مساحت متوازی الاضلاع معادل است با سطح بستهای که بین چهار ضلع آن محصور شده است. اگر برای این شکل هندسی دو جزء مهم به نام قاعده و ارتفاع به شکل و تعریف کنیم، در این صورت مساحت آن برابر میشود با حاصلضرب قاعده در ارتفاع یا . در این مطلب از مجله فرادرس همراه با حل مثال و تمرینهای متنوع به شما کمک میکنیم تا به روشهای پیدا کردن مساحت متوازیالاضلاع در مسائل مختلف کاملا مسلط شوید.
آنچه در این مطلب میآموزید:
-
یاد میگیرید فرمول مساحت متوازیالاضلاع چیست.
-
میآموزید چگونه میتوان مساحت متوازیالاضلاع را با داشتن قطرهای آن بهدست آورد.
-
روش محاسبه مساحت متوازیالاضلاع را بر مبنای اضلاع آن خواهید فهمید.
-
خواهید دانست فرمول مساحت متوازیالاضلاع بر حسب ضرب خارجی چگونه نوشته میشود.
-
تعریف، انواع و ویژگیهای یک متوازیالاضلاع را میشناسید.
-
با حل مسائل مختلف، نحوه استفاده از فرمولهای مساحت متوازیالاضلاع را تمرین خواهید کرد.

فیلم آموزشی مساحت متوازی الاضلاع
مساحت متوازی الاضلاع چیست و چه فرمولی دارد؟
مساحت متوازی الاضلاع به فضای بستهای گفته میشود که داخل یک متوازی الاضلاع قرار گرفته است. متوازیالاضلاع یک چهارضلعی است که در آن اضلاع روبروی هم با هم موازی و برابراند. اگر طول قاعده و ارتفاع متوازی الاضلاع را بدانیم، میتوانیم مساحت آن را با ضرب کردن این دو عدد در یکدیگر محاسبه کنیم. این مساحت با مجذور واحدهای طول مانند سانتیمتر مربع، متر مربع یا اینچ مربع اندازهگیری میشود. فرمول مساحت متوازیالاضلاعی با قاعده و ارتفاع برابر است با :
قاعده × ارتفاع = مساحت متوازی الاضلاع
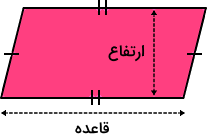
برای اینکه بتوانیم مساحت متوازی الاضلاع را پیدا کنیم، اولین قدم تشخیص قاعده و ارتفاع است. قاعده و ارتفاع یک متوازیالاضلاع همانطور که در شکل زیر نشان داده شده است، همواره بر یکدیگر عمود هستند، یعنی . در بخشهای بعد راجعبه این دو مفهوم بیشتر توضیح میدهیم.
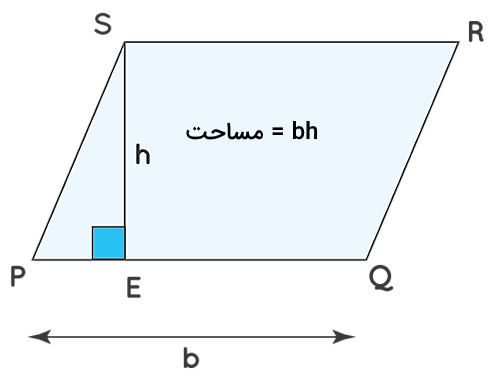
همچنین فرمول بالا را میتوانیم با استفاده از یک مثال به شکل زیر تجزیه و تحلیل کنیم. فرض کنید متوازیالاضلاعی است که روی یک کاغذ شطرنجی ترسیم شده است. به این ترتیب مساحت آن با شمارش مربعها تعیین خواهد شد. حالا مساحت این شکل را به دو روش محاسبه کرده و با هم مقایسه میکنیم. در روش اول و با شمارش مربعها به نتایج زیر میرسیم:
- تعداد کل مربعهای کامل:
- تعداد کل مربعهای نصفه:
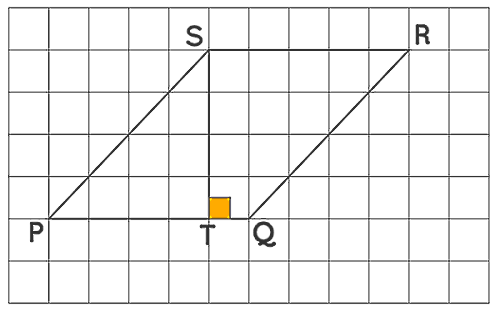
میدانیم مساحت یک مربع برابر است با طول یک ضلع آن به توان دو. همچنین طول هر کدام از اضلاع این مربعهای مساوی هم در کاغذ شطرنجی همواره با عدد یک یا واحد برابر است. به این ترتیب مساحت هر خانه مربع شکل در تصویر بالا برابر است با یک. پس مساحت متوازی الاضلاع بالا با در نظر گرفتن این نکته و به شکل زیر از جمع کردن تعداد خانههای مربعی شکل با مساحت یک بهدست میآید:
از طرفی مساحت این متوازیالاضلاع با استفاده از فرمول معرفی شده و شمارش تعداد مربعها برای رسیدن به اندازه قاعده و ارتفاع، به شکل زیر محاسبه میشود:
- پیدا کردن طول قاعده:
- پیدا کردن طول قاعده:
- پیدا کردن حاصلضرب قاعده و ارتفاع:
ملاحظه میکنید که با استفاده از هر دو روش به پاسخ یکسانی رسیدیم و نشان دادیم که مساحت متوازی الاضلاع داده شده برابر است با حاصلضرب قاعده در ارتفاع.
بهعلاوه، برای درک بهتر مفهوم مساحت متوازی الاضلاع و فرمول آن، میتوانیم فعالیت زیر را انجام دهیم:
- ابتدا متوازی الاضلاع با ارتفاع روی یک مقوا رسم کنید و آن را ببرید.
- سپس قسمت مثلثی را ببرید.
- حالا قسمت باقیمانده یعنی را روی یک صفحه سفید بچسبانید.
- و در نهایت قسمت مثلثی شکل را روی صفحه سفید طوری در کنار هم قرار دهید که اضلاع و به هم وصل شوند.
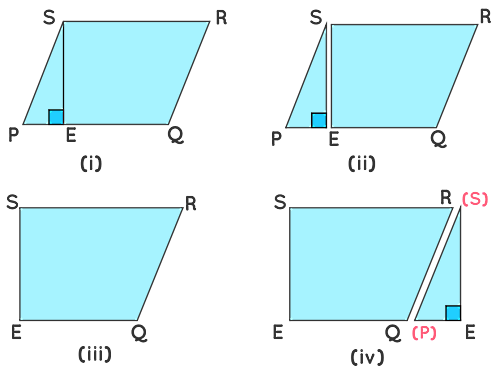
ملاحظه میکنید که مساحت مستطیل بهدست آمده با مساحت متوازی الاضلاع برابر است. همچنین قاعده و ارتفاع متوازی الاضلاع به ترتیب برابر با طول و عرض مستطیل برابر است.
یادگیری فرمول های مساحت با فرادرس
یادگیری مساحت نیازمند این است که ابتدا با ویژگیهای اشکال هندسی مختلف آشنا شوید. سپس باید بتوانید مفاهیمی مانند محیط، مساحت و حجم را از هم تفکیک کنید. یادگیری این تفاوت با مطالعه کتاب ریاضی پایه هفتم آغاز میشود. همچنین در کتابهای درسی ویژگیهای چندضلعیها برای اولین بار در کتاب ریاضی پایه هشتم مطرح شده است. سپس در کتاب ریاضی پایه نهم روش بهدست آوردن مساحت کره یا مساحت و حجم احجامی مانند هرم و مخروط توضیح داده شده است. بنابراین اگر علاقهمند هستید با فرمولهای مربوط به این مباحث همراه با آموزش تصویری و حل مثالهای گسترده آشنا شوید، پیشنهاد میکنیم این فیلمهای آموزشی تهیه شده در مجموعه فرادرس را مشاهده کنید:
روش های محاسبه مساحت متوازی الاضلاع
فرمول مساحت متوازی الاضلاع با توجه به دادههای مسئله متفاوت است. در این بخش سه روش محاسبه مساحت این شکل هندسی را با هم بررسی میکنیم که بر اساس اطلاعات زیر از یکدیگر متمایز میشوند:
- مشخص بودن قاعده و ارتفاع متوازیالاضلاع
- مشخص بودن طول اضلاع مجاور هم و زاویه بین آنها
- مشخص بودن دو قطر متوازیالاضلاع به همراه هر یک از زاویههای متقاطع آنها
۱. مشخص بودن قاعده و ارتفاع
در مورد اولین حالت توضیح دادیم که فرمول مساحت متوازیالاضلاعی با قاعده و ارتفاع برابر است با . برای استفاده از این فرمول، ابتدا باید به تعریف قاعده و ارتفاع در متوازیالاضلاع مسلط باشیم. قاعده یا پایه یکی از اضلاع متوازیالاضلاع است که معمولا آن را بهعنوان ضلع پایینی در نظر میگیرند (برای محاسبه مساحت یا رسم ارتفاع).
از آنجا که در متوازیالاضلاع هر دو ضلع روبهرو با هم برابر و موازی هستند، میتوان گفت که هر ضلعی میتواند به عنوان قاعده انتخاب شود، اما بسته به انتخاب قاعده ارتفاع نیز تغییر خواهد کرد. بنابراین ارتفاع متوازیالاضلاع پارهخطی است عمود که از یک راس بر قاعده (یا امتداد آن) فرود میآید. در واقع ارتفاع همیشه عمود بر قاعده است. اگر قاعده را یک ضلع افقی در نظر بگیریم، ارتفاع بهصورت یک خط عمودی از راس مقابل تا آن ضلع (یا امتداد آن) رسم میشود.
برای مثال، اگر قاعده یک متوازی الاضلاع برابر با سانتیمتر و ارتفاع آن سانتیمتر باشد، مساحت آن برابر است با:
۲. مشخص بودن طول اضلاع مجاور هم و زاویه بین آن ها
مساحت متوازی الاضلاع را میتوان بدون داشتن ارتفاع آن نیز محاسبه کرد. اگر طول اضلاع مجاور هم به ترتیب برابر با و باشند و زاویه بین آنها یعنی برای ما مشخص باشد، میتوانیم به سادگی از فرمول زیر و با توجه به قوانین مثلثات مساحت را تعیین کنیم:
برای نمونه فرض کنید زاویه بین دو ضلع متوازی الاضلاعی قائمه است. اگر طول دو ضلع مجاور هم در این شکل هندسی و سانتیمتر باشند، مساحت آن به شکل زیر حساب میشود:
میدانیم که اگر زاویه بین اضلاع یک متوازی الاضلاع قائمه باشد، آنگاه این متوازی الاضلاع به یک مستطیل تبدیل میشود که مساحت آن برابر است با حاصلضرب دو ضلع آن.
۳. مشخص بودن دو قطر و زاویه بین آن ها
در کنار دو روش قبل، ممکن است در یک سوال فقط طول قطرهای متوازیالاضلاع یعنی و و زاویه بین آنها () را بهجای اندازه اضلاع یا ارتفاع آن داشته باشیم. در این صورت میتوانیم از فرمول معرفی شده در این بخش استفاده کنیم که به شکل زیر است:
میدانیم یک متوازی الاضلاع دو قطر دارد که یکدیگر را در زاویههای خاصی قطع میکنند.
متوازی الاضلاع چیست و چه ویژگی هایی دارد؟
برای اینکه بتوانیم مساحت متوازی الاضلاع را به شکل صحیح و دقیقی محاسبه کنیم، ابتدا باید این شکل هندسی، اجزا و ویژگیهای آن را بهتر بشناسیم. متوازیالاضلاع یک چهارضلعی یا یک شکل هندسی دو بعدی با چهار ضلع است که در آن دو جفت ضلع موازی هم داریم، به این صورت که دو ضلع افقی با هم و دو ضلع مایل نیز با هم موازی هستند. این اضلاع موازی طول یکسانی دارند.
همچنین زاویههای روبروی هم در یک متوازیالاضلاع با هم برابر و مجموع زاویههای داخلی نیز برابر با ۳۶۰ درجه است. بنابراین با اینکه زاویه بین اضلاع مجاور در این چهار ضلعی متفاوت است، اما اضلاع روبروی هم حتما باید موازی هم باشند تا یک متوازیالاضلاع داشته باشیم. به عبارت دیگر، یک چهارضلعی در صورتی متوازی الاضلاع خواهد بود که اضلاع روبروی آن موازی و همنهشت باشند.
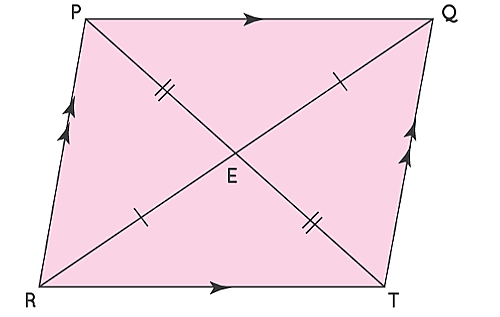
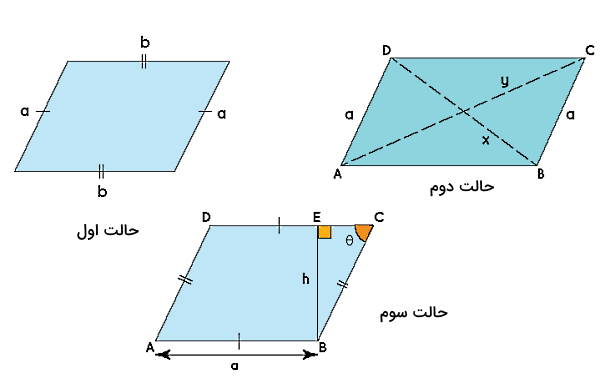
به این ترتیب یک سری ویژگیهای اساسی وجود دارند که به ما در شناسایی متوازیالاضلاعها کمک میکنند. برای مثال، متوازیالاضلاع در شکل بالا دارای ویژگیهای زیر است:
- اضلاع روبروی هم در یک متوازیالاضلاع با هم موازی هستند: و .
- اضلاع روبروی هم در یک متوازیالاضلاع با هم برابراند: و .
- زاویههای روبروی هم در یک متوازیالاضلاع با هم برابراند: و .
- قطرهای یک متوازیالاضلاع یکدیگر را نصف میکنند: و .
- زاویههای داخلی همسو مکمل یکدیگر هستند: و و و .
- قطرهای یک متوازیالاضلاع آن را به دو مثلث همنهشت تقسیم میکنند: با و با همنهشت هستند.
انواع متوازی الاضلاع
متوازیالاضلاعها بر اساس ویژگیهایشان در سه گروه زیر طبقهبندی میشوند:
- مستطیل
- مربع
- لوزی
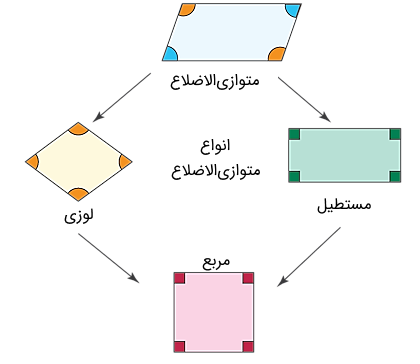
در ادامه ویژگیهای هر کدام را به اختصار توضیح میدهیم.
مستطیل
یک مستطیل نوعی متوازیالاضلاع است که در آن اضلاع روبروی هم با یکدیگر مساوی و موازی هستند. ویژگی مهم این شکل هندسی این است که چهار زاویه قائمه یا ۹۰ درجه دارد.
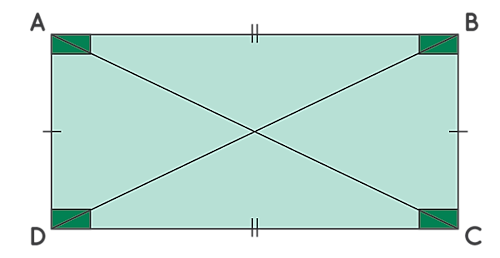
شکل بالا مستطیلی به نام را نشان میدهد که دارای ویژگیهای زیر است:
- یک مستطیل دو جفت ضلع موازی هم دارد: و .
- در یک مستطیل اضلاع روبروی هم با هم برابراند: و .
- یک مستطیل چهار زاویه قائمه دارد: .
- در یک مستطیل دو قطر داریم که مساوی هم هستند: .
- قطرهای یک مستطیل یکدیگر را نصف میکنند.
به این ترتیب مادامی که یکی از زاویهها در یک متوازیالاضلاع برابر با ۹۰ درجه شود، بلافاصله بقیه زاویههای آن نیز قائمه خواهند شد و در نتیجه متوازیالاضلاع ما به مستطیل تبدیل میشود. دقت کنید یک مستطیل همیشه یک متوازیالاضلاع نیز هست، اما هر متوازیالاضلاعی مستطیل نیست. برای مثال، فرض کنید در متوازیالاضلاع زیر داریم . میتوانیم نشان دهیم یا ثابت کنیم که با این فرض، سه زاویه دیگر این متوازیالاضلاع نیز برابر است با ۹۰ درجه و در نتیجه یک مستطیل داریم.
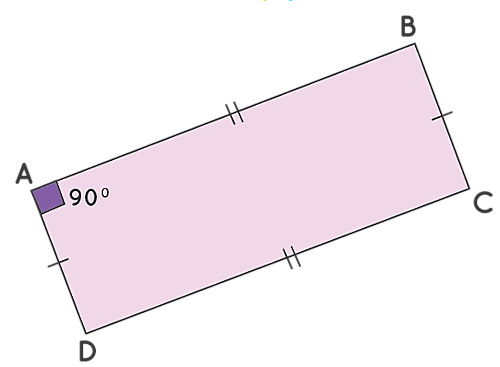
با در نظر گرفتن ویژگیهای یک متوازیالاضلاع، میدانیم که زاویههای روبرو در این شکل هندسی با هم برابراند. بنابراین . از طرفی میدانیم که زاویههای مجاور هم در یک متوازیالاضلاع مکمل هم هستند. بنابراین . این رابطه ما را به این نتیجه میرساند که زاویه برابر است با:
حالا با توجه به اینکه مجموع زاویههای داخلی متوازیالاضلاع برابر است با ۳۶۰ درجه، میتوانیم به این نتیجه برسیم که با قائمه شدن سه زاویه داخلی در این شکل زاویه چهارم یا . در نهایت با توجه به اینکه تمام زاویهها برابر با هم و مساوی ۹۰ درجه بهدست آمدند، پس متوازیالاضلاع ما به یک مستطیل تبدیل شده است.
مربع
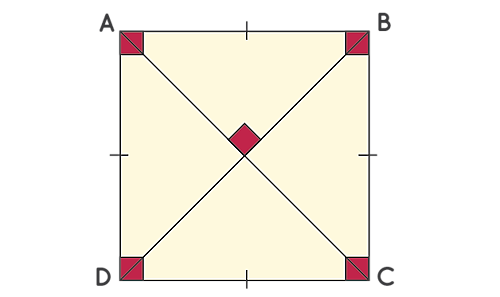
در ادامه بررسی انواع متوازیالاضلاعها، در این بخش با مربع و ويژگیهای آن آشنا میشویم. اگر متوازیالاضلاعی دارای چهار ضلع مساوی هم و چهار زاویه قائمه باشد، آن را مربع مینامیم. شکل زیر مربعی به نام را نشان میدهد که دارای ویژگیهای زیر است:
- در یک مربع چهار ضلع با هم برابراند: .
- در یک مربع اضلاع روبروی هم با هم موازی هستند: و .
- یک مربع چهار زاویه قائمه دارد: .
- در یک مربع دو قطر داریم که مساوی هم هستند: .
- قطرهای یک مربع یکدیگر را نصف میکنند و بر هم عموداند: .
لوزی
به عنوان آخرین نوع از متوازیالاضلاعها، در این بخش به بررسی ویژگیهای یک لوزی میپردازیم تا در محاسبات مربوط به مساحت متوازی الاضلاع موفقتر عمل کنیم. لوزی متوازیالاضلاعی است که چهار ضلع مساوی دارد و در آن زوایای روبروی هم با هم برابرند.
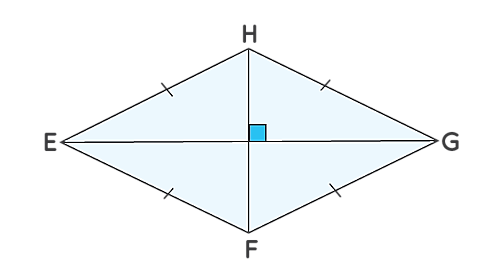
فهرست زیر ویژگیهای لوزی بالا را توضیح میدهد:
- در یک لوزی چهار ضلع با هم برابراند: .
- در یک لوزی اضلاع روبروی هم با هم موازی هستند: و .
- در یک لوزی زاویههای روبروی هم با هم برابراند: و .
- در یک لوزی قطرها بر هم عموداند: .
- قطرهای یک لوزی یکدیگر را نصف میکنند.
با توجه به این ویژگیها میتوانیم تشخیص دهیم چه زمان یک متوازیالاضلاع به لوزی تبدیل شده است. برای نمونه، اگر قطرهای یک متوازیالاضلاع یکدیگر را با زاویه قائمه قطع کنند، لوزی داریم. نشان دادن این تعریف ساده است. کافی است شکل زیر را در نظر داشته باشید:
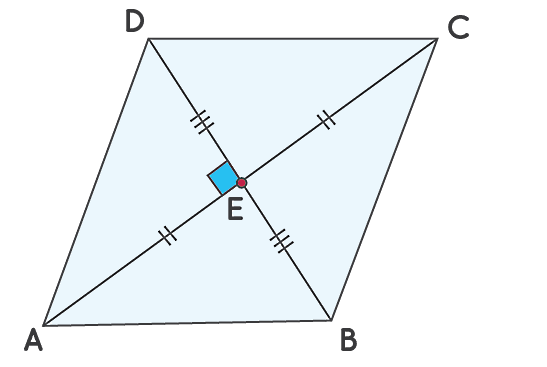
ابتدا ثابت میکنیم که دو مثلث و همنهشت هستند. همنهشتی این دو مثلث با توجه به ضلع مشترک آنها یعنی و اینکه طبق دادهها و است، به روش ض ز ض اثبات میشود. حاصل این همنهشتی این است که خواهیم داشت:
به همین شکل با در نظر گرفتن دو مثلث و و نشان دادن همنهشتی آنها به تساوی و میرسیم. در نهایت با توجه به اینکه شد، میتوانیم بگوییم متوازیالاضلاع بالا یک لوزی است.
سایر فرمول های متوازی الاضلاع
در این بخش مروری داریم بر سایر فرمولهای متوازیالاضلاع، اما پیش از آن پیشنهاد میکنیم برای درک بهتر ویژگیهای انواع چندضلعیها، فیلم آموزش ریاضی پایه هشتم فرادرس را که لینک آن در ادامه برای شما قرار داده شده است، مشاهده کنید:
فرمول های محیط متوازی الاضلاع
فرمول مساحت متوازیالاضلاع را در بخشهای قبل یاد گرفتیم. اما محیط یک متوازیالاضلاع برابر است با کل طول دور آن یا مجموع تمام اضلاع آن. بنابراین فرمول محیط متوازیالاضلاعی با اضلاع و برابر است با:
دقت کنید که برای بهدست آوردن محیط یک متوازیالاضلاع دانستن طول اضلاع آن کافی است و نیازی نیست ارتفاع آن مشخص باشد. البته ممکن است طول اضلاع یک متوازیالاضلاع را ندانیم، اما اطلاعات دیگری در مورد آن به ما داده شده و از ما خواسته شود محیط آن را پیدا کنیم. بنابراین فرمول محیط متوازیالاضلاع بر اساس دادههای زیر به سه شکل مختلف نشان داده میشود:
- اگر اندازه دو ضلع مجاور هم یعنی و مشخص باشد، فرمول محیط متوازیالاضلاع برابر است با .
- اگر اندازه یک ضلع یعنی و طول قطرها یا و مشخص باشد، فرمول محیط متوازیالاضلاع برابر است با .
- اگر قاعده یا ، ارتفاع یا و یکی از زاویهها یعنی مشخص باشد، فرمول محیط متوازیالاضلاع برابر است با .
مساحت متوازی الاضلاع بر حسب ضرب خارجی اضلاع
تا اینجا تمام فرمولهایی که معرفی کردیم فرم اسکالر یا عددی مساحت متوازیالاضلاع را نشان دادند، اما امکان نوشتن این فرمول بهصورت برداری نیز وجود دارد که در این بخش آن را توضیح میدهیم. برای محاسبه شکل برداری مساحت متوازی الاضلاع، به مختصات گوشههای آن نیاز داریم. سپس با استفاده از قوانین جمع برداری، بردار هر یک از ضلعها بهدست میآید:
به این ترتیب فرمول مساحت متوازیالاضلاع بر اساس ضرب خارجی ضلعها به شکل زیر نوشته میشود:
دقت کنید حاصلضرب خارجی بالا در واقع حاصل دترمینان اضلاع متوازیالاضلاع است:
این فرمول به فرمول مساحت متوازی الاضلاع که بر اساس ضرب اسکالر یا عددی اضلاع در سینوس زاویه بین آنها تعریف شد، شباهت زیادی دارد. اما در اینجا به دلیل برداری بودن محاسبات، نیازی به دانستن زاویه نداریم.
مساحت متوازی الاضلاع بر حسب ضرب خارجی قطرها
از بخشهای قبل به خاطر داریم که فرمول مساحت متوازی الاضلاع بر حسب قطر چیست. فرم برداری این فرمول مانند بخش قبل و با حذف سینوس زاویه بین قطرها و در نظر گرفتن ضرب خارجی به شکل زیر نوشته میشود:
اثبات این فرمول آسان است. شکل زیر را در نظر بگیرید که در آن ضلعها و قطرهای یک متوازیالاضلاع بهصورت برداری نمایش داده شده است:
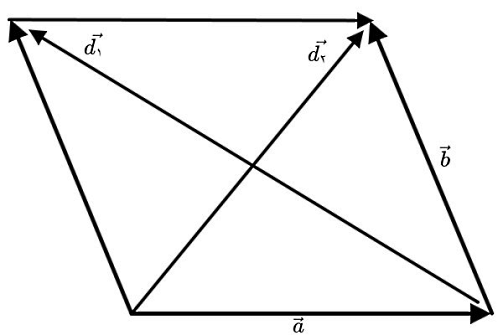
حالا میدانیم که فرمول برداری مساحت متوازی الاضلاع برابر است با:
اما بر اساس شکل بالا میتوانیم رابطه بین ضلعهای متوازیالاضلاع را با قطر آن بهصورت جمع و تفریق برداری بنویسیم:
اگر دو عبارت بالا را در هم ضرب کنیم، خواهیم داشت:
با توجه به اینکه ضرب خارجی هر بردار در خودش برابر با صفر است. بنابراین داریم:
همچنین میدانیم که در ضرب خارجی اگر جای بردارها عوض شود، علامت آنها نیز تغییر میکند:
ضرب خارجی دو بردار همان مساحت متوازی الاضلاع است. پس رابطه بالا را بر حسب این ضرب مینویسیم:
در نتیجه، فرمول مساحت متوازی الاضلاع با استفاده از ضرب خارجی بردارهای قطر آن بهدست خواهد آمد:
یادگیری هندسه متوسطه با فرادرس
در این قسمت قصد داریم مروری داشته باشیم به درس هندسه در مقطع متوسطه. هندسه متوسطه در پایه دهم با درس هندسه ۱ و مباحثی مانند قضیه تالس و چندضلعیها شروع میشود. در هندسه ۲ ویژگیهای دیگری از چندضلعیها مانند منتظم بودن یا محاطی و محیطی بودن مطرح میشود. همچنین در کتاب درسی هندسه ۳ که با عنوان هندسه تحلیلی نیز شناخته میشود، مباحث جدیدی مانند مقاطع مخروطی، ماتریسها و بردارها معرفی میشوند.
مشاهده فیلمهای آموزشی که در ادامه برای شما قرار دادهایم، به شما کمک میکند تا همراه با حل مسائل متنوع و بهرهگیری از آموزش تصویری به کلیه مباحث هندسه متوسطه کاملا مسلط شوید:
حل مثال و تمرین از محاسبه مساحت متوازی الاضلاع
در این قسمت با حل و بررسی چند مثال به شما کمک میکنیم تا به فرمولها و مفاهیم بیان شده در این مطلب کاملا مسلط شوید. همچنین به منظور مرور بیشتر، پیشنهاد میکنیم مطلب «مساحت متوازی الاضلاع به صورت جبری – انواع فرمول ها + حل مثال» از مجله فرادرس را نیز مطالعه کنید.
مثال ۱
مساحت سطح یک پنل خورشیدی به شکل متوازیالاضلاع با قاعده و ارتفاع اینچی چقدر است؟
پاسخ
گفتیم مساحت متوازی الاضلاع در شرایطی که قاعده و ارتفاع آن را داریم از ضرب کردن این دو عدد در یکدیگر بهدست میآید:
مثال ۲
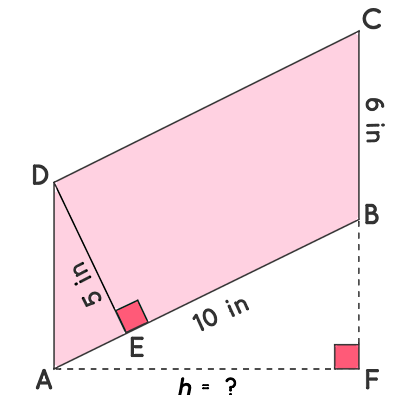
فرض کنید طول اضلاع مجاور هم در یک متوازیالاضلاع برابر است با و اینچ. اگر طبق شکل زیر، ارتفاع مربوط به ضلع اینچی برابر با اینچ باشد، مساحت متوازیالاضلاع و طول ارتفاع مربوط به ضلع اینچی را پیدا کنید:
پاسخ
فرض کنید متوازیالاضلاعی است که در آن و است. با استفاده از فرمول مساحت متوازی الاضلاع، برای قاعده و ارتفاعی به شکل مساحت طبق فرمول زیر بهدست خواهد آمد:
حالا برای پاسخ دادن به سوال بعدی یعنی ارتفاع متناظر با ضلع اینچی، کافی است از مساحت بهدست آمده در بخش قبل استفاده کنیم. با تقسیم کردن این عدد بر قاعده اینچی خواهیم داشت:
در این محاسبه از این واقعیت استفاده کردیم که مساحت یک متوازیالاضلاع با در نظر گرفتن هر جفت قاعده و ارتفاع متناظر با آن همواره مقدار یکسانی بهدست میآید.
مثال ۳
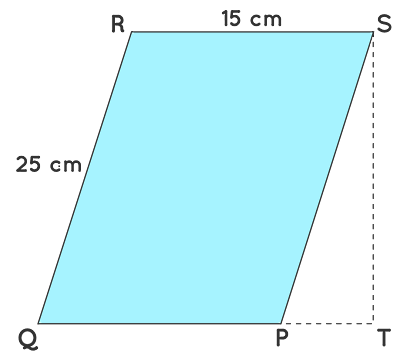
شکل زیر را در نظر بگیرید. با این فرض که مساحت متوازیالاضلاع برابر با واحد است، طول چقدر است؟
پاسخ
در این شکل طول معادل است با ارتفاعی از متوازیالاضلاع که عمود بر امتداد قاعده یا رسم میشود. با توجه به اینکه در متوازیالاضلاع اضلاع روبروی هم با هم موازی و برابراند، پس . بنابراین طبق فرمول مساحت این شکل هندسی، با تقسیم کردن اندازه مساحت به قاعده این ارتفاع بهدست میآید:
مثال ۴
یک نقاش در حال نقاشی یک لوگو در کنار یک ساختمان اداری است. این لوگو از چهار متوازیالاضلاع یکسان تشکیل شده است که در شکل زیر مشاهده میکنید. با این فرض که قیمت هر قوطی رنگ پوند و حاوی رنگ کافی برای پوشش مساحت متر مربع است، هزینه نقاشی این لوگو چقدر خواهد بود؟

پاسخ
ابتدا باید مساحت لوگوی نشان داده شده را بهدست آوریم که شامل چهار متوازیالاضلاع یکسان است. قاعده هر کدام از این متوازیالاضلاعها برابر با است، در حالی که ارتفاع کل لوگو است و لازم است آن را به چهار تقسیم کنیم تا ارتفاع هر متوازیالاضلاع تعیین شود:
حالا ابتدا مساحت هر متوازیالاضلاع را محاسبه میکنیم و سپس عدد بهدست آمده را چهار برابر میکنیم تا مساحت کل لوگو مشخص شود:
پس از اینکه مساحت لوگو را محاسبه کردیم، باید تعداد قوطیهای رنگ موردنیاز برای رنگآمیزی آن را نیز پیدا کنیم. از آنجایی که هر قوطی رنگ مساحتی معادل متر مربع را پوشش میدهد، باید را بر تقسیم کنیم:
پس برای رنگ کردن این لوگو به قوطی رنگ نیاز است که هزینه معادل آن با گرد کردن این تعداد به تعداد عدد قوطی رنگ برابر میشود با پوند:
مثال ۵
مقدار را در شکل زیر تعیین کنید:

پاسخ
شکل صورت سوال متوازیالاضلاعی است که مساحت، ارتفاع و قاعده آن داده شده است، البته قاعده بر حسب است و دقیقا مشخص نیست چه مقداری دارد. برای پیدا کردن کافی است فرمول مساحت متوازیالاضلاع را بنویسیم:
تمرین ۱
مساحت یک زمین بازی به شکل متوازیالاضلاع برابر با است. اگر بدانیم قاعده این زمین بازی است، ارتفاع متناظر با این قاعده برابر است با:
گزینه دوم درست است. طبق فرمول مساحت متوازی الاضلاع که بر اساس حاصلضرب قاعده در ارتفاع متناظر با آن است، میتوانیم ارتفاع را به شکل زیر پیدا کنیم:
تمرین ۲
مساحت بخش صورتی رنگ در شکل زیر برابر با کدام گزینه است؟
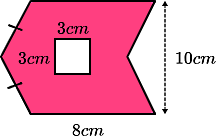
گزینه اول صحیح است. برای محاسبه مساحت این بخش کافی است ابتدا آن را به دو متوازیالاضلاع تقسیم کنیم که هر کدام ارتفاعی برابر با دارند. مساحت هر کدام از این دو برابر خواهد شد با:
و دو برابر آن میشود:
اما برای اینکه مساحت بخش رنگی پیدا شود، لازم است مساحت بخش سفید رنگ که به شکل یک مربع است از آن کم شود. مساحت مربع سفید رنگ با مجذور کردن اندازه ضلع مربع به شکل زیر بهدست میآید:
تمرین ۳
اندازه ضلعهای یک متوازیالاضلاع برابر است با و متر. اگر زاویه بین این دو ضلع درجه باشد، مساحت آن چقدر است؟
گزینه سوم درست است. به منظور حل این سوال، از فرمول مساحت متوازیالاضلاع بر مبنای سینوس زاویه بین دو ضلع آن استفاده میکنیم:
تمرین ۴
اگر اندازه قطرهای یک متوازیالاضلاع برابر با و متر باشد، در حالی که زاویه بین آنها درجه است، مساحت این شکل هندسی برابر است با:
گزینه اول درست است. در این سوال قطرها و زاویه بین آنها داده شده است. پس از فرمول زیر استفاده میکنیم:
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «محاسبه محیط و مساحت متوازی الاضلاع — هر آنچه باید بدانید» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
source
