مساحت شش ضلعی منتظم به سطح بستهای گفته میشود که توسط تمام اضلاع این شکل هندسی احاطه شده است. یک شش ضلعی منتظم دارای ۶ ضلع و ۶ زاویه است که همگی با هم برابراند. اگر طول هر کدام از اضلاع یک شش ضلعی منتظم را با نشان دهیم، در این صورت فرمول محاسبه مساحت آن برابر میشود با . در این مطلب از مجله فرادرس روشها و فرمولهای مختلف محاسبه مساحت شش ضلعی منتظم را همراه با حل مثال و تمرین توضیح میدهیم.
آنچه در این مطلب میآموزید:
-
با فرمولهای مساحت شش ضلعی منتظم آشنا میشوید.
-
محاسبه مساحت شش ضلعی منتظم را همراه با حل مسائل متنوع تمرین خواهید کرد.
-
روش اثبات فرمول مساحت شش ضلعی منتظم را خواهید دانست.
-
میآموزید تفاوت دایره محیطی و محاطی در یک شش ضلعی چیست.
-
یاد میگیرید شش ضلعی منتظم چه ویژگیهایی دارد.
-
انواع شش ضلعی را خواهید شناخت.

به همین منظور پس از اینکه در اولین بخش توضیح دادیم مراحل محاسبه مساحت شش ضلعی منتظم چیست، توضیح میدهیم روشهای مختلف پیدا کردن این عدد با توجه به دادههای مسئله چگونه است. سپس با حل سوالات مختلف در همین زمینه، به شما کمک میکنیم تا به کاربرد این روشها کاملا مسلط شوید. همچنین در بخشهای دیگر این نوشته نشان میدهیم اثبات فرمولهای گفته شده به چه صورت است و یک شش ضلعی منتظم چه ویژگیهایی دارد.
مساحت شش ضلعی منتظم چگونه محاسبه می شود؟
مساحت شش ضلعی منتظم معادل است با سطح بستهای که توسط تمام اضلاع آن احاطه شده است. در یک شش ضلعی منتظم تمام اضلاع با هم برابراند. بنابراین اگر طول هر ضلع را برابر با در نظر بگیریم، مساحت این شکل هندسی توسط فرمول محاسبه میشود.
شش ضلعی یک شکل دو بعدی و یکی از انواع چندضلعی است که دارای ۶ ضلع، ۶ زاویه و ۹ قطر است. برای اینکه بتوانیم مساحت شش ضلعی را محاسبه کنیم، لازم است ابتدا مشخص کنیم که آیا شش ضلعی ما منتظم است یا غیرمنتظم. یک شش ضلعی منتظم دارای ۶ ضلع و ۶ زاویه است که همگی با هم برابراند. همچنین مجموع زاویههای داخلی برای این شکل هندسی برابر است با ۷۲۰ درجه (هر زاویه داخلی آن برابر است با ۱۲۰ درجه).
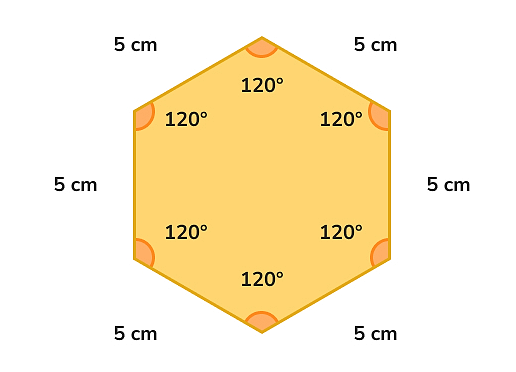
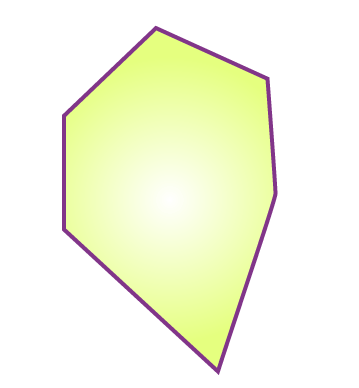
مساحت شش ضلعی منتظم را میتوان به روشهای مختلفی محاسبه کرد که در این ادامه به توضیح هر کدام خواهیم پرداخت. اما در مورد شش ضلعی نامنتظم تمام ۶ ضلع و در نتیجه تمام زاویهها با هم برابر نیستند. تصویر زیر نمونهای از یک شش ضلعی نامنتظم را نشان میدهد که محاسبه مساحت آن نیز روشهای خود را دارد.
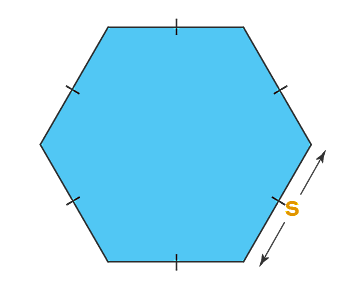
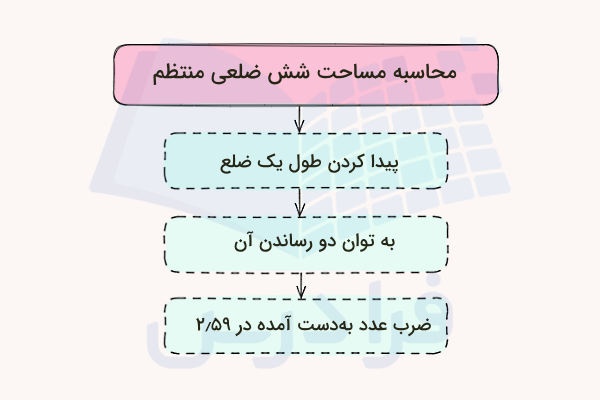
گفتیم فرمول مساحت یک شش ضلعی منتظم با طول ضلعی برابر با میشود . با توجه به اینکه در مورد یک شش ضلعی منتظم صحبت میکنیم، پس طول تمام ضلعها در این محاسبه با هم برابر است. بنابراین اگر طول یکی از اضلاع این شکل هندسی را بدانیم، محاسبه مساحت توسط این فرمول بهراحتی انجام میشود. به این ترتیب مراحل پیدا کردن مساحت شش ضلعی منتظم را میتوانیم به شکل زیر مرتب کنیم:
- مرحله اول: طول یک ضلع از شش ضلعی منتظم یعنی مقدار را مشخص کنید.
- مرحله دوم: فرمول محاسبه مساحت شش ضلعی منتظم یعنی را بنویسید.
- مرحله سوم: با قرار دادن طول یک ضلع در فرمول بالا، مساحت را بهدست آورید.
- مرحله چهارم: واحد مساحت را در مقابل عدد بهدست آمده قرار دهید (واحد مساحت معادل است با واحد طول به توان دو یا مجذور واحد طول).
یادگیری هندسه متوسطه با فرادرس
پیش از اینکه به بررسی روشهای مختلف محاسبه مساحت شش ضلعی منتظم در بخش بعد بپردازیم، در این قسمت قصد داریم مروری داشته باشیم به درس هندسه در مقطع متوسطه. هندسه متوسطه در پایه دهم با درس هندسه ۱ و مباحثی مانند قضیه تالس و چندضلعیها شروع میشود. در هندسه ۲ ویژگیهای دیگری از چندضلعیها مانند منتظم بودن یا محاطی و محیطی بودن مطرح میشود. همچنین در کتاب درسی هندسه ۳ که با عنوان هندسه تحلیلی نیز شناخته میشود، مباحث جدیدی مانند مقاطع مخروطی، ماتریسها و بردارها معرفی میشوند.
مشاهده فیلمهای آموزشی که در ادامه برای شما قرار دادهایم، به شما کمک میکند تا همراه با حل مسائل متنوع و بهرهگیری از آموزش تصویری به کلیه مباحث هندسه متوسطه کاملا مسلط شوید:
روش های محاسبه مساحت شش ضلعی منتظم
در بخش قبل با فرمول اصلی محاسبه مساحت یک شش ضلعی منتظم آشنا شدیم و گفتیم که برای کاربرد آن، کافی است طول یک ضلع از شش ضلعی منتظم مشخص باشد. اما در مسائل پیچیدهتر ممکن است به جای طول ضلع، اطلاعات دیگری به ما داده شده باشد. در این بخش محاسبه مساحت شش ضلعی منتظم را به روشهای دیگر توضیح میدهیم.
۱. اگر مساحت یکی از شش مثلث متساوی الاضلاع داخل آن مشخص باشد
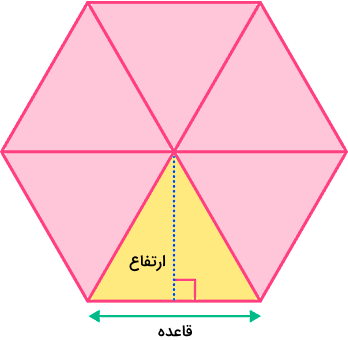
میدانیم یک شش ضلعی منتظم دارای شش ضلع و شش زاویه داخلی برابر است. اگر سطح داخل این شکل هندسی را طبق شکل زیر به شش بخش مساوی تقسیم کنیم، هر کدام از این شش بخش یک مثلث متساویالاضلاع خواهد شد:

نحوه تقسیمبندی سطح داخلی یک شش ضلعی منتظم به شش مثلث متساویالاضلاع به این شکل است که ابتدا باید نقطه مرکزی این شکل را پیدا کنیم. سپس سه قطر داخلی آن را که هر کدام دو زاویه داخلی مقابل هم را به هم وصل میکنند، رسم کنیم. در شکل بالا ملاحظه میکنید که این سه قطر شش ضلعی منتظم از مرکز آن میگذرند.
بنابراین شش ضلعی منتظم بالا معادل است با شش مثلث متساویالاضلاع که در کنار هم قرار گرفتهاند و برای محاسبه مساحت این شش ضلعی، کافی است مساحت یکی از این مثلثها را پیدا کرده و در عدد ۶ ضرب کنیم. با توجه به اینکه مساحت مثلث متساویالاضلاعی با ارتفاع و قاعده توسط فرمول زیر محاسبه میشود:
پس مساحت شش ضلعی منتظم بالا برابر میشود با:
بنابراین فرمول مساحت یک شش ضلعی منتظمی است که از کنار هم قرار گرفتن شش مثلث متساویالاضلاع با ارتفاع و قاعده ساخته شده است. اگر دقت کنید، قاعده هر کدام از این شش مثلث در واقع همان طول ضلع شش ضلعی منتظم است. در بخشهای بعد نشان میدهیم برای یک شش ضلعی منتظم با طول ضلع ، چطور میتوان از فرمول به فرمولی که در ابتدای مطلب گفتیم () برسیم.
۲. اگر شعاع شش ضلعی منتظم مشخص باشد
برای اینکه در این شرایط بتوانیم مساحت شش ضلعی منتظم را پیدا کنیم، ابتدا باید ببینیم منظور از شعاع شش ضلعی منتظم چیست. اما پیش از اینکه به توضیح این بخش بپردازیم، پیشنهاد میکنیم برای اینکه با نحوه محاسبه مساحت انواع چندضلعیهای منتظم بهتر آشنا شوید، فیلم آموزش رایگان مساحت چند ضلعی منتظم + روشهای سریع محاسبه فرادرس را مشاهده کنید. لینک این دوره برای دسترسی راحتتر شما در ادامه قرار داده شده است:
شعاع شش ضلعی منتظم به فاصله مرکز شش ضلعی تا هر یک از رئوس آن گفته میشود. بهعبارت دیگر، اگر دایره محیطی یک شش ضلعی منتظم را رسم کنیم (دایرهای که از تمام راسهای آن عبور میکند)، شعاع این دایره همان شعاع شش ضلعی منتظم است. این دایره خارج از شش ضلعی قرار دارد و به همین علت به آن دایره محیطی گفته میشود. تصویر زیر بیانگر این توضیحات است:
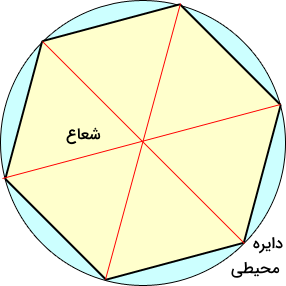
در این حالت با توجه به اینکه در بخش قبل گفتیم هر شش ضلعی منتظم شامل شش مثلث متساویالاضلاع است، بنابراین شعاع این شش ضلعی معادل است با طول هر ضلع مثلث متساویالاضلاع. از طرفی چون هر سه ضلع چنین مثلثی با هم برابراند، پس طول ضلع یک شش ضلعی منتظم نیز برابر است با شعاع آن. به این ترتیب اگر شعاع یک شش ضلعی منتظم برابر با باشد، در واقع طول ضلع آن است و فرمول مساحت به شکلی که قبلا گفتیم خواهد شد:
۳. اگر شعاع دایره محاطی شش ضلعی منتظم مشخص باشد
در بخش قبل شعاع دایره محیطی یا شعاع شش ضلعی منتظم مشخص بود. اما در این بخش فرض میکنیم شعاع دایره محاطی آن را داریم و میخواهیم ببینم در این شرایط چگونه میتوان مساحت شش ضلعی منتظم را پیدا کرد. منظور ما از دایره محاطی یک شش ضلعی، دایرهای است که مانند شکل زیر کاملا در درون آن قرار دارد و به تمام اضلاع شش ضلعی مماس شده است. به تفاوت این شکل با شکل بخش قبل کاملا دقت کنید تا بهتر متوجه شوید تفاوت دایره محیطی و محاطی چیست.
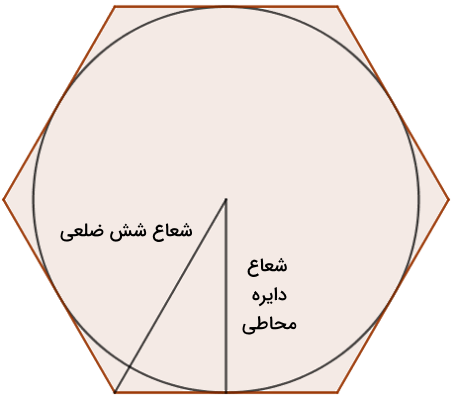
به عبارت دیگر، این دایره کوچکترین دایرهای است که میتوانیم آن را بهصورت کامل داخل شش ضلعی قرار دهیم، به گونهای که هر یک از اضلاع شش ضلعی یک نقطه تماس (در نقطه مماس شده) با دایره داشته باشند. مرکز این دایره همان مرکز شش ضلعی منتظم است اما نکته مهم این است که شعاع این دایره با شعاع شش ضلعی منتظم برابر نیست. در واقع شعاع دایرههای محیطی و محاطی شش ضلعی منتظم با هم فرق دارند.
شعاع دایره محاطی در شش ضلعی منتظم برابر است با فاصله مرکز شش ضلعی تا نقطه میانی هر کدام از اضلاع آن. طبق آنچه پیشتر گفتیم، این فاصله همان ارتفاع مثلث متساویالاضلاع داخل این شکل است. بنابراین اگر بخواهیم مساحت شش ضلعی منتظمی را پیدا کنیم که اندازه شعاع دایره محاطی آن برابر با است، فرمول زیر مناسب است:
اثبات فرمول مساحت شش ضلعی منتظم
گفتیم مساحت یک شش ضلعی منتظم متشکل از شش مثلث متساویالاضلاع با ارتفاع و قاعده برابر است با . در این بخش میخواهیم از این فرمول استفاده کنیم و ببینم چطور میتوان به فرمول رسید. اگر در نگاه اول این دو فرمول را با هم مقایسه کنیم، واضح است که باید ارتفاع در فرمول اول حذف شده و بر حسب نوشته شود تا به دومین فرمول برسیم.
حالا یکی از شش مثلث متساویالاضلاع داخل شش ضلعی منتظم را در نظر بگیرید. طبق خواص و ویژگیهای یک مثلث متساوی الاضلاع، میدانیم ارتفاع این مثلث همواره قاعده آن را در نقطه میانیاش قطع میکند. همچنین هر سه زاویه داخلی در این مثلث برابر با ۶۰ درجهاند:
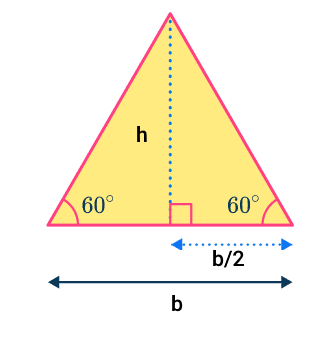
پس با رسم ارتفاع، در واقع مثلث متساویالاضلاع ما به دو مثلث قائمالزاویه تبدیل میشود. حالا اگر با روابط مثلثاتی آشنا باشید، میدانید که در یک مثلث قائمالزاویه برای زاویه بستهای مانند ، تانژانت به شکل زیر تعریف میشود:
ضلع مجاور به زاویه / ضلع روبرو به زاویه
اگر تانژانت زاویه ۶۰ درجه در یکی از دو مثلث قائمالزاویه بالا را طبق فرمول گفته شده بنویسیم، خواهیم داشت:
از طرفی باز هم از مثلثات میدانیم که . بنابراین رابطه بالا مقدار را بر حسب به ما میدهد:
حالا با قرار دادن این در فرمول به فرمول اصلی مساحت شش ضلعی منتظم خواهیم رسید:
حل مثال از مساحت شش ضلعی منتظم
در بخشهای قبل یاد گرفتیم مساحت شش ضلعی چیست و برای محاسبه آن از چه فرمولها یا روشهایی میتوانیم استفاده کنیم. در این بخش با حل و بررسی چندین مثال متنوع میتوانید نحوه استفاده از این فرمولها را تمرین کنید.
مثال ۱
مساحت شش ضلعی منتظمی با طول ضلع اینچ چقدر است؟
پاسخ
چون شش ضلعی ما منتظم است، پس به روشی که در بخش قبل توضیح دادیم میتوان مساحت آن را پیدا کرد. طول ضلع شش ضلعی برابر است با اینچ. پس با نوشتن فرمول مساحت آن به شکل زیر و قرار دادن این مقدار در آن خواهیم داشت:
پاسخ بهدست آمده یعنی برابر است با مساحت این شش ضلعی منتظم.
مثال ۲
مساحت شش ضلعی منتظم را در شکل زیر پیدا کنید:
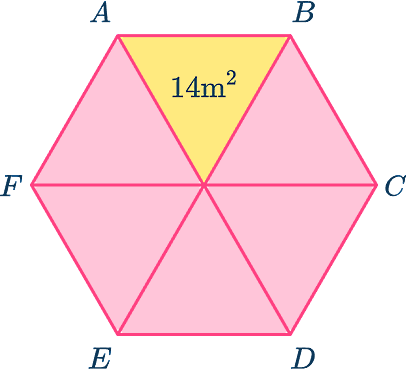
پاسخ
همانطور که ملاحظه میکنید، در این تصویر شش ضلعی منتظم ما به شش مثلث متساوی الاضلاع تقسیم شده است که مساحت هر کدام نیز مشخص است. پس کافی است مساحت یک مثلث را در عدد ۶ ضرب کنیم:
مثال ۳
مساحت شش ضلعی منتظم را در شکل زیر پیدا کنید:
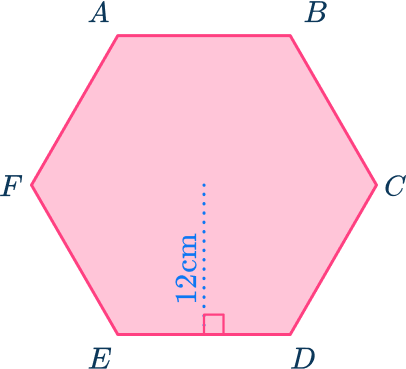
پاسخ
در این سوال طول ضلع شش ضلعی منتظم مشخص نیست. همچنین مساحت مثلثهای متساویالاضلاعی که در داخل شش ضلعی قرار میگیرند نیز داده نشده است. تنها اطلاعاتی که داریم، شعاع دایره محاطی یا همان قاعده مثلث متساویالاضلاع است. در واقع این مثال نمونهای از حالت سوم از روشهای محاسبه مساحت شش ضلعی منتظم است که در بخشهای قبل توضیح داده شد. بنابراین با نوشتن فرمول زیر خواهیم داشت:
دقت کنید حتی اگر فرمول بالا را ندانیم، باز هم میتوانیم محاسبه خود را انجام دهیم. در واقع اگر قاعده این مثلث را پیدا کنیم، طول ضلع این شش ضلعی منتظم تعیین شده است و میتوانیم با فرمول اصلی مساحت را حساب کنیم. از تعریف تانژانت یک زاویه استفاده میکنیم:
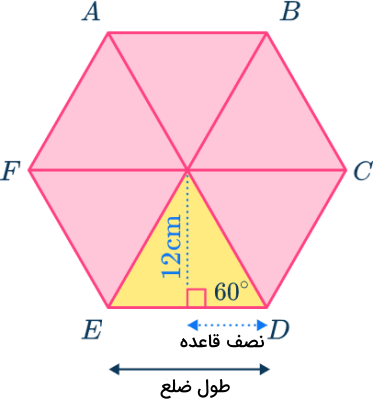
ضلع مجاور به زاویه / ضلع روبرو به زاویه
در آخرین خط از روش گویا کردن کسرها استفاده شده است تا به جواب ساده شدهای برسیم. با مشخص شدن طول ضلع این شش ضلعی مساحت آن برابر است با:
ملاحظه میکنید که با این روش نیز همان پاسخ ابتدا بهدست آمده است.
مثال ۴
فرض کنید مثلث قائمالزاویهای به شکل زیر داریم. اگر بخواهیم با تکرار و کنار هم قرار دادن الگویی به این شکل، یک شش ضلعی منتظم بسازیم، لازم است چند عدد از این مثلثها در کنار هم قرار بگیرند؟ مساحت شش ضلعی منتظم بهدست آمده چقدر خواهد بود؟
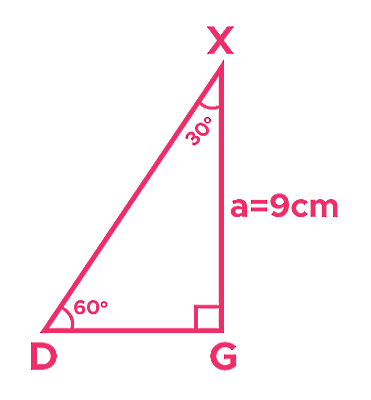
پاسخ
برای حل این سوال به دو روش میتوانیم عمل کنیم. ابتدا روش طولانیتر را توضیح میدهیم و سپس با یادآوری فرمولهای گفته شده، روش کوتاهتر را معرفی میکنیم. در روش طولانیتر، باید ببینیم این مثلث قائمالزاویه چگونه به یک مثلث متساویالاضلاع تبدیل میشود، چون میدانیم که مساحت شش ضلعی منتظم معادل است با شش برابر مساحت مثلثهای متساویالاضلاع تشکیل دهنده آن. پس ابتدا باید مساحت مثلث متساویالاضلاع ساخته شده بر اساس این تصویر را بهدست آوریم.
تبدیل این مثلث قائمالزاویه به مثلث متساویالاضلاع با دو برابر کردن قاعده آن ممکن است، در حالی که ارتفاع تغییری نمیکند. مساحت مثلث برابر است با نصف حاصلضرب قاعده در ارتفاع. ارتفاع برابر است با اما قاعده مثلث قائمالزاویه و در نتیجه قاعده مثلث متساویالاضلاع مشخص نیست. با توجه به زاویههای داده شده، میتوانیم به کمک روابط مثلثاتی قاعده تصویر بالا را پیدا کنیم. کافی است تانژانت زاویه ۳۰ درجه را به شکل زیر بنویسیم:
ضلع مجاور به زاویه / ضلع روبرو به زاویه =
برابر است با قاعده مثلث قائمالزاویه. قاعده مثلث متساویالاضلاع دو برابر این مقدار است:

از اینجا به بعد به دو روش میتوانیم عمل کنیم. در روش اول ابتدا مساحت مثلث متساویالاضلاع را پیدا میکنیم:
شش برابر این مساحت معادل است با مساحت شش ضلعی منتظم:
بنابراین از کنار هم قرار گرفتن شش مثلث متساویالاضلاع و ۱۲ مثلث قائمالزاویه مطابق تصویر داده شده، این شش ضلعی منتظم شکل میگیرد. در روش دیگر از این نکته استفاده میکنیم که قاعده مثلث متساویالاضلاع همان طول ضلع شش ضلعی منتظم است. پس با نوشتن فرمول مساحت آن خواهیم داشت:
که همان نتیجه را خواهد داشت. در روش کوتاهتر برای حل این سوال، با توجه به این مسئله که ارتفاع مثلث قائمالزاویه داده شده همان شعاع دایره محاطی داخل این شش ضلعی است، پس میتوانیم از فرمول زیر برای پیدا کردن مساحت استفاده کنیم:
ویژگی های شش ضلعی منتظم چیست؟
شش ضلعی بهصورت یک شکل دو بعدی بسته تعریف میشود که از شش خط مستقیم تشکیل شده است. در واقع این شکل هندسی یک چندضلعی شش وجهی است، به این معنا که دارای شش ضلع، شش راس و شش زاویه داخلی است. کاشیهای کف حمام، مقطع مداد، لانه زنبورها و … همه و همه به نوعی یک شش ضلعی در نظر گرفته میشوند.
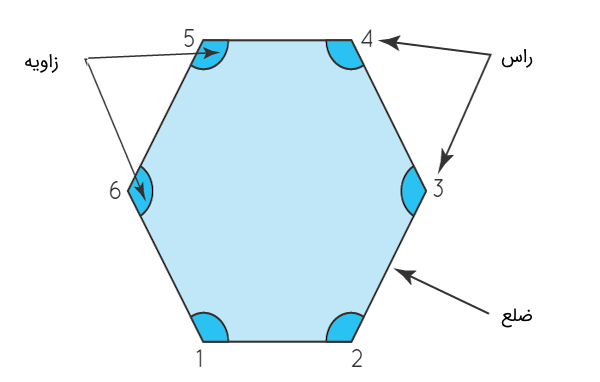
یک شش ضلعی میتواند منتظم یا نامنتظم باشد. در شش ضلعی منتظم ۶ ضلع مساوی و ۶ زاویه داخلی مساوی هم داریم در حالی که یک شش ضلعی نامنتظم، دارای ۶ ضلع با طولهای مختلف و ۶ زاویه با اندازههای مختلف است. در مطلب «چند ضلعی منتظم چیست؟ – به زبان ساده + حل تمرین» از مجله فرادرس، میتوانید اطلاعت بیشتری راجعبه ویژگیهای این اشکال هندسی همراه با حل مثال و تمرین بهدست آورید.
ویژگیهای مهم یک شش ضلعی منتظم را در فهرست زیر ملاحظه میکنید:
- ۶ ضلع برابر دارد.
- ۶ زاویه برابر دارد.
- ۹ قطر دارد.
- هر زاویه داخلی آن برابر با ۱۲۰ درجه است.
- هر زاویه خارجی آن برابر با ۶۰ درجه است.
- مجموع زوایای داخلی آن ۷۲۰ درجه است.
- مجموع زوایای خارجی آن ۳۶۰ درجه است.
- قابلیت محاط شدن در یک دایره را دارد (چون همهی راسهای آن روی محیط یک دایره قرار دارند).
- میتوان برای آن دایره محاطی و محیطی رسم کرد.
- شش محور تقارن دارد.
- دارای تقارن چرخشی از مرتبه ۶ است.
- میتوان آن را به شش مثلث متساویالاضلاع با مساحت برابر تقسیم کرد.
در مورد زوایای خارجی شش ضلعی منتظم، میدانیم مجموع زوایای خارجی هر چندضلعی همواره برابر است با ۳۶۰ درجه. در یک شش ضلعی ۶ زاویه خارجی وجود دارد. بنابراین هر یک از زوایای خارجی در یک شش ضلعی منتظم برابر است با ۶۰ درجه. همچنین برخی از ویژگیهای مشترک بین شش ضلعیهای منتظم و نامنتظم در ادامه آورده شده است:
- در هر دو شش ضلعی ۶ ضلع، ۶ زاویه داخلی و ۶ راس داریم.
- مجموع هر ۶ زاویه داخلی همواره ۷۲۰ درجه است.
- مجموع هر ۶ زاویه خارجی همواره ۳۶۰ درجه است.
انواع شش ضلعی
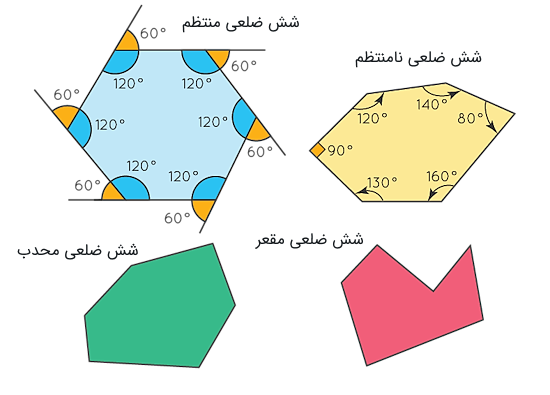
شش ضلعیها را میتوان بر اساس طول اضلاع و زوایای داخلی آنها طبقهبندی کرد. با توجه به این نکته دستهبندی زیر را خواهیم داشت:
- شش ضلعی منتظم: این شش ضلعی دارای اضلاع و زوایههای مساوی است.
- شش ضلعی نامنتظم: این شش ضلعی دارای اضلاع و زوایههایی با اندازههای مختلف است.
- شش ضلعی محدب: در این شش ضلعی اندازه تمام زوایای داخلی کمتر از ۱۸۰ درجه است. شش ضلعیهای محدب میتوانند منتظم یا نامنتظم باشند. همچنین تمام رئوس یک شش ضلعی محدب به سمت بیرون هستند.
- شش ضلعی مقعر: در این شش ضلعی حداقل یکی از زوایای داخلی بزرگتر از ۱۸۰ درجه است. همچنین حداقل یک راس این نوع شش ضلعی به سمت داخل است.
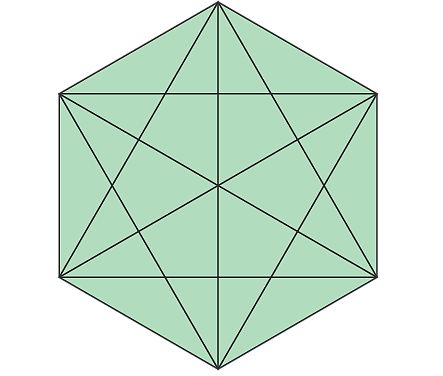
قطرهای شش ضلعی منتظم
در یک ششضلعی منتظم ۹ قطر داریم. در واقع هر پارهخطی که دو راس غیرمجاور یک چندضلعی را به هم وصل میکند، قطر آن است. تعداد قطرهای یک چندضلعی توسط فرمول زیر تعیین میشود که در آن تعداد اضلاع یک چندضلعی است:
بنابراین برای یک شش ضلعی با ، تعداد قطرها برابر میشود با:
دقت کنید از این ۹ قطر، ۳ قطر از مرکز شش ضلعی عبور میکند.
فرمول های شش ضلعی منتظم
اگر طول هر ضلع از یک شش ضلعی منتظم را در نظر بگیریم، فرمولهای مربوط به آن در جدول زیر خلاصه شده است:
| تمام فرمولهای شش ضلعی منتظم با ضلع | |
| محیط | |
| مساحت | |
| شعاع دایره محاطی | |
| شعاع دایره محیطی | |
| قطر اصلی (قطر بلند) | |
| قطر فرعی (قطر کوتاه) | |
چگونه یک شش ضلعی منتظم رسم کنیم؟
برای رسم یک شش ضلعی منتظم میتوانید از پرگار و خطکش استفاده کنید. ابتدا با پرگار یک دایره بکشید. سپس با ثابت نگه داشتن شعاع پرگار، شش نقطه با فواصل مساوی در اطراف محیط دایره را علامت بزنید. برای این منظور، کافی است نوک پرگار را روی دایره قرار دهید و کمانهایی را رسم کنید که دایره را قطع میکنند. در نهایت، این شش نقطه را با خطوط مستقیم و به کمک خطکش به هم وصل کنید تا یک شش ضلعی منتظم تشکیل شود.
یادگیری فرمول های مساحت با فرادرس
یادگیری مساحت نیازمند این است که ابتدا با ویژگیهای اشکال هندسی مختلف آشنا شوید. سپس باید بتوانید مفاهیمی مانند محیط، مساحت و حجم را از هم تفکیک کنید. در کتابهای درسی ویژگیهای فرم دو بعدی کره، یعنی دایره، برای اولین بار در کتاب ریاضی هشتم مطرح میشود. سپس در کتاب ریاضی نهم مبحث حجم و مساحت کره همراه با روش بهدست آوردن حجم احجامی مانند هرم و مخروط توضیح داده شده است. بنابراین اگر علاقهمند هستید با فرمولهای مربوط به این مباحث همراه با آموزش تصویری و حل مثالهای گسترده آشنا شوید، پیشنهاد میکنیم فیلمهای آموزشی تهیه شده در مجموعه فرادرس را مشاهده کنید:
آزمون مساحت شش ضلعی منتظم
در انتهای این مطلب از مجله فرادرس چند سوال چهار گزینهای برای شما تنظیم شده است تا با پاسخدهی به آنها میزان یادگیری و تسلط خود را به روشها و فرمولهای آموزش داده شده در این نوشته بیازمایید. پس از اینکه به تمام سوالات پاسخ دادید، با کلیک روی «دریافت نتیجه آزمون» نمره نهایی شما قابل مشاهده است.
مساحت شش ضلعی منتظم برابر با کدام گزینه است؟
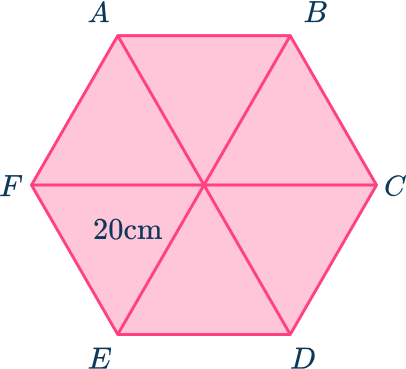
گزینه اول درست است. در این شکل شعاع شش ضلعی منتظم که همان شعاع دایره محیطی است، داده شده است. در دومین بخش از روشهای محاسبه مساحت شش ضلعی منتظم توضیح دادیم که شعاع این شکل هندسی با طول ضلع آن برابر است. بنابراین مساحت آن بهصورت زیر محاسبه میشود:
مساحت شش ضلعی منتظم زیر برابر با کدام گزینه است؟
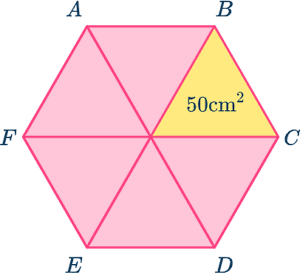
گزینه آخر صحیح است. هر شش ضلعی منتظم از شش مثلث متساویالاضلاع با مساحت برابر تشکیل شده است. بنابراین اگر مساحت یکی از این مثلثها را بدانیم، میتوانیم مساحت شش ضلعی را به شکل زیر پیدا کنیم:
اگر مساحت یک شش ضلعی منتظم برابر با باشد، شعاع آن برابر است با:
گزینه سوم درست است. در این سوال شعاع شش ضلعی منتظم خواسته شده است که معادل همان طول ضلع آن است. پس اگر فرمول مساحت بر حسب اندازه طول را بنویسیم، میتوانیم شعاع را پیدا کنیم:
مساحت شش ضلعی منتظم زیر برابر با کدام گزینه است؟
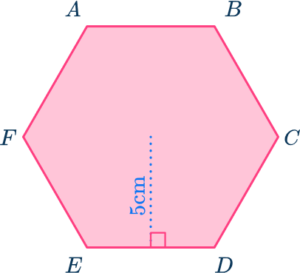
گزینه سوم درست است. در این سوال شعاع محاطی شش ضلعی منتظم داده شده است که با شعاع محیطی یا شعاع ان متفاوت است. فرمول مناسب در این حالت به شکل زیر است:
اگر محیط یک شش ضلعی منتظم برابر با باشد، مساحت آن چقدر است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر یکی از سلولهای خانه زنبور عسلی به شکل یک شش ضلعی منتظم و دارای قطری برابر با باشد، مساحت این سلول تا یک رقم اعشار برابر است با:
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر محیط شش ضلعی منتظمی برابر با باشد، مساحت آن کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
فرض کنید مساحت شش ضلعی منتظمی باشد. هر کدام از شش ضلع آن برابراند با:
نمیتوان تعیین کرد.
طول یک ضلع آن است، اما طول بقیه اضلاع مشخص نیست.
طول هر کدام از شش ضلع است.
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر مساحت شش ضلعی منتظمی باشد. شعاع آن برابر با کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
مجذور شعاع دایره محاطی داخل یک شش ضلعی منتظم با مساحت برابر با کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
source
