مساحت جانبی استوانه، اندازه سطح دور استوانه است. هر استوانه، یک سطح جانبی و دو قاعده دایرهایشکل دارد. اندازه سطح جانبی استوانه از ضرب عدد ۲ در عدد پی در شعاع در ارتفاع استوانه به دست میآید. البته اگر قاعدههای استوانه در یک راستا قرار نداشته باشند (استوانه مایل)، برای محاسبه سطح جانبی، به اندازه طول یال نیاز داریم. در این مطلب از مجله فرادرس، به تعریف مساحت جانبی استوانه و نحوه محاسبه آن به همراه حل چندین مثال و تمرین متنوع میپردازیم.

در ادامه، ضمن ارائه تعریف سطح جانبی استوانه و اصول محاسبه آن، به اثبات فرمول جبری مساحت جانبی استوانه و حل چندین مثال در این رابطه میپردازیم. سپس، فرمول مساحت جانبی استوانه مایل را معرفی میکنیم. علاوه بر این، رابطه بین حجم استوانه و مساحت جانبی آن را مورد بررسی قرار میدهیم. در انتها، با حل چند تمرین در قالب سوالات چندگزینهای، میزان یادگیری شما در این مبحث را میسنجیم.
مساحت جانبی استوانه چگونه بدست می آید؟
مساحت جانبی استوانه، از رابطه زیر به دست میآید:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
منظور از شعاع در رابطه بالا، شعاع قاعدههای دایرهایشکل استوانه است. بسیاری از اجسام اطراف ما، به شکل استوانه هستند. به عنوان مثال، لیوانی که ما در مجله فرادرس از آن استفاده میکنیم، استوانهای است (تصویر زیر).

اگر از دسته لیوان صرفنظر کنیم، شکل استوانهای آن بیشتر به چشم میآید.

استوانه بالا، دارای ارتفاع تقریبی ۱۰ سانتیمتر و قطر قاعده ۷ سانتیمتر است.

با توجه به ابعاد لیوان، میتوانیم مساحت سطح جانبی آن را به دست بیاوریم. به این منظور، مقادیر معلوم را در رابطه زیر قرار میدهیم:
۱۰ × ۳/۵ × ۳/۱۴ × ۲ = مساحت جانبی لیوان
۲۱۹/۸ = مساحت جانبی لیوان
در نتیجه، مساحت جانبی لیوان برابر با ۲۱۹/۸ سانتیمتر مربع است. برای آشنایی بیشتر با نحوه استفاده از رابطه مساحت جانبی استوانه، به حل چند مثال دیگر میپردازیم.
مثال ۱: محاسبه مساحت جانبی استوانه
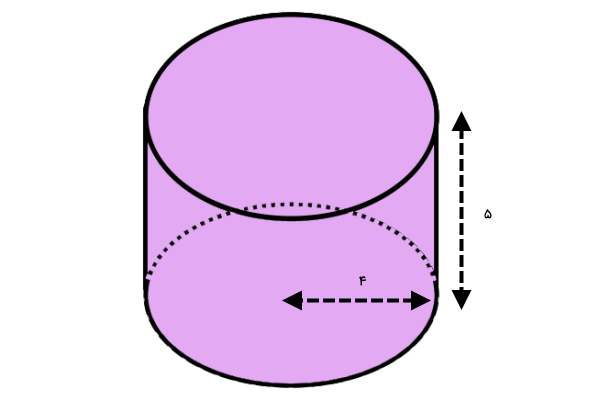
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
با توجه به اطلاعات مسئله، داریم:
- عدد پی: ۳
- شعاع قاعده استوانه: ۴ واحد طول
- ارتفاع استوانه: ۵ واحد طول
این مقادیر را درون رابطه جایگذاری میکنیم:
۵ × ۴ × ۳ × ۲ = مساحت جانبی استوانه
۱۲۰ = مساحت جانبی استوانه
در نتیجه، مساحت جانبی برابر با ۱۲۰ واحد سطح (طول به توان دو) است.
مثال ۲: محاسبه مساحت استوانه با قطر
مساحت جانبی + مساحت قاعدهها = مساحت کل استوانه
قاعدههای استوانه، دو دایره هستند. از اینرو، داریم:
مساحت دایره × ۲ = مساحت قاعدههای استوانه
مساحت دایره با استفاده از فرمول زیر محاسبه میشود:
شعاع × شعاع × عدد پی = مساحت دایره
بر اساس اطلاعات مسئله، میدانیم قطر قاعده استوانه برابر با ۲۰ سانتیمتر است. به این ترتیب، شعاع (نصف قطر)، برابر است با:
۱۰ = ۲ ÷ ۲۰ = شعاع قاعده استوانه
این مقدار را درون فرمول مساحت دایره قرار میدهیم:
۱۰ × ۱۰ × ۳/۱۴ = مساحت دایره
۳۱۴ = مساحت دایره
استوانه، دارای دو قاعده است. بنابراین:
۳۱۴ × ۲ = مساحت قاعدههای استوانه
۶۲۸ = مساحت قاعدههای استوانه
مساحت قاعدههای استوانه برابر با ۶۲۸ سانتیمتر مربع (سانتیمتر به توان ۲) میشود. اکنون، به سراع محاسبه اندازه سطح جانبی استوانه میرویم. فرمول محاسبه این مساحت عبارت است از:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
- عدد پی: ۳/۱۴
- شعاع قاعده استوانه: ۱۰ سانتیمتر
- ارتفاع استوانه: ۱۰ سانتیمتر
با جایگذاری مقادیر معلوم در رابطه، خواهیم داشت:
۱۰ × ۱۰ × ۳/۱۴ × ۲ = مساحت جانبی
۶۲۸ = مساحت جانبی
مساحت سطح جانبی استوانه نیز برابر با ۶۲۸ سانتیمتر مربع است. اکنون میتوانیم با جمع این مساحت و مساحت قاعدهها، مساحت کل استوانه را به دست بیاوریم:
۶۲۸ + ۶۲۸ = مساحت کل استوانه
۱۲۵۶ = مساحت کل استوانه
در نتیجه، مساحت کل استوانه برابر با ۱۲۵۶ سانتیمتر مربع است.
مثال ۳: محاسبه مساحت جانبی استوانه از روی مساحت قاعده
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
- عدد پی: ۳
- شعاع قاعده استوانه: مجهول
- ارتفاع استوانه: ۷ میلیمتر
بر اساس اطلاعات مسئله، شعاع قاعده استوانه را نداریم اما میتوانیم آن را با استفاده از مساحت قاعده به دست بیاوریم. مساحت یکی از قاعدههای استوانه برابر است با:
مساحت دایره = مساحت یک قاعده استوانه
شعاع × شعاع × عدد پی = مساحت یک قاعده استوانه
شعاع × شعاع × ۳ = ۱۰۸
۳ ÷ ۱۰۸ = شعاع × شعاع
۳۶ = شعاع × شعاع
۶ = شعاع
بنابراین، شعاع قاعده استوانه برابر با ۶ میلیمتر است. این مقدار را به همراه دیگر مقادیر معلوم درون فرمول مساحت جانبی قرار میدهیم:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
- عدد پی: ۳
- شعاع قاعده استوانه: ۶ میلیمتر
- ارتفاع استوانه: ۷ میلیمتر
۷ × ۶ × ۳ × ۲ = مساحت جانبی
۲۵۲ = مساحت جانبی
در نتیجه، مساحت جانبی استوانه برابر با ۲۵۲ میلیمتر مربع است.
مساحت جانبی استوانه و گسترده استوانه چیست؟
مساحت جانبی استوانه، اندازه سطحی است که اطراف این حجم منشوری را میپوشاند. یک استوانه را در نظر بگیرید.
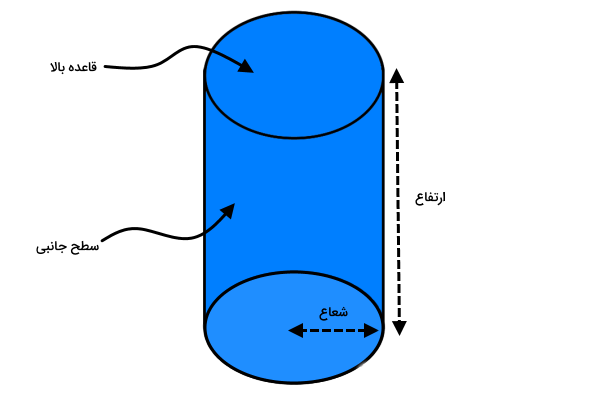
سطح خارجی استوانه، از دو دایره و یک سطح جانبی تشکیل میشود. به سطوح دایرهایشکل در بالا و پایین استوانه، قاعده میگویند.
اگر سطح خارجی یک استوانه را باز کنیم، شکلی مشابه تصویر زیر به دست میآید. به این شکل، گسترده استوانه میگویند.
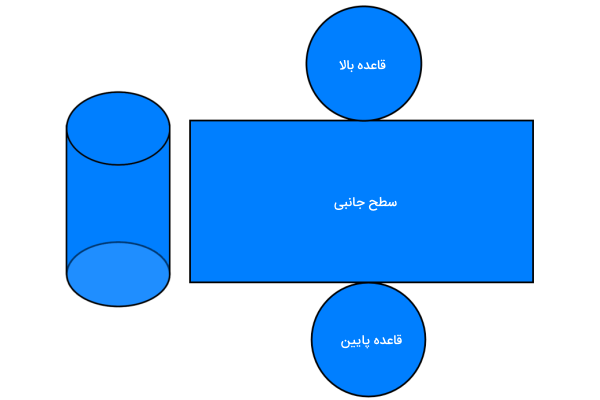
شکل سطح دور استوانه (سطح به وجود آمده در راستای ارتفاع استوانه)، یک مستطیل است. اگر یک استوانه یا دیگر حجمهای منشوری را بر روی یک سطح بغلتانیم، یک مستطیل به وجود میآید. بنابراین، گسترده استوانه، از دو دایره و یک مستطیل تشکیل میشود. در بخشهای بعدی، نحوه محاسبه مساحت این مستطیل یا همان مساحت جانبی سطح استوانه را آموزش میدهیم. پیش از این، بهتر است با تفاوت مساحت جانبی و مساحت کل استوانه آشنا شوید. اشتباه گرفتن این دو مساحت میتواند باعث اشتباه در حل برخی از سوالات امتحانی شود.
تفاوت مساحت جانبی استوانه با مساحت استوانه چیست؟
مساحت استوانه (+)، مجموع مساحتهای سطح جانبی و قاعدههای استوانه است. بنابراین، مساحت جانبی استوانه، بخشی از مساحت کل سطح خارجی استوانه محسوب میشود. گسترده استوانه را در نظر بگیرید.
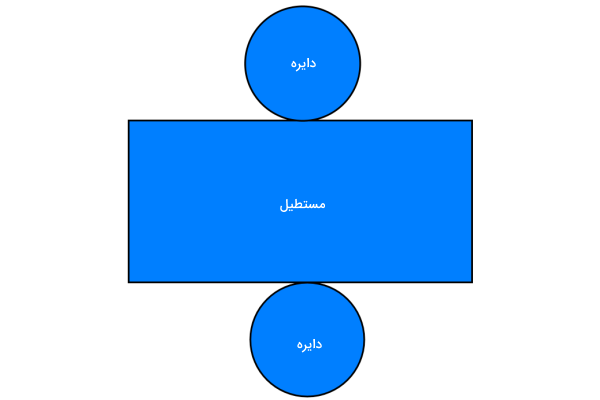
با توجه به گسترده استوانه، تفاوت بین مساحت کل و مساحت جانبی استوانه به صورت زیر تعریف میشود:
مساحت مستطیل + (مساحت دایره × ۲ ) = مساحت کل استوانه
مساحت مستطیل = مساحت جانبی استوانه
فرادرس، یک فیلم آموزشی مفید با عنوان «ریاضی پایه هفتم – جامع و با نکات مهم فرادرس» را تهیه کرده است که به دانشآموزان هفتم و پایههای بالاتر کمک میکند تا مباحث ریاضی هفتم را خیلی سریع و راحت یاد بگیرند. لینک مشاهده این فیلم آموزشی در ادامه آورده شده است.
چگونه مساحت جانبی استوانه و اشکال هندسی را به خوبی یاد بگیریم؟

مبحث مساحت جانبی استوانه، یکی از بخشهای مهم کتاب ریاضی پایه هفتم به شمار میرود. سطح و حجم، در فصل ششم این کتاب آموزش داده میشوند. درس سوم کتاب ریاضی هفتم نیز به مبحث مساحت جانبی و مساحت کل انواع حجمهای منشوری از جمله استوانه میپردازد. با توجه به این توضیحات، برای یادگیری پایهای در رابطه با سطح جانبی استوانه و دیگر اشکال هندسی، بهتر است کتاب ریاضی هفتم را مطالعه کنید. البته به منظور تسلط بر روی این کتاب، باید به دنبال منبع جامعی باشید که نکات تئوری و فرمولهای ریاضی هفتم را به همراه حل مثال ارائه کرده باشد. فرادرس، یک فیلم آموزشی مفید را تهیه کرده است که میتواند به شما در یادگیری سریع و راحت درسهای ریاضی هفتم، از جمله مساحت حجمها کمک کرده و شما را به موفقیت در امتحانات نزدیک کند. لینک مشاهده این فیلم در ادامه آورده شده است:
فرمول جبری مساحت جانبی استوانه چیست؟
فرمول جبری مساحت جانبی استوانه برابر است با:
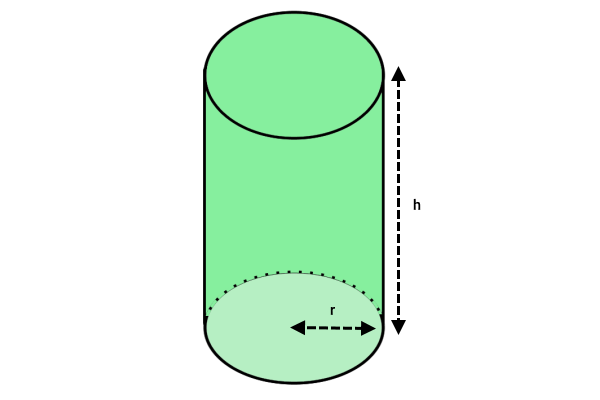
- : مساحت جانبی استوانه
- : عدد پی
- : شعاع قاعده استوانه
- : ارتفاع استوانه
در بخشهای بعدی، نحوه اثبات و رسیدن به فرمول بالا را آموزش خواهیم داد. در ادامه، به حل چند مثال دیگر با استفاده از فرمول جبری اندازه سطح جانبی استوانه میپردازیم.
مثال ۴: محاسبه جبری مساحت جانبی مخزن
- : مساحت جانبی مخزن
- : عدد پی برابر با ۳/۱۴
- : شعاع قاعده مخزن برابر با ۴
- : ارتفاع مخزن برابر با ۳
مقادیر معلوم را درون فرمول قرار میدهیم:
در نتیجه، اندازه سطح جانبی مخزن برابر با ۷۵/۳۶ متر مربع است.
مثال ۵: محاسبه شعاع استوانه از روی مساحت جانبی
- : مساحت جانبی استوانه برابر با ۲۶۷۰ سانتیمتر
- : عدد پی برابر با ۳/۱۴
- : شعاع قاعده استوانه
- : ارتفاع استوانه برابر با ۲۵ سانتیمتر
پس از جایگذاری مقادیر معلوم در فرمول، آن را برای به دست آوردن پارامتر (شعاع قاعده) حل میکنیم:
در نتیجه، شعاع قاعده استوانه، تقریبا برابر با ۱۷ سانتیمتر است (به طور دقیقتر، ۱۷/۰۰۶۴). علامت ، عبارت «تقریبا» را نمایش میدهد.
در مطلب «مساحت استوانه و محاسبه آن | به زبان ساده» (+)، فرمولهای محاسبه مساحت کل استوانه را به طور خلاصه ارائه کردیم. در ادامه این مطلب از مجله فرادرس، نحوه اثبات فرمول مساحت جانبی استوانه را به همراه حل مثال توضیح میدهیم.
اثبات فرمول مساحت جانبی استوانه
برای اثبات فرمول مساحت جانبی استوانه، ابتدا باید به این سوال پاسخ بدهیم که سطح جانبی استوانه به چه شکلی است. سطح جانبی استوانه به شکل مستطیل است.
گسترده استوانه، از یک مستطیل و دو دایره تشکیل میشود. مستطیل، سطح جانبی استوانه و دو دایره، قاعدههای استوانه را تشکیل میدهند.
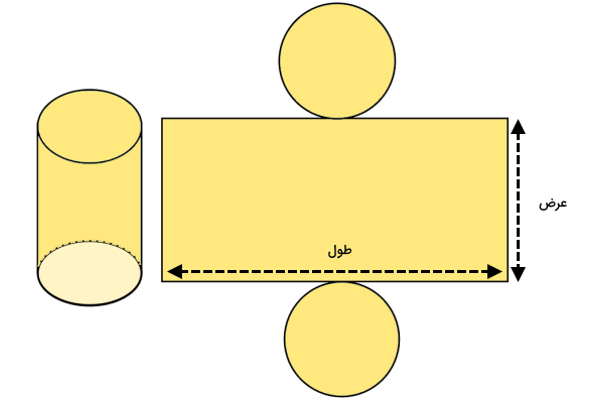
مساحت جانبی استوانه، مساحت مستطیل نمایش داده شده در گسترده آن است. مساحت مستطیل، از رابطه زیر به دست میآید:
عرض × طول = مساحت مستطیل
بنابراین:
عرض مستطیل × طول مستطیل = مساحت جانبی استوانه
فرض کنید مستطیل را برداشته و آن را مانند تصویر زیر، به یک استوانه توخالی تبدیل میکنیم.
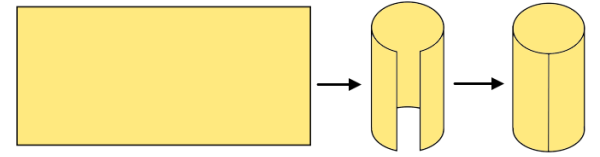
به این ترتیب، عرض مستطیل، معادل ارتفاع استوانه میشود.

طول مستطیل نیز با محیط قاعده استوانه برابری میکند.
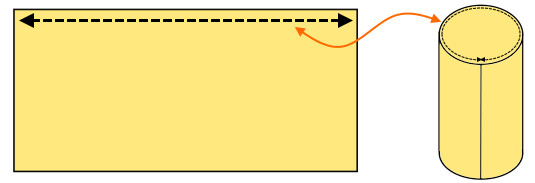
قاعده استوانه، دایرهایشکل بوده و محیط آن برابر است با:
شعاع قاعده × عدد پی × ۲ = محیط قاعده استوانه
به این ترتیب، داریم:
ارتفاع استوانه = عرض مستطیل
و
محیط قاعده استوانه = طول مستطیل
شعاع قاعده × عدد پی × ۲ = طول مستطیل
در نتیجه:
ارتفاع استوانه × شعاع قاعده × عدد پی × ۲ = مساحت جانبی استوانه
یا به طور سادهتر:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
مثال ۶: محاسبه مساحت استوانه از روی ابعاد مستطیل
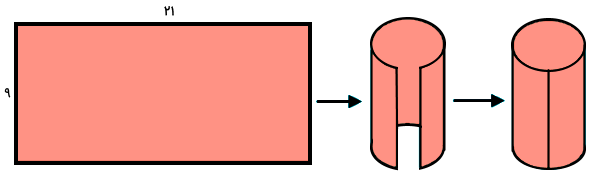
مساحت استوانه چقدر است؟ برای پاسخگویی به این مثال، فرضیات زیر را در نظر بگیرید:
- مستطیل را در راستای طول آن تا زدهایم.
- عدد پی برابر با ۳ است.
برای به دست آوردن مساحت استوانه، به مساحت سطح جانبی و قاعدههای آن نیاز داریم. این مساحت برابر است با:
مساحت قاعدهها + مساحت جانبی = مساحت کل استوانه
مساحت سطح جانبی استوانه، مساحت مستطیلی است که در ابتدا از آن برای ساخت استوانه استفاده کردیم. بنابراین:
مساحت مستطیل = مساحت جانبی
عرض مستطیل × طول مستطیل = مساحت جانبی
۹ × ۲۱ = مساحت جانبی
۱۸۹ = مساحت جانبی
به این ترتیب، مساحت سطح جانبی استوانه برابر با ۱۸۹ سانتیمتر مربع شد. از آنجاییکه مستطیل را از راستای طول آن تا زدهایم، اندازه طول با اندازه محیط قاعده استوانه برابری میکند. بر این اساس، داریم:
طول مستطیل = محیط قاعده
شعاع × عدد پی × ۲ = محیط قاعده
شعاع × عدد پی × ۲ = ۲۱
شعاع × ۳ × ۲ = ۲۱
شعاع × ۶ = ۲۱
۶ ÷ ۲۱ = شعاع
۳/۵ = شعاع
از این محاسبات، شعاع قاعده دایرهایشکل را به دست آوردیم. با استفاده از شعاع میتوانیم مساحت قاعدهها را محاسبه کنیم:
شعاع × شعاع × عدد پی = مساحت قاعده
۳/۵ × ۳/۵ × ۳ = مساحت قاعده
۳۶/۷۵ = مساحت قاعده
هر استوانه، دو قاعده برابر دارد. بنابراین:
مساحت یک قاعده × ۲ = مساحت قاعدههای استوانه
۷۳/۵ = مساحت قاعدههای استوانه
مساحت قاعدههای استوانه برابر با ۷۳/۵ سانتیمتر مربع است. با استفاده از مساحت جانبی و قاعدههای استوانه، مساحت کل آن را به دست میآوریم:
مساحت قاعدهها + مساحت جانبی = مساحت کل استوانه
۷۳/۵ + ۱۸۹ = مساحت کل استوانه
۲۶۲/۵ = مساحت کل استوانه
در نتیجه، مساحت کل استوانه برابر با ۲۶۲/۵ سانتیمتر مربع است.
فرمول مساحت جانبی استوانه مایل چیست؟
فرمولهای معرفی شده در بخشهای قبلی، در محاسبه اندازه سطح جانبی استوانه قائم کاربرد دارند. استوانه قائم، استوانهای با قاعدههای همراستا است.
اگر قاعدههای استوانه، در یک راستا نباشد، استوانه قائم تشکیل میشود. تصویر زیر، نمونهای از یک استوانه مایل را نمایش میدهد.
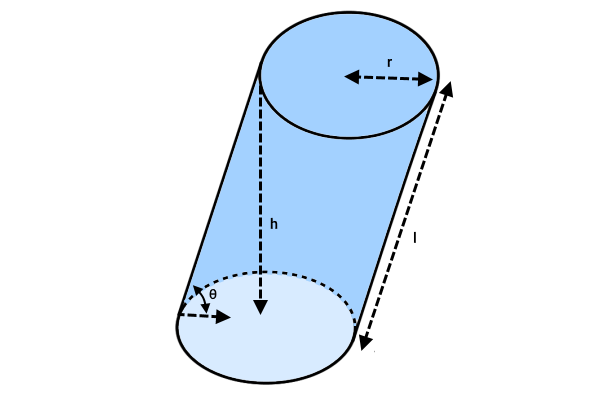
فرمول مساحت جانبی استوانه مایل، با استفاده از فرمول زیر محاسبه میشود:
- : سطح جانبی استوانه مایل
- : عدد پی
- : شعاع قاعده استوانه مایل
- : طول یال استوانه مایل
بین طول یال استوانه مایل و ارتفاع آن، رابطه زیر برقرار است:
- : طول یال استوانه مایل
- : ارتفاع استوانه مایل
- : زاویه انحراف استوانه مایل نسبت به استوانه قائم
در صورت نیاز به محاسبه مساحت کل استوانه مایل میتوان از فرمول زیر استفاده کرد:
یا
مثال ۷: محاسبه مساحت جانبی استوانه مایل
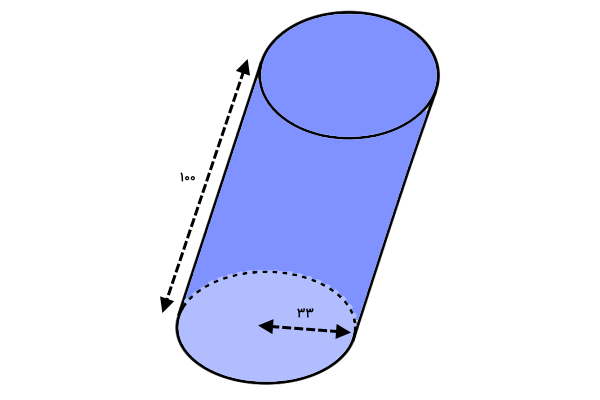
با توجه تصویر، اطلاعات زیر را در اختیار داریم:
- شعاع قاعده استوانه: ۳۳ واحد
- طول یال استوانه: ۱۰۰ واحد
اطلاعات بالا، برای به دست آوردن اندازه سطح جانبی استوانه مایل کفایت میکند. این اطلاعات را در فرمول زیر قرار میدهیم:
- : سطح جانبی استوانه مایل
- : عدد پی برابر با ۳/۱۴
- : شعاع قاعده استوانه مایل برابر با ۳۳
- : طول یال استوانه مایل برابر با ۱۰۰ واحد
در نتیجه، مساحت جانبی استوانه مایل برابر با ۱۰۳۶۲ واحد سطح است.
رابطه بین حجم و مساحت جانبی استوانه
حجم استوانه، از ضرب ارتفاع آن در مساحت قاعده به دست میآید. فرمول جبری حجم استوانه به صورت زیر نوشته میشود:
- : حجم استوانه
- : شعاع قاعده استوانه
- : ارتفاع استوانه
بر اساس این فرمول، اگر حجم و یکی دیگر از پارامترهای اصلی استوانه نظیر شعاع یا ارتفاع را داشته باشیم، میتوانیم مساحت کل، مساحت جانبی و مساحت قاعدههای استوانه را محاسبه کنیم. در ادامه، به حل یک مثال در رابطه با این موضوع میپردازیم.
مثال ۸: محاسبه سطح جانبی استوانه از روی حجم

صورت سوال، حجم و ارتفاع ماگ را به ما داده است. بر اساس فرمول حجم استوانه، داریم:
- : حجم ماگ برابر با ۳۰۰ سیسی
- : شعاع قاعده ماگ
- : ارتفاع ماگ برابر با ۸ سانتیمتر
دقت داشته باشید که یکای سیسی، همان سانتیمتر مکعب است. ۳۰۰ سیسی با ۰/۳ لیتر برابری میکند. با توجه به مقادیر معلوم، داریم:
فرمول را بر حسب حل میکنیم:
با استفاده از روشهای جذر گرفتن سریع میتوان جواب رادیکال بالا را به دست آورد:
به این ترتیب، شعاع ماگ، برابر با ۳/۴۵ سانتیمتر شد. اکنون میتوانیم با استفاده از شعاع قاعده ماگ و ارتفاع آن، مساحت سطح جانبی را به دست بیاوریم. به این منظور، از فرمول زیر استفاده میکنیم:
- : سطح جانبی ماگ
- : عدد پی برابر با ۳/۱۴
- : شعاع قاعده ماگ برابر با ۳/۴۵ سانتیمتر
- : ارتفاع ماگ برابر با ۸ سانتیمتر
در نتیجه، مساحت سطح جانبی ماگ برابر با ۱۷۳/۴۳ سانتیمتر مربع است.
در ادامه و آخرین بخش از این مطلب از مجله فرادرس، به حل چندین تمرین متنوع در قالب یک آزمون چندگزینهای میپردازیم.
آزمون سنجش یادگیری مساحت جانبی استوانه
در این بخش، سطح اطلاعات شما در مبحث اندازه سطح جانبی استوانه را با طرح سوالهای چندگزینهای میسنجیم. پس از جواب دادن به تمام سوالها، نتیجه آزمون برای شما به نمایش درمیآید.
کدامیک از گزینههای زیر، رابطه محاسبه سطح جانبی استوانه را نمایش میدهد.
ارتفاع × شعاع × عدد پی × ۲
ارتفاع × شعاع × شعاع × عدد پی
شعاع × شعاع × عدد پی
شعاع × عدد پی × ۲
اندازه سطح جانبی استوانه، از رابطه زیر به دست میآید:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
نمایش جبری این رابطه با استفاده از فرمول زیر صورت میگیرد:
- : مساحت جانبی استوانه
- : عدد پی
- : شعاع قاعده استوانه
- : ارتفاع استوانه
گزینه دوم، حجم استوانه است. گزینه سوم، برای محاسبه مساحت دایره یا همان قاعده استوانه استفاد میشود. گزینه چهارم نیز رابطه محیط دایره است.
مساحت جانبی استوانهای به شعاع ۲۸ و ارتفاع ۱۵ سانتیمتر، کدامیک از گزینههای زیر است؟ (عدد پی را برابر با ۳ در نظر بگیرید.)
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
اندازه سطح جانبی استوانه، از رابطه زیر محاسبه میشود:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
بر اساس اطلاعات و فرضیات مسئله، عدد پی برابر با ۳، ارتفاع استوانه برابر با ۱۵ سانتیمتر و شعاع قاعده استوانه برابر ۲۸ سانتیمتر است. این مقادیر را در رابطه بالا قرار میدهیم:
۱۵ × ۲۸ × ۳ × ۲ = مساحت جانبی استوانه
۲۵۲۰ = مساحت جانبی استوانه
در نتیجه، مساحت جانبی استوانه برابر با ۲۵۲۰ سانتیمتر مربع است.
استوانهای به مساحت جانبی ۱۰۰ سانتی مربع را در نظر بگیرید. اگر ارتفاع این استوانه برابر با ۴ سانتیمتر باشد، مساحت قاعده آن، تقریبا چقدر خواهد بود؟ (عدد پی را برابر با ۳/۱۴ قرار دهید و نزدیکترین گزینه را انتخاب کنید.)
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
قاعده استوانه، به شکل دایره است. بنابراین، مساحت قاعده دایرهای شکل استوانه از رابطه زیر به دست میآید:
- : مساحت قاعده استوانه
- : عدد پی برابر با ۳/۱۴
- : شعاع قاعده استوانه
با توجه به اطلاعات مسئله، برای محاسبه مساحت قاعده، به شعاع آن نیاز داریم. به منظور تعیین شعاع، دیگر اطلاعات مسئله (مساحت جانبی و ارتفاع) کمک میگیریم. فرمول مساحت جانبی استوانه به صورت زیر نوشته میشود:
- : مساحت جانبی استوانه برابر با ۱۰۰ سانتیمتر مربع
- : عدد پی برابر با ۳/۱۴
- : شعاع قاعده استوانه (مجهول)
- : ارتفاع استوانه برابر با ۴ سانتیمتر
مقادیر معلوم را درون فرمول بالا قرار میدهیم و آن را بر حسب حل میکنیم:
شعاع قاعده استوانه برابر با ۳/۹۸ سانتیمتر است. با جایگذاری این عدد در رابطه مساحت دایره، خواهیم داشت:
مساحت قاعده دایرهای شکل استوانه، تقریبا برابر با ۴۹/۷۴ سانتیمتر مربع است. این مقدار، به گزینه دو نزدیکتر است.
یک قوطی استوانهای را در نظر بگیرید. ارتفاع این قوطی برابر با ۱۲ سانتیمتر و قطر آن برابر با ۸ سانتیمتر است. اگر بالا و پایین قوطی را از آن جدا کنیم، مساحت تقریبی بخش باقی مانده چقدر خواهد بود؟ (عدد پی را برابر با ۳/۱۴ قرار دهید و نزدیکترین گزینه.)
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
با برداشتن بالا و پایین قوطی، سطح جانبی آن باقی میماند. اندازه این سطح، از رابطه زیر به دست میآید:
- : مساحت جانبی قوطی استوانهای (مجهول)
- : عدد پی برابر با ۳/۱۴
- : شعاع قاعده قوطی برابر با نصف قطر آن
- : ارتفاع استوانه برابر با ۱۲ سانتیمتر
در نتیجه، اندازه سطح جانبی قوطی، تقریبا برابر با ۳۰۲ سانتیمتر مربع خواهد بود.
شخصی یک جامدادی استوانهای شکل دارد که از پارچه ساخته شده است. اگر ارتفاع جامدادی برابر با ۲۰ سانتیمتر و شعاع آن برابر با ۳/۵ سانتیمتر باشد، چه مقدار پارچه برای ساخت جامدادی استفاده شده است؟ (عدد پی را برابر با در نظر بگیرید.)
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
پارچهای که برای ساخت جامدادی استفاده شده است، شامل سطح جانبی و قاعدههای دو طرف این سطح میشود. بنابراین، برای محاسبه میزان پارچه مورد استفاده، باید مساحت تمام بخشها را به دست بیاوریم. به عبارت دیگر، مساحت پارچه جامدادی عبارت است از:
مساحت جانبی + مساحت قاعدهها = مساحت پارچه جامدادی
به دلیل استوانهای شکل بودن جامدادی، قاعدههای آن به شکل دایره خواهند بود. از اینرو، مساحت هر قاعده به صورت زیر محاسبه میشود:
- : مساحت قاعده استوانه
- : عدد پی برابر با
- : شعاع قاعده استوانه برابر با ۳/۵ سانتیمتر
با توجه به مقادیر معلوم، داریم:
مساحت هر قاعده جامدادی برابر با ۳۸/۵ سانتیمتر مربع است. بنابراین، مساحت دو قاعده آن برابر خواهد بود با:
مساحت جانبی جامدادی نیز از رابطه زیر به دست میآید:
- : مساحت جانبی جامدادی استوانهای (مجهول)
- : عدد پی برابر با
- : شعاع قاعده جامدادی برابر با ۳/۵ سانتیمتر
- : ارتفاع جامدادی برابر با ۲۰ سانتیمتر
اندازه سطح جانبی جامدادی برابر با ۴۴۰ سانتیمتر مربع است. به این ترتیب، مساحت کل جامدادی برابر میشود با:
در نتیجه، مساحت پارچه مورد استفاده برای ساخت جامدادی برابر با ۵۱۷ سانتیمتر مربع است.
حجم یک تانکر آب استوانهای برابر با ۲۸ متر مکعب است. اگر قطر این تانکر برابر با ۲/۴۴ متر باشد، اندازه سطح جانبی تانکر، کدامیک از گزینههای زیر خواهد بود؟ (عدد پی را برابر با در نظر بگیرید.)
متر مربع
متر مربع
متر مربع
متر مربع
در این سوال، به دنبال مساحت جانبی تانکر استوانهای هستیم. برای به دست آوردن این مساحت، به اندازه شعاع قاعده و طول تانکر (ارتفاع استوانه) نیاز داریم. شعاع قاعده تانکر، برابر با نصف قطر آن، یعنی ۱/۲۲ متر است. به دلیل مجهول بودن طول تانکر، آن را با استفاده از فرمول حجم استوانه و اطلاعات مسئله محاسبه میکنیم. فرمول محاسبه حجم تانکر به صورت زیر نوشته میشود:
- : حجم تانکر برابر با ۲۸ متر مکعب
- : شعاع قاعده استوانه برابر با ۱/۲۲ متر
- : ارتفاع استوانه (مجهول)
طول تانکر یا همان ارتفاع استوانه برابر با ۵/۹۸ متر است. اکنون با داشتن این مقدار میتوانیم مساحت سطح جانبی تانکر را محاسبه کنیم. به این منظور، فرمول زیر را مینویسیم:
- : مساحت جانبی تانکر (مجهول)
- : عدد پی برابر با
- : شعاع قاعده تانکر برابر با ۱/۲۲ سانتیمتر
- : ارتفاع جامدادی برابر با ۵/۹۸ سانتیمتر
در نتیجه، مساحت جانبی تانکر استوانهای برابر با ۴۵/۸۵ متر مربع است.
دو استوانه قائم و مایل را در نظر بگیرید.
- ارتفاع استوانه قائم برابر با ۱۱ سانتیمتر بوده و شعاع قاعده آن برابر با ۲۱ سانتیمتر است.
- ارتفاع استوانه مایل برابر با ۱۱ سانتیمتر بوده و شعاع قاعده آن برابر با ۲۱ سانتیمتر است.
اگر زاویه انحراف راستای استوانه مایل نسبت به افق برابر با ۳۰ درجه باشد، کدامیک از گزینههای زیر صحیح خواهد بود؟ (عدد پی را برابر با قرار دهید.)
سطح جانبی استوانه قائم برابر با سطح جانبی استوانه مایل است.
سطح جانبی استوانه قائم دو برابر سطح جانبی استوانه مایل است.
سطح جانبی استوانه قائم نصف سطح جانبی استوانه مایل است.
سطح جانبی استوانه قائم سه برابر سطح جانبی استوانه مایل است.
برای پاسخ دادن به این سوال، باید مساحت جانبی دو استوانه را به دست بیاوریم. مساحت جانبی استوانه قائم برابر است با:
- : مساحت جانبی استوانه قائم (مجهول)
- : عدد پی برابر با
- : شعاع قاعده استوانه قائم با ۲۱ سانتیمتر
- : ارتفاع استوانه قائم برابر با ۱۱ سانتیمتر
اندازه سطح جانبی استوانه قائم برابر با ۱۴۵۲ سانتیمتر مربع است. به منظور محاسبه این اندازه برای استوانه مایل، از فرمول زیر استفاده میکنیم:
- : مساحت جانبی استوانه مایل (مجهول)
- : عدد پی برابر با
- : شعاع قاعده استوانه مایل برابر با ۲۱ سانتیمتر
- : طول یال استوانه مایل (مجهول)
برای تعیین مساحت جانبی، به اندازه یال استوانه نیاز داریم. این اندازه، از رابطه زیر به دست میآید:
- : طول یال استوانه مایل (مجهول)
- : ارتفاع استوانه مایل برابر با ۱۱ سانتیمتر
- : زاویه انحراف استوانه مایل نسبت به استوانه قائم برابر با ۳۰ درجه
اندازه سطح جانبی استوانه مایل برابر با ۲۹۰۴ سانتیمتر مربع است. به این ترتیب، داریم:
در نتیجه، سطح جانبی استوانه مایل، دو برابر سطح جانبی استوانه قائم است.
یک غلتک روی زمین آسفالت شده باید ۴ مرتبه غلت بزند تا سطح زمین صاف شود. اگر شعاع غلتک ۵۰ سانتیمتر و ارتفاع استوانه آن ۱ متر باشد، برای آسفالت کردن سطح یک کوچه به طول ۲۰ متر و عرض ۴ متر، این غلتک باید به طور تقریبی چند بار بچرخد؟
دور
دور
دور
برای صاف کردن یک کوچه به طور ۲۰ و عرض ۴ متر، غلتک باید ۴ بار سطح کل کوچه را غلت بزند. مساحت کوچه، برابر است با:
عرض کوچه × طول کوچه = مساحت کوچه
۴ × ۲۰ = مساحت کوچه
۸۰ = مساحت کوچه
مساحت کوچه برابر با ۸۰ متر مربع است. به این ترتیب، داریم:
۸۰ × ۴ = مساحت لازم برای صاف کردن کوچه
۳۲۰ = مساحت لازم برای صاف کردن کوچه
غلتک با چهار بار غلت روی سطح کوچه و پوشش ۳۲۰ متر مربع، میتواند کوچه را صاف کند. اکنون میخواهیم تعداد چرخش کامل غلتک را به دست بیاوریم. برای این کار، به مساحت جانبی غلتک نیاز داریم. غلتک، یک جسم استوانهای با شعاع قاعده ۵۰ سانتیمتر (۰/۵ متر) و ارتفاع استوانه ۱ متر است. بنابراین، سطح جانبی آن برابر است با:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی غلتک
۱ × ۰/۵ × ۳/۱۴ × ۲ = مساحت جانبی غلتک
۳/۱۴ = مساحت جانبی غلتک
اندازه سطح جانبی غلتک برابر با ۳/۱۴ متر مربع است. به عبارت دیگر، با یک بار چرخش کامل غلتک بر روی زمین، ۳/۱۴ متر مربع پوشش داده میشود. مساحت مورد نیاز برای صاف کردن کوچه برابر با ۳۲۰ متر مربع بود. بنابراین، تعداد چرخشها برابر خواهد بود با:
۳/۱۴ ÷ ۳۲۰ = تعداد چرخشها
۱۰۱/۹۱ = تعداد چرخشها
در نتیجه، اگر غلتک تقریبا ۱۰۲ بار بچرخد، میتواند کل کوچه را صاف کند.
یک چرخ ماشین که کاملا خیس شده است، با ۱۰ دور چرخیدن روی زمین جای خود را مشخص میکند تا خشک شود. اگر این چرخ به ضخامت ۲۰ سانتیمتر و قطر ۷۰ سانتیمتر باشد، چه مساحتی از زمین را خیس خواهد کرد؟
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
سانتیمتر مربع
با چرخدن چرخ، سطح جانبی آن با زمین برخورد میکند. به دلیل استوانهای بودن شکل چرخ خودروها، اندازه سطح جانبی آنها از رابطه زیر به دست میآید:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی چرخ
در صورت سوال، ضخامت چرخ داده شده است. این ضخامت، همان ارتفاع استوانه است. به علاوه، شعاع با نصف قطر برابری میکند. بنابراین داریم:
۲۰ × ۳۵ × ۳/۱۴ × ۲ = مساحت جانبی چرخ
۴۳۹۶ = مساحت جانبی چرخ
اندازه سطح جانبی چرخ خودرو برابر با ۴۳۹۶ سانتیمتر مربع است. اگر برای خشک شدن، نیاز به ۱۰ دور چرخش کامل بر روی زمین باشد، مساحت خیس شده زمین برابر میشود با:
۴۳۹۶ × ۱۰ = مساحت خیس شدن زمین
۴۳۹۶۰ = مساحت خیس شدن زمین
یک مخزن نفت به شکل استوانهای است که شعاع قاعده آن ۳ متر و ارتفاعش ۵ متر است. میخواهیم بدنه خارجی و سقف آن را رنگ بزنیم. اگر هزینه رنگ کردن هر متر مربع، ۳۰۰۰ تومان باشد، برای رنگ کردن این مخزن چقدر باید هزینه کرد؟
تومان
تومان
تومان
تومان
میخواهیم بدنه خارجی (سطح جانبی) و سقف (قاعده بالایی) یک مخزن استوانهای را رنگ کنیم. مساحت ناحیه قابل رنگ برابر است با:
مساحت جانبی مخزن + مساحت قاعده مخزن = مساحت ناحیه قابل رنگ
مخزن به شکل استوانهای به ارتفاع ۵ متر و شعاع قاعده ۳ متر است. بنابراین، میتوانیم رابطه بالا را به شکل زیر بازنویسی کنیم:
مساحت جانبی استوانه + مساحت قاعده = مساحت ناحیه قابل رنگ
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
شعاع × شعاع × عدد پی = مساحت قاعده
۵ × ۳ × ۳/۱۴ × ۲ = مساحت جانبی استوانه
۹۴/۲ = مساحت جانبی استوانه
۳ × ۳ × ۳/۱۴ = مساحت قاعده
۲۸/۲۶ = مساحت قاعده
به این ترتیب، مساحت جانبی مخزن برابر با ۹۴/۲ متر مربع و مساحت قاعده آن برابر با ۲۸/۲۶ متر مربع میشود. مساحت ناحیه قابل رنگ، از جمع این دو مساحت به دست میآید:
۹۴/۲ + ۲۸/۲۶ = مساحت ناحیه قابل رنگ
۱۲۲/۴۶ = مساحت ناحیه قابل رنگ
برای رنگ کردن مخزن، به ۱۲۲/۴۶ متر مربع رنگکاری نیاز داریم. قیمت هر متر مربع رنگ برابر با ۳۰۰۰ تومان است. بنابراین:
۳۰۰۰ × ۱۲۲/۴۶ = هزینه رنگ کردن مخزن
۳۶۷۳۸۰ = هزینه رنگ کردن مخزن
در نتیجه، هزینه رنگ کردن بدنه خارجی و سقف مخزن برابر با ۳۶۷۳۸۰ تومان (حدود سیصد و هفتاد هزار تومان) میشود.
source
