آشنایی و درک فرمول های فیزیک دوازدهم از اهمیت بسزایی برخوردار است. فیزیک دوازدهم یا فیزیک سه در سال سوم متوسطه یا مقطع دوازدهم برای رشتههای ریاضیفیزیک و علومتجربی تدریس میشود. فیزیک دوازدهم در رشته ریاضیفیزیک از شش فصل و در رشته علومتجربی از چهار فصل تشکیل شده است. مبحثهای حرکت بر خط راست و دینامیک و حرکت دایرهای در فصلهای اول و دومِ فیزیک دوازدهم رشته ریاضیفیزیک تدریس میشوند. این دو فصل، مشابه دو فصل اول فیزیک دوازدهم در رشته تجربی هستند، با این تفاوت که حرکت دایرهای در رشته تجربی تدریس نمیشود. نوسان و موج و برهمکنشهای امواج در فصل سوم و چهارم از فیزیک سه، رشته ریاضیفیزیک تدریس میشوند. اما این دو فصل، در رشته تجربی به صورت خلاصهتر و در یک فصل آموزش داده میشود. فصلهای ۵ و ۶ فیزیک دوازدهم، رشته ریاضیفیزیک، مبحثهای فیزیک اتمی و فیزیک هستهای را توضیح میدهند. این دو فصل نیز برای رشته علومتجربی مشابه فصلهای ۳ و ۴، در یک فصل و به صورت خلاصهتر توضیح داده شدهاند.
حل مسئله و درک فرمول های فیزیک دوازدهم برای موفقیت در آزمون نهایی فیزیک و کنکور، بسیار مهم و ضروری است. در این مطلب از مجله فرادرس، فرمول های فیزیک دوازدهم را به صورت خلاصه همراه با حل مثال توضیح میدهیم. برای هر فصل، ابتدا فرمولها به صورت خلاصه در جدول نوشته شدهاند، سپس توضیح کوتاهی همراه با حل چند مثال برای هر فرمول آورده شده است.
فرمول های فیزیک دوازدهم فصل اول
فرمول های فیزیک دوازدهم فصل اول در فهرست زیر به صورت خلاصه نوشته شدهاند:
- تندی متوسط با رابطه $$s_{ av } = overline{ s } = frac { l } {triangle t } $$ مشخص میشود.
- سرعت متوسط با استفاده از رابطه $$ overline{ v } _ { av } = frac { overrightarrow{ d } } {triangle t } $$ بهدست میآید.
- شتاب متوسط را میتوانیم با استفاده از رابطه $$ overline{ a } _ { av } = frac { overrightarrow{v_2} – overrightarrow{ v _ 1 } } { t _ 2 – t _ 1 } = frac { triangle overrightarrow{ v } } {triangle t } $$ بهدست آوریم
- معادله مکان زمان در حرکت با سرعت ثابت با رابطه $$x = vt + x_0 $$ مشخص میشود.
- معادله سرعت زمان در حرکت با شتاب ثابت به صورت $$v = at + v_0 $$ نوشته میشود.
- معادله سرعت متوسط در حرکت با شتاب ثابت با رابطه $$v_ { av } = frac { v + v_ 0 } { 2 } $$ مشخص میشود.
- معادله مکان زمان در حرکت با شتاب ثابت به صورت $$x = frac { 1 } { 2 } a t ^ 2 + v_ 0 t + x_ 0 $$ نوشته میشود.
- معادله سرعت جابجایی در حرکت با شتاب ثابت با رابطه $$v ^ 2 = v_ 0 ^ 2 + 2 a triangle x $$ نوشته میشود.
- اگر جسمی بدون سرعت اولیه از ارتفاع مشخصی سقوط کند، معادلات حرکت آن به صورت زیر نوشته میشوند:
- $$v = – g t $$
- $$y = – frac { 1 } { 2 } g t ^ 2 + y _ 0 $$
- $$v ^ 2 = – 2 g ( y – y _ 0 ) $$
در ادامه، فرمول های فیزیک دوازدهم فصل اول را با حل مثال به صورت خلاصه توضیح میدهیم.
تندی متوسط و سرعت متوسط
برای آشنایی با سرعت متوسط و تندی متوسط باید با برخی مفاهیم آشنا باشیم.
- مسافت طی شده: به کل مسیر طی شده توسط جسم، مسافت گفته میشود. مسافت کمیتی نردهای است و تنها اندازه دارد.
- جابجایی: به کوتاهترین مسافت بین نقطه ابتدا و انتهای مسیر، جابجایی میگوییم. جابجایی، کمیتی برداری است و تنها به نقاط ابتدا و انتهای مسیر بستگی دارد.
- زمان سپری شده: به هنگام محاسبه تندی متوسط و سرعت متوسط باید مدت زمان صرف شده برای مسافت و جابجایی را داشته باشیم.

به نسبت مسافت طی شده به مدت زمان صرف شده برای طی کردن آن، تندی متوسط گفته میشود.
$$s_{ av } = overline{ s } = frac { l } {triangle t } $$
سرعت متوسط نیز از تقسیم جابجایی بر مدت زمان لازم برای انجام جابجایی بهدست میآید:
$$ overline{ v } _ { av } = frac { overrightarrow{ d } } {triangle t } $$
یکای اندازهگیری سرعت و تندی متوسط در سیستم SI برابر متر بر ثانیه ($$frac { m } { s } $$) است، اما آنها را برحسب کمیتهای دیگری مانند کیلومتر بر ساعت ($$frac { km } { h } $$) نیز میتوان بیان کرد. انتخاب یکای مناسب به صورتِ مسئله و واحدهای مسافت، جابجایی و زمان بستگی دارد.
نکته ۱: تندی و سرعت دو کمیت متفاوت هستند. تندی کمیتی نردهای، اما سرعت کمیتی برداری و به جهت حرکت جسم وابسته است.
نکته ۲: اگر جهت حرکت جسم در بازه زمانی $$triangle t $$ تغییر نکند، مقدارهای تندی متوسط و سرعت متوسط با یکدیگر برابر هستند. اما اگر جهت حرکت جسم تغییر کند، مقدار تندی متوسط بزرگتر از سرعت متوسط خواهد بود.
نمودار مکان زمان
برای توصیف حرکت جسم میتوانیم از نموداری به نام نمودار مکان زمان استفاده کنیم. محور عمودی موقعیت مکانی جسم نسبت به مبدا مکان و محور افقی زمان را نشان میدهد.
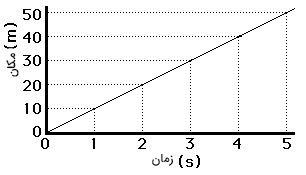
اتومبیلی را در نظر بگیرید که با سرعت مثبت و ثابت ($$+ 10 frac { m } { s } $$) روی خطی مستقیم به صورت نشان داده شده در تصویر زیر حرکت میکند.

با داشتن مکان و زمان حرکت اتومبیل، نمودار مکان زمان آن را به صورت نشان داده شده در تصویر زیر رسم میکنیم. همانطور که مشاهده میکنید، نمودار مکان زمان برای حرکت با سرعت ثابت، خطی مستقیم با شیب ثابت است.
در ادامه، اتومبیلی را در نظر بگیرید که با سرعت مثبت و متغیر، روی خطی مستقیم به صورت نشان داده شده در تصویر زیر حرکت میکند.

با داشتن مکان و زمان حرکت اتومبیل، نمودار مکان زمان آن را به صورت نشان داده شده در تصویر زیر رسم میکنیم. همانطور که مشاهده میکنید، نمودار مکان زمان برای حرکت با سرعت متغیر، منحنی با شیب متغیر است.
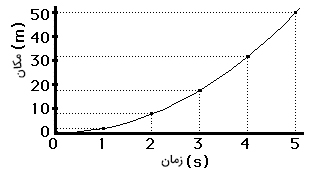
با توجه به توضیحات بالا، شیب خط مماس بر نمودار مکان زمان، بیانگر سرعت حرکت جسم است. بنابراین، مقدار شیبِ خط مماس بر نمودار مکان زمان در هر لحظه از زمان، سرعت جسم را در آن لحظه به ما میدهد. با توجه به نمودارهای مکان زمان برای حرکت با سرعت ثابت و متغیر، شیب نمودار مکان زمان میتواند ثابت یا متغیر باشد. مقدار این شیب، سرعت حرکت جسم را در هر لحظه از زمان به ما میدهد. اگر نمودار، منحنی باشد، از انحنای آن نیز میتوانیم برای توصیف حرکت استفاده کنیم. در نمودارهایی به شکل منحنی، شیب خط مماس بر منحنی، ثابت نیست و از نقطهای به نقطه دیگر، تغییر میکند. شیبِ متغیر به معنای تغییرات سرعت و حرکت شتابدار است. در نتیجه، انحنا در نمودار مکان زمان، حرکت شتابدار را نشان میدهد. هرچه شیبِ نمودار مکان زمان در نقطهای مشخص بیشتر باشد، سرعت حرکت در آن نقطه نیز بزرگتر خواهد بود.
نمودار سرعت زمان
در ادامه، نمودار سرعت زمان اجسام مختلف و نوع حرکت هریک از آنها را با یکدیگر مقایسه میکنیم. علاوه بر نمودار مکان زمان، نمودار دیگری نیز به نام نمودار سرعت زمان وجود دارد. همانطور که میدانیم جسم میتواند به دو صورت حرکت کند، حرکت یکنواخت با سرعت ثابت و حرکت غیریکنواخت با سرعت متغیر. در حرکت یکنواخت با سرعت ثابت، مسافت طی شده توسط جسم در بازههای زمانی یکسان، برابر است و سرعت آن با گذشت زمان تغییر نمیکند. بنابراین، نمودار سرعت زمان در حرکت یکنواخت، خطی افقی و موازی محور زمان است.
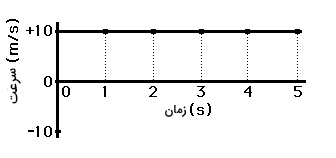
در حرکت یکنواخت با سرعت ثابت، شتاب حرکت برابر صفر است. شیب خط افقی در نمودار بالا چه مقدار است؟ صفر، بنابراین شیبِ نمودار سرعت زمان به ما شتاب را میدهد. اکنون جسمی را در نظر بگیرید که روی خط راست و با سرعت متغیر و افزایشی به سمت راست حرکت میکند. این بدان معنا است که جسم در فاصلههای زمانی برابر، مسافت یکسانی را طی نمیکند. شتاب جسم در حرکت غیریکنواخت میتواند ثابت یا متغیر باشد. فرض کنید جسمی با سرعت افزایشی و شتاب ثابت به سمت راست حرکت میکند. نمودار سرعت زمان آن به صورت نشان داده شده در تصویر زیر است.
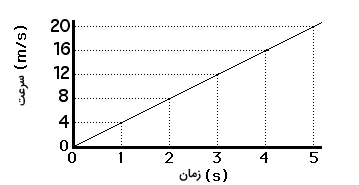
بنابراین، نمودار سرعت زمان در حرکت غیریکنواخت با شتاب ثابت، خطی مستقیم با شیبِ مشخص است. اگر شیب خط مثبت باشد، جسم با شتاب مثبت و اگر شیب خط منفی باشد، جسم با شیب منفی حرکت میکند. فراموش نکنید که شتاب، کمیتی برداری است و اندازه و جهت دارد. توجه به این نکته مهم است که در حرکت غیریکنواخت با شتاب ثابت، مقدار شتاب لحظهای و متوسط با یکدیگر برابر هستند. شتاب لحظهای به ما شتاب حرکت در هر لحظه از زمان، اما شتاب متوسط، مقدار متوسط شتاب را در بازه زمانی مشخص به ما میدهد. حال، فرض کنید جسم با شتاب متغیر حرکت میکند. در این حالت، نمودار سرعت زمان، خطی مستقیم با شیب ثابت نیست، بلکه با توجه به تغییرات شتاب میتواند منحنی به شکلهای مختلف باشد.
فرض کنید نمودار سرعت زمان، جسمی که با شتاب متغیر حرکت میکند به صورت نشان داده شده در تصویر زیر است. شیبِ خط مماس بر نمودار در هر زمان روی نمودار، شتاب حرکت جسم را در آن زمان به ما میدهد.
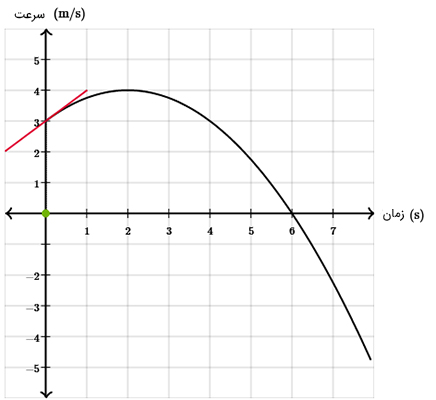
نکته: مساحت زیر نمودار سرعت زمان به ما جابجایی جسم را میدهد.
نمودار شتاب زمان
نمودار شتاب زمان در حرکت غیریکنواخت با شتاب ثابت، خطی افقی، موازی محور زمان است. شیب این نمودار به ما کمیتی به نام «جهش» (Jerk) را میدهد. به تغییرات شتاب نسبت به زمان، جهش گفته میشود. در حرکت غیریکنواخت با شتاب ثابت، مقدار جهش برابر صفر است. نمودار شتاب زمان در حرکت با شتاب ثابت به صورت نشان داده شده در تصویر زیر است. در فیزیک دوازدهم، در مورد حرکت غیریکنواخت با شتاب متغیر توضیحی داده نشده است. بنابراین، در این مطلب در این مورد توضیحی نمیدهیم و تمرکز اصلی را روی حرکت با سرعت ثابت و شتاب ثابت میگذاریم.
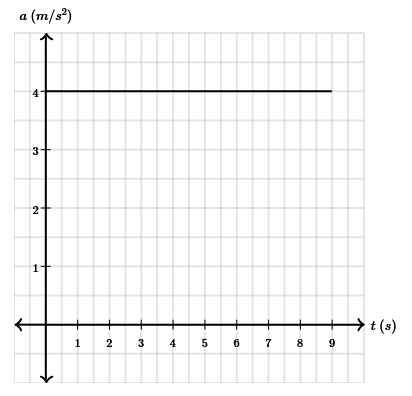
نکته: مساحت زیر نمودار شتاب زمان به ما تغییرات سرعت را میدهد.
همانطور که در مباحث بالا یاد گرفتیم برای توصیف حرکت جسمی بر خط راست از مفاهیم فیزیکی مانند مسافت، سرعت و شتاب استفاده میکنیم. در ادامه، معادلات حرکت یکنواخت و غیریکنواخت را با یکدیگر بررسی میکنیم.
معادله حرکت یکنواخت
اگر جسمی با سرعت ثابت $$v$$ روی محور $$x$$ حرکت کند، معادله مکان برحسب زمان آن به صورت زیر نوشته میشود:
$$x = vt + x_0 $$
در معادله فوق:
- t زمان و برحسب ثانیه یا ساعت است.
- $$x_0 $$ مکان اولیه جسم در زمان صفر است.
- $$x$$ مکان جسم در زمان t است.
- $$v$$ سرعت حرکت جسم است.
اولین معادله حرکت با شتاب یکنواخت
با استفاده از اولین معادله حرکت با شتاب یکنواخت میتوان سرعت جسم را بعد از گذشت زمان معین به دست آورد.
$$a= frac{v_{2}-v_{1}}{t_{2}-t_{1}}$$
با استفاده از فرضهای گفته شده در بخش حرکت یکنواخت، معادله بالا به صورت زیر نوشته خواهد شد.
$$a= frac{v-v_{0}}{t} Rightarrow v= v_{0}+at$$
دومین معادله حرکت با شتاب یکنواخت
مکان جسم پس از گذشت زمان t با استفاده از دومین معادله حرکت با شتاب یکنواخت به دست خواهد آمد. ابتدا فرضهای زیر را در نظر بگیرید.
$$t_{1}=0 \ x_{1}=x_{0} \ v_{1}=v_{0} \ t_{2}=t \ x_{2}=x \ v_{2}=v$$
دومین معادله حرکت با شتاب ثابت
دومین معادله در حرکت با شتاب ثابت به صورت زیر نوشته میشود:
$$ x = x_{0}+v_{0}t + frac{1}{2}at^{2}$$
سومین معادله حرکت با شتاب یکنواخت
اگر مکان، شتاب و سرعت اولیه جسم را داشته باشیم، از معادله زیر برای توصیف حرکت جسم استفاده میکنیم:
$$x-x_{0}= frac{1}{2}(v+v_{0}) t$$
همچنین از اولین معادله حرکت با شتاب ثابت داریم:
$$t=frac{v-v_{0}}{a}$$
با جایگزین کردن معادله فوق در معادله مکان خواهیم داشت.
$$x – x_{0} = frac{1}{2} (v+v_{0})(frac{v-v_{0}}{a}) \ Rightarrow 2a(x – x_{0}) = v^{2}-v_0^2 \ Rightarrow v^{2} = v_0^2 +2a(x – x_{0})$$
در نتیجه سه معادله به دست آمده برای حرکت با شتاب ثابت به صورت زیر نوشته میشوند.
$$v = v_{0}+ at \ x = x_{0} + v_{0}t+frac{1}{2}at^{2} \ v^2 = v_0^2 + 2a(x-x_0)$$
سقوط آزاد
تا اینجا در مورد حرکت جسم بر خط راست در راستای محور $$x$$ صحبت کردیم. جسم میتواند در راستای محور عمودی، y، نیز حرکت کند. هنگامیکه توپی را به سمت پایین رها میکنیم یا سنگی را به سمت بالا میاندازیم، حرکت جسم در راستای محور عمودی است. توپ، پس از رها شدن به سمت زمین حرکت میکند. همچنین، سنگ نیز پس از پرتاب شدن به سمت بالا، تا ارتفاع مشخصی بالا میرود و پس از توقف کامل و تغییر مسیر به سمت زمین برمیگردد. آیا میدانید چه عاملی توپ و سنگ را به سمت زمین برمیگرداند؟ پاسخ نیروی جاذبه زمین است. نیروی جاذبه در جهت عمود بر اجسام وارد میشود. در حرکتِ سقوط آزاد باید به چند نکته توجه داشته باشیم:
- سقوط آزاد جسم به سمت زمین را حرکت با شتاب ثابت در نظر میگیریم.
- در غیاب مقاومت هوا، همه اجسام با هر اندازه و وزنی با شتاب یکسانی سقوط خواهند کرد. در بیشتر مسائل مربوط به سقوط آزاد از مقاومت هوا چشمپوشی میشود.
- شتاب جاذبه با ارتفاع تغییر میکند. اما در فاصلههای بسیار کوچکتر از شعاع زمین، مقدار آن را ثابت در نظر میگیریم.

شتاب جاذبه زمین با g نشان داده میشود و مقدار آن برابر ۹/۸ متر بر مجذور ثانیه است. در بیشتر مسائل مربوط به سقوط آزاد، مقدار g را ۱۰ در نظر میگیریم. جهت g نیز همواره به سمت مرکز زمین است. اگر جسمی از ارتفاع مشخصی رها شود، معادلات حرکت آن به صورت زیر نوشته میشوند:
$$v = -gt \ y = – frac { 1 } { 2 } g t ^ 2 + y _ 0 \ v ^ 2 = – 2 g ( y – y _ 0 ) $$
سه معادله فوق مشابه معادلات حرکت با شتاب ثابت بر خط راست در راستای محور $$ x $$ هستند، با این تفاوت که اندازه a در حرکت با سقوط آزاد همواره برابر g و جهت آن به سمت مرکز زمین است. همچنین، به این نکته توجه داشته باشید که عبارت «رها شدن» در سقوط آزاد به معنای صفر بودن سرعت اولیه جسم خواهد بود.
تا اینجا با انواع نمودارهای حرکت و معادلات حرکت با سرعت ثابت و حرکت با شتاب ثابت آشنا شدیم. در ادامه، با ترکیب نمودارها و معادلاتِ حرکت، مثالهایی را با یکدیگر حل میکنیم.
حل مثال های کاربردی فرمول های فیزیک دوازدهم فصل اول
پس از آشنایی با مفاهیم اصلی و فرمول های فیزیک دوازدهم فصل اول، در این بخش مثالهای متنوعی را با یکدیگر حل میکنیم.
مثال اول
نمودار مکان زمان دو جسم A و B به صورت زیر داده شدهاند. حرکت این دو جسم را با یکدیگر مقایسه کنید.
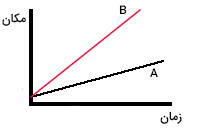
پاسخ
با توجه به توضیحات ارائه شده، شیب نمودار مکان زمان، برابر سرعت حرکت جسم است. نمودارهای مکان زمان دو جسم A و B دو خط مستقیم با شیب ثابت و مثبت هستند. در نتیجه، هر دو جسم با سرعتهای مثبت و ثابت حرکت میکنند. اما شیب خط B بزرگتر از شیب خط A است، بنابراین جسم B با سرعت بیشتری نسبت به جسم A حرکت میکند. به این نکته توجه داشته باشید که در حل مسائل مربوط به حرکت روی خط راست، جهتی را (به طور معمول جهت راست یا بالا) به عنوان جهت مثبت انتخاب میکنیم. اگر جسم در جهت مثبت حرکت کند، سرعت آن مثبت، در غیر این صورت، سرعت آن منفی است.
مثال دوم
نمودار مکان زمان دو جسم A و B به صورت زیر داده شدهاند. حرکت این دو جسم را با یکدیگر مقایسه کنید.
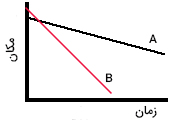
پاسخ
شیب نمودار مکان زمان، برابر سرعت حرکت جسم است. نمودارهای مکان زمان دو جسم A و B دو خط مستقیم با شیب ثابت و منفی هستند. از اینرو، دو جسم با سرعتهای منفی و ثابت حرکت میکنند. اما شیب خط B بزرگتر از شیب خط A است، بنابراین جسم B با سرعت بیشتری نسبت به جسم A حرکت میکند. سرعتِ منفی به معنای حرکت در خلاف جهت مثبت است. به عنوان مثال، اگر جهت راست را به عنوان جهت مثبت انتخاب کنیم، دو جسم به سمت چپ در حال حرکت هستند.
مثال سوم
نمودار مکان زمان دو جسم A و B به صورت زیر داده شدهاند. حرکت این دو جسم را با یکدیگر مقایسه کنید.
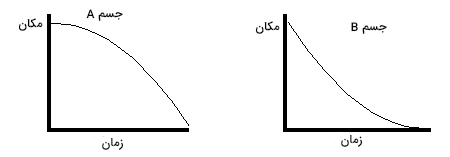
پاسخ
در مثالهای اول و دوم، نمودار مکان زمان، خطی مستقیم با شیب ثابت بود، اما در این مثال، نمودار مکان زمان منحنی است. شیب خطِ مماس بر هر یک از این نمودارها از نقطهای به نقطه دیگر تغییر میکند. برای آنکه بدانیم تغییرات سرعت چگونه است، سه نقطه دلخواه را روی نمودار، انتخاب و خط مماس بر آنها را رسم میکنیم. با مقایسه تغییرات شیب خطهای مماس رسم شده، به راحتی میتوانیم تغییرات سرعت را بهدست آوریم. برای شروع، مراحل زیر را به ترتیب طی میکنیم:
- انتخاب سه نقطه دلخواه روی مکان زمان جسم A
- رسم خط مماس بر هر نقطه روی منحنی
- مقایسه شیب خطهای مماس
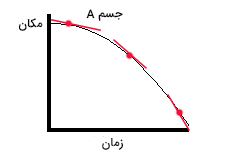
شیب، خطهای مماس رسم شده در سه نقطه، منفی و مقدار آنها در جهت منفی افزایش مییابد. بنابراین، جسم A در جهت منفی حرکت میکند و سرعت آن با گذشت زمان افزایش مییابد. برای جسم B نیز همین روش را انتخاب میکنیم. سه نقطه روی نمودار مکان زمان این جسم، انتخاب و پس از رسم خط مماس بر هم نقطه، شیبِ آنها را با یکدیگر مقایسه میکنیم.
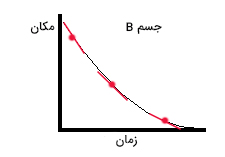
شیب، خطهای مماس رسم شده در سه نقطه، منفی و مقدار آنها در جهت منفی کاهش مییابد. بنابراین، جسم B در جهت منفی حرکت میکند و سرعت آن با گذشت زمان کاهش خواهد یافت.
مثال چهارم
هواپیمایی با سرعت ۱۲۰ کیلومتر بر ساعت از زمین بلند میشود. هواپیما قبل از بلند شدن از زمین باید ۲۴۰ متر روی باند فرودگاه حرکت کند. مقدار شتاب حرکت و مقدار زمان لازم برای آنکه هواپیما از زمین بلند شود را بهدست آورید.

پاسخ
در حل مثالهای مربوط به حرکت با شتاب ثابت، ابتدا معادلات مربوط به این حرکت را مینویسیم:
$$x = x_ 0 + v_ 0 t + frac { 1 } { 2 } a t ^ 2 \ v = v_ 0 + a t \ v ^ 2 = v_0 ^ 2 + 2 a ( x – x_ 0 )$$
در حل بیشتر مسائل مربوط به حرکت، مبدا مکان را صفر انتخاب میکنیم، مگر آنکه مبدا مکان در مسئله داده شده باشد. در این مثال نیز مبدا مکان یا نقطه شروع حرکت هواپیما را صفر در نظر میگیریم، بنابراین مقدار $$x_ 0 $$ برابر صفر است. از آنجا که یکای اندازهگیری سرعت در سیستم SI برابر متر بر ثانیه است، ۱۲۰ کیلومتر بر ساعت را به صورت زیر به متر بر ثانیه تبدیل میکنیم:
$$1 km = 1000 m , enspace 1 h = 3600 s $$
با استفاده از دو رابطه فوق، به راحتی میتوانیم تندی ۱۲۰ کیلومتر بر ساعت را به متر بر ثانیه تبدیل کنیم:
$$72 frac { km } { h } = 120 times frac { { 1000 } } { { 3600 } } frac { m } { s } = 120 times frac { 10} { 36 } frac { m } { s } = 120 times frac { 5 } { 18 } frac{ m } { s } = 33.3 frac { m } { s } $$
هواپیما قبل از بلند شدن، مسافت ۲۴۰ متر را روی باند فرودگاه طی کرده است. همچنین، سرعت اولیه و سرعت هواپیما به هنگام بلند شدن از سطح زمین به ترتیب برابر صفر و ۳۳٫۳ متر بر ثانیه است. از آنجا که زمان حرکت هواپیما داده نشده است، برای یافتن شتاب حرکت باید از معادله مستقل از زمان استفاده کنیم:
$$v ^ 2 = v_0 ^ 2 + 2 a ( x – x_ 0 ) \ ( 33.3 ) ^ 2 = 0 + 2 times 240 times 4 \ 1108.89 = 480 a \ a = frac { 1108.89 } { 480 } = 2.3 frac { m } { s ^ 2 } $$
در ادامه، مدت زمان حرکت هواپیما روی باند فرودگاه و قبل از پرواز را بهدست میآوریم. برای انجام این کار باید از معادلهای استفاده کنیم که برحسب زمان نوشته شده است.
$$v = at + v_ 0 \ 33.3 = 2.3 times t + 0 \ t = frac { 33.3 } { 2.3 } = 14.5 s $$
مثال پنجم
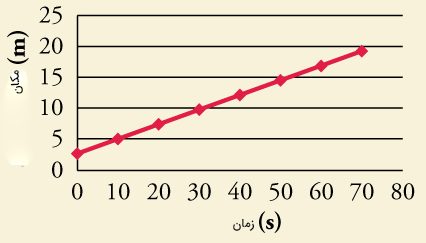
با توجه به نمودار مکان زمان نشان داده شده در تصویر زیر، سرعت متوسط جسم در طول حرکت چه مقدار است؟
۰٫۲۵ متر بر ثانیه
۰٫۳۱ متر بر ثانیه
۳٫۲ متر بر ثانیه
۴٫۰۰ متر بر ثانیه
نمودار مکان زمان در این مثال، خطی مستقیم با شیب ثابت است. اگر نمودار مکان زمان جسمی خطی مستقیم با شیب ثابت باشد، جسم به صورت یکنواخت با سرعت ثابت روی خط مستقیم حرکت میکند. در حرکت یکنواخت با سرعت ثابت، سرعت لحظهای و متوسط با یکدیگر برابر هستند. برای بهدست آوردن سرعت متوسط از روی نمودار مکان زمان، دو نقطه را روی نمودار انتخاب میکنیم و شیب خطِ گذرنده از آنها را بهدست میآوریم:
$$overline { v } = frac { triangle x } {triangle t } = frac { x_ 2 – x_ 1 } { t _2 – t_1 } = frac { 10 – 5 } { 30 – 10 } = frac { 5 } { 20 } \ overline { v } = frac { 1 } { 4 } = 0.25 frac { m } { s } $$
مثال ششم
نمودار مکان زمان جسمی به صورت نشان داده شده در تصویر زیر است. سرعت متوسط جسم در بازه زمانی ۱۵ تا ۲۰ ثانیه کدام است؟
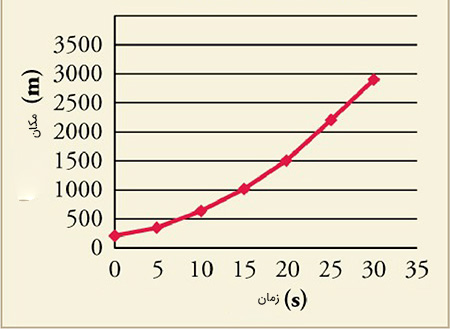
۱۰۰ متر بر ثانیه
۱۵۰ متر بر ثانیه
۵۰ متر بر ثانیه
۲۰ متر بر ثانیه
نمودار مکان زمان در این مثال، منحنی است که شیبِ خط مماس بر آن با گذشت زمان تغییر میکند. برای توصیف حرکت جسم، مراحل زیر را به ترتیب طی میکنیم:
- انتحاب سه نقطه دلخواه روی مکان زمان جسم
- رسم خط مماس بر هر نقطه روی منحنی
- مقایسه شیب خطهای مماس
شیب، خطهای مماس رسم شده در سه نقطه، مثبت و مقدار آنها در جهت مثبت افزایش مییابد. بنابراین، جسم در جهت مثبت حرکت میکند و سرعت آن با گذشت زمان افزایش مییابد. برای بهدست آوردن سرعت متوسط بین زمانهای ۱۵ تا ۲۰ ثانیه، شیب خط گذرنده از دو نقطه $$(15, 1000)$$ و $$(20 , 1500)$$ را بهدست میآوریم:
$$overline { v } = frac { triangle x } {triangle t } = frac { x_ 2 – x_ 1 } { t _2 – t_1 } = frac { 1500 – 1000 } { 20 – 15 } = frac { 500 } { 5 } \ overline { v } = 100 frac { m } { s } $$
مثال هفتم
نمودار مکان زمان جسمی به صورت نشان داده شده در تصویر زیر است. این جسم در لحظه ۱۰ ثانیه در چه فاصلهای از مبدا قرار دارد؟
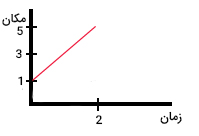
شیب نمودار مکان زمان، برابر سرعت حرکت جسم است. نمودار مکان زمان جسم خطی مستقیم با شیب ثابت و مثبت هستند. در نتیجه، جسم با سرعت مثبت و ثابت حرکت میکنند. برای آنکه بدانیم جسم ۱۲ ثانیه پس از حرکت در چه فاصله از مبدا قرار دارد، باید معادله مکان زمان آن را بنویسیم. معادله مکان زمان جسم در حرکت یکنواخت و با سرعت ثابت به صورت زیر نوشته میشود:
$$x = v t + x_0 $$
با توجه به نمودار مکان زمان، جسم در زمان صفر در فاصله یک متری از مبدا قرار دارد. بنابراین، مقدار $$x_0 $$ برابر یک متر است. در ادامه، برای نوشتن معادله سرعت حرکت جسم را بهدست میآوریم. از آنجا که جسم با سرعت ثابت حرکت میکند، مقدار سرعت متوسط و لحظهای آن با یکدیگر برابر هستند. جسم در آغاز حرکت در یک متری مبدا و ۲ ثانیه پس از شروع حرکت به ۵ متری مبدا میرسد. بنابراین، سرعت متوسط آن برابر است با:
$$overline { v } = frac { triangle x } {triangle t } = frac { x_ 2 – x_ 1 } { t _2 – t_1 } = frac { 5 – 1 } { 2 – 0 } = frac { 4 } { 2 } \ overline { v } = 2 frac { m } { s } $$
در نتیجه، معادله مکان زمان جسم به صورت زیر نوشته میشود:
$$x = 2 t + 1 $$
۱۰ ثانیه پس از شروع حرکت، جسم در فاصله ۲۱ متری مبدا قرار دارد.
مثال هشتم
اتومبیلی با سرعت ۳۶ متر بر ثانیه در حال حرکت در اتوبان است. راننده با مشاهده خروجی، سرعت اتومبیل را در مدت زمان ۳ ثانیه به ۱۵ متر بر ثانیه کاهش میدهد. جابجایی اتومبیل در این مدت زمان چه مقدار است؟

در این مثال، سرعت حرکت اتومبیل در مدت ۳ ثانیه از ۳۶ متر بر ثانیه به ۱۵ متر بر ثانیه کاهش یافته است. بنابراین، نوع حرکت، حرکت غیریکنواخت با شتاب ثابت است. در حل مثالهای مربوط به حرکت با شتاب ثابت، ابتدا معادلات مربوط به این حرکت را مینویسیم:
$$x = x_ 0 + v_ 0 t + frac { 1 } { 2 } a t ^ 2 \ v = v_ 0 + a t \ v ^ 2 = v_0 ^ 2 + 2 a ( x – x_ 0 )$$
در حل بیشتر مسائل مربوط به حرکت، مبدا مکان را صفر انتخاب میکنیم، مگر آنکه مبدا مکان در مسئله داده شده باشد. در این مثال نیز مبدا مکان یا نقطه شروع حرکت اتومبیل را صفر در نظر میگیریم، همچنین، سرعت اولیه برابر ۳۶ متر بر ثانیه و سرعت نهایی برابر ۱۵ متر بر ثانیه داده شده است. کاهش سرعت در طول زمان به معنای، حرکت شتابدار با شتاب منفی است. برای بهدست آوردن جابجایی اتومبیل در مدت ۳ ثانیه، ابتدا مقدار شتاب حرکت را بهدست میآوریم:
$$v = v_ 0 + a t \ 15 = 36 + 3 a \ -21 = 3a \ a = – 7 frac { m } { s } $$
با داشتن شتاب، به راحتی میتوانیم جابجایی اتومبیل را بهدست آوریم:
$$ x = x_ 0 + v_0 t + frac { 1 } { 2 } a t ^ 2 \ x = 0 + 36 times 3 + frac { 1 } { 2 } ( -7 ) ( 3 ) ^ 2 \ x = 108- 31.5 = 76.5 m $$
مثال نهم
راننده اتومبیلی برای فرار از ترافیکِ اتوبان، وارد کندروی ۲۰۰ متری کنار اتوبان میشود. او با سرعت ۱۰ متر بر ثانیه وارد کندرو میشود و به دلیل نبود ترافیک سرعت خود را با شتاب ۲ متر بر مجذور ثانیه افزایش میدهد. راننده در چه مدت زمانی از این کندرو خارج میشود؟
برای حل این مثال، ابتدا آن را به صورت تصویری رسم میکنیم. اتومبیل از اتوبان خارج و با سرعت اولیه ۱۰ متر بر ثانیه وارد کندرو میشود و با شتاب ۲ متر بر مجذور ثانیه به حرکت خود ادامه میدهد. ابتدای کندرو را مبدا مکان، $$x_0 $$، و انتهای آن را $$x $$ در نظر میگیریم.
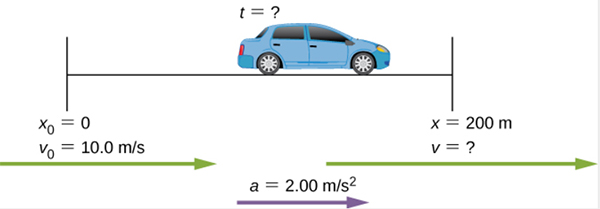
مقدارهای داده شده در این مثال عبارت هستند از:
- سرعت اولیه
- مکان اولیه
- مکان نهایی
- شتاب حرکت
با توجه به مقدارهای داده شده باید زمان را بهدست آوریم. از چه معادلهای میتوانیم استفاده کنیم؟ به معادلات حرکت با شتاب ثابت توجه کنید:
$$x = x_ 0 + v_ 0 t + frac { 1 } { 2 } a t ^ 2 \ v = v_ 0 + a t \ v ^ 2 = v_0 ^ 2 + 2 a ( x – x_ 0 )$$
از آنجا که میخواهیم زمان را بهدست آوریم، از معادله $$v ^ 2 = v_0 ^ 2 + 2 a ( x – x_ 0 )$$ استفاده نمیکنیم، زیرا این معادله مستقل از زمان است و مقدار سرعت نهایی را نیز نداریم. از معادله $$v= v_0 + at $$ نیز به علت نداشتن مقدار سرعت نهایی نمیتوانیم استفاده کنیم. در نتیجه، از معادله $$x = x_ 0 + v_ 0 t + frac { 1 } { 2 } a t ^ 2$$ برای محاسبه زمان استفاده میکنیم:
$$x = x_ 0 + v_ 0 t + frac { 1 } { 2 } a t ^ 2 \ 200 = 0 + 10 t + frac { 1 } { 2 } ( 2 ) t ^ 2 \ 200 = 10t + t ^ 2 \ t ^ 2 + 10 t -200 = 0 $$
برای محاسبه t باید معادله درجه دوم بهدست آمده را حل کنیم. برای این کار معادله بهدست آمده را با استفاده از اتحاد جمله مشترک، تجزیه و ریشهها را بهدست میآوریم:
$$( t + 20 ) ( t – 10 ) = 0 \ t _ 1 = 10 s \ t_ 2 = -20 s $$
از آنجا که زمانِ منفی معنایی ندارد، بنابراین ۲۰- غیرقابلقبول است و اتومبیل پس از ۱۰ ثانیه از کندرو خارج میشود.
مثال دهم
فضاپیمایی با خروج از مدار زمین، به سمت ماه شروع به حرکت میکند. این فضاپیما با شتاب ۲۰ متر بر مجذور ثانیه در مدت ۲ دقیقه، ۱۰۰۰ کیلومتر جابجا میشود. سرعتهای اولیه و نهایی فضاپیما چه مقدار است؟
سرعت اولیه و نهایی به ترتیب برابر ۷۱۳۳/۳ و ۸۵۳۳/۳ متر بر ثانیه است.
سرعت اولیه و نهایی به ترتیب برابر ۷۱۳۳/۳ و ۹۵۳۳/۳ متر بر ثانیه است.
سرعت اولیه و نهایی به ترتیب برابر ۶۱۳۳/۳ و ۷۱۳۳/۳ متر بر ثانیه است.
سرعت اولیه و نهایی به ترتیب برابر ۵۱۳۳/۳ و ۷۵۳۳/۳ متر بر ثانیه است.
در این مثال میخواهیم سرعت اولیه و نهایی فضاپیما را پیدا کنیم. بار دیگر به معادلات حرکت با سرعت ثابت نگاه میکنیم:
$$x = x_ 0 + v_ 0 t + frac { 1 } { 2 } a t ^ 2 \ v = v_ 0 + a t \ v ^ 2 = v_0 ^ 2 + 2 a ( x – x_ 0 )$$
مقدار $$ x_0 $$ برابر صفر و مقدار $$x $$ برابر ۱۰۰۰ متر است. برای بهدست آوردن سرعت اولیه از معادله $$x = x_ 0 + v_ 0 t + frac { 1 } { 2 } a t ^ 2 $$ استفاده میکنیم.
$$x = x_ 0 + v_ 0 t + frac { 1 } { 2 } a t ^ 2 \ 1000000= 0 + v_ 0 times 120 + frac { 1 } { 2 } times 20 times ( 120 )^ 2 \ \ v_ 0 = 7133.3 frac { m } { s }$$
با داشتن سرعت اولیه و معادله $$v= v_ 0 + at $$ به راحتی میتوانیم سرعت نهایی را نیز بهدست آوریم:
$$v = v_0 + at = 7133.3 + 20 times 120 = 9533.3 frac { m } { s } $$
به این نکته توجه داشته باشید که برای حل این مثال زمان را به ثانیه و مسافت را به متر تبدیل کردیم.
مثال یازدهم
دوچرخهسواری برای دوچرخهسواری به دل طبیعت میرود و سه مسیر را با جهتهای یکسان (به سمت شمال) به صورت زیر طی میکند:
- ابتدا به مدت ۲۸ دقیقه با تندی متوسط ۷٫۲ متر بر ثانیه حرکت میکند.
- در ادامه با تغییر تندی متوسط، به مدت ۳۶ دقیقه با تندی متوسط ۴٫۸ متر بر ثانیه به حرکت خود ادامه میدهد.
- در پایان، به مدت ۹ دقیقه با تندی متوسط ۱۳ متر بر ثانیه حرکت میکند و برای استراحت متوقف میشود.
مسافت کل طی شده توسط دوچرخهسوار و سرعت متوسط او در تمام مسیر کدام است؟
مسافت کل طی شده توسط دوچرخهسوار برابر ۲۹٫۴۸۴ کیلومتر و سرعت متوسط او برابر ۴٫۷۳ متر بر ثانیه است.
مسافت کل طی شده توسط دوچرخهسوار برابر ۱۹٫۴۸۴ کیلومتر و سرعت متوسط او برابر ۶٫۷۳ متر بر ثانیه است.
مسافت کل طی شده توسط دوچرخهسوار برابر ۲۹٫۴۸۴ کیلومتر و سرعت متوسط او برابر ۶٫۷۳ متر بر ثانیه است.
مسافت کل طی شده توسط دوچرخهسوار برابر ۲۹٫۴۸۴ کیلومتر و سرعت متوسط او برابر ۲٫۷۳ متر بر ثانیه است.
دوچرخهسوار بدون تغییر جهت به سمت شمال حرکت میکند. مسیر کل او به سه مسیر کوچکتر تقسیم میشود که هر مسیر را با تندی متوسط متفاوتی طی کرده است. برای بهدست آوردن مسافت کل، مسافت طی شده در هر مسیر را بهدست میآوریم و با جمع مسافتهای طی شده در هر مسیر، مسافت کل را محاسبه میکنیم.
مسیر ۱
دوچرخه سوار در شروع حرکت با تندی متوسط ۷٫۲ متر بر ثانیه به مدت ۲۸ دقیقه حرکت میکند. برای بهدست آوردن مسافت طی شده در این مدت از فرمول تندی متوسط استفاده میکنیم. تندی متوسط از تقسیم مسافت بر مدت زمان لازم برای طی کردن این مسافت بهدست میآید:
$$overline { s } = frac { total distance } { total time } \ overline {s } = frac { D } { t } \ 7.2 = frac { D } { ( 28 times 60) } \ D = 7.2 times 60 times 28 = 12096 m = 12.096 km $$
برای محاسبه مسافت، زمان از دقیقه به ثانیه تبدیل شده است.
مسیر ۲
دوچرخه سوار در ادامه حرکت با تندی متوسط ۴٫۸ متر بر ثانیه به مدت ۳۶ دقیقه به حرکت خود ادامه میدهد. مسافت طی شده در این مسیر برابر است با:
$$overline {s } = frac { D } { t } \ 9 = frac { D } { ( 36 times 60) } \ D = 4.8 times 60 times 36 = 10368 m = 10.368 km $$
مسیر ۳
دوچرخه سوار در پایان حرکت با تندی متوسط ۱۳ متر بر ثانیه به مدت ۹ دقیقه به حرکت خود ادامه میدهد. مسافت طی شده در این مسیر برابر است با:
$$overline {s } = frac { D } { t } \ 13 = frac { D } { ( 9 times 60) } \ D = 13 times 60 times 9 = 7020 m = 7.020 km $$
مسافت کل از جمع مسافتهای سه مسیر بهدست میآید:
$$D_ { total } = 7.20 + 10.368+ 12.096 = 29.484 km $$
در ادامه، سرعت متوسط را بهدست میآوریم. برای محاسبه سرعت متوسط، جابجایی را بر زمان صرف شده برای انجام جابجایی تقسیم میکنیم. در این مثال، مسیر حرکت دوچرخهسوار تغییر نکرده است. بنابراین، مسافت و جابجایی با یکدیگر برابر هستند. همچنین، زمان کل حرکت برابر ۷۳ دقیقه یا ۴۳۸۰ ثانیه است.
$$overline { v } = frac { triangle x } {triangle t } = frac { (29.484 times 1000 } { 4380 s } \ overline { v } = 6.73 frac { m } {s } $$
مثال دوازدهم
موتورسواری در مسابقه موتورسواری شامل دو بخش، شرکت کرده است. در بخش اول، موتورسوار از حالت سکون شروع به حرکت میکند و با شتاب ۲٫۶ متر بر مجذور ثانیه به اندازه ۱۲۰ متر جابجا میشود. پس از اتمام بخش اول، بخش دوم بلافاصله شروع میشود. در این بخش، موتورسوار سرعت خود را با شتاب ۱٫۵- متر بر مجذور ثانیه به مقدار ۱۲ متر بر ثانیه کاهش میدهد. جابجایی موتورسوار در بخش دوم چه مقدار است؟

موتورسوار در بخش اول مسیر مسابقه از حالت سکون شروع به حرکت میکند و با شتاب ۲٫۶ متر بر مجذور ثانیه به اندازه ۱۲۰ متر جابجا میشود. سپس، با ورود به بخش دوم مسابقه، سرعت خود را با شتاب ۱٫۵- متر بر مجذور ثانیه به مقدار ۱۲ متر بر ثانیه کاهش میدهد. جابجایی موتورسوار در بخش دوم را میخواهیم. موتورسوار در بخشهای یک و دو با شتاب ثابت حرکت میکند. معادلات حرکت شتاب ثابت عبارت هستند از:
$$x = x_ 0 + v_ 0 t + frac { 1 } { 2 } a t ^ 2 \ v = v_ 0 + a t \ v ^ 2 = v_0 ^ 2 + 2 a ( x – x_ 0 )$$
اطلاعات داده شده برای بخش اول مسابقه عبارت هستند از:
$$v_0 = 0 frac { m } { s } \ triangle x = x – x_ 0 = 120 m \ a = 2.6 frac { m } { s ^ 2 } $$
با استفاده از معادلات بالا میتوانم سرعت نهایی موتور را در انتهای بخش اول بهدست آوریم. برای این کار از معادله مستقل از زمان استفاده میکنیم.
$$v ^ 2 = v_0 ^ 2 + 2 a ( x – x_ 0 ) \ v ^ 2 = 0 + 2 times 2.6 times 120 = 624 \ v = sqrt { 624 } = 24.98 frac { m } { s } $$
بنابراین، موتورسوار با سرعت ۲۴٫۹۸ متر بر ثانیه وارد بخش دوم مسابقه میشود. او در این بخش سرعت خود را با شتاب ۱٫۲- متر بر مجذور ثانیه به ۱۲ متر بر ثانیه کاهش میدهد. برای محاسبه جابجایی در بخش دوم، باز هم از معادله حرکت مستقل از زمان استفاده میکنیم:
$$v ^ 2 = v_0 ^ 2 + 2 a ( x – x_ 0 ) \ (12) ^ 2 = (24.98)^ 2 -2 times 1.5 times triangle x \ 144 = 624 – 3 triangle x \ 3 triangle x = 624 -144 \ triangle x = 160 m $$
مثال سیزدهم
اتوبوسی با تندی ثابت ۲۵ متر بر ثانیه حرکت میکند. اتومبیلی پشت سر اتوبوس و در فاصله ۶۰ متری از آن با سرعت اولیه ۱۲ متر بر ثانیه در حال حرکت است. ناگهان راننده اتومبیل به یاد میآورد که قرار ملاقات مهمی دارد. در نتیجه، سرعت خود را با شتاب ۴٫۲ متر بر مجذور ثانیه افزایش میدهد. پس از چه مدت زمان، اتومبیل از اتوبوس سبقت میگیرد؟

اتومبیل به اتوبوس نمیرسد.
در این مثال دو نوع حرکت یکنواخت با سرعت ثابت و حرکت غیریکنواخت با شتاب ثابت داریم. اتوبوسی با سرعت ثابت ۲۵ متر بر ثانیه حرکت میکند. در همین لحظه اتومبیلی که ۶۰ متر عقبتر از اتوبوس قرار دارد و با سرعت اولیه ۱۲ متر بر ثانیه حرکت میکند، سرعت خود را با شتاب ۴٫۲ متر بر مجذور ثانیه افزایش میدهد. تصویر زیر موقعیت اتوبوس و اتومبیل را نسبت به یکدیگر و لحظه شتاب گرفتن اتومبیل نشان میدهد.
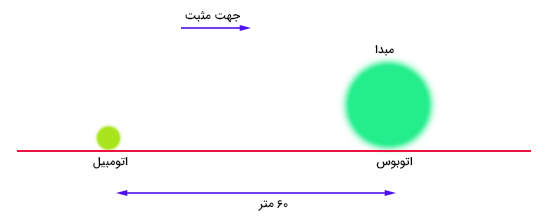
مکان اتوبوس را به عنوان مبدا مکان انتخاب میکنیم. بنابراین، معادله حرکت اتوبوس به صورت زیر نوشته میشود:
$$x= vt + x_ 0 \ x = 25 t $$
سرعت اولیه اتومبیل برابر ۱۲ متر بر ثانیه، مکان اولیه برابر ۶۰- متر و شتاب حرکت آن برابر ۴٫۲ متر بر ثانیه است. در نتیجه معادله حرکت آن به صورت زیر نوشته میشود:
$$x = x_0 + v_0 t + frac { 1 } { 2 } a t ^ 2 \ x = -60 + 12 t + 2.1 t ^ 2 $$
زمان سبقت گرفتن اتومبیل از اتوبوس را میخواهیم بهدست آوریم. اتومبیل برای سبقت گرفتن ابتدا باید به اتوبوس برسد. در لحظه رسیدن اتومبیل به اتوبوس، مکان آنها، $$x$$، یکسان میشود:
$$25 t = -60 + 12 t + 2.1 t ^ 2 \ 2.1 t ^ 2 -13 t – 60 = 0 \ t_1 , t _ 2 = frac { 13 pmsqrt{ (-13) ^ 2 – 4 (2.1)( – 60 ) }} { 2 times (2.1)} \ t_ 1 = 9.3 s , t_ 2 = – 3.07 s $$
از آنجا که زمان منفی معنایی ندارد، بنابراین اتومبیل ۹٫۳ ثانیه پس از شتاب گرفتن به اتوبوس میرسد و از آن سبقت میگیرد.
مثال چهاردهم
نمودار سرعت زمان جسمی به صورت نشان داده شده در تصویر زیر است. کدام یک از گزینههای زیر در مورد شتاب حرکت درست است؟
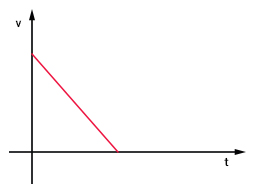
شتاب حرکت مثبت و ثابت است.
شتاب حرکت مثبت و افزایشی است.
شتاب حرکت منفی و کاهشی است.
شتاب حرکت منفی و ثابت است.
همانطور که در توضیحات این بخش گفتیم، شیب نمودار سرعت زمان به ما شتاب حرکت را میدهد. اگر نمودار سرعت زمان، خطی مستقیم با شیبِ ثابت باشد، شتاب حرکت نیز ثابت خواهد بود. در این مثال، نمودار سرعت زمان، خطی مستقیم با شیب ثابت و منفی است. بنابراین، شتاب حرکت نیز منفی و ثابت خواهد بود.
مثال پانزدهم
شخصی توپی را به صورت عمودی با سرعت اولیه مثبت به بالا پرتاب میکند. کدام یک از گزینههای زیر علامت سرعت و شتاب را در ارتفاع بیشینه به درستی توصیف میکند؟
سرعت و شتاب در ارتفاع بیشینه، مثبت هستند.
سرعت و شتاب در ارتفاع بیشینه برابر صفر هستند.
سرعت در ارتفاع بیشینه برابر صفر و شتاب منفی است.
سرعت در ارتفاع بیشینه، مثبت و شتاب، منفی است.
این مثال مربوط به سقوط آزاد است. هر جسمی پس از پرتاب شدن به سمت بالا، تا ارتفاع مشخصی بالا میرود و پس از توقف کامل و تغییر مسیر به سمت زمین برمیگردد. در سقوط آزاد، به طور معمول جهت مثبت را به سمت بالا انتخاب میکنیم. از آنجا که شتاب جاذبه زمین همواره به سمت پایین و مرکز زمین است، علامت آن منفی و اندازه آن در تمام طول حرکت مخالف صفر خواهد بود. اما جهت و اندازه سرعت در پرتاب جسم به سمت بالا، در طول مسیر تغییر میکند. به هنگام پرتاب جسم به سمت بالا، بردار سرعت نیز به سمت بالا و مثبت است. اندازه سرعت با نزدیک شدن به ارتفاع بیشینه، کاهش و در ارتفاع بیشینه برابر صفر میشود.
پس از تغییر مسیر جسم و حرکت آن به سمت پایین، جهت بردار سرعت به سمت پایین و مقدار آن منفی است. بنابراین، با توجه به توضیحات ارائه شده، در ارتفاع بیشینه، مقدار سرعت برابر صفر و بردار شتاب برابر g و علامت آن منفی است.
مثال شانزدهم
توپی از بالای صخرهای به سمت پایین رها میشود. پس از t ثانیه از لحظه پرتاب، سرعت نهایی توپ به $$v$$ میرسد و به اندازه d متر جابجا شده است. اگر زمان آزمایش دو برابر یعنی برابر 2t شود، مقدار سرعت نهایی کدام است؟

معادلات حرکت در سقوط آزاد به صورت زیر نوشته میشوند:
$$v = -gt \ y = – frac { 1 } { 2 } g t ^ 2 + y _ 0 \ v ^ 2 = – 2 g ( y – y _ 0 ) $$
در این مثال، زمان سقوط، سرعت اولیه، سرعت نهایی و جابجایی داده شده است. بار اول، سرعت توپ پس از رها شدن از صخره در مدت زمان t به مقدار نهایی $$v$$ میرسد. همچنین، توپ در این مدت زمان به اندازه d جابجا شده است. حال میخواهیم با فرض دو برابر شدن مدت زمان آزمایش، سرعت نهایی توپ را بهدست آوریم. محل پرتاب شدن توپ را به عنوان مبدا و جهت پایین را به عنوان جهت مثبت انتخاب میکنیم. بنابراین، علامت g در معالات بالا و علامت جابجایی، مثبت خواهند بود. برای بهدست آوردن سرعت نهایی از معادله $$v = gt $$ استفاده میکنیم. سرعت نهایی بار اول به صورت زیر بهدست میآید:
$$v_1 = g t_1 \ v = g t $$
سرعت نهایی در آزمایش دوم نیز به صورت زیر بهدست میآید:
$$v_ 2 = g t_ 2 \ v_ 2 = 2 g t = 2 v $$
در نتیجه با دو برابر شدن زمان، سرعت نهایی نیز دو برابر میشود.
چگونه از فرمول های فیزیک دوازدهم در حل مسئله استفاده کنیم؟
توانایی حل مسئله، به خصوص مسائل فیزیک، از اهمیت بالایی برخوردار است. در مطالب «فرمول های فیزیک دهم» و «فرمول های فیزیک یازدهم» از مجله فرادرس، فرمولهای فیزیک دهم و یازدهم را به همراه حل مساله بیان کردیم. در این مطلب نیز در رابطه با فرمول های فیزیک دوازدهم در مبحثهای حرکت بر خط راست، امواج، حرکت دایرهای، برهمکنشهای موج، آشنایی با فیزیک اتمی و هستهای به صورت خلاصه صحبت میکنیم. توجه به این نکته مهم است که برای موفقیت در امتحان نهایی فیزیک دوازدهم و حل مسائل مختلف آن، باید مفاهیم بنیادی مانند حرکت یکنواخت، حرکت غیریکنواخت، قوانین حرکت نیوتن، حرکت دایرهای، موج، برهمکنش امواج با یکدیگر، مدلهای اتمی و هسته اتم را به خوبی فرا گرفته باشید. از اینرو، تماشای فیلمهای آموزشی، مانند فیلمهای آموزشی تهیه شده در فرادرس، میتواند به شما برای رسیدن به این نقطه کمک فراوانی کند.
در حالت کلی برای حل مسائل فیزیک با استفاده از فرمولهای مرتبط باید مرحلههای زیر را طی کنید:
- ابتدا مسئله داده شده را با دقت مطالعه کنید. پس از خواندن مسئله باید بدانید چه چیزی از شما خواسته شده است.
- پس از خواند مسئله، دادههای معلوم و مجهول را به صورت فهرستوار یادداشت کنید.
- در ادامه، فرمولهای لازم برای حل مسئله را یادداشت کنید.
- مسئلههای فیزیک ممکن است در یک مرحله یا بیش از یک مرحله حل شوند. تشخیص این موضوع به داشتن درک صحیحی از سوال مربوط میشود.
- راهحل را مرتب و گامبهگام پیش ببرید.
- پس از حل مسئله، پاسخ نهایی را برای اطمینان بار دیگر بررسی کنید.
برای آشنایی بهتر با چگونگی حل مسائل مربوط به فرمول های فیزیک دوازدهم میتوانید از فیلم آموزشی زیر استفاده کنید. در این فیلم آموزشی از مجموعه فرادرس با حل سوالات پرتکرار امتحانی، با روند حل مسئلههای مختلف در فیزیک دوازدهم آشنا میشوید.
اگر تسلط کاملی بر مباحث پایه حرکت شناسی، امواج، فیزیک اتمی و هستهای دارید و مسئلههای مرتبط را به خوبی حل میکنید، اما به دنبال یادگیری مبحثها و حل مسئلههای پیشرفتهتر هستید، میتوانید از فیلمهای آموزشی زیر استفاده کنید:
فرمول های فیزیک دوازدهم فصل دوم
در فصل دوم از فیزیک دوازدهم با قوانین حرکت نیوتن، برخی نیروهای خاص، تکانه و قانون دوم نیوتن، حرکت دایرهای یکنواخت و نیروی گرانشی آشنا میشویم. فرمولهای فصل دوم فیزیک دوازدهم در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دهم فصل دوم |
| رابطه نیرو و شتاب در قانون دوم نیوتن | $$overrightarrow { F } _ { net } = m overrightarrow { a } $$ |
| قانون سوم نیوتن | $$overrightarrow { F } _ { 1 2 } = – overrightarrow { F } _ { 2 1 } Rightarrow F _ { 12 } = F _ { 2 1 } $$ |
| نیروی اصطکاک ایستایی بیشینه | $$f_ { s , max } = mu_s F_ N $$ |
| نیروی اصطکاک جنبشی | $$f_ k = mu _ k F_N$$ |
| اندازه نیروی کشسانی فنر | $$F_ s = kx $$ |
| تکانه جسم | $$overrightarrow { p } = m overrightarrow { v } $$ |
| قانون دوم نیوتن برحسب تکانه برای نیروی ثابت | $$overrightarrow { F } _ { net } = frac { triangle overrightarrow { p } }{ triangle t } $$ |
| نیروی خالص متوسط برحسب تکانه | $$overrightarrow { F } _ { a v } = frac { triangle overrightarrow { p }} { triangle t } $$ |
| دوره در حرکت دایرهای یکنواخت | $$T = frac { 2 pi r } { v } $$ |
| اندازه شتاب مرکزگرا | $$a_ c =frac { v ^ 2 } { r } $$ |
| اندازه نیروی مرکزگرا | $$F _ { net } = m frac { v ^ 2 } { r } $$ |
| اندازه نیروی گرانشی بین دو ذره | $$F = G frac { m _ 1 m _ 2 } { r ^ 2 } $$ |
| وزن جسم در سطح زمین | $$W = G frac { H_ e m } { R _ e ^ 2 } $$ |
در ادامه، فرمول های فیزیک دوازدهم فصل دوم نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح میدهیم.
قوانین نیوتن
نیوتن سه قانون معروف دارد:
- قانون اول نیوتن: جسم ساکن، ساکن میماند و جسمی که با سرعت ثابت حرکت میکند، به حرکت خود با سرعت ثابت ادامه میدهد، مگر آنکه نیرویی خارجی بر آن وارد شود. این عبارت، بیانی از قانون اول نیوتن است. قانون اول نیوتن، اینرسی نیز نام دارد. اگر نیروهای خارجی وارد شده بر جسم به گونهای باشند که اثر یکدیگر را خنثی کنند، هیچ تغییر در حالت اولیه جسم به وجود نخواهد آمد.
- قانون دوم نیوتن: شتاب جسم به جرم و مقدار نیروی وارد شده بر جسم وابسته است. در قانون اول نیوتن فرض کردیم که برآیند نیروهای خارجی وارد شده بر جسم برابر صفر است. اما در قانون دوم فرض میکنیم نیروی خالصی برابر F بر جسم وارد میشود. سرعت جسم پس از اعمال نیرو به آن تغییر و شتابی در جهت نیرو پیدا میکند. رابطه نیرو و شتاب به صورت زیر نوشته میشود:
$$overrightarrow { F } = m overrightarrow { a } $$
برطبق رابطه فوق، هرچه نیروی وارد شده بر جسم بزرگتر باشد، شتابِ آن نیز بزرگتر و هرچه جرم جسم بزرگتر باشد، شتاب آن کوچکتر خواهد بود. - قانون سوم نیوتن: دو جسم A و B را در نظر بگیرید. هرگاه جسم A بر جسم B نیرو وارد کند، جسم B نیز نیرویی برابر، اما در جهت مخالف بر جسم A وارد خواهد کرد. قانون سوم نیوتن، قانون عمل و عکسالعمل نیز نام دارد. برای هر عملی (نیرو) در طبیعت، عکسالعملی در جهت مخالف و برابر، وجود خواهد داشت. به بیان دیگر، نیروها نتیجه برهمکنشها هستند. فرض کنید با استفده از چکش، میخی را در چوب فرو میبرید. نیروی وارد شده از طرف چکش بر میخ، سبب فرو رفتن میخ در چوب میشود. همچنین، نیروی وارد شده بر میخ، حرکت چکش را کند میکند. توجه به این نکته مهم است که نیروهای عمل و عکسالعمل همواره به دو جسم وارد میشوند و نوع یکسانی دارند.
معرفی انواع نیروها در فیزیک
نیروهای زیادی در فیزیک وجود دارند. در این بخش، با مهمترین نیروها در فیزیک آشنا میشویم.
نیروی وزن
وزن، W، کلمه دیگری برای نیروی گرانش، $$F_g$$، است. وزن، نیرویی است که همیشه بر اجسام در نزدیکی سطح زمین وارد میشود. جهت نیروی وزن به سمت پایین و مرکز زمین است و با استفاده از رابطه زیر بهدست میآید:
$$overrightarrow { W } = m overrightarrow { g } $$
در رابطه فوق:
- W نیروی وزن است.
- g شتاب جاذبه گرانش و مقدار آن برابر ۹٫۸ متر بر مجذور ثانیه است.
- m جرم جسم است.

نیروی مقاومت شاره
در فصل اول از فیزیک دوازدهم با حرکت سقوط آزاد آشنا شدیم و فرض کردیم به هنگام سقوط جسم، نیروی مقاومت هوا وجود ندارد. اما در واقعیت، این نیرو وجود دارد و در خلاف جهت حرکت جسم بر آن وارد میشود. به عنوان مثال، اگر جسم به سمت پایین سقوط کند، مقاومت هوا به سمت بالا بر آن وارد میشود. این نیرو به اندازه جسم، تندی آن و عاملهای دیگر بستگی دارد.
نیروی عمودی سطح
به طور حتم برای شما پیش آمده است که هنگام راه رفتن به دیوار برخورد کرده و درد زیادی را حس کرده باشید. این درد به دلیل وجود نیرویی به نام نیروی عمودی سطح ایجاد میشود. نیروی عمودی سطح یکی از انواع نیروهای تماسی است و در محاسبه اصطکاک نقش مهمی را ایفا میکند. این نیرو بر سطحِ در تماس عمود است. همانطور که در تصویر زیر مشاهده میکنید نیروی عمودی سطح، به صورت عمود و به طرف بالا بر کتابِ روی میز وارد میشود. این نیرو با نیروی وزن کتاب در تعادل هستند.

نیروی اصطکاک
نیروی اصطکاک یکی از مهمترین انواع نیرو در زندگی روزمره است. این نیرو هنگامی به وجود میآید که دو سطح با یکدیگر در تماس باشند و در خلاف جهت یکدیگر حرکت کنند. اصطکاک از حرکت آسان دو جسم نسبت به یکدیگر جلوگیری میکند. نیروی اصطکاک به دو عامل بستگی دارد:
- نیروی عمودی سطح
- ضریب اصطکاک که به جنس سطوح در تماس بستگی دارد.
در حالت کلی، نیروی اصطکاک به دو نوع اصطکاک جنبشی و ایستایی تقسیم میشود. محاسبه نیروی اصطکاک جنبشی بسیار راحت است. این نیرو با $$f_k$$ نشان داده میشود و با استفاده از رابطه زیر بهدست خواهد آمد:
$$f_k = mu_k N$$
در رابطه فوق، $$N$$ برابر نیروی عمودی سطح و $$mu_k$$ برابر ضریب اصطکاک جنبشی است. نیروی اصطکاک ایستایی کمی با نیروی اصطکاک جنبشی تفاوت دارد. توجه به این نکته مهم است که این نیرو بر جسم ساکن وارد میشود. همچنین، مقدار این نیرو ثابت نیست. به عنوان مثال، جعبه ساکنی روی زمین قرار دارد. برای به حرکت درآوردن جعبه باید به آن نیرویی برابر F وارد کنید. مقدار نیروی اصطکاک ایستایی با توجه به مقدار نیروی F، تغییر میکند. این نیرو در خلاف جهت نیروی F بر جعبه وارد میشود. در نهایت، با افزایش نیروی F و رسیدن آن به مقداری مشخص، جعبه شروع به حرکت خواهد کرد. ادامه حرکت جعبه از به حرکت درآوردن آن آسانتر است. در نتیجه، نیروی اصطکاک جنبشی از بیشینه نیروی اصطکاک ایستایی کمتر خواهد بود. بیشینه مقدار نیروی اصطکاک ایستایی با استفاده از رابطه زیر بهدست میآید:
$$f_{s,max} = mu_s N$$
در رابطه فوق، $$f_{s,max}$$ برابر بیشینه مقدار نیروی اصطکاک ایستایی است.
نیروی کشش طناب
به نیروی وارد شده از طرف طناب بر جسم متصل به آن، نیروی کشش طناب گفته میشود. این نیرو فرمول خاصی ندارد و برای محاسبه مقدار آن از قوانین نیوتن استفاده میکنیم. در ادامه، با حل مثال با چگونگی محاسبه این نیرو آشنا میشویم.
نیروی کشسانی فنر
فنری را در نظر بگیرید که یک انتهای آن به دیوار متصل شده است و به صورت افقی روی میز قرار دارد. جسمی را به آن وصل میکنیم. در حالتی که فنر کشیده یا فشرده نشده باشد، هیچ نیرویی بر جسم وارد نمیشود. حال فرض کنید، فنر به اندازه $$x$$ کشیده یا فشرده میشود. مقدار نیروی وارد شده از طرف فنر بر جسم برابر است با:
$$ F_ e = k x $$
k ثابت فنر نام دارد و به اندازه، شکل و جنس مادهای که فنر از آن ساخته شده است، بستگی دارد.
تکانه و قانون دوم نیوتن
تکانه کمیتی برداری است و از حاصلضرب جرم جسم در سرعت حرکت آن بهدست میآید. همچنین، تکانه همجهت با سرعت است.
$$overrightarrow { p } = m overrightarrow { v } $$
از آنجا که شتاب، برابر تغییرات سرعت نسبت به زمان است، قانون دوم نیوتن برای نیروی ثابتِ F را میتوانیم به صورت زیر بنویسیم:
$$overrightarrow { F } _ { net } = m overrightarrow { a } = m = m frac { v_ 2 – v_ 1 } { t _ 2 – t _ 1 } = frac { triangle overrightarrow { p } } { triangle t } $$
حرکت دایره ای یکنواخت
تا اینجا با معادلات حرکت بر خط راست آشنا شدیم. اما جسم همیشه روی خط راست حرکت نمیکند. گاهی اجسام روی مسیری به شکل دایره حرکت میکنند. به عنوان مثال، زمین روی محوری به شکل دایره به دورِ خورشید میچرخد (مدار واقعی زمین به شکل دایره کامل نیست). فرض کنید جسمی روی مسیری به شکل A قرار دارد و پس از طی کردن محیط دایره به نقطه A میرسد. به مدت زمان لازم برای انجام این کار دوره تناوب گفته میشود و از رابطه زیر بهدست میآید:
$$T = frac { 2 pi r } { v } $$
در رابطه فوق، $$2 pi r $$ محیط دایره و $$v$$ سرعت حرکت جسم است. به این نکته توجه داشته باشید که در حرکت دایرهای یکنواخت، اندازه سرعت جسم ثابت است، اما جهت سرعت، پیوسته تغییر میکند. شتاب به هنگام تغییر اندازه سرعت، جهت آن یا هر دو ایجاد میشود. بنابراین، حرکت دایرهای را میتوانیم حرکتی شتابدار در نظر بگیریم. مقدار این شتاب برابر است با:
$$a_c = frac { v ^ 2 } { 2 } $$
در رابطه فوق، r شعاع دایره و $$v$$ سرعت حرکت جسم روی دایره است. همچنین، نیروی برآیند وارد شده بر جسم در حرکت دایرهای به صورت $$F_ { net } = m frac { v ^ 2 } { r } $$ نوشته میشود.
نیروی گرانشی
دو جسم به جرمهای $$m_1 $$ و $$m_2 $$ را در نظر بگیرید که به فاصله r از یکدیگر قرار گرفتهاند. نیرویی به نام نیروی گرانش بر هر یک از این دو جسم وارد میشود که با حاصلضرب دو جرم رابطه مستقیم و با مربع فاصله آنها، رابطع عکس دارد:
$$F = G frac { m _ 1 m _ 2 } { r ^ 2 } $$
G در رابطه فوق، ثابت گرانش عمومی نام دارد و مقدار آن برابر $$6.67 times 10 ^ { – 11 } frac { N . m ^ 2 } { kg ^ 2 } $$ است.
حل مثال های کاربردی فرمول های فیزیک دوازدهم فصل دوم
در این فصل با قوانین نیوتن، انواع نیروها در فیزیک و حرکت دایرهای آشنا شدیم. در ادامه، با حل چند مثال، چگونگی استفاده از فرمول های فیزیک دوازدهم فصل دوم را در حل مسائل فیزیک با یکدیگر بررسی میکنیم.
حل مثال های مربوط به قوانین نیوتن
با استفاده از قوانین نیوتن میتوانیم مسائل مربوط به حرکت اجسام مختلف را حل و حتی حرکت بسیاری از اجسام را در طبیعت پیشبینی کنیم.
مثال اول
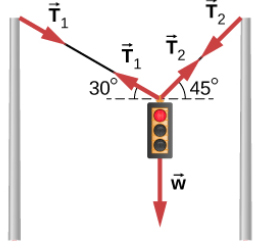
چراغ راهنماییرانندگی به جرم ۱۵ کیلوگرم به صورت نشان داده شده در تصویر زیر توسط دو سیم آویزان شده است. اگر زاویه سیم یک با خط افق، برابر ۳۰ درجه و زاویه سیم دو با خط افق برابر ۴۵ درجه باشد، کشش طناب در هر یک از سیمها برابر است با (از جرم سیمها چشمپوشی شود و مقدار g برابر ۱۰ متر بر مجذور ثانیه فرض شود):
نیروی سیم یک برابر ۱۱۱ و نیروی سیم دو برابر ۱۳۵ نیوتن است.
نیروی سیم یک برابر ۱۳۵ و نیروی سیم دو برابر ۱۱۱ نیوتن است.
نیروی سیم یک برابر ۹۱ و نیروی سیم دو برابر ۱۳۵ نیوتن است.
نیروی کششی سیمهای یک و دو با یکدیگر برابر و مساوی ۱۳۵ نیوتن هستند.
چراغ راهنماییرانندگی توسط دو سیم یک و دو نگه داشته شده است. سه نیرو بر چراغ وارد میشوند:
- نیروی $$T_1 $$ از طرف سیم یک
- نیروی $$T _ 2 $$ از طرف سیم دو
- نیروی وزن
این نیروها در تصویر زیر نشان داده شدهاند.
با توجه به آنکه چراغ راهنماییرانندگی ساکن است، برآیند نیروهای وارد شده بر آن باید برابر صفر باشد. با توجه به صفر بودن برآیند نیروها، به راحتی میتوانیم نیروهای کشش $$T_1 $$ و $$ T _ 2 $$ را بهدست آوریم. نیروهای $$T_1 $$ و $$ T _ 2 $$ را به صورت نشان داده شده در تصویر زیر در راستای محورهای $$x $$ و $$ y $$ تجزیه میکنیم.
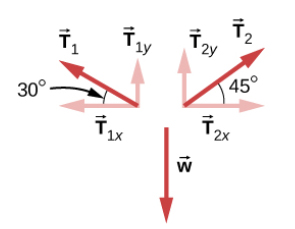
ابتدا نیروهای وارد شده در راستای محور $$x$$ را در نظر میگیریم. دو نیروی $$T_{1x } $$ و $$T _ { 2 x } $$ با یکدیگر برابر هستند:
$$T_ { 1 x } = T_ { 2 x } \ T_ 1 cos 30 = T_ 2 cos 45 \ T_ 1 times frac { sqrt { 3 } } { 2 } = T_ 2 frac { sqrt { 2 } } { 2 } \ sqrt { 3 } T _ 1 = sqrt { 2 } T _2 $$
در ادامه، نیروهای وارد شده در راستای محور $$y$$ را در نظر میگیریم. دو نیروی $$T_{1y } $$ و $$T _ { 2 y } $$ به سمت بالا و نیروی وزن به سمت پایین بر چراغ وارد میشوند. برای آنکه برآیند نیروهای وارد شده بر چراغ در راستای محور y با یکدیگر برابر صفر باشند، مجموع دو نیروی $$T_{1y } $$ و $$T _ { 2 y } $$ باید برابر نیروی وزن باشد:
$$T_ { 1 y } + T_ { 2 y } = W \ T_1 sin 30 + T_ 2 sin 45 = mg \ T_ 1 times frac { 1 } { 2 } + T _ 2 times frac { sqrt { 2 } } { 2 } = 15 times 10 \ T_1 + sqrt { 2 } T_ 2 = 300$$
دو معادله و دو مجهول داریم. بنابراین با کنار هم قرار دادن آنها میتوانی نیروهای کششی سیمهای یک و دو را بهدست آوریم؛
$$sqrt { 3 } T _1 = sqrt { 2 } T _ 2 \ T_ 1 + sqrt { 3 } T _ 1 = 300 \ T_1 + sqrt { 2 } T_ 2 = 300 Rightarrow T_ 1 ( 1 + sqrt { 3 } ) = 300 \ T_ 1 = frac { 300 } { ( 1 + sqrt { 3 } )} \ T_ 1 sim 111 N \ sqrt { 3 } T _ 1 = sqrt { 2 } T _ 2 \ sqrt { 3 } times 111 = sqrt { 2 } T _ 2 \ T_ 2 approx 135 N $$
مثال دوم
مردی به جرم ۷۵ کیلوگرم تصمیم میگیرد وزن خود را با استفاده از ترازو، داخل آسانسور اندازه بگیرد. اگر آسانسور با شتاب ۱٫۲ متر بر مجذور ثانیه به سمت بالا حرکت کند، ترازو چه عددی را نشان میدهد؟ (مقدار g را ۱۰ در نظر بگیرید)
اگر عدد نشان داده شده توسط ترازو در حالت سکون، دقیق باشد، این عدد برابر اندازه نیرویی است که فرد در جهت پایین بر ترازو وارد میکند ($$overrightarrow { F } _ p$$). تصویر زیر نیروهای وارد شده بر آسانسور، ترازو و فرد را نشان میدهد.
- $$overrightarrow { T } $$ نیروی کشش طناب متصل به آسانسور است.
- $$overrightarrow { W} $$ نیروی وزن فرد و به سمت پایین است.
- $$overrightarrow { W} _s $$ نیروی وزن ترازو و به سمت پایین است.
- $$overrightarrow { W} _ e $$ نیروی وزن آسانسور و به سمت پایین است.
- $$overrightarrow { F } _ p$$ نیرویی است که فرد بر ترازو وارد میکند.
- $$overrightarrow { N } $$ نیروی عمودی سطح است.
- $$overrightarrow { F } _ s$$ نیروی وارد شده از طرف ترازو بر فرد است.
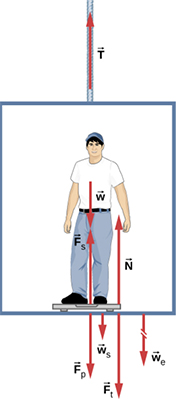
فرد داخل آسانسور، روی ترازو ایستاده است و دو نیروی $$overrightarrow { W} _s $$ به سمت پایین و $$overrightarrow { F } _ s$$ به سمت بالا بر او وارد میشوند. نیروهای $$overrightarrow { F } _ s$$ و $$overrightarrow { F } _ p$$ نیروهای عمل و عکسالعمل یا کنش و واکنش و برطبق قانون سوم نیوتن با یکدیگر برابر، اما در خلاف جهت یکدیگر هستند. بنابراین، برای آنکه بدانیم ترازو چه عددی را نشان میدهد باید مقدار نیروی $$overrightarrow { F } _ s$$ را پیدا کنیم. برای انجام این کار از قانون سوم نیوتن استفاده میکنیم:
$$overrightarrow { F } _ { net } = m overrightarrow { a } $$
تصویر زیر نمودار جسم آزادِ فردِ داخل آسانسور را نشان میدهد.
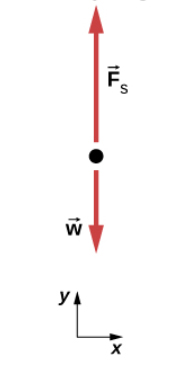
آسانسور با شتاب ۱٫۲ متر بر مجذرو ثانیه به سمت بالا حرکت میکند. بنابراین، جهت بالا را به عنوان جهت مثبت انتخاب میکنیم. نیروی برآیند، $$overrightarrow { F } _ { net} $$ را میتوانیم به صورت زیر بنویسیم:
$$overrightarrow { F } _ { net } = overrightarrow { F } _ s – overrightarrow { w } $$
با قرار دادن رابطه فوق در معادله $$overrightarrow { F } _ { net } = m overrightarrow { a } $$، داریم:
$$F_ s – w = ma \ F_ s = ma + w \ F_ s = ma + mg $$
با قرار دادن مقدارهای داده شده در رابطه بهدست آمده، مقدار $$F_s $$ را بهدست میآوریم:
$$F_ s = ( 75.0 kg ) ( 9.80 frac {m } {s ^ 2 } ) + ( 75.0 kg ) ( 1.20 frac { m } {s ^ 2 } ) = 825 N $$
مثال سوم
ماشین آتوود یکی از مسئلههای مهم در فیزیک است. ماشین آتوود از طنابی تشکیل شده که از روی قرقرهای به صورت نشان داده شده در تصویر زیر رد شده است. دو جسم با جرمهای متفاوت $$m_1 $$ و $$m_2 $$ به دو سر طناب وصل شدهاند. فرض کنید جرمهای $$m_1 $$ و $$m_2 $$ به ترتیب برابر ۲ و ۴ کیلوگرم هستند. اگر جرم $$m_2 $$ رها شود، مقدار شتاب و کشش طناب کدام است؟ (قرقره بدون اصطکاک است و از جرم قرقره و طناب چشمپوشی کنید)
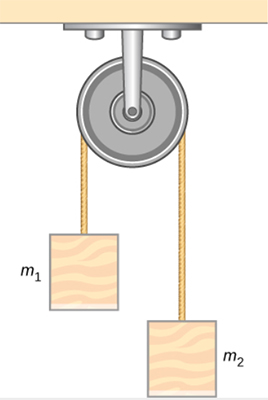
مقدار شتاب برابر ۳٫۲۷ متر بر مجذور ثانیه و مقدار نیرو برابر ۲۶٫۱۴ نیوتن است.
مقدار شتاب برابر ۲٫۳۷ متر بر مجذور ثانیه و مقدار نیرو برابر ۲۶٫۱۴ نیوتن است.
مقدار شتاب برابر ۳٫۲۷ متر بر مجذور ثانیه و مقدار نیرو برابر ۲۴٫۱۴ نیوتن است.
مقدار شتاب برابر ۳٫۲۷ متر بر مجذور ثانیه و مقدار نیرو برابر ۳۶٫۱۴ نیوتن است.
نمودار جسم آزاد و نیروهای وارد شده بر هر یک از جرمها به صورت جداگانه در تصویر زیر نشان داده شدهاند. به این نکته توجه داشته باشید که جرم $$m _ 2 $$ با شتاب $$ a_ 2 $$ به سمت پایین و جرم $$m_1 $$ با شتاب $$ a_ 1 $$ به سمت بالا حرکت میکند. با انتخاب جهت بالا به عنوان جهت مثبت و برابر بودن شتابهای $$ a_ 1 $$ و $$ a _ 2 $$ داریم:
$$a = a_1 = – a_ 2 $$
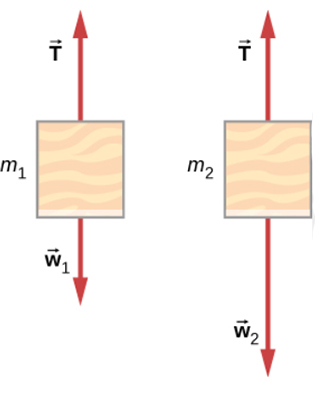
قانون دوم نیوتن را برای جرمهای $$ m _ 1 $$ و $$ m_ 2 $$ استفاده میکنیم:
$$m_1 : enspace T – m_1 g = m_1 a \ m_ 2 : enspace T – m_2 g = – m_ 2 a $$
دو معادله و دو مجهول داریم. ابتدا مقدار شتاب را بهدست میآوریم. برای انجام این کار $$T$$ را از معادلات حذف و معادلهای برای شتاب بهدست میآوریم:
$$m_1 : enspace T – m_1 g = m_1 a \ m_ 2 : enspace T – m_2 g = – m_ 2 a \ T – m_1 g = m_1 a \ -T + m_2 g = + m_ 2 a \ (m_2 – m_ 1 ) g = (m_ 2 + m_ 1 ) a \ a = frac { m_2 – m_1 } { m_ 2 + m_1 } g $$
با قرار دادن مقدارهای $$ m _ 1 $$ و $$m_ 2 $$ در رابطه بهدست آمده، مقدار شتاب را بهدست میآوریم:
$$ a = frac { m_2 – m_1 } { m_ 2 + m_1 } g = frac { 4 – 2 } { 4 + 2 } times (9.8) = frac { 1 } { 3 } times 9.8 = 3.27 frac { m } { s ^ 2 } $$
با قرار دادن شتاب در معادله $$T – m_1 g = m_1 a $$ مقدار $$T$$ را بهدست میآوریم:
$$T – m_1 g = m_1 a \ T = ( 2 times 3.27 ) + ( 2 times 9.8 ) = 26.14 N $$
مثال چهارم
جرم متوسط فردی بزرگسال برابر ۸۶ کیلوگرم است. جرم و وزن این فرد در ماه با شتابی برابر یکششم شتاب زمین چه مقدار است؟ (شتاب جاذبه زمین را برابر ۹٫۸ متر بر مجذور ثانیه در نظر بگیرید)
وزن فرد برابر ۸۶۰ نیوتن و جرم او برابر ۸۶ کیلوگرم است.
وزن فرد برابر ۱۴۰٫۱۸ نیوتن و جرم او برابر ۸۶ کیلوگرم است.
وزن فرد برابر صفر نیوتن و جرم او نیز برابر صفر کیلوگرم است.
قابل محاسبه نیست.
وزن، نیرویی به سمت مرکز سیاره است و با استفاده از رابطه زیر بهدست میآید:
$$W = mg $$
مقدار g در نزدیکی سطح زمین برابر ۹٫۸ متر بر مجذور ثانیه و در نزدیکی سطح ماه، یکششم این مقدار و برابر ۱٫۶۳ متر بر مجذور ثانیه است. با قرار دادن این مقدار در رابطه $$W = mg $$، وزن فرد را روی سطح ماه بهدست میآوریم:
$$W = 86 times 1.63 = 140.18 N $$
نیروی وزن فردی به جرم ۸۶ کیلوگرم را در سطح ماه بهدست آوردیم. سوال مهمی که ممکن است مطرح شود آن است که آیا جرم فرد در سطح ماه نیز برابر ۸۶ کیلوگرم است. بله، جرم به صورت مقدار ماده موجود در جسم تعریف میشود و مقدار آن در همه جای جهان یکسان است. اما وزن، کمیتی برداری است و مقدار آن در نقاط مختلف کیهان با یکدیگر تفاوت دارد.
مثال پنجم
مقدار نیروی موردنیاز برای آنکه اتومبیلی به جرم ۵۴۰ کیلوگرم در مدت ۱۰ ثانیه از حالت سکون به سرعت ۲۷ متر بر ثانیه برسد، چه مقدار است؟
برای حل این مثال باید از معادلات حرکت غیریکنواخت با شتاب ثابت و قانون دوم نیوتن استفاده کنید. برای بهدست آوردن مقدار نیروی موردنیاز، باید شتاب و جرم اتومبیل را داشته باشیم. جرم اتومبیل را داریم، بنابراین تنها کافی است که شتاب را بهدست آوریم. مقدارهای داده شده عبارت هستند از:
- اتومبیل از حالت سکون شروع به حرکت میکند. بنابراین، سرعت اولیه آن برابر صفر است.
- سرعت نهایی اتومبیل برابر ۲۷ متر بر ثانیه است.
- سرعت اتومبیل در مدت ۱۰ ثانیه به ۲۷ متر بر ثانیه میرسد.
با توجه به مقدارهای داده شده، برای بهدست آوردن شتاب از معادله $$v = at + v_ 0 $$ استفاده میکنیم.
$$v = at + v_ 0 \ 27 = a times 10 \ a = 2.7 frac { m } { s ^ 2 } $$
با داشتن شتاب و جرم، به راحتی میتوانیم مقدار نیرو را بهدست آوریم:
$$F = ma \ F = 540 times 2.7 = 1458 N $$
مثال ششم
جسمی به جرم ۱۰ کیلوگرم روی سطح افقی با نیروی افقی ۵۰ نیوتن بهطور یکنواخت (با تندی ثابت) حرکت میکند. اگر بهجای نیروی نیوتونی، به این جسم نیروی افقی نیوتونی وارد کنیم، شتاب آن چند متر بر مجذور ثانیه میشود؟
دو متر بر مجذور ثانیه
یک متر بر مجذور ثانیه
سه متر بر مجذور ثانیه
جسمی روی سطح افقی قرار دارد و نیروی افقی برابر ۵۰ نیوتن بر آن وارد و جسم با تندی ثابت شروع به حرکت میکند. وقتی جسمی ساکن است یا با تندی ثابت روی خط راست حرکت میکند، برآیند نیروهای وارد شده بر آن برابر صفر خواهد بود. نیروی افقی ۵۰ نیوتنی به صورت زیر بر جسم وارد میشود:

پس از اعمال این نیرو، جسم با تندی ثابت شروع به حرکت میکند. حرکت با تندی ثابت به معنای صفر بودن برآیند نیروهای وارد بر جسم است. از آنجا که جسم روی خط راست و افقی حرکت میکند، برآیند نیروهای افقی وارد شده بر آن باید برابر صفر باشد. نیروی F به سمت راست بر جسم وارد میشود. در نتیجه، نیرویی برابر با F باید در خلاف جهت حرکت (به سمت چپ) بر جعبه وارد شود. این نیرو، همان نیروی اصطکاک جنبشی است.

بنابراین، مقدار نیروی اصطکاک جنبشی برابر ۵۰ نیوتن است. در ادامه، نیروی افقی برابر ۶۰ نیوتن بر جسم وارد میشود و جسم با شتاب ثابت شروع به حرکت میکند. دو نیروی ۶۰ نیوتن به سمت راست و اصطکاک جنبشی با مقدار ۵۰ نیوتن به سمت چپ بر جسم وارد میشوند. بر طبق قانون دوم نیوتن، برآیند نیروهای وارد شده بر جسم برابر حاصلضرب جرم جسم در شتاب آن است:
$$F – f_ k – m a \ 60 – 50 = 10 a = 10 = 10 a \ a = 1 frac { m } { s ^ 2 } $$
بنابراین، جسم با شتاب یک متر بر مجذور ثانیه حرکت میکند.
حل مثال های مربوط به انواع نیرو
در این بخش مثالهایی را در رابطه با انواع نیروها در فیزیک با یکدیگر حل میکنیم.
مثال اول
قطعه چوبی به جرم یک کیلوگرم با نیرویی برابر ۱۰ نیوتن روی دیوار نگه داشته شده است. کمینه نیروی عمودی موردنیاز برای آنکه قطعه چوب به سمت بالا حرکت کند چه مقدار است؟ (ضریب اصطکاک ایستایی بین قطعه چوب و دیوار، برابر ۰٫۱۵ و مقدار جاذبه زمین برابر ۱۰ متر بر مجذور ثانیه است)
نیروهای وارد شده بر قطعه چوب در تصویر زیر رسم شدهاند. این نیروها عبارت هستند از:
- نیروی وزن قطعه چوب به سمت پایین
- نیروی اصطکاک ایستایی به سمت پایین و در خلاف جهت حرکت
- کمینه نیروی وارد شده بر چوب برای آنکه به سمت بالا حرکت کند.
- نیروی عمودی سطح وارد شده بر قطعه چوب

توجه به این نکته مهم است که اگر هیچ نیرویی به سمت بالا بر قطعه چوبی وارد نشود، نیروی اصطکاک به سمت بالا بر جسم وارد میشد. زیرا در این صورت نیروی وزن، تنها نیروی وارد شده بر قطعه چوب است که تمایل دارد آن را به سمت پایین حرکت دهد. برای حرکت دادن قطعه چوب به سمت بالا، نیرویی به سمت بالا بر آن وارد میکنیم. برای آنکه قطعه چوبی شروع به حرکت کند، مقدار نیروی وارد شده باید برابر یا بیشتر از مجموع نیروی وزن و اصطکاک ایستایی باشد. مقدار کمینه نیروی وارد شده با استفاده از رابطه زیر بهدست میآید:
$$F_ { min } = mg + f_ { s , max} \ F_ { min } = mg + mu_s N \ F _ { min } = mg + mg mu_S \ F_ { min } = (1 times 10 ) + ( 0.15 times 1 times 10 ) = 10+1.5 = 11.5 N $$
مثال دوم
جعبهای به جرم ۲۰ کیلوگرم روی سطح سیمانی قرار دارد. ضریب اصطکاک ایستایی بین جعبه و سطح برابر ۰٫۲۵ است. مردی نیرویی برابر ۳۵ نیوتن را به صورت افقی به جعبه وارد میکند. اندازه نیروی اصطکاک ایستایی بین جعبه و سطح کدام است؟
برای پاسخ به این سوال باید نیروی اصطکاک ایستایی را به خوبی درک کرده باشید. نکته اصلی در این مثال آن است که نیروی اصطکاک ایستایی بین دو جسم مقداری کمینه و بیشینه دارد. بنابراین این نیرو میتواند هر مقداری بین مقدارهای کمینه و بیشینه را داشته باشد. بیشینه نیروی اصطکاک ایستایی با استفاده از رابطه زیر بهدست میآید:
$$f_ { s, max } = mu_s N $$
در این مثال، نیروی عمودی سطح، N، برابر mg و مقدار آن مساوی ۳۰۰ نیوتن و بیشینه نیروی اصطکاک ایستایی برابر ۵۰ نیوتن است.
مثال سوم
مردی جعبهای به وزن ۵۰ نیوتن را از سطح شیبداری با زاویه ۳۰ درجه نسبت به افق و ارتفاع ۴ متر بالا میبرد. اگر کار انجام شده توسط مرد برابر ۲۷۰ ژول باشد، ضریب اصطکاک سطح شیبدار کدام است؟
باید جرم جعبه را بدانیم.
کار به صورت تغییر انرژی سیستم تعریف میشود. وزن جعبه و جابجایی عمودی آن داده شده است. بنابراین، به راحتی میتوانیم تغییرات انرژی پتانسیل را بهدست آوریم. تغییرات انرژی پتانسیل برابر مقدار کل کارِ موردنیاز برای حرکت جعبه برخلاف جاذبه زمین است:
$$W_ g = triangle PE = mg triangle h \ W_ g = ( 50 N ) ( 4 m ) = 200 J $$
مقدار کار انجام شده برای جابجایی جسم به اندازه ۴ متر در خلاف جاذبه زمین، برابر ۲۰۰ ژول است. اما مرد برای جابجایی جعبه به اندازه ۴ متر، ۲۷۰ ژول کار انجام داده است. ۷۰ ژول کار باقیمانده کجا رفته است؟ مقدار کارِ باقیمانده صرف غلبه بر نیروی اصطکاک بین جعبه و سطح شیبدار شده است.
$$W_ { total } = W_ g + W _ f \ W_ f = 271 J – 200 J = 70 J $$
بنابراین، مقدار کار انجام شده برای غلبه بر نیروی اصطکاک برابر ۷۰ ژول است. در ادامه، مقدار نیروی اصطکاک را بهدست میآوریم. برای انجام این کار به فرمول کار نیاز داریم:
$$W = Fd $$
در رابطه فوق، d مسافت طی شده توسط جعبه روی سطح شیبدار است. برای بهدست آوردن مقدار d از تصویر زیر استفاده میکنیم:
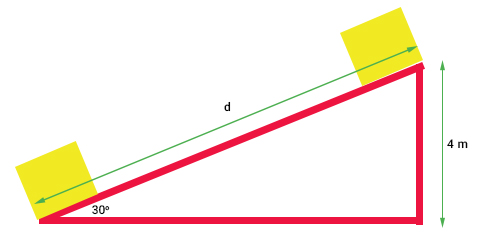
d وتر مثلث قائمالزاویهای با زاویه ۳۰ درجه است. سینوس زاویه ۳۰ درجه به صورت زیر نوشته میشود:
$$sin 30 = frac { 4 } { d m } \ frac { 1 } { 2 } = = frac { 4 m } { d } \ d = 8 m $$
با داشتن d و مقدار کار انجام شده توسط نیروی اصطکاک، به راحتی میتوانیم مقدار این نیرو را بهدست آوریم:
$$W_ f = F_ f times d \ 70 J = F_ f times 8 \ F_ f = frac { 70 J } { 8 m } 8.75 N $$
برای بهدست آوردن ضریب اصطکاک باید نیروی عمودی سطح را نیز بهدست آوریم. برای بهدست آوردن نیروی عمودی سطح، نیروهای وارد شده بر جعبه را رسم و تجزیه میکنیم.
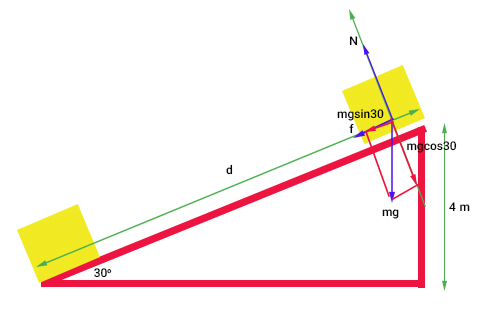
جعبه از روی سطح شیبدار بلند نمیشود، بنابراین برآیند نیروهای وارد بر آن در راستای عمود بر سطح برابر صفر است:
$$N = mg cos 30 \ F_f = N mu = mg cos 30 times mu \ mu = frac { F_f } { mg cos 30 } = frac { 8.75 N } { ( 50 N ) ( 0.866 )} = 0.20 $$
مثال چهارم
جعبهای به جرم ۵ کیلوگرم با سرعت اولیه ۵ متر بر ثانیه روی سطحی حرکت میکند. اگر ضریب اصطکاک ابستایی بین جعبه و سطح، برابر ۰٫۱ باشد، پس از چه مدت زمانی جعبه متوقف میشود؟
جعبهای به جرم ۵ کیلوگرم با سرعت اولیه ۵ متر بر ثانیه روی سطحی حرکت میکند. ضریب اصطکاک ایستایی بین سطح و جعبه برابر ۰٫۱ است. پس از چه مدت زمانی جعبه میایستد. ایستادن جعبه به معنای صفر شدن سرعت نهایی آن است. نیروهای وارد شده بر جعبه در تصویر زیر نشان داده شدهاند:
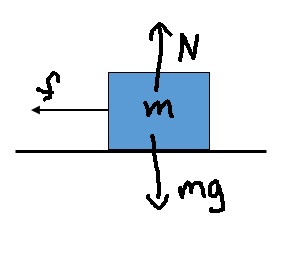
جعبه از روی سطح بلند نمیشود، بنابراین برآیند نیروهای عمودی وارد شده بر آن برابر صفر است:
$$ N = mg $$
همچنین، نیروی اصطکاک، تنها نیروی وارد شده بر جعبه در راستای افقی و به سمت چپ و در خلاف جهت حرکت آن است. با انتخاب جهت راست به عنوان جهت مثبت، سرعت جعبه را مثبت در نظر میگیریم.
$$- f = ma \ f = – ma $$
برای بهدست آوردن مدت زمان توقف جعبه، ابتدا شتاب حرکت آن را بهدست میآوریم:
$$f = mu_k N \ f = 0.1 times 5 times 9.8 = 4.9 N \ f = – m a \ 4.9 = – 5 times 4 \ a = – 0.98 frac { m } { s ^ 2 } $$
شتاب، سرعت اولیه و سرعت نهایی را داریم، بنابراین برای بهدست آوردن شتاب از رابطه $$v = at + v_ 0 $$ استفاده میکنیم:
$$t = frac { v – v_ 0 } { a } \ t = frac { 0 – 5 } { 0.98 } = 5.1 s $$
حل مثال های مربوط به حرکت دایره ای
در این بخش مثالهایی را در رابطه با حرکت دایرهای با یکدیگر حل میکنیم.
مثال اول
سنگی به جرم ۱٫۵ کیلوگرم روی سطح بدون اصطکاکی قرار دارد. این سنگ به طنابی به طول ۸۵ سانتیمتر بسته شده است و روی مسیری به شکل دایره، روی این سطح حرکت میکند. اگر سرعت خطی سنگ برابر ۱٫۸ متر بر ثانیه باشد، نیروی کشش طناب چه مقدار است؟
در حرکت دایرهای یکنواخت، اندازه سرعت جسم ثابت است، اما جهت سرعت، پیوسته تغییر میکند. شتاب به هنگام تغییر اندازه سرعت، جهت آن یا هر دو ایجاد میشود. بنابراین، حرکت دایرهای را میتوانیم حرکتی شتابدار در نظر بگیریم. مقدار این شتاب برابر است با:
$$a_c = frac { v ^ 2 } { 2 } $$
در رابطه فوق، r شعاع دایره و $$v$$ سرعت حرکت جسم روی دایره است. همچنین، نیروی برآیند وارد شده بر جسم در حرکت دایرهای به صورت $$F_ { net } = m frac { v ^ 2 } { r } $$ نوشته میشود. در این مثال، نیروهای کشش طناب، وزن سنگ و نیروی عمودی سطح از طرف میز، تنها نیروهای وارد شده بر سنگ هستند. از آنجا که سنگ از روی میز بلند نمیشود، برآیند نیروهای وارد شده بر آن در راستای عمود برابر صفر هستند. در نتیجه، نیروی کشش طناب، تنها نیرویی است که سبب حرکت دایرهای سنگ میشود و جهت آن به سمت مرکز دایره است.
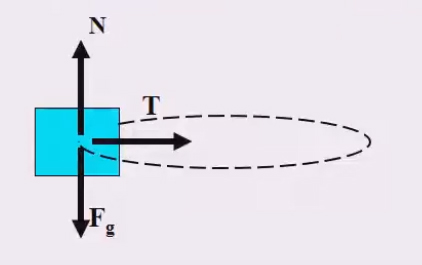
مقدار این نیرو به صورت زیر بهدست میآید:
$$ T = m frac { v ^ 2 } { r } \ T = 1.5 times frac { (1.8) ^ 2 } { 0.85 } = 5.72 N $$
مثال دوم
اتومبیلی باسرعت ۲۴ متر بر ثانیه در جادهای حرکت میکند. اگر ضریب اصطکاک بین چرخهای اتومبیل و جاده، برابر ۰٫۵۳ باشد، کمینه شعاعی که اتومبیل میتواند دور بزند، چه مقدار است؟
مقدارهای داده شده برای محاسبه کمینه شعاع کافی نیستند.
برای حل این مثال، ابتدا نیروهای وارد شده بر اتومبیل را مشخص میکنیم. سه نیروی عمودی سطح، وزن و اصطکاک بر اتومبیل وارد میشوند. سوال مهمی که ممکن است مطرح شود آن است که اگر نیروی اصطکاکِ بین چرخهای اتومبیل و جاده برابر صفر بود، چه اتفاقی رخ میداد؟ اتومبیل روی جاده لیز میخورد و نمیتوانست دور بزند. نیروهای وارد شده بر اتومبیل در تصویر زیر نشان داده شدهاند.
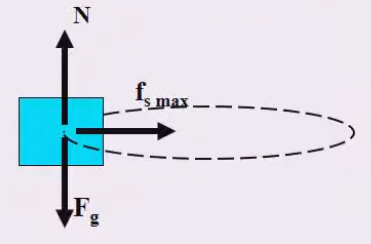
کمینه شعاعی که اتومبیل میتواند دور بزند را میخواهیم بهدست آوریم. در حرکت دایرهای، اندازه سرعت جسم ثابت است، اما جهت سرعت دائما تغییر میکند. شتاب به هنگام تغییر اندازه سرعت، جهت آن یا هر دو ایجاد میشود. بنابراین، حرکت دایرهای را میتوانیم حرکتی شتابدار در نظر بگیریم. مقدار این شتاب برابر است با:
$$a_c = frac { v ^ 2 } { 2 } $$
در رابطه فوق، r شعاع دایره و $$v$$ سرعت حرکت جسم روی دایره است. همچنین، نیروی برآیند وارد شده بر جسم در حرکت دایرهای به صورت $$F_ { net } = m frac { v ^ 2 } { r } $$ نوشته میشود. همانطور که در تصویر فوق مشاهده میکنید، نیروی اصطکاک ایستایی تنها نیرویی است که در راستای شعاع دایره بر اتومبیل وارد و سبب حرکت آن روی مسیری دایرهای میشود.
$$F_ { net } = m frac { v ^ 2 } { r } \ f_ { s, max} = m frac { v ^ 2 } { r } , enspace f_ {s , max } = mu N = mu mg \ mu mg = m frac { v 6 2 } { 2 } \ mu g = frac { v ^ 2 } { r } \ r = frac { v ^ 2 } { mu g } \ r = 110.9 m $$
مثال سوم
آونگی متشکل از سیمی به طول ۱۰ متر و جرمی به جرم ۶۰ کیلوگرم را در نظر بگیرید که از سقف به صورت عمودی آویزان شده است. آونگ را به گونهای حرکت میدهیم که سیم با خط عمودِ گذرنده از محل اتصال سیم زاویه ۵٫۵ درجه بسازد. سپس، جرم را روی مسیری به شکل دایره به صورت نشان داده شده در تصویر زیر به حرکت درمیآوریم. اندازه سرعت حرکت جرم کدام است؟(مقدار g برابر ۱۰ و مقدار سینوس ۵٫۵ درجه برابر ۰٫۰۹۵ است):
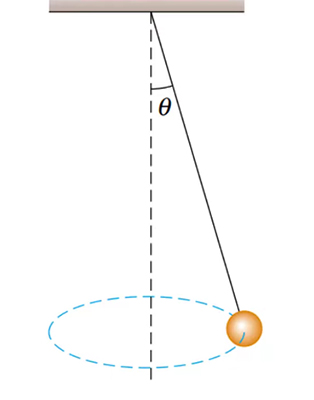
۰٫۹۲ متر بر ثانیه
۰٫۵ متر بر ثانیه
۰٫۷۲ متر بر ثانیه
با مقادیر داده شده نمیتوان سرعت حرکت جسم را بهدست آورد.
ابتدا نیروی وارد شده بر جرم متصل به سیم را رسم میکنیم. دو نیروی کشش سیم و وزن جسم بر آن وارد میشوند.
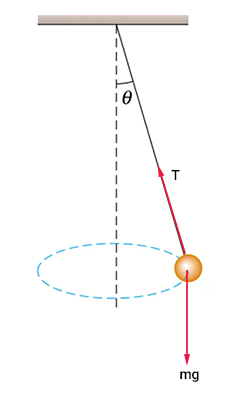
در ادامه، محورهای مختصات $$x$$ و $$y$$ را روی جرم رسم و نیروها را تجزیه میکنیم.
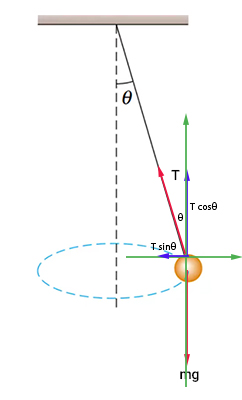
جرم روی دایرهای به شعاع $$10 sin theta $$ حرکت میکند. همانطور که در تصویر بالا مشاهده میکنید،نیروی کشش طناب در راستای محورهای $$ x $$ و $$ y $$ تجزیه شده است:
$$T_ y = T cos theta \ T_ x = T sin theta $$
جسم در راستای محور $$ y $$ حرکت نمیکند، بنابراین برآیند نیروهای وارد شده در این راستا برابر صفر است:
$$T cos theta = mg $$
همچنین، مولفه نیروی کشش سیم در راستای محور $$x$$ تنها نیرویی است که به سمت مرکز دایره بر جسم وارد و سبب حرکت دایرهای آن میشود:
$$T sin theta = m frac { v ^ 2 } { r } $$
برای بهدست آوردن سرعت حرکت جسم در حرکت دایرهای، ابتدا نیروی کشش سیم را بهدست میآوریم:
$$T cos theta = mg \ T = frac { mg } { cos theta } = frac { 60 times 10 } { cos (5.5)} \ T = frac { 600 } { 0.99 } = 602.8 N $$
در ادامه شعاع دایره را نیز بهدست میآوریم:
$$ r = 10 sin theta = 10 sin (5.5 ) = 0.96 m $$
با داشتن شعاع دایره و نیروی کشش سیم، به راحتی میتوانیم سرعت حرکت جسم را بهدست آوریم:
$$T sin theta = m frac { v ^ 2 } { r } \ v = sqrt { frac { ( T sin theta ) r } { m } } \ v = 0.92 frac { m } { s } $$
حل مثال های مربوط به گرانش و رابطه تکانه و قانون دوم نیوتن
در این بخش مثالهایی را در رابطه با نیروی گرانش و رابطه تکانه و قانون دوم نیوتن با یکدیگر حل میکنیم.
مثال اول
توپی به جرم ۰٫۵ کیلوگرم با تندی ۸ متر بر ثانیه به بازیکنی نزدیک میشود. بازیکن با مشت ضربهای به توپ میزند، بنابراین توپ با تندی ۱۲ متر بر ثانیه در جهت مخالف برمیگردد. اگر مشت بازیکن ۰٫۰۲ ثانیه با توپ در تماس باشد، اندازه نیروی متوسط وارد شده بر توپ از طرف مشت بازیکن کدام است؟
تکانه کمیتی برداری است و از حاصلضرب جرم جسم در سرعت حرکت آن بهدست میآید. همچنین، تکانه همجهت با سرعت است.
$$overrightarrow { p } = m overrightarrow { v } $$
از آنجا که شتاب، برابر تغییرات سرعت نسبت به زمان است، قانون دوم نیوتن برای نیروی ثابتِ F را میتوانیم به صورت زیر بنویسیم:
$$overrightarrow { F } _ { net } = m overrightarrow { a } = m frac { v_ 2 – v_ 1 } { t _ 2 – t _ 1 } = frac { triangle overrightarrow { p } } { triangle t } $$
به بیان ساده، تغییرات تکانه نسبت به زمان، به ما اندازه نیروی متوسط را میدهد. در این مثال، جهت راست را به عنوان جهت مثبت انتخاب میکنیم. فرض کنید توپ به جرم ۰٫۵ کیلوگرم از سمت چپ به بازیکنی نزدیک میشود. از آنجا که توپ در خلاف جهت مثبت حرکت میکند، سرعت و در نتیجه تکانه آن منفی هستند.
$$p_ 1 = – m v_1 = – 0.5 times 8 = -4 frac { kg. m } { s } $$
توپ پس از تماسِ۰٫۰۲ ثانیهای با مشت بازیکن، با سرعت ۱۲ متر بر ثانیه، در خلاف جهت مسیر اولیه برمیگردد. تکانه پس از بازگشت برابر است با:
$$p_ 2 = m v_2 = 0.5 times 12 = 6 frac { kg. m } { s } $$
توجه به این نکته مهم است که توپ پس از برخورد با مشت بازیکن، در جهت مثبت (به سمت راست) شروع به حرکت میکند. تغییرات تکانه برابر است با:
$$triangle p= p_2 – p_1 = 6 – ( – 4 ) = 10 frac { kg . m } { s } $$
با تقسیم تغییرات تکانه بر زمان تماس مشت با توپ، نیروی متوسط وارد شده بر توپ را بهدست میآوریم:
$$F_ { average } = frac { triangle p } { triangle t } = frac { 10 } { 0.02 } = 500 N$$
مثال دوم
نیروی گرانشی بین دو جسم A و B برابر ۴ نیوتن است. اگر جرم جسم B نصف شود و جرم جسم A بدون تغییر بماند، نیروی گرانشی بین دو جسم چه مقدار میشود؟
نیروی گرانشی تغییر نمیکند.
دو جسم به جرمهای $$m_A $$ و $$m_B $$ را در نظر بگیرید که به فاصله r از یکدیگر قرار گرفتهاند. نیرویی به نام نیروی گرانش بر هر یک از این دو جسم وارد میشود که با حاصلضرب دو جرم رابطه مستقیم و با مربع فاصله آنها، رابطع عکس دارد:
$$F = G frac { m _ A m _ B } { r ^ 2 } $$
G در رابطه فوق، ثابت گرانش عمومی نام دارد و مقدار آن برابر $$6.67 times 10 ^ { – 11 } frac { N . m ^ 2 } { kg ^ 2 } $$ است. اندازه نیروی گرانشی بین دو جسم قبل از تغییر جرم جسم B برابر ۴ نیوتن است:
$$ 4 = G frac { m _ A m _ B } { r ^ 2 } $$
در ادامه، بدون تغییر فاصله دو جسم و جرم جسم A، جرم جسم B نصف میشود. در این حالت، نیروی گرانشی بین A و B به صورت زیر تغییر میکند:
$$F’ = G frac { m_ A m’_B } { r ^ 2 } \ F’ = G frac { frac { 1 } { 2 } m_ B m_A} { r ^ 2 } = frac { 1 } { 2 } times (G frac { m_ A m_ B } { r ^ 2 } ) \F ‘ = frac { 1 } { 2 } times 4 N = 2 N$$
مثال سوم
وزن جسمی روی سطح زمین برابر ۸۰ نیوتن است. وزن جسم در فاصله $$2R$$ از سطح زمین چه مقدار است؟ (R شعاع زمین است)
اگر جسمی روی زمین یا در فاصله بسیار نزدیک از سطح زمین قرار داشته باشد، نیروی گرانش بین زمین و جسم به صورت زیر نوشته میشود:
$$F = G frac { m M_ e } { R ^ 2 } $$
در رابطه فوق:
- m جرم جسم است.
- $$ M _ e $$ جرم زمین است.
- $$R $$ شعاع زمین است.
با تعریف شتاب جاذبه زمین به صورت $$g = frac { G M_ e } { R ^ 2 } $$ نیروی وزن را میتوانیم به صورت $$W = mg $$ بنویسیم. با افزایش ارتفاع از سطح زمین، شتاب جاذبه و در نتیجه نیروی وزن کاهش مییابند. در این مثال، جسم در ارتفاعی برابر $$2R$$ از سطح زمین قرار میگیرد. مقدار g در این ارتفاع برابر است با:
$$g ‘ = frac { G M _ e } { 2 R } = frac { 1 } { 2 } g $$
بنابراین، شتاب جاذبه زمین در این ارتفاع، نصف میشود. از آنجا که مقدار جرم تغییر نمیکند، وزن جسم نیز در این ارتفاع نصف و برابر ۴۰ نیوتن خواهد شد.
فرمول های فیزیک دهم فصل سوم
فرمول های فیزیک دوازدهم در فصل سوم در مورد موج و نوسان هستند. ابتدا فرمولهای این فصل را به صورت خلاصه بیان، سپس چند مسئله را در این رابطه با یکدیگر حل میکنیم. فرمول های فیزیک دوازدهم فصل سوم در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دهم فصل سوم |
| بسامد یا بسامد | $$f = frac { 1 } { T } $$ |
| معادله مکان زمان در حرکت هماهنگ ساده | $$x ( t ) = A cos omega t $$ |
| بسامد زاویهای | $$omega = frac { 2 pi } { T } = 2 pi f $$ |
| دوره تناوب سیستم جرم و فنر | $$T = 2 pi sqrt { frac { m } { k } } $$ |
| بسامد زاویهای سیستم جرم و فنر | $$omega = sqrt { frac { k } { m } } $$ |
| انرژی مکانیکی سیستم جرم و فنر | $$E = frac { 1 } { 2 } k A ^ 2 $$ |
| انرژی مکانیکی نوسانگر هماهنگ ساده | $$E = 2 pi ^ 2 m A^ 2 f ^ 2 $$ |
| دوره تناوب آونگ ساده | $$T = 2 pi sqrt { frac { L } { g } } $$ |
| تندی انتشار موج | $$v = frac { lambda } { T } = lambda f $$ |
| تندی انتشار موج عرضی در تار یا فنر | $$v = sqrt { frac { F } { mu }} $$ |
| شدت صوت | $$I = frac { P _ { av } } { A } $$ |
| تراز شدت صوت | $$beta = ( 10 dB ) log ( frac { I } { I _ 0 } )$$ |
در ادامه، فرمول های فیزیک دوازدهم فصل سوم نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح میدهیم.
نوسان دوره ای
به انتقال اختلال از مکانی به مکان دیگر در محیط، موج گفته میشود. این انتقال اختلال، بدون انتقال ماده، انرژی را از نقطه اول (منبع) به نقطه دیگر منتقل میکند. هر نقطه در محیطِ انتقالدهنده موج به طور موقت جابجا میشود و سپس به موقعیت تعادلی اصلی خود بازمیگردد. هنگامیکه سیم گیتاری را به حرکت درمیآورید، صدایی ایجاد میشود که برای مدت زمان نسبتا طولانی باقی میماند. مدت زمان هر ارتعاش یا نوسان سیم، برابر مدت زمان ارتعاش قبلی است. دنیای اطراف ما سرشار از نوسان است. نوسانها ممکن است دورهای یا غیردورهای باشند. نوسان دورهای را به صورت تکرار یک حرکت در بازههای زمانی منظم، تعریف میکنیم.
به مدت زمانِ تکرار هر حرکت، دوره تناوب (T) گفته میشود. همچنین، در تعریف نوسان دورهای کمیت دیگری به نام بسامد وجود دارد که به صورت تعداد نوسانها در هر ثانیه تعریف میشود:
$$f = frac { 1 } { T } $$
یکای اندازهگیری بسامد در SI هرتز (Hz) است:
$$1 Hz = 1 frac { 1 } { s } $$
حرکت هماهنگ ساده
به نوسان دورهای که نمودار مکان زمان آن به شکل سینوسی است، حرکت هماهنگ ساده گفته و معادله مکان زمان آن به صورت زیر نوشته میشود:
$$x( t ) = A cos omega t $$
در رابطه فوق:
- A دامنه نوسان است.
- $$omega$$ بسامد زاویهای نام دارد و برابر $$frac { 2 pi } { T } $$ یا $$2 pi f $$ است.
جرم متصل به فنر یکی از معروفترین مثالهای حرکت هماهنگ ساده است. دوره تناوب و بسامد زاویهای سیستم جرم و فنر با استفاده از رابطههای زیر بهدست میآیند:
$$T = 2 pi sqrt { frac { m } { k } } \ omega = sqrt { frac { k } { m } } $$
انرژی در حرکت هماهنگ ساده
جرم متصل به فنری را در نظر بگیرید که حرکتی به صورت حرکت نوسانی هماهنگ ساده انجام میدهد. انرژی مکانیکی این سیستم مقداری ثابت است و با استفاده از رابطه زیر بهدست میآید:
$$E = frac { 1 } { 2 } k A ^ 2 \ E = 2 pi ^ 2 m A ^ 2 f ^ 2 $$
آونگ، جرم کوچکی است که به نخی سبک متصل شده است. در حالت عادی، جرم و نخ متصل به آن به صورت عمودی از نقطهای آویزان شدهاند. اگر جرم را با زاویهای بسیار کوچکی از وضع تعادل رها کنیم، سیستم جرم و نخ میتواند حرکت هماهنگ ساده انجام دهد. دوره تناوب آونگ ساده از رابطه زیر بهدست میآید:
$$ T = 2 pi sqrt { frac { L } { g } } $$
تشدید
اگر جرم متصل به فنر یا جرم متصل به نخ در آونگ ساده، از حالت تعادل خارج و رها شوند، با بسامد یا بسامد مشخصی شروع به نوسان میکنند. به این بسامد، بسامد طبیعی گفته میشود. این نوسانگرها میتوانند با اعمال نیروی خارجی نیز به نوسان درآیند.به چنینی نوسانی، نوسان واداشته میگوییم، زیرا نیرویی خارجی آنها را وادار به نوسان کرده است. در حالت عادی، دامنه نوسان جرم پس از مدتی به دلیل نیروی مقاومت هوا و نیروهای اتلافی دیگر، کوچک و کوچکتر میشود، تا جایی که به صفر برسد. با اعمال نیروی خارجی بر نیروی اتلافی غلبه میکنیم.

اگر دامنه نوسانگر (جرم فنر یا آونگ ساده) پس از اعمال نیرو، بزرگتر شود، دامنه نوسانهای واداشته با بسامد طبیعی نوسانگر برابر شده است. به این حالت تشدید یا رزونانس گفته میشود.
مشخصه های موج
مهمترین مشخصههای امواج عبارت هستند از:
- دامنه: به حداکثر جابجایی ذره محیط از نقطه تعادل، دامنه موج گفته میشود. به بیان دیگر، دامنه فاصله نقطه تعادل از نقاط قله یا فرورفتگی است.
- دوره تناوب: به مدت زمانی که هر ذره در محیط، یک نوسان کامل انجام میدهد، دوره تناوب گفته میشود.
- بسامد: به تعداد نوسانهای ذره محیط در هر ثانیه، بسامد میگوییم.
- تندی انتشار موج: تندی انتشار موج با استفاده از رابطه $$v = frac { lambda } { T } = lambda f$$ بهدست میآید.
موج و انواع آن
امواج به دو دسته کلی تقسیم میشوند.
- امواج عرضی: در موج عرضی، ذرات محیط در امتداد عمود بر جهت حرکت موج منتقل میشوند. امواح سطح آب یا امواج الکترومغناطیسی (مانند نور و امواج رادیویی) امواج عرضی هستند. تندی انتشار موج عرضی در تار یا فنر با استفاده از رابطه زیر بهدست میآید:
$$v = sqrt { frac { F } { mu } } $$
در رابطه فوق، F نیروی کشش و $$mu$$ چگالی خطی است.
- امواج طولی: در موج طولی جابجایی ذرات، موازی با جهت انتشار موج است.
موج الکترومغناطیسی
امواج الکترومغناطیسی میتوانند انرژی را در محیط خلا منتقل کنند. این امواج از طریق نوسان ذرات باردار تولید میشوند.
موج مکانیکی
موج مکانیکی نمیتواند انرژی را در خلا منتقل کند. امواج مکانیکی برای انتقال انرژی از مکانی به مکان دیگر به محیط انتقال نیاز دارند. موج صوتی مثالی از موج مکانیکی است. امواج صوت در محیط خلأ منتقل نمیشوند.
موج صوتی
موج صوتی از نوع امواج طولی است که توسط جسمی مرتعش مانند سیم ویولن، تولید میشود. جسم مرتعش، چشمه صوت نام دارد و صوت ایجاد شده را در تمام جهتها پخش میکند. امواج صوتی با حرکت در محیط، انرژی را از نقطهای به نقطه دیگر منتقل میکنند. تراز و شدت صوت با استفاده از رابطههای زیر بهدست میآیند. در ادامه، با حل چند مثال، چگونگی استفاده از این فرمولها را با یکدیگر بررسی میکنیم.
شدت صوت $$I = frac { P _ { avg }} { A } $$
تراز شدت صوت $$beta = ( 10 db ) log (frac { I } { I + 0 } $$
مثال های حرکت هماهنگ ساده
در این قسمت چند مثال را در رابطه با حرکت هماهنگ ساده با یکدیگر حل میکنیم.
مثال اول
اگر طول نخ آونگی ۴ برابر شود، دوره تناوب آن چگونه تغییر میکند؟
دوره تناوب ۴ برابر میشود.
دوره تناوب $$frac { 1 } { 4 } $$ میشود.
دوره تناوب دو برابر میشود.
دوره تناوب $$frac { 1 } { 2 } $$ میشود.
برای حل این مثال باید به چند نکته توجه داشته باشیم:
- در این مثال در مورد آونگ ساده صحبت میشود. آونگ ساده از نخی بدون جرم تشکیل شده که جرمی کوچک به آن متصل شده است. با انحراف جرم متصل به نخ از حالت تعادل (انحراف با زاویه بسیار کوچک)، آونگ شروع به نوسان میکند. این نوسان را میتوانیم به صورت حرکت هماهنگ ساده در نظر بگیریم.
- دوره تناوب آونگ ساده با استفاده از رابطه زیر بهدست میآید:
$$ T = 2 pi sqrt { frac { L } { g } } $$
در رابطه فوق L طول نخ و g شتاب جاذبه زمین است. نکته جالب آن است که دوره تناوب آونگ ساده به جرم متصل به آن وابسته نیست. در این مثال فرض میشود که طول نخ آونگ ۴ برابر میشود. در این حالت، دوره تناوب آن به صورت زیر تغییر میکند:
$$ T ‘ = 2 pi sqrt { frac { 4 L } { g } } = 2 times 2 pi sqrt { frac { L } { g } } = 2 T $$
بنابراین، با ۴ برابر شدن طول آونگ، دوره تناوب آن نیز دو برابر میشود.
مثال دوم
جسمی به جرم ۰٫۳۵ کیلوگرم به فنر بدون جرمی با ثابت فنر ۷۰ نیوتن بر متر متصل شده است. فنر و جرم متصل به آن به صورت افقی روی سطح بدون اصطکاکی قرار گرفتهاند و نوسان میکنند. اگر دامنه نوسان برابر ۴٫۰ سانتیمتر باشد، مقدار کل انرژی مکانیکی سیستم جرم و فنر کدام است؟
بدون داشتن سرعت نوسان نمیتوانیم انرژی مکانیکی کل را بهدست آوریم.
نوسان سیستم جرم و فنر را نیز میتوانیم به عنوان حرکت هماهنگ ساده در نظر بگیریم. انرژی مکانیکی این سیستم با استفاده از رابطه زیر بهدست میآید:
$$E = frac { 1 } { 2 } k A ^ 2 $$
در رابطه فوق، $$k$$ ثابت فنر و A دامنه نوسان است. در این مثال، مقدارهای ثابت فنر و دامنه نوسان داده شدهاند. با قرار دادن مقدارهای داده شده در رابطه فوق، به راحتی میتوانیم انرژی مکانیکی کل را بهدست آوریم:
$$E = frac { 1 } { 2 } times 70 times ( 0.04 ) ^ 2 = 35 times 16 times 10 ^ { – 4 } = 560 times 10 ^ { -45 } = 0.056 J $$
به این نکته توجه داشته باشید که برای محاسبه انرژی مکانیکی کل، دامنه را از سانتیمتر به متر تبدیل کردیم.
مثال سوم
فنری به صورت عمودی از نقطهای آویزان شده است. جسمی به جرم ۰٫۵ کیلوگرم را به آن وصل میکنیم. پس از اتصال جرم، فنر به اندازه ۰٫۱۲۵ متر کشیده میشود. مقدار ثابت فنر کدام است؟
۴٫۰ نیوتن بر متر
۴۰٫۰ نیوتن بر متر
۰٫۰۶۲۵ نیوتن بر متر
۰٫۲۵۰ نیوتن بر متر
در این مثال، از قانون هوک استفاده میکنیم.
$$F = – k x $$
رابطه فوق را برحسب ثابت فنر مینویسیم:
$$ k = – frac { F } { x } $$
F در این مثال، نیروی وزنِ جسم متصل به فنر است.
$$F = mg = 0.5 times 10 = 5 N $$
فنر قبل از اتصال جرم به آن در حالت تعادل قرار دارد. انتهای فنر را مبدا مکان در نظر میگیریم. پس از اتصال جرم، فنر به اندازه ۰٫۱۲۵ متر کشیده میشود. انتهای فنر در حالت کشیده، پایین مبدا انتخاب شده قرار میگیرد. بنابراین، مقدار کشیدگی فنر را با علامت منفی در نظر میگیریم و در رابطه $$ k = – frac { F } { x } $$ قرار میدهیم.
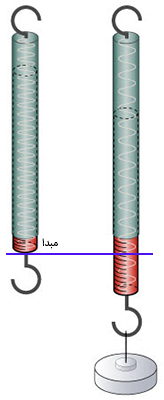
با قرار دادن مقدار F و $$ x $$ در رابطه $$ k = – frac { F } { x } $$، ثایت فنر را بهدست میآوریم:
$$ k = – frac { F } { x } \ k = – frac { 5 N } { – 0.125 m } = 40 frac { N } { m } $$
مثال چهارم
دانشآموزان در کلاس فیزیک در حال انجام آزمایشی در رابطه با حرکت هماهنگ ساده و یادگیری مفاهیم بسامد و دوره تناوب هستند. آنها فنری را به نوسان درمیآورند. این فنر در مدت زمان ۱۸٫۱ ثانیه، ۱۵ سیکل یا چرخه را کامل میکند. دوره تناوب و بسامد فنر برابر هستند با:
دوره تناوب برابر ۱٫۲۱ ثانیه و بسامد برابر ۰٫۸۳ هرتز است.
دوره تناوب برابر ۱٫۴۱ ثانیه و بسامد برابر ۰٫۷۱ هرتز است.
دوره تناوب برابر ۰٫۸۳ ثانیه و بسامد برابر ۱٫۲۱ هرتز است.
دوره تناوب برابر ۲٫۲۱ ثانیه و بسامد برابر ۰٫۴۵ هرتز است.
به مدت زمانِ تکرار هر چرخه یا سیکل، دوره تناوب (T) گفته میشود. به بیان دیگر، دوره تناوب را میتوانیم از تقسیم زمان بر تعداد سیکلهای انجام شده در این زمان بهدست آوریم. در این مثال، فنر تعداد ۱۵ سیکل را در مدت زمان ۱۸٫۱ ثانیه انجام داده است. بنابراین دوره تناوب آن برابر است با:
$$T = frac { 18.1 s } { 15 cyc } = 1.21 س $$
همچنین، در تعریف نوسان دورهای کمیت دیگری به نام بسامد وجود دارد که به صورت تعداد نوسانها در هر ثانیه تعریف میشود:
$$f = frac { 1 } { T } $$
یکای اندازهگیری بسامد در SI هرتز (Hz) است:
$$1 Hz = 1 frac { 1 } { s } $$
با داشتن دوره تناوب، به راحتی میتوانیم بسامد را بهدست آوریم:
$$f = frac { 1 } { 1.21 s } = 0.83 Hz$$
مثال پنجم
جسمی به جرم m مطابق تصویر نشان داده شده در زیر به دو فنر با ثابتهای فنر $$k_1 $$ و $$ k _ 2 $$ وصل شده است و با بسامد زاویهای $$omega $$ نوسان میکند. اگر فنر $$ k _ 2 $$ حذف شود، بسامد زاویهای برابر است با:
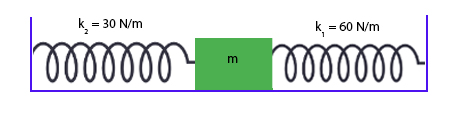
$$sqrt { frac { 3 } { 2 } } omega$$
$$sqrt { frac { 2 } { 3 } } omega$$
$$sqrt { frac { 1 } { 3 } } omega$$
در این مثال، دو فنر با ثابتهای فنر $$k_1 $$ و $$ k _ 2 $$ به صورت موازی به جسمی به جرم m وصل شدهاند. قبل از حل این مثال، فرمولهای محاسبه ثابت فنرِ کل در فنرهای سری و موازی را با یکدیگر مرور میکنیم.
ثابت فنر در فنرهای سری
فنرها ممکن است به صورت سری در کنار یکدیگر قرار گرفته باشند. سری وصل شدن فنرها بدان معنا است که به صورت متوالی و به دنبال یکدیگر قرار گرفتهاند. دو فنر با ثابتهای فنر $$k_1$$ و $$k_2$$ را در نظر میگیریم که به صورت سری به یکدیگر وصل شدهاند. این دو فنر را میتوانیم معادل یک فنر با ثابت فنر موثر K در نظر بگیریم که با استفاده از رابطه زیر بهدست میآید:
$$frac { 1 } { K } = frac { 1 } { k _ 1 } + frac { 1 } { k _ 2 } $$
$$K$$ ثابت فنر موثر دو فنر سری است. اگر بیشتر از دو فنر به صورت سری به یکدیگر متصل شده باشند، ثابت فنر موثر آنها به صورت زیر بهدست میآید:
$$frac { 1 } { K } = frac { 1 } { k _ 1 } + frac { 1 } { k _ 2 } + frac { 1 } { k _ 3 } + … $$
ثابت فنر در فنرهای موازی
فنرها ممکن است به صورت موازی در کنار یکدیگر قرار گرفته باشند. هنگامیکه فنرها به صورت موازی با یکدیگر قرار میگیرند، ثابت فنر معادل آنها از جمع جبری ثابتهای فنرها بهدست میآید. اگر بیشتر از دو فنر به صورت موازی به یکدیگر متصل شده باشند، ثابت فنر موثر آنها به صورت زیر بهدست میآید:
$$K = k_1 + k_2 + k_3 + … $$
از آنجا که دو فنر $$ k _ 1 $$ و $$ k _ 2 $$ به صورت موازی به جرم m بسته شدهاند، ثابت فنر معادل برابر است با:
$$k = k_ 1 + k_ 2 = 30 + 60 = 90 frac { N } { m } $$
در این حالت، بسامد زاویهای برابر است با:
$$ omega = sqrt { frac { k } { m } } = sqrt { frac { 90 } { m } } $$
در ادامه، فنر $$k_2 $$ حذف میشود. در نتیجه بسامد زاویهای به صورت زیر تغییر میکند:
$$ omega’ = sqrt { frac { k_ 1 } { m } } \ omega’ = sqrt { frac { 60 } { m } } \ frac { omega’ } { omega } = sqrt { frac { 60 } { m } times frac { m } { 90 } } = sqrt { frac { 60 } { 90 } } \ frac { omega ‘ } { omega} = sqrt { frac { 2 } { 3 } } $$
مثال ششم
نوسانگر سادهای روی زمین از نقطه $$+ A $$ و در خلاف جهت محور $$x$$ شروع به نوسان میکند. اگر متحرک سه ثانیه پس از شروع حرکت و بدون تغییر جهت به نقطه B برسد، چند ثانیه پس از عبور از نقطه B برای اولین بار به نقطه C میرسد؟
برای حل این مثال، گامهای زیر را به ترتیب طی میکنیم.
گام اول
نوسانگر ۳ ثانیه پس از شروع حرکت به نقطه B که برابر $$0.8 A$$ است، میرسد. فاز نوسانگر را در زمان دو ثانیه بهدست میآوریم. برای انجام این کار ابتدا دایره فازی را رسم و مکان ذره را روی آن مشخص میکنیم.
برای محاسبه زاویه $$phi_1 $$، مقدار $$cos phi_1$$ را بهدست میآوریم:
$$cos phi_1 = frac { 0.8 A } { A} = 0.8 \ phi_1 = 36 enspace degree = frac { pi } { 5 } $$
گام دوم
نوسانگر t ثانیه پس از رسیدن به نقطه B و بدون تغییر جهت به نقطه C میرسد. فاز نوسانگر را در زمان t نیز بهدست میآوریم.
برای محاسبه زاویه $$phi_2 $$، مقدار $$cos phi_2$$ را بهدست میآوریم؛
$$cos phi_2 = frac { 0.6 A } { A} = 0.6 \ phi_1 = 53 enspace degree = frac { 3pi } { 10 } $$
گام سوم
تغییر فاز نوسانگر هنگام رفتن از نقطه B به C برابر است با:
$$triangle phi = phi_2 – phi_1 = frac { 3 pi } { 10 } – frac { pi } { 5 } = frac { 3 pi } { 10 } – frac { 2 pi } { 10 } = frac { pi } { 10 } $$
گام چهارم
زمانی که نوسانگر از B به C میرود را بهدست میآوریم. نوسانگر در مدت ۳ ثانیه از نقطه A به B میرسد. یعنی تغییر فاز نوسانگر در مدت زمان ۳ ثانیه برابر $$frac { pi } { 5 } $$ است. در نتیجه، تغییر فاز $$frac { pi } { 10 } $$ در مدت زمان ۱٫۵ ثانیه اتفاق میدهد.
مثال تشدید
در این قسمت مثالی را در رابطه تشدید با یکدیگر حل میکنیم.
مطابق تصویر زیر چهار فنر با ثابت فنرهای متفاوت از سقف آویزان شدهاند و به هر یک از آنها جسمی با جرم مشخص وصل شده است. اگر سیستم جرم فنر A با بسامد طبیعی خود نوسان کند، پدیده تشدید در کدامیک از سیستمهای جرم فنر مشاهده میشود؟ مشخصات فنرها عبارت هستند از:
- ثابت فنر A برابر ۲۰۰ نیوتن بر متر و جرم متصل به آن برابر ۲ کیلوگرم است.
- ثابت فنر B برابر ۳۰۰ نیوتن بر متر و جرم متصل به آن برابر ۳ کیلوگرم است.
- ثابت فنر C برابر ۱۵۰ نیوتن بر متر و جرم متصل به آن برابر ۲ کیلوگرم است.
- ثابت فنر D برابر ۴۰۰ نیوتن بر متر و جرم متصل به آن برابر ۵ کیلوگرم است.
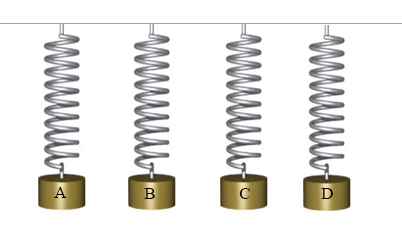
اگر جرم متصل به فنر یا جرم متصل به نخ در آونگ ساده، از حالت تعادل خارج و رها شوند، با بسامد یا فرکانس مشخصی شروع به نوسان میکنند. به این بسامد، بسامد طبیعی گفته میشود. ابتدا بسامد طبیعی سیستم جرم فنر A را بهدست میآوریم. دوره تناوب این سیستم با استفاده از رابطه زیر بهدست میآید:
$$T = 2 pi sqrt { frac { m } { k } }$$
از آنجا که $$f = frac { 1 } { T } $$ بسامد طبیعی نوسانگر A برابر است با:
$$f_A = frac { 1 } { 2 pi } sqrt { frac { k _ A } { m_ A } } $$
ثابت فنر A برابر ۲۰۰ نیوتن بر متر و جرم متصل به آن برابر ۲ کیلوگرم است. در نتیجه، فرکانس آن برابر است با:
$$f_A = frac { 1 } { 2 pi } sqrt { frac { 200 } { 2 } } \ f_A = frac { 1 } { 2 pi } sqrt { 100 } =frac { 1 } { 2 pi } times 10 = frac { 5 } { pi } Hz $$
در ادامه، بسامدهای نوسانگرهای B و C و D را بهدست میآوریم. ثابت فنر B برابر ۳۰۰ نیوتن بر متر و جرم متصل به آن برابر ۳ کیلوگرم است. در نتیجه، فرکانس آن برابر است با:
$$f_A = frac { 1 } { 2 pi } sqrt { frac { 300 } { 3 } } \ f_A = frac { 1 } { 2 pi } sqrt { 100 } =frac { 1 } { 2 pi } times 10 = frac { 5 } { pi } Hz $$
ثابت فنر C برابر ۱۵۰ نیوتن بر متر و جرم متصل به آن برابر ۲ کیلوگرم است. در نتیجه، فرکانس آن برابر است با:
$$f_A = frac { 1 } { 2 pi } sqrt { frac { 150 } { 2 } } \ f_A = frac { 1 } { 2 pi } sqrt { 75 } Hz $$
ثابت فنر D برابر ۴۰۰ نیوتن بر متر و جرم متصل به آن برابر ۵ کیلوگرم است. در نتیجه، فرکانس آن برابر است با:
$$f_A = frac { 1 } { 2 pi } sqrt { frac { 400 } { 5 } } \ f_A = frac { 1 } { 2 pi } sqrt { 80 } Hz $$
بسامد نوسانِ برابر سبب رخ دادن تشدید میشود. بنابراین، این پدیده بین دو نوسانگر A و B رخ میدهد.
مثال های موج، انواع و مشخصه های آن
در این قسمت مثالهایی را در رابطه با انواع موج با یکدیگر حل میکنیم.
مثال اول
تراز شدت موج صوتی با شدت $$4.0 times 10 ^ { -5 } frac { W } { m ^ 2 } $$ کدام است؟
امواج صوتی با حرکت در محیط، انرژی را از نقطهای به نقطه دیگر منتقل میکنند. تراز و شدت صوت با استفاده از رابطههای زیر بهدست میآیند.
شدت صوت $$I = frac { P _ { avg }} { A } $$
تراز شدت صوت $$beta = ( 10 db ) log (frac { I } { I_ 0 } $$
$$I_0 $$ در رابطه فوق شدت مرجع و برابر $$1.00 times 10 ^ { -12 } frac { W } { m ^ 2 } $$ است. برای محاسبه تراز شدت صوت، مقدارهای داده شده را در رابطه $$beta = ( 10 db ) log (frac { I } { I_ 0 }) $$ قرار میدهیم:
$$beta = ( 10 db ) log (frac { 4.0 times 10 ^ { -5 } } { 1.00 times 10 ^ { -12 } } \ beta = 76 dB $$
مثال دوم
اگر تراز صوت در فاصله دو متری از مبدا برابر ۴۰ دسیبل باشد، مقدار آن در فاصله ۴ متری از مبدا کدام است؟
دبیرستانی را فرض کنید که دانشآموزان در ردیفهای مختلف نشستهاند و به سخترانی مدیر گوش میدهند. مدیر با استفاده از بلندگو سخنرانی میکند. بنابراین، بلندگو را در اینجا به عنوان منبع صوت در نظر میگیریم. فاصله ردیف اول از بلندگو برابر ۲ متر و تراز صوت در این نقطه برابر ۴۰ دسیبل است. مقدار تراز صوت در فاصله ۴ متری از بلندگو چه مقدار است؟ شدت صوت با استفاده از دو رابطه زیر بهدست میآید:
$$I = I_ 0 10 ^ { frac { beta } { 10 }} \ I = frac { P } { 4 pi R ^ 2 } $$
$$4 pi R ^ 2 $$ در رابطه فوق سطح مقطع موج کروی خارج شده از منبع صوت است. با استفاده از دو رابطه بالا میتوانیم شعاع کره، R، را به $$ beta $$ مربوط کنیم. ابتدا نسبت شدت صوت در دو فاصله متفاوت از منبع صوت را بهدست میآوریم:
$$frac { I _2 } { I _ 1 } = frac { frac { P } { 4 pi r _ 2 ^ 2 }} { frac { P } { 4 pi r _ 2 ^ 2 }} \ frac { I _ 2 } { I _ 1 } = frac { R _ 1 ^ 2 } { R- 2 ^ 2 } $$
به این نکته توجه داشته باشید که توان در هر فاصلهای از منبع صوت یکسان است، زیرا منبع صوت تغییر نکرده است. رابطه دیگری را نیز میتوانیم برای $$frac { I _ 2 } { I _ 1 } $$ با استفاده از رابطه$$I = I_ 0 10 ^ { frac { beta } { 10 }}$$ بهدست آوریم.
$$frac { I _ 2 } { I _ 1 } = frac { I = I_ 0 10 ^ { frac { beta_2 } { 10 }} } { I = I_ 0 10 ^ { frac { beta_1 } { 10 }} } \ frac { I _ 2 } { I _ 1 } = 10 ^ { frac { beta_2 – beta_1 } { 10 }}$$
دو رابطه برای $$frac { I _ 2 } { I _ 1 } $$ بهدست آوردیم. با برابر قرار دادن آنها داریم:
$$frac { R _ 1 ^ 2 } { R _ 2 ^ 2 } = 10 ^ { frac { beta_2 – beta_1 } { 10 }} $$
از طرفین رابطه فوق $$log$$ میگیریم:
$$log (frac { R _ 1 ^ 2 } { R _ 2 ^ 2 }) = log 10 ^ { frac { beta_2 -beta_1 } { 10 } } \ log (frac { R _ 1 ^ 2 } { R _ 2 ^ 2 }) = frac { beta _ 2 – beta_1 } { 10 } \ 20 log (frac { R _2 } { R _ 1 } ) = beta_2 – beta_1 \ beta_2 = beta_1 + 20 log (frac { R _2 } { R _ 1 } ) beta_ 2 = 40 + 20 log ( frac { 1 } { 2 } ) = 40 – 6.02 = 33.98 db$$
مثال سوم
موجی از محیطی عبور میکند و ذرات محیط را در راستای عمود بر انتشار موج به نوسان درمیآورد. کدام یک از گزینههای زیر در مورد این موج درست است؟
موج عبوری از محیط میتواند موج صوتی باشد.
موج عبوری از محیط میتواند نور مرئی باشد.
این موج میتواند امواج سطحی ایجاد شده در سطح آب باشد.
به صورت سوال دقت کنید. در اثر عبور موج از محیط، ذرات محیط در راستای عمود بر انتشار موج به نوسان درمیآید. به تعریف موج عرضی و طولی دقت کنید. امواج به دو دسته کلی تقسیم میشوند.
- امواج عرضی: در موج عرضی، ذرات محیط در امتداد عمود بر جهت حرکت موج منتقل میشوند. امواح سطح آب یا امواج الکترومغناطیسی (مانند نور و امواج رادیویی) امواج عرضی هستند.
- امواج طولی: در موج طولی جابجایی ذرات، موازی با جهت انتشار موج است.
با توجه به تعریف دو موج عرضی و طولی، موج منتشر شده در محیط از نوع موج عرضی است. گزینه یک، این موج را از نوع موج صوتی میداند که صحیح نیست، زیرا موج صوتی، موجی طولی است. در گزینه ۲ عنوان شده است که این موج از نوع موج رادیویی است. موج رادیوی از نوع موج عرضی است، اما امواج الکترومغناطیسی از میدانهای الکتریکی و مغناطیسی نوسانکننده و نه ذرات، تشکیل شدهاند. نور مرئی نیز نوعی موج الکترومغناطیسی است. بنابراین، گزینه ۴، گزینه صحیح است.
مثال چهارم
امواج عرضی در فنری با نیروی کشش ۶۴ نیوتن، با تندی ۸۰ متر بر ثانیه حرکت میکنند. اگر بخواهیم امواج با تندی ۱۰۰ متر بر ثانیه حرکت کنند، نیروی کشش فنر چه مقدار باید افزایش یابد؟
تندی انتشار موج عرضی در تار یا فنر با استفاده از رابطه زیر بهدست میآید:
$$v = sqrt { frac { F } { mu }} $$
در رابطه فوق، F نیروی کشش و $$mu$$ چگالی خطی است. ابتدا نیروی کشش فنر برابر ۶۴ نیوتن است و امواج با تندی ۸۰ متر بر ثانیه در آن منتشر میشوند. با قرار دادن این دو مقدار در رابطه فوق میتوانیم، چگالی خطی فنر را بهدست آوریم:
$$v = sqrt { frac { F } { mu }} \ v^ 2 = frac { F } { mu } \ mu = frac { F } { v ^ 2 } \ mu = frac { 64 } { 80 times 80 } = 0.01 frac { kg } { m } $$
مقدار $$mu$$ ثابت است. در ادامه، میخواهیم نیروی کشش فنر را تا جایی افزایش دهیم که امواج با تندی ۱۰۰ متر بر ثانیه در آن منتشر شوند. برای بهدست آوردن نیروی کشش فنر، رابطه $$}v = sqrt { frac { F } { mu } $$ را برحسب F مرتب میکنیم:
$$v = sqrt { frac { F } { mu }} \ v^ 2 = frac { F } { mu } \ F = v^ 2 times mu \ F = 10 ^ 4 times 0.01 = 100 N$$
بنابراین، نیروی کشش فنر باید به اندازه ۳۶ نیوتن افزایش یابد.
مثال پنجم
کدام یک از گزینههای زیر صحیح است؟
میدانهای الکتریکی و مغناطیسی همواره در راستای حرکت موج هستند، بنابراین موج الکترومغناطیسی، موجی عرضی است.
میدانها با بسامد متفاوت، اما همگام با یکدیگر تغییر میکنند.
با افزایش بسامد پیشرونده در محیط، طول موج زیاد میشود.
تندی انتشار صوت در محیط به دمای محیط وابسته است.
گزینه ۴ پاسخ صحیح است. در ادامه، هر یک از گزینهها را جداگانه بررسی میکنیم:
- گزینه ۱: موج الکترومغناطیسی، موجی عرضی است و در آن میدانهای الکتریکی و مغناطیسی همواره بر جهت حرکت موج عمود هستند.
- گزینه ۲: میدانهای الکتریکی و مغناطیسی با بسامد یکسان و همگام با یکدیگر تغییر میکنند.
- گزینه ۳: با افزایش بسامد، طول موج کاهش مییابد.
- گزینه ۴: تندی انتشار صوت به جنس محیط و دمای آن بستگی دارد.
مثال ششم
منبع صوتی، صدایی با تراز شدت $$beta_1 $$ برابر ۴۰ دسیبل و منبع صوتی دیگری، صدایی با تراز شدت $$beta_2 $$ برابر ۴۵ دسیبل ایجاد میکند. نسبت شدتهای این دو منبع صوتی ($$frac { I _ 2 } { I _ 1 } $$) برابر است با:
تراز و شدت صوت با استفاده از رابطههای زیر بهدست میآیند.
شدت صوت $$ }I = frac { P _ { avg } { A } $$
تراز شدت صوت $$beta = ( 10 db ) log (frac { I } { I _ 0 } $$
دو چشمه صوت با ترازهای شدت صوت $$beta_1 $$ و $$beta_2 $$ و شدتهای صوت $$ I _ 1 $$ و $$ I _ 2 $$ داریم:
$$beta_1 = ( 10 db ) log (frac { I_1 } { I _ 0 }) \ beta_2 = ( 10 db ) log (frac { I_2 } { I _ 0 }) $$
مقدارهای داده شده را در دو رابطه بالا قرار میدهیم:
$$40 = ( 10 db ) log (frac { I_1 } { I _ 0 }) \ 45 = ( 10 db ) log (frac { I_2 } { I _ 0 }) $$
چگونه نسبت $$frac { I _ 2 } { I _ 1 } $$ را بهدست آوریم؟ برای انجام این کار از ویژگیهای لگاریتم استفاده میکنیم:
$$ log (frac { a } { b } ) = log a – log b \ log ab = log a + log b \ log _ a ^ b = x rightarrow a = b ^ x $$
$$40 = ( 10 db ) log (frac { I_1 } { I _ 0 }) \ 45 = ( 10 db ) log (frac { I_2 } { I _ 0 }) \ 45 – 40 = ( 10 db ) log (frac { I_2 } { I _ 0 }) – ( 10 db ) log (frac { I_1 } { I _ 0 }) \ 5 = 10 ( log ( frac { I _ 2 } { I _ 0 } ) – log ( frac { I _ 1 } { I _ 0 } ) ) \ frac { 1 } { 2 } = log ( frac { frac { I _ 2 } { I _ 0 } } { frac { I _ 1 } { I _ 0 } })= log (frac { I _ 2 } { I _ 1 } ) \ frac { I _ 2 } { I _ 1 } = sqrt { 10 } $$
مثال هفتم
کدام یک از گزینه های زیر نادرست است؟
با افزایش جرم m در سامانه جرم فنر (با فنر یکسان)، نوسانها کند و دوره تناوب افزایش مییابد.
با افزایش طول آونگ، دوره تناوب کاهش مییابد.
موجهای مکانیکی برای انتشار خود به محیط مادی نیاز دارند.
در موجهای پیشرونده، انرژی از نقطهای به نقطه دیگر منتقل میشود.
این مثال، مثالی مفهومی است که برای پاسخ به آن باید مفاهیم فصل سوم فیزیک دوازدهم را به خوبی یاد گرفته باشید. در ادامه، گزینهها را جداگانه با یکدیگر بررسی میکنیم.
گزینه ۱
عبارت «با افزایش جرم m در سامانه جرم فنر (با فنر یکسان)، نوسانها کند و دوره تناوب افزایش مییابد» صحیح است. دوره تناوب سامانه جرم فنر با استفاده از رابطه زیر بهدست میآید:
$$ T = 2 pi sqrt { frac { m } { k } }$$
همانطور که در رابطه فوق مشاهده میکنید، دوره تناوب با جرم رابطه مستقیم دارد. این بدان معنا است که با افزایش جرم، دوره تناوب افزایش و با کاهش جرم، دوره تناوب افزایش مییابد. افزایش T به کند شدن نوسان و کاهش T به معنای تند شدن نوسان است.
گزینه ۲
عبارت «با افزایش طول آونگ، دوره تناوب کاهش مییابد» نادرست است. دوره تناوب آونگ ساده با استفاده از رابطه زیر بهدست میآید:
$$ T = 2 pi sqrt { frac { L } { g }} $$
همانطور که در رابطه فوق مشاهده میکنید، دوره تناوب با طول آونگ رابطه مستقیم دارد. این بدان معنا است که با افزایش طول، دوره تناوب افزایش مییابد.
گزینه ۳
در این گزینه مطرح شده است که موجهای مکانیکی برای انتشار خود به محیط مادی نیاز دارند. این گزینه صحیح است.
گزینه ۴
گزینه ۴ نیز صحیح است و در موجهای پیشرونده، انرژی از نقطهای به نقطه دیگر منتقل میشود.
فرمول های فیزیک دهم فصل چهارم
فرمول های فیزیک دوازدهم در فصل چهارم در مورد برهمکنشهای موج هستند. ابتدا فرمولهای این فصل را به صورت خلاصه بیان، سپس چند مسئله را در این رابطه با یکدیگر حل میکنیم. فرمول های فیزیک دوازدهم فصل چهارم در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دهم فصل چهارم |
| قانون شکست عمومی | $$frac { sin theta _ 2 } { sin theta _ 1 } = frac { v _ 2 } { v _ 1 } $$ |
| ضریب شکست | $$n = frac { c } { v } $$ |
| قانون شکست اسنل | $$n_1 sin theta _ 1 = n_2 sin theta _ 2 $$ |
| طول موجهای تشدیدی تار | $$lambda_n = frac { 2 L } { n } $$ |
| بسامدهای تشدیدی تار | $$f_ n = frac { v } { lambda_ n } = frac { nv } { 2 L } $$ |
در ادامه، فرمول های فیزیک دوازدهم فصل چهارم نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح میدهیم.
بازتاب موج
امواج پس از برخورد به مانع، بازتابیده میشوند. در فصل قبل فهمیدیم امواج به دو دسته کلی امواج الکترومغناطیسی و امواج مکانیکی تقسیم میشوند. در ادامه، بازتاب موج منتشر شده در طناب در دو حالت نشان داده شده است.
بازتاب موج از مانع را میتوانیم با استفاده از جبهههای موج توضیح دهیم. از نموداری با عنوان نمودار پرتویی نیز میتوانیم برای توضیح بازتاب موج از سطح استفاده کنیم. در این نمودار، هر پرتو با پیکانی عمود بر جبهه موج نشان داده میشود. هر پیکان، جهت انتشار موج را نشان میدهد. به تصویر زیر توجه کنید. دو زاویه $$theta_i $$ و $$theta_r$$ در این تصویر نشان داده شدهاند. $$theta_i $$ زاویه فرود یا تابش و $$theta_r$$ زاویه بازتابیده یا بازتابش نام دارند. بر طبق قانون بازتاب عمومی، دو زاویه تابش و بازتابش همواره با یکدیگر برابر هستند. بازتابش نور از سطوح، یکی از بازتابهای معروف در فیزیک است. بازتاب نور ممکن است آینهای (منظم) یا نامنظم باشد.
گاهی امواج به هنگام انتشار ممکن است از محیط یک به محیط دو بروند. آیا میدانید به هنگام عبور موج از محیط یک به محیط دو چه اتفاقی رخ میدهد؟ فرض کنید جبهههای موج تختی با زاویه مشخص به مرز محیطِ یک و دو میرسند. جبهههای موج پس از رسیدن به مرز دو محیط، میشکنند. در این حالت، پرتوهای موج که بر جبهههای موج عمود هستند، تغییر جهت میدهند. همانطور که در تصویر زیر مشاهده میکنید، پرتو فرودی با زاویه $$theta_1 $$ به خط عمود بر مرز میتابد. این زاویه، زاویه تابش نام دارد. پرتو در مرز دو محیط میشکند و با زاویه متفاوت $$ theta_2 $$ (زاویه شکست) وارد محیطِ دوم میشود.
اگر تندی انتشار موج فرودی برابر $$v_1 $$ و تندی انتشار موج شکست یافته برابر $$v_2 $$ باشد، زاویههای فرودی و شکست با تندی انتشار در هر محیط با استفاده از رابطهای به نام قانون شکست عمومی به یکدیگر مربوط میشوند:
$$frac { sin theta_2 } { sin theta_ 1 } = frac { v_ 2 } { v _ 1 } $$
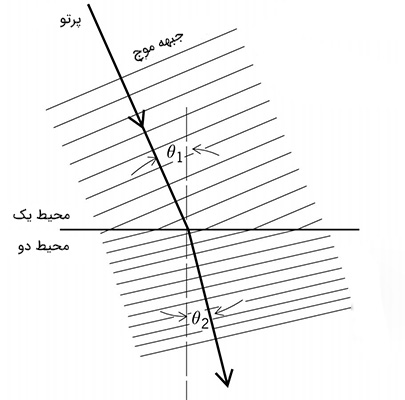
نکته ۱: در صورتی که موج از محیطی با تندی کمتر به محیطی با تندی بیشتر وارد شود، زاویه شکست $$ theta_ 1 $$ بزرگتر از زاویه شکست $$ theta _ 2 $$ است.
نکته ۲: امواج الکترومغناطیسی (مانند نور مرئی) نیز با عبور از محیطی به محیطِ دیگر با تندیهای متفاوت، شکست پیدا میکنند.
نکته ۳: هنگامیکه پرتو نور از محیطی شفاف وارد محیط شفاف دیگری میشود، قسمتی از آن از مرز دو محیط، منعکس میشود و بخشی دیگر، پس از شکست وارد محیط دوم میشود.
برای هر محیط، کمیتی به نام ضریب شکست تعریف میشود که از تقسیم تندی نور در خلا بر تندی نور در محیط، بهدست میآید:
$$ n = frac { c } { v } $$
در رابطه فوق، n ضریب شکست، c تندی نور در خلا و $$v$$ تندی نور در محیط است. با قرار دادن فرمول فوق در رابطه $$frac { sin theta_2 } { sin theta_ 1 } = frac { v_ 2 } { v _ 1 } $$، رابطه قانون شکست عمومی یا قانون اسنل به صورت زیر نوشته میشود:
$$n_ 1 sin theta_ 1 = n_ 2 sin theta _ 1 $$
تداخل امواج
امواج مختلف، مانند امواج صوتی، امواج الکترومغناطیسی و امواج منتشر شده در طنابهای متفاوتِ متصل به هم، با یکدیگر برهمکنش میکنند. به برهمکنش امواج با یکدیگر، تداخل موج میگوییم. طنابی را در نظر بگیرید که یک انتهای آن در نقطهای ثابت است و انتهای دیگر آن را به نوسان درمیآورید. موج پس از انتشار، به نقطه ثابت میرسد و منعکس میشود. این دو موج پس از تداخل یا برهمکنش با یکدیگر، موج برآیندی ایجاد میکنند. پس از تداخل موج تابیده و بازتابیده از یکدیگر و ایجاد موج برآیند، نقاطی از ریسمان ثابت میمانند و هیچ حرکتی انجام نمیدهند. به این نقاط گره میگوییم. همچنین، به وسط دو گره مجاور، شکم گفته میشود. دامنه موج در محل گرهها صفر و در محل شکمها، بیشینه است.
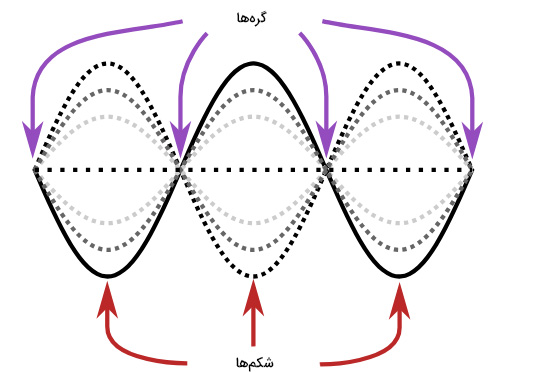
نکته ۴: به نقش موج برآیند، موچ ایستاده گفته میشود، زیرا محل گرهها و شکمهای تغییر نمیکند. تاری با طول L را در نظر بگیرید که در آن موج ایستادهای با n شکم ایجاد شده است. طول تار و طول موج هماهنگ nام با استفاده از رابطه زیر به یکدیگر مربوط میشوند:
$$L = n (frac { lambda_ n } { 2 } \ lambda_n = frac { 2 L } { n } \ f_ n = frac { v } { lambda_ n } = frac { n v } { 2 L } \ n = 1, 2, 3 , …$$
مدهای نوسان با بسامدهای تشدید ($$f_n$$) مشخص میشوند. پایینترین بسامد ($$ n = 1 $$)، بسامد اصلی و مدِ مربوط به آن، مدِ اصلی یا هماهنگ اول نام دارد. به n عدد هماهنگ گفته میشود.
مثال های برهم کنش امواج
تا اینجا با برهمکنش امواج با یکدیگر و فرمولهای مربوط به آنها آشنا شدیم. در ادامه و برای داشتن درک بهتری از این موضوع، چند مثال را با یکدیگر حل میکنیم.
مثال اول
طناب نازکی را در نظر بگیرید که به طناب ضخیمی متصل شده است. در این هنگام موجی در طناب نازک ایجاد و منتشر میشود. به هنگام رسیدن موج به مرز طنابها قسمتی از آن منعکس و قسمت دیگر به طناب ضخیم منتقل میشود. ویژگیهای موج منتقل شده و منعکس شده را با رسم شکل توضیح دهید.
پاسخ
مطابق با تصویر نشان داده شده در ادامه، موج منتقل شده در همان جهت موج فرودی حرکت میکند. ولی موج منعکس شده مانند حالت بازتاب از انتهای ثابت، قرینه شده است. برای امواج بازتابی و انتقالی اتفاقات زیر رخ میدهد.
- موج انتقالی (در محیط با چگالی بیشتر) با سرعت کمتری نسبت به موج بازتابی (در محیط با چگالی کمتر) حرکت میکند.
- موج انتقالی طول موج کوتاهتری نسبت به موج منعکس شده دارد.
- طول موج و سرعت موج منعکس شده با طول موج و سرعت موج فرودی برابر است.
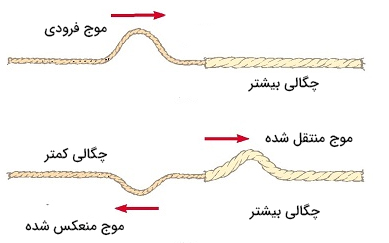
مثال دوم
طناب ضخیمی را در نظر بگیرید که به طناب نازکی متصل شده است. قسمتی از موج ایجاد شده در طناب ضخیم پس از رسیدن به مرز دو طناب، به طناب نازک منتقل میشود و قسمت دیگر از مرز دو طناب منعکس میشود. ویژگیهای موج منتقل شده و منعکس شده را با رسم شکل توضیح دهید.
پاسخ
موج منعکس شده و منتقل شده در تصویر زیر نشان داده شدهاند.
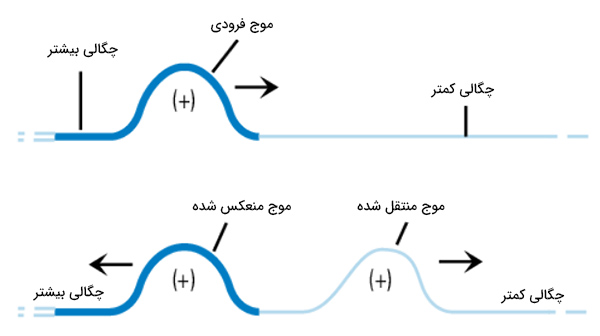
برای امواج بازتابی و انتقالی اتفاقات زیر رخ میدهد.
- موج منعکس شده مانند حالت بازتاب از انتهای آزاد است
- موج انتقال یافته (در محیط با چگالی کمتر) نسبت به موج بازتاب یافته (در محیط با چگالی بیشتر) با سرعت بیشتری حرکت میکند.
- موج انتقال یافته نسبت به موج منعکس شده دارای طول موج بزرگتری است.
- طول موج و سرعت موج بازتاب یافته برابر با طول موج و سرعت موج فرودی است.
نکته: با توجه به توضیحات بالا، رفتار مرزی موجها به صورت زیر خلاصه میشود.
- سرعت موج در محیط با چگالی کمتر، بیشتر است.
- طول موج همواره در محیط با چگالی کمتر، بیشتر است.
- بسامد موج پس از عبور از مرز تغییر نمیکند.
- موج بازتاب یافته به هنگام بازتاب از محیط با چگالی بیشتر قرینه میشود.
- دامنه موج فرودی همواره از دامنه موج بازتاب شده بیشتر است.
مثال سوم
پرتو نوری توسط دو آینه موازی یک و دو در نقطههای A و B منعکس میشود. زاویه انعکاس پرتوی نور در نقطه B چه مقدار است؟
برای حل این مثال، ابتدا قوانین بازتاب از آینه را با یکدیگر مرور میکنیم.
- پرتور نور فرودی، پرتو نور معکس شده و خط عمود بر آینه در صفحهای به نام صفحه برخورد قرار دارند.
- زاویههای تابش و بازتابش با یکدیگر برابر هستند.
برای حل این مثال و مثالهای مشابه، مرحلههای زیر را به ترتیب طی میکنیم.
مرحله اول
پرتو نور ابتدا در نقطه A به آینه یک برخورد میکند. زاویه تابش را نداریم، اما زاویه پرتو با محور تقارن آینهها داده شده است. برای بهدست آوردن زاویه تابش، ابتدا خط عمود بر آینه در نقطه A را به صورت نشان داده شده در تصویر زیر رسم میکنیم. خط $$AA’$$ بر محور تقاون آینهها عمود است.
مرحله دوم
مثلث $$OA’A$$ مثلثی قائمالزاویه است که دو زاویه $$widehat{ A’ }$$ و $$widehat { O } $$ در این مثلث به ترتیب برابر ۹۰ و ۲۵ درجه هستند. بنابراین، به راحتی میتوانیم زاویه $$widehat { A_ 1 } $$ یا زاویه تابش پرتو بر آینه یک را بهدست آوریم:
$$widehat { A_ 1 } + widehat { O } + widehat { A’ } = 180 \ widehat { A_ 1 } = 180 – 90 – 25 = 65 $$
مرحله سوم
از آنجا که زاویه تابش و بازتابش یا یکدیگر برابر هستند، زاویه $$widehat { A_ 2 } $$ نیز برابر ۶۵ درجه است. در ادامه، زاویه تابش در نقطه B را بهدست میآوریم. برای این کار باید زاویه $$widehat { C _ 1 } $$ و $$widehat { C _ 2 } $$ را بهدست آوریم.
مرحله چهارم
مثلث $$AA’C$$ مثلثی قائمالزاویه است که دو زاویه $$widehat{ A’ }$$ و $$widehat { A_2 } $$ در این مثلث به ترتیب برابر ۹۰ و ۶۵ درجه هستند. بنابراین، به راحتی میتوانیم زاویه $$widehat { C _ 1 } $$ را بهدست آوریم:
$$widehat { A _ 2 } + widehat { C_1 } + widehat { A’ } = 180 \ widehat { C _ 1 } = 180 – 90 – 65 = 25 $$
از آنجا که زاویههای $$widehat { C _ 1 } $$ و $$widehat { C _ 2 } $$ متقابل به راس هستند، مقدار زاویه $$ widehat { C _ 2 } $$ نیز برابر ۲۵ درجه است.
مرحله پنجم
برای بهدست آوردن زاویه تابش در نقطه B، ابتدا خط عمود بر آینه دو را در این نقطه، به صورت نشان داده شده در تصویر زیر رسم میکنیم. خط $$BB”$$ بر محور تقاون آینهها عمود است.
مرحله ششم
زاویه تابش $$widehat { B _ 1 } $$ در نقطه B را نیز به صورت مشابه بهدست میآوریم. این زاویه و در نتیجه زاویه بازتابش در نقطه B برابر ۶۵ درجه بهدست میآید.
مثال چهارم
اگر پرتوی فروی A و پرتوی بازتابی B با یکدیگر موازی باشند، زاویه $$alpha$$ چه مقدار است؟
ابتدا زاویههای تابش و بازتابش در هر آینه را مشخص میکنیم.
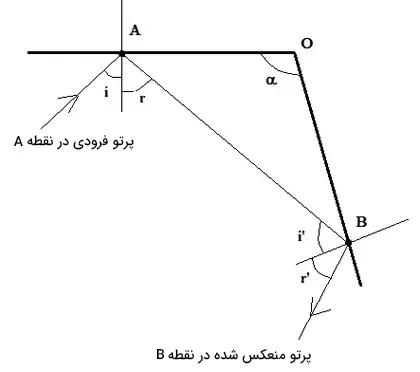
پرتوهای فرودی در نقطه A و منعکس شده در نقطه B با یکدیگر موازی هستند. بنابراین مجموع زاویههای تابش و بازتابش در نقطه A، $$ widehat { i } + widehat { r } $$ با مجموع زاویههای تابش و بازتابش در نقطه A، $$ widehat { i’ } + widehat { r’ } $$ برابر ۱۸۰ درجه است:
$$widehat { i } + widehat { r } + widehat { i ‘ } + widehat { r ‘ } = 180 $$
بر طبق قوانین بازتاب، زاویههای بازتابش و تابش با یکدیگر برابر هستند:
$$widehat { i } = widehat { r } \ widehat { i ‘ } = widehat { r ‘ } $$
با جایگزینی دو تساوی بالا در رابطه $$widehat { i } + widehat { r } + widehat { i ‘ } + widehat { r ‘ } = 180 $$ داریم:
$$widehat { i } + widehat { i’ } + widehat { i } widehat { i’ } = 180 \ 2 (widehat { i } + widehat { i’ }) = 180 \ widehat { i } + widehat { i ‘ } = 90$$
مجموع زوایای داخلی مثلث $$AOB$$ برابر ۱۸۰ درجه است:
$$widehat { alpha } + (90 – widehat { i } ) + (90 – widehat { i ‘ } ) = 180 \ widehat { alpha} + 180 – widehat { i } -widehat { i ‘ } = 180 \ widehat { alpha } = widehat { i } + widehat { i ‘ } = 90$$
مثال پنجم
ضریب شکست الماس برابر ۲٫۲۴ است. تندی انتشار نور در الماس برابر است با:
$$1.24 times 10 ^ 8 frac { m } { s } $$
$$1.24 times 10 ^ 6 frac { m } { s } $$
$$2.24 times 10 ^ 8 frac { m } { s } $$
$$3 times 10 ^ 8 frac { m } { s } $$
هنگامیکه پرتو نور از محیطی شفاف وارد محیط شفاف دیگری میشود، قسمتی از آن از مرز دو محیط، منعکس میشود و بخشی دیگر، پس از شکست وارد محیط دوم میشود. برای هر محیط، کمیتی به نام ضریب شکست تعریف میشود که از تقسیم تندی نور در خلا بر تندی نور در محیط، بهدست میآید:
$$ n = frac { c } { v } $$
در رابطه فوق، n ضریب شکست، c تندی نور در خلا و $$v$$ تندی نور در محیط است. در این مثال، مقدار n را داریم. با توجه به آنکه c برابر $$3 times 10 ^ 8 $$ متر بر ثانیه است، مقدار $$v$$ را بهدست میآوریم:
$$2.42 = frac { 3 times 10 ^ 8 } { v } \ v = frac { 3 times 10 ^ 8 } { 2.42 } = 1.24 times 10 ^ 8 frac { m } { s } $$
مثال ششم
پرتو نور در هوا حرکت میکند و با زاویه ۳۰ درجه نسبت به خط عمود، بر مرز هوا و آب میتابد. این پرتو پس از عبور از مرز، میشکند. اگر زاویه شکست، نصف زاویه فرود باشد، ضریب شکست آب کدام است؟ (ضریب شکست هوا برابر یک است)
رابطه قانون شکست عمومی یا قانون اسنل به صورت زیر نوشته میشود:
$$n_ 1 sin theta_ 1 = n_ 2 sin theta _ 1 $$
در رابطه فوق:
- $$ theta_1 $$ زاویه فرود است.
- $$ theta_2 $$ زاویه شکست است.
- $$ n_ 1 $$ ضریب شکست محیط یک (هوا) است.
- $$ n_ 2 $$ ضریب شکست محیط دو (آب) است.
به این نکته توجه داشته باشید که محیط یک، محیطی است که پرتو ابتدا در آن قرار دارد و محیط دو، محیطی است که پرتو پس از شکست در مرز، به آن وارد میشود. رابطه $$n_ 1 sin theta_ 1 = n_ 2 sin theta _ 1 $$ را برحسب ضریب شکست آب ($$ n_2 $$) مرتب میکنیم.
$$n_ 2 = frac { n_ 1 sin theta_ 1 } { sin theta _ 2 } $$
زاویه $$ theta_ 1 $$ برابر ۳۰ درجه و زاویه $$theta_ 2 $$ برابر ۱۵ درجه است. با قرار دادن مقدارهای داده شده در رابطه فوق، مقدار $$ n_ 2 $$ را بهدست میآوریم:
$$ n_ 2 = frac { ( 1.0 ) times sin (30) } { sin ( 15 ) } = 1.93 $$
مثال هفتم
نور از هوا با ضریب شکست یک، وارد محیطی با ضریب شکست ۱٫۵۲ میشود. اگر طول موج نور فرودی برابر ۵۳۰ نانو باشد، طول موج نور شکست چه مقدار است؟
رابطه قانون شکست عمومی یا قانون اسنل به صورت زیر نوشته میشود:
$$n_ 1 sin theta_ 1 = n_ 2 sin theta _ 1 \ frac { sin theta_! } { sin theta_ 2 } = frac { v_ 1 } { v _ 2 } = frac { lambda _ 1 } { lambda _ 2 } = frac { n_ 2 } { n _ 1 } $$
در رابطه فوق:
- $$ theta_1 $$ زاویه فرود است.
- $$ theta_2 $$ زاویه شکست است.
- $$ n_ 1 $$ ضریب شکست محیط یک است.
- $$ n_ 2 $$ ضریب شکست محیط دو است.
- $$ v_ 1 $$ و $$ v_ 2 $$ به ترتیب تندی انتشار نور در محیطهای یک و دو هستند.
- $$ lambda_1 $$ و $$lambda_ 2 $$ به ترتیب طول موج انتشار نور در محیطهای یک و دو هستند.
به این نکته توجه داشته باشید که محیط یک، محیطی است که پرتو ابتدا در آن قرار دارد و محیط دو، محیطی است که پرتو پس از شکست در مرز، به آن وارد میشود. در این مثال ضریب شکست و طول موج داده شده است، بنابراین برای بهدست آوردن طول موج نور در محیط دو از رابطه زیر استفاده میکنیم:
$$frac { lambda _ 1 } { lambda_ 2 } = frac { n_ 2 } { n _ 1 } \ lambda_ 2 = frac { n_ 1 } { n_ 2 } lambda _ 1 \ lambda _ 2 = frac { 1 } { 1.52 } times 530 nm = 349 nm $$
مثال هشتم
امواج عرضی در امتداد سیمی کشیده به طول ۱۰۰ سانتیمتر حرکت میکنند. تندی انتشار موج در امتداد سیم برابر ۲۵۰ متر بر ثانیه است. اگر فردی تا بسامد ۱۵ کیلوهرتز را بتواند بشنود، بیشینه هارمونیکِ قابلتشخیص توسط این فرد چه مقدار است؟
برای حل این مثال ابتدا مقدارهای داده شده را مینویسیم:
- طول سیم برابر ۱۰۰ سانتیمتر یا یک متر است.
- تندی انتشار موج در سیم برابر ۲۵۰ متر بر ثانیه است.
- بیشینه بسامدی که فرد میتواند بشنود برابر ۱۵ کیلوهرتز یا ۱۵۰۰۰ هرتز است.
بسامد nامین هارمونیک با استفاده از رابطه زیر بهدست میآید:
$$f_ n = frac { n v } { n L } $$
رابطه فوق را برحسب n مرتب میکنیم:
$$n = frac { 2 L f_ n } { v } $$
با قرار دادن مقدارهای داده شده در رابطه فوق، مقدار n را بهدست میآوریم:
$$n = frac { 2 times 1.00 times 15000 } { 250 } = 120$$
مثال نهم
طول لوله بازی برابر ۴ متر است. اگر امواج صوتی با سرعت ۳۲۲ متر بر ثانیه از این لوله عبور کنند، مقدار بسامد اصلی کدام است؟
طول موجهای هماهنگ در لولهای باز که موجی با طول موج $$lambda$$ در آن حرکت میکند با استفاده از رابطه زیر بهدست میآید:
$$lambda=frac { 2 L } { n } $$
در رابطه فوق، L طول لوله، $$lambda$$ طول موجِ موج و n عدد هماهنگ هستند. به این نکته توجه داشته باشید که n عددی طبیعی است. با توجه به رابطه بین $$lambda$$ و $$f$$، بسامد را میتوانیم برحسب طول لوله و عدد هماهنگ به صورت زیر بنویسیم:
$$f = frac { v } { lambda } = frac { vn } { 2 L } $$
مقدار n برای بسامد اصلی برابر یک است:
$$f_ 1 = frac { 1 times 322 } { 2 times 4 } = 40.25 frac { 1 } { s } = 40.25 Hz$$
مثال دهم
طنابی بین دو نقطه به فاصله L از یکدیگر بسته شده است. کشش و جرم خطی طناب به گونهای است که موج با سرعت ۳۴۳ متر بر ثانیه در آن حرکت میکند. امواج صوت در لولهای با شرایط مرزی متقاون و طول L نیز با سرعت ۳۴۳ متر بر ثانیه منتشر میشوند. کدام یک از گزینههای زیر در مورد فرکانسهای هارمونیک در طناب و لوله صحیحی است؟
فرکانسهای هارمونیک طناب و لوله با یکدیگر برابر هستند.
فرکانسهای هارمونیکِ طناب، بزرگتر از فرکانسهای هارمونیک، لوله است.
فرکانسهای هارمونیکِ طناب، کوچکتر از فرکانسهای هارمونیک، لوله است.
فرکانسهای هارمونیکِ طناب و لوله قابلمقایسه نیستند.
این مثال را قدمبهقدم با یکدیگر حل میکنیم.
گام یک
ابتدا فرمول فرکانسهای هارمونیک برای طناب مرتعش را مینویسیم:
$$f_ n = frac { n v } { 2 L } $$
در رابطه فوق:
- $$f_n$$ فرکانس هارمونیک nام در طناب است.
- L طول طناب است.
- n عدد هماهنگ و مقدار آن برابر ۱، ۲، ۳ و … است.
- $$v$$ سرعت انتشار موج در طناب است که مقدار آن در این مثال برابر ۳۴۳ متر بر ثانیه است.
گام ۲
مقدار $$v$$ را در رابطه $$f_ n = frac { n v } { 2 L } $$ قرار میدهیم:
$$f_ n = frac { n (343) } { 2 L } $$
گام ۳
در این مرحله، رابطه فرکانسهای هارمونیک در لوله را مینویسیم.
$$f_ n = frac { 2 n v } { 4 L } $$
گام ۴
مقدار $$v$$ را در رابطه $$f_ n = frac { 2 n v } { 4 L } $$ قرار میدهیم:
$$f_ n = frac { 2 n (343) } { 4 L } \ f_ n = frac { n ( 343 ) } { 2 L } $$
گام ۵
فرکانسهای هارمونیک بهدست آمده برای طناب و لوله در گامهای ۳ و ۴ را با یکدیگر مقایسه میکنیم. این دو فرکانس با یکدیگر برابر هستند. اگر سرعت انتشار موج در طناب دو برابر شود، فرکانس هارمونیک در طناب نیز دو برابر فرکانس هارمونیک در لوله خواهد شد.
فرمول های فیزیک دهم فصل پنجم
فرمول های فیزیک دوازدهم در فصل پنجم در مورد فیزیک اتمی هستند. ابتدا فرمولهای این فصل را به صورت خلاصه بیان، سپس چند مسئله را در این رابطه با یکدیگر حل میکنیم. فرمول های فیزیک دوازدهم فصل پنجم در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دهم فصل پنجم |
| انرژی فوتون | $$E = h f $$ |
| قانون پایستگی انرژی در اثر فوتوالکتریک | $$hf = W + K $$ |
| معادله فوتوالکتریک | $$K_{ maxx } = hf – W$$ |
| بسامد آستانه فوتوالکترونها | $$f_ 0 frac { W_ 0 } { h } $$ |
| معادله بالمر | $$lambda = (364.56 nm ) frac { n ^ 2 } { n ^ 2 – 2 ^ 2 } $$ |
| معادله ریدبرگ | $$frac { 1 } { lambda } = R = (frac { 1 } { n’ ^ 2 } – frac { 1 } { n ^ 2 } ) $$ |
| شعاع مدارهای الکترون برای اتم | $$r_ n = a_ 0 n ^ 2 $$ |
| ترازهای انرژی الکترون در اتم هیدروژن | $$E _ n = frac { – 13.6 eV } { n ^ 2 } $$ |
| معادله گسیل فوتون از اتم | $$E_ U – E_ L = h f $$ |
در ادامه، فرمول های فیزیک دوازدهم فصل پنجم نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح میدهیم.
اثر فوتوالکتریک و فوتون
هنگامیکه نور به فلزی میتابد، الکترونها میتوانند از سطح فلز خارج شوند. به این پدیده، اثر فوتوالکتریک و به الکترونهای خارج شده از فلز، فوتوالکترون گفته میشود. رفتار و ویژگیهای فوتوالکترونها هیچ تفاوتی با الکترونها ندارد. فوتو در فوتوالکترون به این معنا است که الکترونها به دلیل تابش نور به فلز، از سطح آن خارج شدهاند.
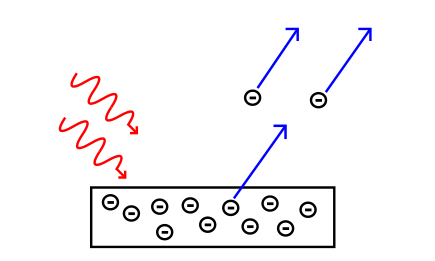
نور در فیزیک کلاسیک به عنوان موج در نظر گرفته میشود. برطبق این دیدگاه:
- انرژی جنبشی فوتوالکترونهای منتشر شده با دامنه نور، افزایش مییابد.
- آهنگ تابش الکترون، با افزایش بسامد نور، افزایش مییابد.
برای تایید این دو نتیجه، آزمایشهایی انجام و نتایج زیر مشاهده شدند:
- انرژی جنبشی فوتوالکترونها با بسامد نور افزایش مییابد.
- جریان الکتریکی با افزایش بسامد نور، ثابت باقی میماند.
- جریان الکتریکی با افزایش دامنه نور، افزایش مییابد.
- انرژی جنبشی فوتوالکترونها با افزایش دامنه نور، ثابت میماند.
تناقض ایجاد شده بین نتایج مشاهده شده و نتایج بهدست آمده از فیزیک کلاسیک، با پیشنهاد اینشتین حل شد، رفتار دوگانه موج ذرهای نور. برطبق این دیدگاه، نور از ذراتی به نام فوتون تشکیل شده است. انرژی هر فوتون را میتوان با استفاده از معادله پلانک بهدست آورد:
$$E = h f $$
در این معادله، E انرژی فوتون برحسب ژول، h ثابت پلانک با مقدار $$6.626 times { 10 ^ { – 34 } J . s } $$ و f بسامد نور برحسب هرتز است. برطبق این معادله، انرژی فوتون با بسامد نور متناسب است. بنابراین، دامنه نور با تعداد فوتونها با بسامد داده شده متناسب است. پس از برخورد نورِ تکفام به سطح فلز، هر فوتون با یک الکترون برهمکنش میکند. اگر انرژی فوتون برای خارج کردن الکترون از فلز کافی باشد، الکترون بلافاصله از فلز جدا میشود. بنابراین، فوتون قسمتی از انرژی خود را برای خروج الکترون از فلز مصرف میکند و مابقی انرژی خود را به صورت انرژی جنبشی، به الکترون میدهد. در نتیجه، انرژی فوتون را میتوانیم به صورت مجموع کار یا انرژی لازم برای خروج الکترون از فلز (W) و انرژی جنبشی الکترون (K) پس از جدا شدن از فلز بنویسیم:
$$hf = W + K $$
برخی الکترونها با صرف انرژی کمتر، به راحتی از سطح فلز جدا میشوند. در نتیجه، هرچه W کمتر باشد، انرژی جنبشی فوتوالکترونها بیشتر خواهد بود. فرض کنید، $$ W_0 $$ کمینه کار یا انرژی لازم برای جدا کردن الکترونها از سطح فلز باشد، در این حالت انرژی جنبشی فوتوالکترونها بیشینه خواهد بود:
$$K _ { max } = hf – W _ 0 $$
$$W_0 $$ یا کمینه انرژی لازم برای جدا کردن الکترون از سطح فلز تابع کار فلز نام و به جنس فلز بستگی دارد. نمودار $$K _ { max} $$ برحسب f، خط راستی است که محور افقی را در $$ f_ 0 $$ قطع میکند. $$ f _ 0 $$ بسامد آستانه نام دارد. فوتون با بسامدی بزرگتر از بسامد آستانه میتواند الکترونها را از سطح فلز خارج کند.
$$ f_ 0 = frac { W _ 0 } { h } $$
طیف خطی
اجسام در دماهای بالا، طیف پیوستهای از امواج الکترومغناطیسی ساطع میکنند. اما هنگامیکه نمونههای خالص تک عنصری گرم میشوند، طیف متفاوتی مشاهده میشود. به عنوان مثال، گاز هیدروژن در فشار کم، به جای گسیل طیف پیوسته، طیفی گسسته به نام طیف خطی از خود ساطع میکند. طیف خطی ایجاد شده و رنگِ نورِ منتشر شده به نوع گاز بستگی دارد. طول موج مربوط به هر یک از خطهای شناخته شده در طیف خطی هیدروژن اتمی با استفاده از رابطهای به نام بالمر بهدست میآید:
$$lambda = (364.56 nm ) frac { n ^ 2 } { n ^ 2 – 2 ^ 2 } $$
n در رابطه فوق ۳ یا بزرگتر از سه و عدی صحیح است. با قرار دادن $$n = 3, 4 , 5 , 6 $$ در معادله بالمر طول موج خطهای طیف گسیلی اتم هیدروژن را برای رنگهای مختلف نور مرئی بهدست میآوریم. چند سال بعد معادله بالمر به صورت زیر بازنویسی و اصلاح شد:
$$frac { 1 } { lambda } = R = (frac { 1 } { n’ ^ 2 } – frac { 1 } { n ^ 2 } ) $$
این معادله، معادله ریدبرگ و R ثابت ریدبرگ نام دارد و مقدار آن برابر $$0.010973731 {( nm ) ^ { – 1 }} $$ است. به هنگام حل مسائل مربوطه میتوانیم مقدار R را برابر ۰٫۰۱۱ در نظر بگیریم.
مدل اتمی رادرفورد-بور
فیزیکدانی نیوزلندی به نام ارنست رادرفورد در آزمایش معروف خود برای تعیین ساختار اتم، از ورقه بسیار نازک طلا استفاده کرد و ذرات آلفا را به آن تاباند. بنابراین این آزمایش به آزمایش ورقه طلا معروف شده است. نتایج بهدست آمده از این آزمایش قابلتوجه بودند. بر طبق نتایج بهدست آمده، رادرفورد مدلی را برای اتم پیشنهاد داد:
- بار مثبت و بیشتر جرم اتم در حجم بسیار کوچکی به نام هسته متمرکز شده است.
- بر طبق مدل رادرفورد، الکترونها با بار منفی، به دور هسته با بار مثبت قرار گرفتهاند. همچنین، رادرفورد ادعا کرد که الکترونها در مسیرهای دایرهای به نام مدار، با سرعت بسیار بالایی به دور هسته میچرخند.
- الکترونها با بار منفی و هسته با بار مثبت توسط نیروی جاذبه الکترواستاتیکی در کنار یکدیگر قرار گرفتهاند.
اما مدل اتمی رادرفورد کاستیهایی داشت. این مدل نمیتوانست پایداری اتم و آرایش الکترونی را توضیح دهد. بور در راستای رفع نقصهای مدل رادرفورد، مدل جدیدی پیشنهاد داد. در مدل رادرفورد، هسته با بار مثبت در مرکز و الکترونها در مدارهایی به دور آن در چرخش هستند. بور از ایده پلانک در مورد گسسته بودن انرژی (انرژی کوانتومی) و یافتههای اینشتین در مورد آنکه نور از ذراتی به نام فوتون تشکیل شده است، برای پاسخ به پرسش اتم چیست و ارائه مدل کاملتری برای ساختار اتم استفاده کرد. بر طبق محاسبات انجام شده توسط بود، شعاع مدارهای الکترون و ترازهای انرژی الکترون در اتم هیدروژن با استفاده از دو رابطه زیر بهدست میآیند:
$$r_ n = a_ 0 n ^ 2 \ E _ n = frac { – 13.6 eV } { n ^ 2 } $$
n در رابطه فوق عدد کوانتومی نام دارد و مدار الکترون به دور هسته را مشخص میکند. اگر الکترون از مداری به مدار دیگر حرکت کند، فوتون را جذب یا ساطع میکند. مقدار انرژی جذب شده یا منتشر شده به صورت زیر بهدست میآید:
$$|triangle E| = |E_f – E_i| = h nu = frac{hc}{lambda}$$
مثال های مربوط به فرمول های فیزیک دوازدهم فصل پنجم
در این قسمت، چند مثال را در رابطه با اثر فوتوالکتریک و مدل های اتمی با یکدیگر حل میکنیم.
مثال اول
بلندترین طول موج نور که میتواند پس از برخورد به تنگستن، فوتوالکترون تولید کند چه مقدار است؟ (تابع کار تنگستن برابر $$4.52 eV$$ است)
برای خروج الکترون از سطح فلز میتوانیم نوری با طول موج مشخص به آن بتابانیم. برخی الکترونها با صرف انرژی کمتر، به راحتی از سطح فلز جدا میشوند. در نتیجه، هرچه کار انجام شده برای جدا کردن الکترونها (W) کمتر باشد، انرژی جنبشی فوتوالکترونها بیشتر خواهد بود. فرض کنید، $$ W_0 $$ کمینه کار یا انرژی لازم برای جدا کردن الکترونها از سطح فلز باشد، در این حالت انرژی جنبشی فوتوالکترونها بیشینه خواهد بود:
$$K _ { max } = hf – W _ 0 $$
$$W_0 $$ یا کمینه انرژی لازم برای جدا کردن الکترون از سطح فلز، تابع کار فلز نام و به جنس فلز بستگی دارد. نمودار $$K _ { max} $$ برحسب f، خط راستی است که محور افقی را در $$ f_ 0 $$ قطع میکند. $$ f _ 0 $$ بسامد آستانه نام دارد. فوتون با بسامدی بزرگتر از بسامد آستانه میتواند الکترونها را از سطح فلز خارج کند.
$$ f_ 0 = frac { W _ 0 } { h } $$
$$W_0 $$ یا کمینه انرژی لازم برای جدا کردن الکترون از سطح فلز تابع کار فلز نام و به جنس فلز بستگی دارد. مقدار آن برای فلز تنگستن برابر ۴٫۵۲ الکترونولت است. فوتون با بسامدی بزرگتر از بسامد آستانه میتواند الکترونها را از سطح فلز خارج کند.
$$ f_ 0 = frac { W _ 0 } { h } $$
با بهدست آوردن بسامد آستانه، به راحتی میتوانیم بلندترین طول موج نور برای خروج الکترون از فلز تنگستن را بهدست آوریم.
$$f_ 0 = frac { W_ 0 } { h } = frac { 4.52 eV } { 6.626 times { 10 ^ { – 34 } J . s } } $$
در این مثال، تابع کار برحسب الکترونولت داده شده است. برای بهدست آوردن بسامد آستانه، باید تابع کار تنگستن را به ژول تبدیل کنیم. هر یک الکترونولت برابر $$1.6 times 10 ^ { – 19 } $$ ژول است. در نتیجه، ۴٫۵۲ الکترونولت، برابر $$4.52 times 1.6 times 10 ^ { – 19 } $$ ژول است:
$$f_ 0 = frac { 4.52 eV } { 6.626 times { 10 ^ { – 34 } J . s }} = frac { 4.52 times 1.6 times 10 ^ { – 19 }} { 6.626 times 10 ^ { – 34 }} = 1.09times 10 ^ { 15 } frac { 1 } { s } $$
حال با استفاده از رابطه $$lambda = frac { c } { f } $$ بلندترین طول موج را بهدست میآوریم:
$$lambda = frac { c } { f } \ lambda = frac { 3 times 10 ^ 8 } { 1.09 times 10 ^ { 15 } } = 2.75 times 10 ^ { -7 } m = 275 nm$$
مثال دوم
نور با طول موج ۲۰۰ نانومتر به فلز تنگستن میتابد. بیشینه انرژی جنبشی فوتوالکترونهای ساطع شده از سطح این فلز چند ژول است؟ (تابع کار فلز تنگستن برابر ۴٫۵۲ الکترونولت است)
$$2.71 times 10 ^ { – 16 } J$$
$$2.71 times 10 ^ { – 19 } J$$
$$1.71 times 10 ^ { – 19 } J$$
$$2.71 times 10 ^ { – 15 } J$$
برخی الکترونها با صرف انرژی کمتر، به راحتی از سطح فلز جدا میشوند. در نتیجه، هرچه W کمتر باشد، انرژی جنبشی فوتوالکترونها بیشتر خواهد بود. فرض کنید، $$ W_0 $$ کمینه کار یا انرژی لازم برای جدا کردن الکترونها از سطح فلز باشد، در این حالت انرژی جنبشی فوتوالکترونها بیشینه خواهد بود:
$$K _ { max } = hf – W _ 0 $$
ابتدا بسامد مربوط به طول موج ۲۰۰ نانومتر را بهدست میآوریم:
$$f = frac { c } { lambda } = frac { 3 times 10 ^ 8 frac { m } { s } } { 200 times 10 ^ { -9 } m } = 0.015 times 10 ^ { 17 } frac { 1 } { s } = 1.5 times 10 ^ { 15 } Hz $$
در ادامه، انرژی جنبشی بیشینه را بهدست میآوریم:
$$K _ { max } = hf – W _ 0 \ K _ {max } = 6.626 times { 10 ^ { – 34 } J . s } times (1.5 times 10 ^ { 15 } frac { 1 } { s } ) – 4.52 eV $$
برای محاسبه انرژی جنبشی بیشینه، باید تابع کار را از الکترونولت به ژول تبدیل کنیم. هر یک الکترونولت برابر $$1.6 times 10 ^ { – 19 } $$ ژول است. در نتیجه، ۴٫۵۲ الکترونولت، برابر $$4.52 times 1.6 times 10 ^ { – 19 } $$ ژول است:
$$4.52 eV = 4.52 times 1.6 times 10 ^ { – 19 } J = 7.23 times 10 ^ { – 19 } J$$
بنابراین، بیشینه انرژی جنبشی برابر است با:
$$ K _ {max } = 6.626 times { 10 ^ { – 34 } J . s } times (1.5 times 10 ^ { 15 } frac { 1 } { s } ) – 4.52 eV \ = 9.34 times 10^ { – 19 } J – 7.23 times 10 ^ { – 19 } J \ K_ { max} = 2.71 times 10 ^ { – 19 } J $$
مثال سوم
تغییرات انرژی جنبشی فوتوالکترونهای خارج شده از سدیم برحسب بسامد در تصویر زیر نشان داده شده است. تابع کار این فلز برحسب الکترونولت کدام است؟
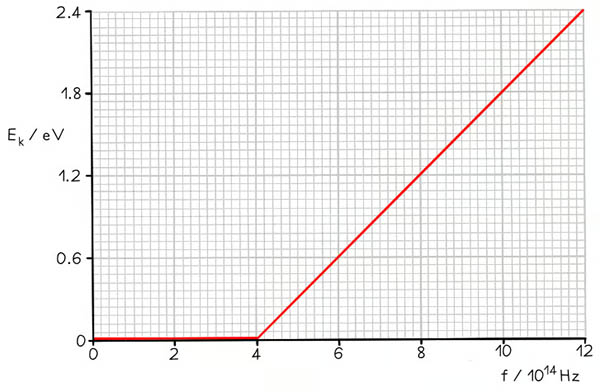
۱٫۵۲ الکترونولت
۲٫۶۵ الکترونولت
۱٫۶۶ الکترونولت
۱/۸۲ الکترونولت
برخی الکترونها با صرف انرژی کمتر، به راحتی از سطح فلز جدا میشوند. در نتیجه، هرچه W کمتر باشد، انرژی جنبشی فوتوالکترونها بیشتر خواهد بود. فرض کنید، $$ W_0 $$ کمینه کار یا انرژی لازم برای جدا کردن الکترونها از سطح فلز باشد، در این حالت انرژی جنبشی فوتوالکترونها بیشینه خواهد بود:
$$K _ { max } = hf – W _ 0 $$
$$W_0 $$ یا کمینه انرژی لازم برای جدا کردن الکترون از سطح فلز تابع کار فلز نام و به جنس فلز بستگی دارد. نمودار $$K _ { max} $$ برحسب f، خط راستی است که محور افقی را در $$ f_ 0 $$ قطع میکند. معادله $$K _ { max } = hf – W _ 0 $$ را میتوانیم با معادله خط راستی با شیب m و عرض از مبدا c مقایسه کنیم:
$$K _ { max } = hf – W _ 0 \ y = m x + c $$
بسامد آستانه همان عرض از مبدا یا محل تقاطع خط راست با محور افقی است.
$$K_ { max } = 0 , f= f _ 0 \ f_ 0 = 4 times 10 ^ { 14 } Hz $$
با داشتن بسامد آستانه به راحتی میتوانیم تابع کار سدیم را بهدست آوریم:
$$W_ 0 = h f _ 0 = ( 6.63 times 10 ^ { – 34 } ) times ( 4 times 10 ^ { 14 } ) = 26.52 times 10 ^ { -20 } J = 2.652 times 10 ^ { – 19 } J $$
در پایان، تابع کار بهدست آمده برحسب ژول را به الکترونولت تبدیل میکنیم:
$$1 eV = 1.6 times 10 ^ { – 19 } J \ W_ 0 = frac { 2.562 times 10 ^ { – 19 } } { 1.6 times 10 ^ { – 19 } } = 1.66 eV $$
مثال چهارم
تابع کار کلسیم برابر $$4.34 times 10 ^ { – 19 } J $$ است. کمینه فرکانس نور برای خروج الکترونها از سطح کلسیم چه مقدار است؟ اگر نور با فرکانس $$1.00 times 10 ^ { 15 } Hz$$ به سطح فلز بتابد، سرعت و انرژی جنبشی الکترونهای خروجی از سطح فلز چه مقدار است؟
کمینه فرکانس، انرژی جنبشی و سرعت خروج الکترونها از کلیسم به ترتیب برابر $$6.55 times 10 ^ { 14 } Hz$$ و $$2.29 times 10 ^ { – 19 } J$$ و $$2.24 times 10 ^ 7 frac { m } { s } $$ است.
کمینه فرکانس، انرژی جنبشی و سرعت خروج الکترونها از کلیسم به ترتیب برابر $$6.55 times 10 ^ { 14 } Hz$$ و $$2.29 times 10 ^ { – 19 } J$$ و $$1.24 times 10 ^ 7 frac { m } { s } $$ است.
نور با فرکانس $$1.00 times 10 ^ { 15 } Hz $$ نمیتواند الکترونی از فلز خارج کند.
کمینه فرکانس، انرژی جنبشی و سرعت خروج الکترونها از کلیسم به ترتیب برابر $$1.55 times 10 ^ { 14 } Hz$$ و $$3.29 times 10 ^ { – 19 } J$$ و $$2.24 times 10 ^ 7 frac { m } { s } $$ است.
برخی الکترونها به راحتی از سطح فلز جدا میشوند. در نتیجه، هرچه W کمتر باشد، انرژی جنبشی فوتوالکترونها بیشتر خواهد بود. فرض کنید، $$ W_0 $$ کمینه انرژی لازم برای جدا کردن الکترونها از سطح فلز باشد، در این حالت انرژی جنبشی فوتوالکترونها بیشینه خواهد بود:
$$K _ { max } = hf – W _ 0 $$
$$W_0 $$ یا کمینه انرژی لازم برای جدا کردن الکترون از سطح فلز تابع کار فلز نام و به جنس فلز بستگی دارد. نمودار $$K _ { max} $$ برحسب f، خط راستی است که محور افقی را در $$ f_ 0 $$ قطع میکند. $$ f _ 0 $$ بسامد آستانه نام دارد. فوتون با بسامدی بزرگتر از بسامد آستانه میتواند الکترونها را از سطح فلز خارج کند.
$$ f_ 0 = frac { W _ 0 } { h } $$
در این مثال، ابتدا کمینه فرکانس موردنیاز برای جدا کردن الکترونها از سطح فلز کلسیم را بهدست میآوریم:
$$ f_ 0 = frac { W _ 0 } { h } \ f_ 0 = frac { 4.34 times 10 ^ { -19} j } { 6.63 times 10 ^ { – 34 } J. s } = 0.655 times 10 ^ { 15 } Hz = 6.55 times 10 ^ { 14 } Hz$$
در ادامه، نور با فرکانس $$1.00 times 10 ^ { 15 } Hz$$ به سطح فلز میتابد، انرژی جنبشی و سرعت الکترونهای خارج شده از فلز را بهدست میآوریم. فرکانس نور تابیده شده از فرکانس آستانه بزرگتر است، بنابراین الکترونها از سطح فلز خارج میشوند.
$$K _ { max } = hf – W _ 0 \ K_{ max} = 6.63 times 10 ^ { – 34 } J . s times ( 1.00 times 10 ^ { 15 } Hz ) – 4.34 times 10 ^ { -19 } J \ K_ { max } = 6.63 times 10 ^ { – 19 } J – 4.34 times 10 ^ { – 19 } J \ K _ { max } = 2.29 times 10 ^ { – 19 } J $$
با داشتن انرژی جنبشی به راحتی میتوانیم سرعت حرکت الکترونهای خارج شده را بهدست آوریم:
$$ K = frac { 1 } { 2 } m v^ 2 \ 2.29 times 10 ^ { – 19 } = frac { 1 } { 2 } times ( 9.12 times 10 ^ { – 31} kg ) times v ^ 2 \ v ^ 2 = frac { 2 times 2.29 times 10 ^ { – 19 } } { 9.12 times 10 ^ { – 34 } }= 0.502 times 10 ^ { 15 } = 5.02 times 10 ^ { 14 } \ v = 2.24 times 10 ^ 7 frac { m } { s } $$
مثال پنجم
انرژی لازم برای جدا کردن سه الکترون و و از سطح فلزی به ترتیب ۲٫۲۶ و ۴٫۲۴ و ۴٫۳۷ الکترونولت است. کدامیک از این الکترونها پس از قرار گرفتن در مقابل نوری با طول موج ۶۰۰ نانومتر، از فلز جدا میشوند؟ (سرعت نور برابر $$3 times 10 ^ 6 frac { m } { s } $$ و ثابت پلانک برابر $$6.63 times 10 ^ { – 34 } J.s $$ است)
هیچیک از سه الکترون
$$W_0 $$ یا کمینه انرژی لازم برای جدا کردن الکترون از سطح فلز تابع کار فلز نام و به جنس فلز بستگی دارد. نمودار $$K _ { max} $$ برحسب f، خط راستی است که محور افقی را در $$ f_ 0 $$ قطع میکند. $$ f _ 0 $$ بسامد آستانه نام دارد. فوتون با بسامدی بزرگتر از بسامد آستانه میتواند الکترونها را از سطح فلز خارج کند.
$$ f_ 0 = frac { W _ 0 } { h } $$
بنابراین، برای خروج الکترون از سطح فلز باید نور با بسامد بزرگتر از $$f_ 0 $$ به سطح آن بتابد. طول موج معادل این بسامد با استفاده از رابطه زیر بهدست میآید:
$$ lambda_0 = frac { c } { f _ 0 } \ lambda_ 0 = frac { c } { frac { W _ 0 } { h } } \ lambda_ 0 = frac { c h } { W _ 0 } $$
در این مثال، انرژی لازم برای جدا کردن سه الکترون از سطح فلز داده شده است. با قرار دادن انرژی لازم برای جدا کردن هر الکترون از سطح فلز، طول موج لازم برای انجام این کار را بهدست میآوریم:
$$lambda_ A = frac { c h } { W _ A }= frac { 3 times 10 ^ 8 times 2.26 eV } { 6.63 times 10 ^ { – 34 } J. s} $$
برای بهدست آوردن طول موج لازم برای خارج کردن الکترون A از سطح فلز باید انرژی لازم برای خروج این الکترون را به ژول تبدیل میکنیم:
$$lambda_ A = frac { c h } { W _ A }= frac { 3 times 10 ^ 8 times 6.63 times 10 ^ { – 34 } J. s} {2.26 eV } \ lambda_ A = frac { 3 times 10 ^ 8 times 6.63 times 10 ^ { – 34 } J. s } { (2.26 times 1.6 times 10 ^ { – 19 } J )} = 5.5 times 10 ^ { – 7 } = 550 times 10 ^ { – 9 } m = 550 nm $$
بنابراین، طول موج لازم برای جدا کردن الکترون A از سطح فلز برابر ۵۵۰ نانومتر است. به طور مشابه، طول موج لازم برای خارج کردن الکترونهای B و C را از سطح فلز بهدست میآوریم:
$$lambda_ B = frac { c h } { W _ B }= frac { 3 times 10 ^ 8 times 6.63 times 10 ^ { – 34 } J. s} {4.24 eV } \ lambda_ B = frac { 3 times 10 ^ 8 times 6.63 times 10 ^ { – 34 } J. s } { (4.24 times 1.6 times 10 ^ { – 19 } J )} = 4.69 times 10 ^ { – 7 } = 469 times 10 ^ { – 9 } m = 469 nm $$
$$lambda_ C = frac { c h } { W _ C }= frac { 3 times 10 ^ 8 times 6.63 times 10 ^ { – 34 } J. s} {4.37 eV } \ lambda_ C = frac { 3 times 10 ^ 8 times 6.63 times 10 ^ { – 34 } J. s } { (4.37 times 1.6 times 10 ^ { – 19 } J )} = 4.55 times 10 ^ { – 7 } = 4.55 nm $$
همچنین، طول موجهای لازم برای جدا کردن الکترونهای B و C از سطح فلز به ترتیب برابر ۴۶۹ و ۴۵۵ نانومتر هستند. در نتیجه، نور با طول موج ۲۰۰ نانومتری نمیتواند هیچ یک از سه الکترون را از سطح فلز جدا کند.
مثال ششم
الکترونی در اتم هیدروژن از تراز $$n = 4 $$ به تراز $$n = 2 $$ میرود، فرکانس فوتون آزاد شده چه مقدار است؟
$$6.15 times 10 ^ { 14 } Hz $$
$$6.15 times 10 ^ { 15 } Hz $$
$$5.15 times 10 ^ { 14 } Hz $$
$$6.15 times 10 ^ { 12 } Hz$$
در تصویر زیر هسته اتم به همراه ترازهای انرژی به دور آن نشان داده شدهاند. الکترونها در هر یک از این ترازها میتواندد قرار داشته باشند، اما در فاصله بین ترازها هیچ الکترونی وجود ندارد. هنگامیکه الکترون از تراز انرژی بالاتر به تراز انرژی پایینتر میآید، انرژی به شکل فوتون آزاد میشود. الکترون در چه صورتی میتواد از تراز انرژی پایینتر به تراز انرژی بالاتر برود؟ الکترون با جذب انرژی کافی میتواند از تراز پایینتر به تراز بالاتر برود.

در این مثال، الکترون در اتم هیدروژن، از تراز چهارم به تراز دوم میرود. در این حالت، فوتونی با مقدار انرژی مشخص آزاد میشود. مقدار انرژی فوتون برابر تفاوت انرژی بین ترازهای چهارم و دوم است.
$$|triangle E| = |E_f – E_i| = h f = frac{hc}{lambda} = hf$$
ترازهای انرژی الکترون در اتم هیدروژن با استفاده از رابطه زیر بهدست میآیند:
$$E _ n = frac { – 13.6 eV } { n ^ 2 } $$
انرژی الکترون در تراز چهارم برابر است با:
$$E _ 4 = frac { – 13.6 eV } { 4 ^ 2 } = – 0.85 eV $$
برای نوشتن انرژی فوق برحسب ژول به صورت زیر عمل میکنیم:
$$E_ 4 = – 0.85 eV = – 0. 85 times 1.6 times 10 ^ { -19 } J = – 1.36 times 10 ^ { – 19 } J $$
به طور مشابه، انرژی الکترون در تراز دوم را نیز بهدست میآوریم:
$$E _ 2 = frac { – 13.6 eV } { 2 ^ 2 } = – 3.4 eV $$
انرژی فوق را برحسب ژول بهدست میآوریم:
$$E_ 4 = – 3.4 eV = – 3.4 times 1.6 times 10 ^ { -19 } J = – 5.44 times 10 ^ { – 19 } J $$
اختلاف انرژی بین دو تراز برابر است با:
$$|triangle E| = |E_2 – E_4| = | -5.44 times 10 ^ { -19 } J – ( -1.34 times 10 ^ { – 19 } J ) | \ triangle E = | – 4.08 times 10 ^ { – 19 } J | = 4.08 times 10 ^ { -19 } J $$
با استفاده از رابطه $$E = hf$$ فرکانس فوتون تابیده شده را بهدست میآوریم:
$$E = h f \ 4.08 times 10 ^ { – 19 } J = 6.63 times 10 ^ { – 34 } times f \ f = frac { 4.08 times 10 ^ { 19 } J } { 6.63 times 10 ^ { – 34 } J. s } = 0.615 times times 10 ^ { 15 } Hz = 6.15 times 10 ^ { 14 } Hz $$
مثال هفتم
الکترونی در اتم هیدروژن در تراز سوم انرژی قرار دارد و فوتونی با طول موج ۱۲۸۳٫۴۵ نانومتر جذب میکند. الکترون پس از جذب این فوتون، به چه تراز انرژی میرود؟
الکترون با جذب انرژی کافی میتواند از تراز پایینتر به تراز بالاتر برود. در این مثال، الکترون ابتدا در تراز سوم قرار دارد و با جذب فوتونی با طول موج ۱۲۸۳٫۴۵ نانومتر به تراز انرژی بالاتر میرود. چه ترازی؟ در ادامه، به این پرسش پاسخ میدهیم. تفاوت انرژی تراز سوم و ترازی که الکترون پس از جذب فوتون به آن میپرد، برابر انرژی فوتون جذب شده است. بنابراین، برای آنکه بدانیم الکترون به چه ترازی میرود، باید انرژی تراز نهایی را بهدست آوریم. برای انجام این کار، ابتدا انرژی فوتون جذب را را محاسبه میکنیم:
$$E = h frac { c } { lambda } \ E = frac { 6.63 times 10 ^ { – 34 } J .s times ( 3 times 10 ^ 8 ) } { 1283.45 times 10 ^ { – 9 } } \ E = 0.0155 times 10 ^ { -1 7 } J = 1.55 times 10 ^ { – 19 } J $$
این انرژی، برابر تفاوت انرژی بین ترازهای اولیه و نهایی الکترون است. انرژی الکترون در تراز سوم برابر است با:
$$$$E _ n = frac { – 13.6 eV } { n ^ 2 } $$ \ E_ 3 = frac { – 13.6 e V } { 9 } =- 1.51 eV = – 1.51 times 1.6 times 10 ^ { – 19 } J = -2.42 times 10 ^ { -19 } J $$
با داشتن تفاوت انرژی بین ترازهای اولیه و نهایی و انرژی تراز اولیه، به راحتی میتوانیم انرژی تراز نهایی را بهدست آوریم:
$$triangle E = E_ f – E_ 3 \ 1.55 times 10 ^ { – 19 } J = E_ f – ( -2.42 times 10 ^ { – 19 } ) \ E_ f = (1.55 -2.44 ) times 10 ^ { -19 } J = – 0.89 times 10 ^ { – 19 } J $$
برای آنکه بدانیم الکترون به چه ترازی پریده است از رابطه $$E _ n = frac { – 13.6 eV } { n ^ 2 } $$ استفاده میکنیم.
$$E _ n = frac { – 13.6 eV } { n ^ 2 } = frac { – 13.6 times 1.6 times 10 ^ { -19 } } { n ^ 2 } \ n ^ 2 = frac { – 13.6 times 1.6 times 10 ^ { -19 } } { – 0.89 times 10 ^ { – 19 } } 24.44 n = 4.94 sim 5 $$
بنابراین، الکترون پس از جذب فوتون با طول موج ۱۲۸۳٫۴۵ نانومتر به تراز پنجم میپرد.
نکته: مثالهای ششم و هفتم را میتوانیم با استفاده از معادله ریدبرگ نیز حل کنیم.
فرمول های فیزیک دهم فصل ششم
فرمول های فیزیک دوازدهم در فصل ششم در مورد فیزیک هستهای هستند. ابتدا فرمولهای این فصل را به صورت خلاصه بیان، سپس چند مسئله را در این رابطه با یکدیگر حل میکنیم. فرمول های فیزیک دوازدهم فصل ششم فیزیک در جدول زیر به صورت خلاصه نوشته شدهاند.
| مبحث موردنظر | فرمول های فیزیک دوازدهم فصل ششم |
| عدد جرمی | $$ A = Z + N $$ |
| واپاشی آلفا | $$^A _ Z Xrightarrow ^{ A – 4 } _ { Z – 2 } Y + ^ 4 _ 2 He$$ |
| واپاشی $$beta^ – $$ | $$^A _ Z Xrightarrow ^{ A } _ { Z + 1 } Y + ^ 0 _ { – 1 } e^ -$$ |
| واپاشی $$beta^ + $$ | $$^A _ Z Xrightarrow ^{ A } _ { Z – 1 } Y + ^ 0 _ { 1 } e^ +$$ |
| واپاشی گاما | $$^A _ Z X ^ *rightarrow ^{ A } _ { Z } X + gamma$$ |
| تعداد هستههای پرتوزای باقیمانده | $$N = N _ 0 ( frac { 1 } { 2 } ) ^ n $$ |
در ادامه، فرمول های فیزیک دوازدهم فصل ششم نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح میدهیم.
هسته اتم
هسته اتم از نوترونها و پروتونها تشکیل شده است. به تعداد پروتونهای موجود در هسته، عدد اتمی (Z) و به تعداد نوترونهای موجود در هسته، عدد نوترونی (N) گفته میشود. عدد جرمی (A) برابر مجموع تعداد پروتونها و نوترونها است:
$$A = Z + N $$
عنصری با نماد شیمیایی X را در نظر بگیرید. نماد هسته در این عنصر به صورت زیر نشان داده میشود:
$$^A _ Z X _ N$$
پروتونهای داخل هسته بار یکسان و مثبت دارند و یکدیگر را توسط نیروی دافعه الکترواستاتیکی دفع میکنند. چرا هسته از هم نمیپاشد؟ زیرا نیرویی بسیار قویتری از نیروی دافعه الکترواستاتیکی بین پروتونها وجود دارد که هسته اتم را نگه داشته است. این نیرو، نیروی هستهای قوی نام دارد. نیروی هستهای بسیار بزرگتر از نیروی دافعه الکترواستاتیکی است. نیروی هستهای قوی کوتاهبرد است و تنها بین نوکلئونهای داخل هسته وارد میشود.
به تفاوت جرم، بین جرم واقعی هسته و جرم پیشبینی شده آن، کاستی جرم هسته گفته میشود. اینگونه به نظر میرسد که قسمتی از جرم هسته از بین رفته است. در واقع، کاستی جرم، هنگام تشکیل هسته به انرژی تبدیل میشود. برای آنکه بدانیم این مقدار جرم به چه مقدار انرژی تبدیل میشود از رابطه معروف اینشتین یعنی $$E = m c ^ 2$$ استفاده میکنیم.
پرتوزایی طبیعی و نیمه عمر
در طی پرتوزایی طبیعی، تمام اتمهای عنصر پرتوزا به صورت خودبهخودی به اتمهای عنصر دیگر تبدیل نمیشوند. برای بیان نرخ واپاشی از مفهومی به نام نیمهعمر استفاده میکنیم. نیمهعمر مدت زمانی است که در طی آن نیمی از ماده آغازین تغییر میکند یا واپاشیده میشود. در پرتوزایی طبیعی سه نوع پرتو ایجاد میشوند.
تابش آلفا
این تابش هنگامی رخ میدهد که از هسته اتم ناپایدار، ذره آلفا شامل دو پروتون و دو نوترون، خارج شود.
$$^A _ Z Xrightarrow ^{ A – 4 } _ { Z – 2 } Y + ^ 4 _ 2 He$$
در واکنش فوق، $$X$$ هسته مادر و $$Y$$ هسته دختر نامیده میشوند.
تابش بتا
گاهی اوقات نوترون در هسته وارد عمل میشود و از بار الکتریکی خنثای خود بهره میبرد و یک الکترون ساطع میکند و به پروتون تبدیل میشود. به تابش الکترون از هسته، واپاشی بتا یا واپاشی الکترونی میگوییم:
$$^A _ Z Xrightarrow ^{ A } _ { Z + 1 } Y + ^ 0 _ { – 1 } e^ -$$
گاهی هسته، یک پوزیترون (الکترون مثبت) تابش میکند. جرم پوزیترون به طور دقیق برابر جرم الکترون و بار الکتریکی آن مثبت است. پروتون پس از تابش پوزیترون به نوترون تبدیل میشود. به خروج پوزیترون از هسته، تابش پوزیترون گفته میشود.
$$^A _ Z Xrightarrow ^{ A } _ { Z – 1 } Y + ^ 0 _ { 1 } e^ +$$
تابش گاما
واپاشی دیگری نیز وجود دارد که در آن تعداد پروتونها و نوترونهای هسته قبل و پس از واپاشی تغییر نمیکند. در این حالت مقدار قابل توجهی انرژی به شکل فوتون از هسته آزاد میشود. به تابش انرژی از هسته، واپاشی گاما میگوییم.
$$^A _ Z X ^ *rightarrow ^{ A } _ { Z } X + gamma$$
نیمه عمر
نیمهعمر مدت زمانی است که در طی آن نیمی از ماده آغازین تغییر میکند یا واپاشیده میشود. اگر تعداد هستههای مادر اولیه در عنصر پرتوزا برابر $$N_ 0 $$ باشد، تعداد هستههای پرتوزای باقیمانده پس از زمان t با استفاده از رابطه زیر بهدست میآیند:
$$N = N_ 0 ( frac { 1 } { 2 } ) ^ n $$
n در رابطه فوق با استفاده از فرمول $$ frac { t } { T _ { frac { 1 } { 2 } }} $$ بهدست میآید.
مثال های مربوط به فرمول های فیزیک دوازدهم فصل ششم
در این قسمت، مثالهایی در رابطه با هسته اتم و پرتوزایی طبیعی و نیمه عمر با یکدیگر حل میکنیم.
مثال اول
نپتونیم $$^ { 237 } _ { 92 } Ne $$ ایزوتوپی است که در راکتورهای هستهای تولید میشود. این ایزوتوپ به شدت ناپایدار است و واپاشی آن با تابش سه ذره آلفا و یک ذره بتای منفی (پوزیترون) انجام میشود. عدد اتمی و عدد جرمی هسته نهایی پس از واپاشی کدام است؟
عدد اتمی و عدد جرمی هسته نهایی پس از واپاشی به ترتیب برابر ۲۳۵ و ۸۸ است.
عدد اتمی و عدد جرمی هسته نهایی پس از واپاشی به ترتیب برابر ۸۸ و ۲۲۵ است.
عدد اتمی و عدد جرمی هسته نهایی پس از واپاشی به ترتیب برابر ۸۸ و ۲۳۳ است.
عدد اتمی و عدد جرمی هسته نهایی پس از واپاشی به ترتیب برابر ۹۱ و ۲۳۳ است.
عنصری با نماد شیمیایی X را در نظر بگیرید. نماد هسته در این عنصر به صورت زیر نشان داده میشود:
$$^A _ Z X _ N$$
در نمایش فوق، A عدد جرمی، Z عدد اتمی و N عدد نوترونی است. تابش آلفا هنگامی رخ میدهد که از هسته اتم ناپایدار، ذره آلفا شامل دو پروتون و دو نوترون، خارج شود.
$$^A _ Z Xrightarrow ^{ A – 4 } _ { Z – 2 } Y + ^ 4 _ 2 He$$
گاهی اوقات نوترون در هسته وارد عمل میشود و از بار الکتریکی خنثای خود بهره میبرد و یک الکترون ساطع میکند و به پروتون تبدیل میشود. به تابش الکترون از هسته، واپاشی بتا یا واپاشی الکترونی میگوییم:
$$^A _ Z Xrightarrow ^{ A } _ { Z + 1 } Y + ^ 0 _ { – 1 } e^ -$$
ایزوتوپ نپتونیم به هنگام واپاشی، سه ذره آلفا و یک ذره بتای منفی گسیل میکند:
$$^{ 237 } _ { 93 } { Np } rightarrow 3 ( ^{ 4 } _ { 2 } {alpha} ) + ^ 0 _ { – 1 } e + ^ A _ B Y \ 237 = 12 + 0 + A \ 93 = 6 + (-1 ) + B \ A = 237 – 12 = 225 \ B = 93 – 5 = 88 $$
در نتیجه، عدد اتمی و عدد جرمی هسته نهایی پس از واپاشی به ترتیب برابر ۸۸ و ۲۲۵ است.
مثال دوم
$$frac { ۷ } { ۸ } $$ ماده پرتوزایی پس از گذشت ۱۳۵ روز واپاشیده میشود. نیمهعمر این ماده چند روز است؟
نیمهعمر مدت زمانی است که در طی آن نیمی از ماده آغازین تغییر میکند یا واپاشیده میشود. اگر تعداد هستههای مادر اولیه در عنصر پرتوزا برابر $$N_ 0 $$ باشد، تعداد هستههای پرتوزای باقیمانده پس از زمان t با استفاده از رابطه زیر بهدست میآیند:
$$N = N_ 0 ( frac { 1 } { 2 } ) ^ n $$
n در رابطه فوق با استفاده از فرمول $$ frac { t } { T _ { frac { 1 } { 2 } }} $$ بهدست میآید. $$frac { ۷ } { ۸ } $$ ماده پرتوزا پس از گذشت ۱۳۵ روز واپاشیده میشود. بنابراین، $$frac { ۱ } { ۸ } $$ ماده پرتوزا باقی مانده است:
$$N = frac { 1 } { 8 } \ N = N _ 0 ( frac { 1 } { 2 } ) ^ n \ frac { 1 } { 8 } N_ 0 = N _ 0 (frac { 1 } { 2 } ) ^ 3 \ n = 3 $$
مقدار n و t را داریم، بنابراین به راحتی میتوانیم نیمهعمر ماده پرتوزا را بهدست آوریم:
$$ n = frac { t } { T _ { frac { 1 } { 2 } }} \ 3 = frac { 135 } { T _ { frac { 1 } { 2 } } \ T_ {frac { 1 } { 2 } }} = frac { 135 } { 3 } = 45 days $$
جمعبندی
در این مطلب از مجله فرادرس، با فرمول های فیزیک دوازدهم آشنا شدیم. فیزیک دوازدهم یا فیزیک سه در سال سوم متوسطه یا مقطع دوازدهم برای رشتههای ریاضیفیزیک و علومتجربی تدریس میشود. فیزیک دوازدهم در رشته ریاضیفیزیک از شش فصل و در رشته علومتجربی از چهار فصل تشکیل شده است. فرمولهای هر فصل ابتدا به صورت خلاصه توضیح داده و در ادامه، برای درک بهتر فرمولها، تعدادی مسئله مرتبط با آنها حل شد.
source