محیط ذوزنقه، اندازه دور این شکل هندسی است که از جمع اندازه چهار ضلع آن به دست میآید. بنابراین، با داشتن اندازه ضلعها (قاعدهها و ساقها)، میتوان اندازه محیط ذوزنقه را به دست آورد. البته در برخی از انواع ذوزنقهها مانند ذوزنقه متساویالساقین (با دو ساق برابر) و ذوزنقه قائمالزاویه (با دو زاویه داخلی راست)، امکان محاسبه محیط به کمک ارتفاع نیز وجود دارد. در این مطلب از مجله فرادرس، نحوه محاسبه محیط ذوزنقه را به همراه حل چندین مثال متنوع آموزش خواهیم داد. در انتهای مقاله، میزان یادگیری شما را با حل چند تمرین میسنجیم. علاوه بر این، چند ابزار اینترنتی کاربردی برای محاسبه آنلاین محیط ذوزنقه را معرفی میکنیم.
در مطالب قبلی مجله فرادرس از جمله «محیط متوازی الاضلاع چیست؟»، «محیط لوزی چگونه بدست می آید؟»، «چگونه محیط مربع را حساب کنیم؟» و بسیاری دیگر از مطالب مرتبط با شکلهای هندسی، محاسبه محیط را به همراه حل چندین مثال و تمرین متنوع آموزش دادهایم. در ادامه این مطلب، به تعریف محیط ذوزنقه و فرمول محاسبه آن میپردازیم.
تعریف محیط ذوزنقه چیست؟
محیط، اندازه دور یک شکل است. در چندضلعیها، به مجموع اندازه ضلعها، محیط میگویند. بنابراین، محیط ذوزنقه، اندازهای است که از جمع اندازه ضلعهای این چهارضلعی به دست میآید.
برای درک این مفهوم، شکل ذوزنقه را در نظر بگیرید.

اگر مداد خود را بر روی یک راس (محل برخورد دو ضلع) ذوزنقه قرار دهیم و آن را بر روی ضلعها حرکت دهیم، پس از رسیدن به نقطه اول، مداد به اندازه محیط ذوزنقه حرکت کرده میکند.
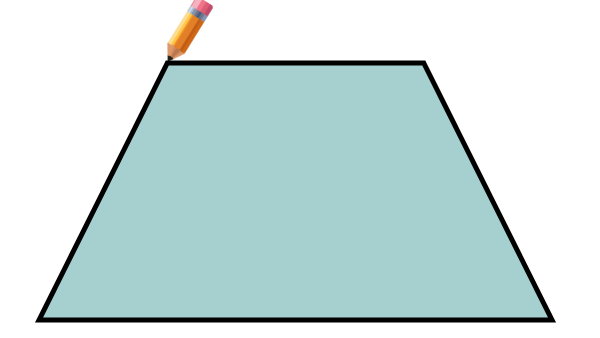
به عبارت دیگر، محیط، مسافت طی شده روی ضلعها است. با توجه به تعریف، این مسافت به صورت زیر محاسبه میشود:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط ذوزنقه
مثال ۱: محاسبه محیط ذوزنقه
تصویر زیر، یک ذوزنقه و اندازه ضلعهای آن را نمایش میدهد.
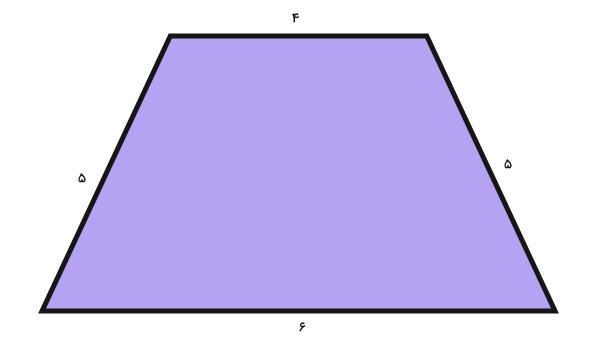
محیط ذوزنقه بالا چند است؟
میدانیم که اندازه محیط، از جمع اندازه ضلعها به دست میآید. بنابراین:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط ذوزنقه
با توجه به تصویر داریم:
- اندازه ضلع اول: $$ ۴ $$
- اندازه ضلع دوم: $$ ۵ $$
- اندازه ضلع سوم: $$ ۶ $$
- اندازه ضلع چهارم: $$ ۵ $$
توجه داشته باشید که عنوان ضلعها را به صورت دلخواه انتخاب کردهایم. شما نیز میتوانید هر ضلع را به صورت دلخواه نامگذاری کنید. این موضوع، تاثیری در نتیجه محاسبات ندارد. با توجه به مقادیر بالا و مفهوم محیط، داریم:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط شکل
$$ ۴ + ۵ + ۶ + ۵ $$ = محیط شکل
$$ ۲۰ $$ = محیط شکل
بنابراین، محیط شکل برابر با $$ ۲۰ $$ است.
فرادرس، چندین فیلم آموزشی مفید را برای شما تهیه کرده است که با مشاهده آنها میتوانید به سادگی و خیلی سریع، روشهای محاسبه مساحت اشکال هندسی را یاد بگیرید. لینک مشاهده این فیلمها در ادامه آورده شده است:
در مطلب «محاسبه مساحت ذوزنقه — به زبان ساده» از مجله فرادرس، در مورد فرمول محاسبه مساحت ذوزنقه صحبت کردیم. در ادامه این مطلب، به معرفی فرمول محاسبه محیط ذوزنقه میپردازیم.
فرمول محاسبه محیط ذوزنقه چیست؟
در بخش قبلی مشاهده کردید که محیط ذوزنقه به صورت زیر محاسبه میشود:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط ذوزنقه
برای نوشتن فرمول محیط ذوزنقه، تصویر زیر را در نظر بگیرید.
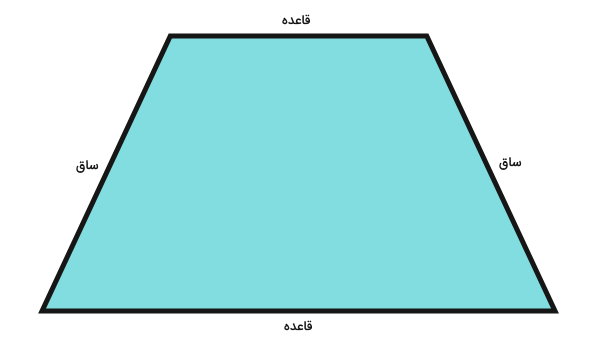
هر یک از ضلعهای ذوزنقه، عنوان مخصوص به خود را دارند. به ضلعهای بالایی و پایینی ذوزنقه (ضلعهای موازی)، «قاعده» یا «پایه» میگویند. دو ضلع کناری ذوزنقه نیز با عنوان «ساق» شناخته میشوند. بر اساس این نامگذاری، فرمول کلامی محاسبه محیط ذوزنقه عبارت است از:
ساق دوم + قاعده دوم + ساق اول + قاعده اول = محیط ذوزنقه
بنابراین، محیط ذوزنقه از مجموع ساقها و قاعدههای این شکل به دست میآید. به عبارت دیگر:
مجموع ساقها و قاعدهها = محیط ذوزنقه
مثال ۲: محاسبه اندازه ساق ذوزنقه از روی محیط آن
ذوزنقهای را در نظر بگیرید که اندازه قاعدهها و یکی از ساقهای آن به صورت زیر باشد:
- اندازه یکی از قاعدهها: $$ ۱۰ $$
- اندازه قاعده دیگر: $$ ۷ $$
- اندازه یکی از ساقها: $$ ۸ $$
اگر محیط ذوزنقه برابر با $$ ۳۳ $$ سانتیمتر باشد، اندازه ساق دیگر ذوزنقه چقدر میشود؟
برای حل این مثال، ابتدا فرمول کلامی محیط ذوزنقه را مینویسیم:
مجموع ساقها و قاعدهها = محیط ذوزنقه
ساق دوم + قاعده دوم + ساق اول + قاعده اول = محیط ذوزنقه
اندازه دو قاعده و یک ساق را داریم. این اندازهها را درون فرمول بالا قرار میدهیم:
ساق دوم + ۷ + ۸ + ۱۰ = محیط ذوزنقه
از طرفی، در صورت سوال، اندازه محیط نیز داده شده است. این اندازه را نیز درون فرمول بالا جایگذاری میکنیم:
ساق دوم + ۷+ ۸ + ۱۰ = ۳۳
به این ترتیب، داریم:
ساق دوم + ۲۵ = ۳۳
ساق دوم را در یک طرف رابطه نگه میداریم و عدد $$ ۲۵ $$ را به طرف دیگر میبریم:
$$ ۳۳ – ۲۵ $$ = ساق دوم
$$ ۸ $$ = ساق دوم
در نتیجه، اندازه ساق دیگر ذوزنقه برابر با $$ ۸ $$ سانتیمتر است.
فرمول جبری محیط ذوزنقه چیست؟
مفاهیم جبر، معادله و متغیر، در پایه هفتم از دوره اول متوسطه آموزش داده میشوند. عبارتهای جبری، نمایش مسائل مختلف به زبان ریاضی هستند. در این عبارتها، معمولا از حروف انگلیسی یا لاتین استفاده میشود. به عنوان مثال، تصویر زیر را در نظر بگیرید.
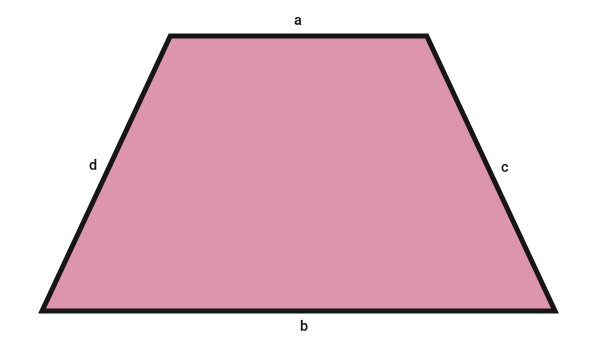
همانطور که مشاهده میکنید، ضلعهای ذوزنقه، با حروف کوچک انگلیسی نمایش داده شدهاند. در دنیای ریاضی، محیط را معمولا با حرف «$$ P $$» نمایش میدهند. این حرف، ابتدای کلمه «Perimeter» به معنای محیط است. البته محیط دایره با حرف «$$ C $$»، ابتدای کلمه «Circumference» نمایش داده میشود. با توجه به تصویر بالا و نکات اشاره شده، فرمول جبری محیط ذوزنقه عبارت است از:
$$ P = a + b + c + d $$
پارامترهای فرمول بالا عبارت هستند از:
- $$ P $$: محیط ذوزنقه
- $$ a $$: یکی از قاعدههای ذوزنقه
- $$ b $$ قاعده دیگر ذوزنقه
- $$ c $$: یکی از ساقهای ذوزنقه
- $$ d $$: ساق دیگر ذوزنقه
نوشتن فرمولها توسط عبارت جبری، حفظ فرمول را راحتتر و حل مسئله را سادهتر میکند. توجه داشته باشید که عنوان انتخابی برای ضلعها، به صورت دلخواه است. به عنوان مثال، میتوانیم فرمول بالا را با استفاده از نام راسهای ذوزنقه بازنویسی کنیم:
$$ P = AB + BC + CD + DC $$
- $$ P $$: محیط ذوزنقه
- $$ AB $$: یکی از قاعدههای ذوزنقه
- $$ BC $$ یکی از ساقهای ذوزنقه
- $$ CD $$: قاعده دیگر ذوزنقه
- $$ DA $$: ساق دیگر ذوزنقه
مثال ۳: محاسبه محیط ذوزنقه به کمک فرمول جبری
محیط ذوزنقهای به اندازه قاعده $$ ۱۰ $$ و $$ ۲۱ $$ و اندازه ساق $$ ۱۶ $$ و $$ ۱۲ $$ را به کمک فرمول جبری محاسبه کنید.
برای محاسبه محیط ذوزنقه، فرمول جبری آن را مینویسیم:
$$ P = a + b + c + d $$
- $$ P $$: محیط ذوزنقه
- $$ a $$: یکی از قاعدههای ذوزنقه برابر با $$ ۱۰ $$
- $$ b $$ قاعده دیگر ذوزنقه برابر با $$ ۲۱ $$
- $$ c $$: یکی از ساقهای ذوزنقه برابر با $$ ۱۶ $$
- $$ d $$: ساق دیگر ذوزنقه برابر با $$ ۱۲ $$
اکنون، مقادیر معلوم را درون فرمول قرار میدهیم:
$$ P = ۱۰ + ۲۱ + ۱۶ + ۱۲ $$
$$ P = ۵۹ $$
توجه داشته باشید که یکا یا واحد اندازه محیط، همان واحد اندازه ضلعها است. به عبارت دیگر، اگر اندازه ضلعها با واحد متر داده شود، اندازه محیط نیز با واحد متر به دست میآید. در صورت عدم بیان واحد ضلع، محیط را بدون واحد مینویسیم.
چگونه محاسبه محیط و مساحت ذوزنقه را به خوبی یاد بگیریم؟
برای یادگیری سریع، ساده و اصولی مباحث ریاضی و هندسه، باید پایه خود را قوی کنید. این کار، با مطالعه کتابهای درسی و حل مثالهای متعدد امکانپذیر است. البته کتابهای درسی به گونهای نوشته میشوند که بسیاری از دانشآموزان، برای درک مثالها و تمرینهایشان به راهنمایی معلم نیاز دارند. از اینرو، دانشآموزان معمولا به دنبال یک منبع کمک آموزشی خوب میگردند. بهترین منبع کمک آموزشی، منبعی است که ضمن توضیح دقیق مبانی یک موضوع، مثالها و تمرینهای متنوعی را برای دانشآموزان حل کند. فرادرس، فیلمهای آموزشی رایگان متعددی را در زمینه نحوه انجام محاسبات مربوط به شکلهای هندسی تهیه کرده است. برای مشاهده این فیلمها، بر روی عنوان آنها کلیک کنید:
مبحث محیط و مساحت، محدود به دوره ابتدایی نیست. دانشآموزان دورههای اول و دوم متوسطه نیز با این مبحث سر و کار دارند. فرادرس، آموزشهای متنوعی را نیز برای این دانشآموزان تهیه کرده است که در ادامه لینک مشاهده آنها را برای شما آوردهایم:
در بخش بعدی این مطلب از مجله فرادرس، نحوه محاسبه محیط انواع ذوزنقه را آموزش میدهیم.
محیط انواع ذوزنقه چگونه محاسبه می شود؟
اصول محاسبه محیط انواع ذوزنقه، یکسان است. به عبارت دیگر، اندازه تمام محیطها، از جمع اندازه ضلعها به دست میآید. با این وجود، فرمول جبری محیط انواع خاص ذوزنقه، کمی متفاوت نوشته میشود.
بر اساس اندازه ساقها و زاویه بین ساق و قاعده، میتوان ذوزنقهها را به سه نوع متساویالساقین، مختلفالاضلاع و قائمالزاویه تقسیم کرد. تصویر زیر، انواع ذوزنقهها را نمایش میدهد.

محیط ذوزنقه متساوی الساقین چگونه محاسبه می شود؟
ذوزنقه متساویالساقین، ذوزنقهای با اندازه ساقهای برابر است. بنابراین، فرمول محیط این نوع ذوزنقه به صورت زیر نوشته میشود:
محیط ذوزنقه متساویالساقین
=
ساق دوم + ساق اول + قاعده دوم + قاعده اول
=
(ساق × ۲) + قاعده دوم + قاعده اول
فرمول جبری محیط متساویالساقین عبارت است از:
$$ P = a+ b + ۲ c $$
- $$ P $$: محیط ذوزنقه متساویالساقین
- $$ a $$: اندازه یکی از قاعدههای ذوزنقه متساویالساقین
- $$ b $$ اندازه قاعده دیگر ذوزنقه متساویالساقین
- $$ c $$: اندازه یکی از ساقهای ذوزنقه متساویالساقین
مثال ۴: محاسبه محیط ذوزنقه متساوی الساقین
محیط یک ذوزنقه متساویالساقین که اندازه قاعدهها و ساقهای آن به ترتیب برابر با ۱۲، ۱۸ و ۷ متر است را به دست بیاورید.
محیط یک ذوزنقه متساویالساقین، از فرمول زیر به دست میآید:
(ساق × ۲) + قاعده دوم + قاعده اول
$$ P = a+ b + ۲ c $$
- $$ a $$: اندازه یکی از قاعدههای ذوزنقه متساویالساقین برابر با $$ ۱۲ $$
- $$ b $$ اندازه قاعده دیگر ذوزنقه برابر با $$ ۱۸ $$
- $$ c $$: اندازه یکی از ساقهای ذوزنقه برابر با $$ ۷ $$
مقادیر معلوم را درون فرمول جایگذاری میکنیم:
$$ P = ۱۲ + ۱۸ + ( ۲ times ۷ ) $$
$$ P = ۳۰ + ۱۴ $$
$$ P = ۴۴ $$
در نتیجه، محیط ذوزنقه متساویالساقین برابر با $$ ۴۴ $$ متر است.
امکان محاسبه محیط یک ذوزنقه متساویالساقین با استفاده از اندازه ارتفاع آن وجود دارد. در بخش محیط ذوزنقه قائمالزاویه، اصول این روش را به همراه حل مثال توضیح میدهیم.
محیط ذوزنقه قائم الزاویه چگونه محاسبه می شود؟
ذوزنقه قائمالزاویه، ذوزنقهای است که یکی از ساقهای آن با دو قاعده، زاویه قائمه یا $$ ۹۰ $$ درجه میسازد. روش محاسبه محیط ذوزنقه قائمالزاویه برای دانشآموزان دورهها و پایههای مختلف میتواند متفاوت باشد. در دوره ابتدایی، محیط یک ذوزنقه قائمالزاویه، توسط فرمول کلی زیر محاسبه میشود:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط ذوزنقه
مجموع ساقها و قاعدهها = محیط ذوزنقه
$$ P = a + b + c + d $$
- $$ P $$: محیط ذوزنقه قائمالزاویه
- $$ a $$: اندازه یکی از قاعدههای ذوزنقه قائمالزاویه
- $$ b $$ اندازه قاعده دیگر ذوزنقه قائمالزاویه
- $$ c $$: اندازه ساق قائم ذوزنقه قائمالزاویه
- $$ d $$: اندازه ساق غیرقائم ذوزنقه قائمالزاویه
در پایه هشتم از دوره متوسطه دوم، دانشآموزان با قضیه فیثاغورس آشنا میشوند. قضیه فیثاغورس، رابطه بین اندازه ضلعهای یک مثلث قائمالزاویه را به صورت زیر تعریف میکند:
$$ a ^ ۲ = b ^ ۲ + c ^ ۲ $$
- $$ a $$: اندازه وتر مثلث قائمالزاویه
- $$ b $$: اندازه یکی از ساقهای مثلث قائمالزاویه
- $$ c $$: اندازه ساق دیگر مثلث قائمالزاویه
از این رابطه میتوان برای محاسبه اندازه اجزای مختلف ذوزنقه قائمالزاویه و حتی ذوزنقه متساویالساقین استفاده کرد. برای این کار، نیاز به اندازه ارتفاع ذوزنقه داریم.
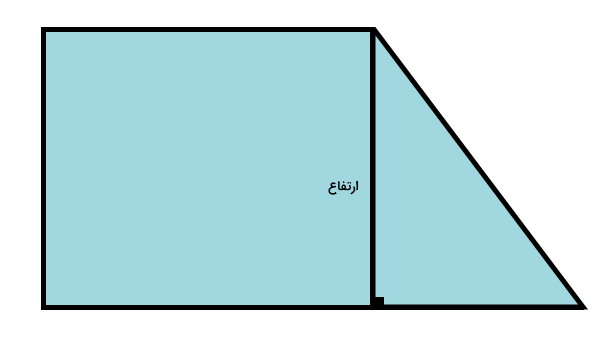
ارتفاع ذوزنقه، پارهخطی است که از به دو قاعده ذوزنقه عمود میشود. بنابراین، اندازه ارتفاع ذوزنقه قائمالزاویه با اندازه ساق قائم آن برابر است. از این نکته و رابطه فیثاغورس میتوان برای محاسبه محیط ذوزنقه قائمالزاویه استفاده کرد. اگر اندازه دو قاعده و ارتفاع ذوزنقه قائمالزاویه را داشته باشیم، در واقع اندازه یکی از ساقها معلوم میشود.
مثال ۵: محاسبه محیط ذوزنقه قائم الزاویه
تصویر زیر یک ذوزنقه قائمالزاویه و اندازه ضلعهای آن را نمایش میدهد.
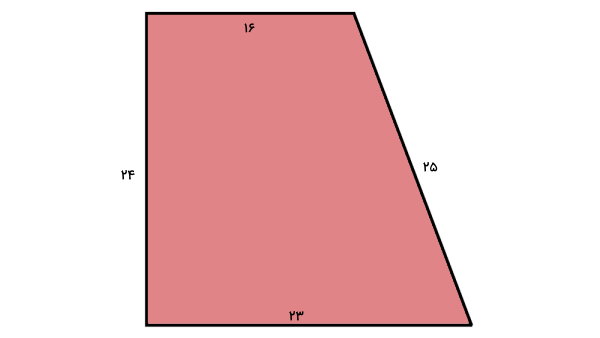
اندازه محیط شکل بالا را به دست بیاورید.
در ذوزنقه قائمالزاویه، اندازه قاعدهها و ساقها به صورت زیر است:
- اندازه قاعده بزرگ: $$ ۲۳ $$ میلیمتر
- اندازه قاعده کوچک: $$ ۱۶ $$ میلیمتر
- اندازه ساق قائم: $$ ۲۴ $$ میلیمتر
- اندازه ساق غیرقائم: $$ ۲۵ $$ میلیمتر
از آنجایی که اندازه تمام ضلعهای ذوزنقه را داریم، محیط آن را با استفاده از فرمول زیر به دست میآوریم:
مجموع ساقها و قاعدهها = محیط ذوزنقه
$$ P = a + b + c + d $$
$$ P = ۲۳ + ۱۶ + ۲۴ + ۲۵ = ۸۸ $$
بنابراین، اندازه محیط برابر با $$ ۸۸ $$ میلیمتر است.
مثال ۶: محاسبه محیط ذوزنقه قائم الزاویه با ارتفاع
اندازه قاعدههای یک ذوزنقه قائمالزاویه برابر با $$ ۲۳ $$ و $$ ۱۶ $$ سانتیمتر است. اگر ارتفاع این ذوزنقه برابر با $$ ۲۴ $$ سانتیمتر باشد، محیط آن چقدر خواهد بود؟
برای حل این مثال، ابتدا شکل ذوزنقه را بر اساس اطلاعات مسئله رسم میکنیم.
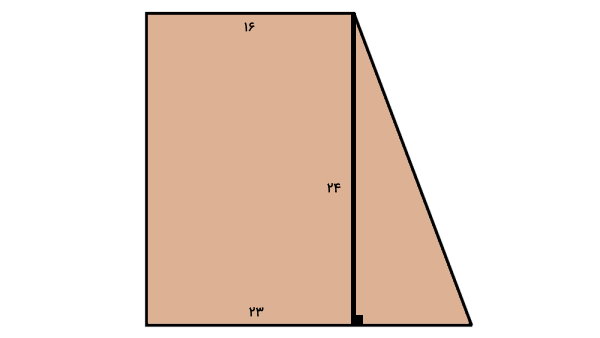
با توجه به اطلاعات مسئله، اندازه دو ضلع ذوزنقه را داریم. برای محاسبه محیط، باید اندازه هر چهار ضلع را داشته باشیم. همانطور که میدانید، ارتفاع ذوزنقه قائمالزاویه با اندازه ساق قائم آن برابر است. بنابراین، علاوه بر اندازه قاعدهها، اندازه یکی از ساقها را هم مشخص کردیم.
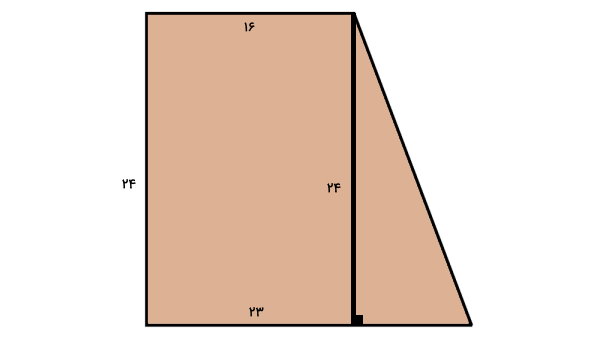
اکنون، فقط به اندازه ساق غیرقائم برای تعیین محیط نیاز داریم. اگر ارتفاع ذوزنقه قائمالزاویه را در تقاطع ساق غیرقائم با قاعده کوچک رسم کنیم، یک مثلث قائمالزاویه به وجود میآید.
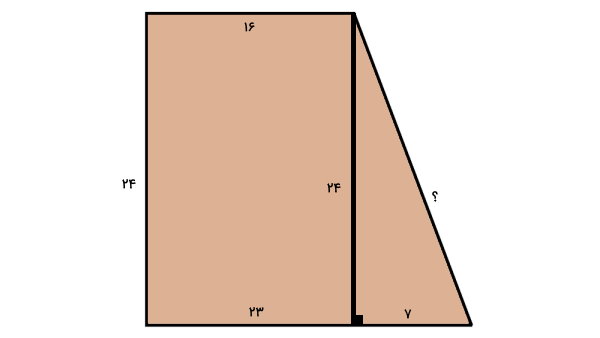
اندازه یکی از ساقهای این مثلث، برابر با ارتفاع ذوزنقه و اندازه ساق دیگر آن، برابر با اختلاف اندازههای قاعده بزرگ و کوچک است. به این ترتیب، داریم:
$$ ۲۴ $$ = اندازه یکی از ساقهای مثلث
$$ ۲۳ – ۱۶ = ۷ $$ = اندازه ساق دیگر مثلث
با کمک قضیه فیثاغورس میتوانیم اندازه وتر این مثلث یا همان ضلع چهارم ذوزنقه را به دست بیاوریم. بر اساس رابطه فیثاغورس، داریم:
$$ a ^ ۲ = b ^ ۲ + c ^ ۲ $$
- $$ a $$: اندازه وتر مثلث قائمالزاویه
- $$ b $$: اندازه یکی از ساقهای مثلث قائمالزاویه برابر با $$ ۲۴ $$ سانتیمتر
- $$ c $$: اندازه ساق دیگر مثلث قائمالزاویه برابر با $$ ۷ $$ سانتیمتر
این مقادیر را درون رابطه قرار میدهیم:
$$ a ^ ۲ = ۲۴ ^ ۲ + ۷ ^ ۲ $$
$$ a ^ ۲ = ۵۷۶ + ۴۹ $$
$$ a ^ ۲ = ۶۲۵ $$
$$ a = sqrt { ۶۲۵ } $$
$$ a = ۲۵ $$
به این ترتیب، اندازه ضلع چهارم ذوزنقه قائمالزاویه یا همان ساق غیرقائم برابر با $$ ۲۵ $$ سانتیمتر به دست آمد. این اندازه را به همراه دیگر اندازههای معلوم در رابطه محاسبه محیط ذوزنقه قائمالزاویه جایگذاری میکنیم:
$$ P = a + b + c + d $$
- $$ P $$: محیط ذوزنقه قائمالزاویه
- $$ a $$: اندازه قاعده بزرگ ذوزنقه قائمالزاویه برابر با $$ ۲۳ $$ سانتیمتر
- $$ b $$ اندازه قاعده کوچک ذوزنقه قائمالزاویه برابر با $$ ۱۶ $$ سانتیمتر
- $$ c $$: اندازه ساق قائم ذوزنقه قائمالزاویه برابر با $$ ۲۴ $$ سانتیمتر
- $$ d $$: اندازه ساق غیرقائم ذوزنقه قائمالزاویه برابر با $$ ۲۵ $$ سانتیمتر
$$ P = ۲۳ + ۱۶ + ۲۴ + ۲۵ = ۸۸ $$
در نتیجه، اندازه محیط، برابر با $$ ۸۸ $$ سانتیمتر شد.
اگر اندازه ارتفاع و دو قاعده ذوزنقه متساویالساقین را داشته باشیم، به کمک فرآیندی مانند روش حل مثال بالا، میتوانیم اندازه دو ساق را به دست بیاوریم. به این ترتیب، امکان محاسبه محیط ذوزنقه با جمع اندازههای تمام ضلعها فراهم میشود. فرادرس، یک فیلم آموزشی مفید را تهیه کرده است که مشاهده آن میتواند شما را در یادگیری سریع و راحت قضیه فیثاغورس و دیگر درسهای کتاب ریاضی هشتم یاری کند. لینک مشاهده این فیلم آموزشی در ادامه آورده شده است:
محیط ذوزنقه مختلف الاضلاع چگونه محاسبه می شود؟
ذوزنقه مختلفالاضلاع، ذوزنقهای است که هیچ دو ضلع هماندازه و هیچ زاویه داخلی قائمه ندارد. این نوع ذوزنقه، حالت عمومی ذوزنقه در نظر گرفته میشود. تصویر زیر، یک ذوزنقه مختلفالاضلاع را نمایش میدهد.
به دلیل برابر نبودن اندازه ضلعها، محیط ذوزنقه مختلفالاضلاع با استفاده از فرمول کلی زیر محاسبه میشود:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط ذوزنقه
مجموع ساقها و قاعدهها = محیط ذوزنقه
$$ P = a + b + c + d $$
- $$ P $$: محیط ذوزنقه مختلفالاضلاع
- $$ a $$: اندازه یکی از قاعدههای ذوزنقه مختلفالاضلاع
- $$ b $$ اندازه قاعده دیگر ذوزنقه مختلفالاضلاع
- $$ c $$: اندازه یکی از ساقهای ذوزنقه مختلفالاضلاع
- $$ d $$: اندازه ساق دیگر ذوزنقه مختلفالاضلاع
مثال ۷: محاسبه اندازه قاعده ذوزنقه مختلفالاضلاع از روی محیط
مجموع اندازههای یک ذوزنقه مختلفالاضلاع برابر با $$ ۷۱ $$ متر است. اگر مجموع اندازه ساقها برابر با $$ ۲۷ $$ متر و اندازه یکی از قاعدهها برابر با $$ ۲۹ $$ متر باشد، اندازه قاعده دیگر چقدر خواهد بود؟
برای به دست آوردن اندازه محیط ذوزنقه مختلفالاضلاع، از فرمول زیر استفاده میکنیم:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط ذوزنقه
مجموع ساقها و قاعدهها = محیط ذوزنقه مختلفالاضلاع
مقادیر معلوم را درون این فرمول قرار میدهیم:
$$ ۲۹ + ۲۷ $$ + قاعده مجهول = $$ ۷۱ $$
$$ ۷۱ – ۲۷ – ۲۹ $$ = قاعده مجهول
$$ ۷۱ – ۵۶ $$ = قاعده مجهول
$$ ۱۵ $$ = قاعده مجهول
در نتیجه، اندازه قاعده دیگر ذوزنقه برابر با $$ ۱۵ $$ متر است.
آزمون سنجش یادگیری محیط ذوزنقه
در این بخش، سطح اطلاعات شما در مبحث محیط ذوزنقه را با طرح سوالهای چندگزینهای میسنجیم. پس از جواب دادن به تمام سوالها، نتیجه آزمون برای شما به نمایش درمیآید. به این ترتیب میتوانید نقاط ضعف و قوت خود را شناسایی کرده و با حل مثالهای بیشتر، بر روی مسائل محیط ذوزنقه تسلط پیدا کنید.
کدام گزینه، اندازه محیط ذوزنقه نمایش داده شده در تصویر زیر است؟
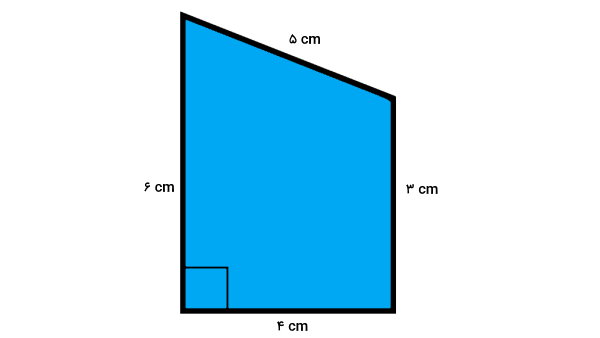
محیط یک چندضلعی، از مجموع اندازه ضلعهای آن به دست میآید. ذوزنقه مورد سوال، چهار ضلع به اندازههای $$ ۵ $$، $$ ۳ $$، $$ ۴ $$ و $$ ۶ $$ دارد. بنابراین، محیط آن برابر است با:
ضلع چهارم + ضلع سوم + ضلع دوم + ضلع اول = محیط ذوزنقه
$$ ۵ + ۳ + ۴ + ۶ $$ = محیط
$$ ۱۸ $$ = محیط
در نتیجه، اندازه محیط برابر با $$ ۱۸ $$ است.
اندازه مجموع اندازه قاعدههای یک ذوزنقه مختلفالاضلاع برابر با $$ ۹۹ $$ سانتیمتر و مجموع اندازه ساقهای آن برابر با $$ ۱۰۱ $$ سانتیمتر است. محیط این ذوزنقه را به دست بیاورید.
۲۰۰ سانتیمتر
۲۰۲ سانتیمتر
۱۸۸ سانتیمتر
۱۸۰ سانتیمتر
اندازه محیط ذوزنقه از مجموع اندازه قاعدهها و ساقهای آن به دست میآید. برای محاسبه این اندازه برای ذوزنقه مختلف الاضلاع، از فرمول زیر استفاده میکنیم:
مجموع ساقها + مجموع قاعدهها = محیط ذوزنقه مختلفالاضلاع
$$ ۹۹ + ۱۰۱ $$ = محیط
$$ ۲۰۰ $$ = محیط
در نتیجه، اندازه محیط برابر با $$ ۲۰۰ $$ است.
در یک ذوزنقه متساویالساقین، اندازه قاعدهها برابر با $$ ۳ $$ و $$ ۴ $$ اینچ است. اگر محیط این ذوزنقه برابر با $$ ۱۰ $$ اینچ باشد، کدامیک از گزینههای زیر، اندازه ساقهای ذوزنقه خواهد بود؟
در ذوزنقه متساویالساقین، اندازه ساقها با یکدیگر برابر است. بر اساس صورت سوال، اندازه دو قاعده و محیط ذوزنقه را داریم. با استفاده از این مقادیر و فرمول زیر میتوانیم اندازه ساقها را به دست بیاوریم:
$$ P = a + b + ۲ c $$
- $$ P $$: محیط ذوزنقه متساویالساقین برابر با $$ ۱۰ $$ اینچ
- $$ a $$: اندازه یکی از قاعدههای ذوزنقه متساویالساقین برابر با $$ ۴ $$ اینج
- $$ b $$ اندازه قاعده دیگر ذوزنقه متساویالساقین برابر با $$ ۳ $$ اینچ
- $$ c $$: اندازه یکی از ساقهای ذوزنقه متساویالساقین
اندازههای معلوم را درون فرمول قرار میدهیم:
$$ ۱۰ = ۴ + ۳ + ۲ c $$
$$ ۱۰ = ۷ + ۲ c $$
$$ ۲ c = ۱۰ – ۷ $$
$$ ۲ c = ۳ $$
$$ c = frac { ۳ } { ۲ } $$
$$ c = ۱/۵ $$
در نتیجه، اندازه ساقهای ذوزنقه برابر با $$ ۱/۵ $$ اینچ است.
یک ذوزنقه قائمالزاویه با اندازه قاعدههای $$ ۶۹ $$ و $$ ۷۸ $$ میلیمتر را در نظر بگیرید. اگر ارتفاع این ذوزنقه برابر با $$ ۴۰ $$ میلیمتر باشد، اندازه محیط ذوزنقه، کدامیک از گزینههای زیر خواهد بود؟
در ذوزنقه قائمالزاویه، اندازه ارتفاع با اندازه ساق قائم برابر است. علاوه بر این، اندازه ساق دیگر، بر اساس قضیه فیثاغورس و رابطه زیر به دست میآید:
$$ a ^ ۲ = b ^ ۲ + c ^ ۲ $$
- $$ a $$: اندازه ساق غیرقائم ذوزنقه قائمالزاویه
- $$ b $$: اندازه ساق قائم ذوزنقه قائمالزاویه برابر با $$ ۴۰ $$ میلیمتر
- $$ c $$: اختلاف اندازه قاعده بزرگ و کوچک ذوزنقه قائمالزاویه برابر با $$ ۷۸ – ۶۹ = ۹ $$
$$ a ^ ۲ = ۴۰ ^ ۲ + ۹ ^ ۲ $$
$$ a ^ ۲ = ۱۶۰۰ + ۸۱ $$
$$ a ^ ۲ = ۱۶۸۱ $$
$$ a = ۴۱ $$
اکنون، اندازه هر چهار ضلع ذوزنقه را داریم. این اندازهها را با هم جمع میکنیم:
$$ P = ۶۹ + ۷۸ + ۴۰ + ۴۱ = ۲۲۸ $$
در نتیجه، اندازه محیط ذوزنقه برابر با $$ ۲۲۸ $$ میلیمتر است.
محیط یک ذوزنقه متساویالساقین به ارتفاع $$ ۸ $$ سانتیمتر و اندازه قاعدههای $$ 44 $$ و $$ ۱۴ $$ سانتیمتر، کدامیک از گزینههای زیر است؟
۱۰۶ سانتیمتر
برای پاسخگویی به این سوال، ابتدا تصویر ذوزنقه متساویالساقین را به همراه اندازههای معلوم رسم میکنیم.
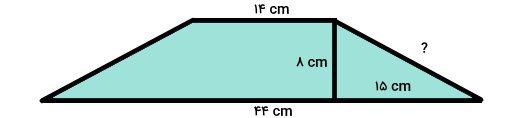
بر اساس اطلاعات موجود، اندازه دو قاعده را داریم. برای تعیین محیط، باید اندازه دو ساق را به دست بیاوریم. این کار، با استفاده از اندازه ارتفاع و نصف اختلاف اندازه قاعدهها انجام میشود. با توجه به قضیه فیثاغورس در مثلث قائمالزاویه، داریم:
$$ a ^ ۲ = ۸ ^ ۲ + ۱۵ ^ ۲ $$
$$ a ^ ۲ = ۶۴ + ۲۲۵ $$
$$ a ^ ۲ = ۲۸۹ $$
$$ a = ۱۷ $$
به دلیل برابر بودن اندازه ساقها در ذوزنقه متساویالساقین، اندازه هر دو ساق برابر با $$ ۱۷ $$ میلیمتر است. اکنون با جایگذاری این اندازه و اندازه قاعدهها در فرمول زیر، محیط ذوزنقه را محاسبه میکنیم:
$$ P = a+ b + ۲ c $$
- $$ P $$: محیط ذوزنقه متساویالساقین
- $$ a $$: اندازه قاعده بزرگ ذوزنقه متساویالساقین برابر با $$ ۲۹ $$ میلیمتر
- $$ b $$ اندازه قاعده کوچک ذوزنقه متساویالساقین برابر با $$ ۱۴ $$ میلیمتر
- $$ c $$: اندازه ساقهای ذوزنقه متساویالساقین برابر با $$ ۱۷ $$ میلیمتر
$$ P = ۴۴ + ۱۴ + ( ۲ times ۱۷ ) = ۹۲ $$
در نتیجه، محیط برابر با $$ ۹۲ $$ میلیمتر است.
محاسبه آنلاین محیط ذوزنقه
ابزارهای اینترنتی، انجام محاسبات ریاضی را سادهتر کردهاند. این ابزارها، با یک جستجوی ساده در اختیار شما قرار میگیرند و امکان حل بسیاری از مسائل مانند مسائل مربوط به محیط ذوزنقه را فراهم میکنند. به عنوان مثال، اگر عبارت «Trapezoid Perimeter» را در گوگل جستجو کنید، یک ماشینحساب مشابه تصویر زیر برایتان به نمایش در میآید.
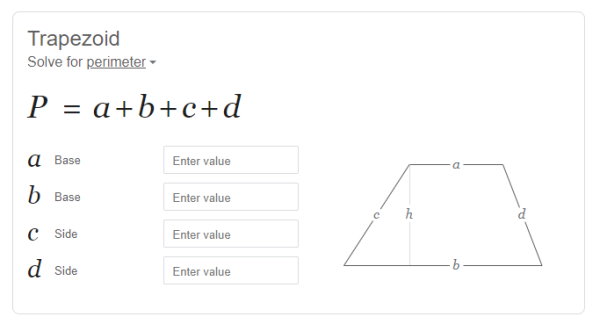
ماشینحساب گوگل از ما میخواهد تا برای محاسبه محیط، اندازه ضلعهای ذوزنقه را وارد کنیم. با انجام این کار، اندازه محیط و فرمول محاسبه آن به نمایش درمیآید.
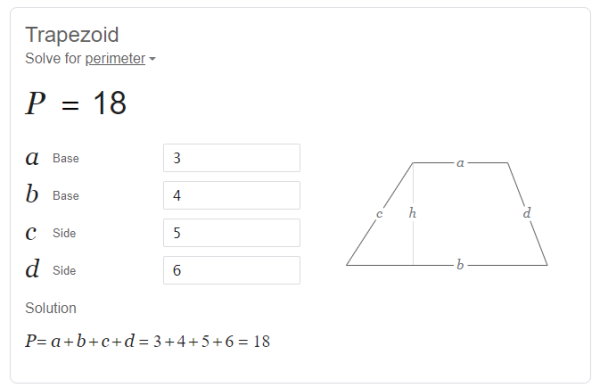
از دیگر سایتهای کاربردی در زمینه ریاضی، میتوان به «OmniCalculator» (+) اشاره کرد. این سایت، سه ماشینحساب زیر را برای انجام محاسبات انواع مختلف ذوزنقه در اختیار کاربران قرار میدهد:
- ماشین حساب محیط ذوزنقه (+)
- ماشین حساب محیط ذوزنقه متساویالساقین (+)
- ماشین حساب محیط ذوزنقه قائمالزاویه (+)
تصویر زیر، رابط کاربری ماشین حساب ذوزنقه در OmniCalculator را نمایش میدهد.
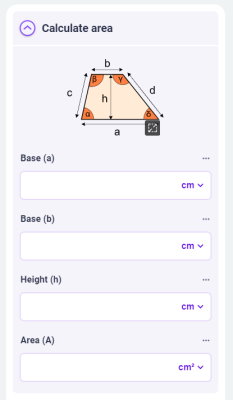
با وارد کردن اندازههای معلوم، OmniCalculator، بسیاری از اندازه مجهول از جمله ارتفاع، زاویههای داخلی و حتی میانه را نیز محاسبه میکند.
source