درخت تصمیم چیست؟

«درخت‌ تصمیم» (Decision Tree) به عنوان یکی از الگوریتم‌های محبوب «یادگیری ماشین» (Machine Learning) محسوب می‌شود که از آن می‌توان برای حل مسائل «طبقه‌ بندی» (Classification) و «رگرسیون» (Regression) استفاده کرد. تفسیر و پیاده‌سازی این الگوریتم آسان است و به همین دلیل، انتخابی مناسب برای افراد مبتدی در حوزه‌ یادگیری ماشین به شمار می‌رود. در این مطلب از مجله فرادرس قصد داریم به این پرسش پاسخ دهیم که درخت تصمیم چیست و چگونه کار می‌کند.

فهرست مطالب این نوشته

در ابتدای مطلب، به مفهوم درخت تصمیم و اصطلاحات تخصصی مرتبط به آن می‌پردازیم و سپس انواع معیارهای انتخاب ویژگی را در این الگوریتم به همراه مثال شرح خواهیم داد. همچنین، به مزایا و معایب این الگوریتم و کاربردهای آن اشاره می‌کنیم و با استفاده از یک مثال برنامه نویسی، نحوه پیاده‌سازی درخت تصمیم را آموزش می‌دهیم.

الگوریتم درخت تصمیم به عنوان یکی از انواع الگوریتم های یادگیری ماشین با رویکرد یادگیری نظارت شده محسوب می‌شود که از آن می‌توان برای حل مسائل رگرسیون و طبقه بندی استفاده کرد. این الگوریتم یک ساختار درختی وارونه دارد که شبیه به فلوچارت است و به سادگی می‌تواند تفکر انسان را در سطوح مختلف تقلید کند. به همین دلیل، درک و تفسیر عملکرد درخت تصمیم‌ آسان است. به عبارتی، از درخت تصمیم‌ به عنوان «جعبه سفید» (White Box) یاد می‌کنند که برخلاف الگوریتم‌های «جعبه سیاه» (Black Box) مانند شبکه‌های عصبی، منطق تصمیم‌گیری داخلی آن قابل درک و تفسیر است.

ساختار سلسله‌مراتبی درخت تصمیم بستری را فراهم می‌کند که این الگوریتم در هر سطح از درخت، بر اساس یک سری قوانین از پیش تعریف شده، درباره تقسیم داده‌ها در شاخه‌های مختلف درخت به تصمیم‌گیری بپردازد. پیش از آن که به توضیح دقیق‌تر عملکرد این الگوریتم بپردازیم، لازم است یک سری اصطلاح تخصصی مرتبط با درخت تصمیم را توضیح دهیم تا به خواننده در درک روال کار این الگوریتم کمک کند.

اصطلاحات مربوط به درخت تصمیم

بالاتر گفتیم که درخت تصمیم چیست و در ادامه قصد داریم برخی اصطلاحات مربوط به این حوزه را نیز بررسی کنیم تا مخاطبان این مطلب بتوانند به راحتی مفاهیم بخش‌های بعدی را درک کنند. در ادامه، فهرستی از این اصطلاحات را ملاحظه می‌کنید:

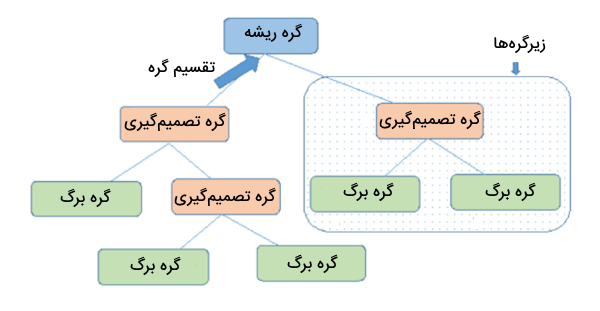
اجزای درخت تصمیم چیست — اجزای درخت تصمیم

«گره» (Node) و «یال» (Edge): درخت تصمیم از چندین گره و شاخه تشکیل شده است. شاخه‌ها، گره‌های درخت را به یکدیگر متصل می‌کنند و گره‌ها بر اساس شرایط و قوانین تعریف شده، داده‌ها را تقسیم می‌کنند.
«گره ریشه» (Root Node): اولین گره در درخت است که تقسیم‌بندی داده‌ها از این گره آغاز می‌شود.
«گره تصمیم‌گیری» (Decision Node): گره‌ای است که به دو یا چند گره دیگر تقسیم می‌شود و نشان‌دهنده‌ یک تصمیم یا شرط میانی است.
«گره برگ» (Leaf Node): به گره‌‌های آخرین سطح درخت، گره برگ گفته می‌شود که دیگر قابل تقسیم به گره‌های دیگر نیستند و نتیجه یا پیش‌بینی نهایی درخت را نشان می‌دهند. از این گره‌ها با عنوان «گره‌های انتهایی» (Terminal Node) نیز یاد می‌شود.
«شاخه» (Branch) یا «زیر درخت» (Sub-Tree): زیرمجموعه‌ای از کل درخت تصمیم‌گیری است که مسیری از درخت را نشان می‌دهد.
«هرس» (Pruning): این فرایند شامل حذف گره‌های غیرضروری از درخت برای جلوگیری از رخداد «بیش برازش» (Overfitting) و ساده‌سازی مدل است.
«گره والد» (Parent Node) و «گره فرزند» (Child Node): در یک درخت تصمیم‌گیری، گره‌ای که به زیرمجموعه‌ای از گره‌ها تقسیم می‌شود، گره‌ والد نامیده می‌شود و گره‌هایی که از گره والد نشأت می‌گیرند، گره‌های فرزند نام دارند. گره‌ والد نشان‌دهنده‌ یک تصمیم یا شرط است، در حالی که گره‌های فرزند نشان‌دهنده‌ نتایج بالقوه یا تصمیمات بیشتر بر اساس آن شرط هستند.

حال که با اجزای اصلی الگوریتم درخت تصمیم آشنا شدید، در ادامه پاسخ به پرسش درخت تصمیم چیست ، لازم است نحوه طراحی و ترسیم این الگوریتم را به همراه ارائه مثال ساده و کاربردی توضیح دهیم تا به درک بهتر آن کمک کند.

رسم درخت تصمیم

در درخت‌های تصمیم‌گیری برخلاف درخت‌های واقعی از بالا به پایین رشد می‌کنند! یعنی گره ریشه در بالای درخت قرار دارد و سپس در سطوح پایین‌تر، به گره‌های متعددی تقسیم می‌شود. به بیان ساده، درخت‌های تصمیم‌گیری مجموعه‌ای از سوالات «اگر-آنگاه» (if-else) هستند. هر گره یک سوال را مطرح می‌کند و بر اساس پاسخ به آن سوال، مسیر حرکت به گره‌های بعدی مشخص می‌شود. این سوالات، مربوط به ویژگی‌های داده‌های مسئله است. به منظور درک بهتر این موضوع، از یک مثال ساده کمک می‌گیریم.

فرض کنید مجموعه داده‌ای داریم که بر اساس آن می‌خواهیم الگوریتم درخت تصمیم را آموزش دهیم تا بتواند پیش‌بینی کند هوا ابری یا بارانی است و آیا می‌توان در آن هوا بیرون از خانه بازی کرد یا خیر؟ مجموعه داده شامل اطلاعاتی از وضعیت هوا برای چندین روز متوالی است که وضعیت هوا (آفتابی، ابری، بارانی)، دما، میزان رطوبت، وضعیت باد را مشخص می‌کند. در تصویر زیر، نمایی از این مجموعه داده را ملاحظه می‌کنید.

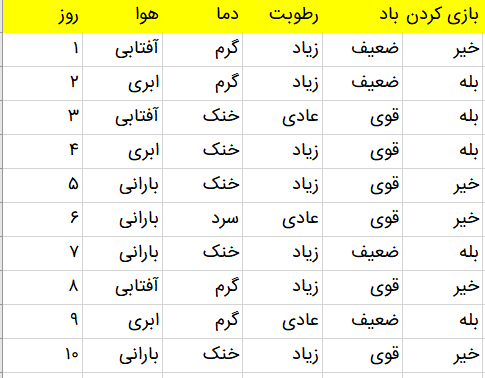
برای این مثال، می‌توانیم یک درخت تصمیم بسازیم که در هر سطح از درخت، داده‌ها را بر اساس ویژگی‌های تعریف شده، تقسیم‌بندی می‌کند تا در نهایت پاسخ مسئله مشخص شود. درخت تصمیم زیر، نمایی از شیوه دسته‌بندی داده‌ها را نشان می‌دهد. در ابتدا، داده به لحاظ وضعیت هوا سنجیده می‌شود. اگر هوا ابری باشد، به پاسخ نهایی مسئله می‌رسیم که نشان می‌دهد در هوای ابری می‌توان در فضای بیرون از خانه بازی کرد. اگر پاسخ سوال در گره ریشه، آفتابی باشد، درخت تصمیم به سراغ بررسی ویژگی بعدی یعنی «میزان رطوبت و وضعیت باد» می‌رود. در این مرحله، سوال دیگری پرسیده می‌شود که آیا میزان باد شدید است یا ضعیف؟ اگر وضعیت باد ضعیف و هوا بارانی باشد، فرد می‌تواند بیرون از خانه بازی کند. به این ترتیب، درخت تصمیم‌گیری با پرسیدن سوالات متوالی پیرامون ویژگی‌های داده‌ها، فرد را به سمت یک تصمیم نهایی هدایت می‌کند.

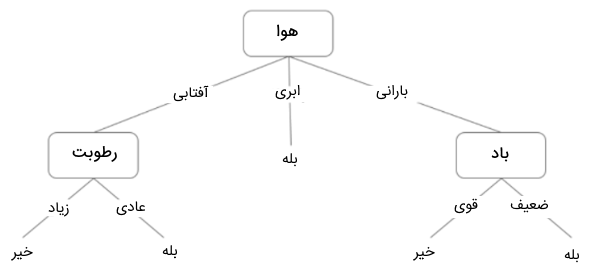
همان‌طور که در تصویر بالا ملاحظه می‌کنید، ویژگی ابری بودن هوا به سایر ویژگی‌ها تقسیم نشده است. علت توقف تقسیم در این نقطه چیست؟ برای پاسخ به این سوال، نیاز به درک چند مفهوم دیگر مانند «آنتروپی» (Entropy)، «کسب اطلاعات» (Information Gain) و «شاخص جینی» (Gini Index) داریم که در بخش‌های بعدی مطلب به آن‌ها می‌پردازیم. اما در اینجا می‌توان به زبان توضیح داد با توجه به داده‌های آموزشی، هرگاه هوا ابری باشد، همیشه می‌توان بیرون از خانه بازی کرد. از آنجایی که در این گره، بی‌نظمی یا تردیدی در خروجی وجود ندارد، نیازی به تقسیم بیشتر آن نیست.

درخت تصمیم‌ چگونه کار می‌کند؟

اگر بخواهیم پاسخ جامع‌تری به این پرسش ارائه دهیم که درخت تصمیم چیست ، لازم است به نحوه عملکرد آن نیز اشاره شود. عملیات درخت تصمیم از چندین مرحله تشکیل شده است که می‌توان مراحل آن را به این صورت خلاصه کرد:

ساخت گره ریشه: کار الگوریتم درخت تصمیم از ساخت گره ریشه شروع می‌شود و کل مجموعه داده در این گره قرار می‌گیرند.
انتخاب بهترین ویژگی: با استفاده از معیارهای انتخاب ویژگی نظیر Gini و بهره‌وری اطلاعاتی، بهترین ویژگی (که بیشترین تمایز را میان داده‌ها ایجاد می‌کند) برای تقسیم داده‌ها در گره ریشه انتخاب می‌شود.
تقسیم داده‌ها: ویژگی انتخاب‌ شده به عنوان یک گره تصمیم‌گیری درنظر گرفته شده و بر اساس آن، مجموعه داده به زیرمجموعه‌های کوچک‌تر تقسیم می‌شود.
تکرار مراحل ۲ و ۳: مراحل انتخاب بهترین ویژگی و تقسیم داده‌ها بر اساس ویژگی‌ها، به صورت «بازگشتی» (Recursive) برای هر زیرمجموعه (گره فرزند) تکرار می‌شود تا زمانی که یکی از شرایط زیر برقرار شود:
1. تمام نمونه‌های موجود در گره فرزند متعلق به یک کلاس یکسان باشند.
2. هیچ ویژگی دیگری برای گسترش درخت تصمیم وجود نداشته باشد.
3. هیچ نمونه‌ دیگری برای ساخت گره فرزند جدید باقی نمانده باشد.

اگر قصد دارید پاسخ مفصل‌تری درباره این سوال دریافت کنید که درخت تصمیم چیست و به دنبال مثال‌هایی با جزئیات بیشتر هستید، پیشنهاد می‌کنیم فیلم آموزش درخت تصمیم فرادرس را ملاحظه کنید که به طور رایگان برای مخاطبان فراهم شده است:

همچنین، اگر مایل هستید مطالب مرتبط بیشتری پیرامون سایر الگوریتم‌های یادگیری ماشین یاد بگیرید و با نحوه پیاده‌سازی آن‌ها با زبان‌ برنامه نویسی پایتون و زبان R آشنا شوید، می‌توانید در دوره‌های مختلف فرادرس شرکت کنید که در ادامه به برخی از آن‌ها اشاره شده است:

همچنین پلتفرم فرادرس، مجموعه دوره‌های آموزشی بسیار متنوع و کاربردی را در زمینه هوش مصنوعی، یادگیری ماشین و داده‌کاوی و شبکه‌های عصبی فراهم کرده است و چنانچه شما به یادگیری این مباحث علاقه‌مند هستید، می‌توانید از طریق لینک‌های زیر دوره‌های مختلف این سایت را ملاحظه کنید:

به منظور درک دقیق‌تر این سوال که درخت تصمیم چیست و بر چه اساسی کار می‌کند، در بخش بعدی به معیارهای انتخاب ویژگی در این الگوریتم می‌پردازیم زیرا این مدل یادگیری ماشین بر پایه این معیارها شکل می‌گیرد.

معیار انتخاب ویژگی در درخت تصمیم

حال که به این پرسش پاسخ دادیم که درخت تصمیم چیست و اصطلاحات فنی آن را شرح دادیم، باید به این نکته اشاره کنیم که برای انتخاب ویژگی‌ها برای هر سطح درخت، از معیارهای خاصی استفاده می‌شود. به عبارتی، معیار انتخاب ویژگی روشی است که از آن در الگوریتم‌های درخت تصمیم برای ارزیابی مفید بودن ویژگی‌های مختلف برای طبقه‌بندی مجموعه داده استفاده می‌شود. هدف اصلی این معیارها یافتن مناسب‌ترین ویژگی است که بتواند همگن‌ترین داده‌ها را در دسته‌های مشابه قرار دهد تا حداکثر سود اطلاعاتی حاصل شود.

روال تقسیم‌بندی داده‌ها به صورت بازگشتی انجام می‌شود و کار الگوریتم زمانی به اتمام می‌رسد که همه داده‌های موجود در یک گره، از ویژگی‌های مشابهی برخوردار باشند یا تقسیم داده‌ها به بهبود نتیجه کمکی نکند. ویژگی مهم تقسیم داده با روش درخت تصمیم این است که این الگوریتم نیازی به استخراج دانشی خاص در مورد داده‌ها ندارد و می‌تواند با داده‌هایی با ابعاد بالا کار کند. سه نوع معیار انتخاب ویژگی در درخت تصمیم استفاده می‌شود که در فهرست زیر به آن‌ها اشاره شده است:

آنتروپی
بهره اطلاعاتی
شاخص جینی

در ادامه، به توضیح هر یک از معیارهای ذکر شده در فهرست بالا می‌پردازیم.

محاسبه آنتروپی در درخت تصمیم به چه شکل است؟

اگر مطالعه مختصری پیرامون این پرسش داشته‌اید که درخت تصمیم چیست و به چه شکل داده‌ها را دسته‌بندی می‌کند، به احتمال زیاد با اصطلاحی با عنوان «آنتروپی» برخورد کرده‌اید. آنتروپی در درخت تصمیم برای اندازه‌گیری میزان بی‌نظمی در مجموعه داده استفاده می‌شود. به منظور درک بهتر این مفهوم، می‌توانیم از یک مثال ساده استفاده کنیم.

فرض کنید گروهی از دوستان می‌خواهند تصمیم بگیرند که یکشنبه به سینما بروند. دو فیلم با نام‌های «جنگ ستارگان» و «پدرخوانده» برای انتخاب وجود دارد. بر اساس آرا، ۵ نفر از دوستان تمایل دارند برای دیدن فیلم جنگ ستارگان به سینما بروند و ۵ نفر دیگر، دیدن فیلم پدرخوانده را ترجیح می‌دهند. در اینجا سوال مطرح می‌شود که در نهایت کدام فیلم باید انتخاب شود؟

انتخاب فیلم در این شرایط دشوار است، زیرا تعداد آرا برای هر دو فیلم تقریباً برابر است. این همان چیزی است که ما آن را بی‌نظمی می‌نامیم. با توجه به تعداد مساوی آرا برای هر دو فیلم، تصمیم‌گیری در مورد این که کدام فیلم را تماشا کنیم، سخت است. اگر ۸ نفر به دیدن فیلم جنگ ستارگان و ۲ نفر به دیدن فیلم پدرخوانده رای می‌دادند، تصمیم‌گیری بسیار آسان‌تر بود. در چنین حالتی، می‌توان به راحتی گفت که اکثریت افراد به دیدن جنگ ستارگان تمایل دارند و بنابراین همه افراد برای دیدن این فیلم به سینما می‌روند.

به عبارتی، می‌توان گفت مقدار آنتروپی برای نسبت نفرات ۵ به ۵ برابر با ۱ است زیرا در این تقسیم‌بندی، میزان بی‌نظمی بالا است و نمی‌توان به راحتی به نتیجه‌گیری نهایی رسید. در حالتی که نسبت نفرات ۸ به ۲ است، مقدار آنتروپی نزدیک به ۰ می‌شود و در این حالت راحت‌تر می‌توان نتیجه‌گیری کرد. در ادامه، فرمول آنتروپی را ملاحظه می‌کنید:

$$ E(S) = – p_{(+)} log p_{(+)} – p_{(-)} log p_{(-)}$$

+p: احتمال کلاس مثبت را نشان می‌دهد. به عبارت ساده‌تر، این نماد نشان‌دهنده میزان احتمال تعلق یک نمونه به دسته مثبت در یک زیرمجموعه خاص از داده‌های آموزشی است.
-p: احتمال کلاس منفی را نشان می‌دهد. به عبارتی، این نماد نشان‌دهنده احتمال تعلق یک نمونه به دسته منفی در همان زیرمجموعه از داده‌های آموزشی است.
S: زیرمجموعه‌ای از نمونه‌های آموزشی است. در ساخت درخت تصمیم، مجموعه داده اولیه اغلب بر اساس ویژگی‌ها یا شرایط خاص به زیرمجموعه‌هایی تقسیم می‌شود. این نماد S نشان‌دهنده یکی از این زیرمجموعه‌ها برای محاسبه آنتروپی است.

حال که فهمیدیم آنتروپی در درخت تصمیم چیست ، لازم است توضیح دهیم این مفهوم چه کاربردی در الگوریتم درخت تصمیم دارد. آنتروپی اساساً میزان ناخالصی یک گره را اندازه‌گیری می‌کند. مقدار ناخالصی نشان دهنده درجه تصادفی بودن است و به ما می‌گوید که داده‌ها تا چه حد تصادفی هستند.

فرض کنید ۱۲ داده آموزشی با ۳ ویژگی در اختیار داریم که با برچسب‌های Yes و No برچسب‌دهی شده‌اند. ۸ داده‌ در این مجموعه دارای برچسب Yes هستند و ۴ داده باقی مانده با No برچسب‌دهی شده‌اند. حال اگر بخواهیم این داده‌ها را بر اساس ویژگی اول تقسیم‌بندی کنیم، گره سمت چپ شامل ۵ داده با برچسب Yes و ۲ داده با برچسب No می‌شود. همچنین، گره سمت راست، ۳ داده با برچسب Yes و ۲ داده با برچسب No را در بر می‌گیرد. حاصل این تقسیم‌بندی را در تصویر زیر ملاحظه می‌کنید.

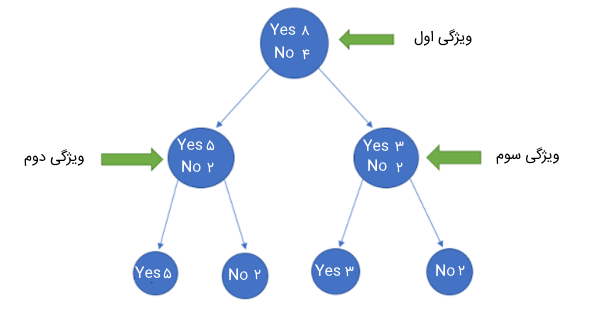
همان‌طور که در تصویر مشخص است، حاصل تقسیم‌بندی داده‌ها بر اساس ویژگی اول خالص نیست زیرا هنوز هم می‌توانیم داده‌های هر دو گره ایجاد شده را تقسیم کنیم تا در نهایت به گره‌هایی دست پیدا کنیم که صرفاً داده‌های یک کلاس را شامل می‌شوند. برای ساختن یک درخت تصمیم، باید مقدار آنتروپی برای هر تقسیم‌بندی را محاسبه کنیم و زمانی که خلوص ۱۰۰٪ شد، آن را به عنوان یک گره برگ در نظر بگیریم. به بیان دیگر، زمانی که تمام داده‌های موجود در گره‌ها از کلاس یکسان باشند، مقدار آنتروپی برابر با عدد صفر است که در این حالت به بهترین نحوه طبقه‌بندی داده رسیدیم. برای بررسی میزان بی‌نظمی (آنتروپی) گره‌های ۲ و ۳ از فرمول‌های زیر استفاده می‌کنیم.

محاسبه آنتروپی برای گره ۲:

$$ – left ( frac {5} {7} right ) log _2 left ( frac {5} {7} right ) – left ( frac {2} {7} right ) log _2 left ( frac {2} {7} right ) $$

$$ = (0.71 * -0.49) – (0.28 * -1.83) $$

$$ = -(-0.34) – (-0.51) $$

$$ = 0.34 + 0.51 $$

$$ = 0.85 $$

محاسبه آنتروپی برای گره ۳:

$$ – left ( frac {3} {5} right ) log _2 left ( frac {3} {5} right ) – left ( frac {2} {5} right ) log _2 left ( frac {2} {5} right ) $$

$$ = (0.6 * -0.73) – (0.4 * -1.32) $$

$$ = -(-0.438) – (-0.528) $$

$$ = 0.438 + 0.528 $$

$$ = 0.966 $$

در تصویر قبل، نحوه تقسیم‌بندی درخت تصمیم به خوبی دیده می‌شود. گره ۲ مقدار آنتروپی کم‌تری دارد یا و میزان ناخالصی آن نسبت به گره ۳ کم‌تر است. همان‌طور که قبلاً گفتیم، هدف کاهش عدم قطعیت یا ناخالصی در مجموعه داده است. در اینجا با استفاده از آنتروپی، ناخالصی یک گره خاص (ویژگی خاص) را بدست می‌آوریم، اما نمی‌دانیم آنتروپی گره والد با تقسیم داده‌ها تا چه حد کاهش می‌یابد. برای این منظور، از معیار جدیدی با نام Information Gain استفاده می‌شود که در ادامه به توضیح آن می‌پردازیم.

معیار بهره اطلاعاتی در درخت تصمیم چیست ؟

معیار Information Gain یا IG میزان اطلاعاتی را مشخص می‌کند که از یک ویژگی به دست می‌آید. به عبارتی، این معیار تعیین می‌کند که یک ویژگی چقدر مهم است. از آنجایی که ساخت درخت تصمیم، به طور کلی در مورد یافتن بهترین گره برای تقسیم داده است، با معیار بهره اطلاعاتی یا همان Information Gain می‌توان میزان اهمیت گره‌ها را مشخص کرد. این معیار بر پایه آنتروپی محاسبه می‌شود. چنانچه قصد دارید به طور مفصل‌تر با این معیار آشنا شوید و نحوه کاربرد آن را در الگوریتم درخت تصمیم بدانید، می‌توانید از فیلم آموزشی فرادرس استفاده کنید که به طور مفصل به این موضوع اختصاص دارد. لینک این دوره آموزشی فرادرس را در ادامه ملاحظه می‌کنید.

می‌توان گفت معیار IG میزان کاهش عدم قطعیت را با توجه به یک ویژگی خاص اندازه‌گیری می‌کند و همچنین یک عامل تعیین کننده برای این است که کدام ویژگی به عنوان گره تصمیم یا ریشه انتخاب شود. در ادامه، فرمول معیار IG را ملاحظه می‌کنید:

$$ Information Gain = E(Y) – E(Y | X) $$

بر اساس فرمول بالا، معیار IG از تفاضل آنتروپی مجموعه داده و آنتروپی مجموعه داده با در نظر گرفتن یک ویژگی خاص حاصل می‌شود. برای درک بهتر این معیار، مثالی را در نظر بگیریم. فرض کنید مسئله ما این است که مشخص کنیم با توجه به داده‌ها، آیا فرد تصمیم می‌گیرد که به باشگاه برود یا خیر؟ برای این مسئله، ۳۰ داده در اختیار داریم که هر داده شامل ۲ ویژگی «میزان انرژی» و «مقدار انگیزه» است. از مجموع کل داده‌ها، ۱۶ نفر به باشگاه می‌روند و ۱۴ نفر قصد رفتن به باشگاه را ندارند. ویژگی‌های میزان انرژی و مقدار انگیزه نیز می‌توانند مقادیر زیر را برای هر فرد شامل شوند:

ویژگی مقدار انرژی: این ویژگی می‌تواند با مقادیر «بالا» و «پایین» مشخص شود.
ویژگی مقدار انگیزه: این ویژگی می‌تواند سه مقدار «بدون انگیزه»، «خنثی» و «انگیزه بالا» را شامل شود.

بیایید ببینیم با استفاده از این دو ویژگی، درخت تصمیم‌ ما چگونه ساخته می‌شود. از معیار IG نیز استفاده می‌کنیم تا بر اساس آن تصمیم بگیریم کدام ویژگی در جایگاه گره ریشه و کدام ویژگی در جایگاه فرزند آن قرار می‌گیرد. در ابتدا، مقدار IG را برای ویژگی انرژی محاسبه می‌کنیم. همان‌طور که قبلا اشاره کردیم، مجموعه داده مسئله، شامل ۳۰ داده است که ۱۶ داده آن شامل افرادی است که به باشگاه می‌روند و ۱۴ داده آن اطلاعات افرادی هستند که به باشگاه نمی‌روند. بر اساس ویژگی انرژی، درخت زیر را شکل می‌دهیم:

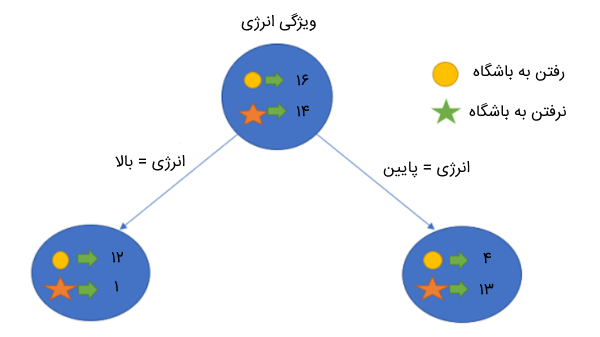
کاربرد معیار بهره اطلاعاتی در درخت تصمیم چیست

سپس، مقدار آنتروپی کل مجموعه داده و مقدار آنتروپی داده‌ها بر اساس ویژگی مقدار انرژی را با استفاده از فرمول زیر محاسبه می‌کنیم:

$$ E(Parent) = – left ( frac {16} {30} right ) log _2 left ( frac {16} {30} right ) – left ( frac {14} {30} right ) log _2 left ( frac {14} {30} right ) approx 0.99 $$

$$ E(Parent | ٍEnergy = ”high”) = – left ( frac {12} {13} right ) log _2 left ( frac {12} {13} right ) – left ( frac {1} {13} right ) log _2 left ( frac {1} {13} right ) approx 0.39 $$

$$ E(Parent | ٍEnergy = ”low”) = – left ( frac {4} {17} right ) log _2 left ( frac {4} {17} right ) – left ( frac {13} {17} right ) log _2 left ( frac {13} {17} right ) approx 0.79 $$

حال، میانگین وزن‌دار را برای آنتروپی‌های هر یک از گره‌های فرزند به صورت زیر محاسبه می‌کنیم:

$$ E(Parent | ٍEnergy) = frac {13} {30} * 0.39 + frac {17} {30} * 0.79 = 0.62 $$

در نهایت، با استفاده از فرمول زیر، مقدار IG را برای ویژگی انرژی محاسبه می‌کنیم:

$$ Information Gain = E(Parent) – E(Parent | Energy) $$

$$ = 0.99 – 0.62 $$

$$ = 0.37 $$

در ابتدا، مقدار آنتروپی برای مجموعه داده‌ اصلی (گره والد) حدود ۰.۹۹ بود. با توجه به مقدار به دست آمده برای معیار IG (یعنی ۰.۳۷)، می‌توانیم بگوییم که اگر ویژگی انرژی را به عنوان گره‌ ریشه انتخاب کنیم، آنتروپی مجموعه داده کاهش پیدا می‌کند. به همین ترتیب، همین کار را برای ویژگی انگیزه انجام می‌دهیم و مقدار IG را نیز برای آن محاسبه می‌کنیم.

$$ E(Parent) = 0.99 $$

$$ E(Parent | ٍMotivation = ”No Motivation”) = – left ( frac {7} {8} right ) log _2 left ( frac {7} {8} right ) – left ( frac {1} {8} right ) log _2 left ( frac {1} {8} right ) =0.54 $$

$$ E(Parent | ٍMotivation = ”Neutral”) = – left ( frac {4} {10} right ) log _2 left ( frac {4} {10} right ) – left ( frac {6} {10} right ) log _2 left ( frac {6} {10} right ) =0.97 $$

$$ E(Parent | ٍMotivation = ”Highly Motivated”) = – left ( frac {5} {12} right ) log _2 left ( frac {5} {12} right ) – left ( frac {7} {12} right ) log _2 left ( frac {7} {12} right ) =0.98 $$

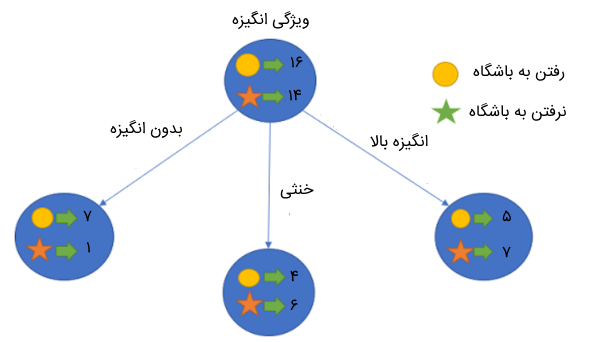
حال، میانگین وزن‌دار را برای آنتروپی‌های هر یک از گره‌های فرزند به صورت زیر محاسبه می‌کنیم:

$$ E(Parent | ٍMotivation) = frac {8} {30} * 0.54 + frac {10} {30} * 0.97 + frac {12} {30} * 0.98 = 0.86 $$

در نهایت، با استفاده از فرمول زیر، مقدار IG را برای ویژگی انگیزه محاسبه می‌کنیم:

$$ Information Gain = E(Parent) – E(Parent | Motivation) $$

$$ = 0.99 – 0.86 $$

$$ = 0.13 $$

همان‌طور که می‌بینیم، ویژگی انرژی با کاهش ۰.۳۷، نسبت به ویژگی انگیزه تأثیر بیشتری در کاهش آنتروپی دارد. بنابراین، برای گره ریشه، آن ویژگی‌ را انتخاب می‌کنیم که بیشترین اطلاعات را به همراه دارد.

در این مثال، ویژگی انرژی را برای گره‌ ریشه‌ انتخاب می‌کنیم و همین کار را برای زیرگره‌ها نیز انجام می‌دهیم. در اینجا می‌بینیم که وقتی انرژی بالا باشد، مقدار آنتروپی پایین می‌آید و بنابراین می‌توانیم بگوییم که فردی با انرژی بالا قطعاً به باشگاه خواهد رفت. اما اگر انرژی فرد کم باشد، دوباره گره را بر اساس ویژگی انگیزه تقسیم خواهیم کرد.

معیار Gini در درخت تصمیم

معیار جینی روشی دیگر برای انتخاب مناسب‌ترین ویژگی برای تقسیم داده‌ها در درخت تصمیم است و از آن برای داده‌های گسسته استفاده می‌شود. از آنجایی که در فرمول بهره‌وری اطلاعات از لگاریتم استفاده شده است، بار محاسباتی آن را بیشتر می‌کند و به همین دلیل در ساخت درخت تصمیم، معیار جینی با فرمول زیر نسبت به IG ترجیح داده می‌شود:

$$ Gini Impurity = 1 – Gini $$

فرمول بالا، میزان ناخالصی یک گره را نشان می‌دهد. مقدار Gini در فرمول بالا مجموع احتمال کلاس‌های مختلف داده‌ها را در گره مشخص می‌کند که فرمول آن را در ادامه ملاحظه می‌کنید:

$$ Gini = sumlimits_{i=1}^n p_{i} ^ {2} $$

در نتیجه می‌توان فرمول ناخالصی جینی را به صورت زیر نوشت:

$$ Gini Impurity = 1 – sumlimits_{i=1}^n p_{i} ^ {2} $$

هرچه مقدار ناخالصی جینی کمتر باشد، همگنی گره بیشتر است. به عبارتی، ناخالصی جینی یک گره خالص برابر با صفر است که در این صورت کلاس تمام داده‌های گره، مشابه هم هستند.

در ادامه، مثالی را برای درک بهتر معیار Gini ارائه کرده‌ایم. فرض کنید می‌خواهیم دانش‌آموزان یک کلاس را بر اساس دو ویژگی قد و وزن دسته‌بندی کنیم تا ببینیم آیا با این مشخصات می‌توانند به عنوان بازیکن بسکتبال انتخاب شوند؟ از بین ۲۰ نفر از دانش‌آموزان، ۱۰ نفرشان می‌توانند به عنوان بازیکن برگزیده شوند. حال، ویژگی قد و وزن مسئله را با استفاده از معیار جینی مورد بررسی قرار می‌دهیم تا مشخص کنیم کدام ویژگی بهترین تفکیک را ارائه می‌دهد و می‌تواند به عنوان گره ریشه در درخت تصمیم انتخاب شود. در ابتدا، داده‌ها را بر اساس ویژگی قد تفکیک می‌کنیم:

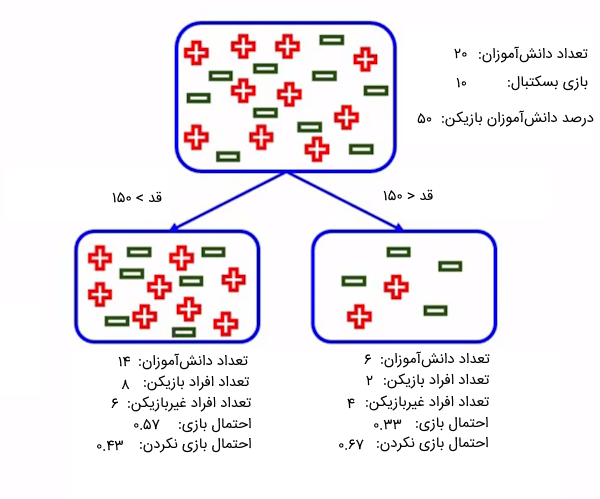
طبق تصویری که در بالا ملاحظه می‌کنید، از میان ۶ نفر از دانش‌آموزان که قدشان از ۱۵۰ سانتی‌متر کوتاه‌تر است، ۲ نفر می‌توانند به عنوان بازیکن بسکتبال انتخاب شوند. همچنین، از بین ۱۴ دانش‌آموزی که قدشان بالای ۱۵۰ سانتی‌متر است، ۸ نفرشان را می‌توان برای بازی برگزید. حال، با استفاده از معیار جینی، بررسی می‌کنیم که این ویژگی چقدر توانسته است اطلاعات مناسب درباره ناخالصی بودن گره‌ها به ما ارائه دهد. در ابتدا، مقدار ناخالصی معیار جینی را برای گره سمت راست (برای افراد با قد کم‌تر از ۱۵۰ سانتی‌متر) محاسبه می‌کنیم:

$$ Gini Impurity = 1 – [(0.33) * (0.33) + (0.67) * (0.67)] = 0.44 $$

سپس، مقدار ناخالصی معیار جینی را برای گره سمت چپ (برای افراد با قد بیشتر از ۱۵۰ سانتی‌متر) محاسبه می‌کنیم:

$$ Gini Impurity = 1 – [(0.57) * (0.57) + (0.43) * (0.43)] = 0.49 $$

در نهایت، مجموع وزن‌دار ناخالصی‌های جینی محاسبه شده را بر اساس فرمول زیر به دست می‌آوریم:

$$ Weighted Gini Impurity = frac {14} {20} * 0.49 + frac {6} {20} * 0.44 = 0.475 $$

در تصویر زیر، تقسیم‌بندی دانش‌آموزان را بر اساس ویژگی وزن ملاحظه می‌کنید. از میان ۱۰ نفر از دانش‌آموزان که وزن‌شان بیشتر از ۵۰ کیلوگرم است، ۲ نفر می‌توانند به عنوان بازیکن بسکتبال انتخاب شوند. همچنین، از بین ۱۰ دانش‌آموزی که وزن‌شان کمتر از ۵۰ کیلوگرم است، ۸ نفرشان را می‌توان برای بازی برگزید. 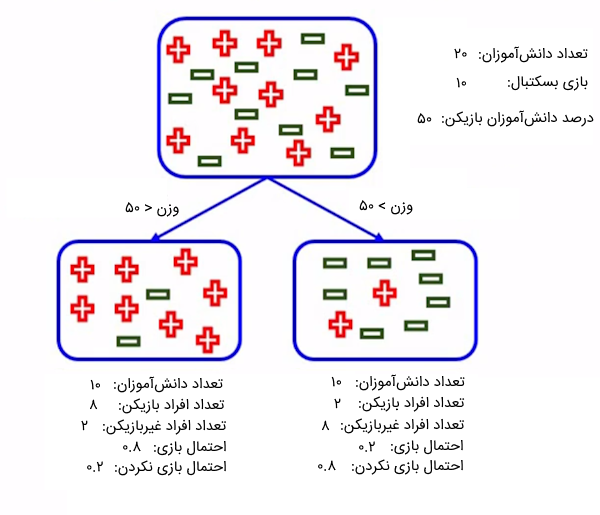مثال معیار جینی در درخت تصمیم

حال، با استفاده از معیار جینی، بررسی می‌کنیم که این ویژگی چقدر توانسته است اطلاعات مناسب درباره ناخالصی بودن گره‌ها به ما ارائه دهد. در ابتدا، مقدار ناخالصی معیار جینی را برای گره سمت راست (برای افراد با وزن بیشتر از ۵۰ کیلوگرم) محاسبه می‌کنیم:

$$ Gini Impurity = 1 – [(0.2) * (0.2) + (0.8) * (0.8)] = 0.32 $$

سپس، مقدار ناخالصی معیار جینی را برای گره سمت چپ (برای افراد با وزن کمتر از ۵۰ کیلوگرم) محاسبه می‌کنیم:

$$ Gini Impurity = 1 – [(0.8) * (0.8) + (0.2) * (0.2)] = 0.32 $$

در نهایت، مجموع وزن‌دار ناخالصی‌های جینی محاسبه شده را بر اساس فرمول زیر به دست می‌آوریم:

$$ Weighted Gini Impurity = frac {10} {20} * 0.32 + frac {10} {20} * 0.32 = 0.32 $$

همان‌طور که از محاسبات پیداست، ویژگی وزن با مقدار Gini برابر با ۰.۳۲ در مقایسه با ویژگی قد با مقدار جینی برابر با ۰.۴۷۵ بهتر توانسته است داده‌ها را تقسیم کند و مقدار ناخالصی داده‌ها پس از تقسیم داده‌ها کمتر شده است. بنابراین، این ویژگی را می‌توان برای گره ریشه در درخت تصمیم انتخاب کنیم.

عمل تقسیم گره ها را چه زمانی متوقف کنیم؟

با مطالعه بخش قبلی مطلب حاضر، ممکن است در ذهن شما این سوال شکل گرفته باشد که چه زمانی باید رشد درخت تصمیم‌ را متوقف کنیم؟ معمولاً در دنیای واقعی با مسائلی سر و کار داریم که داده‌های آن‌ها شامل ویژگی‌های زیادی هستند که این امر باعث می‌شود رشد درخت و تعداد تقسیمات گره‌ها زیاد شوند. ساخت چنین درخت‌های بزرگی زمان‌بر است و ممکن است به وضعیت بیش برازش منجر شود به نحوی که الگوریتم ما بر روی مجموعه داده‌ آموزشی دقت بالایی به دست آورد اما بر روی داده‌های آزمایشی عملکرد ضعیفی داشته باشد. از دو طریق می‌توان عملکرد الگوریتم درخت تصمیم را بهبود داد:

تنظیم «ابرپارامترهای» (Hyperparameter) درخت تصمیم
هرس کردن درخت تصمیم

در تکمیل پاسخ به پرسش درخت تصمیم چیست ، به توضیح هر یک از روش‌های ذکر شده می‌پردازیم.

ابرپارامترهای الگوریتم Decision Tree

از طریق تنظیم ابرپارامترها می‌توان مشکل بیش برازش و رشد بیش از حد درخت تصمیم را رفع کرد. ما می‌توانیم با استفاده از پارامتر max_depth حداکثر عمق درخت تصمیم‌ را تعیین کنیم. هرچه مقدار max_depth بیشتر باشد، درخت شما پیچیده‌تر و بزرگ‌تر خواهد شد. اگر مقدار max_depth را افزایش دهیم، خطای زمان آموزش یا همان Training Error به طور طبیعی کاهش می‌یابد، اما زمانی که الگوریتم را بر روی داده‌های تست امتحان می‌کنیم، دقت بسیار بدی حاصل می‌شود. بنابراین، با امتحان کردن مقادیر مختلف برای این پارامتر باید عملکرد الگوریتم را بررسی کنید و مقداری را برای آن تعیین کنید که نه باعث بیش برازش و نه باعث رخداد وضعیت «برازش ناکافی» (Underfitting) شود. برازش ناکافی نیز زمانی رخ می‌دهد که الگوریتم عملکرد خوبی بر روی داده‌های آموزشی ندارد.

روش دیگری که می‌توان از آن برای بهبود عملکرد درخت تصمیم استفاده کرد، تنظیم حداقل تعداد نمونه برای هر تقسیم است. با استفاده از پارامتر min_samples_split می‌توان حداقل تعداد نمونه را مشخص می‌کنیم. به عنوان مثال، می‌توانیم از مقدار حداقل ۱۰ نمونه برای رسیدن به یک تصمیم استفاده کنیم. این بدان معناست که اگر یک گره کمتر از ۱۰ نمونه داشته باشد، با استفاده از این پارامتر می‌توانیم فراید تقسیم گره را متوقف و آن را به یک گره‌ نهایی (Leaf Node) تبدیل کنیم تا نتیجه نهایی الگوریتم مشخص شود. همچنین، از دو ابرپارامتر دیگر نیز می‌توان در راستای بهبود عملکرد الگوریتم درخت تصمیم استفاده کرد که در ادامه به آن‌ها اشاره شده است:

- ابرپارامتر min_samples_leaf: این ابرپارامتر حداقل تعداد نمونه‌ مورد نیاز برای قرار گرفتن در گره‌ نهایی را مشخص می‌کند. هر چه مقدار این ابرپارامتر بیشتر باشد، احتمال رخداد بیش برازش افزایش می‌یابد.
- ابر پارامتر max_features: این ابرپارامتر به ما کمک می‌کند تصمیم بگیریم هنگام جستجو برای بهترین تقسیم، چند ویژگی را در نظر بگیریم.

هرس کردن در درخت تصمیم چیست ؟

هرس کردن، روش دیگری برای جلوگیری از رخداد وضعیت بیش برازش است. این روش با حذف گره‌ها یا زیرگره‌های کم‌اهمیت به بهبود عملکرد درخت تصمیم‌ کمک می‌کند. همچنین این روش می‌تواند شاخه‌هایی از درخت را حذف کند که اهمیت بسیار پایینی دارند. دو روش اصلی برای هرس کردن درخت تصمیم وجود دارد:

«پیش‌ هرس» (Pre-pruning)
«پس‌ هرس» (Post-pruning)

رباتی در حال هرس کردن درخت تصمیم است - درخت تصمیم چیست

در ادامه، به توضیح هر یک از روش‌های هرس کردن در درخت تصمیم می‌پردازیم.

پیش هرس در درخت تصمیم چیست ؟

یکی از روش‌های هرس کردن در درخت‌های تصمیم‌، تنظیم ابرپارامترها قبل از فرایند آموزش است. این روش برای توقف زودهنگام الگوریتم استفاده می‌شود که از رشد کامل درخت تصمیم‌ جلوگیری کند. هدف از توقف زودهنگام، جلوگیری از ایجاد برگ‌هایی با نمونه‌های کم‌تعداد است. در هر مرحله از تقسیم درخت، «خطای اعتبارسنجی متقابل» (Cross Validation Error) بررسی می‌شود. اگر مقدار این خطا تغییری نکند، رشد درخت متوقف می‌شود. ابرپارامترهایی را که می‌توان برای توقف زودهنگام و جلوگیری از رخداد بیش برازش تنظیم کرد، در ادامه ملاحظه می‌کنید:

ابر پارامتر max_depth: حداکثر عمق درخت تصمیم را مشخص می‌کند.
ابرپارامتر min_samples_leaf: حداقل تعداد نمونه در برگ‌های درخت تصمیم را مشخص می‌کند.
ابرپارامتر min_samples_split: حداقل تعداد نمونه در گره برای ایجاد یک تقسیم جدید را مشخص می‌کند.

این ابرپارامترها همچنین می‌توانند برای تنظیم یک مدل کارآمد استفاده شوند. با این حال، باید احتیاط کنید زیرا توقف زودهنگام می‌تواند منجر به برازش ناکافی نیز بشود.

پس هرس در درخت تصمیم چیست ؟

برخلاف روش پیش‌برش، در روش پس‌برش به درخت تصمیم‌ اجازه داده می‌شود به طور کامل رشد کند. پس از رسیدن به عمق کامل، به منظور جلوگیری از رخداد بیش برازش، برخی از شاخه‌های درخت حذف می‌شوند.

در این روش، الگوریتم تقسیم داده‌ها را به زیرمجموعه‌های کوچک‌تر ادامه می‌دهد تا زمانی که زیرمجموعه‌های نهایی از نظر کلاس، مشابه شوند. زیرمجموعه نهایی درخت تنها شامل چند نقطه داده خواهد بود و به درخت اجازه می‌دهد تا داده‌ها را به طور کامل یاد بگیرد. با این حال، ممکن است درخت تصمیم در زمان تست درباره یک داده جدید به درستی تصمیم نگیرد. ابرپارامتری که می‌توان برای پس‌برش و جلوگیری از رخداد بیش برازش تنظیم کرد، ccp_alpha نام دارد. ccp مخفف عبارت «هرس کردن با پیچیدگی هزینه» (Cost Complexity Pruning) است و می‌تواند به عنوان عاملی برای کنترل اندازه درخت استفاده شود. هر چقدر مقدار ابرپارامتر ccp_alpha بیشتر باشد، تعداد گره‌های هرس‌ شده بیشتر خواهند شد.

ویژگی های درخت تصمیم

الگوریتم درخت تصمیم به منظور حل مسائل چندین فرضیه را در نظر می‌گیرند. این فرضیه‌ها به ساخت صحیح درخت و در بهبود عملکرد آن کمک می‌کنند. در اینجا به برخی از فرضیه‌های رایج و نکات قابل توجه هنگام ایجاد درخت‌های تصمیم‌ اشاره شده است:

تقسیم دوتایی گره‌ها: درخت‌ تصمیم‌ به طور معمول تقسیم‌های دودویی انجام می‌دهد. این بدان معنا است که هر گره را بر اساس یک ویژگی یا شرط به دو زیرمجموعه تقسیم می‌کند. این فرض بر این مبنا است که هر تصمیم را می‌توان به عنوان یک انتخاب دودویی (دو حالته) نشان داد.
«تقسیم‌بندی بازگشتی» (Recursive Partitioning): درخت‌ تصمیم از فرایندی به نام تقسیم‌بندی بازگشتی استفاده می‌کند. در این فرایند، هر گره به زیرگره‌های فرزند تقسیم می‌شود و این فرآیند تا زمانی ادامه می‌یابد که معیار توقف برآورده شود. این فرآیند فرض می‌کند که داده‌ها را می‌توان به طور مؤثر به زیرمجموعه‌های کوچک‌تر تقسیم کرد.
مستقل بودن ویژگی‌ها: درخت‌ تصمیم‌ اغلب این فرض را در نظر می‌گیرد ویژگی‌هایی که برای تقسیم گره‌ها استفاده می‌شوند، مستقل از هم هستند. در عمل، ممکن است این استقلال وجود نداشته باشد، اما حتی با وجود همبستگی بین ویژگی‌ها، درخت‌ تصمیم‌ همچنان می‌تواند به عملکرد خوبی برسد.
همگن بودن داده‌ها در هر گره: درخت‌ تصمیم‌ تلاش می‌کند در هر گره زیرگروه‌های همگن ایجاد کند. به عبارتی، این مدل سعی دارد داده‌هایی را که از کلاس مشابهی هستند، در یک گره مجزا قرار دهد. این فرضیه می‌تواند به ایجاد مرزهای تصمیم‌گیری کمک کند.
«رویکرد حریصانه‌ بالا-به-پایین» (Top-Down Greedy Approach): درخت‌ تصمیم‌ بر پایه رویکرد حریصانه‌ بالا-به-پایین ساخته می‌شود. بر اساس این رویکرد، تقسیم داده‌ها در گره‌ها برای به حداکثر رساندن مقدار معیار IG یا کاهش میزان آنتروپی انجام می‌شود. البته باید به این نکته اشاره داشت که چنین رویکردی تضمین نمی‌دهد همیشه بهینه‌ترین درخت تصمیم ساخته شود.
«ویژگی‌های مقوله‌ای و عددی» (Categorical and Numerical Features): درخت‌ تصمیم‌ می‌تواند با هر دو نوع ویژگی مقوله‌ای و عددی کار کند. با این حال، ممکن است برای هر نوع ویژگی نیاز به استراتژی‌های تقسیم‌بندی متفاوتی باشد.
هرس کردن برای جلوگیری از بیش برازش: با وجود نویز در داده‌ها، درخت‌ تصمیم‌ مستعد بیش برازش می‌شود. این مدل برای مقابله با این شرایط، از هرس کردن و تعیین معیارهای توقف رشد درخت استفاده می‌کند.
«معیارهای ناخالصی» (Impurity Measures): درخت‌ تصمیم‌ از معیارهای ناخالصی مانند معیار جینی یا آنتروپی برای ارزیابی کیفیت تفکیک کلاس‌ها توسط یک گره تقسیم استفاده می‌کند. انتخاب معیار ناخالصی می‌تواند بر ساختار درخت تأثیر بگذارد.
«عدم وجود مقادیر نامشخص» (No Missing Values): درخت‌ تصمیم‌ فرض می‌کند که هیچ مقدار گم‌شده‌ای در مجموعه داده وجود ندارد یا مقادیر گم‌شده به درستی از طریق پر کردن داده با مقادیر مشخص مقداردهی شده‌اند.
برابر بودن ویژگی‌ها: درخت‌ تصمیم‌ ممکن است اهمیت همه ویژگی‌ها را یکسان در نظر بگیرد. البته این مدل می‌تواند برای تأکید بر برخی ویژگی‌های خاص از روش «مقیاس‌بندی ویژگی» (Feature Scaling) یا «وزن‌دهی» (Weighting) استفاده کند.
حساس بودن به «داده‌های پرت» (Outliers): درخت‌ تصمیم‌ نسبت به داده‌های پرت حساس هستند و این مقادیر می‌توانند بر عملکرد الگوریتم تأثیر منفی بگذارند. برای مدیریت موثر داده‌های پرت، ممکن است نیاز به پیش‌ پردازش داده باشد.
حساس بودن به حجم داده‌ها: درخت‌ تصمیم‌ نسبت به حجم داده حساس است. اگر حجم داده‌های آموزشی این الگوریتم کم باشد، ممکن است وضعیت بیش برازش اتفاق بیفتد و اگر حجم داده‌ها زیاد باشد، این احتمال وجود دارد که ساختار درخت‌ تصمیم بسیار پیچیده و بزرگ شود. بنابراین، باید تعادلی بین حجم داده و عمق درخت برقرار کرد تا از مشکلات احتمالی جلوگیری شود.

حال که به این پرسش پاسخ دادیم که الگوریتم درخت تصمیم‌ چیست و به اصطلاحات فنی این مدل یادگیری ماشین پرداختیم، در ادامه این بخش یک مثال ساده برای دسته‌بندی داده‌ها با درخت تصمیم ارائه می‌کنیم.

مثال الگوریتم Decision Tree

در این بخش از مطلب حاضر، به ارائه یک مثال کاربردی می‌پردازیم که نحوه عملکرد درخت تصمیم را نشان می‌دهد. فرض کنید اطلاعاتی از حیوانات مختلف در اختیار داریم و می‌خواهیم هر حیوانی را با استفاده از درخت تصمیم بر اساس ویژگی‌هایش شناسایی و طبقه‌بندی کنیم. در تصویر زیر، مجموعه داده آموزشی این مسئله را ملاحظه می‌کنید.

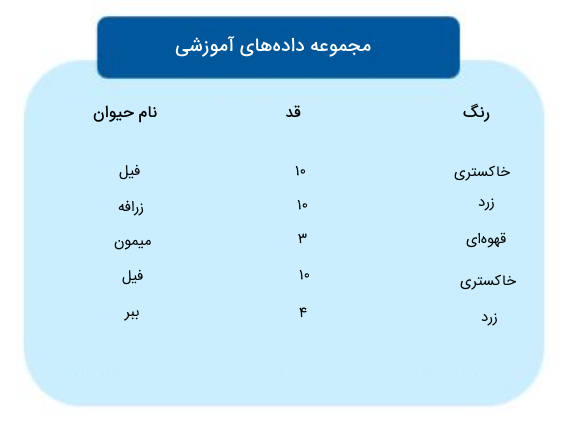
همانطور که گفتیم، باید مشخص کنیم کدام ویژگی باعث می‌شود تقسیم داده‌ها در گروه‌های مختلف به نحوی انجام شود که بیشترین اطلاعات را به دست آوریم و میزان ناخالصی حاصل شده در گره‌های فرزند کمتر شود. در بخش‌های قبلی این مطلب، به طور مفصل درباره نحوه محاسبه معیارهای انتخاب ویژگی صحبت کردیم. برای مسئله فعلی می‌توان از IG یا Gini برای تعیین ویژگی مناسب استفاده کنیم. برای این منظور می‌توانیم چندین ویژگی مختلف نیز برای ساخت درخت و انشعاب گره‌ها در نظر بگیریم. به عنوان مثال، شروط زیر می‌توانند به عنوان عامل تقسیم داده‌ها لحاظ شوند:

اگر از معیار IG برای انتخاب ویژگی رنگ برای گره ریشه استفاده کنیم، می‌بینیم که بیشترین اطلاعات را ارائه می‌دهد و در مقایسه با سایر ویژگی‌ها، ناخالصی داده‌ها را پس از تقسیم، کمتر می‌کند.

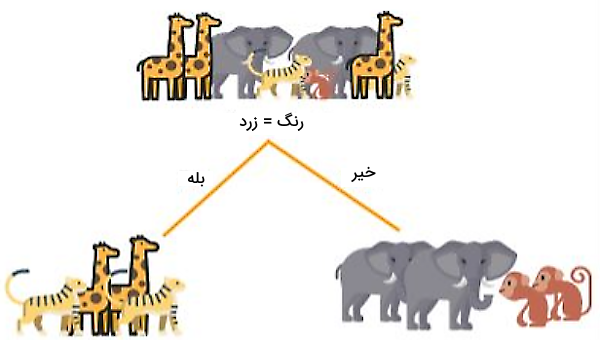
پس از تقسیم داده‌ها بر اساس رنگ حیوانات، مقدار آنتروپی به طور قابل توجهی کاهش می‌یابد. با این حال، برای رسیدن به مقدار آنتروپی صفر، همچنان نیاز است داده‌های گره‌های فرزند را در هر دو شاخه تقسیم کنیم. این بار، هر دو گره را بر اساس ویژگی قد تقسیم و از شرایط قد بلندتر و کوتاه‌تر از ۱۰ سانتی‌متر به عنوان معیار استفاده می‌کنیم.

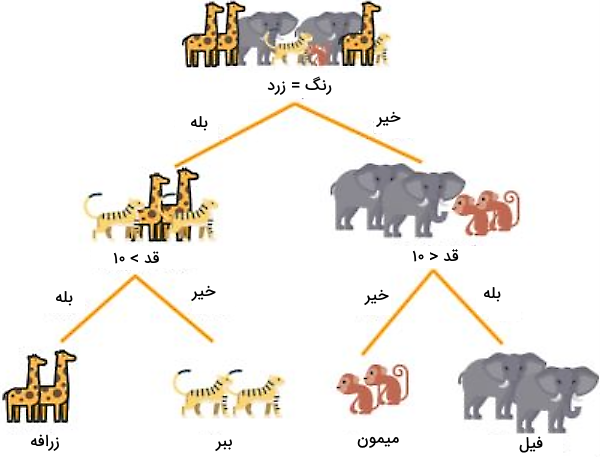
همان‌طور که در تصویر بالا ملاحظه می‌کنید، با تقسیم داده‌ها بر اساس ویژگی قد، در گره‌های جدید، داده‌ها به درستی تفکیک شده‌اند و مقدار آنتروپی در هر یک از گره‌های ایجاد شده برابر با ۰ است. بدین ترتیب، الگوریتم درخت تصمیم متوقف می‌شود و گره‌های نهایی ساخته شده به عنوان گره برگ در نظر گرفته می‌شوند. چنانچه قصد دارید با نحوه پیاده‌سازی یک مسئله با استفاده از درخت تصمیم آشنا شوید، می‌توانید به مطالعه یکی از مطالب کاربردی مجله فرادرس بپردازید که در ادامه لینک آن را ملاحظه می‌کنید:

مزایا و معایب الگوریتم درخت تصمیم چیست ؟

حال که به این پرسش پاسخ دادیم که درخت تصمیم چیست و عملکرد آن به چه نحو است، به نقاط ضعف و قوت آن می‌پردازیم. به دلیل مزیت‌های خوبی که درخت تصمیم دارد، از آن در حل مسائل مختلف ماشین لرنینگ استفاده می‌شود. در ادامه، مهم‌ترین مزایای الگوریتم درخت تصمیم را ملاحظه می‌کنید:

قابل تفسیر و تجسم آسان: درک و تفسیر نحوه‌ عملکرد درخت تصمیم‌گیری بسیار آسان است زیرا قوانین تصمیم‌ به صورت صریح در هر گره نمایش داده می‌شوند.
قابلیت تشخیص الگوهای غیرخطی: درخت‌های تصمیم‌ می‌توانند الگوهای غیرخطی موجود در داده‌ها را به خوبی تشخیص دهند.
نیاز کم به پیش پردازش اطلاعات: برخلاف برخی از الگوریتم‌های یادگیری ماشین، درخت‌های تصمیم‌گیری نیاز کمی به پیش پردازش داده‌ها مانند نرمال‌سازی ویژگی‌ها دارند.
کاربرد در مهندسی ویژگی: درخت‌های تصمیم‌گیری را می‌توان برای مهندسی ویژگی استفاده کرد. به عنوان مثال، می‌توان این الگوریتم را برای پیش‌بینی مقادیر گم‌شده یا انتخاب ویژگی‌های مهم به کار برد.
عدم نیاز به فرض در مورد توزیع داده‌ها: به دلیل این که درخت تصمیم از ماهیت غیرپارامتری برخوردار است، این الگوریتم نیازی به در نظر گرفتن فرضیه خاص در مورد توزیع داده‌ها ندارند.

الگوریتم درخت تصمیم علی‌رغم مزیت‌های مهمی که دارد، دارای معایبی نیز هست که در ادامه به آن‌ها اشاره شده است:

حساسیت به نویز داده‌ها: درخت‌ تصمیم‌گیری نسبت به نویز موجود در داده‌ها حساس است و اگر برای آموزش این الگوریتم از داده‌هایی استفاده کنید که از نویز زیادی برخوردارند، با وضعیت بیش برازش مواجه خواهید شد.
عدم ثبات با تغییرات اندک داده‌ها: اعمال تغییرات کوچک در داده‌ها می‌تواند منجر به ایجاد درخت‌های تصمیم‌گیری متفاوتی شوند.
سوگیری با داده‌های نامتوازن: درخت‌های تصمیم‌گیری ممکن است نسبت به داده‌های نامتوازن «سوگیری» (bias) داشته باشند. بنابراین توصیه می‌شود قبل از ایجاد درخت تصمیم‌گیری، مجموعه داده را متوازن کنید.

کاربرد درخت تصمیم چیست ؟

همانطور که در پست قبلی اشاره شد، درخت‌های تصمیم‌گیری را می‌توان برای مسائل طبقه‌بندی و رگرسیون به کار برد. این ویژگی، آن‌ها را به ابزارهایی بسیار انعطاف‌پذیر و مناسب برای حل طیف وسیعی از مسائل تبدیل می‌کند. رایج‌ترین کاربردهای درخت تصمیم را می‌توان به صورت موارد زیر برشمرد:

تصمیم‌گیری در زندگی روزمره: ما اغلب در زندگی روزمره بدون این که توجه داشته باشیم، از درخت‌های تصمیم‌گیری استفاده می‌کنیم. برای مثال، تصور کنید صبح‌ها در حال تصمیم‌گیری برای لباس پوشیدن هستید. ممکن است از خود بپرسید:

1. وضعیت آب و هوا چگونه است؟ (گره ریشه)
2. اگر هوا گرم باشد، ممکن است تصمیم بگیرید که یک تی‌شرت بپوشید (گره برگ).
3. اگر هوا سرد باشد (گره تصمیم‌گیری)، ممکن است از خود بپرسید:
  1. آیا باران می‌بارد؟ (گره تصمیم‌گیری دیگر)
  2. اگر بله، یک کاپشن می‌پوشید و چتر برمی‌دارید (گره برگ).
  3. اگر خیر، شاید فقط یک ژاکت بپوشید (گره برگ).

مراقبت‌های بهداشتی: در حوزه‌ مراقبت‌های بهداشتی، درخت‌های تصمیم‌گیری می‌توانند به متخصصان پزشکی در تشخیص بیماری‌ها کمک کنند. برای مثال، یک پزشک می‌تواند بر اساس علائم (گره‌های تصمیم‌گیری)، نوع بیماری (گره‌های برگ) را مشخص کند. این امر می‌تواند به ویژه برای غربالگری اولیه یا در مناطق روستایی که کمبود متخصصان مراقبت‌های بهداشتی وجود دارد، مفید باشد.
تحلیل امور مالی: در بخش مالی، از درخت‌های تصمیم‌گیری برای قیمت‌گذاری معامله و توسعه‌ استراتژی استفاده می‌شود. این درخت‌ها می‌توانند بر اساس شرایط مختلف بازار، قیمت‌های آتی احتمالی را مدل‌سازی کنند تا به سرمایه‌گذاران در تصمیم‌گیری آگاهانه کمک کنند.
مدیریت ارتباط با مشتری: شرکت‌ها از درخت‌های تصمیم‌گیری برای پیش‌بینی رفتار مشتری، مانند واکنش مثبت او به یک کمپین بازاریابی، استفاده می‌کنند. بر اساس ویژگی‌های مختلف مشتری (مانند سن، سابقه خرید، رفتار و سلیقه) می‌توان آن‌ها را دسته‌بندی کرد و استراتژی‌های بازاریابی را متناسب با هر دسته تنظیم نمود.
کنترل کیفیت محصولات: در بخش تولید و کنترل کیفیت کارخانه‌ها، از درخت‌های تصمیم‌گیری می‌توان برای پیش‌بینی احتمال عدم موفقیت یک محصول در تست تضمین کیفیت استفاده کرد.
تشخیص کلاه‌برداری: درخت‌ تصمیم‌ می‌تواند با شناسایی الگوها در تراکنش‌ها به تشخیص تقلب کمک کند. این الگوریتم می‌تواند بر اساس پارامترهایی مانند تعداد تراکنش، میزان مبلغ و مکان تراکنش، فعالیت‌های مشکوک را برای بررسی‌های بیشتر مشخص کند.
سیستم‌های توصیه‌گر: بسیاری از پلتفرم‌های آنلاین از درخت‌های تصمیم‌گیری به عنوان بخشی از الگوریتم‌های توصیه‌ خود استفاده می‌کنند. به عنوان مثال، نتفلیکس یا اسپوتیفای ممکن است از درخت‌های تصمیم‌گیری برای تعیین فیلم‌ها یا آهنگ‌های پیشنهادی بر اساس سلایق کاربر و اطلاعات جمعیت‌شناختی استفاده کنند.

درخت تصمیم در پایتون

در مطلب حاضر سعی داشتیم به این پرسش به طور مفصل پاسخ دهیم که درخت تصمیم چیست و بر اساس چه معیارهایی عمل می‌کند. در این بخش به نحوه استفاده از این الگوریتم برای طبقه‌بندی داده‌ها می‌پردازیم تا خوانندگان این مطلب بتوانند با شیوه پیاده‌سازی درخت تصمیم در زبان برنامه نویسی آشنا شوند. به منظور استفاده از الگوریتم درخت تصمیم، از زبان برنامه نویسی پایتون استفاده می‌کنیم که به عنوان یکی از بهترین زبان های برنامه نویسی یادگیری ماشین محسوب می‌شود و کتابخانه های هوش مصنوعی جامعی دارد.

برای پیاده‌سازی درخت تصمیم، می‌توانیم از داده‌های آموزشی مختلفی استفاده کنید. ما در این مطلب، از داده آموزشی سایت Kaggle [+] استفاده کردیم که شامل اطلاعات پزشکی بیمارانی است که قرار است بر مبنای ویژگی‌های مختلف بیماران تشخیص دهیم آیا افراد دارای بیماری دیابت هستند یا خیر؟ کتابخانه‌هایی را که برای پیاده‌سازی درخت تصمیم نیاز داریم، با استفاده از قطعه کد زیر، در برنامه فراخوانی می‌کنیم:

1# Load libraries
2import pandas as pd
3from sklearn.tree import DecisionTreeClassifier # Import Decision Tree Classifier
4from sklearn.model_selection import train_test_split # Import train_test_split function
5from sklearn import metrics #Import scikit-learn metrics module for accuracy calculation

سپس، داده‌های مسئله را بعد از دانلود کردن بر روی سیستم، در برنامه بارگذاری می‌کنیم و نام ویژگی‌ها را تغییر می‌دهیم:

1col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
2# load dataset
3pima = pd.read_csv("diabetes.csv", header=0, names=col_names)

برای ملاحظه چندین سطر از داده‌ها، می‌توان از دستور زیر استفاده کرد:

خروجی دستور بالا را در ادامه ملاحظه می‌کنید:

برای ملاحظه تصویر با مقیاس بزرگتر، بر روی آن کلیک کنید.

با استفاده از قطعه کد زیر، ویژگی‌ها را از مقادیر هدف جدا می‌کنیم تا مقادیر ورودی مدل و مقادیر هدف مشخص شوند:

1#split dataset in features and target variable
2feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
3X = pima[feature_cols] # Features
4y = pima.label # Target variable

سپس، با قطعه کد زیر، داده‌های آموزشی را از داده‌های تست جدا می‌کنیم:

1# Split dataset into training set and test set
2X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1) # 70% training and 30% test

از قطعه کد زیر به منظور آموزش درخت تصمیم و تست آن استفاده می‌کنیم:

1# Create Decision Tree classifer object
2clf = DecisionTreeClassifier()
3
4# Train Decision Tree Classifer
5clf = clf.fit(X_train,y_train)
6
7#Predict the response for test dataset
8y_pred = clf.predict(X_test)

به منظور ارزیابی عملکرد درخت تصمیم، قطعه کد زیر را می‌نویسیم:

1# Model Accuracy, how often is the classifier correct?
2print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

خروجی دستور بالا را در ادامه ملاحظه می‌کنید که دقت مدل را نشان می‌دهد:

Accuracy: 0.6753246753246753

شما می‌توانید درخت نهایی ساخته شده را با استفاده از قطعه کد زیر به نمایش درآورید:

1import six
2import sys
3sys.modules['sklearn.externals.six'] = six
4
5from sklearn.tree import export_graphviz
6from sklearn.externals.six import StringIO  
7from IPython.display import Image  
8import pydotplus
9
10dot_data = StringIO()
11export_graphviz(clf, out_file=dot_data,  
12                filled=True, rounded=True,
13                special_characters=True,feature_names = feature_cols,class_names=['0','1'])
14graph = pydotplus.graph_from_dot_data(dot_data.getvalue())  
15graph.write_png('diabetes.png')
16Image(graph.create_png())

با اجرا کردن قطعه کد بالا، درخت تصمیم ساخته شده را ملاحظه می‌کنید که در تصویر زیر به نمایش در آمده است:

برای مشاهده تصویر با مقیاس بزرگ‌تر، بر روی آن کلیک کنید.

همان‌طور که در تصور بالا ملاحظه می‌کنید، درخت ساخته شده بسیار بزرگ و پیچیده است. می‌توان از روش هرس کردن برای ساده‌سازی درخت استفاده کرد. به عنوان مثال، می‌توانیم مشخص کنیم که سطوح درخت از سه تا بیشتر نشود. بدین منظور می‌توان از قطعه کد زیر استفاده کرد:

1# Create Decision Tree classifer object
2clf = DecisionTreeClassifier(criterion="entropy", max_depth=3)
3
4# Train Decision Tree Classifer
5clf = clf.fit(X_train,y_train)
6
7#Predict the response for test dataset
8y_pred = clf.predict(X_test)
9
10# Model Accuracy, how often is the classifier correct?
11print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

خروجی قطعه کد بالا را در ادامه ملاحظه می‌کنید. همان‌طور که می‌بینید، با هرس کردن درخت، میزان دقت مدل نیز افزایش یافته است:

Accuracy: 0.7705627705627706

حال ساختار درخت تصمیم را پس از هرس کردن با استفاده از قطعه کد زیر به نمایش در می‌آوریم:

1from six import StringIO 
2from IPython.display import Image  
3from sklearn.tree import export_graphviz
4import pydotplus
5dot_data = StringIO()
6export_graphviz(clf, out_file=dot_data,  
7                filled=True, rounded=True,
8                special_characters=True, feature_names = feature_cols,class_names=['0','1'])
9graph = pydotplus.graph_from_dot_data(dot_data.getvalue())  
10graph.write_png('diabetes.png')
11Image(graph.create_png())

خروجی قطعه کد بالا را در ادامه ملاحظه می‌کنید:

حال که با نحوه پیاده‌سازی یک الگوریتم ساده درخت تصمیم آشنا شدید و به پاسخ این پرسش رسیدید که درخت تصمیم چیست ، برای تقویت مهارت خود در این زمینه، می‌توانید به پیاده‌سازی مثال‌های بیشتر بپردازید و با تنظیم مختلف ابرپارامترها و استفاده از شیوه‌های هرس کردن، نتایج مدل را با یکدیگر مقایسه کنید. همچنین، می‌توانید در ادامه مسیر یادگیری خود، به مطالعه سایر روش‌ها و مدل‌های ماشین لرنینگ و مباحث مهم و مرتبط با این حوزه بپردازید و مهارت خود را در پیاده‌سازی آن‌ها با زبان برنامه نویسی بالا ببرید. بدین منظور می‌توانید از مسیر یادگیری پیشنهاد شده فرادرس استفاده کنید که در ادامه به آن‌ها اشاره شده است:

فیلم آموزش تجزیه و تحلیل و آماده‌سازی داده‌ها با پایتون
فیلم آموزش ریاضی برای یادگیری ماشین + پیاده‌سازی در پایتون
فیلم آموزش کتابخانه scikit-learn در پایتون – الگوریتم‌های یادگیری ماشین
فیلم آموزش یادگیری ماشین و پیاده‌سازی در پایتون Python – بخش یکم

جمع‌بندی

در دنیای امروز، از روش‌های مختلف یادگیری ماشین به منظور طراحی ابزارها و سیستم‌های هوش مصنوعی استفاده می‌شوند که می‌توان از آن‌ها در انجام امور مختلف استفاده کرد. یکی از الگوریتم‌های پرکاربرد ماشین لرنینگ، الگوریتم درخت تصمیم است که به دلیل قابلیت تفسیرپذیری و درک عملکرد آن، در بسیاری از مسائل استفاده می‌شود. در این مطلب از مجله فرادرس قصد داشتیم به این پرسش پاسخ دهیم که الگوریتم درخت تصمیم چیست و اصول کارکرد و فرآیند ساخت آن به چه شکل است. همچنین، به روش‌های بهینه‌سازی درخت تصمیم پرداختیم و به مزایا و معایب آن اشاره کردیم. به علاوه، با استفاده از یک مثال برنامه نویسی از زبان پایتون سعی کردیم نحوه پیاده‌سازی این الگوریتم را به مخاطبان این مطلب آموزش دهیم.

source

EXPRESSJS - مجله تکنولوژی نرم افزار و سخت افزار

درخت تصمیم چیست؟ – توضیح به زبان ساده

توسطexpressjs.ir