مقابله با مشکل «داده‌های گمشده» (Missing Data) بخشی اجتناب‌ناپذیر از کار هر دانشمند علم داده و مهندس یادگیری ماشین است. از طرف دیگر، مفهوم «جایگذاری» (Imputation) در آمار، به معنی فرایند جایگذاری مقادیر دیگری به‌جای داده‌های گمشده است. اگر دیتاست یا همان «مجموعه‌داده» (Dataset) ما شامل اطلاعات از دست رفته‌ای باشد، نتایجی که در آخر دریافت می‌کنیم بسیار سوگیری داشته و علاوه‌بر دشوار شدن مرحله پردازش و ارزیابی داده‌ها، کارآمدی مدل یادگیری ماشین نیز کاهش پیدا می‌کند. به‌طور معمول، راه‌حلی که در چنین شرایطی مورد استفاده قرار می‌گیرد، نادیده گرفتن این قبیل از داده‌ها است. اما چنین رویکردی به نتایج قابل اتکایی ختم نمی‌شود و به همین خاطر، در این مطلب از مجله فرادرس، با تکنیک های جایگذاری داده های گمشده آشنا می‌شویم. تحلیل و ارزیابی مجموعه‌داده‌ای که مقادیر گمشده آن جایگذاری شده باشند، برای متخصصان علم داده به‌مراتب راحت‌تر خواهد بود.

در این مطلب، ابتدا با مفهوم و اهمیت جایگذاری داده آشنا می‌شویم و از دلیل گم‌شدن و همچنین انواع داده‌های گمشده می‌گوییم. سپس به معرفی تکنیک های جایگذاری داده های گمشده می‌پردازیم و شرحی از چگونگی انتخاب رویکرد مناسب جایگذاری ارائه می‌دهیم. در انتهای این مطلب از مجله فرادرس نیز به تعدادی از پرسش‌های متداول در این زمینه پاسخ می‌دهیم.

جایگذاری داده چیست؟

به راهکاری برای حفظ اکثریت داده‌ها و اطلاعات دیتاست از طریق جابه‌جا کردن داده‌های گمشده با مقادیری متفاوت، «جایگذاری داده» (Data Imputation) گفته می‌شود. از آنجا که حذف و نادیده گرفتن مداوم داده‌ها از دیتاست امری ناکارآمد است، تا کنون، تکنیک های متنوعی برای جایگذاری داده‌ها پیشنهاد شده است. همچنین با گذشت زمان، حذف داده‌ها باعث کاهش اندازه دیتاست شده و اثر مخربی دارد. توجه داشته باشید که فرایند تعویضِ تنها یک نمونه داده، «جایگذاری یکتا» (Unit Imputation) و جابه‌جایی مجموعه‌ای از داده‌ها «جایگذاری موردی» (Item Imputation) نام دارد.

دلیل گم شدن داده ها چیست؟

پیش از انتخاب از میان تکنیک های جایگذاری داده های گمشده، بهتر است درک مناسبی از چرایی گم‌شدن داده‌ها به‌دست آوریم. سازوکاری که به گم‌شدن داده‌ها ختم می‌شود، ممکن است یکی از سه مورد زیر باشد:

• «داده‌های گمشده به‌طور کامل تصادفی» (Missing Completely at Random | MCAR)
• «داده‌های گمشده به‌صورت تصادفی» (Missing at Random | MAR)
• «داده‌های به‌طور تصادفی گم‌نشده» (Missing Not at Random | MNAR)

دانستن علت گم‌شدن داده‌ها، نگرشی اساسی و اولیه است؛ چراکه انتخاب تکنیک اشتباه در مسائل، به نتایجی نادرست، مدل‌هایی با سوگیری و در نهایت تصمیم‌گیری‌هایی ختم می‌شود که اعتماد ما را نسبت به هوش مصنوعی کم‌رنگ می‌کند.

چگونه جایگذاری داده های گمشده را در SPSS یاد بگیریم؟

مرحله پس از شناسایی و آشنایی با انواع داده‌های گمشده، استفاده از ابزاری کاربردی برای جایگذاری نمونه داده‌های گمشده است. نرم‌افزار اِس‌پی‌اِس‌اِس مخفف عبارت Sciences Statistical Package for the Social است که به عنوان یکی از جامع‌ترین و کاربردی‌ترین نرم‌افزارهای آماری برای تحلیل داده شناخته می‌شود. با استفاده از SPSS می‌توان به‌راحتی داده‌های پیچیده‌ای همچون داده‌های گمشده را مدیریت و بررسی کرد. اگر به این مبحث علاقه‌مند هستید و می‌خواهید نحوه کار کردن با نرم‌افزار SPSS را یاد بگیرید، مشاهده فیلم‌های آموزشی فرادرس را به ترتیب زیر پیشنهاد می‌کنیم:

معرفی تکنیک های جایگذاری داده های گمشده

حالا که یاد گرفتیم جایگذاری داده چیست و به اهمیت آن پی‌بردیم، در این بخش با چند مورد از کاربردی‌ترین تکنیک های جایگذاری داده های گمشده و نحوه پیاده‌سازی هر کدام در زبان برنامه‌نویسی پایتون آشنا می‌شویم؛ تکنیک‌هایی از جمله:

• «جایگذاری میانگین، میانه و نما» (Mean Imputation | Median Imputation | Mode Imputation)
• K نزدیک‌ترین همسایه یا KNN
• «جایگذاری چندگانه از طریق معادلات پیوسته» (Multiple Imputation by Chained Equations | MICE)
• «جایگذاری از طریق درون‌یابی» (Imputing with Interpolation)
• «جایگذاری قبلی و بعدی» (Previous Imputation | Next Imputation)

در ادامه، توضیح بیشتری از هر یک از تکنیک‌های عنوان شده در فهرست فوق ارائه می‌دهیم.

جایگذاری میانگین، میانه و نما

پایه‌ای‌ترین راهکار برای حل مشکل داده‌های گمشده، استفاده از تکنیک‌های «جایگذاری میانگین، میانه و نما» (Mean Imputation | Median Imputation | Mode Imputation) است. برای یادگیری بیشتر درباره مفاهیم آماری می‌توانید فیلم آموزشی مفاهیم آماری در داده کاوی فرادرس که لینک آن در ادامه قرار داده شده است را مشاهده کنید:

مزایا

از جمله مزایای روش‌های جایگذاری میانگین، میانه و نما می‌توان به مورد زیر اشاره کرد:

• سادگی و سرعت: این روش‌ها از نظر محاسباتی کم‌هزینه بوده و به راحتی قابل یادگیری هستند.

معایب

در فهرست زیر، به یکی از مهم‌ترین معایب این روش‌ها اشاره کرده‌ایم:

• ایجاد اختلال در توزیع داده‌ها: در مجموعه‌داده‌هایی که توزیع نابرابری دارند، باعث ایجاد اختلالاتی همچون سوگیری و کاهش «پراکندگی» (Variability) می‌شوند.

برای استفاده از این سه روش، ابتدا باید مانند نمونه کتابخانه scikit-learn را نصب کنیم:

pip install scikit-learn

در قطعه کد زیر، شاهد نحوه پیاده‌سازی تکنیک‌های جایگذاری میانگین، میانه و نما و سپس ترسیم نتایج حاصل از هر کدام هستید:

1import pandas as pd
2import matplotlib.pyplot as plt
3from sklearn.impute import SimpleImputer
4import numpy as np
5
6# Creating a sample dataset with skewed values
7data = {'Scores': [25, 45, 30, 28, np.nan, 32, 29, 80, 85]}
8df = pd.DataFrame(data)
9
10# Mean imputation
11mean_imputer = SimpleImputer(strategy='mean')
12df_mean = pd.DataFrame(mean_imputer.fit_transform(df), columns=df.columns)
13
14# Visual comparison
15plt.figure(figsize=(15, 6))
16plt.subplot(1, 3, 1)
17plt.hist(df['Scores'].dropna(), alpha=0.5, label='Original')
18plt.hist(df_mean['Scores'], alpha=0.5, label='Mean Imputed')
19plt.title('Mean Imputation')
20plt.legend()
21
22# Median imputation
23median_imputer = SimpleImputer(strategy='median')
24df_median = pd.DataFrame(median_imputer.fit_transform(df), columns=df.columns)
25
26plt.subplot(1, 3, 2)
27plt.hist(df['Scores'].dropna(), alpha=0.5, label='Original')
28plt.hist(df_median['Scores'], alpha=0.5, label='Median Imputed')
29plt.title('Median Imputation')
30plt.legend()
31
32# Mode imputation
33mode_imputer = SimpleImputer(strategy='most_frequent')
34df_mode = pd.DataFrame(mode_imputer.fit_transform(df), columns=df.columns)
35
36plt.subplot(1, 3, 3)
37plt.hist(df['Scores'].dropna(), alpha=0.5, label='Original')
38plt.hist(df_mode['Scores'], alpha=0.5, label='Mode Imputed')
39plt.title('Mode Imputation')
40plt.legend()
41
42plt.tight_layout()
43plt.show()

همان‌طور که ملاحظه می‌کنید، برای سادگی بیشتر، از دیتاست‌های آماده استفاده نکرده‌ایم و در عوض، مجموعه‌داده‌ای با یک ویژگی تحت عنوان Scores و ده مقدار تعریف شده است. در تصویر زیر و از چپ به راست، نمودارهای «هیستوگرام» (Histogram) سه روش جایگذاری میانگین، میانه و نما رسم شده‌اند:

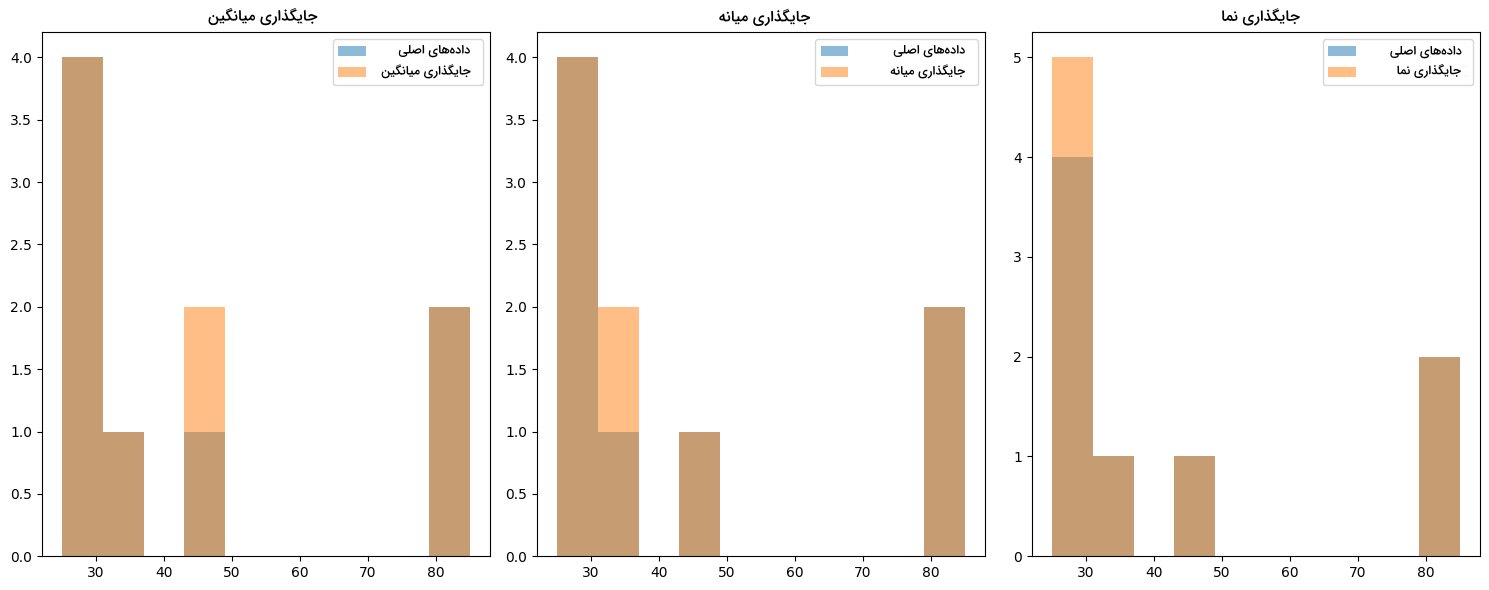
هر چه دیتاست بزرگ‌تر باشد، کاهش مقدار «واریانس» (Variance) و همچنین تغییر در توزیع داده‌ها شدیدتر خواهد بود. در نتیجه بسیار مهم است که پیش از استفاده از روش‌های جایگذاری، درک عمیقی از داده‌ها داشته باشیم.

K نزدیک ترین همسایه

در روش K نزدیک‌ترین همسایه یا KNN، از ویژگی‌ها و شباهت میان نزدیک‌ترین نقاط داده، به‌طور دقیق‌تر، تعداد K عدد از نمونه‌ها، برای پیش‌بینی و جایگذاری داده‌های گمشده استفاده می‌شود.

مزایا

به عنوان یکی از مزایای تکنیک KNN، می‌توانیم به مورد زیر اشاره کنیم:

• حفظ ساختار داده: از آنجا که در KNN، مسئله «همبستگی» (Correlation) میان ویژگی‌ها در نظر گرفته می‌شود، گزینه ایده‌آلی برای توزیع داده‌های پیچیده به شمار می‌رود.

معایب

تکنیک K نزدیک‌ترین همسایه معایبی نیز دارد؛ از جمله:

• هزینه محاسباتی بالا: محاسبه فاصله میان نقاط داده، فرایندی هزینه‌بر است و به همین خاطر، اجرای تکنیک KNN بر روی مجموعه‌داده‌های بزرگ می‌تواند آهسته باشد.

برای پیاده‌سازی روش KNN در زبان برنامه‌نویسی پایتون، مانند نمونه عمل می‌کنیم:

1from sklearn.impute import KNNImputer
2
3# KNN imputation
4knn_imputer = KNNImputer(n_neighbors=2)
5df_knn = pd.DataFrame(knn_imputer.fit_transform(df), columns=df.columns)
6
7# Visual comparison
8plt.hist(df['Scores'].dropna(), alpha=0.5, label='Original')
9plt.hist(df_knn['Scores'], alpha=0.5, label='KNN Imputed')
10plt.title('KNN Imputation')
11plt.legend()
12plt.show()

در نمودار زیر، نتیجه اجرای قطعه کد بالا را مشاهده می‌کنید:

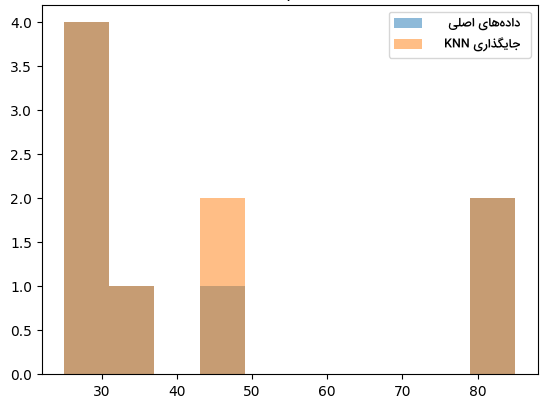
جایگذاری چندگانه از طریق معادلات پیوسته

این روش، یعنی «جایگذاری چندگانه از طریق معادلات پیوسته» (Multiple Imputation by Chained Equations | MICE)، با ساخت چند مدل جایگذاری مختلف و میانگین گرفتن از نتایج به‌دست آمده، راه‌حلی برای مشکل پراکندگی رایج در تکنیک‌های جایگذاری ارائه می‌دهد.

مزایا

از جمله مزایای روش جایگذاری چندگانه، می‌توانیم به مورد زیر اشاره کنیم:

• دقت آماری: به مشکل عدم قطعیت داده‌های گمشده پاسخ داده و به ارزیابی‌های مطمئن‌تری ختم می‌شود.

معایب

یکی از مهم‌ترین معیاب این روش عبارت است از:

• پیچیدگی و هزینه بالا: وجود چندین مدل مختلف، باعث افزایش هزینه محاسباتی و پیچیدگی در قابلیت تفسیرپذیری می‌شود.

پیاده‌سازی تکنیک جایگذاری چندگانه مانند زیر انجام می‌شود:

1from sklearn.experimental import enable_iterative_imputer
2from sklearn.impute import IterativeImputer
3
4# MICE Imputation
5imputer = IterativeImputer(random_state=42, max_iter=10)
6df_mice = pd.DataFrame(imputer.fit_transform(df), columns=df.columns)
7
8# Visual comparison
9plt.hist(df['Scores'].dropna(), alpha=0.5, label='Original')
10plt.hist(df_mice['Scores'], alpha=0.5, label='MICE Imputed')
11plt.title('MICE Imputation')
12plt.legend()
13plt.show()

در تصویر زیر، شاهد نمودار حاصل از پیاده‌سازی روش MICE هستید:

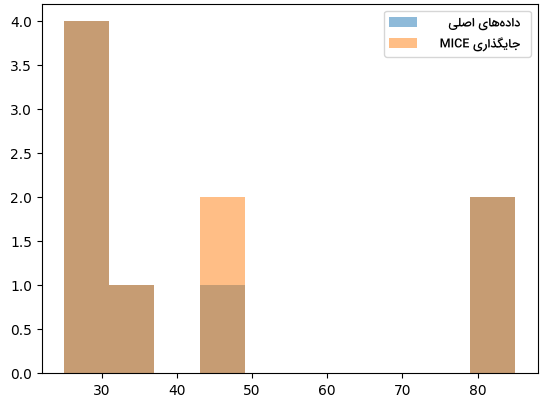
جایگذاری از طریق درون یابی

هنگام کار با داده‌های «سری زمانی» (Time Series)، متوجه می‌شوید که با وجود مرتب بودن نمونه‌ها، گاهی پیش می‌آید که بخشی از اطلاعات گم شده باشد. در چنین شرایطی، استفاده از روش «جایگذاری از طریق درون‌یابی» (Imputing with Interpolation) که «فاصله زمانی» (Temporal Distance) میان نقاط داده را محاسبه می‌کند، کارآمد خواهد بود. برای آشنایی بیشتر با مفهوم داده‌های سری زمانی، مشاهده فیلم آموزشی پیش‌بینی و تحلیل سری‌های زمانی فرادرس را که در لینک زیر آورده شده است به شما پیشنهاد می‌کنیم:

مزایا

در فهرست زیر، تعدادی از مزایای این روش عنوان شده است:

• حفظ ساختار زمانی: تکنیک «درون‌یابی» (Interpolation) با در نظر گرفتن جنبه زمانی داده‌ها، باعث حفظ پیوستگی دنباله نمونه‌ها در طی فرایند جایگذاری می‌شود.
• انعطاف‌پذیری: از ساختار خطی گرفته تا الگوهای پیچیده‌تر، تکنیک درون‌یابی با تغییرات میان داده‌ها سازگار است.

معایب

از جمله معایب جایگذاری از طریق درون‌یابی، می‌توانیم به موارد زیر اشاره کنیم:

• مبتنی‌بر فرضیات: در این روش، فرض می‌شود که تغییرات میان بازه‌های زمانی ثابت است. فرضیه‌ای که گاهی اوقات درست نیست.
• نامناسب برای دنباله‌های طولانی: اگر بخش قابل توجهی از داده‌ها در دسترس نباشد، بهره‌گیری از تکنیک درون‌یابی ممکن است به نتایج نادرستی منتهی شود.

در ادامه، ملاحظه می‌کنید که پیاده‌سازی این روش بر روی داده‌های سری زمانی، به‌طور دقیق‌تر از روز اول ماه ژانویه تا روز دهم ژانویه چگونه انجام می‌شود:

1import pandas as pd
2import matplotlib.pyplot as plt
3import numpy as np
4
5# Creating a sample time series dataset
6date_rng = pd.date_range(start='2024-01-01', end='2024-01-10', freq='D')
7time_series_df = pd.DataFrame(date_rng, columns=['date'])
8time_series_df.set_index('date', inplace=True)
9time_series_df['data'] = [1, 2, 3, 4, np.nan, np.nan, 7, 8, 9, 10]
10
11# Interpolation imputation
12time_series_df_interpolated = time_series_df.interpolate(method='linear')
13
14# Visualization
15time_series_df['data'].plot(kind='line', linestyle='-', marker='o', label='Original', legend=True)
16time_series_df_interpolated['data'].plot(kind='line', linestyle='-', marker='x', label='Interpolated', legend=True)
17plt.title('Time Series Interpolation')
18plt.show()

نمودار نهایی مانند زیر است:

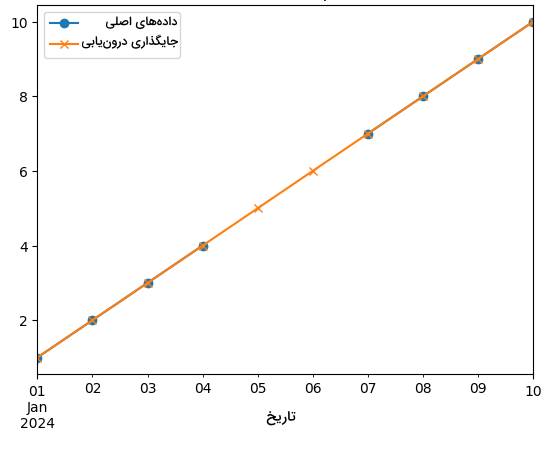
این نمودار، به‌خوبی کارآمدی روش درون‌یابی را به نمایش می‌گذارد. اگر چه میان داده‌های سری زمانی فاصله وجود دارد، تخمین حاصل شده منطقی بوده و روند داده‌ها حفظ شده است.

جایگذاری قبلی و بعدی

تکنیک‌های جایگذاری ویژه‌ای برای داده‌های سری زمانی  و همچنین «داده‌های مرتب‌شده» (Ordered Data) وجود دارند. این تکنیک‌ها مانند «جایگذاری قبلی و بعدی» (Previous Imputation | Next Imputation)، با در نظر گرفتن ساختار ذخیره‌سازی داده‌ها، نتیجه می‌گیرند که مقایسه نمونه‌های نزدیک به یک‌دیگر به مراتب راحت‌تر از نمونه‌هایی است که از یک‌دیگر فاصله دارند. به عنوان مثال در داده‌های سری زمانی، مقدار قبلی و یا بعدی، در موقعیت داده گمشده جایگذاری می‌شود. رویکردی که هم برای مقادیر «عددی» (Numerical) و هم «اسمی» (Nominal) کارآمد است. برای آشنایی بیشتر با انواع داده‌ها در یادگیری ماشین، مطالعه مطلب زیر را از مجله فرادرس به شما پیشنهاد می‌کنیم:

مزایا

از جمله مزایای تکنیک جایگذاری قبلی و بعدی می‌توان به موارد زیر اشاره داشت:

• حفظ پیوستگی: در این روش‌ها، ساختار کلی نمونه داده‌ها حفظ شده و به همین جهت، گزینه مناسبی برای مجموعه‌داده‌های «پیوسته» (continuous) است.
• سادگی: به راحتی قابل درک و پیاده‌سازی هستند.

معایب

در فهرست زیر، تعدادی از معایب این روش را ملاحظه می‌کنید:

• سوگیری: در صورتی که قسمت بزرگی از مجموعه‌داده فاقد اطلاعات باشد، استفاده از چنین تکنیک‌هایی احتمال بروز مشکل سوگیری یا همان Bias را افزایش می‌دهد.
• آسیب‌پذیری نمونه‌های دور افتاده: اگر داده‌های گمشده فاصله زیادی از میانگین داشته باشند، بهتر است از تکینک‌های دیگری استفاده شود.

برای پیاده‌سازی با استفاده از زبان برنامه‌نویسی پایتون، مانند نمونه عمل می‌کنیم:

1# Next fill
2time_series_df_ffill = time_series_df.ffill()
3
4# Previous fill
5time_series_df_bfill = time_series_df.bfill()
6
7# Visualization
8time_series_df['data'].plot(kind='line', linestyle='-', marker='o', label='Original', legend=True)
9time_series_df_ffill['data'].plot(kind='line', linestyle='-', marker='x', label='Next Fill', legend=True)
10time_series_df_bfill['data'].plot(kind='line', linestyle='-', marker='+', label='Previous Fill', legend=True)
11plt.title('Next and Previous Filling')
12plt.show()

نمودار حاصل شده، به‌خوبی روند حفظ پیوستگی داده‌های سری زمانی را به‌وسیله دو تکنیک جایگذاری قبلی و بعدی نشان می‌دهد. مشاهده می‌کنید که چگونه داده‌های گمشده با نمونه‌های قبلی و بعدی خود جایگزین شده‌اند:

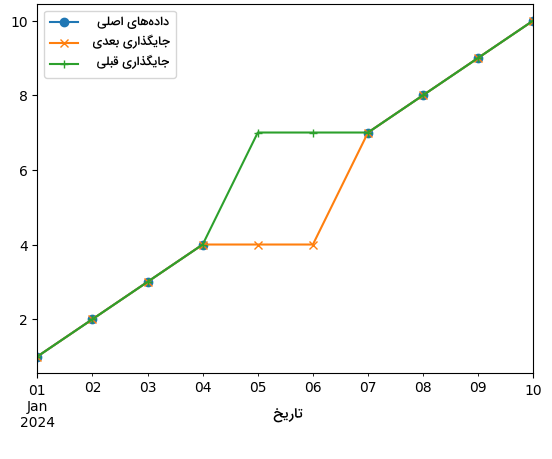
چرا جایگذاری داده اهمیت دارد؟

پس از معرفی تکنیک های جایگذاری داده های گمشده، در این بخش، به شرح اهمیت این فرایند می‌پردازیم. وجود مشکل داده‌های گمشده، دلیل اصلی استفاده ما از رویکرد جایگذاری است. در فهرست زیر، به چند مورد از مشکلاتی که داده‌های گمشده به همراه دارند اشاره شده است:

• ناسازگاری با کتابخانه‌های یادگیری ماشین در زبان برنامه‌نویسی پایتون: با این وجود که ابزارهایی مانند کتابخانه‌های مختلف، کار ما را برای طراحی و پیاده‌سازی الگوریتم‌های یادگیری راحت ساخته‌اند، اما برخی از رایج‌ترین این ابزارها مانند کتابخانه scikit-learn، فاقد مکانیزم‌های مدیریت داده‌های گمشده هستند و در نتیجه به خطا منجر می‌شوند.
• ایجاد اختلال در مجموعه‌داده: حجم زیاد داده‌های گمشده، باعث ایجاد اختلال در توزیع داده‌ها و افزایش یا کاهش اهمیت برخی از ویژگی‌ها در مجموعه‌داده می‌شود.
• تاثیرگذاری بر مدل نهایی: داده‌های گمشده باعث ایجاد «سوگیری» (Bias) در مجموعه‌داده می‌شوند؛ مشکلی که ارزیابی نهایی مدل را با چالش روبه‌رو می‌کند.
• تمایل به بازیابی تمامی نمونه‌های مجموعه‌داده: اهمیت داده‌ها زمانی مشخص می‌شود که بخش زیادی از مجموعه‌داده فاقد اطلاعات باشد یا نمونه داده‌های زیادی را حذف کرده باشیم. در چنین شرایطی و به‌ویژه اگر مجموعه‌داده چندان بزرگ نباشد، حذف بخش کوچکی از داده‌ها نیز بسیار در خروجی نهایی مدل یادگیری ماشین تاثیرگذار خواهد بود.

چگونه رویکرد جایگذاری مناسب را انتخاب کنیم؟

در ادامه معرفی تکنیک های جایگذاری داده های گمشده، آشنایی با چگونگی انتخاب رویکرد مناسب مسئله نیز از اهمیت بالایی برخوردار است. تکنیک جایگذاری که برای پروژه خود انتخاب می‌کنید، باید همگام با ویژگی‌های دیتاست باشد و محدودیت‌های مسئله را نیز در نظر بگیرد. از همین جهت، طرح پرسش‌های زیر می‌تواند کارآمد باشد:

• ساختار داده‌ها چگونه است؟ توزیع، مقیاس و روابط میان‌داده‌ای را بررسی کنید.
• چرا داده‌ها گم شده‌اند؟ با پی بردن به نوع داده‌های گمشده که پیش‌تر نیز به آن‌ها اشاره داشتیم، تکنیک جایگذاری مناسب را انتخاب کنید.
• چه منابع محاسباتی در دسترس است؟ هنگام انتخاب روش‌های جایگذاری، توازن میان دقت و هزینه محاسباتی را در نظر بگیرید.

سوالات متداول پیرامون تکنیک های جایگذاری داده های گمشده

حالا که با انواع تکنیک های جایگذاری داده های گمشده آشنا شدیم، در این بخش به چند مورد از پرسش‌های متداول در این زمینه پاسخ می‌دهیم.

مفهوم جایگذاری برای داده ها چیست؟

جایگذاری داده‌های گمشده با دیگر مقادیر تخمین‌زده شده را جایگذاری داده می‌نامند.

جایگذاری داده متشکل از چه تکنیک هایی است؟

برخی از رایج‌ترین تکنیک های جایگذاری داده های گمشده عبارت‌اند از:

• جایگذاری میانگین، میانه و نما
• K نزدیک‌ترین همسایه یا KNN
• جایگذاری چندگانه از طریق معادلات پیوسته
• جایگذاری از طریق درون‌یابی
• جایگذاری قبلی و بعدی

چه زمان باید از تکنیک های جایگذاری استفاده کنیم؟

در فرایند جایگذاری، موقعیت اطلاعات گمشده با مقادیری منطقی و محتمل تکمیل می‌شود. در نتیجه هر چه تعداد داده‌های گمشده کمتر باشد، نتیجه بهتری نیز از جایگذاری حاصل می‌شود.

نحوه جایگذاری داده های گمشده به چه صورت است؟

از معیارهای آماری مانند میانگین، میانه و نما و یا مقادیر ثابت برای جایگذاری اطلاعات گمشده در سطرهای مجموعه‌داده استفاده می‌شود.

تفاوت میان درون یابی و جایگذاری چیست؟

در حالی که در جایگذاری و به عنوان مثال روش میانگین، داده‌های گمشده با میانگین ستون مرتبط جایگزین می‌شوند، درون‌یابی نوعی تخمین است که برای تولید مجموعه‌ای از نقاط داده در دامنه‌ای «گسسته» (Discrete) از نمونه داده‌های موجود، مورد استفاده قرار می‌گیرد.

جمع‌بندی

جایگذاری نه یک تعویض ساده بلکه بازسازی بخشی بنیادین از مجموعه‌داده است. همان‌طور که در این مطلب از مجله فرادرس خواندیم، هر کدام از تکنیک های جایگذاری داده های گمشده نقاط ضعف و قوت منحصربه‌فردی داشته و یادگیری آن‌ها به اندازه شناخت داده‌ها اهمیت دارد. حالا، با در اختیار داشتن ابزارها و همچنین دانش کافی، می‌توانید با آگاهی بیشتری در مورد انتخاب تکنیک جایگذاری مناسب تصمیم‌گیری کنید.