به طور حتم در دوران کودکی سوار چرخ‌وفلک شده‌اید و احساس عجیبی را تجربه کرده‌اید. تا به حال به انحرافِ توپِ فوتبال در زمینِ چمن دقت کرده‌اید؟ گویی نیرویی نامریی بر توپ وارد می‌شود و مسیر آن را تغییر می‌دهد. این نیروی نامریی، نیروی کوریولیس و شتاب حاصل از آن شتاب کوریولیس نام دارند. زمین، مانندِ چرخ‌وفلکی غول‌پیکر، در حالِ چرخش است. این چرخش، بر حرکت اجسام مختلف، از توپِ فوتبال تا باد و جریانِ آب، اثر می‌گذارد و مسیر حرکت آن‌ها را از خط مستقیم، منحرف می‌کند. شتابِ کوریولیس، شتابی واقعی نیست و اثر چرخش زمین است. در این مطلب از مجله فرادرس، ابتدا به پرسش شتاب کوریولیس چیست به زبان ساده پاسخ می‌دهیم.

در ادامه، در مورد تاثیر شتاب کوریولیس روی الگوهای آب‌وهوایی صحبت و اثر کوریولیس را در سیاره‌های دیگر بررسی می‌کنیم. سپس، فرضیه بسیار مهم تاثیر شتاب کوریولیس بر جهت چرخش آب در سینک ظرف‌شویی در نیمکره شمالی و جنوبی را با چند آزمایش ساده توضیح می‌دهیم. در پایان، فرمول نیرو و شتاب کرویولیس را به‌دست می‌آوریم.

شتاب کوریولیس چیست؟

شتاب کوریولیس از نیروی کوریولیس یا اثر کوریولیس می‌آید. نیروی کوریولیس به نیرویی ظاهری یا شبه نیرو گفته می‌شود که بر اجسام متحرک روی جسم چرخان اثر می‌گذارد. زمین و اجسام قرار گرفته در اطراف آن، بهترین مثال برای درک بهتر این نیرو و شتاب کوریولیس هستند. به عنوان مثال، مسیر پرواز هواپیما به جای خط راست، خطی منحنی است.

اجسام مختلف در کیهان به صورت طبیعی روی خطی راست و مستقیم، با سرعت ثابت حرکت می‌کنند. اگر جسم در مسیر حرکت خود با هیچ نیروی خارجی روبرو نشود، به حرکت خود روی این خط ادامه خواهد داد. در این حالت، حرکت جسم پایسته است. در آینده‌ای نزدیک یا دور، انسان سفر در فضا را آغاز خواهد کرد. برای آن‌که فضانوردان بتوانند سفرهای طولانی در فضا را تحمل کنند، فضاپیماها باید به گونه‌ای طراحی شوند که نیروی جاذبه زمین در آن‌ها احساس شود. دلیل این موضوع به عادت داشتن بدن انسان به نیروی جاذبه زمین مربوط می‌شود. چگونه می‌توان این کار را انجام داد؟ یکی از بهترین ایده‌ها برای شبیه‌سازی جاذبه در فضاپیماها استفاده از سانتریفیوژ است.

سانتریفیوژ به شکل چرخی دورانی و بسیار بزرگ است که نیروی گزیر از مرکزِ داخل آن، فضانوردان را به سمت خارج هل می‌دهد. در این صورت، فضانوردان حالتی مشابه نیروی جاذبه را احساس خواهند کرد. سوال مهمی که ممکن است برای شما مطرح شود آن است که منشا نیروی گریز از مرکز چیست؟ برای پاسخ به این پرسش باید به سانتریفیوژ (چرخ) و فضانوردی که در آن قرار گرفته است، از بیرون نگاه کنیم. فضانورد به همراه چرخش چرخ، می‌چرخد. فرض کنید فضانورد توپی را در دست خود نگه داشته است. مسیر حرکت توپ به شکل دایره است. حال فرض کنید فضانورد توپ را رها می‌کند. چه اتفاقی رخ می‌دهد؟

توپ پس از رها شدن هیچ نیرویی را احساس نمی‌کند. در نتیجه، به جای حرکت روی مسیری به شکل دایره، روی خط مستقیم به مسیر خود ادامه می‌دهد. توپ تا رسیدن به بدنه چرخ به حرکت خود روی خط راست ادامه خواهد داد. از دید ما، به عنوان ناظر خارجی، توپ روی خط مستقیم حرکت می‌کند. اما فضانورد مسیر متفاوتی را مشاهده می‌کند. از دید او توپ به سمت پایین و لبه چرخ سقوط می‌کند.

فضانورد احساس می‌کند نیرویی مجازی به توپ وارد می‌شود، نیروی گریز از مرکز. توجه به این نکته بسیار مهم است که نیروی گریز از مرکز، نیرویی فیزیکی و واقعی نیست. از دید ما به عنوان ناظری خارجی، هیچ نیرویی بر توپ وارد نمی‌شود. توپ پس از رها شدن از دست فضانورد، در مسیری مستقیم و بدون انحراف به حرکت خود ادامه می‌دهد. اما فضانورد قطعا با ما مخالفت خواهد کرد و با قاطعیت خواهد گفت بر توپ نیرو وارد می‌شود. او حرکت توپ در چارچوب مرجع خود را با استفاده از نیروی گریز از مرکز توصیف می‌کند.

اکنون فرض کنید فضانورد به جای رها کردن توپ، آن را به سمت بالا پرتاب می‌کند. باز هم از دید ما به عنوان ناظر بیرونی، توپ پس از پرتاب به سمت بالا، روی خطی مستقیم به سمت دیواره حرکت می‌کند. اما از دید فضانورد، توپ پس از جدا شدن از دست او، به دلیل نیرو گریز از مرکز، روی مسیری به شکل سهمی حرکت می‌کند.

همچنین، فضانورد این موضوع را احساس می‌کند که توپ پس از افتادن جلوی پای او، به مقدار خیلی کمی منحرف شده است. اگر توپ تا ارتفاع بیشتری پرتاب شود، در نقطه دورتری فرود می‌آید. فضانورد با استفاده از نیروی گریز از مرکز به تنهایی نمی‌تواند حرکت توپ را توصیف کند. آیا نیروی دیگری وجود دارد؟ او برای توصیف حرکت توپ باید نیروی مجازی دیگری را نیز اختراع کند. این نیرو، نیروی کوریولیس نام دارد. برای درک بهتر مفهوم این نیرو، آن را از دید ناظر بیرونی بررسی می‌کنیم.

هنگامی‌که چرخ می‌چرخد، هر نقطه داخل آن روی مسیری به شکل دایره حرکت می‌کند. هرچه نقطه از مرکز چرخ دورتر باشد، با سرعت بزرگ‌تری حرکت می‌کند، زیرا باید مسافت بیشتری را طی کند.

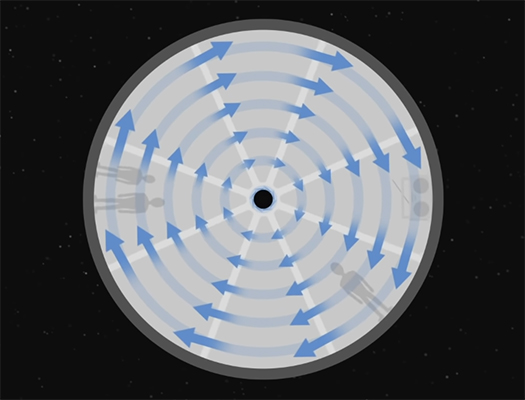
هنگامی‌که فضانورد توپ را نگه داشته است، توپ روی یکی از این دایره‌ها با سرعتی مشخص حرکت می‌کند. توپ پس از پرتاب به سمت بالا، به محور چرخش نزدیک‌تر می‌شود. در این حالت، توپ برای آن‌که بتواند حرکت چرخ را دنبال کند، باید با سرعت کمتری حرکت کند. اما توپ سعی در حفظ حرکت اولیه خود دارد. بنابراین، سریع‌تر از چرخ حرکت می‌کند. از این‌رو، از دید فضانورد مسیر حرکت توپ کمی منحرف می‌شود.

فضانورد نیرو و شتاب کوریولیس را نیز در بدن خود احساس خواهد کرد. سر او به مرکز چرخ نزدیک‌تر است، اما پاهای او در دورترین فاصله از مرکز قرار گرفته‌اند بنابراین، پاهای او با سرعت بیشتری حرکت می‌کنند. در این حالت فضانورد به طور کامل چرخش را احساس و با از دست دادن تعادل، احساس تهوع شدیدی می‌کند. اگر بخواهیم از این نوع سانتریفیوژ در آینده استفاده کنیم، باید آن را در اندازه‌ای بسیار بزرگ بسازیم. در این حالت، اندازه نیرو و شتاب کوریولیس بسیار کوچک می‌شود و هیچ اثری روی فضانورد نخواهد داشت.

نیروی کوریولیس، همانند نیروی گریز از مرکز به هنگام چرخش احساس می‌شود. این نیرو، علاوه بر سانتریفیوژ در چرخ‌وفلک و اجسام چرخان دیگر نیز احساس می‌شود. باید به این نکته توجه داشته باشید که نیروی کوریولیس حتی در مقیاسی به بزرگی زمین نیز وجود دارد. زمین، هر روز به دور خود می‌چرخد. اجسام در نزدیکی دو قطب زمین، با سرعت کمتری نسبت به اجسام نزدیک به استوا حرکت می‌کنند. در این حالت، نیرو و شتاب کوریولیس می‌تواند در مقیاسی به بزرگی زمین وارد شود.

به عنوان مثال، اگر موشکی را به فضا بفرستیم، مسیر موشک به جای مسیری مستقیم، مسیری به شکل منحنی خواهد بود. دلیل این موضوع به چرخش زمین مربوط می‌شود. پرتاب موشک به فضا مشابه پرتاب توپ در سانتریفیوژ است. از دید ناظر روی زمین،‌ موشک روی خط مستقیم حرکت می‌کند، اما از دید ناظری خارج از زمین، مسیر حرکت موشک به شکل منحنی خواهد بود.

نیروی کوریولیس بر حرکت هوا در اتمسفر زمین نیز تاثیر می‌گذارد. به دلیل وجود این نیرو، جهت حرکت طوفان در نیمکره شمالی و جنوبی با یکدیگر تفاوت دارند.

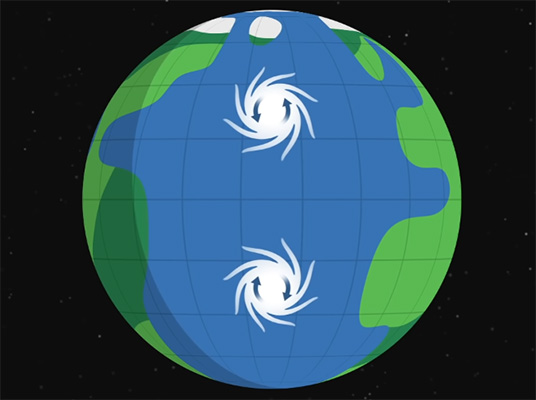
همچنین، هوا در نزدیکی استوا، سریع‌تر از هوا در نزدیکی قطب‌ها حرکت می‌کند. باد به هنگام دور شدن از استوا دوست دارد سرعت اولیه خود را حفظ کند. بنابراین، از چرخش زمین جلوتر می‌رود. این اختلاف سرعت سبب حرکت چرخشی می‌شود. به کمک این موضوع می‌توان جهت حرکت طوفان‌ها را توضیح داد. نیرو و شتاب کوریولیس حتی بر احساس ما از وزن تاثیر می‌گذارد. نیروی گریز از مرکز ما را به سمت خارج از سطح زمین هل می‌دهد. این نیرو در خلاف جهت نیروی جاذبه عمل می‌کند و سبب کاهش وزن ما، هرچند به میزان خیلی کم، می‌شود.

اگر زمین با سرعت بیشتری می‌چرخید، اندازه نیروی گریز از مرکز بزرگ‌تر می‌شد. در این حالت، ترازو وزن ما را کمتر نشان می‌داد. در مقابل، اگر زمین با سرعت کمتری می‌چرخید، نیروی گریز از مرکز مقدار کمتری داشت. در نتیجه، وزن اندازه‌گیری شده توسط ترازو بزرگ‌تر می‌شد. قطاری را فرض کنید که روی خط استوا حرکت می‌کند. اگر قطار به سمت شرق حرکت کند، جهت حرکت آن با جهت چرخش زمین یکسان خواهد بود. در این حالت، قطار با سرعت بزرگ‌تری حرکت و در نتیجه، نیروی گریز از مرکز بزرگ‌تری را احساس می‌کند. از این‌رو، وزن قطار به هنگام حرکت آن به سمت شرق در مقایسه با حالت سکون، کمتر است.

در مقابل، اگر قطار به سمت غرب حرکت کند، جهت حرکت آن مخالفِ جهت چرخش خواهد بود. در این حالت، قطار با سرعت کوچک‌تری حرکت و در نتیجه، نیروی گریز از مرکز کوچک‌تری را احساس می‌کند. از این‌رو، وزن قطار به هنگام حرکت آن به سمت غرب در مقایسه با حالت سکون، بزرگ‌تر است. این حالت عجیب، «اثر اوتووس» (Eotvos effect) نام دارد و حالت خاصی از اثر کوریولیس است. این اثر نشان می‌دهد که وزن اجسام روی زمین به چگونگی حرکت آن‌ها وابسته است.

تا اینجا فهمیدیم نیرو و شتاب کوریولیس، شتاب و نیروی واقعی نیستند. اثر کوریولیس بر جهت وزش باد و شکل‌گیری طوفان‌ها تاثیر می‌گذارد. در ادامه، در مورد تاثیر شتاب کوریولیس بر آب‌وهوا صحبت می‌کنیم.

شتاب کوریولیس چه تاثیری روی آب و هوا می گذارد؟

اثر کوریولیس بر الگوهای آب‌وهوایی تاثیر می‌گذارد. این اثر به دلیل چرخش زمین به وجود می‌آید. همان‌طور که در بخش قبل اشاره کردیم، سرعت چرخش زمین در استوا سریع‌تر از سرعت چرخش آن در قطب‌ها است. زمین در ناحیه استوا پهن‌تر است، بنابراین برای یک چرخش کامل در ۲۴ ساعت، مناطق استوایی با سرعت تقریبی ۱۶۰۰ کیلومتر بر ساعت حرکت می‌کنند. در نزدیکی قطب‌ها، سرعت چرخش زمین بسیار کم و در حدود ۰/۰۰۰۰۸ کیلومتر بر ساعت است.

فرض کنید فردی روی خط استوا ایستاده است و می‌خواهد توپی را برای دوست خود در آمریکای شمالی پرتاب کند. اگر فرد توپ را روی خط مستقیمی پرتاب کند، محل فرود آن سمت راست دوست آمریکایی خواهد بود. زیرا دوست آمریکایی این فرد با سرعت کمتری حرکت می‌کند و به توپ نمی‌رسد. اکنون فرض کنید، این فرد به قطب شمال سفر کرده است و از آنجا می‌خواهد توپ را برای دوست آمریکایی خود پرتاب کند. در این حالت، توپ باز هم سمت راست دوست آمریکایی این فرد فرود می‌آید. اما این بار به دلیل آن است که دوست آمریکایی فرد نسبت به او سریع‌تر حرکت می‌کند و جلوتر از توپ می‌رود. توجه به این نکته مهم است که در هر نقطه از نیمکره شمالی این حرکت را انجام دهید، توپ به سمت راست منحرف خواهد شد.

این موضوع به دلیل شتاب کوریولیس رخ می‌دهد. پرتاب توپ را می‌توان به حرکت شاره‌ها در نواحی بسیار بزرگ، مانند جریان‌ هوا، تعمیم داد. این گونه به نظر می‌رسد که جریان‌ هوا در نیمکره شمالی تمایل دارد به سمت راست حرکت کند. اما اثر کوریولیس در نیمکره جنوبی به طور کامل متفاوت است. جریان‌ هوا در نیمکره جنوبی به سمت چپ حرکت می‌کند. شتاب کوریولیس به سرعت حرکت زمین و سرعت جسم یا شاره، وابسته است. این شتاب در سرعت‌های بالا یا مسافت‌های زیاد، بسیار قابل‌توجه است.

الگوهای آب و هوایی

پیشرفت الگوهای متفاوت آب‌وهوایی، مانند «بادهای بسامان» (Trade Winds) و «چرخندها» (Cyclones)، دو مثال از اثر شتاب کوریولیس هستند. چرخندها، سیستم‌های کم‌فشاری هستند که هوا را، همانند مکنده‌ای قوی، به قسمت مرکزی خود می‌کشند. در سیستم هواشناسی دو سامانه پرفشار و کم‌فشار وجود دارند. به ناحیه‌ای از جو که فشار بالاتری نسبت به محیط اطراف دارد، سامانه پرفشار گفته می‌شود. هوای موجود در این ناحیه، از آن خارج و به ناحیه کم‌فشار می‌رود. در مقابل، سامانه کم‌فشار به ناحیه‌ای از فضا گفته می‌شود که فشاری کمتر از فشار محیط اطراف دارد. بنابراین، هوا از محیط خارج و به ناحیه کم‌فشار وارد می‌شود. به بیان دیگر، جهت جریان هوا در دو ناحیه کم‌فشار و پرفشار با یکدیگر فرق دارد.

همان‌طور که گفتیم، چرخندها سیستم‌های کم‌فشاری هستند که هوا از تمام جهت‌ها وارد قسمت مرکزی آن می‌شود. توده‌های هوا پس از ورود از جهت‌های مختلف به چرخندها، منحرف می‌شوند. این انحراف در نیمکره شمالی به گونه‌ای است که گویا طوفان در جهت خلاف عقربه‌های ساعت می‌چرخد. در مقابل، چرخش طوفان در نیمکره جنوبی در جهت عقربه‌های ساعت است. بنابراین، با کمک اثر کوریولیس می‌توانیم الگوهای آب‌وهوایی در جهان را تعریف کنیم. در ادامه، در مورد بادهای شرقی صحبت می‌کنیم. خط استوا و ناحیه بالا و پایین آن را در نظر بگیرید. بادهای شرقی، بادهایی هستند که در نزدیکی خط استوا از شرق به غرب می‌وزند. همیشه جهت وزش باد را به صورت یکسان حس نمی‌کنید.

گاهی ممکن است باد به سمت شرق بوزد و گاهی به سمت غرب یا شمال. با این وجود، بسیاری از بادها و جهت وزش آن‌ها روی زمین را می‌توان به طور کامل پیش‌بینی کرد. به عنوان مثال،‌ «رودباد یا جت‌استریم» (Jet Streams) در بالای جو زمین از غرب به شرق و بادهای شرقی، جریان‌های هوا نزدیک به سطح زمین هستند که در نزدیکی خط استوا از شرق به غرب می‌وزند. دریانوردان قرن‌ها است که از بادهای شرقی برای مسیریابی استفاده می‌کنند. سوال مهمی که ممکن است مطرح شود آن است که چرا بادهای شرقی از شرق به غرب می‌وزند.

در این جا است که شتاب کوریولیس خودی نشان می‌دهد. بادهای شرقی به دلیل چرخش زمین به دور محور خود، به سمت غرب می‌وزند. ابتدا، هوای گرم و مرطوب در اطراف خط استوا به سمت بالا حرکت می‌کند. در ادامه، هوای سردتر نزدیک به قطب‌ها به سمت پایین حرکت خواهد کرد.

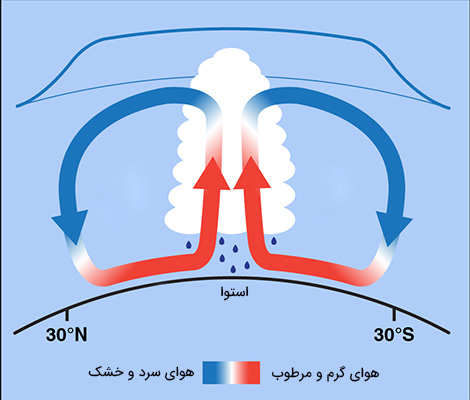
شاید از خود بپرسید اگر هوا از استوا به سمت قطب‌ها جریان دارد، چرا تمام بادها از شمال به جنوب نمی‌وزند؟ اینجا همان جایی است که چرخش زمین پا به میدان می‌گذارد. چرخش زمین به دور محور خود بر جهت حرکت هوا تاثیر می‌گذارد. به دلیل این چرخش، بادها در نیمکره شمالی به سمت راست و در نیمکره جنوبی به سمت چپ، منحرف می‌شوند. این مورد را می‌توان به صورت زیر و در چند مرحله توضیح داد:

• زمین به دور محور خود به صورت پادساعتگرد و در جهت غرب به شرق می‌چرخد.
• هوا در نزدیکی زمین jمایل دارد روی خط مستقیم و بدون انحراف حرکت کند، اما به دلیل چرخش زمین، جهت حرکت آن کمی منحرف می‌شود (مثال فضانورد در سانتریفیوژ چرخان).
• نقاط مختلف روی زمین با سرعت یکسانی نمی‌چرخند، به گونه‌ای که نقاط نزدیک به قطب‌ها با سرعت کمتری نسبت به نقاط نزدیک به خط استوا حرکت می‌کنند.

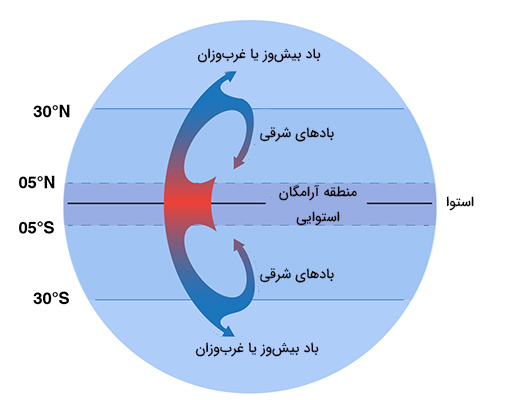
به این دلیل،‌ مسیر جریان هوا به جای حرکت روی خط مستقیم، منحرف می‌شود. همچنین، جهت این انحراف در نیمکره‌های شمالی و جنوبی با یکدیگر تفاوت دارند. همان‌طور که در مطالب بالا اشاره شده به این پدیده، اثر کوریولیس می‌گوییم. به دلیل این اثر است که بادهای شرقی در نیمکره‌‌های شمالی و جنوبی به سمت غرب می‌وزند. بادهای شرقی را می‌توانیم در ۳۰ درجه شمالی و جنوبی خط استوا پیدا کنیم (تصویر زیر). همچنین، روی خط استوا تقریبا هیچ باnی نمی‌وزد. این منطقه «منطقه رکود یا منطقه آرامگان استوایی» (Doldrums) نامیده می‌شود. هوا nv این منطقه به قدری آرام است که کشتی‌های بادی در قدیم به سختی در آنجا حرکت می‌کردند.

اثر کوریولیس در سیاره‌ های دیگر چگونه است؟

سرعت چرخش زمین، در مقایسه با سیاره‌های دیگر در منظومه‌شمسی، بسیار کمتر است. این بدان معنا است که اثر یا شتاب کوریولیس روی زمین به اندازه‌ای قوی نیست که در سرعت‌های کم و مسافت‌های کوتاه، مانند جهت چرخش آب در سینک ظرف‌شویی یا تخلیه آب در وان حمام، تاثیر بگذارد. در ادامه، اثر کوریولیس را در برخی سیاره‌های منظومه‌شمسی با یکدیگر مقایسه می‌کنیم.

شتاب کوریولیس در سیاره زهره

سیاره زهره تقریبا هم‌اندازه زمین است و اتمسفری با چگالی بسیار زیاد، دارد. از آنجا که این سیاره با سرعت بسیار کمی می‌چرخد، اثر کوریولیس روی آن بسیار ضعیف است.

شتاب کوریولیس در سیاره مریخ

جو مریخ بسیار رقیق است. طوفان‌های عظیم گردوغبار، تنها سیستم آب‌وهوایی است که به راحتی در مریخ مشاهده می‌شود. اندازه کوچک سیاره مریخ، شتاب کوریولیس را در سطح آن کاهش می‌دهد.

شتاب کوریولیس در سیاره مشتری

قطر مشتری حدود ۱۱ برابر قطر زمین است. این سیاره، بزرگ‌ترین سرعت چرخش را در میان سیاره‌های منظومه‌شمسی دارد. یک روز در مشتری فقط ۹/۸ ساعت طول می‌کشد، در حالی‌که یک روزِ زمینی، ۲۴ ساعت است. در نتیجه، به دلیل چرخش سریع مشتری به دور خود و اندازه بسیار بزرگ آن، اثر کوریولیسِ بسیار بزرگی در اتمسفر آن اتفاق می‌افتد. از این‌رو، اثر کوریولیس روی این سیاره، بادهای شمالی-جنوبی را به بادهای شرقی-غربی تبدیل می‌کند. این بادها می‌توانند با سرعتی بیش از ۶۱۰ کیلومتر بر ساعت حرکت کنند. از این‌رو، تقسیم‌بندی افقی مشخصی بین بادهای شرقی و غربی ایجاد می‌شود.

این تقسیم‌بندی افقی، نوارهایی به نام کمربند را میان ابرهای سیاره ایجاد می‌کند. مرزهای بین این کمربندهای پر سرعت، منطقه‌های طوفانی بسیار فعالی هستند. لکه سرخ بزرگ با قدمتی ۱۸۰ ساله، به احتمال زیاد یکی از معروف‌ترین طوفان‌ها است. همچنین، اثر کوریولیس،‌ نوارهای رنگی متعددی را در جو مشتری ایجاد می‌کند. هر نوار، نشان‌دهنده یک جریان باد با سرعت و جهت متفاوت است.

شتاب کوریولیس در سیاره زحل

زحل، با قطری حدود ۹/۵ برابر قطر زمین، همانند مشتری، سیاره بسیار بزرگی است. یک روز در سیاره زحل، تنها ۱۰/۵ ساعت طول می‌کشد. از این‌رو، اندازه بزرگ این سیاره، در کنار سرعت چرخش بسیار زیاد، اثر کوریولیس بسیار بزرگی را در اتمسفر آن ایجاد می‌کند. این اثر باعث می‌شود جریان‌های جوی سیاره زحل به صورت چرخشی حرکت کنند. این چرخش‌ها به نوبه خود سبب ایجاد الگوهای راه‌راه در ابرهای زحل می‌شوند.

شتاب کوریولیس در سیاره اورانوس و نپتون

اتمسفرهای اورانوس و نپتون نیز مانند مشتری و زحل از لایه ضخیمی از ابرها تشکیل شده‌اند، اما در جو اورانوس، برخلاف سیارات غول پیکر دیگر، هیچ نوار و توفان برجسته‌ای دیده نمی‌شود. دلیل این امر آن است که اورانوس برخلاف سایر سیاره‌های غول پیکر، منبع گرمای داخلی اضافی ندارد. در نتیجه، حرکت‌های همرفتی (جابجایی توده‌های گرم به بالا و توده‌های سرد به پایین) در جو آن وجود ندارد. ابرهای نپتون به دلیل چرخش بسیار سریع این سیاره به دور خود، به گونه‌ای منحرف می‌شوند تا نوارهایی موازی خط استوای نپتون تشکیل دهند.

همچنین، در جو نپتون ممکن است گرداب‌های آشفته‌ای شکل بگیرند. «کاوشگر وویجر» (Voyager Spacecraft) در سال ۱۹۸۹ میلادی هنگام عبور از کنار نپتون، لکه تاریک بزرگی را به نام «لکه تاریک بزرگ» کشف کرد که تقریبا هم‌اندازه لکه سرخ‌رنگِ مشتری بود. با این حال، عکس‌های اخیر تلسکوپ فضایی هابل نشان می‌دهند لکه تاریک بزرگ به احتمال زیاد ناپدید شده است.

چگونه شتاب کوریولیس را با استفاده از فیلم های آموزشی فرادرس بهتر یاد بگیریم؟

تا اینجا فهمیدیم نیرو و شتاب کوریولیس چیست و چه تاثیری روی شکل‌گیری الگوهای هواشناسی می‌گذارد. شتاب کوریولیس پدیده‌ای فیزیکی است که بر هر جسمِ متحرکی روی سطح زمین، اثر می گذارد و مسیر آن را از خط مستقیم، منحرف می‌کند. با درک این پدیده می‌توانیم راز چرخش طوفان‌ها یا حرکت موشک‌ها را به خوبی متوجه شویم. برای یادگیری شتاب کوریولیس، ابتدا باید با مفاهیم پایه مانند قوانین نیوتن، شتاب، سرعت و بردارها آشنا باشید. این مفاهیم را به خوبی می‌توانید با تماشای فیلم آموزشی زیر یاد بگیرید:

پس از درک مفاهیم پایه، به راحتی می‌توانید با تماشای مجموعه فیلم‌های آموزشی فرادرس برای درس مکانیک تحلیلی، شتاب کوریولیس را فرابگیرید:

شتاب کوریولیس چگونه بر جهت چرخش آب در سینک ظرف‌شویی در نیمکره شمالی و جنوبی تاثیر می گذارد؟

همانطور که در مطالب بالا اشاره شد، اثر کوریولیس بر جهت حرکت باد در نیمکره شمالی و نیمکره جنوبی تاثیر می‌گذارد. باور دیگری که در مورد اثر کوریولیس وجود دارد آن است که جهت حرکت آب در سینک ظرف‌شویی در نیمکره شمالی و جنوبی فرق دارد. آیا این باور درست است؟ مستندهای زیادی در این مورد ساخته شده‌اند. برخی پژوهشگران بر این باور هستند که جهت چرخش آب به این بستگی دارد که در کدام نیمکره زمین قرار گرفته است. اما گروه دیگری از پژوهشگران تاکید دارند که آب هر جهتی که بخواهد داخل سینک حرکت می‌کند و برایش مهم نیست در کدام نیمکره زمین قرار دارد.

بهتر است این موضوع را ابتدا خودتان آزمایش کنید. کنار سینک ظرف‌شویی بایستید و آب را باز و به جهت چرخش آب در سینک ظرف‌شویی، دقت کنید. برخی مواقع آب در جهت عقربه‌های ساعت و مواقعی دیگر در خلاف جهت عقربه‌های ساعت می‌چرخد. بنابراین، این فرضیه که جهت چرخش آب در سینک ظرف‌شویی با تغییر نیمکره، تغییر می‌کند، داستانی ساختگی است و هیچ پشتوانه علمی ندارد. شاید بتوان با انجام آزمایشی دقیق و حذف تمام حرکت‌های اضافی آب، این فرضیه را به طور دقیق‌تری بررسی کرد. برای انجام آزمایش می‌توان از استخر بادی ۱/۵ متری استفاده کرد. این استخر به طور کامل با آب پر می‌شود و به مدت ۲۴ ساعت به حال خود باقی می‌ماند تا تمام حرکت‌های اضافی آب حذف شوند.

همچنین، برای حذف حرکت گردابی آب به هنگام خروج از استخر، به انتهای آن لوله‌ای نازک متصل به شیر وصل شده است. بنابراین، برای تخلیه آب، تنها کافی است شیر متصل به لوله باز شود.

در ادامه، شیر متصل به لوله باز می‌شود. ابتدا، هیچ جهت خاصی برای حرکت آب مشاهده نمی‌شود. برای مشاهده بهتر حرکت آب، مقداری رنگ مصنوعی به آن اضافه می‌شود.

پس از گذشت مدت زمانی مشخص، رنگ‌ها در آب پخش و شروع به حرکت می‌کنند. همان‌طور که در تصویر زیر مشاهده می‌کنید، جهت حرکت رنگ‌ها در آب به صورت پادساعتگرد است. توجه داشته باشید که این آزمایش در نیمکره شمالی انجام شده است.

این حرکت را نمی‌توانید در سینک ظرف‌شویی یا وان حمام مشاهده کنید. زیرا در این دو مکان، تکانه زاویه‌ای به دلیل وجود منابع مختلف سبب حرکت‌های مختلفِ آب، مانند حرکت کاتوره‌ای، می‌شود. با حذف تمام حرکت‌های اضافی آب می‌توان، چرخش پادساعتگرد آن در نیمکره شمالی را مشاهده کرد. اما این نکته را نباید فراموش کنیم که حذف تمام حرکت‌های اضافی کار بسیار سختی است. برای آن‌که بدانیم این آزمایش چگونه کار می‌کند، استخری را در نظر بگیرید که یک سر آن، در نزدیکی قطب جنوب قرار دارد. استخر، نسبت به زمین ساکن است، اما هر روز به دلیل چرخش زمین به دور خود، یک دور کامل حول قطب می‌چرخد.

نقاطی از استخر که در فاصله دورتری از قطب قرار گرفته‌اند در مقایسه با نقاط نزدیک‌تر به قطب،‌ مسافت بزرگ‌تری را طی می‌کنند.

تمام نقاط داخل استخر با چرخش زمین حرکت می‌کنند، اما تکانه نقاطِ نزدیک‌تر به استوا، بزرگ‌تر و تکانه نقاط نزدیک‌تر به قطب، کمتر است. بنابراین، نقاطِ بیرونی‌تر استخر که در فاصله دورتری نسبت به قطب قرار گرفته‌اند، با سرعت بزرگ‌تری حرکت می‌کنند. اما نقاط نزدیک‌تر به قطب با سرعت بسیار کمتری حرکت خواهند کرد.

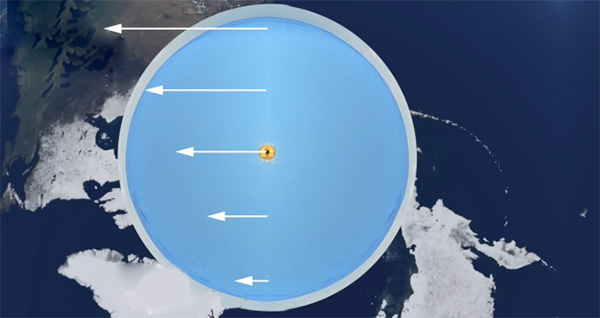
به این سرعت‌ها نسبت به نقطه خروج آب در وسط استخر کمی فکر کنید. اکنون، شیر متصل به استخر باز و آب داخل آن تخلیه می‌شود. به هنگام باز کردن شیر، تمام آب داخل استخر به سمت مرکز آن و محل تخلیه حرکت می‌کند. آبی که در لبه دورتر استخر قرار گرفته است نسبت به نقطه خروج آب، بسیار سریع‌تر حرکت می‌کند. در مقابل، آبِ نزدیک به قطب، به دلیل حرکت با سرعت بسیار کمتر، عقب می‌ماند. بنابراین،‌آب به هنگام نزدیک شدن به نقطه خروج، به صورت پادساعتگرد، می‌چرخد. اما توجه به این نکته مهم است که فاصله نقاط داخل استخر نسبت به یکدیگر در مقایسه با زمین، بسیار بسیار کوچک است. بنابراین، سرعت حرکت آب در نقاط مختلف، تفاوت زیادی با یکدیگر ندارد. از این‌رو، این آزمایش را نمی‌توان به عنوان آزمایشی دقیق و علمی برای پاسخ به پرسش مطرح شده در این بخش در نظر گرفت.

برای انجام آزمایشی مشابه آزمایش فوق باید در نظر داشته باشیم که سطح استخر باید به طور کامل صاف باشد و تمام نقاط کف استخر روی یک صفحه قرار داشته باشند. همچنین، هیچ نیروی خارجی نباید بر استخر و آبِ درون آن وارد شود. بر طبق نظریه‌های مطرح شده، آب به دلیل نیرو و شتاب کوریولیس باید به هنگام حرکت در سینک ظرف‌شویی یا وان حمام، در نیمکره شمالی به صورت پادساعتگرد و در نیمکره جنوبی به صورت ساعتگرد بچرخد. اما عوامل خارجی به اندازه‌ای زیادی که به طور کامل بر حرکت آب درون سینک ظرف‌شویی یا وان حمام اثر می‌گذارند. در نتیجه، آب ممکن است در تمام جهت‌ها حرکت کند.

دو گروه پژوهشی در کمبریج انگلستان و سیدنی استرالیا آزمایش‌های دقیقی را روی جهت چرخش آب در دو نیمکره انجام دادند. تیم‌های پژوهشی در سیدنی و کمبریج به ترتیب چرخش ساعتگرد آب در نیمکره جنوبی و چرخش پادساعتگرد آن در نیمکره شمالی را تایید کردند. در سال ۱۹۶۲، فیزیک‌دانی به نام «آشِر شاپیرو» (Ascher Shapiro) در شهر «واترتاون» (Watertwon)، ماساچوست این کار را انجام داد. شاپيرو سینکی دایره‌ای شکل به قطر تقریبی دو متر و عمق ۱۵۰ میلی‌متر ساخت که سوراخی کوچک در وسط آن تعبیه شده بود و می‌توانست از پایین بسته شود. او سینک را از آب پر کرد و آن را بیش از سه روز به حال خود رها کرد. پس از سه‌ روز آزمایش انجام شد و چرخش پادساعتگرد آب مشاهده شد.

سه سال بعد، گروهی در دانشگاه سیدنی این آزمایش را تکرار کردند و به این نتیجه رسیدند که برای مشاهده چرخش ساعتگرد آب در سینک، باید آبِ داخل سینک حداقل به مدت ۱۸ ساعت به حال خود رها شود. اما نباید فراموش کنیم که تاثیر نیروی کوریولیس در سینک ظرف‌شویی به دلیل عامل‌های مزاحمی مانند جریان آب و شکل سینک، به ندرت قابل مشاهده است.

فرمول شتاب کوریولیس چیست؟

شتاب کوربولیس یا استفاده از رابطه زیر به‌دست می‌آید:

$$overrightarrow{a_c}= 2 overrightarrow{omega} times overrightarrow{v}$$

در رابطه فوق، $$overrightarrow{omega}$$ سرعت زاویه‌ای و $$overrightarrow{v} $$ است سرعت شعاعی هستند. این معادله از کجا می‌آید؟ در این بخش با استفاده از آنالیز برداری، فرمول شتاب کوریولیس را به‌دست می‌آوریم. همان‌طور که در مطالب بالا اشاره شد، شتاب کوریولیس از نیروی کوریولیس یا اثر کوریولیس می‌آید. اثر کوریولیس به نیرویی ظاهری یا شبه نیرو گفته می‌شود که بر اجسام متحرک روی جسم چرخان اثر می‌گذارد. در این قسمت، فرمول شتاب کوریولیس را به‌دست می‌آوریم.

همان‌طور که می‌دانید زمین هر ۲۴ ساعت، یک دور کامل به دور محور عمودی خود، از غرب به شرق، می‌چرخد. بنابراین، زمین را نمی‌توانیم به عنوان چارچوب مرجع لخت در نظر بگیریم. دستگاه مختصات لخت، یا ساکن است یا با سرعت ثابت حرکت می‌کند. با توجه به آن‌که دستگاه مختصات متصل به زمین لخت نیست، قوانین نیوتن باید در آن اصلاح شوند.

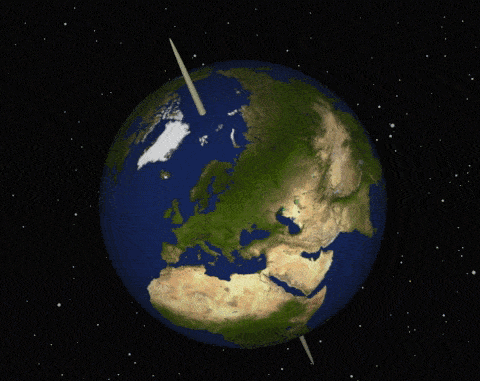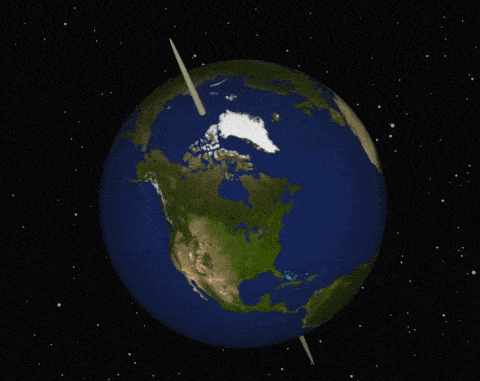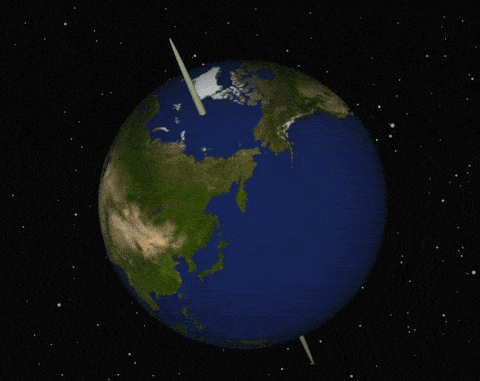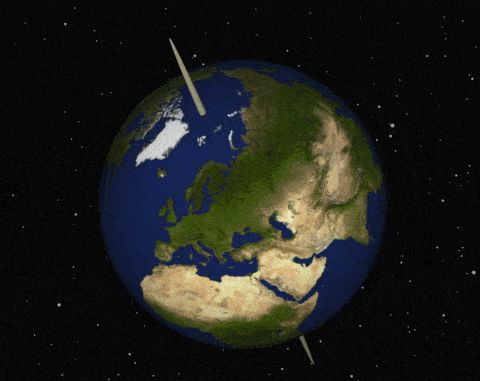
در تصویر فوق، زمین در جهت غرب به شرق به دور محور خود می‌چرخد. توجه به این نکته لازم است محور دروان زمین، به طور کامل افقی نیست. برای به‌دست آوردن رابطه شتاب کوریولیس، ابتدا بردارهای یکه در سه راستای $$y$$، $$x$$ و $$z$$ را را در نظ می‌گیریم و آن‌ها را به ترتیب با $$widehat {i}$$ و $$widehat {j}$$ و $$widehat {k}$$ نشان می‌دهیم. در حالت کلی، دو دستگاه مختصات در این مسئله وجود دارند:

1. دستگا‌هِ لخت که با مختصات دکارتی $$(widehat { i } , widehat { j } , widehat { k } ) $$ نشان داده می‌شود.
2. دستگاه مختصات دوم یا دستگاه مختصات دورانی که در حال دوران است و با مختصات $$(widehat { i } _ r , widehat { j } _ r , widehat { k } _ r ) $$ نشان داده می‌شود. این دستگاه مختصات به همراه زمین، می‌چرخد.

نقطه‌ای روی زمین را در نظر بگیرید که مکان آن با استفاده از بردار واحد $$ overrightarrow { r } $$ نشان داده می‌شود. سرعت این نقطه از مشتق بردار مکان نسبت به زمان به صورت زیر به‌دست می‌آید:

$$ large overrightarrow { v } = frac { d overrightarrow { r } } { d t } = overrightarrow { omega } times overrightarrow { r } $$

در رابطه فوق، $$ overrightarrow { omega } $$ بردار سرعت زاویه‌ای است. در ادامه، بردار $$ overrightarrow { r } $$ را به صورت $$ overrightarrow{r} = (widehat { i } , widehat { j } , widehat { k } ) $$ می‌نویسیم. در نتیجه، $$large overrightarrow { v }$$ یا $$frac{ d overrightarrow{r} }{ dt }  $$ fi به صورت زیر در دستگاه مختصات لخت یا دکارتی نوشته می‌شود:

$$ large overrightarrow { v } = frac{ d overrightarrow{r} }{ dt } \ rightarrow frac{ d widehat { i } } { d t } = overrightarrow { omega } times widehat{i} , frac { d widehat {j} }{dt} = overrightarrow{omega} times widehat{ j } , frac { d widehat { k } } { d t } = overrightarrow{omega} times widehat{k} $$

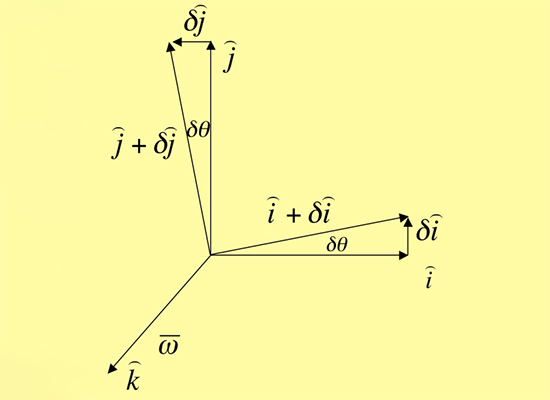
فرض کنید دستگاه مختصات،‌ به صورت نشان داده شده در تصویر زیر، به اندازه $$ delta theta $$ حول محور $$ widehat { k } $$ دوران کند. همان‌طور که در تصویر زیر مشاهده می‌کنید، جهت‌های جدید محورهای $$x$$ و $$y$$، به ترتیب برابر با $$ widehat{i} + delta widehat{i} $$ و $$ widehat{j} + delta widehat{j} $$ خواهد بود. همچنین، جهت محور $$z$$ بدون تغییر باقی می‌ماند. از آنجا که محور $$z $$ محور دوران است، سرعت زاویه‌ای در این راستا خواهد بود. در نتیجه، با استفاده از قانون دست راست در ضرب خارجی بردارها، سرعت دوران محور‌ها را به صورت زیر به‌دست می‌آوریم:

$$ large overrightarrow{omega} times widehat{i} = omega widehat{j}, overrightarrow { omega } times widehat{j} = -omega widehat{i}, overrightarrow{omega} times widehat { k } =0 $$

حال برداری مانند $$ overrightarrow { a } $$ را در نظر می‌گیریم و آن را در دستگاه مختصات دورانی به صورت زیر می‌نویسیم:

$$ overrightarrow{a} = a _ { x } widehat { i} _ { r } + a_{y} widehat{j}_{r} + a_{z} widehat{k}_{r} $$

در ادامه، مشتق بردار $$ overrightarrow {a} $$ نسبت به زمان را در دستگاه مختصات دورانی به‌دست می‌آوریم:

$$ left ( frac { d overrightarrow{a} }{dt} right ) _ { r } = frac { d} { dt } ( a _ { x} widehat {i} _ { r } ) + frac { d } { d t } ( a _ { y } widehat {j}_{r}) + frac { d } { d t }( a _ {z } widehat { k } _ { r }) $$

از آنجا که بردار‌های $$ widehat { i } _ r , widehat { j } _ r , widehat { k } _ r $$ در دستگاه مختصات دوران کننده، نسبت به زمان تغییر نمی‌کنند، مشتق $$left ( frac { d overrightarrow{a} }{dt} right ) _ { r }$$ را می‌توانیم به صورت زیر بنوسیم:

$$large left ( frac { d overrightarrow { a } } { d t } right ) _ { r } = frac { d a _ { x } } { d t } widehat {i}_{r} + frac{ da_{y} } { d t } widehat{j} _ { r } + frac { d a_ { z } } { d t} widehat { k } _ { r } $$

این در حالی است که در دستگاه مختصات اینرسی، بردار‌های $$ widehat { i } _ r , widehat { j } _ r , widehat { k } _ r $$ حرکت می‌کنند. بنابراین مشتق بردار $$ overrightarrow { a } $$ در دستگاه مختصات لخت به صورت زیر نوشته می‌شود:

$$ left( frac{d overrightarrow{a} }{dt} right) _ { I } = frac{d}{dt} (a_{x} widehat{i}_{r}) + frac { d } { d t } ( a _ { y } widehat { j} _ { r } ) + frac{d}{dt} (a_{z} widehat { k} _ { r }) $$

$$ left( frac{d overrightarrow{a} }{dt} right)_{I} = frac{ d a_ { x } } { d t } widehat{i} _ { r } + frac { da_{y} }{dt}widehat{j}_{r} + frac { da _ { z } }{dt}widehat{k}_{r} + a_{x} frac{d widehat{i} _ { r } } { d t } + a _ { y } frac{d widehat{j} _ { r } } { d t } + a _ { z } frac{d widehat { k } _{ r } }{dt} $$

مشتق بردارهای یکه نسبت به زمان برابر است با:

$$ large frac { d widehat{i} _ { r } } { d t} = overrightarrow{omega} times widehat{i} _ { r } , ; ; frac{dwidehat{j}_{r} }{dt} = overrightarrow{omega} times widehat{j} _ { r }, ; ; frac { d widehat { k }_ { r } } { d t } = overrightarrow{omega} times widehat { k } _ { r } $$

در پایان، مشتق زمانی $$ large overrightarrow { a } $$ (نسبت به دستگاه مختصات لخت) به صورت زیر بدست خواهد آمد:

$$ large left( frac{d overrightarrow{a} }{dt} right)_{I} = frac{ da _ { x } }{ d t } widehat{i}_{r} + frac { d a _ { y } }{ d t } widehat{j} _ { r } + frac { d a _ { z } } { d t }widehat{k}_{r} + overrightarrow{omega} times overrightarrow { a } $$

$$ boxed { left ( frac{d overrightarrow { a } } { d t } right) _ { I } = left( frac{d overrightarrow{a} }{dt} right ) _ { r } + ( overrightarrow{omega} times overrightarrow { a } ) } $$

به منظور درک بهتر روابط بدست آمده در بالا، برداری مانند $$ overrightarrow { a } = overrightarrow { r } $$ را در نظر می‌گیریم. این بردار، نقطه‌ای ساکن را روی سطح زمین نشان می‌دهد که به همراه زمین در حال دوران است. بنابراین، جهت این بردار با گذشت زمان تغییر می‌کند. با توجه به رابطه بدست آمده در بالا، مشتق در دستگاه مختصات اینرسی را می‌توان به صورت زیر بیان کرد:

$$ large left ( frac { d overrightarrow { r } } { d t } right ) _ { I } = left ( frac { d overrightarrow { r } } { d t} right)_{r} + (overrightarrow{omega} times overrightarrow{r}) $$

اما این نقطه در دستگاه مختصات دورانی با زمان تغییر نمی‌کند، از این‌رو، مشتق $$ left ( frac { d overrightarrow { r } } { d t} right)_{r} $$ برابر صفر است. در نتیجه:

$$ large left ( frac { d overrightarrow { r } } { d t } right ) _ { I } = (overrightarrow{omega} times overrightarrow{r}) = omega rsin theta$$

در رابطه فوق، $$ large theta $$ زاویه بین محور دوران زمین و عرض جغرافیایی نقطه مفروض است:

$$large theta = 90 ^ 0 – latitude$$

در ادامه، شتاب در چارچوب لخت را برحسب شتاب در چارچوب دورانی به‌دست می‌آوریم:

$$large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ i = large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ r + (overrightarrow{omega} times overrightarrow{r }) $$

برای ساده‌سازی، دو مشتق $$large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ i $$ و $$ large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ r$$ را می‌توانیم به صورت زیر بنویسیم:

$$large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ i = frac{text{d}overrightarrow{ r_ i }}{text{d}t }\ large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ r = frac{text{d}overrightarrow{ r_ r }}{text{d}t }$$

بنابراین، رابطه $$large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ i = large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ r + (overrightarrow{omega} times overrightarrow{r }) $$ را می‌توان به صورت زیر نوشت:

$$large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ i = large left (frac{text{d}overrightarrow{ r }}{text{d} t } large right )_ r + (overrightarrow{omega} times overrightarrow{r }) \ overrightarrow{v _ i } = overrightarrow{ v_ r } + (overrightarrow{ omega } times overrightarrow{ r })$$

اگر از رابطه $$overrightarrow{v _ i } = overrightarrow{ v_ r } + (overrightarrow{ omega } times overrightarrow{ r })$$ شتاب در چارچوب مرجع لخت را می‌توانیم به‌دست آوریم:

$$begin{equation}
left(frac{d vec{v}_i}{d t}right)_i=left(frac{d vec{v}_i}{d t}right)_r+left(vec{omega} times vec{v}_iright)
end{equation}$$

با توجه به آن‌که $$overrightarrow{v _ i } = overrightarrow{ v_ r } + (overrightarrow{ omega } times overrightarrow{ r })$$، داریم:

$$begin{equation}
left(frac{d vec{v}_i}{d t}right)_i=frac{d}{d t}left(vec{v}_r+vec{omega} times vec{r}right)_r+vec{omega} timesleft(vec{v}_r+vec{omega} times vec{r}right)
end{equation}$$

پس از مشتق‌گیری از رابطه فوق داریم:

$$begin{equation}
left(frac{d vec{v}_i}{d t}right)_i=left(frac{d vec{v}_r}{d t}right)_r+frac{d}{d t}left(vec{omega} times vec{r}_rright)+vec{omega} times vec{v}_r+vec{omega} timesleft(vec{omega} times vec{r}_rright)
end{equation}$$

از آنجا که مشتق سرعت نسبت به زمان، شتاب است، رابطه فوق را می‌توانیم به صورت ساده‌تر زیر بنویسیم:

$$begin{equation}
vec{a}_i=vec{a}_r+2 vec{omega} times vec{v}_r+vec{omega} timesleft(vec{omega} times vec{r}_rright)
end{equation}$$

رابطه به‌دست آمده برای شتاب را برحسب شتاب چارچوب دورانی یا شتاب کوریولیس مرتب می‌کنیم:

$$begin{equation} vec{a}_r= vec{a}_i-2 vec{omega} times vec{v}_r- vec{omega} timesleft(vec{omega} times vec{r}_rright)end{equation}$$

برای به‌دست آوردن نیرو در چارچوب دورانی، تنها کافی است طرفین رابطه فوق را در ‌m ضرب کنیم:

$$begin{equation}
m vec{a}_r=m vec{a}_i-2 m vec{omega} times vec{v}_r-m vec{omega} timesleft(vec{omega} times vec{r}_rright)
end{equation}$$

از آنجا که نیرو برابر حاصل‌ضرب جرم در شتاب است، رابطه بالا را می‌توانیم به صورت زیر بنویسیم:

$$begin{equation}
vec{F}_r=vec{F}_i-2 m vec{omega} times vec{v}_r-m vec{omega} timesleft(vec{omega} times vec{r}_rright)
end{equation}$$

همان‌طور که در رابطه فوق می‌بینیم، نیرو در دستگاه دورانی از سه قسمت تشکیل شده است:

• نیروی $$F_ i $$: این عبارت، مقدار نیرو در دستگاه مختصات لخت را نشان می‌دهد.
• عبارت $$2 m vec{omega} times vec{v}$$: این عبارت نیروی کوریولیس نام دارد که در بخش‌های قبل در مورد آن صحبت کردیم. همان‌طور که در رابطه به‌دست آمده برای نیروی کوریولیس مشاهده می‌کنید، مقدار این نیرو به سرعت چارچوب دوارنی وابسته است.
• $$m vec{omega} timesleft(vec{omega} times vec{r}_rright)$$: این عبارت نیروی گریز از مرکز نام دارد. همان‌طور که در رابطه به‌دست آمده برای نیروی گریز از مرکز مشاهده می‌کنید، مقدار این نیرو به مکان جسم در چارچوب دوارنی وابسته است.

جمع‌بندی

در این مطلب از مجله فرادرس فهمیدیم شتاب کوریولیس چیست. شتاب کوریولیس از نیروی کوریولیس یا اثر کوریولیس می‌آید. اثر کوریولیس به نیرویی ظاهری یا شبه نیرویی گفته می‌شود که بر اجسام متحرکی که روی جسم چرخان قرار گرفته‌اند، اثر می‌گذارد. زمین و اجسام قرار گرفته در اطراف آن، بهترین مثال برای درک بهتر این نیرو هستند. به عنوان مثال، مسیر پرواز هواپیما به جای خط راست، خطی منحنی است.