حل نامعادلات بر خلاف معادلات در ریاضی، شامل یک مجموعه جواب است که باید علامت آن‌ها را مشخص کنیم. بدین منظور می‌توانیم ریشه‌های عبارت را مانند یک معادله معمولی بدست آوریم و بعد تعیین علامت کنیم. در این مطلب از مجله فرادرس به بررسی انواع روش‌های تعیین علامت نامعادله می‌پردازیم و مثال‌هایی نیز ارائه می‌کنیم. اگر به این موضوع علاقه‌مند هستید این مطلب را تا آخر مطالعه کنید.

انواع تعیین علامت نامعادله

برخلاف معادلات معمولی، نامعادلات شامل مجموعه‌ای از جواب هستند که در این مطلب به بررسی تعیین علامت نامعادلات به صورت زیر می‌پردازیم:

• تعیین علامت نامعادلات چندجمله‌ای درجه اول
• تعیین علامت نامعادلات چندجمله‌ای درجه دوم
• تعیین علامت نامعادلات کسری درجه اول
• تعیین علامت نامعادلات کسری درجه دوم

برای یادگیری بیشتر و بهتر این موضوع و سایر موضوعات مرتبط با ریاضی دهم، می‌توانید فیلم آموزش ریاضی پایه دهم فرادرس را از لینک زیر مشاهده کنید.

روش تعیین علامت نامعادله چیست؟

برای تعیین علامت نامعادله باید مانند یک معادله معمولی ریشه‌های معادله را تعیین و تعیین علامت کنیم. باید این نکته را در نظر داشته باشیم که اگر کل عبارت در منفی ضرب یا تقسیم شود آنگاه جهت علامت تغییر می‌کند.

تعیین علامت نامعادله را چگونه بیاموزیم؟

برای درک بهتر تعیین علامت در ریاضی، ابتدا باید با مفاهیم پایه آن مانند نحوه محاسبه ریشه در انواع توابع آشنا شوید. در حل نامعادلات به جای یک جواب مشخص، محدوده‌ای از جواب را خواهیم داشت و در مواقعی نیز جواب تعریف نشده خواهد بود. پس ار فهم مفاهیم ابتدایی، دامنه و برد توابع را بررسی کنید. در نهایت، با استفاده از فیلم‌های آموزشی موجود در فرادرس، می‌توانید ویژگی‌های و کار با توابع مختلف از جمله تعیین علامت آن‌ها را به طور کامل یاد بگیرید.

می‌توانید از فیلم‌های آموزشی فرادرس که مرتبط با تعیین علامت معادله و نامعادله هستند نیز استفاده کنید که از لینک‌های زیر قابل بررسی هستند.

همچنین فرادرس دروس متنوع و کاربردی را در زمینه ریاضی منتشر کرده است که اگر به این موضوع علاقه‌مند هستید می‌توانید آن‌ها را از طریق لینک زیر مشاهده کنید.

تعیین علامت نامعادلات کسری

در این قسمت با ارائه مثال‌های گوناگون روش تعیین علامت نامعادلات کسری درجه اول و دوم را می‌آموزیم.

تعیین علامت نامعادلات کسری درجه اول

برای تعیین علامت نامعادله کسری ابتدا تمام جملات را به یک طرف می‌بریم و تا حد امکان ساده کسر را ساده می‌کنیم. سپس ریشه‌های صورت و مخرج را محاسبه می‌کنیم و در جدول تعیین علامت می‌کنیم و در آخر بازه‌ای که نامعادله در آن تعریف شده است را باید انتخاب کنیم.

مثال اول تعیین علامت کسری درجه اول

می‌خواهیم نامعادله $$displaystylefrac{4}{{{x}-{3}}}<{2}$$ را تعیین علامت کنیم.

پاسخ:

ابتدا کل عبارت را به سمت چپ می‌بریم.

$$displaystylefrac{4}{{{x}-{3}}}-{2}<{0}$$

سپس مخرج مشترک می‌گیریم و تا حد امکان ساده می‌کنیم.

$$displaystylefrac{{{4}-{2}{left({x}-{3}right)}}}{{{x}-{3}}}<{0}$$

$$displaystylefrac{{{4}-{2}{x}+{6}}}{{{x}-{3}}}<{0}$$

$$displaystylefrac{{{10}-{2}{x}}}{{{x}-{3}}}<{0}$$

اگر سمت چپ نامعادله را برابر $$f(x)$$ بگیریم مخرج کسر فقط در ۳  تعریف نشده خواهد بود بنابراین دامنه به صورت زیر تعریف می‌شود:

$$displaystyle{D}_{ f{{left({x}right)}}}=mathbb{R}-{leftlbrace{3}rightrbrace}$$

جدول تعیین نامعادله این مثال به شکل زیر است:

$$boxed{begin{matrix}x &-infty &3 & & 5 & +infty\x-3 &- &0 &+ & +&+\ 10-2x&+ &+ &+ & 0&-\ f(x)& -&infty & + & 0&-end{matrix}}$$

بنابراین بازه نامعادله به شکل زیر خواهد بود:

$$displaystyle{x}in{left(-infty,{3}right)}cup{left({5},+inftyright)}$$

مثال دوم تعیین علامت کسری درجه اول

نامعادله $$displaystylefrac{{{x}+{3}}}{{{x}-{1}}}ge{0}$$ را تعیین علامت کنید.

پاسخ:

اگر سمت چپ نامعادله را برابر $$f(x)$$ بگیریم مخرج کسر فقط در ۱  تعریف نشده خواهد بود و تعیین علامت را به صورت جدول زیر انجام می‌دهیم:

$$boxed{begin{matrix}x &-infty &-3 & &1 & +infty\x+3 &- &0 &+ & +&+\ x-1&- &- &- & 0&+\ f(x)& +&0 & – & infty&+end{matrix}}$$

بنابراین بازه نامعادله به شکل زیر خواهد بود:

$$displaystyle{x}in{left(-infty,-{3}right]}cup{left({1},+inftyright)}$$

مثال سوم تعیین علامت کسری درجه اول

می‌خواهیم نامعادله $$displaystylefrac{1}{{4}}<frac{7}{{{7}-{x}}}$$ را تعیین علامت کنیم.

پاسخ:

ابتدا کل عبارت را به سمت چپ می‌بریم.

$$displaystylefrac{7}{{{7}-{x}}}-frac{1}{{4}}>{0}$$

سپس مخرج مشترک می‌گیریم و تا حد امکان ساده می‌کنیم.

$$displaystylefrac{{{28}-{left({7}-{x}right)}}}{{{4}{left({7}-{x}right)}}}>{0}$$

$$displaystylefrac{{{21}+{x}}}{{{4}{left({7}-{x}right)}}}>{0}$$

اکنون سمت چپ نامعادله را برابر $$f(x)$$ می‌گیریم مخرج کسر فقط در ۷  تعریف نشده خواهد بود و تعیین علامت را به صورت جدول زیر انجام می‌دهیم:

$$boxed{begin{matrix}x &-infty &-21 & &7 & +infty\21+x &- &0 &+ & +&+\ 7-x&+ &+ &+ & 0&-\ f(x)& -&0 & + & infty&-end{matrix}}$$

بنابراین بازه نامعادله به شکل زیر خواهد بود:

$$displaystyle{x}in{left(-{21},{7}right)}$$

مثال چهارم تعیین علامت کسری درجه اول

نامعادله $$displaystylefrac{{{x}{left({4}-{x}right)}}}{{{x}+{2}}}ge{0}$$ را تعیین علامت کنید.

پاسخ:

اگر سمت چپ نامعادله را برابر $$f(x)$$ بگیریم مخرج کسر فقط در ۲-  تعریف نشده خواهد بود و تعیین علامت را به صورت جدول زیر انجام می‌دهیم:

$$boxed{begin{matrix}x &-infty &-2 & &0 & &4 & +infty\x+2 &- &0 &+ & +&+&+ &+\x &- &- &+ &0&+& +&+\ 4-x&+ &+ &+ & +&+& 0&-\ f(x)& +&0 & + &0&+ & infty&-end{matrix}}$$

درنتیجه بازه نامعادله به شکل زیر خواهد بود:

$$displaystyle{x}in{left(-infty,-{2}right)}cup{left[{0},{4}right]}$$

مثال پنجم تعیین علامت کسری درجه اول

می‌خواهیم نامعادله $$dfrac{1}{x^{2}-4} leq dfrac{1}{2-x}$$ را تعیین علامت کنیم.

پاسخ:

ابتدا کل عبارت را به سمت چپ می‌بریم.

$$begin{aligned} frac{1}{x^{2}-4}-frac{1}{2-x} &leq 0end{aligned}$$

سپس با مخرج مشترک گرفتن عبارت را ساده می‌کنیم.

$$begin{array}{r} {dfrac{1}{(x+2)(x-2)}-dfrac{1}{-(x-2)} leq 0} \ {frac{1}{(x+2)(x-2)}+frac{1color{Cerulean}{(x+2)}}{color{black}{(x-2)}color{Cerulean}{(x+2)}}color{black}{ leq} 0} \ {dfrac{1+x+2}{(x+2)(x-2)} leq 0} \ boxed{{f(x) = dfrac{x+3}{(x+2)(x-2)}} leq 0}end{array}$$

ریشه‌های عبارت فوق به صورت زیر است:

$$x= -3 , -2, 2$$

مطابق جدول زیر تعیین علامت را انجام می‌دهیم.

$$boxed{begin{matrix}x &-infty &-3 & &-2 & &2 & +infty\ x-2 &- &- &- & -&- &0 &+\ x+2 &- &- &- &0&+& +&+\ x+3&- &0 &+ & +&+ & +&+\ f(x)& -& 0& + &infty&- & infty &+end{matrix}}$$

درنتیجه بازه نامعادله که کوچکتر از صفر باشد به شکل زیر خواهد بود:

$$(-infty,-3] cup(-2,2)$$

مثال ششم تعیین علامت نامعادلات کسری درجه اول

نامعادله $$dfrac{(x-4)(x+2)}{(x-1)} geq 0$$ را تعیین علامت کنید.

پاسخ:

در این مثال نیز یک عبارت کسری چندجمله‌ای درجه اول داریم.

ریشه‌های آن به صورت زیر هستند:

$$begin{array}{r} \x=-2\x=1\x=4end{array}$$

سپس تعیین علامت را در جدول زیر انجام می‌دهیم.

$$boxed{begin{matrix}x &-infty & -2 & & 1 & & 4 & +infty\ x+2 &- & 0 & + & + &+ &+ &+\ x-1 & – & – & – & 0 & + & + &+\ x-4 &- & – & – & – & – &0 &+\ f(x) & – & 0 & + & infty &- & 0 & +end{matrix}}$$

بنابراین بازه قابل قبول که در آن نامعادله مثبت باشد به صورت زیر است:

$$[-2,1) cup[4, infty)$$

مثال هفتم تعیین علامت کسری درجه اول

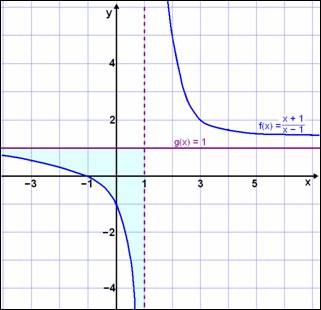
می‌خواهیم نامعادله $$frac{x+1}{x-1}leq 1$$ را تعیین علامت کنیم.

پاسخ:

ابتدا کل عبارت را به سمت چپ می‌بریم.

$$frac{x+1}{x-1}-1leq 0$$

سپس مخرج مشترک می‌گیریم و عبارت را ساده می‌کنیم.

$$frac{x+1-(x-1)}{x-1}leq 0$$

$$frac{2}{x-1}leq 0$$

ریشه مخرج کسر ۱ است و در زیر تعیین علامت کردیم.

$$boxed{begin{matrix}x &-infty &1 & +infty\2/(x-1) &- &infty &+ end{matrix}}$$

بازه‌ای که در آن نامعادله منفی باشد به صورت زیر است:

$$(-infty,1)$$

شکل نامعادله و بازه مربوط به آن در زیر نمایش داده شده است.

تعیین علامت نامعادلات کسری درجه دوم

برای تعیین علامت نامعادله کسری درجه دوم ابتدا تمام جملات را به یک طرف می‌بریم و تا حد امکان ساده کسر را ساده می‌کنیم تا درجه صورت از مخرج کوچکتر شود. سپس ریشه‌های صورت و مخرج را محاسبه می‌کنیم و در جدول تعیین علامت می‌کنیم و در آخر بازه‌ای که نامعادله در آن تعریف شده است را باید انتخاب کنیم.

مثال اول تعیین علامت کسری درجه دوم

می‌خواهیم نامعادله $$displaystylefrac{{{x}-{4}}}{{{x}^{2}+{2}{x}}}le{0}$$ را تعیین علامت کنیم.

پاسخ:

در این مثال یک عبارت کسری داریم که مخرج آن چندجمله‌ای درجه دوم است. ابتدا ریشه‌های صورت و مخرج را محاسبه می‌کنیم.

$$x-4=0 Rightarrow x=4$$

$$x^2+2x=0 Rightarrow x= -2, x=0$$

با داشتن ریشه‌های نامعادله می‌توانیم در جدول زیر تعیین علامت کنیم.

$$boxed{begin{matrix}x &-infty &-2 & &0 & &4 & +infty\x-2 &- &0 &+ & +&+&+ &+\x &- &- &- &0&+& +&+\ x-4&- &- &- & -&-& 0&+\ f(x)& -&infty & + &infty&- & 0&+end{matrix}}$$

بازه قابل قبولی که شرط نامعادله در آن صادق باشد به صورت زیر است:

$$(-infty,-2)cup(0,4]$$

مثال دوم تعیین علامت کسری درجه دوم

نامعادله $$displaystylefrac{{left({x}+{1}right)}^{2}}{{{x}^{2}+{2}{x}-{3}}}le{0}$$ را تعیین علامت کنید.

پاسخ:

در این مثال می‌توانیم مخرج کسر را با استفاده از اتحاد جمله مشترک ساده کنیم.

$$displaystyle{x}^{2}+{2}{x}-{3}={left({x}-{1}right)}{left({x}+{3}right)}$$

$$displaystyle f{{left({x}right)}}=frac{{left({x}+{1}right)}^{2}}{{{left({x}-{1}right)}{left({x}+{3}right)}}}$$

ریشه‌های مخرج به صورت زیر است:

$$x=1, x=-3$$

با توجه به دامنه صورت که به ازای هرمقداری از x تعریف شده است. فقط مخرج را تعیین علامت می‌کنیم.

$$boxed{begin{matrix}x &-infty &-3 & & 1& +infty\x+3 &- &0 &+ & +&+\x-1 &- &- &- & 0&+\f(x) &+ &infty &- & infty&+end{matrix}}$$

تنها بازه‌ای از جدول فوق که شرط نامعادله در آن صادق است به صورت زیر است:

$$xin (-3,1)$$

مثال سوم تعیین علامت کسری درجه دوم

می‌خواهیم نامعادله $$displaystylefrac{{{x}^{2}+{5}{x}}}{{{x}-{3}}}ge{0}$$ را تعیین علامت کنیم.

پاسخ:

در این مثال که در صورت کسر یک عبارت درجه دوم داریم می‌توانیم با فاکتور گرفتن x آن را ساده کنیم.

$$displaystyle f{{left({x}right)}}=frac{{{x}^{2}+{5}{x}}}{{{x}-{3}}}=frac{{{x}{left({x}+{5}right)}}}{{{x}-{3}}}$$

دامنه کل این نامعادله به صورت زیر تعریف می‌شود:

$$displaystyle{D}_{{ f{{left({x}right)}}}}=mathbb{R}-{leftlbrace{3}rightrbrace}$$

ریشه‌های نامعادله به شکل زیر است:

$$begin{array}{r} \x=0\x=-3\x=5end{array}$$

با داشتن ریشه‌ها، تعیین علامت را در جدول زیر انجام می‌دهیم.

$$boxed{begin{matrix}x &-infty & -5 & & 0 & & 3 & +infty\ x+5 &- & 0 & + & + &+ &+ &+\ x & – & – & – & 0 & + & + &+\ x-3 &- & – & – & – & – &0 &+\ f(x) & – & 0 & + & 0 &- & infty & +end{matrix}}$$

درنتیجه بازه نامعادله که بزرگتر از صفر باشد به شکل زیر خواهد بود:

$$[-5,0]cup(3,infty)$$

تعیین علامت نامعادلات چندجمله‌ای

در این بخش به بررسی نحوه تعیین علامت نامعادله‌های چندجمله‌ای درجه اول و دوم می‌پردازیم و مثال‌های متنوعی ارائه می‌کنیم.

تعیین علامت نامعادلات چندجمله‌ای درجه اول

برای حل نامعادله چندجمله‌ای درجه اول می‌توانیم آن را مانند یک معادله معمولی حل می‌کنیم یعنی همه اجزا را به یک طرف نامعادله می‌بریم و آن را مساوی صفر قرار می‌دهیم سپس ریشه معادله را محاسبه می‌کنیم و تعیین علامت می‌کنیم.

نکته مهم: اگر کل عبارت نامعادله را ضرب یا تقسیم بر علامت منفی کنیم یا کل عبارت معکوس کنیم آنگاه جهت نامعادله تغییر می‌کند.

مثال اول تعیین علامت چندجمله‌ای درجه اول

می‌خواهیم نامعادله $$displaystylefrac{1}{{x}}<{4}$$ را تعیین علامت کنیم.

پاسخ:

ابتدا کل عبارت را به سمت چپ می‌بریم و مساوی صفر قرار می‌دهیم.

$$x-frac{1}{4}=0$$

ریشه آن به صورت زیر است:

$$x=frac{1}{4}$$

تعیین علامت آن به صورت زیر است:

$$boxed{begin{matrix}x & & 1/4& & \ x-1/4& – &0 & +end{matrix}}$$

برای اینکه جواب نامعادله درست باشد باید بازه‌ای را انتخاب کنیم که جواب در آن صدق کند. بنابراین بازه به شکل زیر خواهد بود:

$$(-infty,frac{1}{4})$$

مثال دوم تعیین علامت چندجمله‌ای درجه اول

نامعادله $$frac{5}{x}>3$$ را تعیین علامت کنید.

پاسخ:

ابتدا کل عبارت را به سمت چپ می‌بریم و مساوی صفر قرار می‌دهیم.

$$displaystylefrac{5}{{x}}-{3}>{0}$$

$$displaystyle{left({5}-{3}{x}right)}{x}>{0}$$

ریشه‌های آن 0 و $$frac{5}{3}$$ هستند. تعیین علامت آن در جدول زیر آمده است.

$$boxed{begin{matrix}x &&0& & 5/3& & \ frac{5}{x}>3& – &0 &+&0& -end{matrix}}$$

بنابراین بازه نامعادله به شکل زیر خواهد بود:

$$displaystyle{0}<{x}<frac{5}{{3}}$$

مثال سوم تعیین علامت چندجمله‌ای درجه اول

می‌خواهیم نامعادله $$displaystyle{x}^{3}+{5}{x}^{2}-{4}{x}-{20}ge{0}$$ را تعیین علامت کنیم.

پاسخ:

عبارت فوق که به نظر یک چندجمله‌ای درجه سوم است اما با ساده کردن آن تبدیل به یک نامعادله چندجمله‌ای درجه اول می‌شود.

$$displaystyle f{{left({x}right)}}={x}^{3}+{5}{x}^{2}-{4}{x}-{20}=(x+5)(x^2-4)={left({x}+{5}right)}{left({x}+{2}right)}{left({x}-{2}right)}$$

ریشه‌های عبارت فوق به صورت زیر است:

$$begin{array}{r} \x=-5\x=-2\x=2end{array}$$

با داشتن ریشه‌های فوق، در جدول زیر تعیین علامت را انجام می‌دهیم.

$$boxed{begin{matrix}x &-infty &-5 & &-2 & &2 & +infty\ x-2 &- &- &- & -&- &0 &+\ x+2 &- &- &- &0&+& +&+\ x+5&- &0 &+ & +&+ & +&+\ f(x)& -& 0& + &0&- & 0 &+end{matrix}}$$

چون شرط نامعادله اولیه مثبت است درنتیجه بازه‌ای از جدول فوق قابل قبول است که جواب‌های آن مثبت باشند.

$$[-5,-2]cup[2,infty)$$

مثال چهارم تعیین علامت چندجمله‌ای درجه اول

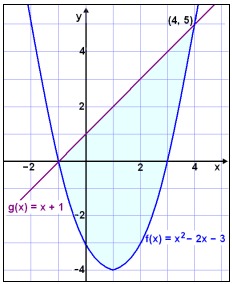
نامعادله $$x^2-2x-3<x+1$$ را تعیین علامت کنید.

پاسخ:

در این مثال ابتدا باید تمام جملات را به سمت چپ ببریم سپس عبارت را ساده می‌کنیم.

$$f(x)=x^2-3x-4$$

از اتحاد جمله مشترک استفاده می‌کنیم.

$$f(x)=(x+1)(x-4)$$

ریشه‌های آن به صورت زیر است:

$$begin{array}{r} \x=-1\x=4end{array}$$

در جدول زیر تعیین علامت کردیم.

$$boxed{begin{matrix}x &-infty &-1 & & 4& +infty\x+1 &- &0 &+ & +&+\x-4 &- &- &- & 0&+\f(x) &+ &0 &- & 0&+end{matrix}}$$

بنابراین بازه‌ای که در آن نامعادله منفی باشد به صورت زیر خواهد بود:

$$(-1,4)$$

این بازه و شکل نامعادله در زیر نمایش داده شده است:

تعیین علامت نامعادلات چندجمله‌ای درجه دوم

برای تعیین علامت نامعادله چندجمله‌ای درجه دوم ابتدا باید همه‌ی جملات را به سمت چپ ببرید، سپس آن را مانند یک معادله معمولی برابر صفر قرار دهید و ریشه‌های آن را محاسبه کنید و بعد در یک جدول تعیین علامت کنید. در آخر فقط بازه‌ای قابل قبول است که در شرط نامعادله صدق کند.

مثال اول تعیین علامت چندجمله‌ای درجه دوم

می‌خواهیم نامعادله $$displaystyle{4}{x}^{2}le{28}{x}$$ را تعیین علامت کنیم.

پاسخ:

ابتدا کل عبارت را به سمت چپ می‌بریم.

$$displaystyle{4}{x}^{2}le{28}{x}Rightarrow{4}{x}^{2}-{28}{x}le{0}$$

سپس مانند یک معادله معمولی ریشه‌های آن را حساب می‌کنیم.

$$displaystyleRightarrow{4}{x}^{2}-{28}{x}={0}$$

$$displaystyleRightarrow{4}{x}{left({x}-{7}right)}={0}Rightarrow{x}={0},{7}$$

اکنون که ریشه‌ها مشخص شدند مطابق جدول زیر تعیین علامت می‌کنیم:

$$boxed{begin{matrix}x &-infty &0 & & 7& +infty\4x^2-28x &+ &0 &- & 0&+end{matrix}}$$

بنابراین بازه نامعادله به شکل زیر خواهد بود:

$$(-infty,0)cup(0,7)cup(7,infty)$$

اما فقط بازه $$(0,7)$$ مورد قبول است زیرا در شرط نامعادله که $$xleq0$$ صدق می‌کند.

روش دوم یک آزمون ساده برای اینکه تشخیص دهیم که کدام بازه در شرط نامعادله صادق است انجام می‌دهیم. برای این منظور به جای $$x$$ مقادیر ۱- و ۱ و ۸ را قرار می‌دهیم و آن را حل می‌کنیم.

$$displaystyle f{{left(-{1}right)}}={4}{left(-{1}right)}^{2}-{28}{left(-{1}right)}={32}>{0}$$

$$displaystyle f{{left({1}right)}}={4}{left({1}right)}^{2}-{28}{left({1}right)}=-{24}<{0}$$

$$displaystyle f{{left({8}right)}}={4}{left({8}right)}^{2}-{28}{left({8}right)}={32}>{0}$$

در سه عددگذاری فوق مشخص است که اگر $$x=1$$ باشد شرط نامعادله برقرارا است که $$x=1$$ نیز در بازه $$(0,7)$$ قرار دارد.

مثال دوم تعیین علامت چندجمله‌ای درجه دوم

نامعادله $$displaystyle{2}{x}^{2}+{5}{x}-{3}>{0}$$ را تعیین علامت کنید.

پاسخ:

این یک نامعادله چندجمله‌ای درجه دوم است که تمام جملات آن در سمت چپ قرار دارند. ریشه‌های آن را باید مانند یک معادله درجه دوم معمولی حساب کنیم.

$$displaystyle f{{left({x}right)}}={2}{x}^{2}+{5}{x}-{3}={0}$$

$$displaystyle{left({2}{x}-{1}right)}{left({x}+{3}right)}={0}$$

$$displaystyle{x}={0.5}$$

$$displaystyle{x}=-{3}$$

اکنون که ریشه‌ها مشخص شدند مطابق جدول زیر تعیین علامت می‌کنیم:

$$boxed{begin{matrix}x &-infty &-3 & & 0.5& +infty\2x^2+5x-3 &+ &0 &- & 0&+end{matrix}}$$

بنابراین بازه نامعادله به شکل زیر خواهد بود:

$$(-infty,-3)cup(-3,0.5)cup(0.5,infty)$$

اما فقط بازه $$(-infty,-3)cup(0.5,infty)$$ مورد قبول است زیرا در شرط نامعادله که $$x>0$$ صدق می‌کند.

مثال سوم تعیین علامت چندجمله‌ای درجه دوم

می‌خواهیم نامعادله $$displaystyle{2}<-{16}{t}^{2}+{6}<{5}$$ را تعیین علامت کنیم.

پاسخ:

این هم یک نامعادله چندجمله‌ای درجه دوم است که بین دو مقدار مختلف قرار گرفته است. نامعادلات به این شکل را باید به دو قسمت تقسیم کنیم و در آخر اجتماع بازه‌های آن‌ها را درنظر بگیریم.

نامعادله اول به صورت زیر حساب می‌کنیم:

$$displaystyle{2}<-{16}{t}^{2}+{6}$$

نامعادله دوم را هم به صورت زیر حساب می‌کنیم:

$$displaystyle-{16}{t}^{2}+{6}<{5}$$

ابتدا ریشه‌های نامعادله اول بدست می‌آوریم و تعیین علامت می‌کنیم.

$$displaystyle{16}{t}^{2}-{6}+{2}<{0}$$

$$displaystyle{16}{t}^{2}-{4}<{0}$$

کل معادله را تقسیم بر ۴ می‌کنیم و سپس از اتحاد مزدوج استفاده می‌کنیم.

$$displaystyle{{f}_{{1}}{left({t}right)}}={16}{t}^{2}-{4}={0}$$

$$displaystyle{4}{t}^{2}-{1}={0}$$

$$displaystyle{left({2}{t}+{1}right)}{left({2}{t}-{1}right)}={0}$$

بنابراین ریشه‌های آن برابر مقادیر زیر خواهد بود:

$$displaystyle{t}=pm{0.5}$$

اکنون که ریشه‌ها مشخص شدند مطابق جدول زیر تعیین علامت می‌کنیم:

$$boxed{begin{matrix}t &-infty &-0.5 & & 0.5& +infty\16t^2-4 &+ &0 &- & 0&+end{matrix}}$$

بازه نامعادله اول به شکل زیر خواهد بود:

$$(-infty,-0.5)cup(-0.5,0.5)cup(0.5,infty)$$

اکنون باید ریشه‌های نامعادله دوم را بدست آوریم و تعیین علامت کنیم.

$$displaystyle-{16}{t}^{2}+{6}-{5}<{0}$$

$$displaystyle{{f}_{{2}}{left({t}right)}}={1}-{16}{t}^{2}={0}$$

از اتحاد مزدوج استفاده می‌کنیم. برای یادگیری «اتحاد مزدوج» می‌توانید مطلب مرتبط با آن را در مجله فرادرس مطالعه کنید.

$$displaystyle{left({1}+{4}{t}right)}{left({1}-{4}{t}right)}={0}$$

بنابراین ریشه‌های آن برابر مقادیر زیر خواهد بود:

$$displaystyle{t}=pm{0.25}$$

با محاسبه ریشه‌های می‌توانیم تعیین علامت کنیم.

$$boxed{begin{matrix}t &-infty &-0.25 & & 0.25& +infty\1-16t^2 &- &0 &+ & 0&-end{matrix}}$$

بازه نامعادله دوم به شکل زیر خواهد بود:

$$(-infty,-0.25)cup(-0.25,0.25)cup(0.25,infty)$$

اکنون که باید اجتماع بازه دو نامعادله را با احتساب شرط نامعادله اولیه بررسی کنیم.

$$boxed{begin{matrix}t &-infty &-5 & &-0.25 & &0.25 & &0.5 &+infty\f_1(t) &+ &0 &- & -&-&- &-&0 &+\f_2(t) &- &- &- &0&+& 0&-& -&-\ f(t)& -&0 & + &0&- & 0&+&0 &-end{matrix}}$$

شرط نامعادله اولیه مقدار عبارت بین ۲ و ۵ بود که مقادیری مثبت هستند، باتوجه به جدول فوق بازه‌ای که این شرط در آن صدق می‌کنپ به صورت زیر است:

$$(-0.5,-0.25)cup(0.25,0.5)$$

مثال چهارم تعیین علامت چندجمله‌ای درجه دوم

نامعادله $$displaystyle{2}{u}^{2}+{5}{u}ge{12}$$ را تعیین علامت کنید.

پاسخ:

این نامعادله درجه دوم را می‌توانیم با استفاده از اتحاد جمله مشترک به صورت زیر ساده کنیم:

$$displaystyle f{{left({u}right)}}={2}{u}^{2}+{5}{u}-{12}={left({2}{u}-{3}right)}{left({u}+{4}right)}$$

ریشه‌های عبارت فوق به شکل زیر است:

$$x=-4, frac{3}{2}$$

با استفاده از ریشه‌های بدست آمده تعین علامت را مطابق جدول زیر انجام می‌دهیم:

$$boxed{begin{matrix}u &-infty &-4 & & 3/2& +infty\u+4 &- &0 &+ & +&+\2u-3 &- &- &- & 0&+\f(u) &+ &0 &- & 0&+end{matrix}}$$

بنابراین بازه‌ای که در آن جواب نامعادله مثبت باشد به صورت زیر است:

$$displaystyle{u}in{left(-infty,-{4}right]}cup{left[frac{3}{{2}},+inftyright)}$$

مثال پنجم تعیین علامت چندجمله‌ای درجه دوم

می‌خواهیم نامعادله $$displaystyle{left({q}+{4}right)}^{2}>{10}{q}+{31}$$ را تعیین علامت کنیم.

پاسخ:

در این مثال که یک نامعادله درجه دوم است، همه‌ی جملات را به سمت چپ می‌بریم و سپس تا حد امکان ساده‌سازی می‌کنیم.

$$displaystyle{q}^{2}+{8}{q}+{16}>{10}{q}+{31}$$

$$displaystyle{q}^{2}+{8}{q}+{16}-{10}{q}-{31}>{0}$$

$$displaystyle{q}^{2}-{2}{q}-{15}>{0}$$

$$displaystyle{left({q}+{3}right)}{left({q}-{5}right)}>{0}$$

$$displaystyle f{{left({q}right)}}={left({q}+{3}right)}{left({q}-{5}right)}$$

با توجه به اینکه ریشه‌های عبارت فوق ۳- و ۵ است، در جدول زیر تعیین علامت می‌کنیم.

$$boxed{begin{matrix}q &-infty &-3 & & 5& +infty\q+3 &- &0 &+ & +&+\q-5 &- &- &- & 0&+\f(q) &+ &0 &- & 0&+end{matrix}}$$

درنتیجه بازه‌ای که در آن جواب نامعادله مثبت باشد به صورت زیر است:

$$displaystyle{q}in{left(-infty,-{3}right)}cup{left({5},+inftyright)}$$

مثال ششم تعیین علامت چندجمله‌ای درجه دوم

نامعادله $$displaystyle{x}^{3}>{2}{x}^{2}+{x}$$ را تعیین علامت کنید.

پاسخ:

برای حل این مثال ابتدا تمام جملات را به طرف چپ می‌بریم و سپس از x فاکتور می‌‌گیریم تا یک عبارت درجه دوم داشته باشیم.

$$displaystyle{x}^{3}-{2}{x}^{2}-{x}>{0}$$

$$displaystyle{x}{left({x}^{2}-{2}{x}-{1}right)}>{0}$$

سپس با استفاده از روش دلتا ریشه‌های عبارت درجه دوم را محاسبه می‌کنیم.

$$displaystyle{x}=frac{{-{b}pmsqrt{{{b}^{2}-{4}{a}{c}}}}}{{{2}{a}}}$$

$$displaystyle{x}=frac{{{2}pmsqrt{{{4}-{4}{left({1}right)}{left(-{1}right)}}}}}{{{2}}}$$

$$displaystyle{x}=frac{{{2}pmsqrt{{8}}}}{{2}}$$

$$displaystyle{x}=frac{{{2}pm{2}sqrt{{2}}}}{{2}}$$

$$displaystyle{x}={1}pmsqrt{{2}}$$

بنابراین تمام ریشه‌های نامعادله به صورت زیر خواهد بود:

$$begin{array}{r} \x=0\x=1pm sqrt{2}end{array}$$

با استفاده از ریشه‌های بدست آمده تعین علامت را مطابق جدول زیر انجام می‌دهیم:

$$boxed{begin{matrix}x &-infty & 1-sqrt{2} & & 0 & & 1+sqrt{2} & +infty\ x &- & – & – & 0&+ &+ &+\ x^2-2x-1 & + & 0 & – & – & – & 0 &+\ f(x) & – & 0 & + & 0 &- & 0 & +end{matrix}}$$

با توجه به شرط نامعادله اولیه در سوال جواب‌هایی که در بازه مثبت هستند قابل قبول است. درنتیجه خواهیم داشت:

$$[1-sqrt{2},0]cup[1+sqrt{2},infty)$$

مثال هفتم تعیین علامت چندجمله‌ای درجه دوم

می‌خواهیم نامعادله $$displaystyle{2}{x}^{3}+{x}^{2}>{6}{x}$$ را تعیین علامت کنیم.

پاسخ:

در این مثال نیز ابتدا باید تمام جملات را به سمت چپ منتقل کنیم سپس با فاکتور گرفتن از x، عبارت را ساده خواهیم کرد.

$$displaystyle{2}{x}^{3}+{x}^{2}-{6}{x}>{0}$$

$$displaystyle{x}{left({2}{x}^{2}+{x}-{6}right)}>{0}$$

$$displaystyle{x}{left({2}{x}-{3}right)}{left({x}+{2}right)}>{0}$$

$$displaystyle f{{left({x}right)}}={x}{left({2}{x}-{3}right)}{left({x}+{2}right)}$$

درنتیجه ریشه‌های نامعادله به صورت زیر خواهد بود:

$$begin{array}{r} \x=0\x=-2\x=frac{3}{2}end{array}$$

اکنون که ریشه‌ها مشخص شدند مطابق جدول زیر تعیین علامت می‌کنیم:

$$boxed{begin{matrix}x &-infty & -2 & & 0 & & 3/2 & +infty\ x+2 &- & 0 & + & + &+ &+ &+\ x & – & – & – & 0 & + & + &+\ 2x-3 &- & – & – & – & – &0 &+\ f(x) & – & 0 & + & 0 &- & 0 & +end{matrix}}$$

بنابراین بازه‌ای که در آن جواب نامعادله مثبت باشد به صورت زیر است:

$$[-2,0]cup[frac{3}{2},infty)$$

مثال هشتم تعیین علامت چندجمله‌ای درجه دوم

نامعادله $$displaystyle{2}{{sin}^{2}{x}}ge sin{{x}}$$ را تعیین علامت کنید.

پاسخ:

در این مثال که توابع مثلثاتی درجه دوم است ابتدا باید تمام جملات را به سمت چپ منتقل کنیم و سپس از $$sin x$$ فاکتور بگیریم.

$$displaystyle{2}{{sin}^{2}{x}}- sin{{x}}ge{0}$$

$$displaystyle sin{{x}}{left({2} sin{{x}}-{1}right)}ge{0}$$

اگر کل عبارت را برابر $$f(x)$$ بگیریم خواهیم داشت:

$$displaystyle f{{left({x}right)}}= sin{{x}}{left({2} sin{{x}}-{1}right)}$$

برای محاسبه ریشه‌های عبارت فوق به شیوه زیر عمل می‌کنیم.

$$sin x =0 Rightarrow x= 0, pi, 2pi$$

$$sin x =frac{1}{2} Rightarrow x= frac{pi}{6} , 5frac{pi}{6}$$

با داشتن ریشه‌های نامعادله مطابق جدول زیر تعیین علامت را انجام می‌دهیم.

$$boxed{begin{matrix}x &-infty &0 & & {pi}/{6}& &{5pi}/{6} & &pi & & 2pi & & infty\sin x &- & 0 & + & + & + &+ & +& 0& -&0 &+\2sin x-1 &- &- &- & 0 & + & 0 &- &- & -& -&-\f(x) & + & 0 &- & 0 &+& 0&- &0 &+ &0 &-end{matrix}}$$

درنتیجه بازه‌ای که در آن شرط مثبت بودن نامعادله صدق کند به شکل زیر خواهد بود:

$$displaystyle{left[frac{pi}{{6}}+{2}{k}pi,frac{5}{{6}}pi+{2}{k}piright]}cup{left[pi+{2}{k}pi,{2}pi+{2}{k}piright]}$$

مثال نهم تعیین علامت چندجمله‌ای درجه دوم

می‌خواهیم نامعادله $$x^{3}+x^{2} leq 4(x+1)$$ را تعیین علامت کنیم.

پاسخ:

در این مثال که به نظر می‌رسد چندجمله‌ای درجه سوم است، ابتدا باید تمام جملات را به سمت چپ منتقل کنیم سپس با فاکتور گرفتن عبارت را ساده خواهیم کرد و به ضرب سه عبارت درجه اول می‌رسیم.

$$begin{aligned}x^{3}+x^{2} &leq 4(x+1) \ x^{3}+x^{2} &leq 4 x+4 \ x^{3}+x^{2}-4 x-4 &leq 0end{aligned}$$

$$begin{aligned} x^{3}+x^{2}-4 x-4 &=0 quadcolor{Cerulean} { .} \ x^{2}(x+1)-4(x+1) &=0 \(x+1)left(x^{2}-4right) &=0 \(x+1)(x+2)(x-2) &=0 end{aligned}$$

ریشه‌های معادله فوق به صورت زیر است:

$$begin{array}{r} \x=-2\x=-1\x=2end{array}$$

تعیین علامت را با داشتن ریشه‌ها انجام می‌دهیم.

$$boxed{begin{matrix}x &-infty & -2 & & -1 & & 2 & +infty\ x+2 &- & 0 & + & + &+ &+ &+\ x+1 & – & – & – & 0 & + & + &+\ x-2 &- & – & – & – & – &0 &+\ f(x) & – & 0 & + & 0 &- & 0 & +end{matrix}}$$

بازه‌ای که در آن نامعادله منفی باشد به شکل زیر خواهد بود:

$$(-infty,-2] cup[-1,2]$$

مثال دهم تعیین علامت چندجمله‌ای درجه دوم

نامعادله $$2 x^{4}>3 x^{3}+9 x^{2}$$ را تعیین علامت کنید.

پاسخ:

در این مثال باید ابتدا همه‌ی جملات را به سمت چپ ببریم سپس با فاکتورگیری یک نامعادله درجه دوم خواهیم داشت.

$$begin{aligned}2 x^{4}&>3 x^{3}+9 x^{2} \ 2 x^{4}-3 x^{3}-9 x^{2}&>0end{aligned}$$

$$begin{array}{r}\2 x^{4}-3 x^{3}-9 x^{2}=0\x^{2}left(2 x^{2}-3 x-9right)=0\x^{2}(2 x+3)(x-3)=0end{array}$$

ریشه‌های این نامعادله به صورت زیر است:

$$begin{array}{r} \x=-frac{3}{2}\x=0\x=3end{array}$$

با داشتن ریشه‌های نامعادله تعیین علامت را در جدول زیر انجام می‌دهیم.

$$boxed{begin{matrix}x &-infty & -3/2 & & 0 & & 3 & +infty\ 2x+3 &- & 0 & + & + &+ &+ &+\ x^2 & + & + & + & 0 & + & + &+\ x-3 &- & – & – & – & – &0 &+\ f(x) & + & 0 & – & 0 &- & 0 & +end{matrix}}$$

بازه‌ای که در آن نامعادله مثبت باشد به شکل زیر خواهد بود:

$$left(-infty,-frac{3}{2}right) cup(3, infty)$$

نتیجه‌گیری

با تعیین علامت نامعادله‌ها می‌توان رفتارشان را در نزدیکی ریشه‌های آن‌ها بررسی کرد. در این مطلب از مجله فرادرس به تعیین علامت انواع عبارت‌های درجه اول و دوم پرداختیم و آموختیم که می‌توانیم نامعادله را مانند یک معادله معمولی با محاسبه ریشه‌هایش تعیین علامت کنیم. مثال‌های زیادی نیز برای درک بهتر این موضوع ارائه شد.