به طور کلی امواج را میتوان به دو دسته طولی و عرضی تقسیم کرد که در امواج طولی جهت ارتعاش و انتشار موج با هم موازی هستند در حالی که در امواج عرضی جهت ارتعاش و انتشار موج عمود بر هم هستند. در این مطلب از مجله فرادرس یاد میگیریم موج طولی و عرضی چیست و چه ویژگیهای دارند. همچنین امواج صوتی و فشاری را به عنوان نمونههایی از امواج طولی توضیح خواهیم داد و در ادامه امواج الکترومغناطیس را به عنوان نمونهای از امواج عرضی شرح خواهیم داد. پس اگر به این موضوع علاقهمند هستید این مطلب را تا انتها مطالعه کنید.
متغیرهای اساسی در حرکت موج
ابتدا لازم است با بعضی از متغیرهای اساسی و مشترک مربوط به امواج طولی و عرضی آشنا شوید و برای یادگیری بیشتر میتوانید فیلم آموزش فیزیک دوازدهم متوسطه فرادرس را از لینک زیر مشاهده کنید.
- طول موج: به کمترین فاصله بین دو قله یا دره در یک موج را طول موج گویند که با $$λ$$ نمایش میدهند و واحد آن $$frac{1}{m}$$ است.
تناوب: مقدار زمان لازم برای آنکه دو نقطه مجاور (مثلا قله) از یک نقطه معین عبور کنند دوره یا تناوب یا پریود میگویند که با $$T$$ نمایش میدهند و واحد آن ثانیه است.
- فرکانس: به تعداد قلهها یا درهها یا هر نقطهای روی موج که از یک نقطه معین در واحد زمان عبور میکند فرکانس گویند که با $$f$$ نمایش میدهند.
رابطه بین فرکانس و دوره تناوب به صورت زیر است:
$$f = dfrac{1}{T}$$
واحد فرکانس در سیستم SI، هرتز تعریف شده است و هر هرتز عکس ثانیه است.
$$ Hz = dfrac{1}{s}$$
- دامنه: بیشینه جابجایی یک ذره در محیط را دامنه گویند که با $$A$$ نمایش میدهند و واحد آن متر است.
مثال اول امواج طولی و عرضی
نور آبی رنگ دارای طول موج ۵۰۰ نانومتر است. با فرض اینکه سرعت نور در محیط $$3times 10^8 (frac{m}{s})$$ است، فرکانس نور را محاسبه کنید.
پاسخ:
با استفاده از فرمول زیر میتوانیم فرکانس را حساب کنیم.
$$f=frac{v}{lambda}=frac{3times 10^8}{500times 10^{-9}}=6.00times 10^{14}$$
اکنون که با متغیرهای اساسی در حرکت موج آشنا شدید در قسمتهای بعد به معرفی موج طولی و عرضی چیست خواهیم پرداخت.

موج طولی و عرضی چیست؟
به طور ساده، در امواج طولی جهت ارتعاش و جهت انتشار موازی یکدیگر هستند درحالیکه در امواج عرضی جهت ارتعاش و جهت انتشار عمود برهم هستند. امواج عرضی برای انتشار به محیط مادی احتیاجی ندارند اما امواج طولی برای انتشار به محیط مادی نیاز دارند. در ادامه این مطلب توضیحات تکمیلی ارائه خواهد شد.
امواج طولی
امواج طولی امواجی هستند که جهت ارتعاش در محیط موازی جهت انتشار موج است و جابجایی محیط همجهت (یا خلاف جهت) انتشار موج است. به امواج طولی مکانیکی، امواج فشاری نیز میگویند زیرا در هنگام حرکت باعث افزایش و کاهش فشار در محیط میشوند. امواج طولی برای انتشار نیاز به محیط مادی دارند. امواج صوتی، زلزله از نمونههای امواج طولی هستند.
رابطه بین فرکانس و طول موج در امواج صوتی هماهنگ که از نوع امواج طولی است به شکل زیر هست:
$$y(x,t)=y_circ cos (omega(t-frac{x}{c}))$$
عوامل به کار رفته در رابطه فوق به شرح زیر است:
- $$y$$: جابجایی یک نقطه در موج صوتی
- $$x$$: فاصله نقطه از منبع تولید موج صوتی
- $$t$$: زمان
- $$y_circ$$: دامنه نوسان
- $$c$$: سرعت موج صوتی
- $$omega$$: سرعت زاویهای موج
مقدار $$frac{x}{c}$$ زمانی که موج فاصله $$x$$ را طی میکند نام دارد.

رابطه فرکانس با سرعت زاویهای به صورت زیر تعریف میشود:
$$f=frac{omega}{2pi}$$
طول موج را میتوان از تقسیم سرعت موج بر فرکانس محاسبه کرد.
$$lambda=frac{c}{f}$$
دامنه در موج صوتی را به صورت اختلاف فشار بین هوای آزاد و بیشینه فشار ایجاد شده ناشی از موج، تعریف میکنند.
سرعت انتشار موج صوتی بستگی به نوع، دما و ترکیب محیطی که موج در آن انتشار مییابد دارد.
امواج فشاری
معادله صوت در سیالات که در قسمت قبل بیان شد، در مورد موج صوتی در محیط جامد کشسان نیز معتبر است. اگرچه امواج عرضی در محیط جامد منتشر میشوند، امواج طولی نیز در محیط جامد منتشر میشوند. سرعت و مقاومت صوتی وابسته به چگالی و سختی محیط جامد است. در زمین شناسی به امواج فشاری، امواج اولیه یا (P-Wave) نیز میگویند.
الکترومغناطیس
معادلات ماکسول، رفتار امواج الکترومغناطیس که جزو امواج عرضی هستند را در خلاء بررسی میکند. با این حال امواج پلاسما جزء امواج طولی به حساب میآیند زیرا آنها جزء امواج الکترومغناطیس نیستند بلکه آنها چگالی امواج ذرات باردار هستند که میتوان آن را با میدان الکترومغناطیس بررسی کرد. البته پیشتر در مجله فرادرس به طور کامل راجع به الکترومغناطیس صحبت کردیم که میتوانید مطلب مربوطه را برای آشنایی بیشتر، مطالعه کنید.
پس از تلاشهای «هویساید» (Oliver Heaviside) برای بسط معادلات ماکسول، او متوجه شد که امواج الکترومغناطیس را نمیتوان در محیط همگن یا امواج طولی در فضای آزاد مشاهده کرد. معادلات ماکسولی که امروزه میشناسیم، این نتیجه را حفظ کرده که در فضای آزاد یا هر دیالکتریکی که خواص مشابه دارند، امواج الکترومغناطیس فقط به صورت عرضی هستند اما امواج الکترومغناطیس را میتوان به عنوان مولفههای طولی در میدانهای الکتریکی و (یا) مغناطیسی هنگام عبور از مواد دوشکستی یا مواد ناهمگن نشان داد. ازجمله این موارد میتوان به «امواج زینک» (Zenneck Wave) اشاره کرد.

در توسعه فیزیک نوین، «الکساندرا پروکا» (Alexandru Proca) فیزیکدان رومانیایی به خاطر تلاشهایش در زمینه معادلات میدان کوانتومی نسبیتی شناخته میشود که منجر به محاسبه جرم مزونها با اسپین ۱ شد. در سالهای اخیر سایر دانشمندان از معادلات او برای توصیف جرم فوتون به عنوان مولفه طولی الکترومغناطیس معادلات ماکسول استفاده کردند. آنها پیشنهاد کردند که احتمال وجود امواج الکترومغناطیس طولی در خلاء قطبیده دیراک وجود دارد. به هر حال جرم فوتون ساکن به نظر بسیاری از فیزیکدانان مورد تردید است و با مدل استاندارد فیزیک همخوانی ندارد.

چگونه امواج طولی و عرضی را با فرادرس یاد بگیریم؟
از امواج صوتی گرفته تا امواج الکترومغناطیس. امواج طولی و عرضی در زندگی روزمره ما وجود دارند. برای درک بهتر موضوع امواج طولی و عرضی ابتدا باید با مفاهیم پایه آنها آشنا شوید. همانطور که پیشتر اشاره شد، در امواج طولی جهت ارتعاش با جهت انتشار موازی است مانند امواج صوتی اما در امواج عرضی جهت ارتعاش عمودبر جهت انتشار است مانند امواج الکترومغناطیس. پس از درک مفاهیم ابتدایی این موضوع، معادلات حاکم بر امواج طولی و عرضی را بررسی کنید. سپس، به تجزیه و تحلیل آنها به صورتهای مختلف بپردازید.
در مرحله بعد، مفاهیم پیشرفتهتری را بررسی کنید، مانند اثر دوپلر در امواج صوتی یا قوانین ماکسول در الکترومغناطیس. در نهایت، با استفاده از فیلمهای آموزشی فرادرس، میتوانید با مفاهیم مربوط به امواج طولی و عرضی را به طور کامل آشنا شوید و برای کاربردهای عملی آنها آماده شوید.
میتوانید فیلمهای آموزشی مرتبط با امواج طولی و عرضی در فیزیک را از لینکهای زیر در فرادرس مشاهده کنید:
همچنین فرادرس دروس متنوع و کاربردی را در زمینه فیزیک منتشر کرده است که اگر به این موضوع علاقهمند هستید میتوانید آنها را از طریق لینک زیر مشاهده کنید.

امواج عرضی
امواج عرضی متضاد امواج طولی هستند که در آن نوسانات در جهت انتشار موج است. امواج عرضی امواجی هستند که جهت ارتعاش در محیط عمود بر جهت انتشار موج است و جابجایی محیط نیز عمود بر جهت انتشار موج است. امواج عرضی برای انتشار نیاز به محیط مادی ندارند و میتوانند در خلا نیز منتشر شوند. تمام امواج میتوانند بدون جابجایی ماده، انرژی را از نقطهای به نقطه دیگر منتقل کنند.
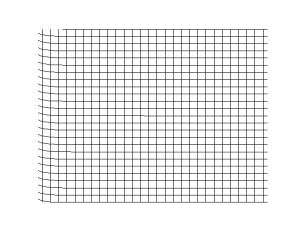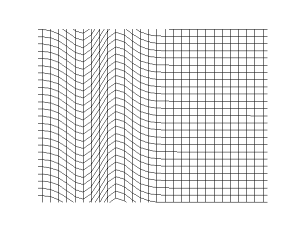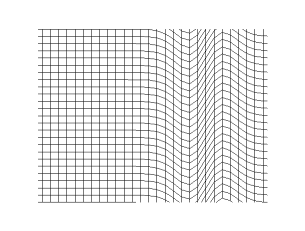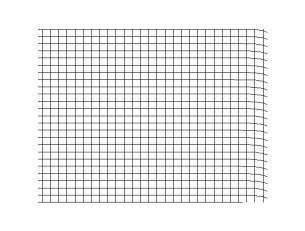
امواج الکترومغناطیسی یک نمونه از امواج عرضی است که برای انتشار نیازی به محیط مادی ندارد. واژه (عرضی) نشاندهنده عمود بودن جهت انتشار موج بر جابجایی ذرات در محیط است. در مورد امواج الکترومغناطیسی نوسان عمود بر جهت انتشار موج است.
یک مثال ساده موج تولید شده در پوسته یک طبل است. امواج موازی با صفحه پوسته طبل منتشر میشوند اما هر نقطه به تنهایی روی پوسته به سمت بالا و پایین جابجا میشود که عمود بر صفحه پوسته طبل است. نور مثال دیگری از امواج عرضی است که در آن نوسانات میدانهای الکتریکی و مغناطیسی هستند که عمود بر جهت انتشار موج است.
امواج عرضی معمولا در جامدات کشسان که «تنش برشی» (Shear Stress) دارند، رخ میدهد. در این مورد نوسانات، جابجایی ذرات جامد از حالت تعادل آنها است که عمود بر جهت انتشار آن هست. این جابجاییها مربوط به تغییر شکل برشی محلی مواد است. بنابراین امواج عرضی با این خصوصیت «امواج برشی» (Shear Wave) نامیده میشوند. از آنجایی که سیالات مقاومتی در برابر نیروی برشی در حالت ساکن ندارند، انتشار امواج عرضی درون سیالات امکان پذیر نیست.
در علم «لرزه شناسی» (Seismology) به امواج برشی امواج ثانویه یا (S-Waves) نیز میگویند.
از دیدگاه ریاضی سادهترین موج عرضی، موج سینوسی قطبیده خطی تخت است. تخت در اینجا به معنی ثابت بودن جهت انتشار در کل محیط است. قطبیده خطی نیز به معنی ثابت بودن جهت جابجایی در کل محیط است و مقدار جابجایی، تنها یک تابع سینوسی از زمان و مکان در جهت انتشار است.
حرکت چنین موجی را میتوان به شکل ریاضی نوشت:
$$S(p,t)= Au sin (frac{t-(p-o)frac{d}{v}}{T}+phi)$$
عوامل به کار رفته در رابطه فوق به شرح زیر است:
- $$d$$: جهت انتشار موج (یک بردار با واحد طول)
- $$o$$: هر ارجاعی به محیط است
- $$u$$: جهت نوسان (یک بردار با واحد طول عمود بر d)
- $$p$$: جابجایی ذرات در ماده
- $$t$$: زمان برحسب ثانیه
- $$A$$: دامنه موج
- $$T$$: دوره تناوب
- $$v$$: سرعت انتشار موج
- $$phi$$: فاز در نقطه مبدا
تمام کمیتهای فوق عدد حقیقی هستند.
با این معادله موج در جهت $$d$$ منتشر شده و در جهت $$u$$ نوسان میکند. موج در جهت $$u$$ قطبیده خطی خوانده میشود. اگر یک ناظر به نقطه ثابت $$P$$ نگاه کند، آنگاه میبیند که حرکت ذرات یک حرکت هماهنگ ساده (سینوسی) با تناوب $$T$$ ثانیه است و بیشینه جابجایی ذرات $$A$$ است که فرکانس برای هر دوره نوسان در هر ثانیه برابر $$f = dfrac{1}{T}$$ است. اگر از همهی ذرات در لحظه ثابت $$t$$ عکس بگیریم، آنگاه ججابجایی همه ذرات در هر صفحه عمود بر $$d$$ خواهد بود. جابجاییها در صفحات متوالی یک الگوی سینوسی تشکیل میدهند. اگر هر دوره کامل را در امتداد $$d$$ گسترش دهیم، آنگاه طول موج به شکل زیر خواهد شد:
$$lambda = v times T=frac{v}{f}$$
کل این الگو در جهت $$d$$ و با سرعت $$v$$ حرکت خواهد کرد.
اصول برهمنهی
در مواد خطی همگن، نوسانات پیچیده (ارتعاش در یک ماده یا شار نور) را میتوان با برهمنهی چندین موج سینوسی طولی یا عرضی توصیف کرد. برای مثال ارتعاش سیم ویالون امواج ایستادهای را تولید میکند که میتوان با جمع تعداد زیادی امواج عرضی با فرکانسهای مختلف که در جهت مخالف یکدیگر حرکت میکند توضیح داد که جابجایی سیم به سمت بالا و پایین یا چپ و راست است. شکمها در برهمنهی امواج روی هم هستند.

قطبیدگی دایرهای
اگر محیط خطی باشد و امکان جابجایی در چندین جهت مستقل را برای یک جهت انتشار d فراهم کند، میتوان دو جهت عمود بر هم را به عنوان جهتهای قطبش انتخاب کرد و هر موج با قطبش خطی در هر جهت دیگری را به عنوان یک ترکیب خطی از این دو موج بیان کرد.
با ترکیب دو موج با فرکانس، سرعت و جهت حرکت یکسان، ولی با اختلاف فاز و جهت جابجایی مستقل میتوان یک موج با قطبش دایرهای یا بیضی شکل به دست آورد. در چنین موجی، ذرات به جای اینکه به عقب و جلو حرکت کنند، مسیرهای دایرهای یا بیضی شکل را طی میکنند.
برای درک بهتر، میتوانیم به آزمایش فوق در مورد سیم ویالون برگردیم. توجه داشته باشید که با تکان دادن دست به چپ و راست به جای بالا و پایین، نیز میتوانید روی آن موج ایجاد کنید. این نکته مهمی است. امواج در دو جهت مستقل (متعامد) میتوانند حرکت کنند. (این برای هر دو جهتی که زاویه قائم با هم تشکیل میدهند صادق است، جهتهای بالا و پایین و چپ و راست برای سادگی انتخاب شدهاند). هر موجی که با تکان دادن دست در یک خط مستقیم ایجاد شود، موج با قطبش خطی است.
حالا تصور کنید دست خود را به صورت دایرهای حرکت میدهید. این حرکت موجب ایجاد یک موج مارپیچی روی سیم میشود. شما به طور همزمان دست خود را هم به بالا و پایین و هم به چپ و راست حرکت میدهید. بیشترین مقدار حرکت چپ و راست یک چهارم طول موج (یا یک چهارم مسافت دور دایره، یعنی ۹۰ درجه یا $$frac{pi}{2}$$ رادیان) پس از بیشترین مقدار حرکت بالا و پایین رخ میدهد. در هر نقطه از سیم، تغییر مکان آن، همان دایرهای را که دست شما توصیف میکند، نشان میدهد، اما تأخیری برابر با سرعت انتشار موج دارد. همچنین توجه داشته باشید که میتوانید دست خود را در یک دایره به صورت ساعتگرد یا پادساعتگرد حرکت دهید. این حرکات دایرهای متناوب، امواج با قطبش دایرهای راست و چپ را تولید میکنند.
هرچه دایره شما ناقصتر باشد، حرکت منظم یک بیضی را توصیف میکند و امواج با قطبش بیضی شکل ایجاد میکند. اگر بیضی خیلی کشیده باشد آنگاه، بیضی شما به یک خط مستقیم تبدیل میشود و قطبش خطی را در امتداد محور اصلی بیضی ایجاد میکند. یک حرکت بیضی همیشه میتواند به دو حرکت خطی متعامد با دامنههای نابرابر و اختلاف فاز ۹۰ درجه تجزیه شود، که در آن قطبش دایرهای حالت خاصی است که در آن دو حرکت خطی دارای دامنه یکسان هستند.
توان در موج عرضی
در این قسمت میانگین توان در یک موج را محاسبه خواهیم کرد. در اینجا چگالی جرم خطی سیم را با $$mu$$ نشان میدهیم.
انرژی جنبشی یک المان جرم در موج عرضی به شکل زیر است:
$${dK} = frac{1}{2} dm v^2 = frac{1}{2} mu dx A^2 omega^2 cos^2left( 2pi x / lambda -omega tright)$$
در یک طول موج انرژی جنبشی به صورت زیر میشود:
$$K = frac{1}{2} mu A^2 omega^2 int_0^lambda cos^2left(2pi x / lambda – omega tright) dx = frac{1}{4} mu A^2 omega^2 lambda. $$
با استفاده از قانون هوک، انرژی پتانسیل در یک المان جرم به شکل زیر است:
$$dU = frac{1}{2} dmomega^2 y^2 = frac{1}{2} mu dxomega^2 A^2 sin^2left( frac{2pi x}{lambda} – omega t right)$$
و انرژی پتانسیل برای یک طول موج به صورت زیر میشود:
$$U = frac{1}{2} mu A^2 omega^2 int_0^lambda sin^2left(frac{2pi x}{lambda} – omega tright) dx = frac{1}{4} mu A^2 omega^2 lambda. $$
بنابراین انرژی کل در یک طول موج به شکل زیر محاسبه میشود:
$$K+U = frac{1}{2} mu A^2 omega^2 lambda. $$
در نتیجه میانگین توان به شکل زیر خواهد بود:
$$ frac{1}{2} mu A^2 omega^2 v_x$$
مثال دوم امواج طولی و عرضی
یک سیم که از دو طرف بسته شده است با مشخصات زیر یک موج سینوسی تولید میکند. توان در آن را حساب کنید.
$$mu = 5.00times10^{-2}(kg/m)$$
$$T=80.0 (N)$$
$$f= 60.0 (Hz)$$
$$A=6.00 (cm)$$
پاسخ:
سرعت موج از رابطه زیر بدست میآید.
$$v=sqrt{frac{T}{mu}}=sqrt{frac{80}{5times10^{-2}}}=40 (m/s)$$
سرعت زاویهای در موج سینوسی به شکل زیر خواهد بود:
$$omega = 2 pi f= 2 pi times 60=377 (frac{1}{s})$$
با جایگذاری مقادیر در فرمول توان موج خواهیم داشت:
$$frac{1}{2} mu A^2 omega^2 v= frac{1}{2}times 5 times 10^{-2}times(377)^2times (6times 10^{-2})^2times 40=512 W$$
مثال سوم امواج طولی و عرضی
یک سیم که یک سر آن آزاد است دارای فرکانس ۵ هرتز هست. فرکانس زاویهای آن را حساب کنید.
پاسخ:
با استفاده از فرمول زیر میتوانیم سرعت زاویهای را محاسبه کنیم.
$$omega = 2 pi f=2 pi times 5=31.4 (rad/s)$$
مثال چهارم امواج طولی و عرضی
یک سیم دو سر بسته دارای طول موج ۴۰ سانتیمتر است. عدد موج آن را محاسبه کنید.
پاسخ:
به راحتی میتوان با استفاده از فرمول زیر عدد موج را حساب کرد.
$$k=frac{2pi}{lambda}=frac{2pi}{40}=0.157 (rad/cm)$$

تفاوت موج طولی و عرضی چیست؟
در جدول زیر به طور خلاصه امواج طولی و عرضی را مقایسه کردهایم. اگر علاقهمند به یادگیری سایر مباحث فیزیک ۳ هستید و دوست دارید که این مباحث را به شکل بهتر و دقیقتری یاد بگیرید، مشاهده فیلم آموزش فیزیک پایه ۳ فرادرس را از لینک زیر به شما پیشنهاد میکنیم.
| امواج عرضی | امواج طولی |
| ارتعاش در محیط عمود بر جهت انتشار موج است. | ارتعاش در محیط موازی جهت انتشار موج است. |
| دو بعدی است. | تک بعدی است. |
| میتواند قطبیده شود. | نمیتواند قطبیده شود. |
| میتواند در جامدات و سطح مایعات تولید شود. | میتواند در هر مادهای تولید شود. |
| میتواند در خلا منتشر شود. | نمیتواند در خلا منتشر شود. |
برهم نهی و تداخل در موج طولی و عرضی چیست؟
در قسمت قبل آموختید موج طولی و عرضی چیست و چه ویژگیهایی دارند. امواج طولی و عرضی هرکدام میتوانند با نوع خود برهمنهی و تداخل داشته باشند. وقتی دو یا چند موج در یک نقطه به هم میرسند به نوعی با هم ادغام میشوند که به اصطلاح برهمنهی امواج گویند.
برهمنهی امواج به دو دسته کلی تقسیم میشود:
- برهمنهی سازنده: اگر دو یا چند موج زمانی که به هم میرسند همفاز باشند یعنی اختلاف فاز صفر یا ۳۶۰ درجه داشته باشند، مطابق شکل زیر قلهها و درههای امواج در یک امتداد باشند، آنگاه دامنه موج تولید شده جدید برابر جمع دامنه امواج اولیه خواهد بود اما طول موج آن ثابت باقی میماند.
- برهمنهی ویرانگر: اگر دو یا چند موج زمانی که به هم میرسند اختلاف فاز ۱۸۰ درجه باشد، مطابق شکل زیر قلهها و درههای امواج در یک امتداد نباشند، باعث میشود که دامنه موج تولید شده جدید صفر باشد، یعنی اصولا امواج یکدیگر را خنثی میکنند.
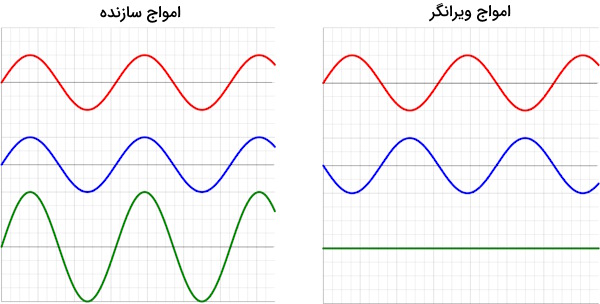
اگرچه برهمنهی سازنده و ویرانگر اتفاق میافتد اما نیازمند آن است که اختلاف فاز دقیقا معادل مقادیر گفته شده باشد و برهمنهی امواج ممکن است ترکیبی از برهمنهی سازنده و ویرانگر همزمان باشد. برای مثال صدای خروجی از یک بلندگو استریو ممکن است که در یک نقطه زیاد و در نقطهای دیگر کم باشد. این تغییر صدا به این معنی است که امواج صوتی در مکانهایی تداخل سازنده دارند و در مکانهایی تداخل ویرانگر دارند. مثال دیگر صدای خروجی از موتورهای جت هواپیما در طی زمانی است که توسط مسافر شنیده میشود. صدای تولید شده توسط دو موتور هواپیما در طی زمان میتواند زیاد یا کم باشد که نشان دهندهی سازنده یا ویرانگر بودن امواج در طول زمان است.
امواج ایستاده
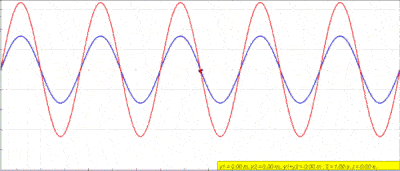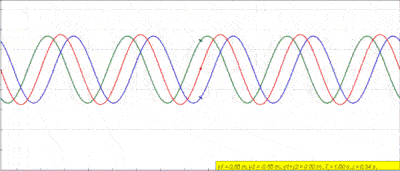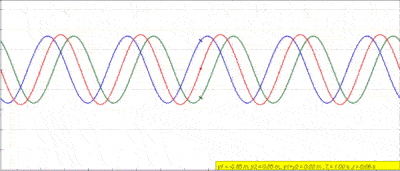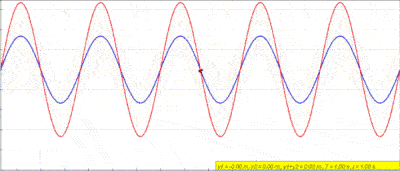
گاهی اوقات به نظر میرسد که امواج حرکت نمیکنند و فقط در یک نقطه ارتعاش میکنند. مطابق شکل زیر وقتی دو موج خلاف جهت یکدیگر حرکت میکنند، اگر دامنه و طول موج یکسان داشته باشند، آنگاه اختلال موج جدید مدام بین حالت سازنده و ویرانگر تغییر میکند. این حالت خاص به نظر شبیه به یک موج ایستاده است که به اصطلاح به این نوع امواج، ایستاده میگویند.
نتیجهگیری
امواج را میتوان به دو دسته طولی و عرضی تفکیک کرد. در این مطلب از مجله فرادرس توضیح دادیم که موج طولی و عرضی چیست و چه ویژگیهایی دارد. همچنین بیان کردیم که در امواج طولی جهت ارتعاش و انتشار موج با هم موازی هستند در حالی که در امواج عرضی جهت ارتعاش و انتشار موج عمود بر هم هستند. از نمونههای امواج طولی در طبیعت میتوان به امواج صوتی و زلزله اشاره کرد همچنین از نمونههای امواج عرضی میتوان امواج الکترومغناطیس را بیان کرد. در تکمیل این موضوع ویژگیها و پدیدههای هر یک را توضیح دادیم. برای یادگیری بیشتر در مورد امواج طولی و عرضی چیست میتوانید فیلم آموزشی فیزیک دوازدهم متوسطه فرادرس را مشاهده کنید.
source