فیزیک یازدهم یا فیزیک دو در سال دوم متوسطه یا مقطع یازدهم برای رشته‌های ریاضی‌فیزیک و علو‌م‌تجربی تدریس می‌شود. سه فصل از فیزیک یازدهم شامل مبحث‌های الکتریسیته ساکن، جریان الکتریکی و مدارهای جریان مستقیم و مغناطیس در دو رشته ریاضی و فیزیک مشترک هستند. علاوه بر سه فصل نامبرده، مبحث القای الکترومغناطیسی و جریان متناوب در فصل چهارم از فیزیک یازدهم به دانش‌آموزان رشته ریاضی‌فیزیک تدریس می‌شود. توجه به این نکته مهم است که القای الکترومغناطیسی در فصل سوم از فیزیک یازدهم رشته تجربی بیان شده است، اما این مبحث در فصلی جداگانه و به صورت مفصل‌تر برای پایه یازدهم رشته ریاضی‌فیزیک تدریس می‌شود. حل مسئله و درک فرمول های فیزیک یازدهم برای موفقیت در آزمون نهایی فیزیک و کنکور، بسیار مهم و ضروری است.

در این مطلب از مجله فرادرس، فرمول‌ های فیزیک یازدهم را به صورت خلاصه همراه با حل مثال توضیح می‌دهیم. برای هر فصل، ابتدا فرمول‌ها به صورت خلاصه در جدول نوشته شده‌اند، سپس توضیح کوتاهی همراه با حل چند مثال برای هر فرمول آورده شده است.

فرمول های فیزیک یازدهم فصل اول

فرمول‌ های فیزیک یازدهم فصل اول در فهرست زیر به صورت خلاصه نوشته شده‌اند:

• کوانتیده بودن بار الکتریکی با فرمول $$q = pm nc enspace , enspace n = 0 , 1 , 2 , …$$ مشخص می‌شود.
• اندازه نیروی الکتریکی بین دو بار نقطه‌ای با رابطه $$ F = k frac { | q _ 1 | | q _ 2 |} { r ^ 2 } $$ به‌دست می‌آید.
• میدان الکتریکیِ‌ جسم باردار با رابطه $$overrightarrow{ E } = frac { overrightarrow{ F } } { q }$$ و $$E = k frac { | q | } { r ^ 2 }$$ محاسبه می‌شود.
• تغییر انرژی پتانسیل الکتریکی بار ذره‌ای q با استفاده از رابطه $$triangle U _ E = – W _ E = – | q | E d cos theta$$ محاسبه می‌شود.
• اختلاف پتانسیل الکتریکی با استفاده از رابطه $$triangle V = V _ 2 – V_1 = frac { triangle U _ E } { q } $$ به‌دست می‌آید.
• پتانسیل الکتریکی در هر نقطه از میدان با استفاده از رابطه $$V = frac { U _ E } { q } $$ به‌دست می‌آید.
• رابطه اختلاف پتانسیل دو نقطه و اندازه میدان الکتریکی یکنواخت برابر $$triangle V = E d $$ است.
• چگالی سطحی بار الکتریکی رسانا با استفاده از رابطه $$sigma = frac { Q } { A } $$ محاسبه می‌شود.
• ظرفیت خازن از رابطه $$C = kappa C _ 0 $$ محاسبه می‌شود.
• ظرفیت خازن با دی‌الکتریک از رابطه $$C = kappa C _ 0 $$ به‌دست می‌آید.
• ظرفیت خازن تخت با مساحت صفحه‌های A و فاصله بین صفحه‌های d از رابطه $$C_0 = epsilon _ 0 frac { A } { d }  $$ محاسبه می‌شود.
• انرژی خازن با استفاده از رابطه‌های $$U = frac { 1 } { 2 } Q V = frac { 1 } { 2 } C V ^ 2 = frac { 1 } { 2 } frac { Q ^ 2 } { C } $$ به‌دست می‌آید.

در ادامه، فرمول‌های نوشته شده در جدول فوق را با حل مثال به صورت خلاصه توضیح می‌دهیم.

بار الکتریکی چیست؟

بار الکتریکی، مفهومی بنیادی در فیزیک و ویژگی بنیادی ذرات زیراتمی است. این ذرات به دلیل داشتن بار الکتریکی، نیرویی را در حضور میدان‌های الکتریکی و مغناطیسی احساس می‌کنند.

این میدان‌ها روی ذرات باردار اثر می‌گذراند. دو نوع بار الکتریکی داریم:

1. بار الکتریکی مثبت: ذر‌ه‌ای زیر‌اتمی مانند پروتون، بار الکتریکی مثبت دارد. این ذره در هسته اتم قرار گرفته است.
2. بار الکتریکی منفی: ذره‌ای زیراتمی مانند الکترون، بار الکتریکی منفی دارد و به دور هسته اتم می‌چرخد.

ذرات با بار الکتریکی یکسان، یکدیگر را دفع و ذرات با بار الکتریکی مخالف، یکدیگر را جذب می‌کنند. مهم‌ترین ویژگی‌های بار الکتریکی عبارت هستند از:

• بار الکتریکی کمیتی اسکالر است.
• بار الکتریکی ذرات باردار را می‌توان به صورت جبری با یکدیگر جمع یا از یکدیگر کم کرد. به عنوان مثال، اگر ذره‌ای با بار الکتریکی ۳+ و ذره دیگری با بار الکتریکی ۲- در کنار یکدیگر، داخل سیستمی بسته قرار داشته باشند، بار الکتریکی کل سیستم برابر ۱+ خواهد بود.
• مقدار بار الکتریکی در سیستمی بسته و ایزوله، پایسته است. این بدان معنا است که مقدار کلِ بار الکتریکی داخلی چنین سیستمی با گذر زمان ثابت می‌ماند.
• بار الکتریکی، کمیتی کوانتیده و گسسته و کوچک‌ترین واحد بار الکتریکی، مقدار باری است که توسط الکترون حمل می‌شود و مقدر آن در حدود $$- 1.6 times 10 ^ { – 19 } $$ کولن است. اگر جسمی خنثی را به جسمی با مقدار مشخصی بار الکتریکی بمالیم، جسم خنثی، الکترون به‌دست می‌‌آورد یا از دست می‌دهد. بار الکتریکی‌ به‌دست آمده توسط الکترون، مضرب صحیح و کاملی از بار بنیادی الکترون، یعنی $$- 1.6 times 10 ^ { – 19 } $$ است:

$$q = pm nc enspace , enspace n = 0 , 1 , 2 , …$$

قانون کولن چیست؟

قانون کولن یکی از مهم‌تریم فرمول‌ های فیزیک یازدهم است. این قانون درباره نیروی بین دو ذره باردار نقطه‌ای صحبت می‌کند. در فیزیک، بار نقطه‌ای به معنای آن است که اندازه بارها در مقایسه با فاصله بین آن‌ها بسیار کوچک است. از این‌رو، آن‌ها را به صورت دو نقطه در نظر می‌گیریم و به راحتی نیروی جاذبه یا دافعه میان آن‌ها را به‌دست می‌آوریم. فیزیک‌دانی فرانسوی به نام «چالز آگوستین کولن» (Charles-Augustin de Columb)‌ در سال ۱۷۸۴ میلادی نیروی بین دو ذره باردار را اندازه گرفت. این فیزیک‌دان به این نتیجه رسید که نیروی بین دو ذره باردار با مربع فاصله بین دو ذره به صورت معکوس و با حاصل‌ضرب اندازه دو بار به صورت مستقیم، متناسب است. بنابراین، اگر دو ذره باردار $$q_1 $$ و $$q_2 $$ به صورت نشان داده شده در تصویر زیر در فاصله r از یکدیگر قرار داشته باشند، نیروی F بین آن‌ها به صورت زیر نوشته می‌شود:

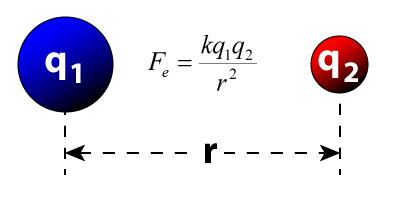
$$F = k frac { q _ 1 } { q _ 2 } { r ^ 2 } $$

در این رابطه:

• $$q_ 1 $$ و $$q _ 2 $$ بارهای الکتریکی دو بار نقطه‌ای برحسب کولن (C)‌ هستند.
• r فاصله بین دو بار برحسب متر است.
• F نیروی الکتریکی وارد بر هر بار بر حسب نیوتن (N) است.
• k ثابت کولن نام دارد و مقدار آن برابر $$8.98755175 times 10 ^ 9  frac { N . m ^ 2 } { C ^ 2 } approx 9.0 times 10 ^ 9 frac { N . m } { C ^ 2 } $$ است.

بر طبق قانون کولن، بارهای هم‌نام، یکدیگر را جذب و بارهای ناهم‌نام، یکدیگر را دفع می‌کنند.

برهم نهی نیروهای الکترواستاتیکی

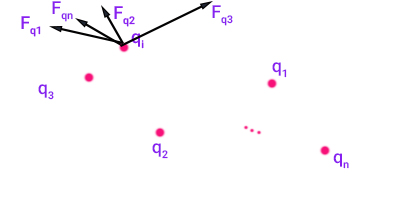
فرض کنید به جای دو ذره باردار، چند ذره باردار با بارهای $$q_1 $$ و $$q_2 $$ و … تا $$q_n$$ داریم. در این حالت، نیروی وارد شده بر بار $$q_i$$ برابر مجموع نیروهای وارد شده از طرف هر یک از ذره‌های باردار دیگر است و به صورت زیر محاسبه می‌شود:

$$overrightarrow{ F _ { q _ i }} = overrightarrow{ F _ { q _ 1 }} + overrightarrow{ F _ { q _ 2 }} + … +overrightarrow{ F _ { q _ n }}$$

میدان الکتریکی چیست؟

همان‌طور که در بخش قبل اشاره شد، قانون کولن در مورد نیروی اعمال شده بین دو ذره باردار در فاصله‌ای مشخص، صحبت می‌کند. این قانون را می‌توانیم با استفاده از مفهومی به نام میدان الکتریکی نیز بیان کنیم که فهرست آن آورده شده است:

• یکی از دو ذره در تمام فضا میدان الکتریکی تولید می‌کند.
• نیروی وارد شده بر ذره دوم به دلیل میدان الکتریکی ایجاد شده توسط ذره اول است.

از این‌رو، دو بار $$q_1 $$ و $$q_2 $$ به کمک میدان الکتریکی به یکدیگر نیرو وارد می‌کنند. برای تعیین میدان الکتریکی ناشی از ذره یا هر جسم باردار در هر نقطه از فضا به صورت زیر عمل می‌کنیم:

• بار کوچک و مثبتِ‌ $$q_0 $$ را در آن نقطه قرار می‌دهیم.
• نیروی الکتریکی وارد شده بر این بار، $$overrightarrow{ F }$$، را اندازه می‌گیریم. در نتیجه میدان الکتریکی ناشی از جسم یا ذره باردار این نقطه به صورت زیر نوشته می‌شود:

$$overrightarrow{ E } = frac { overrightarrow{ F } } { q _ 0 } $$

توجه به این نکته مهم است که میدان الکتریکی کمیتی برداری و یکای اندازه‌گیری آن برابر $$frac { N } { C } $$ است.

میدان الکتریکی حاصل از ذره باردار

میدان الکتریکی حاصل از ذره باردار $$q$$ را می‌توان به صورت زیر نوشت:

$$E = k frac { | q  | } { r ^ 2 } $$

بر طبق رابطه فوق، میدان الکتریکی با اندازه بار، $$q$$، به صورت مستقیم و با مربع فاصله از بار به صورت معکوس متناسب است.

بر هم نهی میدان های الکتریکی

فرض کنید تعدادی ذره باردار در فضا داریم و میدان الکتریکی حاصل از تمام آن‌ها را می‌خواهیم در نقطه‌ای مشخص به‌دست آوریم. برای انجام این کار، میدان الکتریکی حاصل از هر بار را در نقطه موردنظر، با فرض وجود نداشتن سایرِ بارها به‌دست می‌آوریم. سپس، میدان‌ها را به صورت برداری با یکدیگر جمع می‌کنیم.

$$overrightarrow{ E } = overrightarrow{ E _ 1} + overrightarrow{ E _ 2 } + … $$

خطوط میدان الکتریکی

تا اینجا فهمیدیم هر ذره یا جسم بارداری در اطراف خود میدان الکتریکی ایجاد می‌کند. میدان الکتریکی کمیتی برداری است و جهت و اندازه دارد. برای تعیین جهت میدان الکتریکی از ذره آزمونی با بار مثبت و برای نشان داده میدان الکتریکی در فضای اطراف اجسام یا ذرات باردار از خط‌های جهت‌داری به صورت نشان داده شده در تصویر زیر استفاده می‌کنیم. همان‌طور که در تصویر زیر مشاهده می‌کنید، اگر بار جسم یا ذره مثبت باشد، خطوط میدان الکتریکی از جسم یا ذره خارج می‌شوند. در مقابل، اگر بار جسم یا ذره منفی باشد، خطوط میدان به جسم یا ذره وارد می‌شوند.

به بیان دیگر، اگر بار آزمون در میدان جسم باردار مثبت قرار بگیرد، جهت خطوط میدان به گونه‌ای است که ذره آزمون از جسم دور شود. در مقابل، اگر بار آزمون در میدان جسم باردار منفی قرار بگیرد، جهت خطوط میدان به گونه‌ای است که ذره آزمون به جسم نزدیک شود.

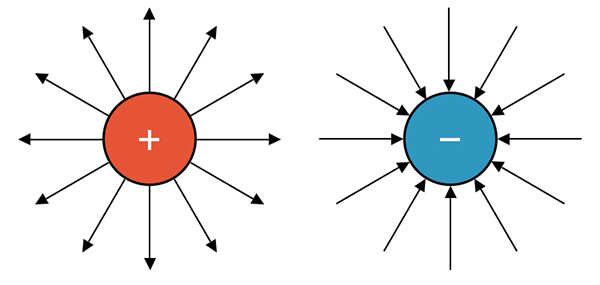
مهم‌ترین ویژگی‌های خطوط میدان الکتریکی عبارت هستند از:

• خطوط میدان الکتریکی هیچ‌گاه یکدیگر را قطع نمی‌کنند. به بیان دیگر، از هر نقطه فضا، تنها یک خط میدان الکتریکی می‌گذرد.
• خطوط میدان الکتریکی بر سطح جسم باردار عمود هستند.
• اندازه بار و تعداد خطوط میدان با یکدیگر متناسب هستند. تعداد خطوط یا چگالی خطوط در اطراف جسم یا ذره‌ای با بار بزرگ‌تر، بیشتر است.
• نقطه شروع خطوط میدان الکتریکی بار مثبت و نقطه پایانی آن‌ها، بار منفی است. اگر تنها یک بار الکتریکی مثبت در فضا وجود داشته باشد، خطوط میدان تا بی‌نهایت می‌روند. همچنین، اگر یک بار الکتریکی منفی در فضا وجود داشته باشد، خطوط میدان از بی‌نهایت می‌آیند و به بار منفی ختم می‌شوند.
• این خطوط هیچ‌گاه حلقه بسته‌ای را تشکیل نمی‌دهند.

اگر بار الکتریکی $$q$$ در میدان الکتریکی $$ overrightarrow{ E } $$ قرار داشته باشد، نیروی وارد شده از طرف این میدان بر بار $$q$$ با استفاده از رابطه $$overrightarrow{ F } = q overrightarrow{ E }$$به‌دست می‌آید.

انرژی پتانسیل الکتریکی چیست؟

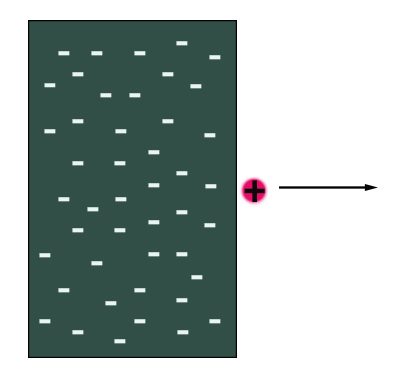
به مقدار انرژی لازم برای آن‌که بتوانیم بار الکتریکی را در خلاف جهت میدان الکتریکی حرکت دهیم، انرژی پتانسیل الکتریکی گفته می‌شود. فرض کنید صفحه‌ای با بار الکتریکی منفی بسیار زیاد داریم. بار الکتریکی مثبت کوچکی از طریق نیروی الکتریکی به این صفحه چسبیده است. اطراف صفحه با بار منفی، میدان الکتریکی وجود دارد که تمام اجسام با بار مثبت را به سمت صفحه جذب می‌کند. بار مثبت چسبیده به صفحه را از آن دور می‌کنیم و در خلاف جهت میدان الکتریکی حرکت می‌دهیم. انجام این کار بسیار سخت است، زیرا نیروی الکتریکی در خلاف جهت بر بار مثبت وارد می‌شود. اگر بار مثبت را رها کنیم، دوست دارد دوباره به صفحه با بار منفی بچسبد. انرژی استفاده شده برای دور کردن ذره مثبت از صفحه، به صورت انرژی پتانسیل الکتریکی داخل ذره ذخیره می‌شود.

اگر بخواهیم ذره را در فاصله دورتری از صفحه قرار دهیم، باید از انرژی بیشتری استفاده کنیم. در نتیجه، انرژی پتانسیل الکتریکی ذخیره شده در ذره، بزرگ‌تر خواهد بود. اگر بار ذره مثبت، دو برابر شود، انرژی بزرگ‌تری برای به حرکت درآوردن آن نیاز است. در مقابل، اگر بار صفحه مثبت باشد، ذره با بار مثبت به جای چسبیدن به صفحه، از آن دور می‌شود. در این حالت، برای نزدیک کردن ذره به صفحه باید انرژی مصرف کنیم. اگر بخواهیم ذره را در فاصله نزدیک‌تری نسبت به صفحه قرار دهیم، باید انرژی بیشتری به آن بدهیم.

اگر ذره بارداری در میدان الکتریکی جابجا شود، کار نیروی الکتریکی وارد شده بر ذره در این جابجایی، برابر منفی تغییرات انرژی پتانسیل الکتریکی است:

$$ W _ E = – triangle U _ E \ triangle U _ E = – W _ E = – |q| E d cos theta  $$

در رابطه فوق:

• $$theta$$ زاویه بین نیروی الکتریکی و جهت جابجایی ذره است.
• $$q$$ بار الکتریکی و واحد اندازه‌گیری آن کولن است.
• E بزرگی میدان الکتریکی و واحد اندازه‌گیری آن نیوتن بر کولن است.
• d جابجایی برحسب متر است.
• $$ triangle U _ E $$ تغییرات انرژی پتانسیل الکتریکی و برحسب ژول اندازه‌ گرفته می‌شود.

پتانسیل الکتریکی چیست؟

به تفاوت انرژی پتانسیل بر واحد بار بین دو نقطه در میدان الکتریکی، پتانسیل یا پتانسیل الکتریکی گفته می‌شود. همان‌طور که در بخش قبل مشاهده کردیم، انرژی پتانسیل الکتریکی ذره‌ای باردار به مقدار بار آن بستگی دارد. از این‌رو، نسبت تغییر انرژی پتانسیل ذره به بار آن از نوع و اندازه بار الکتریکی مستقل است.

$$triangle V = V_ 2 – V _1 = frac { triangle U_ E } { q } $$

در رابطه فوق، $$V $$ کمیتی نرده‌ای است و پتانسیل الکتریکی نام دارد و مقدار آن در دو نقطه یک و دو به ترتیب برابر $$V_ 1 $$ و $$V_ 2 $$ است. همچنین، $$triangle V $$ اختلاف پتانسیل الکتریکی و واحد اندازه‌گیری آن ژول بر کولن یا ولت است. اختلاف پتانسیل الکتریکی را می‌توانیم برحسب رابطه زیر نیز بنویسیم:

$$| triangle V | = Ed $$

میدان الکتریکی داخل رساناها

ماده رسانا به ماده‌ای گفته می‌شود که تعداد زیادی الکترون آزاد دارد. این الکترون‌ها به راحتی در ماده رسانا جابجا می‌شوند.

به دلیل وجود این تعداد الکترون درون ماده رسانا، نیروی دافعه الکتریکی بین آن‌ها نیز بسیار بزرگ است. دو پرسش بسیار مهم در مورد مواد رسانا وجود دارند:

1. اگر بار الکتریکی اضافی به جسم رسانا بدهیم، این بار چگونه در آن توزیع می‌شود؟
2. اگر جسم رسانا را در میدان الکتریکی خارجی قرار رهیم، خطوط میدان چگونه داخل و خارج این جسم توزیع می‌شوند؟

بار الکتریکی اضافی داده شده به جسم رسانا، روی سطح خارجی آن پخش می‌شود. به این نکته توجه داشته باشید که این بار اضافی به گونه‌ای روی سطح رسانا پخش می‌شود که میدان الکتریکی داخل رسانا در شرایط الکترواستاتیکی برابر صفر باشد. جسمی رسانا و خنثی به شکل کره به صورت نشان داده شده در تصویر زیر داخل میدان الکتریکی یکنواختی قرار گرفته است. میدان الکتریکی در نزدیکی جسم رسانا قوی‌تر می‌شود و خطوط میدان به یکدیگر نزدیک‌تر خواهند شد، اما داخل جسم رسانا میدان الکتریکی برابر صفر است.

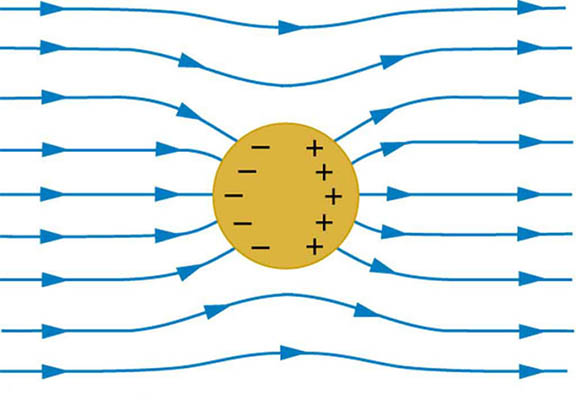
چرا شدت میدان الکتریکی داخل جسم رسانای باردار برابر صفر است؟

میدان الکتریکی به دو دلیل داخل ماده رسانا برابر صفر است. این دو دلیل عبارت هستند از:

• زیرا بارهای الکتریکی اضافی در جسم رسانای خوب، همواره روی سطح خارجی جسم قرار می‌گیرند. از این‌رو، مقدار بار الکتریکی داخل جسم رسانا برابر صفر می‌شود.
• قرار گرفتن بارها روی سطح خارجی جسم رسانا، یکی از ویژگی‌های مهم اجسام رسانا است. زیرا بارهای الکتریکی در جسم رسانا آزادانه می‌توانند به اطراف حرکت کنند. در نتیجه، آن‌ها پایدارترین حالت، یعنی قرار گرفتن روی سطح خارجی جسم رسانا، را برای توزیع انتخاب می‌کنند.

چگالی سطحی بار الکتریکی رسانا

همان‌طور که در بخش قبل گفتیم، بار الکتریکی اضافی روی سطح جسم رسانا توزیع می‌شود. اگر رسانا کره باشد، توزیع بار الکتریکی روی سطح آن کاملا یکنواخت خواهد بود. اما اگر جسم رسانا در برخی مناطق تیزتر و زاویه‌دار باشد، بار الکتریکی روی سطح آن به طور یکنواخت پخش نمی‌شود. برای مقایسه توزیع بار الکتریکی در بخش‌های مختلف سطحِ جسمی رسانا با شکل دلخواه از کمیتی به نام چگالی بار سطحی استفاده می‌کنیم:

$$sigma = frac { Q } { A } $$

در رابطه فوق:

• A مساحت سطحی است که بار روی آن توزیع شده است.
• Q بار الکتریکی موجود روی سطح A و $$sigma$$ چگالی بار سطحی است.

یکای اندازه‌گیری بار الکتریکی برابر کولن بر مترمربع ($$frac { C } { m ^ 2 } $$)‌است. از این‌رو، سطوح نوک‌تیز به دلیل داشتن مساحت کوچک‌تر، چگالی بار سطحی بزرگ‌تری دارند. همان‌طور که در تصویر زیر مشاهده می‌کنید، توزیع بار الکتریکی روی سطوح کروی، کاملا یکنواخت است. اما توزیع بار الکتریکی روی اجسامی با شکل‌های دیگر، یکنواخت نیست و چگالی بار در نقاط نوک‌تیز بسیار زیاد خواهد بود.

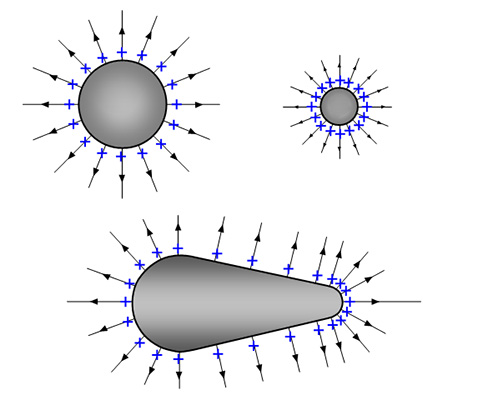
خازن چیست؟

خازن، قطعه‌ای الکتریکی در مدار است که می‌تواند انرژی الکتریکی را به شکل بار الکتریکی در خود ذخیره کند. خازن‌ها اندازه و شکل‌های متفاوتی دارند. آن‌ها به طور معمول از دو صفحه رسانا (صفحه فلزی نازک) به مساحت A ساخته شده‌اند که در فاصله مشخصی از یکدیگر قرار دارند. فاصله خالی بین صفحات خازن گاهی توسط ماده‌ای عایق به نام دی‌الکتریک، پر می‌شود.

باردار یا شارژ کردن خازن

برای شارژ کردن خازن می‌توان آن را در مدار الکتریکی ساده‌ای، شامل یک یا چند باتری، به صورت نشان داده شده در تصویر زیر قرار داد. به محض بستن کلید، بار از طریق سیم‌های رسانا به صفحات خازن می‌رسد. جریان بارها تا زمانی ادامه می‌یابد که اختلاف پتانسیل میان دو صفحه خازن با اختلاف پتانسیل دو سر باتری، برابر شود. صفحات خازن پس از باردار شدن، بار الکتریکی یکسان، اما با علامت مخالف دارند.

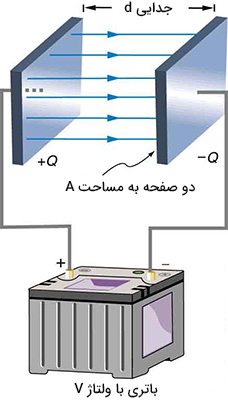
ظرفیت خازن با استفاده از رابطه زیر به‌دست می‌آید:

$$C = frac {  Q } { V } $$

در رابطه فوق، C ظرفیت خازن، Q بار خازن و $$triangle V $$ اختلاف پتانسیل بین صفحه‌های خازن هستند. واحد اندازه‌گیری ظرفیت خازن، کولن بر ولت یا فاراد است. اگر ماده‌ای عایق به نام دی‌الکتریک میان دو صفحه خازن قرار داده شود، ظرفیت خازن به صورت زیر افزایش می‌یابد:

$$C = kappa C_ 0$$

در رابطه فوق، $$kappa$$ ثابت دی‌الکتریک نام دارد. خازن تختی با دو صفحه به مساحت A که به فاصله d از یکدیگر قرار گرفته‌اند را در نظر بگیرید. اگر بین دو صفحه، دی‌الکتریکی با ثابت دی‌الکتریک $$kappa$$ قرار گرفته باشد، ظرفیت خازن با استفاده از رابطه زیر به‌دست می‌آید:

$$C_0 =kappa epsilon _ 0 frac { A } { d }  $$

در رابطه فوق، $$xi_0 $$ ضریب گذردهی خلأ نام دارد و مقدار آن برابر $$8.85 times 10 ^ { – 12 }  frac { F } { m} $$ است.

انرژی خازن

همان‌طور که در بخش قبل اشاره شد خازن، قطعه‌ای الکتریکی در مدار است که می‌تواند انرژی الکتریکی را به شکل بار الکتریکی در خود ذخیره کند. انرژی ذخیره شده در خازن با استفاده از رابطه‌های زیر به‌دست می‌آید:

$$U = frac { 1 } { 2 } Q V = frac { 1 } { 2 } C V ^ 2 = frac { 1 } { 2 } { Q ^ 2 } { C } $$

در رابطه فوق:

• U انرژی الکتریکی خازن و واحد اندازه‌گیری آن ژول است.
• Q مقدار بار روی صفحات خازن و برحسب کولن است.
• $$V$$ اختلاف پتانسیل دو سر خازن و برحسب ولت است.
• C ظرفیت خازن و برحسب فاراد است.

تا اینجا با فرمول های فیزیک یازدهم فصل اول آشنا شدیم. در ادامه، برای درک بهتر این فرمول‌ها، تعدادی مثال با یکدیگر حل می‌کنیم.

مثال اول

مثال دوم

مثال سوم

چهار بار الکتریکی مطابق تصویر نشان داده شده در ادامه، روی چهار راس مربعی به ضلع ۰/۰۵ متر قرار گرفته‌اند. اگر اندازه بار q برابر $$1.0 times 10^ { -7 } $$ کولن باشد، بزرگی نیروی الکترواستاتیکی وارد شده بر بار 2q برابر است با:

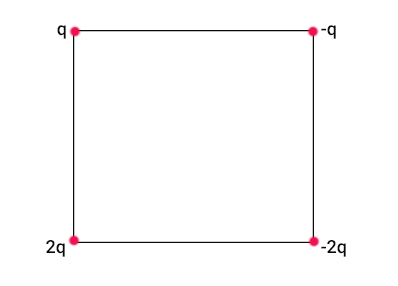
$$F_ { net} = 17.54 times 10 ^ 5 N$$

$$F_ { net} = 12.54 times 10 ^ 5 N$$

$$F_ { net} = 17.54 times 10 ^ 2 N$$

$$F_ { net} = 1.54 times 10 ^ 5 N$$

مشاهده جواب

انداره میدان الکتریکی حاصل از ذره باردار $$q$$ را می‌توان به صورت زیر نوشت:

$$F = k frac { |q _ 1| |q_2|  } { r ^ 2 } $$

چهار بار الکتریکی در چهار گوشه مربعی به ضلع ۰/۰۵ متر قرار گرفته‌اند. میدان الکتریکی وارد شده بر بار 2q را می‌خواهیم به‌دست آوریم. ابتدا جهت میدان الکتریکی حاصل از سه بار دیگر، روی بار 2q را را رسم می‌کنیم. 

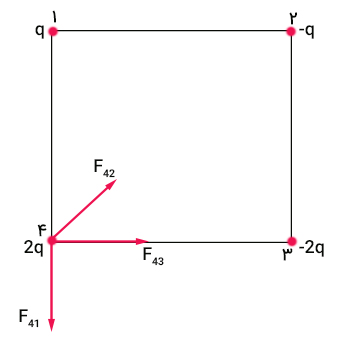
در ادامه مقدار هر یک از سه نیروی الکترواستاتیکی نشان داده شده در تصویر فوق را به‌دست می‌آوریم. $$F_ { 41} $$ نیروی وارد شده از طرف بار یک بر بار ۴، یعنی 2q است و به صورت زیر به‌دست می‌آید:

$$F_{41} = frac { k  (2q) (q)} { r ^ 2 } $$

$$F_ { 42} $$  نیز نیروی وارد شده از طرف بار ۲ بر بار ۴، یعنی 2q است و به صورت زیر به‌دست می‌آید:

$$F_{42} = frac { k times (2q) (q)} { d ^ 2 } $$

$$F_ { 43} $$ نیز نیروی وارد شده از طرف بار ۳ بر بار ۴، یعنی 2q است و به صورت زیر به‌دست می‌آید:

$$ F_{43} = frac { k times (2q) ( 2q) } { r ^ 2 } $$

توجه به این نکته مهم است که برای نوشتن نیروی الکترواستاتیکی بین بارهای الکتریکی در رابطه‌های فوق، علامت بار الکتریکی در فرمول نوشته نشده و از علامت بارها برای تعیین جهت نیرو استفاده شده است. نیروی‌های $$F_ { 4 2 } $$ و $$F_ { 4 3 } $$ از نوع جاذبه و نیروی $$F _ { 41 } $$ از نوع دافعه است. همچنین، فراموش نکنید که فاصله بین دو بار الکتریکی q- و 2q و بارهای 2q- و 2q برابر مقدار ضلع مربع، اما فاصله بین دو بار q- و 2q برابر قطر مربع است. اکر طول هر ضلع مربع برابر r باشد، قطر مربع برابر است با:

$$d ^ 2 = r ^ 2 + r ^ 2 = 2 r ^ 2 // d = sqrt { 2 } r = sqrt { 2 } times 0.05 = 0.07 m$$

با توجه به مقدار قطر، مقدار نیروهای الکترواستاتیکی بین بارها را به صورت زیر به‌دست می‌آوریم:

$$F_{41} = frac { k  (2q) (q)} { r ^ 2 } = 2k frac { q ^ 2 } { r ^ 2 } \F_{42} = frac { k (2q) (q)} { d ^ 2 } = 2k frac { q ^ 2 } { 2 r ^ 2 } = kfrac { q ^ 2 } { r ^ 2 } \ F_{43} = frac { k (2q) ( 2q) } { r ^ 2 } = 4k frac { q ^ 2 } { r ^ 2 } $$

در ادامه، برآیند نیروهای وارد شده بر بار 2q را به‌دست می‌آوریم. برای انجام این کار، تنها کافی است نیروی $$ F_ { 42} $$ را در راستای محورهای افقی و عمودی تجزیه کنیم. زاویه این نیرو با هر یک از محورها برابر ۴۵ درجه است. 

$$F_ { 42, x} = F_ { 42 } cos (45) \ F_ { 42 , y } = F_ { 42 } sin (45) $$

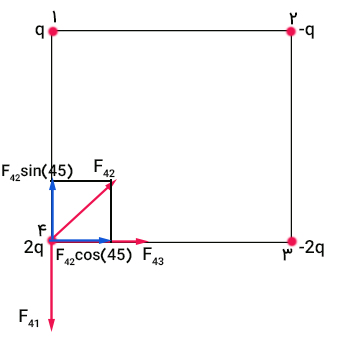
برآیند نیروهای وارد شده بر بار الکتریکی 2q در راستای محور افقی برابر است با:

$$ F_ x = F_ { 42 } cos (45) + F_ { 4 3 } \ F_ x = 4 frac { k q ^ 2 } { r ^ 2 } + frac { sqrt { 2 }} { 2 } frac { k q ^ 2 } { r ^ 2 } = frac { k q ^ 2 } { r ^ 2 } ( 4 + frac { sqrt { 2 } } { 2 } ) $$

همچنین، برآیند نیروهای وارد بر بار الکتریکی 2q در راستای محور عمودی برابر است با:

$$F_ y = F_ { 42 } sin ( 45) – F_ { 4 1 } \ F_y = frac { k q ^ 2 } { r ^ 2 }frac { sqrt { 2 } } { 2 } – 2frac { kq ^ 2 } { r ^ 2 } = frac { k q ^ 2 } { r ^ 2 } ( frac { sqrt { 2 } }{2 } – 2 ) \ F_ y = – frac { k q ^ 2 } { r ^ 2 } ( 2 – frac { sqrt { 2 }} { 2 } )$$

در ادامه و با جایگذاری مقدارهای داده شده، اندازه $$F_x$$ و $$F_ y$$ را به‌دست می‌آوریم:

$$ F_ x = frac { k q ^ 2 } { r ^ 2 } ( 4 + frac { sqrt { 2 } } { 2 } ) = frac { 9 times 10 ^ 9 times 1.0 times 10 ^ { -7 } } { 0.05 ^ 2 } ( 4 + 0.7) = 16.9 times 10 ^ 5 N $$

$$ F_ y = – frac { k q ^ 2 } { r ^ 2 } ( 2 – frac { sqrt { 2 }} { 2 } ) \ F_ y = – frac { 9 times 10 ^ 9 times 1.0 times 10 ^ { – 7 } } { 0.05^ 2 } ( 2 – 0.7) = -4.68 times 10 ^ 5 N$$

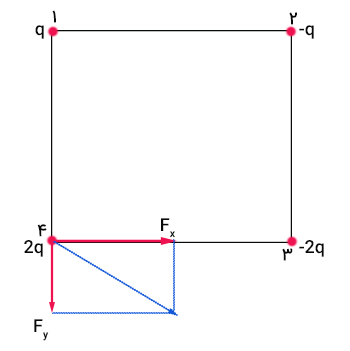
با داشتن نیروهای $$F_ x$$ و $$F_y $$ به راحتی می‌توانیم برآیند نیروهای وارد شده بر بار الکتریکی 2q را به‌دست آوریم. 

$$F_ { net} = 17.54 times 10 ^ 5 N$$

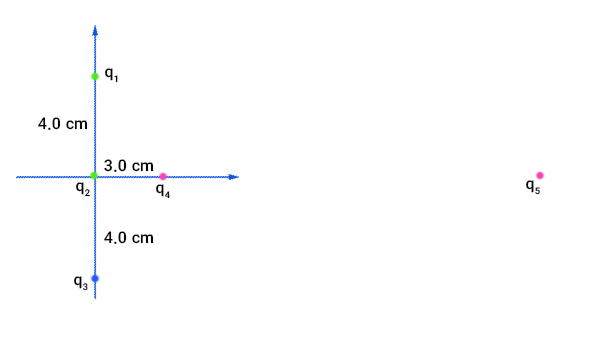
مثال چهارم

سه بار الکتریکی $$q_1 = +20 nc $$ و $$q_ 2 = 10 nC $$ و $$q_3 = -20 nC  $$ به صورت نشان داده شده در تصویر زیر کنار یکدیگر قرار گرفته‌اند. بار $$q_4 $$ از حالت سکون رها می‌شود. سرعت آن در فاصله بسیار دور چه مقدار است؟ (مقدار بار $$q_ 4 $$ برابر ۴۰ نانوکولن و جرم آن برابر $$2.0 times 10 ^ { – 13 } kg$$ است.) 

$$ 1.1 times 10 ^ 4 frac { m } { s } $$

$$ 3.46 times 10 ^ 3 frac { m } { s } $$

$$ 1.1 times 10 ^ 3 frac { m } { s } $$

$$ 3.46 times 10 ^ 4 frac { m } { s } $$

مشاهده جواب

برای حل این مثال از قانون پایستگی انرژی استفاده می‌کنیم:

$$U_ 0 + U_ { q_4} + k_i = U_0 + U_ q{ 4 , f } + k_ f $$

در رابطه فوق:

• $$U_ 0 $$ انرژی سه بار $$q_1 $$ و $$q_2 $$ و $$q_3 $$ قبل از قرار گرفتن بار $$q_4 $$ در نزدیکی آن‌ها است. 
• $$U _ { q_4 } $$ انرژی پتانسیل بار الکتریکی $$q _ 4 $$ است. 
• $$k_i $$ انرژی جنبشی سیستم پس از اضافه شدن بار $$q_4  $$ به آن است. 
• $$U_ q{ 4 , f } $$ انرژی پتانسیل بار $$q_4 $$ در فاصله بسیار دور از سه بار دیگر است. 
• $$k_f $$ انرژی جنبشی نهایی سیستم است.

به هنگام حل این مثال، توجه به این نکات بسیار مهم است:

• بارهای $$q_1 $$ و $$q_2 $$ و $$q_3 $$ در مکان خود ثابت و بدون حرکت هستند.
• بار $$q_ 4 $$ تنها بار متحرک در این مثال است. 
• انرژی پتانسیل الکتریکی سه بار $$q_1 $$ و $$q_2 $$ و $$q_3 $$ یعنی $$U_ 0 $$ قبل و بعد از اضافه شدن بار چهارم بدون تغییر باقی می‌ماند. 

با حذف $$U_0 $$ از طرفین رابطه فوق داریم:

$$ U_ { q_4} + k_i =  U_ q{ 4 , f } + k_ f $$

بار $$q_4 $$ از حالت سکون شروع به حرکت می‌کند، بنابراین انرژی جنبشی اولیه آن، $$k_ i $$ براب صفر است:

$$ U_ { q_4}  =  U_ q{ 4 , f } + k_ f $$

همچنین، بار $$q_4 $$ پس از حرکت از حالت سکون، تا بی‌نهایت می‌رود و در فاصله بسیار دوری از سه بار اول قرار می‌گیرد. از این‌رو، مقدار $$U_ q{ 4 , f }$$ نیز برابر صفر خواهد بود:

$$ U_ { q_4}  =   k_ f \ U_ { q_4} = frac { 1 } { 2 } m v ^ 2 $$

در نتیجه، برای محاسبه سرعت نهایی بار $$q_ 4 $$ تنها کافی است انرژی پتانسیل الکتریکی آن را در مجاروت سه بار دیگر به‌دست آوریم. 

$$U_ { q_ 4 } = q_ 4 V $$

$$V$$ اختلاف پتانسیل تولید شده توسط سه بار دیگر است:

$$V = k (frac { q_ 1 } { r _ 1 }  + frac { q _ 2 } { r _ 2 }  + frac { q_ 3 } { r _ 3 } )  \ V = 9 times 10 ^ 9 ( frac { 20 times 10 ^ { -9 } } { 0.05 } + frac { 10 times 10 ^ { -9 } } { 0.03 } + frac { -20 times 10 ^ { -9 } } { 0.05} ) \ V = 3000 V $$

از این‌رو، مقدار $$U_ { q_ 4 }$$ برابر است با:

$$U_ { q_ 4 } = q_ 4 V \ = 40 times 10 ^ { – 9 } times 3000 = 1.2 times 10 ^ { -4 } J$$

در نتیجه، سرعت بار $$q_ 4 $$ در فاصله بسیار دور از سه بار ثابت، در حدود $$ 3.46 times 10 ^ 4 frac { m } { s } $$ به‌دست می‌آید. 

مثال پنجم

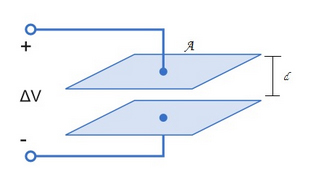
خازن تختی متشکل از دو صفحه به مساحت ۱۵ سانتی‌متر مربع که به فاصله ۳ سانتی‌متر از یکدیگر قرار گرفته‌اند، تشکیل شده است. اگر ولتاژ دو سر خازن برابر ۵ ولت باشد، ظرفیت آن کدام است؟ ($$epsilon_0 = 8.854 times 10 ^ { -12 }  frac { C ^ 2  } { N . m ^ 2 } $$)

$$9.31 times 10 ^ { – 13 } F $$

$$4.43 times 10 ^ { – 13 } F $$

$$1.29 times 10 ^ { – 12 } F $$

$$8.32 times 10 ^ { – 13 } $$

مشاهده جواب

در حالت کلی، ظرفیت خازن با استفاده از رابطه زیر به‌دست می‌آید:

$$C = frac {  Q } { V } $$

در رابطه فوق، C ظرفیت خازن، Q بار خازن و $$triangle V $$ اختلاف پتانسیل بین صفحه‌های خازن هستند. همچنین، ظرفیت خازن تخت با مساحت صفحه‌های A و فاصله بین صفحه‌های d را با استفاده از رابطه $$C = epsilon _ 0 frac { A } { d }  $$ به‌دست می‌آوریم. در این مثال، خازن از دو صفحه تخت با مساحت و فاصله مشخص تشکیل شده است. از آنجا که مشخصات هندسی خازن داده شده است، برای محاسبه ظرفیت آن از رابطه $$C= epsilon _ 0 frac { A } { d }  $$ استفاده می‌کنیم. 

$$C = epsilon _ 0 frac { A } { d }  \ C = frac { 8.854 times 10 ^ { -12 } frac { C ^ 2 } { N . m ^ 2 }  times 0.0015 m ^ 2 } { 0.03 m }  \ C = 4.43 times 10 ^ { – 13 }  F $$

 مثال ششم

 مثال هفتم

 مثال هشتم

خازن تختی متشکل از دو صفحه با فاصله ۱/۵ سانتی‌متر داریم. این خازن را به باتری با اختلاف پتانسیل ۱۵ ولت وصل و پس از شارژ کامل، جدا می‌کنیم. اگر فضای بین صفحه‌های خازن را با ماده دی‌الکتریکی با ثابت ۳، به طور کامل پر کنیم، میدان الکتریکی بین دو صفحه خازن چگونه تغییر می‌کند؟ 

۶۷ درصد کاهش می‌یابد.

۶۷ درصد افزایش می‌یابد. 

۳۳ درصد افزایش می‌یابد. 

۳۳ درصد کاهش می‌یابد.

مشاهده جواب

میدان الکتریکی E بین دو صفحه خازن با فاصله d و اختلاف پتانسیل $$V$$ با استفاده از رابطه زیر به‌دست می‌آید:

$$E = frac { V } { d } $$

میدان الکتریکی بین دو صفحه خازن، قبل از قرار دادن ماده دی‌الکتریک بین دو صفحه آن برابر $$E_0$$ و مقدار آن برابر است با:

$$E_ 0 = frac { V _ 0 } { d  } = frac { 15 } { 1.5 times 10 ^ { -2 }} \ E_ 0  = 1000 V$$

خازن پس از شارژ شدن از باتری جدا می‌شود، بنابراین ولتاژ دو سر آن تغییر اما بار روی صفحه‌ها ثابت می‌ماند. در ادامه، دی‌الکتریکی با ثابت دی‌الکتریک ۳ بین دو صفحه خازن قرار داده می‌شود. از این‌رو، ظرفیت آن به صورت زیر تغییر خواهد کرد:

$$C’ = kappa epsilon_0 frac { A} { d } = 3 epsilon_0 frac { A } { d } = 3 times C$$

با ثابت ماندن بارهای روی صفحه و تغییر ظرفیت، ولتاژ دو سر خازن نیز به صورت زیر تغییر خواهد کرد:

$$V = frac { Q } { C’ } \ V = frac { Q_ 0 } {3 C } \ V = frac { 1 } { 3 } frac { Q _ 0 } { C } = frac { 15 } { 3 } = 5 V $$

میدان الکتریکی بین دو صفحه خازن پس از قرار دادن ماده دی‌الکتریک بین صفحه‌های آن برابر است با:

$$E = frac { V } { d } = frac { 5 V }{ 1.5 times 10 ^ { -2 } } = 333 V  $$

 

چگونه از فرمول های فیزیک یازدهم در حل مسئله استفاده کنیم؟

توانایی حل مسئله، به خصوص مسائل فیزیک، از اهمیت بالایی برخوردار است. در مطلب «فرمول‌ های فیزیک دهم» از مجله فرادرس، فرمول‌ های فیزیک دهم را به همراه حل مساله بیان کردیم. این مطلب نیز در رابطه با الکتریسیته و مغناطیس به صورت خلاصه صحبت و چند مسئله به عنوان مثال و آشنایی با استفاده از فرمول‌ها در حل مسائل مختلف، حل شده است. توجه به این نکته مهم است که برای موفقیت در امتحان نهایی فیزیک یازدهم و حل مسائل مختلف آن باید مفاهیم بنیادی مانند جریان الکتریکی، الکتریسیته ساکن، مقاومت‌ها، خازن‌ها، مغناطیس و القای الکترومغناطیسی را به خوبی فرا گرفته باشید. از این‌رو،‌ تماشای فیلم‌های آموزشی، مانند فیلم‌های آموزشی تهیه شده در فرادرس، می‌تواند به شما برای رسیدن به این نقطه کمک فراوانی کند.

در حالت کلی برای حل مسائل فیزیک با استفاده از فرمول‌های مرتبط باید مرحله‌های زیر را طی کنید:

• ابتدا مسئله داده شده را با دقت مطالعه کنید. پس از خواندن مسئله باید بدانید چه چیزی از شما خواسته شده است.
• پس از خواند مسئله، داده‌های معلوم و مجهول را به صورت فهرست‌وار یادداشت کنید.
• در ادامه، فرمول‌های لازم برای حل مسئله را یادداشت کنید.
• مسئله‌های فیزیک ممکن است در یک مرحله یا بیش از یک مرحله حل شوند. تشخیص این موضوع به داشتن درک صحیحی از سوال مربوط می‌شود.
• راه‌حل را مرتب و گام‌به‌گام پیش ببرید.
• پس از حل مسئله، پاسخ نهایی را برای اطمینان بار دیگر بررسی کنید.

برای آشنایی بهتر با چگونگی حل مسائل فیزیک یازدهم می‌توانیم از فیلم آموزشی زیر استفاده کنید. در این فیلم آموزشی از مجموعه فرادرس با حل سوالات پرتکرار امتحانی، با روند حل مسئله‌های مختلف در فیزیک یازدهم آشنا می‌شوید.

اگر تسلط کاملی بر مباحث پایه الکتریسیته و مغناطیس دارید و مسئله‌های مرتبط را به خوبی حل می‌کنید، اما به دنبال یادگیری مبحث‌ها و حل مسئله‌های پیشرفته‌تر هستید، می‌توانید از فیلم‌های آموزشی زیر استفاده کنید:

فرمول های فیزیک یازدهم فصل دوم

فرمول‌ های فیزیک یازدهم فصل دوم  در جدول زیر به صورت خلاصه نوشته شده‌اند.

مبحث موردنظر	فرمول های فیزیک یازدهم فصل دوم
جریان الکتریکی متوسط	$$frac { triangle q } { triangle t } $$
مقاومت الکتریکی و قانون اهم	$$R frac { V } { I } $$
مقاومت الکتریکی سیمی به طول L و سطح مقطع یکنواخت A که اختلاف پتانسیل V به آن وارد می‌شود.	$$R = rhofrac { L } { A } $$
رابطه مقاومت ویژه و دما	$$rho = rho_0 [ 1 + alpha ( T – T _ 0 )]$$
نیرو محرکه الکتریکی	$$xi = frac { triangle W } { triangle q } \ V_ b – V _ a = xi$$
مدار تک حلقه‌ای و افت پتانسیل در مقاومت	$$ xi – IR = 0 $$
توان در مدارهای الکتریکی	$$P = I triangle V$$
توان مصرفی در مقاومت الکتریکی	$$P = frac { V ^ 2 } { R } = R I ^ 2 $$
توان خروجی منبع نیروی محرکه واقعی	$$ P = xi I – r I ^ 2 $$
مقاومت معادل چند مقاومت سری یا متوالی در مدار	$$ R _ { eq } = R _ 1 + R _ 2 + R _ 3 + … + R _ n $$
مقاومت معادل چند مقاومت موازی در مدار	$$frac { 1} { R_ {eq}} = frac{ 1} { R _1 } + frac { 1 } { R_2 } + … + frac { 1} { R _ { n }}$$

در ادامه، فرمول‌های نوشته شده در جدول فوق را به صورت خلاصه توضیح می‌دهیم.

جریان الکتریکی چیست؟

به حرکت بارهای الکتریکی در جهتی مشخص در مدار، جریان الکتریکی گفته و برحسب آمپر اندازه‌گیری می‌شود.

در حالت عادی وقتی سیمی رسانا داشته باشیم، هیچ جریان الکتریکی از آن عبور نمی‌کند. شاید با خود بگویید الکترون‌ها در این سیم، آزادانه می‌توانند به اطراف حرکت کنند. اما برای داشتن جریان الکتریکی، الکترون‌های آزاد باید به کمک نیروی خارجی به نام ولتاژ قرار بگیرند. در این صورت، جریانی از الکترون‌ها در جهتی مشخص خواهیم داشت. فرض کنید سیمی با سطح مقطع مشخص داریم. اگر در بازه‌ زمانی $$triangle t $$، مقداری باری برابر $$triangle q $$ از سطح مقطع سیم عبور کند، جریان الکتریکی متوسط برابر است با:

$$frac { triangle q } { triangle t } $$

مقاومت الکتریکی و قانون اهم

الکترون‌های آزاد در رسانا به راحتی و بدون مانع نمی‌توانند حرکت کنند. آن‌ها در مسیر خود با اتم‌های ماده رسانا برخورد می‌کنند. از این‌رو، ماده رسانا به هنگام عبور جریان، گرم می‌شود. در نتیجه، الکترون‌های آزاد به هنگام حرکت در ماده رسانا با مقاومت روبرو هستند که به آن مقاومت الکتریکی می‌گوییم. مقاومت الکتریکی به طول و سطح مقطع رسانا، جنس ماده رسانا و دمای آن وابسته است. توجه به این نکته لازم است که اگر به دو مقاومت با مقدارهای متفاوت، ولتاژ یکسانی اعمال کنیم، جریان‌های عبوری از آن‌ها با یکدیگر متفاوت خواهند بود. هرچه مقدار مقاومت کمتر باشد، مقدار جریان عبور بیشتر است. مقاومت الکتریکی بین دو نقطه در رسانا با استفاده از رابطه زیر به‌دست می‌آید:

$$R frac { V } { I } $$

در رابطه فوق، R مقاومت الکتریکی است و برحسب ولت بر آمپر یا اهم اندازه گرفته می‌شود. براساس قانون اهم، جریان عبوری از مقاومت الکتریکی با ولتاژ اعمال شده به دو سر مقاومت، رابطه مستقیم دارد. به بیان دیگر، نمودار جریان برحسب ولتاژ، خطی مستقیم با شیب ثابت و مثبت است.

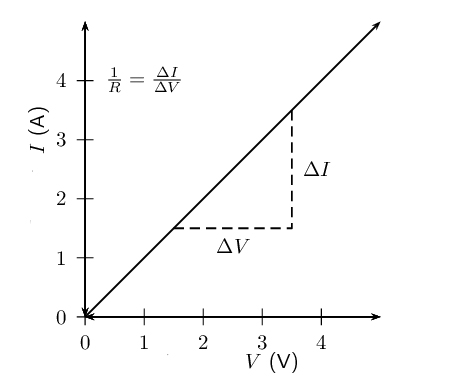
عوامل موثر بر مقاومت الکتریکی

مقاومت الکتریکی به طول و سطح مقطع رسانا، جنس ماده رسانا و دمای آن وابسته است و با استفاده از رابطه زیر به‌دست می‌آید:

$$R = rhofrac { L } { A } $$

در رابطه فوق:

• L طول رسانا و برحسب متر است.
• A سطح مقطع جسم و برحسب مترمربع است.
• R مقاومت جسم و برحسب اهم است.
• $$rho$$ مقاومت ویژه و برحسب اهم-متر است.

تغییر مقاومت ویژه با دما

اگر دمای ماده رسانایی را افزایش دهیم، تعداد الکترون‌های آزادِ آن ثابت می‌ماند، اما اتم‌ها و یون‌ها داخل ماده با سرعت بیشتری نوسان می‌کنند. از این‌رو، الکترون‌های آزاد به هنگام حرکت با احتمال بیشتری به اتم‌ها و یون‌ها برخورد خواهند کرد و مقاومت رسانا افزایش می‌یابد. بر طبق پژوهش‌های انجام شده، مقاومت ویژه با تقریب نسبتا خوبی به صورت خطی با دما تغییر می‌کند و با استفاده از رابطه زیر به‌دست می‌آید:

$$rho = rho_0 [ 1 + alpha ( T – T _ 0 )]$$

نیروی محرکه الکتریکی و مدارها

همان‌طور که در بخش قبل اشاره کردیم، برای آن‌که بارهای آزاد در ماده رسانا بتوانند در جهت مشخصی حرکت و بر مقاومت الکتریکی غلبه کنند، باید نیرویی به نام اختلاف پتانسیل بین دو سر ماده رسانا اعمال کنیم. اختلاف پتانسیل همانند نیروی محرکه الکتریکی عمل می‌کند و بارهای آزاد را در جهت مشخصی حرکت می‌دهد و به آن‌ها برای غلبه بر مقاومت الکتریکی کمک می‌کند. اختلاف پتانسیل به کمک وسیله‌ای به نام باتری به دو سر مقاومت اعمال می‌شود که به آن منبع نیروی محرکه الکتریکی نیز می‌گوییم. باتری با عبور بار الکتریکی، کاری به اندازه $$triangle W $$ روی آن انجام می‌دهد. به مقدار کار انجام شده توسط منبع نیروی محرکه الکتریکی روی واحد بار الکتریکی برای بردن آن از نقطه‌ای با پتانسیل کمتر به نقطه‌ای با پتانسیل بیشتر، نیروی محرکه الکتریکی (emf) گفته می‌شود:

$$xi = frac { triangle W } { triangle q } \ V_ b – V _ a = xi$$

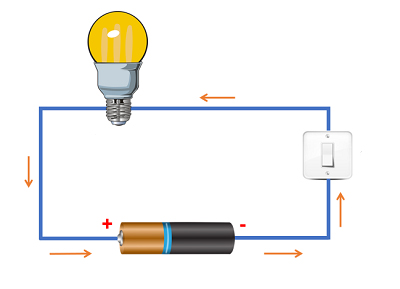
مدار ساده تک حلقه‌ای متشکل از باتری ایده‌ال با نیرو محرکه $$xi$$ و مقاومت R را در نظر بگیرید. اگر به صورت نشان داده شده در تصویر زیر ار نقطه a شروع کنیم و در جهت جریان الکتریکی حرکت کنیم و به این نقطه بازگردیم، رابطه‌ای به صورت زیر خواهیم داشت:

$$V_a + xi – IR = V_a \ xi – IR = 0$$

بنابراین، جمع جبری اختلاف پتانسیل‌ بین اجزای مختلف مدار در هر دور کامل برابر صفر خواهد بود.

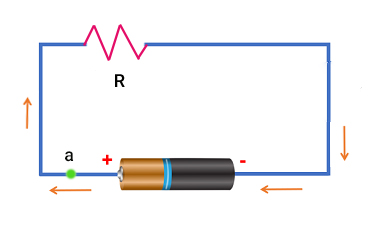
تعیین علامت اختلاف پتانسیل‌ ها در مدار تک حلقه‌ای

فرض کنید مداری تک حلقه‌ای متشکل از باتری با نیروی محرکه الکتریکی $$xi$$ و مقاومت R داریم. هنگام تعیین اختلاف پتانسیل‌ها در این مدار به نکته‌های زیر باید توجه کنیم:

• اگر در جهت جریان الکتریکی حرکت کنیم و به مقاومت R برسیم، اختلاف پتانسیل دو سر مقاومت برابر $$triangle V = – IR $$ خواهد بود.
• اگر در خلاف جریان الکتریکی حرکت کنیم و به مقاومت R برسیم، اختلاف پتانسیل دو سر مقاومت برابر $$triangle V =  IR $$ خواهد بود.
• اختلاف پتانسیل دو سر باتری به هنگام حرکت از پایانه منفی به مثبت برابر $$+ xi $$ و به هنگام حرکت از پایانه مثبت به منفی برابر $$- xi$$ است.

توان در مدارهای الکتریکی

فرمول توان یکی دیگر از فرمول های مهم فیزیک یازدهم است. برای به‌دست آوردن توان دو سر باتری یا هر وسیله الکتریکی دیگر در مدار از رابطه زیر استفاده می‌کنیم:

$$P = I triangle V$$

همچنین، توان مصرفی دو سر مقاومت برابر است با:

$$P = frac { V ^ 2 } { R } = R I ^ 2 $$

توان خروجی منبع نیروی محرکه الکتریکی را نیز می‌توانیم به صورت $$ P = xi I – r I ^ 2 $$ بنویسیم.

ترکیب مقاومت‌ ها

مقاومت‌ها در مدار به صورت سری، موازی یا ترکیبی از این دو حالت در مدار الکتریکی بسته می‌شوند. مقاومت معادل چند مقاومت سری یا متوالی در مدار به صورت زیر به‌دست می‌آید:

$$ R _ { eq } = R _ 1 + R _ 2 + R _ 3 + … + R _ n $$

همچنین، مقاومت معادل چندمقاومت موازی$$  frac { 1 } { R _ { eq } } = frac { 1 } { R _ 1 } + frac { 1 } { R _ 2 } + frac { 1 } { R _ 3 } + … + frac { 1 } {R _ n } $$را با استفاده از رابطه زیر به‌دست می‌آوریم:

$$  frac { 1 } { R _ { eq }} = frac { 1 } { R _ 1 } + frac { 1 } { R _ 2 } + frac { 1 } { R _ 3 } + … + frac { 1 } {R _ n } $$

تا اینجا با فرمول های فیزیک یازدهم فصل دوم آشنا شدیم. در ادامه، برای درک بهتر این فرمول‌ها، تعدادی مثال با یکدیگر حل می‌کنیم.

مثال اول

جریانی برابر ۳/۸ آمپر به مدت ۱۲ دقیقه از سیمی عبور می‌کند. مقدار الکترون عبوری از هر نقطه از مدار در این مدت زمان چه مقدار است؟ 

$$1.71 times 10 ^ { 19 } $$

$$1.71 times 10 ^ { 22 } $$

$$1.6 times 10 ^ { 22 } $$

$$2.71 times 10 ^ { 22 } $$

مشاهده جواب

برای حل این مثال، ابتدا مقدار بار عبوری از مدار را در مدت ۱۲ دقیقه به‌دست می‌آوریم. اگر جریان $$I$$ در مدت زمان t از سیمی بگذرد، مقدار بار عبوری از سیم برابر اسا با:

$$Q= It$$

زمان عبور جریان از سیم برابر ۱۲ دقیقه است. بنابراین، ابتدا آن را به ثانیه تبدیل می‌کنیم. از آنجا که هر دقیقه برابر ۶۰ ثانیه است، ۱۲ دقیقه برابر $$12times 60 $$ یا ۷۲۰ ثانیه خواهد بود. در نتیجه، مقدار Q برابر است با:

$$Q = I t = 3.8 A  times 720 s = 2736 C $$

بار الکتریکی هر الکترون برابر $$1.6 times  10 ^ { -19 }‌ $$ کولن است. بنابراین، برای آن‌که بدانیم چه تعداد الکترون از سیم عبور کرده است، ۲۷۳۶ کولن را بر بار الکترون تقسیم و عدد $$1.71 times 10 ^ { 22 } $$ به‌دست می‌آید. 

مثال دوم

باتری ۹ ولتی به صورت نشان داده در تصویر زیر به مقاومت الکتریکی ۲۵۰ اهمی وصل شده است. مقدار جریان گذرنده از مقاومت، مقدار توان اتلافی توسط مقاومت و مقدار توان منتقل شده توسط آن به ترتیب برابر هستند با: 

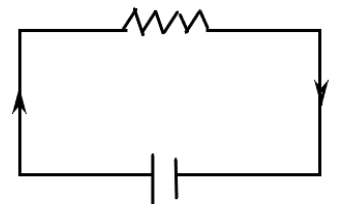
مقدار جریان عبوری از مقاومت برابر ۳۶ میلی آمپر است. همچنین، توان اتلافی در مقاومت با توان منتقل شده توسط باتری با یکدیگر برابر هستند و مقدار آن برابر ۳/۲۴ وات است. 

مقدار جریان عبوری از مقاومت برابر ۳۶۰ میلی آمپر است. همچنین، توان اتلافی در مقاومت با توان منتقل شده توسط باتری با یکدیگر برابر هستند و مقدار آن برابر ۳/۲۴ وات است. 

مقدار جریان عبوری از مقاومت برابر ۳۶ میلی آمپر است. همچنین، توان اتلافی در مقاومت با توان منتقل شده توسط باتری با یکدیگر برابر هستند و مقدار آن برابر ۰/۳۲۴ وات است. 

مقدار جریان عبوری از مقاومت برابر ۳۶ میلی آمپر است. همچنین، توان اتلافی در مقاومت برابر ۰/۳۲۴ وات و توان منتقل شده توسط باتری برابر ۳۲/۴ وات است. 

مشاهده جواب

با توجه به قانون اهم، مقاومت و ولتاژ به صورت خطی با یکدیگر رابطه دارند:

$$V =  I R  $$

مقدار مقاومت برابر ۲۵۰ اهم و ولتاژ دو سر باتری برابر ۹ ولت است. در نتیجه، مقدار جریان عبوری از مقاومت برابر ۰/۰۳۶ آمپر یا ۳۶ میلی ‌آمپر به‌دست می‌آید. در ادامه می‌خواهیم توان تلف شده توسط مقاومت را به‌دست آوریم. برای انجام این کار از رابطه $$P = I R ^ 2 $$ استفاده می‌کنیم. 

$$P = I R ^ 2 =  ( 0.036) ^ 2 times 250 = 0.324 W $$

در پایان، مقدار توان منتقل شده توسط باتری را به‌دست می‌آوریم. 

$$P = V I = 9 times 0.0036 = 0.324 w$$

همان‌طور که مشاهده می‌کنید مقدار توان جذب شده توسط مقاومت یا تلف شده در آن با مقدار توان منتقل شده توسط باتری با یکدیگر برابر هستند. چرا؟ دلیل این موضوع آن است که در مدار، تنها دو قطعه الکتریکی، باتری و مقاومت، وجود دارند و تمام توان منتقل شده توسط باتری به مقاومت منتقل می‌شود

مثال سوم

مداری به صورت نشان داده شده در تصویر زیر است. جریان و ولتاژ عبوری از مقاومت ۱۲ اهمی به ترتیب برابر است با: 

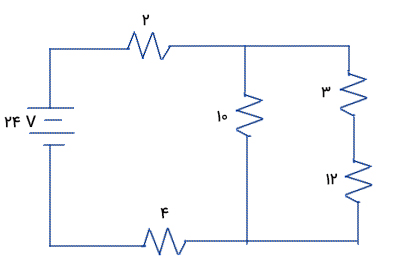
جریان و ولتاژ عبوری از مقاومت ۱۲ اهمی به ترتیب برابر ۰/۸ آمپر و ۹/۶ ولت است. 

جریان و ولتاژ عبوری از مقاومت ۱۲ اهمی به ترتیب برابر ۲ آمپر و ۹/۶ ولت است. 

جریان و ولتاژ عبوری از مقاومت ۱۲ اهمی به ترتیب برابر ۰/۸ آمپر و ۱۲ ولت است. 

جریان و ولتاژ عبوری از مقاومت ۱۲ اهمی به ترتیب برابر ۱/۲ آمپر و ۹/۶ ولت است. 

مشاهده جواب

مقاومت‌ها در مدار به صورت سری، موازی یا ترکیبی از این دو حالت در مدار الکتریکی بسته می‌شوند. مقاومت معادل چند مقاومت سری یا متوالی در مدار به صورت زیر به‌دست می‌آید:

$$ R _ { eq } = R _ 1 + R _ 2 + R _ 3 + … + R _ n $$

همچنین، مقاومت معادل چندمقاومت موازی را با استفاده از رابطه زیر به‌دست می‌آوریم:

$$  frac { 1 } { R _ { eq }} = frac { 1 } { R _ 1 } + frac { 1 } { R _ 2 } + frac { 1 } { R _ 3 } + … + frac { 1 } {R _ n } $$

با استفاده از دو رابطه فوق، مقاومت‌ معادل مدار فوق را به‌دست می‌آوریم. برای محاسبه مقاومت معادل، از دورترین مقاومت‌ها نسبت به باتری شروع می‌کنیم. دو مقاومت ۳ و ۱۲ اهمی، دورترین مقاومت‌ها نسبت به باتری هستند. این دو مقاومت به صورت سری به یکدیگر وصل شده‌اند. بنابراین، مقاومت معادل آن‌ها برابر است با:

$$R_{ net, 3 , 12 } = 3 + 12 = 15 Omega $$

بنابراین، مدار داده شده را می‌توان به صورت زیر ساده کرد.

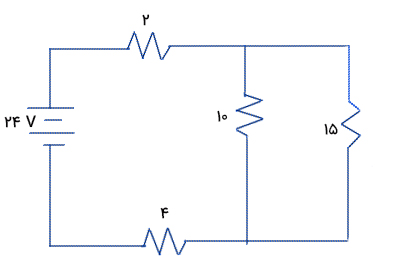
در ادامه، مقاومت معادلِ دو مقاومت ۱۰ و ۱۵ اهمی را که به صورت موازی با یکدیگر قرار گرفته‌اند، حساب می‌کنیم:

$$frac { 1 } { R _ T } = frac { 1 } { R _ 1 } + frac { 1 } { R _ 2 } = frac { 1 } { 10 } + frac { 1 } { 15 } = frac { 15 + 10 } { 150 } = frac { 25 } { 150 } \ R _ T = frac { 150 } { 25 } = 6 Omega$$

از این‌رو، مدار فوق باز به صورت زیر ساده‌تر می‌شود.

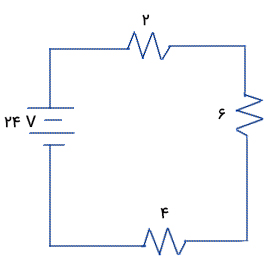
در پایان، سه مقاومتِ سری ۴، ۶ و ۲ اهمی باقی مانده‌اند که مقاومت معادل آن‌ها برابر ۱۲ اهم است. در نتیجه، مقاومت معادل ۵ مقاومت در مدار برابر مقاومت معادل ۱۲ اهمی است که به صورت سری به باتری ۲۴ ولتی وصل شده است. اکنون می‌توانیم جریان کل عبوری از مدار را به‌دست آوریم. 

$$V= I_ { net } R _ { net} \ 24 = I _ { net} times 12 \ I _ { net } = 2 A $$

از مقاومت‌های ۲ و ۴ اهمی نیز جریان کل، یعنی ۲ آمپر می‌گذرد. جریان دو آمپری با رسیدن به نقطه A نشان داده شده در تصویر زیر به دو جریان $$I_ 1 $$ و $$I _ 2 $$ تقسیم می‌شود. 

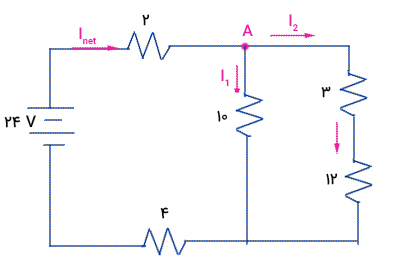
$$I _ { net } = I _ 1 + I _ 2 $$

برای به‌دست آوردن جریان $$I _ 1 $$ و $$I _ 2 $$ به معادله دیگری نیز نیاز داریم. برای نوشتن معادله دوم از مدار حلقه‌ای استفاده می‌کنیم. با شروع از نقطه A داریم:

$$V_ A – 3 I _ 2 – 12 I _ 2 + 10 I _ 1 = V _ A \ 3 I _2 +12 I _ 2 – 10 I _ 1 = 0 \ 15 I _ 2 = 10 I _ i \ 3I _ 2 = 2 I _ I $$

با حل دو معادله به‌دست آمده برای $$I _ 1 $$ و $$I _ 2 $$، مقدار آن‌ها به ترتیب برابرِ $$frac { 6 } { 5 } $$ و $$frac { 4 } { 5 } $$ آمپر به‌دست می‌آید. بنابراین، مقدار جریان عبوری از مقاومت ۱۲ اهمی برابر $$frac { 4 } { 5 } $$ آمپر خواهد بود. برای به‌دست آوردن ولتاژ دو سر این مقاومت نیز به صورت زیر عمل می‌کنیم:

$$V = IR = frac { 4 } { 5 } times 12 = 9.6 V$$

مثال چهارم

جریان عبوری از مقاومت ۱۰۰ اهمی برابر است با:

مشاهده جواب

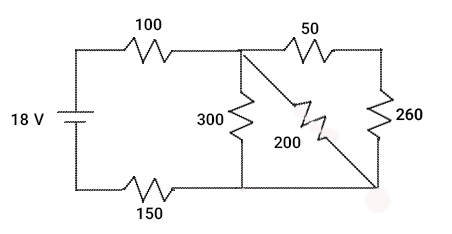
برای حل این مثال، ابتدا قطب‌های مثبت و منفی، باتری و گره‌های A و B و C را روی مدار مشخص می‌کنیم.

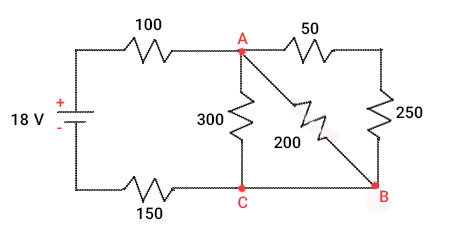
در ادامه، مقاومت معادل در این مدار را به‌دست می‌آوریم. مقاومت‌ها در مدار به صورت سری، موازی یا ترکیبی از این دو حالت در مدار الکتریکی بسته می‌شوند. مقاومت معادل چند مقاومت سری یا متوالی در مدار به صورت زیر به‌دست می‌آید:

$$ R _ { eq } = R _ 1 + R _ 2 + R _ 3 + … + R _ n $$

همچنین، مقاومت معادل چند مقاومت موازی را با استفاده از رابطه زیر به‌دست می‌آوریم:

$$  frac { 1 } { R _ { eq } } = frac { 1 } { R _ 1 } + frac { 1 } { R _ 2 } + frac { 1 } { R _ 3 } + … + frac { 1 } {R _ n } $$

برای به‌دست آوردن مقاومت معادل می‌توانیم مدار فوق را به صورت زیر ساده کنیم. برای انجام این کار از سمت چپ صفحه شروع و قطب مثبت باتری را در نقطه‌ای مشخص قرار می‌دهیم. طبق قرارداد، جریان از قطب مثبت باتری شروع و در قطب منفی آن تمام می‌شود. با حرکت از قطب مثبت، به مقاومت ۱۰۰ اهمی می‌رسیم. بنابراین، پس از نوشتن + به نشانه قطب مثبت باتری، مقاومت ۱۰۰ اهمی را رسم می‌کنیم. سپس به گره A می‌رسیم. 

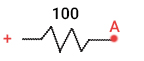
پس از گره A، جریان با سه مسیر با مقاومت‌های متفاوت روبرو می‌شود. مقاومت‌ها در هر مسیر به صورت موازی با یکدیگر قرار گرفته‌اند. این سه مسیر در مدار و پس از گره A را می‌توانیم به صورت ساده‌تر زیر رسم کنیم:

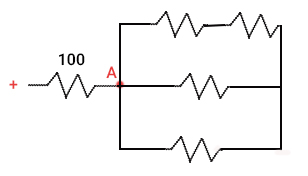
در پایان، مدار به شکل ساده شده زیر در می‌آید: 

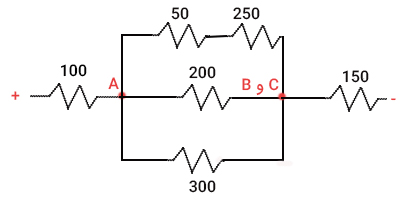
اکنون،‌ مقاومت معادل را به‌دست می‌آوریم. دو مقاومت ۵۰ و ۲۵۰ اهمی به صورت سری با یکدیگر قرار گرفته‌اند. مقاومت معادل آن‌ها برابر است با:

$$R_ { 50 , 250 } =  50 + 250 = 300 Omega $$

در نتیجه، مقاومت‌های ۵۰ و ۲۵۰ اهمی را می‌توانیم با مقاومت ۳۰۰ اهمی جایگزین کنیم. این مقاومت با دو مقاومت ۲۰۰ و ۳۰۰ اهمی به صورت موازی قرار گرفته‌اند. مقاومت معادل این سه مقاومت موازی برابر است با:

$$frac { 1 } { R _ { 300, 200, 300 }} = frac { 1 } { 200 } + frac { 1 } { 300 } + frac { 1 } { 300 } \ R _ { 300, 200, 300 } = 85.7 Omega $$

به راحتی می‌توانیم سه انشعاب موازی از مقاومت‌ها را با مقاومت معادل ۸۵/۶ اهمی جایگزین کنیم. در پایان، سه مقاومت ۱۰۰، ۸۵/۶ و ۱۵۰ اهمی داریم که به صورت سری در کنار یکدیگر قرار گرفته‌اند و مقاومت معادل آن‌ها برابر ۳۳۵/۵ اهم است. اکنون می‌توانیم به راحتی جریانِ کل عبوری از مدار را به‌دست آوریم. 

$$V = IR \ I = frac { V } { R } = frac { 18 } { 335..7 } = 0.054 A$$

جریان کل عبوری از مدار و در نتیجه جریان عبوری از مقاومت ۱۰۰ اهمی برابر ۰/۰۵۴ آمپر است. این جریان پس از رسیدن به گره A به سه جریان $$I_1 $$ و $$I _2 $$ و $$I _ 3 $$ شکسته می‌شود. با استفاده از قانون حلقه‌ها به راحتی می‌توانیم جریان عبوری از مقاومت‌های دیگر را نیز به‌دست آوریم. 

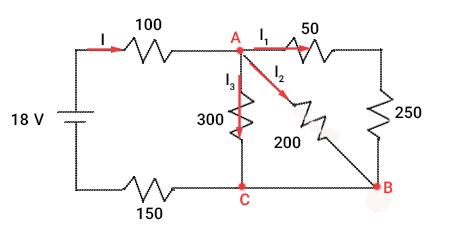
فرمول های فیزیک یازدهم فصل سوم

فرمول‌ های فیزیک یازدهم فصل سوم در جدول زیر به صورت خلاصه نوشته شده‌اند.

مبحث موردنظر	فرمول های فیزیک یازدهم فصل سوم
اندازه نیروی مغناطیسی وارد بر بار الکتریکی در حال حرکت	$$ F = | q | v B sin theta $$
نیروی مغناطیسی وارد بر سیم حامل جریان	$$  F = I l B sin theta  $$
اندازه میدان مغناطیسی در مرکز حلقه‌ای به شعاع R که جریان $$I $$ از آن می‌گذرد.	$$  B = frac { mu_0 I } { 2 R } $$
اندازه میدان مغناطیسی در مرکز پیچه مسطحی با N حلقه و به شعاع R که جریان $$I $$ از آن می‌گذرد.	$$ B = frac {mu _ 0 N I } { 2 R } $$
میدان مغناطیسی سیملوله ایده‌ال	$$ B = frac { mu _ 0 N I } { l }  $$

میدان مغناطیسی چیست؟

به طور حتم در دوران کودکی یکی از سرگرمی‌های شما بازی با آهن‌ربا و براده‌های آهن بوده است. براده‌های آهن توسط آهن‌ربا جذب می‌شوند. همان‌طور که بار الکتریکی در اطراف خود میدان الکتریکی ایجاد می‌کند، میدان مغناطیسی نیز در اطراف آهن‌ربا تشکیل و سبب جذب براده‌های آن توسط آهن‌ربا می‌شود.

خطوط میدان مغناطیسی در اطراف آهن‌ربا به صورت نشان داده شده در تصویر زیر است. همان‌طور که خطوط میدان الکتریکی از بار مثبت خارج و به بار منفی وارد می‌شوند، خطوط میدان مغناطیسی نیز از قطب شمال آهن‌ربا خارج و وارد قطب جنوب آن خواهند شد. به دو نکته در مورد خطوط میدان مغناطیسی باید توجه داشته باشیم:

• خطوط میدان مغناطیسی با عبور از داخل آهن‌ربا، حلقه بسته‌ای را تشکیل می‌دهند.
• این خطوط در نزدیکی قطب‌های آهن‌ربا به یکدیگر نزدیک‌تر هستند.

میدان مغناطیسی وارد شده بر ذره باردار متحرک در میدان مغناطیسی

بار الکتریکی q با سرعت $$v$$ در میدان مغناطیسی به بزرگی B حرکت می‌کند. نیروی وارد شده بر این ذره از طرف میدان مغناطیسی برابر است با:

$$ F = | q | v B sin theta $$

در رابطه فوق، $$theta$$ زاویه جهت حرکت بار و جهت میدان مغناطیسی B است. یکا یا واحد اندازه‌گیری میدان مغناطیسی، تسلا نام دارد:

$$1 T = 1 frac { N } { C. frac { m } { s } }  = frac { N } {A . m } $$

نیروی مغناطیسی وارد بر سیم حامل جریان

فرض کنید سیمی به طول $$l$$ در میدان مغناطیسی به بزرگی B قرار دارد. نیروی وارد شده بر این سیم از طرف میدان با استفاده از رابطه زیر به‌دست می‌آید:

$$  F = I l B sin theta  $$

$$theta $$ زاویه امتداد سیم با خطوط میدان مغناطیسی است.

میدان مغناطیسی در مرکز حلقه‌ای به شعاع R

فرض کنید حلقه‌ای به شعاع R در میدان مغناطیسی به بزرگی B قرار دارد. نیروی وارد شده بر این حلقه از طرف میدان برابر است با:

$$  B = frac { mu_0 I } { 2 R } $$

$$mu_0 $$ در رابطه فوق تراوایی مغناطیسی خلأ نام دارد و مقدار آن برابر $$ 4 pi times 10 ^ { -7 }  frac { T . m } { A } $$ است. اگر به جای یک حلقه، N حلقه داشته باشیم، میدان مغناطیسی به صورت $$ B = frac {mu _ 0 N I } { 2 R } $$ به‌دست می‌آید.

میدان مغناطیسی سیملوله ایده‌ال

در سیملوله ایده‌ال، قطر حلقه‌های سیم در مقایسه با طول آن، $$l$$، بسیار کوچک‌‌تر است. میدان مغناطیسی چنین سیملوله‌ای با استفاده از رابطه زیر به‌دست می‌آید:

$$ B = frac { mu _ 0 N I } { l }  $$

تا اینجا با فرمول های فیزیک یازدهم فصل سوم آشنا شدیم. در ادامه، برای درک بهتر این فرمول‌ها، تعدادی مثال با یکدیگر حل می‌کنیم.

مثال اول

فرض کنید پروتونی با سرعت $$5 times 10 ^ 3 $$ متر بر ثانیه، عمود بر میدان مغناطیسی حرکت می‌کند. اگر نیروی مغناظیسی وارد شده بر پروتون برابر $$1.2 times 10 ^ { – 18 } $$ نیوتن باشد، بزرگی میدان مغناطیسی برابر است با: 

$$1.5 times 10 ^ { -5 } frac { N. s } { C . m } $$

$$2.5 times 10 ^ { -3 } frac { N. s } { C . m } $$

$$1.5 times 10 ^ { -3 } frac { N. s } { C . m } $$

$$1.5 times 10 ^ { -2 } frac { N. s } { C . m } $$

مشاهده جواب

بار الکتریکی q با سرعت $$v$$ در میدان مغناطیسی به بزرگی B حرکت می‌کند. نیروی وارد شده بر این ذره از طرف میدان مغناطیسی برابر است با:

$$ F = | q | v B sin theta $$

در رابطه فوق، $$theta$$ زاویه جهت حرکت بار و جهت میدان مغناطیسی B است. در این مثال، بردار سرعت پروتون با جهت خطوط میدان، زاویه ۹۰ درجه می‌سازد. در نتیجه، نیروی مغناطیسی به صورت زیر نوشته می‌شود:

$$F= qvB sin ( 90 ) = q v B $$

معادله فوق را برحسب B مرتب می‌کنیم:

$$B = frac { F } { q v } $$

با قرار دادن مقدارهای داده شده در رابطه فوق،‌ مقدار B برابر $$1.5 times 10 ^ { -3 } frac { N. s } { C . m } $$ به‌دست می‌آید. 

مثال دوم

جریانی برابر ۳ آمپر از سیمی بسیار بلند می‌گذرد. میدان مغناطیسی در فاصله ۱/۵ سانتی‌متری از این سیم برابر است با:

$$1.27 times 10 ^ { -5 }  T$$

$$12.7 times 10 ^ { -5 }  T $$

$$1.27 times 10 ^ { -7 }  T$$

$$1.27 times 10 ^ { -2 }  T$$

مشاهده جواب

میدان مغناطیسی حاصل از سیمی بسیار بلند که جریانی برابر $$I$$ از آن عبور می‌کند با استفاده از رابطه $$frac { mu _ 0 I } { 2 pi r } $$ به‌دست می‌آید. $$mu_0 $$ در رابطه فوق تراوایی مغناطیسی خلأ نام دارد و مقدار آن برابر $$ 4 pi times 10 ^ { -7 }  frac { T . m } { A } $$ است. با قرار دادن مقدارهای داده شده در این رابطه مقدار میدان مغناطیسی را به‌دست می‌آوریم:

$$B = frac { mu _ 0 I } { 2 pi r } \ B = frac { 4 pi times 10 ^ { -7 } times 3 } { 2 pi times 0.015 } =  1.27 times 10 ^ { -5 }  T$$

مثال سوم

سیملوله‌ای با مقاومت R را به باتری ایده‌الی (بدون مقاومت) وصل می‌کنیم. اگر سیملوله را به سه قسمت مساوی تقسیم و یک‌سوم آن را دوباره به همان باتری وصل کنیم، نسبت میدان مغناطیسی درون سیملوله در این حالت نسبت به حالت قبل، برابر است با: 

میدان مغناطیسی درون سیملوله پس از تقسیم آن به سه قسمت مساوی، ۳ برابر می‌شود. 

میدان مغناطیسی درون سیملوله پس از تقسیم آن به سه قسمت مساوی، یک‌سوم برابر می‌شود. 

میدان مغناطیسی درون سیملوله پس از تقسیم آن به سه قسمت مساوی، بدون تغییر باقی می‌ماند. 

میدان مغناطیسی درون سیملوله پس از تقسیم آن به سه قسمت مساوی، نصف می‌شود. 

مشاهده جواب

مقاومت سیمی به طول $$l$$ و سطح مقطع A با استفاده از رابطه زیر به‌دست می‌آید:

$$R = rho frac { L } { A } $$

همان‌طور که در رابطه فوق مشاهده می‌کنیم، مقاومت با طول سیم رابطه مستقیم و با مساحت آن رابطه عکس دارد. با تقسیم سیملوله به سه قسمت مساوی، مقاومت الکتریکی هر یک از سه قسمت برابر $$frac { 1 } { 3 } $$ مقاومت اولیه سیملوله است. جریان با مقاومت رابطه عکس دارد. بنابراین، با کاهش مقاومت، جریان عبوری از سیملوله افزایش خواهد یافت. از آنجا که مقاومت یک‌سوم شده است، جریان عبوری، سه برابر می‌شود. 

$$B = frac { mu_0 N I } { L } \ B’ = frac { mu_ 0 N’ I’ } { L’ } \ B’ = frac { mu_ 0 frac { N } { 3 } times 3 I } { frac { L } { 3 } } = 3 B $$

مثال چهارم

کدام یک از گزینه‌های زیر نادرست است؟ 

با دور کردن آهن‌ربا از مواد پارامغناطیس، دوقطبی‌های مغناطیسی آن‌ها دوباره به صورت کاتوره‌ای قرار می‌گیرند. 

اتم‌های تشکیل‌دهنده مواد فرومغناطیس به طور ذاتی دارای دوقطبی مغناطیسی هستند. 

مواد دیامغناطیس را می‌توان با قرار دادن در میدان مغناطیسی خارجی، آهن‌ربا کرد. 

مواد فرومغناطیس نرم پس از حذف میدان مغناطیسی خارجی به سرعت خاصیت آهن‌ربایی خود را از دست می‌دهند. 

مشاهده جواب

از میان گزینه‌های داده شده، گزینه ۳ نادرست است. 

مثال پنجم

جریانی برابر ۲ آمپر از سیمی به طول ۸ سانتی‌متر می‌گذرد. اگر این سیم با جهت خطوط میدان مغناطیسی به بزرگی ۶ تسلا زاویه ۳۶ درجه ساخته باشد، نیروی وارد شده بر آن از طرف میدان برابر است با:

هیچ نیرویی بر سیم وارد نمی‌شود. 

مشاهده جواب

فرض کنید سیمی به طول $$l$$ در میدان مغناطیسی به بزرگی B قرار دارد. نیروی وارد شده بر این سیم از طرف میدان با استفاده از رابطه زیر به‌دست می‌آید:

$$  F = I l B sin theta  $$

$$theta $$ زاویه امتداد سیم با خطوط میدان مغناطیسی و در این مثال برابر ۳۶ درجه است. 

$$F = (2 A ) times ( 0.08 m ) times sin ( 36 ) \ F = 0.564 N$$

مثال ششم

ذره‌ای موازی میدان مغناطیسی یکنواختی حرکت می‌کند. کدام یک از عبارت‌های زیر درست است؟

ذره، حول نقطه‌ای در میدان مغناطیسی می‌چرخد. 

میدان مغناطیسی هیچ نیرویی بر ذره وارد نمی‌کند. 

در این حالت، میدان مغناطیسی بیشترین نیرو را بر ذره وارد می‌کند.

مشاهده جواب

بار الکتریکی q با سرعت $$v$$ در میدان مغناطیسی به بزرگی B حرکت می‌کند. نیروی وارد شده بر این ذره از طرف میدان مغناطیسی برابر است با:

$$ F = | q | v B sin theta $$

در رابطه فوق، $$theta$$ زاویه جهت حرکت بار و جهت میدان مغناطیسی B است. دو حالت خاص را در این رابطه بررسی می‌کنیم:

1. اگر ذره در جهت عمود بر میدان مغناطیسی حرکت کند، $$sin theta$$ برابر ۹۰ درجه و نیروی وارد شده بر ذره بیشینه خواهد بود.
2. اگر ذره موازی میدان مغناطیسی حرکت کند، $$sin theta$$ برابر صفر است. در نتیجه، هیچ نیرویی از طرف میدان بر ذره وارد نمی‌شود.

در این مثال، ذره موازی خطوط میدان حرکت می‌کند، بنابراین زاویه بین بردار سرعتِ ذره و خطوط میدان برابر صفر است. از این‌رو، میدان مغناطیسی هیچ نیرویی بر ذره وارد نمی‌کند. 

مثال هفتم

سیستمی ریلی به صورت نشان داده شده در تصویر زیر داخل میدان مغناطیسی قرار گرفته است. میله‌ای در تماس با ریل قرار دارد و با سرعت ۱۵ متر بر ثانیه به سمت راست حرکت می‌کند. فاصله دو ریل از یکدیگر برابر ۰/۰۸۷ متر است. محل تماس ریل و میله هیچ اصطکاکی ندارد و مقاومت میله و ریل‌ها نیز برابر صفر، اما مقاومت الکتریکی متصل به ریل برابر ۰/۰۰۵۵ اهم است. اگر بزرگی میدان مغناطیسی برابر ۰/۰۳۵ تسلا باشد، بزرگی و جهت نیروی خارجی لازم برای آن‌که میله با سرعت ثابت روی ریل حرکت کند، کدام است؟ 

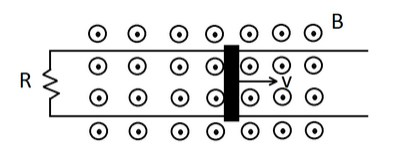
۸/۳ نیوتن به سمت چپ

۰/۰۲۵ نیوتن به سمت راست

۰/۰۲۵ نیوتن به سمت راست

۸/۳ نیوتن به سمت راست

مشاهده جواب

میله‌ به دلیل حرکت روی ریل همانند باتری عمل می‌کند که ولتاژ دو سر آن با استفاده از رابطع زیر به‌دست می‌آید:

$$V = Blv$$

همان‌طور که در تصویر مشاهده می‌کنید، مدار تشکیل شده از مقاومت، ریل و میله، مداری بسته است. بنابراین، جریانی با مقدار مشخص در آن جاری می‌شود:

$$I = frac { V } { R } = frac { B l v } { R } = frac { 0.035 T times 0.087 m times 15 frac { m } { s }}  { 0.0055 Omega } = 8.3 A $$

در این مدار ساده، جریان در همه جا یکسان است. بنابراین، جریان عبوری از سیم برابر ۸/۳ آمپر خواهد بود. میله به دلیل عبور این جریان، نیرویی برابر $$F$$ را احساس می‌کند. 

$$F = B  I l = 0.035 T times 8.3 A times 0.087 m = 0.025 N $$

جهت این نیرو با استفاده از قانون دست راست به سمت چپ به‌دست می‌آید. برای آن‌که میله با سرعت ثابت حرکت کند، نیروی خارجی وارد شده بر آن باید به سمت راست باشد. توان تلف شده در مقاومت را نیز می‌توانیم به راحتی به‌دست آوریم:

$$P = I ^ 2 R = 8.3 ^ 2 times 0.0055 = 0.38 W $$

این توان، برابر تولید شده توسط نیروی خارجی است:

$$P = F v = 0.025 times 15 = 0.38 W$$

فرمول های فیزیک یازدهم فصل چهارم

فرمول‌های فیزیک یازدهم فصل چهارم در جدول زیر به صورت خلاصه نوشته شده‌اند.

مبحث موردنظر	فرمول های فیزیک یازدهم فصل چهارم
شار مغناطیسی عبوری از پیچه‌ای به مساحت A که میدان مغناطیسی B قرار دارد.	$$ Phi = BA cos theta $$
قانون فاراده برای پیچه‌ای که از N دور سیم مشابه تشکیل شده است.	$$  xi _ { av } = – N frac { triangle Phi } { triangle t }  $$
جریان القایی متوسط در پیچه یا سیملوله‌ای به مقاومت R	$$  I _ { av} = frac { xi _ { av } } { R } $$
ضریب القاوری سیملوله‌ای ایده‌ال و بدون هسته به طول $$l$$، سطح مقطع A و N حلقه نزدیک به یکدیگر	$$ L = mu_0 frac { A N ^ 2 } { l }  $$
انرژی ذخیره شده در القاگر	$$U = frac { 1 } L I ^ 2 $$
شار عبوری از پیچه در زمان t	$$Phi = BA cos frac { 2 pi } { T } t$$
نیرو محرکه القایی در پیچه در زمان t	$$xi = xi _ m sin frac { 2 pi } { T } t$$
جریان القایی در پیچه در زمان t	$$I = I _ m sin frac { 2 pi } { T } t $$
رابطه بین ولتاژ و نعداد دورهای دو پیچه در مبدل آرمانی	$$frac { V _ 2 } { V _ 1 } = frac { N _ 2 } { N _ 1 } $$

در فصل‌های قبل با الکتریسیته و مغناطیس آشنا شدیم. الکتریسیته و مغناطیس در کنار یکدیگر مفهومی به نام الکترومغناطیس را تشکیل می‌دهند که نقش مهمی در زندگی روزمره ما ایفا می‌کند. در این فصل با مفاهیم پایه الکترومغناطیس آشنا می‌شویم.

قانون القای الکترومغناطیسی فاراده

پیچه‌ای را در میدان مغناطیسی نظر بگیرید. اگر:

• میدان مغناطیسی در محل پیچه تغییر کند،
• مساحت پیچه تغییر کند،
• پیچه در میدان مغناطیسی بچرخد،

جریان الکتریکی در آن القا می‌شود. القای جریان الکتریکی در پیچه به دلیل تغییر شار مغناطیسی عبوری از پیچه است. شار مغناطیسی کمیتی نرده‌ای است و مقدار آن برای پیچه‌ای به مساحت A که میدان مغناطیسی B قرار دارد برابر است با:

$$ Phi = BA cos theta $$

همان‌طور که در تصویر زیر مشاهده می‌کنید، زاویه $$theta $$ زاویه بین بردار میدان مغناطیسی و نیم‌خط عمود بر سطح حلقه است. واحد اندازه‌گیری شار مغناطیسی، وِبِر نام دارد.

 

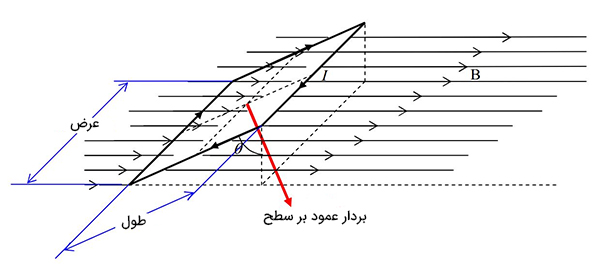
تا اینجا می‌دانیم تغییر شار مغناطیسی عبوری از پیچه یا سیملوله سبب تولید جریان القایی در مدار می‌شود. هرگاه شار مغناطیسی عبوری از مداری بسته تغییر کند، نیروی محرکه‌ای در آن القا خواهد شد. بزرگی این نیروی محرکه متناسب با تغییرات شار مغناطیسی نسبت به زمان است. نیرو محرکه القایی، $$xi_{av} $$ در سیملوله‌ یا پیچه‌ای با N دور سیم با استفاده از رابطه زیر به‌دست می‌آید:

$$xi_{ av } = – frac { triangle Phi} { triangle t } $$

اگر سیملوله یا پیچه مقاومت برابر R داشته باشد، جریان القایی متوسط عبوری از آن با استفاده از رابطه $$I _ { av } = frac { xi _ { a v } } { R } $$ محاسبه می‌شود.

قانون لنز چیست؟

جهت جریان القا شده در مدار یا پیچه به گونه‌ای است که با تغییر شار مغناطیسی مخالفت می‌کند. این موضوع از علامت منفی در رابطه $$xi_{ av } = – frac { triangle Phi} { triangle t } $$ می‌آید.

القاگر چیست؟

القاگر یا سیم‌پیچ یکی از قطعه‌های الکترونیکی لازم در مدارها است که از آن برای تولید میدان مغناطیسی و ذخیره انرژی در میدان استفاده می‌شود. فرض کنید القاگر و مقاومتی به صورت سری به باتری با ولتاژ دلخواه وصل شده‌اند. مقدار مقاومت در مدار می‌تواند تغییر کند. با تغییر مقاومت، چه اتفاقی رخ می‌دهد؟ با تغییر جریان عبوری در مدار، میدان مغناطیسی در القاگر و در نتیجه شار عبوری از آن تغییر خواهد کرد. با تغییر شار، نیروی محرکه‌ای در القاگر القا می‌شود که با تغییر جریان عبوری از القاگر مخالفت می‌کند. به این پدیده اثر خود-القاوری گفته می‌شود. ضریب القاوری سیملوله‌ای ایده‌ال و بدون هسته به طول $$l$$، سطح مقطع A و N حلقه نزدیک به یکدیگر با استفاده از رابطه زیر به‌دست می‌آید:

$$ L = mu_0 frac { A N ^ 2 } { l }  $$

همچنین، انرژی ذخیره شده در القاگر در القاگر را می‌توانیم با استفاده از رابطه $$U = frac { 1 } L I ^ 2 $$ به‌دست آوریم.

جریان متناوب چیست؟

اگر جهت جریان در مدار ثابت باشد و با گذر زمان تغییر نکند، جریان مستقیم و اگر جهت جریان به طور متناوب نسبت به زمان تغییر کند، جریان متناوب داریم. جریان متناوب چگونه تولید می‌شود؟ اثر القای الکترومغناطیسی. در بخش‌های قبل فهمیدیم شار عبوری از پیچه‌ای به مساحت A که در میدان مغناطیسی B قرار دارد با استفاده از رابطه $$ Phi = BA cos theta $$ به‌دست می‌آید. به طور معمول برای تغییر شار و تولید جریان القایی، زاویه $$theta $$ با چرخش حول محوری مشخص، تغییر داده می‌شود. هر چرخش کامل پیچه به دور محور برابر $$2 pi $$ رادیان است. بنابراین، شار عبوری از پیچه در زمان t با استفاده از رابطه زیر به‌دست می‌آید:

$$Phi = BA cos frac { 2 pi } { T } t$$

همچنین، نیروی محرکه القایی در پیچه در زمان t را می‌توانیم با استفاده از رابطه زیر به‌دست آوریم:

$$xi = xi _ m sin frac { 2 pi } { T } t$$

که در آن $$xi_m$$ بیشینه مقدار نیرو محرکه القایی در پیچه یا مدار است.

تا اینجا با فرمول های فیزیک یازدهم فصل چهارم آشنا شدیم. در ادامه، برای درک بهتر این فرمول‌ها، تعدادی مثال با یکدیگر حل می‌کنیم.

مثال اول

مبدلی از دو پیچه با تعداد دورها و ولتاژ‌های متفاوت تشکیل شده است. پیچه اولیه از ۱۵۰ دور و پیچه دوم از ۷۵۰۰۰ دور تشکیل شده است. اگر اختلاف پتانسیل ورودی بین دو سر پیچه اولیه برابر ۱۲۰ ولت باشد، اختلاف پتانسیل خروجی از پیچه ثانویه برابر است با:

مشاهده جواب

رابطه بین ولتاژ و تعداد دورهای دو پیچه در مبدل آرمانی با استفاده از رابطه زیر به‌دست می‌آید:

$$frac { V _ 2 } { V _ 1 } = frac { N _ 2 } { N _ 1 } $$

در این مثال:

$$N_ 1 = 150 \ V_ 1 or triangle V_ 1 = 120 V \ N_2 = 75000 \ V_ 2 or triangle V_ 2 = ? $$

با قرار دادن مقدارهای داده شده در رابطه $$frac { V _ 2 } { V _ 1 } = frac { N _ 2 } { N _ 1 } $$، مقدار ولتاژ خروجی را به‌دست می‌آوریم:

$$frac { V _ 2 } { 120 V } = frac { 75000 } { 150 } \ V_ 2 = frac { 75000 } { 150 } times 120 V = 500 times 120 V = 60000 V = 60 k V $$

مثال دوم

میدان مغناطیسی به بزرگی ۰/۰۵۵ تسلا از حلقه‌ای دایره‌ای به شعاع ۳/۱ سانتی‌متر می‌گذرد. اگر زاویه بین بردار عمود بر حلقه و جهت میدان مغناطیسی برابر ۱۶ درجه باشد، بزرگی شار مغناطیسی عبور از حلقه برابر است با: 

$$0.6 times 10 ^ { -4 } wb $$

$$1.6 times 10 ^ { -3 } wb $$

$$3.6 times 10 ^ { -4 } wb $$

$$1.6 times 10 ^ { -4 } wb$$

مشاهده جواب

شار مغناطیسی کمیتی نرده‌ای است و مقدار آن برای پیچه‌ای به مساحت A که میدان مغناطیسی B قرار دارد برابر است با:

$$ Phi = BA cos theta $$

زاویه $$theta $$ زاویه بین بردار میدان مغناطیسی و نیم‌خط عمود بر سطح حلقه است. در اینجا به جای پیچه، حلقه‌ای دایره‌ای به شعاع ۳/۱ سانتی‌متر در میدان مغناطیسی قرار گرفته است. بنابراین، برای محاسبه شار عبوری از حلقه ابتدا مساحت حلقه را به‌دست می‌آوریم. به این نکته توجه داشته باشید که برای محاسبه شار باید واحد مساحت برحسب مترمربع باشد. بنابراین، شعاع حلقه را به متر تبدیل می‌کنیم:

$$A = pi r ^ 2 = pi ( 3.1 times 10 ^ { – 2 } ) ^ 2 = 3.01 times 10 ^ { -3 } m ^ 2 $$

در نتیجه، شار عبوری از حلقه برابر است با:

$$ Phi = BA cos theta \ Phi = 0.055 times 3 times 10 ^ { -5 }  times cos ( 16 ) = 1.6 times 10 ^ { -4 } wb $$ 

مثال سوم

شار مغناطیسی عبوری از القاگری با ۳۸۵ دور بر متر و قطری برابر ۱۷/۰ سانتی‌متر، برابر $$1.28 times 10 ^ { -4 } T. m ^ 2 $$ است. جریان عبوری از این القاگر برابر است با:

مشاهده جواب

شار مغناطیسی با استفاده از رابطه $$Phi = BA $$ به‌دست می‌آید. در این مثال شار عبوری از القاگر و سطح مقطع آن را داریم. بنابراین، میدان مغناطیسی را می‌توانیم به صورت زیر محاسبه کنیم:

$$B = frac { Phi } { A } = frac { 1.28 times 10 ^ { -4 }} { pi ( 0.085 ) ^ 2 } \ B = 5.6 times 10 ^ { -3 } T $$

همچنین، در سیملوله ایده‌ال، قطر حلقه‌های سیم در مقایسه با طول آن، $$l$$، بسیار کوچک‌‌تر است. میدان مغناطیسی چنین سیملوله‌ای با استفاده از رابطه زیر به‌دست می‌آید:

$$ B = frac { mu _ 0 N I } { l }  $$

رابطه فوق را بر حسب جریان مرتب می‌کنیم:

$$ I = frac { B l } { mu _ 0  N } $$

با قرار دادن مقدارهای داده شده در رابطه جریان، مقدار آن را به‌دست می‌آوریم:

$$I = frac { 5.6 times 10 ^ { – 3 }  times 1 } { 4pi times 10 ^ { -7} times 385 }  \ I = 11.6 A $$

مثال چهارم

میدان مغناطیسی به بزرگی ۰/۴۵ تسلا بر مداری به شکل حلقه با ۴۳ دور سیم به شعاع ۱۵ سانتی‌متر عمود است. اگر میدان مغناطیسی در مدت زمان ۰/۱۲ ثانیه برابر صفر شود، بزرگی نیرو محرکه القایی چه مقدار است؟ 

مشاهده جواب

هرگاه شار مغناطیسی عبوری از مداری بسته تغییر کند، نیروی محرکه‌ای در آن القا خواهد شد. بزرگی این نیروی محرکه متناسب با تغییرات شار مغناطیسی نسبت به زمان است و با استفاده از رابطه زیر به‌دست می‌آید: 

$$|xi | = N | frac { triangle Phi } { triangle t }| $$

شار مغناطیسی را با استفاده از رابطه $$Phi = BA $$ محاسبه می‌کنیم. در این مثال، میدان مغناطیسی عبوری از حلقه در مدت زمان ۰/۱۲ ثانیه از ۰/۴۵ تسلا، صفر می‌شود. در نتیجه، تغییرات شار مغناطیسی عبوری از حلقه برابر است با:

$$triangle Phi = B_2A – B_1 A = 0 – 0.45 times A = – 0.45 times (pi times ( 0..15 ) ^ 2 )  \ triangle Phi =  = – 3.1 times 10 ^ { – 2 } wb$$

نیرو محرکه القا شده در مدت زمان ۰/۱۲ ثانیه برابر است با: 

$$|xi | = N | frac { triangle Phi } { triangle t }| \ = 53 times | frac { 3.1 times { 10 ^ { -2 }}} { 0.12 } | \ | xi | = 13.7 V$$

مثال پنجم

نمودار شار مغناطیسی عبوری از سیم‌پیچی به صورت تابعی از زمان در تصویر زیر نشان داده شده است. در چه زمانی اندازه شار مغناطیسی بیشینه و در چه زمانی نیروی محرکه القایی برابر صفر است؟ 

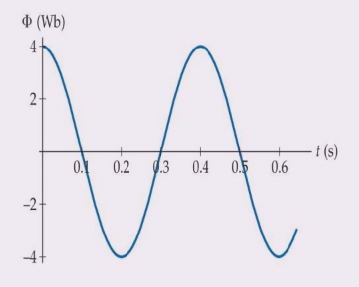
شار مغناطیسی و نیروی محرکه القایی در زمان‌های صفر، ۰/۲، ۰/۴ و ۰/۶ ثانیه به ترتیب بیشینه و صفر هستند. 

شار مغناطیسی و نیروی محرکه القایی در زمان‌های ۰/۱، ۰/۳ و ۰/۵ ثانیه به ترتیب بیشینه و صفر هستند. 

شار مغناطیسی در زمان‌های ۰/۱، ۰/۳ و ۰/۵ بیشینه و نیروی محرکه القایی در زمان‌های صفر، ۰/۲، ۰/۴ و ۰/۶ برابر صفر هستند. 

شار مغناطیسی در زمان‌های صفر، ۰/۲، ۰/۴ و ۰/۶ بیشینه و نیروی محرکه القایی در زمان‌های ۰/۱، ۰/۳ و ۰/۵ برابر صفر هستند. 

مشاهده جواب

در این مثال نمودار شار مغناطیسی برحسب زمان داده شده است. در قسمت اول می‌خواهیم بدانیم شار مغناطیسی گذرنده از سیم‌پیچ در چه زمانی بیشینه می‌شود. برای پاسخ به این پرسش، تنها کافی است به نمودار شار برحسب زمان دقت کنیم. نمودار از تعدادی قله و دره تشکیل شده است. قله‌ها مقدار مثبتِ بیشینه شار عبوری از سیم‌پیچ را نشان می‌دهند. همان‌طور که در نمودار داده شده مشاهده می‌کنید، نخستین قله مثبت در زمان صفر ثانیه رخ داده و مقدار شار عبوری در این زمان برابر ۴ وبر است. اگر علامت شار مهم نباشد، بیشینه بعدی در زمان ۰/۲ ثانیه رخ می‌دهد. 

در ادامه می‌خواهیم بدانیم نیروی محرکه القا شده در چه زمانی برابر صفر است. هرگاه شار مغناطیسی عبوری از مداری بسته تغییر کند، نیروی محرکه‌ای در آن القا خواهد شد. بزرگی این نیروی محرکه متناسب با تغییرات شار مغناطیسی نسبت به زمان است. نیرو محرکه القایی، $$xi_{av} $$ در سیملوله‌ یا پیچه‌ای با N دور سیم با استفاده از رابطه زیر به‌دست می‌آید:

$$xi_{ av } = – frac { triangle Phi} { triangle t } $$

رابطه فوق بدان معنا است که هرگاه شیب نمودار شار برحسب زمان برابر صفر باشد، مقدار نیروی محرکه القایی نیز برابر صفر خواهد بود. شیب نمودار در قله‌ها و دره‌ها، یعنی زمان‌های صفر، ۰/۲، ۰/۴ و ۰/۶ ثانیه برابر صفر و در نتیجه، نیروی محرکه القایی نیز در این زمان‌ها، صفر است. 

مثال ششم

تصویر زیر، شار مغناطیسی گذرنده از سیم‌پیچی تک‌حلقه‌ای برحسب زمان را نشان می‌دهد. نیروی محرکه القایی در زمان ۰/۰۵ و ۰/۱۵ ثانیه به ترتیب برابر است با:

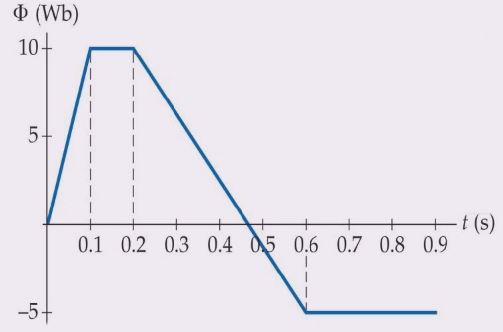
نیروی محرکه القایی در زمان ۰/۰۵ ثانیه برابر ۱۰۰- ولت و در زمان ۰/۵ ثانیه برابر صفر است. 

نیروی محرکه القایی در زمان ۰/۰۵ ثانیه برابر صفر ولت و در زمان ۰/۵ ثانیه برابر ۱۰۰- ولت است. 

نیروی محرکه القایی در زمان ۰/۰۵ ثانیه و ۰/۵ ثانیه برابر ۱۰۰- ولت است. 

نیروی محرکه القایی در زمان ۰/۰۵ ثانیه و ۰/۵ ثانیه برابر صفر است. 

مشاهده جواب

می‌دانیم هرگاه شار مغناطیسی عبوری از مداری بسته تغییر کند، نیروی محرکه‌ای در آن القا خواهد شد. بزرگی این نیروی محرکه متناسب با تغییرات شار مغناطیسی نسبت به زمان است. نیرو محرکه القایی، $$xi_{av} $$ در سیملوله‌ یا پیچه‌ای با N دور سیم با استفاده از رابطه زیر به‌دست می‌آید:

$$xi_{ av } = – frac { triangle Phi} { triangle t } $$

رابطه فوق بدان معنا است که برای محاسبه نیروی محرکه متوسط در بازه زمانی داده شده باید شیب نمودار شار برحسب زمان را در آن بازه زمانی به‌دست آوریم. برای محاسبه نیروی محرکه القایی در زمان ۰/۰۵ ثانیه باید به نمودار شار برحسب زمان مراجعه کنیم. زمان ۰/۰۵ ثانیه و محدوده آن در تصویر زیر نشان داده شده است.

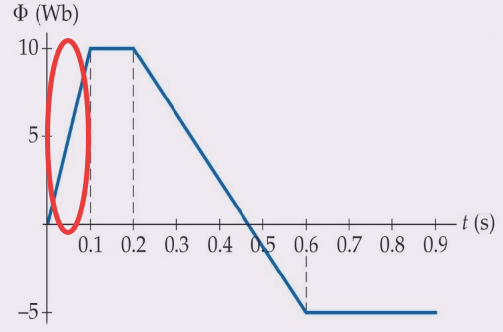
نمودار شار زمان در این بازه، خطی مستقیم با شیب مثبت و ثابت است. بنابراین، با به‌دست آوردن شیب این خط، به راحتی می‌توانیم نیروی محرکه القایی در زمان ۰/۰۵ ثانیه را محاسبه کنیم. برای محاسبه شیب این خط، دو نقطه $$( 0 , 0 ) $$ و $$( 0.1  ,  10 ) $$ را در نظر می‌گیریم و شیبِ خط را به‌دست می‌آوریم:

$$frac { 10 – 0 } { 0.1 – 0 } = frac { 10 } { 0.1} = 100 / V  $$

از آنجا که $$xi_{ av } = – frac { triangle Phi} { triangle t } $$، نیرو محرکه القایی برابر ۱۰۰- ولت خواهد بود. در ادامه، نیروی محرکه را در زمان ۰/۱۵ ثانیه به‌دست می‌آوریم. به طور مشابه، برای محاسبه نیروی محرکه القایی در زمان ۰/۱۵ ثانیه باید به نمودار شار برحسب زمان مراجعه کنیم. زمان ۰/۱۵ ثانیه و محدوده آن در تصویر زیر نشان داده شده است.

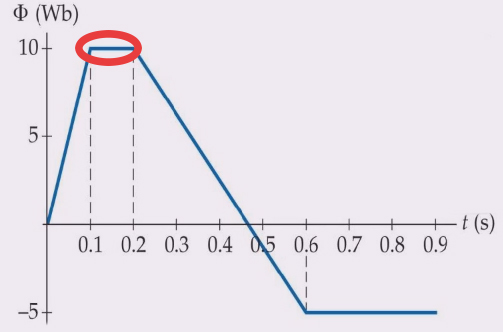
نمودار شار برحسب زمان در این بازه، خطی افقی و مستقیم با شیب صفر است. بنابراین، نیروی محرکه القایی در زمان ۰/۱۵ ثانیه برابر صفر خواهد بود. 

مثال هفتم

جریانی با مقدار مشخص از سیم بلند و مستقیمی می‌گذرد، اگر سیم بر صفحه سیم‌پیچ عمود باشد، کدام یک از گزینه‌های زیر صحیح است؟ 

اگر جریان گذرنده از سیم ثابت باشد، نیروی محرکه القا شده در سیم‌پیچ مخالف صفر است. 

اگر جریان گذرنده از سیم ثابت باشد، نیروی محرکه القا شده در سیم‌پیچ برابر صفر است. 

اگر جریان عبوری از سیم افزایش یابد، نیروی محرکه القایی از سیم‌پیچ مخالف صفر خواهد بود. 

مشاهده جواب

گزینه ۲ پاسخ صحیح است. 

جمع‌بندی

در این مطلب از مجله فرادرس، با فرمول های فیزیک یازدهم آشنا شدیم. فیزیک یازدهم در رشته‌های تجربی و ریاضی‌فیزیک به ترتیب از سه و چهار فصل تشکیل شده است. فرمول‌های هر فصل ابتدا به صورت خلاصه توضیح داده‌ و در ادامه، برای درک بهتر فرمول‌ها، تعدادی مسئله مرتبط با آن‌ها حل شد.