معادله درجه دوم یکی از مباحث اصولی در ریاضیات است که در علوم مهندسی کاربرد فراوانی دارد. در این مطلب از مجله فرادرس به معرفی معادله درجه دوم و انواع روش‌های حل آن می‌پردازیم. یکی از روش‌های جالب برای حل معادله درجه دوم، روش مربع کامل است که در آن سعی می‌کنیم معادله درجه دوم را با استفاده از اتحاد مربع دو جمله‌ای حل کنیم. در ادامه این روش را با چند مثال توضیح خواهیم داد. اگر به این موضوع علاقه‌مند هستید تا انتها این مطلب را مطالعه کنید.

معرفی معادله درجه دوم

معادله درجه دوم یک عبارت جبری است که حداکثر توان (درجه) متغیر آن دو است که شکل کلی و استاندارد آن به صورت زیر است:

$$ax^2+bx+c=0$$

عوامل به کار رفته در آن به شرح زیر است:

• x: متغیر معادله
• b، ‌a و c: ضریب‌های ثابت متغیر هستند

اگر معادله درجه دوم به شکل دیگری بود می‌توان با استفاده از جبر آن را به شکل استاندارد تبدیل کرد.

روش‌های حل معادله درجه دوم

چندین روش برای حل معادله درجه دوم وجود دارد که رایج‌ترین آن‌ها عبارتند از:

• حل معادله درجه دو به روش دلتا
• حل معادله درجه دو به روش مربع کامل
• حل معادله درجه دو به روش هندسی
• حل معادله درجه دو به روش تجزیه
• حل معادله درجه دو به روش ریشه‌گیری

در این مطلب به بررسی جامع حل معادله درجه دوم به روش مربع کامل می‌پردازیم.

حل معادله درجه دوم به روش مربع کامل

روش «مربع کامل» (Complete The Square) یک شیوه ساده و ابتکاری برای حل معادله درجه دوم است. در این روش سعی می‌کنیم که معادله را به اتحاد مجموع دو جمله تبدیل کنیم و در پایان باید از طرفین معادله جذر بگیریم. نکته مهم در این روش این است که ضریب $$x^2$$ باید یک باشد.

بیان هندسی روش مربع کامل در حل معادله درجه دوم

برای درک بهتر این موضوع، روش مربع کامل را با شکل زیر توضیح می‌دهیم. فرض کنید که معادله استاندارد درجه دوم یعنی $$ax^2+bx+c=0$$ را داریم، (در غیر این صورت باید به شکل استاندارد تبدیل کنیم). ضریب $$x^2$$ باید یک باشد. مطابق شکل زیر یک مربع در نظر می‌گیریم که اندازه ضلع آن x و مساحت آن $$x^2$$ است همچنین مستطیل که اضلاع آن x و b است و مساحت آن $$btimes x$$ است.

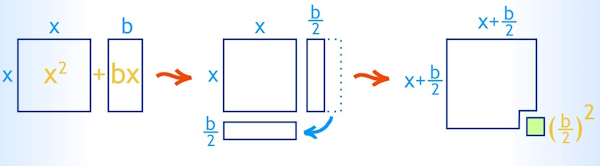
اکنون مستطیل را به دو قسمت مساوی تقسیم می‌کنیم به طوری‌که عرض هر قسمت برابر $$frac{b}{2}$$ باشد. نیمی از مستطیل را به سمت راست مربع و نیمی دیگر را به پایین مربع وصل می‌کنیم.

برای آن‌که مربع جدید کامل شود به یک مربع کوچک در گوشه سمت راست پایین به مساحت $$(frac{b}{2})^2$$ نیاز داریم. اگر مساحت این دو شکل را به صورت جبری بنویسیم خواهیم داشت:

$$x^2+bx+(frac{b}{2})^2=(x+frac{b}{2})^2$$

در نتیجه با اضافه کردن $$(frac{b}{2})^2$$ مربع کامل می‌شود. بنابراین حل معادله درجه اول $$(x+frac{b}{2})^2$$ آسان‌تر از حل معادله درجه دوم خواهد بود.

بنابراین مراحل حل معادله درجه دوم به روش مربع کامل به شرح زیر است:

1. تمام جملات معادله را بر ضریب $$x^2$$ یعنی a تقسیم می‌کنیم.
2. جمله $$(frac{c}{a})$$ را به سمت راست معادله انتقال می‌دهیم.
3. ضریب x یعنی b را باید بر ۲ تقسیم و سپس به توان ۲ رسانده و آن را در طرفین معادله اضافه کنیم.
4. سمت چپ معادله به شکل یک اتحاد مربع کامل تبدیل می‌شود.
5. از طرفین معادله جذر می‌گیریم.

برای درک بهتر این موضوع به مثال‌های زیر توجه کنید:

مثال اول حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$x^2+6x+7=0$$ را به روش مربع کامل حل کنیم.

پاسخ:

معادله به شکل استاندارد هست همچنین ضریب $$x^2$$  یک است، ۷ را به سمت راست معادله می‌بریم در مرحله بعد ضریب x را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+6x+(frac{6}{2})^2=-7+(frac{6}{2})^2$$

سپس سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x+3)^2=2$$

در نتیجه جواب معادله به صورت زیر خواهد بود:

$$x=sqrt{2}-3$$

$$x=-sqrt{2}-3$$

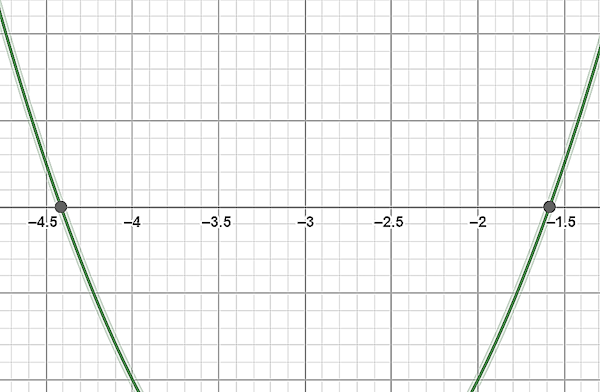
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و یکسان دارد.

مثال دوم حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$x^2+4x+1=0$$ را به روش مربع کامل حل کنیم.

پاسخ:

در این مثال نیز معادله به شکل استاندارد هست همچنین ضریب $$x^2$$  یک است، ۱ را به سمت راست معادله می‌بریم در مرحله بعد ضریب x را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+4x+(frac{4}{2})^2=-1+(frac{4}{2})^2$$

سپس سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x+2)^2=3$$

بنابراین پاسخ معادله به صورت زیر خواهد بود:

$$x=pmsqrt{3}-2$$

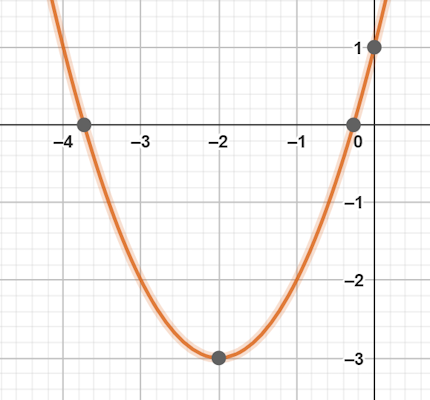
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز دارد.

مثال سوم حل معادله درجه دوم به روش مربع کامل

معادله $$x^2-(frac{3}{2})x=0$$ را می‌خواهیم به روش مربع کامل حل کنیم.

پاسخ:

در اینجا ضریب $$x^2$$  یک است اما عدد ثابت یعنی c نداریم پس ضریب x  یعنی $$(frac{3}{2})$$ را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+(frac{3}{2})x+(frac{3}{4})^2=(frac{3}{4})^2$$

در مرحله بعد سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$frac{1}{16}(4x+3)^2=frac{9}{16}$$

$$(4x+3)^2=frac{1}{2} \ 4x=-frac{5}{2}$$

در نتیجه جواب معادله به صورت زیر خواهد بود:

$$x=0$$

$$x=frac{3}{2}$$

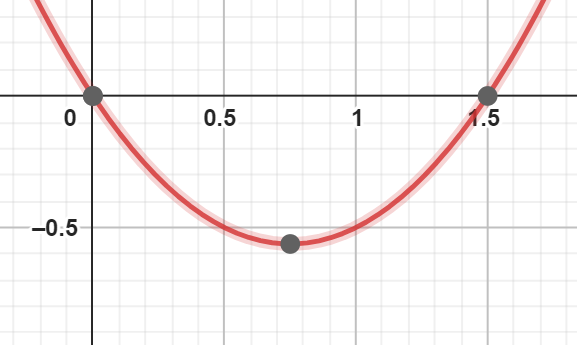
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و یکسان دارد.

مثال چهارم حل معادله درجه دوم به روش مربع کامل

معادله $$x^2+6x=-2$$ را به روش مربع کامل حل خواهیم کرد.

پاسخ:

در این مثال ضریب $$x^2$$  یک است و عدد ثابت یعنی c در سمت راست معادله قرار دارد بنابراین ضریب x  یعنی ۶ را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+6x+(frac{6}{2})^2=(frac{6}{2})^2 = 7$$

سپس سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x+3)^2=7 \ x+3=pmsqrt{7}$$

بنابراین جواب معادله به صورت زیر خواهد شد:

$$x=pmsqrt{7}-3$$

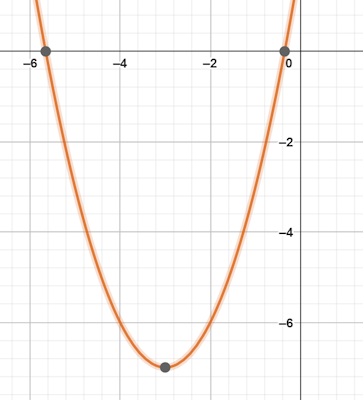
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز دارد.

مثال پنجم حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$x^2-10x=-12$$ را به روش مربع کامل حل کنیم.

پاسخ:

مانند مثال قبل شکل معادله استاندارد است و عدد ثابت یعنی c در سمت راست معادله قرار دارد پس ضریب x  یعنی ۱۰- را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2-10x+25=-12+25=13$$

در مرحله بعد سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x-5)^2=13 \ x-5=pmsqrt{13}$$

در نتیجه جواب معادله به صورت زیر خواهد شد:

$$x=pmsqrt{13}+5$$

با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز دارد.

مثال ششم حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$x^2-8x=5$$ را به روش مربع کامل حل کنیم.

پاسخ:

ضریب $$x^2$$  یک است. ضریب x  یعنی ۱۰- را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2-8x+16=21$$

سپس سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x-4)^2=21 $$

بنابراین جواب معادله به صورت زیر خواهد شد:

$$x=pmsqrt{21}+4$$

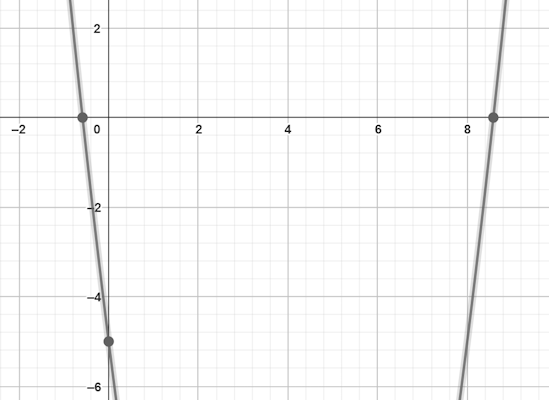
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز دارد.

مثال هفتم حل معادله درجه دوم به روش مربع کامل

معادله $$x^2+3x=-frac{1}{4}$$ را می‌خواهیم به روش مربع کامل حل کنیم.

پاسخ:

در این مثال ضریب $$x^2$$  یک است. ضریب x یعنی ۳ را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+3x+(frac{9}{4})=-frac{1}{4}+(frac{9}{4})=2$$

در نتیجه سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x+frac{3}{2})^2=2$$

بنابراین جواب معادله به صورت زیر خواهد شد:

$$x=pmsqrt{2}-frac{3}{2}$$

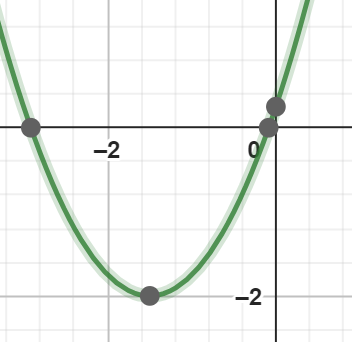
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز دارد.

مثال هشتم حل معادله درجه دوم به روش مربع کامل

معادله $$3x^2-36x=-42$$ را به روش مربع کامل حل خواهیم کرد.

پاسخ:

در این مثال ضریب $$x^2$$  سه است پس ابتدا باید کل معادله را تقسیم بر ۳ کنیم.

$$x^2-12x=-14$$

سپس ضریب x  یعنی ۱۲- را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2-12x+(frac{-12}{2})^2=(frac{-12}{2})^2-14 = 22$$

در مرحله بعد سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x-6)^2=22$$

جواب معادله به صورت زیر است:

$$x=pmsqrt{22}+6$$

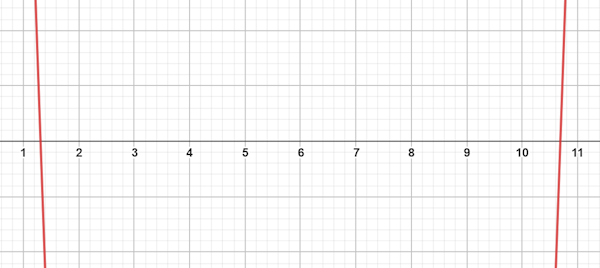
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز دارد.

مثال نهم حل معادله درجه دوم به روش مربع کامل

معادله $$4x^2+20x-3=0$$ را به روش مربع کامل حل خواهیم کرد.

پاسخ:

در این مثال ضریب $$x^2$$  چهار است پس ابتدا باید کل معادله را تقسیم بر ۴ کنیم.

$$x^2+5x=frac{3}{4}$$

در ادامه ضریب x  یعنی ۵ را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+5x+(frac{5}{2})^2=(frac{5}{2})^2+frac{3}{4} = 7$$

سپس سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x+frac{5}{2})^2=7$$

بنابراین جواب معادله به صورت زیر است:

$$x=pmsqrt{7}-frac{5}{2}$$

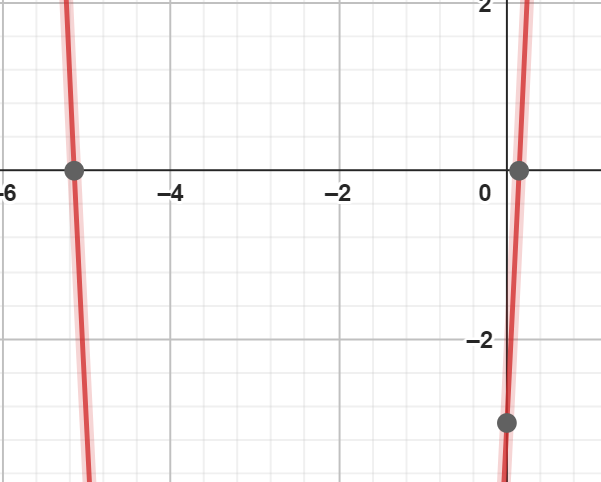
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز دارد.

مثال دهم حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$x^2-9x+14=0$$ را به روش مربع کامل حل کنیم.

پاسخ:

در این مثال ضریب $$x^2$$  یک است و باید ضریب x  یعنی ۹- را تقسیم بر ۲ کنیم و به توان ۲ برسانیم سپس آن را به طرفین معادله اضافه کنیم.

$$x^2-9x+(frac{-9}{2})^2=(frac{-9}{2})^2-14 =frac{25}{4}$$

در ادامه سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x-frac{9}{2})^2=frac{25}{4}$$

پس از جذر گرفتن از طرفین، جواب معادله به صورت زیر است:

$$x=pmfrac{5}{2}+frac{9}{2}$$

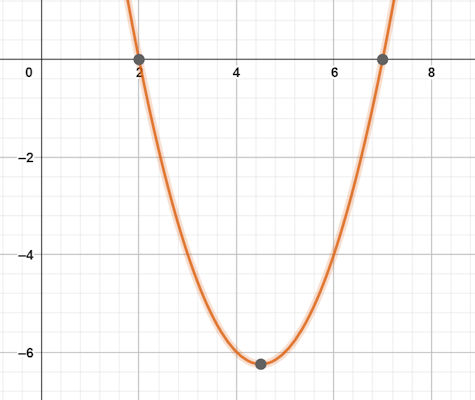
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز یعنی ۷ و ۲ دارد.

مثال یازدهم حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$x^2+8x+2=22$$ را به روش مربع کامل حل کنیم.

پاسخ:

در اینجا ضریب $$x^2$$  یک است در ادامه ۲- را از طرفین کسر می‌کنیم سپس ضریب $$x$$ یعنی ۸ را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+8x+(frac{8}{2})^2=(frac{8}{2})^2+20 $$

در مرحله بعد سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x+4)^2=36$$

پس از جذر گرفتن از طرفین، جواب معادله به صورت زیر خواهد بود:

$$x=-10,x=2$$

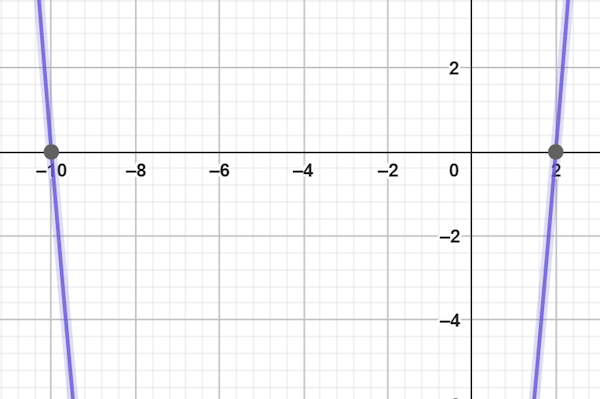
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز یعنی ۱۰- و ۲ دارد.

مثال دوازدهم حل معادله درجه دوم به روش مربع کامل

معادله $$6x^2+69x-36=0$$ را می‌خواهیم به روش مربع کامل حل کنیم.

پاسخ:

در اینجا ضریب $$x^2$$  شش است پس باید طرفین را بر ۶ تقسیم کنیم.

$$x^2+frac{23}{2}x=6$$

در ادامه ضریب x یعنی $$frac{23}{2}$$ را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+frac{23}{2}x+(frac{23}{4})^2=(frac{23}{4})^2+6 =frac{529}{16}$$

در مرحله بعد سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$sqrt{(x+frac{23}{4})^2}=pm sqrt{frac{625}{16}}$$

بعد از جذر گرفتن از طرفین، جواب معادله به صورت زیر خواهد بود:

$$x=pmfrac{25}{4}-frac{23}{4}$$

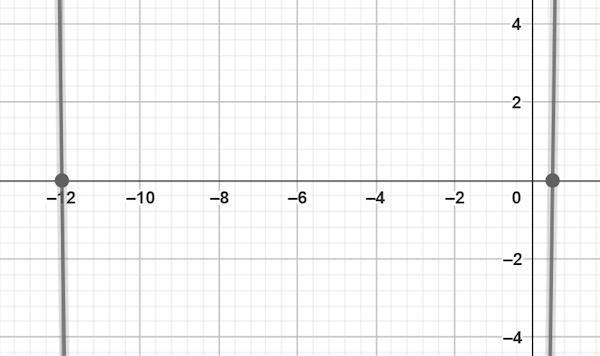
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز یعنی ۱۲- و ۰٫۵ دارد.

مثال سیزدهم حل معادله درجه دوم به روش مربع کامل

معادله $$-x^2+4x−5=0$$ را می‌خواهیم به روش مربع کامل حل خواهیم کرد که در ادامه این مثال از مجله فرادرس به آن می‌پردازیم.

پاسخ:

در این مثال ضریب $$x^2$$، ۱-  است. ضریب x یعنی ۴ را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+4x+(frac{4}{2})^2=(frac{4}{2})^2+5$$

در مرحله بعد سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x+2)^2=9$$

بعد از جذر گرفتن از طرفین، جواب معادله به صورت زیر خواهد بود:

$$(x+2)^2=9 Rightarrow x=1 , x=-5$$

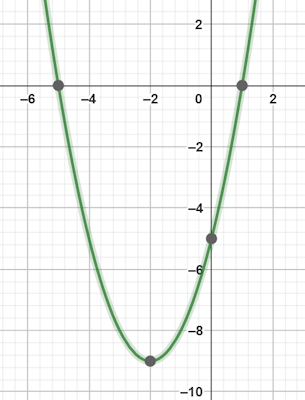
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز یعنی۱ و ۵- دارد.

مثال چهاردهم حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$x^2+6x+9=0$$ را به روش مربع کامل حل کنیم.

پاسخ:

در اینجا ضریب $$x^2$$  یک است پس در ادامه ضریب x یعنی ۶ را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2+6x+(frac{6}{2})^2=(frac{6}{2})^2-9 =0$$

سپس سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x+3)^2=0$$

در مرحله بعد از جذر گرفتن از طرفین، جواب معادله به صورت زیر خواهد بود:

$$x=-3$$

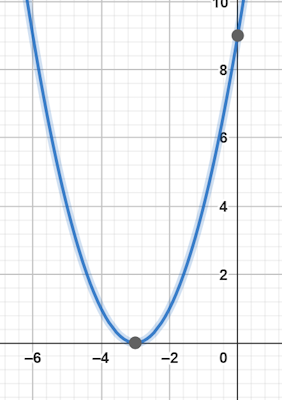
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و یکسان یعنی ۳-  دارد.

مثال پانزدهم حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$2x^2-4x-3=0$$ را به روش مربع کامل حل کنیم.

پاسخ:

در اینجا ضریب $$x^2$$، دو است در نتیجه باید طرفین را بر ۲ تقسیم کنیم.

$$x^2-2x=frac{3}{2}$$

سپس ضریب x یعنی ۲- را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2-2x+(frac{2}{2})^2=(frac{2}{2})^2+frac{3}{2}=frac{5}{2}$$

در ادامه سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x-1)^2=frac{5}{2}$$

بنابراین بعد از جذر گرفتن از طرفین، جواب معادله به صورت زیر خواهد بود:

$$x=1pmsqrt{frac{5}{2}}$$

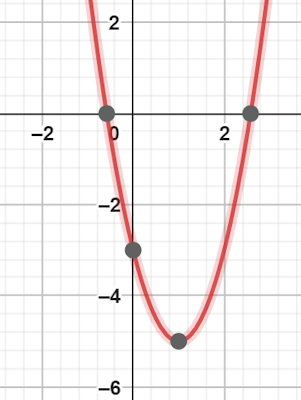
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز دارد.

مثال شانزدهم حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$3x^2-12x+5=0$$ را به روش مربع کامل حل کنیم.

پاسخ:

در اینجا ضریب $$x^2$$، سه است در نتیجه باید طرفین را بر ۳ تقسیم کنیم.

$$x^2-4x=frac{-5}{3}$$

در ادامه ضریب x یعنی ۴- را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم سپس آن را به طرفین معادله اضافه می‌کنیم.

$$x^2-4x+(frac{4}{2})^2=(frac{4}{2})^2+frac{5}{3}=frac{7}{3}$$

سپس سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x-2)^2=frac{7}{3}$$

در نتیجه بعد از جذر گرفتن از طرفین، جواب معادله به صورت زیر خواهد بود:

$$x=2pmsqrt{frac{7}{3}}$$

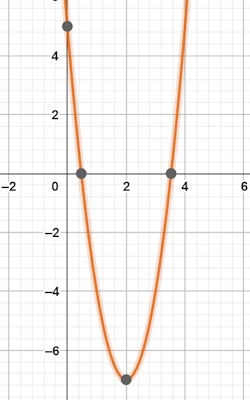
با توجه به جواب متوجه می‌شویم که معادله درجه دوم، دو ریشه حقیقی و متمایز دارد.

مثال هفدهم حل معادله درجه دوم به روش مربع کامل

معادله $$4x^2 +8x−5=0$$ را می‌خواهیم به دو روش مربع کامل و حاصلضرب دو چندجمله‌ای حل کنیم.

پاسخ:

در روش اول ابتدا این معادله را به شکل حاصلضرب دو چند جمله‌ای می‌نویسیم.

$$4x^2 +8x−5= (2x-1)(2x+5)$$

اکنون می‌توانیم هر کدام از عبارت‌های سمت چپ را جداگانه برابر صفر قرار دهیم و معادله درجه یک را حل کنیم.

$$(2x-1)=0 Rightarrow x=frac{1}{2}$$

$$(2x+5)=0 Rightarrow x=-frac{1}{5}$$

در روش دوم همین معادله را با مربع کامل حل می‌کنیم. در اینجا ضریب $$x^2$$، چهار است در نتیجه باید طرفین را بر ۴ تقسیم کنیم.

$$x^2 +2x−frac{5}{4}=0$$

سپس ضریب x یعنی ۲ را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم و آن را به طرفین معادله اضافه می‌کنیم.

$$x^2 +2x+(frac{2}{2})^2=frac{5}{4}+(frac{2}{2})^2$$

در نتیجه سمت چپ معادله را به شکل اتحاد مربع کامل تبدیل می‌کنیم:

$$(x+1)^2=frac{9}{4}$$

بنابراین بعد از جذر گرفتن از طرفین، جواب معادله به صورت زیر خواهد بود:

$$x+1=pm frac{3}{2} Rightarrow x=frac{1}{2} , x=-frac{5}{2}$$

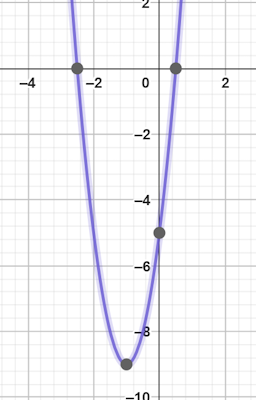
همان‌طور که مشاهده شده جواب معادله در هر دو روش یکسان است.

مثال هجدهم حل معادله درجه دوم به روش مربع کامل

می‌خواهیم معادله $$2x^2 −4x−7=0$$ را به روش مربع کامل حل کنیم.

پاسخ:

چون ضریب $$x^2$$، دو است در نتیجه باید طرفین را بر ۲ تقسیم کنیم.

$$x^2 −2x−frac{7}{2}=0$$

در مرحله بعد ضریب x یعنی ۲- را تقسیم بر ۲ می‌کنیم و به توان ۲ می‌رسانیم و آن را به طرفین معادله اضافه می‌کنیم.

$$x^2 -2x+(frac{-2}{2})^2=frac{7}{2}+(frac{-2}{2})^2$$

سمت چپ معادله به شکل اتحاد مربع کامل تبدیل می‌شود:

$$(x-1)^2=frac{9}{2} $$

بعد از جذر گرفتن از طرفین، جواب معادله به صورت زیر خواهد بود:

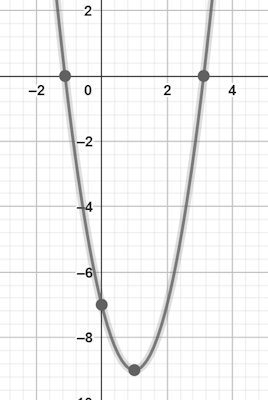
$$x-1=pm frac{3}{sqrt{2}} Rightarrow x=1+frac{3}{sqrt{2}} , x=1-frac{3}{sqrt{2}}$$

تمرین حل معادله درجه دوم با روش مربع کامل

در ادامه تمرین‌هایی برای افزایش مهارت در حل معادله درجه دوم با روش مربع کامل ارائه شده است.