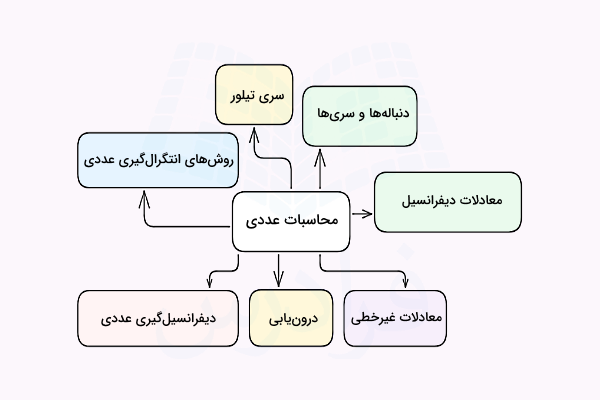
محاسبات عددی که با عنوان Numerical Analysis یا Numerical Methods نیز شناخته میشود، شاخهای از علم ریاضیات است که در آن به دنبال تحلیل و بررسی روشهای عددی حل مسائل مختلف در حوزه علوم پایه و مهندسی هستیم. موضوعاتی که در محاسبات عددی مطرح میشوند عبارتاند از ریشهیابی، درونیابی و تقریب توابع، انتگرالگیری عددی و روشهای مختلف حل معادلات دیفرانسیل. به این ترتیب محاسبات عددی توضیح میدهد که چگونه میتوان از توابع، مشتقها، انتگرالها و معادلات دیفرانسیل بهعنوان مجموعهای از رشتههای عددی در کامپیوترها استفاده کرد. در این مطلب از مجله فرادرس همراه با حل مثال توضیح میدهیم که مفاهیم پایه در محاسبات عددی چیست.

در اولین بخش از این مطلب به معرفی دنبالهها و سریها خواهیم پرداخت و یاد میگیریم معنای همگرایی سریها در محاسبات عددی چیست. همچنین سری تیلور را به عنوان یکی از پرکاربردترین سریها در ریاضیات معرفی میکنیم. در بخش بعد، روشهای تقریبی انتگرالگیری عددی مانند روش تقریب مستطیلی، روش ذوزنقهای، روش نقطه میانی و روش سیمپسون را توضیح میدهیم. در ادامه دیفرانسیلگیری عددی و روشهای مختلف درونیابی مانند روش چند جملهای وندرموند، روش چند جملهای لاگرانژ و اسپلاین مستقیم و مربعی را شرح میدهیم. بخشهای پایانی این نوشته نیز به بررسی معادلات غیرخطی و حل دقیق معادلات دیفرانسیل معمولی اختصاص دارد.
محاسبات عددی چیست؟
محاسبات عددی یا آنالیز عددی علم مطالعه الگوریتمهایی است که در آنها از تقریبهای عددی برای حل مسائل استفاده میشود. در محاسبات عددی با مسائلی روبرو میشویم که نمیتوان آنها را توسط روشهای معمولی و تحلیلی در ریاضیات حل کرد. در نتیجه نیاز داریم با استفاده از روشهای تقریبی، رسم نمودار و بررسی برازش یا درونیابی نمودار، به فرمولهای موردنیاز خود دست پیدا کنیم. به این ترتیب محاسبات عددی فرمولهای ریاضی بهدست آمده را به الگوریتمهایی برای پردازش در کامپیوترها تبدیل میکند.
با توجه به اینکه کاربرد این شاخه از علم ریاضی اغلب به مسائلی محدود میشود که شامل توابع پیوسته، حدگیری و مباحث مرتبط با آن مانند دیفرانسیلگیری، انتگرالگیری، اندازهگیری، دنبالههای بینهایت، سریها و توابع تحلیلی هستند، از این رو میتوانیم محاسبات عددی و حوزه مطالعاتی آن را به نوعی در مقابل ریاضیات گسسته در نظر بگیریم. اغلب دانشمندان و مهندسان در حوزههای مختلف دیر یا زود در کار خود با مسائل محاسباتی از این دست مواجه میشوند. بنابراین یادگیری و کسب مهارت در این شاخه از ریاضیات از اهمیت بالایی برخوردار است. بهطور کلی مهمترین موضوعات محاسبات عددی بهصورت زیر است:
- بسط سریها: از حساب دیفرانسیل و انتگرال تا محاسبات
- انتگرال بهعنوان مجموع و مشتق بهعنوان اختلاف
- درونیابی، اسپلاین و نگاه دیگری به محاسبات عددی
- روشهای عددی برای حل معادلات دیفرانسیل معمولی یا ODE
- پیدا کردن ریشه با روشهایی مانند نیوتن – رافسون
مهارت و دانشی که در این درس آموزش داده میشود برای اغلب دانشمندان و مهندسان مشغول در حوزه شبیهسازی یا تحلیل داده در صنایع مختلف، کاملا مفید و کاربردی است. همچنین یادگیری این شاخه برای علاقهمندان به پژوهش در زمینه ریاضیات محاسباتی ضروری است.
پیشنیازهای درس محاسبات عددی چیست؟
محاسبات عددی یکی از مهمترین دروس دانشگاهی است. بنابراین برای اینکه بهتر متوجه شوید محاسبات عددی چیست، پیشنهاد ما این است که ابتدا با مباحث پیشنیاز این درس آشنا شوید. برای مثال، حساب دیفرانسیل و انتگرال از درس ریاضی عمومی ۱، درس معادلات دیفرانسیل و برخی از مباحث درس جبر خطی به شما کمک میکنند تا پیشرفت بهتری در یادگیری محاسبات عددی داشته باشید. همچنین تکالیفی که در این درس ارائه میشود، اغلب شامل برنامهنویسی اولیه به زبان موردنظر شما است و پیشنهاد ما این است که از متلب برای شروع استفاده کنید. بنابراین اگر با محیط این نرمافزار آشنا نیستید، بهتر است همراه با این درس یادگیری آن را هرچه سریعتر آغاز کنید.
یادگیری محاسبات عددی با فرادرس
پیش از شروع مباحث اصلی درس محاسبات عددی، در این قسمت قصد داریم تمام فیلمهای آموزشی تهیه شده در همین زمینه را به شما معرفی کنیم. مشاهده این دورههای تصویری از مجموعه فرادرس به شما کمک میکند تا یادگیری خود را تکمیل کرده و بهتر متوجه شوید مباحث عددی چیست.
- فیلم آموزش محاسبات عددی – مرور و حل مساله فرادرس
- فیلم آموزش مبانی آنالیز عددی – بخش یکم فرادرس
- فیلم آموزش مبانی آنالیز عددی – بخش دوم فرادرس
- فیلم آموزش رایگان قاعده ذوزنقه ای برای محاسبه انتگرال منحنی فرادرس
- فیلم آموزش رایگان محاسبات عددی – خطاها فرادرس
دنباله ها و سری ها
یکی از مهمترین مباحث در محاسبات عددی، مفهوم دنباله و سری است. بنابراین ابتدا باید بدانیم معنای همگرایی یک سری در محاسبات عددی چیست. به همین منظور، در اولین مبحث از محاسبات عددی ابتدا دنباله و سری را تعریف میکنیم و توضیح میدهیم تفاوت این دو در محاسبات عددی چیست.
پس از اینکه با مفهوم و تعریف دنباله و سری در محاسبات عددی آشنا شدیم، حالا نوبت به پاسخ دادن به این سوالات میرسد که معنای یک دنباله نامتناهی چیست؟ چگونه میتوانیم همگرایی و واگرایی را نشان دهیم و چه زمانی میتوانیم قوانین معمول برای دنبالههای متناهی را در مورد دنبالههای نامتناهی بکار ببریم؟
تعریف دنباله و سری
به مجموعهای نامتناهی از اعداد که با یک ترتیب مشخصی در کنار هم قرار گرفتهاند، یک دنباله یا Sequence گفته میشود. برای مثال، مجموعه زیر را میتوانیم یک دنباله در نظر بگیریم:
این در حالی است که سریها اغلب بهصورت یک مجموع نامتناهی از اعداد به شکل زیر هستند:
برای سادهتر شدن محاسبات میتوانیم اعدادی که در دنبالهها و سریهایی به شکل بالا قرار میگیرند را جزء مجموعه اعداد حقیقی فرض کنیم. اما این به این معنا نیست که اعداد مختلط نمیتوانند در این دنبالهها و سریها قرار بگیرند.
مفهوم همگرایی و واگرایی
یکی از روشهای بررسی جمعهای نامتناهی این است که آنها را بهصورت حد مجموع جزئی در نظر بگیریم. از آنجا که مجموع جزئی همان دنباله است، پس بهتر است ابتدا ببینیم مفهوم همگرایی دنبالهها و سریها در محاسبات عددی چیست. به تعاریف و قضایایی که در ادامه توضیح داده میشوند، دقت کنید.
تعریف ۱
زمانی میگوییم دنبالهای به شکل به اندازه به عدد نزدیک شده است که عددی مانند وجود داشته باشد، طوری که برای تمام داشته باشیم:
در این شرایط دنباله زمانی به همگرا میشود که به اندازه تمام مقادیر بزرگتر از صفر (و هر چقدر کوچک) ممکن به نزدیک شده باشد. همگرایی این دنباله را میتوانیم به شکل زیر نشان دهیم:
اگر چنین شرایطی برای یک دنباله برقرار نباشد، در این صورت میگوییم دنباله موردنظر ما واگرا است. دنبالههای نامحدود برای مثال دنبالههایی که شامل اعداد به دلخواه خیلی زیاد هستند، اغلب واگرا میشوند. همچنین طبق تعریف بالا همگرایی به بینهایت معنایی ندارد، بلکه باید بگوییم یک دنباله به بینهایت واگرا میشود.
به مثالهای زیر در این زمینه توجه کنید:
- اگر ، در این صورت (همگرایی سریع به صفر).
- اگر ، در این صورت (همگرایی آهسته به یک).
- با اینکه محدود است، اما همگرا نمیشود.
- اگر ، در این صورت (این دنباله واگرا است).
برای اینکه ثابت کنیم در آخرین مثال همواره مقادیر دلخواه و بسیار بزرگی میپذیرد، با در نظر گرفتن هر عدد صحیح و بزرگی مانند ، آیا همواره وجود دارد که به ازای آن داشته باشیم ؟ پاسخ این سوال، بله است. کافی است را بهصورت در نظر بگیریم.
تعریف ۲
فرض کنید دنبالهای بهصورت دارید. در این صورت میتوانیم امین مجموع جزئی را به شکل زیر تعریف کنیم:
در این تعریف زمانی سری همگرا میشود که همزمان با ، دنباله مجموع جزئی به عددی مانند همگرا شود. در این صورت میتوانیم بنویسیم:
مجددا این نکته را یادآوری میکنیم که اگر یک سری همگرایی نداشته باشد، میگوییم واگرا است. در ادامه میخواهیم ببینیم برخی قوانین در زمینه همگرایی سریها در محاسبات عددی چیست. سریهای خاصی مطلقا همگرا هستند، در حالی که برخی دیگر از سریها تحت شرایط خاصی همگرا میشوند. دانستن این مسئله به ما کمک میکند تا بتوانیم تشخیص دهیم از چه نوع عملیات جبری برای بررسی همگرایی یک سری میتوانیم استفاده کنیم.
تعریف ۳
یک سری به فرم مطلقا همگرا نامیده میشود، اگر همگرا باشد. اگر یک سری مطلقا همگرا نباشد، اما واگرا هم نباشد، میگوییم این سری همگرای مشروط است. در حقیقت در این نوع همگرایی تناوب علامتهای مثبت و منفی را در سری داریم که همین مسئله منجر به حذف برخی جملات حین جمع کردن و در نتیجه، همگرایی سری میشود. یکی از راههای بررسی و تست همگرایی یک سری استفاده از قضایایی با همین موضوع است که در بخشهای بعدی بیان میشوند.
قضیه ۱ (آزمون سریهای متناوب)
یک سری به شکل را در نظر بگیرید که در آن تمام ها بزرگتر از صفر و مثبت هستند. اگر بهعنوان یک دنباله به همگرا شود، در این صورت این سری همگراست. مشکل اصلی در مورد سریهای همگرای مشروط این است که اگر جملات مجددا مرتب شوند، ممکن است سری به سمت مقدار حدی دیگری همگرا شود. بنابراین اگر بخواهیم با اطمینان بالا یک مجموع نامتناهی را در صورت متناهی بودن بررسی کنیم، بهتر است همگرایی آن مطلق باشد.
قضیه ۲
فرض کنید نوعی تناظر دو طرفه باشد، یعنی آرایش مجددی از اعداد صحیح غیرمنفی است. حالا یک سری به شکل در نظر بگیرید. اگر این سری مطلقا همگرا باشد، در این صورت داریم:
قضیه ۳
انجام عملیات زیر روی سریهای مطلقا همگرا درست است:
- عبور قدر مطلق از بیرون جمع به داخل:
- مبادله جمعها:
نماد O بزرگ
پس از اینکه تا حدی یاد گرفتیم مفهوم همگرایی سریها در محاسبات عددی چیست، در این بخش میخواهیم چند نماد معمول برای مقایسه رشد یا کاهش دنبالهها معرفی کنیم. سه نماد معروف در این زمینه داریم که عبارتاند از:
- نماد بزرگ
- نماد کوچک
- نماد بزرگ
اغلب نماد بزرگ بیشتر از دو نماد دیگر کاربرد دارد و دو نماد دیگر در مواردی مانند مقایسه نرخ کاهش خطاهای برشی یا مقایسه زمان اجرای الگوریتمها استفاده میشوند. فرض کنید دو دنباله غیرصفر به نامهای و داریم. در این صورت برای تمام داریم:
- اگر بزرگتر از صفر و مثبتی وجود داشته باشد به گونهای که ، در این صورت .
- اگر همزمان با داشته باشیم ، در این صورت .
- اگر و ، در این صورت داریم .
را به این صورت میخوانیم: از مرتبه است. برای اینکه بتوانیم بهدرستی از این نمادها استفاده کنیم، برای مثال بهتر است بدانیم در مورد دو دنباله به شکل توابع نمایی و توابع چند جملهای، همواره داریم:
- به ازای هر و مثبتی: .
- به ازای هر و مثبتی: .
برای اینکه قوانین بالا را بهتر متوجه شوید، به مثالهای زیر توجه کنید.
مثال ۱
فرض کنید و است. در این صورت درستی هر کدام از سه مورد بالا را برای برای تمام بررسی کنید:
پاسخ
در اولین مورد باید یک بزرگتر از صفر و مثبتی وجود داشته باشد بهطوری که برقرار باشد تا بتوانیم بگوییم . از آنجا که در ابتدا فرض کردهایم دنبالههای و غیرصفر هستند، بنابراین برای عبارت نمیتوانیم را در نظر بگیریم. به ازای و خواهیم داشت:
و برای و هم خواهیم داشت:
به این ترتیب درستی به ازای یک بزرگتر از صفر و مثبت () و برای تمام ها بهجز صفر برقرار است. پس میتوانیم بگوییم . در دومین مورد، ابتدا را به شکل زیر در نظر میگیریم:
بنابراین اگر ، در این صورت . پس شرایط برای برقراری دومین مورد نیز فراهم است و داریم . در سومین مورد باید علاوهبر ، رابطه نیز برقرار باشد تا بتوانیم بگوییم یا . درستی مستلزم وجود یک بزرگتر از صفر و مثبتی است که به ازای آن همواره داشته باشیم . در حقیقت باید برای درستی مقدار مناسب را پیدا کنیم که چنین مقداری وجود ندارد. بنابراین و در نتیجه .
مثال ۲
درستی و و را به ازای تمام مقادیر و با در نظر گرفتن و بررسی کنید:
پاسخ
طبق تعریف برای برقراری لازم است یک بزرگتر از صفر و مثبتی وجود داشته باشد بهطوری که برقرار باشد:
چون لازم است دنبالههای و غیرصفر باشند، بنابراین نمیتواند برای این بررسی انتخاب درستی باشد. اما برای سایر مقادیر ، برای مثال برای و و با در نظر گرفتن اثر قدر مطلق خواهیم داشت:
پس درستی برای این دو دنباله برقرار است و میتوانیم بگوییم . در ادامه برقراری نیز مستلزم این است که با میل کردن به سمت بینهایت، حاصل نیز به سمت صفر میل کند:
در نتیجه دومین مورد برای این دو دنباله صحیح نیست و داریم . در نهایت برای اینکه داشته باشیم ، لازم است درستی هر دو عبارت و برقرار باشد. اولین مورد در بخش اول بررسی شد، اما برای بررسی دومین مورد یعنی ، باید یک بزرگتر از صفر و مثبتی پیدا کنیم، طوری که . باز هم چون لازم است دنبالههای و غیرصفر باشند، بنابراین نمیتواند برای این بررسی انتخاب درستی باشد. اما برای سایر مقادیر ، برای مثال برای و و با در نظر گرفتن اثر قدر مطلق خواهیم داشت:
پس چون توانستیم یک بزرگتر از صفر و مثبتی پیدا کنیم که نامساوی بالا به ازای آن درست باشد، بنابراین داریم و در نتیجه .
بسط تیلور چیست؟
اگر بتوانیم تابع را حول نقطهای مانند بهصورت زیر بسط دهیم:
در این صورت عبارت بالا بسط تیلور تابع نامیده میشود و فرم فشردهتر آن در قالب سری تیلور به شکل زیر خواهد شد:
این امکان در مورد سری تیلور با جمله وجود دارد که آن را در قالب دو جمله و به شکل زیر بازنویسی کنیم:
با این شرط که عددی بین و است. دقت کنید این فرمول مشخص نمیکند مقدار دقیق عدد چیست، بلکه فقط بیان میکند عددی مانند بهعنوان آخرین جمله یا باقیمانده در بسط بالا وجود دارد. علیرغم اینکه در عبارت بالا مشخص نیست، این شکل از نوشتن بسط تیلور بسیار کاربردیتر از نوشتن آن بهصورت یک سری بینهایت است. در ادامه دو جمعبندی مهم برای بسط تیلور و با کمک گرفتن از آنچه در اولین بخش از مطلب محاسبات عددی آموختیم، بیان میکنیم.
نکته ۱: از آنجا که اغلب اندازه باقیمانده برای ما مهم است، میتوانیم از نامساوی زیر استفاده کنیم:
یا به صورت سادهتر:
که در آن تمام ثوابت در نماد بزرگ مخفی شدهاند. بنابراین میتوانیم بگوییم باقیمانده از مرتبه است. همچنین حد ضمنی در نماد بزرگ بهصورت است.
نکته ۲: فرمول متناهی زمانی معتبر است که تابع ما مرتبه مشتقپذیر باشد و این به آن معنا نیست که بینهایت مرتبه مشتقپذیری داشته باشیم. در حقیقت، سری تیلور با اینکه ممکن است واگرا شود، اما رابطه زیر همچنان معتبر است:
حل مثال از دنباله ها و سری ها
در ادامه چند مثال راجعبه تعاریف و قضایای بیان شده در بخش همگرایی دنبالهها و سریها را با هم بررسی میکنیم تا بهتر متوجه شوید معنای همگرایی در محاسبات عددی چیست.
مثال ۱
ثابت کنید سری که برای مثال شامل جملاتی بهصورت است، به لیمیت همگرا میشود.
پاسخ
برای اثبات این سوال، ابتدا مجموع جزئی زیر را در نظر میگیریم:
حال اجازه دهید با استقرا نشان دهیم که . با قرار دادن ، جمله پایه بهدرستی برابر با محاسبه میشود، چون داریم:
پس با توجه به استقرا میتوانیم به شکلی که در صورت سوال داده شده است را با برابر فرض کنیم. در ادامه به همین ترتیب خواهیم داشت:
مثال ۲
سری هارمونیک را به شکل زیر را در نظر بگیرید و واگرایی آن را نشان دهید:
پاسخ
برای اثبات واگرایی این سری، کافی است نشان دهیم مجموع جزئی با قابل مقایسه است. ابتدا انتگرال آزمون زیر را بکار میبریم:
انتگرال بعدی است، که به عنوان یک دنباله واگرا میشود. بنابراین مجموع جزئی که بزرگتر است نیز باید واگرا شود.
مثال ۳
با فرض عبارت زیر برای تمام های بزرگتر از صفر، اگر این رابطه را به عنوان تابعی از «تابع زتای ریمان» بنامیم و بهصورت نشان دهیم، نشان دهید این تابع که یکی از توابع موردعلاقه نظریهپردازان محاسبات عددی نیز به شمار میرود، برای مقادیر بیشتر از واگرا میشود:
پاسخ
مشابه سوال قبل با بکارگیری انتگرال آزمونی مانند مثال ۲، میتوانیم نشان دهیم که سری برای مقادیر بزرگتر از یک همگرا میشود، در حالی که برای واگرایی داریم.
مثال ۴
یک سری به شکل داریم. آیا این سری همگرایی مطلق دارد؟
پاسخ
خیر، این سری همگرایی مطلق ندارد، چون اگر مقادیر مطلق را از جملات آن حذف کنیم، به یک سری هارمونیک خواهیم رسید. بنابراین با اینکه این سری همگرای مطلق نیست، اما همگرایی مشروط دارد. فرض کنید زوج است و جملات سری را میتوانیم به دو گروه به شکل زیر تقسیم کنیم، طوری که برای داریم:
طبق نامساوی ، نتیجه میگیریم که:
که میدانیم این سری همگرا است. از طرفی اگر فرد باشد، در این صورت . هر دو جمله و دنبالههای همگرایی هستند. بنابراین مجموع آنها نیز همگرا است. پس همگرایی ثابت شد. همچنین مقدار همگرایی برای سری است. این سری حالت خاصی از بسط تیلور حول با در نظر گرفتن محسوب میشود.
مثال ۵
مجددا سری را در نظر بگیرید که همانطور که در مثال قبل دیدیم برابر است با . آیا این سری همگرا است؟
پاسخ
میتوانیم این سری را به شکل دیگری مجددا مرتب کنیم، به این صورت که به ازای هر جمله مثبت، بلافاصله دو جمله منفی بعد از آن قرار دهیم:
این سری هم همگرا است. اما همگرایی آن برابر است با .
روش های انتگرال گیری عددی
پس از اینکه در اولین بخش یاد گرفتید مفهوم دنباله و سری در محاسبات عددی چیست، دومین بخش با توضیح سادهترین روشهای انتگرالگیری عددی شروع میشود. در این بخش یاد میگیریم روشهای انتگرالگیری عددی در محاسبات عددی چیست و هر کدام بر مبنای چه نوع تقریبی پاسخ یک انتگرال را برای ما محاسبه میکنند.
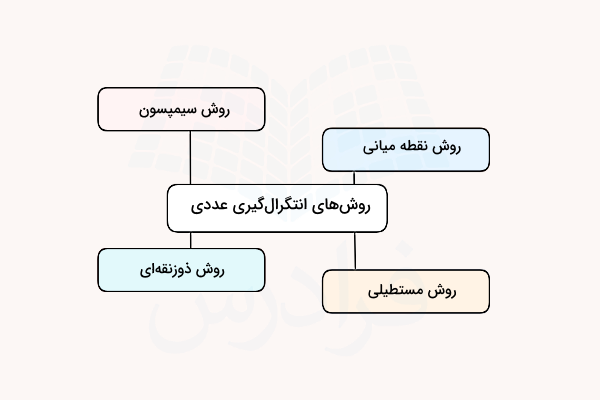
به همین منظور ابتدا لازم است نحوه محاسبه انتگرالهای عددی را به کمک تقریب مرتبه اولی به نام روش مستطیلی شرح دهیم. همچنین در بخشهای بعد روشهای دقیقتری مانند روش نقطه میانی و روش ذوزنقهای را معرفی میکنیم که هر دو از تقریبهای مرتبه دوم برای محاسبه انتگرال استفاده میکنند. در تمام این مباحث هدف ما تعیین پاسخ یک انتگرال معین با روشهای تقریبی است. در نهایت با معرفی روش سیمپسون این بخش را به پایان میرسانیم.
روش مستطیلی
اولین روشی که برای محاسبه انتگرالهای عددی در درس محاسبات عددی معرفی میشود، روش تقریب مستطیلی است. میدانیم مفهوم ابتدایی انتگرال یک تابع معادل است با محاسبه مساحت زیر منحنی آن تابع، که از جمع کردن مساحت تمام مستطیلهای فرضی در این ناحیه بهصورت تقریبی بهدست میآید. این توضیح بیان سادهای از مجموع ریمان است.
با اینکه این روش بسیار ساده بنظر میرسد، اما پاسخ دقیقتر آن با در نظر گرفتن تعداد زیادی مستطیل حاصل میشود. برای شروع، تابعی مانند را در نظر بگیرید که انتگرال آن به شکل زیر محاسبه میشود:
اگر محدوده انتگرالگیری در این انتگرال را بهصورت فرض کنیم و آن را به بازههای کوچکتری به شکل تقسیم کنیم، طوری که داشته باشیم:
در این صورت با در نظر گرفتن اینکه ها شبکه دکارتی یا کارتزین نامیده میشوند، بدون هیچ تقریبی میتوانیم بنویسیم:
اگر انتگرالها را با مقادیری که فقط به نمونههای تابع روی شبکه بستگی دارند، تقریب بزنیم، در این صورت میگوییم انتگرال عددی یا یکچهارم محاسبه شده است. برای مثال، انتگرال تابع را روی بازه میتوانیم به این صورت تقریب بزنیم که مساحت مستطیلی با ارتفاع و عرض را محاسبه کنیم:
در حقیقت در محاسبه بالا روش مستطیلی را برای محاسبه انتگرال عددی انتخاب کردهایم:
برای اینکه دقت این تقریب را بهتر متوجه شویم، نیاز داریم از بسط تیلور استفاده کنیم که در بخش قبل آن را معرفی کردیم. تابع را در طبق بسط تیلور و حول نقطه بسط میدهیم:
که در آن . در نوشتار بالا را به شکل تابعی از نوشتیم تا روی این نکته تاکید کرده باشیم. این رابطه مادامی که یک مشتق داشته باشد، برقرار است. با انتگرالگیری از دو طرف این رابطه و در نظر گرفتن این نکته که نسبت به ثابت است و ، خواهیم داشت:
ما در مورد تابع چیز زیادی نمیدانیم اما میتوانیم با اطمینان نامساوی زیر را برای آن بنویسیم:
با توجه به اینکه طرف دوم نامساوی بالا با عبارت زیر برابر میشود:
بنابراین تا زمانی که تابع انتگرالپذیر باشد، میتوانیم بنویسیم:
که تمام مشتقهای تابع در نماد مخفی شدهاند. پس انتگرال در بازه دارای عدد از چنین جملاتی است و وقتی که این جملات با هم جمع میشوند، مقادیر خطا به شکل با هم ترکیب میشوند، چون . پس با کمک گرفتن از بسط تیلور توانستیم درستی عبارت زیر را نشان دهیم:
مرتبه خطا در این بررسی با خود فاصله شبکه کارتزین یا برابر شد. به همین دلیل میگوییم این روش مرتبه اول است (چون توان برابر با است). اما اینکه طول هر مستطیل را از آخرین نقطه باقیمانده یعنی انتخاب کنیم، چندان روش دقیقی بنظر نمیرسد. در بخشهای بعدی نشان میدهیم روشهای دقیقتر محاسبه انتگرالهای عددی در محاسبات عددی چیست.
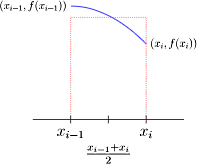
روش نقطه میانی
اگر بخواهیم بدانیم مهمترین تفاوت روش مستطیلی و روش نقطه میانی در محاسبات عددی چیست، کافی است بهجای نقطه را در نظر بگیریم. در این حالت خواهیم داشت:
این رابطه بیان میکند که تابع دو مرتبه مشتقپذیر است، چون در نماد بزرگ مخفی شده است. در این روش از این جهت دقت محاسبات بالاتر است که با میل کردن به سمت صفر، نسبت به بیشتر کوچک میشود. به همین علت روش نقطه میانی را یک روش مرتبه دوم مینامیم. بنابراین روش نقطه میانی برای محاسبه مجموع ریمان در بیشتر تقریبهایی که بر پایه مجموع مساحت مستطیلها محاسبه میشوند، بهتر کار میکند. تعریف دقیق قانون نقطه میانی به شکل زیر است:
اگر تابع روی بازه بستهای به شکل تعریف شده باشد و بتوانیم این بازه را به زیربازه با طول مساوی به شکل تقسیم کنیم، در این صورت با کاربرد نقطه به شکل که برابر میشوند با ، انتگرال با تقریب برابر خواهد شد با:
در عمل روشهای تقریبی زمانی کاربرد درستی خواهند داشت که بدانیم مقدار دقیق انتگرال چقدر است. میدانیم وقتی که پاسخ تقریبی یک انتگرال را بهدست آوردیم، مقدار خطای محاسبات برابر است با اختلاف بین مقدار واقعی و مقدار تقریبی انتگرال. در هر روش تقریبی که در این بخش معرفی میکنیم، بهتر است که کران خطا را نیز تعریف کنیم. مقدار کران خطا از خطای واقعی باید بزرگتر باشد. برای مثال، اگر پاسخ تقریبی انتگرالی و کران خطای متناظر با این پاسخ باشد، در این صورت مطمئن هستیم که مقدار واقعی انتگرال همواره بین دو مقدار و قرار میگیرد.
همچنین در مورد محاسبه تقریبی انتگرالهای عددی مطلوب این است که خطا تابعی از و بهصورت triangle x باشد. در این صورت با کوچک شدن ، خطا هم بهسرعت کاهش خواهد یافت. خوشبختانه برای اغلب توابع، چنین کران خطای متناظری برای تقریب روش میانی وجود دارد. تعریف دقیقتر خطا در روش تقریب نقطه میانی به شکل زیر است:
فرض کنید تابع دارای مشتق دومی بهصورت در هر نقطه از بازه است و برای تمام های این بازه همواره عبارت نیز برقرار است. با در نظر گرفتن ، کران خطا برای تقریب نقطه میانی برابر خواهد شد با:
یکی دیگر از روشهای تقریبی با دقتی از مرتبه دوم، روش ذوزنقهای است که در بخش بعد متوجه خواهید شد روش استفاده از آن در محاسبات عددی چیست.
روش ذوزنقه ای
برخلاف روش مستطیلی و روش نقطه میانی که در هر دو از مستطیلها برای تقریب زدن و حل انتگرال عددی استفاده میکردیم، در روش ذوزنقهای با در نظر گرفتن تعداد زیادی ذوزنقه در بازه سعی میکنیم انتگرال عددی خود را حل کنیم. مساحت ذوزنقهای که از چهار نقطه به شکل ساخته میشود برابر است با:
اگر بخواهیم این مقدار را با انتگرال روی همان بازه مقایسه کنیم، با در نظر گرفتن بسط تیلور کوتاه شده به شکل دو جمله خواهیم داشت:
که دومین مشتق در این عبارت در علامت بزرگ قرار گرفته است. با انتگرالگیری از رابطه اول خواهیم داشت:
از طرفی اگر را در عبارت مساحت ذوزنقه قرار دهیم، خواهیم داشت:
بنابراین میتوانیم بنویسیم:
حالا با جمعبندی روی خواهیم داشت:
بنابراین روش ذوزنقهای هم یک روش تقریبی از مرتبه دوم است. در شکلهای زیر محاسبه تقریبی مساحت زیر یک منحنی به دو روش مستطیلی و ذوزنقهای با هم مقایسه شده و واضح است که روش ذوزنقهای تقریب دقیقتری است:
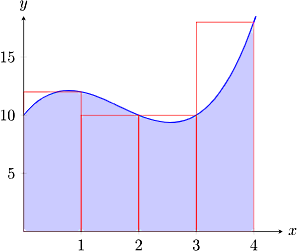

یک روش دیگر برای بررسی جزئی روش ذوزنقهای این است که مانند روش نقطه میانی در بخش قبل، بازه موردنظر خود را به به زیربازه با طول مساوی به شکل تقسیم کنیم. به این ترتیب ذوزنقههای تشکیل شده دارای مساحتی به شکل زیر هستند:
که با جمع کردن مساحت تمام این ذوزنقهها خواهیم داشت:
با سادهسازی عبارت بالا خواهیم داشت:
پس قاعده ذوزنقهای برای محاسبه انتگرال عددی با فرضیاتی کاملا مشابه با قاعده نقطه میانی اما با نتیجهای متفاوت و به شکل زیر تعریف میشود:
اگر تابع روی بازه بستهای به شکل تعریف شده باشد و بتوانیم این بازه را به زیربازه با طول مساوی به شکل تقسیم کنیم، در این صورت با کاربرد نقطه به شکل که برابر میشوند با ، انتگرال با تقریب برابر خواهد شد با:
همانطور که در مورد روش نقطه میانی کران خطا را تعیین کردیم، در اینجا هم کران خطا را به شکل زیر تعریف میکنیم:
فرض کنید تابع دارای مشتق دومی بهصورت در هر نقطه از بازه است و برای تمام های این بازه همواره عبارت نیز برقرار است. با در نظر گرفتن ، کران خطا برای تقریب نقطه میانی برابر خواهد شد با:
نکته: مزیت روش ذوزنقهای در مقایسه با سایر روشهای تقریبی برای محاسبه انتگرالها در محاسبات عددی این است که قسمت بالا یا نوک ذوزنقه طبق شکل بالا میتواند تقریب خیلی خوبی از بخش خمیده شده یا ماکزیمم منحنی تابع داده شده به ویژه در شرایطی که خیلی کوچک میشود، ارائه دهد. این در حالی است که در روشهای تقریبی مستطیلی چنین تقریبی برای این ناحیه نمیتوانیم داشته باشیم.
روش سیمپسون
در انتهای بخش قبل تاکید کردیم که مزیت کاربرد روش ذوزنقهای در مقایسه با روشهای تقریب مستطیلی مانند روش نقطه میانی به جهت محاسبه تقریبی انتگرالها در محاسبات عددی چیست. حال اگر بهجای استفاده از اشکال هندسی با اضلاعی با خطوط راست و مستقیم مانند مستطیل یا ذوزنقه، دنبال تقریب نزدیکتری به منحنی تابع داده شده باشیم، احتمالا از قاعده سیمپسون استفاده کردهایم. عموما بهترین شکلی که میتوانیم برای این روش تقریبی انتخاب کنیم، سهمی است. اگر بخشی از منحنی تابع داده شده در زیر انتگرال را با یک سهمی به معادله تقریب بزنیم، به آسانی میتوانیم مساحت زیر سهمی را محاسبه کنیم.
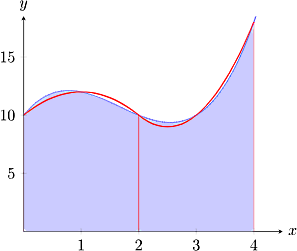
پیش از ادامه این مبحث، بهتر است یادآوری کنیم فرادرس در همین زمینه دورهای با عنوان فیلم آموزش انتگرال عددی با قواعد ذوزنقهای و سیمپسون – پیاده سازی در متلب را تهیه کرده است که با مشاهده این دوره میتوانید پیادهسازی این روش را در متلب نیز فرابگیرید. لینک این آموزش در ادامه برای شما قرار داده شده است:
میدانیم بین هر دو نقطه انتخابی تعداد بینهایت سهمی میتوان رسم کرد، اما بین سه نقطه فقط میتوانیم یک سهمی رسم کنیم. بنابراین اگر بتوانیم بین سه نقطه متوالی روی منحنی مانند و و یک سهمی پیدا کنیم، این سهمی احتمالا در بازه و بسیار نزدیک به منحنی تابع داده شده در زیر انتگرال است.
حالا اگر بازه بسته را به تعداد زوجی زیربازه تقسیم کنیم، میتوانیم منحنی تابع را با چند سهمی جایگزین تقریب بزنیم که هر کدام بخشی از زیربازههای ایجاد شده را پوشش میدهد. اما اول باید فرمول مساحت زیر یک منحنی سهمی شکل را بدانیم. برای بهدست آوردن چنین فرمولی لازم است معادله سهمی یعنی را طوری بنویسیم که از سه نقطه در نظر گرفته شده یعنی و و عبور کند و سپس از آن انتگرالگیری کنیم. البته محاسبات جبری در این سطح کمی پیچیده است و میتوانیم از کامپیوترها کمک بگیریم.
ابتدا باید سه معادله زیر را برای حل کنیم:
حل این سه معادله برای پیدا کردن سه مجهول دشوار است. اما با استفاده از روشهای کامپیوتری میتوان به عبارت زیر رسید:
بنابراین اگر بخواهیم مجموع مساحت زیر تمام سهمیها را حساب کنیم، باید عبارت زیر را بهدست آوریم:
که در حالت سادهتر میشود:
بنابراین مشاهده میکنید که محاسبات برای روش سیمپسون با محاسبات روش ذوزنقهای بسیار متفاوت است. نکته مهم این است که در فرمول بالا نباید ضرایب دو و چهار را فراموش کنیم. همچنین دقت کنیم که بازه موردنظر خود را به تعداد زوجی زیربازه تقسیم کنیم نه تعداد فرد.
بنابراین تعریف دقیق قاعده سیمپسون به این صورت است:
فرض کنید تابع روی بازه بستهای به شکل تعریف شده باشد و بتوانیم این بازه را به زیربازه با طول مساوی به شکل تقسیم کنیم، در این صورت با کاربرد نقطه به شکل که برابر میشوند با ، انتگرال با تقریب برابر خواهد شد با:
همانطور که در مورد روش ذوزنقهای کران خطا را تعیین کردیم، در اینجا هم کران خطا را به شکل زیر تعریف میکنیم:
فرض کنید تابع دارای مشتق چهارمی بهصورت در هر نقطه از بازه است و برای تمام های این بازه همواره عبارت نیز برقرار است. با در نظر گرفتن ، کران خطا برای تقریب سیمپسون برابر خواهد شد با:
با توجه به فاکتور ، کران خطا در این روش دقت بسیار بالاتری نسبت به همتای خود در روش ذوزنقهای یا نقطه میانی دارد. در ادامه این بخش با حل چند مثال بهتر یاد میگیریم که تفاوتهای این روشهای تقریبی در حل مسائل محاسبات عددی چیست.
حل مثال از روشهای انتگرال گیری عددی
در انتهای این بخش چند مثال برای شما در نظر گرفتهایم تا با بررسی و حل آنها کاملا به روشهای مختلف انتگرالگیری عددی در محاسبات عددی مسلط شوید.
مثال ۱
انتگرال تابع را در بازه و با در نظر گرفتن به دو روش ذوزنقهای و مستطیلی محاسبه کنید:
پاسخ
میدانیم حاصل این انتگرال با استفاده از فرمولهای انتگرالگیری برابر است با . میخواهیم ببینیم با این دو روش تقریبی جوابهای بهدست آمده چقدر به نزدیک هستند. در روش مستطیلی، برای مقدار برابر میشود با . حال اگر چند نقطه در شبکه بهصورت در نظر بگیریم و فرض کنیم هر مستطیل دارای طولی است که آخرین نقطه باقی مانده آن است، در این صورت داریم:
این عدد از فاصله زیادی دارد. پس میتوانیم بگوییم با در نظر گرفتن تقریب مرتبه اول پاسخ خیلی دقیق نشد. در روش ذوزنقهای هم همین نقاط را انتخاب میکنیم، با این تفاوت که در اینجا نقطه هم در نظر گرفته میشود:
این جواب به نزدیکتر است. پس با در نظر گرفتن تقریب مرتبه دوم یا پاسخ دقیقتری به دست آوردیم.
مثال ۲
حاصل انتگرال را با قاعده ذوزنقهای تا دو رقم اعشار تقریب بزنید:
پاسخ
ابتدا مشتق دوم را برای تابع زیر انتگرال پیدا میکنیم که طبق فرمولهای مشتقگیری برابر میشود با:
بنابراین همین جا میتوانیم به این نتیجه برسیم که روی بازه بسته ، تابع دارای مقدار ماکزیممی به اندازه است. بنابراین شروع میکنیم به پیدا کردن تعداد زیربازههایی که برای تقریب زدن این انتگرال نیاز داریم. برای اینکه حاصل انتگرال را تا دومین رقم اعشار بهدست آوریم، قطعا باید یا:
با در نظر گرفتن ، کران خطا برابر خواهد شد با . بنابراین تقریب ذوزنقهای را برای شش بازه به شکل زیر محاسبه خواهیم کرد:
در این محاسبه کران خطا به ما نشان میدهد مقدار خطا در دو سمت این تقریب چگونه است. با توجه به مقدار محاسبه شده برای کران خطا و حاصل انتگرال به روش تقریبی، پاسخ درست و واقعی برای انتگرال داده شده همواره بین دو مقدار و قرار دارد. اما اگر بخواهیم به این سوال پاسخ دقیقتری داده باشیم، با دقت در دو پاسخ به دست آمده مشخص میشود که مقدار واقعی اول به سمت و مقدار واقعی دوم به سمت گرد میشوند که اعداد یکسانی نیستند. بنابراین از دومین رقم اعشاری در پاسخ بهدست آمده مطمئن نیستیم.
راهحل چنین مشکلی این است که بزرگتری انتخاب کنیم. برای مثال، با در نظر گرفتن احتمالا دو کرانی خواهیم داشت که هر دو به سمت مقدار یکسانی گرد میشوند. همینجا بهعنوان تمرین میتوانید نشان دهید که کاربرد تقریب مستطیل برای محاسبه مساحت ما را به عدد میرساند که در مقایسه با حاصل بهدست آمده بر اساس تقریب ذوزنقه عدد کم دقتتری است. بهترین روشی که در اینجا میتوانستیم از ابتدا در پیش بگیریم این بود که را در نظر داشته باشیم:
بنابراین بلافاصله میتوانستیم نتیجهگیری کنیم که ما را به پاسخ مطلوب این سوال خواهد رساند.
مثال ۳
حاصل انتگرال را توسط قاعده سیمپسون تا دو رقم اعشار تقریب بزنید:
پاسخ
مشتق چهارم تابع زیر انتگرال برابر میشود با:
بنابراین روی بازه بسته ، تابع دارای مقدار ماکزیممی به اندازه است. حالا شروع میکنیم به پیدا کردن تعداد زیربازههایی که برای تقریب زدن این انتگرال نیاز داریم. برای اینکه حاصل انتگرال را تا دومین رقم اعشار بهدست آوریم، قطعا باید . اما با توجه به سرنخی که از مثال قبلی بهدست آوردیم، انتخاب بهتر است:
چون لازم است تعداد زیربازهها زوج باشند، پس با در نظر گرفتن ، کران خطا برابر خواهد شد با . بنابراین تقریب سیمپسون خواهد شد:
بنابراین مقدار واقعی انتگرال عددی است که بین دو مقدار و قرار میگیرد. هر دو کران خطا به سمت عدد گرد میشوند. بنابراین اگر این مثال را با مثال قبل مقایسه کنید متوجه خواهید شد که چقدر دقت این روش تقریبی در مقایسه با سایر روشهای تقریبی حل انتگرالها در محاسبات عددی بالاتر است. بهویژه اینکه برای رسیدن به این پاسخ در روش ذوزنقهای نیاز داشتیم از تعداد جملات خیلی بیشتری استفاده کنیم در حالی که در این روش تنها با چهار جمله به همان پاسخ رسیدیم.
مثال ۴
پاسخ تقریبی انتگرال زیر را به دو روش ذوزنقهای و سیمپسون و با در نظر گرفتن چهار زیربازه محاسبه کنید:
پاسخ
روی بازه بسته با در نظر گرفتن ، برای خواهیم داشت:
ابتدا تقریب ذوزنقهای را به شکل زیر محاسبه خواهیم کرد:
همچنین خطای این تقریب را میتوانیم بهصورت زیر تعیین کنیم:
که در آن رابطه روی بازه برقرار است، چون داریم:
میبینیم که نامساوی روی این بازه برقرار است. بنابراین را برابر با میگیریم و بر همین اساس قاعده ذوزنقهای پاسخ زیر را به ما خواهد داد:
حالا همین روند را با بکارگیری قاعده سیمپسون امتحان میکنیم:
به تفاوت ضرایب در این دو روش و اثری که در نتیجه خواهد داشت، دقت کنید. با توجه به اینکه ، این تقریب دقیقا به جواب اصلی نزدیک است.
دیفرانسیل گیری عددی
در بخش قبل این موضوع را بررسی کردیم که انواع روشهای تقریبی محاسبه انتگرال در محاسبات عددی چیست. در این بخش میخواهیم ببینیم روشهای مشابه مشتقگیری تقریبی در محاسبات عددی چیست. سادهترین روش محاسبه تقریبی مشتق تابعی مانند از نمونهای مانند این است که تعداد متناهی نسبتهای تفاضلی تشکیل دهیم.
در یک شبهفضای شبکهای که به صورت تعریف میشود، دیفرانسیلها به این شکل تعریف میشوند:
- تفاضلهای راست و چپ یا تفاضل یکطرفه
- تفاضل مرکزی دو طرفه
حالا میخواهیم دقت این تفاضلها را در مشتقهای تقریبی و در شرایطی که ، بررسی کنیم. برای شروع فرض کنید و و . برای محاسبه تفاضل راست، از بسط تیلور حول نقطه صفر استفاده میکنیم و در نتیجه به عبارت زیر برای تابع خواهیم رسید:
فراموش نمیکنیم که . با جایگزینی این عبارت در فرمول تفاضل راست خواهیم داشت:
مادامی که تابع دارای دو مشتق مرزی است، خطا در این عبارت با مشخص میشود. به همین خاطر میگوییم تفاضل راست روشی از مرتبه اول است. بررسی تفاضل چپ هم به شکل مشابهی است. در مورد تفاضل مرکزی، از دو بسط تیلور حول نقطه صفر برای توابع و استفاده میکنیم. به این ترتیب رابطهای از مرتبه سوم به شکل زیر بهدست خواهد آمد:
که در آن بسته به اینکه کدام علامت انتخاب شود میتواند جزء بازه یا باشد. با کم کردن از و حذف جملات شامل خواهیم داشت:
در این محاسبات خطا از مرتبه خواهد بود که نشان دهنده این است که تابع سه مرتبه دیفرانسیلگیری میشود و در نتیجه این روش یک روش مرتبه دوم است. سادهترین انتخاب برای مشتق دوم، تفاضل دوم مرکزی است:
که در آن . در حقیقت در این رابطه فرمول سه نقطهای برای تفاضل دوم با محاسبه تفاضل راست از چپ یا بطور مشابه بهدست میآید.
چون دقت مرتبه دوم است، پس خطا بهصورت خواهد شد. برای اینکه این نکته را ثابت کنیم، بسط تیلور را حول نقطه صفر و برای مرتبه چهارم مینویسیم:
که در آن . جملات فرد در رابطه بالا با محاسبه تفاضل دوم هم را حذف میکنند و آنچه باقی میماند عبارت است از:
بنابراین تا زمانی که تابع چهار مرتبه قابلیت دیفرانسیلگیری داشته باشد، این روش کاملا است. برای مثال، برای تابع ، مشتق اول و دوم برابر است با:
در نتیجه برای تفاضل راست و چپ و تفاضل مرکزی دوم خواهیم داشت:
خطا در تفاضل راست برابر است با ، در حالی که برای تفاضل چپ میشود. پس برای این دو مورد خطا است. همچنین خطا برای و صفر است.
درون یابی چیست؟
در سومین بخش از مباحث محاسبات عددی، به توضیح درونیابی یا Interpolation میپردازیم. اگر بخواهیم مفهوم درونیابی را به زبان ساده و با مثال توضیح دهیم، فرض کنید مقادیر مختلف سرعت رو به بالای موشکی بهصورت تابعی از زمان و در قالب دادههای نقطهای گسسته در اختیار شما قرار داده شده است. اگر بخواهید سرعت این موشک را در یک زمان خاصی پیدا کنید (با این فرض که این برای این زمان دادهای در مورد سرعت ندارید)، میتوانید از روش درونیابی دادههایی که در اختیار دارید استفاده کنید.

در عمل روند استفاده از روش درونیابی برای پیدا کردن پروفایل یا نحوه تغییرات ارتفاع، سرعت و شتاب یک موشک به این شکل است که یک پروب سرعت در موشک، سرعت آن را در هر لحظه اندازهگیری میکند. به این ترتیب به کمک این دادهها میتوانیم سرعت موشک را در هر لحظه خاص درونیابی کنیم. بنابراین درونیابی مسئله فیت کردن یا برازش مجموعهای از نقاط با یک منحنی یا نمودار یک تابع است و در شاخههای مختلفی از جمله تحلیل داده، ریاضیات کاربردی، طراحی صنعتی، پردازش سیگنال و تحلیلهای عددی کاربرد دارد. اگر بخواهیم به زبان آماری صحبت کنیم، درونیابی به نوعی محاسبه رگرسیون است. پس در درونیابی به دنبال یافتن مقادیر تابع در نقاطی هستیم که برای آنها دادهای نداریم و میخواهیم با توجه به دادههایی که داریم این نقاط را تخمین بزنیم.
در مسئله درونیابی با دادههایی به شکل زیر روبرو هستیم که بهصورت نقاطی مجزا و گسسته هستند و برای اینکه بتوانیم مقدار را برای هر تخمین بزنیم، لازم است از یک تابع پیوسته به شکل استفاده کنیم که از این دادههای نقطهای عبور میکند. این روش همان فیت کردن یا برازش است و مقادیر ای که به این روش تعیین شوند، مقادیر درونیابی شده نامیده میشوند.
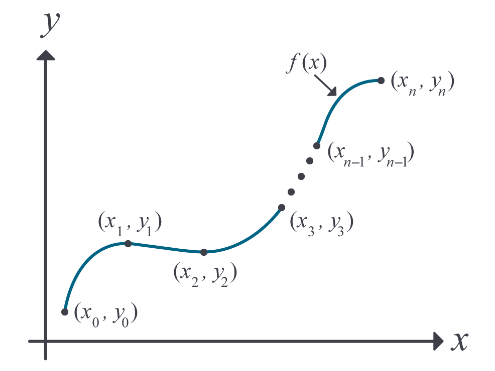
در این روش پیدا کردن تابع مناسب چالش اصلی است و اغلب توابع چندجملهای بهترین انتخاب هستند، به این دلیل که ارزیابی، مشتقگیری و انتگرالگیری از این توابع بسیار آسان است. روشهای مختلف درونیابی که در ادامه راجعبه آنها صحبت خواهیم کرد، عبارتاند از:
- درونیابی چند جملهای
- درونیابی اسپلاین
نکته: اگر جزء دامنه نباشد، در این صورت برای پیدا کردن مقدار متناظر با این باید از برونیابی یا Extrapolation استفاده کنیم.
درون یابی چند جمله ای
درونیابی چند جملهای یکی از روشهای محاسبات عددی برای درونیابی است که در آن از یک چند جملهای درجه که از نقطه عبور میکند، استفاده میکنیم. روشهای مختلفی برای تعیین این چند جملهای وجود دارد که عبارتاند از:
- درونیابی مستقیم یا روش چند جملهای وندرموند
- روش نیوتن
- درونیابی لاگرانژ
با توجه به اینکه در مطلب «درون یابی نیوتن – به زبان ساده» از مجله فرادرس این روش کاملا توضیح داده شده است، در ادامه این بخش فقط به توضیح دو روش دیگر پرداختهایم.
درون یابی مستقیم یا روش چند جمله ای وندرموند
فرض کنید نقطه بهصورت و داریم و مقادیر نمونه یک تابع در این نقاط برابر است با . درونیابی چند جملهای مستقیم در این حالت مسئلهای است که در آن باید یک چند جملهای به شکل با درجه را پیدا کنیم، طوری که مقادیری برابر با را برای بازتولید کند. به عبارت دیگر، نمودار چند جملهای باید از نقاطی به شکل عبور کند.
میدانیم تعریف یک چند جملهای درجه و با ضرایبی بهصورت به شکل زیر است:
ابتدا باید تعداد درجات آزادی در چند جملهای با تعداد نقاطی که میخواهیم تابع با آنها فیت شود، هماهنگ باشد. سپس برای اینکه ببینیم روش مستقیم و عددی حل مسئله درونیابی در محاسبات عددی چیست، تعریف زیر را در نظر میگیریم:
این عبارت برای کلیه برقرار است. در این معادله که با نماد اندیسگذاری شدهاند، مجهولات ما ضرایب هستند. پس با یک سیستم خطی مواجه هستیم:
در رابطه بالا «ماتریس وندرموند» نام دارد که به شکل زیر تعریف میشود:
در ادامه با کاربرد یک نرمافزار عددی مانند متلب میتوانیم شکل برداری ، مقادیر سمت راست و ماتریس را استخراج کنیم و به این ترتیب چنین سیستمی را به شکل و بهصورت عددی در متلب حل میکنیم. بنابراین ضرایب چند جملهای موردنظر ما به این روش بهدست خواهند آمد و حالا میتوانیم آن را بین نقاط شبکه به جهت نمایش درونیابی رسم کنیم. در اولین مثال این بخش، خواهید دید که چگونه ماتریسهای دو در دو یا سه در سه چگونه در فرآیند درونیابی مستقیم خطی و مربعی ایجاد میشوند.
نکته ۱: اگر از یک چند جملهای خطی برای درونیابی مستقیم استفاده کنیم، در این صورت درونیابی خطی انجام دادهایم.
نکته ۲: اگر از یک چند جملهای درجه دو برای درونیابی مستقیم استفاده کنیم، در این صورت درونیابی مربعی انجام دادهایم.
درون یابی چند جمله ای به روش لاگرانژ
در این قسمت توضیح میدهیم که چگونه میتوانیم مسئله درونیابی چند جملهای را در محاسبات عددی به کمک روش لاگرانژ حل کنیم. ابتدا خطای درونیابی را بر اساس نرم یکنواخت اختلاف و به شکل زیر تعریف میکنیم:
که در آن ماکزیمم روی بازه بسته گرفته شده است. حالا با در نظر گرفتن بهصورت یک فضای چند جملهای با درجه آزادی به شکل ، میخواهیم ببینیم روش حل مسئله درونیابی چند جملهای در محاسبات عددی چیست. اجازه دهید مجموعه را بهعنوان مجموعهای از اعداد گسسته در نظر بگیریم که در آن برای هر ، یک چند جملهای خاص مانند از درجه وجود دارد به گونهای که داریم:
در این روند با ثابت در نظر گرفتن میتوانیم بگوییم دارای ریشههایی در برای تمام است، بنابراین باید به شکل زیر باشد:
با ارزیابی این عبارت در ، به روابط زیر میرسیم:
بنابراین تنها عبارت ممکن برای به شکل زیر خواهد شد:
این چند جملهایهای اولیه اساس بسط هر چند جملهای را تشکیل میدهند. در بخش مثالها بهتر متوجه کاربرد این روابط خواهید شد.
قضیه درونیابی لاگرانژ: اگر مجموعهای از اعداد گسسته و حقیقی و مجموعهای از اعداد حقیقی باشد، در این صورت یک خاص داریم به گونهای که رابطه زیر برقرار است:
عبارت گستردهتر برای رابطه بالا با توجه به لم اولی که توضیح داده شد، به شکل زیر است:
که در آن ها همان چندجملهایهای اولیه لاگرانژ هستند.
درون یابی اسپلاین
گفتیم روش درونیابی چند جملهای بر مبنای پیدا کردن یک چند جملهای درجه استوار است. اما اگر خیلی بزرگ باشد، ممکن است با رفتار نوسانی در درونیابی چند جملهای روبرو شویم. این رفتار «پدیده رونگه» نام دارد. با کاربرد درونیابی اسپلاین میتوانیم از رخ دادن پدیده رونگه یا رفتار نوسانی نقاط داده جلوگیری کنیم. درونیابی اسپلاین سه نوع است، خطی، مربعی و مکعبی که در ادامه به اختصار این روشها را توضیح میدهیم.
اسپلاین خطی
شکل زیر را در نظر بگیرید که در آن نقاطی به شکل و و … و همان دادههای نقطهای ما هستند. برای تعیین اسپلاین خطی جهت درونیابی این دادهها باید یک خط مستقیم بین هر دو نقطه رسم کنیم. علت نامگذاری این نوع اسپلاین به شکل خطی یا درجه یک، رسم خط مستقیم بین نقاط است.
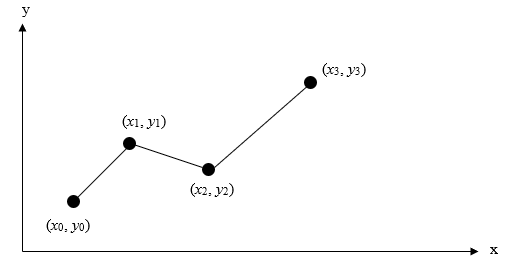
اگر فرض کنیم دادههای بالا بهصورت نزولی مرتب شدهاند، تابع متناظر با این خطوط در هر بازه برابر است با:
و به همین ترتیب برای تمام نقاط. در نتیجه در حالت کلی برای تابع اسپلاین خطی داریم:
اسپلاین مربعی
در اسپلاین مربعی تابع به شکل زیر برای هر دو نقطه در نظر گرفته میشود:
بنابراین تابع اسپلاین مربعی در حالت کلی شکل زیر را دارد:
در این حالت ضریب مجهول داریم که باید با در نظر گرفتن نکات زیر و رسیدن به معادله تعیین شوند:
- اگر تابع اسپلاین مربعی را برای هر دو نقطه پشت سر هم بنویسیم، معادله خواهیم داشت.
- مقدار مشتق اول تابع اسپلاین برای هر دو نقطه پشت سر هم در یک نقطه مشترک برابر است. از این نکته معادله خواهیم داشت.
- تا اینجا معادله داریم. آخرین معادله با توجه به این نکته که اولین جمله در تابع اسپلاین مربعی خطی است ()، بهدست میآید.
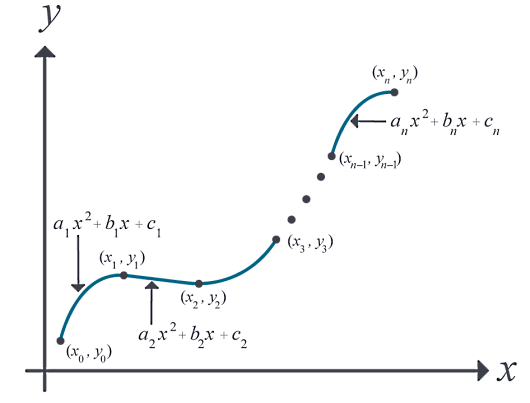
خطای درون یابی توابع هموار
در بخش قبل آموختیم روشهای مختلف درونیابی مانند چند جملهایهای اولیه لاگرانژ یا روش اسپلاین در محاسبات عددی چیست. در این قسمت با توضیح یک قضیه نشان میدهیم روش بررسی خطای درونیابی در محاسبات عددی چگونه است. فرض کنید رابطه برای تمام های مثبت برقرار است. همچنین فرض کنید مجموعهای از اعداد گسسته و حقیقی در بازه بسته است. با در نظر گرفتن بهعنوان چند جملهای درونیابی لاگرانژ تابع در ، برای هر همواره وجود دارد، به گونهای که داریم:
در این رابطه به شکل زیر تعریف میشود:
تخمین خطای درونیابی مستقیما با توجه به این قضیه بهدست خواهد آمد:
دقت کنید طبق فرضهای اولیه برای برقراری این قضیه لازم است تابع پیوسته باشد. در این صورت داریم:
بنابراین اگر شود، برای برخی از ها خطای درونیابی برابر با صفر خواهد شد.
حل مثال از روش های درون یابی
در انتهای این بخش با حل چند مثال به شما کمک میکنیم تا بهتر متوجه شوید مفهوم درونیابی در محاسبات عددی چیست.
مثال ۱
فرض کنید مقادیر سرعت موشکی بر حسب زمان در قالب جدولی به شکل زیر داده شده است. سرعت این موشک را در زمان با استفاده از روش درونیابی مستقیم و در دو حالت با کاربرد چند جملهای خطی و درجه دو پیدا کنید:
پاسخ
در این سوال ابتدا با کاربرد روش درونیابی خطی میتوانیم معادله سرعت را به شکل زیر بنویسیم:
چون از یک چند جملهای خطی استفاده کردهایم، پس کافی است دو نقطه را که به لحظه نزدیکتر هستند، انتخاب کنیم، برای مثال نقاط و :
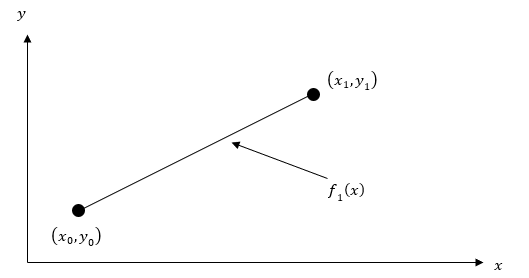
با توجه به اینکه مقادیر سرعت برای این دو لحظه از زمان مشخص هستند، بنابراین با قرار دادن مقادیر زمان و سرعت مشخص در معادله چند جملهای بالا خواهیم داشت:
اگر دو معادله و دو مجهول بالا را حل کنیم، در نهایت معادله سرعت برابر است با:
نکته مهم این است که این معادله برای تمام زمانهای برقرار است. پس سرعت در لحظه به روش درونیابی خطی برابر میشود با:
در مرحله بعدی همین سرعت را با استفاده از یک چند جملهای درجه دو محاسبه میکنیم:
در اینجا باید سه نقطه را که به لحظه نزدیکتر هستند، انتخاب کنیم، برای مثال نقاط و و :
در این حالت سه معادله و سه مجهول داریم که با حل معادلات به روش ماتریسی میتوانیم پس از تعیین مجهولها به معادله زیر برای سرعت برسیم:
این معادله برای بازه برقرار است و سرعت را در لحظه خواسته شده به شکل زیر به ما میدهد:
مثال ۲
درونیابی خطی بین دو نقطه و چگونه است؟
پاسخ
چندجملهای طبق قضیه درونیابی لاگرانژ برابر است با:
برای این مسئله چند جملهای ما بهصورت زیر خواهد شد:
همچنین با توجه به رابطه خواهیم داشت:
مثال ۳
فرض کنید تابعی به شکل داریم. به کمک یک سهمی () این تابع را در سه نقطه و و درونیابی کنید:
پاسخ
ابتدا جمله اولیه لاگرانژ را به شکل زیر و طبق میسازیم:
بهطور مشابه برای سایر جملات خواهیم داشت:
بنابراین درونیابی درجه دو برای این سوال با توجه به فرمول ، به شکل زیر خواهد شد:
همانطور که ملاحظه میکنید، بخشی از پاسخ این محاسبات در قالب توابع هایپربولیک بهدست میآید. البته یکی دیگر از چندجملهایهایی که میتواند برای تقریب تابع نمایی روی بازه بستهای مانند بکار رود، بسط تیلور حول نقطه است:
مثال ۴
بار دیگر اولین مثال از این بخش را در نظر بگیرید و سعی کنید این بار این سوال را به کمک درونیابی اسپلاین حل کنید:
پاسخ
برای استفاده از اسپلاین خطی نیاز داریم دو داده نقطهای نزدیک به نقطه در نظر بگیریم. بهترین انتخابها نقاط و هستند. مقادیر سرعت متناظر با این نقاط در سوال مشخص شدهاند. بنابراین کافی است تابع اسپلاین خطی را همان تابع سرعت بر حسب زمان یعنی در نظر بگیریم. پس خواهیم داشت:
با قرار دادن ثوابت خواهیم داشت:
حالا میتوانیم با قرار دادن سرعت را در این لحظه به روش اسپلاین محاسبه کنیم:
معادلات غیرخطی
در اولین قسمت از این بخش میآموزیم تعریف معادلات غیرخطی در محاسبات عددی چیست و در چه نوع مسائلی به حل این نوع معادلات نیاز داریم. هر معادلهای که در آن توانی بیشتر از یک برای متغیر داشته باشیم، یک معادله غیرخطی نامیده میشود. یک مثال ملموس و ساده از حل معادلات غیرخطی شکل زیر است که اگر در آن وزن مخصوص و شعاع توپ قرمز رنگ مشخص باشد ( و )، با بکار بردن قوانین فیزیکی حاکم بر این مسئله به یک معادله غیرخطی به شکل زیر خواهیم رسید:
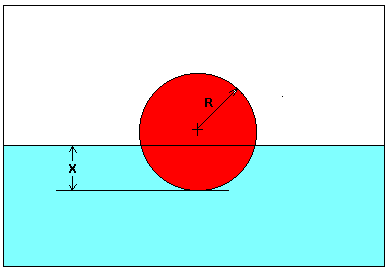
با حل معادله غیرخطی بالا میتوانیم یا عمقی که توپ در آب شناور میماند را پیدا کنیم. بنابراین پس از آشنایی با معادلات غیرخطی، در مرحله بعد باید بدانیم روش پیدا کردن ریشههای این معادلات در محاسبات عددی چیست که در بخش بعد به این موضوع خواهیم پرداخت.
روش های عددی پیدا کردن ریشهها
ابتدا با سادهترین فرم یک معادله غیرخطی یعنی یک معادله درجه دو به شکل شروع میکنیم. میدانیم چنین معادلهای دو ریشه به شکل زیر دارد:
و با توجه به مقدار عبارت ، ریشههای این معادله ممکن است حقیقی، مختلط یا تکراری باشند:
- اگر مثبت باشد، ریشهها حقیقی هستند.
- اگر منفی باشد، ریشهها مختلط هستند.
- اگر مساوی با صفر باشد، ریشهها حقیقی و تکراری هستند.
اما در اغلب مسائل پیچیده عددی با معادلات غیرخطی از مراتب یا درجات بالاتر سروکار داریم. در این موارد باید از روشهای محاسبات عددی برای پیدا کردن ریشهها استفاده کنیم که عبارتاند از:
- روش دو بخشی
- روش نیوتن
- روش وتری
در ادامه دو روش اول را همراه با حل مثال توضیح میدهیم. در مورد سومین روش که Secant Method هم نامیده میشود، میتوانید مطلب «روش وتری – به زبان ساده» از مجله فرادرس را مطالعه کنید.
روش دو بخشی
روش دو بخشی یا Bisection Method که الگوریتم جستجوی دودویی هم نامیده میشود، یکی از اولین روشهایی است که برای پیدا کردن ریشههای یک معادله غیرخطی استفاده شد. این روش بر مبنای قضیه زیر تعریف میشود:
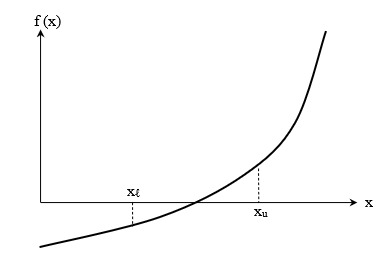
معادلهای به شکل را در نظر بگیرید که در آن یک تابع پیوسته حقیقی است. این معادله حداقل یک ریشه بین و دارد، اگر .
- اگر ، در این صورت ممکن است بین و ریشهای داشته باشیم، همچنان که ممکن است بین و هیچ ریشهای نداشته باشیم.
- اگر ، در این صورت ممکن است بین و بیشتر از یک ریشه هم داشته باشیم، اما وجود یک ریشه قطعی است.
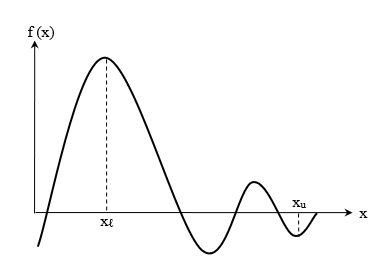
همانطور که مشاهده میکنید، اگر مقدار تابع در دو نقطه و تغییر علامت دهد، در این صورت حتما یک ریشه داریم و تابع ما حداقل در یک نقطه محور افقی را قطع میکند:
اما همانطور که گفتیم اگر ، حداقل یک ریشه داریم. این به این معنا است که ممکن است بیشتر از یک ریشه هم داشته باشیم. در شکل زیر مشاهده میکنید که بین دو نقطه و با توجه به تغییر علامت دادن مقدار تابع در این دو نقطه، سه ریشه وجود دارد:
این در حالی است که اگر تابع پیوسته موردنظر ما در این دو نقطه تغییر علامت ندهد، همچنان ممکن است برای معادله بین این دو نقطه ریشه داشته باشیم. برای مثال، در شکل زیر مشاهده میکنید با اینکه مقدار تابع برای هر دو نقطه و مثبت است، اما در فاصله بین این دو نقطه تابع محور افقی را در دو نقطه قطع کرده است. پس دو ریشه داریم:
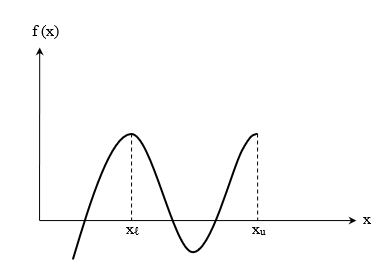
در عین حال برای حالت ممکن است طبق شکلهای زیر هیچ ریشهای نداشته باشیم:
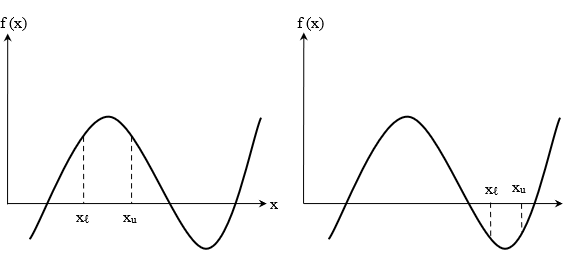
الگوریتم روش دو بخشی برای یافتن ریشههای معادله بهصورت زیر است:
- انتخاب دو ریشه حدسی برای معادله بالا بهعنوان و طوری که برای آنها برقرار باشد.
- تخمین نقطه یا نقطه میانی بهعنوان ریشه دیگر و با در نظر گرفتن .
- اگر ، در این صورت ریشه بین و قرار میگیرد: و .
- اگر ، در این صورت ریشه بین و قرار میگیرد: و .
- اگر ، در این صورت ریشه درست است و الگوریتم متوقف میشود.
در ادامه به مثالی که با این روش حل شده است، دقت کنید.
مثال
با استفاده از روش دو بخشی و حدس اولیه و ، ریشههای معادله غیرخطی زیر را پس از دو تکرار پیدا کنید:
پاسخ
ابتدا معادله بالا را به شکل زیر بازنویسی میکنیم:
سپس چک میکنیم که آیا در دو مقدار و بهعنوان و در این سوال، آیا مقدار تابع تغییر علامت میدهد یا خیر:
پس شرط برقرار است. حالا اولین تکرار را با در نظر گرفتن و شروع میکنیم:
برای انجام تکرار دوم، لازم است ابتدا مقدار تابع را در پیدا کنیم:
بنابراین برقرار است و در نتیجه ریشه ما بین و یا و قرار میگیرد. پس تخمین به شکل زیر خواهد شد:
روش نیوتن – رافسون
روش بعدی پیدا کردن ریشههای معادلات غیرخطی در محاسبات عددی، روش نیوتن – رافسون (Newton-Raphson Method) یا به اختصار روش نیوتن است. فرمولی که در این روش برای حل معادلات استفاده میشود به شکل زیر است:
مثال
با استفاده از روش نیوتن و حدس اولیه ، ریشههای معادله غیرخطی زیر را پس از دو تکرار پیدا کنید:
پاسخ
برای حل معادله ، ابتدا باید مشتق را محاسبه کنیم:
حالا با توجه به حدس اولیه، فرمول روش نیوتن را برای تکرار اول مینویسیم:
در تکرار دوم، مجددا فرمول بالا را مینویسیم، با این تفاوت که یک واحد به اضافه میشود:
مسیر یادگیری معادلات دیفرانسیل با فرادرس
در این نوشته از مجله فرادرس یاد گرفتیم محاسبات عددی چیست و دیدیم که یکی از مهمترین مباحث در این شاخه از ریاضیات به روشهای حل انواع معادلات دیفرانسیل اختصاص دارد. به همین منظور، در این بخش چند فیلم آموزشی مرتبط در این زمینه را برای شما در نظر گرفتهایم تا با مشاهده این دورهها یادگیری خود را در این بخش تکمیل کنید:
- فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد فرادرس
- فیلم آموزش حل عددی معادلات دیفرانسیل جزئی به روش تفاضلات محدود در فرترن FORTRAN فرادرس
- فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica فرادرس
معادلات دیفرانسیل معمولی (ODE)
در این بخش میآموزیم روشهای مختلف حل معادلات دیفرانسیل معمولی یا ODE در محاسبات عددی چیست. معادلات دیفرانسیل معمولی کاربرد گستردهای در حل مسائل مختلف علوم مهندسی دارند. برای مثال، اگر بخواهیم دمای یک گوی کروی حرارت داده شده را به عنوان تابعی از دما پیدا کنیم، باید یک معادله دیفرانسیل معمولی مرتبه اول را حل کنیم. به این ترتیب، فرمولبندی اغلب مسائل فیزیکی و مهندسی به شکلگیری یک معادله دیفرانسیل معمولی منجر میشود.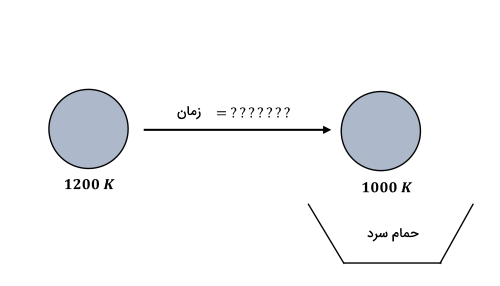
هر معادلهای که شامل مشتقهای متغیرهای موجود در آن معادله باشد، یک معادله دیفرانسیل نامیده میشود. در حالت کلی معادلات دیفرانسیل طبق نمودار زیر دو نوع هستند:
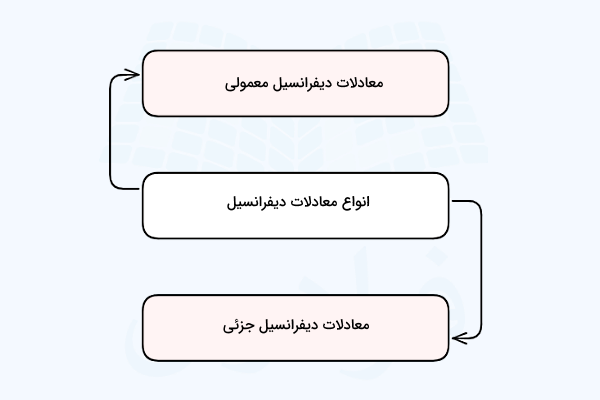
در معادلات دیفرانسیل معمولی فقط یک متغیر مستقل مانند وجود دارد که متغیر وابسته به آن بستگی دارد. مثالهای این نوع معادلات به شکل زیر است:
تقسیمبندی معادلات دیفرانسیل معمولی بر مبنای درجه و مرتبه آنها انجام میشود. مرتبه یک معادله دیفرانسیل معمولی معادل است با بالاترین مرتبه مشتقگیری در آن معادله، در حالی که درجه این نوع معادلات بر اساس توان بالاترین مشتق در این معادلات تعیین میشود. به این ترتیب معادله زیر یک معادله دیفرانسیل معمولی مرتبه سه و خطی یا درجه یک محسوب میشود:
در حالی که معادله زیر یک معادله دیفرانسیل معمولی از مرتبه یک و درجه دو است:
برای اینکه این مبحث را از طریق حل مثال و تمرین بهتر بیاموزید، میتوانید به مطلب «نمونه سوال معادلات دیفرانسیل» از مجله فرادرس مراجعه کنید که لینک آن در ادامه برای شما قرار داده شده است:
روش حل دقیق معادلات دیفرانسیل معمولی مرتبه اول
در این بخش میخواهیم نشان دهیم چگونه میتوان یک معادله دیفرانسیل معمولی را با روش کلاسیکی حل کرد. ابتدا فرم کلی چنین معادلهای را به شکل زیر در نظر میگیریم که در آن ها ضرایب ثابت معادله هستند:
راهحل کلی این معادله شامل دو بخش به شکل زیر است:
- : بخش همگن راهحل
- : بخش ویژه یا ناهمگن راهحل
معادله دیفرانسیل معمولی همگن
این بخش از راهحل با صفر در نظر گرفتن سمت دیگر تساوی در معادله بالا به دست میآید. بنابراین راهحل معادلهای به شکل زیر خواهد بود:
معادله بالا را میتوانیم به صورت سمبولیک به شکل زیر بنویسیم:
که در آن داریم:
در این معادلات عمل روی با عبارت زیر معادل است که یکی پس از دیگری عمل میکنند:
که در آنها فاکتورهای معادله زیر هستند:
از طرفی میدانیم معادله با دو رابطه زیر برابر است:
بنابراین معادله نیز با معادله زیر معادل خواهد بود:
حل چنین معادلهای بر اساس حالتهای مختلفی به شرح زیر انجام میشود:
- ریشهها حقیقی و متفاوت هستند.
- ریشهها حقیقی و مشابه هستند.
- ریشهها مختلط هستند.
ریشههای حقیقی و متفاوت
اگر ، در این صورت کل سمت چپ معادله بالا برابر است با صفر. پس راهحل معادله ، یک راهحل ممکن برای معادله همگن ما است. اصولا به معادلهای با فرم «معادله دیفرانسیل خطی و مرتبه اول لایبنیتس» گفته میشود که راهحل آن به شکل زیر است:
با توجه به اینکه هر کدام از این فاکتور میتوانند قبل از قرار بگیرند، بنابراین راهحل مختلف و متناظر با این فاکتور مختلف توسط ضرایب زیر داده میشوند:
که در آنها ریشههای معادله هستند و نیز ثوابت این معادلهاند. به این ترتیب راهحل کلی معادله همگن با بکارگیری پاسخهای لایبنیتس به شکل زیر خواهد بود:
ریشههای حقیقی و مشابه
اگر دو ریشه یک معادله دیفرانسیل همگن مشابه باشند، برای مثال ، در این صورت داریم:
حال بیاید روی بخش کار کنیم. اگر ، در این صورت و در نتیجه خواهیم داشت:
سپس راهحل بالا را در جایگزین میکنیم:
که با انتگرالگیری از دو طرف این رابطه خواهیم داشت:
بنابراین راهحل نهایی معادله همگن در این بخش برابر است با:
این روند برای دو ریشه مشابه بود. اگر ریشه مشابه هم داشتیم، پاسخ به این صورت است:
ریشههای مختلط
اگر یک جفت از ریشهها مختلط باشند، برای مثال و ، در این صورت خواهیم داشت:
اگر توابع نمایی را بر حسب سینوس و کسینوس بنویسیم، با در نظر گرفتن و خواهیم داشت:
معادله دیفرانسیل معمولی ناهمگن
بار دیگر به معادله دیفرانسیل معمولی در ابتدای این بخش بازمیگردیم:
پاسخ ویژه این معادله از برابر قرار دادن سمت چپ این معادله با حاصل میشود:
تابع میتواند بهصورت نمایی یا مثلثاتی یا ترکیبی از هر دو باشد. جدول زیر نشان میدهد بخش ویژه راهحل این معادله برای توابع مختلف در محاسبات عددی چیست:
source
