تفاوت فرمول STDEV با STDEV.P، در مبنای ریاضی و کاربرد آنها است. فانکشن STDEV، برای محاسبه انحراف معیار در اکسل مورد استفاده قرار میگیرد. البته در این محاسبات، از فرمول انحراف معیار برای نمونه آماری استفاده میشود. در طرف دیگر، تابع STDEV.P قرار دارد. این تابع نیز به منظور تعیین انحراف معیار مورد استفاده قرار میگیرد. البته STDEV.P برای انجام این محاسبات، فرمول انحراف معیار جامعه آماری را بکار میبرد. بنابراین، اگر بخواهیم انحراف معیار کل دادههای موجود را به دست بیاوریم، از فرمول STDEV.P استفاده میکنیم و اگر بخواهیم انحراف معیار زیرمجموعهای از دادهها را به دست بیاوریم، از فرمول STDEV استفاده میکنیم. در این مطلب از مجله فرادرس، به توضیح کامل در مورد تفاوت فرمول STDEV با STDEV.P میپردازیم.

برای شروع، ابتدا در مورد توابع STDEV و STDEV.P و کاربرد اصلی آنها در اکسل به طور مختصر صحبت میکنیم. سپس، تفاوت این دو تابع را از نظر فرمول ریاضی مورد بررسی قرار میدهیم. در ادامه، به معرفی آرگومانهای توابع STDEV و STDEV.P میپردازیم. در نهایت، ضمن حل یک مثال برای نمایش تفاوت فرمول STDEV و STDEV.P، این توابع را با دیگر توابع آماری اکسل مقایسه میکنیم.
توابع STDEV و STDEV.P چه هستند و چه تفاوتی با یکدیگر دارند؟
محاسبه انحراف معیار در نرمافزار اکسل، با استفاده از فانکشن STDEV یا STDEV.S انجام میگیرد. البته کاربرد اصلی این تابع، تعیین انحراف معیار نمونهای از جامعه آماری است. برای به دست آوردن انحراف معیار کل جامعه آماری، باید از تابع دیگری با عنوان STDEVP یا STDEV.P استفاده کرد. بنابراین، اولین و مهمترین تفاوت فرمول STDEV و STDEV.P، هدف از استفاده آنها است.
توابع STDEV و STDEVP، از توابع اکسل ۲۰۰۷ و نسخههای قدیمیتر اکسل محسوب میشوند. مایکروسافت، این توابع را در اکسل ۲۰۱۰ و نسخههای جدیدتر اکسل، با توابع STDEV.S و STDEV.P جایگزین کرد. البته عملکرد تابع STDEV.S با STDEV و تابع STDEV.P با STDEVP، تفاوتی ندارد. 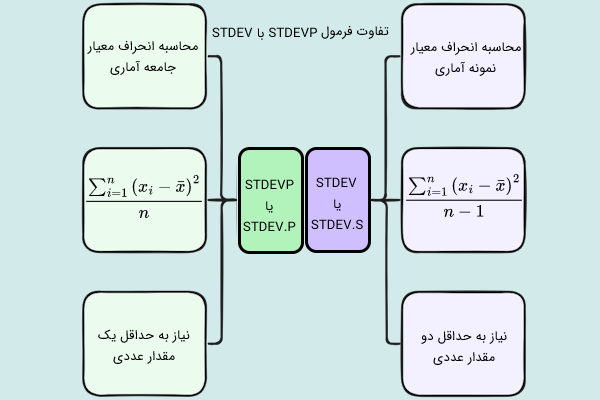
برای اینکه تفاوت فرمول STDEV با STDEV.P در اکسل را بهتر درک کنید، در ادامه، به بررسی مبنای ریاضی، آرگومانها و کاربردهای هر یک از این توابع میپردازیم.
تفاوت فرمول ریاضی STDEV با STDEV.P در اکسل
«انحراف معیار» (Standard Deviation)، معیاری برای ارزیابی میزان پراکندگی یا اصطلاحا انحراف مجموعهای از مقادیر، نسبت به میانگین آنها است. این معیار، از انواع شاخصهای پراکندگی و از مفاهیم آماری مهم به شمار میرود.
به همین دلیل، معمولا از انحراف معیار به عنوان یکی از کمیتهای اصلی هنگام مطالعه بر روی ویژگیهای جامعه آماری و یا نمونه آماری استفاده میشود.
- جامعه آماری: کل مشاهدات، افراد یا آیتمها در یک مطالعه آماری
- نمونه آماری: زیرمجموعه انتخابی از جامعه آماری
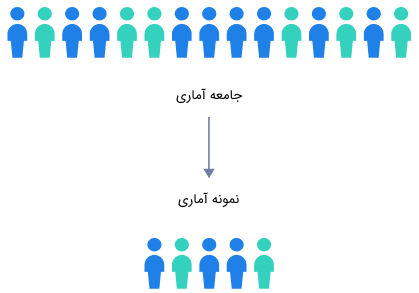
تعداد اعضای نمونه آماری، همواره کمتر از کل جامعه آماری است. انحراف معیار جامعه آماری با استفاده از فرمول زیر به دست میآید:
- : انحراف معیار جامعه آماری
- : مقدار متغیر آماری i-ام
- : تعداد کل اعضای جامعه آماری
- : میانگین جامعه آماری
اگر تعدادی از افراد جامعه را به عنوان نمونه آماری از کل جمعیت جدا کنیم، انحراف معیار آنها برابر میشود با:
- : انحراف معیار نمونه آماری
- : مقدار متغیر آماری i-ام
- : تعداد اعضای نمونه آماری
- : میانگین نمونه آماری
فرمولهای مورد استفاده برای تعیین انحراف معیار جامعه آماری و نمونه آماری را باهم مقایسه کنید:
تفاوت بین روابط بالا، یکی از دلایل تفاوت فرمول STDEV با STDEV.P است. تابع STDEV یا STDEV.S در اکسل، از فرمول انحراف معیار نمونه آماری (S) استفاده میکند. تابع STDEVP یا STDEV.P، فرمول انحراف معیار جامعه آماری (σ) را مورد استفاده قرار میدهد. بنابراین، مبنای محاسبات ریاضی این دو تابع با یکدیگر تفاوت دارد.
تفاوت آرگومانهای فرمول STDEV با STDEV.P در اکسل
یکی از معیارهای مقایسه توابع STDEV و STDEVP در اکسل، آرگومانهای این تابع است. توابع STDEV یا STDEV.S و STDEVP یا STDEV.P، از نظر آرگومان، هیچ تفاوتی با یکدیگر ندارند.
با نوشتن هر یک از این عبارتها درون کادر فرمولنویسی در اکسل (به همراه علامت =)، با آرگومانهای نمایش داده شده در تصویر زیر مواجه میشوید.
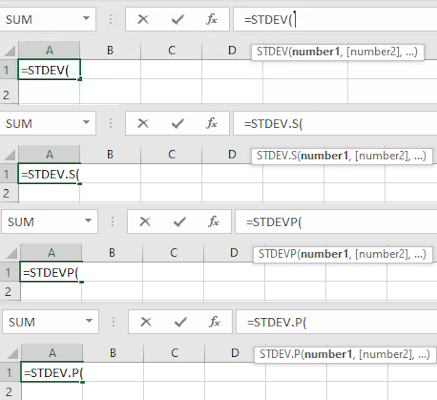
آرگومانهای توابع STDEV و STDEVP در اکسل، عبارت هستند از:
- number1 : اولین آرگومان نمونه آماری (در تابع STDEV) یا جامعه آماری (در تابع STDEVP)
- number2 تا number254: آرگومانهای بعدی نمونه یا جامعه آماری
آرگومان number1، یک آرگومان الزامی است. یعنی برای نمایش صحیح خروجی، حتما باید یک مقدار عددی یا محدودهای از سلولها را به این آرگومان ارجاع دهید. آرگومانهایnumber2 تا number254، اختیاری هستند.
یکی دیگر از تفاوت های فرمول STDEV با STDEV.P در اکسل، ورودی آرگومانهای این دو فرمول است. محاسبه انحراف معیار در اکسل، با حداقل دو مقدار عددی صورت میگیرد. در تابع STDEV یا STDEV.S، اگر محدوده انتخابی برای آرگومان number1، حاوی حداقل دو مقدار عددی باشد، انحراف معیار دو عدد محاسبه میشود و به نمایش درمیآید.
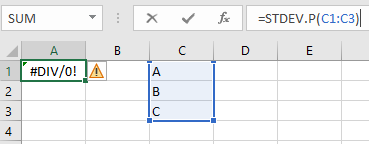
توجه داشته باشید که اگر ورودی آرگومان number1، یک مقدار عددی یا ارجاع به یک سلول حاوی عدد باشد، حتما باید ورودی آرگومان number2 را نیز با یک مقدار عددی یا ارجاع به سلول حاوی عدد، به تابع اضافه کنیم. در صورتی که مقادیر یا محدوده مشخص شده به عنوان ورودیهای تابع STDEV یا STDEV.S، حاوی یک عدد یا بدون عدد باشد، با خطای #DIV/0! مواجه خواهید شد.
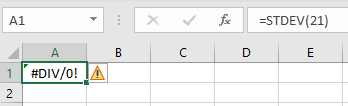
دلیل مشاهده خطای نمایش داده شده در تصویر بالا، به فرمول محاسبه انحراف معیار نمونه آماری ارتباط دارد.
بر اساس این فرمول، اگر نمونه ما تنها یک عضو داشته باشد (n=1)، مخرج کسر برابر با صفر میشود. به این ترتیب، امکان محاسبه جواب وجود ندارد؛ زیرا در ریاضی، حاصل تقسیم عدد بر صفر، تعریف نشده است.
اکنون به سراغ تابع STDEVP یا STDEV.P میرویم. برای محاسبه انحراف معیار توسط این تابع نیز به حداقل دو مقدار عددی نیاز داریم. این مقادیر را میتوان با ارجاع به محدودهای از سلولها (به عنوان ورودی آرگومان number1) تعریف کرد یا هر عدد را به صورت جداگانه در محل آرگومانها نوشت. تفاوت فرمول STDEV.P با STDEV در این است که اگر تنها یک مقدار عددی در آرگومانهای STDEVP یا STDEV.P وجود داشته باشد، هیچ خطایی نمایش داده نمیشود و نتیجه محاسبه انحراف معیار برابر با صفر میشود.
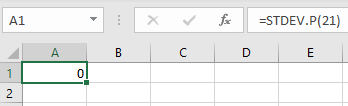
دلیل صفر شدن خروجی تابع STDEV.P در هنگام نوشتن یا ارجاع به تنها یک عدد، در فرمول انحراف معیار جامعه آماری نهفته است.
بر اساس این فرمول، اگر جامعه آماری ما شامل یک عضو عددی باشد، حاصل برابر صفر شده و جواب انحراف معیار نیز برابر با صفر میشود. دقت داشته باشید که در تمام تعاریف و مثالها، به مقادیر عددی اشاره کردیم. هیچ تفاوت خاصی بین فرمول STDEV با STDEV.P در هنگام نوشتن یا ارجاع به مقادیر متنی وجود ندارد.
- آرگومانهای توابع STDEV و STDEV.P، میتوانند عدد، متن، آرایه یا ارجاع به سلولهای حاوی عدد باشند.
- در آرگومانهای توابع STDEV و STDEV.P، میتوان مقادیر منطقی مانند «TRUE» یا «FALSE» و قالب متنی اعداد مانند “1” را نیز به صورت مستقیم تایپ کرد. در این حالت، عبارت TRUE برابر با عدد ۱، عبارت FALSE برابر با عدد ۰ و قالب متنی اعداد برابر با خود عدد در نظر گرفته میشود.
- در صورت ارجاع به یک سلول یا محدودهای از سلولها به عنوان ورودی آرگومانها در توابع STDEV و STDEV.P، فقط ورودیهای عددی در محاسبات مورد استفاده قرار میگیرند. در این حالت، سلولهای خالی، منطقی، متن یا مقادیر خطا، نادیده گرفته میشوند.
به طور کلی، توابع STDEV و STDEV.P، عملکرد بسیار مشابهی دارند و اصلیترین تفاوت این دو تابع، مبنای ریاضی (فرمول محاسبه انحراف معیار) در آنها است. در یکی از مطالب فرادرس با عنوان «انحراف معیار در اکسل چگونه محاسبه می شود؟ – گام به گام»، در مورد توابع و فرمولهای مورد استفاده برای محاسبه انحراف معیار در اکسل صحبت کردیم. در بخشهای بعدی، به معرفی اجمالی این توابع و تفاوت آنها با STDEV و STDEV.P خواهیم پرداخت.
حل مثال برای نمایش تفاوت فرمول STDEV و STDEV.P در اکسل
برای درک بهتر تفاوت فرمول STDEV و STDEV.P از نظر کاربرد و عملکرد، به حل یک مثال در حوزه مالی میپردازیم.
فرض کنید دادههای مربوط به فروش ماهانه یک کسب و کار در سه سال گذشته را مانند تصویر زیر در قالب یک شیت اکسل به ما دادهاند. واحد فروش را میلیون تومان در نظر بگیرید.
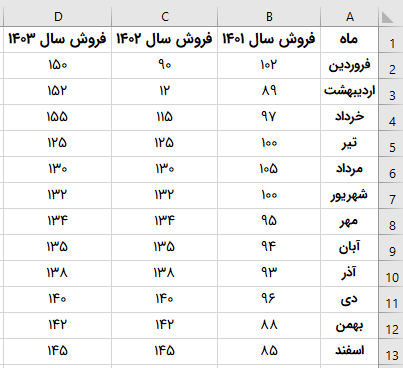
میخواهیم عملکرد فروش کسب و کار مورد نظر را طی این سه سال مورد بررسی قرار دهیم. یکی از شاخصهای آماری مفید برای انجام این کار، انحراف معیار است. با استفاده از این شاخص میتوانیم میزان پراکندگی فروش نسبت فروش میانگین را به دست بیاوریم. دادههای فروش هر سه سال، کل جامعه آماری ما را تشکیل میدهند. برای محاسبه انحراف معیار یک جامعه آماری، باید از فرمول STDEVP یا STDEV.P استفاده کنیم. به این منظور، دو روش داریم. روش اول، وارد کردن جداگانه تمام اعداد به عنوان آرگومانهای تابع است. روش دوم، ارجاع به محدوده سلولهای حاوی آمار فروش است.

پایین بودن انحراف معیار، نشاندهنده عملکرد ثابت و قابل پیشبینی و بالا بودن انحراف معیار، به معنای نوسان و تغییر مثبت یا منفی در عملکرد است. هنگام بررسی فروش، با توجه به اهداف کسب و کار، هم انحراف معیار پایین و هم انحراف معیار بالا میتواند مد نظر باشد. برای درک بهتر عملکرد، علاوه بر انحراف معیار کل، باید انحراف معیار فروش در هر سال را نیز به دست بیاوریم. این کار، با استفاده از فرمول STDEV یا STDEV.S انجام میشود؛ زیرا دادههای فروش ماهانه در هر سال، به عنوان نمونه آماری (زیرمجموعهای از جامعه آماری) هستند.
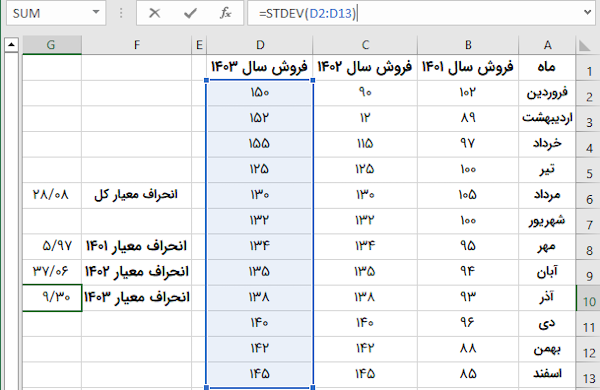
همانطور که مشاهده میکنید، نوسانات فروش در سال ۱۴۰۳، کمتر از سالهای دیگر است. انحراف معیار فروش در سال ۱۴۰۲، به دلیل فروش بسیار پایین در اردیبهشت، نوسانات بسیار بالاتری را نسبت به سالهای دیگر نمایش میدهد. بر اساس انحراف معیار بدستآمده، در سال ۱۴۰۳ نیز میزان فروش دارای نوسان بوده است. به طور کلی، شاخصهای آماری، در کنار یکدیگر معنی بیشتری پیدا میکنند. به عنوان مثال، در اینجا با استفاده از تابع AVERAGE در اکسل، میانگین فروش هر سال را به دست میآوریم.
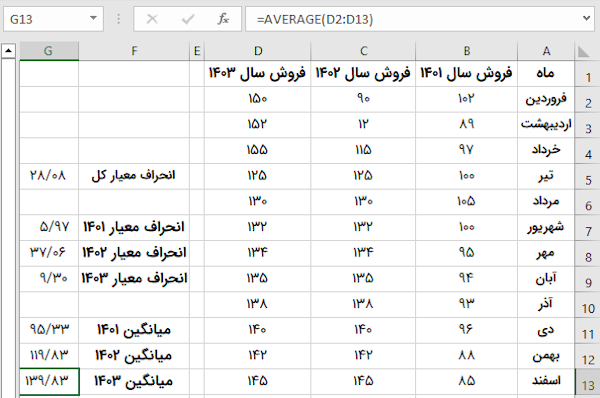
همانطور که مشاهده میکنید، با وجود بالا بودن انحراف معیار، میانگین فروش در هر سال افزایش پیدا کرده است. بنابراین، انحراف معیار کل، نوسانات مثبت و بهبود عملکرد فروش را نمایش میدهد. البته اگر انحراف معیار فروش در هر سال پایین باشد، کسب و کار عملکرد منسجمتری را خواهد داشت.
در این بخش، به حل یک مثال برای آشنایی با نحوه استفاده از توابع STDEV و STDEV.P پرداختیم. در آخرین بخش این مطلب از مجله فرادرس، تفاوت فرمول STDEV و STDEV.P با دیگر فرمولهای انحراف معیار در اکسل را به طور خلاصه مرور میکنیم.
چگونه کار با توابع آماری در اکسل را به خوبی و حرفهای یاد بگیریم؟

رسیدن به تسلط بالا در کار با اکسل، نیازمند یادگیری اصولی ابزارهای اصلی این نرمافزار، حل مثالهای کاربردی متعدد و آشنایی با قابلیتهای پیشرفته آن در گذر زمان است. فرمولها و توابع آماری اکسل، در بسیاری از حوزههای عملی و تئوری کاربرد دارند. قدم اول در یادگیری کار با این توابع، تقویت دانش پایه در زمینه آمار و احتمالات است. آشنایی مقدماتی با اکسل، مرحله بعدی خواهد بود. پس از یادگیری اصول اولیه کار با اکسل، نوبت به یادگیری تخصصی انجام محاسبات آماری در این نرمافزار میرسد. در صورت استفاده از یک منبع آموزشی جامع و کاربردی میتوانید این مسیر را با سرعت بیشتری طی کنید.
فرادرس، مجموعهای از فیلمهای آموزشی جامع و کاربردی را تهیه کرده است که میتوانند شما را در یادگیری کامل و حرفهای توابع آماری اکسل راهنمایی کنند. لینک مشاهده این فیلمهای آموزشی در ادامه آورده شده است:
تفاوت فرمول STDEV و STDEV.P با دیگر فرمولهای انحراف معیار در اکسل
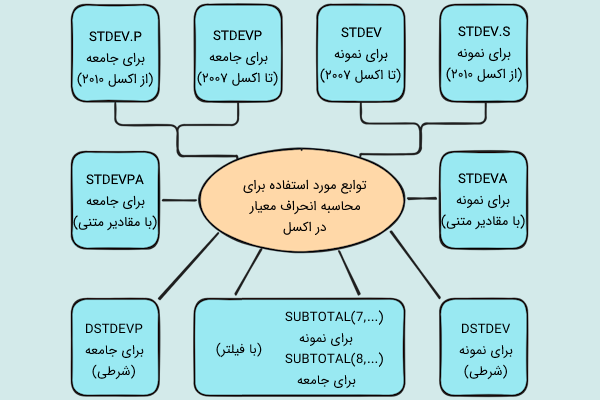
فرمولهای محاسبه انحراف معیار در اکسل، به STDEV و STDEV.P محدود نمیشوند. توابع زیر نیز امکان محاسبه انحراف معیار در اکسل را فراهم میکنند:
- تابع STDEV.S: تابع جایگزین STDEV در اکسل ۲۰۱۰ به بعد برای محاسبه انحراف معیار یک نمونه آماری
- تابع STDEVP: تابع معادل STDEV.P در اکسل ۲۰۰۷ به قبل برای محاسبه انحراف معیار یک جامعه آماری
- تابع STDEVA: تابع مورد استفاده برای محاسبه انحراف معیار یک نمونه آماری با امکان ارجاع به سلولهای حاوی مقادیر منطقی و متنی
- تابع STDEVPA: تابع مورد استفاده برای محاسبه انحراف معیار یک جامعه آماری با امکان ارجاع به سلولهای حاوی مقادیر منطقی و متنی
- تابع DSTDEV: تابع مورد استفاده برای محاسبه انحراف معیار شرطی یک نمونه آماری
- تابع DSTDEVP: تابع مورد استفاده برای محاسبه انحراف معیار شرطی یک جامعه آماری
برای یادگیری کامل نحوه استفاده از توابع آماری و دیگر توابع پرکاربرد در اکسل، باید به فکر مهارت فرمولنویسی باشید. مشاهده «فیلم آموزش استفاده از توابع و فرمولنویسی در اکسل فرادرس» شما را در این مسیر یاری میکند. لینک مشاهده این فیلم آموزشی در ادامه آورده شده است.
در مورد توابع STDEV.S و STDEVP در بخشهای قبلی صحبت کردیم و به بیان تفاوت این توابع با توابع STDEV و STDEV.P پرداختیم. در ادامه، تفاوت دیگر توابع معرفی شده در فهرست بالا با توابع STDEV و STDEV.P را مورد بررسی قرار میدهیم.
تفاوت فرمول STDEV و STDEV.P با STDEVA و STDEVPA
فرمولهای ریاضی مورد استفاده در توابع STDEVA و STDEVPA، دقیقا به توابع STDEV و STDEV.P شباهت دارند. تابع STDEVA مانند تابع STDEV، از فرمول انحراف معیار نمونه آماری استفاده میکند. فرمول تابع STDEVPA نیز مانند STDEV.P، همان فرمول انحراف معیار جامعه آماری است. با این وجود، تفاوت اصلی STDEV و STDEV.P با STDEVA و STDEVPA را میتوان در مقادیر مجاز برای ارجاع در آرگومانها مشاهده کرد.
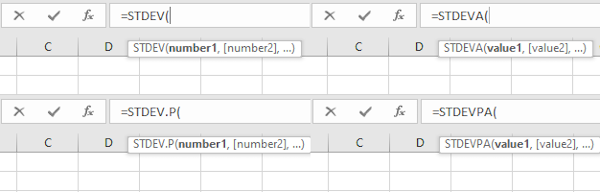
آرگومانهای توابع STDEVA و STDEVPA در اکسل، با عبارت valueنمایش داده میشوند. اگر به خاطر داشته باشید، عبارت مورد استفاده برای نمایش آرگومانهای توابع STDEV و STDEV.P در اکسل، numberبود. در آرگومانهای value، امکان ارجاع به مقادیر عددی، مقادیر منطقی و مقادیر متنی وجود دارد. بنابراین، برخلاف توابع STDEV و STDEV.P، توابع STDEVA و STDEVPA، ارجاع به مقادیر منطقی و متنی را نادیده نمیگیرند. اگر تمام نمونهها دارای مقدار عددی باشند، خروجی تابع STDEV با STDEVA و خروجی تابع STDEV.P با STDEVPA برابر میشود.
تفاوت فرمول STDEV و STDEV.P با DSTDEV و DSTDEVP
توابع DSTDEV و DSTDEVP، امکان محاسبه انحراف معیار بر اساس معیارهای مورد نظر را فراهم میکنند. در این توابع، معمولا از یک فهرست یا پایگاه داده به عنوان مبنای محاسبات استفاده میشود. آرگومانهای توابع DSTDEV و DSTDEVP، تفاوت قابل توجهی با آرگومانهای توابع STDEV و STDEV.P دارند. آرگومانهای توابع DSTDEV و DSTDEVP عبارت هستند از:
- database : سلولهای دربرگیرنده فهرست یا پایگاه داده
- field : ستون حاوی دادههای مورد استفاده برای محاسبات
- criteria :محدوده سلولهای حاوی معیار محاسبات
با استفاده از توابع DSTDEV و DSTDEVP میتوانید به راحتی انحراف معیار مجموعهای از دادهها را با توجه به معیارهای مورد نظر خود به دست بیاورید. به عنوان مثال، فرض کنید آمار فروش چند فروشنده در ماههای مختلف سال را دارید. اگر به دنبال تعیین انحراف معیار فروشهای بیشتر یا کمتر از یک مقدار مشخص در یکی از ماهها باشید، توابع DSTDEV و DSTDEVP، بهترین گزینه برای انجام محاسبات خواهند بود.
تفاوت فرمول STDEV و STDEV.P با SUBTOTAL
تابع SUBTOTAL در اکسل، تابعی بسیار کاربردی است که امکان انجام برخی از محاسبات آماری متداول بر روی بخشی از دادهها را فراهم میکند. این تابع، از امکان محاسبه انحراف معیار نمونه آماری بر اساس تابع STDEV.S و محاسبه انحراف معیار جامعه آماری بر اساس تابع STDEV.P بهره میبرد. تفاوت اصلی فرمول SUBTOTAL با STDEV و STDEV.P، امکان فیلتر کردن دادهها و مشاهده سریع انحراف معیار دادههای فیلتر شده است. توابع STDEV و STDEV.P، قادر به نمایش انحراف معیار دادههای فیلتر شده نیستند و مقادیر پنهان شده را نیز در محاسبات لحاظ میکنند. تابع SUBTOTAL، برای از بین بردن این محدودیت مورد استفاده قرار میگیرد.
source
