یادگیری درس ریاضی برخلاف تصور عموم میتواند بسیار آسان و شیرین باشد، به این شرط که در اولین قدم مفاهیم پایه آن را بهخوبی بیاموزید. قدم بعدی تمرین و تکرار است. با تمرین و تکرار روشها یا فرمولهای مختلف در درس ریاضی، میتوانید تسلط خود را روی یک موضوع کامل کنید. در این نوشته از مجله فرادرس به شما آموزش میدهیم که چگونه مفاهیم پایه در درس ریاضی مانند چهار عمل اصلی را بهتر یاد بگیرید. همچنین روشهایی را بیان میکنیم که با استفاده از آنها بتوانید درس ریاضی را چه در داخل کلاس درس و چه خارج از آن بهخوبی فرا بگیرید. در بخشهای بعدی این مطلب، تمام مباحث مطرح شده در کتابهای درسی ریاضی متوسطه اول و دوم را بهصورت مختصر توضیح خواهیم داد.

چطور درس ریاضی را بهتر یاد بگیریم؟
برای یادگیری درس ریاضی بهتر است پیش از اینکه به جستجو و تلاش برای استفاده از ابزارهای آنلاین بپردازید، در اولین قدم به اصول و مبانی این درس در کلاس درس کاملا مسلط شوید. این فرآیند با روشهای سنتی و تمرین ریاضی روی کاغذ طی میشود. پس از گذراندن این مرحله، ابزارهای آنلاین میتوانند در درک مفاهیم پیچیدهتر، تجسم مفاهیم به روشهای جدید و تقویت درک شما کمک کننده باشند.
در این بخش برای اینکه در فراگیری درس ریاضی موفق شوید و در عین حال از یادگیری آن لذت ببرید، چند پیشنهاد داریم. اولین قدم این است که تلاش کنید یک دانشآموز خوب در درس ریاضی باشید. در این صورت انگیزه و رضایت شما به ادامه این روند رو به رشد کمک میکند. اینکه یک دانشآموز خوب در درس ریاضی محسوب شوید، کار سختی نیست.
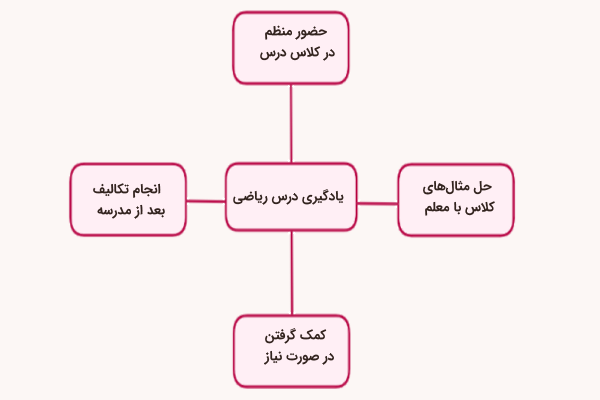
کافی است نکات کلیدی زیر را رعایت کنید:
- حضور منظم و بهموقع در کلاس ریاضی
- حل مثالهای کلاسی همراه با معلم
- انجام تکالیف تعیین شده در همان روز
- کمک گرفتن در صورت نیاز
در ادامه به توضیح هر کدام از این موارد میپردازیم.
حضور منظم و بهموقع در کلاس ریاضی
وقتی که جلسهای از کلاس ریاضی خود را از دست میدهید، مجبور هستید مفاهیم توضیح داده شده در آن جلسه را بهصورت خودخوان مطالعه کرده و یاد بگیرید. این مسئله باعث میشود کیفیت یادگیری شما در مقایسه با زمانی که در کلاس حضور دارید و به توضیحات معلم خود گوش میدهید، افت کند. همچنین سعی کنید به موقع در کلاس ریاضی خود حاضر شوید. حتی اگر کمی زودتر در کلاس حضور داشته باشید، بسیار بهتر است، چرا که میتوانید در این بازه زمانی کتاب درسی خود را باز کرده و به مطالب درس جدید نگاهی بیندازید. دقت کنید لازم نیست در این مرحله کاملا با مفاهیم جدید آشنا شوید. فقط کافی است با نگاهی گذرا به مبحث جدید، بدانید عنوان مبحث درس امروز چیست.

به علاوه حضور زودتر در کلاس درس به شما اجازه میدهد تا کتاب و دفتر خود را باز کرده و کاملا برای نوتبرداری یا مراجعه به متن کتاب در صورت نیاز آماده باشید. بنابراین تا حد امکان سعی کنید در کلاس ریاضی غیبت نداشته باشید، مگر در شرایطی که بیمار هستید. در این صورت حتما از همکلاسیهای خود بخواهید تا در مورد مباحث تدریس شده، تمرینهای حل شده و توضیحات داده شده با شما صحبت کرده و یادداشتهای خود را در اختیار شما قرار دهند.
همچنین سعی کنید حتما تکالیف داده شده در آن جلسه را انجام دهید و در صورت نیاز، برای حل تمرینها از معلم خود کمک بگیرید. اینکه عقبافتادگی خود را همان زمان جبران کنید، بسیار مهم است، چون با گذشت زمان و ناتمام ماندن یادگیری کامل آن مبحث، در درک و یادگیری مباحث بعدی که احتمالا مرتبط با این مبحث باشند، مشکل خواهید داشت و این زنجیره تا سالها ممکن است ادامه پیدا کند. پیشنهاد میکنیم در صورت داشتن چنین تجربهای، حتما در مورد مبحث آن جلسه تمرینهای بیشتری خارج از تکالیف کلاسی حل کنید تا از یادگیری خود مطمئن شوید.
حل مثالهای کلاسی همراه با معلم
دومین نکته کلیدی که بالاتر به آن اشاره کردیم، در مورد حل مثالها یا تمرینهایی است که معلم هنگام تدریس بیان میکند. حتما تا به حال دیدهاید که معلم پس از توضیح یک درس جدید، بلافاصله چند مثال حل میکند. اگر برای حل سوال به شما زمانی داده میشود و سپس سوال توسط معلم حل میشود، حتما دفتر خود را باز کرده و سعی کنید با توجه به توضیحات به سوال پاسخ دهید. با اینکه ممکن است نتوانید سوال را حل کنید، اما حتما این کار را امتحان کنید.در این صورت، پس از اینکه معلم شروع به حل سوال کرد، بهتر متوجه میشوید در کدام قسمت مشکل داشتهاید.

همچنین سعی کنید پس از راهحل خود، راهحل معلم را واضح و مرحله به مرحله یادداشت کنید. گاهی لازم است علاوه بر روابطی که معلم روی تخته مینویسد، توضیحات معلم را نیز حتما یادداشت کنید. در ادامه تمرینها و سوالاتی که معلم تا انتهای کلاس تعیین میکند را سعی کنید همان روز حل کنید تا یادگیری شما تثبیت شود. اگر موفق شدید به سوالی پاسخ دهید، حتما اعلام کنید تا تشویق شوید. فعالیت داوطلبانه در کلاس ریاضی علاقه شما را به یادگیری درس ریاضی تقویت میکند. همچنین اگر در فهم بخشی از مبحث مشکل دارید یا سوالی برای شما مطرح شده است، حتما با بالا بردن دست خود از معلم کمک بخواهید.
انجام تکالیف تعیین شده در همان روز
یکی از کلیدیترین نکات یادگیری بهتر درس ریاضی این است که حتما تکالیف تعیین شده برای پس از کلاس را در همان روز انجام دهید. اغلب ممکن است این تکالیف را شب قبل از جلسه بعدی انجام دهید. این روش باعث میشود یادگیری شما در همان روز کامل نشود و در نتیجه، شاید در حل سوالات با مشکل مواجه شوید. اما اگر بلافاصله پس از اتمام کلاس ریاضی، به حل سوالات بپردازید، چون حضور ذهن بالاتری دارید، در نتیجه، راحتتر و سریعتر میتوانید تکالیف خود را تمام کنید.
کمک گرفتن در صورت نیاز
در بخشهای قبل گفتیم که ممکن است نتوانید در برخی از جلسات کلاس درس ریاضی حضور داشته باشید. حتی ممکن است در کلاس باشید، اما مطالب بیان شده را بهخوبی فرا نگرفته باشید. در این شرایط بهتر است با در نظر گرفتن زمان آزاد معلم خود، در زمانی خارج از وقت کلاس به او مراجعه کنید و از او کمک بگیرید. در این زمینه میتوانید از گروههای مختلف یا سایر افراد نیز استفاده کنید. میتوانید با دوستان خود گروهی تشکیل دهید و از کمک هم بهره ببرید.
دقت کنید که در گروهی عضو شوید که سطح دانش ریاضیات اعضای آن در سطح شما یا از شما بهتر باشد. همچنین میتوانید در صورت نیاز از معلم خصوصی نیز استفاده کنید. مزیت کار با معلم خصوصی این است که تمرکز معلم فقط روی فعالیت و یادگیری شما است. در نتیجه احتمالا بهتر متوجه خواهد شد که مشکل شما در کدام بخشها است.
چگونه درس ریاضی را با فرادرس بهتر یاد بگیریم؟
در این بخش لیستی از فیلمهای آموزشی تهیه شده در مجموعه فرادرس را به شما معرفی کردهایم که به ترتیب از پایه هفتم تا پایه دوازدهم به توضیح مطالب کتابهای درسی پرداختهاند. این دورههای آموزشی که بر اساس سرفصلهای کتابهای درسی طراحی شدهاند، شامل تمام مباحث درس ریاضی در مقطع متوسطه هستند:
- فیلم آموزش ریاضی پایه هفتم فرادرس
- فیلم آموزش ریاضی پایه هشتم فرادرس
- فیلم آموزش ریاضی پایه نهم فرادرس
- فیلم آموزش ریاضی پایه دهم فرادرس
- فیلم آموزش ریاضی پایه یازدهم علوم تجربی فرادرس
- فیلم آموزش ریاضی پایه دوازدهم علوم تجربی فرادرس
مفاهیم پایه در درس ریاضی
گفتیم مهمترین نکته در یادگیری درس ریاضی این است که ابتدا به اصول اولیه و بسیار ساده آن کاملا مسلط شوید. در این بخش میخواهیم به زبانی ساده این مفاهیم پایه را در چهار بخش به شکل زیر توضیح دهیم:
- تسلط بر مبانی ریاضی – جمع
- تسلط بر مبانی ریاضی – تفریق
- تسلط بر مبانی ریاضی – ضرب
- تسلط بر مبانی ریاضی – تقسیم

اما پیش از پرداختن به مباحث بالا، ابتدا باید با مفهوم عدد و بخشهای مختلف ارقام یک عدد آشنا شوید. اولین مشخصه ریاضیات، اعداد هستند. اعداد میتوانند تک رقمی یا یک رقمی، دو رقمی، سه رقمی و … باشند. برای مثال اعداد ، و تک رقمی هستند، در حالی یک عدد دو رقمی و یک عدد سهرقمی محسوب میشود. اعداد یک رقمی فقط دارای یکی یا یکان هستند، در حالی که در اعداد دو رقمی علاوهبر یکیها، دهتاییها یا دهگان هم داریم. اولین رقم از سمت راست در یک عدد دو رقمی، یکیهای آن عدد محسوب میشود و دومین رقم، دهتایی یا دهگان آن است.
به همین ترتیب اعداد سه رقمی شامل سه رقماند که به ترتیب از راست به چپ جزء یکیها، دهتاییها و صدتاییها هستند. اهمیت تشخیص ارزش مکانی هر کدام از رقمهای یک عدد زمانی مشخص میشود که بخواهید هر کدام از چهار عمل اصلی را روی اعداد دو رقمی و بالاتر انجام دهید. با رعایت نکاتی که در ادامه شرح میدهیم، متوجه این نکته خواهید شد و بدون شک روند یادگیری درس ریاضی برای شما آسانتر، سریعتر و لذتبخشتر خواهد بود.
جمع در ریاضی
جمع اعداد با علامت نشان داده میشود. یکی از قواعد ساده در جمع اعداد، قاعده است. طبق این قاعده و با در نظر گرفتن محور اعداد به شکل زیر، جمع عدد با هر عددی، یک واحد به آن عدد اضافه میکند. قاعده بعدی در مورد معنا و مفهوم عدد صفر است. جمع عدد صفر با هر عددی، با خود آن عدد برابر است. بنابراین صفر به معنای هیچ است و اثری در اضافه شدن به یک عدد ندارد.

مورد بعدی جمع اعداد مشابه با هم است که بد نیست حاصل این جمعها را بهخاطر بسپارید. برای مثال، جمع اعداد و یا و . در ادامه یادگیری جمع اعداد، یکی از روشهای موثر استفاده از نگاشت یا پیکانهایی به شکل زیر است تا بتوانید حاصل جمع اعداد مختلف با یک عدد مشخص مانند را راحتتر به خاطر بسپارید. در ادامه موضوع جمع اعداد، با نحوه جمع کردن چند عدد مختلف که زیر هم قرار میگیرند، آشنا میشوید.
جمع اعداد دو رقمی
کاربرد این روش جمع در پیدا کردن حاصل جمع اعداد دو رقمی است. برای مثال، در تصویر زیر مجموع دو عدد دو رقمی و نشان داده شده است. روند جمع دو عدد دو رقمی یا یک عدد یک رقمی با یک عدد دو رقمی به این صورت است که ابتدا دو عدد را کاملا زیر هم مینویسیم، به گونهای که رقم یکان و دهگان هر دو عدد دقیقا زیر هم قرار بگیرند. علامت را برای نشان دادن جمع در سمت چپ دومین عدد به شکل زیر درج میکنیم. همچنین خطی که زیر این عدد کشیده میشود، نشان دهنده علاومت تساوی است.
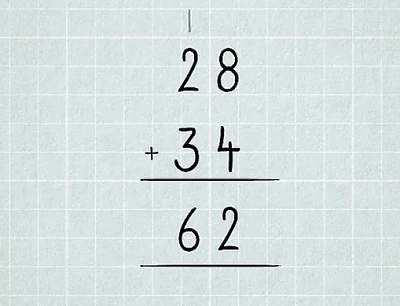
سپس ابتدا اعداد ستون اول یا یکان را با هم جمع میکنیم. همانطور که مشاهده میکنید، حاصل جمع دو عدد و برابر با عدد میشود که یک عدد دو رقمی است. عدد از دو عدد یکتایی و یک عدد دهتایی ساخته شده است. بنابراین اگر بخواهیم آن را زیر خط تساوی بنویسیم، فقط میتوانیم رقم یکان آن یعنی عدد را درج کنیم. رقم دهگان آن که برابر است با یک دهتایی به بالای ستون دوم منتقل میشود.
چون ستون دوم نشاندهنده دهتاییها است، پس نباید این بخش را به شکل بنویسیم، بلکه باید آن را بهعنوان عدد دهتایی در نظر بگیریم. به این ترتیب، عدد در ابتدای ستون دوم، با دو عدد دیگر در این ستون جمع میشوند. مجموع سه عدد این ستون که شامل و و هستند، برابر با عدد میشود.
تفریق در ریاضی
دومین عمل از چهار عمل اصلی در حساب، تفریق یا همان محاسبه اختلاف دو عدد است که با علامت نمایش داده میشود. در مورد تفریق هم قاعدهای مانند قاعده در جمع داریم که در اینجا بهصورت یا یک واحد به عقب رفتن روی محور اعداد است. اگر یک واحد از هر عددی که روی محور اعداد قرار دارد، کم کنیم، حاصل برابر میشود با عدد قبل از آن. این فرآیند را در تصویر زیر مشاهده میکنید:
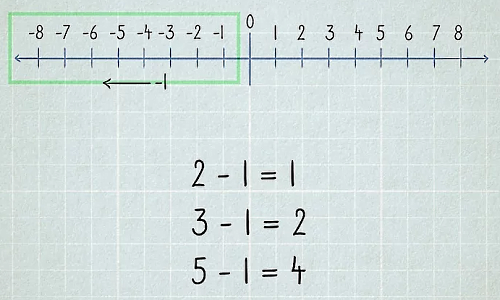
اگر جمع اعداد مشابه در بخش قبل را بهخوبی به خاطر سپرده باشید، در این مرحله میتوانید بهراحتی عدد را از یا را از کم کنید. در این بخش رابطه نزدیک دو عمل اصلی جمع و تفریق مشخص میشود. بهعنوان مثال، وقتی است، حتما برابر با میشود. همچنین حاصل تفریق یک عدد یک رقمی از یک عدد دو رقمی را یاد میگیرید که میتواند شامل قاعده قرض گرفتن هم نباشد.
برای مثال، تصویر زیر تفریق اعداد یک رقمی از دو رقمی را نشان میدهد که زیر هم نوشته شدهاند و در بهدست آوردن پاسخ آنها، کاربرد قاعده قرض گرفتن لازم نیست. برای نمونه در مورد اولین مثال، ابتدا اعداد ستون اول یا ستون یکان را از هم کم میکنیم. حاصل برابر است با که پس از خط نشاندهنده علامت تساوی، نوشته شده است. در ستون بعدی که همان ستون دهگان محسوب میشود، عدد را داریم که از هیچ عدد دیگری کم نمیشود. پس خود این عدد را زیر خط قرار میدهیم.
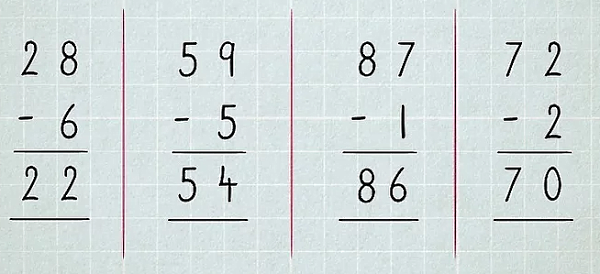
تفریق انتقالی یا تفریق تکنیکی
در مثالهای قبل دیدیم که برای انجام برخی از تفریقها نیازی به کاربرد قاعده قرض گرفتن نیست. اما در مواردی ممکن است تفریق اعداد با استفاده از قاعدهای به نام قاعده قرض گرفتن انجام شود. چنین تفریقی، تفریق تکنیکی، انتقالی یا تفریق در جدول ارزش مکانی هم نامیده میشود. برای اینکه بهتر متوجه شوید چه زمانی باید از این قاعده استفاده کنید، به تصویر زیر دقت کنید. در این سوال میخواهیم ببینیم حاصل کم کردن عدد از عدد چیست. اولین قدم برای انجام تفریق دو عدد دو رقمی این است که این دو عدد را زیر هم و به شکل زیر بنویسیم.

در مرحله بعد ابتدا باید دو عددی را که در اولین ستون از سمت راست، یعنی ستون یکان یا یکیها قرار دارند، از هم کم کنیم، یعنی باید عدد از کم شود. در حالی که میدانیم چنین چیزی امکانپذیر نیست. در این مواقع باید از تفریق انتقالی کمک بگیریم، به این صورت که به اولین عدد از ستون بعدی که ستون دهگان یا دهها نام دارد، نگاه کنید. عدد را در این جایگاه داریم. با قرض گرفتن یک دهتایی از این عدد و انتقال این دهتایی به ابتدای ستون اول، عدد به تبدیل میشود.
معمولا برای اینکه در محاسبات خود اشتباه نکنیم، عدد را خط میزنیم و بالای آن عددی را که یک واحد از آن کمتر است، یعنی را مینویسیم. همچنین این دهتایی به اولین عدد در ستون یکیها اضافه میشود. بنابراین عدد با جمع میشود و حالا بهجای عدد را در این جایگاه داریم و میتوانیم بهراحتی عدد را از آن کم کنیم. حاصل کم کردن از در اولین ستون، عدد است که زیر خط نشاندهنده تساوی آن را مینویسیم.

ضرب در ریاضی
عمل ضرب بهعنوان یکی از چهار عمل اصلی در درس ریاضی یکی از مهمترین و پرکاربردترین بخشها است. برای نشان دادن عمل ضرب بین دو عدد از نماد استفاده میشود. البته ممکن است در برخی متون بهجای این نماد از علامت دات یا استفاده شود. ابتدا با قاعده ضرب هر عدد در و همینطور ضرب هر عدد در شروع میکنیم. ضرب هر عددی در همیشه برابر با است و ضرب هر عدد در همیشه برابر با خود آن عدد است:
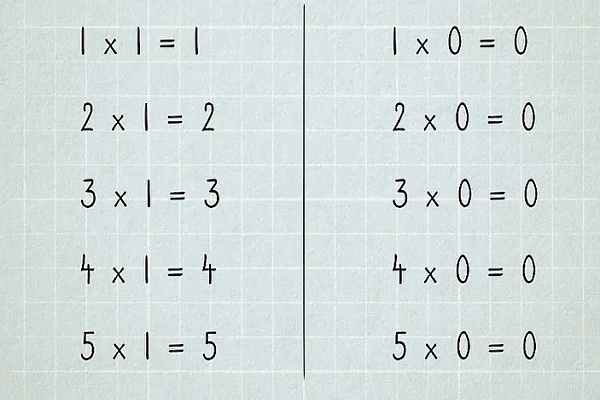
قدم بعدی این است که جدول ضرب را بهخاطر بسپارید. در این جدول حاصل ضرب تمام اعداد تا در یکدیگر نوشته شده است. پیشنهاد میکنیم آنقدر این جدول را تمرین کنید که با مشاهده ضرب هر دو عدد تک رقمی بتوانید بهسرعت حاصل ضرب را بنویسید.
ضرب اعداد دو رقمی
پس از اینکه به ضرب اعداد یک رقمی کاملا مسلط شدید، میتوانید ابتدا ضرب یک عدد تک رقمی در یک عدد دو رقمی را امتحان کنید. برای مثال، تصویر زیر را در نظر بگیرید. در اولین مثال، حاصل ضرب در خواسته شده است. بهتر است مانند بخش جمع و تفریق، در اینجا هم اگر یکی از اعداد ما دو رقمی است، عمل موردنظر را با زیر هم نوشتن دو عدد انجام دهیم، طوری که یکیهای دو عدد کاملا زیر هم و دهتاییها هم کاملا زیر هم و در یک ستون قرار بگیرند.

بنابراین ابتدا باید را در ضرب کنیم، یعنی در اولین مرحله یکیها در هم ضرب میشوند. حاصل ضرب این دو عدد طبق جدول ضرب برابر است با . میدانیم در ستون اول یعنی یکیها مجازیم که فقط یکیهای حاصل جمع را درج کنیم. عدد دارای یکی و تا دهتایی است. بنابراین فقط یکی آن یعنی عدد را زیر خط نشان دهنده تساوی قرار میدهیم و عدد دهتایی آن به ستون دهتاییها منتقل میشود.
در ادامه ممکن است به اشتباه بخواهید مانند عمل جمع یا تفریق عمل کنید، یعنی ضرب دو عددی که در ستون دهتایی قرار دارند یعنی و را انجام دهید. این روش اشتباه است. در اینجا تفاوت مهم دو عمل ضرب و تقسیم با دو عمل جمع و تفریق مشخص میشود. برای اینکه ضرب یک عدد یک رقمی در یک عدد دو رقمی را انجام دهیم، باید عدد یک رقمی را در هر دو رقم عدد دو رقمی ضرب کنیم.
یعنی عدد در این مثال، هم در و هم در ضرب میشود. ضرب در انجام شد و دیدیم که تا دهتایی به ما داد. حالا باید را در ضرب کنیم که میشود . حاصل این ضرب در ستون دهتاییها قرار میگیرد که شامل عدد از مرحله قبل است. پس باید را با در انتها جمع کنیم که میشود . برای اینکه این روند را بهتر درک کنید، به مثال دیگری که در ادامه بیان میشود، دقت کنید.
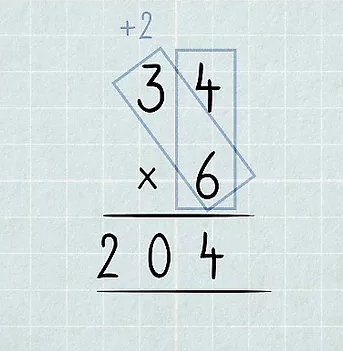
در تصویر بالا، توسط کادرهای آبی رنگ نشان داده شده است که عملیات ضرب چگونه بهصورت تفکیک شده انجام میشود. ابتدا باید عدد در یکیهای عدد یعنی ضرب شود. حاصل این ضرب برابر است با که یک عدد دو رقمی است. پس فقط میتوانیم یکان آن یعنی را در بخش یکان پاسخ درج کنیم و دهگان آن یعنی به ابتدای ستون دوم منتقل میشود. مرحله بعد ضرب در است که میشود . جمع با از مرحله قبل برابر است با که در کنار و در قسمت پاسخ قرار میگیرد. پس پاسخ نهایی این ضرب برابر شد با .
در ادامه میخواهیم حاصل ضرب دو عدد دو رقمی را بهدست آوریم. ابتدا باید دو عدد را کاملا زیر هم بنویسیم، طوری که یکیها زیر هم و دهتاییها هم زیر هم قرار بگیرند. علامت ضرب را سمت چپ دومین عدد قرار میدهیم و خط افقی را زیر همین عدد و به نشانه علامت تساوی درج میکنیم. عدد دوم ما یعنی شامل عدد یکی و عدد دهتایی است. در ضرب دو عدد دو رقمی، باید ابتدا یکیهای عدد دوم یعنی را در عدد اول یعنی بهطور کامل ضرب کنیم. این عملیات با کادر آبی رنگ در شکل مشخص شده است و حاصل آن هم با رنگ آبی نوشته شده است.
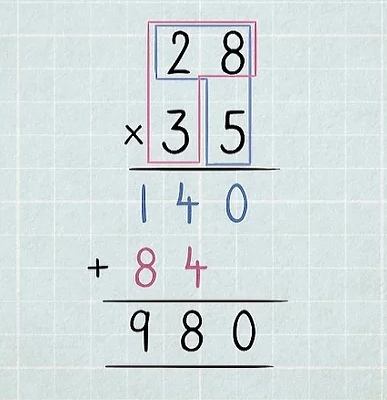
در مرحله بعد، دهتایی عدد دوم یعنی را در عدد اول یعنی بهطور کامل ضرب میکنیم. این فرآیند هم با کادر قرمز رنگ متمایز شده است که حاصل آن نیز عدد قرمز است. در نهایت دو عدد آبی و قرمز باید با هم جمع شوند تا محاسبه حاصل ضرب این دو عدد کامل شود. پس میتوانیم بگوییم ضرب دو عدد دو رقمی برابر میشود با مجموع دو حاصل ضرب که هر کدام از این حاصل ضربها معادل است با ضرب یک عدد یک رقمی در یک عدد دو رقمی. با این توضیحات، عملیات ضرب را شروع میکنیم.
حاصل ضرب در میشود . اما همانطور که توضیح دادیم، مجاز هستیم که فقط یکیهای عدد را زیر خط افقی بنویسیم و دهتاییهای آن که برابر است با عدد به بالای ستون دوم منتقل میشوند. پس فقط را در جایگاه یکیهای جواب مینویسیم. در مرحله بعد عدد در ضرب میشود که حاصل آن برابر است با . عدد با از مرحله قبل جمع میشود و در نهایت عدد بهدست میآید که در کنار از مرحله قبل نوشته میشود. بنابراین برابر شد با اولین حاصل ضرب.
اما عملیات ما هنوز تمام نشده است. همین روند را برای ضرب در باید تکرار کنیم. ابتدا حاصل ضرب در را بهدست میآوریم که میشود . نکته مهم در اینجا این است که رقم در معادل است با تا دهتایی. پس برای نوشتن عدد باید رقم آن را در جایگاه دهتایی از پاسخ و زیر عدد قرار دهیم. رقم آن نیز به ستون بعدی منتقل میشود تا با حاصل ضرب بعدی جمع شود. حاصل ضرب بعدی برابر است با ضرب در که میشود . اگر را با حاصل از مرحله قبل، جمع کنیم، بهدست میآید که آن را کنار با رنگ قرمز مینویسم. بنابراین دومین ضرب ما به عدد ختم شد. در آخرین مرحله باید دو عدد و که با دو رنگ مختلف نمایش داده شدهاند را با هم جمع کنیم که میشود .
تقسیم در ریاضی
آخرین عملیات از چهار عمل اصلی در درس ریاضی، تقسیم است که توسط مشخص میشود. تقسیم عکس ضرب است، بنابراین اگر به ضرب اعداد کاملا مسلط باشید، فرآیند تقسیم برای شما آسان است. برای مثال، میدانیم حاصل ضرب در میشود . پس اگر را بر تقسیم کنیم، پاسخ برابر است با . تصویر زیر این رابطه معکوس را بهخوبی نمایش میدهد:
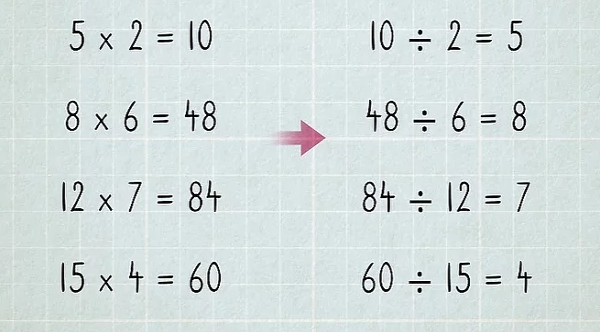
نامگذاری اجزای مختلف در یک تقسیم
هر تقسیم از چهار بخش تشکیل میشود. برای مثال، تقسیم عدد بر را در نظر بگیرید:
- مقسوم: عددی است که میخواهیم آن را بر مقسوم علیه تقسیم کنیم (عدد ).
- مقسوم علیه: عددی است که مقسوم بر آن را تقسیم شده است (عدد ).
- خارج قسمت: عددی است که از تقسیم مقسوم بر مقسوم علیه بهدست میآید (عدد ).
- باقیمانده: عددی است که در انتهای تقسیم با کم کردن حاصلضرب خارج قسمت در مقسوم علیه و کم کردن حاصل از مقسوم بهدست میآید (عدد ).
تقسیم اعداد دو رقمی و بخشپذیری
عملیات تقسیم هم مانند عملیات ضرب با در نظر گرفتن اعداد دو رقمی متفاوت و کمی پیچیدهتر انجام میشود. برای مثال، فرض کنید میخواهید عدد دو رقمی را بر عدد تقسیم کنید. با نوشتن عدد در سمت چپ عدد و قرار دادن علامت بهجای بین این دو عدد، عملیات تقسیم نمایش داده میشود. چنین تقسیمی، تقسیم چکشی نامیده میشود که در آن عدد باید داخل نماد قرار بگیرد. حالا میتوانیم فرآیند تقسیم را شروع کنیم.
ابتدا رقم دهگان را بر تقسیم میکنیم. حاصل تقسیم بر برابر است با . پس عدد را زیر علامت تقسیم مینویسم. سپس این عدد را در ضرب میکنیم که می شود . را از بهعنوان دهگان عدد کم میکنیم. حاصل میشود . این فرآیند تفریق را زیر عدد مانند آنچه که در بخش تفریق توضیح دادیم، زیر هم مینویسیم. در مرحله بعد رقم یکان یعنی را در کنار پاسخ تفریق بخش قبل یعنی درج میکنیم.
حالا باید را بر تقسیم کنیم که میشود . سپس را در ضرب میکنیم و حاصل آن یعنی را از رقم یکان در یعنی کم میکنیم که میشود . پس باقیمانده این تقسیم برابر با شد و حاصل آن که زیر نماد قرار دارد. زمانی که باقیمانده تقسیمی صفر شود، میگوییم عدد اول بر عدد دوم بخشپذیر است. اینکه کدام اعداد بر هم بخشپذیر هستند با تمرین و تکرار مشخص میشود. برای مثال، بر بخشپذیر نیست، چون باقیمانده این تقسیم مخالف صفر و برابر با است.
مباحث درس ریاضی متوسطه اول و دوم
ریاضیات علم مطالعه اعداد، مقادیر، اشکال، ساختارها، الگوها و روابطی است که بین اجزای مختلف هر کدام از این موارد وجود دارد. عمده مطالعات ریاضی اختصاص دارد به پیدا کردن روابط منطقی بین اجزای مختلف، فرمولبندی کردن این روابط و رسیدن به یک دیدگاه سیستماتیک جهت مدلسازی، شبیهسازی و حل مسائل در زندگی واقعی. به همین دلیل یادگیری ریاضیات زیربنا و اساس یادگیری بهتر علومی مانند فیزیک بهشمار میرود و در رشتههای متنوعی از جمله علوم مهندسی، اقتصاد و علوم کامپیوتر کاربرد دارد.

در بخشهای قبل با اصول یادگیری درس ریاضی و مبانی اولیه آن که شامل چهار عمل اصلی است، آشنا شدیم. در این بخش میخواهیم کمی فراتر رفته و برای علاقهمندان توضیح دهیم موضوعات مختلف درس ریاضی در دوره اول و دوم متوسطه چیست. با توجه به اینکه هدف ما در این بخش تنها معرفی مباحث درس ریاضی است، بنابراین در هر قسمت چند مطلب مرتبط از مجله فرادرس برای شما قرار داده شده است تا با مراجعه به این مقالات بتوانید با جزئیات بیشتری این مباحث را یاد بگیرید. مباحث درس ریاضی دورههای اول و دوم متوسطه با توجه به سرفصل کتابهای درسی، به شکل زیر طبقهبندی و معرفی خواهند شد:
- مباحث درس ریاضی پایه هفتم و هشتم
- مباحث درس ریاضی پایه نهم و دهم
- مباحث درس ریاضی پایه یازدهم و دوازدهم
مباحث درس ریاضی پایه هفتم و هشتم
درس ریاضی پایه هفتم شامل مباحث زیر است:
- راهبردهای حل مسئله
- اعداد صحیح
- جبر و معادله
- هندسه و استدلال
- شمارندهها و اعداد اول
- سطح و حجم
- توان و جذر
- بردار و مختصات
- آمار و احتمال
همچنین در کتاب درسی ریاضی پایه هشتم موضوعات زیر توضیح داده میشود:
- اعداد صحیح و گویا
- اعداد اول
- چندضلعیها
- جبر و معادله
- بردار و مختصات
- مثلث
- توان و جذر
- آمار و احتمال
- دایره
همانطور که ملاحظه میکنید، بسیاری از این مباحث با هم مشترک هستند. البته مباحث مشترک در درس ریاضی هفتم شامل اصول و تعاریف اولیه هستند و در ریاضی هشتم، همین موضوعات در سطوح پیشرفتهتر بررسی میشوند. به همین جهت، در ادامه تیترهای مشابه را با در نظر گرفتن تمام مباحث مطرح شده در کتاب ریاضی هفتم و هشتم بهطور کامل توضیح دادهایم.
راهبردهای حل مسئله
فرآیند حل یک مسئله در درس ریاضی را میتوانیم به ترتیب زیر پیش ببریم:
- درک صورت مسئله
- حل مسئله
- چک درستی راهحل و پاسخ بهدست آمده
در زمینه درک مسئله، اولین قدم این است که صورت سوال را به دقت بخوانیم و دقیقا مشخص کنیم که به دنبال محاسبه یا اثبات چه چیزی هستیم. در این بخش میتوانید با هایلایت کردن بخشهای مهم در صورت سوال یا تقسیمبندی کردن دادههایی که در صورت سوال در اختیار شما قرار داده شده است، حل مسئله را برای خود آسانتر کنید. در مرحله بعد، برای حل مسئله و پیدا کردن راهحل مناسب میتوانید از تکنیکهایی نظیر رسم شکل، جدول یا نمودار استفاده کنید.

در برخی از مسائل درس ریاضی لازم است به دنبال پیدا کردن یک الگوی منطقی باشید. همچنین با تشخیص حوزه سوال و نوشتن فرمولهایی که در آن زمینه وجود دارد، ممکن است بتوانید راهحل را سریعتر حدس بزنید. برای مثال، در حل مسائل مربوط به محاسبه حجم یا مساحت اشکال هندسی، با توجه به نام شکل در صورت سوال و نوشتن فرمول مساحت، مساحت جانبی یا حجم آن مقطع، اگر دادههای سوال را به تفکیک یادداشت کرده باشید، بلافصله میتوانید تشخیص دهید برای پیدا کردن پاسخ ابتدا باید چه کمیتی را بهدست آورید. در نهایت، در برخی از سوالات پس از محاسبه پاسخ، میتوانید با معکوس کردن راهحل درستی روش و پاسخ خود را چک کنید.
اعداد صحیح
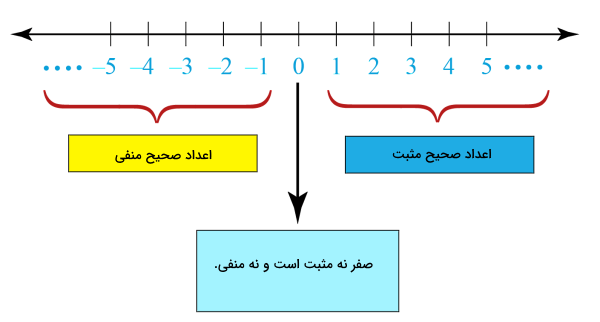
اعداد صحیح به مجموعهای از اعداد گفته میشود که شامل اعداد مثبت، اعداد منفی و صفر میشود. اعداد صحیح منفی همان قرینه اعداد صحیح مثبت هستند، به این معنا که اعدادی دقیقا مشابه با اعداد مثبت هستند و فقط یک علامت منفی به شکل () در سمت چپ خود دارند. برای مثال، قرینه برابر است با و قرینه قرینه میشود .
نکته مهمی که در تشخیص اعداد صحیح باید در نظر گرفته شود این است که اعداد کسری و اعداد اعشاری جزء اعداد صحیح نیستند. پس مجموعه اعداد صحیح شامل سه گروه اعداد زیر میشوند:
- اعداد مثبت یا (مجموعه اعداد طبیعی)
- اعداد منفی یا
- عدد صفر (که نه یک عدد مثبت است و نه یک عدد منفی)
نکته: مجموعه اعداد طبیعی زیرمجموعهای از مجموعه اعداد صحیح است.
همانطور که در شکل بالا مشاهده میکنید، اعداد مثبت یا اعدادی که در سمت راست این محور قرار میگیرند، همواره از اعداد سمت چپ یا اعداد منفی و صفر بزرگتر هستند. مکان قرارگیری عدد صفر مبدا محور نامیده میشود. اعداد منفی همگی در سمت چپ صفر قرار میگیرند. به این ترتیب مجموعه اعداد صحیح را میتوانیم با نماد و به شکل زیر داخل دو علامت آکولاد توصیف کنیم:
نکته مهم دیگری که در مورد اعداد صحیح وجود دارد قواعد جمع، تفریق، ضرب و تقسیم آنها است که با توجه به علامت منفی در مورد اعداد منفی، با قواعد چهار عمل اصلی در مورد اعداد مثبت که قبلا توضیح دادیم، متفاوت است. در ادامه به اختصار این قواعد را با مثال توضیح میدهیم.
قواعد جمع اعداد صحیح
قواعد جمع اعداد صحیح در دو حالت زیر بررسی میشود:
- اگر دو عدد صحیح دارای علامت یکسانی باشند.
- اگر دو عدد علامت متفاوتی داشته باشند.
حالت اول یعنی در حالتی که هر دو عدد مثبت یا منفی باشند. در این صورت، ابتدا باید اعداد را بدون در نظر گرفتن علامت، با هم جمع کنیم. سپس اگر هر دو علامت مثبت داشته باشند، علامت حاصلجمع هم مثبت است و اگر هر دو علامت منفی داشته باشند، علامت پاسخ نیز منفی خواهد بود. در حالت دوم، ابتدا اختلاف دو عدد را بهدست میآوریم (بدون در نظر گرفتن علامتها، عدد بزرگتر از عدد کوچکتر کم میشود). اگر علامت عدد بزرگتر مثبت باشد، پاسخ نیز مثبت است. در غیر این صورت، علامت حاصلجمع منفی خواهد بود.
نکته: اعداد مثبت را میتوانیم با قرار دادن علامت مثبت قبل از عدد یا بدون قرار دادن هیچ علامتی مشخص کنیم. پس قرار دادن علامت مثبت قبل از یک عدد مثبت اجباری نیست.
برای مثال، میخواهیم حاصلجمع دو عدد و را با تعیین مکان قرارگیری این اعداد روی محور اعداد صحیح بهدست آوریم. عدد یک عدد مثبت است که به اندازه پنج واحد به سمت راست و با در نظر گرفتن صفر بهعنوان مبدا، روی محور مشخص میشود:
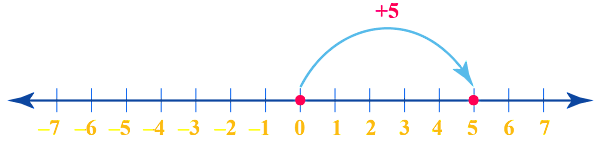
عدد بعدی است که برای مشخص کردن مکان آن روی محور اعداد، کافی است ده واحد در جهت منفی یا به سمت چپ عدد پیش برویم. به این ترتیب، مشخص است که با جمع کردن این دو عدد در نهایت باقی میماند. پاسخ این روش با پاسخ روشی که بالاتر بیان شد، کاملا یکسان خواهد شد.
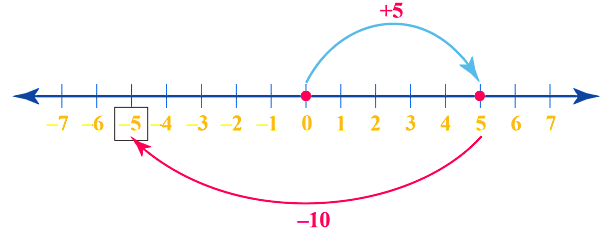
قواعد تفریق اعداد صحیح
قواعد محاسبه اختلاف اعداد صحیح به این صورت است:
- ابتدا لازم است عمیلات تفریق را به جمع تبدیل کنیم.
- سپس دقیقا با قواعدی که برای جمع اعداد صحیح بیان شد، پیش میرویم.
برای نمونه، فرض کنید میخواهید حاصل تفریق را بهدست آورید. ابتدا میتوانیم با قرار دادن عملگر یا علامت جمع بین این دو عدد، این مسئله را از تفریق به مجموع تبدیل کنیم:
نکته: منفی در مثبت یا مثبت در منفی همیشه با منفی برابر است.
با توجه به نکتهای که بیان شد، بهجای منفی، از مثبت در منفی استفاده کردیم. حالا علامت منفی متعلق به عدد دوم است و مجموع یک عدد مثبت و منفی را باید پیدا کنیم. طبق قواعد جمع دو عدد صحیح، چون دو عدد مختلف العلامت داریم، باید عدد کوچک از عدد بزرگ کم شود و در انتها علامت عدد بزرگتر (که منفی است) در کنار پاسخ قرار داده شود:
قواعد ضرب اعداد صحیح
برای اینکه ضرب اعداد صحیح را سریع انجام دهید، کافی است جدول زیر را در این زمینه بهخاطر بسپارید:
| ضرب علامتها | نتیجه | مثال |
قواعد تقسیم اعداد صحیح
در آخرین بخش از مبحث اعداد صحیح در درس ریاضی، برای اینکه تقسیم اعداد صحیح را بهراحتی انجام دهید، کافی است در جدول بخش قبل عملگر تقسیم () را با ضرب () جایگزین کنید. به این ترتیب تقسیم اعداد صحیح مانند تقسیم اعداد طبیعی انجام میشود و در انتها علامت پاسخ با توجه به جدول تعیین خواهد شد.
اعداد گویا
مجموعه اعداد گویا به کلیه اعداد کسری گفته میشود که در حالت کلی با تقسیم یک عدد صحیح بر عدد صحیح دیگر تولید میشوند، با این شرط که مخرج نباید صفر شود. برای مثال، یک عدد گویا است و بهصورت «یک دوم» خوانده میشود. همچنین اعدادی مانند و هم اعداد گویا محسوب میشوند، چون میتوانیم این اعداد را به شکل و بنویسیم.
نکته: مجموعه اعداد صحیح و در نتیجه مجموعه اعداد طبیعی هر دو زیرمجموعهای از مجموعه اعداد گویا هستند.
شکلهای زیر بهخوبی تفاوت اعداد صحیح و گویا را نشان میدهند. و دو عدد صحیح روی محور اعداد هستند که بین آنها هیچ عدد صحیح دیگری وجود ندارد.
اما اگر بخواهیم تمام اعداد گویا بین این دو عدد صحیح را در نظر بگیریم، بینهایت عدد گویا وجود دارد که در شکل زیر تنها چهار عدد از این تعداد بینهایت روی محور اعداد نمایش داده شده است:
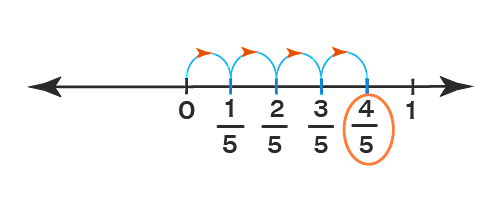
برای اینکه بتوانیم اعداد گویا یا کسری را با هم جمع کرده، از هم کم کنیم یا ضرب و تقسیم این نوع اعداد را انجام دهیم، قواعد و روشهای خاصی وجود دارد که در بخش بعد آنها را توضیح میدهیم.
جمع و تفریق اعداد گویا
برای اینکه بتوانیم دو عدد گویا یا دو کسر را با هم جمع یا از هم کم کنیم، اولین نکته مهم این است که باید مخرجهای دو کسر با هم یکی باشند. برای مثال، در عبارت زیر مخرجها با هم برابر هستند و اگر بخواهیم این تفریق را انجام دهیم، پاسخ شامل مخرجی برابر با مخرج هر یک از دو کسر و صورتی برابر با حاصل تفریق صورتهای دو کسر است:
اما اگر بخواهیم حاصل عبارت زیر را که مخرجهای مختلفی دارد، بهدست آوریم، چگونه باید عمل کنیم؟
در این موارد که مخرج کسرها با هم برابر نیست، باید مخرج مشترک بگیریم تا مخرجها یکسان شوند. در بخش بعد این روش را توضیح خواهیم داد.
مخرج مشترک
روش پیدا کردن مخرج مشترک به این صورت است که ابتدا باید مضربهای هر دو مخرج را لیست کنیم. در بخش «شمارندهها و اعداد اول» توضیح خواهیم داد که منظور ما از مضربهای یک عدد چیست. دقت کنید نیازی نیست تمام مضربهای این دو عدد را بنویسیم و برای مثال، نوشتن چهار یا پنچ مضرب اول کافی است:
اگر مضربهای این دو مخرج را با هم مقایسه کنیم، مشخص است که اولین مضرب مشترک عدد است. پس این عدد مخرج مشترک ما در این مثال است. حالا باید ببینیم مخرجها در سوال بالا در چه عددی ضرب شوند تا به مخرج مشترک برسیم. پس از یافتن این عدد، لازم است صورت و مخرج آن کسر در این عدد ضرب شوند. برای نمونه، مخرج کسر باید در ضرب شود تا به مخرج مشترک برسیم، پس صورت این کسر هم در ضرب میشود. به همین ترتیب، در کسر بعدی یعنی مخرج باید در ضرب شود تا به برسیم، پس صورت این کسر هم در ضرب میشود:
حالا به دو کسر با مخرج یکسان رسیدیم. کافی است مخرج مشترک را بهعنوان مخرج پاسخ قرار داده و صورت کسرها را با هم جمع کنیم تا حاصلجمع این دو کسر محاسبه شود:
ضرب و تقسیم اعداد گویا
پس از اینکه جمع و تفریق اعداد گویا در درس ریاضی را فراگرفتیم، نوبت به یادگیری ضرب و تقسیم این اعداد میرسد. حاصلضرب اعداد گویا یا ضرب کسرها کسری است که صورت آن برابر است با حاصلضرب صورت کسرها و مخرج آن نیز برابر است با حاصلضرب مخرج کسرها:
طبق این قاعده، حاصلضرب دو کسر و میشود:
پیدا کردن حاصل تقسیم کسرها با دانستن این نکته که عملیات تقسیم عکس عملیات ضرب است، آسان میشود. کافی است دومین کسر را معکوس کنیم و با تبدیل تقسیم به ضرب، حاصل را محاسبه کنیم. معکوس کردن یک کسر به معنای جابجایی صورت و مخرج آن است. در حالت کلی اگر دو کسر بهصورت و داشته باشیم، تقسیم آنها به شکل زیر انجام میشود:
نکته: صفر تنها عددی است که معکوس ندارد، چون کسری که مخرج آن صفر باشد در ریاضیات تعریف نشده است.
برای مثال، حاصل برابر است با:
نمایش اعشاری کسرها
اعداد گویا را میتوانیم به شکل اعداد اعشاری یا اعداد مخلوط نمایش دهیم. در این بخش نمایش اعشاری کسرها یا اعداد گویا را بررسی میکنیم. در بخش بعد به نمایش عدد مخلوط برای کسرها خواهیم پرداخت. برای اینکه کسری را به شکل یک عدد اعشاری بنویسیم، کافی است صورت آن را به مخرج تقسیم کنیم. برای مثال، فرض کنید میخواهیم کسر را به یک عدد اعشاری تبدیل کنیم:
حاصل این تقسیم، یک عدد اعشاری شد که رقم اعشار آن تکرار ندارد. اما در تبدیل کسر به عدد اعشاری، حاصل برابر میشود با:
در این تبدیل رقم تا بینهایت تکرار میشود. به این نوع عدد اعشاری، یک عدد اعشاری متناوب میگوییم. عکس این فرآیند هم امکانپذیر است. یعنی میتوانیم با داشتن یک عدد اعشاری، آن را به شکل یک کسر بنویسیم. مثلا اگر عدد اعشاری که به شکل «دو و سه دهم» خوانده میشود را در ضرب کنیم، بهدست میآید. بنابراین میتوانیم بنویسیم:
عدد مخلوط و تبدیل آن به کسر
میتوانیم اعداد گویا یا کسرها را در قالب یک عدد مخلوط نمایش دهیم. عدد مخلوط عددی است که شامل یک عدد کامل مانند یا یا و … میشود که در کنار یک جزء کسری قرار گرفته است. برای مثال، فرض کنید یک پیتزای کامل به همراه پیتزای دیگری که یک اسلایس از آن کم شده است، در اختیار دارید. عدد مخلوط معادل با این دو پیتزا به شکل زیر است:


این عدد بهصورت «یک و سه چهارم» خوانده میشود. اگر بخواهیم معادل کسری این عدد مخلوط را بنویسیم، به شکل زیر پیش میرویم:
دقت کنید بهجای عدد کامل از کسر استفاده کردیم. راهحل سادهتر برای تبدیل عدد مخلوط به کسر این است که مخرج بخش کسری را در عدد کامل ضرب کرده و حاصل را با صورت بخش کسری جمع کنیم. این عدد صورت کسر موردنظر است. مخرج کسر موردنظر نیز، همان مخرج بخش کسری در عدد مخلوط خواهد بود. به مثال زیر توجه کنید:
نکته ۱: هرگاه صورت و مخرج کسری با هم برابر باشند، آن کسر همواره با عدد یک برابر است ().
نکته ۲: در صورتی میتوانیم یک کسر را به عدد مخلوط تبدیل کنیم که صورت آن از مخرجاش بزرگتر باشد.
عکس فرآیند بالا، یعنی تبدیل کسر به عدد مخلوط نیز امکانپذیر است. با توجه به نکته دوم، اگر صورت کسری از مخرج آن بزرگتر باشد، میتوانیم آن کسر را به عدد مخلوط تبدیل کنیم. کافی است ابتدا صورت را بر مخرج تقسیم کنیم. خارج قسمت این تقسیم برابر است با عدد کامل در عدد مخلوط و باقیمانده این تقسیم برابر است با صورت بخش کسری در عدد مخلوط. مخرج کسر در عدد مخلوط نیز همان مخرج کسر داده شده است.
برای نمونه، فرض کنید میخواهیم کسر را به عدد مخلوط تبدیل کنیم. ابتدا را به تقسیم میکنیم. خارج قسمت این تقسیم است و باقیمانده آن . بنابراین عدد مخلوط معادل با این کسر میشود:
جمع و تفریق اعداد مخلوط
برای بهدست آوردن حاصل جمع دو عدد مخلوط، کافی است ابتدا عملیات موردنظر را روی بخش کامل این اعداد اجرا کنیم و سپس روی کسرها. برای مثال، اگر بخواهیم را با $$$3frac{1}{2} $$
دو بخش کسری نیز پس از یافتن مخرج مشترک، با هم جمع میشوند:
بنابراین حاصل این جمع تا اینجا برابر شد با . اگر دقت کنید در بخش کسری این عدد مخلوط همواره صورت کسر از مخرج آن بزرگتر است. پس میتوانیم این کسر را نیز به یک عدد مخلوط تبدیل کنیم و پاسخ سادهتری بهدست آوریم:
برای جمع اعداد مخلوط میتوانیم ابتدا هر دو عدد را به کسر تبدیل کنیم و سپس کسرهای معادل را با هم جمع کنیم. تفریق اعداد مختلط نیز کاملا به همین شکل انجام میشود، با این تفاوت که اعداد کامل و صورت کسرها از هم کم میشوند.
ضرب و تقسیم اعداد مخلوط
در بخشهای قبل ضرب کسرها در درس ریاضی را یاد گرفتیم. ضرب و تقسیم دو عدد مخلوط با تبدیل اعداد مخلوط به کسر و سپس پیروی از قواعد گفته شده، انجام میشود. برای مثال، فرض کنید میخواهیم را بر تقسیم کنیم. ابتدا باید عدد مخلوط را به روشی که گفتیم به کسر تبدیل کنیم:
حالا میتوانیم تقسیم کسر بهدست آمده بر عدد صحیح را انجام دهیم. همانطور که در تعریف اعداد گویا اشاره شد، تمام اعداد صحیح جزء اعداد گویا هستند. پس با نوشتن به شکل یک کسر متعارفی ()، میتوانیم تقسیم بالا را به شیوه توضیح داده شده انجام دهیم:
سایر مباحث مرتبط با اعداد گویا و کسرها
در این قسمت سایر مطالب مرتبط با اعداد گویا و کسرهای متعارفی در مجله فرادرس را برای شما لیست کردهایم:
- مقایسه کسرها – آموزش ریاضی به زبان ساده + مثال و تمرین
- ساده کردن کسر ها – به زبان ساده + سوال با جواب
- کسر تلسکوپی – روش حل به زبان ساده + مثال و تمرین
- تجزیه کسر – به زبان ساده
- کسر مسلسل – به زبان ساده
جبر و معادله
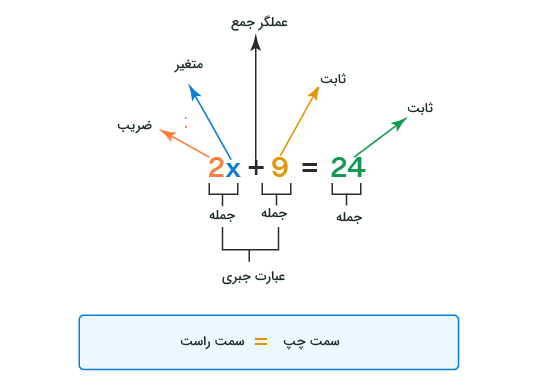
سومین موضوعی که در درس ریاضی پایه هفتم مطرح میشود، جبر و معادله است. معادله در ریاضیات به معنای برابری دو عبارت جبری است. عبارت جبری به مجموعهای از جملات گفته میشود که با علامتهای جمع یا تفریق به هم مربوط شدهاند. برای مثال، و نمونههایی از عبارت جبری هستند. بنابراین منظور ما از جملات در عبارت جبری، هر بخشی است که توسط علامت جمع یا تفریق به دیگری مرتبط شده است. در مثالهای بیان شده، اغلب جملات حاصلضرب یک عدد در متغیر هستند. در حقیقت، در عبارتهای جبری بالا متغیر هستند. هر کمیتی که مقدار عددی آن مشخص نباشد، توسط یک حرف انگلیسی نشان داده میشود و در ریاضیات متغیر نامیده میشود.
به تعریف معادله بازمیگردیم. هر معادله توصیف کننده تساوی بین دو عبارت جبری است که در دو طرف علامت تساوی یا نوشته شدهاند. حل کردن معادله، به معنای پیدا کردن مقدار عددی متغیری است که در آن معادله وجود دارد. اولین قدم برای حل معادله این است که معادله را تشخیص دهید. در این زمینه، به جدول زیر دقت کنید:
| عبارت جبری داده شده | آیا معادله است؟ |
| بله | |
| خیر | |
| بله |
همانطور که ملاحظه میکنید، دومین ردیف جدول بالا یک معادله نیست. چون در آن علامت تساوی بین دو عبارت جبری دیده نمیشود. اما ردیف سوم یک معادله است، با اینکه در آن هیچ متغیری دیده نمیشود، اما برابری دو طرف درست است. پس شرط داشتن معادله این است که بین دو عبارت جبری شامل اعداد بهتنهایی یا اعداد و متغیرها، حتما علامت تساوی داشته باشیم.
تجزیه عبارت های جبری
در بخش قبل تا حدی یاد گرفتیم یک عبارت جبری چیست. در این قسمت یاد میگیریم چگونه میتوان عبارتهای جبری را ساده کرد. فرآیند ساده کردن یا تجزیه عبارتهای جبری به معنای بازنویسی این عبارتها است، طوری که در نهایت هیچ جمله مشابهی وجود نداشته باشد و توانسته باشیم عبارت جبری اولیه را کوتاهتر کرده باشیم. روشهای مختلفی برای تجزیه عبارتهای جبری وجود دارد، اما به طور کلی با رعایت مراحل زیر میتوانیم تجزیه عبارتهای جبری را بهتر انجام دهیم:
- ابتدا جملات داخل پرانتز را با جمع یا تفریق کردن جملات مشابه ساده کنید.
- سپس عوامل خارج از پرانتز را که در آن ضرب شدهاند، در تک تک جملات داخل پرانتز ضرب کنید.
به مثال زیر در این زمینه توجه کنید:
این مثال عددی نمونهای از کاربرد یک ویژگی مهم در عبارتهای جبری به نام خاصیت توزیعپذیری است. طبق خاصیت توزیعپذیری همواره داریم:
عکس این فرآیند یعنی تبدیل جمع بالا به یک ضرب نیز جزئی از عملیات تجزیه است.
اجزای یک معادله چه هستند؟
بخشهای مختلفی که یک معادله میتواند داشته باشد، عبارتاند از:
- ضرایب
- متغیرها
- عملگرها
- ثابتها
- جملات
- عبارتها
- علامت تساوی
انواع معادلات
با توجه به درجه یا توان متغیرهایی که در عبارتهای جبری یک معادله دیده میشوند، میتوانیم انواع معادلات را بهصورت زیر دستهبندی کنیم:
- معادلات خطی
- معادلات درجه دو
- معادلات درجه سه
دستهبندی و تشخیص نوع معادلات از این جهت اهمیت دارد که روش حل انواع معادلات با هم متفاوت است. در نتیجه، میتوانیم روش درست حل هر معادله را بهراحتی انتخاب کنیم.
معادله خطی
هر معادلهای که در آن بیشترین توان متغیرهای موجود در معادله برابر با عدد یک باشد، یک معادله درجه اول یا خطی است. معادلات خطی را با توجه به تعداد متغیرهایی که دارند، میتوان بهصورت معادلات خطی یک متغیره، معادلات خطی دو متغیره و … تقسیمبندی کرد. فرم کلی برای یک معادله خطی با دو متغیر به شکل زیر است:
در این معادله و به ترتیب ضرایب دو متغیر و هستند.
چگونه یک معادله درجه اول را حل کنیم؟
برای حل یک معادله درجه اول، کافی است مراحل زیر را انجام دهیم:
- ابتدا باید تمام جملات دارای متغیر را به یک سمت علامت تساوی برده و تمام جملات بدون متغیر (ثوابت) را به سمت دیگر تساوی منتقل کنیم.
- تمام جملات شامل متغیر در یک سمت تساوی را با هم و تمام ثوابت در سمت دیگر تساوی را نیز با هم جمع میکنیم.
- با تقسیم طرف معلوم بر ضریب مجهول، متغیر بهدست میآید.
نکته: زمانی که جملهای از یک سمت تساوی به سمت دیگر تساوی منتقل میشود، علامت آن در یک منفی ضرب خواهد شد. برای مثال، اگر جملهای در سمت راست معادله علامت مثبت دارد، وقتی آن را به سمت چپ میبریم، علامتش منفی میشود.
فرض کنید میخواهیم معادله را حل کنیم. ابتدا ثابتها را در یک سمت تساوی به شکل قرار میدهیم. ملاحظه میکنید که علامت ثابت یا عدد پس از انتقال به سمت دیگر تساوی در یک منفی ضرب شده و در نتیجه، این عدد مثبت شده است. حالا با جمع کردن ثوابت در سمت راست معادله داریم:
در آخرین قدم، کافی است طرف معلوم یعنی مجموع ثوابت () را بر ضریب مجهول یعنی تقسیم کنیم:
معادله درجه دوم
در معادله درجه دو، بیشترین توان متغیرها برابر با عدد دو است. شکل استاندارد برای یک معادله درجه دو با یک متغیر بهصورت زیر خواهد شد:
همانطور که ملاحظه میکنید، در این معادله توان اول از هم دیده میشود. اما چون بالاترین توان این متغیر دو است، پس این معادله یک معادله درجه دو خواهد بود. اگر نمودار یک معادله درجه دو را رسم کنیم، یعنی با مقداردهی به متغیر ، مقدار را تعیین کنیم و سپس را بر حسب رسم کنیم، شکل نمودار حاصل بهصورت یک سهمی خواهد بود. برای یادگیری روشهای حل معادلات درجه دوم میتوانید به مطلب زیر مراجعه کنید.
معادله درجه سوم
در صورتی که در معادلهای جملاتی با توان سه (نه بیشتر) دیده شود، در این صورت این معادله یک معادله درجه سه است. شکل استاندارد یک معادله درجه سه با یک متغیر بهصورت زیر خواهد بود:
حل معادلات درجه سه کمی نسبت به حل معادلات درجه دو پیچیدهتر است.
نامعادله
اگر بهجای تساوی در یک معادله علامتهای کمتر یا بیشتر یا کمتر مساوی یا بیشتر مساوی را داشته باشیم، در این صورت بهجای معادله یک نامعادله داریم. در مورد نامعادلات نکته مهم این است که با ضرب کردن طرفین یک نامعادله در علامت منفی، جهت نامساوی تغییر میکند.
هندسه و استدلال
درس ریاضی پایه هفتم در چهارمین فصل خود به مبحث هندسه میرسد. در این بخش از کتاب، مفاهیم اولیه هندسه مانند خط، پارهخط، خطوط موازی و متقاطع مطرح میشوند که در ادامه به هر کدام از این موضوعات میپردازیم.
تعریف خط و نیم خط
هر شکل هندسی مستقیم و یک بعدی که ضخامتی ندارد و از هر دو طرف تا بینهایت ادامه دارد، خط نامیده میشود. شکل زیر تصویری از یک خط را نشان میدهد و همانطور که مشاهده میکنید، این خط از هر دو سمت تا بینهایت ادامه دارد (علامتهای پیکان در هر دو سمت خط نشاندهنده ادامهدار بودن آن هستند).

پس یک خط دارای نقطه انتها و ابتدا نیست و اندازهگیری طول آن، امکانپذیر نمیباشد. خطوط مختلف ممکن است بهصورت افقی، عمودی یا مایل رسم شوند. اما خطی که یکی از دو نقطه ابتدا یا انتهای آن مشخص باشد، نیمخط نام دارد. در نیمخط، یک سمت خط بسته است و با یک حرف انگلیسی مشخص میشود، در حالی که سمت دیگر باز است و با علامت پیکان متمایز میشود.
تعریف پاره خط
پارهخط در هندسه، خطی است که دارای نقطه ابتدا و انتها است و طول آن مشخص و قابلاندازهگیری است. برای مثال، در شکل زیر پارهخطی داریم که اندازه آن برابر است با فاصله بین دو نقطه ابتدا و انتهای آن یا فاصله بین دو نقطه و . برای نشان دادن یک پارهخط از نقاط ابتدا و انتهای آن استفاده میشود. برای نمونه، در تصویر زیر پارهخط را داریم که طول آن با نماد مشخص میشود.
خطوط موازی، متقاطع و متعامد
اگر دو یا چند خط داشته باشیم که همگی در یک صفحه باشند و فاصله بین آنها همواره ثابت بماند، در این صورت میگوییم این خطوط موازی هستند. موازی بودن دو خط و را با نمایش میدهیم. دو خط موازی هیچگاه یکدیگر را قطع نمیکنند. این در حالی است که خطوط متقاطع حداقل در یک نقطه یکدیگر را قطع میکنند.
در شکل زیر دو خط موازی را مشاهده میکنید که توسط خط سومی به نام «خط مورب» قطع شدهاند. چون برقرار است، بنابراین خط مورب با زاویههایی مساوی هر کدام از این دو خط را قطع میکند. همچنین سایر زاویههای ایجاد شده در این شکل مکمل یکدیگر هستند (برای مثال، زاویه یک و زاویه دو).
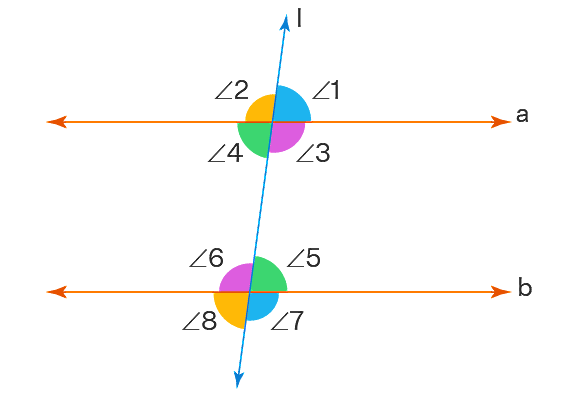
بنابراین هندسه بالا نتایج زیر را به ما میدهد:
همچنین زاویههایی که با رنگ صورتی مشخص شدهاند، مانند و با هم برابر هستند. یکی از انواع خطوط متقاطع خطوطی هستند که متعامداند. اگر خطی خط دیگری را با زاویه قائمه قطع کند، در این صورت میگوییم این دو خط بر هم عمود هستند یا متعامدند. برای نشان دادن تعامد دو خط از نماد استفاده میکنیم.
عمود منصف
در زمینه خطوط متقاطع یکی از مباحث مهم عمود منصف است. عمود منصف یک پارهخط به معنای خطی عمود بر آن است که آن را به دو قسمت کاملا مساوی تقسیم میکند. اگر عمود منصف پارهخطی مانند را در نقطه رسم کنیم، فاصله هر نقطه روی این عمود منصف از دو سر پارهخط همواره برابر است.
تعریف و انواع زاویه
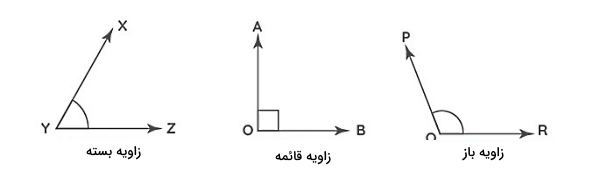
زمانی که دو خط متقاطع یکدیگر را در یک نقطه قطع میکنند، بین این دو خط یک زاویه تشکیل میشود. زاویهها را میتوانیم بر حسب واحدهای مختلفی مانند درجه یا رادیان اندازهگیری کنیم. همچنین بسته به اندازه زاویه، یک دستهبندی به شکل زیر برای زاویهها در نظر گرفته شده است:
زاویه های متمم و مکمل
پس از اینکه با مفهوم زاویه در درس ریاضی آشنا شدیم، حالا میتوانیم روابط بین زاویهها را توضیح دهیم:
نیمساز یک زاویه
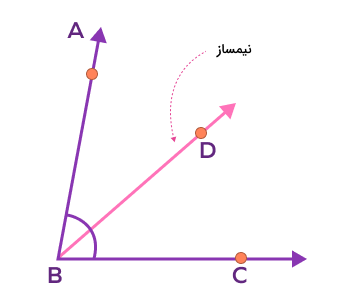
نیمساز یک زاویه خطی است که آن زاویه را به دو زاویه کاملا مساوی تقسیم میکند. برای مثال، در شکل زیر خط نیمساز زاویه است و اگر این زاویه قبل از رسم نیمساز شصت درجه باشد، پس از رسم نیمساز دو زاویه برابر با اندازه سی درجه خواهیم داشت.
انواع مثلث
مثلث یکی از اشکال هندسی است که از سه زاویه داخلی بسته و سه ضلع تشکیل شده است. در حقیقت، زمانی که سه خط مختلف یکدیگر را در سه نقطه قطع کنند، مثلث ساخته میشود. اگر سه زاویه یا سه راس یک مثلث و و باشند، در این صورت این مثلث را با نشان میدهیم. مجموع زاویههای یک مثلث همیشه برابر است با درجه.
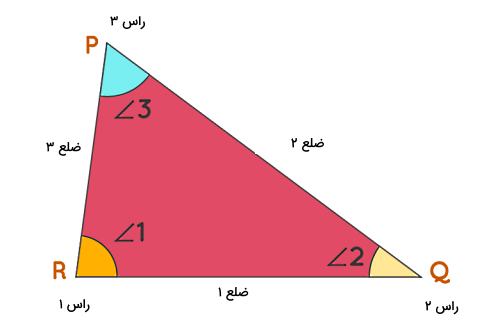
با توجه به اندازه اضلاع و زاویهها در یک مثلث، سه نوع مثلث خاص داریم:
با توجه به اینکه گفتیم مجموع زاویههای یک مثلث همیشه با درجه برابر است، پس اگر در یک مثلث هر سه زاویه آن با هم برابر باشد، میتوانیم نتیجهگیری کنیم که هر زاویه برابر میشود با درجه. به این ترتیب هر کدام از زاویههای یک مثلث متساویالاضلاع درجه است.
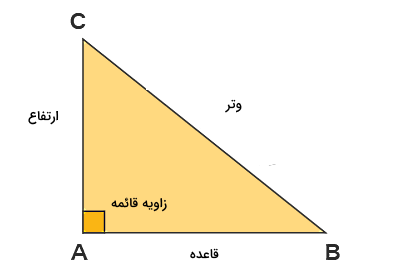
قضیه قیثاغورس
قضیه فیثاغورس در درس ریاضی قضیهای است که به ما کمک میکند با داشتن دو ضلع یک مثلث قائم الزاویه، اندازه سومین ضلع را پیدا کنیم. همانطور که گفتیم، در مثلث قائمالزاویه یک زاویه قائمه داریم که ضلع روبروی این زاویه «وتر» نامیده میشود. طبق این قضیه برای مثلث قائمالزاویهای به شکل زیر همواره مجموع مربعات دو ضلع دیگر یعنی قاعده و ارتفاع برابر است با مربع وتر:
چندضلعی ها
به تمام اشکال هندسی دو بعدی که از خطوط مستقیم و راست (نه خمیده) تشکیل شده و بهصورت یک شکل هندسی بستهاند، چندضلعی گفته میشود. برای مثال، مربع یک چندضلعی است، چون یک شکل هندسی دو بعدی است، دارای اضلاعی بهصورت خط راست است و تمام این اضلاع توسط زاویههایی به هم وصل شدهاند. اما دایره با اینکه یک شکل هندسی دو بعدی است، اما چندضلعی محسوب نمیشود، چون خمیده است و ضلع ندارد.


چندضلعیها با توجه به اندازه اضلاع و زاویههای خود به دو گروه تقسیم میشوند:
- چندضلعی منتظم: تمام اضلاع و زاویههای آن با هم برابر هستند.
- چندضلعی نامنتظم: اضلاع و زاویههای آن با هم برابر نیستند.
بهعلاوه میتوانیم چندضلعیها را بر اساس اندازه زاویههای داخلی آنها نیز تقسیمبندی کنیم. بر این اساس، دو نوع چندضلعی خواهیم داشت:
- چندضلعی محدب: چندضلعی که تمام زاویههای داخلی آن از درجه کوچکتر باشد.
- چندضلعی مقعر: چندضلعی که حداقل یک زاویه داخلی بزرگتر از درجه داشته باشد.
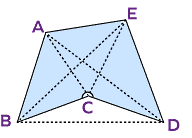
در چندضلعی محدب تمام قطرهای چندضلعی کاملا داخل آن قرار میگیرند. به عبارت دیگر، یکی از راههای تشخیص محدب بودن یک چندضلعی این است که خطوط متصل کننده هر دو زاویه در داخل چندضلعی را رسم کنیم. اگر تمام این خطوط داخل چندضلعی قرار گرفتند، در این صورت چندضلعی ما محدب است. اما در چندضلعی مقعر تمام قطرها داخل شکل قرار نمیگیرند. برای مثال، تصویر بالا نمونهای از یک پنجضلعی مقعر را نشان میدهد که در آن خط متصل کننده دو نقطه و خارج از شکل قرار میگیرد.
- نکته ۱: چندضلعی محدب میتواند منتظم یا نامنتظم باشد.
- نکته۲: چندضلعی مقعر هیچگاه منتظم نیست.
- نکته ۳: مجموع زاویههای داخلی یک چندضلعی محدب با ضلع توسط فرمول محاسبه میشود.
- نکته ۴: برای محاسبه مساحت یک چندضلعی محدب میتوانیم چندضلعی را به چند مثلث تقسیم کنیم و سپس مساحت بخشهای مختلف را با هم جمع کنیم.
چندضلعیها انواع مختلفی دارند، سهضلعیها یا مثلثها، چهارضلعیها که در بخش بعد توضیح داده میشوند، پنجضلعیها، ششضلعیها و به همین ترتیب. در جدول زیر ویژگیهای چندضلعیهای مختلف از جمله منتظم یا نامنتظم بودن، تعداد اضلاع و مجموع زاویههای داخلی نشان داده شده است:
| نام چندضلعی | تعداد اضلاع | منتظم یا نامنتظم | مجموع زاویههای داخلی (بر حسب درجه) |
| مثلث متساویالاضلاع | منتظم | ||
| مثلث متساویالساقین | نامنتظم | ||
| مثلث قائمالزاویه | نامنتظم | ||
| مثلثی با اضلاع متفاوت | نامنتظم | ||
| مربع | منتظم | ||
| مستطیل | نامنتظم |
چهارضلعی ها
یکی از زیرمجموعههای چندضلعیها در درس ریاضی، چهارضلعیها هستند. چهارضلعی یک شکل هندسی بسته است که فقط و فقط دارای چهار ضلع، چهار راس و چهار زاویه است. این چهار ضلع چهار نقطه را در این نوع اشکال هندسی به هم متصل میکنند. اغلب برای نشان دادن یک چهار ضلعی به شکل زیر میتوانیم از نامهایی بهصورت یا یا یا استفاده کنیم. اما برای مثال، انتخاب درستی نیست، چون این نوع نامگذاری با ترتیب رئوس این چهارضلعی همخوانی ندارد.
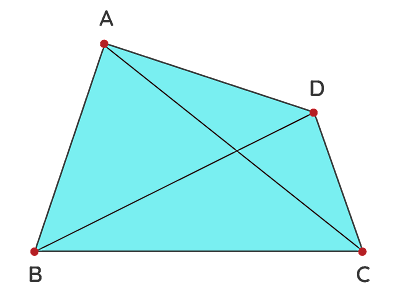
نکات مهم در مورد چهارضلعیها شامل موارد زیر هستند:
- مجموع زاویههای داخلی این اشکال هندسی برابر با درجه است.
- تمام چهارضلعیها دارای چهار ضلع، چهار راس و چهار زاویه اند.
- تمام چهارضلعیها دارای دو قطر هستند.
در ادامه خلاصهای از خصوصیات معروفترین چهارضلعیها را توضیح خواهیم داد. البته چهارضلعیهای دیگری مانند لوزی، ذوزنقه و کایت یا شبهلوزی نیز وجود دارند که با توجه به گستردگی موضوع این نوشته، میتوانید مطالب مرتبط در مجله فرادرس را در این زمینه مطالعه کنید.
مربع
اولین چهارضلعی که در درس ریاضی با ویژگیهای آن آشنا میشویم، مربع است. طبق شکل زیر و خصوصیات کلی که تا اینجا راجعبه چهارضلعیها گفتیم، در مربع هر چهار ضلع و هر چهار زاویه با هم برابر هستند. همچنین در این شکل هندسی دو جفت ضلع داریم که با هم موازی هستند. دو قطر مربع با هم مساوی و بر هم عموداند که این زاویه قائمه در شکل مشخص شده است.
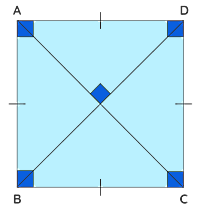
پس اگر بخواهیم ویژگیهای مربع را به زبان ریاضی توصیف کنیم، خواهیم داشت:
- و
مستطیل
ویژگیهای مستطیل بسیار شبیه ویژگیهای مربع است. تفاوت مربع و مستطیل در این است که اندازه تمام اضلاع در مستطیل با هم برابر نیست. به عبارت دیگر مستطیل یک چهارضلعی منتظم محسوب نمیشود، در حالی که مربع یک چهارضلعی منتظم است. در مستطیل فقط اضلاع روبروی هم با هم مساوی و موازی هستند. تفاوت دیگر مستطیل و مربع که از برابر نبودن تمام اضلاع مستطیل ناشی میشود، عمود نبودن قطرهای مستطیل است.
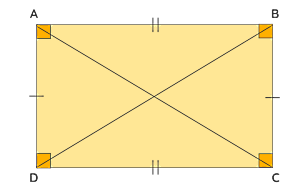
پس اگر بخواهیم ویژگیهای مستطیل را به زبان ریاضی توصیف کنیم، خواهیم داشت:
- و
- و
متوازی الاضلاع
چهارضلعی بعدی که در درس ریاضی به بیان خصوصیات آن پرداخته میشود، متوازیالاضلاع است. این چهارضلعی بسیار شبیه مستطیل است، با این تفاوت که هیچکدام از زاویههای آن قائمه نیستند. با این حال، زاویههای روبروی هم در یک متوزایالاضلاع همواره با هم برابر هستند. همچنین قطرهای متوازیالاضلاع با اینکه یکدیگر را قطع میکنند، اما بر هم عمود نبوده و با هم برابر نیستند.
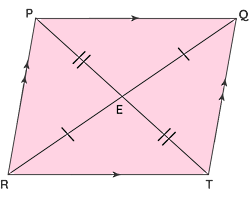
خصوصیات مهم یک متوازیالاضلاع بهصورت زیر خلاصه میشوند:
- و
- و
- و
زاویه داخلی و خارجی
در بخش قبل اشاره کردیم که برای مثال مجموع زاویههای داخلی یک چهارضلعی برابر است با درجه. در این بخش مفهوم زاویه خارجی در درس ریاضی توضیح داده میشود. به شکل زیر توجه کنید. در این تصویر یک پنجضلعی منتظم و محدب را مشاهده میکنید که زاویههای داخلی آن با رنگ قرمز و زاویههای خارجی آن با رنگ آبی نمایش داده شده است. زاویه خارجی به زاویهای گفته میشود که از امتداد هر ضلع از یک چندضلعی بهدست میآید. در حقیقت زاویه خارجی زاویهای است که بین امتداد یک ضلع و ضلع مجاور در یک چندضلعی ایجاد میشود.
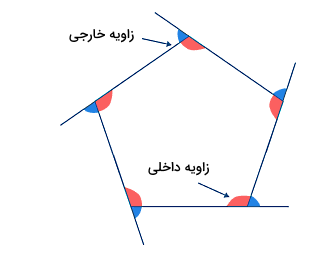
- نکته ۱: مجموع زاویههای خارجی هر چندضلعی همواره برابر است با درجه.
- نکته ۲: زاویه داخلی زاویهای است که بین دو ضلع یک شکل هندسی ایجاد میشود، در حالی که زاویه خارجی زاویهای است که بین امتداد یکی از اضلاع و ضلع دیگر ایجاد میشود.
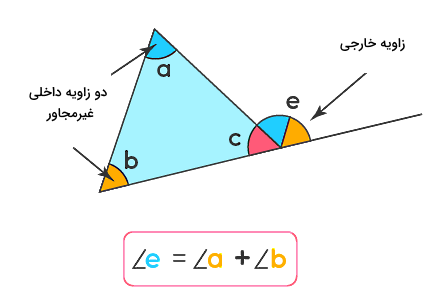
قضیه زاویه خارجی
قضیه زاویه خارجی بیان میکند اندازه هز زاویه خارجی در یک مثلث برابر است با مجموع دو زاویه داخلی غیرمجاور به آن زاویه خارجی. با توجه به اینکه میدانیم هر مثلث دارای سه زاویه داخلی است که مجموع این زوایا برابر است با درجه، در نتیجه شش زاویه خارجی برای هر مثلث خواهیم داشت که از امتداد هر کدام از اضلاع در هر راس ناشی میشوند. این قضیه برای هر کدام از این شش زاویه خارجی صادق است:
سطح و حجم
پیش از اینکه فرمولهای محاسبه محیط، مساحت و حجم در درس ریاضی را برای شکلهای هندسی مختلف بیان کنیم، ابتدا باید ببینیم تفاوت محیط، مساحت و حجم چیست. همچنین مفاهیم دیگری به نام «مساحت جانبی» و «مساحت کل» در مورد حجمهای هندسی مطرح میشوند که باید تفاوت آنها را نیز با مساحت بدانیم:
- محیط: مجموع اضلاع یک شکل هندسی.
- مساحت: ناحیهای که یک شکل هندسی دو بعدی مانند مربع، مستطیل، مثلث یا دایره در یک فضای دو بعدی اشغال میکند.
- مساحت جانبی: مساحت وجههای جانبی (که شامل قاعدهها نمیشود) برای یک شکل هندسی سه بعدی یا یک چندوجهی مانند مکعب یا کره.
- مساحت کل: کل مساحت وجههای خارجی یک شکل هندسی سه بعدی یا یک چندوجهی (مجموع مساحت جانبی و مساحت قاعدهها).
- حجم: کل فضایی که توسط یک شکل هندسی سه بعدی در فضا اشغال میشود. حرکت سطح در فضا حجم را میسازد.
اصلیترین تفاوت مساحت و محیط با حجم، مساحت جانبی یا مساحت کل، ابعاد شکل هندسی موردنظر است. بهطور کلی، محیط و مساحت برای چندضلعیها یا شکلهای هندسی دو بعدی محاسبه میشوند، اما مساحت جانبی، مساحت کل و حجم را برای یک شکل هندسی سه بعدی یا یک چندوجهی حساب میکنیم. شکل زیر تفاوت مساحت، مساحت کل و مساحت جانبی را نشان میدهد:
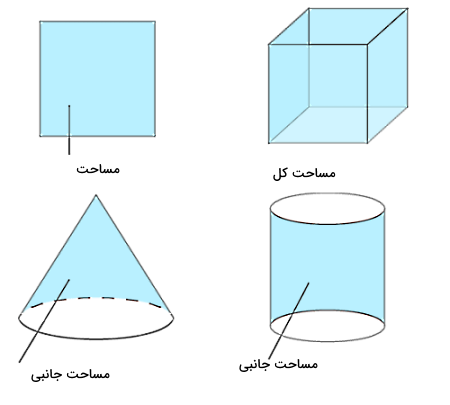
همانطور که ملاحظه میکنید، برای مربع فقط مساحت محاسبه میشود. در واقع مربع حجم ندارد. اما برای شکلهای هندسی سه بعدی یا احجام هندسی مانند مکعب، مخروط یا استوانه میتوانیم مساحت کل یا مساحت جانبی را در کنار حجم پیدا کنیم. در شکل مساحت کل مکعب و مساحت جانبی مخروط و استوانه با رنگ آبی نشان داده شدهاند.
حجمهای هندسی در درس ریاضی دارای شکل هندسی مشخصی هستند، به این معنا که یا در گروه حجمهای کروی، هرمی یا منشوری قرار میگیرند و یا با ترکیبی از این حجمها ساخته شدهاند. تشخیص یک حجم کروی مانند کره آسان است. حجمهای منشوری مانند استوانه، مکعب مستطیل یا منشور شش پهلو همواره از دو صفحه موازی به نام قاعده تشکیل میشوند. در حجمهای هرمی مانند مخروط، بهجای یکی از صفحات موازی در منشور، نقطهای داریم که تمام اضلاع به آن میرسند. به این نقطه، راس هرم گفته میشود. بنابراین حجمهای هروی یک قاعده دارند. در بخشهای بعد با این احجام بیشتر آشنا خواهید شد.
مساحت اشکال هندسی دو بعدی
مساحت برای اشکال هندسی دو بعدی و سه بعدی محاسبه میشود، اما با تغییر ابعاد، فرمولهای مساحت نیز تغییر میکنند. فرمول محاسبه مساحت برای شکلهای دو بعدی بهصورت زیر است:
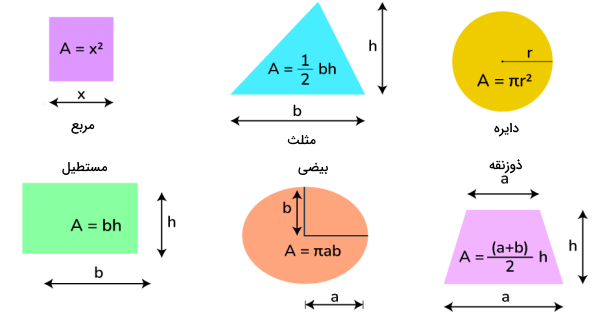
به این ترتیب، نکات مهم در محاسبه مساحت شکلهای دو بعدی بهصورت زیر است:
مساحت اشکال هندسی سه بعدی
اغلب شکلهای هندسی سه بعدی با اضافه کردن یک بعد به اشکال هندسی دو بعدی ساخته میشوند. برای مثال، کره شکل سه بعدی دایره است. مکعب شکل سه بعدی مربع و مکعب مستطیل شکل سهبعدی مستطیل است. سایر احجام هندسی عبارتاند از مخروط، هرم و استوانه. همانطور که در بخشهای قبل گفتیم، مساحت کل یک شکل هندسی سه بعدی همواره برابر است با مجموع مساحت جانبی و مساحت قاعدههای آن شکل.
برای نمونه، فرض کنید میخواهیم مساحت کل مخروطی به شکل زیر را پیدا کنیم. مخروط یک شکل هندسی سه بعدی است که قاعدهای به شکل دایره دارد و همانطور که ملاحظه میکنید، سطح جانبی آن در نقطهای به نام راس مخروط باریک میشود. فاصله راس مخروط تا قاعده آن را ارتفاع مخروط مینامیم که در شکل برابر است با . در حقیقت مخروط نوعی هرم است که قاعده آن دایرهای شکل است.
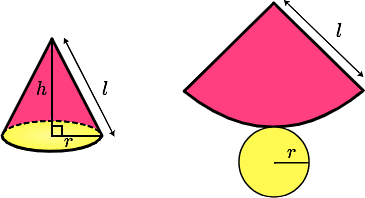
مساحت کل این شکل هندسی را میتوانیم با باز کردن آن به شکل سمت راست در تصویر بالا درآوریم. این بخش را گسترده مخروط مینامیم. در حقیقت دو شکل بالا با هم معادل هستند. پس اگر مجموع مساحت دایره زرد رنگ و قطاع دایرهای صورتی رنگ را پیدا کنیم، کل مساحت این مخروط بهدست آمده است. بهعلاوه مساحت قطاع صورتی رنگ همان مساحت جانبی برای این مخروط محسوب میشود. اولین بخش نامعلوم در این محاسبه این است که قطاع چیست و مساحت آن چگونه بهدست میآید.
با توجه به شکل زیر میتوانیم مساحت قطاع را در نظر بگیریم. بنابراین مساحت کل مخروط بالا برابر است با:
در حالی که معادل است با مساحت جانبی آن.

به همین شکل میتوانیم مساحت جانبی منشور، مساحت جانبی استوانه و مساحت جانبی هرم را محاسبه کنیم. همانطور که گفتیم، کلیه حجمهای منشوری همواره بین دو قاعده قرار میگیرند و بخشهای جانبی یا وجه جانبی در منشور، همان سطح جانبی است. انواع مختلف منشور چند پهلو هستند، یعنی منشور شش پهلو، سه پهلو یا چهار پهلو داریم. با توجه به این تعریف، مساحت کل یک منشور چهار پهلو به شکل زیر است:
حجم اشکال هندسی
پس از اینکه با مهمترین حجمهای هندسی در درس ریاضی آشنا شدیم، در این بخش میخواهیم فرمولهای حجم را برای این اشکال معرفی کنیم:
- حجم مکعبی به ضلع برابر است با .
- حجم مکعب مستطیلی با اضلاع برابر است با .
- حجم کرهای با شعاع برابر است با .
- حجم مخروطی با شعاع قاعده و ارتفاع برابر است با .
- حجم استوانهای با شعاع قاعده و ارتفاع برابر است با .
- حجم منشور با توجه به نوع منشور همواره برابر است با مساحت قاعده در ارتفاع.
- حجم هرم با توجه به نوع هرم همواره برابر است با یک سوم مساحت قاعده در ارتفاع.
انواع تبدیلات هندسی و تقارن
از تبدیلات هندسی در درس ریاضی و بهخصوص در هندسه زیاد استفاده میشود. انواع تبدیلات هندسی عبارتاند از:
- انتقال: در انتقال شکل هندسی نسبت به یک پیکان (خطی با جهت مشخص) منتقل میشود.
- تقارن: در تقارن، شکل هندسی نسبت به یک خط یا محور و بهصورت آینهای تبدیل میشود.
- دوران: در دوران شکل هندسی نسبت به نقطهای به نام مرکز تقارن چرخانده میشود.
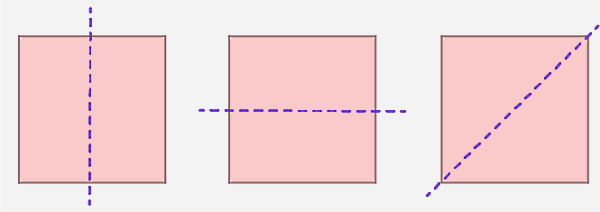
برای مثال، در تصویر زیر خط نقطهچین نشاندهنده خط تقارن یا محور تقارن شکل است، به این معنا که اگر شکل را در راستای این خط به دو قسمت تقسیم کنیم، تمام اجزای شکل اول تصویر آینهای از اجزای متناظر در شکل دوم هستند. اگر جسمی به این شکل تبدیل شود، میگوییم این جسم متقارن است. به این ترتیب ممکن نیست بتوانیم اجسام نامتقارن را با این روش به اجزایی تبدیل کنیم که با هم شباهت دارند.

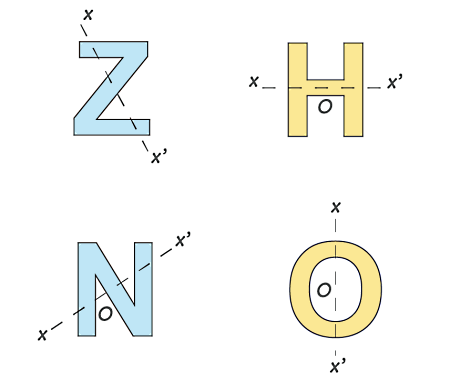
محور تقارن همیشه عمودی نیست، بلکه میتواند افقی یا قطری هم باشد. در واقع، اشکال هندسی مختلف دارای محور تقارنهای مختلفی هستند. برای مثال، مربع هر سه نوع محور تقارن یعنی محور تقارن عمودی، افقی و قطری را دارد. اما یک مثلث که طول اضلاع آن با هم متفاوت است، هیچ محور تقارنی ندارد. این در حالی است که مثلثهای متساویالاضلاع و متساویالساقین بهترتیب سه و یک محور تقارن دارند.
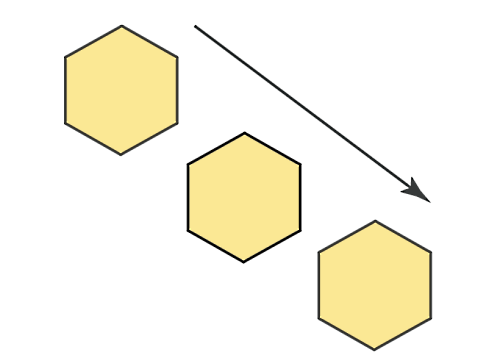
تصویر زیر نشاندهنده نوع دیگری از یک تبدیل هندسی به نام انتقال است. یک شش ضلعی منتظم در این تصویر در راستای برداری که مشاهده میکنید، منتقل شده است. در انتقال، کل یک شکل هندسی از یک موقعیت مکانی به موقعیت مکانی دیگر منتقل میشود. بنابراین جهتگیری شکل، زاویهها و اندازه اضلاع و … تغییری نمیکند.
اگر هر نقطه از یک شکل هندسی به اندازه زاویه درجه منتقل شود، در این صورت میگوییم این شکل دوران داده شده است. نقطهای که دوران حول آن رخ میدهد و در نتیجه، شکل روی خودش منطبق میشود مرکز تقارن نام دارد. به شکل زیر در رابطه با مرکز تقارن دقت کنید:
شکل های همنهشت
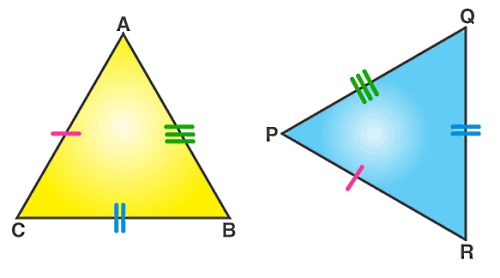
همنهشتی به این معنا است که بتوانیم یک شکل هندسی را کاملا بر شکل دیگر منطبق کنیم. این فرآیند را میتوانیم با کمک گرفتن از انواع تبدیلات هندسی در درس ریاضی که در بخش قبل معرفی شدند، انجام دهیم. برای مثال، اگر بخواهیم همنهشتی دو مثلث را بررسی کنیم، باید علاوهبر اضلاع، زاویههای این دو را نیز با هم مقایسه کنیم.
بهطور کلی در هر کدام از سه حالت زیر میتوانیم بگوییم دو مثلث همنهشت محسوب میشوند:
- سه ضلع دو مثلث با هم برابر باشند (ض ض ض).
- دو ضلع مجاور و زاویه بین این دو ضلع در دو مثلث با هم برابر باشند (ض ز ض).
- دو زاویه و ضلع بین از هر دو مثلث با هم برابر باشند (ز ض ز).
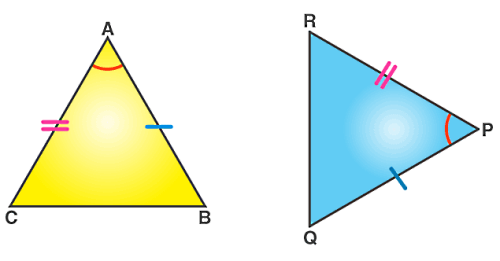
پس از اینکه توانستیم ثابت کنیم دو مثلث همنهشتاند، این امکان وجود دارد تا بتوانیم سایر بخشهای نامعلوم در مثلثها را بهدست آوریم. در مورد مثلث قائمالزاویه میتوانیم دو حالت دیگر به سه حالت بالا اضافه کنیم:
- وتر و یک ضلع از یک مثلث با وتر و یک ضلع از مثلث دیگر برابر است.
- وتر و یک زاویه تند از یک مثلث با وتر و یک زاویه تند از مثلث دیگر برابر است.
دایره
دایره یکی از اشکال هندسی است که مهمترین مشخصه آن شعاع است. فاصله مرکز دایره از هر نقطه روی محیط آن، شعاع نامیده میشود. دو برابر شعاع دایره قطر دایره است. در مورد این شکل دو بعدی چند نکته مهم وجود دارد که در انتهای کتاب ریاضی هشتم مطرح شدهاند:
- اگر بین یک خط و دایره تنها یک نقطه مشترک وجود داشته باشد، در این صورت میگوییم این خط بر دایره مماس است.
- شعاع دایره همواره به محیط داخلی آن عمود است.
- اگر دو کمان از یک دایره با هم برابر باشند،ِ وترهای نظیر آنها هم با هم برابر هستند و برعکس.
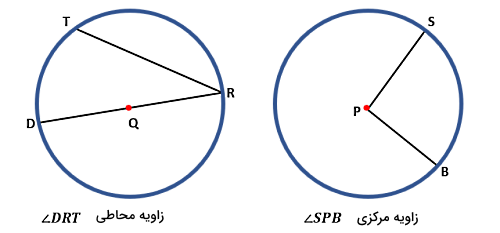
- زاویه مرکزی در دایره به زاویهای گفته میشود که راس آن در مرکز دایره قرار دارد.
- زاویه محاطی در دایره به زاویهای گفته میشود که راس آن روی محیط دایره قرار دارد.
شمارنده ها و اعداد اول
برای اینکه با مفاهیم این بخش از درس ریاضی بهتر آشنا شویم، ابتدا باید ببینیم منظور ما از مفاهیمی مانند شمارنده و بخشپذیری چیست. شمارندههای یک عدد مجموعهای از اعداد هستند که با ضرب برخی از آنها در یکدیگر، عدد موردنظر بهدست میآید. برای مثال تنها شمارندههای عدد عبارتاند از و ، چون داریم . اما برای عددی مانند ، علاوهبر و ، شمارندههایی مانند و هم داریم، چون .
بنابراین میتوانیم بگوییم اگر شمارندههای یک عدد را تعیین کرده باشیم، آن عدد حتما بر تک تک این شمارندهها بخشپذیر است. تعیین تمام شمارندههای یک عدد را تجزیه کردن عدد مینامند. برای مثال، یکی از شمارندههای است، در نتیجه بر بخشپذیر است. بخشپذیری به این معنا است که باقیمانده تقسیم عدد موردنظر به هر کدام از شمارندههای آن برابر است با صفر. پس در واقع ما عدد موردنظر خود را بر شمارنده تقسیم میکنیم و شمارنده همان مقسوم علیه در این تقسیم است.
عدد اول چیست؟
هر عدد طبیعی و بزرگتر از که فقط دو شمارنده داشته باشد، به این صورت که شمارندههای آن فقط عدد و خودش باشند، عدد اول است. عدد اول همیشه از بزرگتر است و تقسیم آن به هر عدد صحیح و مثبت دیگری دارای باقیمانده خواهد بود یا پاسخ کسری یا اعشاری داریم. جدول زیر اعداد اول کوچکتر از را به تفکیک نشان میدهد:
| اعداد کوچکتر از | اعداد اول |
| بین و | |
| بین و | |
| بین و | |
| بین و | |
| بین و | |
| بین و |
بزرگترین شمارنده مشترک یا ب. م. م.
گفتیم شمارندههای یک عدد همان مقسوم علیههای آن عدد هستند. بزرگترین مقسوم علیه مشترک دو عدد همان بزرگترین شمارنده مشترک بین این دو عدد است که به اختصار با ب. م. م. یا نشان داده میشود. برای مثال، فرض کنید دو عدد و را در نظر داریم و میخواهیم ب. م. م. این دو عدد را تعیین کنیم. شمارندهها یا مقسوم علیههای عبارتاند از:
در حالی که مجموعه تمام شمارندهها یا مقسوم علیههای بهصورت زیر است:
حالا باید ابتدا شمارندههای مشترک این دو عدد را مشخص کنیم که برابر است با . پس ب. م. م. این دو عدد یا بزرگترین عدد بین این دو عدد میشود .
کوچکترین مضرب مشترک یا ک. م. م.
برای تعیین ک. م. م. دو عدد، ابتدا باید ببینیم مفهوم مضرب در درس ریاضی چیست. از ضرب هر عدد در یک عدد غیر صفر مضربهای آن عدد بهدست میآید. برای نمونه، اگر بخواهیم مضارب عدد را تعیین کنیم، این عدد را در به ترتیب ضرب میکنیم و خواهیم داشت:
حالا اگر بخواهیم کوچکترین مضرب مشترک دو عدد را پیدا کنیم، کافی است تمام مضارب این دو عدد را بنویسیم. اولین مضرب مشترک معادل است با ک. م. م.. برای مثال، کوچترین مضرب مشترک دو عدد و به شکل زیر مشخص میشود:
عدد مرکب چیست؟
یکی دیگر از تعاریفی که میتوانیم برای اعداد اول ارائه دهیم به این صورت است: هر عدد کامل و بزرگتر از که نمیتوانیم آن را بهصورت حاصلضرب دو عدد دیگر (به جز خودش و ) بنویسیم. این تعریف ما را به گروه دیگری از اعداد میرساند که کاملا در نقطه مقابل این تعریف قرار دارند و اعداد مرکب نامیده میشوند. به این ترتیب، هر عدد مرکب را میتوانیم بهصورت حاصلضرب دو عدد طبیعی و بزرگتر از بنویسیم. به تصویر زیر دقت کنید:
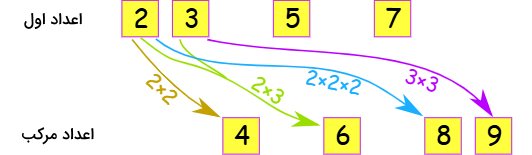
تمام اعداد مرکب در این تصویر را میتوان حاصلضربی از اعداد اول در نظر گرفت.
نکته: عدد نه عدد اول است و نه عدد مرکب.
چه اعدادی نسبت به هم اول هستند؟
اگر دو عدد مرکب هیچ فاکتور مشترکی جز عدد نداشته باشند، در این صورت میگوییم این دو عدد نسبت به هم اول هستند. دقت کنید اینکه دو عدد مرکب نسبت به هم اول هستند به این معنا نیست که این دو عدد اول هستند. هر دو عددی که نسبت به هم اولاند، تنها به یک عدد مشترک بخشپذیر هستند و آن عدد است. به این اعداد، اعداد اول متباین یا اعداد اول متقابل هم گفته میشود. اگر بخواهیم سریع متوجه شویم آیا دو عدد داده شده نسبت به هم اول هستند یا نه، کافی است ب. م. م آنها را پیدا کنیم. اگر ب. م. م. دو عدد برابر با شد، در این صورت این دو عدد حتما نسبت به هم اول هستند. برای مثال، تمام شمارندههای اعداد و را در نظر بگیرید:
بزرگترین مقسوم علیه مشترک این دو عدد است. پس میتوانیم بگوییم با اینکه و اول نیستند، اما نسبت به هم اولاند.
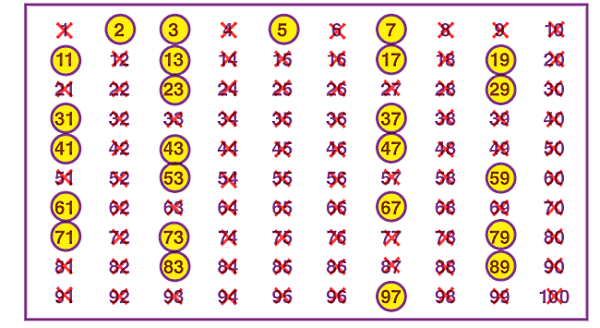
روش غربال اعداد اول
آخرین مبحث مرتبط با اعداد اول در درس ریاضی، توضیح روشی به نام غربال کردن اعداد اول است. از آنجا که تشخیص اعداد اول راحت نیست، اگر بخواهیم بدانیم از تا یک عدد مشخص مانند چند عدد اول داریم، میتوانیم از این روش استفاده کنیم. کافی است مراحل زیر را یکی پس از دیگری مطابق شکل زیر انجام دهیم:
- تمام اعداد طبیعی از تا را یکبار در یک سطر و یکبار در یک ستون مینویسیم.
- ابتدا عدد را خط میزنیم، چون میدانیم این عدد نه اول است و نه مرکب.
- دور عدد دایره میکشیم چون میدانیم عدد اول است.
- تمام مضربهای را خط میزنیم، چون تمام این اعداد مرکب محسوب میشوند.
- دور عدد دایره میکشیم چون میدانیم عدد اول است.
- تمام مضربهای را خط میزنیم، چون تمام این اعداد مرکب محسوب میشوند.
- دور عدد دایره میکشیم چون میدانیم عدد اول است.
- تمام مضربهای را خط میزنیم، چون تمام این اعداد مرکب محسوب میشوند.
- مراحل بالا را برای اعداد و تکرار میکنیم.
- اعداد باقیمانده اول هستند.
توان و جذر
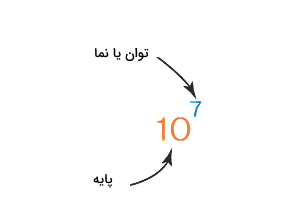
اگر عددی چند بار در خودش ضرب شود، میتوانیم آن را بهصورت یک عدد تواندار بنویسم. برای مثال، فرض کنید داریم . در این عبارت عدد به اندازه مرتبه در خودش ضرب شده است. پس نمایش توانی این عبارت بهصورت زیر است که در آن پایه و توان یا نما نامیده میشود:
قواعد محاسبات اعداد توان دار
برای اینکه در محاسبات اعداد تواندار بهدرستی عمل کنیم، چند قاعده کوتاه در این بخش معرفی میشود که بهتر است آنها را بهخاطر بسپارید:
- عدد به توان صفر:
- عدد به توان یک:
- به توان رسیدن یک عدد تواندار:
- عدد تواندار با توان منفی:
- به توان رسیدن ضرب دو عدد:
- به توان رسیدن تقسیم دو عدد:
ضرب اعداد توان دار
عملیاتی مانند ضرب را میتوان روی اعداد توانی یا تواندار انجام داد. فرض کنید میخواهیم حاصلضرب اعداد توانداری مانند و را پیدا کنیم. یک راهحل این است که عدد را سه بار در خودش ضرب کرده و حاصل را در که همان است، ضرب کنیم. اگر دقت کنید، در این روش و با هم جمع شدهاند و در حقیقت عدد به تعداد بار در خودش ضرب شده است. پس میتوانیم بهجای این کار، از همان ابتدا نماها یا توانهای دو عدد را با هم جمع کنیم و با در نظر گرفتن پایه ، حاصل را بهصورت بنویسیم. به این ترتیب اگر دو عدد توانی با پایه مشترک (پایههای مشابه هم) داشته باشیم، ضرب این دو عدد به شکل زیر انجام میشود:
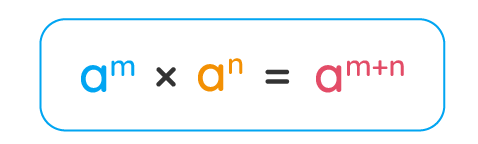
نکته: این قانون زمانی کاربرد دارد که پایههای دو عدد با هم یکی باشند.
تقسیم اعداد توان دار
عملیات تقسیم اعداد توانی با پایههای مشترک مانند ضرب اعداد تواندار است، با این تفاوت که در اینجا توانهای دو عدد از هم کم میشوند. به این ترتیب اگر دو عدد توانی با پایه مشترک (پایههای مشابه هم) داشته باشیم، تقسیم این دو عدد به شکل زیر انجام میشود:
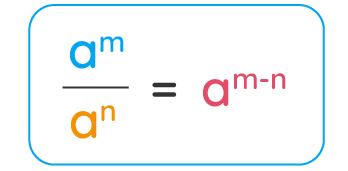
نکته: این قانون هم مانند قاعده ضرب اعداد تواندار، زمانی کاربرد دارد که پایههای دو عدد با هم یکی باشند.
جمع و تفریق اعداد توان دار
در درس ریاضی برای سادهسازی جمع و تفریق اعداد تواندار میتوانیم از قواعد ضرب و تقسیم استفاده کنیم. به مثال زیر در این زمینه توجه کنید:
در این سوال چهار با عدد تواندار با خودش جمع شده است. پس میتوانیم آن را به شکل زیر بازنویسی کنیم:
در نهایت به کمک قاعده ضرب بهراحتی پاسخ بهدست میآید. یا در مثال دیگری، تفریق دو عدد توانی را به شکل زیر داریم:
در این سوال عدد در عامل $5^3$$ و عدد $1$$
جذر و ریشه
عبارتی بهصورت را در نظر بگیرید. در این تساوی، توان دوم یا مجذور عدد و عدد ریشه دوم یا جذر عدد نامیده میشوند. پس به توان دوم هر عدد، مجذور آن عدد و به ریشه دوم هر عدد، جذر آن عدد گفته میشود. نمایش ریشه دوم یک عدد با نماد رادیکال روی آن مشخص میشود.
- نکته ۱: اگر یک عدد حقیقی مثبت باشد، و ریشههای دوم این عدد هستند.
- نکته ۲: اعداد منفی ریشه دوم ندارند.
- نکته ۳: اگر یک عدد حقیقی باشد، و ریشههای سوم این عدد هستند.
جذر تقریبی
گاهی محاسبه جذر یک عدد راحت نیست. اگر مجذور ده عدد اول را بدانیم، میتوانیم بهصورت تقریبی حاصل یک رادیکال را حدس بزنیم. به این روش محاسبه جذر، جذر تقریبی میگویند. برای مثال، را نمیتوانیم بهصورت دقیق و بدون کمک گرفتن از ماشین حساب پیدا کنیم. اما میدانیم جذر برابر است با و جذر برابر است با . پس جذر هم باید بین جذر این دو عدد قرار بگیرد. در نتیجه همواره بزرگتر از و کوچکتر از است.
اعداد توان دار با توان کسری (اعداد رادیکالی)
اگر عدد توانداری دارای توان کسری باشد، عدد تواندار ما معادل خواهد شد با یک عدد رادیکالی:
به این ترتیب برای مثال داریم .
بردار و مختصات
یکی از بخشهای انتهایی درس ریاضی پایه هفتم مبحث بردارها است. بردار پارهخط جهتداری است که علاوه بر اندازه، دارای جهت مشخصی است. بنابراین زمانی از بردار استفاده میکنیم که علاوهبر اندازه یا فاصله، جهت هم برای ما مهم است. برداری که نقطه را به نقطه وصل میکند، بردار نامیده میشود. بردارهای قرینه، اندازهای برابر ولی جهتهای مخالف هم دارند، در حالی که بردارهای مساوی، هم اندازه و هم جهت کاملا یکسانی دارند. هر بردار از سه بخش تشکیل شده است:
- ابتدای بردار
- اندازه بردار
- انتها یا جهت بردار
محورهای مختصات
از مباحث گذشته در درس ریاضی میدانیم محورهای مختصات محورهایی هستند که یک صفحه را به چهار ناحیه مساوی تقسیم میکنند. این محورها متشکلاند از محور افقی (محور ) و محور قائم (محور ) که با زاویه قائمه یکدیگر را در نقطهای به نام مبدا مختصات قطع کردهاند. تصویر زیر بخشهای مختلف یک صفحه مختصات و چهار ناحیه آن را نشان میدهد:
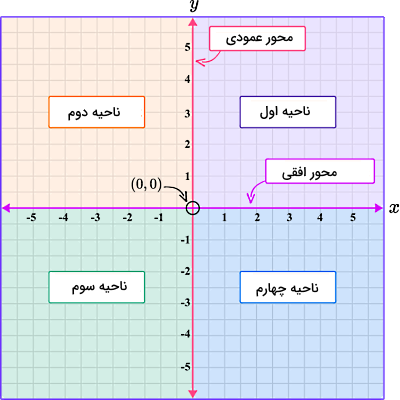
به این ترتیب هر نقطه در این صفحه دارای یک مختصات مشخص است که برای نشان دادن آن از نمادی بهصورت استفاده میشود. در این نمادگذاری، بیانگر این است که نقطه موردنظر ما چقدر نسبت به مبدا روی محور افقی جابجا شده است، در حالی که جابجایی این نقطه نسبت به مبدا در راستای محور قائم را نشان میدهد. برای تعیین مختصات یک نقطه، ابتدا باید ببینیم این نقطه در کدام ناحیه از صفحه مختصات قرار دارد. ویژگیهای چهار ناحیه صفحه مختصات عبارتاند از:
- ناحیه اول: هم مقادیر و هم مقادیر مثبتاند.
- ناحیه دوم: مقادیر منفی و مقادیر مثبتاند.
- ناحیه سوم: هم مقادیر و هم مقادیر منفیاند.
- ناحیه چهارم: مقادیر مثبت و مقادیر منفیاند.
اگر صفحه مختصات را مانند شکل بالا، بهصورت یک صفحه شطرنجی در نظر بگیریم که هر خانه مربعی شکل کوچک آن دارای اضلاعی با اندازه واحد است، در این صورت میتوانیم با شمارش این واحدها بهراحتی مقادیر و را برای هر نقطه فرضی پیدا کنیم. برای مثال، نقاط مشخص شده در تصویر زیر را در نظر بگیرید:
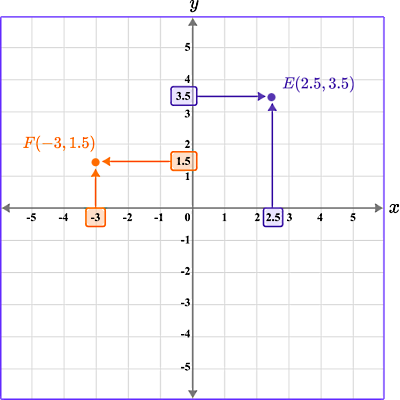
در مورد نقطه که در ناحیه یا ربع دوم صفحه مختصات قرار دارد، مختصات افقی این نقطه توسط برداری مشخص میشود که از مبدا مختصات و موازی با محور افقی تا این نقطه رسم میشود. اما مختصات قائم متناظر با این نقطه، برداری است که از مبدا و موازی با محور قائم تا این نقطه رسم میشود. پس مختصات نقطه برابر است با که با هم نشان داده میشود.
جمع بردارها
برای اینکه بتوانیم دو بردار را با هم جمع کنیم، کافی است مختصات هر بردار را بدانیم. فرض کنید و است. در این صورت مجموع این دو بردار بهصورت زیر خواهد شد:
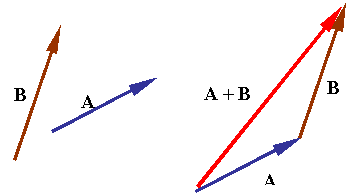
همچنین اگر عدد صحیحی مانند در بردار ضرب شود، در حقیقت این عدد در هر کدام از مولفههای مختصات این بردار ضرب میشود و خواهیم داشت:
بردار واحد
یکی از بهترین روشهای نمایش مختصات بردارها این است که از بردارهای یکه یا بردارهای واحد استفاده کنیم. بردار یکه برداری است با اندازهای برابر با یک یا واحد و همواره دارای جهت مشخصی در راستای یکی از محورهای مختصات است. برای اینکه بین بردار معمولی و بردار یکه تمایز قائل شویم، بردار یکه را با نماد نشان میدهیم، در حالی که بردار معمولی با نشان داده میشود.
کاربرد بردار واحد فقط برای مشخص کردن جهت یک بردار معمولی است، به این صورت که با ضرب این بردار در یک مقدار عددی بردار جدیدی ساخته میشود که اندازه آن برابر است با اندازه آن مقدار عددی و جهت آن برابر است با جهت بردار یکهاش. برای مثال برداری مانند با و معادل است.
نکته: اندازه بردار را میتوانیم با یا نمایش دهیم. اندازه یک بردار همیشه یک مقدار عددی است و جهت ندارد.
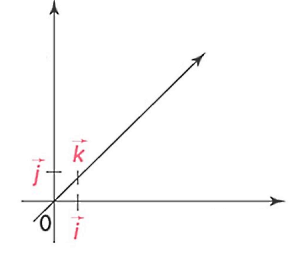
برای اینکه نمایش بردارها با استفاده از بردارهای یکه راحتتر شود، بهتر است برای هر محور مختصات در صفحه یک بردار یکه تعریف کنیم. اگر فضای مختصات را یک فضای سه بعدی در نظر بگیریم، در این صورت هر بردار حداکثر دارای سه مولفه یا مختصه میتواند باشد که هر کدام در راستای یکی از سه محور مختصات قرار دارند. قبلا با دو محور مختصات یعنی محور و آشنا شدیم. در این بخش محور سومی به نام محور را نیز در نظر میگیریم تا یک فضای سه بعدی به شکل بالا داشته باشیم. جدول زیر ویژگیهای بردارهای یکه را برای محورهای مختصات نشان میدهد:
| بردار یکه در راستای محور | بردار یکه در راستای محور | بردار یکه در راستای محور |
به این ترتیب بردار را میتوانیم به شکل زیر در قالب بردارهای یکه نمایش دهیم:
آمار و احتمال
آخرین مبحثی که در درس ریاضی پایه هفتم مطرح میشود، آمار و احتمال است. آمار فرآیند جمعآوری اطلاعات از نمونههای مختلف با هدف سازماندهی، بررسی، مقایسه و انجام تحلیل یا محاسبات آماری مختلف روی آنها است تا بتوان پیشبینی یا تخمین مناسبی در مورد یک موضوع خاص ارائه کرد. اطلاعات اولیهای که در این فرآیند جمعآوری شدهاند، دادههای آماری نام دارند.
در بخش جمعآوری اطلاعات، میتوانیم از روشهای مختلفی مانند جدول یا نمودارهای مناسب برای نشان دادن دادهها استفاده کنیم. بهویژه کاربرد نمودار، در مقایسه اولیه دادهها بسیار کمک کننده است. اگر میخواهید در زمینه آمار و احتمال یادگیری خود را تکمیل کنید، پیشنهاد ما مشاهده فیلم آموزش آمار و احتمال – پایه یازدهم فرادرس است که لینک آن نیز در ادامه برای شما قرار داده شده است:
انواع نمودارهای آماری
در این بخش چند نمودار آماری مهم معرفی میشود:
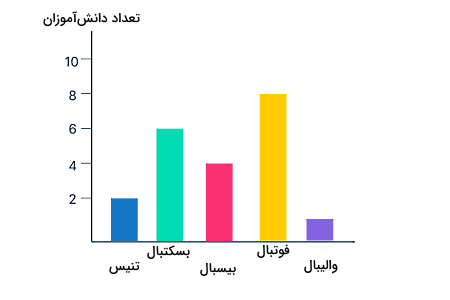
برای مثال، فرض کنید میخواهیم ببینیم دانشآموزان یک کلاس به کدام ورزش بیشتر علاقهمند هستند. اگر پس از نظرسنجی، دادههای جمعآوری شده را توسط یک نمودار نشان دهیم، مقایسه خیلی راحتی خواهیم داشت. یکی از بهترین نمودارهایی که برای نشان دادن دادههای آماری میتوان بکار برد، نمودار میلهای است. در این نوع نمودار، دادههای هر بخش در قالب یک میله مستطیل شکل نشان داده میشوند. طبق نمودار میلهای رسم شده برای این پژوهش، واضح است که فوتبال با تعداد هشت رای، ورزش موردعلاقه دانشآموزان این کلاس است.
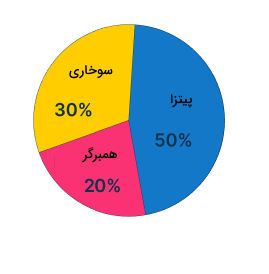
نوع دیگری از نمودارهای آماری، نمودار دایرهای است. این نمودار یک دایره است که سهم بخشهای مختلف یک موضوع در آن با رنگهای مختلف از هم تفکیک میشوند. این نمودار به ما کمک میکند سهم موضوعات یا اجزای مختلف را شبیه به مساحت برشهای مختلف یک پای مقایسه کنیم. بهعنوان مثال، فرض کنید میخواهیم درصد علاقه گروه مشخصی از افراد را به انواع فست فود مقایسه کنیم. پس از جمعآوری دادههای آماری، میتوانیم مقایسه این درصدها را به شکل زیر با یک نمودار دایرهای نشان دهیم:
اگر بخواهیم روند پیشرفت یک موضوع یا یک سری اطلاعات را در گذر زمان را مشخص کنیم، میتوانیم نمودار خطی آن را رسم کنیم. در این نوع نمودار آماری، هر داده آماری توسط یک نقطه مشخص میشود و در انتها، این خطوط به هم وصل میشوند تا روند آن موضوع مشخص شود. برای مثال، فرض کنید میخواهید تغییرات قیمت یک لباس را طی پنج ماه مشخص بررسی کنید. با جمعآوری قیمت این لباس در هر ماه، نمودار خط شکستهای به شکل زیر میتوانید رسم کنید:
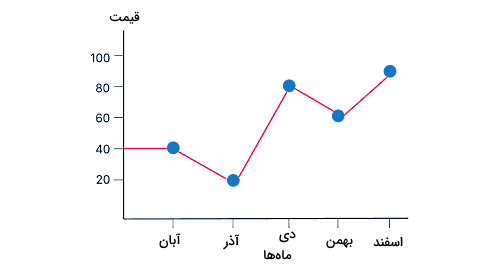
بنابراین از این نمودار میتوانیم وضعیت قیمت این لباس را به این صورت تحلیل کنیم که با اینکه در آذرماه کاهش قیمت داشتهایم، اما در کل روند قیمت این لباس افزایشی بوده است.
دامنه تغییرات
اگر تعداد زیادی داده عددی در مورد یک موضوع جمعآوری کرده باشیم، برای اینکه بتوانیم دید آماری دقیق و درستی نسبت به دادههای خود کسب کنیم، یکی از راهها محاسبه چند کمیتهای آماری مهم مانند دامنه تغییرات است. دامنه تغییرات در درس ریاضی پایه هشتم مطرح شده است و عبارت است از اختلاف بین کمترین و بیشترین مقدار داده.
بنابراین اگر بخواهیم دامنه تغییرات را برای یک مجموعه داده حساب کنیم، اولین قدم این است که دادههای خود را از کوچکترین مقدار تا بزرگترین مقدار بهترتیب مرتب کنیم. سپس با محاسبه اختلاف دو عدد اول و آخر در این لیست، دامنه تغییرات بهدست میآید. اگر دامنه تغییرات عدد بزرگی شود، نشان میدهد تنوع دادههای ما بالا است، در حالی که کوچک بودن دامنه تغییرات به معنای تنوع پایین در دادهها است. مجموعه داده زیر را در نظر بگیرید:
برای محاسبه دامنه تغییرات این مجموعه ابتدا دادهها را از کوچک به بزرگ مرتب میکنیم:
حالا با کم کردن بیشترین مقدار از کمترین مقدار داده، دامنه تغییرات محاسبه میشود:
میانگین
یکی دیگر از روشهای بررسی و تحلیل دادههای آماری، محاسبه میانگین دادهها است. کافی است ابتدا مجموع تمام دادههای عددی را بهدست آوریم. سپس این مجموع را بر تعداد کل دادهها تقسیم کنیم. بنابراین اگر بخواهیم میانگین مجموعه داده بخش قبل راحساب کنیم، به این ترتیب پیش میرویم:
فراوانی
فراوانی در آمار به این معنا است که هر داده مشخص در یک مجموعه داده چند مرتبه تکرار میشود. اگر مجددا به مجموعه داده بازگردیم، میتوانیم جدولی بهصورت زیر به نام جدول فراوانی تنظیم کنیم:
| داده | فراوانی |
مجموع فراوانی دادهها در دومین ستون باید با تعداد کل دادهها برابر شود که همینطور هم هست:
احتمال
در نظریه احتمال شانس وقوع یک پدیده، اتفاق یا پیشامد اندازهگیری میشود. برای مثال، پرتاب یک سکه را در نظر بگیرید. در این آزمایش دو پیشامد یا حالت ممکن است داشته باشیم، یا سکه رو میآید و یا زیر. رو یا زیر آمدن سکه در این آزمایش با شانس کاملا برابری اتفاق میافتد. بنابراین میتوانیم بگوییم احتمال رو آمدن سکه برابر است با یک از دو یا . همچنین احتمال زیر آمدن سکه هم برابر است با یک از دو یا . در واقع این دو حالت یعنی زیر و رو احتمال وقوع برابری دارند.

یک آزمایش معروف دیگر در بررسی احتمال، پرتاب یک تاس است. میدانیم یک تاس شش وجه مختلف با شش عدد دارد و در هر بار پرتاب، یکی از این اعداد ظاهر میشود. بنابراین اگر بخواهیم بدانیم احتمال اینکه تاس دو بیاید، چقدر است، باید یک حالت از شش حالت را در نظر بگیریم که میشود .

پس برای اینکه بتوانیم احتمال را محاسبه کنیم، ابتدا لازم است تمام حالتهای ممکن را بشماریم. سپس تعداد حالتهای موردنظر یا مطلوب را از بین این حالتها تعیین میکنیم. تقسیم این دو عدد به ما احتمال را میدهد. احتمال همیشه عددی بین صفر و یک است. اگر احتمال وقوع رخدادی برابر با یک شود، یعنی قطعیت کامل داریم در حالی که اگر احتمال صفر بهدست آوریم، با قطعیت میتوانیم از عدم پیشامد آن اتفاق صحبت کنیم.
مباحث درس ریاضی پایه نهم و دهم
درس ریاضی پایه نهم شامل مباحث زیر است:
- مجموعهها
- اعداد حقیقی
- استدلال و اثبات در هندسه
- توان و ریشه
- عبارتهای جبری
- خط و معادلههای خطی
- عبارتهای گویا
- حجم و مساحت
همچنین ریاضی پایه دهم موضوعات زیر را پوشش میدهد:
- مجموعه، الگو و دنباله
- مثلثات
- توانهای گویا و عبارتهای جبری
- معادلهها و نامعادلهها
- تابع
- شمارش
- آمار و احتمال
برخی از این مباحث در بخشهای قبل توضیح داده شدهاند. بنابراین در ادامه این بخش تنها به توضیح موضوعات جدید درس ریاضی مانند مفهوم مجموعه اعداد، اتحادها، معادله خط، مثلثات و تابع خواهیم پرداخت. همچنین برای مطالعه کامل مباحث مربوط به شاخه ریاضیات گسسته مانند مفهوم فاکتوریل، ترکیب و جایگشت یا آشنایی با انواع گرافها میتوانید به مطلب «ریاضیات گسسته – مفاهیم پایه به زبان ساده با مثال» از مجله فرادرس مراجعه کنید.
مجموعه ها
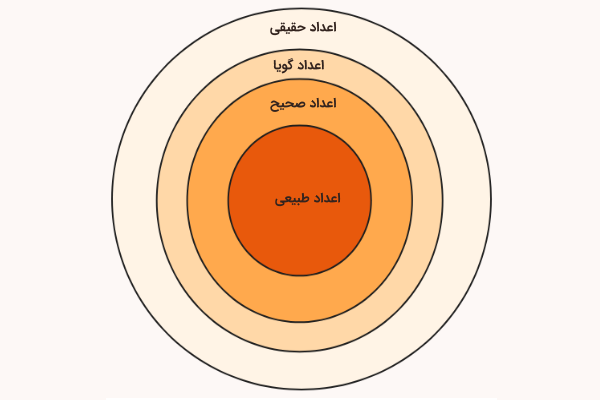
کتابهای ریاضی هفتم و هشتم هر دو با معرفی یک مجموعه اعداد یعنی مجموعه اعداد صحیح و سپس مجموعه اعداد گویا آغاز شدند. در این کتاب هم با مجموعه دیگری از اعداد یعنی مجموعه اعداد حقیقی آشنا خواهیم شد. اما پیش از آن، ابتدا یاد میگیریم یک مجموعه چیست و چه ویژگیهایی دارد.
به مجموعهای از اشیا، اجزا یا اعداد مشخص و غیرتکراری که یک گروه تشکیل میدهند، مجموعه گفته میشود. هر کدام از این اشیا، اجزا یا اعداد یک عضو مجموعه نام دارند. اعضای یک مجموعه ممکن است متناهی یا نامتناهی باشند، اگر مجموعهای دارای بینهایت عضو باشد، میگوییم این مجموعه بینهایت است. برای مثال، مجموعه اعداد طبیعی، مجموعه اعداد صحیح و مجموعه اعداد گویا همگی دارای بینهایت عضو هستند. دقت کنید، روزهای هفته یا نوع خاصی از اتومبیل هم میتوانند یک مجموعه بسازند. بنابراین لازم نیست اعضای مجموعه حتما اعداد باشند.
برای نشان دادن یک مجموعه از آکولادهای باز و بسته بهصورت استفاده میشود. تمام اعضای مجموعه داخل این دو آکولاد قرار میگیرند. هر مجموعه دارای یک اسم است که عموما با یک حرف انگلیسی بزرگ نشان داده میشود. برای مثال داریم:
= مجموعه اعداد طبیعی
= مجموعه اعداد کامل
= مجموعه اعداد صحیح
همچنین برای نمایش مجموعه اعداد گویا میتوانیم از استفاده کنیم. در این عبارت نشان دهنده مجموعه اعداد گویا است، و بیانگر این هستند که در این مجموعه هر عدد بهصورت یک کسر نوشته میشود، با این شرط که همواره مخرج کسر مخالف صفر است. همچنین بخش به این مفهوم است که صورت و مخرج کسرها در مجموعه اعداد گویا عضوی از مجموعه اعداد صحیح هستند.
- نکته ۱: ترتیب اعضا در یک مجموعه مهم نیست. بنابراین با جابجایی اعضا، مجموعه جدیدی ساخته نمیشود.
- نکته ۲: تکرار اعضای یک مجموعه باعث ایجاد مجموعه جدیدی نمیشود.
- نکته ۳: به این معنا است که عضوی از مجموعه است.
- نکته ۴: اگر در مجموعهای هیچ عضوی وجود نداشته باشد، مجموعه تهی یا داریم.
- نکته ۵: برای نشان دادن تعداد اعضای مجموعه از استفاده میکنیم.
نمودار ون
یکی از روشهای نمایش مجموعهها، استفاده از نموداری به نام نمودار وِن است. در این نمودار هر مجموعه را با یک دایره نشان میدهیم و تمام اعضای آن در داخل این دایره قرار میگیرند. رسم نمودار ون از این جهت مفید است که با نگاه به آن میتوانیم به آسانی تشخیص دهیم بین دو یا چند مجموعه چه رابطهای برقرار است. برای مثال، به تصویر زیر دقت کنید:
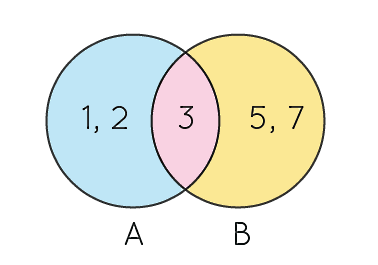
این نمودار ون نشان دهنده دو مجموعه و است و اطلاعات زیر را به ما میدهد:
بهعلاوه مشخص است که عضو مشترک بین دو مجموعه و است.
زیرمجموعه چیست؟
اگر تمام اعضای مجموعهای مانند در مجموعه بزرگتری مانند وجود داشته باشند، میگوییم زیرمجموعهای از است و این عبارت را با نشان میدهیم. برای مثال، همواره مجموعه اعداد طبیعی زیرمجموعهای از مجموعه اعداد صحیح است:
- نکته ۱: هر مجموعهای همواره زیرمجموعهای از خودش است.
- نکته ۲: مجموعه تهی همواره زیرمجموعه تمام مجموعهها محسوب میشود.
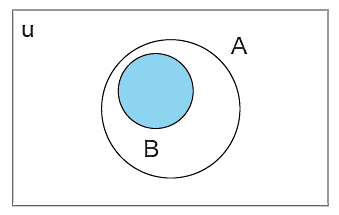
تصویر بالا نمودار ونی است که نشان میدهد . دقت کنید اگر تمام اعضای دو مجموعه با هم برابر باشند، در این صورت دو مجموعه با هم مساوی هستند. پس در زیرمجموعه بودن کافی است فقط اعضای یک مجموعه در مجموعه دیگر وجود داشته باشد، اما ممکن است اعضای مجموعه دیگر در مجموعه کوچکتر وجود نداشته باشند.
اجتماع و اشتراک مجموعه ها
در بخش نمودار ون دیدیم که دو مجموعه و دارای یک عضو مشترک بودند. بنابراین میتوانیم بگوییم اشتراک دو مجموعه و برابر است با مجموعه جدیدی که به شکل زیر نمایش داده میشود:
پس اشتراک دو مجموعه و مجموعه جدیدی است که شامل تمام عضوهای مشترک بین این دو مجموعه است. نمودار ون برای اشتراک دو مجموعه و بهصورت تصویر سمت چپ در شکل زیر نمایش داده میشود:
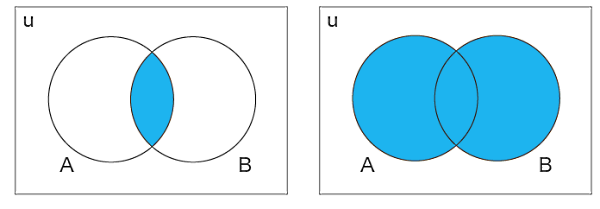
اما در سمت راست این تصویر، اجتماع و نمایش داده شده است. اجتماع دو مجموعه و مجموعه جدیدی است که اعضای آن شامل تمام اعضای دو مجموعه و است. اجتماع و را با نشان میدهیم.
سایر مباحث مرتبط با مجموعهها به همراه معرفی انواع دنبالههای عددی و حسابی در مطالب زیر توضیح داده شدهاند:
- مجموعه متناهی و نامتناهی – تعاریف و خصوصیات
- الگوها و دنباله های متداول عددی – به زبان ساده
- دنباله هندسی و مجموع آن – به زبان ساده
- تصاعد حسابی – به زبان ساده
- فرمول الگویابی | فرمول الگوی عددی – با مثال و به زبان ساده
مجموعه اعداد حقیقی
مجموعه اعداد حقیقی که با حرف مشخص میشوند، شامل تمام اعداد در دنیای واقعی (بهجز اعداد مختلط) هستند. بنابراین مجموعه اعداد طبیعی که به منظور شمارش بکار میروند، مجموعه اعداد صحیح که برای بیان دمای محیط میتوانیم از آنها کمک بگیریم، مجموعه اعداد گویا که برای نمایش کسرها استفاده میشوند یا حتی مجموعه اعداد گنگ یا اصم که در محاسبه جذر اعداد بهدست میآیند، همگی زیرمجموعههایی از مجموعه اعداد حقیقی هستند. بهعنوان مثال، تمام اعداد زیر یک عدد حقیقی محسوب میشوند:
تمام مجموعه اعداد نشان داده شده زیرمجموعهای از مجموعه اعداد حقیقی محسوب میشوند. دو زیرمجموعه اصلی اعداد حقیقی، مجموعه اعداد گویا () و مجموعه اعداد گنگ () هستند. اعداد گنگ اعدادیاند که دارای ارقام اعشاری بینهایت و بدون تکرار هستند. بنابراین میتوانیم بگوییم مجموعه اعداد حقیقی اجتماع دو مجموعه اعداد گویا و اصم است یا .
قدر مطلق
قدر مطلق عدد یا متغیری مانند در حالت کلی با نمایش داده میشود و به معنای اندازه یا مقدار عدد بدون در نظر گرفتن هر گونه علامت مثبت یا منفی است. برای مثال، قدر مطلق با قدر مطلق برابر است:
- نکته ۱: قدر مطلق صفر برابر است با صفر.
- نکته ۲: قدر مطلق هر عدد مثبت برابر است با خودش.
- نکته ۳: قدر مطلق هر عدد منفی برابر است با قرینهاش.
- نکته ۴:
تشابه در هندسه
در بخشهای قبل با حالتهای همنهشتی در مثلثها آشنا شدیم. در این بخش از درس ریاضی به مبحث تشابه در هندسه خواهیم پرداخت. تشابه به معنای تساوی و معادل بودن نیست، بلکه در این حالت یک چندضلعی دارای اضلاعی است که با نسبت مشخصی در چندضلعی دیگر کوچک یا بزرگ شدهاند. همچنین شرط دیگر برای برقراری تشابه این است که زاویهها در دو چندضلعی کاملا باید با هم برابر باشند. بنابراین در حالت کلی تشابه با همنهشتی معادل نیست.
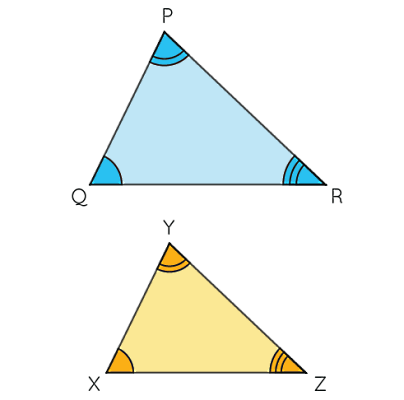
با توجه به تعریف بالا، اگر فرض کنیم دو مثلث متشابه داریم، این دو مثلث با اینکه زاویههای متناظر برابری دارند، اما قطعا هماندازه نخواهند بود. با این حال بین اضلاع متناظر در این دو مثلث، نسبت یکسانی برقرار است، یعنی اضلاع متناظر به یک اندازه کوچک یا بزرگ میشوند. برای مثال، دو مثلث بالا مشابه هم هستند و روابط تشابه آنها یا بهصورت زیر است:
به نسبت مساوی بین اضلاع، زمانی که دو چندضلعی با هم متشابهاند، نسبت تشابه گفته میشود. همچنین روابطی که در بالا بیان شد، برای تمام چندضلعیها از جمله مثلث برقرار است.
توان و نماد علمی
نماد علمی روشی سودمند برای نمایش اعداد خیلی خیلی بزرگ یا خیلی خیلی کوچک است که در آن عدد داده شده را بهشکل مینویسیم، به این شرایط که:
- همواره بزرگتر مساوی و کوچکتر از است.
- یک عدد صحیح است.
برای مثال، نماد علمی برابر است با:
یا نماد علمی میشود:
سایر مباحث مرتبط با توان و ریشه
سایر مطالب مرتبط با مبحث توان و ریشه در درس ریاضی نهم عبارتاند از ضرب و تقسیم رادیکالها، جمع و تفریق رادیکالها، ساده کردن رادیکالها و گویا کردن مخرج کسرها که برای کسب اطلاعات بیشتر در این زمینه میتوانید به مطالب مرتبط در مجله فرادرس به شرح زیر مراجعه کنید:
- ضرب رادیکال – به زبان ساده
- ضرب رادیکال در عدد صحیح – نحوه محاسبه به زبان ساده با مثال
- ضرب عدد در رادیکال – به زبان ساده با مثال و تمرین
- ساده کردن رادیکال ها – به زبان ساده با مثال و تمرین
اتحادها
یکی از مهمترین مباحث درس ریاضی نهم معرفی انواع اتحاد است. در این بخش ابتدا فرمول مهمترین اتحادها را برای شما قرار دادهایم و در ادامه، چند مطلب مرتبط با این موضوع نیز برای شما معرفی شده است تا در صورت نیاز به توضیحات کاملتر به این مقالات مراجعه کنید. اولین و مهمترین اتحادها، اتحادهای مربع دو جملهای هستند:
اتحاد مهم بعدی، اتحاد مزدوج و اتحاد جمله مشترک است:
همچنین مطالب زیر به یادگیری شما در این زمینه بیشتر کمک میکند:
- اتحاد نوع اول – از فرمول تا اثبات + حل تمرین و مثال
- اتحاد مربع چیست؟ – اثبات، فرمول و نمونه سوال با جواب
- اتحاد چاق و لاغر چیست؟ – اثبات، فرمول، نمونه سئوال – به زبان ساده
- اتحاد مربع کامل چیست؟ – توضیح فرمول و محاسبه با مثال و تمرین
- اتحاد مکعب چیست؟ – فرمول، اثبات و مثال – به زبان ساده
- نمونه سوال اتحاد و تجزیه – همراه با جواب
خط و معادلههای خطی
معادله یک خط راست در ریاضی همیشه بهصورت است. در این معادله با دادن مقادیر عددی مختلف به متغیر ، مقادیر روی یک خط راست قرار میگیرند. در چنین معادلهای شیب خط راست و عرض از مبدا آن نام دارد. برای مثال، در تصویر زیر خط راستی را مشاهده میکنید که به اندازه روی محور قائم جابجا شده است. در نتیجه، عرض از مبدا این خط برابر است با .
دستگاه معادله خطی
اگر دو یا چند معادله با متغیرهای مختلف داشته باشیم، طوری که بتوانیم با تعیین یک متغیر متغیر دیگر را بهدست آوریم، در این صورت میگوییم یک دستگاه معادله را حل کردهایم. برای حل دستگاههای معادلات روشهای مختلفی وجود دارد که اولین آن، روش حذف کردن یا جایگزینی است. برای مثال، اگر یک دستگاه معادله شامل دو معادله و دو مجهول و داشته باشیم، ابتدا میتوانیم متغیر را انتخاب کنیم.
سپس به ضرایب این متغیر در دو معادله دقت میکنیم و سعی میکنیم این دو معادله را در دو عدد صحیح مختلف به گونهای ضرب کنیم که در نهایت ضرایب این متغیر در دو معادله با هم قرینه شوند، یعنی اندازه برابر و علامت مخالف هم داشته باشند. با ضرب هر کدام از این دو عدد حدسی خود در هر کدام از معادلات، دو معادله جدید خواهیم داشت که با جمع کردن آنها، قطعا جملات شامل حذف میشوند و در نهایت فقط جملات شامل و مقادیر ثابت را خواهیم داشت. با محاسبه و قرار دادن آن در یکی از دو معادله، هم بهدست میآید.
مطالب زیر به تکمیل یادگیری شما در مورد این مباحث کمک میکنند:
- فرمول شیب خط چیست و چگونه محاسبه می شود؟ + مثال و تمرین
- روش کرامر – از صفر تا صد
مثلثات
یکی از مهمترین مباحث درس ریاضی که در کتاب ریاضی دهم برای اولین بار مطرح میشود، مثلثات است. در مثلثات ابتدا با دایره مثلثاتی آشنا میشویم و بر اساس آن، یاد میگیریم نسبتهای مثلثاتی شامل سینوس، کسینوس، تانژانت و کتانژانت یک زاویه چگونه محاسبه میشوند. طبق شکل زیر، دایره مثلثاتی دایرهای به شعاع واحد است که برای زاویهای مانند میتوانیم نسبتهای مثلثاتی را بهصورت زیر تعریف کنیم:
- سینوس زاویه یا از تقسیم ضلع روبرو به این زاویه بر وتر مثلث حاصل میشود.
- کسینوس زاویه یا از تقسیم ضلع مجاور به این زاویه بر وتر مثلث حاصل میشود.
- تانژانت زاویه یا از تقسیم ضلع روبرو به این زاویه بر ضلع مجاور حاصل میشود.
- سینوس زاویه یا از تقسیم ضلع مجاور به این زاویه بر ضلع روبرو حاصل میشود.
آنچه که در مثلثات حائز اهمیت است، فرمولها، روابط یا اتحادهای مثلثاتی است که در حل مسائل مختلف میتوان از آنها استفاده کرد. برای مثال مهمترین این روابط عبارتاند از:
همچنین اگر میخواهید با نحوه رسم نمودارهای توابع مثلثاتی بهتر آشنا شوید، مطالب زیر راهنمای مناسبی هستند:
مفهوم تابع
تابع مفهومی است که برای بیان رابطه بین دو مجموعه بکار میرود. در تابع دو مجموعه داریم که یکی بهعنوان مجموعه ورودیهای تابع یا دامنه و دیگری مجموعه خروجی تابع یا برد نامیده میشوند. زمانی میتوانیم نام ارتباط دو مجموعه را تابع بنامیم که هر عضو از مجموعه دامنه فقط و فقط با یک عضو از مجموعه برد متناظر شود. برای مثال، در شکل زیر مشاهده میکنید که در اولین تصویر از سمت چپ تابعی داریم که در آن هر عضو از مجموعه اول به یک و فقط یک عضو از مجموعه دوم مرتبط شده است. چنین تابعی را تابع یک به یک مینامیم.
تصویر دوم نیز توصیف کننده یک تابع است، چون باز هم هر عضو از دامنه فقط به یک عضو متصل شده است. اما در تصویر سوم مشاهده میکنید که برای مثال عضو هم به و هم به از مجموعه دوم مرتبط شده است. این نوع ارتباط در تعریف تابع قرار نمیگیرد. بنابراین نمودارهای سوم و چهارم نمایش دهنده تابع نیستند. در حالت کلی اگر تابعی از متغیر باشد، آن را به شکل نشان میدهیم. در این تابع مجموعهای که مقادیر به آن متعلق هستند، دامنه تابع است، در حالی که اثر تابع روی ورودیهای ، مجموعهای به نام برد را برای این تابع را میسازد.
در ریاضیات با انواع مختلفی از توابع مانند توابع درجه دو، توابع لگاریتمی، تابع قدر مطلق، تابع جزء صحیح، توابع مثلثاتی و … سروکار داریم. مطلب «انواع تابع در ریاضی – به زبان ساده + حل مثال» بهطور مفصل توابع مختلف در درس ریاضی را برای شما توضیح داده است. همچنین در ادامه چند مقاله مرتبط با ویژگیهای مختلف توابع برای شما قرار داده شده است:
مباحث درس ریاضی پایه یازدهم و دوزادهم
درس ریاضی پایه یازدهم و دوازدهم برای رشتههای ریاضی و تجربی کمی متفاوت است. از این جهت که کتابهای درسی رشته ریاضی مباحث کاملتری را نسبت به کتابهای درس ریاضی رشته تجربی و انسانی پوشش دادهاند، در این نوشته سعی شده است طبق سرفصلهای این کتابها پیش برویم. کتاب حسابان ۱ شامل مباحث زیر است:
- جبر و معادله
- تابع
- مثلثات
- حد و پیوستگی
حسابان در پایه دوازدهم با عنوان حسابان ۲ شامل موضوعات زیر است:
- تابع
- مثلثات
- حدهای نامتناهی
- مشتق
- کاربردهای مشتق
با توجه به اینکه عمده این مباحث در بخشهای قبل معرفی شدهاند، در ادامه با توضیح حد و پیوستگی این بخش را آغاز میکنیم و در نهایت به مبحث مشتق و کاربردهای آن خواهیم پرداخت.
حد و پیوستگی
حد در ریاضی به معنای برابری تابع با یک عدد حقیقی است، زمانی که متغیر به یک مقدار عددی مشخص مانند نزدیک میشود. برای مثال، اگر به تصویر زیر دقت کنید، با نزدیک شدن مقادیر به سمت از هر دو طرف (چه سمت راست و چه سمت چپ آن)، مقدار تابع به نقطه زرد رنگ نزدیک میشود که طبق نمودار داده شده متناظر است با عدد .
برای اینکه تعریف حد یا لیمیت را به زبان ریاضی ارائه دهیم، از رابطه زیر استفاده میکنیم و آن را به این صورت میخوانیم که حد تابع برابر است با ، زمانی که به سمت میل میکند:
بنابراین اگر بخواهیم حد تابعی که در نمودار بالا مشاهده کردید را به این شکل بنویسیم، داریم:
حد راست و چپ
در نمودار بخش قبل اشاره کردیم که میل کردن به سمت در تعریف حد، میتواند از سمت راست یا چپ باشد. اگر از سمت راست به نزدیک شویم، همسایگی راست و حد راست را بررسی کردهایم، در حالی که اگر از سمت چپ به نزدیک شویم، همسایگی چپ و حد چپ را بررسی کردهایم. به این ترتیب حد راست و چپ که همان حدود یک طرفه نام دارند، به شکل زیر نشان داده میشوند:
با دانستن مفهوم حد چپ و راست حالا میتوانیم تعریف دقیقتری از حد یک تابع ارائه دهیم. زمانی میگوییم حد تابع در نقطه معینی مانند وجود دارد که حد چپ و راست این تابع در وجود داشته باشد. بهعلاوه لازم است حدود یکطرفه علاوه بر وجود داشتن با هم برابر نیز باشند، یعنی داشته باشیم:
پیوستگی
پیوستگی تابع به این معنا است که در یک بازه یا نقطه مشخص، برای تابع مقدار مشخصی داریم. به شکل زیر توجه کنید. در این شکل، تابع در نقطه ناپیوسته است، چون حد چپ و راست این تابع در این نقطه با هم برابر نمیشوند. دقت کنید حد راست در نقطه مقدار بیشتری از حد چپ در همین نقطه دارد.
پیوستگی تابع در نقطهای مانند بهصورت دقیق با برقراری سه شرط زیر ثابت میشود:
- وجود داشته باشد، به این معنا که متعلق به دامنه است و مقدار تابع در نقطهای مانند تعریف شده است.
- حد تابع وجود داشته باشد، به این معنا که حد چپ و راست برای این تابع در این نقطه با هم مساوی هستند.
- برابری نکته اول و دوم یا .
در انتهای این بخش یادآور میشویم که مباحث مهمی مانند قضایای حد که به توضیح نحوه جمع و تفریق یا ضرب و تقسیم حدود میپردازد یا موضوعاتی نظیر روشهای رفع ابهام حد را به همراه دو مبحث مهم حد در بینهایت و حد بینهایت میتوانید با مراجعه به مقالات مرتبط بیاموزید. در اینجا فقط تاکید میکنیم که حد در بینهایت به معنای محاسبه است، در حالی که حد بینهایت زمانی اتفاق میافتد که داشته باشیم:
مشتق و کاربردهای آن
اگر نحوه محاسبه شیب خط که در بخش معادله خط توضیح داده شد را کاملا فرا گرفته باشید، احتمالا با مفهوم مشتق نیز تقریبا آشنا هستید. برای پیدا کردن شیب یک خط با توجه به تغییرات خروجی تابع یا نسبت به تغییرات ورودی یا ، از فرمول زیر استفاده میشود:
این فرمول با توجه به شکل زیر بهصورت زیر خواهد شد:
حالا فرض کنید در شکل بالا خیلی خیلی کوچک شود یا به عبارتی به سمت صفر میل کند. در این صورت فرمول بالا به شکل زیر نوشته میشود:
بنابراین بهطور خلاصه مشتق تابع در نقطه ، بهصورت زیر تعریف میشود:
- محاسبه حد شیب بالا، با فرض اینکه یا تغییرات که با نیز نشان داده میشود، به سمت صفر میل میکند.
- اگر حد بالا وجود داشته باشد، مشتق تابع در نقطه نیز وجود دارد و برابر با این حد است، یعنی داریم:
با فرمول بالا، توصیف کننده مشتق تابع نسبت به متغیر است. یک راه دیگر برای نمایش مشتق، استفاده از نماد بهجای قرار دادن علامت پریم روی تابع است. نمادهای زیر همه یک مفهوم را منتقل میکنند:
برای اینکه بتوانیم مشتق توابع مختلف را محاسبه کنیم، روشهای جبری مختلفی وجود دارد. در مطلب روش های مشتق گیری – به همراه مثال تمام این فرمولها بررسی شده است. برای مثال، مشتق توابع مثلثاتی روابط خاص خود را دارد که نیاز است کاملا به آنها مسلط باشید. همچنین در زمینه کاربردهای مشتق، یادگیری مفاهیمی مانند ماکزیمم و مینیمم توابع، نقطه بحرانی و نقطه عطف حل مسائل مختلف علوم مهندسی میتواند مفید باشد.
یادگیری درس ریاضی در دانشگاه با فرادرس
پیش از اتمام این مطلب از مجله فرادرس و پس از اینکه با موضوعات درس ریاضی متوسطه آشنا شدید، قصد داریم چند فیلم آموزشی در زمینه ریاضیات عمومی دانشگاهی به شما معرفی کنیم. در این دورههای آموزشی فرادرس نیز مباحث مرتبط با مطالبی که توضیح دادیم اما در سطحی پیشرفتهتر وجود دارد. بنابراین اگر تمایل دارید این مباحث را در سطوح دانشگاهی ادامه دهید، پیشنهاد میکنیم فیلمهای زیر را مشاهده کنید:
- فیلم آموزش حسابان پیشرفته فرادرس
- فیلم آموزش ریاضی پایه دانشگاهی فرادرس
- فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد فرادرس
یادگیری درس ریاضی در مدرسه شامل چه مباحثی است؟
پس از اینکه چند راهکار برای یادگیری بهتر درس ریاضی در ابتدای این مطلب ارائه کردیم، در این بخش قصد داریم مباحث کلی درس ریاضی که در مدارس آموزش داده میشوند را معرفی کنیم. این موضوعات عبارتاند از:
- علم حساب
- مقدمات جبر
- جبر یک
- هندسه
- جبر دو
- مثلثات
- حساب دیفرانسیل و انتگرال
مطالعه این بخش به شما کمک میکند تا یک دید کلی در مورد روند یادگیری این درس کسب کنید. برای مثال، متوجه خواهید شد درس ریاضی با چه مبحثی شروع میشود و در سطوح بالاتر، به کجا میرسد.
شروع درس ریاضی با حساب
در اغلب مدارس، دانشآموزان مقطع ابتدایی درس ریاضی را با مبحث حساب شروع میکنند. حساب شامل چهار عمل اصلی یعنی جمع، تفریق، ضرب و تقسیم است. یادگیری حساب کاملا به میزان تمرین شما بستگی دارد. بنابراین تا میتوانید سوالات مختلف در این زمینه حل کنید و سعی کنید همزمان با سرعت، دقت خود را نیز افزایش دهید. در مراحل بعد، میتوانید برای آموزش حساب از نرمافزارها یا ابزارهای مختلفی که با این هدف طراحی شدهاند نیز استفاده کنید.
پیشرفت درس ریاضی تا مقدمات جبر
دومین مبحثی که در یادگیری درس ریاضی با آن آشنا میشوید، مقدمات جبر است که به آن «پیشجبر» هم گفته میشود. این مبحث تمام مفاهیم پایه و پیشنیازهایی که برای حل مسائل جبر یک و جبر دو ممکن است نیاز داشته باشید را ارائه میدهد. لیست زیر موضوعات مختلفی را نشان میدهد که در جبر یک آموزش داده میشوند:
- کسرها و اعداد اعشاری
- نسبتها، تناسب و درصدها
- مربعات و جذر
- مبانی هندسه
- مبانی آمار و احتمال
- مبانی جبر
در اولین مبحث لازم است از مفاهیم آموخته شده در بخش قبل یعنی حساب که شامل انجام چهار عمل اصلی روی کسرها و اعداد اعشاری است، بتوانید استفاده کنید. در ادامه یاد میگیرید چگونه کسرها را کاهش دهید. همچنین با مفهوم اعداد مختلط آشنا میشوید. در زمینه اعداد اعشاری نیز مفهومی به نام ارزش مکانی را خواهید آموخت. موضوع بعدی به نسبتها و تناسب مربوط میشود که کاربرد آن در مطالعاتی شامل مقایسه چند موضوع یا عدد است. در ادامه به منظور یادگیری جذر، لازم است ابتدا مربع کامل چند عدد معروف را بهخاطر بسپارید. این نکته به شما کمک میکند تا بتوانید در مراحل بعدی با معادلات شامل ریشههای مربعی سریعتر کار کنید.

مقدمات جبر خود شامل دو بخش به نام مبانی هندسه و مبانی آمار و احتمال نیز هست. در مبانی هندسه پس از آشنایی با اشکال هندسی معروف و مفاهیم سه بعدی، یاد میگیرید که چگونه کمیتهایی مانند مساحت، محیط، حجم و مساحت جانبی را برای اشکال مختلف محاسبه کنید. همچنین در مورد مفاهیمی مانند خط، پارهخط، خطوط موازی و مورب و زاویهها اطلاعاتی کسب میکنید. در ادامه مبانی آمار و احتمال را داریم که مباحثی مانند رسم انواع گرافها، نمودارهای نقطهای و هیستوگرام را شامل میشود. در انتها و پس از مقدماتی که گفته شد، قادر خواهید بود به حل و بررسی معادلات جبری ساده شامل متغیرهای مختلف بپردازید. همچنین با خواصی مانند توزیع، ترسیم نمودار مربوط به معادلات ساده و حل نامعادلات نیز آشنا خواهید شد.
ارتقای درس ریاضی تا جبر یک
آنچه در جبر یک از درس ریاضی میآموزید، شامل مباحث زیر است:
- حل معادلات خطی
- حل نامعادلات شامل یک یا دو متغیر
- یادگیری نماها
- رسم نمودار خط
- یادگیری حل دستگاه معادلات
در اولین مرحله میآموزید که چگونه معادلات خطی و نامعادلات شامل یک یا دو متغیر را حل کنید. همچنین مادامی که شروع کردید به حل معادلات شامل چند جملهایها (هر عبارتی که از اعداد و متغیرها و توانها تشکیل شده است)، یاد میگیرید که نما یا توان چیست و چگونه باید با آن کار کنید. به این ترتیب قادر خواهید بود چهار عمل اصلی را در مورد چند جملهایها اجرا کنید.

موضوع مهمی که در ادامه یاد میگیرید، مبحث رسم نمودار خط بر اساس معادله خط است، به این صورت که پس از محاسبه شیب خط و عرض از مبدا میتوانید نمودار خط راست را در صفحه مختصات شامل محورهای x و y رسم کنید. در نهایت، حل دستگاه معادلات را یاد میگیرید. دستگاه معادلات شامل دو معادله و دو متغیر x و y است که برای تعیین این متغیرها لازم است هر دو معادله را در نظر بگیرید. روشهای مختلفی برای بررسی و کار کردن با دستگاه معادلات وجود دارد، مانند جمع کردن یا کم کردن معادلات از هم یا رسم نمودار آنها.
ورود درس ریاضی به هندسه
در هندسه با مفاهیمی مانند خط و پارهخط، مقاطع، زاویهها و اشکال هندسی مختلف آشنا میشوید. همچنین قضیههای مختلف و سادهای آموزش داده میشوند که یادگیری و به خاطر سپردن آنها موجب میشود بتوانید مسائل هندسه را راحتتر حل کنید. همچنین با روند محاسبه مساحت و محیط اشکال هندسی و مقاطع مخروطی مانند دایره یا استوانه آشنا میشوید. برای مثال، یکی از مهمترین و پرکاربردترین قوانین هندسه قضیه فیثاغورس است که نشان میدهد رابطه بین اضلاع، وتر و زاویهها در یک مثلث خاص به نام مثلث قائمالزاویه چگونه است.
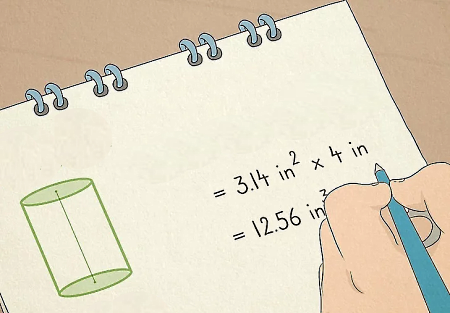
توسعه درس ریاضی تا جبر دو
در مراحل پیشرفتهتر، به مباحث جبر دو در درس ریاضی میرسید. جبر دو بر پایه مفاهیمی که در جبر یک آموزش داده شد، توسعه مییابد. در عین حال شامل یک سری موضوعات پیچیدهتر مانند توابع غیرخطی و ماتریسها است.
مثلثات در درس ریاضی
توابعی به نام سینوس، کسینوس، تانژانت و کتانژانت توابع مثلثاتی نامیده میشوند که در اولین قدم از یادگیری مثلثات در درس ریاضی لازم است با ویژگیها و معادلات حاکم بر این توابع آشنا شوید. مثلثات به شما میآموزد که چگونه زاویهها یا طولهای مختلف در اشکال مثلثی را بهدست آورید. این بخش از ریاضیات در برخی رشتههای مهندسی مانند عمران، ساختمانسازی و معماری بسیار کاربرد دارد.
حساب دیفرانسیل و انتگرال در درس ریاضی
در نهایت آخرین مبحثی که عموما در مدارس تدریس میشود، حساب دیفرانسیل و انتگرال است. شاید یادگیری این بخش سختتر بنظر برسد، اما باید بدانید این بخش کاربرد گستردهای در علوم مهندسی دارد. در این شاخه با مفهومی به نام تابع آشنا میشوید. در ادامه ابزاری به نام حدگیری را یاد میگیرید که به شما در حل بسیاری از مسائل حسابان کمک میکند. حدگیری از توابع بسیار گسترده است، چون با توابع مختلفی ممکن است مواجه شوید که هر کدام ویژگیهای مربوط به خود را دارند. برای مثال توابع نمایی، توابع لگاریتمی یا توابع مثلثاتی هر کدام ویژگیها و قوانین خود را دارند.
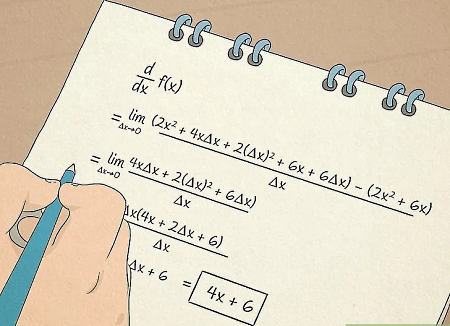
مبحث مهم بعدی در حساب دیفرانسیل و انتگرال، مشتقگیری است. مشتق یک تابع اطلاعات مفیدی به شما خواهد داد. بنابراین لازم است به روند محاسبه مشتق توابع مختلف و فرمولهای آن کاملا مسلط شوید. برای مثال، مشتق اول یک تابع نشان میدهد شیب خط مماس بر آن تابع چیست. در نمونهای دیگر و با در نظر گرفتن یک موقعیت غیرخطی، مشتق نشان دهنده نرخ تغییرات یک کمیت است.
فرآیند مشتقگیری ممکن است بر حسب نیاز، ادامه داشته باشد و مشتقهای بعدی نیز اطلاعات دیگری در اختیار شما قرار دهند. برای نمونه، مشتق دوم به شما میگوید که تابع موردنظر شما در یک بازه مشخص صعودی است یا نزولی. به این ترتیب میتوانید در مورد وضعیت تقعر این تابع صحبت کنید و بر این اساس، به نتایج جالبی در مورد مسئله خود برسید. همچنین ابزاری به نام انتگرال که مفهوم آن عکس مشتق است، در بررسی و محاسبه مساحت یا حجم زیر یک منحنی بکار میرود. یکی دیگر از مباحث حساب دیفرانسیل و انتگرال، انواع سری و تصاعد است. ممکن است با کاربرد این موضوعات در این مقطع خیلی آشنا نشوید، اما اگر بخواهید به مطالعه معادلات دیفرانسیل در سطوح پیشرفتهتر بپردازید، تسلط به سریها مهم است.
source
