یکی از مهمترین قطعات الکترونیکی که به منظور ذخیرهسازی بار و انرژی در مدارها استفاده میشود، «خازن» (Capacitor) است. کارایی یک خازن با کمیتی به نام «ظرفیت» آن سنجیده میشود، به این صورت که هر چه ظرفیت یک خازن بیشتر باشد، بار و انرژی بیشتری را در خود ذخیره میکند. با اینکه رابطه بین ظرفیت، بار و ولتاژ خازن با فرمول توصیف میشود، اما ظرفیت خازن به مشخصات فیزیکی آن مانند مساحت و ابعاد صفحات و نوع مادهای که بین صفحات قرار میگیرد، بستگی دارد. بنابراین فرمول های خازن در مورد انواع خازن متفاوت است.

در این نوشته از مجله فرادرس با هدف معرفی فرمول های خازن، ابتدا تعریف میکنیم که خازن چیست و چه انواعی دارد. سپس با در نظر گرفتن فرمول اصلی ظرفیت خازن بر حسب مقدار بار ذخیره شده روی آن و ولتاژ بین صفحات آن، فرمول ظرفیت انواع خازن شامل خازنهای تخت، کروی و استوانهای را استخراج میکنیم. در ادامه، نحوه اتصال خازنها در مدارهای الکتریکی و فرمول ظرفیت خازن معادل برای اتصال سری و موازی خازنها را به همراه فرمول انرژی خازن، توضیح میدهیم. همچنین در انتهای هر بخش، روند حل چند مثال بررسی میشود تا نحوه استفاده از فرمول های خازن را بهتر بیاموزید.
فرمول های خازن
جدول زیر تمام فرمول های خازن را بهصورت خلاصه نشان میدهد:
| کاربرد | فرمول |
| بار ذخیره شده در خازن | |
| ظرفیت خازن تخت | |
| ظرفیت خازن کروی | |
| ظرفیت خازن استوانهای | |
| انرژی ذخیره شده در خازن | |
| ظرفیت معادل n خازن سری | |
| ظرفیت معادل n خازن موازی |
در این جدول تمام فرمولهای ظرفیت با فرض اینکه در فضای بین صفحات خازن از هیچ ماده عایق یا دیالکتریکی استفاده نشده است، نوشته شدهاند. اگر خازن دیالکتریک داشته باشد، لازم است ضریب را بهعنوان «ثابت دیالکتریک» در این فرمولها ضرب کنیم. در بخشهای آتی نشان میدهیم هر کدام از فرمول های خازن چگونه بهدست میآیند و در حل مسائل چه کاربردی دارند.
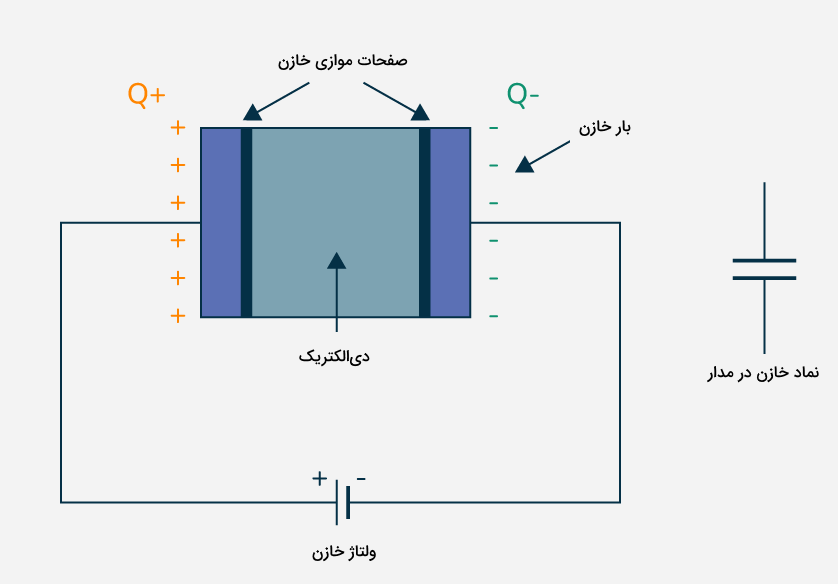
خازن چیست؟
پیش از توضیح تمام فرمول های خازن، ابتدا باید با این قطعه و مشخصات آن کاملا آشنا شویم. خازن یکی از انواع قطعات الکترونیکی است که جهت ذخیره کردن بار و انرژی الکتریکی استفاده میشود. خازنها کاربردهای گستردهای دارند، از ذخیرهسازی انرژی فلاش دوربین گرفته تا ذخیرهسازی انرژی در مدارهای تقویتکننده. این قطعه از دو رسانای الکتریکی ساخته میشود که در فاصله مشخصی از هم قرار دارند. عموما این دو رسانا الکترود نامیده شوند، اما درستتر این است که آنها را صفحات خازن بنامیم.
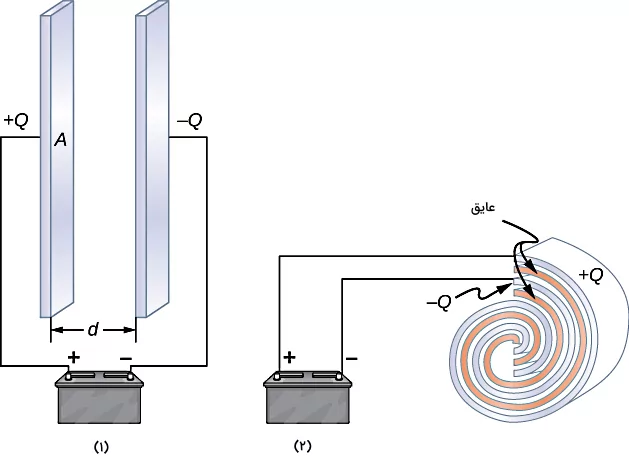
دقت کنید وجود فاصله بین صفحات خازن لازم است و در هیچ خازنی صفحات خازن با هم تماس ندارند. اگر در فاصله بین صفحات خلاء داشته باشیم، در این صورت خازن ما یک «خازن خلاء یا خالی» نامیده میشود. اما اگر این فاصله با یک ماده نارسانای الکتریکی به نام دیالکتریک پر شود، یک «خازن با دیالکتریک» داریم. اغلب خازنها دارای دیالکتریک هستند.
باردار کردن یا شارژ خازن
برای اینکه بتوانیم از توانایی ذخیرهسازی خازن استفاده کنیم، باید آن را باردار کنیم. به باردار کردن خازن، شارژ خازن هم گفته میشود. خازنهایی که در تصویر بخش قبل مشاهده کردید، به خودی خود و بدون اتصال به باتری، هیچ باری ندارند. اما زمانی که توسط سیمهای رسانا به یک باتری یا اختلاف پتانسیل متصل شوند، باردار یا شارژ میشوند. باردار شدن خازن به این معنا است که هر دو صفحه آن باری با اندازه مساوی ولی با علامت مخالف خواهند داشت. پس با اعمال ولتاژ یا اختلاف پتانسیلی برابر با توسط یک باتری، خازن به اندازه باردار یا شارژ میشود.
بار روی صفحات خازن را با نشان میدهیم که همان کمیت بار الکتریکی است و با یکای استاندارد کولن () اندازهگیری میشود. به این ترتیب پس از اینکه خازن شارژ شد، صفحات آن بارهایی برابر با و به شکل زیر خواهند داشت. حالا اگر به دانش خود در زمینه الکتریسیته ساکن رجوع کنیم، میدانیم چون بین صفحات خازن فاصله مشخصی وجود دارد، بار هر صفحه روی سطح همان صفحه باقی میماند.
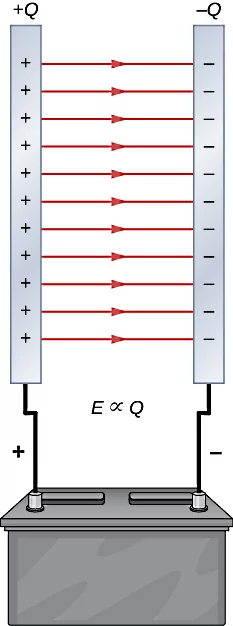
این جدایی بارهای مثبت و منفی از هم، ایجاد یک میدان الکتریکی میکند که خطوط آن از سمت صفحه با بار مثبت به سمت صفحه با بار منفی است. معمولا فاصله بین صفحات خازن خیلی کوچک است، پس میتوانیم میدان الکتریکی بین این دو صفحه را تقریبا یکنواخت در نظر بگیریم و از آثار لبهای صرفنظر کنیم. به این ترتیب، اندازه این میدان در نقطهای بین دو صفحه رسانای موازی با هم به شکل بالا با فرمول زیر محاسبه میشود:
در این رابطه میدان الکتریکی بر حسب نیوتن بر کولن ()، چگالی بار سطحی روی هر صفحه بر حسب کولن بر متر مربع () و گذردهی الکتریکی فضای آزاد یا خلاء بر حسب است. مقدار عددی گذردهی خلاء برابر است با . از طرفی میدانیم ، پس میتوانیم این میدان را به شکل زیر بنویسیم:
بنابراین اندازه میدان با بار خازن نسبت مستقیم دارد، یعنی هر چه بار روی خازن بیشتر باشد، میدان داخل آن هم قویتر است.
انواع خازن
دستهبندی کلی انواع خازن بهصورت زیر است:
- خازنهای معمولی
- خازنهای الکترولیت
- خازنهای متغیر
فرادرس یک فیلم آموزشی جامع را با عنوان «آموزش فیزیک الکتریسیته + مفاهیم کلیدی» تهیه کرده است که میتواند مسیر یادگیری فرمول های خازن و تسلط شما بر حل مسائل مرتبط با این فرمولها را هموار کند. لینک مشاهده این فیلم آموزشی در ادامه آورده شده است:
که البته بررسی خازنهای الکترولیت و متغیر موضوع این مطلب نیست. در شکل زیر نماد انواع خازن در مدار را مشاهده میکنید:
اما میتوانیم خازنها را بسته به شکل صفحاتشان یا نحوه قرارگیری آنها نسبت به هم نیز بهصورت زیر در نظر بگیریم:
- خازن تخت: دو صفحه رسانای موازی با مساحت یکسان
- خارن کروی: دو پوسته کروی رسانای هممرکز با شعاعهای مختلف
- خازن استوانهای: دو پوسته استوانهای رسانا با طول مساوی و شعاعهای مختلف

اگر خازنهایی با مشخصات فیزیکی متفاوت شامل موارد بالا داشته باشیم و همه آنها را توسط باتری مشابهی باردار کنیم، بسته به شکل یا ابعاد صفحات هر کدام مقادیر متفاوتی از بار را در خود ذخیره میکنند.
چگونه فرمول های خازن را با فرادرس بهتر بیاموزیم؟
پیش از اینکه به توضیح هر کدام از فرمول های خازن بپردازیم، در این بخش قصد داریم چند دوره آموزشی تهیه شده در مجموعه فرادرس را به شما معرفی کنیم تا با مشاهده آنها به این مبحث کاملا مسلط شوید. برای مثال، در بخش الکتریسیته ساکن از کتاب درسی فیزیک پایه یازدهم، تعریف خازن و رابطه محاسبه ظرفیت آن به همراه عوامل موثر بر ظرفیت خازن و نحوه به دست آوردن انرژی آن توضیح داده شده است. در آموزش فیزیک پایه یازدهم فرادرس علاوه بر پوشش این موضوعات، به حل چند نمونه تست کنکور سراسری نیز پرداخته شده است. بنابراین مشاهده این فیلمها به یادگیری بهتر شما کمک خواهد کرد. در ادامه لیستی از دورههای مرتبط را مشاهده میکنید:
- فیلم آموزش علوم تجربی پایه هشتم فیزیک فرادرس
- فیلم آموزش فیزیک پایه یازدهم فرادرس
- فیلم آموزش فیزیک پایه یازدهم مرور و حل تمرین فرادرس
فرمول های ظرفیت خازن
پس از اینکه خازن را تعریف کردیم، در این بخش به معرفی مهمترین فرمول از مجموعه فرمول های خازن میپردازیم. گفتیم خازن جهت ذخیرهسازی بار و انرژی در مدارهای الکتریکی بکار میرود. برای اینکه بتوانیم میزان ذخیرهسازی خازن را اندازهگیری کنیم، لازم است آن را با یک کمیت مشخص تعریف کنیم و بتوانیم آن را برای هر خازن محاسبه کنیم. این کمیت، «ظرفیت خازن» (Capacitance of Capacitor) است که با نشان داده میشود.
فرمولبندی ظرفیت خازن به دو شیوه انجام میشود:
- بر اساس کمیتهای الکتریکی تعیینکننده آن یعنی و
- بر اساس مشخصات فیزیکی خازن مانند و و گذردهی الکتریکی بین صفحات
گفتیم خازنها با اتصال به باتری و دریافت اختلاف پتانسیل به اندازه باردار میشوند. بنابراین ظرفیت خازن بهصورت نسبت بیشترین بار الکتریکی ذخیره شده در خازن به اختلاف پتانسیل بین صفحات آن تعریف میشود:
- : بار خازن بر حسب کولن ()
- : اختلاف پتانسیل یا ولتاژ بین صفحات خازن بر حسب ولت ()
- : ظرفیت خازن بر حسب فاراد ()
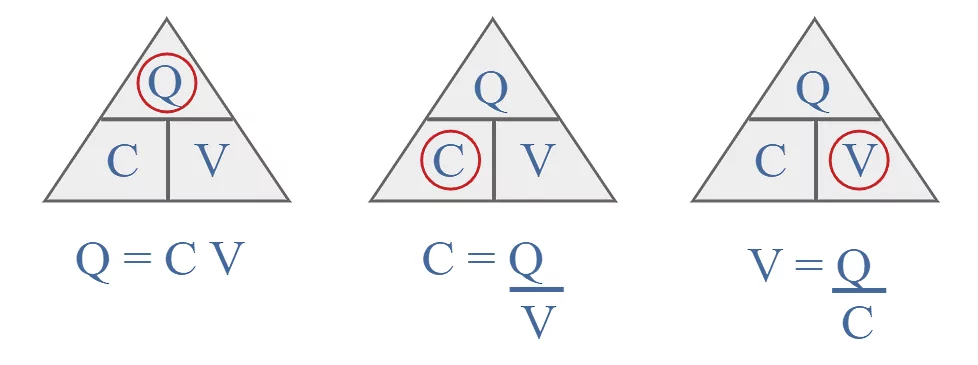
به عبارت دیگر، ظرفیت خازن معادل است با بیشترین بار الکتریکی ذخیره شده در خازن به ازای هر ولت. واحد استاندارد ظرفیت خازن، به افتخار مطالعات آقای «مایکل فارادی» (Michael Faraday) «فاراد» نام دارد. یک فاراد بهصورت یک کولن بر ولت تعریف میشود:
طبق این تعریف، اگر اختلاف پتانسیل بین دو صفحه خازنی با ظرفیت یک فاراد فقط برابر با یک ولت باشد، این خازن میتواند یک کولن بار را ذخیره کند. چون یک کولن بار مقدار بزرگی است، پس میتوانیم نتیجهگیری کنیم که فاراد واحد بزرگی است. در عمل ظرفیت خازنهای مختلف از مرتبه پیکو فاراد () تا میکرو فاراد () و میلی فاراد () متغیر است.
نکته ۱: علامت اختصاری ظرفیت خازن و واحد بار الکتریکی یا کولن یکسان است و لازم است در تشخیص آنها دقت شود.
نکته ۲: ظرفیت خازن از بار و اختلاف پتانسیل بین دو صفحه آن مستقل است. بنابراین اگر بار تغییر کند، ولتاژ هم متعاقبا عوض میشود، به گونهای که همواره نسبت ثابت است.
در ادامه بررسی فرمول های خازن، میخواهیم دومین فرمول ظرفیت خازن را با کمک گرفتن از فرمول اول بهدست آوریم. گفتیم دومین فرمول برای ظرفیت خازن بر اساس مشخصات فیزیکی آن نوشته میشود. پس باید برای انواع خازن با شکلهای متفاوت، فرمولهای مختلفی داشته باشیم.
برای این منظور، ابتدا انواع خازن شامل خازنهای تخت، کروی و استوانهای را با فرض اینکه همگی بدون دیالکتریک هستند، در نظر میگیریم. روند محاسبه ظرفیت انواع خازن بر اساس مشخصات فیزیکی آنها، در بخشهای بعد آمده است. سپس با در نظر گرفتن دیالکتریک، فرمول های خازن را برای هر کدام بازنویسی میکنیم. خواهید دید که در محاسبات خود از مباحث مهم الکتریسته ساکن مانند «قانون کولن» و «قانون گاوس» نیز استفاده میکنیم.
اثبات فرمول ظرفیت خازن تخت
اولین بخش به بررسی ظرفیت خازن تخت اختصاص دارد. یک خازن تخت به شکل زیر در نظر بگیرید که دارای دو صفحه موازی و مشابه هم با مساحت است و این دو صفحه به اندازه از هم فاصله دارند. با اعمال ولتاژ به این خازن، بار روی آن ذخیره میشود. برای شروع از مفهوم قانون کولن استفاده میکنیم. موضوع قانون کولن محاسبه نیروی الکتریکی بین دو گروه بار الکتریکی است که در فاصله مشخصی از هم قرار دارند:

موقعیت توصیف شده در قانون کولن کاملا مشابه وضعیتی است که در خازن داریم. طبق این قانون، هر چه بار الکتریکی بیشتری داشته باشیم، نیروی الکتریکی هم قویتر است و در نتیجه میدان و ظرفیت خازن هم بیشتر خواهد بود. پس اگر صفحات یک خازن تخت بزرگتر باشند، بار بیشتری در خود ذخیره میکنند و در نتیجه ظرفیت بالاتری خواهیم داشت. تا اینجا میتوانیم بگوییم بین مساحت صفحات خازن تخت () و ظرفیت آن () رابطه مستقیمی برقرار است:
نتیجه دیگری که از قانون کولن استخراج میشود، اثر فاصله دو بار روی نیروی الکتریکی و در نتیجه روی میدان و ظرفیت خازن است. هر چه فاصله بین صفحات یک خازن تخت کمتر شود، نیروی جاذبه قویتری بین دو صفحه برقرار میشود و در نتیجه بار ذخیره شده روی صفحات آن بیشتر میشود. پس رابطه بین این دو کمیت عکس هم است:
در اینجا برمیگردیم به رابطه بین میدان و چگالی بار الکتریکی روی صفحات که در بخشهای قبل به شکل زیر نوشته شد:
چون این میدان یکنواخت است، پس اختلاف پتانسیل بین دو صفحه رسانا برابر میشود با حاصلضرب میدان در فاصله بین دو صفحه:
بنابراین با نوشتن فرمول ظرفیت خازن و قرار دادن اختلاف پتانسیل بالا در آن خواهیم داشت:
پس فرمول ظرفیت خازن تخت به شکل زیر محاسبه شد:
پس ظرفیت خازن تخت به مشخصات فیزیکی آن مانند مساحت صفحات و فاصله آنها از هم بستگی دارد. دقت کنید در این بررسی فرض کردیم خازن بدون دیالکتریک است. اما اگر بین دو صفحه رسانای خازن دی الکتریک داشته باشیم، در این صورت گذردهی الکتریکی این ماده نیز در تعیین ظرفیت خازن موثر است.
نکته: با توجه به اینکه واحد استاندارد ظرفیت خازن برابر با فاراد است، میتوانیم واحد گذردهی خلاء را با توجه به فرمول ظرفیت خازن تخت بهصورت زیر هم در نظر بگیریم:
اثبات فرمول ظرفیت خازن کروی
خازن کروی نوع دیگری از انواع خازن است که شامل دو پوسته کروی رسانای هممرکز با شعاعهای (پوسته داخلی) و (پوسته خارجی) است. همانطور که در شکل زیر مشاهده میکنید، هر کدام از پوستهها در این نوع خازن دارای یک نوع بار الکتریکی هستند. با توجه به تقارن، میدان الکتریکی بین صفحات شعاعی و در جهت خارج از خازن است. اگر خاطرتان باشد، در مورد خازن تخت، میدان الکتریکی بین صفحات یکنواخت و دارای مقدار ثابتی بود.
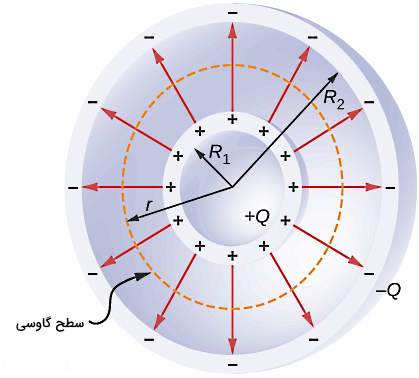
در مورد خازن کروی، میتوانیم از قانون گاوس برای محاسبه میدان بین صفحات استفاده کنیم. اگر سطح گاوسی خود را یک دایره فرضی هممرکز با پوستههای کروی و با شعاع به شکل نقطهچین بالا در نظر بگیریم، در این صورت باری که داخل این سطح گاوسی قرار میگیرد برابر است با . در واقع شعاع سطح گاوسی خود را طوری انتخاب میکنیم که از شعاع پوسته داخلی بیشتر و از شعاع پوسته خارجی خازن کمتر باشد. شکل کلی قانون گاوس عبارت است از:
که در آن میدان الکتریکی و بار الکتریکی کل محصور شده داخل سطح گاوسی با مساحت است. اگر انتگرالگیری بالا را انجام دهیم، برابر میشود با مساحت کرهای با شعاع یا :
پس شکل برداری میدان الکتریکی بین صفحات این خازن کروی محاسبه شد. علامت نشاندهنده این است که این میدان شعاعی است و چون مقدار مثبتی دارد،ِ میتوانیم بگوییم جهت آن به سمت خارج از مرکز پوستهها یا صفحات خازن است. اما محاسبه اختلاف پتانسیل بین صفحات خازن کروی در مقایسه با خازن تخت متفاوت است.
در آنجا چون میدان ثابت بود و با شعاع تغییر نمیکرد، از ضرب مستقیم فاصله بین صفحات در میدان، ولتاژ بهدست آمد. در این مورد اندازه میدان با شعاع تغییر میکند (). پس نمیتوانیم مانند بخش قبل عمل کنیم. راهحل این است که از حاصلضرب برداری میدان در یک فاصله شعاعی خیلی خیلی کوچک مانند ، روی فاصله بین دو پوسته کروی انتگرالگیری کنیم:
چون است، پس عبارت بالا به شکل زیر سادهسازی میشود:
میدانیم انتگرال برابر است با . پس با قرار دادن مقادیر حد بالا و پایین انتگرال، حاصل برابر است با:
حال با داشتن اختلاف پتانسیل، کافی است فرمول ظرفیت خازن را بر حسب بار ذخیره شده روی آن و ولتاژ بین صفحات نوشته و با حذف مقادیر ، ظرفیت خازن کروی را بهدست آوریم:
اثبات فرمول ظرفیت خازن استوانهای
در ادامه فرآیند یادگیری انواع فرمول های خازن، در این بخش روش بهدست آوردن فرمول خازن استوانهای را نشان میدهیم. یک خازن استوانهای متشکل است از دو پوسته استوانهای با محورهای هماندازه به شکل زیر، که پوسته کوچکتر یا داخلی دارای شعاع است. البته این بخش میتواند بهصورت یک پوسته یا استوانه توپر باشد. پوسته خارجی یا بیرونی شعاع بزرگتری مانند دارد. همچنین فرض میکنیم هر دو پوسته رسانا در خازن استوانهای، دارای طول یا محوری برابر با باشند.
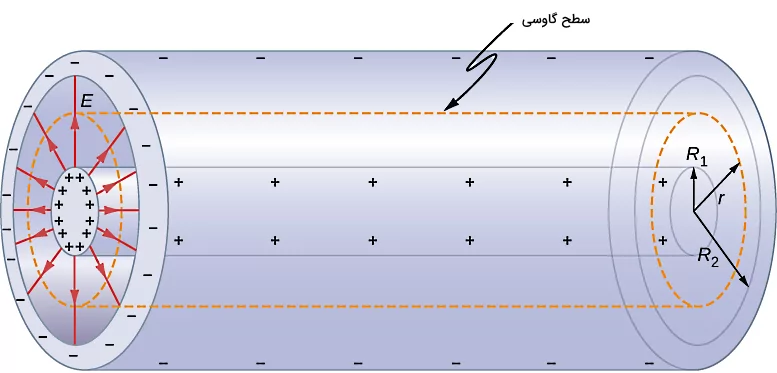
فرض کنید خازن استوانهای فرضی ما یک خازن خلاء یا خالی است، یعنی هیچگونه دیالکتریکی در فاصله بین دو پوسته قرار ندارد. همچنین فرض میکنیم با اتصال این خازن به اختلاف پتانسیل، بارهای و بهترتیب روی پوسته خارجی و داخلی این خازن ذخیره میشوند. برای اینکه فرمول ظرفیت چنین خازنی را بهدست آوریم، مشابه خازن کروی عمل میکنیم. چون در اینجا هم میدان در فضای بین دو پوسته رسانا وابسته به شعاع است، پس با کمک گرفتن از قانون گاوس و انتخاب یک سطح گاوسی مناسب مطابق شکل بالا، مسئله را حل میکنیم:
میدانیم در قانون گاوس میدان الکتریکی و بار الکتریکی کل محصور شده داخل سطح گاوسی با مساحت است. در انتگرال بالا، برابر میشود با مساحت جانبی استوانهای با شعاع و طول که برابر است با :
پس شکل برداری میدان الکتریکی بین صفحات این خازن استوانهای را بهدست آوردیم. مانند مورد خازن کروی، در اینجا هم علامت نشاندهنده این است که این میدان شعاعی است و چون مقدار مثبتی دارد،ِ میتوانیم بگوییم جهت آن به سمت خارج از مرکز پوستهها یا صفحات خازن است. با توجه به اینکه اندازه میدان با شعاع تغییر میکند ()، باید از حاصلضرب برداری میدان در یک فاصله شعاعی خیلی خیلی کوچک مانند ، روی فاصله بین دو پوسته استوانهای انتگرالگیری شود:
چون است، پس عبارت بالا به شکل زیر سادهسازی میشود:
انتگرال برابر است با . پس با قرار دادن مقادیر حد بالا و پایین انتگرال، حاصل برابر است با:
پس از اینکه ولتاژ پیدا شد، کافی است فرمول ظرفیت خازن را نوشته و با حذف مقادیر ، ظرفیت خازن استوانهای را پیدا کنیم:
مانند خازن تخت و خازن کروی، فرمول ظرفیت این نوع خازن هم با وابستگی به مشخصات فیزیکی آن مانند طول و شعاع، بهدست آمد. یکی از مهمترین کاربردهای این فرمول، تعیین ظرفیت به ازای واحد طول کابلهای هممحور است که در انتقال سیگنالهای الکتریکی متغیر با زمان بکار میروند.
فرمول ظرفیت خازن با دی الکتریک
تمام فرمول های خازن در صورتی که داخل خازن از یک مایع عایق بهجای خلاء استفاده شده باشد، باید در ضریبی به نام ثابت دیالکتریک آن ماده عایق ضرب شوند. بنابراین فرمول های خازن با دیالکتریک فقط یک ثابت بیشتر از فرمول های خازن خلاء دارند. معمولا ثابت دیالکتریک خازن را با نماد نشان میدهند که یک عدد بدون بعد است. سرامیک، کاغذ، میکا و تفلون از جمله موادی هستند که بهعنوان دیالکتریک در خازنها کاربرد دارند.
حل مثال و تمرین از فرمول های ظرفیت خازن
در این بخش با حل چند مثال نشان میدهیم که چگونه میتوان با توجه به نوع خازن، از فرمول های خازن مناسب برای محاسبه ظرفیت استفاده کرد.
مثال ۱
ظرفیت یک خازن تخت خالی با صفحات فلزی به مساحت که به اندازه از هم جدا شدهاند، چقدر است؟ اگر ولتاژی برابر با به این خازن اعمال شود، بار ذخیره شده روی آن چند کولن است؟
پاسخ
در بخش اول این سوال، کافی است فرمول ظرفیت خازن تخت را بنویسیم و را محاسبه کنیم:
میدانیم در یک خازن خالی یا خلاء، دیالکتریکی بین صفحات وجود ندارد. پس در فرمول ظرفیت فقط از گذردهی خلاء استفاده میکنیم که برابر است با . این مقدار خیلی کوچک برای ظرفیت خازن تخت نشان میدهد که ساخت وسیلهای با قابلیت ذخیره بالا چقدر میتواند سخت باشد. در بخش دوم سوال، باید بار ذخیره شده را با توجه ولتاژ اعمال شده پیدا کنیم:
مثال ۲
فرض کنید میخواهیم یک خازن تخت خلاء با ظرفیت بسازیم. صفحات این خازن باید چه مساحتی داشته باشند تا در فاصله از هم چنین ظرفیتی تولید شود؟
پاسخ
با نوشتن فرمول ظرفیت خازن تخت خلاء به شکل زیر و در نظر گرفتن مقادیر معلوم در صورت سوال، باید مساحت را در سمت دیگر رابطه قرار دهیم:
این پاسخ نشان میدهد که برای داشتن چنین ظرفیتی، باید صفحات مربعی یک خازن تخت نوعی، عرضی به بزرگی ده کیلومتر داشته باشند!
مثال ۳
ظرفیت خازن کروی که فقط دارای یک پوسته کروی با شعاع است، چقدر است؟
پاسخ
در نگاه نخست شاید به نظر برسد که چون پوسته کروی دیگری نداریم، پس با در نظر گرفتن شعاع برابر با صفر، طبق فرمول ظرفیت خازن کروی، پاسخ صفر است! اما این تحلیل اشتباه است. در حقیقت شعاع پوسته کروی دوم برای چنین خازنی باید در فاصله بینهایت از پوسته کروی اول در نظر گرفته شود. اگر اختلاف پتانسیل را برای چنین خازنی با توجه به فرمول زیر محاسبه کنیم، خواهیم داشت:
نکته مهم در اینجا این است که اگر دقت کنید فرمول بالا علامت منفی ندارد. اما در محاسبات ظرفیت خازن کروی از فرمول مشابهی استفاده شد که علامت منفی داشت. علت این تفاوت این است که فرمول اصلی محاسبه اختلاف پتانسیل بین دو نقطه به شکل زیر است:
مرسوم است که اختلاف پتانسیل بین دو نقطه و را که در واقع بهصورت است، با نماد نشان دهیم. در این سوال، نقطه در بینهایت است و پتانسیل آن صفر میشود. بنابراین رابطه بالا به شکل زیر درمیآید:
حالا به ادامه حل انتگرال میپردازیم. مقدار میدان با آنچه که برای میدان یک خازن کروی محاسبه شد، فرقی ندارد. پس با قرار دادن میدان و انتگرالگیری، داریم:
میدانیم عدد تقسیم بر بینهایت برابر با صفر است. بنابراین با استفاده از فرمول اصلی ظرفیت خازن خواهیم داشت:
بنابراین ظرفیت خازن کروی که فقط یک پوسته به شعاع دارد، همواره از فرمول بهدست میآید. دقت کنید میتوانستیم بدون انتگرالگیری و با استفاده از فرمول ظرفیت خازن کروی هم به این نتیجه برسیم. کافی است شعاع را در بینهایت در نظر گرفته و با توجه به اینکه است، به شکل زیر حدگیری کنیم:
مثال ۴
اگر یک خازن استوانهای تحت ولتاژ به اندازه شارژ شود، ظرفیت آن چقدر است؟ همچنین اگر بدانیم طول محور این خازن است، نسبت شعاعهای آن را محاسبه کنید:
پاسخ
در اولین سوال با داشتن بار ذخیره شده روی خازن و اختلاف پتانسیل، مستقل از اینکه خازن ما چه نوعی است و چه شکلی دارد، کافی است از فرمول اصلی ظرفیت خازن به شکل زیر استفاده کنیم:
میدانیم پیشوند نانو با معادل است. در بخش دوم سوال خواسته شده که نسبت شعاعهای این خازن استوانهای محاسبه شود. با نوشتن فرمول ظرفیت خازن استوانهای میتوانیم به این بخش پاسخ دهیم:
تمرین ۱
اگر ظرفیت یک خازن تخت خالی و مساحت هر کدام از صفحات آن باشد، این دو صفحه در … متری از هم قرار دارند.
گزینه دوم درست است. برای محاسبه فاصله دو صفحه از هم در یک خازن تخت خالی، فرمول زیر را بکار میبریم:
در محاسبات بالا، سانتیمتر مربع را توسط رابطه به متر مربع تبدیل کردهایم.
تمرین ۲
فرض کنید ولتاژ به صفحات دایروی یک خازن تخت با ظرفیت اعمال میشود. در صورتی که شعاع این صفحات دو برابر شود، ظرفیت خازن چقدر خواهد شد؟
گزینه آخر درست است. دقت کنید در این سوال خازن مورد مطالعه ما یک خازن تخت با صفحات دایروی است. بنابراین باید دقت کنیم که از فرمول ظرفیت خازن کروی استفاده نکنیم.
در حالت اول ظرفیت خازن برابر است با مقداری که در سوال داده شده است. برای محاسبه ظرفیت خازن در حالت نهایی یا ، کافی است دو برابر شدن شعاع را در فرمول ظرفیت خازن تخت در نظر بگیریم:
میدانیم مساحت دایرهای با شعاع برابر است با . از رابطه بالا برای ظرفیت و شعاع، میتوانیم به نتیجهگیری زیر برسیم:
تمرین ۳
اگر بار روی صفحات خازن تخت بدون دیالکتریکی با ظرفیت برابر با باشد، کدام گزینه نشاندهنده اندازه میدان الکتریکی بین این صفحات است، در صورتی که فاصله بین آنها باشد؟
گزینه دوم صحیح است. جهت محاسبه میدان بین صفحات باید از فرمول زیر استفاده کنیم که توصیفکننده میدان یکنواخت بین دو صفحه رسانا در خازن است:
که در آن فاصله بین دو صفحه مشخص است، اما ولتاژ داده نشده است. برای محاسبه ولتاژ، کافی است ظرفیت و بار خازن را در فرمول زیر قرار دهیم:
دقت کنید در رابطه بالا باید معادلهای پیکو و میکرو در محاسبات در نظر گرفته شوند. اگر هر دو واحد بر حسب میکرو یا پیکو بودند، میتوانستیم بهراحتی آنها را ساده کنیم.
تمرین ۴
یک کره منفرد و ایزوله شده دارای ظرفیت خازنی برابر با است. شعاع این خازن چقدر است؟
نمیتوان محاسبه کرد.
گزینه اول صحیح است. در مثال سوم گفتیم یک کره منفرد معادل یک خازن کروی است که ظرفیت آن با رابطه زیر محاسبه میشود:
در این سوال ظرفیت مشخص است و شعاع را نداریم. با در نظر گرفتن ، داریم:
نحوه اتصال خازنها در مدارهای الکتریکی
تا اینجا بخشی از مهمترین فرمول های خازن را همراه با حل مثالهای مرتبط آموختیم و گفتیم خازن وسیلهای است که به منظور ذخیرهسازی انرژی الکتریکی در مدارهای الکتریکی استفاده میشود. بنابراین پس از اینکه یاد گرفتیم یک خازن چگونه بار را در خود ذخیره میکند، مرحله بعدی این است که با نحوه اتصال خازنها به هم در مدارهای الکتریکی آشنا شویم.
با یادگیری فرمول های خازن معادل، میتوانیم چند خازن را با یک خازن معادل در مدار جایگزین کنیم و به این ترتیب تحلیل مدارهای پیچیده راحتتر خواهد شد. خازنها به دو شیوه ممکن است به هم متصل شوند، سری و موازی. در ادامه فرمول های خازن معادل را برای هر کدام از این دو نوع اتصال همراه با حل مثال توضیح خواهیم داد. در این زمینه، پیشنهاد میکنیم مطلب «مقاومت الکتریکی چیست؟ – تعریف و توضیح کامل به زبان ساده» از مجله فرادرس را نیز مطالعه کنید.
فرمول ظرفیت معادل خازنهای سری
در شکل زیر، تصویری از نحوه اتصال سری سه خازن با سه ظرفیت متفاوت را مشاهده میکنید که در ادامه با یک خازن معادل با ظرفیت در مدار جایگزین شدهاند. میخواهیم ببینیم فرمول ظرفیت معادل برای چنین خازنی چگونه بهدست میآید. در اتصال سری خازنها، صفحه شامل یک نوع بار از یک خازن به صفحهای شامل بار مخالف از خازن دیگر متصل میشود. در مثال مورد بررسی ما، صفحه با بار منفی خازن اول به صفحه با بار مثبت خازن دوم متصل شده است.

حالا اگر این سه خازن سری را به یک منبع ولتاژ با اختلاف پتانسیل وصل کنیم، باری که هر کدام از خازنها کسب میکنند برابر است با ، یعنی داریم:
اگر بخواهیم بدانیم بارهای مثبت و منفی چگونه روی صفحات این خازنها توزیع میشوند، کافی است ببینیم کدام صفحه به کدام پایانه باتری یا منبع ولتاژ متصل شده است. در شکل بالا، صفحهای از خازن اول که به پایانه مثبت منبع وصل شده، دارای بار مثبت میشود و صفحهای از خازن سوم که به پایانه منفی منبع متصل شده، دارای بار منفی خواهد شد. سایر صفحات خازن بر مبنای القای بار مخالف باردار میشوند، به گونهای که مجموع بار هر دو صفحه یک خازن و مجموع بار کل صفحات سه خازن برابر با صفر شود. در چنین چینشی، افت پتانسیل برای هر خازن با دیگری متفاوت است. علت این مسئله به تفاوت ظرفیت هر خازن بازمیگردد:
اما مجموع این افت پتانسیلها برابر است با ولتاژ منبع یا باتری:
حالا با توجه به روابط بالا، میتوانیم ظرفیت خازن معادل را پیدا کنیم:
چون ، پس میتوانیم بار را از طرفین رابطه بالا حذف کنیم:
میتوانیم این رابطه را برای چند خازن تعمیم دهیم. پس فرمول ظرفیت معادل n خازن سری برابر است با:
نکته ۱: همواره ظرفیت معادل چند خازن سری از ظرفیت هر کدام از خازنها کمتر است.
نکته ۲: علت یکسان بودن بار خازن معادل با بار هر یک از خازنهایی که بهصورت سری به هم وصل شدهاند، اصل بقای بار در مدار است.
فرمول ظرفیت معادل خازنهای موازی
اتصال موازی خازنها شکلی بهصورت زیر دارد. در این نوع اتصال، صفحه با بار مثبت تمام خازنها به پایانه مثبت و صفحه با بار منفی تمام خازنها به پایانه منفی منبع ولتاژ یا باطری متصل میشود. در این نوع اتصال هم میتوانیم خازنها را با یک خارن معادل به نام در مدار جایگزین کنیم. چون دو صفحه هر خازن به منبع ولتاژ مدار متصل است، پس اختلاف پتانسیل دو سر هر خازن با دیگری برابر و معادل با ولتاژ منبع است:
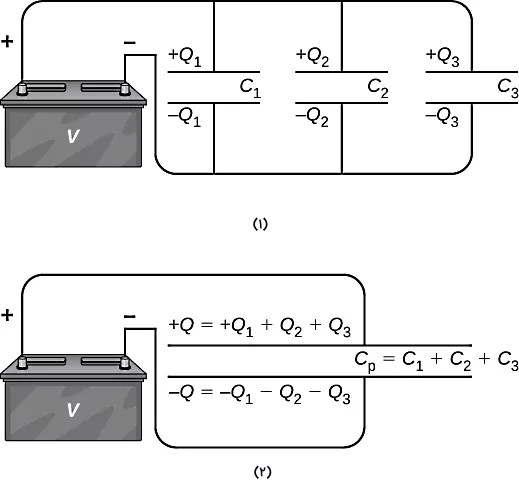
تفاوت دیگر اتصال موازی با اتصال سری خازنها در این است که بار ذخیره شده در هر خازن با دیگری برابر نیست. در این شرایط بار خازن معادل با مجموع بار تمام خازنهایی که بهصورت موازی به هم متصل شدهاند، برابر است:
بنابراین وضعیت بار و اختلاف پتانسیل در دو نوع اتصال خازنها کاملا عکس یکدیگر است. حالا با نوشتن فرمول ظرفیت خازن میتوانیم از رابطه بالا استفاده کنیم تا ظرفیت معادل خازنهای موازی در شکل را محاسبه کنیم:
در نوشتن رابطه بالا از استفاده شد. با ساده کردن ولتاژ از طرفین، ظرفیت معادل میشود:
با تعمیم این فرمول برای چند خازن موازی، فرمول ظرفیت معادل n خازن موازی برابر است با:
نکته: همواره ظرفیت معادل چند خازن موازی از ظرفیت هر کدام از خازنها عدد بزرگتری است.
حل مثال و تمرین از خازنهای سری و موازی
در دو بخش قبل با فرمول های خازن معادل در اتصال سری و موازی خازنها کاملا آشنا شدیم. حالا میخواهیم در قالب حل چند مثال و تمرین، نحوه کار با این فرمولها را آموزش دهیم.
مثال ۱
ظرفیت معادل سه خازن سری که ظرفیتهایی بهصورت و و دارند را پیدا کنید. اگر همین سه خازن را به شکل موازی ببندیم، ظرفیت معادل چقدر خواهد شد؟
پاسخ
با نوشتن فرمول ظرفیت معادل برای خازنهای سری داریم:
در بخش دوم سوال، باید ظرفیت معادل سه خازن موازی را با فرمول زیر محاسبه کنیم:
مثال ۲
در مدار زیر، ظرفیت معادل چقدر است؟
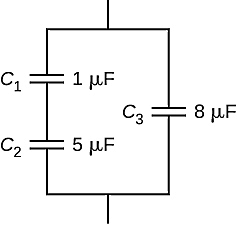
پاسخ
در این سوال دو خازن یک و دو بهصورت سری به هم وصل شدهاند. اما اتصال خازن یک و دو به خازن سه از نوع سری نیست. اگر دقت کنید دو گره در بالا و پایین این مدار وجود دارد که باعث میشود خازن سوم با معادل دو خازن اول موازی شود. پس ابتدا معادل دو خازن یک و دو را با نوشتن فرمول ظرفیت معادل خازنهای سری بهدست میآوریم:
ظرفیت معادل دو خازن یک و دو را با نماد نشان دادهایم. بنابراین تا اینجا مسئله به شکل زیر ساده شده است:

واضح است که نحوه اتصال دو خازن بالا موازی است:
مثال ۳
با توجه به شکل زیر و ظرفیتهای و و ، چنانچه ولتاژی به اندازه به مجموعه اعمال شود، بار و اختلاف پتانسیل متناظر با هر خازن را پیدا کنید:
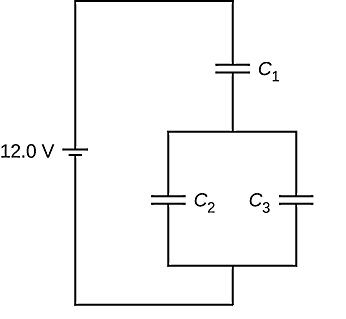
پاسخ
در مدار این سوال، دو خازن شماره دو و سه کاملا موازی به هم متصل شدهاند. اگر معادل این دو خازن را در مدار جایگزین کنیم، در نهایت دو خازن سری در مدار خواهیم داشت. پس اولین قدم، محاسبه ظرفیت معادل مدار است:
مدار معادل تا اینجا به شکل زیر خواهد شد:

پس ظرفیت خازن معادل با این سه خارن در مدار محاسبه شد. حالا اگر مدار بالا را در نظر بگیریم که در آن دو خازن سری داریم، میدانیم ولتاژ کل با مجموع ولتاژ این دو خازن برابر است:
ولتاژ کل همان مقدار است. از طرفی میدانیم طبق فرمول اصلی ظرفیت خازن، میتوانیم ولتاژ را برای هر خازن بر حسب بار ذخیره شده در آن و ظرفیتش به شکل زیر بنویسیم:
همچنین بار روی هر کدام از این دو خازن با بار خازن معادل برابر است، یعنی داریم . پس رابطه بالا بهصورت زیر ساده میشود:
دقت کنید چون ظرفیت خازنها بر حسب میکروفاراد بود، بار هم بر حسب میکروکولن بهدست میآید. پس بار ذخیره شده در خازن اول تعیین شد. برای بهدست آوردن ولتاژ آن، کافی است از فرمول زیر استفاده کنیم:
بلافاصله از فرمول که بالاتر نوشتهایم، میتوانیم ولتاژ دو سر خازن معادل دو و سه را پیدا کنیم:
حالا میرویم سراغ دو خازن دیگر. خازنهای شماره دو و سه موازی هم بودند. پس ولتاژ هر کدام با ولتاژ دو سر خازن معادل آنها یکی است، یعنی داریم:
در نهایت فقط بار خازنهای دو و سه را باید پیدا کنیم:
مسئله حل شد. برای اینکه راهحل خود را امتحان کنیم، اگر بار خازنهای دو و سه را با هم جمع کنیم باید با بار خازن اول برابر باشد. چون خازن اول با خازن معادل دو و سه، سری است و بار برابری دارند:
مثال ۴
اگر چهار خازن با ظرفیتهای و و و به شکل زیر در اتصال با هم قرار داشته باشند، با در نظر گرفتن اختلاف پتانسیل برای کل مجموعه، بار روی هر خازن را محاسبه کنید:
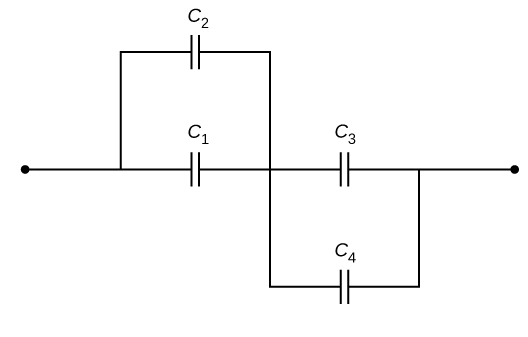
پاسخ
برای پیدا کردن بار روی هر خازن، ابتدا باید ببینیم ساده شده مدار بالا به چه صورت است. خازنهای یک و دو با هم و خازن سه و چهار نیز با هم موازی هستند. معادل هر جفت از این خازنها، دو خازن سری میشود:
پس در مرحله آخر دو خازن سری داشتیم که معادل آنها خازنی با ظرفیت شد. از بخش مربوط به اتصال سری خازنها، میدانیم بار روی این خازن با بار روی هر کدام از دو خازن سری یکسان است:
پس اگر بار کل را حساب کنیم، بار دو خازن معادل مرحله قبلتر هم پیدا میشود:
حالا با داشتن بار و ظرفیت، میتوانیم ولتاژ هر کدام از خازنهای معادل یعنی و را پیدا کنیم:
طبق دانشی که در مورد خازنهای موازی بهدست آوردیم، میدانیم ولتاژ دو سر هر کدام از خازنهای موازی با ولتاژ کل مجموعه خازنهای موازی یکسان است. پس داریم:
پس بار روی هر کدام از خازنهای اول و دوم بهصورت زیر محاسبه میشود:
برای خازن سه و چهار هم به همین روش عمل میکنیم:
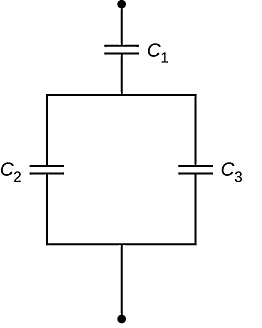
تمرین ۱
ظرفیت معادل مدار زیر با در نظر گرفتن و و ، برابر با کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
تمرین ۲
فرض کنید به مدار زیر که شامل خازنهایی با ظرفیتهای و و است، ولتاژی به اندازه اعمال میشود. بار ذخیره شده روی این خازنها به ترتیب چقدر است؟
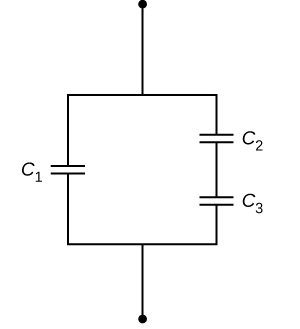
و و
و و
و و
و و
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
فرمول انرژی خازن
فرمول دیگر از مجموعه فرمول های خازن، رابطهای است که انرژی ذخیره شده در خازن را به ما میدهد. این انرژی که با نشان داده میشود، نوعی انرژی پتانسیل الکتروستاتیکی است که با توجه به مقادیر بار ذخیره شده در خازن و اختلاف پتانسیل آن یا تعیین میشود. خازن انرژی الکتریکی را در میدان الکتریکی بین صفحات خود ذخیره میکند، به این ترتیب که با شارژ شدن آن، میدان الکتریکی تشکیل میشود. حالا اگر اتصال خازن از باتری قطع شود، این انرژی در میدان بین صفحات خازن باقی میماند.
در ادامه نشان میدهیم چگونه میتوان فرمول انرژی خازن را بهدست آورد. فرض کنید یک خازن تخت و بدون دیالکتریک داریم که فضای بین صفحات آن خلاء است. طبق چیزی که گفتیم، اگر حجم این فضا را با نشان دهیم، یک میدان الکتروستاتیکی یکنواخت مانند در این فضا وجود دارد. از طرفی میدانیم چگالی انرژی برابر است با انرژی تقسیم بر حجم:
فرمول چگالی انرژی الکتروستاتیکی را میتوانیم با توجه به دانش خود در زمینه امواج الکترومغناطیسی بنویسیم. طبق این فرمول، چگالی انرژی در یک فضای خلاء که شامل میدان الکتریکی است، فقط به اندازه این میدان بستگی دارد:
بنابراین فرمول انرژی الکتریکی بهصورت زیر میشود:
در اینجا میتوانیم میدان الکتریکی یکنواخت در فضای بین دو صفحه چنین خازنی را بهصورت زیر در نظر بگیریم:
اگر دقت کنید در انتهای این رابطه میتوانیم بهجای از استفاده کنیم. پس فرمول انرژی خازن میشود:
اگر از فرمول استفاده کنیم، فرمول انرژی خازن را به شکلهای زیر هم خواهیم داشت:
روابط بالا برای انرژی خازن در مورد انواع خازن برقرار است.
حل مثال و تمرین از فرمول انرژی خازن
در ادامه به حل چند سوال در مورد نحوه محاسبه انرژی خازن میپردازیم.
مثال ۱
اگر اختلاف پتانسیل یک خازن پیکوفارادی برابر با ولت باشد، انرژی ذخیره شده در این خازن چقدر است؟ چنانچه اختلاف پتانسیل را تا ولت افزایش دهیم، انرژی ذخیره شده چقدر افزایش مییابد؟
پاسخ
در اولین بخش از این سوال، فرمول محاسبه انرژی را به شکل زیر مینویسیم:
در ادامه با ولتاژ جدید مجددا انرژی را حساب میکنیم:
جهت مقایسه انرژیها، کافی است انرژی در حالت دوم را بر انرژی در حالت اول تقسیم کنیم:
پس انرژی نه برابر میشود.
مثال ۲
انرژی ذخیره شده در شبکه خازنی زیر را در شرایطی که ظرفیت هر خازن به شکل و و است و تمام خازنها کاملا شارژ شدهاند، پیدا کنید:

پاسخ
با بکار بردن فرمول های خازن برای انرژی و در نهایت جمع کردن انرژیهای بهدست آمده، انرژی کل شبکه خازنی بهدست میآید. چون ظرفیت هر خازن و ولتاژ کل را داریم، بهتر است از فرمول استفاده کنیم. اما ابتدا باید ولتاژ هر خازن پیدا شود. این کار را در مثال ۳ بخش قبل انجام دادهایم و نتایج به شکل زیر بودند:
بنابراین انرژی کل این مجموعه خازن برابر است با:
یک راه دیگر برای محاسبه انرژی کل در نظر گرفتن خازن معادل این مدار و ولتاژ کل است. ظرفیت خازن معادل این مدار طبق حل مثال ۳ بخش قبل برابر است با:
تمرین ۱
فرض کنید خازن تخت و بدون دیالکتریکی با ظرفیت در اختیار داریم که در حال شارژ شدن توسط یک منبع ولتی است. اگر اتصال این خازن را با اختلاف پتانسیل اعمال شده به آن قطع کنیم و فاصله بین صفحات آن را نصف کنیم، نسبت انرژی ذخیره شده در خازن پس از قطع ولتاژ به قبل از آن چیست؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
تمرین ۲
ظرفیت یک خازن خالی که با اتصال به ولتاژ شارژ میشود برابر است با . اگر اتصال باتری و خازن قطع شود و مقداری تفلون با ثابت دیالکتریک فضای بین صفحات خازن را کاملا پر کند، انرژی ذخیره شده در خازن با و بدون تفلون به ترتیب برابر است با:
و
و
و
و
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
مسیر یادگیری فیزیک الکتریسیته دانشگاهی با فرادرس
فیزیک پایه دانشگاهی شامل موضوعات مهمی مانند فیزیک مکانیک، فیزیک الکتریسیته و مغناطیس است که در اغلب رشتههای علوم پایه و مهندسی آشنایی با این سه موضوع از اهمیت بالایی برخوردار است. در این نوشته، در مورد مبحث خازن از فیزیک الکتریسیته صحبت کردیم. به همین دلیل در ادامه چند فیلم آموزشی مرتبط از مجموعه فرادرس برای شما انتخاب شده است تا با مشاهده آنها به حل مسائل این حوره مسلط شوید:
- فیلم آموزش رایگان محاسبه ظرفیت خازن سری فرادرس
- فیلم آموزش فیزیک الکتریسیته فرادرس
- فیلم آموزش رایگان الکتریسیته ساکن – حل تمرین فرادرس
- فیلم آموزش فیزیک ۲ دانشگاه فرادرس
- فیلم آموزش رایگان خازن ها و دیالکتریک در فیزیک عمومی ۲ – حل مساله فرادرس
- فیلم آموزش فیزیک عمومی ۲ – حل مساله فرادرس
- فیلم آموزش الکترومغناطیس مهندسی فرادرس
- فیلم آموزش رایگان اسیلاتور RC + حل مثال فرادرس
- فیلم آموزش رایگان محاسبه ظرفیت خازن از روی کد رنگ فرادرس
- فیلم آموزش رایگان تعمیر لوازم خانگی حرارتی ۱ – الکتریسیته، خازن و مقاومت فرادرس
جمعبندی
در این آموزش از مجله فرادرس فرمول های خازن را بهطور کامل بررسی کردیم و با نحوه استفاده از این فرمولها در حل بخشی از مسائل الکتریسیته آشنا شدیم. اصلیترین فرمول خازن، است که رابطه بین ظرفیت، بار ذخیره شده و ولتاژ اعمال شده به دو سر خازن جهت شارژ کردن آن را توصیف میکند. همچنین انرژی الکتریکی ذخیره شده در خازن را میتوانیم توسط روابط یا یا محاسبه کنیم.

فرمول مهم بعدی، فرمول ظرفیت خازن است که برای انواع خازن متفاوت است، چون ظرفیت خازن به مشخصات فیزیکی آن بستگی دارد. برای مثال فرمول ظرفیت خازن تخت است، در حالی که برای محاسبه ظرفیت خازن کروی از و برای محاسبه ظرفیت خازن استوانهای از استفاده میشود.
همچنین در صورتی که داخل هر کدام از این خازنها دیالکتریک داشته باشیم، ثابت دیالکتریک به فرمولهای بالا اضافه میشود. برای مثال، ظرفیت خازن تخت با دیالکتریک میشود. بخش دیگر فرمول های خازن به نحوه اتصال چند خازن در مدار و محاسبه ظرفیت خازن معادل مربوط میشود. این مبحث بهطور خلاصه در جدول زیر گردآوری شده است:
| اتصال سری n خازن | اتصال موازی n خازن | |
| ظرفیت خازن معادل یا | ||
| ولتاژ معادل یا | ||
| بار معادل یا |
source
