آیا تا به حال هنگام شنا کردن فشار آب را روی بدن خود حس کرده‌اید؟ این پدیده ناشی از «فشار در شاره ها» (Fluid Pressure) است. در هر نقطه‌ داخل یک شاره، به‌علت نیروی وزن آن، همیشه فشاری وجود دارد که به آن فشار در شاره ها گفته می‌شود. آب دریا، هوای اطراف‌مان و هر نوع مایع یا گاز دیگری یک شاره یا سیال در نظر گرفته می‌شوند و چنین فشاری در هر نقطه از این مواد وجود دارد. در این مطلب از مجله فرادرس می‌خواهیم مفهوم فشار در شاره ها را توضیح دهیم و ببینیم این نوع فشار به چه عواملی بستگی دارد و مقدار آن چگونه محاسبه می‌شود. همچنین با قوانینی مانند اصل ارشمیدس و اصل پاسکال آشنا می‌شویم.

فشار در شاره ها

فشار در شاره ها برابر است با نیرویی که به واحد سطح یک جسم جامد داخل یک شاره وارد می‌شود. این فشار از نیروی وزن شاره ساکن ناشی می‌شود. تمام شاره‌ها شامل مایعات و گازها فشار ایجاد می‌کنند. اگر بخواهیم فشار یک نقطه مشخص داخل یک مایع را بدانیم، کافی است عمق آن نقطه را به همراه چگالی مایع بدانیم. سپس طبق فرمول $$P=rho gh$$

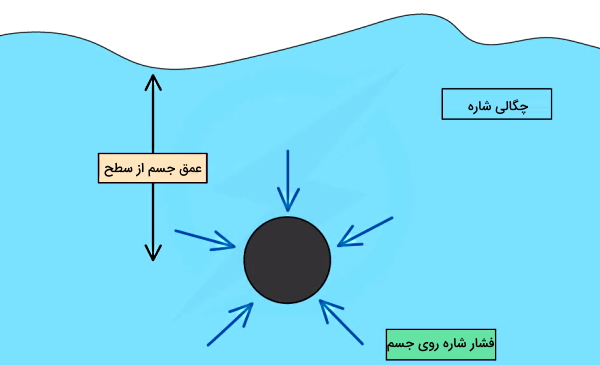
در رابطه بالا P فشار مایع با واحد پاسکال (Pa)، ρ چگالی مایع با واحد کیلوگرم بر متر مکعب (kg/m³)، g شتاب جاذبه زمین بر حسب متر بر مجذور ثانیه (m/s²) و h عمق یا ارتفاع مایع بر حسب متر (m) است. در بخش‌های بعد نشان می‌دهیم که چگونه می‌توان با در نظر گرفتن نیروی وزن شاره، رابطه بالا را از فرمول اصلی فشار استخراج کرد.

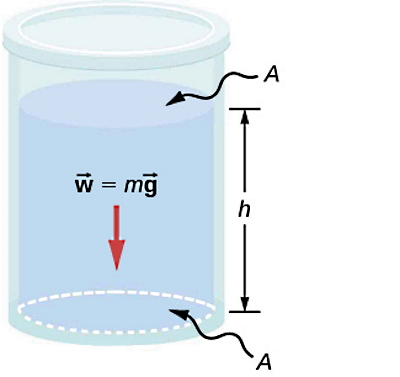
گفتیم فشار در شاره ها برابر است با نیرویی که به‌صورت عمودی بر واحد سطح جسمی که داخل آن شاره قرار دارد، وارد می‌شود. این نیرو به دیواره‌های محفظه یا ظرفی که شاره در آن قرار دارد نیز وارد می‌شود. پس هر جسمی که داخل شاره قرار بگیرد یا هر ظرفی که شاره در آن قرار داشته باشد، می‌تواند فشاری از سمت شاره دریافت کند.

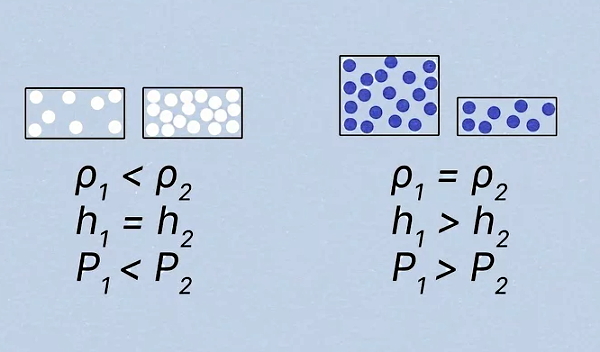
نکته مهم در مورد اندازه‌گیری مقدار فشار در شاره ها این است که برای مثال اگر یک ستونی از مایع را در نظر بگیریم، فشار شاره با افزایش عمق مایع بیشتر می‌شود. پس عمق نقطه‌ای که مدنظر است، در محاسبه فشار موثر است.

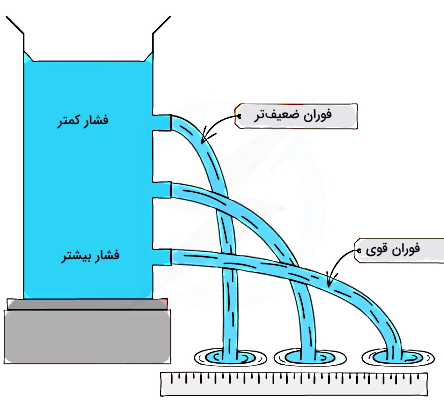
مورد دیگری که روی اندازه فشار در شاره ها تاثیرگذار است، چگالی آن شاره است. هر چه شاره‌ای چگال‌تر باشد، فشار آن هم بیشتر است. برای نمونه فرض کنید فشار دو مایع مختلف مثل آب و نفت در یک نقطه با عمق یکسان مقایسه شود. چون آب از نفت چگالی بیشتری دارد، پس فشار آب از نفت در این مورد بیشتر است. این در حالی است که برای مقایسه فشار یک مایع در نقاط مختلف، تنها پارامتری که تعیین‌کننده است، عمق آن نقاط است. چون چگالی یک مایع در تمام نقاط آن یکسان است. به این ترتیب پارامترهایی مثل جرم شاره، حجم یا شکل آن روی فشار تاثیری ندارند.

یادگیری فشار در شاره ها با فرادرس

برای تسلط بیشتر به مبحث فشار در شاره ها که در کتاب‌های درسی علوم نهم و فیزیک دهم به آن‌ها پرداخته شده است، پیشنهاد می‌کنیم فیلم‌های آموزشی زیر از مجموعه فرادرس را مشاهده کنید:

1. فیلم آموزش علوم تجربی نهم – بخش فیزیک فرادرس
2. فیلم آموزش فیزیک دهم فرادرس
3. فیلم آموزش فیزیک دهم – مرور و حل تمرین فرادرس

شاره چیست؟

به هر ماده‌ای که قابلیت جاری شدن داشته باشد، «شاره یا سیال» (Fluid) گفته می‌شود. می‌دانیم تمام مواد در یکی از سه حالت جامد، مایع و گاز هستند که دو گروه از این سه حالت، یعنی مایع و گاز در طبقه‌بندی شاره‌ها قرار می‌گیرد. پیش از شروع مبحث مفهوم فشار در شاره ها، لازم است ابتدا بدانیم یک شاره چه خصوصیاتی دارد.

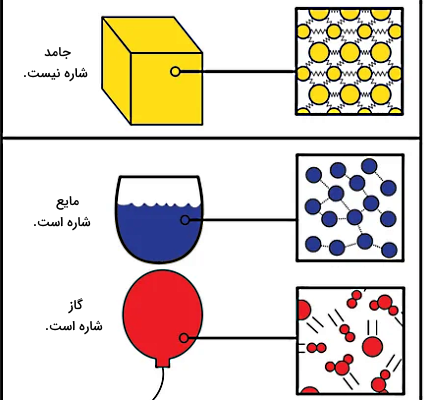
طبق شکل زیر در یک جامد اتم‌ها یا ذرات سازنده ماده در فاصله خیلی نزدیکی از هم قرار دارند، طوری که نیروهای قوی بین هر ذره و ذره مجاورش وجود دارد. بنابراین ذرات یک جامد آزادی عمل برای حرکت در داخل ماده ندارند. اما در مایعات و گازها، ذرات سازنده ماده می‌توانند داخل ماده حرکت کنند. علت این مسئله این است که در این دو حالت ماده، ذرات فواصل بیشتری از هم دارند و نیروهای جاذبه بین آن‌ها نسبت به جامد خیلی ضعیف‌تر است.

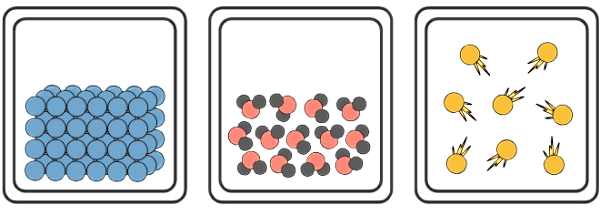
در گازها ذرات آزادی عمل بیشتری دارند، اما در مایعات هم ذرات تشکیل دهنده ماده می‌توانند روی هم بلغزند. بنابراین هر دو گروه ویژگی مهم یک شاره که همان قابلیت جاری شدن است را دارند. یکی از خواص شاره ها، فشاری است که ایجاد می‌کنند. تمام مایعات و گازها فشار ایجاد می‌کنند، چون تمام آن‌ها از ماده ساخته شده‌اند که این ماده دارای وزن است و قادر است جاری شود تا فضا یا حجمی را پر کند. 

مفهوم فشار در شاره ها

تا اینجا آموختیم که فشار به چه عواملی وابسته است. حالا می‌خواهیم ببینیم فشار در شاره ها چه معنایی دارد. همان‌طور که یک جسم جامد می‌تواند به جسم جامد دیگری فشار وارد کند، شاره‌ها (شامل مایعات و گازها) هم می‌توانند به اجسام جامد فشار وارد کنند.

پس فشار در شاره ها، فشاری است که ناشی از وزن مایع یا گاز است. این فشار به هر جسمی که داخل مایعی غوطه‌ور است یا در محفظه‌ حاوی هر نوع گازی قرار دارد، اعمال می‌شود.

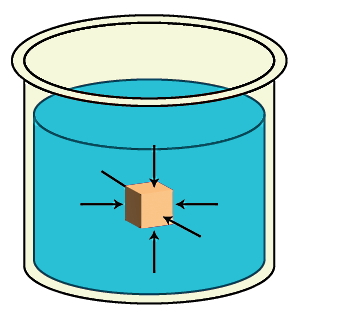
بنابراین فشار در شاره ها به دو قسمت تقسیم می‌شود، فشار مایعات و فشار گازها. در ادامه با دو مثال مفهومی و ملموس در زندگی روزمره، فشار در شاره ها را توضیح می‌دهیم. در اولین مثال فشار آب بر بدن انسان و در مثال دوم فشار هوا به‌عنوان نوعی گاز بر بدن انسان بررسی می‌شود.

• نکته ۱: مانند شکل بالا، نیروی وارد بر واحد سطح برای بررسی فشار همیشه عمود بر آن سطح و به سمت داخل آن در نظر گرفته می‌شود.
• نکته ۲: چون یک شاره شکل مشخصی ندارد، فشار در تمام نقاط‌‌‌ آن پخش می‌شود. در ادامه خواهید دید در تمام مثال‌هایی که بیان می‌کنیم، برای نشان دادن فشار از پیکان‌هایی در جهت‌های مختلف استفاده می‌شود.
• نکته ۳: گفتیم فشار یک کمیت نرده‌ای یا عددی است، یعنی جهت ندارد. اما در شکل‌های مربوط به آن، برای نشان دادن جهت فشار تولید شده از پیکان جهت‌دار استفاده می‌کنیم. باید دقت کنیم این مسئله نباید باعث شود فکر کنیم فشار یک کمیت برداری است و جهت دارد، بلکه این پیکان‌ها فقط نشان‌دهنده جهت نیرویی هستند که به واحد سطح از ماده وارد می‌شود.
• نکته ۴: ارتفاع یا عمقی که اندازه‌ می‌گیریم با اینکه ممکن است زیر سطح دریا باشد، اما همیشه مقدار مثبتی در فرمول دارد.

فشار مایعات

یکی از بهترین مثال‌ها برای فشار در شاره ها، شنا کردن است که در آن فشار ایجاد شده از سمت یک مایع را می‌توانید به‌خوبی حس کنید. فرض کنید در عمق مشخصی از آب فرو رفته‌اید. در این شرایط آبی که بالاتر از بدن شما قرار دارد، در اثر نیروی جاذبه‌ای که دریافت می‌کند، شما را به پایین می‌کشد. پس نیروی جاذبه باعث می‌شود تا شما فشار آب را کاملا حس کنید.

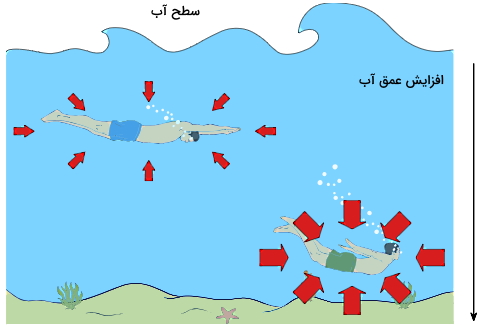
با رفتن به قسمت‌های عمیق‌تر، مقدار آبی که بالاتر از بدن شما قرار دارد، بیشتر است. در نتیجه، نیرو بزرگ‌تر است و شدت فشاری که حس می‌کنید نیز بیشتر خواهد شد. اگر به شکل بالا دقت کنید، افزایش فشار وارد بر بدن با بزرگ‌تر شدن اندازه پیکان‌های قرمز مشخص است. بنابراین با تغییر عمق خود در آب، کاملا متوجه تغییرات فشار وارد بر بدن خود خواهید شد.

فشار گازها

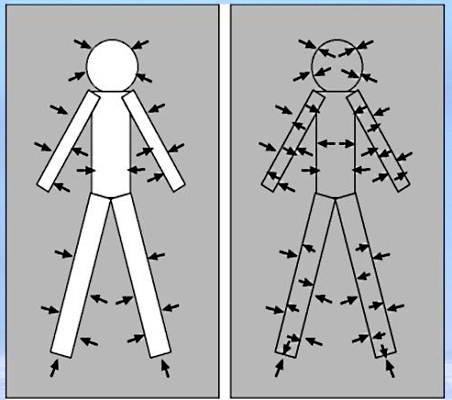
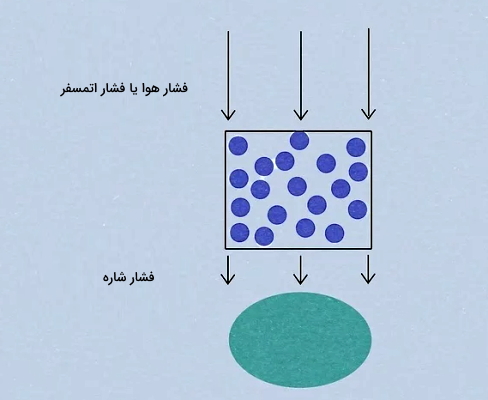
در این قسمت مثال دیگری از فشار در شاره ها را بررسی می‌کنیم. باید بدانیم نه تنها وزن مایعات فشار ایجاد می‌کند، بلکه وزن گازها نیز فشار تولید می‌کند. به‌عنوان مثال دوم از فشار در شاره ها، بدن خود را در نظر بگیرید. همواره به بدن انسان فشار بزرگی که ناشی از نیروی وزن هوای اطراف است، وارد می‌شود. به‌عبارت دیگر، بدن انسان فشار ناشی از وزن هوای اطراف خود را کاملا دریافت می‌کند.

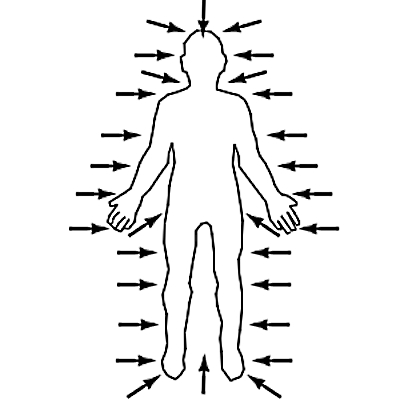
همان‌طور که توضیح دادیم، چون ذرات یک شاره در حال حرکت در جهت‌های مختلفی هستند، پس فشاری که یک شاره ایجاد می‌کند نیز در تمام جهات است. این نکته در تصویر بالا کاملا مشخص است. اما علت اینکه ما چنین فشار بزرگی را حس نمی‌کنیم، چیست؟ چون داخل بدن انسان هم چنین فشاری وجود دارد، پس اختلاف فشار داخل و خارج از بدن انسان صفر است. به همین علت است که فشار هوا را حس نمی‌کنیم و بدن انسان تنها مقادیری از فشار را حس می‌کند که از فشار هوا یا فشار اتمسفر بیشتر یا کمتر باشد، مثلا زمانی که در عمقی از آب فرو می‌رویم یا داخل یک هواپیما در حال پرواز هستیم.

تاثیر عمق مایع روی فشار

در قالب دو مثال یاد گرفتیم که فشار در شاره ها چگونه است. اگر بار دیگر به مثال فشار مایعات برگردیم، به خاطر داریم که عمق شاره یکی از عوامل موثر در فشار آن است. اگر عمق یا ارتفاع از سطح مایع را با h نشان دهیم، می‌توانیم رابطه بین h و P یا فشار را به شکل زیر نشان دهیم:

$$h uparrow Rightarrow P uparrow$$

بنابراین ارتباط عمق شاره و فشار آن یک رابطه مستقیم است، یعنی با افزایش یا کاهش h، فشار هم زیاد یا کم می‌شود. برای اینکه اثر عمق روی فشار را بهتر متوجه شویم، در مثال بعدی یک قوطی را در نظر بگیرید که داخل آب غوطه‌ور است. با توجه به اینکه گفتیم فشار ناشی از مایع در تمام جهات به جسم وارد می‌شود، پس شکل زیر را خواهیم داشت:

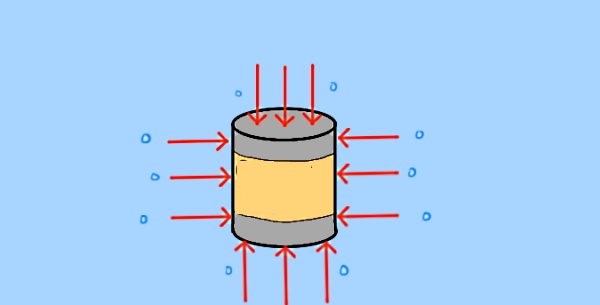
اما اگر بیشتر دقت کنیم، کف قوطی در عمق بیشتری نسبت به سر قوطی قرار دارد. پس فشار آب وارد بر قوطی در قسمت کف نسبت به سر بیشتر خواهد بود. اما مقدار فشار در دو طرف سمت و راست قوطی کاملا با هم برابر است. همین مسئله باعث می‌شود فشار آب در حالت کلی و با در نظر گرفتن تمام جهات، باعث حرکت قوطی به سمت بالا شود.

تاثیر چگالی مایع روی فشار

مجددا مثال شنا در آب را در نظر بگیرید. عامل موثر دیگر روی فشار در شاره ها که در این بخش معرفی می‌کنیم، چگالی مایعی است که بدن در آن غوطه‌ور است. چگالی هم مانند فشار یک کمیت نرده‌ای در فیزیک است که با حرف یونانی ρ نشان داده می‌شود. چگالی هر ماده‌ای به‌صورت جرم واحد حجم آن تعریف می‌شود و دارای فرمولی به شکل زیر است:

$$rho=frac{m}{V}$$

که در آن m جرم ماده بر حسب کیلوگرم (kg) و V حجم ماده بر حسب متر مکعب (m³) است. پس واحد ρ یا چگالی، کیلوگرم بر متر مکعب یا kg/m³ به‌دست می‌آید. هر چه چگالی شاره بیشتر باشد، فشار بیشتری ایجاد می‌کند. این نکته توضیح می‌دهد که چرا در شرایط مشابه، فشاری که از سمت هوا به بدن ما وارد می‌شود با فشار آب فرق دارد. در واقع کلید این اختلاف، تفاوت در چگالی مایعات با چگالی گازها است.

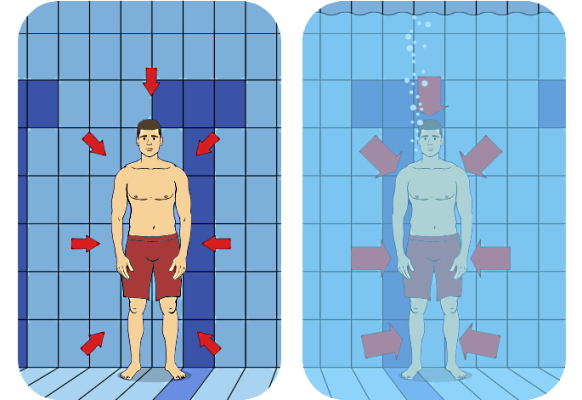
برای درک بهتر این مسئله، شکل بالا را در نظر بگیرید که در آن شخصی در حالت اول، در کف یک استخر خالی قرار گرفته است. در حالت دوم باز هم در موقعیت قبلی است، اما در این حالت استخر از آب پر شده است. پس در دو حالت، دو نوع شاره داریم، هوا و آب. می‌دانیم هر شار‌ه‌ای فشار تولید می‌کند. اگر چگالی آب و هوا را مقایسه کنیم، می‌بینیم که آب از هوا چگال‌تر است یا چگالی بیشتری دارد:

$$rho_{water}=997 frac{kg}{m^3}$$

$$rho_{air}=1.225 frac{kg}{m^3}$$

واضح است که در حالت دوم، شخص داخل آب فشار بیشتری حس می‌کند که می‌توانیم آن را به بیشتر بودن چگالی آب نسبت به هوا نسبت دهیم. بیشتر شدن فشار در داخل آب، با پیکان‌های قرمز بزرگ‌تر نشان داده شده است. پس رابطه بین فشار شاره و چگالی آن، یک رابطه مستقیم است، یعنی هر چه شاره چگالی بیشتری داشته باشد، فشار بیشتری هم ایجاد می‌کند.

$$rho uparrow Rightarrow P uparrow$$

• نکته: مایعات عملا قابلیت تراکم‌پذیری ندارند، به این معنا که نمی‌توان حجم آن‌ها را با اعمال فشار تغییر داد. به همین دلیل به جز در موارد خاصی که همراه با تغییرات دمایی است، چگالی یک مایع در تمام عمق‌ها و در تمام نقاط آن همیشه یکسان است.

تاثیر جاذبه روی فشار

آخرین عاملی که روی اندازه فشار در شاره ها تاثیرگذار است، شتاب ناشی از جاذبه است که با g نشان داده می‌شود. تاثیر شتاب جاذبه برای تمام شاره‌‌های روی زمین یکسان است، چون به تمام مواد روی زمین شامل انواع شاره ها، شتاب جاذبه یکسانی وارد می‌شود. اما اگر وضعیت فشار یک شاره را در دو شتاب جاذبه مختلف بررسی کنیم، تفاوت فشار مشخص است. برای مثال زمین و ماه را در نظر بگیرید.

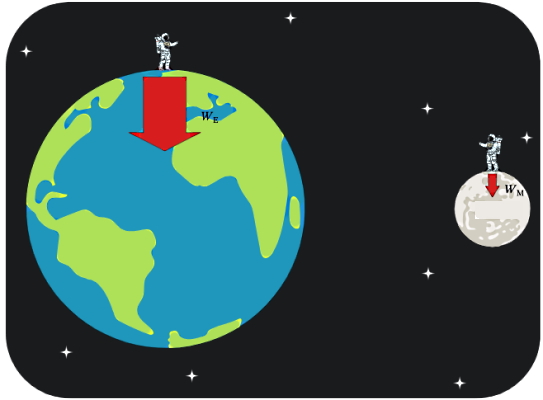
اندازه شتاب روی زمین برابر است با $$g_e=9.8 frac{m}{s^2}$$

$$g uparrow Rightarrow P uparrow$$

به‌عبارت دیگر بزرگتر شدن شتاب جاذبه روی زمین باعث می‌شود نیروی وزن‌ (W_E) بیشتری به همان شاره روی زمین وارد شود، در نتیجه فشار بیشتری ایجاد می‌کند. در بخش بعد خواهیم دید چگونه می‌توان با در نظر گرفتن همه عوامل موثر روی فشار در شاره ها شامل عمق شاره، چگالی آن و شتاب جاذبه زمین، مقدار دقیق این کمیت را محاسبه کرد.

اصل ارشمیدس

در بخش تاثیر عمق روی فشار در شاره ها، گفتیم با انداختن یک قوطی در آب، در مدت زمان خیلی کوتاهی قوطی کمی بالاتر از عمق اولیه خود دیده می‌شود. به این اثر برآیند، «نیروی شناوری» (Buoyant Force) اجسام غوطه‌ور هم گفته می‌شود. این مسئله موضوع «اصل ارشمیدس» (Archimedes’ Principle) است که طبق آن نیروی شناوری وارد بر یک جسم با وزنی از شاره که توسط جسم غوطه‌ور در آن جابجا شده است، برابر است:

$$F_B=W_{fl}$$

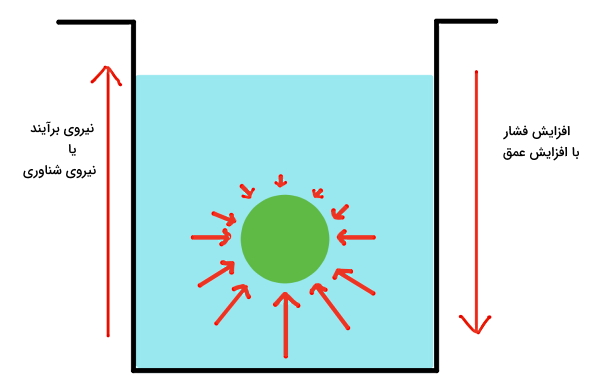
در رابطه بالا F_B همان نیروی شناوری است و W_fl برابر است با نیروی وزن شاره‌ای است که به خاطر حضور جسم جابجا می‌شود. طبق اصل ارشمیدس و اثر عمق روی فشار شاره، نیروی شناوری وارد شده به سر جسم نسبت به نیروی وارد شده به ته آن، بیشتر است.

اگر مقدار نیروی شناوری از وزن جسم داخل شاره بیشتر باشد، جسم در شاره بالا می‌رود. اگر این نیرو از وزن جسم کمتر باشد، جسم داخل شاره غرق می‌شود. اگر نیروی شناوری با وزن جسم برابر باشد، جسم در همان ارتفاعی که هست باقی‌ می‌ماند.

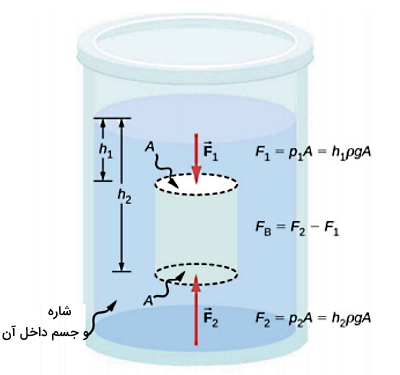
در شکل بالا، مفهوم نیروی شناوری به این صورت نشان داده شده است:

1. اگر فاصله سر جسم تا سطح شاره را h₁ در نظر بگیرید، فشار وارد بر سر جسم P₁ است که نیروی F₁ به سمت پایین را ایجاد می‌کند.
2. اگر فاصله ته جسم تا سطح شاره را h₂ در نظر بگیرید، فشار وارد بر ته جسم P₂ است که نیروی F₂ به سمت بالا را ایجاد می‌کند.
3. اختلاف این دو نیرو، برابر است با نیروی شناوری.

فرمول فشار در شاره ها

در بخش‌های قبل به‌صورت تجربی یا گرفتیم که عوامل موثر روی فشار در شاره ها چیست. در این بخش خواهیم دید که پس از محاسبه فرمول فشار در شاره ها، نتایج قبلی تایید می‌شوند. گفتیم که وزن یک شاره می‌تواند به اجسامی که در داخل آن قرار گرفته‌اند یا در تماس با آن هستند، فشار اعمال کند. اما چگونه می‌توانیم مقدار دقیق این فشار را محاسبه کنیم؟ آیا فشار تولید شده در عمق‌های مختلف برای مایعات متفاوتی که جاذبه به آن‌ها نیرو وارد می‌کند، با هم فرق دارد؟ در ادامه این بخش، به این سوالات پاسخ خواهیم داد.

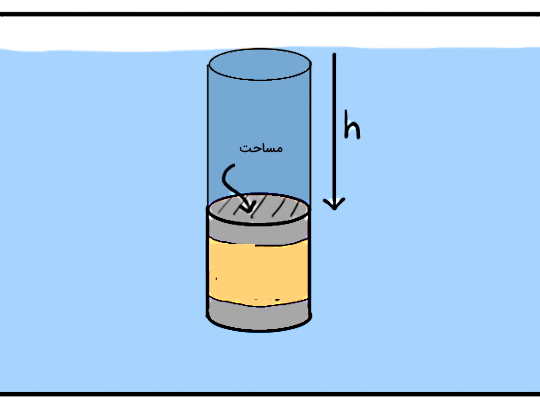
قوطی لوبیایی را در نظر بگیرید که داخل یک استخر افتاده است و فاصله سطح بالای آن از سطح آب برابر است با h. انتظار داریم در اثر نیروی وزن آب بالای قوطی که دارای ارتفاع یا عمق h است، به سطح بالایی قوطی فشار اعمال شود. طبق تعریف کلی، فشار برابر است با نیروی عمودی وارد بر واحد سطح که با فرمول زیر مشخص می‌شود:

$$P=frac{F}{A}$$

به‌جای نیروی F وزن ستون آب بالای قوطی را قرار می‌دهیم که برابر است با:

$$W=m_wg$$

$$Rightarrow P=frac{m_wg}{A}$$

m_w جرم مقدار آبی است که دقیقا در بالای در قوطی قرار گرفته است. در این مرحله با نوشتن m_w بر حسب چگالی و حجم، رابطه را ساده‌تر می‌کنیم. می‌دانیم چگالی یک ماده برابر است جرم واحد حجم آن که به شکل زیر نشان داده می‌شود:

$$rho=frac{m}{V}$$

$$Rightarrow m=rho V$$

بنابراین می‌توانیم به‌جای m_w بنویسیم $$rho_w V_w$$

$$P=frac{rho_w V_wg}{A}$$

برای محاسبه حجم باید از فرمول حجم استوانه استفاده کنیم. حجم استوانه‌ای با ارتفاع h و سطح مقطع A برابر است با:

$$V=Ah$$

در مسئله ما با در نظر گرفتن مساحت مقطع دایره‌ای قوطی به‌صورت A و با علم به اینکه ارتفاع ستون آب روی قوطی برابر با h است، خواهیم داشت:

$$V_w=Ah$$

با جای‌گذاری حجم در فرمول فشار، داریم:

$$Rightarrow P=frac{rho_w Ahg}{A}=rho_w hg$$

برای هر مایع دیگری می‌توانستیم فرمول مشابهی به‌دست آوریم. تنها تفاوت در چگالی و ارتفاع مایع است. پس با قرار دادن نیروی وزن به‌جای F و استفاده از فرمول چگالی به‌جای جرم مایع، توانستیم فرمول فشار در مایعات را از فرمول اصلی فشار استخراج کنیم:

$$P=rho gh$$

طبق این فرمول، بار دیگر با استفاده از روابط ریاضی به این نتیجه می‌رسیم که فشار در مایعات فقط و فقط به عمق شاره، چگالی آن و شتاب جاذبه وارد بر آن بستگی دارد.

• نکته ۱: طبق فرمول $$P=rho gh$$
• نکته ۲: طبق فرمول $$P=rho gh$$
• نکته ۳: طبق فرمول $$P=rho gh$$
• نکته ۴: طبق فرمول $$P=rho gh$$
• نکته ۵: این فرمول برای یک مایع ساکن صادق است، یعنی اگر شاره در حال حرکت باشد یا به اصطلاح جاری شود، شرایط متفاوت است.

اگر دانش‌آموز پایه دهم هستید، در مطلب «فرمول های فیزیک دهم در یک نگاه» از مجله فرادرس خلاصه‌ای از فرمول‌های فیزیک دهم گردآوری شده است که شامل فرمول‌های این مبحث هم می‌شود.

فرمول فشار کل

پس از یادگیری فرمول فشار در شاره ها که با در نظر گرفتن یک مایع به‌عنوان شاره، به‌دست آمد، در این بخش فرمول فشار کل یا P_t را معرفی می‌کنیم. اگر به مثال قوطی در بخش قبل برگردیم، ممکن است این سوال برای شما مطرح شود که اثر فشار هوای بالای سطح آب روی قوطی چیست؟

این سوال، نکته درستی است و لازم است اثر فشار هوا را به علت وزنی که دارد، در محاسبات در نظر بگیریم. در واقع فشار کل روی قوطی، فشاری است که از مجموع فشار ستون آب و فشار ستون هوای بالای آن ناشی می‌شود. کافی است مقدار فشار هوای وارد بر سطح مایع یا P₀ را با فشار آب جمع کنیم تا اثر فشار کل ناشی از هر دو شاره یعنی آب و هوا روی جسم غوطه‌ور در آب را داشته باشیم:

$$P_t=P_0+rho gh$$

در ابتدای مطلب گفتیم که فشار مطلق، فشار گیج و فشار اتمسفر چه ارتباطی با هم دارند. در اینجا فشار مایع یا $$rho gh$$، همان فشار گیج، فشار مطلق همان فشار کل یا P_t و فشار اتمسفر یا P_atm همان فشار هوا یا P₀ است. 

$$P_t=P_0+P_g$$

• نکته ۱: فشار اتمسفر در تمام سطح زمین با تقریب مقدار یکسانی دارد و برابر است با $$1.01times10^5 Pa = 1 atm$$

$$P_t=1.01times10^5 Pa +rho gh$$

• نکته ۲: فرمول بالا برای محاسبه فشار وارد بر جسمی که در یک محفظه خلاء  قرار دارد، استفاده نمی‌شود.
• نکته ۳: معمولا در مسائل اگر مقدار فشار کل خواسته شود، حتما از کلمه «کل» یا «مطلق» استفاده می‌شود. در غیر این صورت منظور همان فشار مایع یا فشار گیج است که با فرمول $$rho gh$$ قابل محاسبه است.
• نکته ۴: در نظر گرفتن فشار کل در اندازه‌گیری‌ها و محاسبات عددی واقعی در زندگی کمک کننده نیست، چون اثر فشار هوا روی تمام اجسام به شکل یکسانی وجود دارد. برای مثال فرض کنید می‌خواهید فشار هوای داخل لاستیک ماشین را اندازه‌گیری کنید. افزودن مقدار  $$1.01times10^5 Pa$$
• نکته ۵: طبق شکل بالا، صفر فشار کل یا فشار مطلق همان فشار خلاء است که مقدار آن صفر است، یعنی این فشار نسبت به خلاء سنجیده می‌شود. اما صفر فشار گیج، فشار هوا است که برابر است با ‎1 atm.

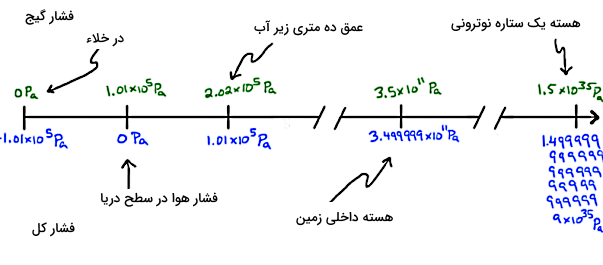
شکل بالا تفاوت مقادیر عددی فشار کل و فشار گیج را برای عمق‌های مختلف نشان می‌دهد. می‌دانیم تفاوت فشار گیج و فشار کل با فشار اتمسفر برابر می‌شود که یک عدد ثابت به شکل $$1.01times10^5 Pa$$

مثال و تمرین از فشار در شاره ها

در بخش قبل، آموختیم که برای محاسبه دقیق فشار وارد بر یک جسم غوطه ور در آب از چه فرمولی باید استفاده کنیم. در این بخش با حل مثال‌‌های گوناگون به شما کمک می‌کنیم تا کاربرد این رابطه را در حل مسائل بهتر یاد بگیرید.

مثال ۱

فشار و نیروی وارد بر جسم دایره‌ای شکلی با مساحت ‎100 cm² که در عمق ‎100 m از آب قرار دارد، چقدر است؟ (چگالی آب ‎1000 kg/m³ است و شتاب g برابر است با ‎10 m/s²)

پاسخ

فشار وارد بر جسم دایره‌ای شکل همان فشاری است که توسط نیروی وزن آبی که روی آن قرار می‌گیرد، ایجاد می‌شود. بنابراین با استفاده مستقیم از فرمول فشار در مایعات می‌توانیم P را حساب کنیم:

$$P=rho gh$$

طبق این فرمول فشار آب فقط به چگالی آب و عمقی که جسم در داخل آب غوطه‌ور است، بستگی دارد. پس اینکه مساحت سطح جسم چقدر است اهمیتی ندارد و یک داده اضافی در صورت سوال است که اگر دقت نکنید ممکن است باعث سردرگمی شما شود. حالا می‌رویم سراغ فرمول فشار مایعات و عددگذاری می‌کنیم:

$$Rightarrow P=1000times 10 times100=10^6 Pa$$

مثال ۲

اگر آب داخل استخر فشاری برابر با ‎20 kPa ایجاد کند، عمق آن را محاسبه کنید: (چگالی آب را ‎1000 kg/m³ و شتاب g را ‎ 9.8 m/s²در نظر بگیرید)

پاسخ

در این سوال فشار ستون مایع داده شده است. چگالی و شتاب جاذبه هم طبق صورت سوال مشخص هستند. با استفاده از فرمول فشار مایعات می‌توانیم مجهول مسئله را که عمق یا ارتفاع آب است، پیدا کنیم:

$$P=rho gh$$

$$Rightarrow h =frac{P}{rho g}$$

اما پیش از عددگذاری لازم است واحد فشار را به پاسکال تبدیل کنیم تا عمق آب بر حسب متر محاسبه شود. می‌د‌انیم پیشوند کیلو به معنای 10³ است. بنابراین داریم:

$$20 kPa=20 times 10^3 Pa=2 times 10^4 Pa$$

حالا اعداد را در فرمول فشار قرار می‌دهیم:

$$Rightarrow h =frac{2 times 10^4}{10^3 times 9.8}=frac{20}{9.8}=2.04 m$$

مثال ۳

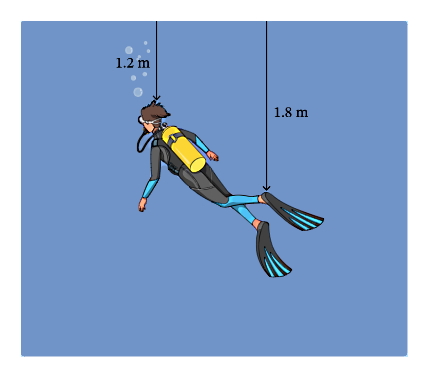
شناگری داخل آبی با چگالی ‎1025 kg/m³ به‌صورت شکل زیر در حال شنا کردن است. با در نظر گرفتن شتاب g به اندازه ‎9.8 m/s² اختلاف فشار آب بین سر و پاهای شناگر چقدر است؟

پاسخ

طبق شکلی که در صورت سوال داریم، عمق سر شناگر در آب ‎1.2 m و عمق پاهای شناگر از سطح آب ‎1.8 m است. برای اینکه اختلاف فشار بین این دو نقطه را حساب کنیم، باید اول فشار آب را در هر کدام از این نقاط جداگانه محاسبه کنیم. پس با کاربرد فرمول فشار مایعات، برای مقدار فشار آب روی سر شناگر داریم:

$$P_{head}=rho gh_{head}$$

$$Rightarrow P_{head}=1025times 9.8times 1.2=12054 Pa$$

حالا فشار آب روی پاهای شناگر را پیدا می‌کنیم:

$$P_{feet}=rho gh_{feet}$$

$$Rightarrow P_{feet}=1025times 9.8times 1.8=18081 Pa$$

با محاسبه اختلاف این دو فشار سوال حل می‌شود. دقت کنید طبق شکل چون پاهای شناگر در عمق بیشتری نسبت به سر او قرار دارند، انتظار داریم مقدار فشار در این نقطه بیشتر باشد که بیشتر هم به‌دست آمد:

$$triangle P = P_{feet} – P _{head}$$

$$Rightarrow triangle P = P_{feet} – P _{head}=18081-12054=6027 Pa$$

• نکته: یک راه ساده‌تر برای حل این سوال این بود که ابتدا اختلاف دو عمق را محاسبه کنیم. سپس این عدد را در فرمول فشار قرار دهیم. چون هر دو نقطه موردنظر ما در مایعی با چگالی یکسان قرار دارند:

$$triangle h =h_{feet} – h _{head}=1.8-1.2=0.6 m$$

$$Rightarrow triangle P = rho gtriangle h=1025times 9.8times 0.6=6027 Pa$$

تمرین ۱

تمرین ۲

اصل پاسکال

یکی از مهم‌ترین مباحث فشار در شاره ها، قانون پاسکال است که برای تمام شاره‌های ساکن صادق است. می‌دانیم مجموع تمام نیروهای وارد بر یک شاره ساکن یا شاره‌ای که جریان ندارد، صفر است. طبق اصل پاسکال، زمانی که تغییری در فشار یک شاره ایجاد شود، این تغییر بدون کاهش، به تمام نقاط آن شاره و حتی به دیواره‌های ظرفی که شاره در آن قرار گرفته است، منتقل می‌شود.

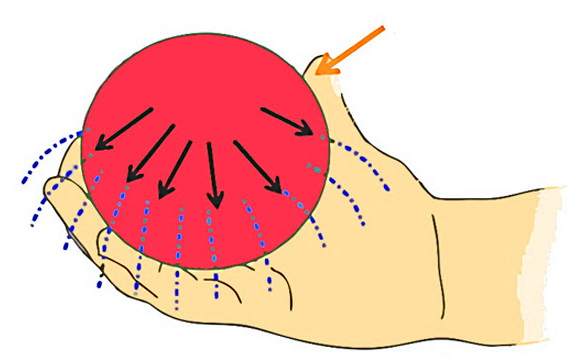
به عبارت دیگر فشار خارجی اعمال شده به یک شاره محدود شده در یک محفظه، به‌صورتی کاملا برابر در سراسر شاره و در تمام جهات منتقل می‌شود. شکل بالا این مفهوم را به‌خوبی نشان می‌دهد. کاربرد اصل پاسکال در موقعیت‌هایی است که می‌خواهیم اختلاف فشار را محاسبه کنیم، مثلا در طراحی شوکرها یا ماشین‌های سنگین بالابرنده از این اصل استفاده می‌شود.

• نکته: اصل پاسکال به این معنا نیست که فشار تمام نقاط یک شاره یکسان است. همان‌طور که بارها اشاره شد، فشار نقاط مختلف یک مایع با مقدار ارتفاع یا عمق مایع تغییر می‌کند.

فرمول‌هایی که در مسائل مربوط به اصل پاسکال استفاده می‌شوند، همان فرمول‌هایی است که تا اینجا معرفی کردیم. در ادامه با بررسی دو مثال مهم شامل سیستم «بالابر هیدرولیکی» (Hydraulic Lift) و «مانومتر» (Manometer)، چگونگی کاربرد این اصل در موقعیت‌های مختلف را بهتر متوجه خواهید شد.

بالابر هیدرولیکی

شاید مهم‌ترین کاربرد اصل پاسکال، انتقال فشار در شاره ها در یک سیستم بالابر هیدرولیکی باشد. شکل زیر را برای این بالابر در نظر بگیرید. دو پیستون A و B را داریم که توسط یک محفظه‌ پر شده از مایعی، از هم جدا شده‌اند. یکی از این پیستون‌ها دارای سطح مقطع یا مساحت کوچک‌تری (A₁) است که از آن برای اعمال نیروی F₁ روی مایع استفاده می‌شود. F₂ نیرویی است که در پیستون دیگر بر اثر اعمال نیروی F₁ روی سطح A₁ احساس می‌شود.

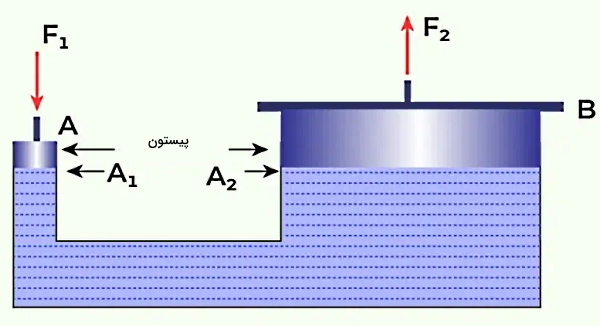
اگر از فرمول اصلی فشار برای محاسبه فشار روی پیستون A استفاده کنیم، داریم:

$$P=frac{F_1}{A_1}$$

این فشار طبق اصل پاسکال به تمام نقاط مایع، از جمله پیستون B که در تماس با مایع است، منتقل می‌شود. بنابراین به پیستون B با سطح مقطع A₂، فشاری به اندازه P وارد می‌شود. پس فشار روی پیستون A و فشار روی پیستون B طبق اصل پاسکال برابر با P است، اما چون این دو پیستون مساحت‌های مختلفی دارند، پس نیرویی که اعمال شده است (F₁) با نیرویی که در B حس می‌شود (F₂)، برابر نیست:

$$P=frac{F_2}{A_2}$$

به عبارت دیگر برای این سیستم داریم:

$$frac{F_1}{A_1}=frac{F_2}{A_2}$$

$$Rightarrow F_2=F_1frac{A_2}{A_1}$$

نتیجه بالا این مفهوم را دارد که با اعمال یک نیروی ثابت به پیستون A، اگر نسبت مساحت دو پیستون را زیاد کنیم، نیروی بالابرنده پیستون B افزایش خواهد یافت، بدون اینکه لازم باشد نیروی F₁ بیشتری وارد کنیم:

$$frac{A_2}{A_1} uparrow Rightarrow F_2 uparrow$$

مانومتر

برای اندازه‌گیری فشار در شاره ها از ابزارهای مختلفی استفاده می‌شود که یکی از آن‌ها مانومتر است. در شکل زیر، یک نمونه مانومتر با لوله باز نشان داده شده است. این وسیله از یک لوله U شکل تشکیل شده است که در آن مایعی با چگالی ρ قرار می‌گیرد. معمولا یک انتهای لوله در معرض فشار هوا است و انتهای دیگر، به سیستمی که قرار است فشار آن اندازه گرفته شود، متصل می‌شود.

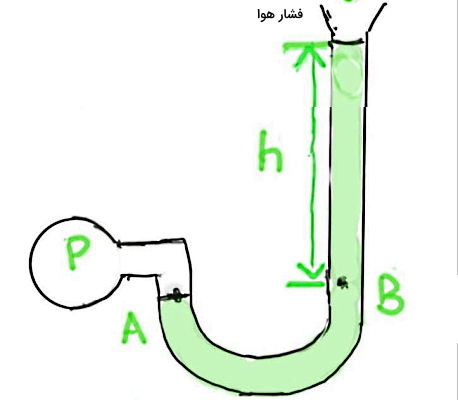
فرض کنید می‌خواهیم فشار سیستمی که به سر دیگر لوله متصل است (P) را با این مانومتر اندازه‌گیری کنیم، در حالی که سمت دیگر لوله در معرض هوا قرار دارد. در این قسمت با کمک گرفتن از اصل پاسکال، فشار این سیستم محاسبه می‌شود. فشار دو نقطه از یک مایع که هر دو در ارتفاع یکسانی هستند، برابر است. بنابراین اگر دو نقطه A و B را طبق شکل در نظر بگیریم، فشار در این دو نقطه باید برابر باشد:

$$P_{A}=P_{B}$$

فشار در نقطه A برابر با همان فشاری است که می‌خواهیم پیدا کنیم. فشار در نقطه B طبق فرمول فشار کل برای یک مایع برابر است با:

$$P_B=P_0+rho gh$$

با مساوی قرار دادن این دو فشار، داریم:

$$P=P_0+rho gh$$

پس فشار کل برای سیستم متصل به نقطه A به این صورت محاسبه می‌شود. اما عموما فشار کل را نمی‌خواهیم، پس باید بنویسیم:

$$P-P_0=rho gh$$

مثال و تمرین از اصل پاسکال

در این بخش پس از اینکه با کاربرد اصل پاسکال در سیستم‌های هیدرولیکی آشنا شدیم و دیدیم که فشار در شاره ها چگونه منتقل می‌شود، چند مثال را به کمک اصل پاسکال حل می‌کنیم.

مثال ۱

یک بالابر هیدرولیکی از دو پیستون با مساحت‌های A₂=1 m² و A₁=0.2 m² تشکیل شده است که توسط مایعی با هم ارتباط دارند. اگر نیرویی به اندازه ‎80 N به پیستون با مساحت کمتر وارد شود، مقدار نیروی بالابر چقدر است؟

پاسخ

طبق اصل پاسکال فشاری که به یک پیستون وارد می‌شود، توسط مایع داخل محفظه به تمام نقاط از جمله به پیستون دیگر منتقل می‌شود. پس اگر این فشار را P₁ در نظر بگیریم و فشار وارد شده به پیستون A₂ را P₂ در نظر بگیریم، خواهیم داشت:

$$P_1=P_2$$

با کمک گرفتن از فرمول اصلی فشار به‌صورت نیروی عمودی وارد بر واحد سطح، خواهیم داشت:

$$P=frac{F}{A}$$

$$Rightarrow frac{F_1}{A_1}= frac{F_2}{A_2}$$

حالا با قرار دادن مقادیر عددی، F₂ محاسبه می‌شود:

$$Rightarrow frac{80}{0.2}= frac{F_2}{1} Rightarrow F_2=frac{80}{0.2}=400 N$$

دقت کنید در سوال اشاره شده است که نیروی وارد شده یعنی F₁ به پیستونی با مساحت کمتر یعنی A₁ وارد می‌شود.

مثال ۲

یک سیستم هیدرولیکی دو پیستون دایره‌ای با شعاع‌های ‎30 cm و ‎60 cm دارد که توسط محفظه‌ای پر شده از یک مایع، به هم متصل شده‌اند. اگر یک جعبه ‎50 kg را روی پیستون با شعاع بزرگ‌تر قرار دهیم، نیروی وارد شده به پیستون دیگر چقدر است؟ (g=10 m/s²)

پاسخ

جعبه‌ای که روی پیستون قرار می‌گیرد، نیروی وزن خود را به پیستون وارد می‌کند. طبق اصل پاسکال، فشار حاصل از این نیرو توسط مایع یا شاره این سیستم، به تمام نقاط آن از جمله به پیستون دیگری که در تماس با این شاره است، منتقل می‌شود. بنابراین اگر پیستون با شعاع ‎60 cm را پیستون 1 بنامیم، داولین قدم این است که نیروی ورن وارد بر این پیستون و مساحت آن را حساب کنیم:

$$P_1=frac{F_1}{A_1}$$

$$F_1=W=mg=50times10=500 N$$

$$A_1=pi R_1^2=pi (0.6)^2$$

دقت کنید مقدار شعاع به سانتی‌متر داده شده است که باید به متر تبدیل شود. بنابراین P₁ به‌دست می‌آید:

$$Rightarrow P_1=frac{500}{pi (0.6)^2}$$

با محاسبه مساحت پیستون دیگر و نوشتن اصل پاسکال به‌صورت برابری دو فشار، خواهیم داشت:

$$A_2=pi R_2^2=pi (0.3)^2$$

$$P_2=frac{F_2}{A_2}$$

$$P_1=P_2Rightarrow frac{500}{pi (0.6)^2}= frac{F_1}{pi (0.3)^2}$$

$$Rightarrow F_1=frac{500timespi (0.3)^2}{pi (0.6)^2}$$

$$Rightarrow F_1=frac{500times 0.3times0.3}{0.6 times0.6}=frac{500}{4}=125 N$$

تمرین ۱

آزمایش توریچلی و بارومتر

در بخش‌های گذشته کاملا یاد گرفتیم که مفهوم و فرمول فشار در شاره ها چیست. در این بخش یکی از مهم‌ترین و ساده‌ترین ابزارهای اندازه‌گیری در این مبحث را معرفی می‌کنیم. «بارومتر جیوه‌ای» (Mercury Barometer) توسط فیزیکدان ایتالیایی به نام «اوانجلیستا توریچلی» (Evangelista Torricelli) در سال ۱۶۴۳ اختراع شد. بارومتر تک ستونی از جیوه است که فشار اتمسفر را اندازه می‌گیرد. این وسیله لوله‌‌ای است شیشه‌ای با یک انتهای بسته و با طول ‎،100 cm که در داخل ظرفی حاوی مایع جیوه قرار گرفته است.

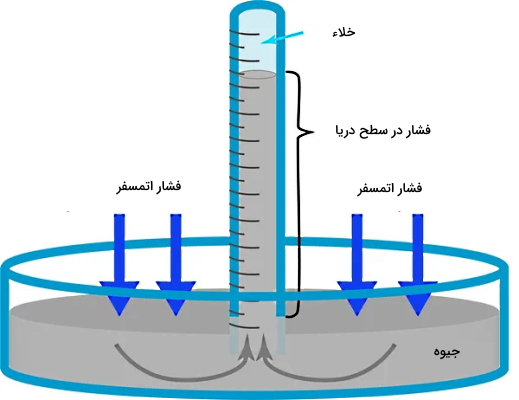
برای قرار دادن لوله داخل ظرف جیوه، باید ابتدا داخل آن را کمی جیوه بریزیم. سپس با قرار دادن انگشت روی دهانه باز آن، لوله را معکوس کنیم و در داخل ظرف حاوی جیوه قرار دهیم. با برداشتن انگشت از انتهای لوله، جیوه در لوله پایین می‌رود و همزمان در داخل ظرف بالا می‌رود. در نهایت، جیوه داخل لوله در ارتفاعی حدود ‎76 cm یا ‎760 mm بالاتر از سطح جیوه داخل ظرف، به حالت پایدار و تعادلی می‌رسد.

در این شرایط می‌گوییم فشار ستون جیوه با فشار اتمسفر یا فشار هوای اطراف برابر است.  برای اینکه بهتر متوجه شوید، سه نقطه A و ‌B و C را طبق شکل زیر در نظر بگیرید. چون این نقاط همه در یک ارتفاع قرار دارند، پس فشار در این سه نقطه برابر است:

$$P_{B}=P_{C}=P_{A}$$

از طرفی دو نقطه B و C در معرض فشار هوا یا فشار اتمسفر هستند، پس فشار این نقاط با فشار اتمسفر برابر است:

$$P_{B}=P_{C}=P_{atm}$$

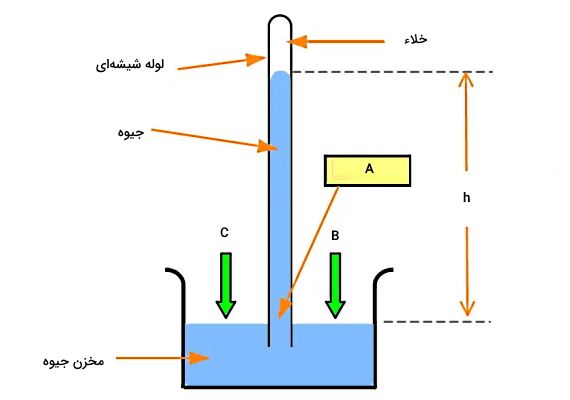
فشار در نقطه A معادل فشار ستون مایع جیوه است. پس با کاربرد فرمول فشار مایعات داریم:

$$P_A=rho gh$$

حالا با برابر قرار دادن مقادیر داریم:

$$P_{atm}=rho gh$$

یعنی فشار ستون جیوه در لوله بارومتر با فشار اتمسفر برابر است. حالا اگر بخواهیم فشار اتمسفر را به‌دست آوریم، ‌می‌توانیم مقادیر عددی را در رابطه بالا قرار دهیم تا فشار اتمسفر محاسبه شود. با علم به اینکه این برابری زمانی اتفاق می‌افتد که جیوه به ‌اندازه ‎76 cm در لوله بالا رود و اینکه چگالی جیوه برابر است با ‎13545.848 kg/m³، خواهیم داشت:

$$P_{atm}=13545.848times 9.8 times 0.76=100889.47 Pa approx100000 Pa=10^5 Pa$$

این مقدار همان فشار اتمسفری است که قبلا معرفی کرده بودیم. پس به کمک بارومتر توانستیم فشار اتمسفر را اندازه بگیریم.

فشار در لوله‌های U شکل

یادگیری مبحث فشار در شاره ها و تمام مفاهیمی که تا اینجا یاد گرفتیم، با حل مسائلی از لوله‌های U شکل که حاوی یک یا چند نوع شاره مختلف هستند، تکمیل می‌شود. برای آشنایی بهتر با مسائل این چنینی به روند بررسی مثال‌ زیر توجه کنید.

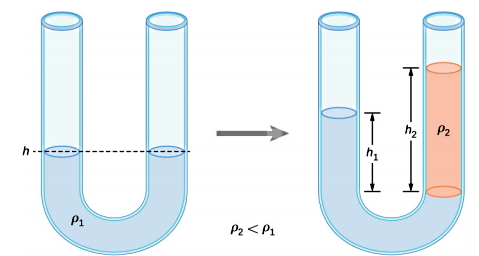
لوله U شکلی با دو دهانه باز طبق تصویر سمت چپ در شکل بالا در نظر بگیرید که از مایعی با چگالی ρ₁ تا ارتفاع h در هر دو طرف لوله پر شده است. حالا فرض کنید مایع دیگری با چگالی ρ₂ در یک سمت این لوله ریخته شود. برای اینکه مایع دوم روی سطح مایع اول قرار بگیرد باید ρ₂<ρ₁ باشد. مشاهده می‌کنید که ارتفاع مایع اول در دو طرف لوله U شکل فرق خواهد کرد، در سمت راست پایین ‌می‌رود و در سمت چپ بالا.

گفتیم برای یک شاره مشخص، مقدار فشار شاره در نقاطی با عمق یا ارتفاع یکسان همواره برابر است. پس فشار دو نقطه با یک ارتفاع در دو طرف لوله U شکل، تا زمانی که از مایع یکسان پر شده باشد، برابر است. دو نقطه‌ای که برای برابری فشار انتخاب می‌کنیم، به صورت شکل زیر هستند:

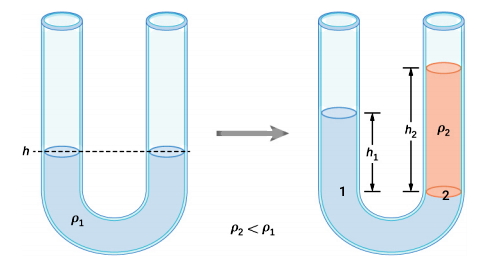
پس برای ارتفاع و فشار در نقاط 1 و 2 داریم:

• فاصله سطح مشترک با هوا در مایع دوم تا سطح مشترک‌ آن با مایع اول = h₂
• $$P_2=P_0+rho_2 gh_2$$
• فاصله سطح مشترک با هوا در مایع اول تا سطحی موازی با سطح پایین برای مایع دوم = h₁
• $$P_1=P_0+rho_1 gh_1$$

$$P_1=P_2$$

$$Rightarrow P_0+rho_1 gh_1=P_0+rho_2 gh_2$$

با حذف فشار اتمسفر یا P₀ از دو طرف و ساده شدن مقدار g، در نهایت رابطه زیر را خواهیم داشت:

$$Rightarrow rho_1 h_1=rho_2 h_2$$

• نکته: طبق رابطه بالا اگر روی مایع اول، مجددا از همان مایع بریزیم یعنی ρ₁=ρ₂، در این صورت ارتفاع مایع در دو طرف لوله کاملا برابر خواهد بود (h₁=h₂).

مثال و تمرین از فشار لوله‌های U شکل

در این بخش با حل چند مثال، کاربرد فرمول فشار در شاره ها و سایر مفاهیمی که بیان شد را در حل مسائل شامل لوله‌های U شکل یاد می‌گیریم.

مثال ۱

در یک لوله U شکل به‌صورت زیر سه مایع مختلف ریخته شده است. در سمت چپ مایعی با چگالی ρ به اندازه ‎20 cm طول لوله را اشغال کرده است و در سمت راست، مایع دیگری با چگالی 1.5ρ به اندازه ‎10 cm بالا رفته است. بین این دو، مایع سومی با چگالی 2ρ داریم که تا ارتفاع h در طرف راست لوله زیر مایع دیگر افزایش ارتفاع نسبت به سطح سمت چپ لوله داشته است. مقدار h را محاسبه کنید:

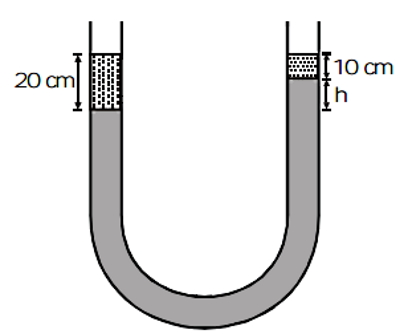
پاسخ

به کمک اصل پاسکال می‌دانیم که فشار تمام نقاطی که روی یک سطح افقی قرار می‌گیرند، با هم برابر است. پس دو نقطه در دو سمت لوله بالا در نظر می‌گیریم که کاملا در یک سطح قرار دارند، یکی در ابتدای ارتفاع ‎20 cm با نام A و دیگری در ابتدای ارتفاع h با نام B. اگر فشار هر کدام از این نقاط را بنویسیم، داریم:

$$P_A=P_0+rho gtimes0.2$$

دقت کنید در رابطه بالا مقادیر ارتفاع همه برحسب متر نوشته شده‌اند. همچنین در سمت لوله بالای نقطه B، دو مایع مختلف داریم که لازم است فشار هر دو با فشار هوا جمع شود. با مساوی قرار دادن این دو فشار خواهیم داشت:

$$P_A=P_B$$

$$Rightarrow P_0+rho gtimes0.2=P_0+1.5rho gtimes 0.1+2rho gh$$

P₀ها از دو طرف حذف می‌شوند. در نتیجه با ساده‌سازی مقدار h به‌دست می‌آید:

$$Rightarrow 0.2rho g=0.15rho g+2rho gh$$

$$Rightarrow 0.05rho g=2rho gh$$

$$Rightarrow 0.05=2h$$

$$Rightarrow h=0.025 m=2.5 cm$$

تمرین ۱

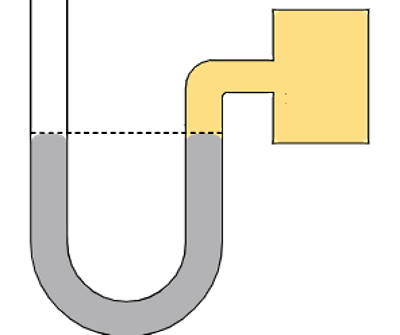
شکل زیر تصویری از یک مانومتر را نشان می‌دهد که یک سمت آن به منبع گازی متصل است و سر دیگر لوله در معرض فشار هوا قرار دارد. کدام گزینه به‌درستی ارتباط بین فشار گاز و فشار هوا را نشان می‌دهد؟

$$P_{atm} > P_{gas}$$

$$P_{atm} < P_{gas}$$

$$P_{atm}=P_{gas}$$

نمی‌توان مشخص کرد.

مشاهده جواب

گزینه سوم درست است. دو نقطه روی خط افقی رسم شده در شکل در نظر می‌گیریم. یکی در سمت راست لوله که فشار آن همان فشار منبع گاز است (P_gas). در سمت چپ لوله، اگر نقطه‌ای روی این خط انتخاب کنیم، فشار آن کاملا با فشار هوا برابر است.

طبق اصل پاسکال تمام نقاط روی خط افقی در شکل دارای فشار برابری هستند، چون همه این نقاط در ارتفاع مشابهی قرار دارند. پس $$P_{atm}=P_{gas}$$

تمرین ۲

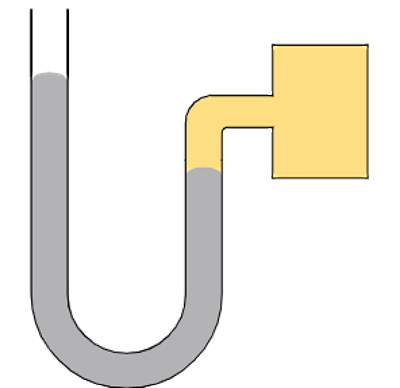
برای مانومتری با شکل زیر کدام گزینه صحیح است؟

$$P_{atm} > P_{gas}$$

$$P_{atm} < P_{gas}$$

$$P_{atm}=P_{gas}$$

نمی‌توان مشخص کرد.

مشاهده جواب

گزینه دوم درست است. تفاوت این تمرین با تمرین قبلی در این است که در اینجا سطح مایع در سمت چپ لوله بالاتر رفته است. بنابراین اگر مجددا دو نقطه دقیقا در مکان‌‌های تمرین قبل در نظر بگیریم، فشار برای نقطه سمت راست همان P_gas است، در حالی که در سمت چپ علاوه بر فشار هوا، فشار ستون مایع هم اضافه شده است. پس با مساوی قرار دادن فشار این دو نقطه خواهیم داشت:

$$P_{atm}+rho gh=P_{gas}$$

در نتیجه همواره فشار گاز داخل محفظه به اندازه فشار ستون مایع از فشار هوا بیشتر است.

اصل برنولی

مبحث فشار در شاره ها به یافته‌های دو دانشمند به نام‌های «بلز پاسکال» (Blaise Pascal) و «دانیل برنولی» (Daniel Bernoulli) بازمی‌گردد. در ادامه مطالعات این دانشمندان «معادله برنولی» (Bernoulli’s Equation) ارائه شد که تقریبا در هر موقعیتی می‌توان از آن برای تعیین فشار در هر نقطه از یک سیال استفاده کرد.

البته کاربرد این معادله با در نظر گرفتن یک سری فرضیات باید انجام شود. برای مثال، سیال باید اید‌ه‌آل و تراکم‌ناپذیر باشد. سیال ایده‌آل سیالی است که در آن هیچ گونه اصطکاکی وجود ندارد و ویسکوزیته یا چسبندگی آن، صفر است. معادله برنولی برای سیالی که در تمام نقاط خود دارای مقدار چگالی ثابتی است، به شکل زیر است:

$$frac{P}{gamma}+frac{v^2}{2g}+z=constant$$

• P فشار شاره با واحد پاسکال (Pa)
• v سرعت شاره در حال حرکت بر حسب m/s
• g شتاب جاذبه زمین بر حسب m/s²
• z با واحد متر (m) مقدار ارتفاعی است که مایع بالا می‌رود.

طرف دوم رابطه بالا برابر است با مقداری ثابت. برای γ یا «وزن مخصوص شاره» رابطه زیر را داریم:

$$gamma=rho g$$

• ρ چگالی سیال با واحد kg/m³
• P/γ «هد فشار» (Pressure Head)
• v²/2g «هد سرعت» (Velocity Head)

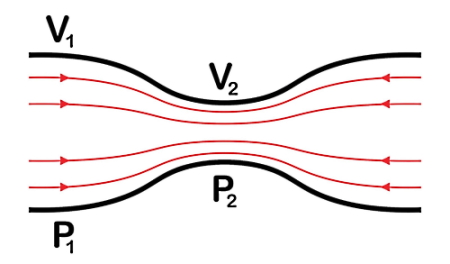
بنابراین اصل برنولی که از معادله برنولی استخراج می‌شود، به‌صورت زیر است:

در جریانی از شاره که به صورت افقی در حال حرکت است، نقاطی که سرعت بیشتری دارند، فشار کمتر و نقاطی که سرعت کمتری دارند، فشار بیشتری ایجاد می‌کنند.

ما در بخش‌های قبل فرمول فشار در مایعات ساکن را با استفاده از فرمول اصلی فشار به‌دست آوردیم. در این بخش می‌خواهیم با شروع از معادله برنولی به‌عنوان معادله اصلی حاکم بر فشار در شاره ها، فرمول فشار در مایعات را مجددا به‌دست آوریم. ابتدا معادله برنولی را می‌نویسیم:

$$frac{P}{gamma}+frac{v^2}{2g}+z=constant$$

سرعت سیال در رابطه بالا با توجه به موقعیتی که برای این مطلب فرض کردیم، صفر است. بنابراین جمله دوم صفر می‌شود و عبارت زیر باقی خواهد ماند:

$$frac{P}{gamma}+z=constant$$

اگر به‌جای γ عبارت معادل یعنی ρg را قرار دهیم و z را با h جایگزین کنیم، خواهیم داشت:

$$frac{P}{rho g}+h=constant$$

رابطه بالا معادل فرمول فشار در مایعات به‌دست آمد.

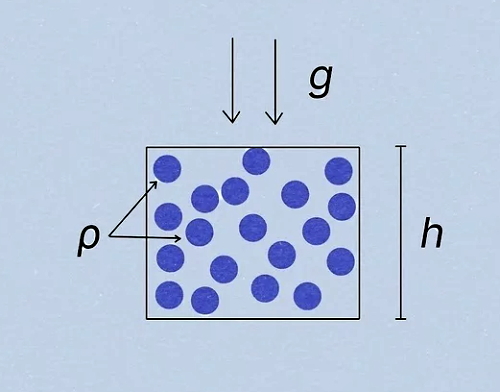
اگر دقت کنید تمام مفاهیمی که در این مطلب بیان شدند، برای هر دو گروه زیر صادق است:

1. شاره‌ای که در یک محیط باز قرار دارد، مثل آب اقیانوس، آب استخر در فضای آزاد یا هوای اطراف‌مان
2.  شاره‌ای در یک محیط بسته قرار دارد، مانند آب داخل لوله یا گاز داخل لوله‌های خط انتقال گاز

در واقع فشار شاره ساکن در یک محیط باز را معمولا با تقریب «فشار استاتیک» (Static Pressure) در نظر می‌گیرند، حتی با اینکه در شرایطی مثل اقیانوس، امواج و جریان‌های آب جزئی وجود دارد. علت صرف نظر کردن از این پویایی این است که این امواج عملا تاثیر چندانی در مقدار فشار ندارند. استاتیک شاره ها به مطالعه وضعیت شاره در چنین شرایطی می‌پردازد. اما اگر شاره در حال حرکت باشد، یعنی سرعت شاره مخالف صفر باشد، با علم دینامیک شاره ها مواجه هستیم، مثل وقتی که سیالی در حال حرکت در یک لوله است یا حتی سیالی که در حال متراکم شدن داخل یک محفظه بسته است.

یادگیری مکانیک سیالات با فرادرس

اگر تمایل دارید دانش خود را در مورد مباحث استاتیک و دینامیک سیالات و در سطح مقاطع دانشگاهی بیشتر کنید، در مجموعه فرادرس فیلم‌های آموزشی با این هدف به شرح زیر تهیه شده‌ است. شما می‌توانید با مشاهده این فیلم‌ها در قالب تصویر، یادگیری بهتری داشته باشید:

1. فیلم آموزش فیزیک پایه ۳ فرادرس
2. فیلم آموزش فیزیک ۳ حل تمرین فرادرس
3. فیلم آموزش مکانیک سیالات ۱ فرادرس
4. فیلم آموزش مکانیک سیالات ۱ مرور و حل تمرین فرادرس
5. فیلم آموزش مقدماتی مکانیک سیالات ۲ فرادرس
6. فیلم آموزش مکانیک سیالات مرور و حل تست کنکور ارشد فرادرس

فشار چیست؟

فشار کمیتی است که برای تمام حالت‌های مواد تعریف می‌شود و برابر است با نیروی عمودی وارد بر واحد سطح یک جسم. برای اینکه درک عمیق‌تری نسبت به مفهوم فشار در شاره ها به‌دست آوریم، بهتر است ابتدا با مفهوم فشار در حالت کلی آشنا شویم. این کمیت نرده‌ای در فیزیک با نماد P نشان داده می‌شود و با توجه به تعریفی که برای آن ارائه شد، دارای فرمول کلی به شکل زیر است:

$$P=frac{F}{A}$$

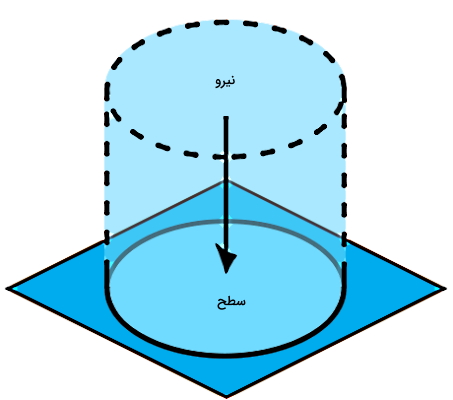
در این رابطه نیروی F بر حسب نیوتن (N) و مساحت سطح A بر حسب متر مربع (m²) است. پس واحد فشار یا P به‌صورت نیوتن بر متر مربع به‌دست خواهد آمد که آن را «پاسکال» (Pascal) می‌نامند. بنابراین واحد استاندارد فشار در سیستم بین‌المللی یکاها یا SI، پاسکال است که با Pa نشان داده می‌شود.

برای فهم بهتر فرمول فشار، فرض کنید طبق شکل زیر تلاش می‌کنید تا با وارد کردن نیروی زیادی به یک چکش، بتوانید پین بولینگی را وارد دیوار کنید. حالا همین آزمایش را به‌جای پین، برای یک میخ تکرار کنید. مشخص است که با وارد کردن همان مقدار نیرو یا حتی نیروی کمتری، میخ به‌راحتی به داخل دیوار نفوذ خواهد کرد. این آزمایش نشان می‌دهد گاهی فقط وارد کردن نیروی زیاد راه حل مسئله نیست. بلکه لازم است بدانیم این نیرو روی چه سطحی توزیع می‌شود.

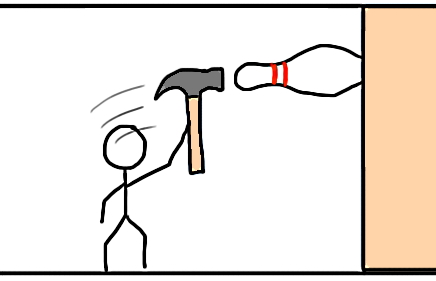
در حالت دوم، تمام نیروی بین چکش و دیوار در سطح خیلی کوچکی یعنی در نوک میخ جمع شده است. اما برای پین بولینگ، همان مقدار نیرو روی سطح بزرگ‌تری توزیع می‌شود، به همین دلیل نیرو نسبت به حالت دوم کمتر متمرکز است. به‌عبارت دیگر با وارد کردن نیروی برابر روی میخ، توزیع نیرو در یک سطح خیلی کوچک باعث می‌شود نیروی متمرکزتری به دیوار وارد شود. پس در واقع هر دو کمیت نیرو و سطح مقطعی که نیرو روی آن توزیع می‌شود، مهم هستند.

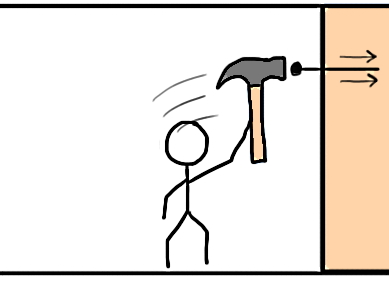
تمام توضیحات بالا در فرمول فشار خلاصه می‌شود. بنابراین با نگاه کردن به فرمول فشار متوجه خواهیم شد که برای افزایش فشار دو راه داریم:

• راه اول این است که نیرو را افزایش دهیم. با بیشتر شدن مقدار F در صورت کسر، P هم افزایش خواهد یافت.

$$F uparrow Rightarrow P uparrow$$

• راه دوم این است که مساحت سطحی که نیرو به آن وارد می‌شود را کم کنیم. در نتیجه با کمتر شدن مقدار A در مخرج کسر، P زیاد خواهد شد.

$$A downarrow Rightarrow P uparrow$$

در مثال چکش و پین بولینگ حتی با زیاد کردن نیرو، ایجاد فشار بیشتر برای ورود به دیوار سخت است. اما اگر سطحی که نیرو به آن وارد می‌شود را کم کنیم، مثلا به‌جای پین بولینگ از وسیله نوک تیزی مانند میخ با سطح خیلی کوچک استفاده کنیم، فشار به قدری زیاد می‌شود که میخ به‌راحتی می‌تواند به داخل دیوار نفوذ کند.

واحدهای فشار

یکی از مباحث مهم در محاسبه فشار در شاره ها، واحدهایی است که برای این نوع فشار استفاده می‌شود. در بخش قبل یاد گرفتیم که واحد SI فشار، پاسکال است. پیش از اینکه به معرفی سایر واحدهای فشار بپردازیم، پیشنهاد می‌کنیم اگر علاقه‌مند هستید تا با مشاهده نحوه حل تمرین‌ مبحث فشار را یاد بگیرید، از فیلم آموزشی فیزیک دهم – مرور و حل تمرین فرادرس که لینک آن در ادامه قرار داده شده است، استفاده کنید.

واقعیت این است که در مسائل فشار از واحدهای مختلفی ممکن است استفاده شود. برای مثال ممکن است فشار در قالب فشار استاندارد اتمسفری بیان شود. در این حالت واحد فشار، اتمسفر است که با atm نشان داده می‌شود. با دانستن واحد اتمسفر برای فشار، واحد دیگری به نام تور یا torr را می‌توانیم معرفی کنیم که برابر است با 1/760 اتمسفر.

واحدهای مانومتریکی مثل میلی‌متر جیوه یا mmHg نیز برای بیان فشار بکار می‌روند. فشار در این سیستم‌ها بر اساس محاسبه ارتفاع ستونی از یک مایع خاص مثل جیوه در یک «مانومتر» (Manometer) اندازه‌گیری می‌شود. همچنین یکی دیگر از واحدهای مرسوم برای فشار، واحد بار است. جدول زیر مهم‌ترین واحدهای فشار و ارتباط آن‌ها با مقدار یک پاسکال را نشان می‌دهد.

فشار پیمانه‌ای

مفهوم دیگری که احتمالا در مبحث فشار در شاره ها با آن برخورد خواهید داشت، اصطلاح «فشار پیمانه‌ای یا فشار گیج» (Gauge Pressure) است. فشار پیمانه‌ای همان فشار نسبی یا فشاری است که نسبت به فشار اتمسفر سنجیده می‌شود. معمولا فشار اندازه‌گیری شده توسط فشارسنج‌ها یا فشاری که در موقعیت‌های مختلف اندازه‌گیری می‌شود، همان فشار گیج است. برای مثال، وقتی که فشار لاستیک ماشین اندازه‌گیری می‌شود، عدد اعلام شده نسبت به فشار اتمسفر محاسبه شده است.

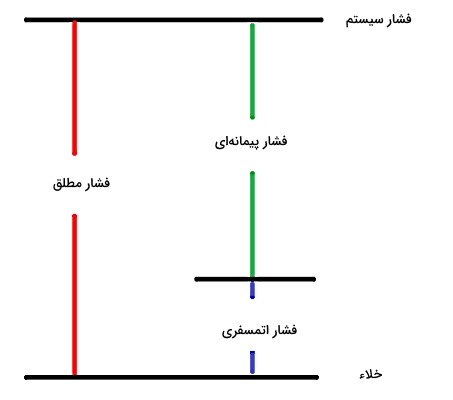
شکل بالا نموداری را نشان می‌دهد که در آن ارتباط بین فشار گیج با فشار مطلق و فشار اتمسفر مشخص است. همان‌طور که مشاهده می‌کنید، اندازه‌گیری فشار گیج از فشاری برابر با یک اتمسفر انجام می‌شود، به عبارت دیگر صفر فشار گیج برابر است با یک اتمسفر. رابطه بین سه فشار گیج (P_g)، فشار مطلق یا فشار سیستم (P_s) و فشار اتمسفر (P_atm) به شکل زیر است:

$$P_g=P_s-P_{atm}$$

مثال و تمرین از مفهوم فشار

در بخش قبل یاد گرفتیم فرمول کلی برای فشار چیست، چه واحدهایی دارد و چگونه می‌توانیم با کم یا زیاد کردن نیرو و مساحت، فشار را کم یا زیاد کنیم. در این قسمت برای اینکه با این فرمول بهتر آشنا شوید، به بررسی چند مثال و تمرین در این زمینه می‌پردازیم.

مثال ۱

فرض کنید جعبه مکعب شکلی با ضلع ‎1 m و جرم ‎ 10 kgروی یک میز قرار دارد. فشاری که این جعبه به میز وارد می‌کند را محاسبه کنید (شتاب جاذبه زمین برابر است با $$g=9.8 frac{m}{s^2}$$

پاسخ

برای محاسبه فشار جعبه به میز، فرمول فشار را بکار می‌بریم:

$$P=frac{F}{A}$$

نیرویی که باعث ایجاد فشار جعبه به میز می‌شود، نیروی وزن آن است. پس ابتدا باید نیروی وزن را حساب کنیم:

$$F=W=mg$$

$$Rightarrow F=W=10times9.8=98 N$$

در مرحله بعدی برای محاسبه فشار، لازم است مساحتی که نیرو به آن وارد می شود را پیدا کنیم. برای یک جعبه روی میز به شکل مکعبی با ضلع یک متر، نیروی وزن روی مربعی با اضلاع 1 در 1 توزیع خواهد شد. پس مساحت A برابر است با مساحت مربعی با ضلع ‎1 m:

$$A=1times1=1 m^2$$

حالا که مساحت و نیرو هر دو مشخص شدند، می‌توانیم فشار را به‌دست آوریم:

$$Rightarrow P=frac{F}{A}=frac{98}{1}=98 Pa$$

مثال ۲

فشار ناشی از یک صندلی با جرم ‎7.2 kg چند پاسکال است، اگر هر پایه آن دارای سطح مقطع گردی با شعاع ‎1.3 cm باشد و وزن صندلی به‌صورت مساوی روی چهار پایه آن تقسیم شده باشد:

پاسخ

برای محاسبه فشار ناشی از چهار پایه صندلی به زمین، از فرمول کلی فشار به شکل $$P=frac{F}{A}$$

$$F=W=mg$$

با در نظر گرفتن مقدار 10 برای شتاب جاذبه زمین و جای‌گذاری جرم صندلی خواهیم داشت:

$$Rightarrow F=W=7.2times10=72 N$$

این نیرو روی چهار پایه صندلی به مقدار برابری توزیع می‌شود. پس با محاسبه مساحت یک پایه (A₁) و ضرب آن در عدد 4، می‌توانیم مساحت کلی که نیرو به آن وارد شده است یعنی A را داشته باشیم. ابتدا مساحت یک پایه صندلی که طبق سوال دایره‌ای به شعاع ‎1.3 cm است را حساب می‌کنیم و قبل از آن بهتر است شعاع را برحسب متر بنویسیم.

$$1 m = 100 cm Rightarrow 1 cm = frac{1}{100} m = 10^{-2} m$$

$$Rightarrow 1.3 cm = 1.3 times 10^{-2} m$$

$$A_1=pi r^2$$

$$Rightarrow A_1 = pi times (1.3 times 10^{-2})^2=5.3times 10^{-4} m^2$$

$$P=frac{F}{A}=frac{F}{4A_1}$$

$$Rightarrow P=frac{72}{4times5.3times 10^{-4}}approx3.4times 10^{4}approx34000 Pa$$

تمرین

آزمون فشار در شاره ها

در انتهای این مطلب از مجله فرادرس، می‌توانید میزان تسلط خود بر مفاهیم بیان شده را با پاسخ‌دهی به سوالات زیر بیازمایید. در پایان با کلیک روی بخش «دریافت نتیجه آزمون» نمره نهایی شما قابل مشاهده است.

فشار اتمسفر یا فشاری که هوای اطراف به بدن ما وارد می‌کند، ‎101325 Pa است که مقدار خیلی بزرگی است. علت اینکه این فشار به بدن ما آسیب نمی‌زند، چیست؟

فشار داخل بدن نیز همین مقدار است.

نیروی وزن این فشار با نیرویی که از داخل به بدن وارد می‌شود، در تعادل است.

گزینه اول و دوم درست است.

مشاهده جواب

گزینه سوم صحیح است. علت اینکه فشار هوا را روی بدن خود حس نمی‌کنیم این است که فشار داخل بدن ان را خنثی می‌کند.

فشاری که مایعی در عمق ‎2.5 m ایجاد می‌کند، با ‎36750 Pa برابر است. چگالی این مایع کدام گزینه است؟ (شتاب g را ‎ 9.8 m/s²در نظر بگیرید)

$$2500 frac{kg}{m^3}$$

$$1000 frac{kg}{m^3}$$

$$1500 frac{kg}{m^3}$$

$$2000 frac{kg}{m^3}$$

مشاهده جواب

گزینه سوم درست است. می‌دانیم فرمول چگالی مایع به شکل زیر است:

$$P=rho gh$$

اگر بخواهیم چگالی را از این رابطه استخراج کنیم، خواهیم داشت:

$$Rightarrow rho=frac{P}{gh}$$

حالا با قرار دادن مقادیر عددی چگالی محاسبه می‌شود:

$$Rightarrow rho=frac{36750}{9.8times 2.5}=1500 frac{kg}{m^3}$$

کدام گزینه مقدار فشار مایع را تغییر می‌دهد؟

چگالی جسمی که در مایع غوطه‌ور است.

شکل ظرفی که مایع در آن قرار دارد.

مشاهده جواب

گزینه دوم درست است. طبق فرمولی که برای فشار در مایعات داشتیم، فشار مایع فقط و فقط به چگالی و عمق مایع و مقدار شتاب جاذبه وارد بر آن بستگی دارد. پس هر کمیت یا عاملی به جز این سه مورد، اثری روی فشار ندارد.

دقت کنید چگالی خود مایع مهم است و چگالی جسمی که در آن غوطه‌ور است، اهمیتی ندارد. در واقع در این فرمول فقط مشخصات مایع در نظر گرفته می‌شود. همچنین حجم و شکل ظرف مایع نیز از ویژگی‌هایی هستند که در فشار تاثیری ندارند.

بدنه یک قایق غرق شده حدودا ‎12 m زیر سطح آب است. اگر متوسط چگالی آب دریا ‎1025 kg/m³ و مساحت بدنه ‎15 m² باشد، نیروی وارد شده به بدنه قایق از سمت دریا چقدر است؟ (شتاب g را ‎ 9.8 m/s²در نظر بگیرید)

$$1808100 N$$

$$120540 Pa$$

هر دو گزینه اول و دوم درست هستند.

مشاهده جواب

گزینه اول صحیح است. برای محاسبه نیروی کل، باید ابتدا فشاری که آب دریا به بدنه قایق وارد می‌کند را محاسبه کنیم. سپس با داشتن فشار و مساحت بدنه، می‌توانیم از فرمول اصلی فشار برای محاسبه نیرو استفاده کنیم. پس اول می‌رویم سراغ محاسبه فشار آب دریا که یک مایع است و فرمول فشار آن به شکل زیر است:

$$P=rho gh$$

$$Rightarrow P=1025times9.8times 12=120540 Pa$$

حالا فرمول اصلی فشار در ابتدای این مطلب را بکار می‌بریم:

$$P=frac{F}{A}$$

$$Rightarrow F=PA$$

$$Rightarrow F=120540times 15=1808100 N$$

شناگری تا عمق ‎1.25 m زیر سطح آب دریا شنا می‌کند. اگر چگالی آب دریا ‎1025 kg/m³ باشد، فشار کلی که بدن شناگر حس می‌کند، چقدر است؟ (شتاب g را ‎ 9.8 m/s²در نظر بگیرید)

$$101000 Pa$$

$$12556 Pa$$

$$110000 Pa$$

$$113556 Pa$$

مشاهده جواب

گزینه چهار درست است. دقت کنید در این سوال مقدار فشار کل خواسته شده است. پس باید از فرمول فشار کل استفاده کنیم. فشار کل وارد به بدن شناگر مجموع فشار آب دریا و فشار هوای سطح دریا است:

$$P_t=P_0+rho gh$$

می‌دانیم مقدار فشار اتمسفر یا فشار در سطح دریا برابر با عدد ثابت $$1.01times10^5 Pa$$

$$P_w=rho gh$$

$$Rightarrow P_w=1025 times9.8times1.25= 12556 Pa$$

حالا با جمع این عدد با P₀، فشار کل به‌دست خواهد آمد:

$$Rightarrow P_t=P_0+rho gh=1.01times10^5 +12556=101000+12556=113556 Pa$$

علت اینکه طبق تصویر زیر، دیواره سدها را به‌صورت گوه‌ای شکل می‌سازند، چیست؟

تاثیر شکل محفظه روی فشار ایجاد شده

تحمل فشار بیشتری که در کف مخزن ایجاد می‌شود.

تحمل فشار بیشتری که در سطح بالای شاره ایجاد می‌شود.

مشاهده جواب

گزینه دوم صحیح است. با توجه به اینکه مقدار فشار مایع با عمق آن رابطه مستقیم دارد، پس در کف مخزن سد، فشار نسبت به فشار در سطح آب خیلی بیشتر است. برای اینکه تحمل این فشار برای دیواره‌های داخلی سد آسان‌تر شود، شکل سد را به صورت گوه می‌سازند.

 نیروی شناوری برابر است با

نیروی وزن جسم داخل شاره

نیروی وزن شاره‌ای که بر اثر حضور جسم جابجا شده است.

مجموع نیروی وزن جسم و نیروی وزن شاره‌ای که بر اثر حضور جسم جابجا شده است.

نیروی وارد بر ته جسم داخل شاره

مشاهده جواب

گزینه دوم درست است. نیروی شناوری برابر است با اختلاف نیروی وارد بر سر و ته جسم داخل شاره. پس گزینه آخر غلط است. همچنین نیروی شناوری معادل نیروی وزن شاره‌ای است که جابجا می‌شود نه وزن جسم.

در یک سیستم هیدرولیکی، دو پیستون دایره‌ای توسط یک شاره‌ با هم در ارتباط هستند. اگر نسبت شعاع این دو پیستون برابر با ‏1/2 باشد و روی پیستون بزرگ‌تر جعبه‌ای با جرم ‎100 kg قرار داده شده باشد، نیرویی که لازم است به پیستون دیگر اعمال شود … نیوتن است (g=10).

مشاهده جواب

گزینه آخر صحیح است. گفتیم در سیستم‌های هیدرولیکی اصل پاسکال برقرار است. بنابراین فشار حاصل از وزن این جعبه روی یک پیستون، توسط شاره به پیستون دیگر منتقل می‌شود. پس اگر فشار روی پیستون بزرگ‌تر که جعبه روی آن قرار دارد را P₁ بنامیم و فشار روی پیستون دیگر P₂ باشد، داریم:

$$P_1=P_2$$

که در آن برای هر فشار فرمول زیر برقرار است:

$$P_1=frac{F_1}{A_1}$$

$$P_2=frac{F_2}{A_2}$$

$$Rightarrow frac{F_1}{A_1}=frac{F_2}{A_2}$$

$$Rightarrow F_2=F_1frac{A_2}{A_1}$$

نیروی F₁ که باعث ایجاد فشار می‌شود، نیروی وزن جعبه است و باید محاسبه شود. همچنین مساحت سطح پیستون‌ها هم با استفاده از فرمول مساحت دایره حساب می‌شود:

$$F_1=W=mg$$

$$F_1=100times10=1000 N$$

$$A=pi R^2$$

$$Rightarrow frac{A_2}{A_1}= frac{pi R_2^2}{pi R_1^2}=(frac{R_2}{ R_1})^2$$

در اینجا باید دقت کنید جعبه روی پیستون با شعاع بزرگ‌تر قرار داده شده است . ما برای نیروی وارد بر این پیستون اندیس 1 را در نظر گرفتیم. پس اندیس شعاع پیستون بزرگ‌تر باید 1 باشد. بنابراین نسبت 1/2 در صورت سوال به‌صورت زیر است:

$$frac{R_2}{ R_1}=frac{1}{ 2}$$

$$Rightarrow frac{A_2}{A_1}=(frac{1}{ 2})^2=frac{1}{ 4}$$

حالا با قرار دادن مقادیر به‌دست آمده در فرمولی که برای F₂ داشتیم، مقدار این نیرو پیدا می‌شود:

$$Rightarrow F_2=1000 timesfrac{1}{ 4}=250 N$$

کدام گزینه برای اندازه‌گیری فشار هوا بکار می‌رود؟

مشاهده جواب

گزینه اول درست است. همان‌طور که گفتیم از بارومتر جیوه‌ای برای سنجش فشار اتمسفر یا هوا استفاده می‌شود.

فشار شاره معادل … است.

مشاهده جواب

گزینه اول درست است. طبق فرمول فشار کل برابر است با مجموع فشار شاره (فشار گیج) و فشار اتمسفر (فشار هوا) روی سطح آن. البته در صورتی که شاره سطح بازی داشته باشد.