استدلال ریاضی فرآیندی است که در آن با استفاده از ریاضیات و منطق، درست یا نادرست بودن یک گزاره را ثابت میکنیم. ریاضیات تنها مجموعهای از فرمولها، اعداد و محاسبات نیست، بلکه زبانی است برای درک، توصیف و پیشبینی هر آنچه که در دنیای اطراف ما اتفاق میافتد. برای اینکه بتوانیم از این زبان به شکل موثری استفاده کنیم، نیاز به ابزاری داریم که به ما اطمینان دهد نتایج ما درست و قابلاعتماد هستند. این ابزار استدلال ریاضی است. در این مطلب از مجله فرادرس توضیح میدهیم استدلال ریاضی چیست.
آنچه در این مطلب میآموزید:
-
با انواع روشهای استدلال در ریاضی آشنا میشوید.
-
میآموزید در استدلال استقرایی چگونه میتوان از جزء به کل رسید.
-
مراحل استدلال استنتاجی را خواهید شناخت.
-
یاد میگیرید تفاوت اثبات مستقیم و غیرمستقیم چیست.
-
کاربرد مثال نقض در اثبات نادرستی یک گزاره را خواهید شناخت.
-
با حل نمونه سوالهای مختلف کاربرد روشهای استدلال ریاضی را تمرین خواهید کرد.



در بخش اول به تعریف و بررسی انواع استدلال در ریاضی میپردازیم. سپس مراحل استدلال استقرایی و استدلال استنتاجی را کاملا توضیح میدهیم و در مورد هر کدام چند نمونه سوال حل میکنیم تا بهتر متوجه شوید روند حل مسائل به کمک این روشها چگونه است. همچنین با سایر روشهای اثبات درستی یا نادرستی یک گزاره کلی مانند برهان خلف، اثبات به روش مستقیم و استفاده از مثال نقض آشنا خواهید شد.
استدلال ریاضی چیست؟
استدلال در درس ریاضی به فرآیندی گفته میشود که در آن با استفاده از دانستههای قبلی مانند شواهد، مشاهدات یا حقایق پذیرفته شده سعی میکنیم به یک نتیجهگیری یا حکم جدید برسیم. بنابراین استدلال کردن به ما کمک میکند تا چراها و چگونگیها در ریاضیات را پیدا کنیم. همچنین در هندسه نیز از استدلال برای اثبات برابری زاویهها یا اضلاع، تشابه شکلها و حل مسائل پیچیده استفاده میشود.
فهرست زیر نشان میدهد مهمترین روشهای استدلال در ریاضی چیست و چه تفاوتهایی با هم دارند:
- استدلال استقرایی: پیدا کردن الگو از چند مثال و حدس زدن یک قانون (رسیدن از جزء به کل)
- استدلال استنتاجی: استفاده از تعریفها و قضیهها برای اثبات قطعی یک حکم (رسیدن از کل به جزء)
در واقع استقرا به ما میآموزد که چگونه از مشاهده چند مثال به یک الگوی مشترک کلی برسیم، در حالی که استنتاج به ما یاد میدهد که چگونه آن الگو را به شکل درستی اثبات کرده و از کل به جزء دست پیدا کنیم. فراموش نکنید که به کمک استدلال استقرایی حدس میزنیم، اما در استدلال استنتاجی اثبات میکنیم.
یادگیری استدلال ریاضی با فرادرس
مبحث استدلال در ریاضی در بخشهای مختلفی از کتابهای درسی ریاضیات و هندسه متوسطه مطرح شده است. فهرست زیر راهنمای جامعی است که نشان میدهد این مباحث دقیقا در کدام کتابهای درسی قرار دارند:
- استدلال و اثبات در هندسه ریاضی نهم: فصل سه کتاب ریاضی پایه نهم
- استدلال استقرایی و استنتاجی هندسه دهم: درس دوم از فصل یک کتاب هندسه یک
- استدلال و قضیه تالس ریاضی یازدهم: درس پنجم از فصل دو کتاب ریاضی یازدهم تجربی
- آشنایی با منطق و استدلال ریاضی یازدهم انسانی: درس یک تا چهار کتاب ریاضی و آمار یازدهم علوم انسانی
- استدلال در ریاضیات گسسته: درس اول از فصل یک کتاب ریاضیات گسسته
بنابراین اگر قصد دارید بهتر متوجه شوید که مفهوم استدلال ریاضی چیست، پیشنهاد میکنیم فیلمهای آموزشی زیر از مجموعه فرادرس را مشاهده کنید تا با حل نمونه سوالات متنوع کاملا به این مبحث مسلط شوید:
استدلال و اثبات در هندسه ریاضی نهم
در کتاب ریاضی نهم قدم به قدم یاد میگیریم که کلیات و اصول استدلال ریاضی چیست. برای شروع باید بدانیم اثبات هندسی چیست. اثبات یعنی بیان مرحله به مرحله اینکه چرا یک حکم همیشه درست است. هر اثبات هندسی از سه بخش تشکیل میشود:
- دادهها شامل اطلاعات مسئله
- دلایل شامل تعریفها، قضیهها، اشکال و قوانین هندسی
- نتیجه یا همان حکم یا رابطهای که باید ثابت شود.
در ادامه برخی از مهمترین تعریفها و قوانین هندسه را به شکلی خلاصه بیان کردهایم:
- مثلث متساویالساقین: اگر دو ضلع مثلثی برابر باشند، زاویههای مقابل آن دو ضلع نیز با هم برابراند. دقت کنید عکس این تعریف نیز درست است، یعنی اگر دو زاویه مثلثی برابر باشند، اضلاع مقابل آنها نیز با هم برابر هستند.
- همنهشتی مثلثها: دو مثلث همنهشتاند، اگر تمام زاویهها و اضلاع متناظر آنها با هم برابر باشند. البته برای اثبات همنهشتی لازم نیست تمام اضلاع و زوایا را بدانیم، بلکه تسلط بر سه قانون زیر کافی است. پس از اثبات همنهشتی، قسمتهای متناظر برابر خواهند شد:
- برابری هر سه ضلع
- برابری دو ضلع و زاویه بین آنها
- برابری دو زاویه و ضلع بین آنها
- تشابه مثلثها: دو مثلث مشابهاند، اگر سه ضلع آنها با هم برابر باشد یا نسبت دو ضلع و زاویه بین آنها برابر باشد یا نسبت سه ضلع متناظر آنها برابر باشد. در مثلثهای مشابه، نسبت اضلاع متناظر ثابت است و زاویههای متناظر نیز برابراند.
- میانخط در مثلث: اگر نقاط وسط دو ضلع مثلثی را به هم وصل کنیم، این خط با ضلع سوم موازی و طول آن نصف ضلع سوم است. این گزاره مستقیما از تشابه مثلثها نتیجهگیری میشود.
- خطوط موازی: اگر دو خط موازی توسط خط سومی به نام خط مورب قطع شوند، زاویههای متناظر برابر و زاویههای داخلی همجهت مکمل هم هستند.
بنابراین با تشخیص دادهها و مجهولات، رسم شکل دقیق، انتخاب قضیه مناسب و استفاده از تشابه، همنهشتی و خواص مثلثها میتوان یک فرآیند اثبات هندسی را کامل کرد.
نمونه سوال استدلال ریاضی نهم
در این بخش با حل چند نمونه سوال بهتر متوجه خواهید شد که روند استدلال ریاضی چیست و چگونه میتوان از آن در حل مسائل استفاده کرد.
مثال ۱
در چند مثلث مختلف، دو ضلع را برابر در نظر بگیرید و زاویههای متناظر آنها را محاسبه کنید. الگو چیست؟
پاسخ
در این سوال با مساوی در نظر گرفتن دو ضلع در چند مثلث مختلف، میتوانیم به حدس زیر برسیم:
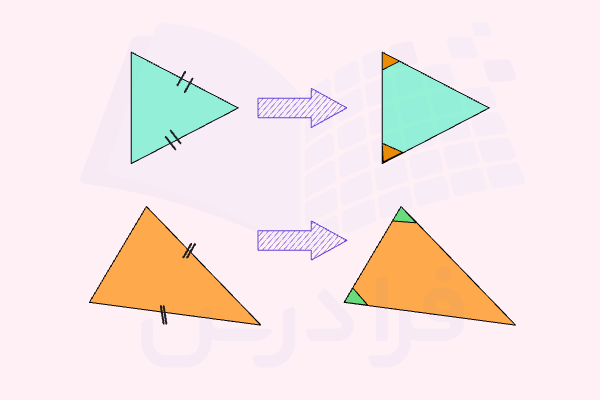
اگر دو ضلع مثلثی با هم برابر باشند، دو زاویه متناظر آنها نیز با هم برابراند. این مسئله همان قضیه مثلث متساویالساقین است که از همنهشتی دو مثلث فرضی به دست میآید.
مثال ۲
اگر در مثلثی و باشد، اندازه زاویه چقدر است؟
پاسخ
چون در این مثلث است، پس با یک مثلث متساویالساقین روبرو هستیم که در آن زاویههای متناظر با این دو ضلع برابر اندازه یکسان دارند. بنابراین زاویه نیز برابر با و است.
استدلال استقرایی چیست؟
در این بخش توضیح میدهیم اولین و سادهترین روش استدلال در ریاضی چیست. استدلال استقرایی یا Inductive Reasoning نوعی روش استدلالی است که در آن با در نظر گرفتن مشاهدات و کشف یک سری الگوهای مشترک تلاش میکنیم تا یک قانون کلی را حدس بزنیم. در این نوع استدلال بر اساس مشاهدات خود به الگوی مشترکی میرسیم که طبق آن میتوان یک حدس یا گمان را مطرح کرد.
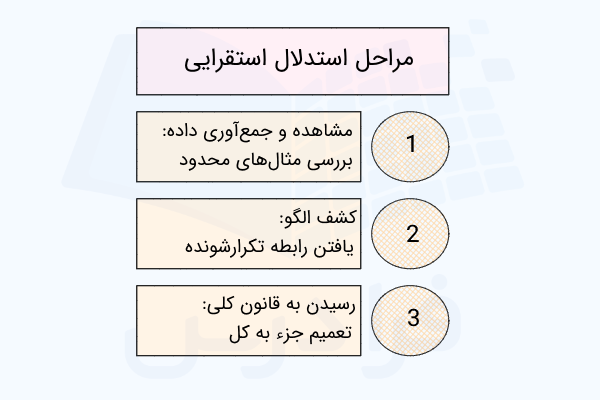
استدلال استقرایی نه تنها در هندسه، بلکه در سایر شاخههای ریاضیات مانند دنبالهها یا اثبات روابط عددی کاربرد دارد. سه مرحله اصلی در استدلال استقرایی عبارتاند از:
- مشاهده: بر اساس دیدن یا انجام چند مثال یا فرآیند خاص
- پیدا کردن الگوی مشترک: یافتن یک ویژگی مشترک یا یک روند تکراری در مثالها
- استخراج حدس، گمان یا تعمیم کلی: مطرح کردن یک حکم کلی که فکر میکنیم برای تمام موارد مشابه درست باشد.
با اینکه استدلال استقرایی به ما کمک میکند تا الگوها را کشف کنیم و به فرضیههای جدید برسیم، اما یک محدودیت بزرگ دارد. نتیجه استدلال استقرایی هرگز از نظر ریاضیاتی قطعیت ندارد، به این معنا که هر چقدر مثالهای بیشتری پیدا کنیم که حدس ما را تایید کنند، باز هم ممکن است مثال دیگری وجود داشته باشد که آن حدس یا فرض را نقض کند. به مثالی که حدس ناشی از استدلال استقرایی را باطل کند، «مثال نقض» گفته میشود. برای نمونه، مجموعه زیر را به عنوان زیرمجموعهای از اعداد اول در نظر بگیرید:
طبق استدلال استقرایی میتوانیم حدس بزنیم که تمام اعداد اول فرداند. چون در مشاهده اول عدد فرد است و به همین شکل در مشاهدات بعدی اعداد و و … نیز فرد هستند. اما مثال نقض برای حدس بالا این است که عدد به عنوان یک عدد اول، فرد نیست. در نتیجه عدد مثال نقض فرض فرد بودن اعداد اول است و حدس ما باطل است. به همین دلیل استدلال استقرایی را میتوانیم به عنوان اولین قدم در فرآیند استدلال ریاضی در نظر بگیریم. اما در مراحل بعدی برای قطعیت بخشیدن به حدس خود و اثبات آن به نوع قویتری از استدلال نیاز داریم که در بخشهای بعد با آن آشنا خواهید شد.
مشاهده در استدلال استقرایی
اولین مرحله در فرآیند استدلال استقرایی این است که مثالها، نمونهها یا موارد خاص و محدود را در مورد یک مسئله بررسی کرده و یک سری داده اولیه جمعآوری کنیم. لازم است مشاهده دقیق و بدون پیشداوری انجام شود.
کشف الگو در استدلال استقرایی
در بخش قبل توضیح دادیم مشاهده در استدلال ریاضی چیست و چگونه انجام میشود. پس از مشاهده، لازم است به دنبال رابطه یا الگوی تکرارشوندهای باشیم که بین دادههای ما وجود دارد. اغلب کشف الگو نیازمند بررسی چندین مثال دیگر است تا اطمینان حاصل کنیم که جواب دادن الگوی ما تصادفی نبوده است. روشهایی مانند رسم شکل یا شمارش میتوانند در کشف چنین الگویی به ما کمک کنند.
حدس یا استنتاج در استدلال استقرایی
در نهایت در آخرین مرحله از استدلال استقرایی با بررسی و تعمیم موارد خاص میتوانیم به یک حکم یا قانون کلی برسیم. علت اینکه گفتیم نتیجه استدلال استقرایی قطعیت کامل ندارد این است که حدس به دست آمده نیاز به اثبات ریاضیاتی دارد. همچنین نتیجه حاصل از این نوع استدلال در ریاضی موارد استثنا و فرضیات در نظر گرفته شده را به ما نمیدهد.
حل مثال از استدلال استقرایی
در این بخش با بررسی چند نمونه سوال بهتر متوجه خواهید شد که روش استقرا در فرآیند استدلال در ریاضی چیست و چگونه میتوان از آن استفاده کرد.
مثال ۱
مجموع زاویههای داخلی یک چند ضلعی را به روش استدلال استقرایی پیدا کنید:
پاسخ
گفتیم استدلال استقرایی روشی است که در آن با مشاهده الگوهای خاص در مورد چند نمونه مثال، به یک قانون کلی در مورد تمام مثالهای ممکن میرسیم. در این سوال ابتدا نشان میدهیم چگونه میتوان یک چند ضلعی با ضلع را به مثلث تقسیم کرد. سپس با استفاده از استدلال استقرایی فرمول مجموع زاویههای داخلی یک چند ضلعی را پیدا خواهیم کرد.
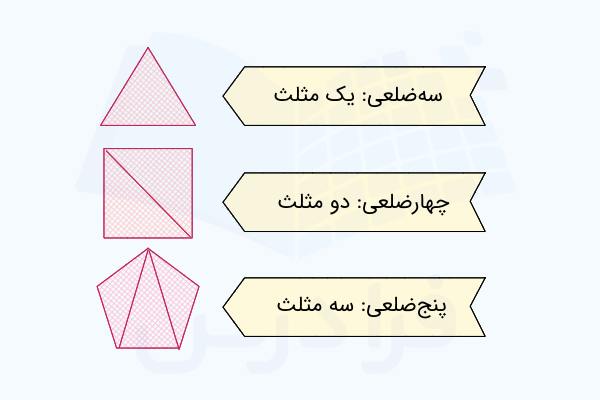
برای شروع، جدولی به شکل زیر تنظیم میکنیم که رابطه بین تعداد اضلاع یا را با تعداد مثلثهای تشکیل شده نشان میدهد. دقت کنید برای تقسیم یک چندضلعی به تعدادی مثلث کافی است فقط از یک راس دلخواه خطوطی را به تمام راسهای غیرمجاور آن راس رسم کنیم:
| نام چند ضلعی | تعداد اضلاع یا | تعداد مثلثها |
| سه ضلعی (مثلث) | ||
| چهار ضلعی | ||
| پنج ضلعی | ||
| شش ضلعی |
به این ترتیب برای مثلث هیچ خطی نخواهیم داشت و همان یک مثلث (خودش) را در جدول یادداشت میکنیم. برای چهار ضلعی، یک خط مورب و در نتیجه دو مثلث داریم. برای پنج ضلعی دو خط مورب از یک راس داریم و حاصل سه مثلث خواهد شد. همانطور که ملاحظه میکنید، این جدول بر اساس چهار مثال اولیه یعنی و و و تنظیم شده است و به ما کمک میکند تا الگوی موردنظر را پیدا کنیم. فراموش نکنید که حداقل تعداد اضلاع برای تشکیل یک چند ضلعی است.
در همین مرحله با توجه به اعداد ستون دوم و سوم میتوانیم الگویی به شکل زیر را توسط استدلال استقرایی استخراج کنیم:
اگر تعداد اضلاع یک چند ضلعی برابر با باشد، تعداد مثلثهای داخل آن برابر است با .
از طرفی میدانیم مجموع زاویههای داخلی یک مثلث همیشه برابر است با . بنابراین مجموع زوایای داخلی هر چند ضلعی نیز برابر میشود با مجموع زاویههای داخلی مثلثهای تشکیل دهنده آن. به این ترتیب جدول زیر نشان میدهد رابطه بین تعداد اضلاع یک چند ضلعی و مجموع زوایای داخلی آن به چه صورت است:
| نام چند ضلعی | مجموع زاویههای داخلی آن |
| سه ضلعی (مثلث) | |
| چهار ضلعی | |
| پنج ضلعی | |
| شش ضلعی |
با در نظر گرفتن دومین ستون از جدول بالا میتوانیم به روش استدلال استقرایی به فرمول زیر برای مجموع زاویههای داخلی یک ضلعی دست پیدا کنیم:
دقت کنید فرمول به دست آمده برای هر چند ضلعی سادهای چه منتظم یا نامنتظم صادق است، با این شرط که اضلاع آن متقاطع نباشند. با اینکه این جدول فقط چهار مثال را پوشش داده است، اما میتوان آن را برای چند ضلعیهایی با تعداد اضلاع بیشتر نیز گسترش داد. برای مثال، در مورد یک هفت ضلعی طبق فرمول بالا مجموع زاویههای داخلی برابر است با
مثال ۲
به روش استدلال استقرایی ثابت کنید برای هر عدد طبیعی داریم:
پاسخ
برای اینکه ببینیم در این مسئله روش استفاده از استدلال ریاضی چیست، ابتدا از اولین قدم یعنی مشاهده و محاسبه چند مثال اولیه شروع میکنیم:
در مرحله بعد باید با بررسی و دقت در روابط بالا سعی کنیم یک الگوی مشترک بین پاسخها به دست آوریم که قابلتعمیم به یک نتیجه کلی نیز باشد. اگر اعداد به دست آمده در روابط بالا را به شکل زیر بازنویسی کنیم، خواهیم داشت:
به این ترتیب الگوی تکرار شونده به شکل بالا است که با تعمیم آن به حالت کلی در مورد هر عدد طبیعی خواهیم داشت:
استدلال استنتاجی چیست؟
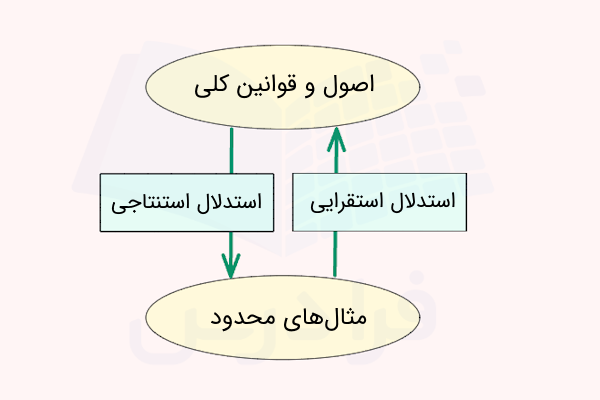
در بخش قبل آموختیم که فرآیند استدلال استقرایی به عنوان نوعی استدلال ریاضی چیست و گفتیم که در این روش ابتدا مشاهده میکنیم، سپس الگوی مشترکی را پیدا میکنیم و در نهایت به یک قانون کلی میرسیم. با توجه به اینکه استدلال استقرایی نوعی کشف است و نه اثبات ریاضیاتی، پس نتیجه آن میتواند درست یا نادرست باشد تا زمانی که توسط روشهای منطقی مانند استدلال استنتاجی یا اصل استقرا اثبات شود.

استدلال استنتاجی روشی است برای اثبات قطعی گزارهها با استفاده از قوانین، تعریفها و قضیههای شناخته شده در علم ریاضیات و هندسه. در این نوع استدلال بر خلاف استدلال استقرایی مسیر تفکر از کل به جزء است، یعنی ابتدا یک اصل یا قانون کلی را میپذیریم، سپس با بکارگیری منطق و قوانین مختلف به یک نتیجهگیری خاص و دقیق میرسیم.
استنتاج پایه تمام اثباتهای ریاضیاتی است، به این معنا که هر برهان هندسی، اثبات جبری یا هر نتیجه منطقی در ریاضیات نوعی استدلال استنتاجی به شمار میرود. برای مثال، اگر دو گزاره زیر را بدانیم:
- تمام زاویههای قائمه درجهاند.
- زاویه قائمه است.
نتیجه میگیریم که زاویه نیز یک زاویه درجه است. در اینجا از دو گزاره کلی (تعریف زاویه قائمه و قانون زاویهها) نتیجهای خاص گرفته شد که بر پایه قوانین پذیرفته شده و بدون هیچ حدسی یا گمانی انجام شده است. بنابراین فرآیند نتیجهگیری ما بر پایه استدلال استنتاجی بوده است.
در هندسه نیز اغلب اثباتها استنتاجی هستند. برای نمونه، اگر در مثلثی دو زاویه برابر باشند، به روش استدلال استنتاجی و بر اساس تعاریف مربوط به همنهشتی مثلثها و قضیههای ثابت شده میتوانیم به این نتیجه برسیم که ضلعهای مقابل این دو زاویه نیز با هم برابراند. در این فرآیند هیچ مشاهده یا حدسی نداریم، بلکه هر گام منطقی از گام قبلی ناشی میشود.
ساختار استدلال استنتاجی عموما شامل سه مرحله است:
- مقدمات: شامل فرضها یا قوانین شناخته شده است.
- روند منطقی: به معنای استفاده از قواعد استنتاجی است.
- نتیجهگیری: رسیدن به گزاره خاصی که از مقدمات به دست آمده است.
برای مثال در مورد برهانهای هندسی، مقدمات شامل دادههای مسئله یا قضایای قبلا اثبات شده هستند و با استفاده از منطق ریاضی (مانند همنهشتی، قضیه تالس، قضیه کسینوسها و …) نتیجه خاص حاصل میشود.
نکته: فرآیند استدلال استنتاجی مکمل یا اثبات فرآیند استدلال استقرایی است.
استدلال استنتاجی محدودیتهای زیادی ندارد، اما ذکر چند نکته در مورد این نوع استدلال مهم است:
- وابستگی به مفروضات اولیه: اگر مقدمات مسئله اشتباه باشند، نتیجه استنتاج نیز نادرست خواهد بود. برای مثال، اگر بگوییم «تمام اعداد فرد اول هستند»، نتیجه استنتاج بر پایه این مقدمه اشتباه نیز غلط خواهد بود.
- عدمکشف روابط جدید بدون مقدمات: در استدلال استنتاجی نمیتوانیم بدون داشتن قوانین یا اطلاعات قبلی یک رابطه جدید را کشف کنیم. به همین علت برای کشف الگوهای جدید معمولا از استدلال استقرایی استفاده میشود و سپس به کمک استنتاج میتوان آنها را اثبات کرد.
- نیاز به دقت منطقی: هر خطای منطقی در روند استدلال استنتاجی نتیجه را بیاعتبار میکند. به همین دلیل در ریاضیات و هندسه هر برهان استنتاجی با دقت زیادی نوشته میشود.
در همین راستا چنانچه علاقهمند هستید با قضیه استقرا و نحوه اثبات آن از طریق حل مثالهای کاربردی آشنا شوید، پیشنهاد میکنیم فیلم آموزش رایگان اثبات قضیه استقرا + مثالهای کاربردی فرادرس را مشاهده کنید که لینک آن نیز برای دسترسی راحتتر شما در ادامه قرار داده شده است:
فرض های اولیه در استدلال استنتاجی
در این بخش توضیح میدهیم مفروضات و قوانین اولیه استدلال ریاضی چیست. فرضهای اولیه یا مقدمات میتوانند شامل قواعد کلی، تعریفها یا قضایای اثبات شدهای باشند که موردقبولاند و نتیجه استنتاج ما در یک مسئله همواره بر اساس این مقدمات شکل میگیرد. فرض کنید میخواهیم نشان دهیم زاویههای مقابل اضلاع برابر در یک مثلث متساویالساقین با هم برابراند. در این بررسی مفروضات ما عبارتاند از:
- فرض اول: تعریف مثلث متساویالساقین است (مثلثی که دو ضلع آن برابرند).
- فرض دوم: یک قضیه هندسی است با این عنوان که در هر مثلث، زاویههای مقابل به اضلاع مساوی با هم برابرند.
روند منطقی در استدلال استنتاجی
روند منطقی مرحلهای است که در آن از مقدمات استفاده میکنیم و با قواعد و قوانین ریاضیات یا هندسه به نتیجه نزدیک میشویم. این مرحله شامل تحلیل و استنتاج مرحله به مرحله است. برای نمونه در مورد مثال بخش قبل با این فرض که در مثلث متساویالساقین دو ضلع برابر داریم، پس طبق قضیه هندسی گفته شده زاویههای مقابل این دو ضلع برابر نیز با هم مساوی هستند.
نتیجه گیری در استدلال استنتاجی
در نهایت پس از بررسی مقدمات و اعمال روند منطقی، نتیجهگیری به دست میآید. اگر مقدمات و روند منطقی صحیح باشند، نتیجه حاصل از استدلال استنتاجی بر خلاف نتیجه حاصل از استدلال استقرایی کاملا قطعی و معتبر است. در مورد مثال بخش قبل، این نتیجه که «زاویههای مقابل دو ضلع برابر در مثلث متساویالساقین برابراند»، برای تمام مثلثهای متساویالساقین و نه فقط در مورد موارد مشاهده شده همواره درست و معتبر است.
حل مثال از استدلال استنتاجی
تا این قسمت آموختیم که استنتاج در استدلال ریاضی چیست و چگونه به ما کمک میکند تا مسائل مختلف ریاضیات و هندسه را اثبات کنیم. در این روش از قواعد، تعاریف و قضایای پذیرفته شده برای رسیدن به یک نتیجهگیری استفاده میکنیم و مسیر از کل به جزء است. به بیان دیگر، اگر مفروضات و مقدمات درست باشند و استدلال ما کاملا منطقی باشد، نتیجه همیشه درست است. برای مثال، با در نظر گرفتن دو فرض زیر به این نتیجه میرسیم که علی فانی است:
- همه انسانها فانی هستند.
- علی یک انسان است.
در ادامه چند نمونه سوال در همین راستا حل میکنیم تا بهتر متوجه شوید فرآیند استنتاج در استدلال ریاضی چیست.
مثال ۱
فرض کنید در مثلث دو ضلع و برابراند، یعنی یک مثلث متساویالساقین داریم با قاعده . اگر از راس یک خط عمودی بر ضلع رسم کنیم که آن را در نقطه قطع کند (یعنی )، به کمک استدلال استنتاجی درستی دو عبارت زیر را ثابت کنید:
پاسخ
با کمک گرفتن از استدلال استنتاجی، ابتدا دو مثلث و را در نظر میگیریم. طبق صورت سوال سه فرض در مورد این دو مثلث داریم که عبارتاند از:
- ضلع بین این دو مثلث مشترک است.
- از نتیجه میگیریم که
بنابراین دو مثلث و هر دو قائمالزاویه هستند. همچنین در این دو مثلث وترها برابراند، چون گفتیم و ارتفاع نیز بین این دو مشترک است. حالا زمان آن رسیده که از قوانین هندسی استفاده کنیم که از قبل میدانیم.
در مورد دو مثلث قائمالزاویه، اگر وتر و یک ساق در دو مثلث با هم برابر باشند، آن دو مثلث همنهشتاند. بنابراین در اینجا دو مثلث و همنهشت هستند. در سومین قدم، از همنهشتی این دو مثلث به این نتیجه میرسیم که سایر قسمتهای متناظر نیز برابراند:
- برابری زاویههای متناظر:
- برابری ضلعهای متناظر:
این عبارتها همان گزارههایی هستند که در سوال خواسته شده است.
مثال ۲
در مثلث نقاط و به ترتیب نقاط وسط اضلاع و هستند. با استفاده از استدلال استنتاجی نشان دهید که و .
پاسخ
ابتدا مثلث را رسم میکنیم. سپس نقاط و را روی اضلاع و طوری قرار میدهیم که هر کدام دقیقا در وسط ضلع باشند:
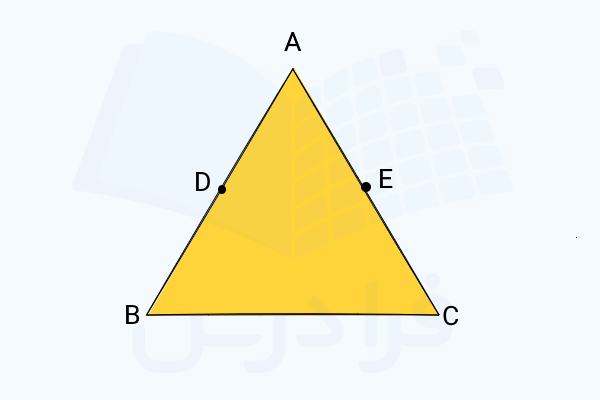
طبق این فرض که هر کدام از این نقاط در وسط یک ضلع قرار دارد، میتوانیم بنویسیم:
حالا طبق قضیه تالس میتوانیم بگوییم اگر نقاط و روی این دو ضلع به گونهای باشند که تساوی برقرار باشد، آنگاه موازی خواهد بود. در این سوال دو نسبت اشاره شده هر دو برابر هستند با . در نتیجه بخش اول سوال با استفاده از قضیه تالس ثابت شد:
در مرحله بعد برای استنتاج بخش دوم سوال لازم است از قوانین حاکم بر تشابه مثلثها بهره ببریم. ثابت کردیم که است. مثلث کوچک و مثلث بزرگ مثلثهای مشابه هم هستند، چرا که اگر اندازههای دو ضلع از مثلثی با اندازههای دو ضلع از مثلث دیگر متناسب باشد و زاویه بین آنها نیز برابر باشد، دو مثلث متشابهاند. پس طبق قوانین تشابه، سایر زاویههای متناظر در این دو مثلث نیز با هم برابر خواهند شد. همچنین تمام نسبتهای بین اضلاع در این دو مثلث نیز با هم برابر هستند، یعنی داریم:
استدلال ریاضی گسسته دوازدهم
در آخرین بخش این مطلب از مجله فرادرس قصد داریم توضیح دهیم در کتاب ریاضیات گسسته دوازدهم روشهای استدلال ریاضی چیست و شامل چه موضوعاتی میشود. در اولین درس از این کتاب به توضیح مفاهیمی مانند گزاره، گزاره باز، ارزش گزاره، نقیض و ترکیب گزارهها و … پرداخته میشود که در ادامه به شکلی مختصر هر کدام را معرفی کردهایم:
- گزاره: نوعی جمله خبری است که میتوان آن را به طور دقیق درست یا نادرست تشخیص داد. برای مثال، عبارت «عدد هفت یک عدد اول است» یک گزاره درست و عبارت «مثلثی با چهار ضلع وجود دارد» نوعی گزاره نادرست است. دقت کنید جملات پرسشی، امری یا مبهم گزاره محسوب نمیشوند.
- گزاره باز: جملهای که درستی آن به مقدار یک متغیر بستگی دارد، برای نمونه عبارت «» یک گزاره باز است.
- ارزش گزاره: همان تعریف دو ارزش درست (True) و نادرست (False) است، در واقع هر گزاره باید یک ارزش مشخص داشته باشد.
- نقیض گزاره: جملهای است که ارزش آن، عکس ارزش گزاره اصلی است.
- ترکیب گزارهها: ترکیب گزارهها را میتوان به صورت یکی از سه مورد زیر در نظر گرفت:
- عطف گزارهها: عطف دو گزاره زمانی درست است که هر دو گزاره درست باشند.
- فصل گزارهها: فصل دو گزاره زمانی اشتباه است که هر دو گزاره اشتباه باشند.
- گزاره شرطی: عبارت یک گزاره شرطی است و فقط زمانی نادرست است که درست و نادرست باشد. این گزاره در بقیه حالتها درست است.
به علاوه سه روش مهم و ساده استدلال ریاضی که از آنها برای نشان دادن درستی یا نادرستی گزارهها استفاده میشود، عبارتاند از:
- اثبات مستقیم
- مثال نقض
- اثبات غیرمستقیم (برهان خلف)
| اثبات مستقیم | از فرض شروع میکنیم و گام به گام به گزاره اصلی نزدیک میشویم. |
| مثال نقض | برای گزارههایی که ادعای درستی همیشگی دارند، یک مثال نقض پیدا میکنیم. |
| برهان خلف | فرض میکنیم گزارهای اشتباه است، یک تناقض پیدا میکنیم تا درستی آن ثابت شود. |
اولین روشی که در این بخش از ریاضیات گسسته با آن آشنا میشوید، روش «اثبات مستقیم» است. در این نوع اثبات از فرضها یا مقدمات شروع میکنیم و با استفاده از قواعد منطقی، تعاریف و قضیههای شناخته شده قدم به قدم به نتیجه میرسیم، یعنی با پیروی کردن از ، از شروع میکنیم و به میرسیم. پس ایده اصلی در اثبات مستقیم این است که از فرضها حرکت کنیم و به نتیجه برسیم.
همچنین اگر بخواهیم ثابت کنیم یک گزاره کلی نادرست است، لازم نیست تمام حالتها را بررسی کنیم. بلکه تنها کافی است یک مثال پیدا کنیم که آن گزاره را نقض کند. به این شیوه اثبات، «مثال نقض» گفته میشود. برای مثال، فرض کنید گزارهای داریم به این صورت که «مجموع دو عدد اول همیشه اول است». برای اثبات نادرستی آن، کافی است یک مورد مثال نقض پیدا کنیم:
:مثال نقض
یک عدد اول نیست، پس ادعای بالا درست نیست. اما در روش «اثبات غیرمستقیم یا برهان خلف» برای ثابت کردن درستی یک گزاره، ابتدا فرض میکنیم آن گزاره درست نیست، یعنی نقیض گزاره موردنظر را در نظر میگیریم. سپس با استفاده از این فرض و قوانین منطقی، به یک تناقض میرسیم که این تناقض میتواند تناقض با یک حقیقت بدیهی، تناقض با یک قانون ریاضیاتی یا تناقض با فرضهای مسئله باشد. زمانی که تناقض به وجود آمد، نتیجه میگیریم که گزاره نقیض ما غلط بوده است. پس خود گزاره درست است.
در مطلب زیر از مجله فرادرس مفهوم و کاربرد برهان خلف را توضیح دادهایم.
نمونه سوال استدلال ریاضی گسسته دوازدهم
در این بخش با حل چند نمونه مثال بهتر متوجه خواهید شد که چگونه با روشهایی مانند اثبات مستقیم یا مثال نقض میتوانیم برخی گزارهها را اثبات کنیم و سایر روشهای استدلال ریاضی چیست.
مثال ۱
به روش اثبات مستقیم نشان دهید که اگر عددی زوج باشد، نیز زوج است.
پاسخ
در روش اثبات مستقیم با در نظر گرفتن فرض داده شده در صورت سوال خواهیم داشت:
چون زوج است
بنابراین برای خواهیم داشت:
عبارت بالا نشان میدهد که بر بخشپذیر است، پس زوج است.
مثال ۲
با استفاده از برهان خلف ثابت کنید در یک مثلث حاصل جمع دو ضلع همیشه از ضلع سوم بزرگتر است.
پاسخ
اگر اضلاع یک مثلث را به شکل فرض کنیم، هدف اثبات این است که . در روش برهان خلف فرض میکنیم که این رابطه برقرار نیست، یعنی با در نظر گرفتن نقیض آن داریم:
در این صورت با چیدن دو ضلع و در کنار هم، طول آنها از کمتر یا مساوی است. اما این سه نقطه نمیتوانند یک مثلث تشکیل دهند، زیرا شرط تشکیل مثلث نقض شده است. پس به تناقض رسیدیم، چون فرض کرده بودیم شکل ما یک مثلث است. چون فرض نادرست شد، پس نقیض آن یعنی درست است.
مثال ۳
به روش برهان خلف ثابت کنید اگر یک عدد صحیح و زوج باشد، آنگاه نیز زوج است.
پاسخ
برای اثبات به روش برهان خلف، ابتدا فرضی مخالف با آنچه داریم را در نظر میگیریم، یعنی اگر زوج باشد، آنگاه فرد است. بنابراین اگر فرد باشد، میتوان آن را به شکل زیر نوشت:
حالا را محاسبه میکنیم:
حاصل محاسبه بالا برابر شد با دو برابر یک عدد صحیح دیگر به اضافه یک. پس فرد است. اما طبق فرض سوال زوج است. اینجا به تناقض میرسیم. به این ترتیب فرض خلاف ما اشتباه و گزاره همواره درست است.
مثال ۴
اگر برای هر عدد حقیقی داشته باشیم ، آیا گزاره همواره درست است؟
پاسخ
برای اثبات درستی یا نادرستی عبارت داده شده میتوانیم دنبال مثال نقض باشیم. اگر مثال نقضی پیدا شد، گزاره همیشه صحیح نیست. برای مثال، با در نظر گرفتن خواهیم داشت:
پس برای عبارت برقرار است، در حالی که نیست. بنابراین یک مثال نقض برای این سوال است.
source
