الگوریتم مرتب سازی حبابی برای مرتب کردن عناصر همسان به کار برده می‌شود. فرض کنیم که لیستی از اعداد وجود دارد که مقادیر آن به صورت تصادفی تولید شده‌اند. با کمک این الگوریتم می‌توانیم تمام مقادیر داخل لیست را به ترتیب از کوچک به بزرگ یا برعکس بچینیم. به این نوع الگوریتم‌ها الگوریتم‌های مرتب سازی گفته می‌شود. در این تکنیک از ابتدای لیست شروع کرده و عناصر مجاور هم را مقایسه می‌کنیم. اگر ترتیب قرارگیری این عناصر برعکس جهت درست، صعودی یا نزولی، بود، آن‌ها را با همدیگر جابه‌جا می‌کنیم. به احتمال زیاد مرتب سازی حبابی، کار‌آمدترین الگوریتم مرتب سازی برای مجموعه داده‌های بزرگ نیست، اما به راحتی می‌توان آن را فهمید. در ضمن فرایند پیاده‌سازی مرتب سازی حبابی در پایتون ساده‌‌ است. در نتیجه برای کمک به یادگیری مهارت‌های برنامه نویسی توسط افراد مبتدی، ابزار بسیار با ارزشی است.

در این مطلب از مجله فرادرس با روش پیاده‌سازی مرتب سازی حبابی در پایتون آشنا می‌شوید. به این منظور لازم است که هم الگوریتم مرتب سازی حبابی را بشناسید و هم با اصول کدنویسی با زبان پایتون آشنایی داشته باشید. بعد از معرفی الگوریتم، روش کار آن را هم توضیح می‌دهیم. سپس تکنیک‌های مختلف بهینه‌سازی مرتب‌ سازی حبابی و کاربردهای این الگوریتم را هم معرفی می‌کنیم.

مرتب سازی حبابی در پایتون چیست؟

مرتب سازی حبابی به الگوریتمی گفته می‌شود که با مقایسه دوبه‌دوی مقادیر و جابه‌جا کردن آن‌ها در صورت نیاز، کل داده‌های موجود در مجموعه همگن را مرتب می‌کند. این الگوریتم ساده بوده و با کمک زبان پایتون به راحتی می‌توان آن را پیاده‌سازی کرد. برای نوشتن کدهای این روش، باید با الگوریتم مرتب سازی آشنا باشید و قواعد کلی برنامه‌نویسی با پایتون را نیز بدانید. در این بخش، ابتدا مرتب سازی حبابی را به صورت خلاصه توضیح می‌دهیم و سپس روش پیاده‌سازی آن را در پایتون بررسی می‌کنیم.

الگوریتم مرتب سازی حبابی

مرتب سازی حبابی، الگوریتمی است که بر اساس مقایسه عناصر مجاور هم کار می‌کند. هدف این الگوریتم آن است که مقادیر موجود در سری داده شده به صورت صعودی یا نزولی مرتب شوند. در فهرست پایین،‌ شبه کد مرتب سازی حبابی را نوشته‌ایم.

1. از ابتدای سری، یعنی عناصر با اندیس ۰ و ۱، شروع کرده و دو عنصر اول را با همدیگر مقایسه می‌کنیم.
2. اگر ترتیب این دو عنصر، درست نبود جای آن‌ها را با همدیگر عوض می‌کنیم. ترتیب صعودی یا نزولی در لحظه تعریف مسئله مشخص می‌شود.
3. سپس به اندازه یک عنصر به سمت راست، انتهای سری، حرکت می‌کنیم.
4. عناصر مجاور، با اندیس ۱ و ۲، را با همدیگر مقاسه می‌کنیم. در صورتی که مقادیر آن‌ها در جایگاه درست قرار نگرفته‌ بودند، آن‌ها را با هم جابه‌جا می‌کنیم. در غیر این صورت به شکل دست‌نخورده باقی می‌مانند.
5. همین روش را تا انتهای سری ادامه می‌دهیم.
6. در این مرحله، به ابتدای لیست برمی‌گردیم و دوباره از مرحله اول شروع می‌کنیم. در الگوریتم ساده مرتب سازی حبابی، عملیات پیمایش به تعداد عناصر موجود در لیست انجام می‌شود. فرض کنید لیستی با ۱۰ عنصر داریم. در این صورت باید آن را ۱۰ بار پیمایش کنیم.

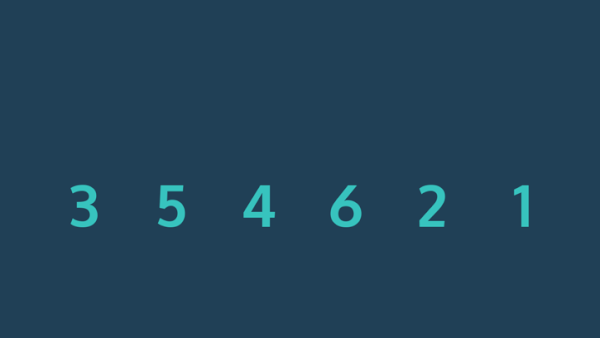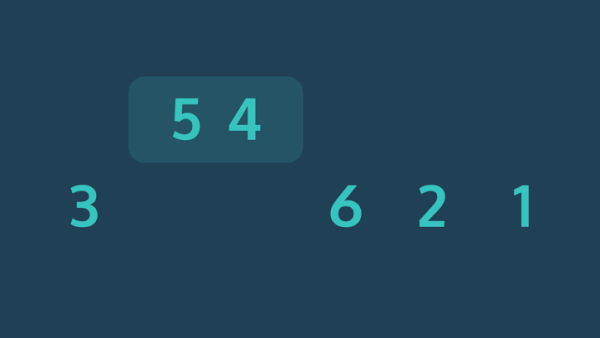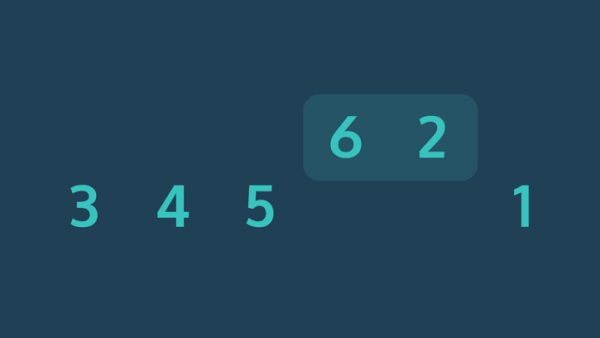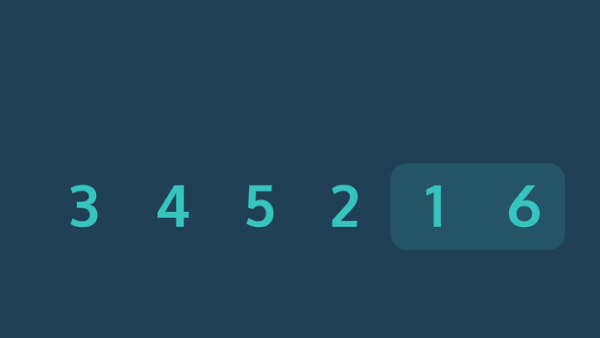
این حرکت خانه به خانه عناصر بزرگ از ابتدای سری به سمت انتهای آن، شبیه به حرکت حباب‌ها از پایین تا بالا در مایعات است. برای همین به این الگوریتم، مرتب سازی حبابی گفته می‌شود.

پیاده سازی مرتب سازی حبابی در پایتون

برای پیاده‌سازی الگوریتم مرتب سازی حبابی در پایتون باید تمام مراحل گفته شده در قسمت قبل را گام‌به‌گام شبیه‌سازی کنیم. ابتدا کدی را برای مقایسه عناصر مجاور هم و جابه‌جایی آن‌ها می‌نویسیم. البته فقط به شرطی مقادیر را جابه‌جا می‌کنیم که در جایگاه مناسب قرار نگرفته باشند. سپس این کد را بر روی تمام جفت‌های سری از ابتدا تا انتها اجرا می‌کنیم. این کار تا جایی تکرار می‌شود که تمام داده‌های موجود در سری (برای مثال در اینجا از لیست استفاده کرده‌ایم) مرتب شوند.

در کادر پایین، نسخه ساده‌ای از الگوریتم مرتب سازی حبابی در پایتون را پیاده‌سازی کرده‌ایم.

بعد از اجرای کد بالا، خروجی زیر توسط مفسر پایتون تولید شده و در کنسول، نمایش داده می‌‌شود.

[11, 12, 22, 25, 34, 64, 90]

در فهرست پایین تمام مراحل اجرای کد بالا را نوشته‌ایم. توجه کنید که در این کد می‌خواهیم عناصر لیست را به شکل صعودی مرتب کنیم.

1. def bubble_sort(arr): در این خط، تابع bubble_sort() را تعریف کرده‌ایم. این تابع پارامتری به نام arr  دریافت می‌کند.
2. n = len(arr): پارامتر arr  از نوع لیست‌های پایتون است. در این خط، طول لیست را محاسبه کرده و در متغیر n ذخیره می‌کنیم.
3. for i in range(n): برای حل این مسئله از دو حلقه for به صورت تو در تو استفاده می‌کنیم. در این خط، حلقه بیرونی به اندازه n  تعریف شده است. زیرا الگوریتم مرتب سازی حبابی باید n  بار بر روی لیست پیمایش بکند.
4. for j in range(0, n-i-1): از این حلقه یعنی حلقه درونی، برای مقایسه خانه‌های مجاور استفاده می‌کنیم.
5. if arr[j] > arr[j+1]: با کمک این عبارت شرطی، دو خانه مجاور هم را مقایسه می‌کنیم. این حلقه به همین ترتیب از اول تا آخر لیست را پیمایش می‌کند.
6. arr[j], arr[j+1] = arr[j+1], arr[j]: اگر خانه اول از خانه دوم بزرگ‌تر بود باید مقادیر آن‌ها را با همدیگر جابه‌جا بکنیم.
7. return arr: این دستور، لیست مرتب شده را برمی‌گرداند.
8. my_list: در خط ۱۳ لیست دلخواهی تعریف کرده‌ایم.
9. sorted_list = bubble_sort(my_list): در خط ۱۵ تابع خود را بر روی لیست نمونه اجرا کرده و نتیجه را ذخیره می‌کنیم.
10. print(sorted_list): با کمک این دستور، لیست مرتب شده را چاپ می‌کنیم.

پیچیدگی زمانی مرتب سازی حبابی در پایتون

پیچیدگی زمانی مرتب سازی حبابی در پایتون برابر با $$O(n^2)$$ است. n  در این فرمول تعداد عناصر لیست را نشان می‌دهد. $$O(n^2)$$ یعنی آن که با افزایش تعداد عناصر لیست، کارایی الگوریتم به شکل چشم‌گیری کاهش پیدا می‌کند. البته الگوریتم مرتب سازی در مقابل مجموعه داده‌های کوچک و لیست‌های نسبتا مرتب، عملکرد خوبی از خود نشان می‌دهد.

یادگیری پایتون با پیاده سازی پروژه واقعی

روش‌های مختلفی برای یادگیری برنامه نویسی وجود دارد. بهترین روش آن است که دانشجو علاوه بر یاد گرفتن نکات برنامه نویسی، تجربه نوشتن کدهای صحیح و غلط را نیز بدست بیاورد. پایتون جزو پرطرفدارترین زبان‌های برنامه نویسی در دنیاست. برای همین افراد زیادی برای یادگیری آن اقدام می‌کنند. این زبان در حوزه‌های متنوعی مانند توسعه نرم‌افزار، هوش مصنوعی، امنیت سایبری و غیره کاربرد دارد. کاربرد گسترده پایتون در صنعت باعث شده است، فرصت‌های شغلی زیادی هم برای برنامه نویسان پایتون، وجود داشته باشد.

فرادرس جزو منابع معتبر و حرفه‌ای برای یادگیری این زبان برنامه نویسی است. در این وب‌سایت آموزشی، فیلم‌های متنوعی درباره پایتون ارائه شده‌اند. بیشتر فیلم‌های آموزشی فرادرس با رویکرد پروژه‌محور طراحی می‌شود تا فرایند یادگیری همراه با کسب تجربه باشد. در نتیجه، به غیر از تقویت مهارت‌های برنامه نویسی، دانشجویان یاد می‌گیرند که چگونه فناوری‌های مختلف را با هم ترکیب کنند.

در پایین، چند مورد از فیلم‌‌های آموزش پروژه‌محور پایتون را معرفی کرده‌ایم.

در صورت تمایل با کلیک بر روی تصویر بالا به صفحه اصلی این مجموعه آموزشی، هدایت شده و از فیلم‌های پروژه‌محور بیشتری دیدن کنید. در بخش بعد روش کار الگوریتم مرتب سازی حبابی را با کمک فلوچارت، بررسی کرده‌ایم.

روش کار الگوریتم مرتب سازی حبابی چیست؟

در قسمت قبل با الگوریتم مرتب سازی حبابی و روش پیاده‌سازی آن در پایتون آشنا شدید. اما حالا می‌خواهیم ببینیم این کدها چگونه کار می‌کنند. در این روش، ابتدا هر دو عنصر کنار هم را مقایسه می‌کنیم. اگر ترتیبشان اشتباه باشد، آن‌ها را با هم جابه‌جا می‌کنیم. این عملیات از ابتدا تا انتهای لیست انجام می‌شود.این پیمایش چند بار تکرار می‌شود، تا زمانی که تمام عناصر لیست به درستی مرتب شوند.

ChatGPT said:

در زیر، عملکرد الگوریتم مرتب سازی حبابی را به صورت تصویری نشان داده‌ایم. فرض کنیم که آرایه ورودی شامل عناصر {7,4,1,6} است. در مرحله اول، بزرگترین عنصر در اولین جایگاه این مجموعه قرار دارد.

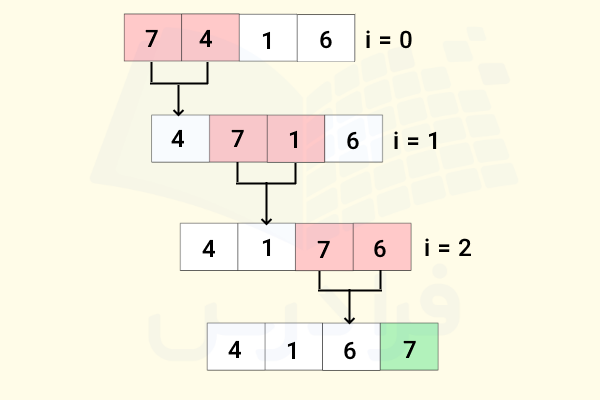
با یک دور پیمایش کامل مجموعه، عدد 7  به انتهای آن منتقل می‌‌شود. در دور بعد، دومین عنصر بزرگ در جایگاه درست خودش قرار گرفته است. بنابرین پیمایش مجموعه به شکل زیر می‌شود.

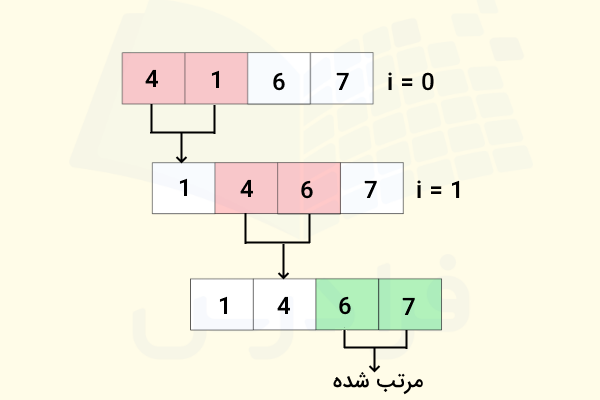
در دور سوم هم، عناصر سوم و چهارم در جایگاه درست خودشان قرار گرفته‌اند. این تغییر در پیمایش قبلی مجموعه اتفاق افتاد.

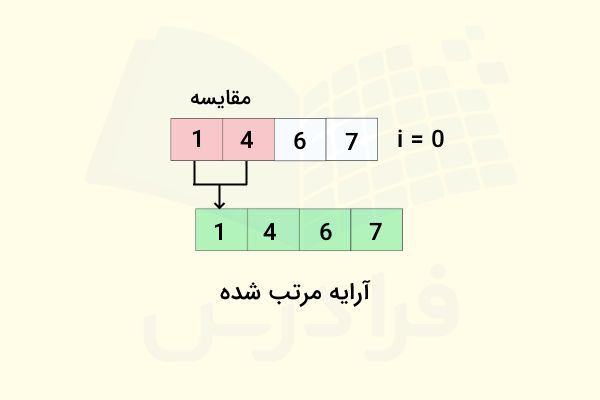
اکنون تمام عناصر با ترتبی صعودی و درست در جایگاه خودشان قرار دارند. بنابراین پیمایش مجموعه به پایان رسیده و عملیات مرتب سازی با موفقیت انجام شد.

بهینه سازی مرتب سازی حبابی در پایتون

مرتب سازی حبابی را نمی‌توان به عنوان کارآمدترین الگوریتم مرتب سازی در نظر گرفت. اما با اجرای چند تکنیک بهینه‌سازی می‌توانیم کارایی این الگوریتم را بهتر کنیم. در این قسمت از مطلب، سه روش بهینه‌سازی الگوریتم مرتب سازی حبابی را معرفی کرده‌ایم.

• «مرتب سازی حبابی پرچمدار» (Flagged Bubble Sort)
• «مرتب سازی حبابی بازگشتی» (Recursive Bubble Sort)
• «مرتب سازی کوکتلی» (Cocktail Shaker Sort)

برای بهینه‌سازی الگوریتم‌ها هم باید با تکنیک‌های برنامه نویسی به خوبی آشنا باشید هم الگوریتم‌ها را بشناسید. در صورت تمایل به کسب این مهارت، پیشنهاد می‌کنیم که فیلم آموزش نکات برنامه نویسی پایتون و حل مسائل الگوریتمی را در فرادرس مشاهده کنید. با هدف کمک به مخاطبان مجله، لینک دسترسی به این فیلم را در پایین نیز قرار داده‌ایم.

مرتب سازی حبابی پرچمدار

در این تکنیک مرتب سازی حبابی برای بررسی انجام شدن یا نشدن جابه‌جایی در هربار پیماش‌ لیست از پرچم، استفاده می‌کنیم. اگر در طول پیمایش لیست، هیچ جا‌به‌جایی اتفاق نیافتد، نتیجه می‌گیریم که لیست مرتب شده است. بنابراین، الگوریتم می‌تواند سریع‌تر کار خود را متوقف کند.

در کادر زیر، الگوریتم مرتب سازی حبابی پرچمدار را با زبان پایتون پیاده‌سازی کرده‌ایم.

در فهرست پایین، روش اجرای کدهای بالا را توضیح داده‌ایم.

1. def bubbleSort(arr): با این کد، تابع bubbleSort() را تعریف می‌کنیم. این تابع، پارامتری به نام arr  دریافت می‌کند.
2. n = len(arr): پارامتر arr  از نوع لیست است. در این خط، طول لیست را محاسبه کرده و در متغیر n  ذخیره می‌کنیم.
3. for i in range(n): حلقه بیرونی را به اندازه n  تعریف می‌کنیم تا در بدترین حالت، لیست به تعداد عناصر داخل آن پیمایش بشود.
4. swapped = False: متغیر swapped  همان پرچمی است که وظیفه نظارت بر انجام جابه‌جایی عناصر را در هر پیمایش بر‌عهده دارد. بخاطر وجود این پرچم، اسم این الگوریتم را «مرتب سازی حبابی پرچمدار» گذاشته‌اند.
5. for j in range(0, n-i-1): در این خط، حلقه درونی را تعریف می‌کنیم. این حلقه وظیفه دارد تا خانه‌های مجاور را بررسی کرده و در صورت نیاز مقادیر آن‌ها را با هم جابه‌جا بکند.
6. if arr[j] > arr[j+1]: این شرط بررسی می‌کند که آیا خانه اول بزرگ‌تر از خانه دوم است یا نه.
7. arr[j], arr[j+1] = arr[j+1], arr[j]: اگر شرط برقرار بود، با این کد، مقادیر دو خانه را جابه‌جا می‌کنیم تا بزرگ‌ترها به سمت انتهای لیست بروند.
8. swapped = True: هر وقت جابه‌جایی انجام شد، باید مقدار swapped  را True  بکنیم.
9. if (swapped == False): بعد از هربار پیمایش کامل لیست، این شرط بررسی می‌کند که آیا جابه‌جایی انجام شده است یا نه. اگر هیچ جابه‌جایی انجام نشده بود، یعنی لیست مرتب است. پس حلقه بیرونی را با دستور break در پایتون متوقف می‌کنیم.
10. خطوط آخر برنامه: از خط ۲۲ به بعد، لیست دلخواهی تعریف کرده‌ایم. تابع را روی آن اجرا کرده و در نهایت لیست مرتب شده را چاپ می‌کنیم.

در این الگوریتم هم برای اجرای مرتب سازی حبابی با پرچم از حلقه for  به صورت تو در تو استفاده کرده‌ایم. برای پیاده‌سازی بیشتر الگوریتم‌ها باید از حلقه‌های پایتون استفاده کنیم. در صورت نیاز به آشنایی بیشتر با این عناصر بسیار مهم برنامه نویسی، پیشنهاد می‌کنیم که مطلب مربوط به آن‌ها را در مجله فرادرس مطالعه کنید.

مرتب سازی حبابی بازگشتی

این الگوریتم نوعی از همان الگوریتم مرتب سازی حبابی معمولی است. با این تفاوت که برای حل مسئله در آن از تکنیک بازگشتی استفاده می‌کنیم. در این تکنیک، لیست به دو قسمت مختلف تقسیم می‌شود، عنصر اول و مابقی لیست که هنوز مرتب نشده است. الگوریتم در هر دفعه فقط بر روی بخش مرتب نشده پیمایش می‌کند. بعد از هر پیمایش، اندازه قسمت اول لیست (بخش پیمایش شده) بزرگتر و اندازه بخش دوم کوچکتر می‌شود.

نکته: این تکنیک‌ مزیت خاصی از نظر پیاده‌سازی یا زمان اجرا ندارد. بلکه بیشتر برای بررسی درک افراد از تکنیک مرتب سازی حبابی و آزمودن مهارت‌های آن‌ها، پیاده‌سازی می‌شود.

در کد بالا الگوریتم مرتب سازی حبابی را با استفاده از کلاس‌های پایتون پیاده‌سازی کرده‌ایم. در فهرست پایین، تمام مراحل اجرای کد بالا را گام‌به‌گام نوشته‌ایم.

1. class bubbleSort: با این خط، کلاسی به نام bubbleSort  تعریف می‌کنیم که وظیفه مرتب سازی حبابی را دارد.
2. def __init__(self, array): متد init در پایتون به عنوان سازنده کلاس شناخته می‌شود. این متد، پارامتر array  را دریافت کرده و در self.array  ذخیره می‌کند. از متغیر self.length  نیز برای نگهداری طول لیست استفاده می‌کنیم.
3. def __str__(self): با کمک این تابع، نمای مناسبی برای شیء خروجی به شکل رشته درست می‌کنیم.
4. def bubbleSortRecursive: در خط ۱۱ تابع مرتب سازی حبابی را به صورت بازگشتی تعریف می‌کنیم.
5. در خطوط ۱۲ و ۱۳: اگر n  مشخص نشده باشد، طول لیست را به آن اختصاص می‌دهیم.
6. count = 0: از این متغیر برای شمارش جابه‌جایی‌ها در هربار پیمایش لیست، استفاده می‌کنیم.
7. if n == 1: شرط پایه برای بازگشت است. یعنی اگر فقط یک عنصر باقی مانده باشد، عملیات بازگشت تابع تمام می‌شود.
8. for i in range(n – 1): در این خط، حلقه‌ای را برای پیمایش خانه‌های مجاور تعریف می‌کنیم.
9. if self.array[i] > self.array[i + 1]: بررسی می‌کنیم که آیا عنصر اول بزرگ‌تر از بعدی است یا نه.
10. اگر شرط برقرار باشد: عناصر را جابه‌جا می‌کنیم.
11. count = count + 1: با هر جابه‌جایی، به اندازه یک‌ واحد شمارنده را افزایش می‌دهیم.
12. if (count == 0): این شرط بررسی می‌کند که آیا عنصری جابه‌جا شده است یا نه. اگر شرط برقرار باشد، لیست مرتب است و تابع پایان می‌یابد.
13. خط ۲۹: اگر شرط برقرار نباشد self.bubbleSortRecursive(n – 1)، تابع را برای n-1  عنصر بعدی اجرا می‌کنیم. اینجا از عبارت else استفاده نشده است. زیرا همین‌ که شرط بالا برقرار نباشد برای اجرا شدن این دستور کافی است. نیازی به else نیست.
14. از خط ۳۱ به بعد: در خطوط آخر هم لیست دلخواه تعریف می‌کنیم. سپس شیئی از کلاس می‌سازیم. تابع مرتب سازی بازگشتی را اجرا کرده و در نهایت لیست مرتب شده را چاپ می‌کنیم.

مرتب سازی کوکتلی

به این تکنیک، «مرتب‌ سازی حبابی دوطرفه» (Bidirectional Bubble Sort) هم گفته می‌شود. این الگوریتم نسخه بهینه‌سازی شده‌ای از مرتب سازی حبابی است که لیست داده شده را از هر دو جهت مرتب می‌کند. با استفاده از مرتب سازی کوکتلی تعداد پیمایش‌ها کمتر می‌شود. در نتیجه، ممکن است که الگوریتم سریع‌تر اجرا شود.

روش کار الگوریتم مرتب سازی کوکتلی را در فهرست پایین نوشته‌ایم.

1. پیمایش به جلو:‌ ابتدا آرایه از چپ به راست پیمایش می‌شود. در این مرحله، عناصر همجوار را به روش قبلی و دوبه‌دو مقایسه می‌کنیم. اگر عنصر سمت چپ از عنصر سمت راست کوچک‌تر بود، آن‌ها را با همدیگر جابه‌جا می‌کنیم. بعد یک‌بار پیمایش داده‌ها بزرگترین عنصر به سمت راست یا انتهای آرایه منتقل می‌شود.
2. پیمایش رو به عقب:‌ در مرحله بعد هم آرایه را از راست به چپ پیمایش می‌کنیم. با همان روش قبلی اما این‌ بار عناصر کوچک‌تر جابه‌جا می‌شوند. یعنی اینکه در انتهای این پیمایش، کوچک‌ترین عنصر به سمت چپ یا ابتدای آرایه منتقل شده است.
3. تکرار:‌ دوباره هر دو روش پیمایش را تکرار می‌کنیم. این مراحل تاجایی تکرار می‌شوند که دیگر هیچ دو عنصری با همدیگر جابه‌جا نشوند.

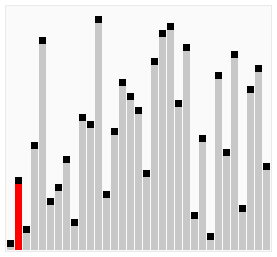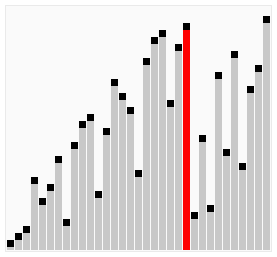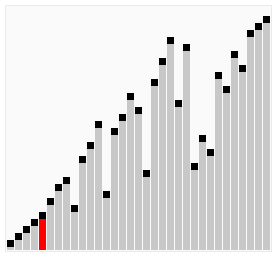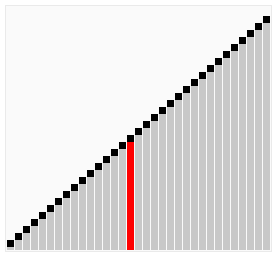
در کادر پایین، کدهای مربوط به الگوریتم مرتب سازی کوکتلی را با زبان پایتون نوشته‌ایم.

مراحل انجام کار توسط الگوریتم مرتب سازی کوکتلی در فهرست زیر توضیح داده شده‌اند.

1. n = len(a): تعداد کل عنصر موجود در لیست a  را محاسبه کرده و در متغیر n  ذخیره می‌کند.
2. swapped = True: در این خط کد، متغیر swapped  را تعریف می‌کنیم. این متغیر مانند پرچم عمل می‌کند. با کمک این پرچم می‌فهمیم که آیا در طول پیمایش لیست، جابه‌جایی بین عناصر انجام شده است یا نه.
3. for i in range(start, end):‌ این حلقه برای پیمایش رو به جلو لیست به کار برده می‌‌شود.
4. در خطوط ۱۰ و ۱۱: با کمک عبارت شرطی if در پایتون، بزرگ‌ترین عنصر را به سمت راست حرکت می‌دهیم.
5. if (swapped == False): این عبارت شرطی برای بررسی رویدادن جابه‌جایی در هر پیمایش به کار می‌رود. هر وقت این شرط برقرار باشد، به معنای آن است که لیست با موفقیت مرتب شده است.
6. for i in range(end – 1, start – 1, -1): این حلقه هم برای پیمایش از عقب به جلو استفاده می‌شود. وظیفه این حلقه، انتقال کوچک‌ترین عنصر لیست به ابتدای آن است.
7. if (a[i] > a[i + 1]): این عبارت شرطی برای انجام جابه‌جایی معکوس به کار برده می‌شود.

یادگیری نوشتن الگوریتم‌ها در فرادرس

برای یاد گرفتن نوشتن الگوریتم‌ها می‌توانید از وب‌سایت فرادرس کمک بگیرید. این سایت از دو روش ارائه مطالب و فیلم‌های آموزشی درباره الگوریتم نویسی استفاده می‌کند. هر چند مهارت طراحی و نوشتن الگوریتم برای توسعه‌دهندگان نرم‌افزار بسیار مفید است. اما در بین این افراد، عده کمی به سراغ طراحی الگوریتم می‌روند. درحالی که الگوریتم‌ها نقش بسیار مهمی در پلتفرم‌ها و برنامه‌های بزرگ، بازی ‌می‌کنند. فرادرس، فیلم‌های آموزشی بسیار خوبی درباره طراحی و نوشتن الگوریتم‌ها منتشر کرده است.

در فهرست پایین چند مورد از فیلم‌های آموزش الگوریتم نویسی در فرادرس را معرفی کرده‌ایم.

با کلیک بر روی تصویر زیر می‌توانید به صفحه اصلی این مجموعه آموزشی هدایت شده و از سایر فیلم‌ها نیز دیدن کنید.

کاربردهای مرتب سازی حبابی در پایتون

در هر سناریو‌یی که به مرتب کردن داده‌ها احتیاج داریم، می‌توانیم از مرتب سازی حبابی استفاده کنیم. به طور معمول، بیشترین کاربرد این تکنیک در مرتب سازی لیست‌ها، آرایه‌ها و ساختمان داده‌هایی مانند لیست‌های پیوندی و درخت‌های باینری است. علاوه بر این با کمک مرتب سازی حبابی می‌توانیم وظایف مربوط به مجموعه داده‌های بزرگ را هم اجرا بکنیم. هرچند باید توجه داشت که سرعت آن نسبت به الگوریتم‌های دیگر کمتر است و برای مجموعه‌های خیلی بزرگ، کارایی بالایی ندارد.

در فهرست زیر، چند مورد از کاربردهای الگوریتم مرتب سازی حبابی را نوشته‌ایم.

• مرتب سازی لیست‌ها و آرایه‌ها: مرتب سازی حبابی می‌تواند لیست‌ها و آرایه‌هایی با هر نوع داده را مرتب بکند. به خصوص اگر اندازه مجموعه داده کوچک باشد یا از قبل کمی مرتب‌شده باشد، این الگوریتم عملکرد بسیار خوبی از خود نشان می‌دهد.
• مرتب سازی ساختمان‌های داده: از مرتب سازی حبابی برای اصلاح چیدمان عناصر موجود در لیست‌های پیوندی و درخت‌های باینری هم می‌توان استفاده کرد. هر چند این الگوریتم چندان برای کار بر روی مجموعه داده‌های بزرگ بهینه نیست.
• مرتب سازی مجموعه داده‌های بزرگ: می‌دانیم که سرعت مرتب سازی حبابی با افزایش تعداد داده به شدت کاهش پیدا می‌کند. اما در سناریو‌هایی که سرعت اجرای عملیات از اهمیت زیادی برخوردار نیست هم می‌توان از این الگوریتم کمک گرفت. هر چند توصیه شده که در زمان کار با چنین مجموعه داده‌هایی از الگوریتم‌های مرتب سازی کارآمدتر استفاده کنیم.

جمع‌بندی

در این مطلب از مجله فرادرس، پیاده‌سازی الگوریتم مرتب سازی حبابی در پایتون را بررسی کرده‌ایم. روش کار آن را با کمک نوشتن شبه‌ کد توضیح داده‌ایم. پیچیدگی زمانی مرتب سازی حبابی برابر با $$O(n^2)$$ است. البته با کمک تکنیک‌هایی مانند «مرتب سازی حبابی با پرچم»، «مرتب سازی حبابی بازگشتی» و «مرتب سازی کوکتلی» می‌توان به بهینه‌سازی عملکرد این الگوریتم و افزایش سرعت آن کمک کرد. این الگوریتم با مقایسه تکراری عناصر مجاور هم از ابتدا تا انتهای سری، تمام داده‌ها را مرتب می‌کند.

از مرتب سازی حبابی در پایتون می‌توان برای مرتب کردن عناصر لیست‌ها، آرایه‌ها و حتی ساختمان‌های داده‌ای مانند لیست‌های پیوندی و درخت‌های باینری استفاده کرد. با مطالعه این مطلب به راحتی می‌توانید از مرتب سازی حبابی در پروژه‌های خود استفاده کنید. علاوه بر این مورد، پیاده‌سازی الگوریتم‌های مرتب سازی روش بسیار خوبی برای تمرین کدنویسی و افزایش تسلط بر روی مفاهیم پایتون است.