استوانه یا Cylinder یک شکل هندسی سه بعدی است، دارای دو قاعده دایرهای شکل و یکسان در قسمت بالا و پایین که توسط یک سطح خمیده به هم متصل شدهاند. اگر شعاع قاعده یک استوانه را و ارتفاع آن را در نظر بگیریم، در این صورت محیط این استوانه به شکل تقریبی توسط فرمول یا بهدست میآید. در این مطلب از مجله فرادرس به زبانی ساده توضیح میدهیم محیط استوانه چگونه محاسبه میشود.
آنچه در این مطلب میآموزید:
-
میآموزید محیط استوانه را با چه روشی محاسبه کنید.
-
فرمول تقریبی محاسبه محیط استوانه را فرا خواهید گرفت.
-
با تعریف و ویژگیهای استوانه آشنا خواهید شد.
-
یاد میگیرید که فرمول محیط استوانه با فرمول مساحت و حجم آن چه تفاوتی دارد.
-
در قالب چند مثال نحوه کاربرد فرمول محیط استوانه را تمرین خواهید کرد.
-
انواع استوانه و تفاوتهای آنها را خواهید شناخت.

محیط استوانه چگونه محاسبه می شود؟
اگر به یک استوانه نگاه کنیم، متوجه میشویم که از دو دایره در بخشهای بالا و پایین و یک بدنه منحنی شکل در سطح جانبی خود تشکیل شده است که اگر آن را باز کنیم به شکل یک مستطیل در میآید. پس محیط استوانه با تقریب برابر با محیط این مستطیل است. اگر محیط دایرهای با شعاع را طول این مستطیل و ارتفاع استوانه یا را عرض این مستطیل در نظر بگیریم، محیط استوانه حاصل برابر میشود با .
دقت کنید یک استوانه برخلاف اشکال هندسی دو بعدی مانند مربع، مستطیل، دایره، لوزی و متوازیالاضلاع یک شکل هندسی سه بعدی محسوب میشود. به همین علت است که معمولا برای آن مساحت و حجم را محاسبه میکنیم نه محیط. اما اگر بخواهیم به مفهومی مانند محیط در مورد این شکل بپردازیم، یک روش تقریبی این است که آن را باز کنیم و محیط اجزای تشکیلدهنده آن را محاسبه کنیم. در ادامه با جزئیات بیشتری نشان میدهیم که فرمول محیط استوانه چگونه محاسبه میشود.

میدانیم محیط هر شکل هندسی برابر است با مجموع کل مرزها، لبهها یا دور آن شکل. بنابراین محیط استوانه نیز به معنای پیدا کردن دور آن یا جمع کردن تمام مرزهای آن است. برای شروع بیایید ببینیم هر کدام از اجزای استوانهای با شعاع و ارتفاع مطابق شکل زیر چه هستند:
- قاعده بالا یا دایره بالایی با شعاع
- قاعده پایین یا دایره پایینی با شعاع
- بدنه مستطیلی شکل که به دور دایرهها پیچیده شده است.
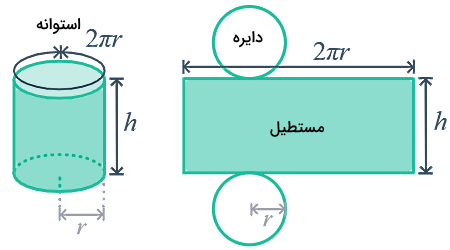
پس اگر این استوانه را باز کنیم، به شکل یک مستطیل درخواهد آمد که عرض آن برابر است با ارتفاع استوانه یا و طول آن برابر است با محیط هر کدام از دو دایره بالا یا پایین. از طرفی میدانیم محیط دایرهای با شعاع طبق فرمول زیر محاسبه میشود:
به این ترتیب فرض میکنیم بهجای استوانه بالا مستطیلی داریم با عرض و طول . میدانیم فرمول محیط یک مستطیل برابر است با دو برابر مجموع طول و عرض آن. پس فرمول محیط استوانهای با شعاع و ارتفاع به شکل زیر در نظر گرفته میشود:
دقت کنید در برخی از منابع از عدد پی در این محاسبات صرفنظر میشود و فرمول محیط استوانه را به شکل سادهتر در نظر میگیرند.
یادگیری محیط و مساحت با فرادرس
یادگیری نحوه محاسبه محیط نیازمند این است که ابتدا با ویژگیهای اشکال هندسی مختلف آشنا شوید. سپس باید بتوانید محیط، مساحت و حجم را از هم تفکیک کنید. یادگیری این تفاوت با مطالعه کتاب ریاضی پایه هفتم آغاز میشود. همچنین در کتابهای درسی ویژگیهای چندضلعیها برای اولین بار در کتاب ریاضی پایه هشتم مطرح شده است. سپس در کتاب ریاضی نهم روش بهدست آوردن مساحت کره یا مساحت و حجم احجامی مانند هرم و مخروط توضیح داده شده است. بنابراین اگر علاقهمند هستید با فرمولهای مربوط به این مباحث همراه با آموزش تصویری و حل مثالهای گسترده آشنا شوید، پیشنهاد میکنیم این فیلمهای آموزشی تهیه شده در مجموعه فرادرس را مشاهده کنید:
حل مثال و تمرین از محیط استوانه
پس از اینکه در بخش قبل یاد گرفیتم محیط استوانه چگونه محاسبه میشود، در این قسمت ابتدا تمام فرمولهای مربوط به یک استوانه را معرفی میکنیم. سپس با حل و بررسی مثالها و تمرینهای متنوع، به شما کمک میکنیم تا به نحوه استفاده از این فرمولها بهویژه فرمول محیط استوانه مسلط شوید. هر شکل هندسی سه بعدی حداقل دارای دو فرمول اصلی است (مساحت سطح و حجم) و لازم است برای مثال در مورد محاسبه مساحت استوانه، تفاوت مساحت کل و مساحت جانبی آن را در نظر بگیرید.
به این ترتیب سه فرمول مهم برای مساحت سطح و حجم این شکل داریم که همراه با فرمول محیط آن در جدول زیر آورده شدهاند:
| فرمولهای استوانهای با شعاع و ارتفاع | |
| فرمول محیط استوانه | |
| فرمول مساحت جانبی استوانه | |
| فرمول مساحت کل استوانه | |
| فرمول حجم استوانه | |
در همین راستا، برای اینکه با مسائل مربوط به حجم استوانه بیشتر آشنا شوید، پیشنهاد میکنیم مطلب «حجم استوانه و محاسبه آن – به زبان ساده» از مجله فرادرس را مطالعه کنید.
مثال ۱
محیط استوانهای که قطری برابر با و ارتفاعی به اندازه دارد را محاسبه کنید:
پاسخ
همانطور که گفتیم، محیط استوانه توسط فرمول زیر محاسبه میشود:
در این فرمول لازم است شعاع قاعده مشخص باشد، پس باید قطر را بر عدد دو تقسیم کنیم:
حالا با جایگذاری این مقادیر در فرمول بالا، محیط این استوانه به شکل زیر به دست میآید:
البته میتوانستیم با در نظر گرفتن محیط دایره به شکل از ابتدا با فرمول مسئله را حل کنیم.
مثال ۲
اگر حجم استوانهای برابر با سانتیمتر مکعب باشد و بدانیم که ارتفاع این استوانه نیز سانتیمتر است، محیط آن چقدر میشود؟
پاسخ
در این سوال حجم استوانه داده شده و محیط آن از ما خواسته شده است. با توجه به اینکه برای پیدا کردن محیط طبق فرمول لازم است هم شعاع و هم ارتفاع استوانه را داشته باشیم، بنابراین با استفاده از فرمول حجم استوانه ابتدا باید شعاع آن را به شکل زیر محاسبه کنیم:
حالا فرمول محیط استوانه را مینویسیم:
تمرین
محیط استوانهای با شعاع و ارتفاع برابر با کدام گزینه زیر است؟
گزینه سوم درست است. برای محاسبه محیط استوانه کافی است شعاع قاعده و ارتفاع آن را بدانیم. سپس این دو مقدار را در فرمول زیر قرار دهیم:
یادگیری هندسه متوسطه با فرادرس
در این بخش از این مطلب مجله فرادرس قصد داریم مروری داشته باشیم به درس هندسه در مقطع متوسطه. هندسه متوسطه در پایه دهم با درس هندسه ۱ و مباحثی مانند قضیه تالس و چندضلعیها شروع میشود. در هندسه ۲ ویژگیهای دیگری از چندضلعیها مانند منتظم بودن یک شش ضلعی یا محاطی و محیطی بودن آنها مطرح میشود. همچنین در کتاب درسی هندسه ۳ که با عنوان هندسه تحلیلی نیز شناخته شده است، مباحث جدیدی مانند مقاطع مخروطی، ماتریسها و بردارها معرفی میشوند.
مشاهده فیلمهای آموزشی که در ادامه برای شما قرار دادهایم، به شما کمک میکند تا همراه با حل مسائل متنوع و بهرهگیری از آموزش تصویری به کلیه مباحث هندسه متوسطه کاملا مسلط شوید:
استوانه چیست و چه ویژگی هایی دارد؟
برای اینکه در درک محیط استوانه و محاسبات مربوط به آن موفقتر عمل کنید، در این بخش قصد داریم به شکلی مختصر توضیح دهیم که یک استوانه چیست و چه ویژگیهایی دارد. رولهای دستمال و قوطیهای نوشابه مثالهایی از استوانه در زندگی واقعی هستند. همچنین آیا میدانستید که برج کج پیزا نیز شکلی استوانهای دارد؟ معادل انگلیسی استوانه یا Cylinder از کلمهای یونانی به معنای غلتاندن گرفته شده است. این اصطلاح نخستین بار برای توصیف شکل هندسی جسمی با قاعده دایرهای شکل و اضلاع مستقیم استفاده شد و بعدها برای سایر اجسام استوانهای شکل دیگر مانند لولهها، ظروف و قطعات موتور نیز بکار رفت.
فهرست زیر تعریف جامع و کاملی از یک استوانه را ارائه میدهد:
- استوانه یک شکل سه بعدی است، متشکل از دو قاعده دایرهای یکسان و موازی هم که به وسیله یک سطح خمیده به هم متصل شدهاند.
- قاعدهها مانند دیسکهای دایرهای شکل هستند.
- خطی که از مرکز یکی از دایرهها عبور کرده و به مرکز دایره دیگر میرسد، «محور استوانه» نام دارد.
- فاصله عمودی بین دو قاعده را «ارتفاع استوانه» مینامند که عموما با حرف نمایش داده میشود.
- فاصله مرکز قاعده تا لبه آن «شعاع استوانه» نام دارد که با حرف نشان داده میشود.
- استوانه ترکیبی از دو دایره و یک مستطیل است.
با در نظر گرفتن این ویژگیها یک استوانه مطابق تصویر زیر ساخته میشود:
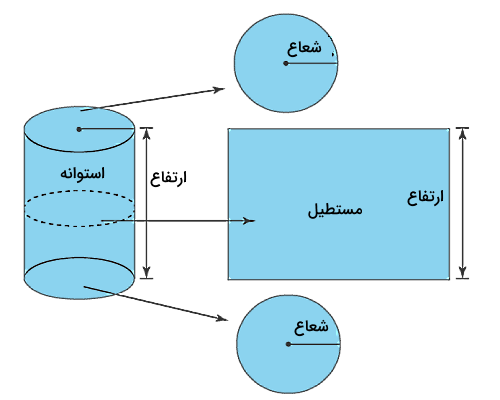
پس اندازه یک استوانه به شعاع قاعده و ارتفاع سطح منحنی شکل آن بستگی دارد. همچنین برخلاف اشکال هندسی سه بعدی مانند مخروط، مکعب یا مکعب مستطیل استوانه هیچ راسی ندارد، یعنی هیچ گوشه مشخصی در استوانه وجود ندارد. بهعلاوه قاعده و سطح بالایی یک استوانه همیشه مشابه هم هستند، یعنی اگر قاعده دایره باشد، سطح بالایی نیز یک دایره است و اگر قاعده بیضی باشد، سطح بالایی به شکل یک بیضی است.
انواع استوانه
در هندسه چهار نوع استوانه داریم که به شکل زیر از هم متمایز میشوند:
- استوانه دایرهای قائم: محور بین دو قاعده موازی عمود بر مرکز قاعدهها است (مثال: قوطی نوشابه).
- استوانه مایل: اضلاع بهصورت مایل قرار دارند و عمود بر قاعده نیستند (مثال: برج کج پیزا).
- استوانه بیضوی: قاعده استوانه بهجای دایره به شکل بیضی است (مثال: عدسیهای اپتیکی).
- استوانه تو خالی دایرهای قائم یا پوسته استوانهای: دو استوانه دایرهای قائم که یکی درون دیگری قرار دارد و هر دو دارای محور مشترک و عمود بر قاعده هستند (مثال: سیلندرهای هیدرولیکی).
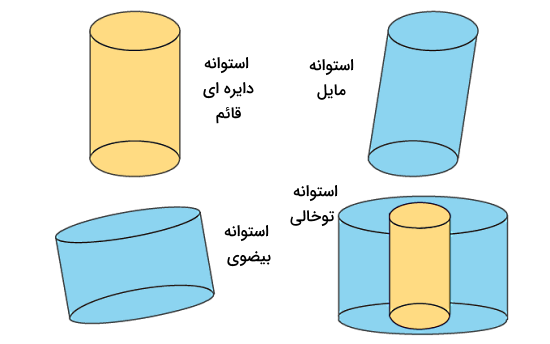
تفاوت پوسته استوانهای با استوانه دایرهای قائم در این است که این نوع تو خالی است، یعنی درون آن یک فضای خالی وجود دارد.
رئوس، یال ها و وجوه استوانه
گفتیم یک استوانه دارای دو سطح دایرهای و یک سطح خمیده است. این دو سطح دایرهای که در دو انتهای استوانه قرار دارند، هماندازه و همشکل یعنی مساوی و همنهشت هستند. اگر سطح خمیده متصل کننده این دو دایره را باز کنیم، به یک مستطیل میرسیم که در واقع به شکل لولهای پیچیده شده است. به این ترتیب وجوه، یالها و رئوس استوانه به شکل زیر توصیف میشوند:
- وجهها: یک استوانه در مجموع سه وجه دارد (دو وجه دایرهای تخت + یک وجه خمیده).
- یالها: یک استوانه دو یال دارد (یکی در بالا و یکی در پایین، در محل اتصال سطح خمیده به دایرهها).
- رئوس: یک استوانه هیچ راسی ندارد (چون یالهای آن در هیچ نقطهای به هم نمیرسند).
پس استوانه هیچ گوشه یا نقطه تقاطع تیزی ندارد.
source
