درصد یکی از مفاهیم کاربردی درس ریاضی است که برای بیان نسبت، مقایسه و تحلیل دادههای عددی بکار میرود. این کلمه از عبارت لاتین Per Centum گرفته شده است که به معنی «از صد» یا «در هر صد» است. به این ترتیب درصد روشی است برای نمایش یک عدد به صورت کسری از . به عنوان مثال، وقتی میگوییم ، منظور ما واحد از واحد کل است. در این مطلب از مجله فرادرس توضیح میدهیم نحوه محاسبه درصد چگونه است.
آنچه در این مطلب میآموزید:
-
یاد میگیرید نحوه محاسبه درصد در حالتهای مختلف چگونه است.
-
با روش تبدیل درصد به کسر متعارفی و برعکس آشنا میشوید.
-
میآموزید چگونه میتوان درصد را به عدد اعشاری تبدیل کرد.
-
با مفهوم و فرمولهای درصد تغییرات آشنا میشوید.
-
نحوه محاسبه درصد را با حل سوالات متنوع تمرین خواهید کرد.
-
فرآیند محاسبه درصد در اکسل را میآموزید.

پس از اینکه در اولین بخش نشان دادیم درصد چگونه محاسبه میشود، ابتدا مروری داریم بر حالتهای مختلفی که ممکن است در محاسبات درصد با آنها روبرو شویم. سپس به تعریف درصد، اهمیت و کاربرد آن در ریاضیات خواهیم پرداخت و ارتباط آن را با کسر متعارفی یا اعداد اعشاری توضیح میدهیم. همچنین به نحوه محاسبه درصد با اکسل اشاره کوتاهی داریم و در نهایت با حل مثالها و تمرینهای متنوع، به شما کمک میکنیم تا به این موضوع کاملا مسلط شوید.
نحوه محاسبه درصد چگونه است؟
اگر چند عدد داشته باشیم که مجموع آنها برابر با باشد، هر عدد مستقیما نشاندهنده مقدار درصدی نیز هست. در غیر این صورت نحوه محاسبه درصد به این صورت است که ابتدا هر مقدار جزئی را بر مجموع اعداد یا مقدار کل تقسیم میکنیم تا یک کسر متعارفی تشکیل شود. سپس این کسر را در عدد ضرب میکنیم تا درصد هر عدد بهدست آید.
بنابراین درصد به کسر یا نسبتی گفته میشود که در آن مخرج یا مقدار کل است. برای مثال، اگر سام در امتحان ریاضی خود نمره کسب کرده باشد، به این معنی است که نمره او از مقدار کل عددی برابر با شده است.
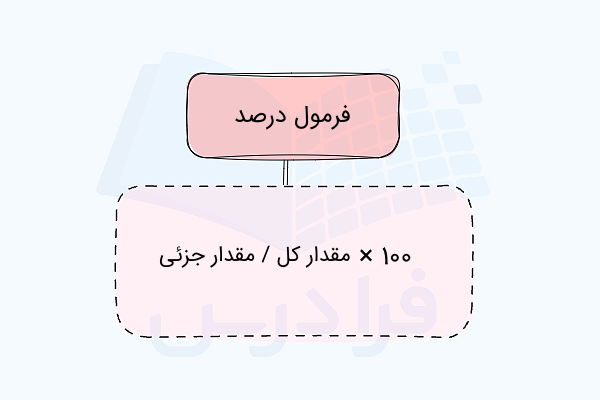
جدول زیر فرمول درصد را به شکل دقیقتری نشان میدهد:
| محاسبه درصد ، اگر مقدار از را داشته باشیم | |
| محاسبه درصد ، اگر را داشته باشیم |
فهرست زیر چند مثال از نحوه محاسبه درصد و تبدیل آن به کسر متعارفی یا عدد اعشاری را نشان میدهد:

محاسبه درصد یعنی یافتن سهم یا نسبت یک مقدار از مقدار کلی که بر پایه عدد تعریف میشود. برای محاسبه درصد، دو روش به نام تبدیل مخرج کسر به و روش واحدی (روش تناسب ساده) وجود دارد که در ادامه هر کدام را توضیح میدهیم. همچنین ممکن است با مواردی مواجه شویم که مجموع دو یا چند عدد داده شده برابر با عدد باشد (یا نباشد) که برای هر کدام از این دو حالت نیز نحوه محاسبه درصد متفاوت است.
محاسبه درصد با تبدیل مخرج کسر به ۱۰۰
اگر در صورت سوال یک کسر متعارفی داشته باشیم و بخواهیم معادل درصدی آن را پیدا کنیم، بهتر است از این روش استفاده کنیم. ابتدا باید مخرج کسر داده شده را طوری بنویسیم که مخرج آن به تبدیل شود. در این صورت، عددی که در صورت قرار دارد همان مقدار درصدی است.
برای مثال، اگر بخواهیم بدانیم کسر چند درصد است، کافی است ابتدا مخرج آن را با ضرب کردن در عدد به تبدیل کنیم. طبیعی است که برای درست بودن محاسبات، صورت کسر نیز در عدد ضرب میشود. پس داریم:
به محض اینکه مخرج کسر داده شده به تبدیل شد، صورت آن همان مقدار درصدی موردنظر است:
دقت کنید کاربرد این روش در مواردی که مخرج کسر یکی از عوامل عدد نباشد، توصیه نمیشود. در این شرایط بهتر است از روش دوم یعنی روش واحدی استفاده شود.
محاسبه درصد با روش واحدی (روش تناسب ساده)
روش دیگری که نحوه محاسبه درصد را آسان میکند، روش واحدی یا روش تناسب ساده است. در این روش هم مانند روش قبل، یک کسر متعارفی داریم و میخواهیم ببینیم معادل درصدی آن چیست. کافی است کسر را مستقیما در عدد ضرب کنیم تا درصد بهدست آید.
برای نمونه، درصد مربوط به کسر بهصورت زیر محاسبه میشود:
محاسبه درصد زمانی که مجموع کل برابر ۱۰۰ باشد
علاوهبر موقعیتهای گفته شده، ممکن است دو یا چند عدد داشته باشیم که جمع آنها دقیقا برابر با است. در چنین شرایطی درصد هر مقدار نسبت به کل، برابر با خود آن عدد است. برای مثال، سارا کاشیهایی با سه رنگ مختلف برای خانهاش خریده است. جزئیات این خرید در جدول زیر نشان داده شده است:
| رنگ | تعداد کاشیها |
| زرد | |
| سبز | |
| قرمز |
اگر دقت کنید مجموع تعداد کاشیها با رنگها مختلف برابر است با :
بنابراگر اگر بخواهیم بدانیم چند درصد از کاشیهای سارا سبز است، کافی است به جدول نگاه کنیم و بگوییم .
محاسبه درصد زمانی که مجموع کل برابر ۱۰۰ نباشد
در مقایسه با بخش قبل، حالتی را در نظر بگیرید که مجموعه اعداد داده شده نشود. میخواهیم ببینیم در این حالت نحوه محاسبه درصد چگونه است. در چنین شرایطی بهتر است از روش واحدی (تناسب) استفاده کنیم. برای نمونه، فرض کنید الهام دستبندی دارد که شامل مهره قرمز و مهره آبی است. واضح است که مجموع مهرههای دستبند الهام برابر است با نه .
حالا اگر بخواهیم بدانیم چند درصد از مهرههای دستبند الهام قرمز و چند درصد آبی است، کافی است ابتدا کسر متناسب با این دو مورد را بنویسیم. سپس طبق روش واحدی، کسر بهدست آمده را در عدد ضرب کنیم:
- دستبند قرمز است:
- دستبند آبی است:
یادگیری محاسبات ریاضی با فرادرس
در بخش قبل آموختیم که درصد یک ابزار قدرتمند و انعطافپذیر در بیان و تحلیل مقادیر نسبی است. تسلط بر مفهوم درصد و نحوه محاسبه و تفسیر آن نهتنها برای دانشآموزان و دانشجویان، بلکه برای هر فردی در زندگی روزمره و محیط کار ضروری است. یادگیری این مفهوم پایهگذار مهارتهای تحلیلی و تصمیمگیریهای بهتر در بسیاری از زمینهها خواهد بود. در کنار این مفهوم، تسلط به کلیه محاسبات ریاضی نیز از اهمیت بالایی برخوردار است. در ادامه چند فیلم آموزشی از مجموعه فرادرس در همین زمینه به شما معرفی میشود:
همچنین یکی از سریعترین و دقیقترین روشهای محاسبه درصد استفاده از اکسل (Excel) است. در بخشهای بعد راجعبه این موضوع توضیحات کوتاهی ارائه میشود. در این زمینه علاوهبر اینکه میتوانید به مطلب «تبدیل عدد به درصد در اکسل – به زبان ساده» از مجله فرادرس مراجعه کنید، مشاهده فیلمهای آموزش رایگان فرادرس نیز به شما کمک خواهد کرد:
ارتباط درصد با کسر متعارفی و اعداد اعشاری
همانطور که در نحوه محاسبه درصد نشان داده شد، درصد شکل خاصی از یک کسر است که مخرج آن همیشه است. بهعلاوه این امکان وجود دارد تا درصد را به عدد اعشاری نیز تبدیل کنیم و برعکس. این ویژگی درصد را به یک ابزار قدرتمند در محاسبات عددی تبدیل کرده است، چرا که به راحتی میتوان آن را در معادلات، تحلیلها و مدلسازیهای ریاضی بکار گرفت.
تبدیلات بین درصد و عدد اعشاری
نماد همواره میتواند با تقسیم بر صد یا جایگزین شود. پس از یادآوری این نکته، در این قسمت توضیح میدهیم تبدیل درصد به اعشار و برعکس چگونه است:
- برای تبدیل درصد به اعشار، کافی است علامت را با تقسیم بر صد یا جایگزین کنیم.
- برای تبدیل عدد اعشاری به درصد، کافی است آن را در ضرب کنیم.
به عنوان مثال اگر بخواهیم را به یک عدد اعشاری تبدیل کنیم، با جایگزین کردن بهجای علامت درصد خواهیم داشت:
این در حالی است که برای حالت دوم، میتوانیم بگوییم عدد معادل است.
تبدیلات بین درصد و کسر متعارفی
درصد و کسر هر دو روشهایی برای نمایش اعداد و نسبتهایشان هستند. درصد را میتوان به عنوان کسری با مخرج ثابت و برابر با تعریف کرد. میدانیم کسر متعارفی رابطهای بین یک جزء () و یک کل () است که به صورت نوشته میشود و در آن مخالف صفر و و هر دو اعداد صحیح هستند.
برای تبدیل درصد به کسر ابتدا باید نماد درصد () را حذف کنید. سپس عدد داده شده را بر تقسیم کنید تا یک کسر متعارفی تشکیل شود. در نهایت کسر به دست آمده را به کوچکترین اجزای آن کاهش دهید. به مثال زیر در این زمینه توجه کنید:
اگر بخواهیم را به کسر تبدیل کنیم، با حذف علامت درصد و ضرب این عدد در خواهیم داشت:
دقت کنید برای اینکه سادهسازی راحتتری داشته باشیم، صورت و مخرج کسر اولیه را در ده ضرب کردهایم. اما عکس این تبدیل یعنی تبدیل کسر به درصد به معنای تبدیل عدد کل یا مخرج به و یافتن تعداد بخشهای است. به عنوان مثال اگر بخواهیم تبدیل کسر به درصد را انجام دهیم، کافی است کسر را در عدد ضرب کنیم:
حل مثال از نحوه محاسبه درصد
در این قسمت راهحل چند مثال را با هم بررسی میکنیم تا بهتر متوجه شوید نحوه محاسبه درصد در مسائل مختلف چگونه است.
مثال ۱
اگر نمره دانشآموزی در درس ریاضی از مقدار شده باشد، چگونه درصد آن را محاسبه میکنیم؟
پاسخ
در این سوال فقط یک عدد داده شده است. پس برای محاسبه درصد کافی است از روش تناسب ساده استفاده کنیم. ابتدا کسر متعارفی متناسب با این سوال را که به شکل از است مینویسیم و سپس آن را در ضرب میکنیم تا درصد این نمره محاسبه شود:
مثال ۲
اگر بدانیم در یک کلاس نفری دختر وجود دارد، چند درصد این کلاس پسر هستند؟
پاسخ
طبق صورت سوال از تعداد نفر دانشآموز در یک کلاس، نفر دختر هستند. پس تعداد پسران این کلاس برابر است با:
بنابراین نحوه محاسبه درصد پسران این کلاس به شکل زیر است:
پس این کلاس را پسرها تشکیل میدهند. اگر در این سوال درصد دختران نیز خواسته شده بود، میتوانستیم به یکی از دو روش زیر این درصد را محاسبه کنیم:
یا
مثال ۳
یک محلول شکر یک لیتری حاوی شکر است. چه کسری از این محلول شکر است؟
پاسخ
برای یافتن پاسخ، باید را به کسر تبدیل کنیم. گفتیم در تبدیل درصد به کسر، درصد داده شده را پس از حذف علامت درصد بر تقسیم میکنیم:
درصد تغییر چیست و چه فرمولی دارد؟
یکی از مفاهیم مهم در مبحث درصد، درصد تغییرات است. این مفهوم برای محاسبه میزان افزایش یا کاهش یک مقدار نسبت به مقدار اولیه بکار میرود. درصد تغییر میتواند مثبت (نشاندهنده افزایش) یا منفی (نشاندهنده کاهش) باشد و معادل است با تغییرات مقدار یک کمیت در یک دوره زمانی که بر حسب درصد نوشته شده است. این کمیت در تحلیلهای اقتصادی، آماری و مدیریت مالی بسیار کاربرد دارد. معادل دیگر این مفهوم در ریاضیات آهنگ تغییرات است.
درصد تغییر مثبت
درصد تغییر مثبت به درصد تغییر در مقدار اشاره دارد، زمانی که در یک دوره زمانی افزایش مییابد. افزایش جمعیت، افزایش تعداد باکتریها روی یک سطح و … نمونه مثالهایی از این روند است. درصد تغییر مثبت را میتوان با استفاده از فرمول زیر محاسبه کرد:
۱۰۰ × مقدار اولیه / (مقدار اولیه – مقدار افزایش یافته) = درصد تغییر مثبت
برای نمونه، فرض کنید قیمت یک ژاکت از دلار به دلار افزایش پیدا کرده است و میخواهیم ببینیم چند درصد افزایش قیمت داشتهایم. کافی است فرمول بالا را بکار ببریم تا درصد تغییر مشخص شود:

درصد تغییر منفی
کاهش درصد تغییر یا درصد تغییر منفی به درصد تغییر در مقدار اشاره دارد، زمانی که در یک دوره زمانی کاهش مییابد. کاهش سطح بارندگی، کاهش تعداد بیماران کووید و … نمونه مثالهای مرسوم در این بخش هستند. محاسبه درصد تغییر منفی توسط فرمول زیر انجام میشود:
۱۰۰ × مقدار اولیه / (مقدار اولیه – مقدار کاهش یافته) = درصد تغییر منفی
برای مثال، فرض کنید نرخ بارندگی از میلیمتر به میلیمتر کاهش یافته است و میخواهیم ببینیم درصد تغییر متناظر با این کاهش چقدر است. کافی است فرمول بالا را بنویسیم:
ملاحظه میکنید که حاصل عددی منفی شد. البته دقت کنید ممکن است در برخی از منابع فرمول درصد تغییر در این شرایط به شکل زیر نوشته شود که نتیجه آن یک عدد مثبت است. در این حالت نیز نباید فراموش کنید که تغییرات روند کاهشی داشته است نه افزایشی:
۱۰۰ × مقدار اولیه / (مقدار کاهش یافته – مقدار اولیه) = درصد تغییر کاهشی
حل مثال از محاسبه درصد تغییر
در بخش قبل آموختیم که درصد تغییر چیست و از چه فرمولهایی برای محاسبه آن میتوان استفاده کرد. در این قسمت با حل چند مثال روش استفاده از این فرمولها را تمرین خواهید کرد.
مثال ۱
اگر قیمت یک کتاب از دلار به دلار افزایش پیدا کرده باشد، درصد تغییرات قیمت آن چقدر است؟
پاسخ
در این سوال تغییرات قیمت روند افزایشی داشته است. پس لازم است از فرمول درصد تغییر مثبت به شکل زیر استفاده کنیم:
۱۰۰ × مقدار اولیه / (مقدار اولیه – مقدار افزایش یافته) = درصد تغییر مثبت
اگر درصد تغییر مثبت را با نشان دهیم، خواهیم داشت:
مثال ۲
اگر تعداد استخدامیهای یک شرکت از نفر به نفر کاهش پیدا کرده باشد، نرخ استخدام این شرکت چند درصد تغییر کرده است؟
پاسخ
در این سوال همانطور که از صورت سوال پیدا است، کاهش تعداد استخدامیها را داریم. پس از فرمول درصد تغییر منفی استفاده میکنیم:
۱۰۰ × مقدار اولیه / (مقدار اولیه – مقدار کاهش یافته) = درصد تغییر منفی
علامت منفی بهدست آمده نشاندهنده کاهش نرخ استخدام در این شرکت است.
مثال ۳
اگر قیمت یک خانه طی سه سال از دلار ابتدا به اندازه افزایش و سپس به اندازه کاهش پیدا کند، درصد تغییرات قیمت این خانه در کل این سه سال چقدر بوده است؟
پاسخ
برای اینکه بتوانیم درصد تغییرات را در طول این سه سال پیدا کنیم، لازم است ابتدا ببینیم قیمت خانه پس از افزایش بیست درصدی چقدر میشود. سپس بیست و پنج درصد کاهش را روی قیمت نهایی بهدست آمده از مرحله قبل اعمال کنیم تا در نهایت مشخص شود قیمت خانه پس از عبور از این دو تغییر چقدر شده است.
با داشتن این مقدار و مقدار اولیه دلار درصد تغییر در طول این سه سال محاسبه خواهد شد. دقت کنید اینکه مجموع تغییرات را به شکل برای پاسخ این سوال در نظر بگیریم، کاملا اشتباه است. پس ابتدا باید قیمت نهایی خانه را پس از اولین تغییر بهدست آوریم. اگر این قیمت را با نشان دهیم، خواهیم داشت:
در مرحله دوم بیست و پنج درصد کاهش قیمت روی این قیمت جدید اعمال میشود. دقت کنید چون در این حالت درصد تغییر منفی است، باید حتما علامت منفی را در محاسبات خود در نظر بگیریم. پس داریم:
حالا با توجه به اینکه قیمت نهایی طی این دو مرحله افزایشی و کاهشی بهدست آمده است، میتوانیم درصد تغییرات کلی در این دو فرآیند را حساب کنیم. اما برای اینکه بتوانیم تشخیص دهیم از کدام فرمول باید استفاده کنیم (درصد تغییر مثبت یا منفی)، کافی است مقادیر اولیه و نهایی قیمت این خانه را با هم مقایسه کنیم. قیمت خانه در طول این سه سال از دلار به دلار کاهش پیدا کرده است. پس لازم است فرمول درصد تغییر منفی نوشته شود:
۱۰۰ × مقدار اولیه / (مقدار اولیه – مقدار کاهش یافته) = درصد تغییر منفی
به این ترتیب قیمت این خانه در طول این سه سال ده درصد کاهش یافته است.
درصد چیست و یادگیری آن چه اهمیت و کاربردی دارد؟
برای اینکه بتوانیم درصد را بهدرستی محاسبه کنیم، ابتدا باید ببینیم درصد چیست و تسلط بر آن چه اهمیت و کاربردی دارد. درصد کسری است که مخرج آن برابر با عدد است. در واقع درصد رابطهای است بین جزء و کل که در آن مقدار کل همیشه عدد در نظر گرفته میشود.
نحوه محاسبه درصد به این شکل است که ابتدا عدد موردنظر را نسبت به مقدار کل محاسبه کرده و سپس حاصل را در ضرب میکنیم. این عملیات باعث میشود که عدد نهایی بهصورتی استاندارد و قابلفهم برای عموم تبدیل شود.

برای مثال، اگر نمرات یک دانشآموز در درس ریاضی برابر با از باشد، در این صورت درصد متناسب با این نسبت بر اساس کسری محاسبه میشود که رابطه بین جزء (نمرات کسب شده) و کل (نمره کل) را توصیف میکند. سپس باید این کسر در ضرب شود تا فرم درصد را داشته باشیم:
همچنین این عدد در شکل کسری خود بهصورت و در نسبت بهصورت نوشته میشود. در اینجا نماد درصد است که به شکل «درصد» خوانده میشود. نماد درصد را همواره میتوانیم با عبارت «تقسیم بر » نیز جایگزین کنیم تا به یک کسر یا معادل اعشاری تبدیل شود. درصد یک عدد بدون بعد است.
درصد به دلیل سادگی و قابلیت درک بالا، در حوزههای مختلفی از جمله مسائل علمی، مالی، تجاری و آماری بکار برده میشود. این مفهوم امکان مقایسه آسان بین مقادیر مختلف را فراهم میکند، بهویژه زمانی که مقیاسها متفاوت هستند. از مقایسه نرخ تورم و سود بانکی گرفته تا تحلیل نتایج آزمونها و سهم بازار شرکتها، همه و همه به کمک درصد سادهتر و دقیقتر انجام میشوند.
البته کاربرد درصد فقط محدود به ریاضیات و مباحث پیشرفته نیست، بلکه در زندگی روزمره نیز بهطور گستردهای مورد استفاده قرار میگیرد. درصد در تعیین تخفیفها، مالیات، بهرههای بانکی، رشد یا کاهش جمعیت، شاخصهای اقتصادی و حتی در علوم طبیعی مانند شیمی و زیستشناسی نیز نقش بسیار مهمی دارد. در حوزه آموزش نیز از درصدها برای بیان نمره، درصد موفقیت و تحلیل نتایج دانشآموزان استفاده میشود. لیست زیر بخشی از این کاربردها را بهصورت جزئیتر نشان میدهد:
- در ریاضیات و مدرسه برای محاسبه نمرات
- در اقتصاد برای محاسبه بازده سرمایه، تورم، کاهش یا افزایش قیمتها
- در علوم طبیعی برای بررسی ترکیب گازها یا عناصر در نمونهای از مواد
- در سلامت برای محاسبه درصد چربی بدن یا میزان اکسیژن خون
- درک عمیقتر کسرها و اعداد اعشاری
- سرعت و دقت بیشتر در کار با حجم زیادی از داده
- سهولت انجام مقایسه بین گروههای مختلف با مقیاسهای متفاوت (برای مثال درمقایسه نمرات، بودجه، یا بازده شغلی)
نحوه محاسبه درصد با اکسل
در بخش قبل نحوه محاسبه درصد را همراه با حل مثال و تمرین کاملا یاد گرفتیم. در این بخش بهصورت کوتاه اشارهای داریم به روش محاسبه درصد در اکسل. چنانچه تمایل دارید اشراف بیشتری نسبت به این موضوع داشته باشید، پیشنهاد ما مشاهده فیلم آموزش رایگان محاسبه درصد در اکسل + مثالهای عملی فرادرس است که لینک آن نیز در ادامه برای شما قرار داده شده است:
برای محاسبه درصد در اکسل طبق آنچه در بخشهای قبل گفتیم، چند روش ساده وجود دارد که عبارتاند از:
- محاسبه درصد یک عدد از عدد دیگر
- محاسبه درصد تغییر (درصد افزایش یا کاهش)
- محاسبه مقدار بر اساس درصد
برای مثال، در حالت اول اگر بخواهیم بدانیم که عدد چند درصد از است، کافی است در یک سلول از اکسل فرمول =20/80 را بنویسیم. بلافاصله نتیجه 0.25 را در همان سلول خواهیم داشت. حالا برای اینکه مقدار درصدی این عدد را داشته باشیم، ابتدا این سلول را انتخاب میکنیم. سپس از تب Home در نوار بالای محیط اکسل، گزینه Number را پیدا کرده و روی علامت درصد یا گزینه Percent Style کلیک میکنیم. در این صورت عدد بهدست آمده به 25% تبدیل خواهد شد.
در روش دوم و با هدف محاسبه درصد تغییر، برای نمونه فرض کنید عدد اولیه را داریم که تا افزایش یافته است و میخواهیم درصد افزایش آن را حساب کنیم. ابتدا فرمول =(80-50)/50 را در یک سلول از اکسل مینویسیم. سپس مانند روش قبل با کلیک روی گزینه Percent Style حاصل این محاسبه به شکل درصدی در سلول نمایش داده میشود که برابر است با 60%.
در سومین بخش برای مثال فرض کنید میخواهیم از را حساب کنیم. فرمول =25% * 200 را در یک سلول از اکسل مینویسیم و بلافاصله نتیجه محاسبه شده در همان سلول ظاهر میشود که برابر است با =(80-50)/50.
یادگیری صفر تا صد کسرها با فرادرس
همانطور که در بخشهای قبل ملاحظه کردید، مفهوم کسر به معنای نسبت یا بخشی از کل به مفهوم درصد و کاربردهای آن بسیار نزدیک است. به همین دلیل در این بخش قصد داریم چند فیلم آموزشی رایگان در زمینه مباحث مختلف مربوط به کسرها مانند تساوی، مقایسه، سادهسازی، جمع، ضرب، مخرج مشترک گرفتن، کسرهای مساوی و بزرگتر از واحد، کسرهای مخلوط و تبدیل کسر به اعشار را به شما معرفی کنیم. مشاهده این فیلمهای آموزشی فرادرس به شما کمک میکند تا کاملا به مبحث کسرها در ریاضیات مسلط شوید:
آزمون نحوه محاسبه درصد
در انتهای این مطلب از مجله فرادرس برای اینکه به نحوه محاسبه درصد کاملا مسلط شوید و میزان یادگیری خود را بیازمایید، ده سوال چهار گزینهای برای شما در نظر گرفتهایم. پس از اینکه به تمام سوالات پاسخ دادید، با کلیک روی گزینه «دریافت نتیجه آزمون» نمره نهایی شما قابل مشاهده است. پیش از شروع، خلاصهای از مهمترین نکات مربوط به محاسبات درصد بهصورت زیر برای شما خلاصه شده است:
- برای محاسبه درصد یک عدد کافی است از فرمول «۱۰۰ × عدد کل (یا مجموع اعداد) / عدد» استفاده کنید.
- افزایش یا کاهش هر کمیتی را میتوان بهصورت درصد و در قالب کمیتی به نام «درصد تغییر» بیان کرد.
- یک کسر را میتوان به درصد و برعکس تبدیل کرد.
- برای تبدیل کسر به درصد آن را در عدد ضرب و برای تبدیل درصد به کسر آن را بر عدد تقسیم کنید.
- درصدها معکوسپذیراند، برای مثال از برابر است با از .
اگر بدانیم حقوق علی افزایش یافته، در حالی که حقوق فعلی او دلار است. حقوق علی پس از ارتقا چقدر است؟
گزینه اول صحیح است. این سوال مربوط به مبحث درصد تغییر است. با توجه به اینکه حقوق افزایش داشته، پس فرمول درصد تغییر مثبت را به شکل زیر مینویسیم:
۱۰۰ × مقدار اولیه / (مقدار اولیه – مقدار افزایش یافته) = درصد تغییر مثبت
اگر حقوق دریافتی پس از افزایش را با نشان دهیم، خواهیم داشت:
نیل یک تلفن همراه جدید به قیمت دلار خریده است. اگر بدانیم ارزش تلفن هر سال از قیمت اولیهاش کاهش مییابد، قیمت تلفن همراه او پس از دو سال چقدر است؟
گزینه اول درست است. در این سوال باید از فرمول درصد تغییر کاهشی یا درصد تغییر منفی استفاده کنیم:
۱۰۰ × مقدار اولیه / (مقدار اولیه – مقدار کاهش یافته) = درصد تغییر منفی
اگر قیمت نهایی تلفن در انتهای سال اول را با نشان دهیم، خواهیم داشت:
دقت کنید حتما باید علامت منفی را برای درصد تغییر در نظر بگیریم تا به پاسخ درستی برسیم:
مریم روزانه دقیقه مطالعه میکند. او دقیقه از این زمان را به مطالعه و تمرین ریاضی، دقیقه را به علوم و دقیقه را به مطالعات اجتماعی اختصاص میدهد. کدام گزینه در مورد زمانبندی مطالعاتی او صحیح است؟
زمان به درس ریاضی اختصاص داده شده است.
زمان به درس علوم اختصاص داده شده است.
زمان به درس مطالعات اجتماعی اختصاص داده شده است.
تمام گزینههای بالا درست هستند.
گزینه آخر درست است. در این سوال سه موضوع مطالعاتی داریم که برای هر کدام مدت زمان مشخصی از زمان کل دقیقه اختصاص داده شده است. بنابراین چون مجموع کل بازههای زمانی برابر نیست، لازم است به روش تناسب ساده یا روش واحدی پیش برویم:
- زمان به درس ریاضی اختصاص داده شده است:
- زمان به درس علوم اختصاص داده شده است:
- زمان به درس مطالعات اجتماعی اختصاص داده شده است:
از برابر است با:
گزینه دوم درست است. کافی است را به شکل کسر بنویسیم و در ضرب کنیم:
برابر است با:
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
مینا میخواهد کسر را به درصد تبدیل کند. کدام گزینه پاسخ درست خواهد بود؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر دمای هوا از درجه به درجه کاهش پیدا کند، درصد تغییرات متناظر با این تغییر برابر است با:
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر حجم آب مخزنی طی یک فرآیند از لیتر به اندازه افزایش پیدا کند و سپس در فرآیند دیگری نیز به میزان مجددا افزایش یابد، درصد تغییرات کلی آب این مخزن برابر با کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
تعداد افرادی که به نگهداری زنبور در یک کشور مشغولاند از سال ۲۰۰۸ تا ۲۰۱۳ از نفر به نفر افزایش پیدا کرده است. اگر بدانیم این تعداد از سال ۲۰۱۳ تا کنون افزایش داشته است، در حال حاضر چند نفر به نگهداری زنبور در این کشور مشغول هستند و درصد تغییرات نهایی از سال ۲۰۰۸ تا ۲۰۲۵ چقدر است؟
و
و
و
و
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
فرض کنید قیمت خرید یک مدل تلویزیون خاص طی مدت زمان دو سال از دلار به اندازه کاهش پیدا کرده است. اگر طی دو هفته مجددا کاهش قیمت برای این مدل تلویزیون داشته باشیم، قیمت نهایی و درصد تغییرات کل قیمت این کالا در انتهای این مدت به ترتیب برابراند با:
و
و
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
source
