بهینه سازی محدب، روشی است که بهوسیله آن میتوانیم مقدار بهینه یک تابع ریاضی را پیدا کنیم. یادگیری ماشین یکی از محبوبترین حوزههایی است که این روزها با آن رو به رو هستیم. با بیشتر شدن دادههای حجیم، نیاز به روشها و الگوریتمهایی که بتوانند این حجم از اطلاعات را بهدرستی تحلیل کرده و نکات مهم موجود در آن را بفهمند، بیشتر از قبل احساس میشود. یکی از ابزارهای بسیار مهم که در این مسیر به کمک پژوهشگران و مهندسان آمده، بهینهسازی محدب است. اگر بخواهیم ساده بگوییم، بهینهسازی محدب بهدنبال پیدا کردن بهترین پاسخ ممکن برای مسائلی است که در آن، تابع هدف شکلی محدب دارد و محدودیتها یا قیدهای آن بهصورت خطی تعریف شدهاند. این روش، پایه بسیاری از الگوریتمهای محبوب در یادگیری ماشین را تشکیل میدهد. به همین دلیل، این نوشتار از مجله فرادرس را به تشریح بهینه سازی محدب در یادگیری ماشین و جنبههای گوناگون تئوری و عملی آن به مثال پرداختهایم.
آنچه در این مطلب میآموزید:
-
مباحث نظری بهینهسازی محدب از جمله مجموعه محدب، اپیگراف، تابع محدب و غیره را میآموزید.
-
با روند و مراحل گام به گام فرایند بهینهسازی محدب در یادگیری ماشین آشنا خواهید شد.
-
مهم ترین ویژگی های بهینهسازی محدب را درک خواهید کرد.
-
مفاهیم پایه دوگانگی و شرایط KTT را یاد میگیرید.
-
با نقش، مزایا، معایب و کاربردهای بهینه سازی محدب آشنا میشوید.
-
بهینهسازی محدب را از طریق مثال و پیادهسازی در پایتون، بهتر درک خواهید کرد.


در ابتدای این مطلب، مروری بر تعریف بهینهسازی محدب به زبان ساده خواهیم داشت و نقش مهم بهینه سازی محدب در یادگیری ماشین را به شما توضیح میدهیم تا بدانید که این مبحث ریاضی چگونه به ابزاری مهم در تحلیل دادهها تبدیل شده است.
بهینه سازی محدب چیست؟
برای درک راحتتر مفهوم بهینه سازی محدب یا کوژ، مثال سادهای را بیان میکنیم. فرض کنید ظرفی کاسهمانند پیش روی شما قرار دارد و میخواهید پایینترین نقطه درون این کاسه که معمولاٌ در عمق آن قرار دارد را پیدا کنید. بهینهسازی محدب در واقع به همین فرایند پیدا کردن کمینهمقدار در اَشکال محدب اشاره دارد.
منظور از اشکال محدب، شکلهایی صاف و هموار و بدون پستی و بلندی هستند. برای درک بهتر میتوانید همان کاسه یا حتی یک تپه را تصور کنید که کاملا صاف و بدون فرورفتگی یا برآمدگی هستند و مانند یک کاسه صاف و یکدست، روی آنها از برآمدگی و فرورفتگی خبری نیست. در واقع بهدلیل همین صاف و همواتر بودن، میتوانیم نقطهای را روی آن پیدا کنیم که پایینترین جای آن شکل باشد.
تصاویر زیر، اشکال محدب و همچنین غیرمحدب را بهخوبی نشان دادهاند.
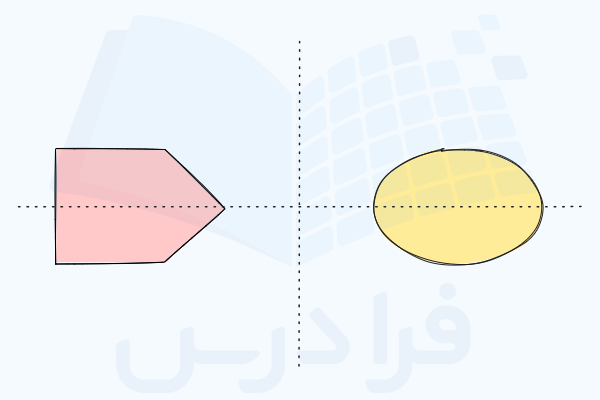
در بهینهسازی محدب، برخی مفاهیم ریاضی وجود دارند که نقش مهمی در حل مسائل ایفا میکنند و به کمک آنها میتوانیم نقاطی را که کمترین – یا حتی بیشترین مقدار – را در این شکلهای محدب دارند پیدا کنیم. در واقع، با استفاده از یک تابع یا شاخص، میزان ارتفاع – یا همان بالا پایین بودن – نقطه را میسنجیم. چیزی که در این توابع به دنبال آن هستیم، پیدا کردن نقطهای است که مقدار تابع را کمینه کند.
علاوه بر موارد اشاره شده، برای اینکه شکلی منظم با ساختاری مناسب داشته باشیم، لازم است که نقاط درون منحنی، برخی قیدها و شرایط را داشته باشند. در واقع همسو بودن با این قواعد به ما اطمینان میدهند که شکل موجود قابل پیشبینی، مناسب و بدون پستی و بلندی است.
با استفاده از مفاهیم مرتبط در ریاضیات و استفاده از برخی روشها میتوانیم پایینترین جای شکل را پیدا کنیم. این شیوه حل مسئله در حوزههای مختلفی از جمله موارد فهرست شده در زیر میتوان بسیار مفید و ارزشمند باشد.
- پیدا کردن بهترین راه برای چیدن برخی اقلام درون یک جعبه
- برنامهریزی مسیرهای بهینه برای رفت و آمد اتومبیلها
- آموزش کامپیوترها برای آموختن از دادهها و پیدا کردن الگوهای پنهان در آنها
- کمینه کردن واریانس بازدهی در بازار سهام، به شرط حداقل بازدهی تعیین شده
بهطور کلی، بهینه سازی محدب را میتوان کمک گرفتن از برخی مفاهیم ریاضی برای پیدا کردن نقطهای با کمترین ارتفاع در یک منحنی فاقد ناهمواری در نظر گرفت که برای حل بهتر و هوشمندانهتر انواع گوناگونی از مسائل مورد استفاده قرار میگیرد.
مجموعه محدب
مجموعههای محدب نقش بسیار مهمی در بهینهسازی بر عهده دارند. برای درک بهتر، این مجموعهها را میتوان اشکالی در نظر گرفت که اگر ۲ نقطه را در درون آنها انتخاب و به هم وصل کنیم، هیچگاه این خط از محدوده شکل خارج نمیشود. به دلیل وجود همین ویژگی، به آنها محدب میگوییم. در شکل زیر نمونهای از اشکال محدب و غیرمحدب و خطوط اشاره شده را مشاهده میکنید.
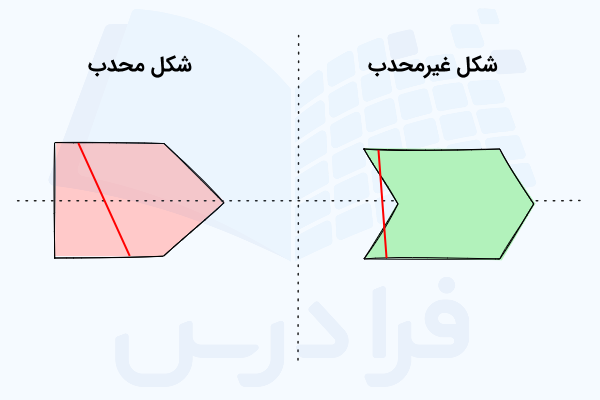
مجموعه محدب را میتوان بهشکل زیر توصیف کرد.
اپی گراف
همانطور که در تصویر زیر قابل مشاهده است، اپیگراف، ناحیهای است که روی نمودار یک تابع مانند یا بالاتر از آن قرار میگیرد.
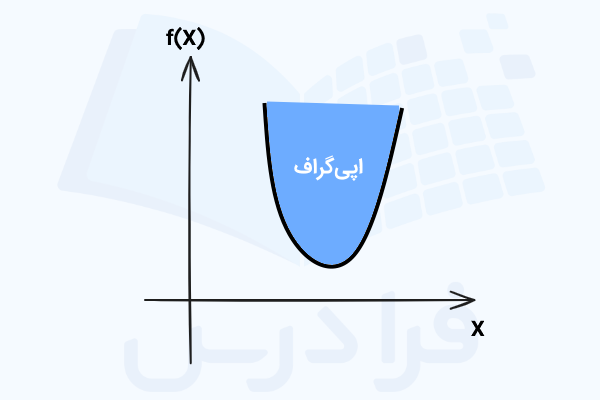
اکنون و پس از آشنایی با اپیگراف و مجموعههای محدب به سراغ یکی از مهمترین عناصر بهینهسازی یعنی توابع محدب میرویم.
تابع محدب چیست؟
تابع محدب نوعی تابع در ریاضیات است، با این مشخصه که میتوان بین هر ۲ نقطه دلخواه روی منحنی آن خطی مستقیم رسم کرد و این خط یا «وتر» همیشه در بالا یا روی نمودار قرار خواهد گرفت و از خود منحنی رد نمیشود. به بیان دیگر، شکل منحنی تابع این امکان را فراهم کرده که هر خط مستقیمی بین ۲ نقطه، در جایگاهی بالاتر از خود تابع قرار میگیرد.
توابع محدب دارای رفتاری قابل پیشبینی و قابل اطمینان هستند. یعنی وقتی بهدنبال نقطهای با کمترین مقدار روی نمودار آنها هستیم، میتوانیم مطمئن باشیم که نقطه مدنظر در ته نمودار قرار گرفته است. به این دلیل که ۲ طرف نمودار همیشه به سمت بالا خم شده است. بدینترتیب، برای پیدا کردن نقطهای با بیشینه مقدار هم میدانیم که باید بالاترین نقطه نمودار را در نظر داشته باشیم. این ویژگیها کمک میکنند تا کار با چنین توابعی بسیار راحت باشد.
تقریبا در هر جایی که صحبت از حل مسئله و بهینهسازی باشد، یعنی بسیاری از زمینههای ریاضیاتی، یادگیری ماشین و غیره، توابع کوژ یا محدب و کاربرد آنها را نیز میتوان دید. چون به کمک آنها میتوانیم سریعتر و بهینهتر به جوابهای مسئله دست پیدا کنیم.
از دید هندسی و دقیقتر که به این موضوع نگاه کنیم، در نمودار توابع محدب میتوان خطی از نقطه دلخواه به نقطه دلخواه دیگر مانند رسم کرد که همیشه در بالای نمودار قرار میگیرد تصویر زیر این مورد را به خوبی نشان داده است.
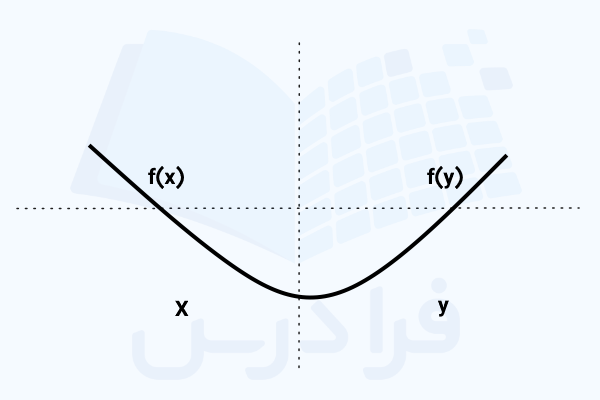
خوب است بدانید که اپیگراف تابع محدب، یک مجموعه محدب است.
به لحاظ ریاضی و جبری نیز، اگر برای هر دو نقطه دلخواه x و y و هر عددی بین صفر و ۱ مانند t رابطه زیر برقرار باشد، آنگاه میگوییم که تابع f محدب است.
حال اگر منفی یک تابع یعنی ، ویژگیهای یک تابع محدب را داشته باشد، آنگاه با تابع «مقعر» (Concave) رو به رو هستیم. در چنین حالتی خطی که بین ۲ نقطه x و y روی نمودار f رسم میکنیم، در زیر یا روی نمودار قرار خواهد گرفت. این نکته را نیز خوب است بدانید که هر تابع خطی، با نموداری مشابه یک خط صاف و بدون انحنا، در عین حال هم محدب و هم مقعر محسوب میشود. تابع سینوس و توابعی که تلفیقی از محدب و مقعر هستند و انحنا و خمیدگی رو به بالا و پایین دارند، جزو توابع «غیرمحدب» (Non-Convex) بهشمار میروند.
بررسی محدب بودن توابع
برای اینکه تابعی مانند محدب باشد، مشتق مرتبه دوم آن میبایست بزرگتر یا مساوی با صفر باشد. یعنی داریم:
فرق تابع محدب با تابع غیرمحدب
برای اینکه بتوانیم روشهای بهینهسازی خوب و کارآمدی ایجاد کنیم، لازم است با تفاوتهای موجود میان توابع محدب و توابع غیرمحدب آشنا باشیم. دو مثال زیر را در نظر بگیرید.
- تابع محدب:
- تابع غیرمحدب:
تابع محدب اشاره شده تنها یک مینیموم یا مقدار بهینه سراسری دارد. بههمیل دلیل به راحتی میتوان آن را پیدا کرد. از سوی دیگر، تابع غیرمحدب ما چندین مینیموم یا مقادیر بهینه محلی را در بر میگیرد که همین مورد باعث دشواری در پیدا کردن بهترین مینیموم خواهد شد. جدول زیر، دید خوبی در مورد این تفاوتها به شما میدهد.
| ویژگی | توابع محدب | توابع غیرمحدب |
| تعریف | دارای ویژگیهای محدب | نداشتن ویژگیهای محدب |
| تعداد نقاط بهینه | یک نقطه بهینه | چند نقطه بهینه |
| دشواری بهینهسازی | راحتتر | سختتر |
| شکل و ظاهر | سطح صاف | سطح نامنظم |
| مثال | ||
| کاربرد | رگرسیون خطی و غیره | شبکههای عصبی پیچیده |
| مصورسازی | یک نقطه کمینه | پستی و بلندیهای متعدد |

چگونه الگوریتم های بهینه سازی هوشمند را با فرادرس یاد بگیریم؟
درک مفاهیم پایهای مانند بهینهسازی محدب و همچنین آشنایی با روشهای پیشرفتهتری همچون الگوریتمهای بهینهسازی هوشمند، جزو مواردی هستند که در عصر حاضر برای بسیاری از پژوهشگران، دانشجویان، مهندسان و سایر علاقهمندان اهمیت بسیار بالایی دارند. بهینهسازی محدب بهعنوان سنگبنای طیف بسیاری از مسائل در حوزه علم داده و یادگیری ماشین عمل کرده و یادگیری صحیح آن مسیر آشنایی با الگوریتمهای پیشرفتهتر را هموار میکند. از سوی دیگر، الگوریتمهای هوشمند مانند الگوریتم ژنتیک، ازدحام ذرات و کلونی مورچگان، ابزارهایی قدرتمند برای حل مسائل پیچیده و غیرخطی هستند که با روشهای کلاسیک قابل حل نیستند.
با توجه به اینکه مشاهده فیلمهای آموزشی یکی از روشهای جدید و بسیار مؤثر در امر یادگیری مهارتهای گوناگون بهشمار میرود، شما میتوانید از فیلمهای آموزشی فرادرس مانند مجموعه فیلمهای آموزش الگوریتمهای بهینهسازی هوشمند مقدماتی تا پیشرفته از فرادرس برای این منظور استفاده کنید.
عناوین برخی از این فیلمهای آموزش موجود در این مجموعه را در ادامه فهرست کردهایم.
فرایند بهینه سازی محدب در یادگیری ماشین
نموداری که در ادامه آورده شده به شما کمک میکند تا درک بهتری از روند کلی حل مسائل بهینه سازی محدب در یادگیری ماشین بهدست آورید.
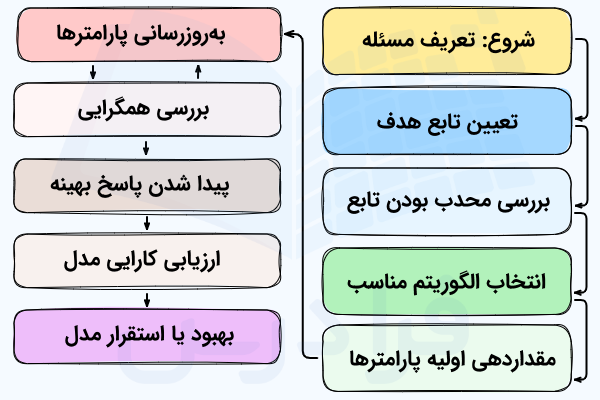
توجه داشته باشید که در مرحله بهروزرسانی پارامترها، طی چندین مرحله یا تکرار و با روشهایی مانند الگوریتم نقطه داخلی، گرادیان نزولی و غیره مقدار پارامترها تعیین میشود. در مرحله بعد نیز پیشرفت فرایند حل مسئله را بررسی میکنیم تا مطمئن شویم که به همگرایی و مینیموم سراسری دست پیدا کردهایم.
این نمودار، گامهای لازم برای حل مسائل بهینهسازی محدب و همچنین تکرارشونده بودن چنین الگوریتمهایی را برای رسیدن به پاسخ بهینه نشان میدهد.
مهم ترین ویژگی های بهینه سازی محدب
بهینهسازی کوژ چندین ویژگی شاخص از جمله موارد اشاره شده در زیر را دارد که آن را از سایر روشها متمایز میکند.
- تابع هدف محدب: تابع هدفی که میبایست بهینه کنیم از نوع محدب است. به بیان دیگر، شکل منحنی آن بهگونهای است که تنها یک نقطه بهینه – کمینه یا بیشینه – سراسری دارد و خبری از نقاط بهینه محلی نیست. مشتقدوم چنین توابعی که بهدنبال کمینه یا بیشینهسازی آن هستیم نیز نامنفی است.
- قیدهای محدب: در مسائل بهینهسازی با قیدهای محدب، راهحلهای مجاز و «قابل قبول» (Feasible) در ساختاری قرار میگیرند که شکلی ساده و قابل پیشبینی دارد. این قیدها که بیشتر تابعی محدب یا خطی هستند، مرزهایی را برای جست و جوی راهحل مشخص میکنند. به بیان دیگر فضای جست و جو توسط این قیدها محدود میشود.
- شرایط بهینگی: در مسائل بهینهسازی محدب، قواعد واضح و مشخصی برای تشخیص نقطه بهینه وجود دارد. در چنین توابعی، دستیابی به یک مقدار کمینه یا حتی بیشینه، به معنای رسیدن به نقطه کمینه یا بیشینه سراسری است. در این مسائل فرقی بین بهینه محلی و سراسری وجود ندارد.
- الگوریتمهای کارآمد: برای حل مسائل بهینهسازی محدب، میتوان از الگوریتمهای گوناگونی، از متدهای «نقطه درونی» (Interior-Point) گرفته تا روشهای مبتنی بر گرادیان و زیرگرادیان استفاده کرد که این کار را با سرعت بالا و بهشکلی کارآمد انجام میدهند. خصوصیت محدب بودن در این نوع مسائل کمک میکند تا الگوریتمهای اشاره شده بهشکل مؤثری راهحل بهینه را پیدا کنند.
مسائل بهینه سازی محدب چه هستند؟
این دسته از مسائل که جزو مسائل بهینهسازی دستهبندی میشوند در تلاش هستند تا یک تابع هدف با ویژگیهای محدب را با در نظر گرفتن محدودیتها و قیدهای محدب، کمینه یا بیشینهسازی کنند. خصوصیات مسائل بهینهسازی محدب کمک میکنند تا بتوان آنها را با الگوریتمهای مطمئن و با سرعت زیادی حل کرد.
نکات کلیدی در تعریف مسئله محدب
مسئله بهینهسازی محدب بهطور معمول به شکل زیر تعریف میشود.
- کمینهسازی تابع:
- با قیدهای:
در واقع، به دنبال این هستیم که تابعی محدب، مانند را تا جایی که بشود کمینه کنیم. در این میان، قیدهایی مانند برای های ۱ تا و نیز باید مدنظر قرار گیرند. ضمن اینکه نیز توابعی محدب هستند.
متغیرهای تصمیم، تابع هدف، قیدها
مؤلفه های مهم در تعریف مسئله شامل موارد زیر هستند.
- متغیرهای تصمیمگیری: مجهولهایی هستند که میبایست مقدار بهینه آنها را در طول فرایند بهینهسازی پیدا کنیم و در فضای تعریف میشوند.
- تابع هدف یا : تابعی محدب که سعی در کمینهسازی آن داریم. بهطور مثال، نُرمها، لگاریتم دترمینانت یا «log-det»
- قیدها: مؤلفههایی که میبایست خاصیت محدب بودن مسئله را حفط کنند. مانند معادلات خطی و
شکل استاندارد در مقابل شکل متعارف
جدول زیر، شباهتها و تفاوتهای این دو فرم را نشان میدهد.
| ویژگی | شکل استاندارد | شکل متعارف |
| هدف | کمینهسازی تابع محدب | کمینهسازی تابع خطی |
| قیدهای نابرابری | ||
| قیدهای برابری | – |
بازنویسی و تغییر شکل مسئله این امکان را فراهم میکند تا الگوریمهای حل مسئله از روشهای تخصصی و بهینه برای حل استفاده کنند.
روش های فرمول بندی مجدد
این روشها را در ادامه آوردهایم.
- اضافه کردن متغیرهای کمکی معروف به «اسلک» (Slack) برای تبدیل نامساویها به معادلات که در راستای سادهتر کردن مسئله انجام میشود.
- تبدیل اپیگراف، روش دیگری برای فرمولهسازی مجدد محسوب میشود که در آن متغیر کمکی با شرط را برای بهینهسازی هدف خطی را داریم.
- نمایش مخروطی بهعنوان تکنیکی دیگر، نرمها را با استفاده از ساختارهای مخروطی مرتبه دوم مدل میکند.
مفاهیم پایه دوگانگی و شرایط KTT
در اینجا قصد داریم تا نگاهی به خصوصیات ریاضی مسائل داشته باشیم. البته باید بگوییم که آشنایی با چنین مفاهیمی برای استفاده از ابزارهای بهینهسازی ضروری نیست و میتوانید بدون در نظر گرفتن آن نیز مدل خود را با یک زبان مدلسازی بنویسید و حل آن را به سیستم کامپیوتری بسپارید. با این تفاصیل، آشنا بودن با مفاهیمی مانند شرایط KTT و دوگانگی، درک بهتری از عملکرد الگوریتمهای مورد استفاده به شما خواهد داد.
دوگانگی
در زمینه بهینهسازی خطی، برای هر مسئله که با آن رو به رو میشویم و با نام «مسئله اصلی» (Primal Problem) شناخته میشود، یک مسئله آینهای یا متناظر به نام «مسئله دوگان» (Dual Problem) نیز وجود دارد. نکته جالب در اینجا، این است که با انجام مجموعهای از کارها و استفاده از قواعدی مشخص چه با کامپیوتر و چه بهصورت دستی میتوانیم مسئله مورد نظر را به شکل دوگان آن تبدیل کنیم. بدینترتیب با بهدست آوردن مسئله دوگان با قواعدی که در ادامه تشریح میشود، به فرصتها و شیوههای سودمندی برای حل مسئله دست خواهیم یافت.

برای اینکه درک و شناخت خوبی از مسئله دوگان پیدا کنید، مثال ساده زیر را در نظر بگیرید.
بیشینهسازی تابع زیر:
با شرایط زیر:
در واقع قصد داریم تا مقدار تابع هدف را بیشینهسازی کنیم. در این میان، قیدهای زیر میبایست رعایت شوند.
- مقدار نباید از ۴ بیشتر باشد.
- مقدار نباید از ۱۲ تجاوز کند.
- بیشترین مقداری که میتواند داشته باشد حداکثر ۱۸ است.
- مقادیر و نیز میباست عددی مثبت یا صفر باشد.
اکنون اگر بخواهیم مسئله دوگان متناظر با این مدل را بنویسیم، به شکل زیر خواهد بود.
کمینهسازی تابع زیر:
با شرایط زیر:
به کمک تصویر زیر میتوانید درک بهتری از رابطه بین مسئله اصلی و مسئله دوگان متناظر با آن پیدا کنید.

- رنگ سبز: اگر در مسئله اصلی به دنبال بیشینه کردن مقدار تابع باشیم، در مسئله دوگان آن با کمینهسازی رو به رو هستیم و عکس این قضیه نیز وجود دارد.
- رنگ زرد: هر متغیر در مسئله اصلی متناظر با یک قید در مسئله دوگان است. ضرایب تابع هدف اصلی مانند ۳ و ۵، در واقع قیدهای دوگان هستند.
- بنفش: کرانهای موجود در متغیرهای اصلی مانند ، بر قیدهای مسئله دوگان تأثیر میگذارند.
- آبی: قیدهای مسئله اصلی در مسئله دوگان بهصورت متغیر ظاهر میشوند. پارامترهای قیدهای اصلی مانند ۴، ۱۲ و ۱۸ نیز به ضرایب تابع هدف مسئله دوگان تبدیل میشوند.
- فیروزهای: در قیدهای مسئله اصلی، را داریم که به کرانهای در متغیرهای مسئله دوگان تبدیل میشود.
- قرمز: ماتریس ضرایب قیدها در مسئله دوگان نیز ترانهاده ماتریس ضرایب قیدها در مسئله اصلی محسوب میشود.
اکنون که با مفهوم دوگانگی در بهینهسازی خطی آشنا شدید میتوانیم به نسخه کلیتر آن در مسائل محدب یعنی دوگانگی لاگرانژی نگاه کنیم.
تابع دوگانه لاگرانژی
فرض کنید مجموعهای از ضرایب لاگرانژ شامل با عناصر غیرمنفی یعنی و همچنین بردار را داریم. در چنینی حالتی معادله زیر برقرار است.
تابع دوگان نیز بهصورت زیر خواهد بود.
به کمک اصل دوگانگی در بهینهسازی میتوانیم پایینترین حد ممکن پاسخ بهینه را تخمین بزنیم و شناخت بهتری از حساسیت مسئله به شرایط پیدا کنیم.
شرایط KKT
در این قسمت، با شرایط KKT آشنا خواهید شد. KKT در واقع مجموعهای از قواعد مهم در حل مسائل بهینهسازی محدب را شامل میشود که قیدهایی از نوع معادل و نامساوی دارند. این شرایط به زبان ساده، ساختاری هستند که با آنها میتوان پاسخهای بهینه مسائل محدب را شناسایی کرد. بسیاری از روشهای عددی حل مسئله بهینهسازی بر پایه همین شرایط ساخته شدهاند. در موقعیتهای سادهتر نیز امکان پیدا کردن پاسخ نهایی را بهصورت تحلیلی فراهم میکنند. ویژگی دیگر این رویکرد، ترکیب متغیرهای اصلی یا اولیه و همچنین متغیرهای دوگان است که باعث میشود اطلاعات ارزشمندی در مورد پاسخ پیدا کنیم. بهطور مثال مشخص میکند که کدام قیدها در تعیین پاسخ نهایی تأثیر داشتهاند یا اینکه بهطور مثال در یک سیستم قدرت، قیمت برق بهچه صورتی یا به چه مقداری تعیین شده است.
برای اینکه راهحلی متشکل از متغیرهای اولیه و ضرایب لاگرانژ یعنی بهینه باشد، میبایست ۴ شرط مهم را بر آورده کند. در ادامه این شرایط تشخیص بهینگی را آوردهایم.
- «تحققپذیری اولیه» (Primal Feasibility): یعنی تمامی قیدهای نامساوی بهصورت و قیدهای مساوی بهصورت باشند.
- «تحققپذیری دوگانه» (Dual Feasibility): ضرایب لاگرانژِ مربوط به قیود نامساوی، یعنی ، نباید منفی باشند. یعنی داریم:
- «آهستگی مکمل» (Complementary Slackness): در اینجا میخواهیم مطمئن شویم که حاصلضرب میبایست برای تمامی قیدها برقرار باشد. به بیان دیگر اگر محدودیتی نداریم، ضریب آن هم صفر شود.
- «ایستایی» (Stationarity): شرط بیانگر این است که در نقطه بهینه، ترکیب گرادیان تابع هدف، گرادیان قیدها و اثر قیدهای مساوی باید صفر باشد.
میتوان گفت که هرگاه این چهار اصل برقرار باشند، به نقطه بهینه رسیدهایم.
برداشت های اقتصادی و هندسی
در این قسمت به ۲ برداشت مهم و کاربردی اقتصادی و هندسی مسائل بهینهسازی اشاره کردهایم.
- «قیمتهای سایهای» (Shadow Prices): با نشان داده میشود و بیانگر هزینه نهایی است که در ازای کاهش محدودیتها پرداخت میشود.
- «ابرصفحههای پشتیبان» (Supporting Hyperplanes): متغیرهای دوگانه، خطهای مماس را برای اپیگرافها تعریف میکنند.
دلیل اهمیت بهینه سازی محدب
در این قسمت توضیح میدهیم که چرا بهینه سازی محدب تا این اندازه مهم است.
نقاط قوت در مقابل سایر روش ها
مزایای زیر را نسبت به روش های غیرمحدب ارائه میدهد.
- بهینگی سراسری: یکی از مهمترین ویژگیهای بهینهسازی محدب این است که راهحل نهایی همیشه بهترین حالت ممکن در سطح سراسری است و در نقاط مینیموم محلی گیر نمیافتد.
- قابل حل بودن در زمان چندجملهای: بسیاری از مسائل محدب با شرایط معمولی میتوانند با روشهایی همچون الگوریتم «نقطه درونی» و در زمان معقولی حل شوند.
- امکان تحلیل حساسیت دقیق با استفاده از مفهوم «دوگانگی» (Duality) را نیز دارد.
کاربرد در کنترل سیستم و یادگیری ماشین
در ادامه به نقش محدب بودن در زمینههای گفته شده اشاره کردهایم.
- SVM-ها: برای دستهبندی دادهها از «برنامهریزی درجه دوم» (QP) استفاده میشود که در ساختار بهینهسازی محدب قرار دارد.
- رگرسیون Lasso: وجود مدل را به سمت تنکتر شدن هدایت میکند.
- MPC: در سیستمهای کنترلی برای حفظ پایداری سیستم از بهینهسازی خطی یا درجه دوم بهصورت بلادرنگ استفاده میشود.
چالشهای رایج در شرایط غیرمحدب
در مسائل غیرمحدب با مشکلاتی مانند آنچه در ادامه اشاره شده رو به رو هستیم.
- گرفتار شدن در کمینه محلی: یکی از مشکلات رایج در اینگونه مسائل، گیر افتادن در کمینه محلی و جوابهای غیرقابل پیشبینی و غیربهینه است.
- در چنین مسائلی بهجای اتکا بر روشهای دقیق مانند «Convex Relaxation» یا «تبدیل محدب»، از تنظیم اکتشافی استفاده میشود.
- عدم تضمین همگرایی در اینگونه مسائل، ممکن است زمان اجرای نامعینی را بهدنبال داشته باشد.

مثال ساده حل مسئله بهینه سازی محدب
در این قسمت، مثال عملی سادهای از یک مسئله بهینه سازی محدب را آوردهایم.
در خط نخست، کتابخانه cvxpy را برای مدلسازی و حل مسائل بهینهسازی محدب وارد میکنیم. سپس تعریف متغیرهای x و y را داریم که قرار است مقدار آنها در طول حل مسئله محاسبه شود. در ادامه تعریف تابع هدف objective را داریم که سعی در کمینهسازی مجموع مربع فاصله از دارد. قید ما در این مسئله در متغیر constraintsتعریف شده که میگوید مجموع x و y میبایست بزرگتر یا مساوی با 1 باشد. مسئله را در problem تعریف کردهایم که تابع هدف و قید را در بر میگیرد. برای حل مسئله و پیدا کردن مقدار بهینه برای x و y از متد .solve() استفاده کردهایم. در نهایت نیز مقدار بهینه متغیرها و همچنین مقدار کمینه تابع هدف مشابه زیر، در خروجی چاپ میشود.
Optimal Solution: x = 0.99999999 y = 2.00000001 Optimal Objective Value: 1.01953125e-15
بهینه سازی محدب در یادگیری ماشین
بسیاری از مسائل مرتبط با یادگیری ماشین را میتوان در قالب مسائل بهینهسازی محدب مدلسازی کرد. به همین دلیل بهینهسازی محدب را میتوان یکی از مهمترین ابزارهای این حوزه برشمرد. بهطور مثال، در مسائل مربوط به «دستهبندی» (Classification) سعی داریم که بهترین ابرصفحه یا مرز را برای تقسیم دادهها در قالب کلاسهای متفاوت پیدا کنیم. بنابراین کافیست تا مسئله را به شکل مسائل بهینهسازی محدب تبدیل کنیم. در چنین حالتی تابع هدف برابر با فاصله ابرصفحه با دادهها است. از سوی دیگر قیدهای مسئله نیز، معادلات خطی هستند که دستهبندی صحیح دادهها توسط ابرصفحه را تضمین میکنند.
در حوزه یادگیری ماشین، مدلهایی میسازیم که توانایی آموختن از دادهها و دیتاستها را داشته باشند و بههمین ترتیب عملکرد قابل قبولی را نیز روی دادههای جدید ارائه دهند. برای این منظور میبایست پارامترهای مدل را بهشکلی انتخاب کنیم که میزان خطای پیشبینی را تا حد ممکن کاهش دهند. بهینهسازی محدب بهعنوان یک روش ریاضی در اینجا وارد عمل میشود و بهکمک آن میتوان مقدار بهینهای را برای «تابع زیان» (Loss Function) پیدا کرد. این چالش را میتوان در قالب مسئله بهینهسازی محدب، با تابع هدف محدب و قیدهای خطی حل کرد.
بهینهسازی محدب به دلیل مزایای متعددی مانند تضمین همگرایی و رسیدن به جواب، روشهای مؤثر و کارآمد و سایر ویژگیها، ابزار بسیار قدرتمندی در حوزه یادگیری ماشین محسوب میشود.

روش های بهینه سازی محدب در یادگیری ماشین
فهرست زیر برخی از مهمترین روشهای حل مسائل یادگیری ماشین که با بهینهسازی محدب فرمولهبندی شدهاند را نشان میدهد.
- گرادیان نزولی
- روش نیوتن
- روشهای نقطه درونی
- گرادیان نزولی تصادفی
با در نظر گرفتن اینکه اولویت ما سرعت پیدا کردن پاسخ باشد یا میزان پیچیدگی محاسباتی، میتوانیم روش مناسبی را برای پروژه خود انتخاب کنیم.
کاربرد بهینه سازی محدب در الگوریتم های یادگیری ماشین
روشهایی مانند گرادیان نزولی میتوانند بهخوبی مسائل بهینهسازی محدب را حل کنند. بهطور مثال، در رگرسیون خطی قصد پیدا کردن وزنهایی را داریم که میزان اختلاف بین خروجیهای پیشبینی شده و دادهها واقعی یا به بیان دیگر خطای میانگین مربعات را کمینه کند. همچنین میتوان ماشینهای بردار پشتیبان را مثال زد که در آن بهدنبال پیدا کردن ابرصفحهای هستیم که دادهها را به شکل کارآمدی به دو دسته تقسیم کند.
بهینهسازی محدب نقش مهمی در یادگیری ماشین دارد و در الگوریتمهای مختلفی مانند موارد زیر بهکار میرود.
- رگرسیون خطی
- رگریون لجستیک
- ماشینهای بردار پشتیبان
- شبکههای عصبی
رگرسیون خطی
در رگرسیون خطی بهدنبال این هستیم که مقدار «MSE» بین خروجیهای پیشبینی شده و خروجیهای واقعی را کمینه کنیم. در اینجا، MSE که فرمول آن در ادامه آورده شده، نسبت به پارامترهای مدل یعنی ، شکلی محدب دارد.
در چنین حالتی مقدار مینیموم پیدا شده، همان بهینه سراسری موجود در دادههایمان محسوب میشود.
رگرسیون لجستیک
در رگرسیون لجستیک به دنبال ایجاد مدلی هستیم که توانایی پیشبینی احتمال تعلق یک نمونه به یک دسته مشخص را داشته باشد. در ادامه، تابع هزینه یا همان معیار خطا که محدب است و میبایست کمینه شود را آوردهایم.
محدب بودن در اینجا، کمک میکند تا بهترین مقادیر موجود برای پارامترها مشخص شوند.
ماشین های بردار پشتیبان
SVM یا ماشین بردار پشتیبان یکی از قدرتمندترین روشهایی است که میتوان برای حل مسائل دستهبندی بهکار برد. در این روش با تابع هدف محدب رو به رو هستیم و قصد داریم تا با بهینهسازی آن ابرصفحه و مرزی را برای دستهبندی دادهها بهبهترین شکل، بیابیم. در ادامه، شکل کلی مسئله SVM را آوردهایم.
کمینهسازی تابع هدف:
با رعایت قیدهای:
این مسئله، نوعی بهینهسازی با تابع هدف درجه دوم محدب است که برای حل آن میتوان از الگوریتمهای گوناگون استفاده کرد.
شبکه های عصبی
در زمینه یادگیری عمیق، مدلهایی مانند شبکههای عصبی معمولاٌ دارای تابع زیان غیر محدب هستند که از پیچیدگی معماری آنها ناشی میشود. با این وجود نمیتوان از نقش محدب بودن در بسیاری از جنبههای این مدل مانند توابع فعالساز و توابع زیان غافل شد.
- توابع زیان: خیلی از توابعی که برای بررسی میزان خطا در یادگیری عمیق بهکار میروند، خاصیت محدب بودن دارند و در رسیدن به پاسخ بهینه بسیار مفید هستند. بهطور مثال، «هِنج» (Hinge) در ماشینهای بردار پشتیبان و «کراسانتروپی» در مسائل دستهبندی جزو همین موارد بهشمار میروند.
- توابع فعالساز: تابع ReLU یکی از رایجترین توابع فعالساز در شبکههای عصبی است که همزمان با اضافه کردن عناصر غیرخطی به مدل، در قسمتهایی از دامنه خود همچنان ویژگی محدب بودن را دارد. سادگی این تابع با فرمول زیر و خطی بودن آن در برخی نواحی، امکان یادگیری سریعتر و بهتر را برای شبکههای عصبی را فراهم میکند.
تکنیک های رایج برای بهینه سازی محدب در یادگیری ماشین
در این قسمت میخواهیم تعدادی از روشهای متداول برای حل مسائل بهینه سازی محدب در یادگیری ماشین را بررسی کنیم.

گرایان نزولی
یکی از رایجترین روشهای بهینهسازی در این حوزه که با توجه به اصول بهینهسازی محدب ایجاد شده، «گرادیان نزولی» (Gradient Descent) نام دارد و بر اساس مشتق تابع هدف کار میکند. در این روش، پارامترها به سمت کاهش مقدار تابع هدف حرکت میکنند. به بیان دیگر، هر بار یک گام کوچک در جهت عکس شیب یا گرادیان منفی تابع هدف برداشته میشود. اندازه این گامها با نرخ یادگیری تعیین میشود. در صورتیکه این نرخ به درستی تنظیم شود و تابع هدف نیز محدب باشد، با این تکنیک میتوان خیلی سریع بهترین راهحل ممکن را پیدا کرد. پیادهسازی این روش نیز ساده است.
بهطور مثال، گرادیان نزولی را میتوانید مانند کوهنوردی تصور کنید که هنگام پایین آمدن، در راستای شیب تند سرازیری گام بر میدارد. از دید ریاضی نیز همین کار بهصورت تکرار شونده و برای بهروز کردن پارامترهای مدل یعنی انجام میشود.
لازم است اشاره کنیم که همان نرخ یادگیری و تعیین کننده اندازه قدمهاست.
گرادیان نزولی تصادفی
«SGD» یا گرادیان نزولی تصادفی، روشی است که هنگام کار با دیتاستهای بزرگ و حجیم میتوان از آن استفاده کرد. در این روش، بهجای بررسی کل دیتاست، تنها از بخش کوچکی از دادهها که بهطور تصادفی نیز انتخاب شده و «Batch» نام دارد، برای بهدست آوردن گرادیان استفاده میشود. اندازه بخش انتخابی نیز با «اندازه Batch» مشخص میشود. تصادفی بودن این الگوریتم ممکن است باعث شود که روند کندتری نسبت به آموزش دستهای برای رسیدن به جواب داشته باشد.
روش نیوتن
این روش بهینهسازی، از مشتق دوم تابع هدف برای تعیین مسیر حرکت بهروزرسانیها استفاده میکند. با اینکه روش نیوتن در برخی مسائل میتواند نسبت به گرایان نزولی خیلی سریعتر به جواب برسد اما پیچیدگی بیشتری دارد. همچنین در صورتیکه حجم دادهها بسیار زیاد باشد، محاسبات نیوتن سنگینتر شده و وابستگی بیشتری به شرایط اولیه مسئله پیدا میکند.
روش های شبه نیوتنی
روشهای شبهنیوتن به دستهای از تکنیکهای بهینهسازی اشاره دارند که بهجای محاسبه مشتق دوم تابع هدف بهطور مستقیم، از اطلاعات مشتق اول برای این منظور کمک میگیرند. چنین روشی علاوه بر اینکه میتواند سریعتر از روش نیوتن عمل کند، حساسیت کمتری نیز به شرایط شروع خواهد داشت. از رایجترین الگوریتمهای این دسته میتوان به روش «BFGS» اشاره کرد.
گرادیان مزدوج
گرادیان مزدوج، روشی است که میتواند برای حل دستگاههای معادلات خطی بزرگ مورد استفاده قرار گیرد. در واقع هنگامیکه با ماتریس خلوت بزرگی رو به رو هستیم و حل مستقیم آن به لحاظ پردازشی ممکن است پرهزینه باشد، استفاده از این تکنیک بسیار مفید خواهد بود و عملکرد خوبی نسبت به سایر روشها ارائه میدهد. الگوریتم گرادیان مزدوج با تکیه بر فرایندی تکرارشونده و با کمینهسازی یک تابع درجه دوم، بهتدریج به جواب میرسد.
روش نقطه داخلی
از دیگر الگوریتمهای قدرتمند برای حل مسائل بهینهسازی محدب میتوان به روشهای «نقطه درونی» (Interior-Point) اشاره کرد. این روشها بهطور خاص برای حل مسائل بزرگ و پیچیده در برنامهریزی درجه دوم و خطی بسیار کارآمد و مفید هستند. شیوه کار آنها نیز به این صورت است که طی تکرارهایی، از داخل فضای مجاز حل و بدون خارج شدن از ناحیه تعریف شده برای پاسخ، به سمت مرزهای آن پیش روند. مزیت این روشها را در ادامه آوردهایم.
- پیچیدگی زمانی چندجملهای: این مزیت که بیانگر کارایی بالایی این روشهاست کمک میکند تا با تعداد تکرارهای محدود و قابل پیشبینی، راهحل را پیدا کنند.
- پایدار بودن: حساسیت کمی به اندازه مسئله و دادهها دارند. به همین دلیل، پایداری خوبی در مسائل پیچیده با ابعاد بالا ارائه میدهند.

مزایا و معایب بهینه سازی محدب در یادگیری ماشین
بهینهسازی محدب چند مزیت و نقطه ضعف مهم دارد که در این قسمت به آن پرداختهایم.
نقاط قوت
فهرست زیر شامل مزایای بهینهسازی محدب است.
- اطمینان از همگرایی و دستیابی به پاسخی بهینه با استفاده از روشهای اشاره شده
- وجود الگوریتمهای کارآمد برای بهینهسازی محدب
- اختلالپذیری و نویزپذیری کمتر نسبت به مسائل غیرمحدب
- کابردهای فراوان روشهای بهینهسازی محدب در زمینههای، بانکداری، مهندسی، ماشینلرنینگ و غیره
نقاط ضعف
فهرست زیر شامل معایب بهینهسازی محدب است.
- کاربردهای محدود، به دلیل عدم کارایی روشهای بهینهسازی محدب برای مسائل غیرمحدب
- پیچیدگی محاسباتی زیاد برای مسائل بزرگ، علیرغم حل سریع و کارآمد مسائل بهینهسازی
- احتمال دستیابی به راهحل بهینه غیریکتا در صورت وجود پاسخهایی به همان اندازه خوب و ایجاد مشکل در فرایند تصمیمگیری در چنین حالتی
- وابسته بودن خروجی به صحت فرضیات مرتبط با دادهها و ساختار مسئله
مثال SVM با بهینه سازی محدب
ماشین بردار پشتیبان یکی از الگوریتمهای شناخته شده در حوزه یادگیری ماشین محسوب میشود که میتوان با آن مسائل دستهبندی را حل کرد. برای اینکه درک بهتری از کاربرد بهینهسازی محدب در ماشینلرنینگ پیدا کنید، این قسمت را به پیادهسازی الگوریتم SVM در پایتون اختصاص دادهایم.
در شروع کدنویسی، لازم است ابزارهای مختلفی از جمله کتابخانههای نامپای، matplotlib، سایکیتلرن را وارد کنید، همانطور که در کد زیر آورده شده است.
کتابخانه CVXOPT یک ابزار پایتونی است که با استفاده از آن میتوانید مسائل بهینهسازی محدب را بهسادگی با این زبان محبوب پیادهسازی کنید. make_blobs از کتابخانه سایکیتلرن نیز برای تولید دیتاست برای مسئله مورد استفاده قرار گرفته است.
در ادامه کدهای کلاس اصلی برنامه یعنی SVM را آوردهایم.
دیتاست و ویژگیهای مربوط به دادهها، جزو مهمترین عناصر در حوزه ML بهشمار میروند. به همین دلیل، یکی از مهمترین کارهایی که در پیادهسازی الگوریتم SVM میبایست انجام دهیم این است که ویژگیها یا فیچرهای مربوطه را از دادههای مسئله بیرون بکشیم. با دسترسی به ویژگیها و انتخاب مهمترین آنها میتوانیم از این مرحله عبور کرده و به سراغ محاسبه ریاضیاتی مدل برویم. تابع fit که قرار است مدل را آموزش بدهد، ویژگیها و برچسب را به عنوان پارامتر ورودی میگیرد. برای اینکه بدانیم دادههای ما شامل چند نمونه و هر نمونه دارای چند ویژگی است از متد x.shape استفاده کردهایم.
پیش از توضیح ادامه کدها باید بگوییم که در SVM با مفهومی به نام کِرنل و ایجاد آن رو به رو هستیم. در کلاس SVM چندین روش کرنل مختلف وجود دارد تا مدل ما با توجه به ماهیت دادهها بتواند بهترین الگوی ممکن را پیدا کند.
در یکی از مطالب پیشین مجله فرادرس، روش های کرنل در یادگیری ماشین از طرز کار گرفته تا استفاده از آن در مسائل را به زبان ساده توضیح دادهایم که مطالعه آن میتواند اطلاعات مفیدی را در این باره در اختیارتان قرار دهد.
در خط شماره ۸ از کدهای بالا، ماتریسی به نام k ، با ابعاد «n_samplesدر n_samples » ایجاد کردهایم که قرار است مقدار کرنل را نگه دارد. مقدار هر خانه آن نیز در خط آخر و با ضرب داخلی و متد np.dot کتابخانه نامپای محاسبه میشود.

مفاهیم ریاضی
برای درک بهتر اینکه چرا رویکرد اشاره شده را بهکار گرفتهایم، تابع محدب ریاضی در ادامه آورده شده را در نظر داشته باشید.
در فرمول بالا، ساختار رایج برای مسائل برنامهریزی درجه دوم را مشاهده میکنید که قرار است در این بخش پیادهسازی کنیم. در واقع چنین مسئلهای که شامل پارامترهای است را به ابزار CVXOPT میدهیم.
توجه داشته باشید که از میان این پارامترها، تنها و ضروری هستند.
کدهای زیر نشان میدهند که مفهوم ریاضی گفته شده و دوگان تابع را به چهشکلی میتوان کدنویسی کرد.
در خط نخست ماتریس را تعریف کردهایم که از ضرب خارجی برچسب در خودش و سپس ضرب عنصر به عنصر آن در ماتریس هسته یا محاسبه می شود. خط شماره ۲، بیانگر پارامتر یا بردار است که از n_samples عدد ۱- تشکیل شده است. پس از آن تعریف مربوط به ماتریس G یا همان قیدهای نامساوی را داریم. دستور np.diag در اینجا یک ماتریس قطری ایجاد میکند که در قطر اصلی آن، عناصر np.ones(n_samples) * -1 که در واقع شامل اعداد ۱- است جای گرفته است. در خط شماره ۴، بردار را تعریف کردهایم که شامل n_samples عدد صفر است. پس از آن، پارامتر A را داریم که ماتریسی برای قید تساوی موجود در فرمول ریاضی اشاره شده محسوب میشود. با توجه به پارامترهای تعریف این ماتریس یعنی y, (1, n_samples) میتوان مشاهده کرد که نتیجه یک بردار سطری شامل برچسبهای می شود. در خط آخر نیز پارامتر را تعریف کردهایم که همان بردار سمت راست قید مساوی است. این ماتریس شامل یک عنصر با مقدار صفر است.
تا این قسمت از مثال پیادهسازی الگوریتم SVM توانستیم پارامترهای برنامه را مشخص کنیم. اکنون زمان آن رسیده تا معادله ایجاد شده را حل کنیم. برای حل از ابزارهایی به نام حل کننده استفاده میکنیم که با مراجعه به مستندات CVXOPT میتوانید فهرستی از آنها پیدا کنید. برای تسهیل پیادهسازی در اینجا از حل کننده استفاده میکنیم.
تعیین کران ها و سایر پارامترها
کدهای زیر را در نظر بگیرید.
در خط نخست، با دادن پارامترهای به دست آمده از مرحله قبل به حل کننده، به سراغ پیدا کردن راهحل مسئله میرویم. خروجی تابع qp که همان جوابهای مسئله است درون یک دیکشنری به نام sol قرار میگیرد. این دیکشنری شامل گزینههای متعددی است اما با توجه به اینکه در حال پیادهسازی SVM هستیم، عنصر X را از آن بیرون میکشیم. سپس و در خط بعد، به کمک تابع ravel از کتابخانه نامپای، خروجیها را بهصورت یک ماتریس خطی در میآوریم.
وزن ها و مقادیر بایاس
محاسبه بایاس و همچنین وزنها در مدل SVM برای حل مسئله بهینهسازی محدب، به کدهای زیر نیاز دارد.
در خط نخست تعریف بایاس یا b را داریم که مقدار اولیه آن صفر است. سپس درون حلقه مقدار بایاس طی تکرارهایی با استفاده از کرنل، بردار پشتیبان و برچسب آن به دست میآید. حلقه دوم نیز وزن نهایی را محاسبه میکند. تعیین کردن وزن و بایاس برای کلاسها در SVM اهمیت زیادی دارد. به دلیل اینکه لازم است نویزها و دیتاست را بهخوبی مدیریت کنیم تا برای مدل مشکلاتی مانند کمبرازش یا بیشبرازش پیش نیاید. این پارامترها درون حلقه قرار گرفتهاند و بهطور مداوم بهروزرسانی میشوند.
تابع پیش بینی
حالا و در این قسمت به سراغ مهمترین بخش پیادهسازی یا همان تابع پیشبینی میرویم. تابع predict با بررسی علامت خروجی، نشان میدهد که هر نمونه به کدام کلاس تعلق دارد. با توجه به اینکه مسئله ما ۲ کلاس دارد، در اینجا با حالتهای «۱+» و «۱-» به عنوان خروجی رو به رو هستیم.
در خط نخست تعریف تابع پیشبینی را داریم که داده آزمایشی یا xtest را به عنوان ورودی دریافت میکند تا کلاس آن مشخص شود. در بدنه تابع، ضرب داخلی داده تست و وزن، محاسبه شده سپس با بایاس جمع میشود. تابع np.sign علامت خروجی را بر میگرداند. بهطور مثال اگر مثبت باشد، پیشبینی ۱+ است و در صورت منفی بودن یعنی ۱- را پیشبینی کرده است.
تابع f
این تابع برای مصورسازی استفاده میشود که برای موفقیت SVM اهمیت زیادی دارد.
مرحله تست
اکنون به مرحلهای رسیدهایم که میتوانیم عملکرد الگوریتم دستهبندی را ببینیم.
همانطور که پیشتر نیز اشاره شد، دیتاست ما با تابع make_blobs ساخته شده و با توجه به ماهیت مسئله آن را آماده کردهایم. اکنون برای درک بهتر عملکرد مدل آن را به تصویر میکشیم.
تصویر زیر، خروجی این مثال دستهبندی با الگوریتم بهینهسازی محدب را نشان میدهد.
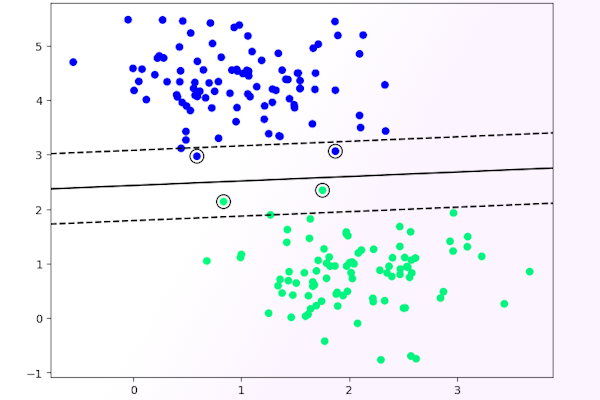
کاربردهای بهینه سازی محدب و استفاده از آن در مسائل دنیای واقعی
تا این قسمت از مطلب، با مباحث نظری بهینهسازی محدب و همچنین پیادهسازی عملی آن در قالب یک مثال آشنا شدید. اما توانمندیهای بهینهسازی محدب به همین زمینهها ختم نمیشود و در بسیاری از حوزه و صنایع گوناگون همچون مهندسی، امور مالی، یادگیری ماشین و غیره نیز میتوان از مزایای آن بهرهمند شد. در این قسمت از مطلب برخی از این کاربردها را توضیح دادهایم.
بهینه سازی سبد سرمایه گذاری
نخستین کاربردی که از بهینهسازی محدب در دنیای واقعی بیان میکنیم، بهینهسازی پرتفوی سرمایهگذاری است که بهعنوان نمونهای شناخته شده، به حوزه امور مالی تعلق دارد. مهمترین هدفی که از بهبود سبد سرمایهگذاری بهدنبال آن هستیم، این است که ترکیبی صحیح و بهینه از داراییها را برای سرمایهگذاری انتخاب کنیم که ضمن بیشینه کردن سود ما، کمترین میزان ریسک و ضرر را بههمراه داشته باشد.

در چنین مدلهایی بهطور معمول برای نمایش میزان ریسک و بازده از تابع درجه دوم بهعنوان تابع هدف استفاده میشود و از سوی دیگر قیدهای مدل نیز خطی هستند. روشهای بهینهسازی محدب، ابزاری مؤثر برای حل این مسئله و پیدا کردن بهترین ترکیب داراییها محسوب میشود و سرمایهگذاران بهکمک نتایج آن میتوانند تصمیمگیری و برنامهریزی بهتری در مورد نحوه ترکیب سبد دارایی مناسب خود داشته باشند.
در صورت علاقهمندی به این موضوع، مشاهده فیلم آموزش بهینهسازی سبد سهام با روشهای بهینه سازی کلاسیک و هوشمند در متلب از فرادرس که لینک آن نیز در ادامه آورده شده میتواند اطلاعات خوبی را در این باره در اختیارتان قرار دهد.
پردازش سیگنال
یکی از مهمترین چالشهای موجود در حوزه تحلیل و پردازش سیگنال، این است که بتوانیم از دادههای نویزی، سیگنال اصلی را بهدست بیاوریم. بهینهسازی محدب در اینگونه مسائل نیز میتواند مورد استفاده قرار گرفته و نقش مؤثری ایفا کند. «حسگری فشرده» (Compressed Sensing) یکی از نمونههای بارز این مسائل است که در آن به دادههای محدودی از سیگنال دسترسی داریم و سیگنال نیز ساختاری پراکنده دارد. در چنین حالتی که تنها بخشی از اطلاعات موجود است، روشهای بهینهسازی محدب مانند «Lasso» و «جست و جوی پایه» (Basis Pursuit) میتوانند برای بازیابی سیگنال پراکنده و دادههای آن مورد استفاده قرار گیرند. این روشها در زمینههای مختلفی مانند پردازش تصویر، صدا و ویدیوها بهشکل گستردهای استفاده میشوند.
سیستم های قدرت
در مدیریت سیستمهای برق و قدرت نیز شاهده استفاده از بهینهسازی محدب برای ایجاد هماهنگی در عرضه و تقاضای برق و همچنین بهبود بهرهوری عملیاتی این سیستمها هستیم. هدفی که در اینجا وجود دارد این است که در کنار حفظ تعادل در تقاضا و انتقال برق، هزینه تولید نیز میبایست کمینه شود. بهکمک این روشها میتوان برنامهریزی تولید و جریان انرژی را بهینه کرد و از نقاط قوت آن در طراحی، بهرهبرداری و کنترل سیستمهای قدرت بهره گرفت.
هوش مصنوعی
بهینهسازی محدب در حوزه هوش مصنوعی و یادگیری ماشین نیز بهعنوان ابزاری مهم، کاربرد فراوانی دارد. بهخصوص هنگامیکه روی توسعه و آموزش مدلهایی تمرکز داریم که قرار است روی دادههای نادیده و جدید هم عملکرد مناسبی داشته باشند. نقش بهینهسازی محدب در اینجا این است که مقدار بهینه پارامترهای مدل را با کمینهسازی تابع زیان پیدا کند. قیدهای موجود بهطور معمول معادلات خطی هستند و تابع زیان نیز ساختاری محدب دارد. در ماشینلرنینگ، بیشتر روشهای بهینهسازی بر پایه الگوریتم گرادیان نزولی و نسخههای گوناگون آن ساخته میشوند. مدلهایی مانند ماشینهای بردار پیشتیبان، رگرسیون لجستیک و رگرسیون خطی، نمونههای بارزی از کاربردهای بهینهسازی محدب در این زمینه بهشمار میروند.
- انتخاب ویژگی و پراکندگی: رگرسیون Lasso با افزایش «پراکندگی» (Sparsity) در ضرایب، گزینه خوبی برای دادههایی با تعداد ویژگیهای زیاد و ابعاد بالا بهشمار میرود.
- بینایی کامپیوتر: کارهایی مانند بخشبندی تصاویر و بازسازی آنها در قالب مسائل بهینهسازی محدب حل میشوند.
- پردازش زبان طبیعی: در مسائلی مانند دستهبندی متن و مدلسازی موضوعات از روشهای قابل حل با بهینهسازی محدب مانند رگرسیون لجستیک استفاده میشود.
آشنایی با سایر روش های بهینه سازی با فرادرس
در این مطلب، مبحث بهینه سازی محدب در یادگیری ماشین را بررسی کردیم و جزئیات آن را یاد گرفتید. اکنون در ادامه مسیر یادگیری خود، اگر به دنبال روشهایی هستید که از تکنیکهای کلاسیک فراتر بروند و بتوانند مسائل پیچیده دنیای واقعی را بهتر حل کنند، الگوریتمهای فراابتکاری گزینههای بسیار قدرتمندی در این زمینه محسوب میشوند. این دسته از الگوریتمها با الهام از طبیعت، رفتارهای جانداران و غیره میتوانند به بهینهسازی در زمینههای گوناگون کمک کنند.
چند فیلم آموزشی کاربردی در قالب مجموعه فیلمهای آموزش الگوریتم های فراابتکاری – مقدماتی تا پیشرفته از فرادرس را در ادامه معرفی کردهایم که برای یادگیری مفاهیم پایه و استفاده از این الگوریتمها بهطور عملی در پروژهها بسیار مفید خواهند بود.
از طریق این مجموعه میتوانید به فیلمهایی از جمله موارد زیر دسترسی داشته باشید.
جمعبندی
در این مطلب از مجله فرادرس در مورد بهینه سازی محدب صحبت کردیم و جنبههای گوناگون آن از مباحث نظری گرفته تا الگوریتمها و حتی پیادهسازی عملی در زبان برنامهنویسی پایتون را مورد بررسی قرار دادیم.
در ریاضیات، مبحثی با عنوان بهینه سازی محدب داریم که در تلاش است تا بهترین جواب را برای مسائل دارای محدودیت بهینهسازی پیدا کند. به بیان دیگر، بهینهسازی محدب میتواند پاسخ خوبی را برای مسائلی با تابع هدف محدب و قیدهای خطی پیدا کند. در این روش بهینهسازی، تابع هدفی را که قیود خطی دارد، کمینهسازی میکنیم. یکی از مشخصههای مهم توابع محدب این است که اگر ۲ نقطه دلخواه را در چنین توابعی انتخاب و به هم وصل کنیم، خط مستقیمی که آنها را به هم وصل میکند همیشه در بالای نمودار تابع قرار خواهد گرفت.
بهینه سازی محدب را میتوان ابزاری بسیار قدرتمند و کارآمد برای حل قاعدهمند انواع گوناگونی از مسائل بهینهسازی دانست که سرعت و دقت خوبی را در این زمینه فراهم میکند. این دسته از الگوریتمها در زمینه یادگیری ماشین و در مدلهایی همچون مانند رگرسیون خطی، ماشینهای بردار پشتیبان، رگرسیون لجستیک، آموزش شبکههای عصبی و بسیاری از روشهای دیگر نیز مورد استفاده قرار میگیرند. هنگامیکه مسائل خود را در قالب یک مسئله بهینهسازی محدب، مطرح یا به اصطلاح فرمولهسازی میکنیم، این فرصت را داریم که از تئوری قدرتمند پشت آن و الگوریتمهای کارآمد موجود بهرهمند شویم و جوابهای بهینهای را به دست بیاوریم. بهینه سازی محدب به دلیل خصوصیات و کابردهای فراوانی که دارد جزو ابزارهای مهم در زمینههایی همچون یادگیری ماشین، تحقیق در عملیات، اقتصاد، مهندسی و امور مالی محسوب میشود.
source
