مکانیک کلاسیک یکی از بنیادیترین شاخههای فیزیک است که در آن وضعیت حرکت یک جسم با در نظر گرفتن تمام نیروها و گشتاورهای وارد بر آن تحلیل و بررسی میشود. با اینکه در مطالعه کلاسیکی برخی موقعیتها مانند ابعاد بسیار ریز، سرعتهای خیلی بالا و میدانهای گرانشی قوی محدودیت داریم، اما تسلط به مکانیک کلاسیک پیشنیاز مطالعه فیزیک کوانتوم و نظریه نسبیت محسوب میشود. در این مطلب از مجله فرادرس توضیح میدهیم مکانیک کلاسیک چیست و شامل چه موضوعات و فرمولهایی میشود.
آنچه در این مطلب میآموزید:
-
میآموزید مقدمات یادگیری مکانیک کلاسیک چیست.
-
با دستهبندیهای مختلف مکانیک کلاسیک آشنا خواهید شد.
-
قوانین حاکم بر مکانیک کلاسیک را خواهید شناخت.
-
یاد میگیرید که چگونه برآیند نیروها و گشتاورهای وارد بر یک جسم را پیدا کنید.
-
با حل سوالات متنوع به نحوه استفاده از فرمولهای مکانیک کلاسیک مسلط خواهید شد.
-
میتوانید معادله حرکت را برای انواع حرکت بهدست آورید.

به همین منظور پس از اینکه در اولین بخش با کلیات و زیربنای مکانیک کلاسیک آشنا شدیم، توضیح میدهیم مقدمات یادگیری مکانیک کلاسیک چیست. در ادامه به بررسی قوانین مختلف حاکم بر این شاخه از فیزیک خواهیم پرداخت و نحوه بهدست آوردن معادله حرکت و پیدا کردن برآیند نیروها را نیز توضیح میدهیم. در انتها با پاسخدهی به سوالات آزمونی که برای شما تهیه شده است، میتوانید میزان تسلط خود به فرمولهای مکانیک کلاسیک را بیازمایید.
مکانیک کلاسیک چیست؟
مکانیک کلاسیک حرکت یک جسم را با توجه به نیروهای وارد بر آن توصیف میکند و چارچوبی را ارائه میدهد تا بتوانیم متوجه شویم اجسام در دنیای ماکروسکوپیک (با صرفنظر کردن از آثار کوانتومی و نسبیتی) چگونه حرکت میکنند یا چگونه با هم برهمکنش دارند. این شاخه از علم فیزیک را به افتخار بنیانگذار آن «آیزاک نیوتن» (Isaac Newton)، «مکانیک نیوتنی» نیز مینامند.
مکانیک کلاسیک مطالعه وضعیت حرکتی اجسام و بررسی اثر نیروهایی است که به آنها وارد میشود. به این ترتیب اولین مفهومی که باید در این شاخه از علم فیزیک بشناسیم، نیرو یا Force است. هر عاملی که موجب تغییر سرعت جسم یا ذرهای شود، نیرو نام دارد.
سپس باید ببینیم منظور ما از جسم یا ذره چیست. هر چیزی از یک ذره بنیادی تا یک کهکشان میتواند به عنوان یک جسم در مکانیک کلاسیک در نظر گرفته شود. البته میدانیم که اجسام بسیار بزرگی مانند کهکشانها در حقیقت خود مجموعهای از ذرات بنیادی هستند. اما در مکانیک کلاسیک هر جسمی فارغ از ابعاد یا اجزای تشکیلدهندهاش اغلب بهصورت یک جسمی که با دست میتوان نگه داشت، در نظر گرفته میشود.
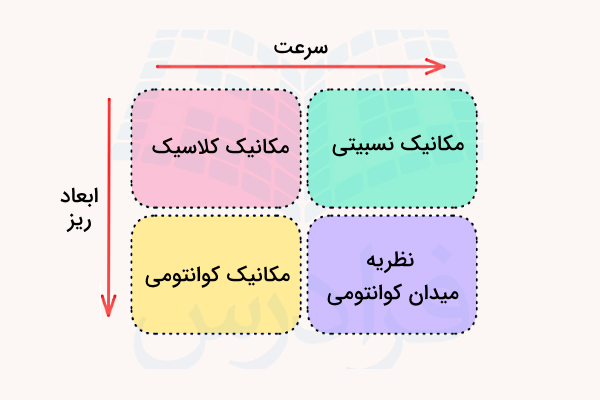
با توجه به این فرضیات میتوانیم بگوییم مکانیک کلاسیک نوعی مدلسازی فیزیکی و تقریب است، بنابراین محدودیتهای خود را خواهد داشت. مهمترین محدودیتهای مکانیک کلاسیک در مقیاسهای بسیار کوچک و ابعاد ریز، سرعتهای خیلی بزرگ در حد سرعت نور و در میدانهای گرانشی بسیار قوی است. به جز این موارد، در سایر موقعیتها مکانیک کلاسیک عملکرد کاربردی و قابلقبولی در ارائه توضیح و درک بسیاری از پدیدههای اطراف ما داشته است.
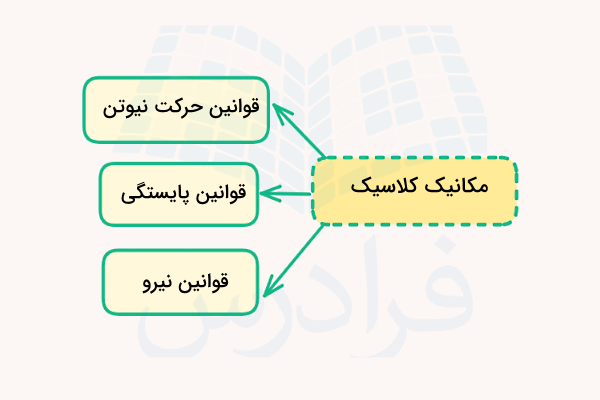
شالوده اصلی مکانیک کلاسیکی چند قانون فیزیکی مهم است که بر مبنای فرمولبندی ریاضیاتی مشاهدات فیزیکی توسعه داده شدهاند. برخی از این قوانین را میتوانیم از برخی دیگر استخراج کنیم، اما امکان اثبات همه آنها وجود ندارد. در واقع برخی از این قوانین بدیهی هستند و ما آنها را همواره معتبر فرض میکنیم. این قوانین مهم در سه دستهبندی زیر قرار میگیرند:
- قوانین حرکت نیوتن
- قوانین پایستگی
- قوانین نیرو
حتما با قوانین حرکت نیوتن آشنا هستید، با این وجود چون این قوانین مبدا مطالعات کلاسیکی محسوب میشوند، در بخشهای بعد به صورت مختصر به معرفی آنها خواهیم پرداخت. همچنین سه قانون برای بررسی پایستگی داریم که عبارتاند از:
شکل ریاضیاتی این قوانین را از قانون دوم و سوم نیوتن میتوانیم استخراج کنیم. در این میان شاید قوانین نیرو کمی مبهم بنظر برسند. منظور ما از قوانین نیرو در این نوشته قوانینی هستند که بر اساس آنها میتوانیم کلیه نیروهای اعمال شده به جسم یا اجسام موردمطالعه خود را شناسایی کنیم. با توجه به نوع سیستم فیزیکی که در نظر داریم، این قوانین ممکن است متفاوت باشند.
برای مثال، در مورد یک فنر فشرده شده یا کشیده شده از فرمولبندی «قانون هوک» بهعنوان قانون نیرو استفاده میکنیم، در حالی که در مورد دو ذره دارای بار الکتریکی «قانون کولن» قانون نیرویی است که به ما پاسخ درستی در محاسبات خواهد داد. البته باید توجه داشته باشید که این قوانین تنها در ترکیب با قوانین حرکت نیوتن میتوانند تحلیل درستی از فیزیک کلاسیک مسئله در اختیار ما قرار دهند. در عین حال این دو مثال نمونهای از فرمولهای کلاسیکی هستند که بر مبنای آزمایش و تجربه بهدست آمدهاند، به این معنا که با استفاده از قوانین حرکت نیوتن یا قوانین پایستگی نمیتوانیم به فرمول نیروی فنر یا نیروی الکتریکی برسیم.
موضوع دیگری که در مطالعه فیزیک کلاسیک باید به آن توجه داشته باشیم، مفاهیم و کمیتهای مختلفی است که در این شاخه تعریف شدهاند و نباید آنها را با قوانین اشتباه بگیریم. اصولا تعاریف به گونهای انتخاب میشوند تا درک دقیق و راحتتری از یک پدیده داشته باشیم. برای مثال، عدد پی در ریاضیات بهصورت نصف نسبت محیط به شعاع دایره تعریف میشود. همچنین همه بر سر این مسئله در مرود عدد پی توافق دارند که برای آن نماد خاصی در نظر گرفته شود.
یادگیری مکانیک کلاسیک برای دانشآموزان با فرادرس
اگر دانشآموز هستید، یکی از بهترین روشها برای یادگیری مکانیک کلاسیک این است که فیلمهای آموزشی تهیه شده در این زمینه را مشاهده کنید. در ادامه، لیستی از تمام دورههای آموزشی فرادرس با این موضوع را برای شما قرار دادهایم تا بهتر متوجه شوید مکانیک کلاسیک چیست:
- فیلم آموزش فیزیک دهم مرور و حل تمرین فرادرس
- فیلم آموزش فیزیک دوازدهم سوالات امتحانات نهایی با حل تشریحی فرادرس
- فیلم آموزش فیزیک دوازدهم مرور و حل تمرین فرادرس
- فیلم آموزش فیزیک دوازدهم نکته و حل تست کنکور فرادرس
- فیلم آموزش رایگان دینامیک و حرکت دایره ای فرادرس
- فیلم آموزش رایگان نمودار سرعت زمان فرادرس
مقدمات یادگیری مکانیک کلاسیک چیست؟
پیش از ورود به مباحث اصلی فیزیک کلاسیک از جمله قوانین آن، ابتدا لازم است مقدمات و ابزارهایی معرفی شوند تا بتوانیم درک بهتر و دقیقتری از این شاخه کسب کنیم. در این بخش با الفبای این مقدمات آشنا میشویم که در قالب دو مبحث «کمیتهای مکانیک کلاسیک» و «تحلیل مسائل مکانیک کلاسیک» ارائه شده است.
کمیتهای مکانیک کلاسیک
کمیتهای قابلاندازهگیری در علم فیزیک فقط اعداد محض نیستند و تمام آنها با یک ویژگی فیزیکی متناظراند. به همین دلیل است که برای مثال ۱۰ ثانیه با ۱۰ متر یا ۱۰ کیلوگرم در فیزیک یکی نیست. کلمهای که در کنار این اعداد برای معرفی کمیت موردنظر در فیزیک بکار میرود، واحد اندازهگیری است که از اهمیت بالایی برخوردار است. به این ترتیب یک کمیت در فیزیک به این صورت تعریف میشود: هر ویژگی یا خاصیتی که بتوان آن را اندازه گرفت و دارای واحد و وسیله اندازهگیری مورد توافق جهانی باشد.
جدول زیر مهمترین کمیتهای مطرح شده در فیزیک کلاسیک را به همراه واحدهای اندازهگیری استاندارد یا SI برای هر کدام و نمادی که برای نمایش آنها در فرمولها بکار میرود، نشان میدهد:
| کمیت – نماد | واحد استاندارد | نماد واحد |
| مکان – | متر | |
| جرم – | کیلوگرم | |
| زمان – | ثانیه | |
| زاویه – | رادیان | |
| جابهجایی – | متر | |
| مسافت – | متر | |
| سرعت – | متر بر ثانیه | |
| تندی – | متر بر ثانیه | |
| سرعت زاویهای – | رادیان بر ثانیه | |
| شتاب – | متر بر مجذور ثانیه | |
| شتاب زاویهای – | رادیان بر مجذور ثانیه | |
| تکانه خطی – | کیلوگرم متر بر ثانیه | |
| نیرو – | نیوتن | |
| گشتاور – | نیوتن در متر | |
| انرژی جنبشی – | ژول | |
| کار – | ژول |
نکته ۱: دقت کنید برای مثال کمیتی مانند طول را میتوان با واحدهای مختلفی توصیف کرد. به همین دلیل برای اینکه بتوانید حل مسائل این حوزه را راحتتر انجام دهید، بهتر است به انواع تبدیل واحدها مانند تبدیل اینچ به سانتیمتر و … مسلط شوید.
نکته ۲: نکته دیگری که در مورد کمیتهایی مانند طول، جرم و زمان در جدول بالا مهم است این است که این سه کمیت جزء کمیتهای اصلی در فیزیک هستند. در واقع سه مورد از هفت کمیت اصلی در فیزیک (شامل طول، جرم، زمان، دما، مقدار ماده، شدت جریان الکتریکی و شدت روشنایی) بهعنوان کمیتهای مهم فیزیک کلاسیک شناخته میشوند.
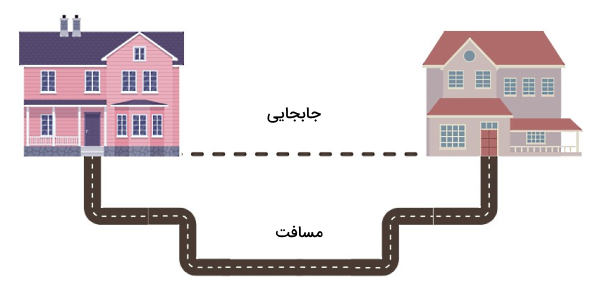
نکته ۳: مسافت و جابجایی با هم یکی نیستند. اگر بخواهیم بدانیم تفاوت مسافت و جابجایی در مکانیک کلاسیک چیست، باید به برداری و نردهای بودن این دو کمیت توجه کنیم. جابجایی یک کمیت برداری است، در حالی که مسافت یک کمیت نردهای یا عددی است. تصویر بالا بهخوبی این تفاوت را نشان میدهد. اگر بخواهیم از خانه سمت راست به خانه سمت چپ برویم، جهت بردار جابجایی از راست به چپ و اندازه آن معادل با فاصلهای است که در تصویر میبینید. همچنین اگر مسافت نشان داده در شکل را برای رسیدن به خانه سمت چپ طی کنیم، با اینکه بیشتر راه رفتهایم، اما باز هم جابجایی ما معادل همان فاصله بالا است.
نکته ۴: تفاوت تندی و سرعت مانند تفاوت مسافت و جابجایی است. تندی همان اندازه بردار سرعت و یک کمیت بدون جهت است.
تحلیل مسائل مکانیک کلاسیک
در فیزیک تلاش بر این است تا کمیتهای مختلف را توسط روابط یا قوانین مشخصی به هم ربط دهیم. برای مثال، اگر سوال ما این است که برای جابجایی یک جعبه از روی زمین تا طبقه سوم چقدر انرژی لازم است، اولین نکتهای که از مکانیک کلاسیک در مورد این سوال باید در نظر بگیریم این است که این انرژی لازم معادل است با همان کار انجام شده.
سپس لازم است کمیتهای قابلاندازهگیری در این سوال که بهعنوان ورودی داده شدهاند را بدانیم، برای مثال جرم جعبه و فاصله طبقه سوم از سطح زمین. در مرحله بعد باید قانون یا فرمولی که این ورودیها را به خروجی موردنظر ما مرتبط میکند، استفاده کنیم که در این سوال فرمول نیروی وزن و فرمول کار فیزیکی است. همچنین لازم است با برخی از مهمترین ثوابت در فیزیک کلاسیک مانند اندازه شتاب جاذبه زمین بهطور حدودی آشنا باشیم. نکته بعدی این است که دقت کنیم ابعاد و نوع حرکت ما در مسئله مکانیک کلاسیک چیست. انواع حرکت را از نظر ابعاد به شکل زیر میتوان دستهبندی کرد:
همچنین دو نوع حرکت در مکانیک کلاسیک عبارتاند از:
دسته بندی مکانیک کلاسیک
طبقهبندی مکانیک کلاسیک ممکن است با در نظر گرفتن پارامترهای مختلفی انجام شود. برای مثال در یک دستهبندی مکانیک کلاسیک را از نظر رویکردی که برای تحلیل و حل مسائل بکار میگیرد، به سه گروه زیر تقسیمبندی میکنیم:
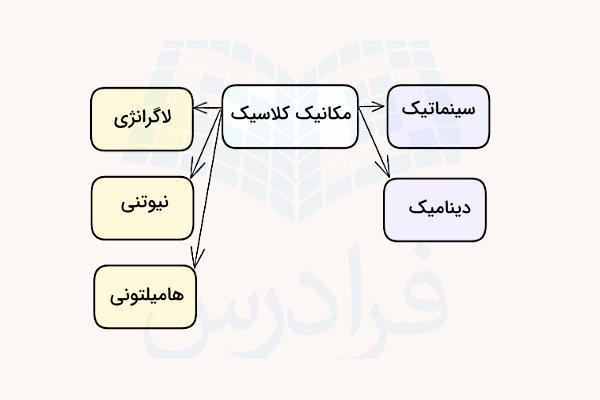
در این نوشته ما با رویکرد نیوتنی پیش رفتهایم، اما در سطوح دانشگاهی و در درسی با عنوان «مکانیک تحلیلی» نحوه استفاده از رویکرد لاگرانژی در زمینه حل مسائل توضیح داده شده است. همچنین برای اینکه بتوانیم مطالعات کلاسیکی خود را به شکل تفکیک شدهای انجام دهیم، میتوانیم این شاخه علم فیزیک را به دو گروه سینماتیک (حرکتشناسی) و دینامیک تقسیمبندی کنیم.
فرمولهای سینماتیک برای پیدا کردن مکان جسم، مدت زمان حرکت آن، جابجایی و مسافت طی شده توسط جسم و یا در محاسبه کمیتهایی مانند سرعت، شتاب، تکانه و انرژی جنبشی بکار میروند. جدول زیر تمام فرمول های سینماتیک مربوط به حرکت خطی یک جسم را نشان میدهد:
| نام کمیت | فرمول |
| سرعت متوسط | |
| معادله مکان – زمان | |
| سرعت متوسط | |
| شتاب متوسط | |
| معادله سرعت – زمان | |
| معادله مستقل از شتاب | |
| معادله درجه دوم مکان – زمان | |
| معادله مستقل از زمان |
همچنین تمام فرمولهای حرکت زاویهای در سینماتیک به شکل زیر خلاصه میشوند:
| نام کمیت | فرمول |
| سرعت زاویهای متوسط | |
| معادله زاویه – زمان | |
| شتاب زاویهای متوسط | |
| معادله سرعت زاویهای – زمان | |
| معادله مستقل از شتاب زاویهای | |
| معادله زاویه – زمان (درجه دو) | |
| معادله مستقل از زمان |
اگر علاقهمند هستید با نحوه استفاده از این فرمولها بیشتر آشنا شوید، پیشنهاد میکنیم مطلب «تمام فرمول های سینماتیک با مثال و تمرین» از مجله فرادرس را مطالعه کنید.
قوانین حرکت نیوتن
قوانین حرکت نیوتن اولین مجموعه از قوانین بدیهی فیزیک کلاسیک هستند که در این بخش به معرفی آنها میپردازیم. این قوانین بر مبنای مشاهدات دانشمندی به نام «آیزاک نیوتن» (Isaac Newton) ارائه شدند و برای فرمولبندی آنها، لازم است سه کمیت سرعت لحظهای، شتاب و تکانه یک ذره یا جسم را بشناسیم. اگر موقعیت مکانی ذره یا جسم موردنظر ما در هر لحظه از زمان توسط داده شود، در این صورت سرعت لحظهای این ذره یا جسم برابر است با مشتق معادله مکان:
در رابطه بالا معادل است با اولین مرتبه مشتقگیری از که در فیزیک مکانیک معادل سرعت است.
همچنین میدانیم واحد سرعت طبق این تعریف برابر میشود با واحد مکان تقسیم بر واحد زمان یا متر بر ثانیه. اگر از معادله بهدست آمده برای سرعت مجددا مشتق بگیریم، به شتاب لحظهای ذره یا جسم موردنظر خواهیم رسید:
شتاب با دو مرتبه مشتقگیری از مکان نیز معادل است:
همچنین تکانه خطی را داریم که از حاصلضرب جرم در سرعت بهدست میآید:
حالا برای اینکه سه قانون نیوتن را معرفی کنیم، آمادهایم.
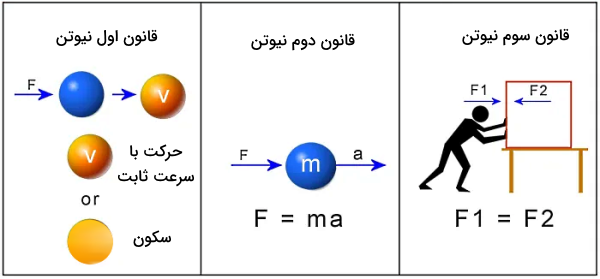
قانون اول نیوتن
اولین قانون نیوتن که به «قانون لختی، اینرسی یا ماند» نیز معروف است، بیان میکند تا زمانی که هیچ نیرویی به جسم وارد نشود، جسم اگر ساکن است، ساکن میماند و اگر در حال حرکت است، به حرکت خود با سرعت ثابت ادامه میدهد. بنابراین قانون اول نیوتن توصیف کننده وضعیت حرکت برای تمام ذرات یا اجسام در حال سکون () است. فرمول مناسب برای توصیف وضعیت جسم در قانون اول نیوتن به شکل زیر است:
علامت سیگما در رابطه بالا به معنای مجموع یا برآیند است. طبق این قانون میتوانیم نتیجهگیری کنیم هر عاملی که موجب تغییر سرعت جسم شود، نیرو نامیده میشود که در بخش بعد به این موضوع میپردازیم.
قانون دوم نیوتن
در قانون دوم نیوتن وضعیت حرکت در شرایطی بررسی میشود که جسم تحت تاثیر نیرو است. اگر مجموع یا برآیند نیروهای وارد بر یک جسم مخالف صفر باشد، سرعت آن تغییر میکند. تغییرات سرعت در جسم موجب میشود حرکت آن شتابدار شود، چون . به این ترتیب فرمول قانون دوم نیوتن با این فرض که جرم جسم ثابت میماند، به شکل زیر است:
همچنین این امکان وجود دارد تا فرمول قانون دوم نیوتن را بر حسب تکانه بنویسیم:
قانون دوم نیوتن به ما کمک میکند تا دیمانسیون نیرو را مشخص کنیم. طبق فرمول بالا واحد نیرو از ضرب کردن واحد جرم در واحد شتاب حاصل میشود. به این ترتیب حاصلضرب یک کیلوگرم در یک متر بر مجذور ثانیه معادل با یک نیوتن نیرو تعریف شد:
بنابراین در اصول از قانون دوم نیوتن برای اندازهگیری نیرو میتوان استفاده کرد. همچنین به درستی قانون اول بر اساس قانون دوم توجه کنید. اگر نیرویی به جسم وارد نشود، تغییرات تکانه یا تغییر در سرعت هم نخواهیم داشت. به این ترتیب شتاب جسم مساوی با صفر است. در این شرایط حرکت جسم را تحت عنوان «حرکت با سرعت ثابت یا حرکت یکنواخت» میشناسیم. اما در قانون دوم که نیروی وارد بر جسم مخالف است، جسم شتاب میگیرد و اگر شتاب آن نسبت به زمان تغییر نکند، میگوییم جسم «حرکت با شتاب ثابت» دارد.
قانون سوم نیوتن
سومین نتیجه مشاهدات نیوتن در مورد نیروهایی که در اطراف خود مشاهده کرد، «قانون عمل – عکسالعمل یا قانون کنش – واکنش» نام دارد. اگر جسم اول نیرویی برابر با را به جسم دو اعمال کند، جسم دو نیز نیرویی مساوی اما در خلاف جهت به نام را به جسم اول وارد میکند. نکته قانون سوم نیوتن این است که اندازه این دو نیرو برابر اما جهتهایشان مخالف هم است:
قوانین نیرو
در ادامه بررسی مهمترین قوانین و اصول حاکم بر مکانیک کلاسیک، در این بخش قوانین و فرمولهای برخی از نیروهای خاص را معرفی خواهیم کرد، از جمله قانون هوک، قانون گرانش نیوتن، قانون کولن، اصطکاک و نیروی درگ. با اینکه قانون دوم نیوتن به ما نشان میدهد نتیجه اعمال یک نیرو چیست (تغییر تکانه جسم)، اما در مورد منشا آن صحبتی نمیکند. این نکته قانون دوم باعث شده است تا این فرمول ساده بسیار کاربردی باشد، چون برای انواع نیروها بکار میرود.
در عین حال برای تحلیل کلاسیکی بهتر نیاز داریم در مورد منشا نیروها اطلاعاتی داشته باشیم تا بتوانیم آنها را کنترل کنیم. بنابراین تسلط به این قوانین در کنار سه قانون نیوتن به شما کمک میکند تا مسائل مکانیک کلاسیک را بهطور دقیق و کاملی حل کنید. این بخش را با توضیح قانون هوک آغاز میکنیم.
قانون هوک
قانون هوک توصیف کننده نیروی لازم برای کشیدن یا فشردن یک فنر است. طبق قانون سوم نیوتن اگر فنر را با اعمال یک نیرو فشرده کنید، فنر در مقابل نیرویی برابر اما در خلاف جهت به شما وارد خواهد کرد. در این مثال سادهترین جسمی را در نظر گرفتهایم که میتوان به آسانی آن را فشرد یا کشید که یک فنر ایدهآل است. منظور از ایدهآل بودن فنر این است که رابطه بین نیروی لازم برای فشردن یا کشیدن فنر و میزان فشردگی یا کشیدگی آن خطی است. این رابطه خطی توسط قانون هوک و با فرمول زیر توصیف میشود:
- : نیروی فنر بر حسب نیوتن ()
- : جابجایی فنر (میزان کشیدگی یا فشردگی آن) بر حسب متر ()
- : ثابت فنر بر حسب نیوتن بر متر ()
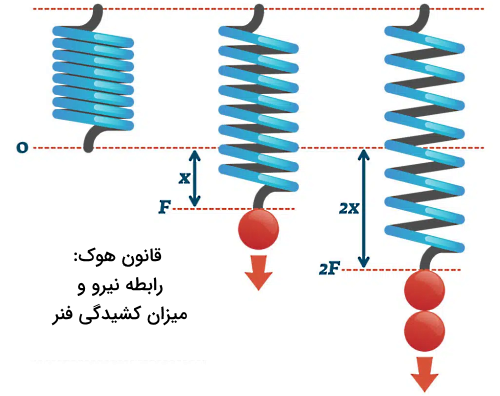
اندازه ثابت فنر به مشخصات فیزیکی و جنس آن وابسته است. برای مثال، فنرهای سفتتر دارای ثابت فنر بزرگتری هستند. نکته مهمی که از قانون هوک در مورد تعریف واحد نیرو یا نیوتن میتوانیم برداشت کنیم این است که یک نیوتن نیرو برای یک متر کشیدن یا یک متر فشردن فنری با ثابت یک نیوتن بر متر لازم است.
قانون گرانش نیوتن
دومین قانون نیرویی که در این بخش از مطلب مکانیک کلاسیک معرفی میکنیم، قانون جهانی گرانش نیوتن است. گرانش یکی از ملموسترین نیروهایی است که اغلب ما با آن آشنا هستیم و آثار آن را حس کردهایم. برای مثال، نیروی جاذبه زمین از نوع گرانش است و طبق قانون گرانش نیوتن، زمین با تقریب هموار فرض میشود و هر جسم دیگری را که دارای جرم است به سمت خود جذب میکند.
نیروی گرانش بین چهار نیروی بنیادی طبیعت، ضعیفترین نیرو است. به همین علت است که نیروی گرانشی که از سمت یک کتاب به شما وارد میشود را حس نمیکنید، در حالی که نیروی گرانش حاصل از زمین را به علت جرم بالای آن کاملا احساس میکنید. همچنین به دلیل جرم بالای زمین است که اگر جسمی را پرتاب کنید یا بیندازید، همواره آن جسم بلافاصله به سمت زمین شتاب میگیرد. در همین راستا، دانشمندی به نام «گالیلئو گالیله» (Galileo Galilei) نشان داد شتابی که تمام اجسام در نتیجه نیروی جاذبه یا گرانش زمین بهدست میآورند، با هم برابر است. این مقدار با نماد نشان داده میشود:
به این ترتیب نیرویی که زمین به هر جسم وارد میکند، از فرمولی به شکل حاصلضرب جرم آن جسم در این شتاب ثابت بهدست میآید و نشاندهنده وزن آن جسم است:
- : نیروی جاذبه زمین یا نیروی وزن بر حسب نیوتن ()
- : جرم جسم بر حسب کیلوگرم ()
- : شتاب جاذبه زمین بر حسب متر بر مجذور ثانیه ()
این نیرو را اغلب با نماد نیز نشان میدهند. با توجه به اینکه جرم زمین بهصورت یکنواخت توزیع نشده است، اندازه در مناطق مختلف ممکن است به اندازه خیلی کمی متفاوت باشد، اما در کل تقریب بالا برای این شتاب در همه جای دنیا پذیرفته شده است. همچنین باید این نکته را مدنظر داشته باشید که کاربرد فرمول بالا محدود است به فواصلی در حدود هزاران کیلومتر بالاتر از سطح زمین. در مورد فواصل بیشتر و اجرامی با جرم خیلی بزرگتر از جرم زمین، این فرمول به شکل زیر خواهد بود:
- : نیروی گرانشی بر حسب نیوتن ()
- و : جرم اجسام بر حسب کیلوگرم ()
- : فاصله بین دو جسم بر حسب متر ()
- : ثابت جهانی گرانش یا ثابت نیوتن بر حسب نیوتن در متر مربع بر مجذور کیلوگرم ()
- : بردار واحد در راستای خطی که دو جرم را به هم متصل میکند.
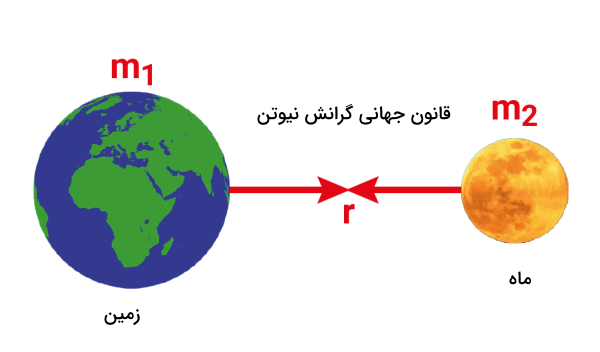
رابطه بالا فرمول قانون گرانش نیوتن است که در مورد سیستمهایی مانند سیستم زمین و ماه یا سیستم زمین و خورشید بکار میرود. همچنین ثابت جهانی گرانش که یکی از مهمترین ثابتهای مکانیک کلاسیک محسوب میشود، دارای مقدار زیر است:
در مورد این فرمول چند نکته مهم دیگر وجود دارد که در ادامه به آنها اشاره میکنیم:
- علامت منفی در فرمول قانون گرانش نشاندهنده این است که نیروی گرانشی از نوع جاذبه است.
- به کمک این فرمول میتوانیم برای مثال گرانشی را که یک کتاب به ما وارد میکند، محاسبه کنیم. با انجام این محاسبه دقیق خواهیم دید عدد بهدست آمده بسیار کوچک است و همین نکته موجب میشود تا این گرانش را احساس نکنیم.
- مقدار شتاب جاذبه زمین یا از قرار دادن مقادیر جرم و شعاع زمین در این فرمول بهدست آمده است.
- برای دانستن مقدار شتاب جاذبه روی سیارات دیگر، کافی است از جرم و شعاع آن سیاره در فرمول بالا استفاده کنیم.
- این فرمول با فرض هموار و صاف بودن زمین به تبدیل میشود.
- در مورد مکانیک اجرام آسمانی و ماهوارهها بهتر است از معادله استفاده کنیم.
قانون کولن در الکتروستاتیک
در بخش قبل آموختیم همواره هر دو جرمی که در فاصله مشخصی از هم قرار دارند، به یکدیگر نیرویی از نوع گرانش وارد میکنند. مشابه این وضعیت را برای دو ذره یا جسم باردار داریم. نیرویی که در چنین سیستمی ایجاد میشود، از نوع گرانشی نیست، بلکه به علت وجود خاصیتی به نا بار الکتریکی، از نوع الکتریکی است. قانون کولن فرمولبندی این نیرو را به شکل زیر توصیف میکند:
- : نیروی الکتریکی بر حسب نیوتن ()
- و : اندازه بار اجسام بر حسب کولن ()
- : فاصله بین دو جسم بر حسب متر ()
- : ثابت کولن بر حسب نیوتن در متر مربع بر مجذور کولن ()
- : بردار واحد در راستای خطی که دو جرم را به هم متصل میکند.
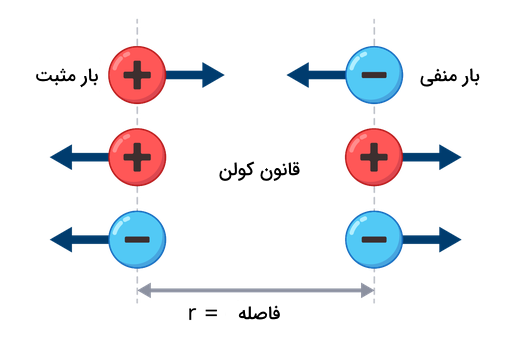
همانطور که ملاحظه میکنید، این فرمول به فرمول قانون گرانش بسیار شبیه است. همچنین مقدار عددی ثابت کولن به صورت زیر است:
نکته مهمی که در مقایسه این نیرو با نیروی گرانشی باید بدانید این است که در مقیاس فواصل زندگی روزمره، اغلب نیروی کولن از نیروی گرانشی بسیار بزرگتر است.
اصطکاک و نیروی درگ
با اینکه گالیله و نیوتن برای معرفی قانون اول نیوتن تلاشهای زیادی کردند، اما پذیرفتن این قانون توسط سایر دانشمندان و صاحبنظران طول کشید. یکی از مهمترین دلایل آنها این بود که اگر نیرویی به جسمی وارد نشود، جسم به حرکت خود تا ابد ادامه نخواهد داد و بهتدریج متوقف میشود. این مشاهده قانون اول را نقض میکرد. اما امروز میدانیم دلیل توقف تدریجی اجسام در حال حرکت وجود نیروهایی مانند نیروی اصطکاک یا نیروی مقاومت هوا (نیروی درگ) است.
بنابراین چون آن زمان این دو نیرو شناخته شده نبودند، گمان بر این بود که قانون اول نیوتن درست نیست. اما امروز با اطلاع از وجود این دو نیرو میتوانیم بگوییم قانون اول نیوتن همواره درست است. طبق این قانون اگر هیچ نیرویی به جسم وارد نشود (از جمله نیروهایی مانند نیروی اصطکاک و نیروی درگ)، در این صورت جسم متحرک میتواند تا ابد به حرکت خود با سرعت ثابت ادامه دهد. درک ماهیت نیروی اصطکاک نشان میدهد که چرا راندن اتومبیل روی یک سطح یخی از یک جاده معمولی آسانتر است (اصطکاک روی یخ کمتر است).
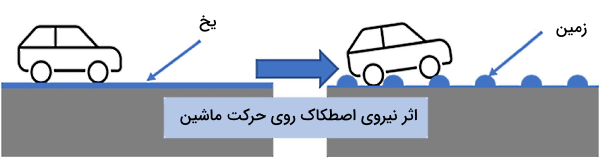
همچنین میدانیم محیطی که میتوانیم در آن حرکت کنیم، همواره نیرویی به نام نیروی درگ به ما وارد میکند و همین مسئله نشان میدهد که چرا راه رفتن در هوا از راه رفتن در آب راحتتر است (نیروی درگ در آب بیشتر است). در ادامه این بخش به معرفی فرمولهای این دو نوع نیروی مهم در مکانیک کلاسیک میپردازیم.
نیروی درگ چیست؟
در سرعتهای پایین، نیروی درگ با سرعت جسم در حال حرکت رابطه خطی دارد. همچنین این نیرو در مورد اجسام در حال حرکت در محیطی مانند یک سیال به ویژگیهای آن محیط مانند ویسکوزیته (گرانروی یا ) و سطح مقطع جسم نیز بستگی دارد. به این ترتیب اگر یک جسم کروی با شعاع و با سرعت در حال حرکت در یک محیط باشد، نیروی درگ توسط «قانون استوکس» و بهصورت زیر فرمولبندی خواهد شد:
- : نیروی درگ بر حسب نیوتن ()
- : ویسکوزیته محیط بر حسب نیوتن در ثانیه بر متر مربع ()
- : شعاع جسم کروی بر حسب متر ()
- : سرعت جسم بر حسب متر بر ثانیه ()
البته فرم کلیتر فرمول مناسب برای محاسبه نیروی درگ به شکل زیر است که در آن شکل جسم در حال حرکت دلخواه و ضریب تناسب است:
قانون استوکس در سرعتهای بالا تغییر میکند و به شکل زیر تبدیل میشود (نیروی درگ با مربع سرعت متناسب است):
- : نیروی درگ بر حسب نیوتن ()
- : چگالی محیط بر حسب کیلوگرم بر متر مکعب ($$ $$ frac{kg}{m^3} $$ $$)
- : سطح مقطع جسم بر حسب متر مربع ()
- : سرعت جسم بر حسب متر بر ثانیه ()
- : ضریب درگ و بدون واحد
ضریب درگ در این فرمول به شکل و خصوصیات سطحی جسم بستگی دارد. مقادیر معمول برای این ضریب عبارتاند از برای یک دوچرخهسوار، برای یک دونده و برای یک اتومبیل آیرودینامیکی مدرن. دقت کنید جهت نیروی درگ مانند نیروی اصطکاک همواره در خلاف جهت حرکت جسم است. پس از معرفی نیروی درگ، میرسیم به معرفی نیروی اصطکاک. تمام نیروهای با منشا اصطکاکی در اثر تماس دو سطح با هم ایجاد میشوند. همانطور که اشاره کردیم، جهت این نیرو همواره در خلاف جهت حرکت جسم و اندازه آن وابسته به ویژگیهای سطوح است.
نیروی اصطکاک چیست؟
همچنین یکی دیگر از مهمترین عوامل تعیین کننده در اندازه نیروی اصطکاک این است که دو سطح چه مقدار نیروی عمودی به هم وارد میکنند. این نیروها طبق قانون سوم نیوتن همواره با هم برابر هستند (نیرویی که سطح اول به سطح دوم وارد میکند، با نیرویی که سطح دوم به سطح اول وارد میکند از نظر اندازه یکسان است). چون این نیروها همیشه عمود بر سطح هستند، در مکانیک کلاسیک آنها را «نیروی عمودی سطح» مینامیم و با یا نشان میدهیم.
طبق «قانون اصطکاک کولن»، اندازه نیروی اصطکاک بین دو سطح (سطح جسم و سطحی که روی آن در حال حرکت است یا ساکن قرار دارد) همیشه در رابطه زیر صدق میکند:
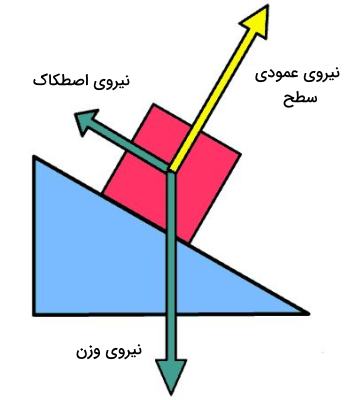
ضریب اصطکاک و یک کمیت بدون واحد است که به ویژگیهای هر دو سطح بستگی دارد. همچنین در مورد این ضریب مهم است که بدانیم آیا دو سطح در حال تماس نسبت به هم ساکناند یا در حال حرکت. اگر سطوح نسبت به هم در حال حرکت نباشند، پیکربندی سیستم موردمطالعه ما یک پیکربندی استاتیکی است و ضریب اصطکاک در این شرایط با (ضریب اصطکاک ایستایی) نشان داده میشود. اما زمانی که اجسام شروع به حرکت میکنند، ضریب اصطکاک ایستایی به ضریب اصطکاک جنبشی یا تبدیل میشود که معمولا از کمتر است. به این ترتیب فرمول اصطکاک جنبشی به شکل زیر خواهد شد:
به دست آوردن معادله حرکت
در بخشهای گذشته با قوانین حاکم بر مکانیک کلاسیک از جمله قوانین نیوتن و قوانینی که در مورد نیروهای مختلف وجود دارند، کاملا آشنا شدیم. در این بخش قصد داریم روند ترکیب کردن این قوانین را به منظور تحلیل مسائل مکانیک کلاسیک و نوشتن معادله حرکت با هم مرور کنیم. معادله حرکت معادلهای است که حرکت یک ذره را با در نظر گرفتن نیروهای وارد بر آن بهخوبی توصیف میکند. دقت کنید در نوشتن معادله حرکت معمولا جسم یا کل سیستم موردنظر خود را مانند یک ذره در نظر میگیریم. در ادامه معادله حرکت دو مورد از مسائل معروف در مکانیک کلاسیک را با هم بررسی میکنیم.
معادله حرکت در سقوط آزاد
برای مثال، فرض کنید میخواهیم معادله حرکت سنگی با جرم را که از ارتفاع از سطح زمین رها شده است، بنویسیم. با صرفنظر کردن از مقاومت هوا، تنها نیرویی که به این سنگ وارد میشود، جاذبه زمین است. به این ترتیب با در نظر گرفتن قانون دوم نیوتن به شکل زیر و جایگذاری تنها نیرویی که به سنگ در این مثال وارد میشود، خواهیم داشت:
دقت کنید در فرمول بالا به معنای دو مرتبه مشتقگیری از مکان نسبت به زمان است. برای اولین مشتق، از یک علامت نقطه استفاده میشود. در ادامه به نکاتی که میتوانیم از این مثال دریافت کنیم، توجه کنید:
- این معادله حرکت به ما نشان میدهد جرم جسم در سقوط آزاد اهمیتی ندارد.
- این معادله یک معادله دیفرانسیل مرتبه دوم است، به این معنا که اگر بخواهیم حرکت واقعی سنگ را تحلیل کنیم، لازم است دو شرط اولیه را بدانیم. این دو شرط در مثال بالا همان مشخص بودن ارتفاع سنگ از زمین () و صفر بودن سرعت اولیه سنگ هنگام رها شدن است.
- معادله حرکت بالا یک معادله حرکت یک بعدی است، چون حرکت سنگ در راستای یک خط مستقیم و عمودی رخ میدهد.
اگر بخواهیم این معادله دیفرانسیل را حل کنیم، لازم است دو مرتبه انتگرالگیری روی زمان انجام دهیم که یک پاسخ کلی به شکل زیر به ما میدهد:
با اعمال دو شرط مرزی گفته شده، معادله بالا به شکل زیر ساده میشود:
معادله حرکت در سقوط آزاد با در نظر گرفتن نیروی درگ
اگر در سقوط آزاد مقاومت هوا (نیروی درگ) را در نظر بگیریم، معادله حرکت متفاوتی خواهیم داشت. فرض کنید سنگ کروی شکلی با شعاع داریم که از ارتفاع در رها میشود. میخواهیم ببینم در چه زمان و با چه سرعتی این سنگ به زمین میرسد. در بخش قبل شکل سادهتر این سوال را حل کردیم. در این بخش با اضافه شدن نیروی درگ قانون دوم نیوتن به شکل زیر خواهد شد:
دقت کنید نیروی درگ با نیروی وزن جمع میشود. چون جهت حرکت سنگ به سمت پایین است، پس نیروی درگ در خلاف این جهت یعنی به سمت بالا است. از طرفی میدانیم جهت نیروی وزن همیشه به سمت زمین (پایین) است. پس این دو نیرو باید با یک علامت منفی در سمت دیگر قانون دوم نیوتن متمایز شوند. همچنین در نوشتن فرمول نیروی درگ قانون استوکس را به شکل زیر در نظر گرفتهایم:
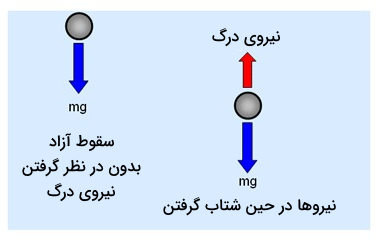
در این معادله حرکت نیروهای ما به زمان و مکان بستگی ندارند، اما وابستگی به سرعت را داریم (). همچنین یکی از جملات در سمت راست تساوی بالا مقدار ثابتی دارد (نیروی وزن)، بنابراین معادله حرکت ما یک معادله همگن در نظر گرفته نمیشود. اگر این معادله را به صورت زیر مرتب کنیم، ناهمگن بودن معادله بهتر مشخص میشود:
پس میتوانیم معادله حرکت را مجموعی از دو معادله همگن و یک بخش ویژه در نظر بگیریم. با در نظر گرفتن بخش ویژه به پاسخ زیر خواهیم رسید:
همچنین معادله همگن برابر است با:
اگر به روش جداسازی متغیرها این معادله را حل کرده، انتگرالگیری کنیم و را صفر در نظر بگیریم، به پاسخ زیر خواهیم رسید:
این معادله نشان میدهد اگر هیچ نیروی دیگری وجود نداشته باشد، نیروی درگ بهصورت نمایی کم میشود. همچنین دقت کنید که ما در این محاسبه سرعت اولیه را صفر در نظر نگرفتیم، چون پاسخ معادله همگن با پاسخ کلی یکسان نیست. سرعت اولیه در حقیقت ثابت انتگرالگیری است که پس از نوشتن راهحل کلی میتوانیم آن را صفر در نظر بگیریم:
با در نظر گرفتن ، خواهیم داشت:
همچنین با انتگرالگیری از معادله بالا روی زمان، معادله مکان به شکل زیر خواهد شد:
حالا برای اینکه ببینیم در چه زمانی سنگ به زمین برخورد میکند، کافی است را مساوی قرار دهیم و را بهدست آوریم. همچنین تعیین سرعت برخورد نیز با قرار دادن زمان بهدست آمده در معادله امکانپذیر است.
معادله حرکت در سیستم جرم و فنر
یکی دیگر از سیستمهای مورد علاقه در مطالعه مکانیک کلاسیک، جرم متصل به یک فنر است. واضح است که اگر بخواهیم نیروهای وارد بر جرم را در این آزمایش بررسی کنیم، در نظر گرفتن نیروی جاذبه به ما کمکی نخواهد کرد. این نیرو در راستای عمودی به جرم وارد میشود و چون در این راستا جرم هیچگونه حرکتی ندارد، بنابراین نوشتن این معادله به کار نمیآید.
اما اگر حرکت جرم در راستای محور افقی را در نظر بگیریم، باید تمام نیروهایی که در این راستا به آن وارد میشوند را در نظر بگیریم. تنها نیروی وارد به جرم در این شرایط نیرویی است که از قانون هوک بهدست میآید. پس با قرار دادن این نیرو در قانون دوم نیوتن داریم:
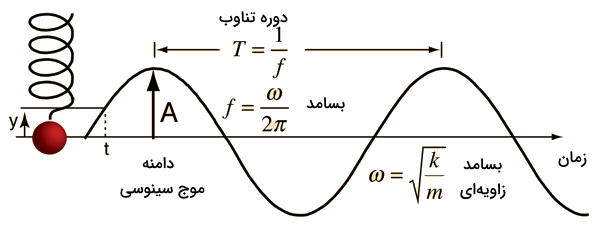
مجددا معادله حرکت بهصورت یک معادله دیفرانسیل مرتبه دوم بهدست آمد. پس برای حل آن لازم است حداقل دو شرط اولیه را داشته باشیم، برای مثال مکان و سرعت اولیه جرم متصل به فنر. پاسخ کلی برای معادله بالا ترکیبی از توابع سینوسی و کسینوسی است:
این پاسخ نشان میدهد جرم متصل به فنر در این مثال در واقع نوسانگری است که با بسامد نوسان میکند.
بررسی معادله حرکت در سه حالت خاص
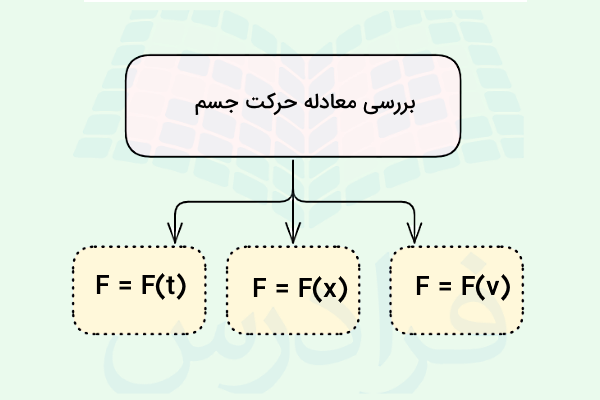
در سه بخش قبل با بررسی چند مثال آموختیم چگونه با کمک گرفتن از قانون دوم نیوتن و قوانین نیرو میتوان به معادله حرکت جسم رسید. در حالت کلی برای نیرو در قانون دوم باید علاوهبر وابستگی به مکان و زمان، وابستگی به سرعت هم در نظر گرفته شود. به این ترتیب فرمول جامع قانون دوم در یک بعد به شکل زیر خواهد بود:
حل این معادله برای نیروهای پیچیده با وابستگی همزمان به هر سه متغیر دشوار است. با این وجود در شرایطی که نیرو فقط به یکی از سه متغیر بالا وابسته باشد، بهراحتی میتوان مسئله را بررسی کرد. در ادامه این بخش وابستگی به هر کدام از این سه پارامتر را در نظر میگیریم تا ببینیم معادله حرکت چه میشود:
در این زمینه میتوانید فیلم آموزش رایگان معادله دیفرانسیل حرکت یک سیستم فرادرس را مشاهده کنید که با زبانی ساده اما کاربردی این مبحث را توضیح داده است. جهت دسترسی آسانتر لینک این دوره در ادامه برای شما قرار داده شده است:
وابستگی نیرو به زمان
در اولین حالت خاص، فرض میکنیم نیرو در قانون دوم نیوتن فقط به زمان وابسته است. با انتگرالگیری از قانون دوم نیوتن به شکل زیر خواهیم داشت:
با این فرض که در زمان اولیه ، سرعت جسم برابر است با . با انتگرالگیری مجدد از سرعت میتوانیم به معادله مکان برسیم:
وابستگی نیرو به مکان
در این حالت که مشابه مسئله نوسانگر هارمونیک است، امکان انتگرالگیری روی زمان را نداریم. اما میتوانیم از قاعده زنجیرهای در مشتقگیری استفاده کنیم تا بتوانیم معادله دیفرانسیل خود را بهگونهای بازنویسی کنیم که در آن مکان متغیر ما است:
پس قانون دوم نیوتن در این نوع وابستگی برای نیرو بهتر است به شکل زیر نوشته شود:
حالا میتوانیم انتگرالگیری کنیم:
برای اینکه به معادله حرکت یا برسیم، از فرمول و البته به شکل استفاده میکنیم. با انتگرالگیری داریم:
وابستگی نیرو به سرعت
اگر نیرو فقط به سرعت جسم بستگی داشته باشد، دو راه برای رسیدن به معادله حرکت جسم وجود دارد. روش اول این است که قانون دوم را به شکل بنویسیم و با استفاده از جداسازی متغیرها، آن را ساده کنیم:
پس از معکوس کردن را خواهیم داشت و نیز با انتگرالگیری از آن طبق آخرین معادلهای که در بخش وابستگی نیرو به زمان بهدست آمد، پیدا میشود. روش دوم این است که معادله حرکت خود را در بر حسب مکان بهجای زمان بهدست آوریم:
انتگرالگیری بالا به ما را میدهد. با کاربرد آخرین رابطهای که در بخش وابستگی نیرو به مکان بهدست آمد، میتوانیم را داشته باشیم.
پیدا کردن برآیند نیروها
مهمترین موضوعی که در حل مسائل مکانیک کلاسیک لازم است بررسی شود، تشخیص تمام نیروهای وارد بر جسم موردنظر و سپس محاسبه برآیند یا مجموع این نیروها است. در بخش قوانین نیرو با بخشی از این نیروها آشنا شدیم. همچنین آموختیم که چگونه میتوان با استفاده از قانون دوم نیوتن، و معادله حرکت جسم را بهدست آورد. در تکمیل بخش قبل، در این بخش قصد داریم با یک مثال توضیح دهیم اگر چندین نیرو با جهتهای مختلف به یک جسم وارد شود، تحلیل مسئله به چه صورت خواهد بود.
فرض کنید طبق شکل زیر کتابی روی یک میز شیبدار قرار داده شده است. انتظار داریم در این وضعیت کتاب به سمت پایین میز سر بخورد و میخواهیم ببینیم شتاب حرکت کتاب در این وضعیت چقدر است. نیروهای وارد بر آن به شرح زیراند:
- نیروی جاذبه زمین یا که همواره در جهت منفی محور y وارد میشود.
- نیروی عمودی سطح یا که از طرف میز و عمود بر کتاب به آن وارد میشود.
- نیروی اصطکاک که در خلاف جهت حرکت کتاب به آن وارد میشود.
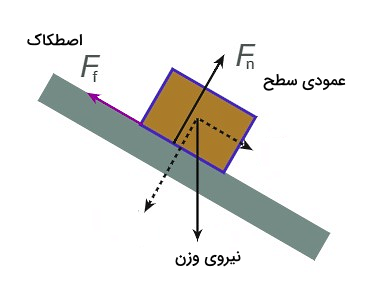
با مشخص شدن نیروها، حالا بهتر میتوانیم متوجه شویم که علت سر خوردن کتاب به سمت پایین دقیقا چه نیرویی است. در مرحله اول برای پیدا کردن برآیند نیروهای وارد بر کتاب لازم است دستگاه مختصات را مشخص کنیم. این کار به ما کمک میکند تا بدانیم دقیقا جهت مثبت محورهای x و y چیست. انتخاب این دستگاه کاملا اختیاری است و البته به نوع تقارن مسئله و نیروهایی که داریم بستگی دارد. اغلب تلاش بر این است که دستگاهی را انتخاب کنیم که بیشتر نیروهای ما کاملا در راستای یکی از دو محور آن قرار داشته باشند.
برای مثال، انتخاب جهتهای x و y به شکل قراردادی برای وضعیت بالا، انتخاب خوبی نیست، چون فقط نیروی وزن در راستای محور y (با جهت منفی) قرار دارد. اما اگر جهت مثبت محور y را در جهت نیروی عمودی سطح و جهت مثبت محور x را خلاف جهت نیروی اصطکاک در نظر بگیریم، در این صورت دو نیرو از سه نیروی ما در راستای محورهای مختصات قرار دارند. بنابراین محاسبه برآیند نیروها در این حالت بسیار سادهتر است. حالا با نوشتن قانون دوم نیوتن شروع میکنیم:
در این قانون نیرو و شتاب بردار هستند، پس برای اینکه تحلیل مسئله آسانتر شود، برای نیروی برآیند یا مجموع نیروها دو مولفه x و y با توجه به جهتهایی که برای این دو محور برگزیدیم، در نظر میگیریم:
به این ترتیب فرمول اولیه به دو فرمول بالا تبدیل شد و از حالت برداری خارج شد. به این فرآیند تجزیه کردن نیروها گفته میشود. حالا کافی است ابتدا نیروهایی که در راستای محور x هستند، را مشخص کنیم:
- نیروی اصطکاک در خلاف جهت محور x
- مولفهای از نیروی وزن در جهت محور x
همچنین نیروهایی که در راستای محور y هستند، عبارتاند از:
- نیروی عمودی سطح در جهت محور y
- مولفهای از نیروی وزن در خلاف جهت محور y
اگر زاویه بین راستای نیروی وزن و سطح میز را در نظر بگیریم، قانون دوم نیوتن برای این مسئله به شکل زیر خواهد شد:
دقت کنید در ابتدا گفتیم که کتاب به سمت پایین میز سر میخورد. بنابراین در این مسئله کتاب حرکتی در راستای محور y ندارد و شتاب کتاب در این راستا برابر با صفر است. پس داریم:
به این ترتیب بکار بردن قانون دوم در این راستا به ما نشان داد مقدار نیروی عمودی سطح چقدر است. در راستای x نیز میتوانیم با استفاده از قانون دوم را به شکل زیر بنویسیم:
با جایگذاری نیروی عمودی سطحی که از قانون دوم در راستای y بهدست آوردیم، خواهیم داشت:
حالا با در نظر گرفتن شتاب کل این کتاب به شکل ، داریم:
بنابراین فقط با داشتن زاویه و مقدار میتوانیم شتاب این کتاب را محاسبه کنیم.
مثال سیستم طناب و قرقره
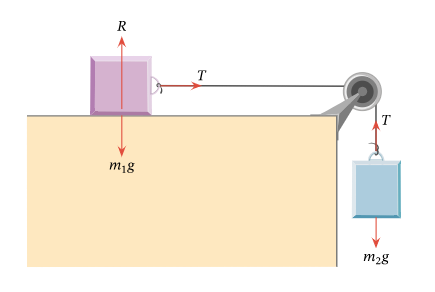
در شکل زیر فرض کنید دو جسم و توسط یک طناب بدون جرم و یک قرقره به هم متصل شدهاند. همچنین سطحی که جسم اول روی آن قرار داده شده است را یک سطح بدون اصطکاک در نظر بگیرید. مقدار کشش طناب و شتاب سیستم را محاسبه کنید.
پاسخ
با توجه به اینکه دو جسم با یک طناب بهم متصل شدهاند، شتاب برای کل سیستم مقدار یکسانی خواهد داشت. نیروهای وارد بر اجسام با توجه به نبود اصطکاک برابر با کشش طناب یکسان برای دو جسم و نیروی وزن است. نکات مهم در حل این مسئله اول این است که شتاب جسم اول در راستای محور x و جسم دوم در راستای محور y است. این دو شتاب به هم تبدیل شده و بهعنوان شتاب a سیستم در نظر گرفته میشوند. نکته بعدی انتخاب دستگاه مختصات است. برای راحتی جهت مثبت محور x را به سمت راست و جهت مثبت محور y را به سمت پایین در نظر میگیریم. حالا با نوشتن قانون دوم نیوتن برای هر جسم ابتدا شتاب و سپس نیروی کشش را برای سیستم بدست خواهیم آورد:
در نهایت مسئله بهصورت یک دستگاه دو معادله دو مجهول خواهد شد که با حل آن، مقدار T برابر با و شتاب بدست می آید.
مرکز جرم و سیستم ذرات
مکانیک کلاسیک با معرفی مفهومی به نام مرکز جرم به ما کمک میکند تا بتوانیم در تحلیل مسائل شامل اشکال هندسی خاص دقیقتر عمل کنیم. ابتدا باید ببینیم تعریف مرکز جرم در مکانیک کلاسیک چیست. فرض کنید در صفحه xy دارای جرمهای نقطهای متفاوتی به شکل در ، جرم در و به همین ترتیب، هستیم. مرکز جرم این سیستم از ذرات یا دارای مختصاتی بهصورت زیر است:
که در آن معادل جرم کل یا است. اگر این جرمهای نقطهای در سه بعد توزیع شده باشند، مختصات مرکز جرم به شکل زیر خواهد شد:
پس فرمول جامعتر برای محاسبه مرکز جرم برابر است با:
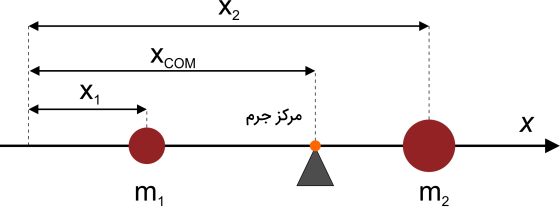
برای مثال، اگر دو جرم کاملا مساوی در فاصله مشخصی از یکدیگر قرار داشته باشند، مرکز جرم دقیقا در وسط این فاصله است. اما اگر یکی از این دو جرم از دیگری بزرگتر باشد، مطابق شکل زیر مرکز جرم که با هم نشان داده میشود، به جرم بزرگتر نزدیکتر خواهد بود.
مفهوم گشتاور و شتاب زاویه ای
وارد نشدن نیرو به جسم، ضمانتی در مورد حرکت نکردن آن به ما نمیدهد. ممکن است شرایطی داشته باشیم که علیرغم صفر شدن مجموع نیروها، جسم شروع به چرخش کند. تا اینجا فقط به بررسی حرکت خطی اجسام پرداختیم. در این بخش میخواهیم ببینیم حرکت زاویهای یا چرخش در مکانیک کلاسیک چیست و چه متغیرهایی در آن باید مطالعه شود.
هر نیرویی چرخش ایجاد نمیکند، بلکه فقط نیروهایی منجر به چرخش میشوند که دارای مولفهای عمود بر خط متصل کننده نقطه اثر نیرو و محور یا بازوی چرخشاند. به این ترتیب در این نوع حرکت علاوهبر نیرو و بازو یا محور چرخش (بازوی گشتاور)، با مفاهیم جدیدی به نام گشتاور نیرو یا ، تکانه زاویهای یا و شتاب زاویهای یا سروکار داریم. گشتاور نیرو یکی از مهمترین کمیتهای برداری در مکانیک کلاسیک است که بهصورت زیر محاسبه میشود:
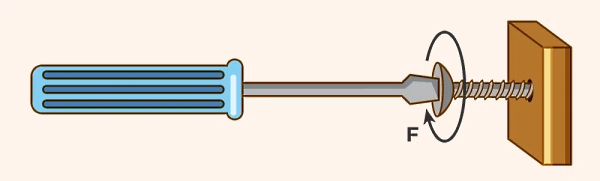
در این رابطه علامت به معنای ضرب خارجی دو بردار است. بنابراین گشتاور برداری است که بر نیروی ایجاد کننده آن و بر بازوی گشتاور عمود است (تعیین جهت توسط قانون دست راست انجام میشود). همچنین طبق فرمول ضرب برداری میتوانیم فرمول بالا را با در نظر گرفتن زاویه بین نیرو و بازوی گشتاور به شکل بهصورت زیر نیز بنویسیم:
ممان اینرسی و تکانه زاویه ای
تکانه زاویهای همتای زاویهای تکانه خطی در مکانیک کلاسیک است که توسط فرمول زیر محاسبه میشود:
اگر ضرب خارجی بالا را باز کنیم، خواهیم داشت:
اما مهمترین کاربرد تکانه زاویهای در نوشتن قانون دوم نیوتن بر حسب گشتاور و به شکل زیر است:
این رابطه دقیقا با در حرکت خطی معادل است. بنابراین شکل دیگر قانون دوم نیوتن در حرکت زاویهای را به صورت زیر نیز میتوانیم نشان دهیم:
همچنین در بررسی حرکت زاویهای یکی از مهمترین روابطی که در حل مسائل به ما کمک میکند، قانون پایستگی تکانه زاویهای است که معادل همتای آن در حرکت خطی است:
در این روابط اندیسهای و به ترتیب به معنای تکانه جسم در حالت اولیه و نهایی هستند. اگر فرمول تکانه را باز کنیم، فرمولهای بالا برابر میشوند با:
مثال از گشتاور برآیند
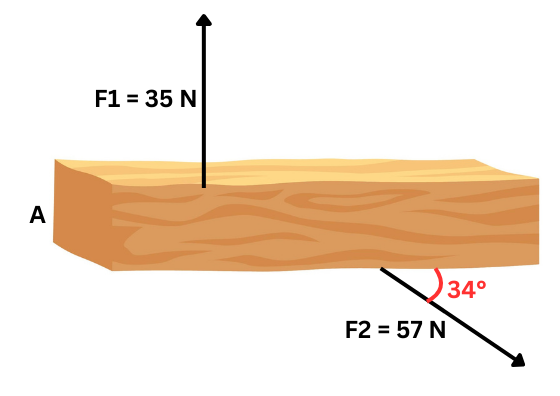
به تخته چوب زیر دو نیرو مطابق شکل وارد میشود. اگر نیروی در فاصله از گوشه سمت چپ و نیروی در فاصله از گوشه سمت راست به آن اعمال شوند، گشتاور برآیند نسبت به نقطه A را محاسبه کنید:
پاسخ
برای پیدا کردن گشتاور برآیند کافی است جهت نیرو و بازوی هر گشتاور را با توجه به نقطه A پیدا کنیم. همچنین لازم است جهت مثبت گشتاور را تعریف کنیم. فرض میکنیم در این سوال خارج صفحه معادل با جهت مثبت است. به این ترتیب برای مثال گشتاور حاصل از نیروی مثبت و گشتاور حاصل از نیروی منفی خواهد شد. پس نیازی به نوشتن شکل برداری فرمول گشتاور نیست، چون جهتها تعیین شدند. با نوشتن فرمولهای زیر محاسبات خود را ادامه میدهیم:
دقت کنید جهت بازوی گشتاور در تعیین جهت گشتاور هر نیرو مهم است. جهتبندی بازوی گشتاور همواره از نقطه اثر نیرو تا نقطه موردنظر (در اینجا A) در نظر گرفته میشود. همچنین در مورد دومین نیرو لازم است طول بازوی گشتاور را به شکل زیر بهدست آوریم:
بنابراین گشتاور برآیند از جمع کردن این دو گشتاور محاسبه میشود:
تفاوت استاتیک و دینامیک چیست؟
در بخشهای قبل آموختیم هرگاه چندین نیروی مختلف به یک جسم وارد شوند، اگر نیرو و گشتاور برآیند صفر شوند، جسم ما هیچ نوع شتابی چه خطی و چه زاویهای نخواهد داشت. پس طبق قانون اول نیوتن، این جسم به حرکت خود با سرعت ثابت یا وضعیت خود در حالت سکون ادامه خواهد داد. استاتیک شاخهای از مکانیک کلاسیک است که در آن به بررسی وضعیت اجسامی با این وضعیت پرداخته میشود.
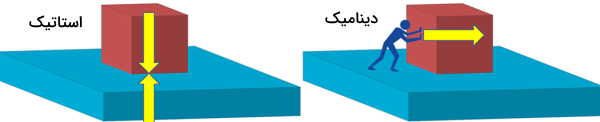
جدول زیر تفاوت استاتیک و دینامیک را بهخوبی نشان میدهد:
| مکانیک کلاسیک | |
| استاتیک (جسم در تعادل است) | دینامیک (جسم در تعادل نیست) |
مطالعه استاتیک مطالعه وضعیت تعادلی اجسام است، به این معنا که در مجموع هیچ نیرو یا گشتاوری به جسم موردبررسی وارد نمیشود. اما اگر نیرو یا گشتاوری جسم ما وارد شود، مطالعه وضعیت آن دیگر در حوزه استاتیک قرار نمیگیرد. پس در دینامیک با اجسامی سروکار داریم که از نیروها و گشتاورهای وارد بر آنها مخالف صفر هستند.
یادگیری مکانیک کلاسیک دانشگاهی با فرادرس
یکی از مهمترین مباحث فیزیک دانشگاهی در اغلب رشتههای مهندسی و علوم پایه، فیزیک مکانیک است. به همین دلیل در این بخش قصد داریم چند فیلم آموزشی مرتبط با این موضوع را به شما معرفی کنیم. مشاهده این دورههای فرادرس به شما کمک میکند تا با حل مثالها و تمرینهای متنوعتر در قالب صدا و تصویر درک بسیار عمیقتری نسبت به این مبحث کسب کنید:
- فیلم آموزش رایگان بردارها در فیزیک ۱ دانشگاهی
- فیلم آموزش فیزیک پایه ۱
- فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله
- فیلم آموزش فیزیک پایه ۱ مرور و حل مساله
- فیلم آموزش فیزیک پایه ۱ مرور و حل تست
- فیلم آموزش رایگان فیزیک پایه ۱ حرکت دورانی
- فیلم آموزش رایگان حرکت ذره در سه بعد در مکانیک تحلیلی
آزمون مکانیک کلاسیک
در این مطلب از مجله فرادرس یاد گرفتیم مکانیک کلاسیک چیست و پیرامون چه موضوعاتی در آن صحبت میشود. در انتها ده سوال چهار گزینهای برای شما در نظر گرفتهایم تا با پاسخدهی به آنها بتوانید دانش و یادگیری خود را بیازمایید. پس از اینکه پاسخ درست تمام سوالات را انتخاب کردید، با کلیک روی گزینه «مشاهده نتیجه آزمون» میتوانید نمره نهایی خود را مشاهده کنید.
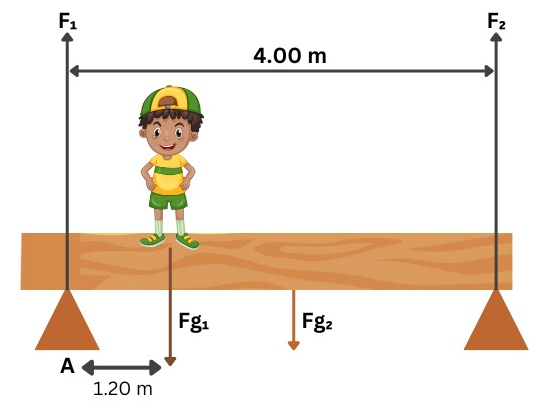
شخصی مطابق شکل زیر با جرم در فاصله از لبه سمت چپ یک تیر بلند با طول ایستاده است. اگر جرم این تیر باشد، برای حفط تعادل و ماندن شخص در این وضعیت، وزن نیروهای و به ترتیب برابراند با:
و
و
و
و
گزینه اول درست است. این مسئله به نوعی یک سوال استاتیکی محسوب میشود که در آن میخواهیم شخص در حالت تعادل باشد و هیچ نیرو یا گشتاور برآیندی به او وارد نشود. پس ابتدا تمام نیروهایی که در این سوال داریم را مشخص کرده و طبق قانون دوم نیوتن برآیند نیروها را پیدا میکنیم:
پس تا اینجا مجموع دو نیروی مورد نظر در سوال را به کمک برقراری شرط تعادل خطی پیدا کردیم. اما برای برقراری تعادل چرخشی لازم است هیچ گشتاور برآیندی نداشته باشیم. ابتدا یک نقطه مناسب تعریف میکنیم که گشتاورها را نسبت به آن بسنجیم. چون میخواهیم در این سوال کل مجموعه در تعادل باشد، انتخاب این نقطه دلخواه است، اما بهتر است طوری این نقطه را انتخاب کنیم که محاسبات ما آسانتر شود.
برای مثال، اگر نقطه A را طبق شکل سوال در نظر بگیریم، نیروی در محاسبات حذف میشود، چون بازوی گشتاوری در این شرایط برای این نیرو نخواهیم داشت. به این ترتیب گشتاور نیروهای و و را به شکل زیر حساب میکنیم:
حالا با در نظر گرفتن جهت نیروها و بازوی هر گشتاور، لازم است علامت مقادیر بهدست آمده را مشخص کنیم. اگر خارج صفحه را مثبت بگیریم، فقط مثبت است و دو گشتاور دیگر مقدار منفی دارند. بنابراین قانون دوم نیوتن به شکل زیر خواهد شد:
از رابطهای که بالاتر بهدست آمد، برای نیروی داریم:
موشکی با نرخ در طول پرتاب شتاب میگیرد. چقدر طول میکشد تا این موشک به سرعت برسد؟
گزینه آخر صحیح است. سرعت نهایی موشک و شتاب آن را داریم. همچنین میتوانیم نتیجهگیری کنیم که در هنگام پرتاب سرعت اولیه موشک صفر است. پس با نوشتن فرمول زیر که یکی از فرمولهای مهم حرکت با شتاب ثابت است، خواهیم داشت:
فرض کنید در داخل آسانسوری روی یک ترازو ایستادهاید. اگر وزن واقعی شما 610 N باشد اما ترازوی داخل آسانسور وزن شما را 730 N نشان دهد، شتاب آسانسور کدام گزینه است؟
شتاب متر بر مجذور ثانیه و به سمت پایین است.
شتاب متر بر مجذور ثانیه و به سمت بالا است.
شتاب متر بر مجذور ثانیه و به سمت بالا است.
گزینه دوم درست است. میدانیم به شخص ایستاده در داخل آسانسور روی ترازو، فقط دو نیرو در راستای قائم وارد میشود. نیروی وزن و نیروی عمودی سطح از سمت ترازو. زمانی وزن ظاهری (وزنی که ترازو میخواند) از وزن واقعی بیشتر میشود که شتاب به سمت بالا باشد. پس اگر قانون دوم را بنویسیم، داریم:
کودکی در حال راندن یک اسکوتر است. میدانیم که برای راندن اسکوتر لازم است پای خود را روی زمین به سمت عقب هل دهیم. این عقب دادن پا باعث میشود کودک شتابی برابر با داشته باشد. اگر وزن کودک باشد، نیرویی که کودک به اسکوتر وارد کرده است، کدام گزینه است؟ (فرض کنید شتاب جاذبه زمین برابر با است)
چون کودک میتواند با سرعت زیادی اسکوتر را حرکت دهد، پس نیرویی که کودک به اسکوتر وارد کرده است از بیشتر است.
مقدار این نیرو را نمیتوان محاسبه کرد. فقط میتوانیم بگوییم مقدار این نیرو با نیرویی که اسکوتر به کودک وارد میکند، برابر است.
گزینه سوم درست است. کودک در اثر نیرویی که از اسکوتر دریافت کرده است، شتاب دارد. طبق قانون دوم نیوتن است. پس اگر جرم کودک را بدانیم، با توجه به مقدار شتابی که در صورت سوال داریم میتوانیم نیروی اسکوتر به کودک را محاسبه کنیم. برای محاسبه جرم می توانیم از نیروی وزن که در صورت سوال داده شده است، استفاده کنیم. میدانیم برای وزن یا جاذبه زمین داریم:
حالا با داشتن جرم، آن را در فرمول قانون دوم نیوتن قرار میدهیم:
پس نیروی اسکوتر به کودک به دست آمد. طبق قانون سوم، نیروی کودک به اسکوتر نیز همین مقدار و در جهت مخالف است. پس اطلاعات کافی برای محاسبه نیرو در این سوال وجود دارد و گزینه ۴ اشتباه است.
شخصی با ممان اینرسی اولیه روی یک صندلی چرخان در اداره نشسته و در حال چرخیدن با سرعت زاویهای حول مرکز جرم صندلی است. اگر ممان اینرسی این شخص تا افزایش پیدا کند، سرعت زاویهای او در این حالت چقدر است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
فرض کنید شخصی با جرم و با سرعت در حال اسکی روی یک سطح شیبدار به سمت پایین است که ناگهان میافتد و شروع به سر خوردن روی سطح میکند. چنانچه دقیقا بعد از افتادن، سرعت شخص به برسد، شتاب شخص در هنگام لیز خوردن چقدر است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
در سوال قبلی، مدت زمان لیز خوردن شخص تا لحظهای که روی زمین به سکون میرسد، چقدر است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
یک نیروی به میلهای وارد میشود، به گونهای که این میله حول مرکز خود میچرخد. اگر این نیرو در نقطهای به فاصله از مرکز میله و با زاویه درجه به آن وارد شود، گشتاور حاصل از آن برابر است با:
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
فرض کنید نمودار مکان – زمان حرکت جسمی بهصورت زیر داده شده است. کدام گزینه معادله مکان – زمان این حرکت را در بازه تا نشان میدهد؟
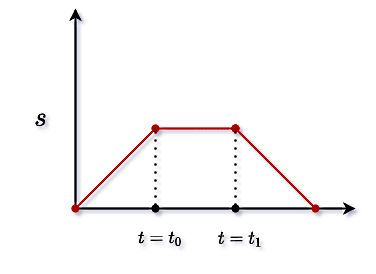
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
source
