خازن معادل خازنی است که اگر جایگزین گروهی از خازنها در مدار شود، عملکردی معادل با عملکرد آنها در مدار خواهد داشت. پیدا کردن ظرفیت این خازن که با یا نمایش داده میشود، تحلیل مدارهای الکتریکی را بسیار آسانتر خواهد کرد. در این مطلب از مجله فرادرس توضیح میدهیم خازن معادل در مدارهای سری و موازی چیست و ظرفیت آن چگونه محاسبه میشود.
آنچه در این مطلب میآموزید:
-
میآموزید مفهوم و کاربرد خازن معادل چیست.
-
نحوه پیدا کردن ظرفیت خازن معادل در اتصال سری را فراخواهید گرفت.
-
نحوه پیدا کردن ظرفیت خازن معادل در اتصال موازی را یاد میگیرید.
-
میتوانید مدارهای ترکیبی شامل اتصال سری و موازی خازنها را ساده کنید.
-
با فرمولهای اتصال سری و موازی خازنها بهطور کامل آشنا خواهید شد.
-
نحوه پیدا کردن ظرفیت خازن معادل در مدارهای الکتریکی را تمرین خواهید کرد.

ابتدا توضیح میدهیم مفهوم خازن معادل چیست و چرا بهتر است در بررسی مدارهای شامل چند خازن به پیدا کردن این خازن و محاسبه ظرفیت آن بپردازیم. در ادامه پس از اشاره به ساختار، فرمول و کاربرد خازن در الکترونیک، نشان میدهیم اتصال سری و موازی خازنها چه تفاوتی دارد و فرمول خازن معادل برای هر کدام چگونه بهدست میآید. همچنین با حل مثال و تمرین به شما کمک میکنیم تا بتوانید در مدارهای پیچیدهتر که شامل ترکیبی از اتصال سری و موازی خازنها میشوند، بهراحتی ظرفیت خازن معادل را محاسبه کنید.
خازن معادل چیست؟
اگر بتوانیم گروهی از خازنهای متصل شده به هم را تنها با یک خازن جایگزین کنیم، به گونهای که عملکرد این تک خازن با عملکرد مجموعه خازنهای قبلی کاملا یکسان باشد، در این صورت این خازن را «خازن معادل» مینامیم. برای خازن سری با ظرفیت تا ، ظرفیت خازن معادل توسط فرمول محاسبه میشود، در حالی که در اتصال خازن موازی، ظرفیت خازن معادل برابر است با .
اگر مطابق تصویر زیر صفحاتی از دو خازن به هم متصل شوند که بارهای مخالف هم دارند، در این صورت اتصال سری یا مدار سری داریم. در این حالت برای سادهتر شدن محاسبات میتوانیم دو خازن سری را با یک خازن معادل جایگزین کنیم. نکته مهم این است که بار خازن معادل در اتصال سری با بار هر کدام از خازنهای متصل شده به هم برابر است. این در حالی است که ولتاژ خازن معادل در این نوع اتصال برابر است با مجموع ولتاژ هر کدام از دو خازن.
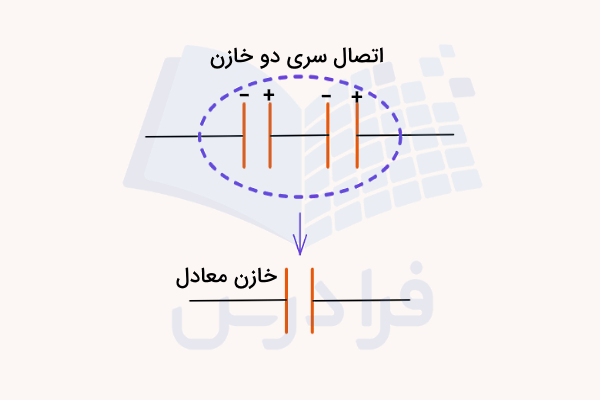
اما اگر طبق تصویر زیر صفحاتی از دو خازن به هم متصل شوند که بارهای مشابه هم دارند، در این صورت اتصال موازی یا مدار موازی داریم. در این حالت هم میتوانیم برای سادهتر شدن محاسبات دو خازن موازی را با یک خازن معادل جایگزین کنیم. نکته مهم این است که در اتصال موازی، ولتاژ خازن معادل همواره با ولتاژ دو سر خازنهای متصل شده به هم برابر است. اما بار خازن معادل در این نوع اتصال برابر است با مجموع بار هر کدام از دو خازن.
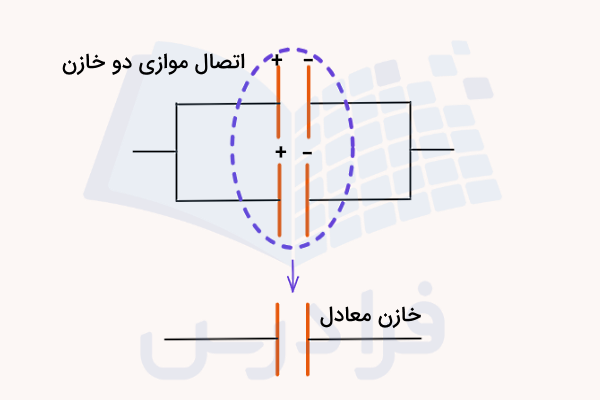
جدول زیر مروری است بر فرمول بار، ولتاژ و ظرفیت خازن معادل در هر کدام از دو نوع اتصال سری و موازی:
| خازنهای سری | خازنهای موازی |
| اتصال صفحات ناهمنام | اتصال صفحات همنام |
بنابراین برای اینکه بتوانیم خازن معادل مجموعهای از خازنها را پیدا کنیم، لازم است این خازنها به شکل سری یا موازی به هم متصل شده باشند. پس اولین قدم در محاسبه ظرفیت خازن معادل تشخیص اتصال سری یا موازی خازنها است. البته در برخی از مسائل ممکن است با ترکیبی از اتصال سری و موازی خازنها روبرو شویم که در بخشهای بعدی با حل مثال میآموزید چگونه میتوان خازن معادل را در چنین مدارهایی نیز پیدا کرد.
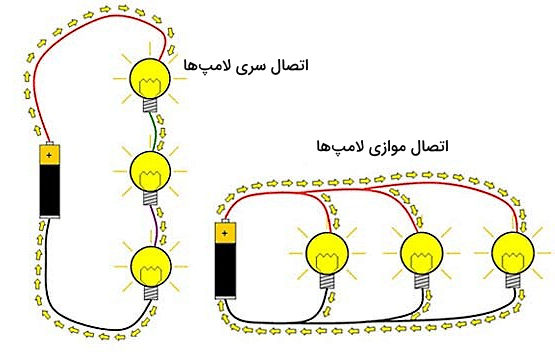
پیدا کردن خازن معادل و محاسبه ظرفیت آن به شما این امکان را میدهد تا یک مدار الکتریکی پیچیده را به مدار سادهتری تبدیل کنید. همچنین میدانیم ویژگی مهم یک خازن در مدار، ظرفیت آن است. پس بهتر است فرمولهای خازن را بهگونهای پیدا کنیم که ظرفیت خازن معادل را به ما بدهند. اگر خازنها به شکل سری به هم متصل شده باشند، محاسبه ظرفیت خازن معادل آنها فرمول مخصوص به خود را دارد، در حالی که ظرفیت خازن معادل در اتصال موازی خازنها فرمول دیگری دارد. تصویر بالا اتصال سری و موازی چند لامپ را در دو مدار مختلف نشان میدهد. اتصال سری و موازی خازنها نیز به همین شکل است. در ادامه توضیح میدهیم که برای هر نوع اتصال و یا در مدارهایی شامل ترکیبی از این دو نوع اتصال، چگونه میتوان خازن معادل را پیدا کرد.
ساختار و فرمول خازن
برای اینکه بهتر متوجه شوید اتصال سری و موازی خازنها به چه صورت است، ابتدا باید با ساختار خازن آشنا شوید. خازن یکی از قطعات الکترونیکی است که وظیفه ذخیرهسازی و آزاد کردن بار و انرژی الکتریکی در مدار را بر عهده دارد. این قطعه از دو صفحه رسانا موازی هم ساخته میشود که بین آنها معمولا یک دیالکتریک قرار گرفته است. میزان توانایی یک خازن جهت ذخیرهسازی بار الکتریکی توسط کمیتی به نام ظرفیت خازن مشخص میشود.
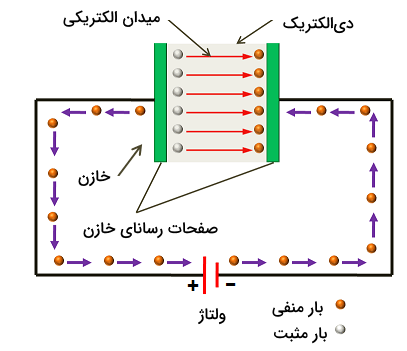
در تصویر بالا خازنی را مشاهده میکنید که در حال شارژ شدن است، به این صورت که با اتصال پایانه مثبت باتری به صفحه رسانای سمت چپ خازن و پایانه منفی آن به صفحه راست خازن اختلاف پتانسیل () به دو سر این قطعه اعمال میشود. در نتیجه با برقراری جریان، تعداد زیادی بار منفی از طریق سیم رسانا به سمت صفحه سمت راست خازن حرکت میکنند. این بارها دافعه شدیدی را از بار منفی موجود در دیالکتریک خازن حس میکنند.
در نتیجه مقدار زیادی بار منفی () روی صفحه سمت راست خازن جمع میشود. دقت کنید به همین شکل بار مثبت و برابر با روی صفحه چپ خازن جمع میشود. بین ظرفیت خازن، بار ذخیره شده روی آن و اختلاف پتانسیل اعمال شده به دو سر آن (دو صفحه آن) رابطه زیر برقرار است:
همچنین خازن در مدار با نماد زیر مشخص میشود:
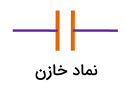
چگونه خازن و محاسبات آن را با فرادرس بهتر بیاموزیم؟
پیش از اینکه به توضیح دو نوع اتصال خازنها و نحوه پیدا کردن خازن معادل در هر کدام بپردازیم، در این بخش قصد داریم چند دوره آموزشی تهیه شده در مجموعه فرادرس را به شما معرفی کنیم تا با مشاهده آنها به این مبحث کاملا مسلط شوید. برای مثال، در بخش الکتریسیته ساکن از کتاب درسی فیزیک پایه یازدهم، تعریف خازن، فرمول محاسبه ظرفیت آن به همراه عوامل موثر بر ظرفیت خازن و نحوه به دست آوردن انرژی آن توضیح داده شده است. همچنین در آموزش فیزیک پایه یازدهم فرادرس علاوه بر پوشش این موضوعات، به حل چند نمونه تست کنکور سراسری نیز پرداخته شده است. بنابراین مشاهده این فیلمها به یادگیری بهتر شما کمک خواهد کرد. در ادامه لیستی از دورههای مرتبط را مشاهده میکنید:
خازن معادل در مدار سری
فرض کنید دو خازن با ظرفیتهای و به شکل زیر به هم متصل شدهاند، یعنی صفحه مثبت خازن اول به سیم حامل جریان ورودی، صفحه منفی خازن اول به صفحه مثبت خازن دوم و صفحه منفی خازن دوم به سیم خروجی متصل شده است. چنین اتصالی را اتصال سری خازنها و مدار حاصل از آن را یک مدار سری مینامیم. در اتصال سری خازنها، صفحات با بار مخالف هم به شکل زنجیرهای و در راستای یک خط به هم متصل میشوند.
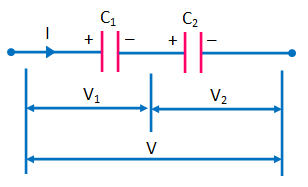
حالا میخواهیم خازن معادل در چنین اتصالی را به همراه ظرفیت آن پیدا کنیم. نکته مهم در مورد اتصال سری خازنها این است که بار ذخیره شده روی تمام خازنهایی که به شکل سری به هم وصل شدهاند، با هم برابر است. برای اینکه این نکته را بهتر متوجه شوید، به صفحات داخلی اتصال سری در تصویر بالا توجه کنید. منظور ما از صفحات داخلی، صفحه منفی خازن اول و صفحه مثبت خازن دوم است.
این دو صفحه از نظر فیزیکی از بقیه مدار مجزا هستند و به همین دلیل لازم است که بار کل روی آنها ثابت باقی بماند. در واقع اگر هیچ اختلاف پتانسیلی به دو سر این خازنها اعمال نشود، این دو صفحه هیچ باری نخواهند داشت و به همین ترتیب، اگر اختلاف پتانسیلی برابر با به دو سر این دو خازن اعمال شود، بار روی صفحه مثبت خازن دوم و بار روی صفحه منفی خازن اول ذخیره میشود. علت منفی و مثبت بودن بار صفحات داخلی در این اتصال برقراری تعادل است.
پس تا اینجا متوجه شدیم که هر دو خازن در اتصال سری بالا بار برابری با اندازه دارند. اما همانطور که در شکل ملاحظه کردید، افت پتانسیل هر کدام از این دو خازن با دیگری متفاوت است، اگر چه هر دو به منبع یکسانی با ولتاژ متصل شدهاند. مجموع این افت ولتاژها با کل ولتاژ اعمال شده به ورودی و خروجی این اتصال سری برابر است، یعنی داریم:
با توجه به آنچه گفته شد، حالا میتوانیم ظرفیت خازن معادل را برای شکل بالا محاسبه کنیم. کافی است از فرمول خازن به شکل زیر استفاده کنیم و آن را بر حسب ولتاژ بنویسیم:
با جایگزین کردن کسر بالا بهجای مقادیر ولتاژ در فرمول خواهیم داشت:
در نوشتن عبارت بالا از این واقعیت استفاده کردیم که مشخصات خازن اول برابر با ، مشخصات خازن دوم و مشخصات خازن معادل است. دقت کنید طبق توضیحاتی که دادیم، مقادیر بار روی دو خازن اول و دوم با بار روی خازن معادل برابر است و به همین علت برای هر سه خازن بار را قرار دادیم. حالا میتوانیم با فاکتورگیری از عامل مشترک در دو طرف تساوی بالا به رابطه زیر برسیم:
آنچه بهدست آمد، فرمول خازن معادل در اتصال سری دو خازن است. همچنین میتوانیم با مخرج مشترک گرفتن و معکوس کردن کسر اول، فرمول بالا را به شکل زیر هم بنویسیم:
تعمیم این فرمول برای تعداد زیادی () خازن که به شکل سری به هم متصل شدهاند، ما را به فرمول زیر میرساند:
نکته ۱: ظرفیت خازن معادل در اتصال سری همواره از ظرفیت هر کدام از خازنها کوچکتر است.
نکته ۲: اگر خازن با ظرفیتی مساوی به شکل سری به هم متصل شوند، ظرفیت خازن معادل این خازنها برابر است با .
حل مثال از خازن معادل در اتصال سری
در این بخش نحوه استفاده از فرمول ظرفیت خازن معادل در مدار سری را با حل مثال بهتر متوجه خواهید شد. پیش از شروع، پیشنهاد میکنیم جدول زیر را حاوی تمام فرمولهای اتصال سری خازنها است، مرور کنید:
| اتصال سری خازن |
|
| رابطه بار خازن معادل و بار ذخیره شده روی هر خازن | |
| رابطه ولتاژ خازن معادل با افت ولتاژ در عبور از هر خازن | |
| رابطه ظرفیت خازن معادل با ظرفیت هر خازن | |
همچنین فرادرس یک فیلم آموزشی جامع را با عنوان «آموزش فیزیک الکتریسیته + مفاهیم کلیدی» تهیه کرده است که میتواند مسیر یادگیری فرمولهای خازن و تسلط شما بر حل مسائل مرتبط با تعیین خازن معادل را هموار کند. لینک مشاهده این فیلم آموزشی در ادامه آورده شده است:
مثال ۱
ظرفیت خازن معادل برای دو خازن با ظرفیت که بهصورت سری به هم وصل شدهاند، چقدر است؟ همچنین افت ولتاژ هر کدام از این دو خازن را محاسبه کنید، در صورتی که ولتاژی برابر با به این اتصال اعمال شده باشد:
پاسخ
محاسبه ظرفیت خازن معادل برای دو خازن سری توسط فرمول زیر انجام میشود:
برای اینکه افت ولتاژ در هر کدام از این دو خازن محاسبه شود، فرمول زیر را برای خازن معادل مینویسیم و میدانیم که در اتصال سری :
حالا با نوشتن فرمولهای زیر برای هر کدام از دو خازن میتوانیم افت ولتاژ هر کدام را بهدست آوریم:
مثال ۲
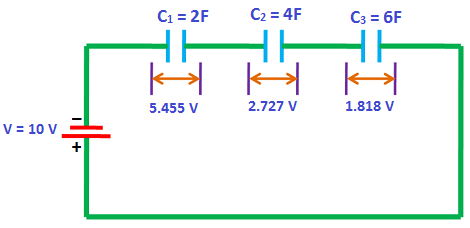
در شکل زیر مداری را ملاحظه میکنید که شامل سه خازن است. خازن معادل این مدار چه ظرفیتی دارد و بار ذخیره شده روی آن چقدر است؟ همچنین بار ذخیره شده روی هر کدام از سه خازن را به همراه ولتاژ هر کدام بهدست آورید:
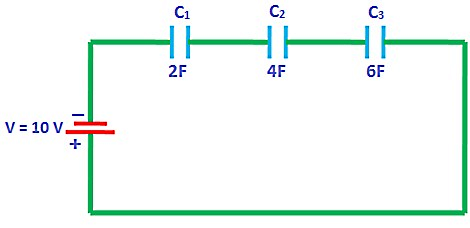
پاسخ
این سه خازن بهصورت سری به هم متصل شدهاند، چون پایانه منفی منبع ولتاژ یا باتری در مدار به یک صفحه خازن اول متصل شده است و اگر دقت کنیم، در ادامه نیز صفحات ناهمنام خازنها در این چیدمان به هم متصل شدهاند. بنابراین با نوشتن فرمولهای خازن معادل در اتصال سری خواهیم داشت:
در بخش دوم این سوال بار ذخیره شده روی خازن ظرفیت از ما خواسته شده است. با توجه به اینکه ولتاژ کل اعمال شده به سه خازن سری در شکل مشخص است، اگر از فرمول استفاده کنیم، بار خازن معادل این سه خازن سری برابر میشود با:
همچنین گفتیم که بار روی هر کدام از سه خازن سری با بار خازن معادل برابر است. بنابراین برای خازنهای تا بار به شکل زیر خواهد بود:
در نهایت برای محاسبه ولتاژ هر کدام از خازنهای تا با استفاده از فرمول زیر خواهیم داشت:
بنابراین توزیع ولتاژ روی هر کدام از این سه خازن در مدار سری به شکل زیر است:
مثال ۳
اگر یک خازن را به یک خازن بهصورت سری ببندیم و به دو سر این جفت خازن نیز ولتاژ را اعمال کنیم، بار و افت ولتاژ در عبور از هر خازن چقدر است؟
پاسخ
دو خازن سری داریم و میدانیم بار روی هر کدام از خازنهای سری با بار روی خازن معادل آنها برابر است. پس اگر ظرفیت خازن معادل این دو خازن را پیدا کنیم، میتوانیم بار کل این مدار سری و بار هر یک از دو خازن را همزمان بهدست آوریم:
به این ترتیب بار روی هر کدام از این دو خازن بهدست آمد. در مرحله بعد برای تعیین ولتاژ هر خازن، کافی است از فرمول زیر برای هر کدام استفاده کنیم:
خازن معادل در مدار موازی
در بخش قبل آموختیم اتصال سری خازنها چگونه است و فرمول مناسب برای محاسبه ظرفیت خازن معادل در این حالت چیست. در این بخش ابتدا توضیح میدهیم اتصال موازی خازنها به چه صورت است. اگر دو خازن با ظرفیتهای و به شکل زیر به هم وصل شوند، طوری که صفحه مثبت خازن اول به صفحه مثبت خازن دوم و صفحه منفی خازن اول نیز به صفحه منفی خازن دوم متصل شود، در این حالت میگوییم این دو خازن موازی شدهاند.
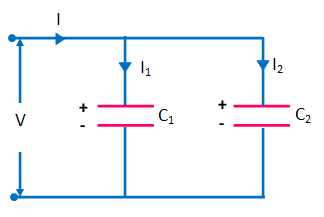
در این حالت صفحات مثبت هر دو خازن به سیم جریان ورودی و صفحات منفی هر دو خازن نیز به سیم خروجی متصل است. حالا برای اینکه بتوانیم ظرفیت معادل این دو خازن را پیدا کنیم، کافی است به ولتاژ و بار روی هر خازن توجه کنیم و ببینیم این مدار با مدار بخش قبل چه تفاوتی دارد. در این نوع مدار اختلاف پتانسیل اعمال شده به کل مدار یا با اختلاف پتاسیلی که به دو سر هر کدام از دو خازن وارد میشود، برابر است.
اما برخلاف مدار سری، در این مدار موازی بار کل بین دو خازن تقسیم میشود. در واقع این بار باید بهگونهای توزیع شود که افت ولتاژ در عبور از هر کدام از دو خازن یکسان باقی بماند. بنابراین دو خازن بالا با ظرفیتهای و دارای بارهای متفاوتی به شکل و هستند. بنابراین با در نظر گرفتن ظرفیت خازن معادل بهصورت زیر خواهیم داشت:
حالا با کمک گرفتن از رابطه که معادل است با نحوه توزیع بار خازن معادل روی هر کدام از دو خازن موازی، خواهیم داشت:
در نوشتن عبارت بالا از این واقعیت استفاده کردیم که مشخصات خازن اول برابر با ، مشخصات خازن دوم و مشخصات خازن معادل است. دقت کنید طبق توضیحاتی که دادیم، ولتاژ خازن اول و دوم با ولتاژ کل باتری در مدار برابر است و به همین علت برای هر سه خازن اختلاف پتانسیل را قرار دادیم. سمت دیگر تساوی بالا معادل است با مجموع ظرفیت خازنهای یک و دو:
آنچه بهدست آمد، فرمول خازن معادل در اتصال موازی دو خازن است. تعمیم این فرمول برای تعداد زیادی () خازن که به شکل موازی به هم متصل شدهاند، ما را به فرمول زیر میرساند:
نکته ۱: ظرفیت خازن معادل در اتصال موازی همواره از ظرفیت هر کدام از خازنها بزرگتر است.
نکته ۲: اگر خازن با ظرفیتی مساوی به شکل موازی به هم متصل شوند، ظرفیت خازن معادل این خازنها برابر است با .
حل مثال از خازن معادل در اتصال موازی
پس از اینکه با مدار موازی و نحوه محاسبه ظرفیت خازن معادل در آن آشنا شدید، در این بخش میتوانید پس از مطالعه جدول زیر با حل چند مثال روش استفاده از فرمول خازن معادل در اتصال موازی را تمرین کنید:
| اتصال موازی خازن |
|
| رابطه بار خازن معادل و بار ذخیره شده روی هر خازن | |
| رابطه ولتاژ خازن معادل با افت ولتاژ در عبور از هر خازن | |
| رابطه ظرفیت خازن معادل با ظرفیت هر خازن | |
دقت کنید فرمولهای مربوط به اتصال سری و موازی خازنها کاملا برعکس فرمولهای متناظر برای قطعهای به نام مقاومت الکتریکی در مدار است. در این زمینه، پیشنهاد میکنیم مطلب «مقاومت الکتریکی چیست؟ – تعریف و توضیح کامل به زبان ساده» از مجله فرادرس را نیز مطالعه کنید.
مثال ۱
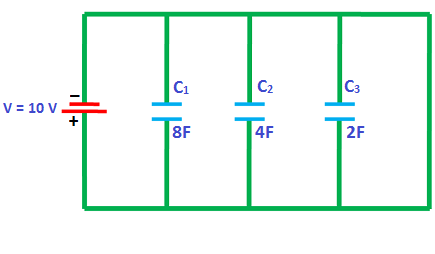
سه خازن بهصورتی که در تصویر زیر ملاحظه میکنید، به هم متصل شدهاند. خازن معادل این سه خازن چه ظرفیتی دارد؟ ولتاژ دو سر هر کدام از سه خازن و بار روی هر یک چقدر است؟ همچنین نشان دهید بار کل ذخیره شده روی این سه خازن با بار خازن معادل برابر است:
پاسخ
همانطور که در تصویر بالا ملاحظه میکنید، مدار این سوال سه خازن موازی هم را نشان میدهد. گفتیم برای خازنهای موازی، ظرفیت خازن معادل با جمع کردن ظرفیت خازنها بهدست میآید. در اینجا سه خازن داریم، پس فرمول با در نظر گرفتن به شکل زیر خواهد شد:
همچنین گفتیم در مورد خازنهای موازی، همواره ولتاژ دو سر هر خازن با ولتاژ کل اعمال شده به مدار برابر است. بنابراین در اینجا داریم:
پس از اینکه ولتاژ هر خازن تعیین شد، بار ذخیره شده روی هر یک نیز توسط فرمول زیر محاسبه میشود:
به این ترتیب بار کل این مدار با جمع کردن باری که روی هر کدام از سه خازن ذخیره شده است، بهدست میآید:
همچنین اگر بار ذخیره شده روی خازن معادل را توسط فرمول زیر پیدا کنیم، ملاحظه میکنید که این بار با مجموع بارهای روی هر خازن برابر است:
مثال ۲
اگر ظرفیت معادل چند خازن با ظرفیتهای و و برابر با باشد، مقدار چقدر است؟
پاسخ
ظرفیت خازن معادل در اتصال موازی از مجموع ظرفیت خازنها حاصل میشود:
مثال ۳
اگر سه خازن با ظرفیتهای و و بهصورت موازی بسته شوند و یک باتری با ولتاژ به دو سر این مجموعه متصل شود، بار و ولتاژ هر خازن را محاسبه کنید:
پاسخ
با توجه به اینکه سه خازن موازی داریم، طبق قوانین این نوع اتصال خازنها میدانیم ولتاژ کل مجموعه با ولتاژ دو سر هر کدام از خازنها برابر است، یعنی داریم:
پس بخشی از سوال در همینجا پاسخ داده شد. در مورد محاسبه بار روی هر خازن نیز طبق فرمول زیر عمل میکنیم:
خازن معادل در مدارهای ترکیبی
مدارهای الکتریکی همیشه بهصورت یک اتصال سری یا موازی از خازنها طراحی نمیشوند، بلکه اغلب با شکلی پیچیدهتر و بهصورت ترکیبی از اتصالات سری و موازی روبرو هستیم. در این بخش با حل مثال نشان میدهیم که در مدارهای شامل هر دو نوع اتصال چگونه میتوان ظرفیت خازن معادل را محاسبه کرد.
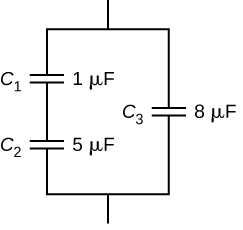
فرض کنید مداری به شکل بالا داریم و میخواهیم خازن معادل را در این مدار ترکیبی از اتصال سری و موازی پیدا کنیم. اولین قدم برای ساده کردن چنین مدارهایی این است که بخشهایی از مدار را که فقط شامل یک اتصال سری یا موازی هستند، شناسایی کنیم. سپس باید خازن معادل این بخش را پیدا کنیم. این فرآیند آنقدر تکرار میشود تا هیچ خازن دیگری جز خازن معادل در مدار باقی نماند.
در مداری که مشاهده کردید، شاخه سمت چپ دو خازن سری را نشان میدهد که صفحات آنها به هم وصل شدهاند. پس اولین قدم پیدا کردن خازن معادل این دو خازن سری یعنی و است که در شکل زیر با نشان داده شده است:
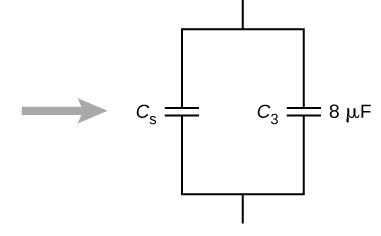
ملاحظه میکنید که مدار اولیه به شکل بالا ساده شد. حالا از موازی بودن خازن معادل با سومین خازن یعنی استفاده میکنیم. به این ترتیب خازن معادل با سه خازن اولیه در مدار را به شکل زیر خواهیم داشت:
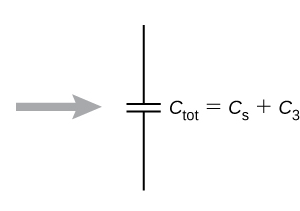
مثال ۱
در مدار شکل زیر، ظرفیت خازن معادل چقدر است؟
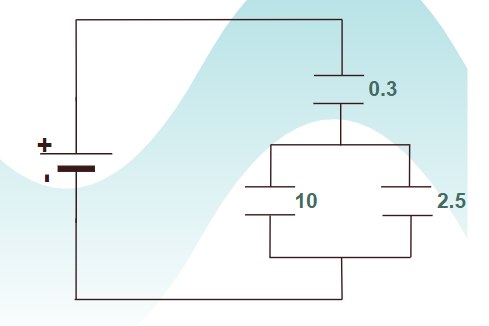
پاسخ
در این مدار سه خازن داریم که نوع اتصال آنها ترکیبی از اتصال سری و موازی است. اگر دقت کنید خازنهایی با ظرفیت و موازی هم بسته شدهاند. اگر خازن معادل این دو را پیدا کنیم، این خازن با خازن یک اتصال سری را تشکیل خواهد داد و میتوانیم با محاسبه ظرفیت خازن معادل این دو به سوال پاسخ دهیم. پس اولین قدم، در نظر گرفتن دو خازن موازی با ظرفیت و است:
حالا مدار ما از ترکیب سه خازن با ظرفیتهای و و به اتصال سری دو خازن با ظرفیت و تبدیل شده است. پس کافی است فرمول خازن معادل در اتصال سری را برای این دو خازن بنویسیم تا ظرفیت خازن معادل این مدار محاسبه شود:
مثال ۲
ابتدا ظرفیت خازن معادل در مدار زیر را با این فرض که و و است، محاسبه کنید. سپس ولتاژ و بار روی هر خازن را بهدست آورید:
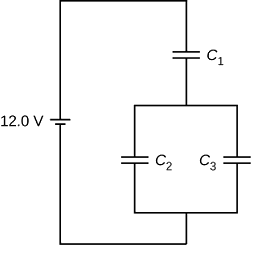
پاسخ
مدار داده شده یک اتصال ترکیبی از اتصالهای سری و موازی است. بنابراین ابتدا باید ببینیم در کدام بخش از این مدار یک اتصال سری یا موازی به وضوح دیده میشود. با دقت در حلقه سمت راست این مدار، واضح است که خازنهای و موازی هم بسته شدهاند. پس ابتدا ظرفیت خازن معادل این دو خازن را به شکل زیر پیدا میکنیم:
با تبدیل خازنهای شماره دو و سه به یک خازن معادل با ظرفیت مدار تا حدی سادهتر شده است. این خازن با خازن شماره یک سری است. پس معادل و را اگر پیدا کنیم، خازن معادل کل این مدار تعیین شده است:
در دومین بخش از سوال میخواهیم بار و ولتاژ روی هر خازن را پیدا کنیم. برای رسیدن به این هدف، بهصورت معکوس عمل میکنیم و به اتصال سری دو خازن و بازمیگردیم. دو خازن سری دارای باری برابر با هم و برابر با بار خازن معادل خود هستند. پس همینجا میتوانیم نتیجهگیری کنیم که .
همچنین ولتاژ کل اعمال شده به این مدار برابر است با مجموع افت ولتاژ در خازن شماره یک و خازن معادل :
حالا با توجه به فرمول و با در نظر گرفتن رابطه بالا برای بار هر کدام از این سه خازن، میتوانیم مقادیر ولتاژ را به شکل زیر داشته باشیم:
با جایگذاری مقادیر عددی در رابطه بالا خواهیم داشت:
پس تا اینجا بار روی اولین خازن بهدست آمد. افت ولتاژ این خازن نیز با داشتن بار و ظرفیت آن برابر است با:
حالا یک پله عقبتر میرویم تا بتوانیم مشخصات بار و ولتاژ خازنهای شماره دو و سه را نیز پیدا کنیم. خازنهای و موازی هستند، بنابراین طبق قوانین خازنهای موازی انتظار داریم ولتاژ برابر داشته باشند. همچنین ولتاژ خازن معادل این دو یعنی نیز باید با ولتاژ هر کدام از این دو خازن برابر باشد:
را میتوانیم توسط فرمول خازن و به شکل زیر محاسبه کنیم:
البته یک راه دیگر برای پیدا کردن ولتاژ این خازن معادل این بود که ولتاژ کل را از ولتاژ خازن شماره یک یعنی کم کنیم. حاصل این تفریق نیز خواهد شد. بنابراین ولتاژ خازنهای شماره دو و سه نیز خود به خود پیدا شدند:
بار روی این دو خازن نیز با مشخص شدن ولتاژ و دانستن ظرفیت به شکل زیر بهدست میآید:
پس بار و ولتاژ خازنهای شماره یک تا سه تعیین شد.
مثال ۳
خازن معادل مدار زیر با فرض و و و ، چه ظرفیتی دارد؟ همچنین بار روی هر کدام از این چهار خازن را با در نظر گرفتن اختلاف پتانسیل کل محاسبه کنید:
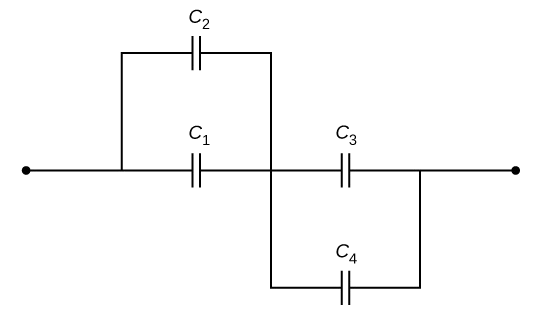
پاسخ
در مدار بالا ترکیبی از اتصال سری و موازی را داریم. در واقع دو حلقه در مدار است که هر کدام به شکل موازی بسته شدهاند و اگر برای هر کدام از این حلقهها یک خازن معادل را در نظر بگیریم، در نهایت مدار بالا بهصورت یک اتصال سری از دو خازن ساده میشود. ابتدا حلقه سمت راست را در نظر میگیریم که اتصال موازی از دو خازن و است. خازن معادل این دو ظرفیتی به شکل زیر دارد:
سپس حلقه سمت چپ را در نظر میگیریم که اتصال موازی از دو خازن و است. خازن معادل این دو نیز ظرفیتی به شکل زیر دارد:
پس مدار بالا از چهار خازن با اتصال ترکیبی به دو خازن با اتصال سری کاهش پیدا کرد. در نهایت ظرفیت خازن معادل این مدار توسط فرمول زیر محاسبه میشود:
حالا میرویم سراغ بخش دوم این سوال که محاسبه بار روی هر خازن است. برای پاسخدهی به این فرم از سوالات در مدارهای ترکیبی بهتر است از انتها به ابتدا روند مرحله قبل را تکرار کنیم. در انتهای کار دو خازن سری داشتیم که خازن معادل آنها ظرفیت دارد، در حالی که ولتاژ دو سر این خازن معادل طبق صورت سوال است. بنابراین با استفاده از فرمول اصلی خازن میتوانیم بار خازن معادل را پیدا کنیم:
از طرفی میدانیم بار روی دو خازن سری با هم و با بار روی خازن معادلشان برابر است. پس داریم:
اما هنوز بار روی هر کدام از چهار خازن شماره یک تا چهار مشخص نیست. پس یک پله عقبتر میرویم. خازن معادل با دو خازن موازی یک و دو، ظرفیت و بار مشخصی دارد. پس ولتاژ آن را به شکل زیر محاسبه میکنیم:
و چون خازنهای یک و دو موازی هم هستند، پس داریم:
حالا میتوانیم با داشتن ولتاژ و ظرفیت هر کدام از خازنهای شماره یک و دو بار روی این دو خازن را به شکل زیر تعیین کنیم:
همین روند را برای خازنهای موازی سه و چهار اجرا میکنیم:
مثال ۴
ظرفیت خازن معادل در مدار زیر چقدر است؟
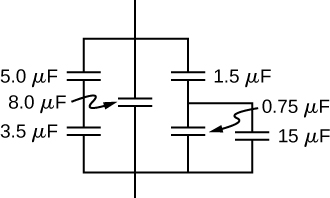
پاسخ
این مدار ترکیبی از اتصال سری و موازی چند خازن است. اگر از سمت راست شروع کنیم، خازنهایی با ظرفیت و موازی هم هستند. بنابراین خازن معادل این دو ظرفیتی به اندازه زیر دارد:
خازن معادل این دو را با نشان میدهیم. با خازن بالایی خود که ظرفیت میکروفاراد دارد، سری بسته شده است. اگر معادل این دو را بنامیم، محاسبه آن طبق فرمول ظرفیت خازنهای سری به شکل زیر انجام میشود:
خازن با خازن میکروفارادی موازی است، پس معادل این دو یا برابر میشود با:
به همین شکل نیز با دو خازن باقیمانده در شاخه سمت چپ مدار موازی است. برای سادهسازی، بهتر است ابتدا معادل این دو خازن را که بهصورت سری به هم متصل شدهاند، پیدا کنیم. اگر این معادل را بنامیم، معادل خازنهای موازی و به ما خازن معادل این مدار را میدهد:
یادگیری فیزیک الکتریسیته دانشگاهی با فرادرس
فیزیک پایه دانشگاهی شامل موضوعات مهمی مانند فیزیک مکانیک، فیزیک الکتریسیته و مغناطیس است که در اغلب رشتههای علوم پایه و مهندسی آشنایی با این سه موضوع از اهمیت بالایی برخوردار است. در این نوشته، در مورد مبحث خازن از فیزیک الکتریسیته صحبت کردیم. به همین دلیل در ادامه چند فیلم آموزشی مرتبط از مجموعه فرادرس برای شما انتخاب شده است تا با مشاهده آنها به حل مسائل این حوره مسلط شوید:
- فیلم آموزش رایگان الکتریسیته ساکن – حل تمرین
- فیلم آموزش رایگان اسیلاتور RC + حل مثال
- فیلم آموزش رایگان محاسبه ظرفیت خازن از روی کد رنگ
- فیلم آموزش رایگان تعمیر لوازم خانگی حرارتی ۱ – الکتریسیته، خازن و مقاومت
آزمون خازن معادل
در انتهای این مطلب از مجله فرادرس ده سوال چهار گزینهای برای شما تنظیم شده است تا با پاسخدهی به آنها بتوانید میزان یادگیری خود را بسنجید. پس از اینکه به تمام سوالات جواب دادید، با کلیک روی گزینه «مشاهده نتیجه آزمون» نمره نهایی شما قابل مشاهده است.
ظرفیت خازن معادل با چهار خازن سری با ظرفیتهای و و و برابر با کدام گزینه است؟
گزینه سوم صحیح است. فرمول محاسبه ظرفیت خازن سری به شکل زیر است:
که در اینجا با توجه به اینکه چهار خازن داریم، است:
ظرفیت معادل سیستمی از خازنها با ظرفیت و و که به شکل موازی به هم متصل شدهاند، برابر است با:
گزینه اول درست است. ظرفیت معادل این سه خازن موازی از جمع کردن ظرفیت خازنها بهدست میآید:
اگر بدانیم ظرفیت خازن معادل برای سه خازن با ظرفیتهای و و که بهصورت سری به هم متصل شدهاند، برابر است با ، مقدار چقدر است؟
گزینه دوم درست است. میدانیم برای محاسبه ظرفیت خازن معادل سه خازن سری فرمول مناسب به شکل زیر است:
در مدار زیر با فرض و و و اختلاف پتانسیل کل ، بار روی خازن شماره دو چقدر است؟
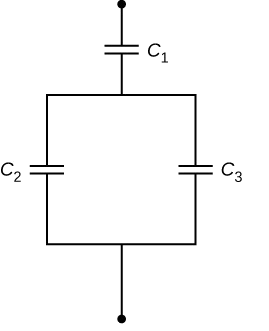
گزینه سوم صحیح است. در این مدار که به شکل ترکیبی از اتصال سری و موازی است، در نگاه اول میتوانیم سریع به این نتیجه برسیم که دو خازن شماره دو و سه موازی هم بسته شدهاند.
بنابراین برای محاسبه بار روی خازن دو طبق فرمول ، ابتدا باید افت ولتاژ در عبور از این خازن مشخص باشد. چون خازنهای دو و سه موازی هستند، ولتاژ خازن معادل این دو خازن با ولتاژ هر کدام از دو خازن شماره دو و سه برابر است:
اگر ظرفیت خازن معادل یا را محاسبه کنیم:
با توجه به فرمول میتوانیم و در نتیجه را داشته باشیم. اما در این فرمول نیز مجهول است و لازم است ابتدا این کمیت محاسبه شود. پس یک قدم جلوتر میرویم و معادل دو خازن سری و را در نظر میگیریم که به شکل زیر بهدست میآیند:
دو خازن سری در انتهای سادهسازی این مدار باری برابر با هم و برابر با بار روی خازن معادل خود دارند:
و مقدار این بار توسط فرمول زیر قابل محاسبه است:
اگر بار روی خازن اول خواسته شده بود، پاسخ را داشتیم. ولی در سوال بار روی خازن دوم خواسته شده و لازم است به روند ابتدای راهحل بازگردیم. با جایگزینی مقدار عددی در فرمول ولتاژ خازن دوم یا بهدست خواهد آمد:
در نهایت با داشتن ولتاژ خازن دو، بار آن بهراحتی حساب میشود:
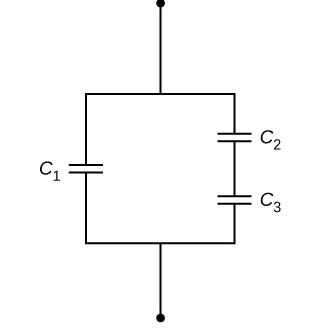
مداری به شکل زیر داریم که در آن و و است. اگر ولتاژ کلی برابر با به این مدار اعمال شود، بار روی خازن اول چقدر است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
فرض کنید برای بستن مداری به یک بانک خازنی با ظرفیت کل نیاز دارید، اما خازنهایی که در اختیار شما است، همه دارای ظرفیت هستند. کمترین تعداد خازنهایی که باید به هم متصل شوند تا به هدف خود برسید چقدر است و در چه نوع اتصالی؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
فرض کنید یک خازن ابتدا به منبع ولتاژ متصل شود. اگر دو سر این خازن را به یک خازن بدون بار با ظرفیت وصل کنیم، بار اولیه و نهایی خازن بهترتیب برابر با کدام گزینه است:
و
و
و
و
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر و و و باشند، ظرفیت معادل در مدار زیر برابر با کدام گزینه است؟

مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر چهار خازن با ظرفیت به شکل زیر بسته شده باشند، ظرفیت خازن معادل آنها چقدر است؟

مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
ولتاژ دو سر یک مجموعه از چهار خازن سری چقدر است اگر بدانیم افت ولتاژ در عبور از هر خازن برابر با است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
source
