الگوریتم‌های گوناگونی برای خوشه‌بندی داده‌ها وجود دارند که با توجه طرز کار و عملکردشان می‌توان آن‌ها را در دسته‌های مختلفی جای داد. آشنایی با خصوصیات هر یک از این الگوریتم‌ها و همچنین حجم دیتاست مورد استفاده، به شما کمک می‌کند تا بهترین انتخاب را برای به‌کارگیری این الگوریتم‌ها در پروژه‌های خود داشته باشید. الگوریتم K-Means یکی از همین الگوریتم‌هاست که با داشتن پیچیدگی زمان مناسب، برای داده‌های حجیم نیز عملکرد خوبی ارائه می‌دهد. در این مطلب از مجله فرادرس می‌خواهیم نگاه دقیق‌تری به الگوریتم K-Means برای خوشه بندی داشته باشیم و مزایا، معایب و کاربردهای آن را نیز مورد بررسی قرار دهیم.

در ابتدای مطلب، تعریفی از K-Means ارائه داده‌ایم که شما را با این الگوریتم محبوب آشنا می‌سازد. سپس، به شما می‌گوییم که این تکنیک جزو کدام‌یک از الگوریتم‌های خوشه‌بندی محسوب می‌شود و کاربرد‌های اصلی آن در دیتاساینس را نیز بررسی می‌کنیم. طرز کار الگوریتم K-Means، موضوع دیگری است که مراحل آن را برایتان شرح خواهیم داد. پس از آن نیز به سراغ پیاده‌سازی عملی این الگوریتم در زبان پایتون خواهیم رفت.

الگوریتم K-Means برای خوشه بندی چیست؟

K-Means یکی از الگوریتم‌های شناخته شده برای خوشه‌بندی داده‌ها در حوزه یادگیری ماشین است که داده‌ها را به تعداد «K» خوشه یا کلاستر، تقسیم می‌کند. در این شیوه که عملکردی گام به گام یا تکرار شونده دارد، داده‌های مشابه در خوشه‌های یکسانی قرار می‌گیرند تا از این طریق الگوهای پنهان در داده‌ها را شناسایی کنیم. این الگوریتم در واقع، جزو روش‌های یادگیری «بدون نظارت» (Unsupervised) محسوب می‌شود که برای گروه‌بندی داده‌های بدون برچسب در قالب تعداد مشخصی خوشه مورد استفاده قرار می‌گیرد.

الگوریتم K-Menas را می‌توان یکی از معروف‌ترین و پرکاربردترین روش‌های ماشین‌لرنینگ برای خوشه‌بندی داده‌ها دانست. فرقی که این روش خوشه‌بندی با «یادگیری نظارت شده» (Supervised Learning) دارد این است که داده‌های آموزشی مورد استفاده در آن، الزامی برای داشتن برچسب ندارند. به بیان دیگر، مشخص نیست که داده‌های خام الگوریتم به چه گروه یا دسته‌ای تعلق دارند.

K-Means جزو کدام دسته از الگوریتم ها است؟

در حال حاضر، مدل‌های گوناگونی از الگوریتم‌های خوشه‌بندی وجود دارند که برخی را در ادامه فهرست کرده‌ایم.

• خوشه‌بندی «انحصاری» (Exclusive)
• خوشه‌بندی «‌هم‌پوشانی» (Overlapping)
• خوشه‌بندی «سلسله‌مراتبی» (Hierarchical)
• خوشه‌بندی «احتمالی» (Probabilistic)

الگوریتم خوشه‌بندی K-Menas جزو روش‌های خوشه‌بندی انحصاری یا سخت محسوب می‌شود. به بیان دیگر در این نوع خوشه‌بندی، هر داده تنها به یک خوشه یا کلاستر تعلق دارد و نمی‌تواند همز‌مان عضوی از چندین دسته باشد.

در یکی از مطالب پیشین مجله فرادرس، خوشه‌بندی سلسله‌مراتبی به همراه کدهای R را مورد بررسی قرار دادیم که مطالعه آن می‌تواند برایتان مفید باشد.

کاربردهای K-Means در علوم داده چیست؟

خوشه‌بندی با K-Means جزو روش‌هایی است که در بیشتر حوزه‌ها می‌توان شاهد کاربردهایی از آن بود. در یادگیری ماشین، هنگامی‌که داده‌هایمان به‌صورت عددی و به‌راحتی قابل گروه‌بندی هستند و همچنین ابعاد کمی دارند می‌توان از مزایای این الگوریتم بهره‌مند شد. پژوهشگران و افراد فعال در این زمینه با تلفیق الگوریتم محبوب K-Means با مدل‌های شبکه عصبی و یادگیری عمیق مانند CNN و RNN، بازدهی و دقت برنامه‌های گوناگون یادگیری ماشین مانند بینایی کامپیوتر، پردازش زبان طبیعی و غیره را بهبود داده‌اند.

این روش خوشه‌بندی داده‌ها کاربردهای زیادی در دیتاساینس دارد که برخی را در ادامه فهرست کرده‌ایم.

• بخش‌بندی مشتریان: گروه‌بندی مشتریان بر اساس رفتار
• تحقیقات بازار: بررسی ترندهای بازار و سلایق مشتریان
• فشرده‌سازی تصاویر: کاهش حجم تصاویر
• تشخیص ناهنجاری: تشخیص الگوهای غیرعادی

بخش بندی مشتریان

تقسیم‌بندی مشتریان به این معنی است که مشتریان شرکت یا کسب و کاری را بر مبنای برخی ویژگی‌های مشابه گروه‌بندی کنند. بدین‌ترتیب می‌توان تبلیغاتی خاص را برای هر یک از این گروه‌ها یا خوشه‌ها در نظر گرفت و به‌شکل بهتری بازاریابی کرد.

گروه بندی اسناد

طی این فرایند می‌توان دسته یا گروه خاصی را برای اسناد در نظر گرفت. این کار به شرکت‌ها کمک می‌کند تا روی محتوا نظارت داشته باشند.

بخش بندی تصاویر

این روش در حوزه بینایی کامپیوتر برای تجزیه تصویر دیجیتال به مجموعه‌ای از پیکسل‌های جدا از هم مورد استفاده قرار می‌گیرد. پژوهش‌های مرتبط بیان‌گر این هستند که مدل‌های K-Means به چه صورت می‌توانند مرزهای موجود در تصاویر پزشکی را تشخیص دهند.

سیستم های توصیه گر

این‌گونه سیستم‌ها کاربردهای گسترده‌ای در اپلیکیشن‌ها و وب‌سایت‌های اینترنتی دارند. روش‌هایی مانند K-Means و PCA، تکنیک‌هایی هستند که در توسعه سیستم‌های پیشنهاد محصولات در فروشگاه‌ها آنلاین مورد استفاده قرار می‌گیرند.

دلیل استفاده زیاد و محبوب بودن K-Means برای خوشه‌بندی داده‌ها این است که علاوه بر سادگی، بهره‌وری و اثربخشی بالایی دارد.

چگونه یادگیری ماشین را با فرادرس یاد بگیریم؟

یادگیری ماشین یکی از مهم‌ترین شاخه‌های هوش مصنوعی است که به کمک آن، سیستم‌های کامپیوتری می‌توانند از داده‌های فراهم شده یاد بگیرند و سپس از آموخته‌های خود برای تصمیم‌گیری استفاده کنند. برای یادگیری ماشین‌لرنینگ، شیوه‌های مختلفی وجود دارد که مطالعه مقالات، مشاهده ویدیو‌ها و وبینارهای آموزشی تنها چند نمونه از این روش‌ها محسوب می‌شوند. با توجه به اینکه مشاهده فیلم‌های آموزشی یکی از روش‌های جدید و بسیار مؤثر در امر یادگیری مهارت‌های گوناگون به‌شمار می‌رود، شما می‌توانید از فیلم‌های آموزشی فراهم شده توسط پلتفرم فرادرس مانند مجموعه فیلم‌های آموزش یادگیری ماشین Machine Learning – مقدماتی تا پیشرفته از فرادرس برای این منظور استفاده کنید.

این نوع فیلم‌های آموزشی با کیفیتی بالا و توسط اساتید باتجربه تهیه شده‌اند و می‌توانند جنبه‌های گوناگون یادگیری ماشین را به همراه تمرین‌ها و پروژ‌های گوناگون به شما یاد دهند. با یادگیری مفاهیم مرتبط از جمله الگوریتم K-Means که موضوع اصلی این مطلب را تشکیل داده، می‌توانید مهارت‌های خود را در کشف الگو‌های پنهان در داده‌ها تقویت کنید.

عناوین برخی از این فیلم‌های آموزش موجود در این مجموعه را در ادامه فهرست کرده‌ایم.

طرز کار الگوریتم K-Means برای خوشه بندی چگونه است؟

همان‌طور که پیش‌تر نیز اشاره کردیم، الگوریتم K-Means برای خوشه‌بندی، به‌صورت تکرارشونده عمل می‌کند و به بیان دیگر، فرایندی چند مرحله‌ای دارد. به‌طور کلی هدف اصلی که طی این مراحل به دنبال آن هستیم، این است که فاصله بین داده‌ها و مرکز خوشه اختصاص یافته به آن‌ها را به کمترین میزان خود برسانیم.

الگوریتم خوشه‌بندی K-Means داده‌ها را با در نظر گرفتن فاصله‌ای که از مرکز هر خوشه دارند به چندین گروه تقسیم می‌کند. در این شیوه برای سنجیدن فواصل از معیارهایی مانند فاصله اقلیدسی می‌‌توان استفاده کرد. K در این الگوریتم بیان‌گر تعداد خوشه‌ها یا گروه‌هایی است که داده‌ها به آن‌ها تخصیص داده می‌شوند. طبیعی است که با افزایش مقدار K، گروه‌های کوچکتر با جزئیات بیشتری خواهیم داشت و عکس این قضیه نیز صادق است. یعنی اگر مقدار K را کمتر در نظر بگیریم، خوشه‌‌های بزرگ‌تری خواهیم داست که جزئیات کمتری از داده‌ها را نشان می‌دهند.

الگوریتم K-Means برای خوشه بندی از چندین گام تشکیل شده است که در ادامه توضیح داده‌ایم.

تعیین مقادیر اولیه مرکز K خوشه

همان‌طور که پیش‌تر نیز اشاره شد، K نشان دهنده تعداد خوشه‌هایی است که برای گروه‌بندی داده‌هایمان در نظر داریم. بنابراین، به‌عنوان اولین قدم می‌بایست مقدار اولیه برای K مرکز خوشه‌ها را تعیین کنیم. برای انجام این کار، هم می‌توان به‌صورت تصادفی عمل کرد و هم از سایر تکنیک‌های انتخاب اولیه مراکز خوشه‌ها بهره‌مند شد.

اختصاص داده ها به خوشه ها

در گام دوم با روشی تکرار شونده و ۲ مرحله‌ای رو به رو هستیم که مانند الگوریتم یادگیری ماشین «امید ریاضی – بیشینه‌سازی» (Expectation Maximization) یا EM کار می‌کند. در ادامه این ۲ بخش را توضیح داده‌ایم.

• امید ریاضی: در این مرحله،‌ با استفاده از معیارهایی همچون فاصله اقلیدسی، فاصله داده‌ها از مراکز خوشه‌ها، تعیین شده و بر همین اساس، هر داده‌ای به نزدیکترین مرکز خوشه تخصیص داده می‌شود.
• بیشینه‌سازی: در این مرحله نیز با میانگین‌گیری از داده‌های هر خوشه، مرکز کلاسترها را به‌روزرسانی می‌کنیم.

این روند به میزان «تعداد تکرار مشخص» یا «همگرا شدن مرکز خوشه‌ها» تکرار خواهد شد.

همان‌طور که مشخص است، الگوریتم خوشه‌بندی K-Means فرایند ساده‌ای دارد. با این وجود، عملکرد صحیح آن تا حد زیادی به شرایط اولیه از جمله مقداردهی اولیه مراکز خوشه‌ها و همچنین «پرت بودن داده‌ها» (Outliers) و غیره وابسته است. برای اینکه بتوان خوشه‌های بهتری را تشکیل داد و داده‌ها به‌طور صحیح تفکیک شوند، لازم است مقداردهی اولیه مراکز خوشه‌ها و همچنین تعیین تعداد خوشه‌ها به شکلی بهینه انجام شود.

برای اینکه بتوان میزان کیفیت خوشه‌بندی را اندازه گرفت یا آن را بهبود داد شیوه‌های مختلفی وجود دارد. به بیان دیگر، برای انجام چنین کاری از معیارهای سنجش و روش‌های انتخاب مراکز اولیه خوشه‌ها استفاده می‌شود. در ادامه، آشنایی بیشتری با این معیارها پیدا خواهید کرد.

معیارهای ارزیابی خوشه ها

در این قسمت با معیارهای سنجش خوشه‌بندی آشنا خواهید شد. به‌طور کلی، خوشه‌بندی خوب و با کیفیت دارای خصوصیاتی است که در ادامه فهرست کرده‌ایم.

• داده‌های درون خوشه شباهت زیادی با هم دارند.
• هر خوشه از سایر خوشه‌ها جدا و قابل تفکیک است.

در واقع، برای رسیدن به چنین خصوصیاتی می‌بایست فاصله بین داده‌های درون خوشه را تا حد ممکن از هم کاهش داده و فاصله بین خوشه‌‌ها را نیز تا جایی که امکان دارد، افزایش دهیم. به‌شکل ساده‌تر می‌توان گفت که خوشه‌هایی بهتر هستند که قابل تفکیک، فشرده و جمع‌وجورتر باشند. الگوریتم K-Means به‌عنوان یکی از رایج‌ترین روش‌های خوشه‌بندی داده‌ها، به دنبال این است که مجموع مربعات خطا یا همان «SSE» را تا حد ممکن کاهش دهد. با محاسبه مجموع مربع فواصل اقلیدسی هر داده با نزدیک‌ترین مرکز خوشه می‌توان از کیفیت خوشه مطلع شد. به بیان دیگر، با این کار متوجه می‌شویم که داده‌های هر خوشه چقدر به هم نزدیک هستند.

با استفاده از معیارهای ارزیابی و سنجش می‌توان فهمید که خوشه‌بندی تا چه اندازه با کیفیت و خوب بوده و همچنین جنبه‌‌های گوناگون نتایج را مورد بررسی قرار داد. بدین‌ترتیب می‌توانیم بهترین مقدار را برای تعداد خوشه‌ها و همچنین موقعیت اولیه آن‌ها در نظر بگیریم. با استفاده از معیارهایی ارزیابی که در ادامه معرفی شده، می‌توانید فاصله بین داده‌های هر خوشه و همچنین فاصله بین خوشه‌ها را بسنجید.

اینرسی

الگوریتم خوشه‌بندی K-Means به‌دنبال این است موقعیت‌هایی را برای مرکز خوشه‌ها انتخاب کند که مقدار فاصله داده‌ها تا این مراکز، در پایین‌ترین میزان ممکن باشد. با کمینه‌سازی اینرسی، داده‌ها به شکلی بهینه در خوشه‌ها قرار خواهند گرفت. برای به‌دست آوردن اینرسی،‌ فاصله بین هر داده و مرکز خوشه آن اندازه‌گیری می‌شود. سپس، مربع این فاصله محاسبه شده و در نهایت مجموع مربعات برای تمامی داده‌های درون خوشه به دست می‌آید. اینرسی یا مجموع محاسبه شده، فاصله داده‌های درون خوشه و نزدیکی آن‌ها را نشان می‌دهد. بنابراین هر چه مقدار آن کمتر باشد بهتر است. چون داده‌ها به هم نزدیک‌تر و شبیه‌تر هستند.

شاخص Dunn

دومین خصوصیت برای خوشه‌های بهینه که پیش‌تر اشاره شد با «شاخص Dunn» سنجیده می‌شود. این معیار، رابطه بین کمترین فاصله بین خوشه‌ها و بیشترین فاصله بین داده‌های هر خوشه را بررسی می‌کند. در چنین حالتی، خوشه‌هایی بهتر هستند که فاصله بیان آن‌ها زیاد است و تاحد ممکن متفاوت و جدا از هم هستند.

بهبود عملکرد K-Means برای خوشه بندی

برای اینکه بتوان نتایج خوبی از الگوریتم از K-Means برای خوشه بندی به‌دست آورد، لازم است عملکرد آن را بهینه‌سازی کنیم.

با توجه به اینکه مقداردهی اولیه در الگوریتم K-Means به‌صورت تصادفی صورت می‌گیرد، می‌توان آن را جزو الگوریتم‌های غیرقطعی در نظر گرفت که در هر بار اجرا روی داده‌های مشابه، خروجی‌های متفاوتی را به ما ارائه می‌دهد. یعنی ممکن است خوشه‌بندی‌هایی که در این اجراها انجام می‌دهد، متفاوت باشند.

برای اینکه الگوریتم K-Means عملکرد خوبی داشته باشد و خوشه‌بندی را به بهترین شکل برایمان انجام دهد، لازم است تعیین تعداد خوشه‌ها و همچنین مقداردهی اولیه مراکز آن‌ها به‌شکل مناسبی انجام شود. بدین‌ترتیب، الگوریتم خوشه‌بندی سرعت و دقت بالاتری نیز خواهد داشت.

تعیین موقعیت اولیه مرکز خوشه ها

الگوریتم K-Means داده‌ها را در قالب تعدادی خوشه، گروه‌بندی می‌کند و هر یک از این خوشه‌ها با نقطه‌ای مشخص می‌شود که نشان دهنده «مرکز» (Centroid) آن است. خوشه‌بندی در این روش به شکلی انجام می‌شود که داده‌های داخل گروه، بیشترین شباهت را به هم داشته باشند و فاصله هر داده تا مرکز خوشه تا حدد ممکن کم باشد. این الگوریتم عمل خوشه‌بندی را در طی چندین مرحله انجام می‌دهد و به اصطلاح تکرار شونده است. این مورد که در شروع کار الگوریتم، انتخاب مراکز خوشه‌ها به چه صورتی باشد می‌تواند تأثیر زیادی در خوشه‌های ایجاد شده برای گروه‌بندی داده‌ها داشته باشد.

گفتیم که مقداردهی اولیه مراکز خوشه‌ها ممکن است به‌طور تصادفی انجام شود. در چنین حالتی، ممکن است نتایج متفاوت و ناپایداری داشته باشیم. برای رهایی از چنین مشکلاتی، روش‌های گوناگونی از جمله «K-Means ++‎» برای مقداردهی مراکز خوشه‌ها معرفی شده است.

K-Means ++‎

روش K-Means ++‎ که توسط محققانی به نام‌های «آرتور» و «واسیلویتسکی» معرفی شده،‌ نوعی الگوریتم K-Means محسوب می‌شود که مراکز خوشه‌ها را در شروع الگوریتم، به‌شکلی بهینه انتخاب می‌کند. استفاده از این تکنیک همچنین، نتایج بهتری را در تخصیص داده به خوشه‌ها و خوشه‌بندی به‌دنبال خواهد داشت.

روند کار الگوریتم K-Means ++‎ را در ادامه آورده‌ایم.

• نخستین کار الگوریتم K-Means ++‎ برای انتخاب مراکز اولیه خوشه‌ها این است که از بین داده‌ها، مقداری به‌عنوان مرکز خوشه برگزیده می‌شود.
• برای هر یک از سایر مراکز خوشه‌ها، فاصله هر داده تا نزدیک‌ترین مرکز خوشه به‌دست می‌آید.
• مرکز خوشه جدید به‌شکلی انتخاب می‌شود که نقاط دورتر از مراکز قبلی، احتمال بیشتری برای انتخاب داشته باشند.
• با توجه به ماهیت تکرار شونده بودن این الگوریتم، مراحل بالا تا پیدا شدن و مقداردهی اولیه مرکز تمام خوشه‌ها تکرار خواهد شد.

نحوه انتخاب تعداد خوشه ها

الگوریتم K-Means به‌طور معمول و در بهترین حالت، تا زمان پیدا شدن تعداد مناسبی از مراکز خوشه‌ها تکرار خواهد شد. این تکرار‌ها می‌توانند تا همگرایی مرکز خوشه‌ها ادامه داشته باشند.

روش Elbow

تکنیک «آرنج» (Elbow Method) یکی از روش‌هایی است که برای پیدا کردن تعداد مناسب خوشه‌ها می‌توان از آن بهره‌مند شد. در این روش نموداری مانند آنچه در ادامه آورده شده به شما نشان می‌دهد که برای الگوریتم K-Means به چه تعداد مرکز خوشه نیاز خواهید داشت.

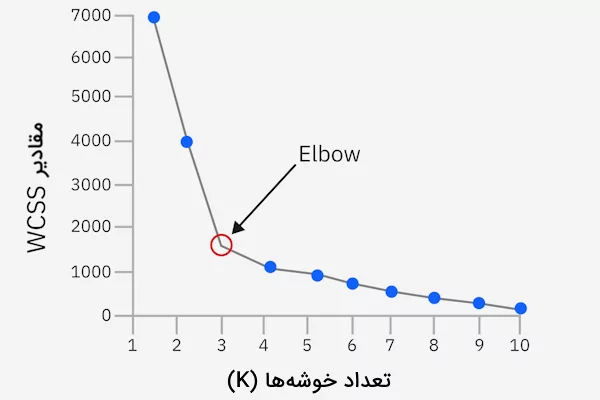
این تکنیک، فاصله اقلیدسی هر داده از مرکز خوشه مربوطه را محاسبه می‌کند. سپس تعداد خوشه‌ها به‌نحوی انتخاب می‌شود که از آنجا به بعد، تغییر قابل‌توجهی در «مجموع مربعات درون‌خوشه» (WCSS) وجود نداشته باشد. این نقطه را در نمودار بالا با برچسب «Elbow» نشان داده‌ایم. مقدار WCSS در واقع بیان‌گر میزان پراکندگی داده‌ها در هر خوشه است که در تصویر بالا با توجه به تعداد خوشه‌ها قابل مشاهده است.

نخستین گام برای پیدا کردن تعداد مراکز خوشه به روش Elbow، این است که مقدار WCSS را برای هر یک از خوشه‌ها به‌دست بیاوریم. در ادامه، مقدار WCSS را در محور عمودی یا Y و تعداد خوشه‌ها را در محور افقی یا X ترسیم می‌کنیم. همان‌طور که در تصویر بالا نیز مشخص شده، با زیاد شدن K که بیان‌گر تعداد خوشه‌ها است، نمودار نیز شکلی تثبیت شده پیدا می‌کند. با در نظر همین الگو می‌توانید تعداد مناسب برای خوشه‌های K-Means را پیدا کنید.

یکی از نکاتی که هنگام تعیین تعداد خوشه‌ها می‌بایست به آن توجه داشته باشید این است که تعداد خوشه‌های بیشتر، بار محاسباتی بیشتری هم برایتان به‌دنبال خواهد داشت. این مورد حتی در دیتاست‌های بزرگ بیشتر خود را نشان می‌دهد.

علی‌رغم مزیت‌های روش Elbow، در مواردی که داده‌ها دارای ویژگی‌های زیاد و ابعاد بالا هستند یا اینکه شکل و ساختار منظمی ندارند، شاید بهتر باشد که از سایر تکنیک‌های جایگزین استفاده کنید. روش‌های دیگری مانند «تحلیل سیلوئت» (Silhouette Analysis) و سایر شیوه‌ها نیز برای انتخاب تعداد بهینه خوشه‌ها وجود دارد که می‌توانید از آن‌ها بهره‌مند شوید.

مزایا و معایب الگوریتم K-Means برای خوشه بندی

اکنون که تعریف و طرز کار الگوریتم K-Means برای خوشه بندی را می‌دانید خوب است که با نقاط قوت این روش و معایبی که دارد نیز آشنا شوید.

مزایای الگوریتم K-Means برای خوشه بندی

در ادامه، به برخی مزایای الگوریتم محبوب K-Means اشاره کرده‌ایم.

• سادگی: الگوریتم K-Means عملکرد قابل فهم و ساده‌ای دارد و به‌راحتی می‌توانید آن را در پروژه‌های خود به‌کار بگیرید. این تکنیک جزو محبوب‌ترین الگوریتم‌های بدون نظارت یادگیری ماشین محسوب می‌شود.
• سرعت: الگوریتم K-Means به‌طور تکرار شونده کار می‌کند و بار محاسباتی زیادی ندارد. این تکنیک همچنین نسبت به روش خوشه‌بندی سلسه‌مراتبی دارای سرعت بیشتری است. به این دلیل که نیازی نیست تا ساختار درختی خوشه‌ها را ایجاد کند و فواصل بین تمامی داده‌ها با هم را به دست آورد.
• مقیاس‌پذیری: مزیت دیگر استفاده از الگوریتم K-Means برای خوشه بندی این است که می‌تواند برای دیتاست‌های حجیم نیز مورد استفاده قرار گیرد. همچنین می‌تواند با خوشه‌هایی در اندازه و اَشکال متفاوت نیز کار کند. در نتیجه گزینه خوبی برای تحلیل خوشه‌ای محسوب می‌شود. به‌طور کلی می‌توان گفت که سرعت بالا و بهینه بودن این الگوریتم باعث شده تا نسبت به سایر روش‌ها مقیاس‌پذیرتر بوده و برای داده‌های حجیم نیز گزینه مناسبی باشد.

نقاط ضعف الگوریتم K-Means برای خوشه بندی

اکنون که با نقاط قوت الگوریتم K-Means برای خوشه بندی آشنا شدید، خوب است که معایب آن را نیز بدانید.

• وابستگی به پارامترهای ورودی: برای اینکه عملکرد خوبی را از الگوریتم K-Means شاهد باشیم، لازم است ورودی مناسبی را نیز به آن بدهیم. به بیان دیگر، مقداردهی اولیه مراکز خوشه‌ها و همچنین تعداد خوشه‌ها می‌تواند تأثیر زیادی روی فرایند خوشه‌بندی و خروجی‌ها داشته باشد. به‌همین ترتیب، در صورتی‌که مراکز اولیه خوشه‌ها به‌درستی انتخاب نشوند،‌ ممکن است ضعف‌هایی را در خوشه‌بندی داده‌ها و کاهش سرعت خوشه‌بندی شاهد باشیم. پژوهش‌گران تاکنون تحقیقات زیادی را در رابطه با بهبود مقداردهی اولیه مراکز خوشه‌ها انجام داده‌اند تا فرایند خوشه‌بندی سریع‌تر و بهتر انجام شود.
• عملکرد ضعیف روی برخی داده‌ها: الگوریتم K-Means به‌طور معمول در مواردی می‌تواند درست کار کند که داده‌های پروژه دارای خوشه‌هایی تقریباٌ هم‌اندازه باشد. ضمن اینکه داده‌های پرت یا تراکم‌های بسیار متغیر در داده‌ها وجود نداشته باشند. هنگامی‌که داده‌ها دارای ویژگی‌های متعدد یا نوسانات قابل توجهی باشد نیز K-Means ممکن است نتایج خوبی نداشته باشد.
• تأثیر زیاد داده‌های پرت: وجود داده‌های پرت در دیتاست ممکن است روی خروجی‌های الگوریتم K-Means و خوشه‌های تشکیل شده تأثیر منفی بگذارد. گروه‌های تشکیل شده با اینکه می‌بایست از هم قابل تفکیک باشند اما نباید فاصله آن‌ها به حدی باشد که روی داده‌ها تأثیر بگذارند و آن‌ها را سمت خود منحرف کنند. با توجه به اینکه K-Means مرکز خوشه‌ها را با میان‌گیری از داده‌ها به‌دست می‌آورد، وجود داده‌های پرت می‌تواند روی این موضوع اثر منفی بگذارد. ضمن اینکه ممکن است باعث بیش‌برازش شود و داد‌ه‌های پرت را نیز در تعیین مرکز خوشه‌ها مدنظر قرار دهد.

پیاده سازی الگوریتم K-Means برای خوشه بندی در پایتون

در این قسمت، نحوه کدنویسی و پیاده‌سازی الگوریتم K-Means را به‌صورت گام به گام در زبان برنامه‌نویسی پایتون توضیح می‌دهیم. مجموعه داده‌ای که قرار است الگوریتم روی آن اجرا شود، دیتاست ساختگی «Blobs» است که از طریق کتابخانه Scikit Learn می‌توانید به آن دسترسی داشته باشید.

گام ۱: وارد کردن کتابخانه های مورد نیاز به برنامه

برای این پیاده‌سازی لازم است کتابخانه‌های نام‌پای، Matplotlib و همچنین «Scikit Learn» را به برنامه اضافه کنیم. کدهای زیر این مورد را به‌خوبی نشان داده‌اند.

در صورت نصب نبودن هر یک از این ابزارها، با خطا رو به رو خواهید شد. در چنین حالتی می‌توانید با دستور pip می‌توانید کتابخانه مربوطه را نصب کنید.

گام ۲: ایجاد دیتاست

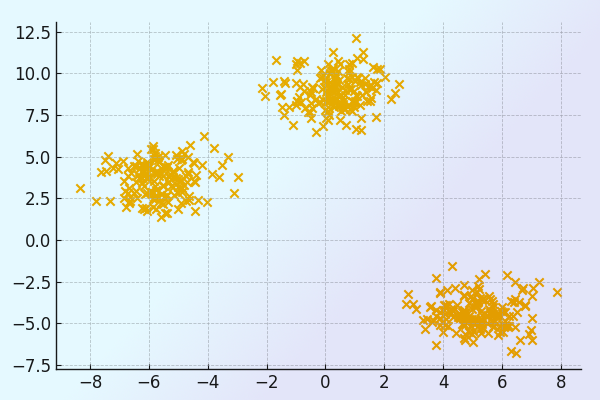
اکنون نوبت به ایجاد یک دیتاست سفارشی و ساختگی رسیده که این کار با تابع make_blobs از کتابخانه sklearn.datasets به سادگی‌ قابل انجام است.

در خط شماره ۱، متغیر‌های X و y برای نگهداری از ویژگی‌ها و برچسب خوشه تعریف شده است. پارامترهای تابع sklearn.datasets نیز به‌ترتیب تعیین کننده تعداد نمونه‌های مورد نیاز، تعداد ویژگی‌ها و تعداد خوشه‌ها هستند. تا اینجا، داده‌های ما ایجاد می‌شوند. در خط شماره ۳ از کدها یک پنجره جدید برای رسم نمودار می‌سازیم. در خط بعد، grid یا همان خطوط شبکه‌ای روی نمودار را فعال می‌کنیم. این کدها برای درک بهتر جزئیات نمودار مفید خواهند بود. در خط شماره ۵، داده‌ها را روی نمودار و با ویژگی مشخص شده ایجاد می‌کنیم. در نهایت خط آخر هم برای نمایش نمودار به‌کار می‌رود.

اجرای کدهای بالا، خروجی مشابه تصویر زیر را تولید می‌کند.

گام ۳: تنظیم مقادیر اولیه تصادفی برای مراکز خوشه ها

در این مرحله می‌بایست مقداردهی اولیه الگوریتم K-Means را انجام دهیم. برای این منظور کدهای زیر را می‌نویسیم.

در خط شماره ۱، متغیر K را داریم که تعداد خوشه‌های الگوریتم K-Means را برابر با ۳ مقداردهی می‌کند. خط شماره ۳ شامل تعریف یک ساختار داده دیکشنری به نام clusters است. در خط شماره ۴، مقدار Seed برای تولید عدد تصادفی را تنظیم کرده‌ایم. خط شماره ۶ شامل تعریف حلقه‌ای است که به تعداد خوشه‌ها تکرار می‌شود. درون حلقه، مرکز خوشه جاری با در نظر گرفتن تعداد ویژگی‌ها و در محدوده مشخص شده به‌صورت تصادفی تعیین می‌شود. لیست points  در خط شماره ۸ برای نگهداری داده‌های این خوشه تعریف شده است. خطوط شماره ۹ تا ۱۱ شامل تعریف دیکشنری برای نگهداری مرکز خوشه و داده‌های آن هستند. در خط شماره ۱۴، خوشه تشکیل شده به دیکشنری clusters اضافه می‌شود. در نهایت نیز خوشه‌ها به شکل زیر نمایش داده می‌شود.

{
    0: {'center': [0.06919154, 1.78785042], 'points': []},
    1: {'center': [1.06183904, -0.87041662], 'points': []},
    2: {'center': [-1.11581855, 0.74488834], 'points': []}
}

گام ۴: ترسیم مراکز تصادفی خوشه ها و داده ها

برای این منظور کدهای زیر را نوشته‌ایم.

همان‌طور که در تصویر زیر نیز قابل مشاهده است، این کد، یک نمودار پراکندگی از داده‌ها و مراکز اولیه خوشه‌ها ترسیم می‌کند که به‌ترتیب با علامت X نارنجی‌رنگ و ستاره‌های قرمز رنگ نشان داده شده‌اند.

گام ۵: نحوه تعریف فاصله اقلیدسی

در این قسمت تابعی به نام distance داریم که با دریافت ۲ نقطه، فاصله اقلیدسی بین آن‌ها را محاسبه می‌کند.

در این کدها، اختلاف مؤلفه‌های ۲ نقطه p1 و p2 محاسبه شده و سپس به توان ۲ می‌رسد. در ادامه مجموع آن ها را به‌دست آورده و در نهایت جذر می‌گیرد. فرمول زیر این موضوع را به‌خوبی نشان داده است.

$$text{distance}(p1, p2) = sqrt{sum_{i=1}^n (p1_i – p2_i)^2}$$

گام ۶: تابع تخصیص و به روز رسانی مرکز خوشه

در این قسمت می‌خواهیم تابعی بنویسیم که ۲ عمل زیر را انجام دهد.

• تخصیص داده‌ها به نزدیک‌ترین مرکز خوشه
• به‌روزرسانی و بهینه‌سازی مراکز هر خوشه با توجه به میانگین داده‌های اختصاص داده شده

برای این منظور می‌توانید کدهای زیر را بنویسید.

در ابتدا تابعی به نام assign_clusters تعریف کرده‌ایم که با دریافت داده‌‌ها و اطلاعات خوشه‌ها به عنوان پارامتر ورودی، می‌تواند تشخیص دهد هر یک از داده‌ها از کدام خوشه فاصله کمتری دارد. تا از این طریق آن داده را جزو همان خوشه در نظر بگیرد. در خط شماره ۲، حلقه‌ای داریم که روی داده‌ها پیمایش می‌‌کند. لیست dist برای نگهداری فاصله‌ها تعریف شده است. در خط شماره ۷ حلقه داخلی را داریم که فاصله داده تا مرکز خوشه را سنجیده و در لیست فاصله‌ها ذخیره می‌شود. با np.argmin کمترین فاصله را پیدا کرده و در خط شماره ۱۱، داده را به مجموعه داده‌های آن خوشه اضافه می‌کنیم. در انتهای تابع نیز لیست clusters برگردانده می‌شود.

تابع دیگری که در این کد تعریف کرده‌ایم update_clusters نام دارد و قرار است با دریافت داده‌ها و همچنین لیست خوشه‌ها به‌عنوان ورودی، مرکز خوشه را با داده‌های جدیدی که دارد مجدد محاسبه و به‌روزرسانی کند. درون این تابع حلقه‌ای داریم که روی خوشه‌ها پیمایش می‌کند. درون حلقه داده‌های موجود در خوشه فعلی را به آرایه نامپای تبدیل می‌کند. در ادامه، درصورتی‌که داده‌ای درون خوشه وجود داشته باشد، مرکز خوشه را با میانگین‌گیری از داده‌ها به‌روز می‌کند. سپس، لیست داده‌های این خوشه خالی می‌شود. در انتهای تابع نیز لیست clusters برگردانده می‌شود.

گام ۷: تابع پیش بینی خوشه مربوط به داده ها

در این مرحله قصد داریم تابعی بنویسیم که مشخص کند هر داده به کدام یک از خوشه‌ها تعلق دارد. بنابراین، کدهای زیر را می‌نویسیم.

تابع پیش‌بینی ما pred_cluster نام دارد که در خط شماره ۱ تعریف شده است و داده‌های ارزیابی به‌همراه لیست خوشه را به عنوان ورودی دریافت می‌کند. در خط شماره ۳، حلقه‌ای داریم که روی داده‌‌ها پیمایش می‌کند. حلقه داخلی در خط شماره ۵ با پیمایش روی هر خوشه، فاصله داده‌ها را با مرکز خوشه را محاسبه کرده و به لیست dist که برای ذخیره فواصل داده با خوشه‌‌ها در نظر گرفته شده، اضافه می‌کند. پس از خروج از حلقه داخلی، کمترین مقدار در لیست فواصل که همان نزدیک‌ترین خوشه به داده است به لیست pred اضافه می‌شود. در نهایت نیز همین لیست به‌عنوان خروجی تابع پیش‌بینی برگردانده می‌شود.

گام ۸: تخصیص و به روزرسانی و پیش بینی مرکز خوشه

در این مرحله، نوبت به استفاده از توابع تعریف شده مانند تخصیص داده به نزدیک‌ترین خوشه، به‌روزرسانی مرکز خوشه با توجه به داده‌های جدید و پیش‌بینی خوشه مناسب برای داده‌های جدید رسیده که کدهای زیر این کار را انجام خواهند داد.

گام ۹: ترسیم داده ها به همراه خوشه پیش بینی شده

در این گام قصد داریم تا داده‌ها را به‌همراه خوشه‌ای که برای آن‌ها پیش‌بینی شده ترسیم کنیم. برای این کار لازم است کدهای زیر را بنویسیم.

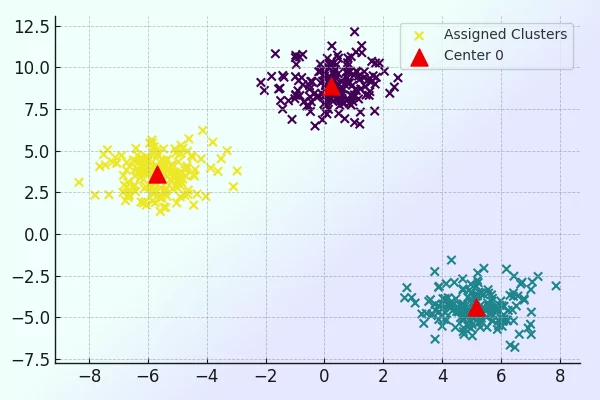
در خط شماره ۱،‌ داده‌ها را روی صفحه ترسیم می‌کنیم. همچنین، با توجه به خوشه‌ای که برای آن‌ها پیش‌بینی شده رنگ‌های مختلفی به آن‌ها اختصاص داده می‌شود. در خط شماره ۲ حلقه for را داریم که به تعداد خوشه‌‌ها تکرار می‌شود و مراکز جدید آن‌ها را با علامت مثلث و رنگ قرمز روی صفحه درج می‌کند. در نهایت نیز نمودار با دستور plt.show() به‌شکل زیر به نمایش در می‌آید.

یادگیری پروژه‌ محور K-Means با فرادرس

در این مطلب، به بررسی الگوریتم خوشه‌بندی K-Means به عنوان یکی از محبوب‌ترین شیوه‌های گروه‌بندی داده‌های بدون برچسب پرداختیم. اکنون اگر قصد یادگیری بیشتر در مورد استفاده کاربردی از این الگوریتم و سایر الگوریتم‌های خوشه‌بندی را دارید، می‌توانید فیلم‌های آموزشی فرادرس که در ادامه فهرست شده را مشاهده کنید.

جمع‌بندی

در این مطلب از مجله فرادرس الگوریتم K-Means برای خوشه‌بندی را مورد بررسی قرار دادیم. این الگوریتم جزو روش‌های معروف ماشین‌لرنینگ است که به‌طور متداول برای گروه‌بندی داده‌‌ها مورد استفاده قرار می‌گیرد.

با مطالعه این نوشتار درک خوبی از الگوریتم K-Means برای خوشه بندی پیدا خواهید کرد. همچنین خواهید دانست که طرز کار و مراحل خوشه‌بندی توسط این الگوریتم به چه صورتی است. با معیارهای گفته شده برای ارزیابی الگوریتم می‌توانید کارایی این روش را سنجیده و با شیوه‌های اشاره شده، عملکرد آن را بهبود دهید. روش Elbow را نیز به عنوان شیوه‌ای برای انتخاب تعداد بهینه خوشه‌ها توضیح دادیم. علاوه بر این موارد، به مزایا و معایب این الگوریتم و پیاده‌سازی آن نیز پرداختیم تا بتوانید به آسانی این الگوریتم را در پروژه‌های خود به‌کار بگیرید.