مساحت کره چطور محاسبه می شود؟ – به زبان ساده + فرمول و مثال – EXPRESSJS

به همین منظور در اولین بخش فرمول‌‌های مساحت کره و نیم‌کره را همراه با حل چند مثال معرفی می‌کنیم. نحوه استفاده از این فرمول‌ها در حل مسائل مختلف درس ریاضی به شما کمک می‌کند تا به مفهوم مساحت کره و فرمول‌های مرتبط با آن کاملا مسلط شوید. سپس با ویژگی‌های این حجم هندسی در حالت کلی بیشتر آشنا می‌شوید. همچنین در بخش‌های بعد اثبات فرمول مساحت کره را توضیح می‌دهیم. بخش انتهایی این نوشته به آزمون مساحت کره اختصاص دارد تا با پاسخ‌دهی به این سوالات، یادگیری خود را در این مبحث تکمیل و تثبیت کنید.

فرمول مساحت کره چیست؟

مساحت کره همان مساحت خارجی‌ترین سطح از آن است. این کمیت مانند مساحت هر شکل هندسی دیگری باید دارای بخشی به‌صورت مجذور طول (طول به توان دو) باشد. در یک کره فاصله تمام نقاط روی سطح خارجی از مرکز به یک اندازه و برابر با «شعاع کره» یا $r$

در فرمول بالا معمولا عدد پی با تقریب برابر با $π = 3.14 pi = 3.14$ منشور، استوانه و مخروط کمیتی به نام «مساحت جانبی» تعریف می‌شود. در مورد این احجام، مساحت جانبی با «مساحت کل» فرق دارد. اما در مورد کره مساحت جانبی نداریم. تعریف مساحت جانبی زمانی بکار می‌رود که حجم موردنظر ما از دو بخش به نام «قاعده» و «سطح جانبی» تشکیل شده باشد. در مورد کره، کل حجم در یک بخش گرد و یکپارچه قرار می‌گیرد.

تصویری از یک نارنگی داخل پوسته کروی - مساحت کره

نکته ۱: یک کره کامل مساحت جانبی ندارد یا به عبارتی، مساحت جانبی آن همان مساحت کل آن است.

نکته ۲: فرض کنید استوانه‌ای به شکل زیر یک کره را احاطه کرده است، طوری که ارتفاع استوانه با قطر کره برابر است. «ارشمیدس» (Archimedes) نشان داد مساحت جانبی این استوانه‌ با مساحت کره داخل آن برابر است.

کره‌ای داخل یک استوانه — مساحت جانبی استوانه‌ با مساحت کره داخل آن برابر است.

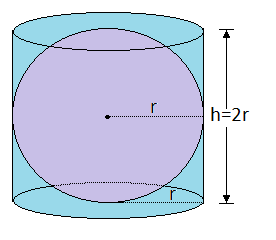
فرمول مساحت کره بر حسب قطر

ممکن است در برخی از مسائل به‌جای شعاع کره، قطر آن یا $d$

$pi d^2$

رسیدن به فرمول بالا بسیار آسان است. کافی است با در نظر گرفتن این واقعیت که همواره قطر هر کره دو برابر شعاع آن است، پیش برویم:

$d = 2r Rightarrow r = frac{d}{2}$

$4 pi r^2 Rightarrow 4 pi (frac{d}{2})^2$

$4 pi (frac{d}{2})^2 = 4 pi (frac{d^2}{4}) = pi d^2$

فرمول مساحت کره‌ای با شعاع $r$	$4 pi r^2$
فرمول مساحت کره‌ای با قطر $d$	$pi d^2$

یادگیری فرمول های مساحت با فرادرس

یادگیری مساحت نیازمند این است که ابتدا با ویژگی‌های اشکال هندسی مختلف آشنا شوید. سپس باید بتوانید مفاهیمی مانند محیط، مساحت و حجم را از هم تفکیک کنید. در کتاب‌های درسی ویژگی‌های فرم دو بعدی یک کره، یعنی دایره، برای اولین بار در کتاب ریاضی هشتم مطرح می‌شود. سپس در کتاب ریاضی نهم مبحث حجم و مساحت کره همراه با روش به‌دست آوردن حجم احجامی مانند هرم و مخروط توضیح داده شده است. بنابراین اگر علاقه‌مند هستید با فرمول‌های مربوط به این مباحث همراه با آموزش تصویری و حل مثال‌های گسترده آشنا شوید، پیشنهاد می‌کنیم فیلم‌های آموزشی تهیه شده در مجموعه فرادرس را مشاهده کنید:

مجموعه آموزش دروس متوسطه دوم و کنکور – درس، تمرین، حل مثال و تست فرادرس — برای مشاهده مجموعه فیلم‌های آموزش دروس متوسطه دوم و کنکور – درس، تمرین، حل مثال و تست فرادرس، روی تصویر کلیک کنید.

فرمول مساحت نیم کره چیست؟

در بخش‌های قبل آموختیم مساحت کره چیست و چه فرمولی دارد. در این بخش می‌خواهیم ببینیم فرمول مساحت نیم‌کره چیست و چگونه به‌دست می‌آید. مساحت جانبی نیم‌کره برابر است با نصف مساحت کره یا $frac{4 pi r^2}{2} = 2 pi r^2$

برش هندوانه از وسط و تبدیل آن به دو نیم‌کره مساوی — برش هندوانه کروی از وسط و تبدیل آن به دو نیم‌کره

در محاسبه مساحت نیم‌کره نکته مهمی که باید در نظر بگیریم این است که آیا کف نیم‌کره را در محاسبات خود وارد می‌کنیم یا نه. ابتدا بهتر است ببینیم منظور ما از نیم‌کره چیست. هندوانه‌ای را در نظر بگیرید که از مرکز به دو بخش کاملا مساوی تقسیم شده است. اگر با تقریب این هندوانه را یک کره کامل فرض کنیم، پس از برش، دو نیم‌کره مساوی به شکل زیر داریم:

بنابراین زمانی که صحبت از محاسبه مساحت هر کدام از دو برش هندوانه بالا می‌شود، سوالی که پیش می‌آید این است که می‌خواهیم مساحت هر کدام از این دو نیم‌کره را با در نظر گرفتن سطح دایره‌ای و قرمز رنگ آن محاسبه کنیم یا بدون در نظر گرفتن این بخش، فقط سطح خمیده و سبز رنگ (سطح پوسته هر برش هندوانه) را می‌خواهیم به‌دست آوریم؟

در ریاضیات این بخش دایره‌ای و قرمز رنگ از هر کدام از دو نیم‌کره بالا را «قاعده نیم‌کره» می‌نامیم. همچنین سطح خمیده و سبز رنگ هر کدام از دو برش هندوانه «سطح جانبی نیم‌کره» نامیده می‌شود. در ادامه این بخش با هم بررسی می‌کنیم مساحت نیم‌کره در هر کدام از دو حالت چگونه پیدا می‌شود. پس یک نیم‌کره برخلاف یک کره کامل دارای دو بخش زیر است:

یک قاعده صاف و دایره‌ای شکل
یک سطح جانبی خمیده شکل

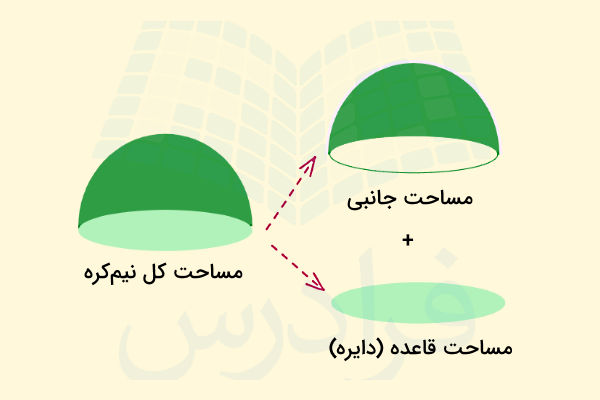
مساحت جانبی نیم‌ کره

همان‌طور که توضیح دادیم، هر نیم‌کره از دو بخش تشکیل شده است: قاعده و سطح جانبی یا سطح خمیده. سطح خمیده شکل نیم‌کره همان سطح جانبی آن است. اگر بخواهیم مساحت یک نیم‌کره را فقط با در نظر گرفتن این بخش حساب کنیم، در حقیقت مساحت جانبی نیم‌کره را به‌دست آورده‌ایم. مساحت جانبی نیم‌کره‌ای با شعاع $r$

$frac{4 pi r^2}{2} = 2 pi r^2$

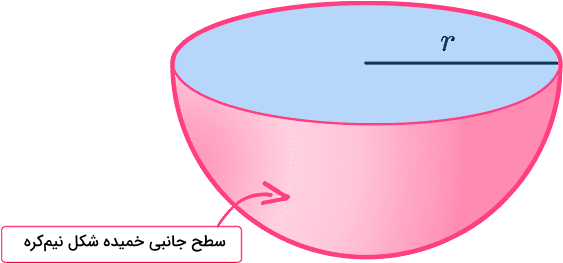
مساحت کل کره

اما اگر بخواهیم مساحت کل یک نیم‌کره را پیدا کنیم، حتما لازم است علاوه‌بر سطح جانبی قاعده دایره‌ای شکل آن را نیز در نظر بگیریم. قاعده یک نیم‌کره همیشه به شکل دایره‌ است. اگر نیم‌کره موردنظر ما دارای شعاع $r$

$pi r^2 + 2 pi r^2 = 3 pi r^2$

مثال مساحت کره

محاسبه مساحت اشکال هندسی تعریف شده عموما توسط فرمول‌های مشخصی انجام می‌شود. برای مثال، فرمول مساحت دایره‌ای با شعاع $pi r^2$ دایره یک شکل هندسی دو بعدی است و حجم ندارد. در واقع اگر بخواهیم برای دایره بعد سومی در نظر بگیریم، تبدیل به کره می‌شود. با بخاطر سپردن دقیق این جدول می‌توانید این فرمول‌ها را در مسائل مختلف به‌خوبی از هم تفکیک کنید:

فرمول قطر کره‌ یا دایره‌ای به شعاع $r$	$d=2r$
فرمول محیط دایره‌ای به شعاع $r$	$2 pi r$
فرمول محیط کره‌ای به شعاع $r$	$2 pi r$
فرمول مساحت دایره‌ای به شعاع $r$	$pi r^2$
فرمول مساحت کره‌ای به شعاع $r$	$4 pi r^2$
فرمول حجم کره‌ای به شعاع $r$	$frac{4}{3} pi r^3$
فرمول مساحت ‌جانبی نیم‌کره‌ای به شعاع $r$	$2 pi r^2$
فرمول مساحت کل نیم‌کره‌ای به شعاع $r$	$3 pi r^2$

برای حل سوالات متنوع‌تر در این زمینه و با نگاهی به آزمون‌های ورودی دبیرستان‌های نمونه دولتی یا تیزهوشان، فرادرس یک فیلم آموزشی با عنوان فیلم آموزش ریاضی نهم – نکته و تست آزمون نمونه دولتی و تیزهوشان تهیه کرده است که جهت دسترسی آسان‌تر، لینک آن نیز در ادامه برای شما قرار داده شده است:

مثال ۱

مساحت کره‌ای با شعاع پنج چقدر است؟

پاسخ

برای به‌دست آوردن مساحت کره کافی است فرمول آن را بنویسیم و مقدار شعاع را در فرمول جای‌گذاری کنیم:

$S = 4 pi r^2 Rightarrow S = 4 times 3.14 times (5)^2 = 314$

مثال ۲

مساحت کره‌ای که در تصویر زیر مشاهده می‌کنید، چقدر است؟

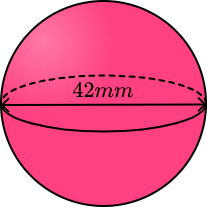
پاسخ

در این سوال قطر کره روی تصویر مشخص شده است. پس برای محاسبه مساحت کافی است از فرمول زیر استفاده کنیم:

$pi d^2$

$S = pi d^2 Rightarrow S = 3.14 times (42 mm)^2 = 5541.76 {mm}^2$

مثال ۳

مساحت جانبی نیم‌کره زیر چقدر است؟

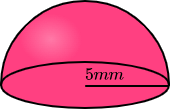
پاسخ

طبق تصویر داده شده نیم‌کره‌ای با شعاع پنج میلی‌متر داریم و می‌خواهیم مساحت جانبی آن را به‌دست آوریم. با توجه به اینکه کره یک حجم هندسی کاملا متقارن است، بنابراین نیم‌کره معادل است با نصف کره و می‌توانیم فرمول مساحت آن را با تقسیم کردن فرمول مساحت یک کره کامل بر دو به‌دست آوریم. پس داریم:

$S = frac{4 pi r^2}{2} = 2 pi r^2$

همان‌طور که در بخش‌‌های قبل توضیح داده شد، در محاسبه مساحت جانبی نیم‌کره فقط بخش خمیده شکل آن را در نظر می‌گیریم. پس نیازی به اضافه کردن مساحت قاعده به پاسخ بالا نیست، چون مساحت کل از ما خواسته نشده است.

کره چیست و چه ويژگی‌هایی دارد؟

برای اینکه بهتر متوجه شویم فرمول مساحت کره چیست، ابتدا باید با تعریف دقیق کره آشنا شویم. «کره» (Sphere) نوعی حجم سه بعدی و گرد است که برخلاف اغلب اشکال سه بعدی دیگر مانند مکعب، مخروط و … هیچ راس، گوشه یا لبه‌ای ندارد.

در یک کره تمام نقاط روی سطح از مرکز آن فاصله برابری دارند. در دنیای اطراف ما حجم‌های کروی بسیاری وجود دارند، از سیاره زمین گرفته (که البته دقیقا یک کره محسوب نمی‌شود) تا اتم‌های ماده، یک توپ بسکتبال، حباب صابون، توپ تنیس همه و همه در محاسبات با تقریب به شکل یک کره مدل‌سازی می‌شوند.

شعاع کره

شعاع کره معادل است با خطی که مرکز کره را به هر نقطه روی سطح آن متصل می‌کند. بنابراین اگر مانند شکل زیر مرکز کره را با نماد $O$

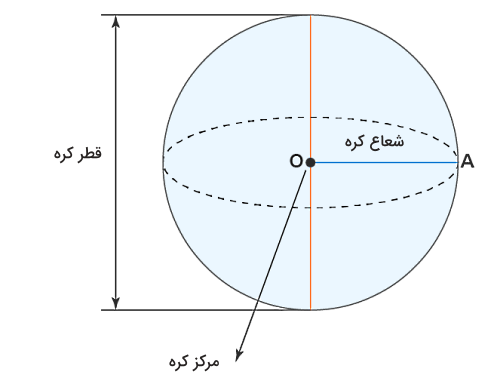
تصویر کره آبی رنگ همراه با معرفی اجزای آن - مساحت کره — مرکز، شعاع و قطر کره

قطر کره

قطر کره معادل با خطی است که یک نقطه فرضی روی سطح آن را به نقطه‌ای که دقیقا در مقابل آن و باز هم روی سطح قرار می‌گیرد، متصل می‌کند. قطر کره حتما از مرکز کره عبور می‌کند، به این شکل که مرکز کره دقیقا نقطه میانی هر کدام از قطرهای یک کره محسوب می‌شود. همچنین قطر کره همیشه دو برابر شعاع آن است. بنابراین اگر قطر کره با $d$

$d=2r$

محیط کره

شاید محاسبه محیط کره در مقایسه با محاسبه مساحت یا حجم آن مبهم بنظر برسد. محیط کره معادل است با دور بزرگترین دایره‌ای که در داخل کره وجود دارد. در شکلی که در ادامه مشاهده می‌کنید، مثالی از این دایره توسط خطوط نقطه‌چین مشخص شده است. به بیان دقیق‌تر، برای محاسبه محیط کره لازم است مقطعی از آن را در نظر بگیریم که حتما شامل مرکز آن است. این مقطع شامل بزرگترین دایره‌ای است که در داخل یک کره وجود دارد.

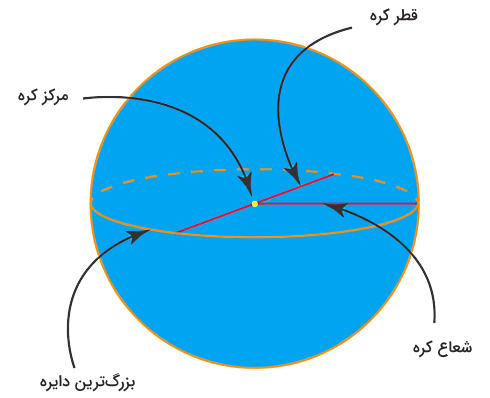
یک روش دیگر برای تشخیص این مقطع این است که کره را در در راستای یکی از قطرهای آن برش دهیم، در این صورت سطح مقطع ایجاد شده دایره‌ای است که محیط آن همان محیط کره است. پس فرمول محیط کره‌ای با شعاع $r$

$2 pi r$

با اینکه فرمول محیط کره دقیقا مشابه فرمول محیط دایره است، اما باید دقت کنیم که در مورد کره محیط کدام‌یک از دایره‌های داخل کره را در نظر گرفته‌ایم. پیشنهاد می‌کنیم برای اینکه با نحوه محاسبه محیط و مساحت اشکال هندسی مختلف بیشتر آشنا شوید، مطلب «فرمول های محیط و مساحت اشکال هندسی» از مجله فرادرس را مطالعه کنید.

حجم کره

مشابه هر جسم سه بعدی دیگر، کره نیز فضای مشخصی را اشغال می‌کند، پس حجم مشخصی دارد. فرمول حجم کره به شکل زیر است:

$frac{4}{3} pi r^3$

این فرمول به ما نشان می‌دهد چه مقدار فضا توسط این کره اشغال شده است. واحد حجم کره با توجه به توان سوم شعاع، همواره توان سومی از واحد طول یا فاصله است. نکته جالب‌توجه در مورد کره این است که بین تمام حجم‌های هندسی با مساحت سطحی مشابه با مساحت یک کره، کره بیشترین حجم را دارد.

اثبات فرمول مساحت کره

تا اینجا آموختیم مساحت کره چگونه تعریف می‌شود و چه فرمولی دارد. همچنین با ویژگی‌‌های مختلف یک کره و خواص آن کاملا آشنا شدیم. در این بخش می‌خواهیم نشان دهیم فرمول مساحت کره چگونه به‌دست می‌آید. برای اینکه فرمول مساحت کره‌ای با شعاع $r r$ انتگرال‌، مشتق‌گیری و دوران کاملا مسلط باشید.

ابتدا کمانی مطابق شکل زیر در نظر می‌گیریم. طول این کمان توسط دو معادله به شکل کلی $x(t)$

$S = int_{a}^{b} sqrt{ (frac{dy}{dt})^2 + (frac{dx}{dt})^2 dt}$

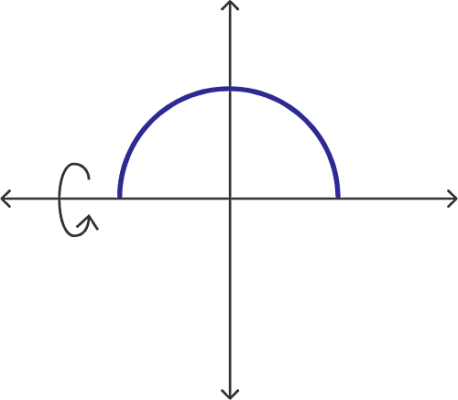
اگر این منحنی را حول محور xها دوران دهیم، یک نیم‌کره به‌دست می‌آید. در واقع با دوران این منحنی حول محور x، مساحت حجم به‌دست آمده از این دوران را از فرمول زیر می‌توانیم به‌دست آوریم:

$A = 2 pi int_{a}^{b} y sqrt{ (frac{dy}{dt})^2 + (frac{dx}{dt})^2 dt}$

همچنین برای اینکه به یک کره کامل برسیم، می‌توانیم نیم‌کره به‌دست آمده در مرحله قبل را حول محور x بچرخانیم. می‌دانیم یک ‌نیم‌دایره برای $0 le t le pi$

$x ( t) = r cos ( t )$

$y ( t) = r sin ( t)$

با مشتق‌گیری از این دو معادله خواهیم داشت:

$frac { d x } { d t } = – r sin ( t )$

$frac { d y } { d t } = r cos ( t )$

از جایگزینی عبارت‌های بالا در انتگرال مساحت خواهیم داشت:

$large begin {aligned} A & = 2 pi int _ 0 ^ pi r sin ( t ) sqrt { big ( – r sin ( t ) big ) ^ 2 + big ( r cos ( t ) big ) ^ 2 } d t \ & = 2 pi int _ 0 ^ pi r sin ( t ) sqrt { r ^ 2 big ( sin ( t) ^ 2 + cos ( t ) ^ 2 big ) } dt \ & = 2 pi int _ 0 ^ pi r ^ 2 sin ( t ) d t \ & = 2 pi r ^ 2 int _ 0 ^ pi sin ( t ) d t \ & = 4 pi r ^ 2 . end{aligned}$

ملاحظه می‌کنید که مساحت کره به‌دست آمد.

آزمون مساحت کره

در انتهای این مطلب از مجله فرادرس چند سوال به‌صورت چهار گزینه‌ای برای شما در نظر گرفته شده است تا با حل آن‌ها میزان یادگیری خود را بیازمایید. پس از پاسخ‌دهی به تمام سوالات با کلیک روی گزینه «مشاهده نتیجه آزمون» می‌توانید نمره نهایی خود را مشاهده کنید.

مساحت سطح خمیده شکل نیم‌کره‌ای با شعاع $12 cm$

گزینه سوم درست است. می‌دانیم مساحت کل نیم‌کره مجموع مساحت جانبی و مساحت قاعده آن است. اما در این سوال مساحت سطح خمیده شکل یعنی سطح جانبی خواسته شده است که فرمول آن به شکل $2 pi r^2$

$Rightarrow 2 pi (12)^2 = 904.32$

اگر حجم کره‌ای برابر با $36pi$

گزینه آخر درست است. دقت کنید چون حجم کره را داریم، پس باید با استفاده از فرمول حجم کره ابتدا شعاع آن را تعیین کنیم. سپس می‌توانیم مساحت جانبی آن را که همان مساحت کل آن است، با داشتن شعاع محاسبه کنیم:

$V = frac{4}{3} pi r^3 Rightarrow 36 pi = frac{4}{3} pi r^3$

$Rightarrow 36 = frac{4}{3} r^3 Rightarrow r^3 = 27$

$Rightarrow r = 3$

$S = 4 pi r^2 Rightarrow S = 4 pi 3^2 = 36pi$

اگر مساحت جانبی کره‌ای برابر با $4000 {cm}^2$

$r =sqrt{ frac{4000}{ pi } }$

$r =sqrt{ frac{1000}{ pi } }$

$r =sqrt{ frac{3000}{ pi } }$

$r =sqrt{ frac{2000}{ pi } }$

گزینه دوم صحیح است. گفتیم که در مورد کره مساحت جانبی همان مساحت کل است. بنابراین فرمول مساحت کره را می‌نویسیم تا بتوانیم شعاع کره را پیدا کنیم:

$S = 4 pi r^2 Rightarrow 4000 = 4 pi r^2$

$Rightarrow r^2 = frac{4000}{4 pi } = frac{1000}{ pi }$

$Rightarrow r =sqrt{ frac{1000}{ pi } }$

اگر یک توپ کروی مطابق شکل زیر کاملا استوانه‌ای را پر کرده باشد و بدانیم مساحت جانبی این استوانه برابر است با $45$

گزینه اول صحیح است. طبق قضیه ارشمیدس، اگر استوانه‌ای یک کره را کاملا احاطه کرده باشد، مساحت جانبی این استوانه‌ با مساحت کره داخل آن برابر است.

اگر مساحت جانبی کره‌ای برابر با $1386 {cm}^2$

$20.5 cm$

$10.5 cm$