در کتاب درسی هندسه ۳ یا هندسه تحلیلی رشته ریاضی، مباحث مختلفی از جمله ماتریس و کاربردهای آن، آشنایی با مقاطع مخروطی و بردارها مطرح میشوند. در این نوشته از مجله فرادرس پس از ارائه توضیحاتی مختصر در مورد مفاهیم هر یک از این سه بخش، تمام فرمول های هندسه تحلیلی دوازدهم را معرفی میکنیم. همچنین با حل مثالهای متنوع در هر بخش به شما کمک میکنیم تا به کاربرد این فرمولها در حل سوالات درس هندسه کاملا مسلط شوید.

فرمول های هندسه تحلیلی دوازدهم
فرمول های هندسه تحلیلی دوازدهم شامل کلیه فرمولهای سه فصل این کتاب با عناوین «ماتریس و کاربردها»، « آشنایی با مقاطع مخروطی» و «بردارها» است. عملیات جبری در ماتریسها، فرمول وارون ماتریس و دترمینان، معادله دایره، بیضی و سهمی، روابط بین بردارها در فضای سه بعدی و فرمولهایی مانند ضرب داخلی و خارجی بردارها از جمله فرمولهای این کتاب محسوب میشوند.
در ادامه این مطلب، شروع هر بخش با معرفی فرمولهای مرتبط با عنوان آن همراه است. در زیربخشهای بعدی به توضیح مختصر هر کدام از این فرمولها میپردازیم تا با تعاریف و مفاهیم پشت هر فرمول کاملا آشنا شوید. در انتهای هر بخش نیز چند مثال برای شما در نظر گرفتهایم تا با تمرین بیشتر فرمول های هندسه تحلیلی دوازدهم کاملا به آنها مسلط شوید.
فرمول های هندسه فصل اول: ماتریس و کاربردها
اولین فصل از کتاب هندسه سه به مبحث ماتریس و کاربردهای آن اختصاص دارد. جدول زیر تمام فرمول های هندسه تحلیلی دوازدهم مرتبط با این عنوان را نشان میدهد:
| توضیحات | فرمول |
| نمایش ماتریسی به نام با سطر و ستون | |
| درایههای ماتریس ( شماره سطر و شماره ستون درایه) | |
| جمع دو ماتریس و | |
| اختلاف دو ماتریس و | |
| خاصیت جابجایی جمع دو ماتریس | |
| خاصیت شرکتپذیری جمع دو ماتریس | |
| ضرب یک عدد حقیقی مانند در یک ماتریس | |
| ضرب ماتریس در ماتریس همانی یا واحد | |
| تعریف وارون ماتریسی مانند | |
| دترمینان ماتریس | |
| وارون ماتریس |
در ادامه این بخش ابتدا ماتریس، ویژگیها و انواع آن را معرفی میکنیم.
ویژگیهای ماتریس
برای یادگیری بهتر فرمول های هندسه تحلیلی دوازدهم مرتبط با این بخش، ابتدا باید ببینیم ماتریس چیست و چگونه تعریف میشود. ماتریس یک جدول یا یک آرایه منظم و مستطیل شکلی از اعداد، نمادها یا عباراتی است که در ردیفها و ستونهای مرتبی در کنار هم قرار گرفتهاند. هر کدام از این اعداد یا نمادها یک «درایه ماتریس» نامیده میشوند
ماتریسی به نام با سطر و ستون بهصورت نمایش داده میشود. تعداد درایههای یک ماتریس برابر است با حاصلضرب تعداد سطرهای آن در تعداد ستونها. همچنین هر درایه ماتریس را با یک حرف لاتین کوچک مانند نشان میدهیم که در آن شماره سطر و شماره ستون آن درایه است.
انواع ماتریس چه هستند؟
آشنایی با انواع ماتریس به ما کمک میکند تا بتوانیم از فرمول های هندسه تحلیلی دوازدهم بهتر استفاده کنیم. انواع ماتریسها بهصورت زیر طبقهبندی میشوند:
- ماتریس سطری: ماتریسی که فارغ از تعداد ستونها فقط و فقط شامل یک سطر باشد.
- ماتریس ستونی: ماتریسی که فارغ از تعداد سطرها فقط و فقط شامل یک ستون باشد.
- ماتریس یکه: ماتریسی که دارای یک سطر و یک ستون است.
- ماتریس مستطیلی: ماتریسی است که در آن تعداد سطرها و ستونها برابر نیستند.
- ماتریس مربعی: ماتریسی است که در آن تعداد سطرها و ستونها برابر هستند.
- ماتریس صفر: ماتریسی است که تمام درایههای آن برابر است با عدد . این ماتریس را با نشان میدهیم.
- ماتریس قطری: نوعی ماتریس مربعی است که تمام درایههای روی قطر اصلی آن مخالف و سایر درایههای آن برابر با است.
- ماتریس اسکالر: نوعی ماتریس قطری است که تمام درایههای روی قطر اصلی آن مخالف و برابر با هم هستند، در حالی که سایر درایههای آن است.
- ماتریس واحد یا همانی: نوعی ماتریس اسکالر است که تمام درایههای روی قطر اصلی آن برابر با و سایر درایههای آن برابر با است.
- ماتریس بالامثلثی: نوعی ماتریس مربعی است که اعداد بالای قطر اصلی آن مخالف و اعداد زیر قطر اصلی آن برابر با هستند.
- ماتریس پایینمثلثی: نوعی ماتریس مربعی است که اعداد بالای قطر اصلی آن برابر با و اعداد زیر قطر اصلی آن مخالف هستند.
- ماتریس تکین: ماتریسی که دترمینان آن صفر است.
- ماتریس غیرتکین: ماتریسی که دترمینان آن مخالف صفر است.
- ماتریس متقارن: ماتریسی است که برای درایههای آن رابطه برقرار است.
- ماتریس تقارنپذیر: ماتریسی است که تمام مقادیر دترمینان آن برابر است با صفر.
فرمول جمع و تفریق ماتریس ها
گفتیم از ماتریسها برای لیست کردن دادهها و نمایش سیستمها میتوان استفاده کرد. از آنجایی که درایههای یک ماتریس در ریاضیات اعداد هستند، پس این امکان وجود دارد که بتوانیم عملیاتی مانند جمع یا تفریق را روی ماتریسها اجرا کنیم. جمع و تفریق ماتریسها با جمع و تفریق کردن درایههای متناظر آنها انجام میشود. بنابراین زمانی مجاز به این کار هستیم که ابعاد یا مرتبه ماتریسها کاملا مشابه هم باشند.
برای مثال، دو ماتریس را میتوانیم با هم جمع یا از هم کم کنیم اما اگر یکی از این دو ماتریس مرتبه داشته باشد، مجاز به اجرای این عملیات نیستیم. قانون کلی جمع و تفریق ماتریسها به این صورت است که اگر دو ماتریس و را با ابعاد یکسان در نظر بگیریم، مجموع و تفاضل این دو ماتریس ماتریسهایی مانند و را با ابعادی مشابه ایجاد میکنند:
همچنین در مورد جمع و تفریق ماتریسها قواعد جابجایی و شرکتپذیری به شکل زیر همواره برقرار است:
فرمول ضرب ماتریس ها
یکی دیگر از چهار عمل اصلی که در مورد ماتریسها تعریف و بررسی میکنیم، ضرب ماتریسها است. البته پیش از اینکه به روش ضرب کردن دو ماتریس بپردازیم، ابتدا لازم است با نحوه ضرب کردن یک عدد حقیقی در یک ماتریس آشنا شویم. اگر بخواهیم یک عدد حقیقی مانند را در ماتریسی به شکل ضرب کنیم، حاصل به شکل زیر خواهد بود:
همچنین برای این نوع ضرب قوانین زیر همیشه برقرار است:
نکته: قرینه ماتریسی مانند از ضرب کردن عدد حقیقی در آن حاصل میشود. واضح است که .
در ادامه یادگیری فرآیند ضرب ماتریسها، باید به این نکته توجه کنید که ضرب دو ماتریس در یکدیگر زمانی امکانپذیر است که تعداد ستونهای ماتریس اول با تعداد سطرهای ماتریس دوم برابر باشد. برای مثال، اگر ماتریس از مرتبه و ماتریس از مرتبه باشند، در این صورت حاصلضرب این دو ماتریس یعنی یک ماتریس خواهد بود.
حالا فرض کنید ماتریسهای و به شکل زیر داده شده باشند، برای بهدست آوردن حاصلضرب این دو به روش زیر عمل میکنیم:
درایهای که متناظر با اولین سطر و اولین ستون در ماتریس است از ضرب کردن اولین سطر در اولین ستون و جمع کردن مقادیر بهدست آمده حاصل خواهد شد:
به همین شکل، درایهای که متناظر با اولین سطر و دومین ستون در ماتریس است از ضرب کردن اولین سطر در دومین ستون و جمع کردن مقادیر بهدست آمده حاصل خواهد شد:
و در نهایت درایهای که متناظر با اولین سطر و سومین ستون در ماتریس است از ضرب کردن اولین سطر در سومین ستون و جمع کردن مقادیر بهدست آمده حاصل خواهد شد:
این روند به ما اولین سطر از ماتریس حاصلضرب را خواهد داد و به شکل مشابهی سطر دوم این ماتریس نیز بهدست خواهد آمد. چون ماتریس از مرتبه و از مرتبه است، پس انتظار داریم ماتریس حاصلضرب از مرتبه باشد. تصویر زیر ضرب یک ماتریس سطری در یک ماتریس ستونی را نشان میدهد که سادهترین شکل ضرب ماتریسی است و حاصل آن یک عدد است:
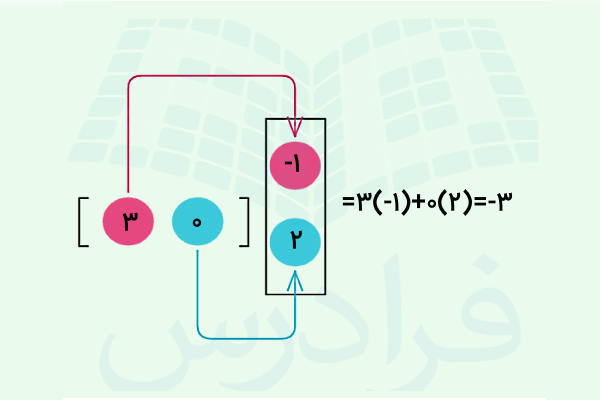
همچنین برای ضرب چند ماتریس در هم قوانین زیر همیشه برقرار هستند:
نکته مهم: ضرب ماتریسهای دارای خاصیت جابجایی نیست.
همچنین در ضرب ماتریسها یک عضو خنثی به نام ماتریس واحد یا همانی داریم که با نماد متمایز میشود. از بخش قبل به یاد دارید که ماتریس واحد نوعی ماتریس اسکالر است که تمام درایههای روی قطر اصلی آن برابر با و سایر درایههای آن برابر با است. به این ترتیب اگر ماتریسی مانند در این ماتریس ضرب شود، همواره رابطه زیر برقرار است:
فرمول وارون ماتریس
پس از اینکه با فرمول های هندسه تحلیلی دوازدهم در زمینه روش انجام عملیات مختلف در ماتریسها آشنا شدیم، در این بخش روشهای بهدست آوردن وارون یک ماتریس را توضیح میدهیم. ابتدا باید ببینیم تعریف وارون یک ماتریس چیست. یک ماتریس مربعی مانند زمانی دارای ماتریس وارونی به نام است که همواره رابطه زیر برای این دو برقرار باشد:
برای مثال اگر ماتریس را داشته باشیم و بخواهیم بدانیم آیا ماتریس وارون این ماتریس محسوب میشود یا خیر، کافی است حاصلضرب این دو ماتریس را بهدست آوریم و ببینیم آیا یک ماتریس همانی میشود یا نه:
حاصل این ضرب یک ماتریس همانی شد. بنابراین ماتریس وارون ماتریس است. اما اگر ماتریسی به ما داده شود و بخواهیم وارون آن را پیدا کنیم، باید چه کنیم؟ برای پاسخ دادن به این سوال، مجددا ماتریس را به شکل بالا در نظر بگیرید و فرض کنید وارون آن را نمیدانید. با در نظر گرفتن ماتریس وارونی به شکل زیر (ماتریسی با درایههای مجهول)، میتوانیم به کمک فرمول ماتریس وارون را پیدا کنیم:
رابطه بالا به ما دو دستگاه معادله با دو معادله و دو مجهول میدهد:
حل این دو دستگاه به ما مقادیر زیر را میدهد که مشخص کننده ماتریس واروناند:
بنابراین یکی از کاربردهای ماتریس وارون پیدا کردن راهحل برای سیستم معادلات خطی است. فرض کنید یک سیستم ماتریسی به شکل داریم. با دانستن ماتریس وارون یعنی ، اگر دو طرف این معادله را در ضرب کنیم، خواهیم داشت:
در رابطه بالا ماتریس ضرایب، ماتریس مقادیر معلوم و ماتریس مجهولات نامیده میشود.
فرمول دترمینان و محاسبه ماتریس وارون
در بخش قبل آموختیم فرمول مناسب از مجموعه فرمول های هندسه تحلیلی دوازدهم برای محاسبه وارون یک ماتریس چیست. در این بخش نشان میدهیم اگر بدانیم چگونه دترمینان یک ماتریس را محاسبه کنیم، بهدست آوردن ماتریس وارون بسیار آسانتر خواهد شد. طبق تعریف، دترمینان ماتریسی به شکل از فرمول زیر بهدست میآید:
تعریف بالا سادهترین تعریف برای دترمینان است، چون یک ماتریس مربعی از مرتبه داریم. اما در مورد مراتب بالاتر، محاسبه دترمینان پیچیدهتر است. اگر دترمینان ماتریس یا را بدانیم، محاسبه معکوس آن توسط فرمول زیر انجام میشود:
به تغییراتی که در درایههای ماتریس داده شده است، توجه کنید. طبق این تعریف اگر شود، وارون آن وجود ندارد. در همین راستا اگر علاقهمند به یادگیری روش بهدست آوردن دترمینان و سپس وارون یک ماتریس سه در سه هستید، پیشنهاد میکنیم مطلب «ماتریس معکوس ۳×۳ – به زبان ساده» از مجله فرادرس را مطالعه کنید.
مثال و تمرین ماتریس
پس از اینکه آموختیم ماتریس چیست و فرمول های هندسه تحلیلی دوازدهم مرتبط با این موضوع چه هستند، در این بخش قصد داریم با حل چند مثال به شما کمک کنیم تا به کاربردهای این فرمولها کاملا مسلط شوید:
مثال ۱
با در نظر گرفتن ماتریس زیر، به سوالات داده شده پاسخ دهید:
- ابعاد این ماتریس چیست؟
- درایههای متناظر با و کدامند؟
- همچنین مجموع دو ماتریس زیر را بهدست آورید:
پاسخ
- ابعاد ماتریس داده شده است، چون این ماتریس دارای سه سطر و سه ستون است.
- درایه متناظر با برابر است با درایهای که در سطر سوم و ستون اول قرار دارد یعنی .
- درایه متناظر با برابر است با درایهای که در سطر دوم و ستون دوم قرار دارد یعنی .
در مورد سومین سوال، با توجه به اینکه مرتبه این دو ماتریس کاملا یکسان و برابر با است، بنابراین مجازایم به جمع کردن درایههای متناظر به شکل زیر:
مثال ۲
- اگر ماتریس برابر باشد با ، ماتریس را پیدا کنید:
- همچنین حاصلضرب دو ماتریس و را بهدست آورید:
پاسخ
برای پاسخ به اولین سوال، کافی است عدد صحیح را در تمام درایههای ماتریس داده شده ضرب کنیم:
در بخش بعدی حاصلضرب دو ماتریس داده شده به شکل زیر محاسبه میشود:
مثال ۳
فرض کنید جدول زیر نشان دهنده وسایل لازم برای بازی دو تیم فوتبال است:
| تیم یک | تیم دو | |
| تعداد دروازهها | ||
| تعداد توپها | ||
| تعداد پیراهنها |
همچنین هزینه هر کدام از این وسایل نیز در جدول زیر ارائه شده است:
| دروازه | دلار |
| توپ | دلار |
| پیراهن | دلار |
هزینه کل وسایل لازم برای هر کدام از این دو تیم چقدر است؟
پاسخ
ابتدا باید دادههای این دو جدول را در قالب دو ماتریس تنظیم کنیم. ماتریس اول که توصیفکننده تجهیزات موردنیاز برای هر دو تیم است به شکل زیر تنظیم میشود:
ملاحظه میکنید که ستون اول این ماتریس تجهیزات تیم یک و ستون دوم تجهیزات تیم دو است. همچنین برای اینکه بتوانیم دو ماتریس تنظیم شده را در یکدیگر ضرب کنیم، ماتریس هزینهها را بهصورت یک ماتریس سطری به شکل زیر در نظر میگیریم:
به این ترتیب حاصلضرب دو ماتریس و برابر میشود با:
یادگیری هندسه دبیرستان با فرادرس
پیش از توضیح ماتریسها، ابتدا قصد داریم چند فیلم آموزشی در زمینه کلیه مباحث مطرح شده در کتابهای درسی هندسه دبیرستان را معرفی کنیم. مشاهده این دورهها به شما کمک میکند تا از طریق مشاهده تصاویر یادگیری عمیقتری داشته باشید. ضمن اینکه اغلب این آموزشها همراه با حل مثالها و تمرینهای متنوعی است که به درک بهتر شما از هر موضوع کمک خواهد کرد:
فرمول های هندسه فصل دوم: آشنایی با مقاطع مخروطی
فصل دوم از کتاب هندسه ۳ رشته ریاضی مبحثی به نام «مقاطع مخروطی» (Conic Sections) را توضیح میدهد. مطالعه و کشف مقاطع مخروطی به یونان باستان بازمیگردد و در حال حاضر از نتایج بهدست آمده در این موضوع در علوم مختلفی از جمله مهندسی و طراحی سازهها، طراحی تلسکوپهای رادیویی، معماری، نجوم و … استفاده میشود. نامگذاری مقاطع مخروطی بر این اساس انجام شده است که این مقاطع از تقاطع یک صفحه با یک مخروط ایجاد میشوند.
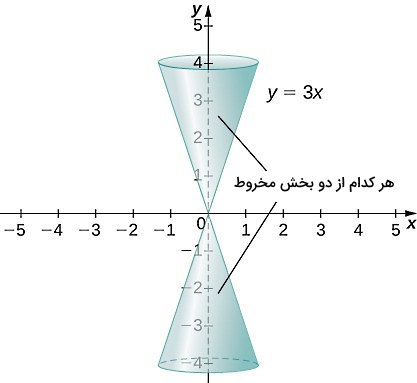
مخروط واقعی از دو بخش مشابه به شکل زیر تشکیل شده است، اما ما هر کدام از بخشهای آن را بهعنوان یک مخروط میشناسیم (در واقع هر کدام از این بخشهای شبیه یک کلاه تولد هستند). تعریف دقیقتر مخروط دایرهای به این شکل است: مکان هندسی تمام نقاطی که از چرخش یک خط مستقیم عبوری از مبدا مختصات حول محور y ایجاد میشوند. در بخش بعد راجعبه مفهوم «مکان هندسی» صحبت خواهیم کرد. در تصویر زیر مشاهده میکنید که مخروط نشان داده شده از چرخش خطی با معادله حول محور yها حاصل شده است و این چرخش دو بخش به شکل زیر ایجاد میکند:
همچنین در تصویر زیر ملاحظه میکنید که مقاطع مخروطی مختلف چگونه از تقاطع یک صفحه با یک مخروط بهدست میآیند. در تصویر سمت چپ، با قرار گرفتن یک صفحه در زاویههای مختلف و تقاطع آن فقط با یکی از دو بخش مخروط به مقاطع مختلفی به نام دایره، بیضی و سهمی میرسیم. در تصویر سمت راست تقاطع یک صفحه با هر دو بخش مخروط واقعی نشان داده شده است. این تقاطع منجر به شکلگیری مقطعی به نام هذلولی خواهد شد.
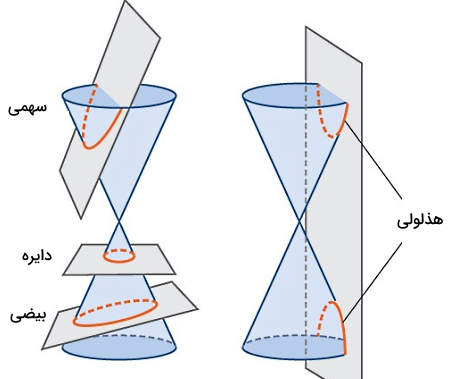
همچنین میتوانیم بگوییم نوع مقطع مخروطی که از این تقاطع ایجاد میشود به زاویه صفحه با محور مخروطها بستگی دارد. در مورد هذلولی این زاویه صفر و در مورد دایره این زاویه قائمه است. در ادامه برای اینکه بهتر این نکات را بهخاطر بسپارید، آنها را فهرست کردهایم:
- اگر صفحه با محور مخروط موازی باشد، تقاطع آن با مخروط یک هذلولی ایجاد میکند.
- اگر صفحه با یکی از یالهای مخروط موازی باشد، تقاطع آن با مخروط یک سهمی ایجاد میکند.
- اگر صفحه به محور مخروط عمود باشد، تقاطع آن با مخروط یک دایره ایجاد میکند.
- تقاطع صفحه با مخروط اگر جزء سه مورد بالا نباشد، حاصل ایجاد یک بیضی است.
مجموعه تمام فرمول های هندسه تحلیلی دوازدهم برای مهمترین مقاطع مخروطی در ریاضیات یعنی سهمی، دایره، و بیضی در جدول زیر جمعآوری شده است:
| نام مقطع مخروطی | توضیحات | معادله |
| دایره | دایرهای با مرکز و شعاع | |
| سهمی | سهمی رو به بالا (راس و کانون ) | |
| سهمی رو به پایین (راس و کانون ) | ||
| سهمی راست (راس و کانون ) | ||
| سهمی چپ (راس و کانون ) | ||
| معادله کلی سهمی رو به بالا یا پایین | ||
| معادله کلی سهمی راست یا چپ | ||
| بیضی | معادله بیضی افقی (مرکز و طول محور اصلی ) | |
| معادله بیضی عمودی (مرکز و طول محور اصلی ) | ||
| معادله کلی بیضی |
مکان هندسی چیست؟
به مجموعهای از تمام نقاطی که دارای یک ویژگی مشترک هستند، مکان هندسی گفته میشود. دانستن مفهوم مکان هندسی برای تعریف مقاطع مخروطی و در نتیجه بهتر بهخاطر سپردن فرمول های هندسه تحلیلی دوازدهم ضروری است. نتیجه در نظر گرفتن مکان هندسی رسیدن به یک منحنی یا سطح است.
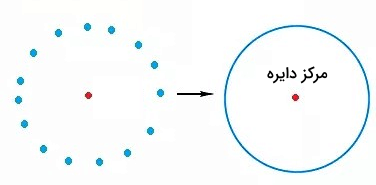
برای مثال، یک دایره مکان هندسی تمام نقاط روی یک صفحه است که دارای فاصله مشخصی از یک نقطه مشخص به نام مرکز دایره هستند. تصویر بالا نشان میدهد چگونه میتوانیم از اتصال این نقاط بهعنوان مکان هندسی دایره به یک دایره برسیم.
معادله دایره
دایره سادهترین مقطع مخروطی است که در کتاب هندسه ۳ بررسی میشود و تعریف آن به این صورت است: مکان هندسی تمام نقاطی از صفحه که از یک نقطه ثابت به نام «مرکز دایره» به یک فاصلهاند. این فاصله ثابت همان «شعاع دایره» است. همچنین معادله دایره بهعنوان یکی از مهمترین فرمول های هندسه تحلیلی دوازدهم به شکل زیر است:
- نقطه : مختصات مرکز دایره
- فاصله : شعاع دایره
رسیدن به این معادله آسان است و با استفاده از فرمول فاصله میتوانیم آن را بهدست آوریم:
با مربع کردن طرفین این تساوی داریم:
طبق تعریف دایره، هر نقطهای روی آن مانند دارای فاصلهای برابر با از مرکز دایره است. پس در فرمول بالا برابر با میشود، در حالی که نقطه معادل است با مرکز دایره با مختصات :
معادله دایره همیشه به صورت استاندارد داده نمیشود. اغلب در مسائل مختلف با شکل پیچیدهتری از این معادله سروکار داریم و لازم است با استفاده از اتحادها یا سایر روشهای سادهسازی معادله داده شده را به شکل استاندارد آن تبدیل کنیم. در بخش مثالها این نکته را بهتر میآموزید.
معادله سهمی
سهمی یا Parabola از تقاطع صفحه با تنها یکی از دو بخش مخروط واقعی ایجاد میشود و در این تقاطع صفحه با یکی از یالهای مخروط موازی است. همچنین تعریف دیگری که برای یک سهمی میتوانیم ارائه دهیم به این صورت است:
- مجموعهای از تمام نقاط یک صفحه که فاصله آنها از یک نقطه ثابت (کانون) برابر با فاصله آنها از یک خط ثابت (خط هادی سهمی) در همان صفحه است.
- نقطهای که در میانه فاصله بین کانون و این خط قرار دارد، «راس سهمی» نامیده میشود.
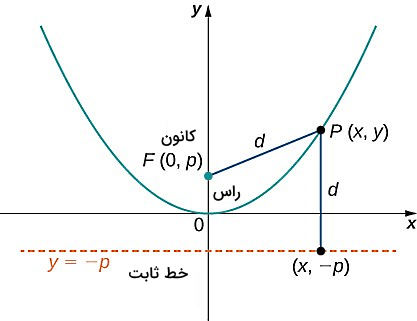
در تصویر بالا این اجزا را مشاهده میکنید. اگر از این تصویر در کنار فرمول فاصله به شکل زیر استفاده کنیم، میتوانیم به معادله سهمی برسیم. میدانیم فاصله بین دو نقطه به نام با مختصات و با مختصات ، توسط فرمول زیر تعیین میشود:
حالا با توجه به تعریفهایی که در مورد سهمی داشتیم، باید با طبق تصویر برابر باشد:
با مجذور کرن دو طرف تساوی بالا و کاربرد اتحاد مربع کامل خواهیم داشت:
حالا فرض کنید بخواهیم راس سهمی را در تصویر بالا جابجا کنیم. در این صورت بهتر است برای اینکه به یک معادله جامعی از سهمی برسیم، از بهعنوان مختصات راس استفاده کنیم. به این ترتیب اگر کانون سهمی بالای راس آن قرار داشته باشد، مختصات آن برابر است با . همچنین معادله خط ثابت به شکل است. به این ترتیب معادله سهمی به شکل زیر میشود:
اگر این معادله را برای بهدست آوردن حل کنیم، خواهیم داشت:
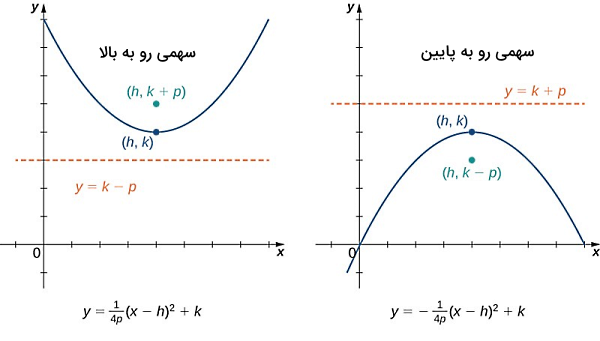
این رابطه معادله استاندارد یک سهمی رو به بالا (با تقعر بالا) است که مختصات راس و کانون آن بهترتیب برابراند با و ، در حالی که یک عدد ثابت است. سهمیها همیشه تقعر رو به بالا ندارند، بلکه ممکن است رو به پایین باشند یا به سمت چپ یا راست تقعر داشته باشند. در تصویر بالا و پایین زیر معادلات استاندارد سهمی برای هر چهار حالت ممکن نمایش داده شده است:
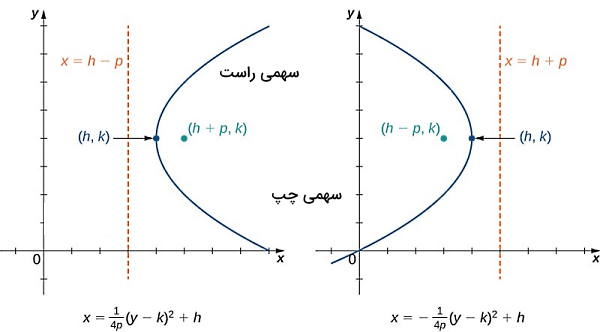
البته حالت کلیتری که برای معادله یک سهمی و بدون توجه به مختصات راس و کانون آن میتوانیم در نظر بگیریم، به شکل زیر است:
معادله اول در مورد سهمیهایی با تقعر بالا یا پایین و معادله دوم برای سهمیهای راست یا چپ است. در بخش مثالها با کاربرد این معادلات بیشتر آشنا خواهید شد.
معادله بیضی
بیضی یا Ellipse مجموعهای از تمام نقاط یک صفحه است که همواره مجموع فواصل آنها از دو نقطه ثابت به نام «کانونهای بیضی» ثابت است. در این بخش میخواهیم ببینیم فرمول های هندسی تحلیلی دوازدهم مرتبط با این مقطع مخروطی چگونه بهدست میآیند.
همانطور که در تصویر زیر ملاحظه میکنید، دو کانون بیضی که با نماد و مشخص شدهاند، دارای فاصله ثابتی از مرکز بیضی هستند و این فاصله با نشان داده شده است. به این ترتیب مختصات کانون برابر با و مختصات کانون برابر با است:
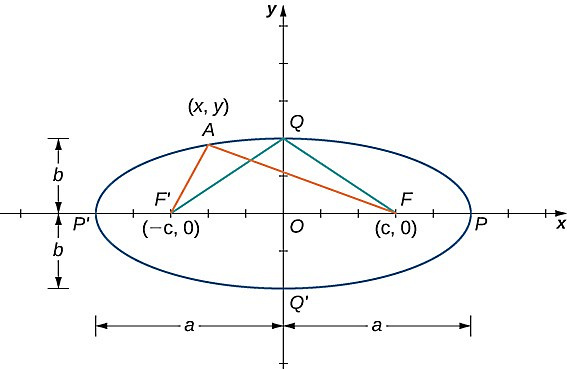
همچنین دو نقطه و را داریم که «راسهای بیضی» نامیده میشوند و در دو انتهای محور یا قطر اصلی (محور بزرگتر) بیضی قرار دارند. این محور الزاما افقی نیست و میتواند عمودی هم باشد. طول محور اصلی بیضی بالا برابر است با . مشابه این دو نقطه، نقاط و را داریم که در دو انتهای محور فرعی (محور کوچکتر) بیضی با طول قرار گرفتهاند. دقت کنید محورهای بیضی همیشه بر هم عموداند. با انتخاب هر نقطه دلخواه روی بیضی و بهدست آوردن مجموع فواصل این نقطه از دو کانون، میتوانیم معادله بیضی را تعیین کنیم. برای مثال، فرض کنید نقطهای مانند با مختصات را در نظر داریم:
بنابراین مجموع فواصل هر نقطه دلخواهی مانند با مختصات روی این بیضی همواره برابر میشود با مقدار ثابت :
اگر طرفین آخرین رابطه را به توان دو برسانیم و در انتها جملات شامل متغیرهای x و y را در یک طرف تساوی قرار دهیم، خواهیم داشت:
با تقسیم طرفین این عبارت بر ، خواهیم داشت:
همچنین با توجه به قضیه فیثاغورث در شکل ابتدای بخش، میدانیم . پس معادله بالا را میتوانیم به شکل زیر ساده کنیم:
این معادله را بر مبنای تصویر بالا بهدست آوردیم که در آن مرکز بیضی روی مبدا مختصات است. اما حالت کلی و جامع معادله بیضی با در نظر گرفتن مختصات برای مرکز آن بهدست میآید:
این معادله توصیف کننده یک بیضی افقی با مرکز ، محور اصلی و افقی با طول و محور فرعی عمودی با طول است. در این بیضی محل قرارگیری کانونها است که در آن . اما اگر محور اصلی بیضی ما عمودی باشد، معادله آن کمی متفاوت است. معادله یک بیضی عمودی با مرکز ، محور اصلی و عمودی با طول و محور فرعی و افقی با طول به شکل زیر است:
که در آن محل قرارگیری کانونها است و داریم . حالت کلی معادله یک بیضی به شکل زیر است، اما در اغلب مسائل علاقهمندیم شکل استاندارد آن را که یکی از دو معادله بالا است، پیدا کنیم:
مثال و تمرین مقاطع مخروطی
در انتهای این بخش چند سوال برای شما در نظر گرفتهایم تا بتوانید از طریق تمرین بیشتر به فرمول های هندسه تحلیلی دوازدهم مرتبط با موضوع این بخش کاملا مسلط شوید. دقت کنید بررسی معادلات مقاطع مخروطی و نوشتن آنها به شکل استاندارد نیازمند تسلط بر اتحادها و استفاده از روشی به نام «مربع کامل کردن» است. در مطلب «حل معادله درجه دوم به روش مربع کامل – به زبان ساده + مثال و تمرین» از مجله فرادرس در مورد این روش صحبت کردهایم.
مثال ۱
مرکز و شعاع هر کدام از دایرههای زیر را تعیین کنید:
پاسخ
در مورد اولین مورد کافی است آن را به شکل زیر بنویسیم و با معادله اصلی دایره مقایسه کنیم تا مختصات مرکز و اندازه شعاع بهدست آید:
به این ترتیب داریم:
در دومین مورد ابتدا طرفین تساوی را بر عدد دو تقسیم میکنیم:
حالا میتوانیم این معادله را با مقایسه کنیم و به نتیجه زیر برسیم:
در سومین معادله باید از روش مربع کامل کردن استفاده کنیم. با قرار دادن تمام جملات شامل x در کنار هم و تمام جملات شامل y در کنار هم خواهیم داشت:
به معادله استاندارد دایره رسیدیم. پس برای مرکز و شعاع آن داریم:
مثال ۲
معادله کلی یک سهمی به شکل را در قالب فرم استاندارد آن بازنویسی کرده و سپس این سهمی را رسم کنید:
پاسخ
دقت کنید چون توان دوم متغیر را در این معادله نداریم، پس میتوانیم مطمئن شویم که این سهمی یا تقعر بالا دارد و یا تقعر پایین. همچنین لازم است این معادله را برای حل کنیم تا به فرم استاندارد برسیم. اگر به طرفین این معادله را اضافه کنیم، خواهیم داشت:
مرحله بعدی این است که یک سمت این معادله را به شکل مربع کامل بنویسیم تا بتوانیم با کمک گرفتن از اتحادها آن را ساده کنیم. این ترفند با اضافه و کم کردن عدد چهار در یک سمت جواب خواهد داد:
با تقسیم کردن طرفین بر عدد هشت داریم:
بنابراین به فرم استاندارد معادله سهمی داده شده رسیدیم. این پاسخ به ما نشان میدهد مختصات راس و کانون سهمی چه هستند:
همچنین معادله خط ثابت زیر این سهمی به شکل زیر خواهد شد:
حالا رسم منحنی این سهمی با مشخصاتی که بهدست آوردیم، آسان است:

مثال ۳
معادله زیر به ما داده شده است. با نوشتن آن به شکل استاندارد تعیین کنید این معادله توصیف کننده کدام مقطع مخروطی و با چه مشخصاتی است. همچنین نمودار آن را رسم کنید:
پاسخ
اولین کاری که میکنیم بردن عدد ثابت به سمت دیگر تساوی، قرار دادن جملات شامل x در کنار هم و قرار دادن جملات شامل y در کنار هم است:
حالا باید از روش مربع کامل کردن در مورد هر دو متغیر x و y استفاده کنیم. فقط نباید فراموش کنیم که دو ضریب عددی نیز در خارج از هر دو پرانتز داریم و باید در نظر گرفته شوند:
با تقسیم کردن تمام جملات این تساوی بر عدد معادله به شکل استاندارد خود درمیآید:
اگر به این معادله دقت کنیم، متوجه میشویم که این معادله مربوط به یک بیضی عمودی است، چون مخرج جمله دارای متغیر y بزرگتر از مخرج جملهای است که متغیر x دارد. بنابراین معادله استاندارد ما به شکل است. از مقایسه این معادله با معادله بهدست آمده نتیجه میگیریم که یک بیضی با مختصات مرکز داریم. همچنین در این بیضی و است. پس نمودار آن به شکل زیر رسم میشود:

تمرین ۱
اگر معادله یک مقطع مخروطی به شکل باشد، کدام گزینه صحیح است؟
این معادله مربوط است به یک سهمی راست با راس و کانون
این معادله مربوط است به یک سهمی چپ با راس و کانون
این معادله مربوط است به یک سهمی راست با راس و کانون
این معادله مربوط است به یک سهمی چپ با راس و کانون
گزینه سوم درست است. ابتدا باید شکل استاندارد این معادله را بنویسیم. با توجه به اینکه توان دوم در معادله وجود دارد، پس همینجا میتوانیم نتیجهگیری کنیم که یک سهمی راست یا چپ خواهیم داشت و لازم است را در یک طرف تساوی پیدا کنیم. ابتدا به طرفین معادله داده شده اضافه میکنیم:
حالا پس از تقسیم طرفین بر عدد دو، یک سمت را مربع کامل میکنیم:
اگر این معادله را با معادله استانداردی که برای یک سهمی راست معرفی کردیم، مقایسه کنیم، خواهیم داشت:
مختصات راس به شکل بالا شد. مختصات کانون این سهمی نیز به شکل زیر است:
تمرین ۲
معادله توصیفکننده کدام یکی از گزینههای زیر است؟
یک بیضی افقی با مرکز و و
یک بیضی عمودی با مرکز و و
یک بیضی افقی با مرکز و و
یک بیضی عمودی با مرکز و و
گزینه اول صحیح است. ابتدا عدد ثابت را به سمت دیگر تساوی میبریم. سپس جملات شامل x و y را در کنار هم قرار میدهیم تا بهتر بتوانیم مربع کامل کردن را برای هر کدام انجام دهیم:
عبارت بالا را با فاکتورگیری میتوانیم سادهتر کنیم:
همچنین نباید فراموش کنیم که دو ضریب عددی نیز در خارج از هر دو پرانتز داریم که باید در نظر گرفته شوند:
با تقسیم کردن تمام جملات این تساوی بر عدد معادله به شکل استاندارد خود درمیآید:
این معادله مربوط به یک بیضی افقی است، چون مخرج جمله دارای متغیر x بزرگتر از مخرج جملهای است که متغیر y دارد. بنابراین معادله استاندارد ما به شکل است. از مقایسه این معادله با معادله بهدست آمده نتیجه میگیریم که یک بیضی با مختصات مرکز داریم. همچنین در این بیضی و است.
فرمول های هندسه فصل سوم: بردارها
در آخرین فصل از کتاب هندسه ۳ رشته ریاضی به مبحث بردارها پرداخته شده است. ابتدا باید ببینیم منظور ما از بردار در درس ریاضی و هندسه چیست. بردار به هر کمیتی گفته میشود که دارای اندازه و جهت است و از آن در علوم مختلفی از جمله فیزیک و مهندسی استفاده زیادی میشود. اغلب کمیتهای فیزیکی مانند سرعت، شتاب و نیرو از جنس برداراند، به این معنا که علاوهبر اندازه، دانستن جهت آنها نیز در حل مسائل بسیار مهم است.
در این فصل ابتدا در مورد فضای دو بعدی با عنوان «فضای » صحبت میشود تا پس از تسلط کامل به این فضا بتوانید با یک بعد بالاتر یعنی «فضای » نیز بهتر آشنا شوید. همچنین از هندسه ۱ و ۲ و ریاضیات پایه مانند کتاب ریاضی هفتم بهخاطر داریم که مفهوم صفحه، دستگاه مختصات دو بعدی یا مختصات یک نقطه در فضا چیست. در همین راستا پیشنهاد میکنیم اگر نیاز به بازبینی مفاهیم پایه دارید، فیلم آموزش ریاضی پایه هفتم فرادرس را مشاهده کنید که لینک آن در ادامه برای شما قرار داده شده است:
در این کتابهای درسی توضیح داده شد که میتوانیم برای مشخص کردن موقعیت هر نقطه فرضی در صفحه از زوجی به نام مولفه x و مولفه y استفاده کنیم. این دو مولفه توصیف کننده مختصات یک نقطه در صفحه هستند و مقادیر عددی متناظر با آنها میتواند یک عدد حقیقی باشد. با توجه به اینکه مجموعه اعداد حقیقی را با نماد نشان میدهیم، بنابراین اگر مختصات هر کدام از نقاط صفحه را با مشخص کنیم، در این صورت میتوانیم بگوییم مجموعه زیر شامل تمام نقاط صفحه است:
یکی دیگر از مفاهیم مهم در درس هندسه معادله خط است که صورت کلی آن به شکل زیر است (). در این معادله و نمیتوانند همزمان صفر باشند:
فرمول های هندسه تحلیلی دوازدهم برای این فصل از کتاب در جدول زیر خلاصه شدهاند:
| توضیحات | فرمول |
| مجموعه تمام نقاط یک صفحه یا فضای | |
| معادله خط با | |
| مجموعه تمام نقاط فضای سه بعدی یا | |
| فاصله بین دو نقطه و | |
| اندازه یک بردار | |
| ضرب عدد در بردار | |
| جمع دو بردار و | |
| اختلاف دو بردار و | |
| خاصیت جابجایی در جمع دو بردار | |
| خاصیت شرکتپذیری در جمع بردارها | |
| خاصیت توزیعپذیری در جمع دو بردار | |
| حاصلجمع یک بردار با بردار صفر | |
| حاصلجمع یک بردار با قرینهاش | |
| تجزیه یک بردار بر حسب بردارهای یکه | |
| بردار یکه در راستای برداری مانند |
دقت کنید در پیدا کردن اندازه یک بردار یا محاسبه مجموع دو بردار، به محض صفر شدن یکی از مولفههای x یا y یا z، با یک بردار در فضای دو بعدی سروکار داریم. در ادامه توضیحات مختصری در مورد بخشهای مختلف این فصل از کتاب ارائه میشود.
معرفی فضای سه بعدی
در حقیقت هر کدام از سه محور مختصات در یک دستگاه مختصات سه بعدی، محوری از اعداد است که میتوانیم روی آن تمام اعداد حقیقی یا را نمایش دهیم. به همین علت کل دستگاه متشکل از سه محور را یک فضای مینامیم. تصویر زیر نحوه قرارگیری محورهای مختصات و صفحات حاصل از تقاطع این محورها در دو فضای و را نشان میدهد:
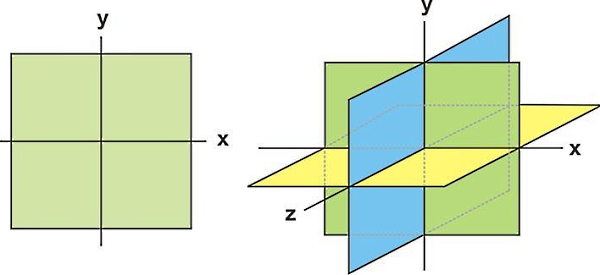
ملاحظه میکنید که در فضای دو بعدی (تصویر سمت چپ) تقاطع دو محور x و y فقط یک صفحه با نام صفحه xy ایجاد کرده است. اما در فضای (تصویر سمت راست) علاوهبر این صفحه، در نتیجه اضافه شدن محور جدیدی به نام محور z، دو صفحه دیگر با عنوان صفحه zx و صفحه yz نیز ایجاد شدهاند. همچنین تصویر زیر نشان میدهد که مختصات یک نقطه در چنین فضایی چگونه تعیین میشود:

طبق این شکل اگر x واحد در راستای محور xها، y واحد در راستای محور yها و z واحد در راستای محور zها پیش برویم، به این نقطه با مختصات میرسیم. در فضای سه بعدی تقاطع محورهای مختصات منجر به شکلگیری هشت ناحیه میشود که علامت هر کدام از سه مولفه x و y و z در آنها در تصویر زیر نشان داده شده است:

یکی دیگر از مهمترین نکات مربوط به فضای سه بعدی فرمول فاصله است. اگر دو نقطه با مختصات و در یک صفحه (صفحه xy) داشته باشیم، فاصله بین این دو نقطه توسط فرمول زیر بهدست میآید:
این فرمول را در فصل آشنایی با مقاطع مخروطی به کرات استفاده کردیم و حالا آن را به فضای تعمیم میدهیم. فاصله بین دو نقطه و توسط فرمول زیر تعیین میشود:
اگر دقت کنید در مورد نقاطی با مختصات و با توجه به صفر بودن مولفههای z، فرمول بالا خود به خود به فرمول فاصله برای دو بعد کاهش مییابد. پس از اینکه یاد گرفتیم چگونه مختصات یک نقطه یا فاصله بین دو نقطه را در یک فضای سه بعدی بررسی کنیم، میخواهیم نتیجه معادله سادهای به شکل را در سه فضای یک، دو و سه بعدی طبق تصویر زیر مقایسه کنیم:
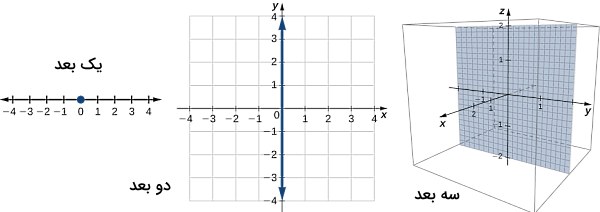
این مقایسه به شما نشان میدهد تفاوت ابعاد چه تغییراتی را در مسائل ایجاد میکند. در یک بعد حاصل معادله تنها یک نقطه است، اما در دو بعد نتیجه برابر است با محور yها و در سه بعد، این معادله به ما صفحه yz را میدهد. به عبارت دیگر، در فضای سه بعدی معادله توصیف کننده تمام نقاطی با مختصات است. به این ترتیب میتوانیم به نتایج زیر برسیم:
- در فضای معادل است با صفحه yz.
- در فضای معادل است با صفحه xz.
- در فضای معادل است با صفحه xy.
همچنین نتایج زیر تعمیمی از یافتههای بالا خواهد بود:
- صفحهای موازی با صفحه xy و شامل نقطه را میتوانیم توسط معادله نمایش دهیم.
- صفحهای موازی با صفحه xz و شامل نقطه را میتوانیم توسط معادله نمایش دهیم.
- صفحهای موازی با صفحه yz و شامل نقطه را میتوانیم توسط معادله نمایش دهیم.
فرمول جمع و تفریق بردارها در دو بعد
پس از آشنایی با فضای دو و سه بعدی و چگونگی نمایش نقاط در هر کدام از این دو فضا، میخواهیم به نمایش بردارها در این دو فضا بپردازیم. هر پارهخط جهتداری که دارای سه مشخصه به نام نقطه ابتدایی، نقطه انتهایی و طول باشد، یک بردار نامیده میشود. نقطه انتهایی یک بردار تعیینکننده جهت آن است.
مهمترین نکاتی که در مورد بردارها در فضای باید بدانیم، به شرح زیر هستند:
- برداری با نقطه ابتدایی ، نقطه انتهایی به شکل نمایش داده میشود.
- اندازه توسط یا نمایش داده میشود که از فرمول فاصله بین این دو نقطه بهدست میآید.
- دو بردار زمانی با هم برابر هستند که همسنگ باشند، یعنی علاوه بر اندازه، جهت آنها نیز کاملا با هم برابر باشد.
- دو بردار موازی دارای اندازه و راستای یکسان هستند، اما جهت آنها ممکن است مانند هم یا مخالف هم باشد.
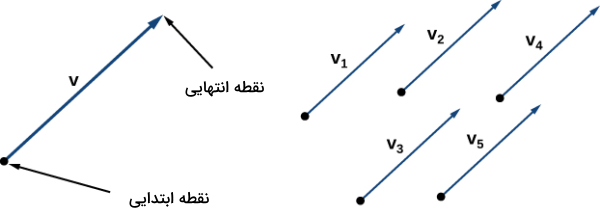
تصویر بالا مشخصات مهم یک بردار را نشان میدهد. همچنین تمام بردارهای تا در این تصویر بردارهایی هماندازه هستند. مفاهیم دیگری که در مورد بردارها باید در نظر بگیریم، ترکیب آنها و عملیات مختلفی است که میتوانیم روی آنها انجام دهیم. در ادامه قوانینی که لازم است در این زمینه بدانید را فهرست کردهایم. ابتدا به ضرب یک عدد یا اسکالر در یک بردار می پردازیم که در تصویر زیر چند نمونه از آن را مشاهده میکنید:
- ضرب یک اسکالر در بردار: برداری است که از حاصلضرب یک عدد مانند در برداری به نام حاصل شده است.
- در ضرب اسکالر در بردار، اگر مثبت باشد، بردار با بردار همجهت است.
- در ضرب اسکالر در بردار، اگر منفی باشد، بردار در خلاف جهت بردار است.
- در ضرب اسکالر در بردار، اگر یا اندازه بردار برابر با صفر باشد، اندازه بردار نیز صفر است.
- قرینه بردار برداری است که از حاصلضرب عدد در بردار حاصل میشود.
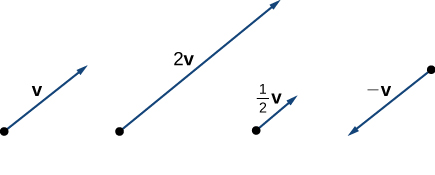
اگر بردار ابتدایی را به شکل در نظر بگیریم، ضرب اعدادی مانند و $$ $$ frac{1}{2} $$ $$ و به نتایجی مطابق تصویر بالا منجر خواهد شد. همچنین ملاحظه میکنید که عدد جزئی از مجموعه اعداد حقیقی است. در مرحله بعد به جمع بردارها در فضای دو بعدی میرسیم. جمع بردارها بهسادگی جمع اعداد نیست، چون در مورد بردارها جهت را نیز باید در نظر بگیریم. دو روش معروف برای جمع دو بردار و ، روش مثلث و روش متوازیالاضلاع است:
- روش متوازیالاضلاع: نقطه ابتدای دو بردار را روی هم قرار میدهیم تا یک متوازیالاضلاع تشکیل شود. قطر این متوازیالاضلاع بردار حاصلجمع است (تصویر سمت راست).
- روش مثلث: دومین بردار را از انتهای بردار اول رسم میکنیم تا یک مثلث تشکیل شود. وتر این مثلث بردار حاصلجمع است (تصویر سمت چپ).
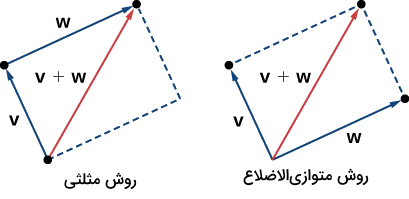
عملیات مهم بعدی در مورد دو بردار تفریق یا کم کردن آنها از هم است که باز هم به یکی از دو روش بالا انجام میشود. بردار معادل است با حاصلجمع بردار و منفی بردار . حالا فرض کنید نقطه ابتدایی بردار مختصاتی بهصورت و نقطه انتهایی آن دارای مختصات باشد، در این صورت مولفههای x و y برای این بردار به شکل زیر خواهد شد:
اگر اندازه هر کدام از دو مولفه بردار بالا را به شکل و در نظر بگیریم، در این صورت برای پیدا کردن اندازه چنین برداری از فرمول زیر میتوانیم استفاده کنیم:
به این ترتیب تمام قوانینی که بالاتر توضیح دادیم، برای دو بردار به شکل و و عدد به شکل زیر میشوند:
- ضرب اسکالر در بردار:
- جمع دو بردار:
- خاصیت جابجایی در جمع دو بردار:
- خاصیت شرکتپذیری جمع سه بردار:
- خاصیت توزیعپذیری در جمع دو بردار:
- حاصلجمع یک بردار با بردار صفر یا عضو خنثی:
- حاصلجمع یک بردار با قرینهاش:
فرمول جمع و تفریق بردارها در سه بعد
در بخش قبل با کلیه نکات و فرمول های هندسه تحلیلی دوازدهم برای مبحث بردارها در فضای آشنا شدیم. با اضافه کردن یک بعد دیگر به فضا، در این بخش کلیه عملیات انجام شده روی بردارها در فضای را با هم مرور و بررسی میکنیم. دقت کنید صورت کلی قوانینی مانند تعریف و قرینه یک بردار، ضرب یک اسکالر در بردار و تساوی یا توازی دو بردار که در بخش قبل توضیح دادیم، همچنان در سه بعد نیز درستاند.
تصویر زیر یک بردار سه بعدی به نام را نشان میدهد که نقطه ابتدایی آن منطبق بر مبدا و نقطه انتهایی آن مختصاتی به شکل دارد. همانطور که ملاحظه میکنید، تمام بردارها در فضای دارای سه مولفه x و y و z هستند:
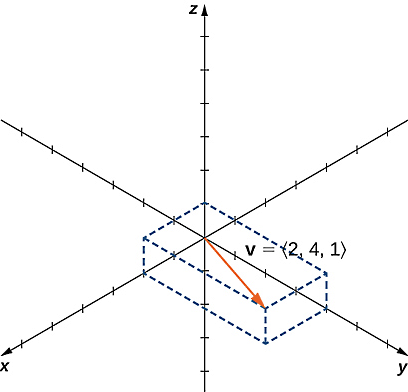
به این ترتیب برای دو بردار به شکل و و عددی مانند عملیات جبری به شکل زیر انجام میشود:
- ضرب اسکالر در بردار:
- جمع دو بردار:
سایر قوانین مانند خاصیت جابجایی، انجمنی، توزیعپذیری و … همگی در این فضا نیز برقراراند.
بردارهای یکه
برای آسانتر شدن محاسبات بردارها میتوانیم از ابزاری به نام بردارهای یکه استفاده کنیم. بردارهای استاندارد یکه طبق جدول زیر تعریف میشوند و ملاحظه میکنید که اندازه هر کدام برابر با واحد است:
| بردار یکه در راستای محور xها | بردار یکه در راستای محور yها | بردار یکه در راستای محور zها |
بنابراین اگر بخواهیم برداری مانند را بر حسب این بردارها بنویسیم، کافی است در کنار هر کدام از مولفهها بردار یکه مناسب با محور مختصات آن را قرار دهیم:
بردار یکه فقط مختص محورهای مختصات نیست. در مورد هر بردار نوعی مانند با شرط صفر نبودن، میتوانیم بردار یکهای به شکل زیر تعریف کنیم:
مثال و تمرین بردارها
در این بخش با مطرح کردن چند سوال و در قالب حل مثال و تمرین به شما کمک میکنیم تا به فرمول های هندسه تحلیلی دوازدهم مرتبط با مباحث این فصل کاملا مسلط شوید.
مثال ۱
- ابتدا تعیین کنید فاصله بین دو نقطه در تصویر زیر چقدر است.
- سپس معادله صفحهای که از نقطه عبور کرده و با صفحه yz موازی است، را بنویسید.
- همچنین معادله صفحهای که از سه نقطه و و عبور میکند را بنویسید.
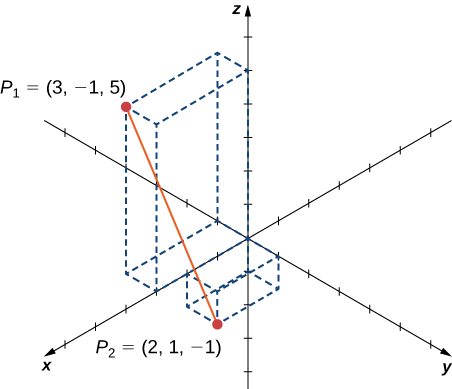
پاسخ
در پاسخ به اولین سوال، مختصات هر یک از دو نقطه در شکل مشخص است. بنابراین برای بهدست آوردن فاصله کافی است فرمول زیر را بنویسیم:
در مورد سوال دوم گفتیم که اگر صفحهای موازی با صفحه yz و شامل نقطهای با مختصات باشد، معادله آن به شکل است. پس در مورد نقطه معادله صفحه میشود . در آخرین سوال این مثال با توجه به اینکه هر سه نقطه داده شده دارای یک مولفه مشترک (مولفه y) هستند، بنابراین معادله مناسب برای صفحهای که از هر سه نقطه بگذرد، است.
مثال ۲
فرض کنید نقاط و را به شکل زیر داریم و خط متصلکننده این دو نقطه معادل است با قطر یک کره. معادله این کره را پیدا کنید: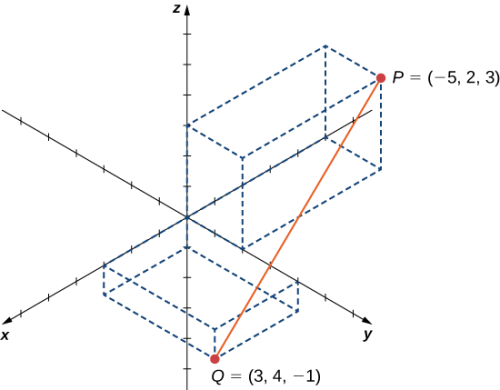
پاسخ
برای اینکه معادله یک کره را بنویسیم، کافی است از معادله دایره در بخش قبل استفاده کنیم و آن را به سه بعد تعمیم دهیم. معادله دایرهای با مرکز و شعاع به شکل زیر است:
برای رسیدن به معادله یک کره که معادل سه بعدی یک دایره است، کافی است یک بعد دیگر به این معادله اضافه کنیم:
این معادله با در نظر گرفتن دو نقطه و بهدست میآید که در آن مختصات مرکز کره است. پس برای اینکه معادله کره متناظر با این مسئله را بنویسیم لازم است شعاع و مرکز کره را بهدست آوریم. ابتدا نصف قطر کره را که از فرمول فاصله بین دو نقطه بهدست میآید، محاسبه میکنیم تا شعاع کره حاصل شود:
سپس مختصات مرکز کره را تعیین میکنیم، با در نظر گرفتن این نکته که مرکز کره دقیقا در وسط قطر آن قرار میگیرد. بنابراین اگر میانگین دو مولفه x را برای هر دو نقطه و به همین شکل میانگین دو مولفه y و z را برای هر دو نقطه محاسبه کنیم، مختصات مرکز کره تعیین میشود:
بنابراین معادله کره با توجه به اینکه و شدند، به شکل زیر نمایش داده میشود:
مثال ۳
اگر نقطه ابتدایی بردار معادل با و نقطه انتهایی آن باشد و بدانیم ، به سوالات زیر پاسخ دهید:
- بردار را در قالب مولفههای آن بنویسید و اندازه آن را بهدست آورید:
- و و را نیز محاسبه کنید:
پاسخ
نوشتن بردار در قالب مولفههایش با توجه به مختصات دو نقطه داده شده توسط فرمول زیر انجام میشود:
اندازه چنین برداری برابر میشود با:
در سوال دوم باید عملیات خواسته شده روی بردارهای صورت سوال را انجام دهیم:
مثال ۴
اگر بدانیم و ، بردارها و مقادیر عددی خواسته شده را بهدست آورید:
- بردار یکه در راستای
پاسخ
در مورد اولین سوال، باید ابتدا اعداد داده شده را در بردارها ضرب کنیم، سپس بردارهای بهدست آمده را از هم کم کنیم:
در سوال دوم نگاهی به مجموعه فرمول های هندسه تحلیلی دوازدهم میاندازیم. ابتدا اندازه بردار را محاسبه کرده و سپس پاسخ را در عدد پنج ضرب میکنیم:
در سوال سوم، اندازه حاصلضرب اسکالر در بردار خواسته شده است. پس به شکل زیر عمل میکنیم:
به تفاوت پاسخها در این سوال و سوال قبل دقت کنید. در نهایت بردار یکه را در راستای بردار میخواهیم:
تمرین
معادله صفحه عبوری از نقطه و موازی با صفحه xy معادل کدام گزینه است؟
گزینه اول درست است. با توجه به اینکه گفتیم صفحهای موازی با صفحه xy و شامل نقطه را میتوانیم توسط معادله نمایش دهیم، برای نقطه معادله صفحه موردنظر ما میشود .
یادگیری هندسه در سطوح پیشرفته با فرادرس
در این بخش قصد داریم چند دوره آموزشی از مجموعه فرادرس را به شما معرفی کنیم که شامل مباحث پیشرفتهتری از هندسه مانند هندسه منیفلد است. همچنین در کلیه کتابهای ریاضی عمومی ۲ نیز موضوعاتی مشابه با موضوعات این مطلب مطرح شده است. مشاهده این فیلمهای آموزشی به شما کمک میکند تا در صورت تمایل یادگیری خود را به این سطح گسترش دهید، بهویژه اینکه دسترسی برخی از این فیلمها بهصورت رایگان است و در هر کدام روی یک مبحث خاص تمرکز شده است تا بتوانید با تمرین و توضیح بیشتر، کاملا به آن بخش تسلط پیدا کنید:
فرمول های حاصلضرب بردارها
آخرین مبحث کتاب درسی هندسه سه رشته ریاضی به توضیح ضرب داخلی و خارجی بردارها اختصاص دارد. مهمترین فرمول های هندسه تحلیلی دوازدهم مرتبط با این موضوع در جدول زیر فهرست شده است:
| ضرب داخلی دو بردار و با زاویه | |
| ضرب خارجی دو بردار و با زاویه | |
| خاصیت جابجایی در ضرب داخلی | |
| خاصیت توزیعپذیری در ضرب داخلی | |
| خاصیت شرکتپذیری در ضرب داخلی | |
| ضرب داخلی یک بردار در خودش | |
| زاویه بین دو بردار | |
| ضرب داخلی دو بردار غیرصفر و عمود بر هم | |
| تصویر در راستای | |
| خاصیت جابجایی در ضرب خارجی | |
| خاصیت توزیعپذیری در ضرب خارجی | |
| خاصیت شرکتپذیری در ضرب خارجی | |
| ضرب خارجی یک بردار در خودش | |
| حجم متوازیالسطوح ساخته شده توسط سه بردار |
ضرب داخلی و خارجی موجب سادهسازی بسیاری از مسائل و فرمولبندیها در علوم مختلفی از جمله فیزیک، مهندسی و اقتصاد شده است. برای مثال، حاصلضرب داخلی دو بردار نیرو و جابجایی فرمول کار در فیزیک را میدهد، در حالی که از ضرب خارجی این دو بردار به یک کمیت برداری به نام گشتاور نیرو میرسیم.
فرمول ضرب داخلی بردارها
ضرب داخلی دو بردار که با ضرب دات هم شناخته میشود، برای دو بردار به شکل و بهصورت زیر تعریف میشود:
مسلما اگر دو بردار و در چنین ضربی دو بردار دو بعدی باشند، این فرمول به شکل زیر کاهش خواهد یافت:
نکته مهمی که باید در نظر داشته باشیم این است که در عملیات جبری مانند جمع و تفریق بردارها حاصجمع یا اختلاف یک بردار میشد. اما در مورد ضرب بردارها بردار بودن پاسخ کاملا به نوع ضرب بستگی دارد. در ضرب داخلی دو بردار، حاصلضرب همیشه یک عدد یا اسکالر است و به همین دلیل این نوع ضرب را ضرب عددی، اسکالر یا نردهای هم مینامند. اثبات فرمول بالا با کمک گرفتن از قاعده کسینوسها انجام میشود. همچنین خواص زیر برای ضرب داخلی دو بردار برقرار هستند ( یک عدد است):
- خاصیت جابجایی در ضرب داخلی:
- خاصیت توزیعپذیری در ضرب داخلی:
- خاصیت شرکتپذیری در ضرب داخلی:
- ضرب داخلی یک بردار در خودش:
از آخرین نکته به این نتیجه میرسیم که اگر ضرب داخلی برداری در خودش صفر شد، خود آن بردار برابر با صفر است. همچنین تعریف هندسی ضرب داخلی دو بردار که زاویهای برابر با دارند، به شکل زیر است:
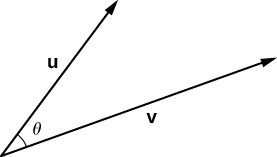
از این فرمول مهم به نتایج زیر میرسیم:
- زاویه در فرمول بالا همواره در نامساوی صدق میکند.
- کسینوس زاویه بین دو بردار برابر است با .
- دو بردار غیرصفر و عمود بر هم هستند، اگر و فقط اگر .
در انتهای بررسی فرمول های هندسه تحلیلی دوازدهم مرتبط با مبحث ضرب داخلی بردارها، با موضوعی به نام «تصویر بردارها» آشنا میشویم. تصویر برداری مانند روی بردار مطابق شکل زیر تعریف میشود:
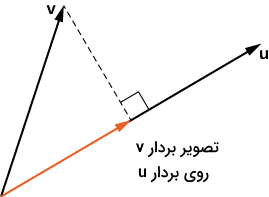
همانطور که ملاحظه میکنید، مولفه حاصل از تصویر کردن روی ، برداری است همجهت با و با نقطه شروعی منطبق بر نقطه شروع این بردار. این بردار در حقیقت مولفهای از است که در راستای عمل میکند. از این نکته در تجزیه بردارها و پیدا کردن مولفههای مختلف یک بردار استفاده میشود. اگر زاویه بین دو بردار و در شکل بالا باشد، در این صورت اندازه تصویر در راستای دارای فرمول زیر است:
در حالی که شکل برداری آن بهصورت زیر است:
فرمول ضرب خارجی بردارها
محاسبه حاصلضرب خارجی یا ضرب برداری بردارها در مقایسه با ضرب داخلی آنها پیچیدهتر است و در آخرین بخش این مطلب از مجله فرادرس به توضیح این موضوع میپردازیم. در ضرب خارجی دو بردار، حاصلضرب به شکل برداری عمود بر دو بردار اولیه است. بنابراین خروجی این نوع ضرب برداری برخلاف ضرب داخلی که یک عدد بود، بردار است. اگر دو بردار غیرصفر و در هم ضرب خارجی شوند، حاصل بهشکل زیر تعیین میشود:
دقت کنید ضرب خارجی و داخلی بهترتیب با علامتهای و از هم متمایز میشوند. همچنین برای تعیین جهت بردار حاصلضرب باید از قاعده دست راست به شکل زیر استفاده کنیم. ابتدا انگشتان خود را در جهت بردار اول قرار میدهیم. با چرخش انگشتان به سمت دومین بردار، جهت انگشت شست تعیین کننده جهت حاصلضرب است:
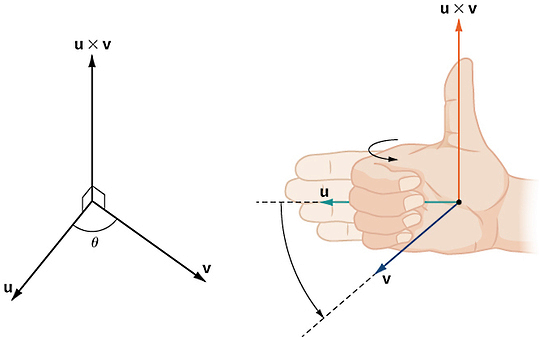
بهعلاوه با در نظر گرفتن بهعنوان یک عدد برای ضرب خارجی دو بردار غیرصفر و داریم:
- خاصیت جابجایی در ضرب خارجی:
- خاصیت توزیعپذیری در ضرب خارجی:
- خاصیت شرکتپذیری در ضرب خارجی:
- ضرب خارجی یک بردار در خودش:
همچنین دو قانون مهم زیر را برای ضربهای سهگانه داریم:
اولین فرمول توصیفکننده ضرب سهگانه عددی است، در حالی که فرمول دوم برای محاسبه ضرب برداری سهگانه بکار میرود. همچنین شکل هندسی ضرب خارجی دو بردار با زاویه توسط فرمول زیر توصیف میشود:
در بخش مثالها نشان میدهیم که چگونه میتوانیم ضرب خارجی دو بردار را توسط دترمینانگیری محاسبه کنیم. یکی از مهمترین کاربردهای ضرب داخلی و خارجی، محاسبه آسان حجم متوازیالسطوحی به شکل زیر است که از سه بردار و و ساخته شده است:
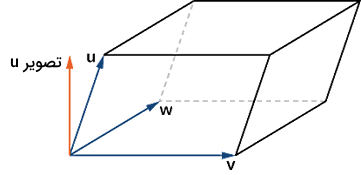
ضرب بالا همان ضرب سهگانه داخلی است که بالاتر فرمول حالت کلی آن را بیان کردیم. حاصل چنین ضربی یک عدد است، همچنان که انتظار داریم حجم فقط اندازه داشته باشد، نه جهت.
فرمول ضرب بردارهای یکه
اگر در محاسبات ضرب برداری بردارهای داده شده بر حسب بردارهای یکه نوشته شده باشند، لازم است حاصلضرب داخلی و خارجی این بردارها را بدانیم. در ادامه روابط مهم در ضرب خارجی بردارهای یکه را فهرست کردهایم:
همچنین برای ضرب داخلی این بردارها روابط زیر را داریم:
مثال و تمرین ضرب بردارها
با حل مثالهای این بخش بهتر متوجه میشوید که چگونه میتوانیم محاسبات مربوط به هر کدام از این دو نوع ضرب را با انتخاب فرمول مناسب از مجموعه فرمول های هندسه تحلیلی دوازدهم به درستی انجام دهیم.
مثال ۱
- حاصلضرب داخلی را برای بردارهای و پیدا کنید:
- اگر باشد، را محاسبه کنید:
پاسخ
با نوشتن فرمول ضرب داخلی به شکل زیر پیش میرویم:
در مورد سوال دوم، ابتدا باید را پیدا کنیم:
حالا باید ضرب اسکالر را در بردار انجام دهیم:
مثال ۲
زاویه بین دو بردار و چقدر است؟
پاسخ
از فرمول استفاده میکنیم:
مثال ۳
اگر و باشند، بردار یکه عمود بر این دو بردار را پیدا کنید:
پاسخ
میدانیم حاصلضرب خارجی این دو بردار برداری است که به هر دو عمود است. پس ابتدا با محاسبه دترمینان زیر حاصلضرب خارجی را پیدا میکنیم:
$$ = left|begin{array}\2&-1\-1&4end{array}right|hat{i} $$
$$ – left|begin{array}\5&-1\0&4end{array}right|hat{j} $$
$$ + left|begin{array}\5&2\0&-1end{array}right|hat{k} $$
دترمینان بالا به سه دترمینان دیگر تبدیل شد که حاصل آن به شکل زیر میشود:
اما در صورت سوال بردار یکه عمود بر این دو بردار خواسته شده است، نه خود بردار. پس لازم است بردار یکه متناظر با بردار را به روش زیر و با تقسیم بردار حاصل به اندازهاش بهدست آوریم:
تمرین ۱
مقدار چقدر باشد تا بردار عمود بر بردار باشد؟
گزینه دوم درست است. گفتیم شرط عمود بودن دو بردار این است که ضرب داخلی آنها صفر شود. با صفر قرار دادن این حاصلضرب به معادلهای میرسیم که را به ما میدهد:
تمرین ۲
حاصل برابر با کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
source
