در مطالب قبلی مجله فرادرس در مورد مفهوم مشتق و دیفرانسیل و تفاوت آنها صحبت کردیم. در این مقاله قصد داریم به یکی دیگر از مفاهیم مرتبط با این مباحث یعنی آهنگ تغییرات یا Rate of Change بپردازیم. آهنگ تغییرات در ریاضی توصیفکننده چگونگی رفتار یک تابع است و نشان میدهد تابع موردنظر ما در چه بازههایی صعودی یا نزولی است. به بیان دقیقتر، اگر مشتق تابعی مانند را با نشان دهیم، این عبارت همان آهنگ تغییرات کمیت نسبت به کمیت است.

در اولین بخش این نوشته کاملتر توضیح دادهایم که آهنگ تغییرات چیست. بخش دوم به معرفی و حل مثال و تمرین از فرمول متوسط آهنگ تغییرات اختصاص دارد. سپس کاربردهای آهنگ تغییرات در ریاضیات را بیان کردهایم که شامل تعیین صعودی یا نزولی بودن یا بهدست آوردن نقاط اکسترمم نسبی و مطلق یک تابع است. همچنین توضیح دادهایم آهنگ تغییرات لحظهای و متوسط چه تفاوتی با هم دارند و چگونه میتوانیم مسائل مربوط به این مفهوم را به کمک مشتقگیری حل کنیم. با حل و بررسی مثالها و آزمونی که در این مطلب برای شما تهیه شده است میتوانید به کلیه سوالات در زمینه آهنگ تغییرات و کاربردهای آن مسلط شوید.
آهنگ تغییرات در ریاضی چیست؟
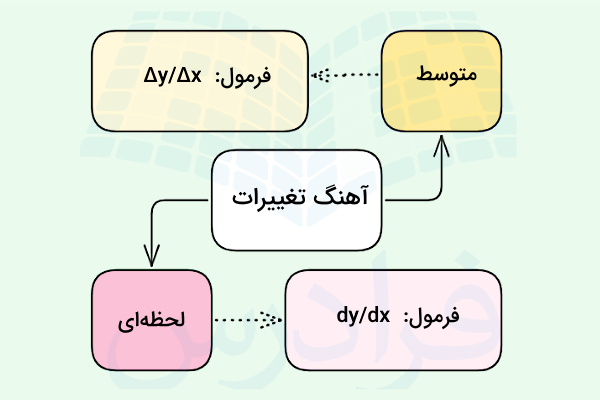
آهنگ تغییرات یا نرخ تغییرات چگونگی تغییرات خروجی یک تابع نسبت به تغییرات ورودی آن را توصیف میکند. متوسط آهنگ تغییرات برای تابعی مانند و روی بازه معادل است با . این فرمول شیب خط متصل کننده دو نقطه متناظر با ابتدا و انتهای بازه (شیب خط سکانت) را به ما میدهد. اما آهنگ تغییرات آنی یا لحظهای توسط فرمول محاسبه میشود که همان مشتق یا شیب خط مماس بر نمودار تابع است.
در درس ریاضی پس از آشنایی با مفهوم تابع و ویژگیهای آن مانند دامنه و برد، زوج یا فرد بودن، یک به یک یا پوشا بودن میرسیم به مبحث بررسی آهنگ تغییرات یک تابع. آهنگ تغییرات یک تابع اطلاعات جالبتوجهی در مورد آن تابع به ما میدهد که میتوانیم از این اطلاعات در زمینه شناسایی نقاطی که تابع موردنظر ما صعودی یا نزولی است یا در تعیین اکسترممهای نسبی و مطلق و وضعیت تقعر آن استفاده کنیم. به عبارت دیگر، بررسی و تحلیل آهنگ تغییرات یک تابع به ما نشان میدهد رفتار آن تابع چگونه است.
یادگیری درس حسابان با فرادرس
در ریاضی متوسطه مفاهیمی مانند آهنگ تغییرات، حد، مشتق، دیفرانسیل و مقدمات انتگرال در درسی به نام «حسابان» مطرح میشوند. به همین دلیل در این قسمت قصد داریم چند فیلم آموزشی در مورد این کتاب درسی به شما معرفی کنیم که در مجموعه فرادرس تهیه شدهاند. مشاهده این فیلمها به شما کمک میکند تا با بهرهگیری از آموزش تصویری و حل مثالها و تمرینهای متنوع به مباحثی مانند آهنگ تغییرات و کاربردهای آن کاملا مسلط شوید:
متوسط آهنگ تغییرات یک تابع چیست و چه فرمولی دارد؟
در این بخش ابتدا با یک مثال توضیح میدهیم آهنگ تغییرات یک تابع چیست و چه اطلاعاتی به ما میدهد. سپس متوسط آهنگ تغییرات و فرمول آن را معرفی میکنیم. فرض کنید جدول زیر متوسط هزینه یک گالن بنزین در سالهای ۲۰۰۵ تا ۲۰۱۲ را نشان میدهد. اگر قیمت بنزین را بهصورت تابعی از سال نشان دهیم، میتوانیم تحلیل بهتری از نوسانات قیمت بنزین در این سالها ارائه دهیم.
با نگاه اجمالی به جدول زیر متوجه خواهید شد که روند کلی تغییرات قسمت بنزین از سال ۲۰۰۵ تا ۲۰۱۲ به صورت افزایشی بوده است. حتی میتوانیم بگوییم این افزایش قیمت با دلار برابر است. اما جالبتر از این نتیجهگیری این است که نشان دهیم قیمت بنزین سالانه چگونه تغییر میکند. تغییر قیمت بنزین به ازای هر سال را آهنگ تغییرات مینامیم. این پارامتر توصیف کننده چگونگی تغییرات خروجی تابع نسبت به ورودی آن است.
| سال () | قیمت بنزین بر حسب دلار () |
| ۲۰۰۵ | ۲٫۳۱ |
| ۲۰۰۶ | ۲٫۶۲ |
| ۲۰۰۷ | ۲٫۸۴ |
| ۲۰۰۸ | ۳٫۳۰ |
| ۲۰۰۹ | ۲٫۴۱ |
| ۲۰۱۰ | ۲٫۸۴ |
| ۲۰۱۱ | ۳٫۵۸ |
| ۲۰۱۲ | ۳٫۶۸ |
با کمی دقت ملاحظه میکنید که تغییرات قیمت بنزین در هر سال با سال دیگر متفاوت است. بنابراین میتوانیم به این نتیجه برسیم که در این مثال آهنگ تغییرات ثابت نیست و این نکته در تحلیل مسئله به ما کمک زیادی خواهد کرد. در ادامه توضیح میدهیم فرمولبندی و روش محاسبه آهنگ تغییرات یک تابع چگونه است.
اگر بدون توجه به اینکه آهنگ تغییرات در مثال قبل ثابت نیست، فقط و فقط به نقاط شروع و پایان در تغییرات قیمت بنزین طی سالهای ۲۰۰۵ تا ۲۰۱۲ توجه کنیم، در این صورت «متوسط آهنگ تغییرات» را در این بازه زمانی در نظر گرفتهایم. محاسبه متوسط آهنگ تغییرات یک تابع توسط فرمول زیر امکانپذیر است:
تغییرات خروجی تقسیم بر تغییرات ورودی تابع = متوسط آهنگ تغییرات تابع
در این فرمولبندی از حرف یونانی دلتا برای نشان دادن تغییرات یک کمیت استفاده کردهایم. عموما برای تابعی که بهصورت تعریف میشود، بهجای میتوانیم از استفاده کنیم، در هر دو حالت این دو عبارت نشان دهنده تغییرات مقادیر خروجی تابع بر اساس تغییرات ورودی آن هستند. حالا به مثال بالا برمیگردیم. در این مثال افزایش قیمت بنزین از شروع بازه موردنظر ما یعنی سال ۲۰۰۵ تا انتهای این بازه یعنی سال ۲۰۱۲ معادل با متوسط آهنگ تغییراتی بهصورت زیر است:
این محاسبه به ما نشان میدهد بهطور متوسط قیمت بنزین حدود ۰٫۱۹۶ دلار در هر سال افزایش داشته است. پس اگر مقادیر یک تابع را به ازای نقاط مختلف داشته باشیم، روند محاسبه متوسط آهنگ تغییرات آن تابع در بازهای بین دو مقدار و بهصورت زیر است:
- محاسبه اختلاف دو خروجی متناظر با نقاط ابتدا و انتهای بازه:
- محاسبه اختلاف نقاط ابتدا و انتهای بازه:
- یافتن نسبت دو عدد بالا:
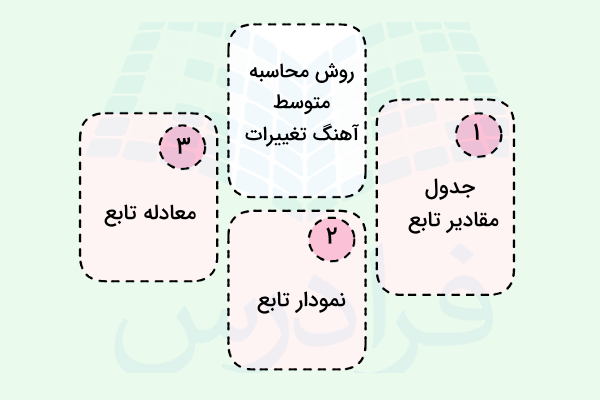
نمودار زیر نشان میدهد روشهای مختلف محاسبه متوسط آهنگ تغییرات چیست.
حل مثال و تمرین از محاسبه متوسط آهنگ تغییرات
در این بخش به حل و بررسی چند مثال در زمینه محاسبه متوسط آهنگ تغییرات یک تابع خواهیم پرداخت. خواهید دید که میتوانیم این محاسبه را با کمک گرفتن از جدول مقادیر تابع، از روی نمودار آن و یا با توجه به معادله یا ضابطه تابع انجام دهیم.
مثال ۱
متوسط آهنگ تغییرات را برای مثال این بخش در دو بازه ۲۰۰۷ تا ۲۰۰۹ و ۲۰۰۵ تا ۲۰۱۰ پیدا کنید:
پاسخ
برای پاسخ به این سوال کافی است از روی جدول، خروجی متناظر با هر کدام از سالهای ۲۰۰۷ و ۲۰۰۹ را بهعنوان اولین بازه و ۲۰۰۵ و ۲۰۱۰ را بهعنوان دومین بازه پیدا کنیم و سپس طبق روشی که توضیح داده شد، پیش برویم:
- محاسبه اختلاف دو خروجی متناظر با نقاط ابتدا و انتهای بازه:
- محاسبه اختلاف نقاط ابتدا و انتهای بازه:
- یافتن نسبت دو عدد بالا:
ملاحظه میکنید که متوسط آهنگ تغییرات بین سالهای ۲۰۰۷ تا ۲۰۰۹ منفی است. اما برای بازه بعدی حاصل محاسبات مثبت خواهد شد:
- محاسبه اختلاف دو خروجی متناظر با نقاط ابتدا و انتهای بازه:
- محاسبه اختلاف نقاط ابتدا و انتهای بازه:
- یافتن نسبت دو عدد بالا:
مثال ۲
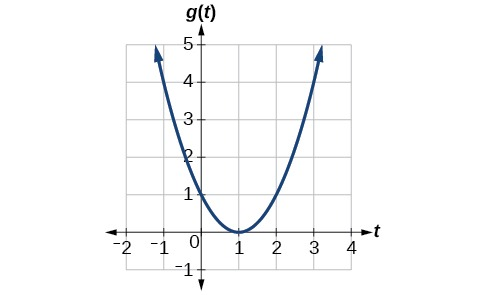
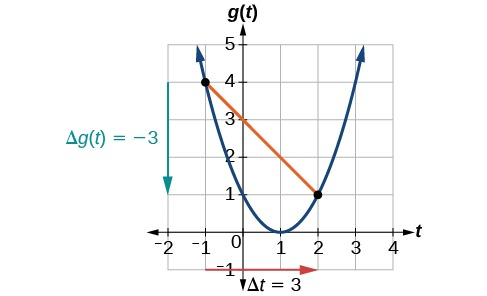
با توجه به نمودار تابع به شکل زیر، متوسط آهنگ تغییرات این تابع را در بازه بهدست آورید:
پاسخ
محاسبه متوسط آهنگ تغییرات در این مثال هم به شیوه سوال قبلی است، با این تفاوت که در اینجا لازم است مقادیر تابع یا خروجیهای موردنظر خود را با توجه به نمودار آن مشخص کنیم. ابتدا باید نقطه ابتدای بازه یعنی را در نظر بگیریم. خروجی متناظر با این نقطه طبق نمودار برابر است با . همچنین انتهای بازه یعنی متناظر میشود با . بنابراین خواهیم داشت:
- محاسبه اختلاف دو خروجی متناظر با نقاط ابتدا و انتهای بازه:
- محاسبه اختلاف نقاط ابتدا و انتهای بازه:
- یافتن نسبت دو عدد بالا:
تصویر زیر این روند را نشان میدهد. خط افقی قرمز رنگ نشان دهنده تغییرات مقادیر ورودی تابع یا است، در حالی که خط عمودی سبز رنگ یا تغییرات خروجی تابع یا مقادیر متناظر با ابتدا و انتهای بازه را نشان میدهد. به این ترتیب حاصل تقسیم این دو مقدار نشان میدهد متوسط آهنگ تغییرات تابع در این بازه منفی است. دقت کنید برای محاسبه آهنگ تغییرات، ترتیب مقادیر اولیه و نهایی بسیار مهم و تعیین کننده است.
مثال ۳
فرض کنید آلیس با شروع رانندگی از خانه، فاصله خود از خانه را همزمان با گذر زمان در قالب جدول زیر ثبت کرده است. سرعت متوسط حرکت او در شش ساعت اولیه رانندگیاش چقدر است؟
| زمان (ساعت) () | فاصله (مایل) () |
| ۰ | ۱۰ |
| ۱ | ۵۵ |
| ۲ | ۹۰ |
| ۳ | ۱۵۳ |
| ۴ | ۲۱۴ |
| ۵ | ۲۴۰ |
| ۶ | ۲۹۲ |
| ۷ | ۳۰۰ |
پاسخ
در این مثال نمونهای از کاربرد مفهوم آهنگ تغییرات در بررسی یک کمیت فیزیکی به نام سرعت نشان داده شده است. سرعت در فیزیک به معنایی جابجایی یا تغییر مکان یک جسم یا ذره در گذر زمان است. بنابراین اگر تعریف سرعت را با آهنگ تعییرات مقایسه کنیم، میتوانیم بگوییم سرعت در فیزیک همان آهنگ تغییرات مکان نسبت به زمان است. با توجه به اینکه فرمول آهنگ تغییرات در حقیقت متوسط این کمیت را به ما میدهد، پس در اینجا هم آنچه که محاسبه میشود همان سرعت متوسط آلیس است. طبق آنچه که در سوال از ما خواسته شده، لازم است انتهای ساعت اول و ششم رانندگی آلیس را در نظر بگیریم که به ترتیب متناظر است با فواصل ۱۰ و ۲۹۲ مایل:
- محاسبه اختلاف دو خروجی متناظر با نقاط ابتدا و انتهای بازه:
- محاسبه اختلاف نقاط ابتدا و انتهای بازه:
- یافتن نسبت دو عدد بالا:
به این ترتیب سرعت متوسط یا متوسط آهنگ تغییرات فاصله آلیس در گذر زمان برای این بازه برابر شد با ۴۷ مایل بر ساعت. دقت کنید در این سوال سرعت حرکت آلیس ثابت نیست و به همین دلیل متوسط سرعت او به بازهای که انتخاب میکنیم، بستگی دارد. برای نمونه، سرعت متوسط آلیس در بازه مقدار متفاوتی میشود و به شکل زیر بهدست میآید:
- محاسبه اختلاف دو خروجی متناظر با نقاط ابتدا و انتهای بازه:
- محاسبه اختلاف نقاط ابتدا و انتهای بازه:
- یافتن نسبت دو عدد بالا:
مثال ۴
متوسط آهنگ تغییرات تابعی با معادله روی بازه بسته چه معادلهای دارد و پاسخ بهدست آمده به چه معنا است؟
پاسخ
در این سوال ضابطه تابع داده شده است. کافی است نقاط ابتدا و انتهای بازه داده شده را در نظر گرفته و مقادیر متناظر با این نقاط را حساب کنیم:
همانطور که ملاحظه میکنید، نقطه انتهایی بازه داده شده خودش یک مجهول بهصورت است. بدون اینکه به این نکته توجه کنیم، محاسبات خود را ادامه میدهیم:
- محاسبه اختلاف دو خروجی متناظر با نقاط ابتدا و انتهای بازه:
- محاسبه اختلاف نقاط ابتدا و انتهای بازه:
- یافتن نسبت دو عدد بالا:
در سادهسازی آخرین رابطه از اتحاد جمله مشترک کمک گرفتیم. پاسخ بهدست آمده بر حسب مجهول و همان معادله موردنظر در سوال برای متوسط آهنگ تغییرات تابع است. این پاسخ به این معنا است که اگر در نظر گرفته شود، یعنی بازه ما به شکل است و در نتیجه متوسط آهنگ تغییرات تابع میشود.
تمرین ۱
متوسط آهنگ تغییرات تابعی با معادله در بازه برابر با کدام گزینه است؟
گزینه دوم درست است. کافی است ابتدا مقادیر متناظر با ابتدا و انتهای بازه داده شده را بر اساس معادله تابع بهدست آوریم:
حالا طبق روشی که گفتیم، پیش میرویم:
- محاسبه اختلاف دو خروجی متناظر با نقاط ابتدا و انتهای بازه:
- محاسبه اختلاف نقاط ابتدا و انتهای بازه:
- یافتن نسبت دو عدد بالا:
تمرین ۲
نیروی الکتروستاتیکی در فیزیک با نماد نشان داده شده و بر حسب نیوتن اندازهگیری میشود. اگر رابطه این نیرو با فاصله بین دو ذره باردار یا که بر حسب سانتیمتر اندازهگیری میشود، به شکل باشد، متوسط آهنگ تغییرات این نیرو چند نیوتن بر سانتیمتر است، اگر فاصله بین دو ذره باردار از به افزایش داده شود؟
گزینه چهارم صحیح است. برای محاسبه متوسط آهنگ تغییرات در این سوال با توجه به اینکه ضابطه تابع موردنظر یعنی تابع نیرو مشخص است، کافی است ابتدا و انتهای بازه خود را مشخص کنیم. این دو نقطه همان فواصل و هستند. پس ابتدا مقادیر متناظر با این دو را مشخص میکنیم:
حالا میتوانیم به روش قبل ادامه دهیم:
- محاسبه اختلاف دو خروجی متناظر با نقاط ابتدا و انتهای بازه:
- محاسبه اختلاف نقاط ابتدا و انتهای بازه:
- یافتن نسبت دو عدد بالا:
آهنگ متوسط تغییر و آهنگ لحظهای تغییر
در بخش قبل فرمول متوسط آهنگ تغییرات برای یک تابع را معرفی کردیم. در این بخش مجددا به آن فرمول بازمیگردیم و توضیح میدهیم تفاوت متوسط آهنگ تغییرات با آهنگ تغییرات لحظهای یا آنی چیست. متوسط آهنگ تغییرات تابعی مانند روی بازه معادل است با فرمول زیر:
تصویر زیر دو نقطه ابتدا و انتهای بازه و مقادیر متناظر با آنها را نشان میدهد. متوسط آهنگ تغییرات تابع در این بازه معادل است با شیب خطی که از این دو نقطه عبور کرده است. چنین خطی را «خط سکانت» مینامیم. با توجه به اینکه شیب خط سکانت برای هر دو نقطه فرضی ممکن است متفاوت باشد، پس متوسط آهنگ تغییرات نیز بسته به بازهای که مدنظر داریم، متفاوت است.
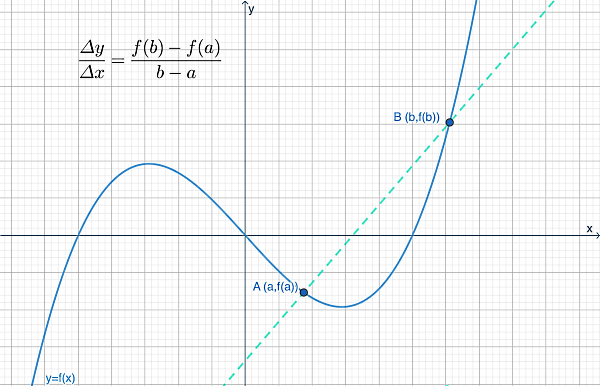
حالا فرض کنید بازه موردنظر ما بسیار بسیار کوچک شود. در این حالت دو نقطه ابتدا و انتهای بازه بسیار به هم نزدیک هستند و خط متصل کننده آنها یا خط سکانت به خط مماس بر نمودار در یک نقطه نزدیک میشود. هر چه انتخاب بازه ما کوچکتر باشد، این خط سکانت بیشتر به خط مماس نزدیک میشود. این نوع نزدیک شدن در ریاضیات با مفهومی به نام «میل کردن یا حدگیری» بیان میشود.
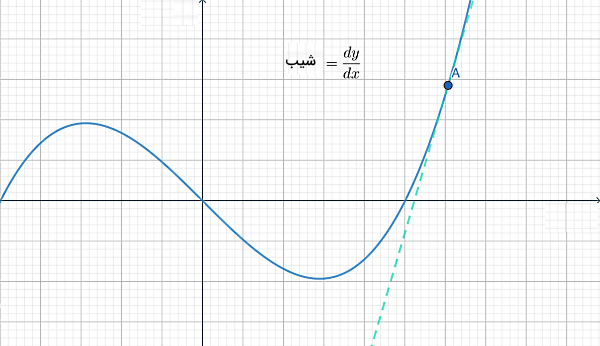
تصویر بالا نشان میدهد آهنگ تغییرات لحظهای برای بررسی روند تغییرات یک تابع در یک نقطه بکار میرود. به این ترتیب آهنگ تغییرات آنی تابعی مانند در نقطهای با مختصات معادل است با . این فرمول با حدگیری از فرمول متوسط آهنگ تغییرات بهدست میآید و این موضوع را در ادامه نشان میدهیم.
فرض کنید نقاط و در تصویر ابتدای این بخش را به هم نزدیک و نزدیکتر کنیم. اگر این روند را ادامه دهیم، این دو نقطه در نهایت به یک نقطه تبدیل خواهند شد. اما بهتر است برای اینکه دقیقتر پیش برویم، نزدیک کردن نقاط را با مفهوم حد نشان دهیم که به معنای نزدیکی دو نقطه و یکی نبودن آنها است ( و ). با کم شدن فاصله بین این دو نقطه، همانطور که اشاره شد، خط متصل کننده آنها نیز به خط مماس تبدیل میشود.
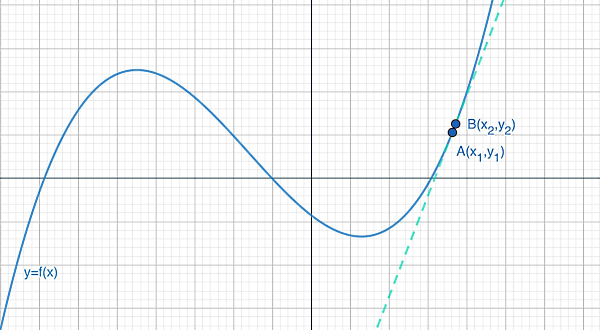
اگر مختصات نقطه را با و مختصات نقطه را با نشان دهیم، روند تبدیل آهنگ تغییرات متوسط به لحظهای به شکل زیر است:
کاربردهای آهنگ تغییرات در ریاضی چیست؟
پس از اینکه با روشهای محاسبه متوسط آهنگ تغییرات آشنا شدیم، در این بخش قصد داریم کاربردهای آهنگ تغییرات را در بررسی نمودار یک تابع و نتایجی که میتوان از این تحلیل استخراج کرد، توضیح دهیم. برای مثال، یکی از این کاربردها تشخیص صعودی یا نزولی بودن یک تابع با توجه به آهنگ تغییرات آن در یک بازه خاص است.
در ادامه راجعبه این کاربردها بیشتر صحبت خواهیم کرد اما در همین راستا، فیلم آموزش ریاضی عمومی ۱ – مرور و حل مساله فرادرس میتواند مسیر یادگیری این مبحث را برای شما هموارتر کند. لینک مشاهده این فیلم آموزشی در ادامه آورده شده است:
تشخیص صعودی یا نزولی بودن یک تابع
ابتدا باید ببینیم صعودی یا نزولی بودن یک تابع با آهنگ تغییرات آن چه ارتباطی دارد. زمانی یک تابع را در یک بازه خاص صعودی در نظر میگیریم که همزمان با افزایش مقادیر ورودی آن، خروجی نیز زیاد شود. در مقابل، اگر همزمان با افزایش مقادیر ورودی یک تابع روی یک بازه خاص، تغییرات خروجی آن کاهشی باشد، در این صورت این تابع یک تابع نزولی است. به این ترتیب متوسط آهنگ تغییرات برای یک تابع صعودی همواره مثبت است، در حالی که برای یک تابع نزولی این کمیت منفی است.
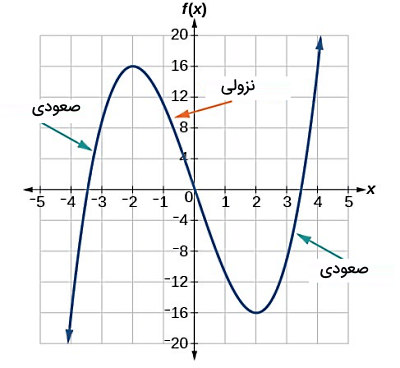
تصویر بالا نشان میدهد یک تابع میتواند در بازههای مختلف رفتار متفاوتی از نظر صعودی یا نزولی بودن داشته باشد. این نمودار مربوط به تابعی با معادله است که در بازه باز نزولی و در اجتماع دو بازه باز صعودی است. البته توابعی هم داریم که در سرتاسر دامنه خود فقط صعودی یا فقط نزولی هستند. همچنین واضح است که اگر تابعی روی یک بازه مشخص نه صعودی باشد و نه نزولی، به آن یک «تابع ثابت» میگوییم. جدول زیر وضعیت صعودی یا نزولی بودن برخی توابع را روی دامنه آنها نشان میدهد:
| نام تابع | صعودی یا نزولی بودن | نمودار تابع |
| تابع ثابت
|
نه صعودی و نه نزولی |
 |
| تابع همانی
|
صعودی |
 |
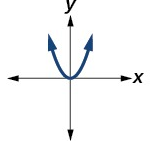
| تابع درجه دو
|
در صعودی
در نزولی در مینیمم |
 |
تعیین اکسترمم های نسبی یک تابع
در مورد توابعی مانند تابع بالا، همواره نقطه یا نقاطی وجود دارند که در آنها وضعیت تابع از صعودی به نزولی یا برعکس تبدیل میشود. به این نقاط «اکسترمم محلی یا اکسترمم نسبی» (Local Extrema) گفته میشود. تعریف دقیقتر این نقاط به شکل زیر است:
- ماکزیمم یا بیشینه نسبی: معادل است با ورودی یک تابع که با رفتن به سمت مقادیر بیشتر از آن، وضعیت تابع از صعودی به نزولی تغییر میکند.
- مینیمم یا کمینه نسبی: معادل است با ورودی یک تابع که با رفتن به سمت مقادیر بیشتر از آن، وضعیت تابع از نزولی به صعودی تغییر میکند.
نکته ۱: یک تابع در نقاط اکسترمم نسبی خود نه صعودی محسوب میشود و نه نزولی.
نکته ۲: با توجه به اینکه هر اکسترمم نسبی تنها با در نظر گرفتن یک بازه خاص تعریف میشود، بنابراین ممکن است این نقاط لزوما ماکزیمم یا مینیمم مطلق در سرتاسر دامنه تابع محسوب نشوند.
به این ترتیب برای تابعی که نمودار آن را مشاهده کردید، دو نقطه اکسترمم نسبی داریم:
- یک ماکزیمم نسبی در نقطهای با مختصات
- یک مینیمم نسبی در نقطهای با مختصات
اغلب نمودار تابع به ما کمک میکند تا خیلی راحت تشخیص دهیم متوسط آهنگ تغییرات یک تابع مثبت است یا منفی. به تصویر زیر دقت کنید. نمودار یک تابع در ماکزیمم نسبی خود از تمام نقاط قبل و بعد از خود در بازه موردنظر خروجی بالاتری دارد. به همین شکل در مینیمم نسبی مقدار تابع نسبت به تمام مقادیری که قبل و بعد از آن در بازه مورد بررسی وجود دارند، کمتر است.
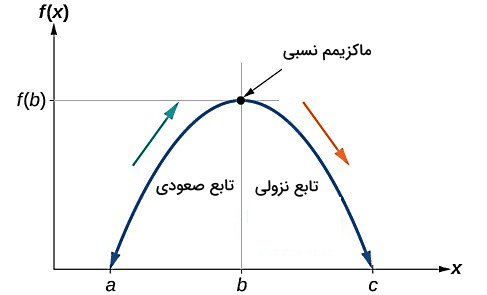
با توجه به توضیحاتی که در این بخش ارائه شد، تعریف دقیقتر توابع صعودی و نزولی و نقاط ماکزیمم و مینیمم در زبان ریاضیات عبارتاند از:
- تابع روی یک بازه باز صعودی محسوب میشود، اگر برای هر در این بازه به شکل ، داشته باشیم: .
- تابع روی یک بازه باز نزولی محسوب میشود، اگر برای هر در این بازه به شکل ، داشته باشیم: .
- تابع در نقطه روی بازه باز دارای یک ماکزیمم نسبی است، اگر به ازای هر در این بازه، بزرگتر یا مساوی با باشد.
- تابع در نقطه روی بازه باز دارای یک مینیمم نسبی است، اگر به ازای هر در این بازه، کوچکتر یا مساوی با باشد.
تعیین اکسترمم های مطلق یک تابع
در بخش قبل اشاره کردیم که در تعیین اکسترممهای نسبی یک تابع باید به بازه موردنظر دقت کنیم. در حقیقت اگر به بررسی نقاطی با بیشترین یا کمترین مقدار در یک بازه مشخص تمرکز کنیم، به دنبال نقاط اکسترمم نسبی آن تابع هستیم. اما اگر بررسی خود را در سرتاسر دامنه یک تابع انجام دهیم، نقاط بهدست آمده «اکسترمم مطلق» (Absolute Extrema) آن تابع نامیده میشوند.
دقت کنید در این بخش مانند بخش قبل نقاط اکسترمم را با توجه به نمودار تابع و روند آهنگ تغییرات آن تعیین میکنیم. اما در بخشهای آتی از روش دقیقتری به نام مشتقگیری کمک خواهیم گرفت. در تصویر زیر نمودار تابعی را ملاحظه میکنید که ابتدا و انتهای آن با یک دایره بسته مشخص شده است (نشان دهنده بسته بودن بازه). این تابع دامنه محدودی به شکل زیر دارد. پس با مشاهده کل این دامنه میتوانیم اکسترممهای مطلق آن را که شامل یک ماکزیمم مطلق و یک مینیممم مطلق هستند، مطابق شکل تعیین کنیم.
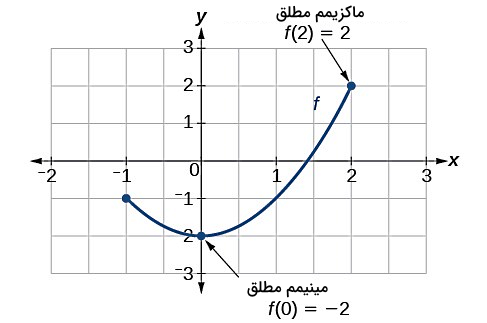
نکته: توابعی داریم که نه ماکزیمم مطلق دارند و نه مینیمم مطلق. برای مثال تابعی با معادله .
تعریف دقیقتر نقاط اکسترمم مطلق به زبان ریاضیات بهصورت زیر است؛
- ماکزیمم مطلق تابع در برابر است با ، اگر برای تمام های موجود در دامنه این تابع داشته باشیم: .
- مینیمم مطلق تابع در برابر است با ، اگر برای تمام های موجود در دامنه این تابع داشته باشیم: .
حل مثال از کاربرد آهنگ تغییرات در ریاضی
در این بخش با حل چند مثال در زمینه کاربردهای آهنگ تغییرات مانند تشخیص نقاط اکسترمم یک تابع و … به شما کمک میکنیم تا به این موضوع کاملا مسلط شوید. دقت کنید در این بخش سعی داریم فقط با توجه به نمودار تابع وضعیت آن را مشخص کنیم. اما در بخشهای بعد توضیح میدهیم روش دقیقتر تعیین نقاط اکسترمم تابع بر اساس مشتقگیری چگونه است.
مثال ۱
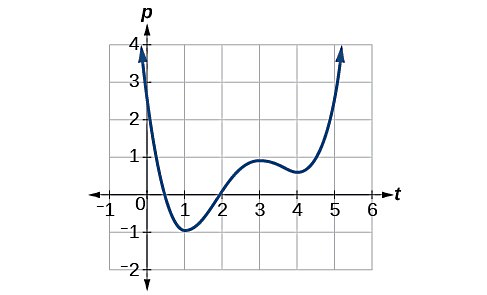
فرض کنید نمودار تابع به شکل زیر داده شده است. بازههایی را که بنظر میرسد در آنها تابع داده شده یک تابع صعودی است، مشخص کنید:
پاسخ
واضح است که در هیچ بازهای تابع داده شده یک تابع ثابت محسوب نمیشود. در بازههایی مانند از نقطه تا نقطه و از نقطه تا بینهایت (با توجه به علامت پیکان)، تابع داده شده صعودی است که بهتر است این دو فاصله را به شکل دو بازه باز و نشان دهیم. در سایر فواصل تابع نزولی است. دقت کنید علت اینکه از بازه باز استفاده میکنیم این است که نقاط ابتدا و انتهای بازه همان نقاط اکسترمم نسبی ما هستند و توضیح دادیم که در این نقاط تابع داده شده نه صعودی است و نه نزولی.
مثال ۲
برای تابعی که نمودار آن را ملاحظه میکنید، تمام نقاط اکسترمم نسبی را پیدا کنید:
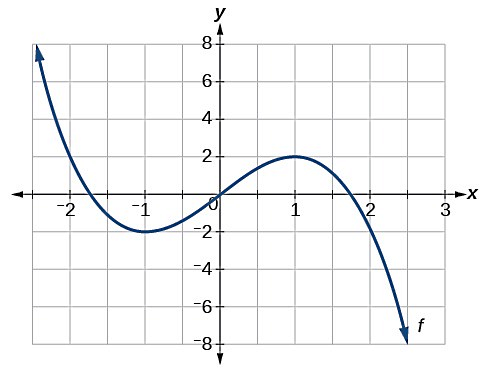
پاسخ
با توجه به توضیحاتی که در زمینه تعیین نقاط اکسترمم تابع داده شد، واضح است که تابع بالا در نقطه روی تمام نقاط حول آن دارای یک ماکزیمم نسبی است، چون به ازای هر در این بازه، بزرگتر یا مساوی با است. بهعلاوه، این تابع در نقطه روی تمام نقاط حول آن دارای یک مینیمم نسبی است، چون به ازای هر در این بازه، کوچکتر یا مساوی با است. به این ترتیب ماکزیمم نسبی این تابع معادل است با مولفه y متناظر با نقطه ، یعنی . همچنین مینیمم نسبی این تابع معادل است با مولفه y متناظر با نقطه ، یعنی .
مثال ۳
تابعی که نمودار آن را ملاحظه میکنید، چند اکسترمم دارد؟ این اکسترممها نسبی هستند یا مطلق؟
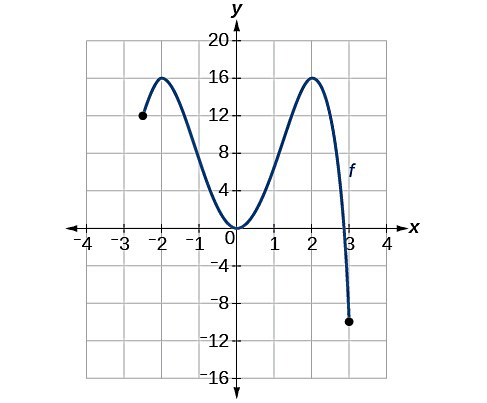
پاسخ
با توجه به اینکه ابتدا و انتهای این نمودار با نقاط بسته و نه پیکان نمایش داده شدهاند، پس میتوانیم بگوییم تمام دامنه این تابع در تصویر مشخص است. در نقاطی مانند و ماکزیمم داریم و چون مقدار تابع در این دو نقطه با هم برابر است ()، پس میتوانیم هر دو نقطه را بهعنوان نقاط ماکزیمم مطلق در نظر بگیریم. از طرفی در نقطه تابع داده شده دارای مینیمم مطلق است با مقداری برابر با .
محاسبه آهنگ تغییرات با مشتق
اگر بخواهیم کاربردهای مشتق را یک به یک برشماریم، یکی از مهمترین کاربردهای آن محاسبه آهنگ تغییرات است که این بخش را به این موضوع اختصاص دادهایم. مشتقگیری میتواند اطلاعات مهمی در زمینه رفتار یک تابع، نمودار و روشهای بهینهسازی آن به ما بدهد. برای شروع میدانیم نشان دهنده مشتق یک تابع است و بهصورت زیر تعریف میشود:
این تعریف به نوعی با تعریفی که برای متوسط آهنگ تغییرات ارائه کردیم، مشابه است. بنابراین میتوانیم مشتق یک تابع را با آهنگ تغییرات آن معادل در نظر بگیریم. شیوه دیگر برای نمایش یک تابع و مشتق آن این است که تابع را بهصورت تعریف کنیم، به گونهای که ارتباط بین دو کمیت و توسط ضابطه این تابع تعیین شود. در این صورت مشتق این تابع با نمایش داده میشود که بیانگر آهنگ تغییرات نسبت به است. بنابراین به ما میگوید همزمان با تغییر ، کمیت چگونه تغییر میکند.
بنابراین اگر بخواهیم آهنگ تغییرات را در مسئلهای تعیین کنیم، میتوانیم مشتقگیری انجام دهیم. اما پیش از آن لازم است به روشهای مشتقگیری و تمام فرمولهای آن کاملا مسلط باشیم. مطلب «فرمول های مشتق مهم + سوال با جواب» از مجله فرادرس جمعبندی کاملی از تمام فرمولهای مشتق ارائه میدهد که در صورت نیاز میتوانید آن را مطالعه کنید. در بخش بعد با توضیح تفاوت آهنگ متوسط تغییر و آهنگ لحظهای تغییر ارتباط آهنگ تغییرات و مشتقگیری را بهتر متوجه خواهید شد.
تشخیص تابع صعودی و نزولی با مشتق
یکی دیگر از کاربردهای مشتقگیری تعیین نقاط اکسترمم و وضعیت تابع داده شده از نظر صعودی یا نزولی بودن است. در بخشهای قبل توضیح دادیم که چه ارتباطی بین آهنگ تغییرات و صعودی یا نزولی بودن یک تابع وجود دارد. برای مثال گفتیم تابع درجه دوم در بازه نزولی و در بازه صعودی است. در این قسمت به کمک مشتق به تعیین این ویژگیها خواهیم پرداخت.
فرض کنید تابع روی بازه بسته پیوسته و روی بازه باز مشتق پذیر است. در این صورت وضعیت صعودی یا نزولی بودن این تابع با توجه به علامت مشتق آن به شکل زیر است:
- تابع روی بازه باز صعودی است، اگر مشتق آن در بازه بسته مثبت باشد یا داشته باشیم: .
- تابع روی بازه باز نزولی است، اگر مشتق آن در بازه بسته منفی باشد یا داشته باشیم: .
- تابع روی بازه باز ثابت است، اگر مشتق آن در بازه بسته صفر باشد یا داشته باشیم: .
بنابراین اگر معادله یک تابع را داشته باشیم و از آن مشتقگیری کنیم، میتوانیم با توجه به نتیجه بهدست آمده مشخص کنیم که این تابع صعودی است یا نزولی. یکی دیگر از روشهای تعیین وضعیت تابع با استفاده از مشتق و به کمک نمودار این است که در آن بجای مشتقگیری، از روش خط مماس بر نمودار استفاده کنیم. این روش در مواردی که به فرمولهای مشتقگیری مسلط نیستیم، کارگشا است. میدانیم شیب خط مماس بر نمودار در هر نقطه، معادل است با مشتق تابع در آن نقطه.
به این ترتیب اگر نمودار یک تابع را در اختیار داشته باشیم، برای تعیین آهنگ تغییرات یا مشتق آن کافی است خط مماس بر نمودار را در نقاط مختلف رسم کنیم و ببینیم این خطوط چه شیبی دارند. برای مثال، اگر بخواهیم خط مماس بر نمودار زیر را رسم کنیم، لازم است حتما بازههای مختلف را مدنظر داشته باشیم. البته در برخی از بازهها مانند شیب خط مماس بر نمودار در تمام نقاط بازه تقریبا یکسان است. دقت کنید این روش هم چون بر اساس نمودار تابع است، یک روش تقریبی است و دقیق نیست.
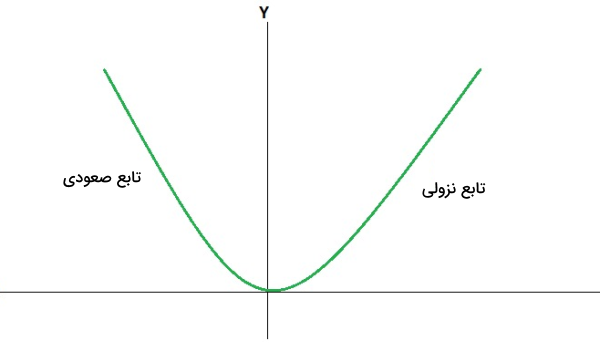
با رسم خطوط مماس بر نمودار در دو بازه و و در نقطه به نتیجه زیر میرسیم:
- در بازه شیب خط مماس بر نمودار و در نتیجه مثبت است. پس در این بازه تابع صعودی است.
- در بازه شیب خط مماس بر نمودار و در نتیجه منفی است. پس در این بازه تابع نزولی است.
- در نقطه شیب خط مماس بر نمودار و در نتیجه صفر است. پس در این بازه تابع نه صعودی است و نه نزولی.
بنابراین اگر به روش مشتقگیری بخواهیم ثابت کنیم تابع بالا در بازه صعودی است، ابتدا مشتق تابع را محاسبه میکنیم:
این عبارت همواره به ازای تمام هایی که در بازه قرار دارند، مقداری مثبت خواهد داشت. بنابراین طبق تعاریفی که بالاتر ارائه شد، تابع در این بازه صعودی است.
تشخیص نقطه عطف و تقعر نمودار با مشتق
گفتیم یکی دیگر از کاربردهای بررسی آهنگ تغییرات یک تابع این است که میتوانیم نقطه عطف و تقعر را مشخص کنیم. این بخش به توضیح این موضوع اختصاص دارد. اگر تابع یک تابع مشتقپذیر روی بازه باشد، در این صورت تعریفهای زیر را خواهیم داشت:
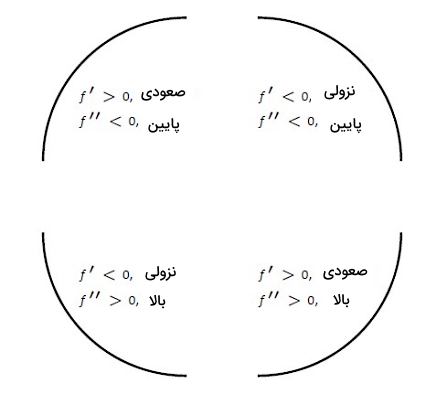
- تقعر نمودار رو به بالا است، اگر صعودی باشد.
- تقعر نمودار رو به پایین است، اگر نزولی باشد.
- نمودار هیچگونه تقعری ندارد، اگر ثابت باشد.
به این ترتیب در مورد اولین تعریف اینطور میتوانیم تحلیل کنیم که اگر به یک نمودار دارای تقعر بالا از چپ به راست نگاه کنیم، شیب خط مماس بر این نمودار افزایش خواهد یافت. به تصویر زیر که نمونهای از نمودار یک تابع با تقعر رو به بالا است، دقت کنید. در سمت چپ نمودار شیب زیاد و در عین حال منفی است. هر چه به مرکز نمودار نزدیک میشویم، از شدت شیب کاسته میشود تا اینکه در مبدا شیب به صفر میرسد. با عبور از مبدا و حرکت به طرف سمت راست نمودار، مجددا شیب افزایش مییابد، اما این بار با مقداری مثبت. پس روند افزایش شیب از چپ به راست در نمودار تابعی با تقعر رو به بالا به این صورت است.
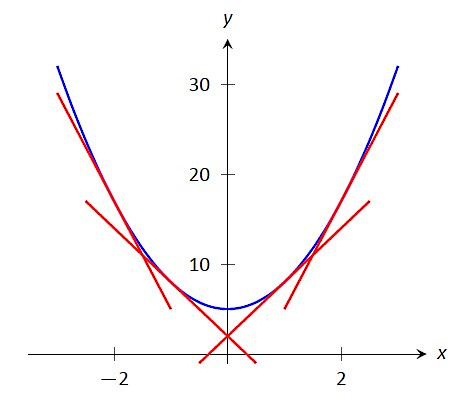
همچنین گفتیم اگر نزولی باشد، در این صورت تابع تقعر رو به پایین دارد. این تعریف به این معنا است که اگر از چپ به راست به یک تابع دارای تقعر پایین نگاه کنیم، شیب خطوط مماس بر این نمودار کاهش مییابد. در تصویر زیر ابتدا شیب تند و مثبتی داریم اما در سمت راست نمودار، شیب تند و منفی است.
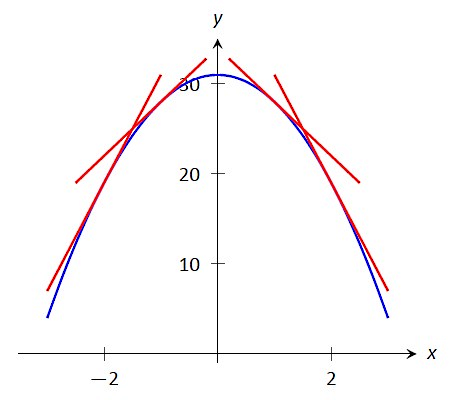
تعریف دقیقتر تقعر نمودار تابع با این شرط که روی بازه دو مرتبه مشتقپذیر باشد، بهصورت تصویر زیر است:
- تقعر نمودار رو به بالا است، اگر مثبت باشد.
- تقعر نمودار رو به پایین است، اگر منفی باشد.
- نمودار هیچگونه تقعری ندارد، اگر صفر باشد.
پس از اینکه با تعریف تقعر تابع آشنا شدیم، میتوانیم نقطه عطف را نیز شناسایی کنیم. نقطه عطف نقطهای روی نمودار تابع است که در آن جهت تقعر نمودار عوض میشود. برای مثال، در شکل زیر دو نقطه عطف روی نمودار تابع داریم. پس همانطور که ملاحظه میکنید، اگر تقعر تابع در نقطهای مانند عوض شود، در این صورت وضعیت نیز در این نقطه از صعودی به نزولی یا برعکس تغییر کرده است و این به این معنا است که علامت از منفی به مثبت یا برعکس تغییر کرده است.
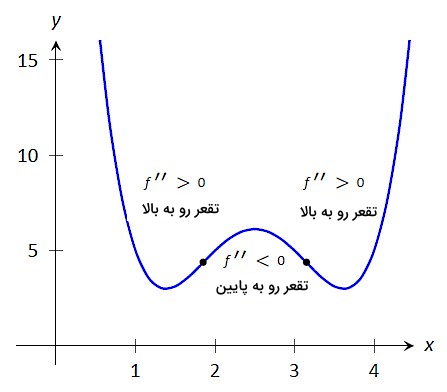
پس تعریف دقیقتر برای نقطه عطف یک تابع به این صورت است: اگر نقطه عطف روی نمودار تابع باشد، در این صورت یا و یا در نقطه تعریف نشده است.
سایر کاربردهای محاسبه آهنگ تغییرات با مشتق
در بخشهای قبل توضیح دادیم کاربرد محاسبه آهنگ تغییرات با مشتق در علم ریاضیات چیست و دیدیم که از این مفهوم میتوان در تعیین صعودی یا نزولی بودن یک تابع، تشخیص نقاط اکسترمم و تقعر آن استفاده کرد. در این بخش میخواهیم با برخی از کاربردهای این مفهوم در علوم دیگری مانند فیزیک، اقتصاد و زیستشناسی آشنا شویم. مشتقگیری از یک تابع به ما کمک میکند تا معادلات شتاب و سرعت در فیزیک، نرخ افزایش جمعیت در زیستشناسی و نرخ تغییر در اقتصاد را محاسبه کنیم. در ادامه این بخش با نحوه محاسبه این پارامترها بیشتر آشنا میشویم.
تخمین مقدار یک تابع
یکی از کاربردهای آهنگ تغییرات به روش مشتقگیری تخمین مقدار نامعلوم یک تابع در یک نقطه است، به این صورت که با کمک گرفتن از مقدار معلوم تابع همراه با آهنگ تغییرات آن در نقطهای دیگر اما نزدیک به نقطه موردنظر میتوانیم این محاسبه را انجام دهیم. فرض کنید تابع تابعی است که روی یک بازه بسته تعریف شده است. در این صورت مقدار تغییرات روی این بازه برابر است با فرمول زیر:
از طرفی میدانیم متوسط آهنگ تغییرات تابع روی این بازه از فرمول زیر بهدست میآید:
همچنین توضیح دادیم که آهنگ تغییرات آنی یا لحظهای برای این تابع در نقطهای مانند معادل است با مشتق آن که به شکل زیر نمایش داده میشود:
و برای مقادیر خیلی کوچک ، تقریب زیر را میتوانیم در نظر بگیریم:
در نتیجه با سادهتر کردن عبارت بالا خواهیم داشت:
بنابراین اگر فقط و را داشته باشیم، میتوانیم با استفاده از این فرمول مقدار را تخمین بزنیم. برای مثال، اگر جمعیت در حال حاضر یک شهر را به همراه آهنگ تغییرات رشد جمعیت بدانیم، میتوانیم جمعیت آن شهر را در آینده تخمین بزنیم. در تصویر زیر مشاهده میکنید که با رسم خط مماس بر نمودار در نقطه ، میتوانیم مقدار را تخمین بزنیم. نکته مهم در این تخمین این است که هر چه کوچکتر باشد، تقریب بهتری داریم.
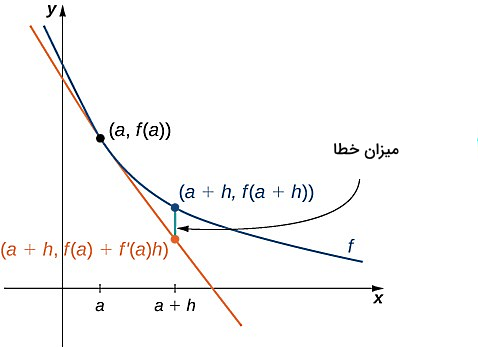
بررسی تغییرات جمعیت
از جمله کاربردهای آهنگ تغییرات در بررسی تغییرات جمعیت است که میتواند در مباحث آماری مربوط به بررسی جمعیت شهرها باشد یا جمعیت باکتریها در موضوعات زیستشناسی. با داشتن جمعیت کنونی و استفاده از نرخ رشد جمعیت قادریم جمعیت آینده را تخمین بزنیم. بنابراین اگر جمعیت در حال حاضر را با نشان دهیم، نرخ رشد آن همواره برابر است با .
بررسی حرکت اجسام در فیزیک
یکی دیگر از کاربردهای مشتقگیری برای محاسبه آهنگ تغییرات بررسی حرکت یک جسم در بخشی از علم فیزیک به نام «سینماتیک یا حرکتشناسی» است. اگر معادله حرکت جسمی را داشته باشیم، میتوانیم با محاسبه سرعت و شتاب اطلاعات مفیدی از حرکت آن بهدست آوریم. با توجه به اینکه سرعت جسم بهصورت آهنگ تغییرات مکان و شتاب آن نیز بهصورت آهنگ تغییرات سرعت تعریف میشود، کافی است از معادله مکان دو مرتبه مشتق بگیریم تا به معادله هر کدام از این دو کمیت برسیم:
- سرعت یک جسم در زمان برابر است با .
- تندی یک جسم در زمان برابر است با .
- شتاب یک جسم در زمان برابر است با .
محاسبه درآمد و سود در اقتصاد
یکی از مهمترین بخشهایی که محاسبه آهنگ تغییرات و مشتقگیری میتواند کمک کننده باشد، حوزه اقتصاد و بررسی سود، درآمد و هزینهها است. در این زمینه کمیت مهمی به نام «هزینه نهایی» (Marginal Cost) داریم که با نماد اختصاری MC نمایش داده میشود و برابر است با مشتق تابع هزینه. همچنین درآمد نهایی یا Marginal Revenue را داریم که از مشتق تابع درآمد بهدست میآید و به همین ترتیب، سود نهایی را داریم که از مشتقگیری تابع سود حاصل میشود. تابع سود را با توجه به تابع درآمد و تابع هزینه میتوان تعیین کرد. بنابراین تعاریف زیر را در حالت کلی خواهیم داشت:
- اگر هزینه تولید آیتم باشد، در این صورت تابع هزینه یا برابر است با .
- اگر درآمد آیتم باشد، در این صورت تابع درآمد یا برابر است با .
- اگر سود حاصل از فروش آیتم باشد، در این صورت تابع سود یا برابر است با .
همچنین طبق تعریفهایی که بالاتر ارائه شد و با انتخاب مقدار مناسب، میتوانیم تقریب زیر را نیز در نظر بگیریم:
کوچکترین و منطقیترین انتخاب برای در رابطه بالا برابر است با . به این ترتیب خواهیم داشت:
در بخش بعد با حل مثال بیشتر متوجه خواهید شد که کاربرد آهنگ تغییرات در بررسی و تخمین این توابع اقتصادی به چه صورت است.
حل مثال از محاسبه آهنگ تغییرات با مشتق
در تمام مثالهایی که در بخشهای گذشته حل شدند، از نمودار توابع برای محاسبه آهنگ تغییرات و نتایج حاصل از آن مانند تعیین نقاط اکسترمم استفاده کردیم. اما در این بخش با حل و بررسی چند مثال نشان میدهیم که مشتقگیری سریعترین، دقیقترین و آسانترین روش برای بررسی آهنگ تغییرات یک تابع است.
مثال ۱
اگر تمام اضلاع یک مکعب با نرخ یکسانی به اندازه افزایش پیدا کنند، آهنگ تغییرات حجم این مکعب چقدر است؟
پاسخ
ابتدا باید ببینیم ضابطه این تابع چگونه است. در مورد یک مکعب رابطه بین حجم و طول ضلع آن برابر است با . بنابراین برای اینکه آهنگ تغییرات حجم مکعب را پیدا کنیم، کافی است از آن نسبت به زمان مشتق بگیریم. اینکه چرا باید مشتقگیری را نسبت به زمان انجام دهیم به نرخ تغییرات ضلع آن یعنی برمیگردد. در این کمیت واحدی که داده شده است، متر بر ثانیه است. بنابراین چون ضلع مکعب با زمان تغییر میکند، پس باید تغییرات حجم را نیز با زمان در نظر بگیریم:
همانطور که ملاحظه میکنید، در محاسبات بالا برای اینکه مشتقگیری به درستی انجام شود از روش زنجیرهای استفاده کردهایم. حالا کافی است بهجای مقدار را قرار دهیم و از مشتق بگیریم:
مثال ۲
فرض کنید دایرهای داریم که شعاع آن مرتب در حال افزایش است. آهنگ تغییرات مساحت این دایره را همزمان با افزایش شعاع بهدست آورید، اگر شعاع آن باشد.
پاسخ
ابتدا باید رابطه مساحت دایره و شعاع آن را بنویسیم:
در صورت سوال تغییرات مساحت نسبت به شعاع آن خواسته شده است، بنابراین از رابطه بالا نسبت به مشتق میگیریم:
در نهایت برای اینکه در آهنگ تغییرات را تعیین کنیم، کافی است این مقدار را در رابطه بالا قرار دهیم:
مثال ۳
اگر بدانیم و ، مقدار را تخمین بزنید:
پاسخ
در این سوال کافی است از فرمول برای تخمین مقدار تابع استفاده کنیم:
مثال ۴
اگر توپی از ارتفاع رها شده و معادله مسافت آن به شکل باشد، سرعت لحظهای آن زمانی که به زمین میرسد و سرعت متوسط آن در طول این افتادن چقدر است؟
پاسخ
در این سوال که کاملا یک مبحث فیزیکی است، معادله حرکت توپ داده شده است. برای پیدا کردن سرعت لحظهای کافی است از معادله مکان مشتقگیری کنیم:
اما مقدار این سرعت در لحظهای که به زمین میرسد، خواسته شده است و باید این زمان را نیز محاسبه کنیم. با توجه به اینکه در لحظه رسیدن توپ به زمین مکان آن صفر میشود، پس میتوانیم از رابطه زیر استفاده کنیم:
حل معادله درجه دو بالا به پاسخ زیر منجر میشود:
پس سرعت لحظهای در لحظه برخورد توپ به زمین برابر میشود با:
در بخش دوم از سوال سرعت متوسط را برای کل پروسه افتادن توپ میخواهیم که در مدت زمان دو ثانیه رخ داده است. پس با نوشتن فرمول سرعت متوسط به شکل زیر خواهیم داشت:
دقت کنید باید ابتدا و را با مقداردهی به معادله مکانی که در اختیار داریم، محاسبه کنیم و سپس در عبارت بالا قرار دهیم.
مثال ۵
فرض کنید تعداد وعدههای غذایی که در کسب و کار خانگی خود میتوانیم بفروشیم با کمیت و سود حاصل از این فروش نیز توسط معادله بهدست میآید. با این شرط که ، اگر تابع درآمد حاصل از فروختن این وعدهها با معادله داده شود، درآمد حاصل از فروش امین آیتم را تخمین بزنید. همچنین پاسخ بهدست آمده را با حاصلی که از فرمول تخمین مقدار یک تابع میتوانید بهدست آورید، مقایسه کنید:
پاسخ
در مورد اولین سوال با توجه به اینکه تخمین درآمد خواسته شده، کافی است را محاسبه کنیم که برابر است با :
از طرفی برای مقایسه این جواب با پاسخ حاصل از فرمول تخمین مقدار یک تابع، لازم است از اختلاف و استفاده کنیم:
ملاحظه میکنید که جوابهای نزدیک به هم برای هر دو روش بهدست آمد.
تمرین ۱
اگر بدانیم جمعیت یک شهر هر پنج سال سه برابر میشود در حالی که جمعیت کنونی آن برابر با ۱۰۰۰۰ نفر است، جمعیت این شهر دو سال بعد چقدر خواهد بود؟
گزینه اول درست است. در این سوال میتوانیم با استفاده از آهنگ تغییرات و مشتقگیری به تخمین جمعیت بپردازیم. جمعیت کنونی برابر است با و طبق اطلاعات سوال، میدانیم هر پنج سال جمعیت سه برابر میشود. پس میتوانیم دو نتیجه زیر را داشته باشیم:
حالا برای اینکه آهنگ تغییرات را بهدست آوریم، کافی است فرمول متوسط آهنگ تغییرات را به شکل زیر بنویسیم:
با داشتن آهنگ تغییرات میتوانیم جمعیت در دو سال آینده را تخمین بزنیم:
تمرین ۲
ذرهای در راستای محور x و به سمت راست در حال حرکت است. اگر معادله حرکت این ذره بر حسب زمان بهصورت داده شود، در لحظه حرکت این ذره از راست به چپ است یا از چپ به راست؟
ذره حرکتی ندارد.
چون اطلاعات مسئله کامل نیست، نمیتوان تعیین کرد.
گزینه اول صحیح است. ابتدا با مشتقگیری از معادله مکان سرعت حرکت این ذره را تعیین میکنیم:
با قرار دادن زمان داده شده در این معادله، علامت سرعت در این لحظه تعیین میشود:
چون سرعت در این لحظه مثبت است، پس همجهت با حرکت اولیه یعنی از چپ به راست حرکت میکند.
تمرین ۳
اگر معادله تابعی به شکل داده شود، نقاط عطف آن کدامند؟
تمام گزینهها درست هستند.
گزینه اول درست است. طبق تعریف در نقاط عطف یا و یا مشتق دوم تعریف نشده است. بنابراین اولین قدم محاسبه مشتق دوم تابع داده شده است:
طبق شروط گفته شده، تنها نقطه عطف ما است، چون روی تمام نقاط تعریف شده است و از معادله به میرسیم.
چگونه ریاضی عمومی ۱ را با فرادرس بهتر یاد بگیریم؟
در این بخش قصد داریم چند دوره آموزشی از مجموعه فرادرس را با موضوع ریاضی عمومی ۱ و مباحث مطرح شده در آن، به شما معرفی کنیم. مشاهده این فیلمهای آموزشی به شما کمک میکند تا یادگیری خود را در این زمینه تکمیل کنید، بهویژه اینکه دسترسی برخی از این فیلمها بهصورت رایگان است و در هر کدام روی یک مبحث خاص تمرکز شده است تا بتوانید با تمرین و توضیح بیشتر، کاملا به آن بخش تسلط پیدا کنید:
- فیلم آموزش ریاضی عمومی ۱ – مرور و حل مساله فرادرس
- فیلم آموزش ریاضی عمومی ۱ + مرور و حل تست کنکور کارشناسی ارشد فرادرس
- فیلم آموزش رایگان حد و پیوستگی ریاضی عمومی ۱ + مثالهای کاربردی فرادرس
- فیلم آموزش رایگان قضیه فشردگی یا ساندویچ + مثالهای کاربردی فرادرس
- فیلم آموزش رایگان روابط اساسی مشتق + حل مثال فرادرس
- فیلم آموزش رایگان مشتق پارامتری و زنجیری + حل مثال فرادرس
- فیلم آموزش رایگان روش حل مشتق ضمنی + حل مثالهای مختلف فرادرس
- فیلم آموزش رایگان روش حل انتگرال تغییر متغیر + به زبان ساده با مثال فرادرس
آزمون آهنگ تغییرات
در این مطلب از مجله فرادرس توضیح دادیم آهنگ تغییرات چیست و چگونه محاسبه میشود. همچنین با کاربردهای این مفهوم در تعیین نقاط اکسترمم و بررسی رفتار تابع آشنا شدیم و یاد گرفتیم محاسبه آهنگ تغییرات به روشهای مختلفی ممکن است، از جمله بررسی نمودار تابع، استفاده از معادله آن، بررسی جدول مقادیر و مشتقگیری.
در انتها میتوانید با پاسخ دادن به سوالات چهار گزینهای زیر که در قالب یک آزمون برای شما تهیه شده است، میزان یادگیری خود را بیازمایید. برای مشاهده نمره نهایی کافی است پس از پاسخدهی به تمام سوالات، روی بخش «دریافت نتیجه آزمون» کلیک کنید.
مستطیلی داریم که اندازه اضلاع آن در هر ثانیه تغییر میکند. اگر نرخ افزایش طول این مستطیل برابر با باشد، در حالی که عرض آن با نرخ زیاد میشود، آهنگ تغییرات مساحت این مستطیل در طول و عرض برابر با کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
کدام گزینه نشان دهنده متوسط نرخ تغییرات روی بازه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
متوسط آهنگ تغییرات تابع روی بازه کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
وضعیت صعودی یا نزولی بودن تابع در کدام گزینه به درستی بیان شده است؟
این تابع در بازه نزولی است.
این تابع در بازه صعودی است.
این تابع در بازه نزولی و در بازه صعودی است.
گزینه اول و دوم صحیح است.
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر معادله تابعی بهصورت باشد، نقاطی را پیدا کنید که به ازای آنها آهنگ تغییرات صفر است:
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر بدانیم و ، مقدار تقریبی برابر با کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
ذرهای در حال حرکت در راستای مثبت محور xها و به سمت راست است و معادله حرکت آن به شکل داده شده است. در لحظه این ذره در حال سرعت گرفتن به سمت بالا است یا پایین؟
در این لحظه ذره متوقف شده است.
چون اطلاعات سوال کامل نیست، نمیتوان تعیین کرد.
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر باشد، نقاط بحرانی تابع کدامند؟
گزینه اول و دوم درست هستند.
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
اگر فروش محصول خاصی طی سه سال توسط معادله مدلسازی شده باشد و بدانیم که در دو سال اول این فروش روند کاهشی داشته است، نقاطی منطبق با بیشترین آهنگ تغییرات کاهشی برای فروش کدامند؟
تمام گزینهها درست هستند.
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
آهنگ تغییرات نسبت به برای تابع در نقطه برابر با کدام گزینه است؟
مشاهده پاسخ تشریحی برخی از سوالات، نیاز به عضویت در مجله فرادرس و ورود به آن دارد.
source
