با اینکه مشتق و دیفرانسیل و فرمولهای آنها در درس ریاضی بسیار شبیه به یکدیگر بنظر میرسند، اما واقعیت این است که تعریف و کاربرد هر کدام با دیگری کاملا متفاوت است. اگر بخواهیم نرخ تغییرات مقدار یک تابع را نسبت به ورودی آن بدانیم، باید مشتق آن تابع را محاسبه کنیم، در حالی که اگر بخواهیم میزان تغییرات بینهایت کوچک از یک متغیر را بهدست آوریم، از آن دیفرانسیلگیری میکنیم. بنابراین دانستن تفاوت مشتق و دیفرانسیل برای انجام محاسباتی کاملا درست و دقیق و اجتناب از کاربرد یکی به جای دیگری، ضروری است. به همین دلیل در این مطلب از مجله فرادرس به توضیح این موضوع پرداختهایم.

پس از اینکه در اولین بخش بهصورت کلی توضیح دادیم تفاوت مشتق و دیفرانسیل چیست، در دو بخش جداگانه به تعریف هر کدام، معرفی فرمولها و کاربردهای آنها خواهیم پرداخت. همچنین در انتهای این مطلب مثالها و تمرینهای متنوعی در همین زمینه برای شما در نظر گرفته شده است تا با حل و بررسی این سوالات به مبحث تفاوت مشتق و دیفرانسیل و کاربردهای هر کدام کاملا مسلط شوید.
تفاوت مشتق و دیفرانسیل چیست؟
مشتق و دیفرانسیل در علم حساب ارتباط نزدیکی با هم دارند، اما یکی نیستند. مشتقگیری فرآیندی است که در آن نرخ تغییرات خروجی یک تابع نسبت به تغییرات ورودی آن اندازهگیری میشود. اما اگر بخواهیم نشان دهیم چطور با اعمال یک تغییر خیلی کوچک در ورودی یک تابع، خروجی متناظر با آن نیز تغییر خیلی کوچکی خواهد داشت، از دیفرانسیل استفاده میکنیم. با توجه به این تعاریف، مشتق بهعنوان شیب خط مماس بر نمودار تابع در نقطه موردنظر شناخته میشود و فرمولی بهصورت دارد، در حالی که فرمول مناسب برای محاسبه دیفرانسیل یک تابع عبارت است از .
طبق فرمولهای بالا، واضح است که برای محاسبه دیفرانسیل یک تابع باید مشتق آن را بدانیم. پس میتوانیم بگوییم این دو مفهوم با هم در ارتباط هستند، در حالی که با هم فرق هم دارند. برای اینکه با تفاوت مشتق و دیفرانسیل بهتر آشنا شوید، به مثال ساده زیر توجه کنید. فرض کنید تابع موردنظر ما به شکل باشد:
- طبق قواعد مشتقگیری میدانیم مشتق این تابع یا برابر است با و این محاسبه نشان میدهد به ازای هر مقداری از ، نرخ تغییرات این تابع همیشه برابر با عدد ثابت است.
- دیفرانسیلگیری برای این تابع طبق فرمول گفته شده معادل است با . این فرمول نشان میدهد که برای مثال اگر ورودی این تابع یعنی به اندازه خیلی کوچکی به شکل تغییر کند، در این صورت تغییرات خروجی نیز یک عدد کوچک و تقریبا برابر با است.
پس تا اینجا یاد گرفتیم مهمترین تفاوت مشتق و دیفرانسیل بنا به تعریف هر کدام چیست. یکی دیگر از تفاوتهای این دو مبحث این است که دیفرانسیل تابعی از دو متغیر و مشتق تابعی از یک متغیر است. گفتیم دیفرانسیل یک تابع توسط معادلهای به شکل ٰ تعیین میشود و ملاحظه میکنید که در این معادله دو متغیر به شکل و داریم. از طرفی در مورد مشتقگیری فرمول را بکار میبریم که تنها به متغیر وابسته است.
بخش دیگری از انواع تفاوت مشتق و دیفرانسیل به کاربردهای هر کدام از این دو بازمیگردد. از دیفرانسیل اغلب در محاسبات تقریبی برای دستیابی به میزان تغییرات یک تابع یا بررسی خطا استفاده میشود. به عبارت دیگر این فرآیند ما را به یک جواب تقریبی در محاسبات خود میرساند. بهعلاوه میتوانیم از دیفرانسیلگیری در مسائل بهینهسازی و یافتن مقادیر بیشینه یا کمینه یک تابع نیز استفاده کنیم، در حالی که کاربردهای مشتق در حل مسائل حوزههای مختلفی از جمله فیزیک، اقتصاد و مهندسی است. جدول زیر نشان میدهد تفاوت مشتق و دیفرانسیل با در نظر گرفتن جنبههای مختلف هر کدام چیست:
| مشتق | دیفرانسیل | |
| تعریف | نرخ تغییرات یک تابع نسبت به تغییرات ورودی آن | تغییرات بینهایت کوچک یک متغیر |
| ارتباط | مشتق معادل است با نسبت دیفرانسیل خروجی به ورودی تابع. | محاسبه دیفرانسیل یک تابع با داشتن مشتق آن امکانپذیر است. |
| نحوه نمایش یا فرمول برای تابع |
یادگیری درس حسابان با فرادرس
در ریاضیات متوسطه مفاهیمی مانند حد، مشتق، دیفرانسیل و مقدمات انتگرال در درسی به نام «حسابان» مطرح میشوند. به همین دلیل در این قسمت قصد داریم چند فیلم آموزشی در مورد این کتاب درسی را به شما معرفی کنیم که در مجموعه فرادرس تهیه شدهاند. مشاهده این فیلمها به شما کمک میکند تا با بهرهگیری از آموزش تصویری و حل مثالها و تمرینهای متنوع کاملا به مباحثی مانند تفاوت مشتق و دیفرانسیل مسلط شوید:
مشتق چیست و چه کاربردهایی دارد؟
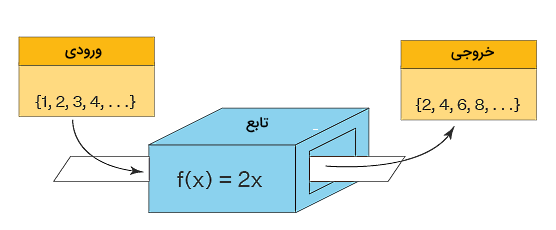
«مشتق» (Derivative) نوعی فرآیند ریاضیاتی است که روی یک تابع اجرا میشود، به این معنا که میگوییم مشتق یک تابع برابر است با تابع جدیدی که «تابع مشتق» یا «نرخ تابع» نامیده میشود. اگر بخواهیم تعریف دقیقتری از مشتق ارائه دهیم، بهتر است از مفهوم متغیرهای مستقل و وابسته استفاده کنیم. مشتق یک تابع نرخ آنی یا لحظهای تغییرات مقدار یک متغیر وابسته نسبت به تغییرات مقدار یک متغیر مستقل است.
در همین راستا قدم اول برای یادگیری بهتر تفاوت مشتق و دیفرانسیل این است که ببینیم تعریف تابع چیست و چگونه میتواند بین متغیرهای مختلف ارتباط برقرار کند. یک تابع بین دو مجموعه از مقادیر با نامهای ورودی و خروجی یا دامنه و برد ارتباط برقرار میکند. مقادیر ورودی یک تابع متغیرهای مستقلی هستند که با توجه به مقدار آنها، خروجی یا متغیر وابسته در آن تعیین میشود. حال اگر برای مثال بخواهیم ببینیم در یک لحظه زمانی خاص یک تابع با چه سرعتی تغییر میکند، در حقیقت باید مشتق آن تابع را نسبت به زمان بررسی کنیم.
مشتق یک تابع با شیب خط مماس بر نمودار آن تابع معادل است و این توضیح کوتاه به ما اطلاعات زیادی در مورد روند تغییرات آن تابع خواهد داد. برای مثال، اگر نمودار تابعی با معادله و بر حسب زمان رسم شود، شکل آن بهصورت یک نیمسهمی رو به بالا خواهد شد. اگر شیب خط مماس بر این نمودار را رسم کنیم، حاصل یک خط مستقیم است. به این ترتیب مشتق به ما نشان میدهد نرخ تغییرات این تابع با زمان خطی است، اگرچه خود تابع بر حسب زمان یک تابع درجه دو محسوب میشود.
برای مثال، تابعی به شکل را به همراه دو نقطه روی آن با مختصات و در نظر بگیرید. در این شرایط شیب خطی که از این دو نقطه میگذرد (خط سکانت) توسط رابطه زیر مشخص خواهد شد:
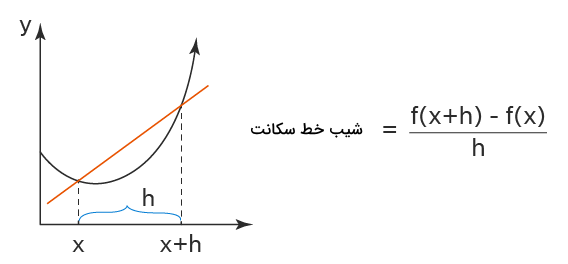
با دقت در نمودار این تابع و مکان این دو نقطه انتخابی، ملاحظه میکنید که هر چه فاصله بین این دو نقطه کمتر و کمتر شود یا به زبان ریاضی این پارامتر به سمت صفر میل کند ( )، نقطه دوم به نقطه اول نزدیک و نزدیکتر میشود تا حدی که با قرار گرفتن دو نقطه روی هم میتوانیم خط سکانت را با خط مماس بر نمودار در یک نقطه معادل بدانیم. تصویر زیر نشان میدهد اگر شود، چگونه خط سکانت در تصویر قبل به خط مماس بر نمودار در نقطه تبدیل خواهد شد:
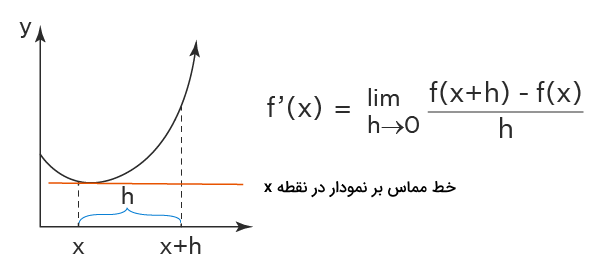
حال اگر روند کوچک شدن را به کمک مفهومی به نام حد نشان دهیم، در این صورت شیب خط سکانت که حالا به خط مماس بر نمودار در نقطه تبدیل شده است، برابر است با مشتق تابع در نقطه . این توضیح در زبان ریاضیات به شکل زیر نوشته میشود:
رابطه بالا دقیقترین تعریفی است که میتوانیم در مورد مشتق تابع ارائه کنیم. بر اساس این فرمول اگر تابع فرضی ما به شکل باشد، فرآیند مشتقگیری بهصورت زیر خواهد بود:
با توجه به قوانین محاسبه حد، پاسخی به شکل بالا برای این مشتقگیری بهدست میآید. اما محاسبه مشتق با این فرمول بسیار دشوار و وقتگیر است، بهویژه برای توابع پیچیدهتری مانند توابع مثلثاتی یا توابع معکوس. در این زمینه و با توجه به اینکه برای محاسبه دیفرانسیل نیز لازم است مشتقگیری انجام شود، پیشنهاد میکنیم حتما مطلب «فرمول های مشتق + سوال با جواب و دانلود PDF» از مجله فرادرس را مطالعه کنید تا به تمام فرمولهای موردنیاز برای انواع مشتقگیری کاملا مسط شوید.
آزمونهای مشتق گیری
در ادامه توضیح تفاوت مشتق و دیفرانسیل، بهتر است با کاربردهای هر کدام آشنا شویم که موضوع این بخش و بخشهای بعد است. اما پیش از شروع این مبحث، میخواهیم به شما فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد فرادرس را معرفی کنیم که لینک آن نیز در ادامه برای شما قرار داده شده است. مشاهده این دوره به شما کمک میکند تا پس از تسلط کامل بر فرآیند مشتقگیری بتوانید با انواع معادلات دیفرانسیل و روش حل آنها کاملا آشنا شوید.
یکی از سادهترین کاربردهای مشتق و فرمولهای آن در علم فیزیک، محاسبه کمیتهایی مانند سرعت، شتاب و … است. با داشتن معادله حرکت یک جسم میتوانیم سرعت آن را تعیین کنیم، کافی است فرآیند مشتقگیری از آن را شروع کنیم. اگر مشتقگیری از معادله حرکت را دو مرتبه انجام دهیم، معادله شتاب حرکت جسم تعیین خواهد شد. همچنین با توجه به مفهوم شیب خط مماس بر نمودار میتوانیم از روی نمودار حرکت یک جسم، نمودارهای سرعت – زمان، شتاب – زمان و نحوه تبدیلات آنها به هم را ارزیابی کنیم.
کاربرد دیگر مشتقگیری در یافتن بازههایی است که یک تابع صعودی یا نزولی است یا بازههایی که در آن تابع مورد نظر ما دارای تقعر خاصی است. این موارد در تحلیل و ارزیابی نمودارهای مختلف در علوم مهندسی بسیار مهم هستند. در حالت کلی هرگاه با عبارتهایی نظیر شیب، گرادیان، نرخ تغییرات، آهنگ تغییرات، بیشینه یا کمینه، صعودی یا نزولی، نقطه عطف و … مواجه شدیم، لازم است از مفهوم مشتق استفاده کنیم.
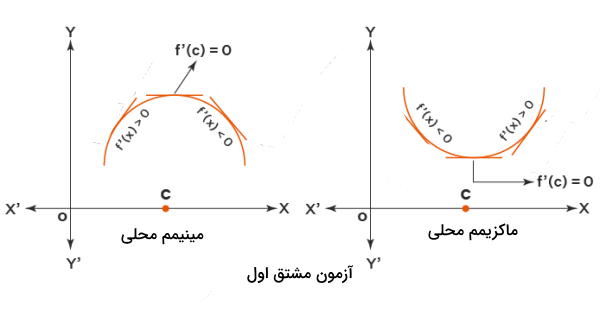
روش یافتن نقاطی مانند ماکزیمم یا مینیمم یا نقطه عطف برای یک تابع این است که آزمونهای مشتق اول و دوم را روی آن اجرا کنیم. روند آزمون مشتق اول به شکل زیر است:
- نشاندهنده مشتق تابع یا شیب خط مماس بر نمودار در نقطه است.
- اگر مقدار در نقطه موردنظر ما بزرگتر از صفر شود، تابع یک تابع صعودی است.
- اگر مقدار در نقطه موردنظر ما کوچکتر از صفر شود، تابع یک تابع نزولی است.
- اگر در نقطهای علامت مشتق عوض شود، در آن نقطه یک اکسترمم محلی داریم.
- اگر تغییر علامت مشتق از منفی به مثبت باشد، اکسترمم محلی یکی از مینیممهای تابع است.
- به خاطر داشته باشید که در مینیمم یا ماکزیمم محلی همواره عبارت برقرار است.
همچنین برای آزمون مشتق دوم که در تعیین نقاط بحرانی تابع کمک کننده است، میتوانیم به شکل زیر عمل کنیم:
- با مساوی صفر قرار دادن ، نقاط بحرانی را پیدا کنید.
- هر کدام از نقاط بحرانی حاصل از تساوی بالا را در مشتق دوم تابع یا قرار دهید.
- اگر مثبت شد، تابع در آن نقطه مینیمم مطلق دارد.
- اگر منفی شد، تابع در آن نقطه ماکزیمم مطلق دارد.
- اگر مساوی با صفر شد، تابع ما نه ماکزیمم مطلق دارد و نه مینیمم مطلق.
دیفرانسیل چیست و چه کاربردهایی دارد؟
«دیفرانسیل» (Differential) یکی از شاخههای بنیادی علم حساب است که با هر دو مبحث انتگرالگیری و مشتقگیری کاملا مرتبط است. در این حوزه با تغییرات بینهایت کوچک یک کمیت در حال تغییر سروکار داریم. همانطور که میدانید، جهان اطراف ما پر است از توابعی که مدام ورودی آنها در حال تغییر است. برای مثال، مساحت جسم دایرهای شکلی که شعاع آن در حال افزایش است یا حرکت پرتابهای که با تغییرات سرعت پرتابه همراه است. بررسی نرخ تغییرات هر کدام از این متغیرها نسبت به دیگری همان مشتقگیری است و معادلهای که نمایشدهنده ارتباط بین این متغیرها است، «معادله دیفرانسیل» نام دارد.
پس یک معادله دیفرانسیل معادلهای است که ارتباط بین یک سری متغیر، توابع و برخی از مشتقات این توابع را توصیف میکند. بهطور کلی در فرمولهای دیفرانسیلگیری همیشه لازم است مشتق را بدانیم و به همین دلیل است که میگوییم مشتق و دیفرانسیل با هم مرتبط هستند. همچنین یک معادله دیفرانسیل میتواند شامل مشتقها و توابع مختلفی از تمام مراتب مشتقگیری باشد. دیفرانسیلگیری با توجه به نوع مسئلهای که با آن سروکار داریم، انواع مختلفی دارد که در ادامه این بخش به آنها اشاره میکنیم.
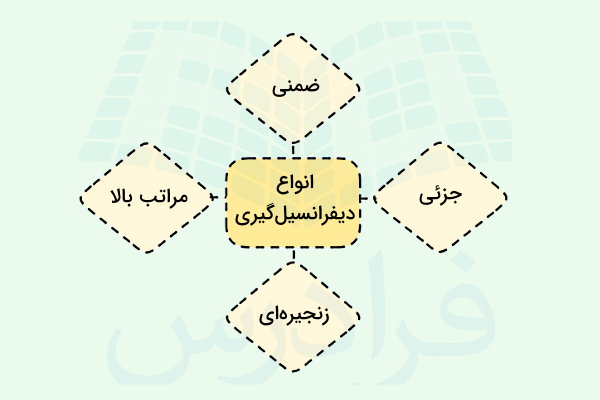
دیفرانسیل گیری زنجیره ای
برای اینکه بهتر متوجه شوید تفاوت مشتق و دیفرانسیل در کاربرد چگونه است، در این قسمت به نحوه دیفرانسلگیری بر حسب پارامترهای مختلف میپردازیم. اگر و باشند، این بدین معنا است که در اینجا خود متغیرهای و ما به متغیر سومی به نام وابسته هستند. بنابراین اگر بخواهیم نسبت دو دیفرانسیل و را بهدست آوریم، به شکل زیر عمل میکنیم:
با توجه به اینکه طبق تعریف مشتق میدانیم معادل است با و معادل است با ، پس عبارت بالا بهصورت زیر ساده میشود:
به همین شکل اگر و باشند، یعنی هر دو بر حسب باشند، در این صورت دیفرانسیلگیری نسبت به به شکل زیر داده میشود:
دیفرانسیل گیری ضمنی
فرض کنید تابع مورد نظر شما با مشخص میشود، به این معنا که به دو متغیر وابسته است. در این بخش با حل یک مثال عددی نشان میدهیم برای دیفرانسیلگیری از این توابع باید چگونه عمل کنیم. فرض کنید عبارت به شما داده شده است و میخواهید را پیدا کنید. با دیفرانسیل گرفتن از طرفین عبارت داده شده به شکل زیر خواهیم داشت:
دیفرانسیل گیری لگاریتمی
در دو بخش قبل با بخشی از انواع روشهای دیفرانسیلگیری آشنا شدیم. این روشها به ما کمک میکنند تا پس از تفکیک تفاوت مشتق و دیفرانسیل بتوانیم روش حل درست مسائل را تشخیص دهیم. در ادامه با یک مثال نشان میدهیم تکنیک دیفرانسیلگیری لگاریتمی چیست و چگونه به ما کمک میکند. فرض کنید یک تساوی بر حسب متغیرهای و به شکل داریم و میخواهیم نسبت دیفرانسیل را به دیفرانسیل محاسبه کنیم. اولین مرحله این است که از طرفین رابطه بالا لگاریتم بگیریم:
دیفرانسیل گیری مراتب بالاتر
عموما برای محاسبه مراتب بالاتر دیفرانسیلگیری از نمادهایی مانند یا بهعنوان دومین مرتبه و در حالت کلی از بهعنوان nامین مرتبه استفاده میشود. این نمادها در مشتقات مراتب بالاتر نیز بکار میروند، اما بیان درستتر این است که بهجای مشتق مراتب بالاتر از عبارت دیفرانسیلگیری مراتب بالاتر استفاده کنیم.
برای مثال دیفرانسیلگیری مرتبه دوم بهصورت و دیفرانسیلگیری مرتبه nام بهصورت نوشته میشوند یا اگر بخواهیم برای تابع مراتب یک تا چهار دیفرانسیلگیری را انجام دهیم، به شیوه زیر عمل میکنیم:
دیفرانسیل گیری جزئی
در دیفرانسیلگیری جزئی تابعی شامل دو یا چند متغیر مانند داریم و روند کار به این صورت است که اگر برای نمونه تابعی به شکل داشته باشیم و بخواهیم را پیدا کنیم، کافی است را ثابت در نظر بگیریم و اگر بخواهیم را بهدست آوریم، لازم است را ثابت در نظر بگیریم. به این ترتیب محاسبات به شکل زیر انجام خواهد شد:
همچنین نکته مهم در مرود این محاسبات این است که اگر تابعی از دو متغیر باشد، در این صورت هر دو نسبت دیفرانسیلی و وجود دارند. بهعلاوه میتوانیم برای مثال دیفرانسیلگیری جزئی مرتبه دوم را به شکل یا نیز بنویسیم.
یادگیری معادلات دیفرانسیل با فرادرس
در بخش قبل در کنار توضیح تفاوت مشتق و دیفرانسیل آموختیم تعریف یک معادله دیفرانسیل چیست. معادلات دیفرانسیل زبان استاندارد مدلسازی ریاضی به منظور توصیف رفتار سیستمها و طبیعت هستند. به همین دلیل یکی از مهمترین درسهایی که در مقطع کارشناسی بسیاری از رشتههای فنی و مهندسی یا علوم پایه تدریس میشود، درس «معادلات دیفرانسیل معمولی» (Ordinary Differential Equations) است. در این بخش تصمیم داریم به معرفی چند فیلم آموزشی رایگان با موضوع معادلات دیفرانسیل بپردازیم تا با مشاهده این دورهها و حل مثالها و تستهای متنوع در این زمینه به انواع معادلات دیفرانسیل و روش حل آنها کاملا مسلط شوید:
همچنین در مجموعه زیر میتوانید فیلمهای آموزشی فرادرس در زمینه حل معادلات دیفرانسیل با استفاده از نرمافزارهایی مانند «متمتیکا» (Mathematica)، «فرترن» (Fortran)، «میپل» (Maple) و «فلکس پیدیای» (Flex PDE) را مشاهده کنید:

حل مثال و تمرین از تفاوت مشتق و دیفرانسیل
در بخشهای گذشته با تفاوت مشتق و دیفرانسیل آشنا شدیم. در آخرین بخش از این مطلب از مجله فرادرس با بررسی چند مثال نشان میدهیم که در مسائل مربوط به علم حساب این دو مفهوم چگونه مطرح میشوند. همچنین در انتهای این بخش چند سوال چهار گزینهای بهعنوان تمرین برای شما در نظر گرفته شده است تا با پاسخدهی به آنها میزان یادگیری خود را در این زمینه بیازمایید.
مثال ۱
دیفرانسیل تابع زیر را بهدست آورید:
پاسخ
برای محاسبه دیفرانسیل هر متغیری از جمله که یک تابع است، از فرمول زیر استفاده میکنیم:
طبق این فرمول ابتدا باید مشتق تابع را بدانیم که مستلزم دانستن فرمول مشتق سکانت در دومین جمله این تابع است. مشتق سکانت همواره برابر است با . بنابراین با مشتقگیری از این تابع دو جملهای داریم:
مثال ۲
دیفرانسیل تابع را به ازای تغییر از تا محاسبه کنید:
پاسخ
حل این سوال به کمک فرمول دیفرانسیل امکانپذیر است:
اما طبق این فرمول در اولین قدم باید مشتق تابع نمایی را محاسبه کنیم که به شکل زیر بهدست میآید:
حالا با توجه به صورت سوال و تغییرات از تا ، داریم:
و چون این مقدار خیلی کوچک است، پس میتوانیم تقریب زیر را در نظر بگیریم:
به این ترتیب حاصل دیفرانسیلگیری بالا با توجه به اینکه است، برابر میشود با:
مثال ۳
مقادیر عددی و را در مورد تابع در صورتی که از تا کاهش داده شود، پیدا کنید:
پاسخ
این سوال مشابه مثال قبلی است، با این تفاوت که در اینجا هم در کنار خواسته شده و این به ما کمک میکند تا بهتر متوجه دیفرانسیل و تفاوت آن با مفهومی به نام تغییرات یک متغیر شویم. همچنین در این سوال مقدار متغیر مستقل یا ما به اندازه کوچکی کاهش داده شده است و انتظار داریم پاسخ نهایی برای دیفرانسیلگیری و محاسبه تغییرات منفی شود. در اولین مرحله برای محاسبه تغییرات یا به ازای تغییر در متغیر به شکل زیر پیش میرویم:
دقت کنید برای بهدست آوردن تغییرات، کافی است مقدار تابع در حالت نهایی از مقدار تابع در حالت اولیه کم شود:
در بخش دوم این سوال باید دیفرانسیل را محاسبه کنیم و همانطور که میدانید پیش از آن باید مشتقگیری از تابع داده شده انجام شود:
تغییرات از تا است. پس داریم:
و چون این مقدار کوچک است، پس میتوانیم تقریب زیر را در نظر بگیریم:
به این ترتیب مقدار عددی دیفرانسیلگیری بالا در برابر میشود با:
دقت کنید در این نوع محاسبات مقداری که برای در عبارت بالا قرار میدهیم، همواره مقدار اولیه است نه مقداری که به آن پس از تغییر کوچکی میرسد. ملاحظه میکنید پاسخی که در هر دو حالت بهدست آمد، نزدیک به هم است و با کوچکتر کردن مقدار عددی تغییرات ، این دو پاسخ نیز به هم نزدیک و نزدیکتر میشوند.
مثال ۴
فرض کنید اضلاع یک مکعب به اندازه و با خطایی کمتر از تخمین زده شدهاند. اگر از این اندازهگیری برای محاسبه حجم مکعب استفاده شود، بیشترین خطای ممکن در محاسبه حجم چقدر است؟
پاسخ
در این سوال میتوانید با جنبههای کاربردی مطالبی که تا اینجا گفتیم، کاملا آشنا شوید. ابتدا باید بدانیم حجم مکعبی با طول ضلع توسط رابطه زیر تعیین میشود:
در این سوال است و . اولین قدم این است که اینچ را به فوت تبدیل کنیم. تبدیل واحد اینچ به صورت زیر انجام میشود:
حالا با نوشتن فرمول دیفرانسیل به شکل زیر میتوانیم خطای محاسباتی در حجم را بهدست آوریم:
تمرین ۱
دیفرانسیل برابر با کدام گزینه است
گزینه دوم درست است. دقت کنید در اینجا دیفرانسیل تابعی به نام را میخواهیم که بر حسب متغیر نوشته شده است. بنابراین برای مثال گزینههای اول و سوم بر حسب متغیر هستند و این اشتباه است. دیفرانسیلگیری از این تابع با فرمول زیر و بر اساس محاسبه مشتق تابع به شکل زیر انجام میشود:
تمرین ۲
و به ترتیب برابر با کدام گزینه هستند اگر باشد و از تا تغییر کند؟
و
و
و
و
گزینه اول درست است. ابتدا باید دیفرانسیل را محاسبه کنیم و همانطور که میدانید پیش از آن باید مشتقگیری با توجه به فرمول مشتق تابع کسینوسی انجام شود:
تغییرات از تا است. پس داریم:
و چون این مقدار کوچک است، پس میتوانیم تقریب زیر را در نظر بگیریم:
به این ترتیب مقدار عددی دیفرانسیلگیری بالا در بهعنوان مقدار اولیه متغیر برابر میشود با:
در مرحله بعد برای محاسبه به ازای تغییر در متغیر به شکل زیر پیش میرویم:
تمرین ۳
شعاع کرهای با حداکثر خطایی به اندازه ، برابر با اندازهگیری شده است. حداکثر خطایی که در محاسبه حجم آن ممکن است داشته باشیم، چقدر است؟
گزینه آخر درست است. ابتدا باید فرمول حجم کره بر حسب شعاع را بنویسیم:
در این سوال است و . با نوشتن فرمول دیفرانسیل به شکل زیر میتوانیم خطای محاسباتی در حجم را بهدست آوریم:
source
