«فرآیند بی دررو یا آدیاباتیک» (Adiabatic Process) یکی از انواع فرآیندهای ترمودینامیکی است که در آن هیچ گرمایی از طریق مرزهای سیستم به داخل آن وارد یا از آن خارج نمیشود. بنابراین در فرآیند بی دررو گرمای کل سیستم ثابت میماند و هیچگونه تبادل گرما یا جرم بین سیستم و محیط اطراف آن وجود ندارد (که البته این به معنای ثابت ماندن دما در این فرآیند نیست). در این مطلب از مجله فرادرس توضیح میدهیم فرآیند بی دررو چه ویژگیهایی دارد و تفاوت آن با سایر فرآیندهای ترمودینامیکی چیست.

به همین منظور پس از اینکه با تعریف و ویژگیهای این نوع فرآیند در بخش اول کاملا آشنا شدید، در بخش بعدی به توضیح و معرفی فرمولهای آن میپردازیم. سپس انواع فرآیند بی دررو شامل برگشتپذیر و برگشتناپذیر را توضیح میدهیم. به این ترتیب با «فرآیندهای آیزنتروپیک» نیز آشنا خواهید شد. همچنین نشان میدهیم که چگونه با استفاده از قانون اول ترمودینامیک میتوانیم فرمول این فرآیند را بهدست آوریم. یکی دیگر از بخشهای این نوشته به بررسی فرمول کار در فرآیند بی دررو اختصاص دارد و خواهید دید که در این نوع فرآیند کار عامل انتقال انرژی بین سیستم و محیط محسوب میشود. در انتها با حل مثالهای متنوع به شما کمک میکنیم تا به این مبحث کاملا مسلط شوید.
فرآیند بی دررو چیست؟
فرآیند بی دررو یا آدیاباتیک نمونهای از یک فرآیند ترمودینامیکی است که در آن هیچگونه تبادل گرمایی بین سیستم و محیط اطراف آن وجود ندارد (). این نوع فرآیند میتواند برگشتپذیر یا برگشتناپذیر باشد و مشخصه اصلی آن، ثابت ماندن گرمای کل سیستم است. در فرآیند بی دررو قابلیت انبساط یا تراکم سیستم به ترتیب با مصرف انرژی داخلی آن یا از طریق کار انجام شده روی آن وجود دارد. بنابراین فشار، حجم و دمای سیستم طی این فرآیند ممکن است تغییر کنند.
برای اینکه بتوانیم یک فرآیند بی دررو داشته باشیم، لازم است شرایط زیر برقرار باشد:
- سیستم باید به شکل کاملا ایدهآلی از محیط اطراف عایق شده باشد.
- لازم است فرآیند خیلی سریع انجام شود، به گونهای که زمان کافی برای انتقال گرما وجود نداشته باشد، حتی اگر سیستم از نظر حرارتی بهخوبی عایق نشده باشد.
بنابراین در صورت برقراری این دو شرط میتوانیم شاهد رخ دادن نمونهای از یک فرآیند بی دررو یا آدیاباتیک باشیم. گفتیم در فرآیند بی دررو گرمای کل سیستم ثابت میماند و این به معنای ثابت ماندن دمای سیستم نیست. اگر دما در یک فرآیند ترمودینامیکی ثابت بماند، «فرآیند همدما یا ایزوترمال» را داریم که موضوع بخشهای بعدی است. درک تفاوت این دو نوع فرآیند به درک تفاوت دما و گرما برمیگردد. دما متوسط انرژی جنبشی اتمها یا مولکولهای یک سیستم است، در حالی که حرارت یا گرما نوعی انرژی است که در نتیجه اختلاف دما بین دو سیستم جاری میشود.
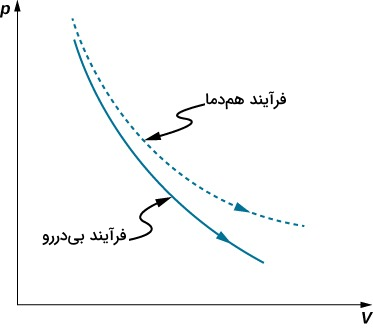
در تصویر بالا نمودار یک فرآیند بیدررو را در مقایسه با یک فرآیند همدما مشاهده میکنید که هر دو انبساط یک گاز کامل را نشان میدهند. یکی از مثالهای رایج برای تراکم بیدررو که در بخشهای بعد با آن بیشتر آشنا میشوید، خارج شدن هوای داخل یک لاستیک پنوماتیکی است. همچنین از بازدهی آدیاباتیکی در ساخت وسایلی مانند نازلها، کمپرسورها و توربینهای گازی یا در روند سردسازی یا تبرید در یخچالها استفاده میشود. جالب است بدانید که یک نوسانگر هارمونیک کوانتومی را میتوانیم نمونهای از یک سیستم بیدررو در نظر بگیریم. بهعلاوه یکی از مرسومترین فرآیندهای بیدررو در محیط اطراف ما، انبساط بیدرروی هوا است. وقتی که هوای گرم از سطح زمین به بالا میرود، بهصورت آدیاباتیک منبسط میشود و در نتیجه، بخار آب سرد شده در قالب قطرات آب ابرها را میسازد.
یادگیری ترمودینامیک متوسطه با فرادرس
مباحث دما، گرما و قوانین ترمودینامیک کلاسیک در آخرین فصل از کتاب درسی فیزیک پایه دهم مطرح میشوند که فرآیند بی دررو یکی از موضوعات آن است. در این بخش قصد داریم چند دوره آموزشی مرتبط با این عناوین را به شما معرفی کنیم تا از طریق مشاهده فیلم و حل مثالها و تمرینهای بیشتر یادگیری خود را در این زمینه تکمیل کنید:
فرمول فرآیند بی دررو چیست؟
پس از اینکه در بخش قبل آموختیم مفهوم و تعریف فرآیند بی دررو چیست، در این قسمت میخواهیم به معرفی فرمول این فرآیند ترمودینامیکی بپردازیم. فرآیند بی دررو برای یک گاز ایدهآل با فرمول زیر توصیف میشود:
- : فشار گاز ایدهآل بر حسب پاسکال ()
- : حجم گاز ایدهآل بر حسب متر مکعب ()
- : ضریب بیدررو (بدون واحد)
دقت کنید در تمام مباحث مطرح شده در این نوشته منظور ما از سیستمهای ترمودینامیکی سیستمهایی شامل گازهایی با مشخصات گاز ایدهآل است. ضریب بیدررو را میتوانیم بر اساس نسبت ظرفیت گرمایی در فشار و حجم ثابت یا نسبت گرمای ویژه در فشار و حجم ثابت تعریف کنیم. هر دو تعریف به ما فرمولهایی با نتایج یکسان میدهد، چون اگر به تعریف این دو کمیت دقت کنیم، تنها تفاوت آنها در پارامتر جرم است.
ظرفیت گرمایی که با نشان داده میشود، عبارت است از میزان گرمایی که برای افزایش دمای ماده به اندازه یک درجه لازم است به کل ماده داده شود. این در حالی است گرمای ویژه هم تعریف مشابهی دارد، با این تفاوت که در آن گرمای داده شده به یک کیلوگرم از ماده (و نه کل ماده) را در نظر میگیریم. پس محاسبه ضریب بیدررو به هر دو روش زیر درست است:
- نسبت گرمای ویژه در فشار ثابت به گرمای ویژه در حجم ثابت:
- نسبت ظرفیت گرمایی در فشار ثابت به ظرفیت گرمایی در حجم ثابت:
این ضریب با عنوان «نسبت ظرفیت گرمایی» یا «فاکتور انبساط آیزنتروپیک» نیز شناخته میشود. بهطور کلی میتوانیم بگوییم اندازه این ضریب به ماهیت ماده یا گاز مورد بررسی در مسئله ترمودینامیکی ما بستگی دارد. فرمول فرآیند بی دررو این واقعیت را بیان میکند که اگر از حالت تعادل اولیه با پارامترهای به حالت تعادل ثانویه با پارامترهای بهصورت بیدررو برویم، رابطه زیر همواره برقرار است:
در بخش «فرآیند بی دررو و قانون اول ترمودینامیک» از همین مطلب، نحوه استخراج فرمول ابتدای این بخش را بر اساس قانون اول ترمودینامیک بهصورت کامل توضیح میدهیم. یکی دیگر از روشهای تعمیم فرمول بالا این است که از قانون گاز ایدهآل به شکل زیر استفاده کنیم:
- : فشار گاز ایدهآل بر حسب پاسکال ()
- : حجم گاز ایدهآل بر حسب متر مکعب ()
- : دمای گاز ایدهآل بر حسب کلوین ()
- : مقدار گاز ایدهآل بر حسب مول ()
- : ثابت جهانی گازها با مقدار
با قرار دادن فشار بهدست آمده از قانون گازها در فرمول ابتدای بخش خواهیم داشت:
حالا اگر ثوابتی مانند و را در رابطه بالا به سمت راست تساوی ببریم، ثابت جدیدی خواهیم داشت که باز هم میتوانیم آن را با نماد کلی constant نشان دهیم:
ساده کردن این عبارت ما را به فرمول زیر میرساند:
این فرمول تغییر حالت بیدرروی سیستم را از حالت تعادل اولیه با پارامترهای به حالت تعادل ثانویه با پارامترهای به ما نشان میدهد که با رابطه زیر معادل است:
به همین شکل میتوانیم فرمول اول این بخش برای فرآیند بی دررو را بر حسب دو متغیر فشار و دما نیز بنویسیم:
اگر تمایل دارید با قوانین ترمودینامیکی و فرمولهای آن بهصورت کامل و جامع آشنا شوید، پیشنهاد ما مطالعه مطلب «ترمودینامیک چیست؟ – آموزش علم و قوانین به زبان ساده» از مجله فرادرس است.
فرمول کار در فرآیند بی دررو چیست؟
در این قسمت میخواهیم ببینم کار انجام شده طی یک فرآیند بی دررو چگونه محاسبه میشود. مقدار مول از یک گاز ایدهآل محبوس شده در داخل استوانهای به شکل زیر را در نظر بگیرید که تمام سطوح تماسی آن عایق حرارتی هستند. اگر یک پیستون عایق با سطح مقطع را که کاملا با مساحت دهانه این سیلندر استوانهای همخوانی دارد، به سمت پایین حرکت دهیم، در حقیقت روی این گاز کاری توسط یک نیروی خارج از سیستم انجام دادهایم.
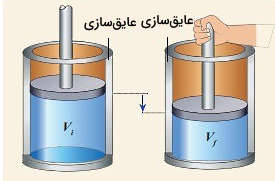
در این شرایط سیستم بهصورت بیدررو از حالت اولیهای با مشخصات به حالت نهایی با پارامترهای میرسد. برای محاسبه کار خارجی لازم برای وقوع چنین تغییری، کافی است فرمول زیر را بنویسیم:
همچنین با در نظر گرفتن این واقعیت که فرآیند بی دررو به شکل شبه استاتیکی رخ میدهد، پس در هر نقطه از این فرآیند قانون گازهای ایدهآل برقرار است. بنابراین میتوانیم از رابطه استفاده کنیم:
اما بهجای مقادیر ثابت در رابطهای که در نهایت بهدست آوردیم، میتوانیم از فرمول به شکل زیر استفاده کنیم:
بهعلاوه میتوانیم این رابطه را مجددا بر اساس قانون گازهای ایدهآل به شکل زیر نیز بنویسیم:
نکته مهم: این رابطه کار انجام شده توسط نیروی خارجی یا همان کار خارجی روی گاز ایدهآل یا سیستم ترمودینامیکی موردنظر ما را محاسبه میکند. کار انجام شده توسط گاز ایدهآل همواره اندازهای برابر با این مقدار ولی علامتی مخالف دارد.
فرآیند بی دررو برگشت پذیر
فرآیند بی دررو برگشتپذیر که به آن فرآیند «همآنتروپی یا آیزنتروپیک» (Isentropic) هم گفته میشود، نوعی فرآیند ایدهآل ترمودینامیکی و بیدررو است که طی آن کار منتقل شده در سیستم با هیچگونه اتلافی همراه نیست، به این معنا که هیچ نوع انتقال گرما یا ماده نداریم. بنابراین فرآیند برگشتپذیر است. از چنین فرآیند ایدهآلی در علوم مهندسی بهعنوان یک مدل پایه جهت مقایسه با سیستمهای واقعی استفاده میشود.
اگر بخواهیم کمی دقیقتر وارد جزئیات این فرآیند شویم، ابتدا بهتر است بدانیم تعریف فرآیند آیزنتروپیک چیست. فرآیند آیزنتروپیک به فرآیندی گفته میشود که تغییرات آنتروپی در آن صفر است. با توجه به تعریف فرآیند بی دررو که در آن انتقال گرما صفر است، نتیجه میگیریم که تغییرات آنتروپی هم باید صفر باشد. در واقع آنتروپی که با نماد نمایش داده میشود، برابر است با و به همین دلیل است که اگر باشد، هم برابر با صفر است. بنابراین فرآیندهای بیدررو میتوانند آیزنتروپیک هم در نظر گرفته شوند. تراکم هوای داخل کمپرسورها یا انبساط بخار در توربینهای بخار نمونههایی از فرآیند آیزنتروپیک یا فرآیند بی دررو برگشتپذیر هستند.
فرآیند بی دررو برگشت ناپذیر
در مقابل فرآیند بی دررو برگشتپذیر، فرآیند بی دررو برگشتناپذیر را داریم و به این معنا است که طی آن سیستم امکان بازگشت به حالت اولیه خود را ندارد. برای مثال، اگر یک انبساط بیدرروی برگشتناپذیر را در نظر بگیریم، تغییراتی در آنتروپی خواهیم داشت که در نتیجه اتلافهای ناشی از اصطکاک است. تفاوت مهم این نوع فرآیند با فرآیند آیزنتروپیک این است که در نوع برگشتناپذیر سیستم حالت شبه استاتیکی خود را حفط نمیکند، چون فرآیند آنقدر آهسته رخ میدهد که حالت تعادل حفظ نمیشود. به همین علت فرمولهایی که برای فرآیند بی دررو در بخشهای قبل معرفی شدند، در مورد این نوع فرآیند برقرار نیستند.
برای اینکه بتوانید به این مفاهیم کاملا مسلط شوید و رابطه بین پارامترهای ترمودینامیکی مختلف مانند دما، آنتروپی، آنتالپی، انرژی داخلی و … را بهتر متوجه شوید، لازم است تمرین بیشتری از طریق مشاهده دورههای آموزشی مرتبط داشته باشید. فرادرس یک فیلم آموزشی با عنوان آموزش ترمودینامیک ۲ – مرور و تست کنکور ارشد در همین زمینه تهیه کرده است که لینک آن در ادامه برای شما قرار داده شده است:
انبساط بی دررو
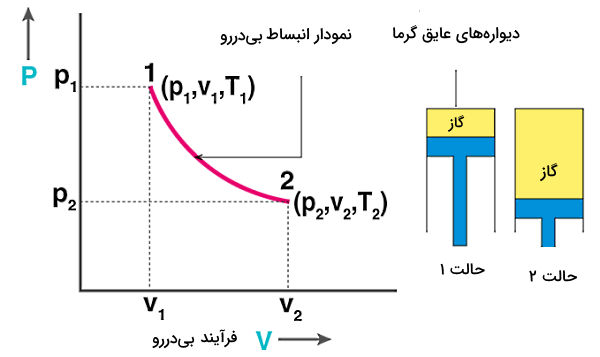
انبساط بیدررو نوعی فرآیند انبساط است که در آن هیچ نوع برهمکنش گرمایی بین سیستم و محیط وجود ندارد و کار انجام شده توسط سیستم به کمک انرژی داخلی آن انجام میشود. دقت کنید در انبساط بیدررو کار انجام شده توسط گاز ایدهآل مثبت است، چون در این فرآیند فشار گاز طبق شکل زیر کم میشود. پس اگر به فرمول کار که در بخش قبل بهدست آمد مراجعه کنیم، حاصل عددی منفی است و با توجه به اینکه کار خارجی منفی شده است، پس کار انجام شده توسط سیستم مثبت است.
تراکم بی دررو
برای اینکه با تراکم بیدررو آشنا شوید، تراکم بیدرروی هوای داخل سیلندری مطابق شکل زیر را در نظر بگیرید. در این فرآیند تراکم به گونهای انجام میشود که هیچ گرمایی از محیط بیرون به هوا اضافه نشود یا هیچ گرمایی از داخل سیلندر به خارج نرود. به این ترتیب انرژی داخلی هوا به اندازه کار خارجی انجام شده روی آن افزایش مییابد. پس با اعمال نیروی دست به پیستون مطابق تصویر سمت راست، فشردهسازی هوای داخل سیلندر در قالب یک فرآیند بی دررو انجام خواهد شد.
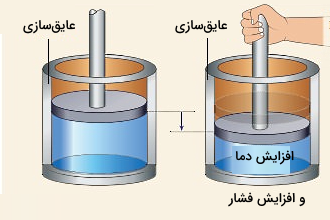
اگر بخواهیم کار انجام شده توسط سیستم در یک فرآیند تراکم بیدررو را محاسبه کنیم، کافی است ابتدا کار خارجی در این فرآیند را مطابق فرمول برآورد کنیم. چون طی تراکم فشار سیستم در حالت نهایی افزایش مییاید، بنابراین مقدار کار خارجی مثبت است، در حالی که کار سیستم روی محیط منفی است.
نمودار فرآیند بی دررو چگونه رسم میشود؟
در بررسی فرآیندهای ترمودینامیکی برای یک سیستم، میدانیم که اگر بخواهیم از حالت اولیه به حالت نهایی برسیم، مسیرهای مختلفی وجود دارند. همچنین این نکته مهم است که متغیرهای ترمودینامیکی توصیف کننده یک سیستم فقط در حالت تعادل سیستم با محیط اطرافش تعریف میشوند. تصویر زیر انواع فرآیندهای ترمودینامیکی را نشان میدهد که فرآیند بی دررو یکی از آنها است:

در هر کدام از این فرآیندها یکی از انواع پارامترهای ترمودینامیکی شامل دما، گرما، فشار یا حجم ثابت میماند و بر همین اساس نام گذاری آنها انجام شده است. برای نمونه، در «فرآیند همفشار یا ایزوبار»، است. برای رسم نمودارهای مرتبط با فرآیندهای ترمودینامیکی عموما مقادیر فشار بر حسب حجم رسم میشود. شکل زیر نمودارهای برای انبساط و تراکم بیدررو را نشان میدهد:
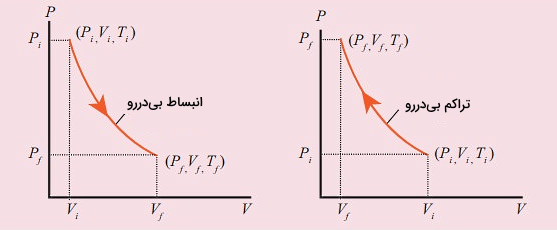
یکی دیگر از روشهای محاسبه کار انجام شده طی یک فرآیند آدیاباتیک این است که پس از رسم نمودار مساحت زیر آن را پیدا کنیم. این روش با توجه به اینکه نمودار فرآیند بی دررو مانند نمودار فرآیند همدما منحنی شکل و خطی نیست، اغلب دشوار است و نیاز به انتگرالگیری دارد. اگر به یاد داشته باشید، این روند را در بخش مربوط به استخراج فرمول کاملا توضیح دادیم.
فرآیند بی دررو و قانون اول ترمودینامیک
در این بخش میخواهیم ارتباط فرآیند بی دررو و قانون اول ترمودنیامیک را توضیح دهیم. خواهید دید که با توجه به فرمول قانون اول میتوانیم برای فرآیند بی دررو رابطه مناسبی را استخراج کنیم که در بخشهای قبل آن را به عنوان فرمول فرآیند بی دررو معرفی کردیم. ابتدا باید ببینیم قانون اول ترمودینامیک چیست و چه فرمولی دارد. این قانون رابطه بین تغییرات انرژی داخلی (انرژی درونی) سیستم، کار انجام شده و تغییر گرمای سیستم را به شکل زیر توصیف میکند:
- : تغییرات انرژی داخلی (انرژی درونی) سیستم
- : کار انجام شده
- : گرمای اضافه یا کم شده
حالا اگر بخواهیم این فرمول را در مورد یک فرآیند بی دررو بازنویسی کنیم، با توجه به تعریف چون تبادل گرما در این نوع فرآیند وجود ندارد، پس داریم:
و قانون اول ترمودینامیک برای آن به شکل زیر میشود:
یا
جمله در رابطه بالا به گرمای ویژه بستگی دارد. همانطور که اشاره شد، گرمای ویژه (Specific Heat Capacity یا Specific Heat) را میتوانیم بهصورت مقدار گرمایی در نظر بگیریم که به ازای یک واحد تغییر دما به یک مول ماده اضافه میشود. واحد این کمیت مهم ترمودینامیکی طبق تعریف برابر است با ژول بر کیلوگرم در کلوین یا . بنابراین این گرمای اضافه شده موجب افزایش انرژی داخلی یا سیستم میشود، به گونهای که میتوانیم گرمای ویژه در حجم ثابت را به شکل زیر تعریف کنیم:
در این رابطه معادل است با تعداد مولهای سیستم ترمودینامیکی ما. از طرفی کار انجام شده در حجم را میتوانیم به شکل زیر تعریف کنیم:
با قرار دادن دو عبارت بهدست آمده در فرمول قانون اول ترمودینامیک برای فرآیند بی دررو خواهیم داشت:
در اینجا از قانون گازهای ایدهآل به شکل کمک میگیریم، به این صورت که اگر از طرفین آن دیفرانسیل بگیریم، خواهیم داشت:
با جایگزین کردن رابطه بالا در آخرین فرمولی که نوشتیم، داریم:
اگر تمام پارامترهای این رابطه را در یک سمت تساوی قرار دهیم و به شکل زیر آن را ساده کنیم، خواهیم داشت:
زمانی که گرما در فشار ثابت به این سیستم اضافه میشود، گرمای ویژه در فشار ثابت را به شکل زیر میتوانیم بنویسیم:
پس از این رابطه در آخرین فرمول ساده شده استفاده میکنیم که با توجه به تعریف زیر خواهیم داشت:
حال با توجه به قوانین لگاریتم طبیعی داریم:
پس میتوانیم رابطه بالا را به شکل زیر بازنویسی کنیم:
در آخرین مرحله صفر شدن دیفرانسیل عبارت داخل پرانتز ما را به این نتیجه میرساند که این عبارت باید با یک عدد یا مقدار ثابت برابر باشد. پس موفق شدیم فرمول فرآیند بی دررو را از قانون اول ترمودینامیک استخراج کنیم.
فرآیند بی دررو و آنتالپی
یکی دیگر از فرمهای نمایش معادلات ترمودینامیکی این است که آنها را بر اساس کمیتی به نام آنتالپی با نماد بنویسیم. در حالت کلی آنتالپی به شکل زیر محاسبه میشود:
اگر از طرفین این رابطه دیفرانسیلگیری کنیم، به عبارت زیر میرسیم:
که در آن همان انرژی داخلی سیستم است. از طرفی گفتیم قانون اول ترمودینامیک برابر است با . حالا فرض کنید میخواهیم این قانون را برای یک فرآیند بی دررو فشار ثابت اعمال کنیم. به این ترتیب میشود و میتوانیم برای جمله از استفاده کنیم. پس قانون اول در مورد این فرآیند به شکل درمیآید. با جایگذاری این عبارت در فرمول بالا خواهیم داشت:
به این ترتیب تغییرات آنتالپی با کار انجام شده توسط سیستم برابر شد. از این فرمول در سیستمهایی مانند توربینها یا پمپها استفاده میشود.
فرآیند ایزوترمال چیست و چه تفاوتی با فرآیند بی دررو دارد؟
«فرآیند ایزوترمال یا همدما» (Isothermal Processes) یکی دیگر از انواع فرآیندهای ترمودینامیکی است که طی آن دما ثابت میماند. همانطور که در ابتدای مطلب ذکر شد، با توجه به اینکه در یکی از این دو فرآیند دما و در دیگری گرما ثابت میماند، ممکن است این دو فرآیند مشابه هم تصور شوند، در حالی که این چنین نیست.
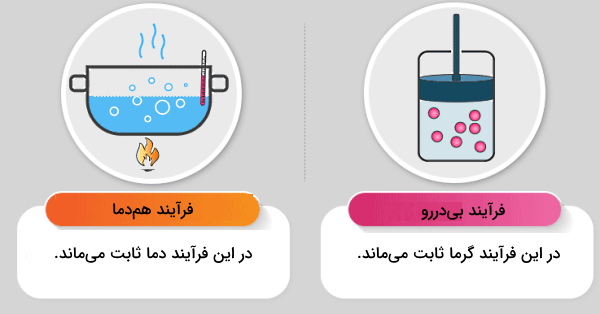
در فرآیند ایزوترمال بر خلاف فرآیند بی دررو انتقال گرما به محیط اطراف انجام میشود تا به این وسیله دمای سیستم ثابت بماند. مقایسه این فرآیند با فرآیند بی دررو در جدول زیر انجام شده است:
| فرآیند بی دررو یا آدیاباتیک | فرآیند ایزوترمال یا همدما |
| در طول این فرآیند ترمودینامیکی هیچگونه انتقال گرمایی بین سیستم و محیط وجود ندارد (). | در طول این فرآیند ترمودینامیکی همواره دما ثابت میماند (). |
| کار انجام شده در نتیجه تغییرات انرژی داخلی سیستم است. | کار انجام شده در نتیجه تغییرات گرمای خالص درون سیستم است. |
| در طول این فرآیند دما میتواند تغییر کند. | در طول این فرآیند دما تغییر نمیکند. |
| در طول این فرآیند هیچ انتقال گرمایی وجود ندارد. | در طول این فرآیند انتقال گرما داریم تا دما ثابت نگه داشته شود. |
| فشار در یک حجم مشخص پایین است. | فشار در یک حجم مشخص بالا است. |
همچنین تصویر زیر نشان میدهد که از نظر نموداری یک فرآیند همدما چگونه است. میتوانیم با در نظر گرفتن تغییرات حجم سیستم از حالت به حالت ، کار انجام شده را به شکل زیر محاسبه کنیم:
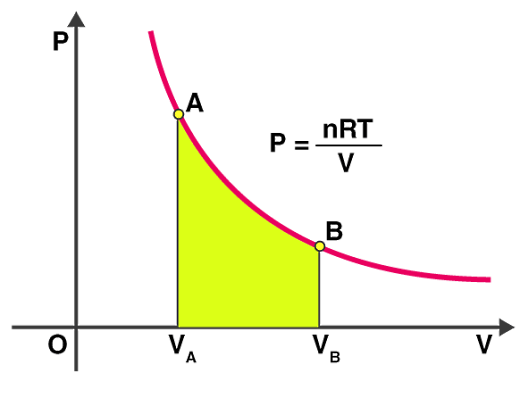
با کمک گرفتن از قانون گازهای ایدهآل میتوانیم رابطه بالا را به شکل زیر بنویسیم:
یادگیری ترمودینامیک دانشگاهی با فرادرس
پیش از شروع یادگیری علم ترمودینامیک در سطوح دانشگاهی، ابتدا باید به بخشهایی از مباحث فیزیک پایه ۳ دانشگاهی کاملا مسلط شوید. در ادامه دو فیلم آموزشی در همین زمینه برای شما فهرست شدهاند:
ترمودینامیک یکی از مهمترین مباحث در رشتههای فیزیک، شیمی، مهندسی مکانیک و مهندسی شیمی است، بهویژه در مطالعه مکانیک سیالات و انتقال حرارت از قوانین این علم استفاده زیادی میشود. این مبحث در سطوح پیشرفتهتر خود از ترمودینامیک کلاسیک عبور کرده و میرسد به «مکانیک آماری» که در بیشتر گرایشهای رشته فیزیک در قالب یک درس سه واحدی تدریس میشود و یکی از مباحث پرکاربرد در پیشبینی خیلی از سیستمهای بینظم و آشفته است. در مکانیک آماری سیستمهایی که شامل تعداد بسیار زیادی ذره هستند با استفاده از قوانین کوانتومی مورد مطالعه قرار میگیرند. در ادامه چند دوره تصویری در این راستا نیز معرفی شدهاند:
حل مثال و تمرین از فرآیند بی دررو
در این نوشته از مجله فرادرس با ویژگیها و فرمولهای فرآیند بی دررو کاملا آشنا شدیم. در انتها قصد داریم با حل و بررسی چند مثال به شما در تسلط بیشتر به این مفاهیم کمک کنیم. همچنین میتوانید با حل سوالات چهار گزینهای داده شده در این بخش و در قالب تمرین، میزان یادگیری خود را بیازمایید. در جدول زیر تمام فرمولهای مربوط به فرآیند بی دررو را برای شما جمعآوری کردهایم:
| فرمولهای فرآیند بی دررو () | |
| سیستم از حالت به میرود: | |
| سیستم از حالت به میرود: | |
| سیستم از حالت به میرود: | |
| فرمول کار | |
| قانون اول ترمودینامیک | |
مثال ۱
اغلب ما تجربه پمپ کردن هوا به داخل لاستیک یک دوچرخه را ممکن است داشته باشیم. فرض کنید هوای داخل پمپ مخصوص برای این کار مانند یک سیستم ترمودینامیکی عمل میکند و دارای حجم مشخص در فشار اتمسفر و دمای محیط یعنی است. در صورتی که نازل این پمپ دچار مشکل شده و حجم هوای داخل آن شود، اگر ضریب بیدرروی هوا باشد، دمای نهایی هوای داخل پمپ چقدر است؟
پاسخ
فرآیند فشردهسازی هوای داخل این پمپ به شکل بیدررو انجام شده است. بنابراین باید از فرمولهای مخصوص این فرآیند استفاده کنیم که بهترین انتخاب فرمولی است که در آن حجم و دما را داشته باشیم (چون فشار تغییری نمیکند):
دقت کنید اگر حجم اولیه باشد، حجم نهایی برابر است با . پس داریم:
همانطور که ملاحظه میکنید دمای هوای داخل پمپ از نقطه جوش آب بسیار بالاتر بهدست آمد. بنابراین اگر در این شرایط قرار دارید، باید از تماس با نازل پمپ اجتناب کنید.
مثال ۲
فرض کنید مقداری بخار بنزین به سیلندر موتور یک اتومبیل در شرایطی که پیستون آن در موقعیت انبساطی خود قرار دارد، تزریق شده است. در نتیجه فشار، دما و حجم مخلوط گاز و هوا به ترتیب برابر میشوند با و و . همچنین ضریب بیدرروی هوا برابر است با .
- چنانچه این مخلوط بهصورت بیدررو تا حجم متراکم شود، فشار و دمای این مخلوط پس از تراکم چقدر است؟
- محاسبه کنید چه میزان کار توسط مخلوط گاز و هوا در طول این فرآیند تراکم بیدررو انجام شده است. دقت کنید در شرایط واقعی عملکرد موتور یک اتومبیل، تراکم یک فرآیند شبه استاتیکی نیست. اما در اینجا فرض میکنیم این چنین نیست.
پاسخ
با توجه به فرض این سوال که در آن فرآیند اتفاق افتاده به شکل یک تراکم بیدررو و شبه استاتیکی برای گاز ایدهآل مدلسازی شده است، فرمولهای و برقراراند. پس میتوانیم فرمول اول را به شکل زیر بنویسیم و با توجه به تغییرات حجم، فشار نهایی را محاسبه کنیم:
دقت کنید در محاسبات بالا با اینکه واحد حجم بهصورت استاندارد نوشته نشده است، اما مانعی ایجاد نمیکند. چون نسبت حجمها در فرمول قرار داده شده و نیازی به تبدیل واحد در اینجا نداریم. پس فشار در حالت نهایی محاسبه شد. برای پیدا کردن دمای نهایی، کافی است به کمک قانون گازهای کامل و به شکل زیر عمل کنیم:
در مرحله بعدی برای محاسبه کار انجام شده توسط سیستم ترمودینامیکی که در اینجا مخلوط هوا و گاز است، کافی است فرمول زیر را بنویسیم:
نکته مهم در اینجا این است که این فرمول کار خارجی را حساب میکند،در حالی که هدف ما محاسبه کاری است که سیستم ترمودینامیکی در این فرآیند انجام میدهد. به همین دلیل باید پس از محاسبه، پاسخ خود را با علامت مخالف در نظر بگیریم:
بهعلاوه حتما لازم است در این فرمول تبدیل واحدها برای حجم انجام شود تا در انتها کار محاسبه شده بر حسب ژول بهدست آید. کاری که پیستون روی مخلوط هوا و گاز انجام داده است، مطابق انتظار ما برای تراکم مقداری منفی بهدست آمد. بنابراین کار مخلوط گاز و هوا روی پیستون مثبت است و برابر است با .
مثال ۳
یک نمودار را مطابق شکل زیر در نظر بگیرید و فرض کنید که این نمودار نشاندهنده مسیر ترمودینامیکی یک مول گاز کامل در یک محفظه استوانهای شکل است (ضریب بیدرروی گاز برابر است با ).
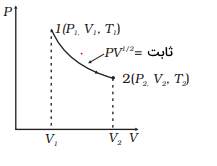
- کار انجام شده برای رفتن از حالت یک به دو را محاسبه کنید.
- نسبت دمایی را با در نظر گرفتن عبارت پیدا کنید:
- اگر بدانیم انرژی داخلی یک مول از این گاز در دمای برابر است با ، گرمایی که باید به این گاز داده شود تا نتیجه مشابهی بگیریم با زمانی که طی یک فرآیند آدیاباتیکی گاز از حالت یک به حالت دو برده میشود و را بهدست آورید:
پاسخ
با توجه به اینکه روی نمودار فرمول در مورد یک گاز کامل نوشته شده است و همچنین در حالت دوم حجم زیاد و فشار کم شده است، پس در حقیقت یک فرآیند انبساط بیدررو داریم. در مورد اولین سوال کافی است از فرمول کار انجام شده روی گاز برای یک فرآیند بی دررو به شکل زیر استفاده کنیم:
دقت کنید چون مقادیر فشار و حجم داده نشده است، نمیتوانیم پاسخ را از این سادهتر کنیم. در مورد سوال بعدی، میتوانیم از فرمول زیر استفاده کنیم تا نسبت دو دمای خواسته شده بهدست آید:
در سومین سوال ابتدا لازم است تغییرات انرژی داخلی گاز را محاسبه کنیم. با توجه به توضیح داده شده، میتوانیم بنویسیم:
دما در حالت دوم در بخش قبل برابر شد با . پس داریم:
همچنین تغییرات کار را با توجه به اولین بخش و اینکه مقدار گاز داده شده برابر است با یک مول ()، میتوانیم به شکل زیر بنویسیم:
بنابراین طبق قانون اول ترمودینامیک خواهیم داشت:
مثال ۴
فرض کنید مقداری هوای خشک در دمای در دو حالت آهسته و ناگهانی متراکم شود و به حجم برابر حجم اولیه خود برسد. تغییرات دمایی در دو حالت را با در نظر گرفتن بهدست آورید:
پاسخ
اگر این تراکم به آهستگی انجام شود، یک فرآیند ایزوترمال یا همدما رخ داده است و در نتیجه دما تغییر نخواهد کرد. یعنی در این حالت داریم:
پس تغییر دما صفر است:
اما اگر تراکم بهصورت ناگهانی انجام شود طوری که فرصتی برای تبادل گرما نداشته باشیم، یک فرآیند بی دررو داریم که لازم است برای پیدا کردن دمای نهایی از فرمول زیر استفاده کنیم:
مثال ۵
روی گازی با که در حالت اولیهای با دمای اتاق و فشار اتمسفر قرار دارد، تراکم سریعی انجام میشود که طی آن داریم .
- دمای نهایی این گاز زا تخمین بزنید.
- اگر در محفظه مول گاز داشته باشیم، چه میزان کار برای این تراکم لازم است ()؟
پاسخ
چون تراکم به سرعت انجام شده است، پس یک فرآیند آدیاباتیک داریم که برای محاسبه دما در حالت دوم و با توجه به تغییرات حجمی داده شده، میتوانیم از فرمول زیر استفاده کنیم:
دمای اتاق را در نظر میگیریم. اما مقدار ضریب بیدررو مشخص نیست و لازم است با توجه به فرمول زیر آن را محاسبه کنیم:
برای پاسخ دادن به سوال دوم، طبق قانون اول ترمودینامیک و با توجه به بیدررو بودن این تراکم، میتوانیم از فرمول زیر استفاده کنیم:
تمرین ۱
کدام گزینه درست است؟
در فرآیند بی دررو هیچ گونه تبادل گرما و جرمی وجود ندارد.
ضریب بی دررو برابر است با نسبت طرفیت گرمایی در فشار ثابت به گرمای ویژه در حجم ثابت.
در یک فرآیند بی دررو همواره برقرار است.
گزینه اول و سوم درست است.
گزینه چهارم صحیح است. دقت کنید در دومین گزینه، نسبت دو کمیت مختلف یعنی ظرفیت گرمایی و گرمای ویژه ذکر شده است، در حالی که طبق تعریف لازم است هر دو کمیت مشابه هم باشند.
تمرین ۲
دو سیلندر و با ابعاد کاملا مشابه هم داریم که هر دوی آنها شامل مقدار یکسانی گاز ایدهآل در دمای اتاق هستند. در سیلندر پیستون آزادانه حرکت میکند، در حالی که در سیلندر پیستون در جای خود ثابت شده است. وقتی که سیلندر گرم میشود، تغییرات دمایی گاز داخل آن برابر است با . اگر همان مقدار گرما به سیلندر تزریق شود، دمای گاز داخل این سیلندر چقدر تغییر میکند (فرض کنید ضریب بیدرروی این گاز برابر است با )؟
دادههای سوال کافی نیست.
گزینه اول صحیح است. در این سوال باید از فرمولی استفاده کنیم که مقدار گرمای لازم برای تغییر دمای یک گاز را در شرایطی که فشار یا حجم آن ثابت میماند، به ما بدهد.
ر مورد سیلندر طی افزایش گرما و تغییرات دمایی همراه با آن، با توجه به اینکه پیستون میتواند حرکت کند، پس حجم گاز زیاد شده و این فرآیند ترمودینامیکی در فشار ثابت انجام میشود. بنابراین فرمول مناسب برای این سیلندر به شکل زیر است:
دقت کنید برابر با ظرفیت گرمایی در فشار ثابت است. از طرفی در مورد سیلندر با توجه به ثابت بودن پیستون، حجم گاز تغییر نمیکند ولی فشار آن در این فرآیند قطعا افزایش مییاید. پس فرمول مناسب در این حالت با در نظر گرفتن ظرفیت گرمایی در حجم ثابت نوشته میشود:
چون گرمای داده شده به هر دو سیلندر یکسان است، پس با مساوی قرار دادن این دو فرمول میتوانیم تغییرات دمایی برای دومین سیلندر را پیدا کنیم:
همچنین مقدار یا تعداد مولهای هر دو گاز طبق فرض صورت سوال یکسان است، پس از دو طرف ساده میشود. بنابراین داریم:
از طرفی میدانیم ضریب بیدررو بر حسب ظرفیت گرمایی برابر است با . پس داریم:
تمرین ۳
گازی با ضریب بیدرروی ، حجم و فشار بهصورت آدیاباتیکی متراکم میشود و به حجم میرسد. کار انجام شده روی گاز در این فرآیند برابر با کدام گزینه است؟
گزینه دوم درست است. میدانیم برای یک فرآیند بی دررو همواره رابطه برقرار است. پس با نوشتن این فرمول به شکل زیر میتوانیم در اولین مرحله فشار گاز پس از تراکم را پیدا کنیم:
سپس با نوشتن فرمول کار مشخص میشود کار انجام شده روی گاز برای اینکه متراکم شود، چقدر است:
این فرمول کار انجام شده روی گاز توسط عامل خارجی را بهدست میدهد که همین کمیت هم در سوال از ما خواسته شده است.
تمرین ۴
کدام گزینه در مورد یک فرآیند بی دررو صحیح است؟
هر سه فرمول بالا درست هستند.
گزینه آخر صحیح است و هر سه فرمول بالا برای یک فرآیند بیدررو درست هستند. در مورد اولین و سومین فرمول در متن توضیحات لازم داده شده است. در مورد فرمول دوم در توضیحات اثبات فرمول این فرآیند بر اساس قانون اول ترمودینامیک دیدیم که است و به فرمولی به شکل نیز رسیدیم. پس فرمول درستی است.
source
