$$ln Y = ln k + alpha ln X$$

$$P(X) = k X^ {-alpha}$$

به علامت منفی در این فرمول دقت کنید. با لگاریتم گرفتن از طرفین این رابطه خواهیم داشت:

$$ln P = ln k – alpha ln X$$

در اغلب توزیع‌های توانی همواره تعداد زیادی مقادیر عددی کوچک و تعداد خیلی کمی مقادیر عددی بزرگ داریم. به این ترتیب توزیع توانی می‌تواند برای توصیف پدیده‌هایی بکار رود که در آن‌ها تعداد خیلی کمی از آیتم‌ها در بالای یک توزیع (یا پایین آن) دسته‌بندی شده‌اند. به عبارت دیگر، این توزیع بیان می‌کند که یک مقدار کوچک از رویدادها معمول است، در حالی که مقدار بیشتری از آن‌‌ها مرسوم نیست. برای مثال، زمانی که توزیع درآمد را در نظر بگیریم، مشاهده می‌کنیم که فقط تعداد خیلی کمی از افراد را می‌توانیم به‌عنوان بیلیونر در نظر بگیریم.

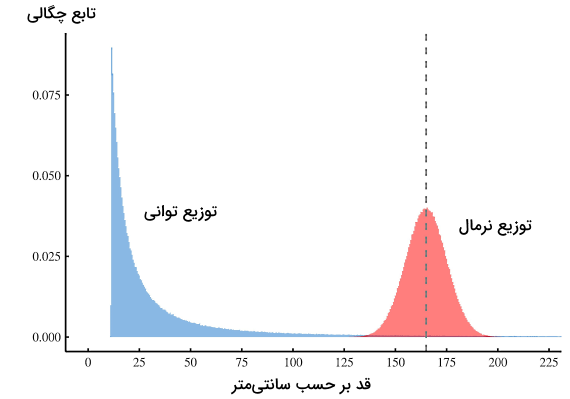
همچنین در تصویر بالا که مربوط به یک آزمایش خیالی است، ملاحظه می‌کنید که اگر بخواهیم توزیع قد افراد را با یک توزیع توانی نمایش دهیم، نتیجه به چه صورت است. در این تصویر این توزیع با توزیع نرمال مقایسه شده است. اگر محاسبات خود را به‌درستی انجام دهیم، هر دو نوع توزیع میانگین یکسانی از قد افراد به‌دست می‌دهند. نکته مهمی که از مشاهده نمودار توزیع توانی در مقایسه با توزیع نرمال دریافت می‌شود این است که عده زیادی از افراد قد چندان بلندی ندارند! در حالی که اگر بخواهیم فقط به توزیع استاندارد نرمال برای این داده‌‌ها توجه کنیم، به این نتیجه‌گیری در اولین نگاه نمی‌رسیم.

توزیع‌های توانی برای توصیف توزیع ابعاد و اندازه‌ها مناسب‌اند. برای مثال، موارد زیر نمونه‌های رایجی از توزیع‌هایی هستند که با یک توزیع توانی به بهترین شکل توصیف می‌شوند:

• توزیع درآمد خانواده‌ها: تعداد زیادی از خانواده‌ها دارای درآمد کم و تعداد کمی دارای درآمد بالا هستند.
• تعداد کارگران: تعداد خیلی زیادی از کارخانه‌ها و شرکت‌ها دارای تعداد کمی کارگر و تعداد کمی از کارخانه‌ها یا شرکت‌ها دارای تعداد زیادی کارگر‌اند.

به همین شکل تعداد زمین‌لرزه‌ها، طبقه‌بندی شهرها بر اساس جمعیت‌شان و حجم معاملات در بازار سهام می‌توانند به‌عنوان مثال‌های دیگری از این نوع توزیع محسوب شوند. توزیع توانی با عنوان توزیع نمایی هم شناخته می‌شود.

انواع توزیع‌‌ احتمال چیست؟

گفتیم توزیع توانی یکی از انواع توزیع‌های احتمال است. انواع توزیع‌های احتمال را می‌توانیم در دو گروه توزیع‌های پیوسته و گسسته طبقه‌بندی کنیم. برای مثال، چند نمونه توزیع‌ احتمال گسسته یا Discrete عبارت‌اند از:

• «توزیع پواسون» (Poisson Distribution)
• «توزیع یکنواخت گسسته» (Uniform Distribution)
• «توزیع دو جمله‌ای» (Binomial Distribution)
• «توزیع هندسی» (Geometric Distribution)
• «توزیع فوق‌هندسی» (Hyper Geometric Distribution)
• «توزیع برنولی» (Bernoulli Distribution)

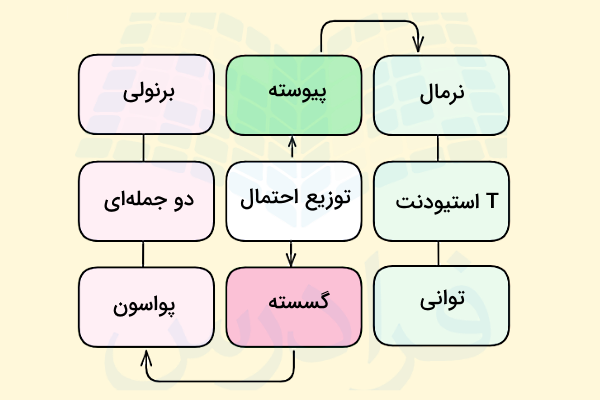
از طرفی انواع دیگری از توزیع‌های احتمال را داریم که بیشتر با هدف سنجش فرضیات استفاده می‌شوند و توزیع‌ احتمال پیوسته یا Continuous نامیده می‌شوند:

• «توزیع نرمال استاندارد» (Standard Normal)
• «توزیع تی – استیودنت» (Student’s t Distribution)
• «توزیع یکنواخت پیوسته» (Uniform Distribution)
• «توزیع توانی» (Power Law Distribution)

البته در بخش‌‌های آتی خواهید دید که قانون زیف نمونه‌ای از یک توزیع توانی گسسته محسوب می‌شود که در آن پارامترسازی فرمول توزیع توانی متفاوت است. در مورد مفهوم توزیع احتمال و انواع آن، پیشنهاد می‌کنیم مطلب زیر از مجله فرادرس را مطالعه کنید که جهت دسترسی آسان‌تر لینک آن در ادامه برای شما قرار داده شده است.

مسیر یادگیری آمار و احتمال با فرادرس

برای اینکه با مبحث توزیع توانی و کاربردهای آن بیشتر آشنا شوید، در این بخش قصد داریم چند فیلم آموزشی از مجموعه فرادرس و با موضوع آمار و احتمال را به شما معرفی کنیم تا با مشاهده این دوره‌ها و بهره‌گیری از آموزش تصویری به همراه حل مثال‌ها و تمرین‌های بیشتر بتوانید به شکلی کاملا کاربردی به این مباحث مسلط شوید. آمار و احتمال یکی از مهم‌ترین مباحث درس ریاضی در مقطع متوسطه به‌شمار می‌رود که بسته به رشته شما (علوم انسانی یا علوم ریاضی و علوم تجربی) استفاده از فیلم‌های زیر در یادگیری مفاهیمی مانند آمار توصیفی، احتمال و توزیع‌های احتمالاتی کمک می‌کند:

به علاوه این توزیع‌ها در شاخه‌های مهمی مانند یادگیری ماشین (Machine Learning)، علم داده (Data Science) و تحلیل داده (Data analysis) بکار می‌روند. بنابراین اگر قصد دارید در سطوح پیشرفته‌تری به مباحث بیان شده در این نوشته مسلط شوید، پیشنهاد ما این است که ابتدا با کلیات مباحث آمار و احتمال در علوم مهندسی آشنا شوید. مشاهده این فیلم‌های آموزشی از فرادرس در مسیر یادگیری مقدمات موثر است:

1. فیلم آموزش تئوری احتمالات فرادرس
2. فیلم آموزش آمار و احتمال مهندسی با مثال های مختلف فرادرس
3. فیلم آموزش رایگان مبانی احتمالات فرادرس
4. فیلم آموزش رایگان متغیرهای تصادفی پیوسته فرادرس
5. فیلم آموزش رایگان مسائل توزیع های گسسته و پیوسته در آمار و احتمال فرادرس

پس از اینکه کاملا به مباحث آمار و احتمال مسلط شدید، در زمینه کاربردهای آمار و احتمال یا یادگیری نرم‌افزارهای آماری می‌توانید به این دوره‌ها مراجعه کنید:

1. مجموعه آموزش اس پی اس اس SPSS – مقدماتی تا پیشرفته فرادرس
2. فیلم آموزش محاسبات آماری در اکسل Excel فرادرس
3. فیلم آموزش طراحی و آنالیز داده ها با نرم افزار اوریجین پرو OriginPro فرادرس
4. فیلم آموزش برنامه نویسی R و نرم افزار RStudio مقدماتی فرادرس
5. فیلم آموزش آمار و کاربرد آن در مدیریت فرادرس
6. فیلم آموزش آمار و احتمال در پایتون Python فرادرس

نمودار توزیع توانی چگونه است؟

پس از توریع نرمال، توزیع توانی مرسوم‌ترین نوع از انواع توزیع‌ها است که برای توصیف داده‌ها بکار می‌رود. می‌دانیم اگر نمودار توزیع داده‌ها یه شکل یک زنگ و دارای تقارن واضحی باشد، در این صورت توزیع نرمال داریم. حالا اگر بخواهیم برای نمودار توزیع توانی یک مشخصه پیدا کنیم، آن چیست؟ در این بخش نحوه رسم و شکل نمودار یک توزیع توانی را توضیح می‌دهیم تا بتوانید این توزیع را از روی نمودار آن به‌راحتی تشخیص دهید.

دو نکته مهم در مورد نمودار توزیع توانی عبارت‌اند از:

• به‌جای رسم $$X$$ و $$P(X)$$، باید لگاریتم هر دو را رسم کنیم.
• نمودار توزیع توانی تقریبا نزدیک به یک خط راست است (رفتار تقریبا خطی دارد).

بنابراین اگر نمودار دو کمیت این توزیع را نسبت به هم و با در نظر گرفتن محورهای لگاریتمی رسم کنید، یک رفتار تقریبا خطی را مشاهده خواهید کرد. پس چنین رفتاری نشان دهنده این است که می‌توانیم تغییرات دو کمیت را نسبت به هم توسط یک توزیع توانی توصیف کنیم:

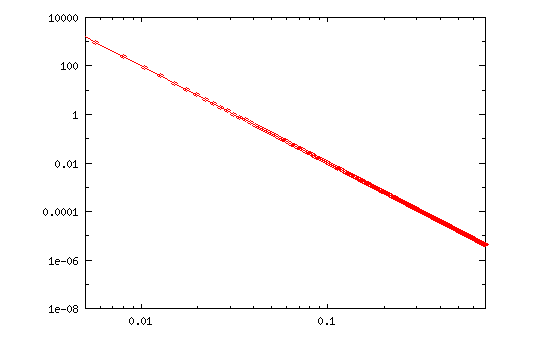
با اینکه نمودار بالا نوعی توزیع توانی با یک رفتار کاملا خطی را نشان می‌دهد، اما در عمل نویز‌هایی داریم که در مقادیر بالا دیده نمی‌شوند. همان‌طور که در توضیح مثال‌های این توزیع اشاره کردیم، در نمودار این توزیع معمولا مقادیر بزرگی با فراوانی پایین وجود دارند، همچنان که بیشتر مقادیر کوچک دارای فراوانی بالایی هستند.

بنابراین برای رسم نمودار توزیع توانی بهتر است به یکی از دو روش زیر عمل کنیم:

• به‌جای اینکه بازه‌‌هایی با طول برابر در نظر بگیرید، از بازه‌های لگاریتمی استفاده کنید (برای مثال، $$10 – 100 – 1000$$
• روش بهتر این است که از همان ابتدا نمودار $$ln X$$ و $$ln P(X)$$ را رسم کنید.

همچنین یکی از مهم‌ترین نکاتی که باید در رسم نمودار این توزیع مدنظر داشته باشید این است که توزیع توانی معمولا تمام مقادیر را پوشش نمی‌دهد و فقط برای مجموعه‌ای از مقادیر ممکن عمل می‌کند. برای نمونه در مثال درآمد خانواده، همواره حداقل درآمدی وجود دارد ($$X_{min}$$

توزیع توانی پیوسته و مشخصات آن

در این بخش می‌خواهیم به بررسی مشخصه‌های مختلفی که برای یک توزیع توانی پیوسته می‌توانیم در نظر بگیریم، بپردازیم و فرمول‌های هر کدام را معرفی کنیم. در کنار توزیع توانی پیوسته، توزیع‌های توانی گسسته را هم داریم که در بخش‌های بعد به توزیع مشابه و معروف آن یعنی «قانون زیف» خواهیم پرداخت.

تابع چگالی توزیع توانی پیوسته

یکی از مهم‌ترین مفاهیم آماری که در ارتباط با انواع توزیع‌ها تعریف می‌شود، پارامتری به نام تابع چگالی است. در بررسی توزیع توانی پیوسته هم لازم است ابتدا تابع چگالی متناظر با آن را معرفی کنیم که به شکل زیر است:

$$f(x) = frac{alpha -1 }{x_{min}} (frac{x}{x_{min}})^ {-alpha}$$

پس توزیع توانی باید از تابع چگالی بالا پیروی کند که در آن مقادیر $$x$$ و $$alpha$$ به‌صورت زیر تعریف می‌شوند:

$$x > x_{min}$$

$$alpha > 1$$

پس باید توجه داشته باشیم که طبق این تعریف لازم است مقادیر $$alpha$$ از یک بیشتر باشند. در عمل، چنین شرایطی سخت نیست، چون پیدا کردن داده‌هایی که برای آن‌ها $$alpha$$ از یک کمتر باشد، دشوار است.

تابع توزیع توزیع توانی پیوسته

پس از آشنایی با تابع چگالی، توابع توزیعی به شکل زیر برای توزیع توانی پیوسته خواهیم داشت که احتمالات بر اساس آن‌ها محاسبه می‌شوند:

$$F(x) = P (X < x )= 1 – (frac{x}{x_{min}})^ {1-alpha}$$

$$bar{ F(x)} = P (X > x )= (frac{x}{x_{min}})^ {1-alpha}$$

مقدار انتظاری توزیع توانی پیوسته

در ادامه اگر بخواهیم امید ریاضی یا مقدار انتظاری را برای یک توزیع توانی پیوسته پیدا کنیم، فرمول زیر را باید بنویسیم:

$$E(X) = (frac{alpha -1 }{alpha -2}) x _{min}$$

دقت کنید این رابطه به ازای تمام مقادیر بزرگتر از دو یعنی $$alpha > 2$$

مقدار انتظاری ماکزیم در یک نمونه

حالا اگر فرض کنیم اندازه نمونه ما برابر است با $$n$$، در این صورت مقدار انتظاری برابر است با:

$$E(X_{max}) = n ^ {frac{1 }{alpha -1}}$$

به این ترتیب با در نظر گرفتن $$alpha > 1$$

منحنی لورنتس در توزیع توانی پیوسته

همان‌طور که گفتیم در مورد توزیع درآمد، توزیع مناسب توزیع توانی است. فرض کنید می‌خواهیم بدانیم $$A$$ درصد از ثروت کل مربوط به $$P$$ درصد از ثروتمندترین خانواده‌ها چقدر است. به این منظور می‌توانیم از فرمولی به شکل زیر استفاده کنیم:

$$A= P ^ {frac{alpha -2 }{alpha -1}}$$

که برای تمام $$alpha > 2$$

توزیع های شرطی در توزیع توانی پیوسته

با در نظر گرفتن یک توزیع توانی با مینیمم مقدار $$x_{min}$$

$$P [frac{X > x}{X > x_0} ]=frac{P[X > x]}{P[X > x_0]} = frac{(frac{x}{x_{min}})^ {1-alpha}}{(frac{x_0}{x_{min}})^ {1-alpha}}$$

یا به شکل ساده‌تر، داریم:

$$P [frac{X > x}{X > x_0} ]=frac{P[X > x]}{P[X > x_0]} = (frac{x}{x_0})^{1-alpha}$$

همان‌طور که ملاحظه می‌کنید، آخرین عبارت کاملا به شکل یک توزیع توانی نوشته شده است.

تخمینی از پارارمتر آلفا در توزیع توانی پیوسته

فرمول زیر نشان می‌دهد تخمین پارامتر $$alpha$$ در یک توزیع توانی پیوسته چگونه است:

$$hat{ alpha } = 1 + n [sum_{i=1}^n ln frac{x_i}{x_{min}}]$$

توزیع های مشابه با توزیع توانی کدامند؟

در این بخش می‌خواهیم دو توزیع مشابه با توزیع توانی را معرفی کنیم. شناخت این توزیع‌ها به شما کمک می‌کند تا در شناسایی و استفاده از توزیع توانی موفق‌تر عمل کنید. به‌علاوه اگر می‌خواهید با انواع توزیع‌های گسسته و پیوسته آماری بیشتر آشنا شوید، مشاهده فیلم آموزش رایگان مسائل تشریحی توزیع های گسسته و پیوسته در آمار و احتمال فرادرس را به شما پیشنهاد می‌کنیم که لینک آن جهت دسترسی آسان‌تر شما در ادامه قرار داده شده است:

توزیع پارتو

یکی از انواع خاص توزیع توانی، توزیع پارتو یا Pareto Law است که نوعی قانون غیرعلمی است و بیان می‌کند ۸۰ درصد اتفاقات از تنها ۲۰ درصد از علت‌ها ناشی می‌شود. به بیان دیگر، بخش زیادی از آنچه که ما انجام می‌دهیم، اثر ناچیزی دارد. توزیع پارتو نمونه‌ای از یک توزیع توانی پیوسته است. این توزیع بر اساس نام اقتصاددان معروف ایتالیایی «ویلفردو پارتو» (Vilfredo Pareto) نام‌گذاری شده است و فرمولی به شکل زیر دارد:

$$F (x )=1- (frac{x_{min}}{x})^{alpha}$$

پس در توزیع پارتو پارامتر $$alpha$$ به شکل $$alpha -1$$

قانون زیف

در ادامه بررسی توزیع‌های مشابه با توزیع توانی، در این بخش توزیعی به نام قانون زیف یا Zipf’s Law را معرفی می‌کنیم که معمولا فراوانی یک رویداد را نسبت به رتبه آن مشخص می‌کند. قانون زیف بیان می‌کند که برای مثال، اگر لیستی از کلماتی با بیشترین فراوانی کاربرد در یک کتاب دلخواه را داشته باشیم، کلمه‌ای که بیشترین کاربرد را دارد، دو برابر نسبت به کلمه‌ای با فراوانی بعدی بیشتر تکرار شده است. به همین شکل کلمه‌ای که در جایگاه دوم تکرار یا فراوانی در این کتاب است، دو برابر نسبت به کلمه‌ای در جایگاه سوم بیشتر تکرار شده است و به همین صورت تا انتها.

بنابراین قانون زیف در ساده‌ترین شکل خود کاملا با توزیع توانی معادل است. این قانون باعث ایجاد توزیعی به نام «توزیع زتا» (Zeta Distribution) یا توزیع زیف می‌شود. اگر به خاطر داشته باشید، در بخش‌های قبل توضیح دادیم که در مورد توزیع‌های توانی پیوسته چگونه می‌توانیم برخی مفاهیم آماری مانند تابع چگالی، مقدار انتظاری و … را محاسبه کنیم. همچنین گفتیم توزیع پارتو یک نمونه توزیع توانی پیوسته با پارامترسازی متفاوت است. در این بخش ابتدا کمی در مورد توزیع‌های توانی گسسته صحبت می‌کنیم و سپس نمونه‌ مشابهی از این نوع توزیع یعنی قانون زیف را توضیح می‌دهیم.

اگر متغیرهای ما گسسته یا کیفی باشند (برای مثال، اندازه شهرها، فراوانی‌های یک کلمه، تعداد بازدیدها از یک مقاله و …)، در این صورت توزیع توانی ما از نوع گسسته خواهد بود. به عنوان مثال، بزرگترین شهر واقعا از نظر ابعاد و اندازه بزرگ است، اما در توصیف مابقی شهرها می‌گوییم شهرهای کوچک و کوچکتر. بنابراین اگر بخواهیم ابعاد شهرهای مختلف را با هم مقایسه کنیم، ممکن است برای شهرهای زیادی از صفت کوچکتر استفاده کنیم. به همین ترتیب، خانواده‌های زیادی با دو فرزند وجود دارند، اما تعداد خانواده‌هایی با سه، چهار یا پنج فرزند کمتر است.

«جرج زیف» (George Zipf) زبان‌شناسی در دانشگاه هاروارد بود که مشاهده کرد فراوانی کلمات در زبان انگلیسی تقریبا از فرمولی به شکل زیر پیروی می‌کند:

$$f= frac{0.1}{k}$$

در این فرمول $$k$$ رتبه یا جایگاه کلمه در این بررسی است. برای مثال، اگر برای کلمه خاصی $$k = 1$$

$$f= frac{0.1}{1} = 0.1 =10$$

به همین شکل، کلمه‌ای که در دومین جایگاه از نظر تکرار قرار می‌گیرد، ۵ درصد فراوانی دارد. این مطالعه او قانونی به نام قانون زیف را توسعه داد که بر اساس آن، همواره رتبه یا جایگاه با فراوانی یا اندازه مرتبط می‌شود. شکل دقیق‌تر قانون زیف به‌صورت زیر نوشته می‌شود:

$$f= frac{1}{k^ {a}}$$

• $$f$$ فراوانی یا اندازه است.
• $$k$$ رتبه یا جایگاه فراوانی یا اندازه است.
• $$a$$ پارامتر ثابت و معمولا بزرگتر از یک است.

زمانی که تعداد عناصر یا داده‌های ما ثابت است، برای اینکه که مجموع تکرارهای ما برابر با با یک شود، لازم است فراوانی‌ها بر مجموع تمام فراوانی‌ها تقسیم شود. به این ترتیب فراوانی نرمالایز شده‌ای به‌صورت $$f_z$$

$$f_z =frac{ frac{1}{k^ {a}} }{sum_{k=1}^N frac{1}{k^ {a}} }$$

نمودار قانون زیف چگونه رسم می شود؟

برای رسم نمودار توزیعی که از قانون زیف به‌عنوان یک نمونه توزیع توانی گسسته پیروی می‌کند، کافی است لگاریتم محدوده مقادیر $$k$$ و فراوانی‌ها یا اندازه‌های $$f$$ را پیدا کنیم. اگر نتایج حاصل از رسم نمودار تقریبا به شکل یک خط مستقیم شد، قانون زیف درست است.

مثال از قانون زیف

فرض کنید در ناحیه‌ای شش شهر داریم که قانون زیف با رابطه‌ای به شکل $$f= frac{3}{k}$$

پاسخ

برای اینکه بتوانیم به این سوال پاسخ دهیم، اولین قدم رسم جدولی بر اساس قانون زیف به شکل $$f= frac{3}{k}$$

در اولین ردیف با قرار دادن $$k = 1$$

$$f_z =frac{ frac{3}{k} }{sum_{k=1}^6 frac{3}{k} }$$

ابتدا بهتر است مخرج کسر بالا را پیدا کنیم که برابر است با:

$$sum_{k=1}^6 frac{3}{k} = frac{3}{1} + frac{3}{2} + frac{3}{3} + frac{3}{4} + frac{3}{5} + frac{3}{6} =7.35$$

به این ترتیب در مورد اولین رتبه، فراوانی نرمالایزه شده به شکل زیر محاسبه خواهد شد:

$$f_z =frac{ f}{sum_{k=1}^N frac{1}{k^ {a}} } = frac{ 3}{7.35 }=0.4$$

مابقی ردیف‌ها نیز به همین شکل پیدا می‌شوند. در نتیجه شهری که دارای بیشترین جمعیت در این ناحیه است یا شهری که در رتبه اول این جدول قرار گرفته است، $$0.4 times 100 = 40$$