اسپین ویژگی است که برای ذرات بنیادی اتم بررسی میشود. خاصیت و مفهوم اسپین با چرخشهای فیزیک کلاسیک متفاوت است اما برای درک این مفهوم از قوانین فیزیک کلاسیک نیز استفاده میشود. اسپین را اغلب با عبارت تکانه زاویهای ذاتی ذرات بنیادی تعریف میکنند. در این مطلب از مجله فرادرس میآموزیم اسپین چیست و چه ویژگیهایی دارد. در ابتدای این مطلب میآموزیم اسپین چیست و آزمایش اشترن گرلاخ را برای درک مفهوم آن بررسی میکنیم. سپس ویژگیهای اسپین مانند مقدار آن، جهت و عدد کوانتومی اسپینی را توضیح میدهیم. در ادامه مطلب، اصل برهمنهی را بررسی کرده و به شرح تفاوت اسپین در پدیدههای مختلف میپردازیم. در نهایت، کاربردهای مفهوم اسپین را برشمرده و تاریخچه آن را توضیح میدهیم. با مطالعه این مطلب تا انتها با این ویژگی کوانتومی به خوبی آشنا شوید.

اسپین چیست؟
اسپین با استفاده از مشاهده رفتار ذرات بنیادی مانند الکترون در میدان مغناطیسی تعریف شده است. اسپین یک ویژگی بدون واحد است و میتواند برای ذرات بنیادی مختلف مقادیر صحیح و نیم صحیح کوانتومی متفاوتی داشته باشد. اسپین الکترون با مفهومی به نام عدد کوانتومی اسپینی اندازهگیری میشود که میتواند مقادیر + و داشته باشد.
درک نادرست از مفهوم اسپین
از آنجا که در قوانین فیزیک کلاسیک، ذرات باردار و متحرک در میدان مغناطیسی منحرف میشوند، این نظریه بیان شد که الکترونها نیز به دلیل انحراف در میدان مغناطیسی باید دارای نوعی کمیت مانند چرخش باشند. به این ویژگی اسپین گفته شد.
بعدها اثبات شد که فرضیه چرخش الکترونها ماند اجسام فیزیک کلاسیک اشتباه است. فیزیکدانها به این نتیجه دست یافتند که سرعت چرخش الکترون باید بسیار بالاتر از سرعت نور باشد تا بتواند این رفتار را در میدان مغناطیسی داشته باشد که این فرضیه در جهان واقعی ممکن نیست.
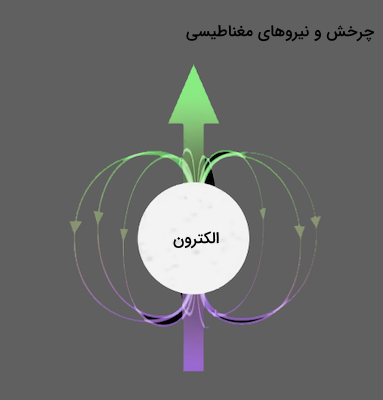
اسپین کوانتومی به این دلیل نام اسپین را گرفت که بین این مفهوم و رفتار بارهای متحرک در میدان مغناطیسی زمین رفتاری مشابه دیده شد. این پدیده در این جهان ممکن نیست. دلیل دیگر رد این نظریه این بود که به نظر میرسد الکترون شکل خاصی نداشته باشد. الکترون به عنوان ذرهای بدون بعد در نظر گرفته میشود که در میلیاردها متر هیچ ساختاری ندارد. داشتن یک ویژگی بدین شکل بدون داشتن ساختار ممکن نیست.
با وجود تمامی این موارد، برای ذرات بنیادی به دلیل رفتاری که در میدان مغناطیسی از خود نشان میدهند، ویژگی اسپین در نظر گرفته میشود. درک این مفهوم که اسپین چیست، با دانستههای ما از فیزیک کلاسیک ممکن است.
درک مفهوم اسپین با قوانین فیزیک کلاسیک
اسپین برابر با مقدار تکانه زاویهای ذاتی ذرات بنیادی درنظر گرفته میشود. برای درک بهتر این عبارت بهتر است این تعریف را به دو قسمت تکانه زاویهای و ذاتی تقسیم کنیم. مفهوم تکانه زاویهای در فیزیک کلاسیک، مقدار بزرگی حرکت به دور یک محور است. محور در تعریف تکانه مغناطیسی میتواند از مرکز جسم گذشته و جسم به دور خود بچرخد (تکانه زاویهای چرخشی) و یا محور بیرون از جسم باشد و جسم به دور محور بچرخد (تکانه زاویهای مداری).
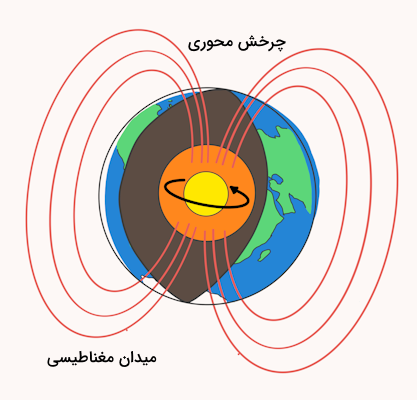
به دلیل اینکه ذرات بنیادی به عنوان ذرات نقطهای در نظر گرفته میشوند، نمیتوانند تکانه زاویه چرخشی داشته باشند زیرا محور عبور کننده از مرکز آنها بر خود ذره مطابق میشود. در تعریف اسپین، این خاصیت یک خاصیت ذاتی برای ذرات در نظر گرفته میشود. این بدین معنا است که صرف نظر از اینکه ذره بنیادی است یا کلاسیک، میتواند تکانه زاویهای داشته باشد.
یادگیری شیمی کوانتومی با فرادرس
برای درک بهتر این موضوع که اسپین چیست، باید با مفاهیمی چون ساختار اتم، اوربیتالهای اتمی و آرایش الکترونی عناصر آشنا شویم. همچنین، شناخت برخی از قوانین مانند اصل طرد پائولی و قانون هوند، به ما در درک مفهوم اسپین کمک میکند. پیشنهاد میکنیم برای درک بهتر این مفاهیم، به مجموعه فیلم آموزش دروس شیمی از دروس دانشگاهی تا کاربردی مراجعه کنید که با زبانی ساده ولی کاربردی به توضیح این مفاهیم میپردازد.
همچنین، با مشاهده فیلمهای آموزش فرادرس که لینک آنها در ادامه اورده شده است، میتوانید به آموزشهای بیشتری در زمینه شیمی کوانتومی دسترسی داشته باشید.
آزمایش اشترن گرلاخ
اولین بار در سال ۱۹۲۲ میلادی دانشمندان با انجام آزمایشهایی متوجه شدند که الکترونها و دیگر ذرات بنیادی، کمیت مغناطیسی ناشناختهای دارند. دانشمندان در این آزمایشات، اتمهای نقره را در یک میدان مغناطیسی آزاد کردند و از آن عبور دادند و مکان فرود آمدن آنها را پس از عبور از میدان مغناطیسی بررسی کردند. نام این آزمایش با اقتباس از نام دانشمندان انجام دهنده آن، اشترن گرلاخ (Stern – Gerlach) نام گرفت.

این اتمها در این آزمایش در زمان فرود، تنها مکانهای مشخصی را اختیار کردند. درحالی که اگر یک آهنربای معمولی را از این میدان عبور دهیم میتواند با توجه به قدرت و جهت گیریاش در مکانهای مختلفی فرود بیاید. اتمهای نقره تنها نقاط بالا و پایین نزدیک قطب مثبت و منفی میدان مغناطیسی را اشغال کردند. این آزمایش پایه درک این مفهوم که اسپین چیست را تشکیل داد.
مقدار اسپین ذرات بنیادی
در قسمت قبل آموختیم اسپین چیست. در مکانیک کوانتومی هر فرمی از تکانه زاویهای اعم از اسپین یا اوربیتال مقداری کوانتومی دارد و مقدار اعشاری ندارد. اسپین مواد تنها میتواند مقادیر صحیح یا نیم صحیح داشته باشد. اسپین صحیح به این معنی است که ذره با یک چرخش به موقعیت ابتدایی خود میرسد. به همین ترتیب، اسپین نیم صحیح بدین معنی است که ذره با دو چرخش کامل به وضعیت اولیه خود میرسد.
در قسمت قبل اشاره کردیم که اسپین ذرات میتواند مقادیر منفی و مثبت و … داشته باشد. مقادیر نیم صحیح و صحیح اسپین برای ذرات بنیادی مختلف به یک دستهبندی برای این ذرات بر اساس مقدار اسپین آنها انجامیده است. بر اساس این دسته بندی، ذرات بنیادی به دو دسته بوزون و فرمیون تقسیم میشوند.
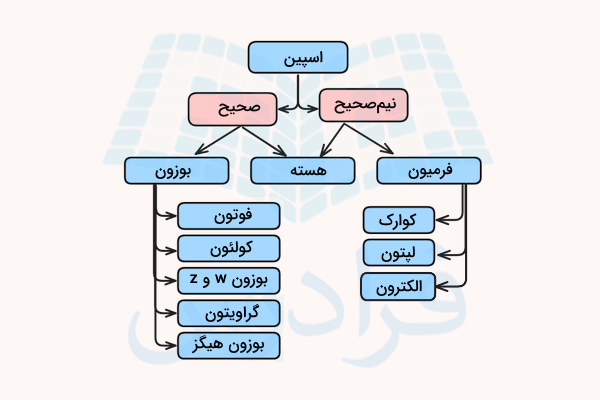
بوزونها
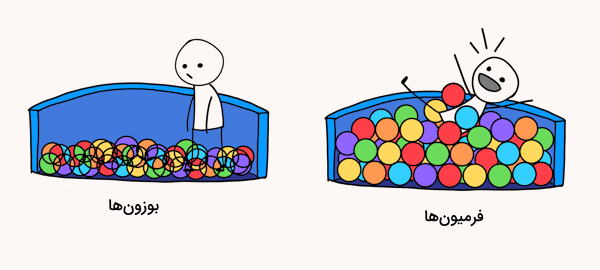
بوزونها ذراتی هستند که با اسپین صحیح انرژی را انتقال می دهند. برای مثال، فوتونها انرژی را بین دو ذره باردار منتقل میکنند. یک خاصیت مهم بوزونها این است که هرتعدادی از آنها میتواند مقدار مشابهی از خواص مکانیکی را در همان مکان و زمان داشته باشند.
این پدیده دلیلی است که باریکههای لیزر یکدیگر را دفع نمیکنند. بوزونها از آماز بوز انشتین پیروی میکنند. به همین دلیل میتوانند در یک مکان در کنار هم قرار گیرند. برای مثال، اتم هلیوم ۴ در حالت پایه اسپین ۰ دارد و با اینکه از فرمیونهایی مانند الکترون و کوارک تشکیل شدهاست، مانند یک بوزون رفتار میکند.
انواع بوزونها
ذرات بنیادی که انرژی را با خود حمل میکنند، همگی بوزونهایی با اسپین ۱ هستند. بوزونها شامل فوتونها (که نیروی الکترومغناطیسی دارند) ، گلوئونها (انرژی بالا) و بوزونهای z و w با انرژی کم هستند. توانایی بوزونها برای قرارگیری در کنارهم حتی در صورت داشتن یک وضعیت کوانتومی مشابه، منجر به ساخت دستگاههای لیزر شده است. همچنین، مواد دیگری مانند هلیوم فوق مایع (که مانند بوزون رفتار میکند) و مواد ابررسانا که در آنها جفتهای الکترونی مانند بوزون رفتار میکنند، همگی با استفاده از این خاصیت بوزونها به دست آمدهاند.
بوزونهایی با اسپین غیر یک
بوزونهای بنیادی با اسپینی غیر از عدد یک (۰، ۲، ۳ و .. ) در تاریخ کشف نشدهاند. هرچند وجود این مواد از نظر تئوریک اثبات شده است. دانشمندان به صورت محاسباتی وجود ذراتی به نام گراویتون (با اسپین ۲) و بوزون هیگز (با اسپین ۰) را اثبات کردهاند. وجود خارجی بوزون هیگز در سال ۲۰۱۳ اثبات شد.
فرمیونها
فرمیونها ذرات بنیادی هستند که مقدار اسپین آنها نیم عدد صحیح است. الکترونها نوعی از فرمیونها هستند. این ذرات یکی از مهمترین و اصلیترین ذرات سازنده ماده هستند. درواقع تمامی جهان از الکترونها به وجود آمده است. درک اینکه اسپین چیست میتواند به ما در درک رفتار الکترونها و مواد کمک کند. فرمیونها از اصل طرد پائولی پیروی میکنند. فرمیونها از آمار فرمی دیراک پیروی میکنند.
یکی از مهم ترین خواص فرمیونها این است که نمیتوانند با خواص مشابه در یک زمان و یک مکان وجود داشته باشند. برای مثال، دو الکترون با اسپین مشابه (هردو + یا ) نمیتوانند یک زیرلایه اوربیتال را اشغال کنند. این همان قانونی است که با نام اصل طرد پائولی شناخته میشود. طبق این اصل، هیچ دو الکترونی در اتم نمیتوانند خواص کاملا مشابه و اعداد کوانتومی کاملا یکسانی داشته باشند و حداقل عدد کوانتومی اسپینی آنها متفاوت است.
کوارکها و لپتونها
کوارکها و لپتونها که شامل الکترونها و نوترینوها هستند، هرچیزی که با نام ماده شناخته میشوند را تشکیل میدهند. اسپین تمامی این ذرات است. این نظریه که هر مادهای حجم دارد از این مطلب نشات گرفته است که بنابر اصل طرد پائولی، فرمیونهایی با یک وضعیت کوانتومی مشابه نمیتوانند در کنار هم قرار بگیرند. نیروی دافعهای از نزدیک شدن این ذرات به یکدیگر جلوگیری میکند.
هسته اتم
هسه اتم دارای اسپین هسته است که میتواند مقداری نیم صحیح و صحیح داشته باشد. پس هسته اتم هم میتواند خواص فرمیون و هم خواص بوزونها را داشته باشد.
ذرات ذکر شده در قسمت قبل همگی از ذرات ریزی هستند که در ساخار اتم و الکترونها، نوترونها و پروتون اتم یافت میشوند و ویژگیهای خاص خود را دارند که باعث میشود ساختار اتم پایدار بماند. پیشنهاد میکنیم برای آشنایی بیشتر با این ذرات، مطلب ذرات زیراتمی مجله فرادرس را مطالعه کنید.
جهت اسپین
در قسمت قبل آموختیم مقادیر ممکن برای اسپین چیست. اسپین جهت خاصی دارد که تنها با قرار گرفتن در میدان مغناطیسی مشخص میشود. اگر یک الکترون از یک میدان مغناطیسی عبور کند و مقدار اسپین آن را اندازهگیری کنیم تنها میتوانیم یکی از مقادیر + و را مشاهده کنیم. این در حالی است که این مشخص شدن اسپین ذرات تا زمانی که در میدان مغناطیسی قرار نگرفتهاند مشخص نیست.
فیزیکدانان به این اسپینها اسپین بالا و اسپین پایین میگویند. اسپین بالا و پایین با استفاده از میدان مغناطیسی تعریف میشود. اسپین الکترونها تنها میتواند یکی از مقادیر اسپین بالا و اسپین پایین را اختیار کند.
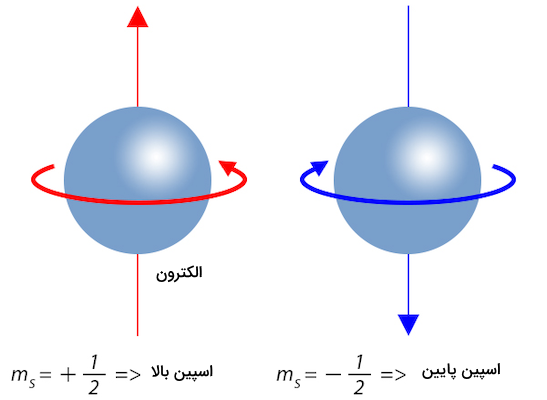
با وجود این به دلیل وجود تعداد زیادی الکترون در اتمها اینطور به نظر میرسد که الکترون هر دو حالت اسپین را دارد و تنها با عبور از میدان مغناطیسی میتوان تشخیص داد که الکترون اسپین بالا دارد یا اسپین پایین.
اسپین ذرات بنیادی بر خلاف چرخش در فیزیک کلاسیک، با بردار تعریف نمیشود و نمیتواند در بعد تعریف شود. چرخش به دور محور یک جسم تنها زمانی تعریف میشود که جسم دارای طول، عرض و ارتفاع باشد و با توجه به اندازه ذرات بنیادی، این پدیده برای آنها صادق نیست.
روش تعیین اسپین در شیمی
جهت اسپین الکترونهای موجود در اتمها و یونها را میتوان به روش تئوریک و با استفاده از رسم آرایش الکترونی حدس زد. برای این کار باید ۳ قدم اساسی را دنبال کنیم.
- پیدا کردن تعداد الکترونهای اتم یا یون با استفاده از عدد اتمی و بار آن
- نوشتن آرایش الکترونی اتم طبق اصل آفبا و مشخص کردن اعداد کوانتومی
- تقسیم الکترونها در اوربیتالهای رسم شده با استفاده از فلشهای بالا و پایین
رسم آرایش الکترونی عناصر یکی از مهمترین مباحث شیمی برای درک رفتار اتمها و مولکولها و پیوند شیمیایی بین آنها است. پیشنهاد میکنیم برای درک بهتر این مفهوم، فیلم آموزش آرایش الکترونی عناصر فرادرس که لینک آن در ادامه امده است را مشاهده کنید.
برای مثال، فرض کنید میخواهیم آرایش الکترونی اتم گوگرد را با ۱۶ اتم رسم کرده و جهت اسپین الکترونهای لایه ظرفیت آن را پیدا کنیم. با دانستن اینکه این اتم ۱۶ الکترون دارد، آرایش الکترونی آن را طبق اصل آفبا رسم میکنیم.
اوربیتال s یک زیرلایه، اوربیتال p سه زیرلایه، اوربیتال d پنج زیرلایه و اوربیتال f هفت زیرلایه دارند و در هر زیرلایه دو الکترون با اسپینهای مخالف هم جای میگیرند.
طبق اصل هوند، الکترونها ابتدا با اسپین مشابه به ترتیب و به صورت تکی زیرلایههای هر اوربیتال را پر میکنند و سپس باقی الکترون در اوربیتال با الکترونهای قبلی با اسپین مخالف جفت میشود. در لایه آخر اتم گوگرد (لایه سوم) یک اوربیتال 3s و یک اوربیتال 3p وجود دارد. در اوربیتال s دو الکترون با اسپین مخالف جای میگیرند. در اوربیتال p چهار الکترون وجود دارد. ابتدا سه الکترون به صورت تکی و با اسپین مشابه (بالا) این زیرلایهها را پرکرده و الکترون آخر با اسپین مخالف با یکی از الکترونهای اسپین بالا جفت میشود.
الکترون اسپین پایین میتواند هریک از سه زیرلایه را اشغال کند. شکل جایگیری این الکترونها در زیرلایهها به صورت زیر است.
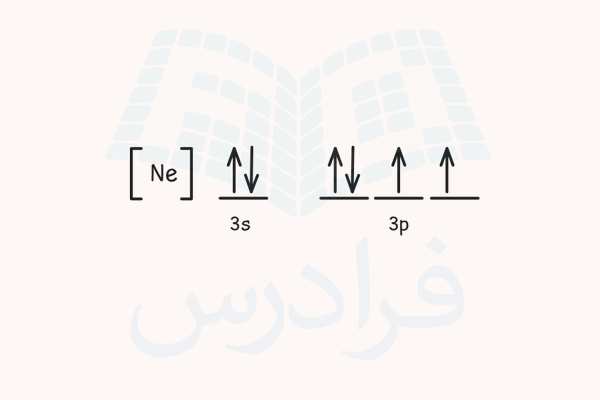
در ادامه برای درک بهتر تعیین اسپین از روی آرایش الکترونی، به مثالهای زیر توجه کنید.
مثال ۱
چند الکترون در یک اتم میتوانند عدد کوانتومی اصلی ۵ و عدد کوانتومی فرعی ۱ داشته باشند؟
پاسخ
برای پاسخ به اینگونه سوالات باید هر ۴ عدد کوانتومی اصلی و فرعی، مغناطیسی و مغناطیسی اسپین را بررسی کنیم. برای پاسخ بهتر به این سوال بهتر است یک جدول رسم کرده و مقادیر ممکن این اعداد کوانتومی را در آن بنویسیم.
| عدد کوانتومی | مقدار |
| عدد کوانتومی اصلی | ۵ |
| عدد کوانتومی فرعی | ۱ |
| عدد کوانتومی مغناطیسی | -۱، ۰، +۱ |
| عدد کوانتومی اسپینی |
مقادیر عدد کوانتومی مغناطیسی مقادیر عدد صحیح بین مثبت و منفی عدد کوانتومی فرعی است. به ازای هر عدد کوانتومی فرعی (زیرلایه)، دو عدد الکترون جفت با اسپینهای بالا و پایین میتواند وجود داشته باشد. پس جمعا ۶ الکترون با این مشخصات وجود خواهد داشت.
مثال ۲
با عدد کوانتومی اصلی ۶ و عدد کونتومی اسپین چند الکترون در یک اتم وجود دارد؟
پاسخ
مانند مثال قبل، یک جدول از مقادیر همه اعداد کوانتومی ممکن رسم میکنیم.
| عدد کوانتومی | مقدار |
| عدد کوانتومی اصلی | ۵ |
| عدد کوانتومی فرعی | ۰، ۱، ۲، ۳، ۴ |
| عدد کوانتومی مغناطیسی | ۰، ±۱، ±۲، ±۳، ±۴ |
| عدد کوانتومی اسپینی |
مانند مثال قبل، به ازای هر عدد کوانتومی مغناطیسی، دو عدد کوانتومی اسپینی وجود دارد که یکی از آنها اسپین منفی پایین و یکی از آنها اسپین مثبت و بالا دارد. در نتیجه به ازای هر مقدار عدد کوانتومی مغناطیسی، یک الکترون با اسپین منفی وجود دارد. برای مثال، با عدد کوانتومی فرعی ۴، ۹ زیرلایه با مقادیر عدد کوانتومی مغناطیسی از -۴ تا +۴ خواهیم داشت که هریک از اینها میتوانند یک الکترون با اسپین منفی را در خود جای دهند.
بدین ترتیب، ۲۵ الکترون با این مشخصات در اتم وجود دارند.

عدد کوانتومی اسپینی
عدد کوانتومی اسپینی یا اسپین الکترون چهارمین عدد کوانتومی تعریف شده برای الکترونهای یک اتم است. این عدد کوانتومی با حرف نمایش داده میشود و میتواند مقادیر + و داشته باشد. اسپین + با فلش رو به یالا و اسپین منفی با فلش رو به پایین نمایش داده میشوند و به آنها اسپین بالا و اسپین پایین گفته میشود.
الکترونها اسپین نیم صحیح دارند و این بدین معنا است که آنها میتوانند با دو چرخش کامل به حالت اولیه خود باز گردند. بنابر اصل برهم نهی، هر الکترون میتواند ترکیبی از اسپین + و را داشته باشد.
معادله زیر احتمال حضور الکترون در یکی از حالتهای اسپین را نشان می دهد.
احتمال اندازهگیری اسپین بالای الکترون ۰٫۷۵ و احتمال اندازهگیری اسپین پایین الکترون ۰٫۲۵ خواهد بود. قبل از انجام آزمایش و اندازهگیری یک سیستم کوانتومی بدون شک نمیتوانیم حدس بزنیم که کدام اسپین را خواهد داشت اما احتمال حضور آن در هریک از این حالتها به شکل بالا است و تا دیدن نتیجه آزمایش مشخص نخواهد بود.
محاسبه عدد کوانتومی اسپینی
تعریف قراردادی عدد کوانتومی اسپینی به شکل فرمول زیر نشان داده میشود.
که در این تعریف، n میتواند یک عدد صحیح غیر منفی مانند ۰، ۱، ۲، ۳ و … باشد. مقادیر s برای یک ذره بنیادی به نوع ذره بستگی دارد و نمیتواند تغییر کند و برای هر ذره مقداری مشخص یا مجموعهای از مقادیر مشخص دارد. (برای مثال برای الکترون که میتواند رو به بالا یا رو به پایین باشد.)
میزان تکانه زاویهای اسپین در سیستمهای فیزیکی مقداری کوانتومی دارد. مقادیر ممکن برای مقدار عدد کوانتومی اسپینی از طریق فرمول زیر به دست میآید.
در این فرمول h ثابت پلانک و ثابت پلانک کاهش یافته است.
اصل بر هم نهی
اصل برهمنهی به این معنی است که یک ذره میتواند همزمان دو حالت را اختیار کند. تا زمانی که ذره از میدان مغناطیسی عبور نداده شده باشد، مشخص نخواهد بود که اسپین آن منفی یا مثبت است. این اصل به ما کمک می کند درک کنیم مفهوم همزمانی دو اسپین الکترون چیست.
برای درک بهتر این پدیده، یک سکه را در نظر بگیرید. در فیزیک کلاسیک، این سکه فقط میتواند یکی از دو حالت شیر یا خط را داشته باشد. در فیزیک کوانتوم، این سکه میتواند یک حالت برهمنهی داشته باشد که از هر دو حالت شیر و خط تشکیل شده است و تا زمانی که روی آن کاری انجام ندهیم، مشخص نخواهد شد که روی سکه شیر یا خط است.
تفاوت اسپین و تکانه زاویه ای کلاسیک
در مطالب علمی اسپین به کمیت تکانه زاویهای کوانتومی ذاتی و تکانه زاویهای در تعریف کلاسیک آن و برای ذرات دارای حجم و جرم استفاده میشود. در این مطلب اشاره کردیم که اسپین در ذرات کوانتومی مشابه اسپین در فیزیک کلاسیک است اما این دو تعریفهایی کاملا متفاوت دارند. ذرات بنیادی ذرات نقطهای در نظر گرفته میشوند که نمیتوانند تکانه زاویهای چرخشی کلاسیک را داشته باشند زیرا محور عبور کننده از مرکز آنها بر خود آنها منطبق است.
با اینحال گفتیم که ذرات صرف نظر از بنیادی یا کلاسیک بودنشان تکانه زاویهای دارند. این بدین معنا است که برای ذرات بنیادی مقدار تکانه زاویه ای برابر صفر نیست. حال این پرسش پیش میآید که این ذرات که در فضای اتم نمیچرخند، چگونه میتوانند تکانه زاویهای داشته باشند؟ پاسخ به این پریش به ما کمک می کند بدانیم ماهیت اسپین چیست.
برای پاسخ به این سوال از مکانیک نیوتنی بهره میگیریم. طبق تعریف مکانیک نیوتوی، یک ذره تنها در صورتی میتواند انرژی داشته باشد که در حال حرکت باشد و انرژی جنبشی داشته باشد یا اینکه در حال دریافت انرژی از یک منبع خارجی باشد و دارای انرژی پتانسیل باشد. طبق قانون نسبیت، میزان انرژی یک ذره آزاد از طریق رابطه زیر به دست میآید.
این بدین معنی است که ذره آزاد هیچ نیرویی را حس نمیکند. همچنین، برای ذرهای که در حال حرکت نباشد، این معادله به شکل زیر نوشته میشود.
این معادله بیان میکند که ذرهای که در حال حرکت نباشد و نیرویی نیز بر آن وارد نشده باشد، به هرحال دارای انرژی است. این تعریف کاملا با تعریف مکانیک نیوتنی همخوانی دارد. به بیان دیگر، ذرات دارای انرژی ذاتی هستند. پس برای ایجاد ذرات دارای جرم، نیاز به صرف انرژی داریم. اسپین نیز کاملا مشابه همین است.
در مکانیک کوانتومی میتوانیم ذراتی نقطهای داشته باشیم که کاملا ایستا هستند اما همچنان تکانه زاویهای دارند. و اگر بخواهیم همچین ذراتی را ایجاد کنیم باید به آن اندازه تکانه زاویهای ایجاد کنیم. این مقدار تکانه زاویهای دقیقا همان اسپین ذرات کوانتومی است. این موضوع که تعریف کلاسیک تکانه زاویهای با تعریف اسپین کوانتومی را اشتباه نکنیم بسیار مهم است.
کاربرد اسپین
در این مطلب آموختیم اسپین چیست و چه مقادیری دارد. اسپین، کاربردهای تئوری و عملی بسیاری را در فرآیندها و پدیدههای مختلف دارد. در قسمت قبل نقش این مفهوم را در مفاهیم تئوری آموختیم. حال کاربردهای عملی آن را در مفاهیم، فرآیندها و دستگاههای مختف بررسی میکنیم.
اسپین ذرات یکی از عوامل مهم تعیین کننده خواص مختلف ذرات کوانتومی و مواد فیزیکی هستند. در ادامه میآموزیم کاربرد اسپین چیست.
ساختار جدول تناوبی
عدم تمایل ذرات فرمیون مانند الکترونها برای داشتن اعداد کوانتومی یکسان و متفاوت بودن اسپین آنها در هر اوربیتال و زیرلایه، دلیلی شکل گرفتن ساختار جدول تناوبی به شکل امروزی شده است. هر اتم عدد اتمی منحصر به فرد خود را دارد و هر الکترون در هر اتم یا یونی، خواص منحصر به فرد خود را دارد.
از مفهوم اسپین در دستگاههای طیف سنجی، دستگاه تصویر برداری رزونانس مغناطیسی (MRI)، حافظه رایانه، ساعتهای اتمی، ترانزیستور اسپین، وسایل الکترونیکی نیز استفاده میشود.
تصویربرداری رزونانس مغناطیسی
در این مطلب آموختیم اسپین چیست. با وجود اینکه اسپین یک ویژگی ملموس نیست و درک کردن آن سخت است، اما یکی از عوامل مهم برای ساخت دستگاههایی چون دستگاه تصویربرداری رزونانس مغناطیسی (MRI) شده است.
اساس کار این دستگاهها به این شکل است که بدن انسان از آب زیادی تشکیل شده است که دارای یونهای هیدروژن مثبت است که تنها از یک پروتون تشکیل شدهاند. این پروتونها از دسته فرمیونها هستند، اسپین نیم صحیح دارند و با ایجاد میدان مغناطیسی قوی در دستگاه، جهتگیری کرده و با بازگشت به جهت اولیه سیگنالهایی آزاد میکنند که در نهایت به تشکیل تصویر مربوطه میانجامد.
دستگاههای طیف سنجی
از مفهوم اسپین در دستگاههای مختلف طیف سنجی استفاده میشود. دستگاههایی چون دستگاه طیف سنجی رزونانسی مغناطیسی هسته (NMR)، طیف سنجی رزونانس مغناطیسی الکترون (ESR یا EPR)، از امواج رادیویی و رزونانس مغناطیسی هسته استفاده میکنند.
کامپیوتر کوانتومی
به دلیل نقش مهمی که اسپین در درک خواص مغناطیسی مواد دارد، از این مفهوم در حافظه رایانههای کوانتومی استفاده شده است.
ساعت اتمی
جفت شدن اسپین مداری به دستیابی به طیف اتمی خالصی میانجامد که از آن در ساخت ساعتهای اتمی استفاده میشود. این طیف که با استفاده از مفهوم اسپین به دست آمده است، در ساعتهای اتمی، مفهوم مدرنی را از ثانیه بیان میکند.
یادگیری مکانیک کوانتومی با فرادرس
درک این مفهوم که اسپین چیست و کاربردهای آن کدامند، به درک مفاهیم دیگری مانند خواص کوانتومی مواد، نظریه کوانتومی ماده، عملگرهای خطی و تصویرگر و … وابسته است. پیشنهاد میکنیم برای آشنایی بیشتر با این مفاهیم، به مجموعه فیلم آموزش مکانیک کوانتومی فرادرس مراجعه کنید که با زبانی ساده ولی کاربردی به توضیح این مفاهیم میپردازد.
همچنین با مراجعه به فیلمهای آموزش فرادرس که لینک آنها در ادامه آورده شده است، میتوانید به آموزشهای بیشتری در زمینه مکانیک کوانتومی دسترسی داشته باشید.
تاریخچه
در این مطلب از مجله فرادرس آموختیم اسپین چیست. خاصیت کوانتومی اسپین اولین بار در بررسی طیف نشری فلزات قلیایی کشف شد. در سال ۱۹۴۳، ولفگانگ پائولی (Wolfgang Pauli) با استفاده از دادههایی که جمعآوری کرده بود، درجه آزادی جدیدی برای الکترون لایه ظرفیت اتمها بیان کرد. سپس دانشمندانی مانند رالف کرونیگ (Ralph Kronig)، ساموئل گودسمیت (Samuel Goudsmit) و جرج اولنبک (George Ohlenbeck) در مورد اینکه الکترون میتواند خاصیت مغناطیسی و تکانه زاویهای مغناطیسی داشته باشند بحث کردند.

در نهایت، پائولی با استفاده از معادلات کوانتومی شرودینگر و اصل عدم قطعیت هایزنبرگ و درنهایت با استفاده از مطالعات پاول دیراک (Paul Dirac) توانست اثبات کند که برخی ذرات زیراتمی اسپین نیم صحیح و برخی اسپین صحیح دارند.
اولین آزمایش انجام شده در اثبات این نظریف آزمایش اشترن گرلاخ با اتم نقره بود. این آزمایش پایه درک اینکه مفهوم اسپین چیست را برای مطالعات آینده تشکیل داد.
source
