احتمال، یکی از شاخههای علم ریاضی است که با شانس وقوع پدیدههای مختلف سر و کار دارد. به عنوان مثال، بازی شطرنج را در نظر بگیرید. برای شروع بازی و انجام اولین حرکت، ۲۰ حالت وجود دارد (۱۶ حرکت احتمالی برای سربازها و ۴ حرکت احتمالی برای اسبها). با ادامه بازی، حالتهای ممکن برای انجام حرکات بعدی، به میزان قابلتوجهی افزایش مییابد. حدس زدن حرکتها و محاسبه میزان شانس وقوع آنها، در حیطه علم احتمال است. در مثال ساده و معروف پرتاب سکه نیز همین شرایط وجود دارد. پس از پرتاب، یا روی سکه یا پشت آن نمایان میشود. مفاهیم و قوانین احتمال، در بسیاری از حوزهها به کار میروند. در این مطلب از مجله فرادرس، قصد داریم ببینیم احتمال چیست و چه قوانینی دارد.

در ابتدای مطلب، به تعریف احتمال و بیان اهمیت، کاربرد، نحوه نمایش و پیشنیازهای یادگیری این علم میپردازیم. سپس، به سراغ تعریف برخی از مفاهیم و اصطلاحات پایه در دنیای احتمال میرویم. در نهایت، ضمن ارائه فرمولها و قوانین اصلی احتمال، تفاوت آمار و احتمال را توضیح میدهیم.
تعریف احتمال چیست؟
«احتمال» (Probability)، امکان وقوع یک رویداد است که با عددی بین ۰ تا ۱ بیان میشود. اگر امکان رخ دادن یک رویداد وجود نداشته باشد، میگوییم احتمال آن برابر با ۰ است. در صورت مطمئن بودن از رخ دادن حتمی یک رویداد، میگوییم احتمال آن برابر با ۱ است.
احتمال، یکی از شاخههای پرکاربرد ریاضی محسوب میشود. این علم، به منظور پیشبینی بسیاری از پدیدههای دنیای واقعی مورد استفاده قرار میگیرد. قوانین و فرمولهای احتمالاتی برای حل مسائل گوناگون در حوزههای مختلف مانند کسب و کار، مهندسی، هوش مصنوعی و غیره به کار برده میشوند.
برای درک بهتر موضوع، سادهترین مثال دنیای احتمال، یعنی پرتاب یک سکه به هوا را در نظر بگیرید. یک طرف سکه را «پشت» و طرف دیگر آن را «رو» مینامیم. هنگام پرتاب سکه به هوا و پس از فرود آمدن آن، مطمئن نیستیم که با کدام طرف مواجه خواهیم شد.
علم احتمال به ما کمک میکند تا امکان وقوع هر حالت (پشت یا رو آمدن سکه) را به صورت یک عدد قابل درک بیان کنیم. در مثال پرتاب سکه، احتمال پشت آمدن سکه برابر با ۰/۵ و احتمال رو آمدن سکه نیز برابر ۰/۵ است. بنابراین، امکان رخ دادن هر یک از حالتها، به اندازه مساوی وجود دارد. در بخشهای بعدی، به معرفی قوانین و فرمولهای احتمال برای محاسبه این اعداد خواهیم پرداخت.
اهمیت و کاربرد احتمال چیست؟
یکی از سوالات پرتکرار دانشآموزان هنگام مطالعه بسیاری از مفاهیم ریاضی، کاربردی بودن این مفاهیم در دنیای واقعی است. احتمال، یکی پرکاربردترین شاخههای ریاضی است که کاربردهای گستردهای در دنیای واقعی و حوزههای مختلف دارد. این کاربردها، از بازیهای ساده تا علوم پیشرفته را دربرمیگیرند. همین موضوع، درک مفهوم احتمال را بسیار سادهتر از مفاهیم پیچیده ریاضی میکند.
هدف اصلی احتمال، پیشبینی وقوع رویدادها است. بنابراین، این علم، برای افزایش آگاهی در مورد حالتهای مختلف یک رویداد و اتخاذ تصمیمهای آگاهانه برای موفقیت در صورت رخ دادن هر حالت استفاده میشود. اهمیت و کاربردهای احتمال را میتوان در موارد زیر خلاصه کرد:
- تصمیمگیری و مدیریت ریسک: احتمال، با کمیسازی خروجیهای ممکن، امکان اتخاذ تصمیمهای آگاهانهتر و کاهشهای ریسکهای مختلف را فراهم میکند. این ویژگی، کاربرد گستردهای در علوم اقتصادی، درمان و مهندسی دارد.
- تحلیل پیشگویانه: با تحلیل توزیع دادههای قدیمی توسط ابزارهای احتمالاتی، امکان پیشگویی در مورد رویدادهای آتی فراهم میشود. این ویژگی، معمولا در علوم داده و یادگیری ماشین مورد استفاده قرار میگیرد.
- تحقیق علمی و استنباط آماری: آزمون فرضیه و تحلیل آماری، به محققان کمک میکند تا دادههای مشاهده شده را با فرضیههای مورد انتظار تطابق دهند. این ویژگی به درک ماهیت تصادفی و تغییرپذیر رویدادها در علوم فیزیک، زیستشناسی، روانشناسی و اقتصاد کمک میکند.
- زندگی روزمره: امکان استفاده از احتمال در فعالیتهای روزمره مانند بازیها، پیشبینی وضعیت آب و هوا، پیشبینی مسابقات ورزشی و غیره وجود دارد. این علم به افراد در تقویت مهارت تفکر انتقادی و درک عدم قطعیتها و شانس کمک میکند.
درک احتمال، هم از نظر ریاضی و هم از نظر فلسفی مهم است. قوانین احتمال میتوانند پلی میان پدیدههای علمی و عقاید شخصی باشند. به عنوان مثال، هنگام پرتاب یک تاس، امکان مواجهه با اعداد ۱ تا ۶ (با احتمال برابر) وجود دارد. با این وجود، پیش از پرتاب، هر کسی میتواند نظر شخصی خود را در مورد عدد احتمالی بیان کند. یادگیری احتمال، باعث درک بهتر فرآیندهای طبیعی و استدلال انسانی میشود.
احتمال در ریاضی چگونه نمایش داده میشود؟
احتمال با حرف انگلیسی P (اولین حرف عبارت Probability) نمایش داده میشود. به عنوان مثال، برای اشاره به احتمال رخ دادن پیشامد A، مینویسیم:
عبارت بالا، به معنی احتمال پیشامد A است. در بخش بعدی، راجع به اصطلاحات و مفاهیم پایه در احتمال، از جمله پیشامد، فضای نمونه و غیره صحبت میکنیم.
پیشنیاز یادگیری احتمال چیست؟
پیش از یادگیری احتمال، بهتر است دانش خود را در زمینه منطق ریاضی (گزاره ها و سورهای منطقی)، مجموعهها (اجتماع، اشتراک و تفاضل مجموعهها)، شمارش، جایگشت و ترکیب تقویت کنید. این مفاهیم ریاضی، باعث درک بهتر شما از احتمال و قواعد آن میشوند.
اصطلاحات و مفاهیم احتمال
در این بخش، به تعریف برخی از مفاهیم و اصطلاحات پایه و پرکاربرد احتمال میپردازیم.
نظریه احتمال چیست؟
«نظریه احتمال» (Probability Theory) یا «حساب احتمالات» (Probability Calculus)، یکی از شاخههای ریاضی است که به مطالعه احتمال میپردازد. در نظریه احتمال، مسائل با استفاده از مجموعه اصول احتمالاتی بیان و حل میشوند. در بخشهای بعدی، راجع به این اصول صحبت خواهیم کرد.
آزمایش در احتمال چیست؟
«آزمایش» (Experiment)، فعالیتی است که نتایج یا خروجیهای آن از قبل مشخص نباشد. هر آزمایش، چند نتیجه مطلوب و چند نتیجه نامطلوب دارد. به عنوان مثال، توماس ادیسون برای اختراع لامپ، بیش از هزار بار تلاش و آزمایش کرد. نتیجه بیش از هزار آزمایش، نامطلوب بود اما نتیجه یکی از این آزمایشها، مطلوب بود و منجر به اختراع لامپ شد. مفاهیم آزمایش، نتیجه مطلوب و نتیجه نامطلوب در احتمال نیز مورد استفاده قرار میگیرد.
آزمایش تصادفی در احتمال چیست؟
«آزمایش تصادفی» (Random Experiment)، آزمایشی است که با وجود مشخص بودن مجموعه نتایج ممکن آن، امکان اظهار نظر قطعی در مورد رخ دادن یک خروجی خاص، پیش از انجام آزمایش وجود ندارد. به عنوان مثال، پرتاب سکه و پرتاب تاس، آزمایشهای تصادفی هستند.
در آزمایش تصادفی پرتاب سکه، میدانیم که نتایج ممکن، پشت یا رو آمدن سکه هستند. در آزمایش تصادفی پرتاب تاس نیز اعداد ۱ تا ۶، نتایج ممکن در نظر گرفته میشوند. با وجود دانستن نتایج ممکن، نمیتوانیم به طور قطعی بگوییم که پس از اجرای آزمایش تصادفی، چه نتیجهای به دست میآید.
اگر بخواهید احتمال پشت آمدن سکه را محاسبه کنید، مشاهده پشت به عنوان نتیجه مطلوب و مشاهده رو به عنوان نتیجه نامطلوب در نظر گرفته میشود. بنابراین، خروجی مورد نظر در آزمایشهای تصادفی، نتیجه مطلوب است و خروجیهای دیگر، نتیجه نامطلوب هستند.
تلاش آزمایشی یا آزمون در احتمال چیست؟
تلاش آزمایشی یا «آزمون» (Trial)، تکرارهای متعدد فرآیند اجرای آزمایش است. به عبارت دیگر، به هر تلاش برای اجرای یک آزمایش تصادفی، آزمون میگویند. به عنوان مثال، یک آزمایش تصادفی را در نظر بگیرید که در آن، یک سکه دو بار به هوا پرتاب میشود. به هر پرتاب سکه در این آزمایش تصادفی، یک آزمون یا تلاش آزمایشی میگویند.
نتیجه یا برآمد در احتمال چیست؟
برآمد یا «نتیجه» (Outcome)، خروجی یک آزمون است. به عنوان مثال، یک فوتبالیست را در حال زدن ضربه پنالتی در نظر بگیرید. در این شرایط، یا توپ گل میشود یا گل نمیشود. هر یک از این خروجیها، یک برآمد است.
نتایج احتمالی در احتمال چیست؟
«نتایج احتمالی» (Possible Outcome)، فهرستی از تمام خروجیهای ممکن در یک آزمایش است. در پرتاب سکه، پشت یا رو آمدن سکه، نتایج احتمالی هستند.
نتایج همشانس در احتمال چیست؟
نتایج هماحتمال یا «نتایج همشانس» (Equally likely Outcomes)، خروجیهای یک آزمایش هستند که تمام آنها با احتمال برابر رخ میدهند. به عنوان مثال، در آزمایش پرتاب تاس، احتمال مشاهده هر عدد، برابر با (یکششم) است. در آزمایش پرتاب سکه نیز احتمال مشاهده پشت یا رو، برابر با (یکدوم) است.

نتایج غیرهمشانس در احتمال چیست؟
«نتایج غیرهمشانس» (Non-Equally Likely Outcomes)، خروجیهای یک آزمایش هستند که با احتمال برابر رخ نمیدهند. فضای نمونه در این شرایط، دارای احتمال غیرهمشانس خواهد بود. به عنوان مثال، یک قوطی کبریت را در نظر بگیرید. این جسم نیز مانند تاس، دارای شش وجه است. با این وجود، اگر آن را به هوا پرت کنیم، احتمال ظاهر شدن هر وجه آن برابر با نخواهد بود؛ زیرا ابعاد وجههای قوطی کبریت با یکدیگر تفاوت دارند. به آزمایش پرتاب قوطی کبریت، یک آزمایش تصادفی با احتمال غیرهمشانس میگویند.
رویداد یا پیشامد در احتمال چیست؟
پیشامد یا «رویداد» (Event)، آزمونی با نتیجه از پیش تعیین شده است. به عنوان مثال، مشاهده عدد ۱ پس از پرتاب تاس، یک پیشامد به شمار میرود.
رویداد یا پیشامد تصادفی در احتمال چیست؟
«پیشامد تصادفی» (Random Event)، پیشامدی است که امکان پیشگویی راحت آن وجود ندارد. احتمال رخ دادن این پیشامد، بسیار کوچک است. به عنوان مثال، تشکیل رنگینکمان در حین بارندگی، یک پیشامد تصادفی است.
فضای نمونه در احتمال چیست؟
«فضای نمونه» (Sample Space)، مجموعهای از تمام نتایج ممکن در یک آزمون است. توجه داشته باشید که به هر عضو فضای نمونه، یک برآمد و به هر زیرمجموعه فضای نمونه، یک پیشامد میگویند. فضای نمونه، معمولا با حرف S نمایش داده میشود. به عنوان مثال، پرتاب تاس را در نظر بگیرید. در یک مرتبه پرتاب تاس، احتمال مشاهده اعداد ۱ تا ۶ وجود دارد. بنابراین، هر یک از این اعداد، یک برآمد هستند. مجموعه این برآمدها، به صورت زیر نوشته میشود:
مجموعه بالا، فضای نمونه پرتاب تاس را نشان میدهد. هر یک از اعداد ۱ تا ۶، یک برآمد از فضای نمونه در آزمون پرتاب تاس هستند. در پرتاب تاس، اگر مشاهده عدد زوج، به عنوان حالت یا نتیجه مطلوب در نظر گرفته شود، مجموعه اعداد ، یک پیشامد از فضای نمونه بالا خواهد بود. پیشامدها، انواع مختلفی دارند که در بخشهای بعدی به تعریف برخی از آنها میپردازیم.
فضای نمونه گسسته در احتمال چیست؟
«فضای نمونه گسسته» (Discrete Sample Space)، مجموعهای متناهی یا نامتناهی است که امکان شمارش آنها وجود دارد. به عنوان مثال، فضای نمونه در آزمایش پرتاب تاس، یک فضای نمونه گسسته است؛ زیر میتوان تعداد اعضای آن را شمرد. در ریاضیات دبیرستان، فقط در مورد نوع متناهی فضاهای نمونه گسسته بحث میشود.
فضای نمونه پیوسته در احتمال چیست؟
«فضای نمونه پیوسته» (Continuous Sample Space)، مجموعهای نامتناهی است که بازههایی از اعداد حقیقی یا اشکال و احجام هندسی را در برمیگیرد. به عنوان مثال، کمیتهای فیزیکی مانند دما، شتاب و فشار، از انواع فضاهای نمونه پیوسته هستند.
پیشامد مستقل در احتمال چیست؟
«پیشامد مستقل» (Independent Event)، پیشامدی است که وقوع آن به هیچ پیشامد دیگری وابسته نباشد. به عنوان مثال، پرتاب سکه را در نظر بگیرید. اگر سکهای را یک بار پرتاب کنیم، یا با پشت یا با روی آن مواجه میشویم. فرض کنید در پرتاب اول، پشت آمده باشد. اکنون، سکه را برای بار دوم پرتاب میکنیم. از خود سوال کنید که آیا پشت آمدن سکه در پرتاب اول، تاثیری بر روی پشت یا رو آمدن آن در پرتاب دوم دارد. جواب این سوال، منفی است.
نتیجه هر پرتاب سکه، مستقل از پرتاب دیگر است و هیچ تاثیری بر روی شانس یا احتمال پرتابهای دیگر ندارد. ممکن است شما به عنوان مثال سکه را ده مرتبه پرتاب کنید و پشت بیاید. این نتیجه، دلیلی بر افزایش احتمال رو آمدن سکه در پرتاب یازدهم نیست؛ زیرا در پرتاب یازدهم نیاز دوباره شانس پشت آمدن سکه با رو آمدن آن برابر خواهد بود.
پیشامد وابسته در احتمال چیست؟
«پیشامد وابسته» (Dependent Event)، پیشامدی است که وقوع آن به پیشامد دیگری بستگی دارد. به عنوان مثال، یک سکه و یک تاس را در نظر بگیرید. برای شروع آزمایش، ابتدا سکه را پرتاب میکنیم. اگر پشت بیاید، سکه را برای مرتبه دوم پرتاب کرده و در صورت رو آمدن، تاس را برای مرتبه اول پرتاب میکنیم. دقت داشته باشید که پیشامد مرحله دوم، به پیشامد مرحله اول بستگی دارد. این پیشامدها را وابسته میگویند.
فرادرس، یک فیلم آموزشی جامع را با عنوان «آموزش ریاضی پایه دهم برای رشته های تجربی و ریاضی» تهیه کرده است میتواند شما را در یادگیری مفاهیم پایه احتمال و حل مسائل مرتبط با این موضوع کمک کند. لینک مشاهده این آموزش کاربردی و مفید در ادامه آورده شده است.
پیشامد محتمل در احتمال چیست؟
«پیشامد محتمل» (Probable Event)، پیشامدی است که میتوان احتمال وقوع آن را محاسبه کرد. به عنوان مثال، امکان محاسبه احتمال قبولی یک دانشآموز در مقطع فعلی و ادامه تحصیل در مقطع بالاتر وجود دارد. بنابراین، به این پیشامد (احتمال ارتقا به مقطع بالاتر)، یک پیشامد محتمل میگویند.
پیشامد غیرمحتمل یا غیرممکن در احتمال چیست؟
پیشامد غیرمحتمل یا «پیشامد غیرممکن» (Impossible Event)، پیشامدی است که به عنوان بخشی از آزمایش محسوب نمیشود و یا در فضای نمونه جای ندارد. به عنوان مثال، در مناطقی با آب و هوای بسیار گرم، برف نمیبارد. در این مثال، بارش برف به عنوان یک پیشامد غیرمحتمل در نظر گرفته میشود؛ زیرا احتمال رخ دادن آن نزدیک به ۰ یا برابر با ۰ است.
پیشامدهای مکمل یا متمم در احتمال چیست؟
پیشامدهای متمم یا «پیشامدهای مکمل» (Complementary Event)، دو پیشامدی هستند که اگر یکی از آنها رخ دهد، دیگری رخ نمیدهد. این پیشامدها، از نظر وقوع، دقیقا در مقابل یکدیگر قرار دارند. به عنوان مثال، در پرتاب سکه، پیشامد پشت آمدن و رو آمدن را در نظر بگیرید. اگر پیشامد پشت آمدن سکه رخ دهد، پیشامد رو آمدن رخ نمیدهد و بالعکس. این دو پیشامد، مکمل یکدیگر هستند. در یک آزمایش، نتیجه مطلوب و نامطلوب، به عنوان پیشامدهای مکمل در نظر گرفته میشوند.
دقت داشته باشید که مجموعه تهی، زیرمجموعهای از تمام مجموعهها است. از طرفی، هر مجموعه، زیرمجموعه خودش محسوب میشود. از اینرو، مجموعه تهی و فضای نمونه S، زیرمجموعهای از فضای نمونه S هستند. به این ترتیب، این دو مجموعه، دو پیشامد از فضای نمونه S به شمار میروند. مجموعه S، یک پیشامد حتمی و مجموعه تهی، یک پیشامد نشدنی است. پیشامدهای حتمی و نشدنی، متمم یکدیگرند.
پیشامدهای دوبهدوی ناسازگار در احتمال چیست؟
«پیشامدهای دوبهدوی ناسازگار» (Mutually Exclusive Events)، دو پیشامدی هستند که رخ دادن یکی از آنها باعث جلوگیری از رخ دادن دیگری میشود. به عبارت دیگر، امکان وقوع همزمان این دو پیشامد وجود ندارد. به عنوان مثال، یک مسابقه فوتبال را در نظر بگیرید. اگر احتمال به ثمر نرسیدن هیچ گل (اتمام بازی با نتیجه ۰-۰) برابر با ۰/۲ و احتمال به ثمر رسیدن تنها یک گل در کل مسابقه برابر با ۰/۱۵ باشد، احتمال رخ دادن همزمان این دو پیشامد برابر با ۰ خواهد بود؛ زیرا وقوع هر یک از این پیشامدها، از وقوع پیشامد دیگر جلوگیری میکند. بنابراین، این دو پیشامد، ناسازگار هستند.
چگونه احتمال را به طور کامل و اصولی یاد بگیریم؟
به منظور یادگیری کامل و اصولی احتمال، پیش از هر چیزی باید اصول و مبانی این علم را یاد بگیرید. آشنایی با مجموعهها و اصول شمارش، اقدام خوبی برای شروع است. سپس، به سراغ یادگیری اصطلاحات و مفاهیم اصلی احتمال بروید. دروس ریاضی دوره متوسطه دوم، از جمله «ریاضی ۱»، «ریاضی ۲»، «آمار و احتمال» و «جبر و احتمال»، بسیاری از مفاهیم مورد نیاز شما را در این زمینه پوشش میدهند. با وجود کامل بودن مطالب کتابهای درسی، برای تقویت مهارتهای خود در حل مسائل مربوط به احتمال، باید به حل مثالها و تمرینهای متعدد بپردازید.
فرادرس، مجموعهای از فیلمهای آموزشی جامع و مفید را تهیه کرده است که میتوانند به شما در یادگیری و تسلط بر روی احتمال کمک کنند. لینک مشاهده برخی از این فیلمهای آموزشی در ادامه آورده شده است:
فرمولها و قوانین احتمال چه هستند؟
در دنیای احتمال، قوانین و فرمولهای مختلفی وجود دارند که در این بخش به معرفی برخی از مهمترین آنها میپردازیم.
کاربرد علائم جبری در احتمال چیست؟
برای یادگیری احتمال، باید با مفهوم مجموعه آشنا باشید. بسیاری از مفاهیم احتمال، با استفاده از مباحث مرتبط با مجموعهها تعریف میشوند. جدول زیر، اصلیترین علائم ریاضی مجموعهها را نمایش میدهد.
| علامت مجموعه | توضیح |
| مجموعه سراسری | |
| مجموعه A | |
| متمم مجموعه A (مجموعهای شامل تمام اعضای U است که هیچیک از اعضای A در آن حضور ندارند.) | |
| مجموعه B | |
| متمم مجموعه B | |
| اشتراک مجموعههای A و B | |
| اجتماع مجموعههای A و B | |
| تفاضل مجموعههای A و B |
جدول زیر، حاوی علائم مورد استفاده برای نمایش ریاضی پارامترهای احتمالاتی است.
| علامت احتمال | توضیح |
| مجموعه شامل فضای نمونه | |
| تعداد اعضای فضای نمونه | |
| پیشامد A | |
| متمم پیشامد A | |
| پیشامد B | |
| متمم پیشامد B | |
| احتمال رخ دادن پیشامد A | |
| احتمال رخ دادن پیشامد B | |
| احتمال رخ دادن همزمان پیشامدهای A و B | |
| احتمال رخ دادن حداقل یکی از پیشامدهای A یا B | |
| احتمال رخ دادن پیشامد A و رخ ندادن پیشامد B | |
| احتمال رخ دادن پیشامد A به شرط رخ دادن پیشامد B |
آشنایی با مفاهیم مرتبط با مجموعهها، دانش پایه شما برای درک فرمولهای احتمال را افزایش میدهد. مطلب «نمودار ون – از صفر تا صد» در مجله فرادرس، به معرفی یکی از ابزارهای کاربردی برای یادگیری روابط بین مجموعهها میپردازد. این ابزار میتواند شما را در مطالعه فرمولها و قوانین احتمال نیز کمک کند.
روش محاسبه فضای نمونه چند آزمایش در احتمال چیست؟
در صورتی که آزمایشی متشکل از دو آزمون با فضاهای نمونه و باشد، فضای نمونه آن برابر خواهد بود با:
رابطه بالا برای هر تعداد آزمایش همزمان نیز صدق میکند. به عنوان مثال، پرتاب یک تاس را در نظر بگیرید. فضای نمونه این آزمون، دارای ۶ عضو (اعداد ۱ تا ۶) است. اگر تاس را برای مرتبه دوم پرتاب کنیم، فضای نمونه آزمون دوم نیز برابر با ۶ عضو خواهد بود. با این وجود، فضای نمونه کل آزمایش برابر میشود با:
بنابراین، اگر یک تاس را دو مرتبه یا دو تاس را به طور همزمان پرتاب کنیم، اندازه فضای نمونه کل آزمایش برابر با ۳۶ میشود.
مثال ۱: محاسبه اندازه فضای نمونه در پرتاب همزمان تاس و سکه
در یک آزمایش تصادفی، یک تاس و یک سکه را به طور همزمان پرتاب میکنیم. اندازه فضای نمونه را به دست بیاورید.
برای به دست آوردن اندازه فضای نمونه در آزمایش پرتاب همزمان یک تاس و یک سکه، از رابطه زیر استفاده میکنیم:
- : اندازه فضای نمونه کل آزمایش
- : اندازه فضای نمونه در پرتاب تاس برابر با ۶
- : اندازه فضای نمونه در پرتاب سکه برابر با ۲
به این ترتیب داریم:
در نتیجه، فضای نمونه کل آزمایش برابر با ۱۲ است.
احتمال پیشامد و بازه مجاز آن چیست؟
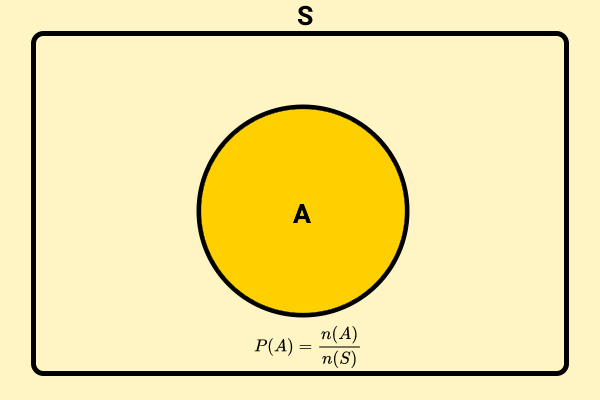
محاسبه احتمال یک پیشامد، با استفاده از فرمول زیر صورت میگیرد:
- : احتمال پیشامد A
- : تعداد برآمدهای مطلوب A
- : تعداد تمام برآمدهای موجود در فضای نمونه
فرمول بالا، در محاسبه احتمال در فضاهای گسسته همشانس کاربرد دارد. این نوع احتمال، با عنوان احتمال کلاسیک شناخته میشود.
احتمال یک پیشامد، همواره عددی حقیقی بین ۰ تا ۱ است. عدد ۰، غیرممکن بودن پیشامد را نمایش میدهد. عدد ۱ نیز بیانگر وقوع قطعی پیشامد است. مقدار عددی احتمال را با درصد نیز بیان میکنند. به عنوان مثال، برای اشاره به قطعی بودن یک پیشامد، میگویند احتمال آن برابر با ۱۰۰ درصد است.
مثال ۲: محاسبه احتمال یک پیشامد
در آزمایش پرتاب تاس، احتمال مشاهده عدد ۶ چقدر است؟
برای به دست آوردن احتمال، ابتدا باید فضای نمونه و پیشامد را مشخص کنیم. یک تاس، شش وجه دارد که بر روی هر یک از آنها، یک عدد منحصر به فرد (از ۱ تا ۶) نوشته شده است. این اعداد، فضای نمونه را تشکیل میدهند. به این ترتیب، داریم:
فضای نمونه، ۶ عضو دارد. بنابراین:
اکنون به سراغ عضوهای پیشامد میرویم. در این مثال، پیشامد مورد نظر، رو شدن عدد ۶ است. به این ترتیب، داریم:
پیشامد، ۱ عضو دارد. بنابراین:
اکنون، میتوانیم احتمال رو شدن عدد ۶ را در یک پرتاب تاس محاسبه میکنیم. این احتمال با استفاده از رابطه زیر به دست میآید:
- : احتمال رو شدن عدد ۶
- : تعداد برآمدهای مطلوب برابر با ۱
- : تعداد تمام برآمدهای موجود در فضای نمونه برابر با ۶
مقادیر معلوم را درون فرمول قرار میدهیم:
بنابراین، احتمال رو شدن عدد ۶ پس از پرتاب تاس، برابر با یا تقریبا ۰/۱۷ است. به عبارت دیگر، نزدیک به ۱۷ درصد احتمال مشاهده عدد ۶ در هر پرتاب تاس وجود دارد. احتمال مشاهده اعداد دیگر نیز به همین مقدار (تقریبا ۰/۱۷ یا ۱۷ درصد) است.
مثال ۳: محاسبه احتمال پرتاب همزمان تاس و سکه
یک سکه و یک تاس را به طور همزمان پرتاب میکنیم. احتمال اینکه سکه به پشت بیاید و عددی کوچکتر از ۵ روی تاس نمایان شود را به دست بیاورید.
برای شروع، ابتدا فضای نمونه را مشخص میکنیم. با وجود اشاره به پرتاب همزمان تاس و سکه، میتوانید پرتاب سکه و پرتاب تاس را به صورت جداگانه در نظر بگیرید تا امکان تعیین فضای نمونه فراهم شود. پس از پرتاب سکه، امکان مشاهده پشت یا رو وجود داشته و پس از پرتاب تاس، امکان مشاهده اعداد ۱ تا ۶ وجود دارد.
پشت سکه را با حرف T و روی آن را با حرف H در نظر بگیرید. فرض کنید پس از پرتاب سکه، پشت آن مشخص شود. در این حالت و پس از پرتاب تاس، با برآمدهای زیر روبرو میشویم:
اگر پس از پرتاب سکه، روی آن مشخص شود. در این حالت و پس از پرتاب تاس، با برآمدهای زیر روبرو میشویم:
به این ترتیب، برای فضای نمونه، داریم:
در صورت سوال، از ما خواسته شده است تا احتمال مشاهده پشت سکه و عددی کوچکتر از ۵ روی تاس را به دست بیاوریم. برای این کار، باید تمام حالتهایی که در شرایط صورت سوال صدق نمیکنند. را از فضای نمونه حذف کنیم. به این ترتیب، خواهیم داشت:
مجموعه بالا، اعضای پیشامد مورد سوال را نمایش میدهد. تعداد اعضای این مجموعه برابر با ۴ است. تعداد اعضای فضای نمونه نیز برابر ۱۲ است. به عبارت دیگر:
اکنون، فرمول محاسبه احتمال را مینویسیم:
- : احتمال مشاهده پشت سکه به همراه عددی کوچکتر از ۵ روی تاس
- : تعداد برآمدهای مطلوب برابر با ۴
- : تعداد تمام برآمدهای موجود در فضای نمونه برابر با ۱۲
مقادیر معلوم را درون رابطه جایگذاری میکنیم:
در نتیجه، احتمال مشاهده پشت سکه به همراه عددی کوچکتر از ۵ روی تاس برابر با یا حدود ۳۳ درصد است.
احتمال مجموع برآمدها چیست؟
مجموع احتمال رخ دادن تمام برآمدها، برابر با ۱ میشود. به عبارت دیگر، مجموع احتمالات در فضای نمونه برابر با ۱ است. به این ترتیب، داریم:
- : احتمال رخ دادن پیشامد زیرمجموعه فضای نمونه
- : مجموعه فضای نمونه (مجموعه تمام برآیندها)
احتمال تهی چیست؟
مجموعه تهی (ø)، مجموعهای است که هیچ عضوی ندارد. به عبارت دیگر، تعداد اعضای این مجموعه برابر با ۰ است. احتمال رخ دادن مجموعه تهی، برابر با صفر میشود. به این ترتیب، داریم:
احتمال اشتراک دو پیشامد چیست؟
احتمال اشتراک دو پیشامد، به مستقل یا وابسته بودن پیشامدها بستگی دارد. اگر دو پیشامد مستقل باشند، احتمال اجتماع آنها با استفاده از رابطه زیر به دست میآید:
- : احتمال اشتراک دو پیشامد مستقل A و B
- : احتمال پیشامد A
- : احتمال پیشامد B
در صورت وابسته بودن یکی از پیشامدها به دیگری، از فرمول زیر برای محاسبه احتمال اشتراک آنها استفاده میشود:
- : احتمال اشتراک دو پیشامد A و B
- : احتمال پیشامد A
- : احتمال پیشامد وابسته B بعد از پیشامد A (احتمال شرطی)
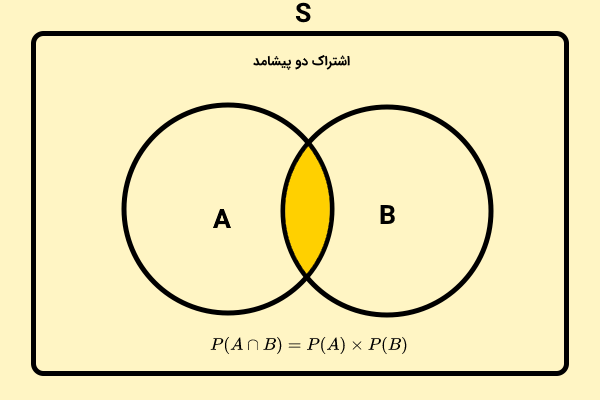
در رابطه بالا، احتمال وقوع پیشامد B به برآمد پیشامد A بستگی دارد. به همین دلیل، فرمول احتمال اشتراک این دو پیشامد، به صورت بالا نوشته میشود. احتمال اشتراک دو پیشامد A و B، یعنی هم پیشامد A اتفاق بیفتد و هم پیشامد B اتفاق بیفتد. عبارت راهنما برای تشخیص سریع مسائل قابل حل با فرمول بالا، «و» است. بنابراین، اگر این عبارت به طور مستقیم در مسئله قابل مشاهده بود یا امکان بیان مسئله با استفاده از این عبارت وجود داشت، میتوانید از فرمول بالا برای تعیین احتمال اشتراک دو پیشامد استفاده کنید. در ادامه، به توضیح بهتر این نکته با حل یک مثال میپردازیم.
مثال ۴: محاسبه احتمال دو پیشامد مستقل
یک تاس را دو مرتبه پرتاب میکنیم. چقدر احتمال دارد در پرتاب اول تاس عدد ۳ و در پرتاب دوم تاس عدد ۵ مشاهده شود؟
برای حل این مسئله، دو روش وجود دارد. روش اول، نوشتن تمام اعضای فضای نمونه، مشخص کردن حالتهای مطلوب، شمارش تعداد اعضای فضای نمونه، شمارش تعداد حالتهای مطلوب و محاسبه احتمال با استفاده از فرمول احتمال پیشامد است. در روش دوم، میتوان از فرمول احتمال اشتراک دو پیشامد استفاده کرد.
هر پرتاب تاس، یک آزمایش مجزا است و نتیجه پرتاب اول بر روی احتمال مشاهده هر عدد در پرتاب دوم تاثیر نمیگذارد. بنابراین، این آزمایش، دو پیشامد مستقل را نمایش میدهد. برای محاسبه احتمال مشاهده عدد ۳ در پرتاب اول تاس و مشاهده عدد ۵ در پرتاب دوم تاس، از فرمول احتمال اشتراک دو پیشامد مستقل استفاده میکنیم. برای تشخیص این موضوع میتوانید از عبارت «و» کمک بگیرید (پیشامد مشاهده عدد ۳ در پرتاب اول و پیشامد مشاهده عدد ۵ در پرتاب دوم). فرمول احتمال اشتراک دو پیشامد عبارت است از:
- : احتمال مشاهده عدد ۳ در پرتاب اول و مشاهده عدد ۵ در پرتاب دوم تاس
- : احتمال پیشامد مشاهده عدد ۳ در پرتاب اول تاس برابر با
- : احتمال پیشامد مشاهده عدد ۵ در پرتاب دوم تاس برابر با
در نتیجه، احتمال مشاهده عدد ۳ در پرتاب اول و مشاهده عدد ۵ در پرتاب دوم تاس برابر با یا حدود ۲/۸ درصد است. دقت داشته باشید که اگر دو تاس را همزمان پرتاب میکردیم، احتمال اینکه یکی از تاسها عدد ۳ و دیگری عدد ۵ را نمایش دهند، با مقدار به دستآمده در این مثال متفاوت میشد.
مثال ۵: محاسبه احتمال دو پیشامد وابسته
در یک کلاس دانشگاه، ۲۰ دانشجوی دختر و ۱۰ دانشجوی پسر حضور دارند. استاد، قصد دارد دو نفر را به صورت تصادفی برای پرسیدن سوالات شفاهی انتخاب کند. احتمال پسر بودن هر دو شخص انتخاب شده چقدر است؟
برای پاسخ به این سوال، ابتدا آنها را تحلیل میکنیم. در مجموع، ۳۰ دانشجو در کلاس حضور دارند. اگر استاد قصد انتخاب تصادفی یکی از آنها را داشته باشد، احتمال انتخاب شدن هر شخص برابر با خواهد بود. به دلیل حضور ۱۰ دانشجوی پسر، احتمال پسر بودن شخص انتخاب شده برابر است با:
- : احتمال پسر بودن شخص انتخاب شده
- : تعداد برآمدهای مطلوب برابر با ۱۰ (تعداد دانشجویان پسر)
- : تعداد تمام برآمدهای موجود در فضای نمونه برابر با ۳۰ (تعداد کل دانشجویان حاضر در کلاس)
بنابراین، در انتخاب شخص اول، احتمال دارد که دانشجوی انتخابی، پسر باشد. نکته مهم در انتخاب دانشجوی بعدی این است که دانشجوی انتخاب شده در مرحله اول، دیگر در فضای نمونه قرار ندارد. بنابراین، یک نفر از فضای نمونه کم میشود و تعداد فضای نمونه به ۲۹ میرسد. این موضوع، بر روی احتمال انتخاب هر دانشجو تاثیر میگذارد. بنابراین، پیشامد پسر بودن دانشجوی انتخابی دوم، وابسته به پیشامد پسر یا دختر بودن دانشجوی انتخابی اول است.
پس از انتخاب دانشجوی اول، فضای نمونه برابر با ۲۹ و تعداد دانشجویان پسر برابر با ۹ میشود. تعداد دانشجویان دختر تغییری نمیکند. به این ترتیب، احتمال پسر بودن دانشجوی دوم از رابطه زیر به دست میآید:
- : احتمال پسر بودن شخص انتخاب شده در مرحله دوم
- : تعداد برآمدهای مطلوب برابر با ۹ (تعداد دانشجویان پسر در مرحله دوم)
- : تعداد تمام برآمدهای موجود در فضای نمونه برابر با ۲۹ (تعداد کل دانشجویان حاضر در کلاس، پس از کم کردن شخص انتخاب شده در مرحله اول)
احتمال پسر بودن هر دو دانشجوی انتخابی، یعنی پسر بودن دانشجوی انتخابی اول و پسر بودن دانشجوی انتخابی دوم. عبارت «و»، راهنمای ما برای استفاده از فرمول محاسبه احتمال اشتراک دو پیشامد است. به دلیل وابسته بودن یکی از پیشامدها به دیگری، این فرمول به صورت زیر نوشته میشود:
- : احتمال پسر بودن هر دو دانشجوی انتخابی
- : احتمال پسر بودن دانشجوی انتخابی اول برابر با
- : احتمال پسر بودن دانشجوی انتخابی دوم به شرط پسر بودن دانشجوی انتخابی اول برابر با
با جایگذاری مقادیر معلوم در رابطه بالا، خواهیم داشت:
در نتیجه، احتمال انتخاب تصادفی دو دانشجوی پسر در کلاسی با ۲۰ دانشجوی دختر و ۱۰ دانشجوی پسر، برابر با یا تقریبا ۱۰/۳ درصد است.
احتمال اجتماع دو پیشامد چیست؟
احتمال اجتماع دو پیشامد مستقل از رابطه زیر به دست میآید:
- : احتمال اجتماع دو پیشامد A و B
- : احتمال پیشامد A
- : احتمال پیشامد B
- : احتمال اشتراک دو پیشامد A و B
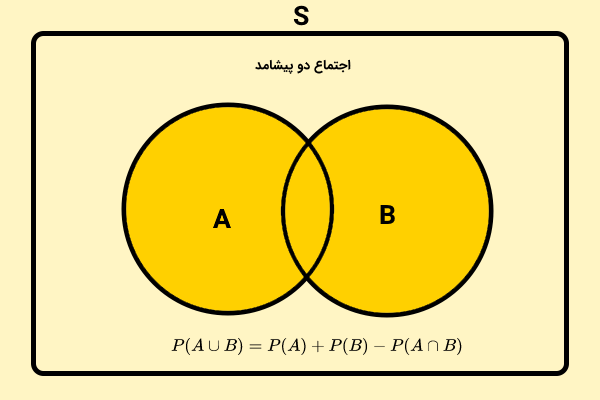
احتمال اجتماع دو پیشامد A و B، یعنی یا پیشامد A اتفاق بیفتد یا پیشامد B اتفاق بیفتد. بنابراین، کلمه کلیدی برای تشخیص بهتر مسائل قابل حل با فرمول بالا، عبارت «یا» است. اگر توانستید این عبارت را به طور مستقیم در مسئله پیدا کنید یا مسئله به گونهای بیان کنید که این عبارت درون آن ظاهر شود، میتوانید از فرمول بالا برای رسیدن به جواب کمک بگیرید. در ادامه، این موضوع را با حل یک مثال توضیح میدهیم.
مثال ۶: محاسبه احتمال اجتماع دو پیشامد
جدول زیر، دادههای یک مطالعه بر روی تخلف عبور از سرعت مجاز در حین رانندگی و استفاده از تلفن همراه را نمایش میهد.
| عنوان | تعداد تخلف عبور از سرعت غیرمجاز در سال گذشته | بدون تخلف عبور از سرعت مجاز در سال گذشته | جمع |
| استفاده از تلفن همراه | ۲۵ | ۲۸۰ | ۳۰۵ |
| عدم استفاده از تلفن همراه | ۴۵ | ۴۰۵ | ۴۵۰ |
| جمع | ۷۰ | ۶۸۵ | ۷۵۵ |
از میان مشارکتکنندگان این پژوهش، یک نفر را به صورت تصادفی انتخاب میکنیم. احتمال اینکه این شخص، دارای تلفن همراه باشد یا در سال گذشته، هیچ تخلف مرتبط با عبور از سرعت مجاز نداشته باشد، چقدر است؟
اگر صورت سوال را به دقت خوانده باشید، متوجه عبارت «یا» در آن میشوید. این عبارت، یعنی باید از فرمول احتمال اجتماع پیشامدها برای حل مسئله استفاده کنیم. این فرمول عبارت است از:
- : احتمال اجتماع دو پیشامد A و B
- احتمال اینکه این شخص، دارای تلفن همراه باشد یا در سال گذشته، هیچ تخلف مرتبط با عبور از سرعت مجاز نداشته باشد.
- : احتمال پیشامد A
- احتمال اینکه شخص، دارای تلفن همراه باشد.
- : احتمال پیشامد B
- احتمال اینکه شخص در سال گذشته، هیچ تخلف مرتبط با عبور از سرعت مجاز نداشته باشد.
- : احتمال اشتراک دو پیشامد A و B
- احتمال اینکه هم شخص دارای تلفن همراه باشد و هم در سال گذشته، هیچ تخلف مرتبط با عبور از سرعت مجاز نداشته باشد.
برای حل مسئله، ابتدا باید مقدار پارامترهای مجهول را به دست بیاوریم. این کار با محاسبه احتمال اینکه شخص، دارای تلفن همراه باشد، شروع میکنیم. فرمول محاسبه این احتمال به صورت زیر نوشته میشود:
- : احتمال اینکه شخص، دارای تلفن همراه باشد.
- : تعداد افراد دارای تلفن همراه برابر با ۳۰۵
- : تعداد کل افراد مشارکتکننده در مطالعه برابر با ۷۵۵
اکنون به سراغ محاسبه احتمال اینکه شخص در سال گذشته، هیچ تخلف مرتبط با عبور از سرعت مجاز نداشته باشد میرویم. مقدار این احتمال، با استفاده از فرمول زیر به دست میآید:
- : احتمال اینکه شخص، در سال گذشته، هیچ تخلف مرتبط با عبور از سرعت مجاز نداشته باشد.
- : تعداد افراد بدون تخلف عبور از سرعت مجاز در سال گذشته برابر با ۶۸۵
- : تعداد کل افراد مشارکتکننده در مطالعه برابر با ۷۵۵
احتمال اینکه شخص انتخاب شده دارای تلفن همراه باشد و در سال گذشته، هیچ تخلف مرتبط با عبور از سرعت مجاز نداشته باشد، برابر است با:
- : احتمال اینکه هم شخص دارای تلفن همراه باشد و هم در سال گذشته، هیچ تخلف مرتبط با عبور از سرعت مجاز نداشته باشد.
- : تعداد افراد دارای تلفن همراه، بدون تخلف عبور از سرعت مجاز در سال گذشته برابر با ۲۸۰
- : تعداد کل افراد مشارکتکننده در مطالعه برابر با ۷۵۵
اکنون، مقادیر معلوم را درون فرمول احتمال اجتماع پیشامدها قرار میدهیم:
در نتیجه، احتمال اینکه این شخص، دارای تلفن همراه باشد یا در سال گذشته، هیچ تخلف مرتبط با عبور از سرعت مجاز نداشته باشد، برابر با یا تقریبا ۹۴ درصد است.
اگر به یادگیری فرمولهای احتمال در سطح دبیرستان علاقه دارید، «فیلم آموزش آمار و احتمال پایه یازدهم فرادرس» را مشاهده کنید. لینک مشاهده این فیلم آموزشی در ادامه آورده شده است.
احتمال تفاضل دو پیشامد چیست؟
برای محاسبه احتمال تفاضل دو پیشامد، از رابطه زیر استفاده میکنیم:
- : احتمال تفاضل دو پیشامد A و B
- : احتمال پیشامد A
- : احتمال پیشامد B
- : احتمال اشتراک دو پیشامد A و B
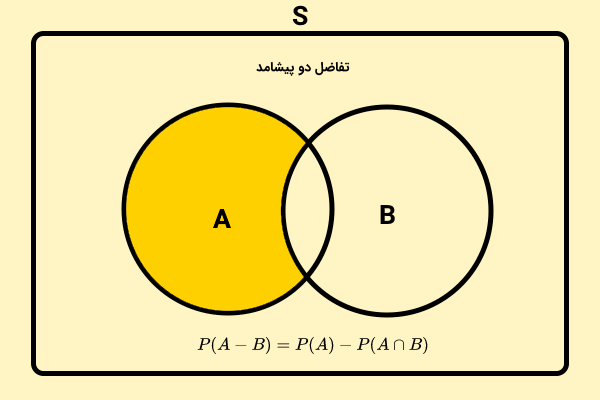
احتمال تفاضل دو پیشامد، یعنی یکی از پیشامدها رخ دهد و پیشامد دیگر رخ ندهد. اگر پیشامد A، زیرمجموعهای از پیشامد B باشد، احتمال پیشامد A، کوچکتر مساوی احتمال پیشامد B میشود و احتمال رخ دادن B و رخ ندادن A برابر خواهد بود با:
در این شرایط، پیشامد A درون پیشامد B قرار میگیرد و اشتراک پیشامدها، برابر با پیشامد کوچکتر میشود. به همین دلیل، فرمول محاسبه احتمال تفاضل، به فرم بالا درمیآید.
مثال ۷: محاسبه احتمال تفاضل دو پیشامد
کیسهای حاوی ۱۲ توپ با شمارههای ۱ تا ۱۲ را در نظر بگیرید. میخواهیم یک توپ را به صورت تصادفی از درون کیسه بیرون بیاوریم. احتمال پیشامد زیر را به دست بیاورید:
- شماره روی توپ، عددی فرد باشد اما اول نباشد.
پیش از حل این مسئله، به عبارت «اما» در صورت سوال دقت کنید. این عبارت مسئله را به ما نشان میدهد. در اینجا قصد داریم احتمال فرد بودن عدد روی توپ و اول نبودن آن را به دست بیاوریم. برای شروع، به سراغ محاسبه احتمال فرد بودن عدد روی توپ میرویم. اعداد فرد روی توپها برابر هستند با:
این مجموعه، دارای ۶ عضو است. فضای نمونه نیز ۱۲ عضو دارد. به این ترتیب:
- : احتمال فرد بودن عدد روی توپ انتخابی
- : تعداد برآمدهای مطلوب (تعداد توپهای دارای عدد فرد برابر با ۶)
- : تعداد تمام برآمدهای موجود در فضای نمونه (تعداد تمام توپهای درون کیسه برابر با ۱۲)
به این ترتیب، احتمال فرد بودن عدد روی توپ انتخابی برابر با است. اعداد اول بین ۱ تا ۱۲ عبارت هستند از:
احتمال اینکه شماره روی توپ انتخابی، عددی فرد باشد اما اول نباشد، به صورت زیر نوشته میشود:
برای محاسبه این احتمال، از رابطه زیر استفاده میکنیم:
- : احتمال فرد بودن عدد روی توپ و اول نبودن آن
- : احتمال فرد بودن عدد روی توپ برابر با
- : احتمال اول بودن عدد روی توپ
- : احتمال فرد بودن و اول بودن عدد روی توپ
از بین پارامترهای بالا، را هنوز محاسبه نکردهایم. برای تعیین این پارامتر، باید به دنبال اعدادی بین ۱ تا ۱۲ باشیم که هم فرد و هم اول هستند. این اعداد در مجموعه زیر آورده شدهاند:
مجموعه بالا، دارای ۴ عضو است. با در نظر گرفتن ۱۲ عضو فضای نمونه، خواهیم داشت:
اکنون، تمام مقادیر مورد نیاز برای حل مسئله را داریم. این مقادیر را درون فرمول احتمال تفاضل دو پیشامد قرار میدهیم:
در نتیجه، احتمال اینکه شماره روی توپ انتخابی، عددی فرد باشد اما اول نباشد، برابر با است.
احتمال متمم یک پیشامد چیست؟
اگر A یک پیشامد از فضای نمونه S باشد، متمم پیشامد A (پیشامد ‘A یا AC)، زمانی رخ میدهد که پیشامد A رخ ندهد. مجموع احتمال یک پیشامد و احتمال متمم آن پیشامد برابر با ۱ است. به عبارت دیگر:
بنابراین، اگر بخواهیم احتمال یک پیشامد را به دست بیاوریم، میتوانیم از رابطه زیر استفاده کنیم:
البته، فرمول دیگری برای محاسبه احتمال متمم یک پیشامد وجود دارد که به صورت زیر نوشته میشود:
- : احتمال متمم یک پیشامد
- : تعداد اعضای فضای نمونه
- : تعداد اعضای پیشامد A
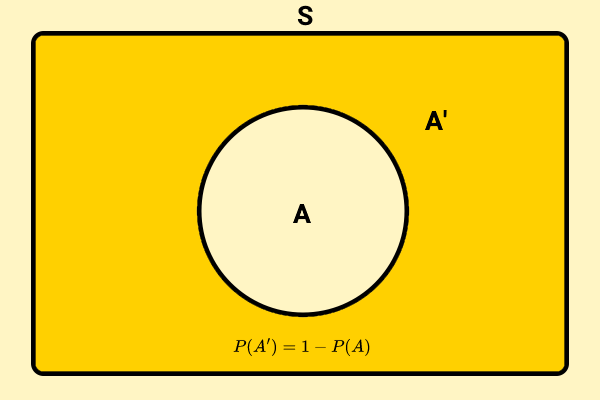
اگر به تصویر بالا دقت کنید، میتوانید به روابط زیر برسید:
اجتماع یک پیشامد با متمم آن پیشامد، فضای نمونه را تشکیل میدهد. علاوه بر این، اشتراک یک پیشامد با متمم آن پیشامد، برابر با مجموعه تهی است؛ زیرا این دو، هیچ نقطه اشتراکی ندارند.
مثال ۸: محاسبه احتمال متمم یک پیشامد
دو تاس را به طور همزمان پرتاب میکنیم. احتمال اینکه دو عدد منحصر به فرد روی هر یک از تاسها ظاهر شود، چقدر است؟
اولین روشی که برای حل این مسئله به ذهن اغلب افراد میآید، نوشتن تمام اعضای فضای نمونه، تعیین زوجمرتبهای دارای اعداد منحصر به فرد و محاسبه احتمال با استفاده از فرمول احتمال پیشامد است. این روش میتواند کمی زمانبر باشد و احتمال خطا را افزایش میدهد. در چنین شرایطی، استفاده از مفهوم احتمال متمم یک پیشامد، فرآیند حل را سادهتر میکند. فضای نمونه، در پرتاب همزمان دو تاس برابر است با:
اعضای این فضای نمونه به صورت زیر نوشته میشوند:
صورت سوال، احتمال نمایان شدن دو عدد منحصر به فرد روی هر تاس، مانند را میخواهد. زوجمرتبهای حاوی اعداد منحصر به فرد در فضای نمونه S را A مینامیم. متمم A، مجموعهای زیرمجموعهای زوجمرتبهای حاوی اعداد تکراری مانند است. اکنون، به جای نوشتن تمام اعضای A، اعضای متمم آن، یعنی ‘A را مینویسیم:
متمم A، دارای ۶ عضو است. احتمال رخ دادن ‘A برابر است با:
- : احتمال یکسان بودن اعداد تاسها
- : تعداد برآمدهای مطلوب برابر با ۶
- تعداد حالتهایی که در آنها، اعداد هر دو تاس با هم برابر میشود.
- : تعداد تمام برآمدهای موجود در فضای نمونه برابر با ۳۶
احتمال متمم A (احتمال یکسان بودن اعداد دو تاس)، برابر با است. بنابراین، احتمال A (احتمال متفاوت بودن اعداد دو تاس) برابر میشود با:
در نتیجه، به احتمال یا تقریبا ۸۳ درصد، اعداد نمایان شده بر روی دو تاس، با یکدیگر تفاوت خواهند داشت. اگر میخواستیم این مسئله را با روش معمولی حل کنیم، باید تمام ۳۰ عضو A را مینوشتیم. این کار، زمان حل را افزایش میداد. در عوض، با استفاده از قوانین احتمال و فرمول احتمال متمم، با سرعت بیشتری به جواب سوال رسیدیم.
احتمال اشتراک، اجتماع و تفاضل دو پیشامد ناسازگار چیست؟
اگر A و B، دو پیشامد از فضای نمونه S باشند و هیچ اشتراکی بین آنها وجود نداشته باشد ، آنها را دو پیشامد ناسازگار مینامیم. احتمال اشتراک دو پیشامد ناسازگار برابر با ۰ است. با توجه به تعریف، هر پیشامد تصادفی (مانند A) و متمم آن (مانند ‘A)، همواره ناسازگارند.
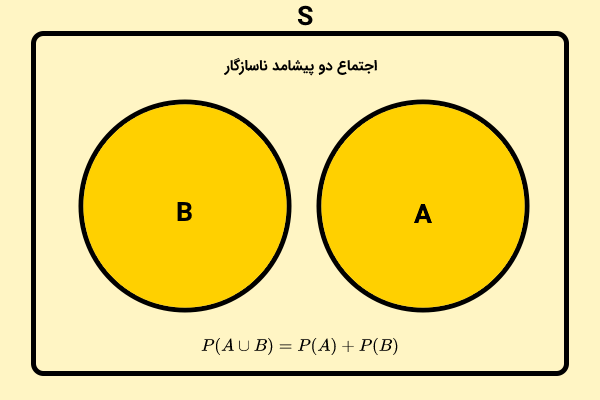
رابطه محاسبه احتمال اجتماع دو پیشامد ناسازگار به صورت زیر نوشته میشود:
- : احتمال اجتماع دو پیشامد ناسازگار A و B
- : احتمال پیشامد A
- : احتمال پیشامد B
- : اشتراک دو پیشامد ناسازگار A و B برابر با ۰
اشتراک دو پیشامد ناسازگار A و B، مجموعه تهی است. میدانیم که احتمال مجموعه تهی برابر با ۰ میشود. بنابراین، احتمال اشتراک دو پیشامد ناسازگار A و B، برابر با صفر است (). به این ترتیب، داریم:
مجموع احتمالات دو پیشامد ناسازگار، همیشه کمتر از ۱ و در شرایط خاص، برابر با ۱ است. رابطه تفاضل دو پیشامد ناسازگار به صورت زیر نوشته میشود:
- : احتمال تفاضل دو پیشامد ناسازگار A و B
- : احتمال پیشامد A
- : احتمال پیشامد B
- : احتمال اشتراک دو پیشامد ناسازگار A و B برابر با ۰
به همین صورت، داریم:
احتمال اشتراک و اجتماع سه پیشامد دوبهدو ناسازگار چیست؟
اگر B ،A و C، سه پیشامد دوبهدو ناسازگار یا مجزا باشند، اشتراک هر جفت از آنها، برابر با ۰ یا مجموعه تهی میشود:

اشتراک هر سه پیشامد دوبهو ناسازگار، مجموعه تهی است:
اجتماع سه پیشامد دوبهو ناسازگار، با استفاده از رابطه زیر محاسبه میشود:
احتمال شرطی چیست؟
در صورتی که B پیشامدی با احتمال بزرگتر از ۰ باشد ، احتمال پیشامد A به شرط رخ دادن پیشامد B، با استفاده از رابطه زیر به دست میآید:
- : احتمال رخ دادن پیشامد A به شرط رخ دادن پیشامد B
- : احتمال رخ دادن همزمان پیشامدهای A و B
- : احتمال رخ دادن پیشامد B
اگر باشد، احتمال هیچ پیشامدی به شرط B وجود ندارد. زیرا پیشامد B، هیچگاه رخ نخواهد داد. در پیشامدهای همشانس میتوان از رابطه زیر برای به دست آوردن احتمال شرطی استفاده کرد:
- : احتمال رخ دادن پیشامد A به شرط رخ دادن پیشامد B
- : تعداد اعضای مشترک بین برآمدهای پیشامدهای A و B
- : تعداد اعضای موجود در مجموعه برآمدهای پیشامد B
برای درک بهتر مفهوم احتمال شرطی، به حل و توضیح یکی از مثالهای کتاب آمار و احتمال یازدهم میپردازیم. این مثال به ظاهر ساده اما دارای نکات بسیار مهمی است.
مثال ۹: محاسبه احتمال شرطی در آزمایش پرتاب سکه
سکهای را سه بار پرتاب میکنیم. میدانیم که دستکم سه بار رو آمده است. در این صورت، احتمال اینکه هر سه بار رو آمده باشد چقدر است؟
پیش از شروع حل، صورت مسئله را به دقت بررسی کنید. در این مثال، با آزمایش پرتاب سکه روبرو هستیم. هر پرتاب سکه، دارای فضای نمونه شامل دو عضو (پشت و رو) با احتمال همشانس () است. پرتاب سکه، سه بار تکرار میشود. نتیجه حداقل یکی از این پرتابها، رو آمدن سکه است. بنابراین، احتمال حداقل یک بار رو آمدن سکه، به عنوان شرط در نظر گرفته میشود. اکنون باید احتمال سه بار رو آمدن سکه با توجه به شرط مذکور را به دست بیاوریم. برای شروع، رابطه احتمال شرطی را مینویسیم:
- : احتمال سه بار رو آمدن سکه به شرط اطمینان از حداقل یک بار رو آمدن سکه
- : احتمال سه بار رو آمدن سکه و حداقل یک بار رو آمدن سکه
- : احتمال حداقل یک بار رو آمدن سکه
برای به دست آوردن جواب رابطه بالا، پارامترهای مجهول را محاسبه میکنیم. در ابتدا، به سراغ میرویم. محاسبه این احتمال با استفاده از رابطه صورت میگیرد:
- : تعداد حالتهایی که در آنها، حداقل یک بار رو و سه بار رو آمده باشد.
- : تعداد اعضای فضای نمونه
در آزمایشهای چندمرحلهای مانند سه بار پرتاب سکه یا پرتاب سه سکه به طور همزمان، فضای نمونه هر مرحله را در فضای نمونه مرحله بعدی ضرب میکنیم تا فضای نمونه کل آزمایش به دست بیاید. در اینجا، فضای نمونه پرتاب سکه، دارای ۲ عضو است. بنابراین، داریم:
- : فضای نمونه آزمایش سه بار پرتاب سکه
- : فضای نمونه آزمون پرتاب سکه در مرحله اول برابر با ۲
- : فضای نمونه آزمون پرتاب سکه در مرحله دوم برابر با ۲
- : فضای نمونه آزمون پرتاب سکه در مرحله سوم برابر با ۳
در نتیجه، فضای نمونه کل آزمایش برابر با ۸ است. اکنون به سراغ تعیین تعداد حالتهایی میرویم که در آنها، حداقل یک بار رو و سه بار رو آمده باشد. در اینجا یک نکته بسیار مهم وجود دارد. تنها در یک حالت، نتیجه هر سه پرتاب، رو آمدن سکه است که در همان حالت، حداقل یک رو مشاهده میشود. بنابراین، برابر با ۱ است. به این ترتیب، داریم:
اکنون، احتمال حداقل یک بار رو آمدن سکه یا را محاسبه میکنیم. سادهترین روش برای محاسبه این احتمال، استفاده از احتمال متمم پیشامد B، یعنی ‘B است. پیشامد ‘B، حالتهایی را دربرمیگیرد که در آنها، سکه اصلا رو نیامده باشد. فقط در صورت پشت آمدن هر سه پرتاب، این حالت به وجود میآید. بنابراین، احتمال پیشامد ‘B برابر است با:
به این ترتیب داریم:
بنابراین، احتمال حداقل یک بار رو آمدن سکه، برابر با است. این مقدار را به همراه مقدار درون رابطه احتمال شرطی قرار میدهیم:
در نتیجه، در سه بار پرتاب سکه، اگر حداقل یک بار رو آمده باشد، به احتمال یا تقریبا ۱۴ درصد، هر سه پرتاب رو خواهد بود.
قضیه بیز در احتمال چیست؟
«قضیه بیز» (Bayes Theorem)، قضیهای برای تعیین احتمال رخ دادن یک پیشامد بر اساس پیشامدهای قبلی است. فرمول قضیه بیز به صورت زیر نوشته میشود:
- : احتمال رخ دادن پیشامد A به شرط رخ دادن پیشامد B
- : احتمال رخ دادن پیشامد B به شرط رخ دادن پیشامد A
- : احتمال رخ دادن پیشامد A
- : احتمال رخ دادن پیشامد B
قضیه بیز در بسیاری از فعالیتهای دنیای واقعی نظیر پیشبینی هوا، آزمایش DNA، تحلیل مالی، تشخیص شکست مهندسی، آزمایش مواد مخدر و غیره کاربرد دارد.
نمودار درختی در احتمال چیست؟
«نمودار درختی» (Tree Diagrams)، یکی از ابزارهای کاربردی برای نمایش گرافیکی مسائل احتمال و سادهسازی درک نحوه حل آنها است.
نمودارهای درختی از شاخه، مقدار احتمال و خروجی تشکیل میشوند. نمودار درختی زیر، آزمایش پرتاب سکه را نمایش میدهد.
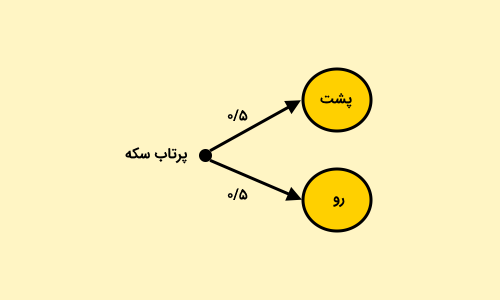
در مسائل ساده، شاید نیازی به رسم نمودار درختی نباشد. با این وجود، این ابزار در حل مسائل چندمرحلهای و پیچیده، بسیار کاربردی و راهگشا خواهد بود. به عنوان مثال، آزمایش دو مرتبه پرتاب سکه یا پرتاب همزمان دو سکه را در نظر بگیرید. در این مثال، نمودار درختی مانند تصویر زیر رسم میشود.
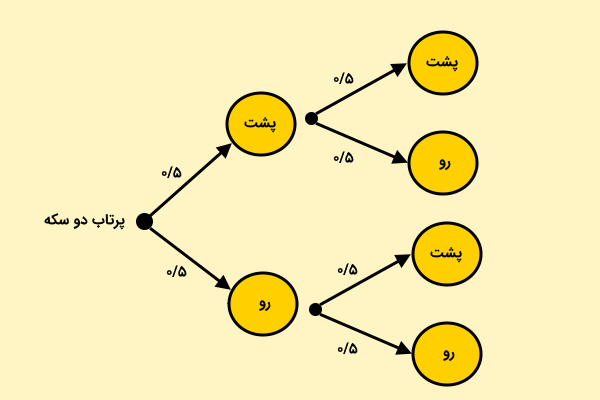
با استفاده از نمودار درختی بالا، به راحتی میتوانیم احتمال پیشامدهای دلخواه را به دست بیاوریم. به عنوان مثال، برای تعیین احتمال پشت آمدن هر دو سکه (پشت آمدن سکه در هر دو مرحله)، اندازه احتمال روی شاخههای مسیر مورد نظر را در هم ضرب میکنیم. به این ترتیب، داریم:
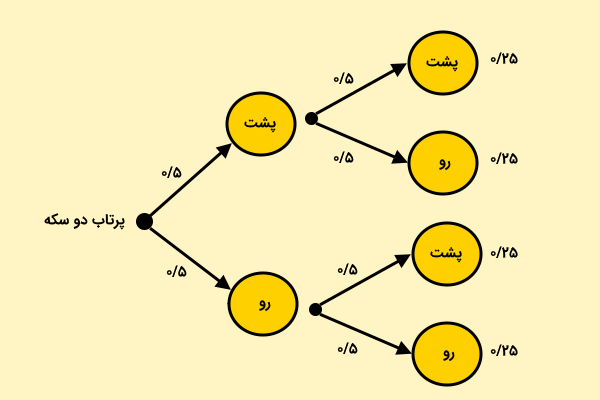
در نتیجه، احتمال پشت آمدن هر دو سکه برابر با ۰/۲۵ یا ۲۵ درصد است. به منظور محاسبه احتمال مشاهده حداقل یک پشت، احتمال تمام مسیرهایی که دارای حداقل یک پشت هستند را با هم جمع میکنیم. بر اساس نمودار بالا، سه مسیر دارای این ویژگی هستند. بنابراین، داریم:
در نتیجه، احتمال مشاهده حداقل یک پشت، برابر با ۰/۷۵ یا ۷۵ درصد است. نمودار درختی، کاربرد خوبی در حل مسائل احتمال با پیشامدهای مستقل دارد. با این وجود، کاربرد اصلی آن را میتوان در مسائل احتمال با پیشامدهای وابسته و مسائل احتمال شرطی مشاهده کرد. در ادامه، به حل یک مثال مرتبط با این موضوع میپردازیم.
مثال ۱۰: محاسبه احتمال با استفاده از نمودار درختی
سه نفر را در نظر بگیرید که به طور تصادفی، عددی بین ۱ تا ۵ را انتخاب کردهاند. احتمال اینکه دو نفر از آنها، یک عدد را انتخاب کرده باشند، چقدر است؟
استفاده از نمودار درختی درک و حل این مسئله را سادهتر میکند. برای شروع، نفر اول و دوم، را در نظر بگیرید. احتمال اینکه این دو نفر، عدد یکسانی را انتخاب کرده باشند، است. بنابراین، احتمال اینکه عدد انتخاب شده توسط این دو نفر، یکسان نباشد، برابر با خواهد بود.
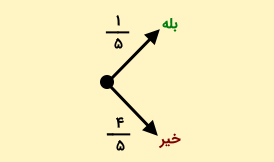
اکنون به سراغ عدد انتخاب شده توسط نفر سوم میرویم. اگر دو نفر قبلی، عدد یکسانی را انتخاب کرده باشند، مسیر بله با احتمال یکپنجم ادامه پیدا نمیکند. توجه داشته باشید که احتمال اینکه نفر سوم هم همان عدد را انتخاب کرده باشد، یکپنجم است؛ زیرا تنها یک عدد از پنج عدد برای مقایسه وجود دارد.
در صورت متفاوت بودن اعداد انتخابی توسط نفر اول و دوم، عدد انتخابی توسط نفر سوم، با آن دو عدد مقایسه میشود. بنابراین، احتمال یکسان بودن عدد انتخابی توسط نفر سوم با یکی از این اعداد، برابر با دوپنجم خواهد بود.
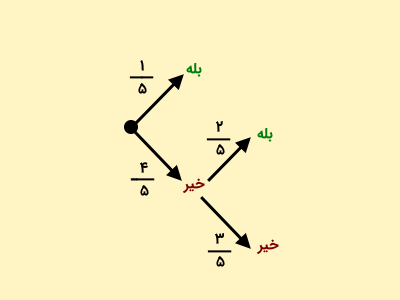
احتمال اینکه عدد انتخابی توسط نفر سوم با هیچکدام از اعداد انتخابی توسط نفر اول و دوم یکسان نباشد، برابر با سهپنجم میشود. برای به دست آوردن احتمال اینکه حداقل دو نفر، یک عدد را انتخاب کرده باشند، با استفاده از مسیرهای مشخص شده با عبارت «بله» قابل محاسبه است. بر اساس نمودار درختی، دو مسیر چنین ویژگی دارد. احتمال هر یک از این مسیرها با ضرب احتمال شاخههای موجود در آنها تعیین میشود. به این ترتیب، احتمال مسیر اول برابر است با:
احتمال مسیر دوم نیز برابر است با:
با جمع مقادیر بالا، به احتمال مورد نظر میرسیم:
در نتیجه، احتمال اینکه دو نفر از آنها، یک عدد را انتخاب کرده باشند، برابر با یا ۵۲ درصد خواهد بود. اگر تعداد نفرات را بیشتر کنیم، شاخههای نمودار درختی و تعداد مسیرهای آن بیشتر میشود. برای این مثال، بیشتر شدن تعداد نفرات، به معنی افزایش احتمال یکسان شدن حداقل دو عدد انتخابی است.
به منظور تمرین بیشتر، همین مسئله را با چهار نفر در نظر بگیرید و به کمک نمودار درختی آن را حل کنید.
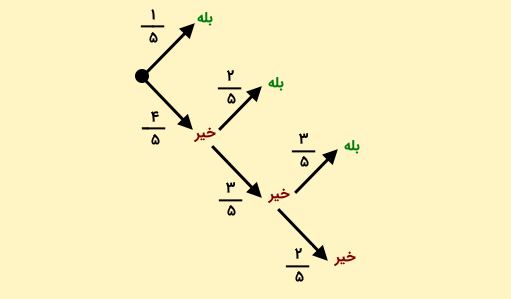
مسیرهای دارای عبارت «بله» در این شرایط به صورت زیر خواهند بود:
در نهایت باید به جواب میرسیم.
بهترین منبع و مسیر برای یادگیری احتمال چیست؟

انتخاب بهترین منبع و مسیر برای یادگیری احتمال، به مقطع تحصیلی و سطح دانش پایه شما بستگی دارد. برای دانشآموزان متوسطه دوم، آشنایی با اصطلاحات و مفاهیم اولیه، استفاده از منابع آموزشی مرتبط با کتابهای درسی و حل مثالهای متعدد در سطح دبیرستان کفایت میکند. فرادرس، مجموعهای از فیلمهای آموزشی مفید را برای دانشآموزان تهیه کرده است که سطح دانش آنها در زمینه احتمال و مهارتهای حل مسئله آنها را ارتقا میدهند. لینک مشاهده برخی از این آموزشها در ادامه آورده شده است:
پس از یادگیری اصول و مفاهیم اولیه، به منظور ارتقا دانش تخصصی خود میتوانید به سراغ مباحث پیشرفتهتر احتمال بروید. مجموعه آموزشهای آمار و احتمالات فرادرس، شما را برای موفقیت در این مسیر یاری میکنند. لینک مشاهده فیلمهای آموزشی این مجموعه در ادامه آورده شده است:
در آخرین بخش این مطلب از مجله فرادرس، به مقایسه یکی از علوم مرتبط با احتمال، یعنی آمار میپردازیم.
تفاوت آمار و احتمال چیست؟
آمار و احتمال، دو شاخه پرکاربرد از ریاضی هستند که ارتباط نزدیکی با یکدیگر دارند. این شاخههای ریاضی، به مطالعه و تحلیل تداوم وقوع رویدادها میپردازند.
با این وجود، تفاوتهای بنیادی متعددی بین آمار و احتمال وجود دارد. تفاوتهای اصلی آمار و احتمال عبارت هستند از:
- احتمال، علم پیشبینی شانس رخ دادن رویدادها در آینده است. در حالی که آمار، به عنوان علم تحلیل تکرار رویدادهای گذشته شناخته میشود.
- احتمال، در اصل یکی از شاخههای تئوری ریاضی به شمار میرود که نتایج تعاریف و مفاهیم ریاضی را مورد مطالعه قرار میدهد. در حالی که آمار، در اصل یکی از شاخههای کاربردی ریاضی است که با مشاهده و درک دنیای واقعی سر و کار دارد.
متخصصان آمار در مقایسه با متخصصان احتمال، نگاه متفاوتی نسبت به دنیای اطراف خود دارند. به عنوان مثال، پرتاب یک تاس را در نظر بگیرید. فردی که بر روی احتمالات تسلط دارد، شکل و تعداد وجههای تاس را بررسی میکند. سپس، با فرض برابر بودن اندازه وجهها، شانس ظاهر شدن هر عدد را برابر با یکششم به دست میآورد.
در طرف مقابل، فردی که بر روی آمار تخصص دارد، به راحتی برابر بودن اندازه وجهها و یکسان بودن شانس ظاهر شدن هر عدد را نمیپذیرد. این شخص، ابتدا به مشاهده چندین پرتاب تاس میپردازد و فراوانی اعداد ظاهر شده را مورد بررسی قرار میدهد. به این ترتیب و با توجه به دادههای جمعآوری شده، در مورد شانس ظاهر شدن هر عدد تصمیم میگیرد.
آمار و احتمال، هر دو از مباحث مهم و کاربردی در حوزههای مختلف هستند. یادگیری این علوم، درک ما از پدیدههای دنیای واقعی را بهبود میبخشد. احتمال، امکان تعیین خروجیهای ممکن در یک دنیای ایدهآل را فراهم میکند. آمار، میزان نزدیک بودن دنیای واقعی با دنیای ایدهآل را اندازه میگیرد.
source
