فانکشن STDEV در اکسل، امکان محاسبه انحراف معیار داده‌های عددی را فراهم می‌کند. البته این فانکشن در نسخه‌های جدید اکسل با عنوان STDEV.S‌ شناخته می‌شود. STDEVP و STDEV.P‌ نیز از دیگر فانکشن‌های مرتبط با STDEV در اکسل هستند که به منظور تعیین انحراف معیار کل یک جامعه آماری مورد استفاده قرار می‌گیرند. در این مطلب از مجله فرادرس، قصد داریم به معرفی کامل فانکشن STDEV در اکسل بپردازیم و روش‌های استفاده از انواع آن را به همراه حل مثال‌های تصویری آموزش دهیم.

برای درک عملکرد فانکشن STDEV در اکسل، ابتدا باید با مبانی ریاضی آن آشنا شوید. به همین دلیل، در اولین بخش این مطلب، نگاهی سریع به مفهوم انحراف معیار و فرمول آن خواهیم داشت. سپس، ویژگی‌ها و نحوه استفاده از فانکشن STDEV را مرور می‌کنیم. در ادامه، تفاوت‌های این فانکشن با فانکشن STDEV.S را مورد بررسی قرار می‌دهیم. بررسی انواع فانکشن‌های مرتبط با STDEV و آموزش نحوه رسم نمودار بر اساس داده‌های انحراف معیار نیز در این مطلب پوشش داده می‌شود. پس از این موارد، به آموزش روش پیدا کردن داده‌های پرت، رفع خطاهای رایج و نحوه محاسبه انحراف معیار داده‌های فیلتر شده می‌پردازیم. در نهایت، ضمن توضیح اجمالی تفاوت فانکشن‌های STDEV و VAR، در مورد عملکرد فانکشن STDEV در گوگل شیت صحبت می‌کنیم.

انحراف معیار چیست و چه کاربردی دارد؟

«انحراف معیار» (Standard Deviation)، یکی از انواع شاخص‌های پراکندگی و از مفاهیم آماری مهم است که به منظور توصیف پراکندگی یا اصطلاحا انحراف داده‌ها نسبت به مقدار میانگین مورد استفاده قرار می‌گیرد.

انحراف معیار با استفاده از فرمول زیر به دست می‌آید:

$$sigma = sqrt { frac { 1 } { n – 1 } sum _ { i = 1 } ^ n left ( x _ i – bar { x }right ) ^ 2 }$$

هر یک از پارامترهای فرمول بالا عبارت هستند از:

• $$sigma$$: انحراف معیار
• $$n$$: تعداد افراد یا نمونه‌های انتخاب شده از جامعه آماری
• $$x_i$$
• $$bar { x }$$

فانکشن STDEV در اکسل، از رابطه بالا برای محاسبه انحراف معیار نمونه‌ای از جامعه استفاده می‌کند.

فانکشن STDEV در اکسل چیست؟

تابع STDEV در اکسل، مقدار انحراف معیار را بر اساس داده‌های یک نمونه از جامعه آماری تخمین می‌زند. پیش از بررسی بیشتر عملکرد و ویژگی‌های این تابع، باید به این نکته اشاره کنیم که فانکشن STDEV در اکسل ۲۰۰۷ به قبل وجود دارد. این فانکشن از اکسل ۲۰۱۰ به بعد منسوخ شد و جای خود را به STDEV.S داد.

آرگومان‌های فانکشن STDEV در اکسل چه هستند؟

برای مشاهده آرگومان‌های فانکشن STDEV، عبارت = STDEV(  را درون سلول یا کادر فرمول‌نویسی در اکسل وارد می‌کنیم.

به محض تایپ پرانتز اول پس از عبارت STDEV، آرگومان‌های تابع در ادامه آن ظاهر می‌شوند. ساختار تابع انحراف معیار در اکسل به شکل STDEV(number1,[number2],…) است. آرگومان‌های این تابع عبارت هستند از:

• number1 : نمونه اول از جامعه آماری (الزامی)
• number2 تا number255: نمونه بعدی از جامعه آماری (اختیاری)

دقت داشته باشید که آرگومانnumber1 ، می‌تواند مجموعه‌ای از اعداد را شامل شود و یک آرگومان الزامی برای تابع STDEV محسوب می‌شود. در صورت وارد کردن یک عدد یا ارجاع به یک سلول منفرد در محل این آرگومان، ورودی‌های تابع ناقص خواهد بود و به حداقل یک آرگومان دیگر مانند number2نیاز است. در این شرایط، وارد کردن آرگومان دوم نیز الزامی می‌شود. STDEV می‌تواند تا ۲۵۵ آرگومان را به صورت ورودی‌های منفرد یا آرایه دریافت کند.

حل مسئله انحراف معیار با فانکشن STDEV در اکسل

تصویر پایین، نحوه استفاده از فانکشن STDEV برای محاسبه انحراف معیار مجموعه‌ای از اعداد را نمایش می‌دهد. این مجموعه، شامل ۱۰ عضو در سلول‌های «A2» تا «A11» است.

اعضای این مجموعه به صورت آرایه و به روش ارجاع محدوده (A2:A11) در جایگاه آرگومان اول (number1) قرار می‌گیرند. عدد نمایش داده شده در سلول «A13»، خروجی تابع STDEV یا همان انحراف معیار اعداد موجود در سلول‌های A2 تا A11 است.

اگر تعداد اعداد کم باشد، می‌توان آن‌ها را به صورت آرگومان‌های جداگانه درون فانکشن STDEV وارد کرد و انحراف معیار مجموعه آن‌ها را به دست آورید. به عنوان مثال، در تصویر زیر، اعداد موجود در سلول‌های A2 تا A11، هر کدام به صورت جداگانه و به روش ارجاع منفرد در جایگاه آرگومان‌های number1 تا number10 قرار می‌گیرند.

خروجی تابع STDEV در روش ارجاع به سلول منفرد با روش ارجاع به محدوده سلول‌ها تفاوتی ندارد. با این وجود، در صورت افزایش تعداد اعداد، استفاده از روش ارجاع محدوده توصیه می‌شود.

ویژگی‌های فانکشن STDEV در اکسل چیست؟

هنگام استفاده از فانکشن STDEV در اکسل، نکات زیر را به خاطر داشته باشید:

• تابع STDEV، داده‌های شما را به عنوان یک نمونه از جامعه آماری در نظر می‌گیرد. اگر داده‌هایتان، تمام جامعه آماری را دربرمی‌گیرد، باید از توابع دیگری به منظور محاسبه انحراف معیار استفاده کنید.
• تابع STDEV، از فرمول $$sqrt { frac { 1 } { n – 1 } sum _ { i = 1 } ^ n left ( x _ i – bar { x }right ) ^ 2 }$$
• آرگومان‌‌های تابع STDEV می‌تواننند عدد، نام، آرایه یا ارجاع به سلول‌های حاوی عدد باشند.
• مقادیر منطقی مانند «TRUE» یا «FALSE» و قالب متنی اعداد مانند “1” نیز در صورت تایپ مستقیم درون فهرست آرگومان‌ها، به عنوان ورودی‌های مجاز تابع STDEV در نظر گرفته می‌شوند.
• اگر یک آرگومان به صورت آرایه یا ارجاع وارد شده باشد، فقط ورودی‌های عددی در محاسبات مورد استفاده قرار می‌گیرند. سلول‌های خالی، منطقی، متن یا مقادیر خطا در آرایه یا ارجاع، نادیده گرفته می‌شوند.
• آرگومان‌های حاوی مقادیر خطا یا متن‌های غیرقابل تبدیل به عدد، باعث رخ دادن خطا در خروجی تابع STDEV می‌شوند.
• در صورت نیاز به محاسبه انحراف معیار با ارجاع به مقادیر منطقی یا قالب متنی اعداد، باید از تابع دیگری استفاده کنید که در بخش‌های بعدی به معرفی آن خواهیم پرداخت.

در بخش بعدی، به معرفی دیگر توابع مرتبط با STDEV و آموزش نحوه استفاده از آن‌ها می‌پردازیم. برای اینکه تسلط بیشتری بر روی نحوه استفاده از توابع مختلف اکسل داشته باشید، باید مهارت فرمول‌نویسی خود را بهبود بخشید. به این منظور، مشاهده «فیلم آموزش استفاده از توابع و فرمول‌نویسی در اکسل فرادرس» را به شما پیشنهاد می‌کنیم. لینک مشاهده این آموزش در ادامه آورده شده است.

چگونه محاسبه انحراف معیار در اکسل را به طور کامل یاد بگیریم؟

انحراف معیار، یکی از شاخص‌های پراکندگی پرکاربرد در تحلیل‌های آماری است. نرم‌افزار اکسل، به عنوان یک ابزار کامپیوتری پرکاربرد، امکان محاسبه این شاخص را با استفاده از توابع مختلف فراهم می‌کند. برای اینکه انجام این محاسبات را به خوبی و به طور کامل یاد بگیرید، باید مهارت خود در کار با اکسل را بالا ببرید. با حل مثال‌های کاربردی متنوع، آشنایی با دیگر توابع آماری اکسل و تمرین، قطعا به این هدف می‌رسید. البته نباید نقش یک منبع آموزشی خوب را نادیده بگیرید.

فرادرس، یک فیلم آموزشی مفید و کاربردی را تهیه کرده است که می‌تواند شما را با انواع توابع آماری اکسل، از جمله تابع STDEV آشنا کند. لینک مشاهده این آموزش در ادامه آورده شده است:

فانکشن STDEV.S در اکسل چیست و چه کاربردی دارد؟

STDEV.S، تابعی برای محاسبه انحراف معیار در اکسل ۲۰۱۰ به بعد است. حرف «S» در انتهای این تابع، ابتدای کلمه «Sample» به معنای «نمونه» را نمایش می‌دهد. به عبارت دیگر، فانکشن STDEV.S، به منظور تعیین انحراف معیار نمونه یا نمونه‌هایی از یک جامعه آماری مورد استفاده قرار می‌گیرد. برای به دست آوردن انحراف معیار کل جامعه آماری، باید از یک تابع دیگر استفاده کرد.

تفاوت فانکشن STDEV با STDEV.S در اکسل چیست؟

فانکشن STDEV از نظر عملکرد، تفاوتی با فانکشن STDEV.S ندارد. فانکشن STDEV.S در نسخه‌های جدیدتر اکسل (نسخه‌های ۲۰۱۰ به بعد) معرفی شد. البته در این نسخه‌ها، هنوز هم می‌توان فانکشن STDEV را مشاهده کرد اما حضور آن‌ها، به منظور سازگاری فایل‌های اکسل با نسخه‌های ۲۰۰۷ به قبل است.

از تفاوت‌های جزئی فانکشن STDEV با STDEV.S می‌توان به تعداد آرگومان‌های ورودی اشاره کرد. STDEV، قادر به دریافت حداکثر 255 آرگومان و STDEV.S، قادر به دریافت 254 آرگومان است. در هر دوی این فانکشن‌ها، از یک فرمول مشابه برای محاسبه انحراف معیار استفاده می‌کنند.

آرگومان‌های فانکشن STDEV.S در اکسل چه هستند؟

با تایپ فرمول =STDEV.S(  در یک سلول یا کادر فرمول‌نویسی اکسل، آرگومان‌های فانکشن STDEV.S به نمایش درمی‌آیند.

این آرگومان‌ها، عبارت هستند از:

• number1 : نمونه اول از جامعه آماری (الزامی)
• number2 تا number254: نمونه بعدی از جامعه آماری (اختیاری)

توجه داشته باشید که به غیر از تعداد آرگومان‌های قابل تعریف، تفاوت خاصی بین STDEV.S و STDEV وجود ندارد. بنابراین، روش استفاده از تابع STDEV.S نیز مشابه تابع STDEV است. برای اثبات این موضوع، مثال حل شده در بخش قبلی را این بار با استفاده از STDEV.S انجام می‌دهیم.

حل مسئله انحراف معیار با فانکشن STDEV.S در اکسل

در اکسل زیر می‌خواهیم انحراف معیار یک نمونه آماری با ۱۰ عضو عددی را به دست بیاوریم. این نمونه، بخشی از یک جامعه آماری بزرگ‌تر است. به همین دلیل، از فانکشن STDEV.S برای به دست آوردن انحراف معیار استفاده می‌کنیم.

به منظور تعیین انحراف معیار، دو روش پیش روی ما قرار دارد. در روش اول، آرگومان اول تابع (number1) را با ارجاع به محدوده اعضای نمونه (A2:A11) تعیین می‌کنیم و سپس پرانتز تابع را می‌بندیم. با فشردن کلید Enter، انحراف معیار نمونه آماری به دست می‌آید و در سلول حاوی فرمول تابع نمایش داده می‌شود. همان‌طور که مشاهده می‌کنید، خروجی تابع (انحراف معیار نمونه) با خروجی مثال قبلی (مثال حل شده با تابع STDEV) تفاوتی ندارد.

در روش دوم، هر یک از اعضای نمونه آماری را به عنوان یک آرگومان جداگانه (ازnumber1 تا number10) در نظر می‌گیریم و به خانه‌های حاوی اعداد آن‌ها ارجاع می‌دهیم. این روش نیز خروجی مشابهی را به دست می‌آورد.

اگر در یک پروژه گروهی کار می‌کنید و از یکسان بودن نسخه‌های اکسل نصب شده بر روی سیستم افراد گروه اطمینان ندارید یا احتمال می‌دهید برخی از افراد از نسخه‌های قدیمی اکسل استفاده می‌کنند، بهتر است محاسبات انحراف معیار را با فانکشن STDEV انجام دهید.

فانکشن STDEVP و STDEV.P در اکسل چیست و چه کاربردی دارد؟

STDEVP، تابعی در اکسل است که به منظور محاسبه انحراف معیار کل جامعه آماری مورد استفاده قرار می‌گیرد. این تابع، برای انجام محاسبات خود، از فرمول زیر استفاده می‌کند:

$$sqrt { frac { 1 } { n } sum _ { i = 1 } ^ n left ( x _ i – bar { x }right ) ^ 2 }$$

حرف «P» پس از عبارت STDEV، ابتدای کلمه «Population» به معنای «جمعیت یا جامعه» است. فانکشن STDEVP در اکسل ۲۰۱۰ به بعد، جای خود را به فانکشن STDEV.P داد. البته به منظور سازگاری با توابع اکسل ۲۰۰۷ به قبل، امکان استفاده از تابع STDEVP در نسخه‌های جدید اکسل وجود دارد.

توابع STDEVP و STDEV.P از نظر عملکرد و کاربرد، مشابه یکدیگر هستند. البته، در اینجا نیز مانند تفاوت بین توابع STDEV و STEDV.S، تعداد آرگومان‌های ورودی در فانکشن STDEVP برابر با ۲۵۵ و در فانکشن STDEV.P برابر ۲۵۴ است.

چه زمانی از فانکشن STDEV و چه زمانی از فانکشن STDEVP استفاده کنیم؟

هنگام نیاز به محاسبه انحراف معیار کل جامعه آماری، باید از فانکشن STDEVP یا STEDV.P استفاده کنید. اگر نیاز به تعیین انحراف معیار بخشی از جامعه داشته باشید، باید به سراغ فانکشن STDEV یا STEDV.S بروید. دقت داشته باشید که در صورت استفاده نادرست از تابع STDEV به جای STDEVP، انحراف معیار به دست آمده بیشتر می‌شود؛ زیرا مخرج کسر در فرمول انحراف معیار نمونه $$( n – 1 )$$

با وجود متفاوت بودن خروجی فانکشن STDEV با خروجی فانکشن STDEVP، اگر اندازه نمونه جامعه بزرگ باشد، انحراف معیارهای به دست آمده از دو فانکشن، تقریبا برابر می‌شوند. با این وجود، بهتر است از هر فانکشن برای کاربرد متناسب با آن استفاده کنید تا به نتایج دقیق‌تری برسید.

آرگومان‌های فانکشن STDEVP در اکسل چه هستند؟

با تایپ = STDEVP(  یا =STDEV.P(  در یک سلول یا کادر فرمول‌نویسی، نرم‌افزار اکسل از شما می‌خواهد تا آرگومان‌های زیر را به عنوان ورودی تابع وارد کنید:

• number1 : اولین آرگومان یک جامعه آماری (الزامی)
• number2 تا number254: آرگومان‌های بعدی جامعه آماری (اختیاری)

دقت داشته باشید که امکان ارجاع به محدوده‌ای از سلول‌ها برای محاسبه انحراف معیار کل جامعه آماری وجود دارد. بنابراین، هم می‌توان تمام اعضای جامعه آماری را به روش ارجاع محدوده در اولین آرگومان وارد کرد و هم می‌توان هر یک از اعضای کل جامعه را به صورت منفرد و جداگانه در جایگاه آرگومان‌های اول، دوم و غیره قرار داد. انتخاب هر یک از این روش‌ها، کاملا اختیاری است.

حل مسئله انحراف معیار با فانکشن STDEV و STDEVP در اکسل

برای درک بهتر نحوه استفاده از توابع STDEV یا STDEV.S و STDEVP یا STDEV.P در اکسل، به حل یک مسئله نزدیک به واقعیت می‌پردازیم. مسئولین یک دبیرستان می‌خواهند میانگین معدل دانش‌آموزان مقاطع دهم، یازدهم و دوازدهم را به طور جداگانه و کلی محاسبه کنند و سپس انحراف معیار این معدل را برای هر مقطع و تمام مقاطع به دست بیاورند. داده‌های مربوط به معدل دانش‌آموزان کلاس‌های دهم، یازدهم و دوازدهم برای این دبیرستان در تصویر زیر نمایش داده شده است.

همان‌طور که مشاهده می‌کنید، جامعه آماری ما، شامل معدل دانش‌آموزان کلاس‌های دهم، یازدهم و دوازدهم یک دبیرستان است. این جامعه آماری، ۵۷ عضو دارد. برای به دست آوردن میانگین معدل هر یک از کلاس‌ها، از توابع زیر و ارجاع محدوده استفاده می‌کنیم:

• میانگین معدل کلاس دهم: =AVERAGE(A2:C20)
• میانگین معدل کلاس دهم: =AVERAGE(B2:B20)
• میانگین معدل کلاس دهم: =AVERAGE(C2:C20)

میانگین معدل کل سه کلاس را نیز با استفاده از =AVERAGE(A2:C20)  به دست می‌آوریم. تصویر زیر، مقادیر میانگین محاسبه شده را نمایش می‌دهد.

اکنون به سراغ محاسبه انحراف معیار می‌رویم. در اینجا ۵۷ معدل داریم که جامعه آماری ما را تشکیل می‌دهند. بنابراین، معدل هر کلاس، یک نمونه آماری محسوب می‌شود. برای محاسبه انحراف معیار نمونه آماری باید از فانکشن STDEV یا STDEV.S در اکسل استفاده کنیم. به عنوان مثال، انحراف معیار معدل دانش‌آموزان کلاس دهم با =STDEV(A2:A20)  محاسبه می‌شود.

برای محاسبه انحراف معیار معدل دانش‌آموزان کلاس‌های یازدهم و دوازدهم نیز از همین فرمول با ارجاع به محدوده‌های (B2:B20 و C2:C20) استفاده می‌کنیم. تابع مورد استفاده برای به دست آوردن انحراف معیار تمام معدل‌ها، متفاوت است. از آنجایی که تمام معدل‌ها، کل جامعه آماری ما را نمایش می‌دهند، محاسبه انحراف معیار آن‌ها توسط فانکشن STDEVP یا STDEV.P انجام می‌شود.

با توجه خروجی‌های به دست آمده برای میانگین و انحراف معیار، مشاهده می‌شود که میانگین معدل دانش‌آموزان کلاس دهم بهتر از بقیه کلاس‌ها است. علاوه بر این، میزان انحراف معیار معدل دانش‌آموزان این کلاس نسبت به کلاس‌های دیگر کمتر است. به عبارت دیگر، اغلب دانش‌آموزان کلاس دهم عملکردی نزدیک به میانگین دارند و پراکندگی کمتری در معدل آن‌ها نسبت به کلاس‌های دیگر مشاهده نمی‌شود.

عملکرد دانش‌آموزان کلاس‌های یازدهم و دوازدهم به طور قابل توجهی کمتر از دانش‌آموزان کلاس دهم است. در این کلاس‌ها، ضمن پایین آمدن میانگین معدل، انحراف معیار نیز افزایش یافته است. این مسئله، پراکندگی نسبتا بالای معدل دانش‌آموزان را نمایش می‌دهد. به عبارت دیگر، اغلب دانش‌آموزان از نظر معدل یا عملکرد خوبی دارند یا نتیجه ضعیفی را کسب کرده‌اند.

از نظر کلی، عملکرد دبیرستان را نمی‌توان بسیار خوب ارزیابی کرد. میانگین کل جامعه آماری (میانگین معدل‌ها) در سطح متوسط قرار دارد اما انحراف معیار کل جامعه آماری (پراکندگی معدل‌ها) نسبتا بالا است. بنابراین، باید بر روی پیدا کردن دلایل این عملکرد بیشتر تحقیق شود. مسئولان مدرسه باید به دنبال بالا بردن میانگین معدل‌ها و پایین آوردن انحراف معیار باشند.

فانکشن STDEVA و STDEVPA در اکسل چیست و چه کاربردی دارد؟

توابع STDEVA و STDEVPA، از دیگر توابع آماری اکسل هستند که به ترتیب به منظور محاسبه انحراف معیار نمونه آماری و جامعه آماری مورد استفاده قرار می‌گیرند. تفاوت اصلی این توابع با STDEV یا STDEV.S و STDEVP یا STDEV.P، نوع داده‌های ورودی مجاز است.

اگر در آرگومان‌های فانکشن STDEV یا STDEV.S، به مقادیر منطقی مانند TRUE (مقدار ۱) و FALSE (مقدار ۰) ارجاع داده شود، فانکشن، این مقادیر را نادیده می‌گیرد و از محاسبات حذف می‌کند. این ویژگی در فانکشن STDEP یا STDEV.P نیز وجود دارد. البته توجه داشته باشید که در صورت نوشتن مستقیم عملگرهای منطقی در فرمول این توابع (بدون استفاده از روش‌های ارجاع)، مقادیر آن‌ها در محاسبات انحراف معیار در نظر گرفته می‌شود.

فانکشن STDEVA و فانکشن STDEVPA در اکسل، امکان ارجاع به سلول‌های دارای مقادیر منطقی و متنی را فراهم می‌کنند. اگر سلول ارجاع داده شده دارای یک متن یا عبارت FALSE باشد، مقدار عددی آن برابر با صفر در نظر گرفته می‌شود. در صورت نوشتن عبارت TRUE در یک سلول، مقدار عددی آن سلول برابر با ۱ خواهد بود. این قابلیت معمولا در تحلیل‌های مالی کاربرد دارد. در بخش‌های بعدی با حل یک مثال، کاربرد فانکشن STDEVA و STDEVPA را توضیح خواهیم داد.

آرگومان‌های فانکشن STDEVA و STDEVPA در اکسل چه هستند؟

هنگام تایپ = STDEVA(  و =STDEVPA(  در اکسل، آرگومان‌های زیر به عنوان ورودی‌های تابع نمایش داده می‌شوند:

• value1 : اولین آرگومان یک نمونه آماری (الزامی)
• value2 تا value255: آرگومان‌های بعدی نمونه آماری (اختیاری)

اگر عبارت ابتدای آرگومان‌های فانکشن STDEV در اکسل را به خاطر بیارید (عبارت number)، متوجه تفاوت عملکرد آن با STDEVA می‌شوید. در ابتدای آرگومان‌های فانکشن STDEVA، عبارت «value» به معنای «مقدار» وجود دارد. البته مبنای ریاضی هر دوی این توابع یکسان است و هر دوی آن‌ها از فرمول زیر برای محاسبه انحراف معیار نمونه آماری استفاده می‌کنند:

$$sigma = sqrt { frac { 1 } { n – 1 } sum _ { i = 1 } ^ n left ( x _ i – bar { x }right ) ^ 2 }$$

فانکشن STDEVPA نیز مانند تابع STDEVP، از فرمول زیر برای تعیین انحراف معیار جامعه آماری استفاده می‌کند:

$$sqrt { frac { 1 } { n } sum _ { i = 1 } ^ n left ( x _ i – bar { x }right ) ^ 2 }$$

بنابراین، اگر تمام داده‌های شما عددی باشد، خروجی STDEV و STDEVPA با خروجی STDEVA و STDEVPA یکسان می‌شود. شاید این سوال برایتان پیش بیاید که کاربرد دقیق توابع STDEVA و STDEVPA چیست. این سوال را با حل یک مثال توضیح می‌دهیم.

حل مسئله انحراف معیار با فانکشن STDEVA و STDEVPA در اکسل

فرض کنید می‌خواهید داده‌های فروش محصولات یک شرکت در شعبه‌های مختلف را مورد تحلیل قرار دهید. به این منظور، شرکت، داده‌های زیر را در اختیار شما قرار داده است.

در ستون فروش، هم داده‌های عددی و هم داده‌های متنی وجود دارند. شعبه‌هایی که میزان فروش آن‌ها هنوز مشخص نیست، با عبارت «نامشخص» نمایش داده شده‌اند. می‌خواهیم انحراف معیار تمام این داده‌ها (داده‌های مشخص و نامشخص) را به دست بیاوریم. به این منظور، عبارت =STDEVA(  را درون یک سلول دلخواه تایپ می‌کنیم و آرگومان اول را به محدوده داده‌های خود ارجاع می‌دهیم.

به دلیل استفاده از فانکشن STDEVA، داده‌های متنی به عنوان ۰ در نظر گرفته می‌شوند. به علاوه، این داده‌ها در محاسبه n در فرمول انحراف معیار مورد استفاده قرار می‌گیرند. به این ترتیب، خروجی نمایش داده شده در تصویر بالا به دست می‌آید. وجود داده‌های متنی، معمولا باعث افزایش انحراف معیار می‌شود.

همان‌طور که در تصویر بالا مشاهده می‌کنید، انحراف معیار داده‌های بالا را با استفاده از فانکشن STDEV به دست بیاوریم، به عدد پایین‌تری می‌رسیم. دلیل این موضوع، حذف داده‌های غیرعددی از محاسبات توسط فانکشن STDEV است. انتخاب زمان مناسب برای استفاده از تابع STDEVA یا STDEV، به هدف تحلیل شما بستگی دارد.

در یکی از مطالب مجله فرادرس با عنوان «محاسبات آماری با اکسل – راهنمای کاربردی»، به معرفی برخی از پرکاربردترین شاخص‌های آمار توصیفی در اکسل و محاسبه آن‌ها با استفاده از افزونه‌های تخصصی پرداختیم. در ادامه، دو فانکشن مشابه با فانکشن STDEV در اکسل را معرفی می‌کنیم که برای محاسبه انحراف معیار شرطی کاربرد دارند.

فانکش DSTDEV و DSTDEVP در اکسل چیست و چه کاربردی دارد؟

DSTDEV و DSTDEVP، توابعی هستند که به منظور محاسبه انحراف معیار داده‌های موجود در یک فهرست یا پایگاه داده مورد استفاده قرار می‌گیرد. فانکشن DSTDEV، در تعیین انحراف معیار نمونه آماری و فانکشن DSTDEVP، در تعیین انحراف معیار جامعه آماری کاربرد دارد. تفاوت اصلی توابع DSTDEV و DSTDEVP با توابع STDEV و STDEVP، امکان تعریف معیار برای انتخاب داده‌های مورد استفاده در محاسبات است. برای درک این موضوع، در ادامه به معرفی آرگومان‌های DSTDEV و DSTDEVP می‌پردازیم.

آرگومان‌های فانکشن DSTDEV و DSTDEVP در اکسل چه هستند؟

هنگام تایپ =DSTDEV(  یا =DSTDEVP(  در یک سلول یا کادر فرمول‌نویسی، نرم‌افزار اکسل از ما می‌خواهد تا آرگومان‌های الزامی زیر را وارد کنیم:

• database : در این آرگومان، محدوده سلول‌های دربرگیرنده فهرست یا پایگاه داده مشخص می‌شود. پایگاه داده، شامل مجموعه‌ای از ردیف‌ها و ستون‌ها است. به ردیف‌های حاوی اطلاعات، «رکورد» (Record) و به ستون‌ها، «فیلد» (Field) می‌گویند. ردیف اول، شامل برچسب یا «لیبل» (Label) هر است.
• field : در این آرگومان، ستون مورد استفاده برای محاسبات مشخص می‌شود. برای مشخص کردن ستون می‌توان از لیبل آن‌ها در میان علامت نقل قول (مانند “فروش”) یا عدد معرف موقعیت ستون (عدد ۱ برای ستون اول، عدد ۲ برای ستون دوم و غیره) استفاده کرد.
• criteria : در این آرگومان، محدوده سلول‌های حاوی معیار محاسبات مشخص می‌شود. به این منظور باید از حداقل یک لیبل ستون و حداقل یک داده زیر لیبل استفاده کرد.

هر سه آرگومان توابع DSTDEV و DSTDEVP، الزامی هستند. نحوه استفاده از این توابع را در بخش بعدی به همراه حل یک مثال توضیح می‌دهیم.

حل مسئله انحراف معیار با فانکشن DSTDEV و DSTDEVP در اکسل

در این بخش، به حل یک مسئله انحراف معیار شرطی با فانکشن DSTDEV در اکسل می‌پردازیم. داده‌های زیر را در نظر بگیرید.

داده‌های بالا، میزان فروش پنج فروشنده را برای دو ماه مختلف نمایش می‌دهد. می‌خواهیم انحراف معیار فروش‌های بالای ۲۰۰ را برای ماه فروردین به دست بیاوریم. به این منظور، ابتدا معیار محاسبات را در با در نظر گرفتن لیبل ستون‌های اصلی در دو ستون جداگانه ایجاد می‌کنیم.

دقت داشته باشید که ردیف لیبل ستون معیارها و ردیف اطلاعات معیارها باید متوالی باشند. اکنون، به سراغ محاسبه انحراف معیار با استفاده از فانکشن DSTDEV می‌رویم. به این منظور، ابتدا را تایپ می‌کنیم تا عنوان آرگومان‌های تابع ظاهر شود.

در مرحله اول، باید آرگومان database را وارد کنیم. این آرگومان، محدوده داده‌های ما را می‌خواهید. بنابراین، به کل داده‌ها به همراه ردیف لیبل از سلول A1 تا C6 ارجاع می‌دهیم. با تایپ کاراکتر «,» آرگومان بعدی از ما خواسته می‌شود.

در مرحله بعد، باید آرگومان field را وارد کنیم. در این آرگومان، با استفاده از روش متنی یا عددی، به ستون حاوی اطلاعات مورد نظرمان ارجاع می‌دهیم. قصد ما از بکارگیری فانکشن DSTDEV، محاسبه انحراف معیار فروش‌های بالای ۲۰۰ در ماه فروردین است. بنابراین، باید به ستون فروش در تابع ارجاع دهیم. به این منظور، هم می‌توانیم از لیبل این ستون در میان علامت نقل قول، یعنی «”فروش”» استفاده کرده و هم می‌توانیم عدد ستون نسبت به کل محدوده مرجع (یعنی ۳) استفاده کنیم.

در انتها، نوبت به وارد کردن آرگومان criteria می‌رسد. برای این آرگومان، باید به ردیف لیبل و ردیف اطلاعات معیار محاسبات ارجاع دهیم. به این منظور، محدوده سلول‌های F1 تا G2 را انتخاب می‌کنیم.

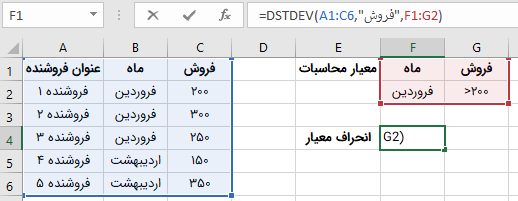
پس از وارد کردن تمام آرگومان‌های تابع DSTDEV و فشردن کلید Enter، انحراف معیار با توجه به معیارهای انتخابی محاسبه می‌شود و به نمایش درمی‌آید.

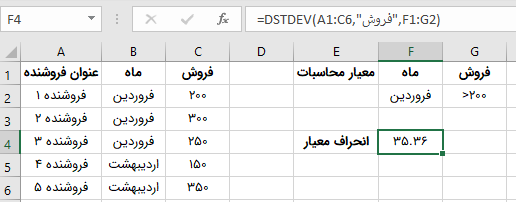
در مثال بالا، فانکشن DSTDEV، در ستون ماه، به دنبال فروردین می‌گردد. سپس، فروش‌هایی که مقدار آن‌ها بیشتر از ۲۰۰ است را پیدا می‌کند. در این مثال، سه داده با ماه فروردین وجود دارد که دو مورد از آن‌ها بیشتر از ۲۰۰ (فروش‌های فروشنده ۲ و ۳) است. به این ترتیب، انحراف معیار این دو عدد محاسبه می‌شود. اگر انحراف معیار فروش‌های مذکور را با استفاده از فانکشن STDEV در اکسل محاسبه کنیم، دقیقا به نتیجه نمایش داده شده در تصویر بالا می‌رسیم.

در پایگاه‌های داده بزرگ و فایل‌های حاوی داده‌های زیاد، تابع DSTDEV، کار ما را برای جدا کردن نمونه‌های آماری مورد نظر بسیار ساده می‌کند. به علاوه، با استفاده از این تابع، امکان انجام تحلیل‌های گوناگون با معیارهای متنوع فراهم می‌شود.

نکات و ویژگی‌های فانکشن DSTDEV و DSTDEVP در اکسل

مهم‌ترین نکات و ویژگی‌های فانکشن DSTDEV و فانکشن DSTDEVP در اکسل عبارت هستند از:

• امکان استفاده از هر محدوده‌ای برای آرگومان criteria در توابع DSTDEV و DSTDEVP وجود دارد. البته تا زمانی که این محدوده دارای حداقل یک ستون لیبل و حداقل یک سلول حاوی اطلاعات در زیر لیبل باشد.
• با وجود عدم محدودیت در محل قرارگیری محدوده criteria، بهتر است این محدوده را زیر فهرست داده‌ها قرار ندهید. این کار در هنگام اعمال تغییرات بر روی داده‌ها نظیر اضافه کردن داده‌های جدید، باعث ایجاد مشکل می‌شود.
• همواره از عدم هم‌پوشانی محدوده criteria با فهرست داده‌ها اطمینان حاصل کنید.

تصویرسازی فانکشن STDEV در اکسل چگونه انجام می‌شود؟

رسم نمودار میانگین و انحراف معیار در اکسل با استفاده از خروجی‌های فانکشن STDEV، طی مراحل زیر انجام می‌شود:

1. آماده‌سازی داده‌ها
2. محاسبه میانگین و انحراف معیار
3. رسم نمودار میله‌ای از روی میانگین‌ها
4. اضافه کردن انحراف معیارها به نمودار

در ادامه، با حل یک مثال به توضیح هر یک از بالا می‌پردازیم.

آماده‌سازی داده‌ها

داده‌های زیر را در نظر بگیرید. این داده‌ها، امتیازات ۱۱ بازیکن اصلی سه تیم فوتبال را نمایش می‌دهد.

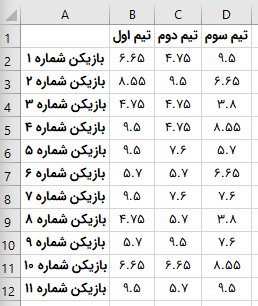
می‌خواهیم میانگین امتیازات و انحراف معیار امتیازات بازیکنان هر تیم را به شکل یک نمودار میله‌ای دربیاوریم.

محاسبه میانگین و انحراف معیار

میانگین و انحراف معیار داده‌های موجود را با استفاده از توابع AVERAGE و STDEV مورد محاسبه قرار می‌دهیم. در مرحله بعدی، سلول‌های حاوی اطلاعات مربوط به میانگین امتیازات را انتخاب می‌کنیم.

رسم نمودار میله‌ای از روی میانگین‌ها

پس از انتخاب سلول‌های حاوی میانگین‌ امتیازات، به زبانه «Insert» می‌رویم و از پنل «Charts»، نمودار میله‌ای ساده را انتخاب می‌کنیم.

با انتخاب گزینه نمایش داده شده در تصویر بالا، نمودار میله‌ای داده‌های انتخابی به صورت زیر نمایش داده می‌شود.

با انجام یک‌سری تنظیمات سفارشی ساده، نمودار بالا را به شکل زیر درآوردیم.

اگر می‌خواهید رسم انواع نمودارها در اکسل و اعمال تنظیمات سفارشی بر روی آن‌ها را به طور کامل و کاربری یاد بگیرید، «فیلم آموزش رسم نمودار در اکسل – طراحی انواع نمودار و تنظیمات فرادرس» را مشاهده کنید. لینک مشاهده این آموزش در ادامه آورده شده است.

اضافه کردن انحراف معیار به نمودار میله‌ای

با کلیک چپ بر روی نمودار میله‌ای، چند آیکون در گوشه بالا-راست کادر نمودار ظاهر می‌شود. نشانگر ماوس را بر روی آیکون علامت مثبت (+) می‌بریم و بر روی آن کلیک می‌‌کنیم. پس از کلیک بر روی آیکون علامت مثبت، گزینه‌های مختلفی برای اضافه کردن المان‌های دلخواه به نمودار به نمایش درمی‌آیند.

نشانگر ماوس را به روی گزینه «Error Bars» می‌بریم و بر روی فلش ظاهر شده در سمت راست آن کلیک می‌کنیم. با کلیک بر روی گزینه «More Options»، خطوط معرف انحراف معیار بر روی نمودار ظاهر می‌شوند.

از منوی کناری «Format Error Bars»، به بخش «Error Amount» می‌رویم و گزینه «Custom» را فعال می‌کنیم. با کلیک بر روی «Specify Value»، امکان تنظیم سفارشی مقدار انحراف معیار فراهم می‌شود.

در هر دو بخش «Positive Error Value» و «Negative Error Value»، به محدوده انحراف معیارهای محاسبه شده توسط فانکشن STDEV ارجاع می‌دهیم و سپس بر روی دکمه «OK» کلیک می‌کنیم. به این ترتیب، محدوده انحراف معیار داده‌ها بر اساس مقادیر انتخابی ما بر روی نمودار ظاهر می‌شود.

با یک تغییر کوچک بر روی ظاهر نمودار می‌توانیم انحراف معیار را به شکل بهتری نمایش دهیم.

تصویرسازی خروجی‌های فانکشن STDEV در اکسل به ما کمک می‌کند تا در بهتری از داده‌ها داشته باشیم و بتوانیم راحت‌تر به تفسیر آن‌ها بپردازیم. در صورت علاقه به یادگیری نحوه کار با ابزارهای رسم نمودار ساده تا حرفه‌ای در اکسل، مشاهده «مجموعه فیلم‌های آموزش مقدماتی تا پیشرفته رسم انواع نمودار در اکسل فرادرس» را به شما پیشنهاد می‌کنیم. لینک مشاهده فیلم‌های آموزشی این مجموعه در ادامه آورده شده است.

پیدا کردن داده‌های پرت با استفاده از فانکشن STDEV در اکسل

یکی از کاربردهای فانکشن STDEV در اکسل، پیدا کردن «داده‌های پرت» (Outliers) است. به داده‌هایی که در فاصله غیرعادی از بقیه مقادیر یک جامعه آماری قرار داشته باشند، داده پرت یا داده دورافتاده می‌گویند. داده‌های پرت معمولا به دلیل خطاهای مختلف به وجود می‌آیند. با این وجود، در برخی از موارد، این داده‌ها به صورت طبیعی و بدون هیچ خطایی در جامعه آماری ظاهر می‌شوند.

در علم آمار و تحلیل داده‌های آماری، پیدا کردن داده‌های پرت از اهمیت بالایی برخوردار است. روش‌های مختلفی برای انجام این کار وجود دارد که یکی از آن‌ها، استفاده از میانگین و انحراف معیار است. بر اساس این روش، هر داده‌ای که در محدوده زیر قرار نداشته باشد، به عنوان داده پرت در نظر گرفته می‌شود:

$$AVERAGE() pm STDEV.P()$$

برای درک بهتر فرآیند پیدا کردن داده‌های پرت با استفاده از فانکشن STDEV در اکسل، تصویر زیر را در نظر بگیرید.

می‌خواهیم داده‌های پرت موجود در داده‌های نمایش داده شده در تصویر بالا را به دست بیاوریم. به این منظور، ابتدا میانگین داده‌ها را با استفاده از تابع AVERAGE به دست می‌آوریم.

میانگین داده‌های موجود در محدوده A2 تا B:12 برابر با ۱۸/۱۸ شد. علاوه بر میانگین، به مقدار انحراف معیار نیز نیاز داریم. از آنجایی که کل جامعه آماری به ما داده شده است، از تابع STDEVP یا STDEV.P برای تعیین انحراف معیار کل جامعه استفاده می‌کنیم.

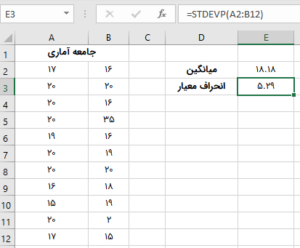
خروجی تابع STDEVP، عدد ۵/۲۹ را به عنوان انحراف معیار جامعه آماری ما نمایش می‌دهد. اکنون می‌توانیم توسط میانگین و انحراف معیار به دست آمده، بازه داده‌های معمولی را مشخص کنیم. حد پایینی این بازه بر اساس فرمول زیر محاسبه می‌شود:

$$AVERAGE – ( 3 * STDEVP)$$

حد پایینی داده‌ها برابر با ۲/۳۲ است. بنابراین، هر داده‌ای که کمتر ۲/۳۲ باشد، به عنوان داده پرت در نظر گرفته می‌شود. حد بالایی با استفاده از فرمول زیر به دست می‌آید:

$$AVERAGE + ( 3 * STDEVP)$$

حد بالایی داده‌ها برابر با ۳۴/۰۵ است. بنابراین هر داده‌ای که بیشتر از ۳۴/۰۵ باشد، به عنوان داده پرت در نظر گرفته می‌شود. با توجه به محاسبات صورت گرفته، داده‌های بین ۲/۳۲ و ۳۴/۰۵، داده‌های عادی به شمار می‌روند. هر داده‌ای که خارج از این بازه قرار داشته باشد، داده پرت است.

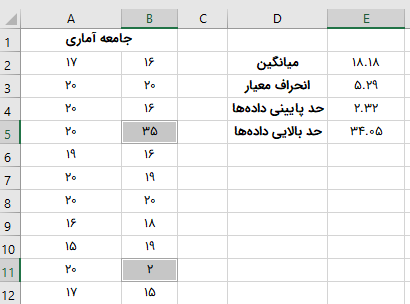
اگر داده‌های جامعه آماری را بررسی کنید، متوجه خواهید شد که عدد ۳۵ (در سلول B5) و عدد ۲ (در سلول B11)، در محدوده داده‌های معمولی قرار ندارند. بنابراین، این دو عدد، به عنوان داده پرت در نظر گرفته می‌شوند. البته باید به ارزیابی‌های بیشتر برای پیدا کردن علت احتمالی رخ دادن داده‌های پرت پرداخت. در صورتی که این موضوع به علت خطا باشد، داده‌های پرت از جامعه آماری حذف می‌شوند.

یکی از روش‌های سریع و کاربردی برای پیدا کردن داده‌های پرت در میان داده‌های جامعه آماری، استفاده از قابلیت قالب‌بندی شرطی در اکسل است. با استفاده از این قابلیت، داده‌های پرت با ظاهر متفاوت (به عنوان مثال، رنگ پس‌زمینه متفاوت) به نمایش درمی‌آیند.

خطاها و رفع خطاهای رایج فانکشن STDEV در اکسل

هنگام استفاده از فانکشن STDEV در اکسل، امکان مواجهه با خطاهای مختلفی وجود دارد که در این بخش به معرفی این خطاها و آموزش برطرف کردن آن‌ها می‌پردازیم.

خطای !DIV/0 هنگام استفاده از فانکشن STDEV در اکسل

خطای #DIV/0! ، زمانی رخ می‌دهد که مقادیر کافی برای محاسبه انحراف معیار وجود نداشته باشند. فانکشن STDEV در اکسل، به حداقل دو داده عددی برای محاسبه انحراف معیار نیاز دارد. بنابراین، اگر فقط یک مقدار عددی را وارد کنید یا اگر محدوده ارجاعی شما دارای یک مقدار عددی باشد، #DIV/0! رخ می‌دهد.

فانکشن STDEVA نیز به حداقل دو داده (عددی و یا متنی) نیاز دارد. در صورت کافی نبودن داده‌ها، خروجی این فانکشن نیز #DIV/0! خواهد بود. برای رفع این خطا، داده‌های خود و سلول‌‌های خالی را مورد بررسی قرار دهید. ارجاع به محدوده اشتباه نیز می‌تواند باعث رخ دادن این خطا شود. بنابراین، همواره از وجود دو مقدار در محدوده انتخابی اطمینان حاصل کنید.

خطای !REFهنگام استفاده از فانکشن STDEV در اکسل

خطای #REF! ، زمانی رخ می‌دهد که ارجاع به یک سلول اشتباه باشد. پاک شدن داده‌ها می‌تواند باعث نمایش این خطا شود. برای رفع این خطا، ارجاع‌های درون فرمول تابع را مورد بررسی قرار دهید تا سلول به وجودآورنده خطا را پیدا کنید.

خطای !VALUE هنگام استفاده از فانکشن STDEV در اکسل

اگر محدوده ارجاع در فانکشن STDEV، دارای مقدار غیرمعتبر مانند یک خطا باشد، #VALUE!  رخ می‌دهد. برای رفع این خطا، بهتر است مقادیر سلول‌ها را مورد بررسی قرار دهید و حتی از ابزار فیلتر در اکسل برای اطمینان از فرمت درست مقادیر استفاده کنید. البته توجه داشته باشید که در صورت فیلتر کردن داده‌ها، فانکشن STDEV، باز هم تمام داده‌های محدوده انتخابی را درون محاسبات خود در نظر می‌گیرد. بنابراین، باید قابلیت فیلتر را به همراه یکی دیگر از توابع کاربردی اکسل مورد استفاده قرار دهید. در بخش بعدی، به معرفی این تابع می‌پردازیم.

ترکیب فانکشن STDEV با SUBTOTAL در اکسل

ابزار فیلتر، یکی از ابزارهای پرکاربرد نرم‌افزار اکسل است که امکان نمایش سفارشی داده‌ها بر اساس معیارهای مختلف را فراهم می‌کند. در هنگام استفاده از فانکشن STDEV در اکسل، در صورت فیلتر کردن داده‌ها، هیچ تغییری در خروجی انحراف معیار مشاهده نمی‌کنید. با این وجود، در برخی از موارد، نیاز دارید تا انحراف معیار داده‌های فیلتر شده را به دست بیاورید. تابع SUBTOTAL در اکسل، این کار را برای شما انجام می‌دهد.

SUBTOTAL، تابعی است که برای انجام محاسبات بر روی بخشی از داده‌ها مورد استفاده قرار می‌‌گیرد. این تابع، امکان بکارگیری برخی از توابع اکسل را به همراه قابلیت فیلتر فراهم می‌کند. توابع STDEV.S و STDEV.P نیز از توابع قابل استفاده در SUBTOTAL هستند. برای آشنایی با نحوه استفاده از SUBTOTAL به منظور محاسبه انحراف معیار داده‌های فیلتر شده، تصویر زیر را در نظر بگیرید.

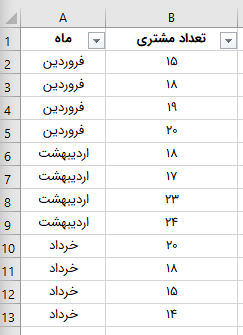
تصویر بالا، داده‌های مربوط به تعداد مشتریان یک کسب کار در ماه‌های فروردین، اردیبهشت و خرداد را نمایش می‌دهد. داده‌های مربوط به هر ماه، در چهار مرحله جمع‌آوری و ثبت شده‌اند. می‌خواهیم انحراف معیار تعداد مشتریان را به دست بیاوریم. اگر از فانکشن STDEV استفاده کنیم، نتیجه زیر به دست می‌آید.

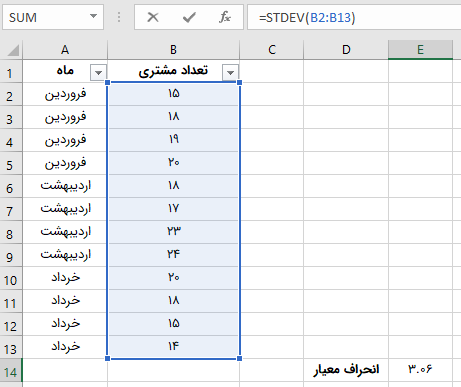
با استفاده از ابزار «Sort & Filter» در زبانه «Home»، پنل «Editing»، قابلیت فیلتر را به داده‌ها اضافه کرده‌ایم. اکنون می‌خواهیم انحراف معیار تعداد مشتریان در ماه فروردین را به دست بیاوریم. برای این کار، عبارت «فروردین» را در ستون «ماه» فیلتر می‌کنیم. به این ترتیب، نتیجه زیر به دست می‌آید.

همان‌طور که مشاهده می‌کنید، با فیلتر داده‌ها، هیچ تغییری در خروجی فانکشن STDEV در اکسل رخ نداد و مقدار انحراف معیار ثابت مانند. برای رفع این مشکل، عبارت =SUBTOTAL(  را جایگزین تابع قبلی می‌کنیم.

اولین آرگومان تابع SUBTOTAL، یک عدد را از ما می‌خواهد. این عدد، تابع مورد نظر را مشخص می‌کند. همان‌طور که مشاهده می‌کنید، عدد 7 در فهرست توابع SUBTOTAL، به تابع STDEV.S اختصاص دارد. بنابراین، این عدد را انتخاب می‌کنیم.

آرگومان بعدی تابع SUBTOTAL، محدود داده‌ها را از ما می‌خواهد. در اینجا نیز همان محدوده قبلی (B2:B13) را وارد می‌کنیم. با فشردن کلید Enter، انحراف معیار داده‌های موجود در محدوده انتخابی محاسبه می‌شود و به نمایش درمی‌آید.

تا به اینجا، خروجی تابع SUBTOTAL تفاوتی با تابع STDEV ندارد. با این وجود، اگر یک ماه دلخواه مانند فروردین را فیلتر کنیم، نتیجه انحراف معیار به صورت زیر محاسبه و نمایش داده می‌شود.

همان‌طور که مشاهده می‌کنید، فیلتر داده‌ها بر روی محاسبات انحراف معیار توسط تابع SUBTOTAL تاثیر گذاشت. عدد نمایش داده شده در تصویر بالا، انحراف معیار تعداد مشتریان در ماه فروردین است.

تفاوت فانکشن VAR با فانکشن STDEV در اکسل چیست؟

تابع VAR در اکسل، به منظور محاسبه واریانس داده‌ها مورد استفاده قرار می‌گیرد. واریانس بیشتر برای تحلیل‌های آماری و شناسایی پراکندگی داده‌ها استفاده می‌شود. در برخی از موارد، این شاخص به عنوان معیاری برای تشخیص نرمال بودن توزیع داده‌ها مورد استفاده قرار می‌گیرد.

در طرف دیگر، انحراف معیار به طور گسترده در تحلیل‌های مالی و اقتصادی برای اندازه‌گیری نوسانات به کار برده می‌شود. این شاخص به سرمایه‌گذاران در درک بهتر ریسک‌های موجود در سرمایه‌گذاری‌ها کمک می‌کند. انحراف معیار، جذر واریانس است. بنابراین، خروجی فانکشن STDEV، از ترکیب تابع VAR و SQRT به دست می‌آید. به عبارت دیگر:

$$text { STDEV() = SQRT(VAR()) }$$

هر دو تابع VAR و STDEV، از توابع آماری اکسل محسوب می‌شوند. اگر به دنبال طی کردن یادگیری کامل اکسل برای انجام تحلیل‌های مختلف هستید، باید با این تابع نیز آشنا شوید. در بخش بعدی، بهترین مسیر یادگیری تحلیل‌های آماری در اکسل را به همراه معرفی چند فیلم آموزشی جامع و کاربردی برای شما تشریح می‌کنیم.

مسیر یادگیری تحلیل آماری در اکسل چیست؟

در این مطلب، ویژگی و کاربردهای فانکشن STDEV در اکسل را به طور کامل مورد بررسی قرار دادیم. این فانکشن، تنها یکی از کاربردهای بی‌شمار اکسل در حوزه‌های مختلف، بخصوص تحلیل‌های آماری را نمایش می‌دهد. اغلب افرادی که قصد فعالیت به عنوان حسابدار، تحلیل‌گر مالی، مدیر یا حتی مهندس را دارند، از تحلیل‌های آماری برای تهیه و یا تفسیر گزارش‌های گوناگون استفاده می‌کنند. اکسل، به عنوان محبوب‌ترین و پرکاربردترین ابزار کامپیوتری در این زمینه محسوب می‌شود. اولین قدم در یادگیری تحلیل‌های آماری، آشنایی با اصول آمار و احتمالات است. مرور مباحث دبیرستان و سپس رفتن به سراغ یادگیری دروس دانشگاهی، دانش پایه شما را ارتقا می‌بخشد. فیلم‌های آموزشی فرادرس، بخصوص مجموعه آموزشی زیر، تمام نیازهای شما را برطرف می‌کنند.

پس از اصول تئوری، باید به سراغ یادگیری ابزارهای اکسل بروید. این کار را با یادگیری ابزارهای ابتدایی شروع کنید و سپس، قابلیت‌های پیشرفته اکسل در حوزه تحلیل‌های آماری را یاد بگیرید. فیلم‌های آموزشی فرادرس، منابع جامع و کاربردی زیادی را در اختیار شما قرار می‌دهند. لینک مشاهده این فیلم‌های آموزشی، در ادامه آورده شده‌اند.

پس از یادگیری ابزارهای تخصصی تحلیل آماری در اکسل و تسلط بر روی آن‌ها، یادگیری نرم‌افزارهای تخصصی‌تر در این حوزه نظیر SPSS می‌تواند مهارت‌های فنی شما را افزایش دهد و زمینه پیشرفت شما را فراهم کند. در واقع اکس، پیش‌زمینه‌ای برای کار با نرم‌افزارهای تخصصی تحلیل آماری نیز محسوب می‌شود. فرادرس، چندین فیلم آموزشی مفید و کاربردی نیز در این زمینه تهیه کرده است که لینک مشاهده آن‌ها را در ادامه آورده‌ایم:

در آخرین بخش از این مطلب مجله فرادرس، به معرفی عملکرد فانکشن STDEV در گوگل شیت می‌پردازیم.

فانکشن STDEV در گوگل شیت چیست؟

«گوگل شیت» (Google Sheets)، یک برنامه صفحه‌گسترده رایگان و مبتنی بر وب است که از قابلیت‌های مشابه اکسل بهره می‌برد. با وجود نسخه آنلاین اکسل در مجموعه مایکروسافت ۳۶۵، گوگل شیت، به عنوان محبوب‌ترین برنامه صفحه‌گسترده آنلاین محسوب می‌شود. فانکشن STDEV در گوگل شیت نیز وجود دارد.

اگر می‌خواهید قابلیت‌ها و ابزارهای گوگل شیت را به خوبی یاد بگیرید، «فیلم آموزش گوگل شیت فرادرس» را مشاهده کنید. لینک مشاهده این آموزش در ادامه آورده شده است.

تمام توابع موجود برای محاسبه انحراف معیار نمونه و جامعه آماری در اکسل را در گوگل شیت نیز می‌توان مشاهده کرد. عملکرد این توابع، دقیقا مانند معادل آن‌ها در اکسل است. البته در گوگل شیت، توابع محاسبه انحراف معیار، قادر به دریافت حداکثر ۳۰ آرگومان هستند.