انحراف معیار یا «Standard Deviation» نشاندهنده میزان پراکندگی یا تغییرپذیری مقادیر مختلف در یک مجموعه داده است. به بیان دقیقتر، این انحراف معیار است که مشخص میکند فاصله دادههای ما از مقدار میانگین بهطور متوسط چقدر است. اگر بخواهیم از نتایج بررسی سایر مفاهیم آماری مانند واریانس، ضریب تغییرات و فواصل اطمینان مطمئن شویم، لازم است انحراف معیار را نیز محاسبه کنیم. به این ترتیب، یادگیری نحوه محاسبه انحراف معیار در اکسل به ما کمک میکند تا در زمانی سریعتر و با دقت بالاتری محاسبات آماری خود را انجام دهیم.

در اولین بخش این نوشته از مجله فرادرس، مراحل محاسبه انحراف معیار در اکسل را بهصورت کلی بیان میکنیم و در بخشهای بعد، به توضیح تک تک این مراحل با جزئیات خواهیم پرداخت. برای مثال، یکی از مهمترین نکاتی که باید به آن دقت شود، تفاوت فرمول انحراف معیار برای نمونه و جمعیت (جامعه آماری) است. این نکته باعث میشود برای محاسبه انحراف معیار در اکسل با توجه به نوع دادهها (نمونه، جمعیت، دادههای منطقی یا ترکیبی از انواع مختلف داده)، از توابع مختلفی مانند STDEV.P() ، STDEV.S() ، STDEVA() یا STDEVPA() استفاده کنیم که در این زمینه نیز توضیحات لازم ارائه شده است. بهعلاوه در این نوشته یاد میگیریم که چگونه میتوان نتایج محاسبه انحراف معیار در اکسل را تفسیر کرد و در همین راستا، نشان میدهیم که اهمیت رسم error bar روی نمودار دادهها در مشاهده تنوع و پراکندگی دادهها چیست. موضوع بخشهای انتهایی این مطلب، معرفی و تعریف انحراف معیار به همراه توضیح فرمولهای محاسبه آن است تا با اساس محاسبات انحراف معیار در اکسل بیشتر آشنا شوید.
مراحل محاسبه انحراف معیار در اکسل
انحراف معیار یکی از مهمترین شاخصهای پراکندگی در آمار است که نشان میدهد نحوه توزیع و فاصله مقادیر مختلف داده از مقدار میانگین بهطور متوسط چقدر است. محاسبه انحراف معیار در کنار سایر شاخصها به ما کمک میکند پس از تحلیل نتایج بتوانیم پیشبینی مطمئنتری ارائه دهیم. یکی از آسانترین ابزارهای محاسبه انحراف معیار، «نرم افزار اکسل» (Excel Software) از مجموعه برنامههای نرم افزار «مایکروسافت آفیس» (Microsoft Office) است. کافی است یکی از سینتکسهای زیر را در اکسل اجرا کنید:
سینتکس اول:
=STDEV.S(number1,[number2],…)
سینتکس دوم:
=STDEV.P(number1,[number2],…)
دستور اول انحراف معیار نمونه و دستور دوم انحراف معیار جمعیت را محاسبه میکند. اما اگر میخواهید با جزئیات بیشتری گام به گام مراحل محاسبه انحراف معیار در اکسل را بدانید، میتوانید به روش زیر عمل کنید:
- وارد کردن دادهها به یک ستون از اکسل
- انتخاب تابع انحراف معیار مناسب (نمونه یا جمعیت)
- انتخاب یک سلول برای درج نتیجه
- وارد کردن فرمول انحراف معیار
- مشخص کردن آرگومان یا محدوده تابع انحراف معیار
- فشار دادن کلید اینتر و محاسبه انحراف معیار
شاید مهمترین نکته در مبحث انحراف معیار در اکسل، مرحله دوم از مراحل بالا باشد. برای اینکه بدانیم برای محاسبه انحراف معیار از کدام تابع اکسل باید استفاده کنیم، بهتر است ابتدا به سوالات زیر پاسخ دهیم:
- آیا میخواهید انحراف معیار را برای یک نمونه آماری محاسبه کنید یا برای یک جامعه آماری؟
- کدام ورژن از نرمافزار اکسل را استفاده میکنید؟
- آیا مجموعه دادههای شما فقط شامل اعداد یا مقادیر منطقی است یا مقادیر متنی هم دارید؟
در ادامه هر یک از گامهای محاسبه انحراف معیار در اکسل را توضیح میدهیم. همچنین برای درک بهتر این مراحل، لازم است بدانیم مفهوم انحراف معیار در آمار چیست و چه فرمولی دارد که در بخشهای انتهایی به این مباحث پرداختهایم. در صورت نیاز میتوانید ابتدا این بخشها را مطالعه کنید.
۱. وارد کردن دادهها به یک ستون از اکسل
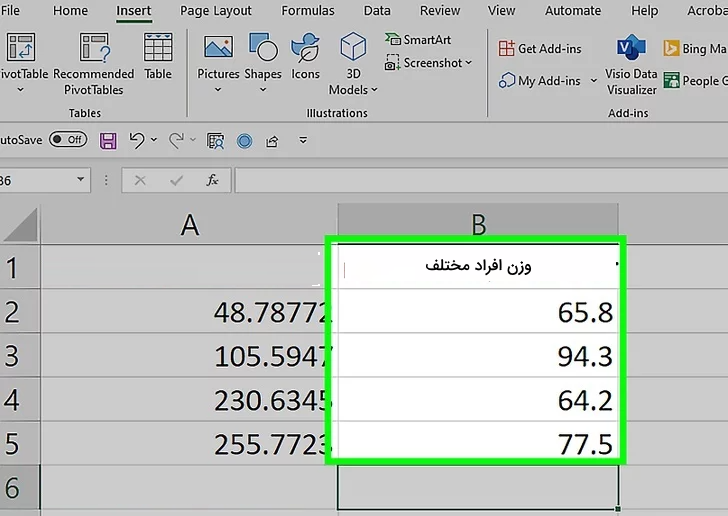
اولین مرحله برای محاسبه انحراف معیار در اکسل، وارد کردن دادهها به اکسل است. اگر دادههای شما از قبل در اکسل قرار دارد، در این مرحله فقط کافی است آنها را در یک ستون و پشت سر هم قرار دهید. در غیر این صورت، باید ابتدا دادههای خود را به محیط اکسل وارد کنید. برای مثال، در تصویر برای محاسبه انحراف معیار مقادیر وزن چهار شخص مختلف، دادههای مرتبط در ستونی با کادر سبز رنگ پشت سر هم مرتب شدهاند.
۲. انتخاب تابع انحراف معیار مناسب (نمونه یا جمعیت)
در واقع امتیاز محاسبه انحراف معیار در اکسل این است که با استفاده از توابع داخلی این برنامه میتوانیم محاسبات خود را با دقت بالا و بدون خطا انجام دهیم. در اکسل توابع مختلفی با اهداف محاسباتی خاص وجود دارد که از میان آنها دو تابع STDEV.P() و STDEV.S() برای محاسبه انحراف معیار استفاده میشوند.
تفاوت مهم این دو تابع در این است که تابع STDEV.S() به منظور محاسبه انحراف معیار روی دادههای یک نمونه و تابع STDEV.P() برای پیدا کردن انحراف معیار روی یک جمعیت بکار میرود. پس همینجا نتیجه میگیریم که پیش از شروع محاسبات، ابتدا باید مشخص کنیم آیا دادههای ما مربوط به یک نمونه آماری است یا یک جمعیت یا جامعه آماری.
اگر بخواهیم به بررسی تفاوت این دو تابع بپردازیم، ابتدا باید تفاوت فرمول محاسبه انحراف معیار در مورد این دو وضعیت را بدانیم. این موضوع در بخشهای بعد بیشتر توضیح داده میشود. فعلا فقط به این نکته بسنده میکنیم که تابع STDEV.P() بر تعداد کل مقادیر دادههای نقطهای یا تقسیم میشود، در حالی که تابع STDEV.S() بر تعداد کل دادههای نقطهای با یک واحد کمتر یعنی تقسیم میشود تا تنوعی که در دادههای نمونه وجود دارد، در نظر گرفته شود.
بد نیست در اینجا به این نکته اشاره کنیم که در نسخههای قدیمیتر اکسل (۲۰۰۷ یا قبلتر)، از یک تابع کلی به نام STDEV() بهجای این دو تابع استفاده میشد. STDEV() در اکسل انحراف معیار نمونه را بر اساس روش میانگین مربعات محاسبه میکند. اغلب نتایج حاصل از محاسبات این تابع با نتایج بهدست آمده از تابع STDEV.S() یکسان است. در ادامه برای اینکه با کاربرد دو تابع STDEV.S() و STDEV.P() بهتر آشنا شوید، به تفکیک آنها را در دو بخش جداگانه بررسی میکنیم.
تابع ()STDEV.P برای محاسبه انحراف معیار جمعیت در اکسل
تابع STDEV.P() مشخصا برای محاسبه انحراف معیار در اکسل و برای یک جمعیت یا جامعه آماری استفاده میشود. این تابع فرض میکند که آرگومانهای داده شده شامل کل جمعیت آماری ما هستند. این تابع از فرمول انحراف معیار برای جمعیت که در بخشهای بعد آن را معرفی خواهیم کرد، برای محاسبه انحراف معیار استفاده میکند. به عنوان مثال، اگر بخواهیم نمرات آزمون تمام دانشآموزان یک مدرسه مشخص را بررسی و تحلیل کنیم، کاربرد این تابع در اکسل مفید است، چون در این مثال مجموعه داده ما کل جمعیت را شامل میشود.
تابع ()STDEV.S برای محاسبه انحراف معیار نمونه در اکسل
اگر بخواهیم انحراف معیار در اکسل را برای یک نمونه آماری پیدا کنیم، از تابع STDEV.S() استفاده میکنیم. در این تابع آرگومان داده شده یک نمونه از جمعیت (و نه کل جمعیت) در نظر گرفته میشود. فرمولی که این تابع اکسل بکار میبرد، فرمول انحراف معیار برای نمونه است. برای مثال، فرض کنید میخواهید انحراف معیار در اکسل را برای نمرات آزمون زیرمجموعهای تصادفی از دانشآموزان یک مدرسه مشخص بهدست آوردید. در این شرایط ما با یک نمونه آماری سروکار داریم.
۳. انتخاب یک سلول برای درج نتیجه
پیش از اینکه محاسبه انحراف معیار در اکسل را شروع کنید، لازم است ابتدا سلولی که میخواهید انحراف معیار در آن نشان داده شود را انتخاب کنید. با کلیک روی این سلول، انتخاب آن انجام شده است. دقت کنید این سلول باید خالی باشد و هیچ نوع داده عددی یا متنی در آن نباشد.
۴. وارد کردن فرمول انحراف معیار
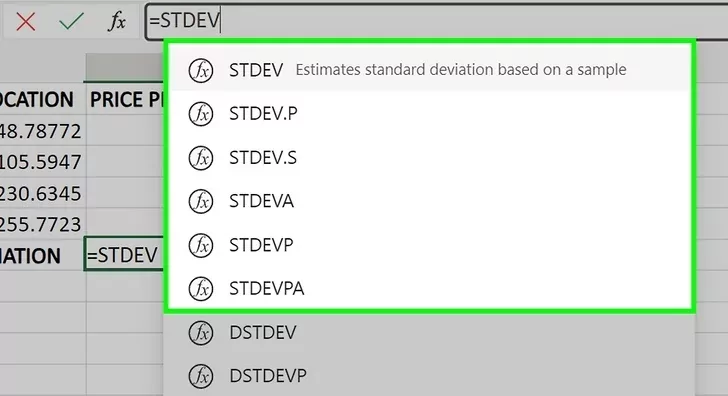
مرحله بعد نوشتن فرمول انحراف معیار است که همانطور که اشاره شد، با توجه به نوع دادهها و آنچه که در مسئله از ما خواسته شده است، باید تابع مناسب را انتخاب کنیم. برای نوشتن فرمول در تب بالای صفحه اکسل، ابتدا باید حتما علامت مساوی را قرار دهیم. سپس با نوشتن یک الی دو حرف از توابع انحراف معیار، لیست پیشنهادی توابع را مشاهده میکنید. همچنین میتوانید توابع را بهصورت STDEV.P() یا STDEV.S() تایپ کنید.
۵. مشخص کردن آرگومان یا محدوده تابع انحراف معیار
تا اینجا فقط تابعی که میتواند انحراف معیار را برای ما محاسبه کند، در جایگاه خود قرار دادهایم. در این قسمت باید دادههایی را که میخواهیم انحراف معیار آنها را داشته باشیم در آرگومان این تابع قرار دهیم. منظور از آرگومان تابع، همان پرانتزی است که در عبارت STDEV.P() یا STDEV.S() وجود دارد. برای قرار دادن دادهها در آرگومان، ابتدا باید داخل این پرانتز کلیک کنیم.
سپس روی اولین سلول از ستون دادهها کلیک میکنیم. با درگ کردن یا کشیدن علامت مثبت گوشه این سلول تا انتهای ستون (آخرین سلولی که شامل عدد است)، آرگومان تابع انحراف معیار ما مشخص شده است. البته میتوانید شماره اولین و آخرین سلول از دادههای خود را بهترتیب و با قرار دادن علامت بینشان، تایپ کنید (برای مثال به شکل ).
۶. محاسبه انحراف معیار
آخرین مرحله این است که مکاننمای خود را در انتهای فرمول محاسبه انحراف معیار در اکسل قرار دهیم. با زدن اینتر، انحراف معیار دادههای شما در سلولی که انتخاب کرده بودید، ظاهر میشود. برای مثال اگر دادههای شما از سلول تا سلول در یک ستون از اکسل قرار داشته باشند، چنانچه این دادهها نمایشگر یک نمونه باشند، فرمول محاسبه انحراف معیار به صورت زیر است:
= STDEV.S(A1:A10)
در حالی که محاسبه انحراف معیار در اکسل برای یک جامعه آماری توسط تابع زیر انجام میشود:
= STDEV.P(A1:A10)
یادگیری انحراف معیار و شاخصهای پراکندگی در آمار با فرادرس
در این بخش پیشنهاد میکنیم اگر علاقهمند به یادگیری مباحث آماری هستید، فیلمهای آموزشی زیر از مجموعه فرادرس را مشاهده کنید:

- فلیم آموزش رایگان روش حل انحراف معیار و واریانس + توابع محاسباتی در اکسل فرادرس
- فیلم آموزش آمار و احتمال مهندسی فرادرس
- فیلم آموزش رایگان آمار توصیفی چیست؟ + مفاهیم، روشها و کاربردها فرادرس
بررسی چند مثال از محاسبه انحراف معیار در اکسل
پس از اینکه با مراحل محاسبه انحراف معیار در اکسل کاملا آشنا شدیم، در این بخش میخواهیم آموختههای خود را در قالب حل چند مثال بررسی کنیم.
مثال اول محاسبه انحراف معیار در اکسل
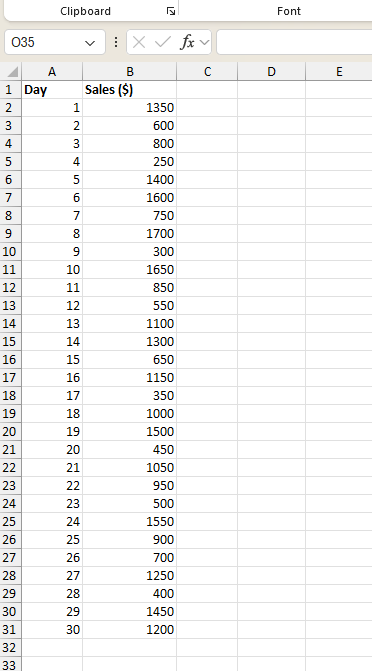
فرض کنید میخواهید دادههای مربوط به فروش یک فروشگاه را تحلیل و بررسی کنید. هدف این است که تنوع فروش روزانه طی یک ماه گذشته بررسی شود تا بتوانید موجودی کالای خود را بهتر مدیریت کنید. اگر دادههای شما به شکل زیر طی سی روز گذشته جمعآوری شده باشند، انحراف معیار چقدر است؟
پاسخ
در تصویر بالا میزان فروش برای هر کدام از روزهای ماه مشخص شده است. برای نمونه، فروش در روز دهم برابر است با دلار. پس دادههای ما در این مثال، ستون دوم یا ستون است. برای محاسبه انحراف معیار در اکسل، پیش از انتخاب تابع محاسباتی موردنظر، ابتدا سلولی را انتخاب میکنیم که میخواهیم نتیجه محاسبات انحراف معیار در آن ظاهر شود. در این مثال ما سلول را انتخاب کردهایم. همچنین نوع دادههای ما در این سوال جمعیت است. پس باید از تابع STDEV.P() استفاده کنیم، به این صورت که در بخش مربوط به تایپ فرمول، ابتدا علامت مساوی و سپس عبارت STDEV.P() را تایپ میکنیم.
برای انتخاب آرگومان این تابع که داخل پرانتز قرار میگیرد، کافی است ابتدا داخل پرانتز در عبارت تایپ شده STDEV.P() کلیک کنیم. سپس اولین سلول از ستون دادهها یعنی را انتخاب کرده و آن را تا سلول بکشیم یا درگ کنیم. حالا در بخش فرمول باید عبارتی بهصورت = STDEV.P(B2:B31) داشته باشیم. با قرار دادن مکاننما در این بخش و زدن کلید اینتر، محاسبات انجام شده و نتیجه در سلول موردنظر ظاهر میشود که بهصورت زیر است:
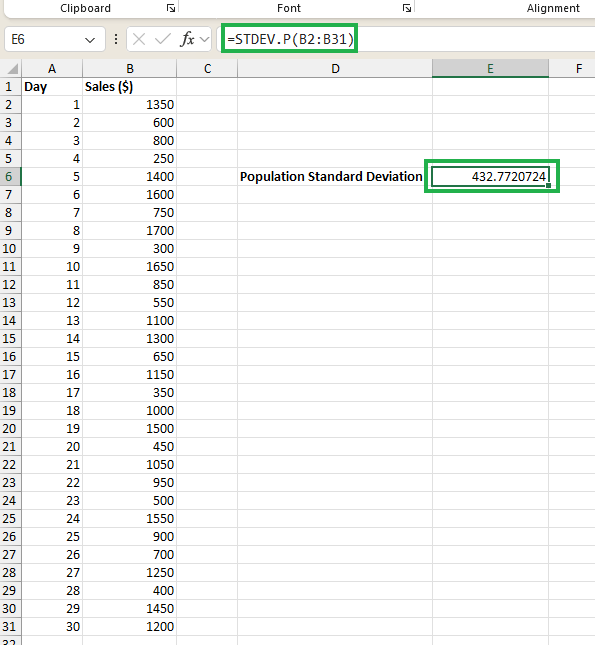
مثال دوم محاسبه انحراف معیار در اکسل
بار دیگر به دادههای فروش در مثال اول دقت کنید و این بار انحراف معیار را برای کل سال گذشته محاسبه کنید:
پاسخ
تفاوت این دو مثال توصیف کننده تفاوت توابع STDEV.P() و STDEV.S() است. در مثال اول، بررسی ما روی جمعیت بود، اما در این مثال بررسی ما روی نمونه است، چون در سوال انحراف معیار کل سال گذشته خواسته شده است، در حالی که دادههای ما مربوط به بخشی از کل سال است. پس یک نمونه آماری داریم و باید از STDEV.S() برای محاسبه انحراف معیار در اکسل استفاده کنیم. اولین قدم انتخاب سلولی است که میخواهیم پاسخ محاسبات در آن قرار داده شود. برای اینکه بتوانیم عدد حاصل از این محاسبه را با عدد بهدست آمده از مثال اول برای جمعیت مقایسه کنیم، سلول زیر ، یعنی را انتخاب میکنیم.
سپس عبارت = STDEV.S() را در بخش فرمولنویسی تایپ کرده و با کلیک داخل پرانتز، انتخاب سلول و درگ تا سلول ، آرگومان تابع انحراف معیار را کامل میکنیم. حالا با زدن اینتر در انتهای عبارت = STDEV.S(B2:B31) ، نتیجه محاسبه انحراف معیار در اکسل در سلول به شکل زیر ظاهر میشود:
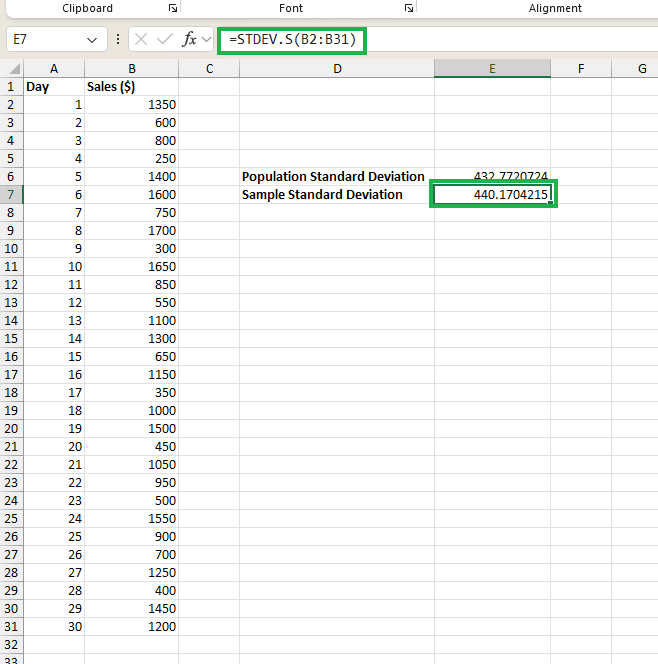
مثال سوم محاسبه انحراف معیار در اکسل
در این سوال میخواهیم تابع مناسب برای محاسبه انحراف معیار در اکسل را برای هر یک از موقعیتهای زیر مشخص کنید:
در موقعیت اول، نمرات آزمون پنج نفر از دانشآموزان یک کلاس بهصورت داده شده است. پس از قرار دادن این دادهها در ستونی مانند ، میخواهیم میزان تنوع این دادهها را با محاسبه انحراف معیار تحلیل کنیم. در سناریوی بعدی، فرض میکنیم تیم کوچکی را برای جمعآوری داده در زمینه تعداد تماسهای روزانه در یک شرکت در نظر گرفتهایم. این دادهها بهصورت در ستونی به نام قرار میگیرند و میخواهیم انحراف معیار را برای آنها محاسبه کنیم:
پاسخ
در اولین موقعیت، کاملا مشخص است که با یک نمونه از جامعه آماری بزرگتر (کل کلاس) سروکار داریم. پس باید از تابع محاسبه انحراف معیار در اکسل برای نمونه و به شکل زیر استفاده شود:
= STDEV.S(B1:B5)
در مورد دومین سناریو، محاسبه انحراف معیار روی یک جامعه آماری را داریم:
= STDEV.P(B1:B5)
دقت کنید ترتیب قرار گرفتن دادهها در ستون مهم نیست. با نوشتن فرمولهای بالا، هر پنج داده در محاسبات لحاظ میشوند.
تفسیر مقادیر انحراف معیار در اکسل
در بخشهای گذشته آموختیم که مراحل محاسبه انحراف معیار در اکسل چیست. برای نمونه در مثال اول و دوم از بخش قبل، دو مقدار عددی برای انحراف معیار با توجه به نوع سوال محاسبه شد. پیش از پرداختن به موضوع این بخش، چنانچه تمایل دارید با توابع مختلف اکسل و نحوه فرمولنویسی در آن بیشتر آشنا شوید، میتوانید فیلم آموزش استفاده از توابع و فرمول نویسی در اکسل Excel فرادرس را که لینک آن در ادامه قرار داده شده است، مشاهده کنید:
در این قسمت قصد داریم توضیح دهیم تفسیر این اعداد چگونه انجام میشود. اولین قدم برای تحلیل و مقایسه انحراف معیار، محاسبه میانگین یا Mean Value است. محاسبه میانگین در اکسل روندی شبیه محاسبه انحراف معیار در اکسل دارد، فقط کافی است تابع متناظر با این هدف را انتخاب کنیم که عبارت است از AVERAGE () . به مثال زیر در این زمینه توجه کنید:
مثال
در مثالهای محاسبه انحراف معیار برای فروش، تفسیر نتایج بهدست آمده چگونه است؟
پاسخ
ابتدا مقدار میانگین را پیدا میکنیم، به این صورت که روی سلولی مانند کلیک کرده و عبارت = AVERAGE () را در بخش فرمول تایپ میکنیم. سپس با کلیک داخل پرانتز و انتخاب سلولهای موردنظر که شامل دادههای فروش هستند، عبارتی به شکل داریم. با قرار دادن مکاننما در انتهای عبارت = AVERAGE (B2:B31) و زدن کلید اینتر، مقدار میانگین به شکل زیر محاسبه میشود:
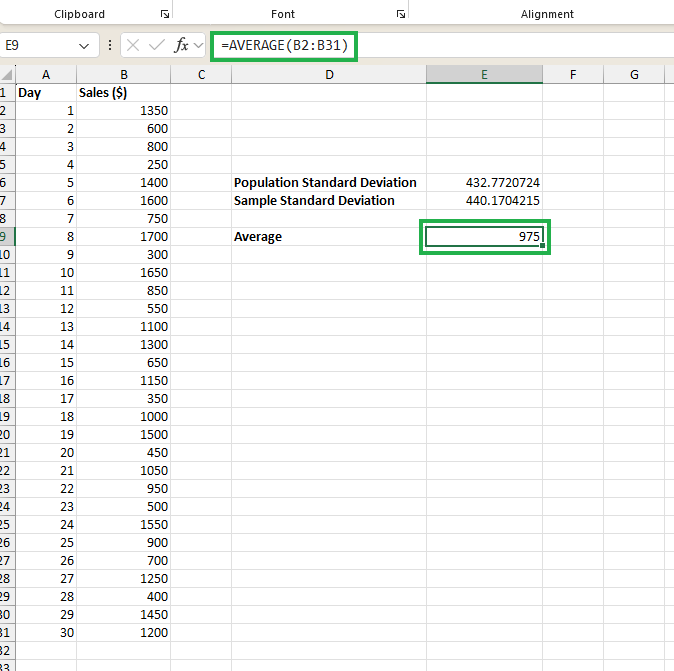
حالا با توجه به عددی که برای میانگین بهدست آمده است، بهراحتی میتوانیم در مورد مقادیر انحراف معیار صحبت کنیم. هر دو مقدار انحراف معیار چه برای جمعیت و چه برای نمونه، از میانگین فاصله زیادی دارند. مقدار انحراف معیار جمعیت با عدد تقریبی نشاندهنده این است که بهطور متوسط، فروش روزانه به اندازه از میانگین انحراف یا فاصله دارد.
انحراف معیار نمونه با عدد تقریبی با اینکه کمی از عدد بهدست آمده برای انحراف معیار جمعیت بزرگتر است، اما توصیفکننده فاصله متوسطی به اندازه از مقدار میانگین است. باید توجه داشته باشید این عدد در صورتی مرتبط و قابل استفاده است که دادههای مربوط به نمونه (در اینجا سی روز ماه گذشته) جزئی از یک جمعیت بزرگتر باشد. زمانی که مقدار انحراف معیار نمونه کمی از انحراف معیار جمعیت بیشتر میشود، میتوانیم به این نتیجه برسیم که عدمقطعیت یا Uncertainty داریم. این عدمقطعیت به کاربرد نمونه جهت تخمین وضعیت تنوع دادههای فروش طی یک سال گذشته مربوط میشود.
در مجموع، هر دو مقدار انحراف معیار با توجه به پراکندگی بالا در مقایسه با مقدار میانگین، نشاندهنده تنوع و تغییر زیاد در فروش روزانه هستند. به عبارت دیگر، نوسان فروش روزانه حول مقدار میانگین زیاد است. بنابراین این سطح از تنوع و تغییرپذیری در فروش نیازمند مدیریت موجودی و پرسنل است، چرا که ممکن است برخی روزها فروش خیلی کمتر یا خیلی بیشتر از مقدار میانگین شود و در نتیجه، با کمبود یا انباشتگی کالا در انبار مواجه شویم.
اگر بخواهیم تحلیل دقیقتری در این زمینه ارائه کنیم، بهتر است سایر کمیتهای آماری نیز محاسبه و بررسی شوند. در مطلب «ضریب پراکندگی چیست؟ – به زبان ساده + فرمول محاسبه» از مجله فرادرس، به معرفی و توضیح انواع ضرایب پراکندگی مانند ضریب دامنه، ضریب انحراف میانگین، ضریب تغییرات و ضریب انحراف چارک پرداخته شده است که در صورت علاقه میتوانید به این آموزش مراجعه کنید.
رسم نمودار دادهها و قرار دادن Error Bar برای انحراف معیار
یکی دیگر از ابزارهایی که به شما در تحلیل، بررسی و مقایسه نتایج حاصل از محاسبات انحراف معیار در اکسل کمک میکند، استفاده از نمودارهای مختلف مانند نمودار میلهای، نمودار خطی یا نقاط پراکنده است. این نمودارها در نشان دادن میزان تنوع دادهها بسیار موثراند. مثال بخش قبل را در نظر بگیرید که در آن مقادیر انحراف معیار و میانگین محاسبه و تفسیر شدند.
با انتخاب دادههای فروش ماه گذشته از سلول تا ، رفتن روی منوی Insert و انتخاب نمودار موردنظر که در اینجا Line Chart است، نمودار خطی دادههای فروش به شکل زیر رسم میشود. همانطور که مشاهده میکنید، نوسان دادهها کاملا مشخص است:
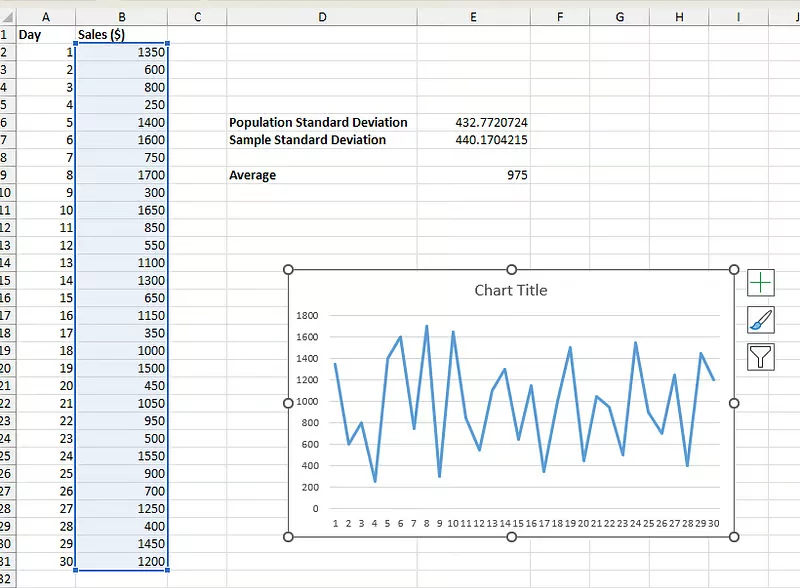
پس از اینکه نمودار به شکل بالا رسم شد، نکته مهم قرار دادن Error Bars است. با انتخاب نمودار و ظاهر شدن منوی Chart Design، روی آن کلیک کنید. سپس با کلیک روی گزینه Add Chart Element مطابق شکل زیر، لیستی را مشاهده میکنید که لازم است در آن گزینه Error Bars و سپس Standard Deviation انتخاب شود. در این صورت error barها به شکل خطوط عمودی روی نمودار قرار میگیرند:
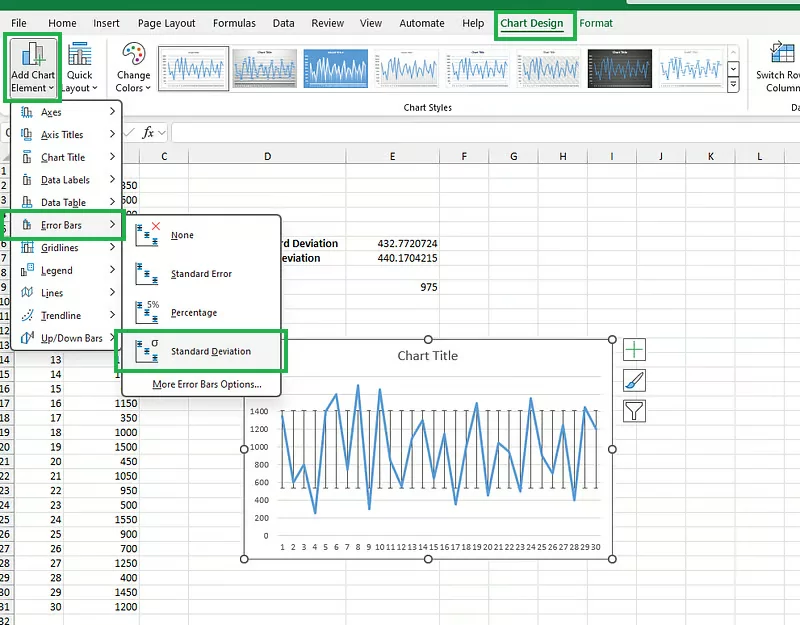
برای تنظیم فرمت error bar میتوانید به بخش تنظیمات آن، یعنی Format Error Bars مراجعه کنید. در این بخش شکل خطوط عمودی error bar روی نمودار شامل رنگ، پهنا و استایل قابل تغییر است. بنابراین قرار دادن Error Bars روی نمودار توزیع دادهها، میزان تغییرات و پراکندگی دادههای فروش را بهتر نشان داده است.
محاسبه انحراف معیار در اکسل برای دادههای منطقی
گاهی اوقات ممکن است با دادههای منطقی شامل درست یا TRUE و نادرست یا FALSE در اکسل مواجه شویم. اکسل مقادیر درست را معادل و مقادیر نادرست را معادل در نظر میگیرد. برای محاسبه انحراف معیار در مورد چنین دادههایی تابع مشخصی به نام STDEVA () در اکسل داریم که نحوه کار با آن را در مثال زیر خواهید دید:
مثال
تابع مناسب برای محاسبه انحراف معیار در اکسل در مورد دادههایی به شکل که در ستون قرار گرفتهاند، چیست؟ فرض کنید این دادهها پاسخهایی هستند که در مورد رضایت مشتریان از خدمات یک شرکت جمعآوری شده است.
پاسخ
همانطور که ملاحظه میکنید، دادههای این سوال از نوع دادههای منطقی بهشمار میروند. پس تابع مناسب برای محاسبه انحراف معیار این مقادیر به شکل زیر است:
=STDEVA (B1:B5)
محاسبه انحراف معیار در اکسل برای انواع مختلف دادهها
ممکن است در مسائلی انواع دادههای مختلف شامل اعداد و گزارههای منطقی به شکل درست و نادرست داشته باشیم. در چنین شرایطی تابع مناسب جهت محاسبه انحراف معیار در اکسل به شکل STDEVPA () است. در ادامه با بررسی یک مثال بهتر متوجه این نوع مسائل خواهید شد.
مثال
فرض کنید میخواهید عملکرد تیم کوچکی را با محاسبه انحراف معیار بررسی کنید. اینکه شخصی برای دریافت پاداش واجد شرایط است یا نه، توسط گزارههای منطقی درست و نادرست مشخص شده است. همچنین نمره عملکرد برخی از اعضای دیگر تیم توسط اعداد مختلف نشان داده شده است:
پس از قرار دادن این مقادیر در ستونی به نام در اکسل، تابع مناسب برای محاسبه انحراف معیار چیست؟
پاسخ
در این مثال دادههای ما شامل عدد و گزارههای منطقی درست و نادرست هستند. بنابراین باید از تابع STDEVPA () به شکل زیر برای محاسبه انحراف معیار استفاده کنیم:
= STDEVPA (B1:B6)
نکته: در مثال این بخش و بخش قبل، توابعی که برای محاسبه انحراف معیار استفاده شد، محاسبه را روی جمعیت انجام میدهند.
توابع محاسبه انحراف معیار در اکسل چیست؟
در بخشهای قبل این توابع را به مرور و همراه با مثال معرفی کردیم. جدول زیر جمعبندی کاملی از این توابع ارائه میدهد:
| نوع داده | تابع محاسبه انحراف معیار در اکسل | نسخه اکسل |
| نمونه | STDEV() | ۲۰۰۳ تا ۲۰۱۹ |
| نمونه | STDEV.S() | ۲۰۱۰ تا ۲۰۱۹ |
| نمونه | STDEVA () | ۲۰۰۳ تا ۲۰۱۹ |
| جمعیت | STDEVP() | ۲۰۰۳ تا ۲۰۱۹ |
| جمعیت | STDEV.P() | ۲۰۱۰ تا ۲۰۱۹ |
| جمعیت | STDEVPA () | ۲۰۰۳ تا ۲۰۱۹ |
دقت کنید هیچکدام از این توابع نمیتوانند یک سلول خالی اکسل را در محاسبات در نظر بگیرند. همچنین نوع دادههایی که این توابع میتوانند پردازش کنند، با هم متفاوت است. جدول زیر این تفاوت را نشان میدهد. برای مثال دادههای منطقی در توابع STDEVA () و STDEVPA () قابل پردازش بهصورت یا هستند، در حالی که همین توابع کلیه دادههای متنی را در نظر میگیرند.
| تابع محاسبه انحراف معیار در اکسل | دادههای منطقی | دادههای متنی |
| STDEV() | ||
| STDEV.S() | ||
| STDEVA () | ||
| STDEVP() | ||
| STDEV.P() | ||
| STDEVPA () |
انحراف معیار چیست؟
همانطور که در ابتدای مطلب توضیح دادیم، انحراف معیار یک کمیت یا پارامتر آماری است که به ما نشان میدهد میزان پراکندگی یا انحراف در یک مجموعه داده چقدر است. همچنین با دانستن انحراف معیار میتوانیم متوجه شویم در یک مجموعه داده اختلاف یا فاصله دادهها با مقدار میانگین چقدر است.

انحراف معیار نشاندهنده میزان گستردگی، پراکندگی یا پخششدگی دادههای ما است. برای مثال، اگر مقدار انحراف معیار پایین باشد، یعنی دادههای نقطهای ما به مقدار میانگین نزدیک هستند. این نکته نشان میدهد که بین مقادیر مختلف دادههای ما سازگاری یا Consistency بیشتری وجود دارد. بنابراین پخش یا گستردگی دادهها نیز کم است. در حالی که انحراف معیار بزرگ بیانگر این است که مقادیر مختلف دادهها در یک مجموعه داده از مقدار میانگین فاصله زیادی دارند. بنابراین دادههای ما در این حالت محدوده گستردهتری از مقادیر را شامل میشوند و دارای تنوع یا Variability بیشتری هستند.
برای مثال دادههای زیر را در نظر بگیرید. با اینکه مقدار میانگین برای هر دو مجموعه داده یکسان و برابر با عدد است، اما به وضوح میتوان تشخیص داد که تنوع و گستردگی مقادیر در گروه دوم بیشتر است:
بنابراین انحراف معیار با در اختیار گذاشتن یک دید منطقی از وضعیت دادهها، به شما در بررسی تنوع یا سازگاری دادهها کمک میکند. همچنین محاسبه انحراف معیار در ارزیابی دقت و صحت مدلهای رگرسیونی نیز مهم است، چرا که این عدد میتواند میزان انحراف مقادیر باقیمانده که همان خطاهای مدل جهت انجام پیشبینی هستند را نشان دهد. به عبارت دیگر، با محاسبه انحراف معیار باقیماندهها میتوان تخمین زد که مدل رگرسیونی مورد استفاده با دادههای واقعی تا چه اندازه فیت شده است.
سرمایهگذارها و مشاوران مالی انحراف معیار را بهعنوان یکی از مهمترین پارامترهای ارزیابی ریسک در نظر میگیرند. صاحبان این مشاغل عموما با دادههای گستردهای سروکار دارند، به همین علت به دنبال ابزارهای قابلاعتمادی هستند که تحلیل معناداری از این دادهها ارائه کند. نرم افزار اکسل یکی از این ابزارهای تجزیه و تحلیل داده محسوب میشود که امتیاز آن در دسترسی آسان و کاربرپسند بودن آن است. بهطور کلی، محاسبه انحراف معیار در اکسل یا به کمک سایر نرم افزارها میتواند جهت پیشبینی و یا تحلیل نتایج در موضوعات زیر بکار رود:
- پیشبینی ریسکهای اقتصادی
- کنترل کیفیت
- پزشکی و سلامت
- تحصیلات و پژوهش
- پیشبینی شرایط آب و هوایی
فرمول محاسبه انحراف معیار چیست؟
اولین نکتهای که در مورد فرمول مناسب برای محاسبه انحراف معیار مطرح میشود این است که آیا میخواهیم انحراف معیار یک نمونه آماری را محاسبه کنیم یا محاسبات ما روی یک جامعه آماری است. پس ابتدا بهتر است تفاوت نمونه و جامعه را بدانیم. یک «جامعه یا جمعیت آماری» (Population) شامل تمام اعضای یک مجموعه داده است، در حالی که یک «نمونه» (Sample) زیر مجموعهای از مجموعه دادههای موردنظر ما است. در نتیجه نمونه شامل یک یا چند عضو از جامعه است نه تمام اعضای آن.

بنابراین تحلیل دادهها با توجه به اینکه دادههای مورد نظر ما جزئی از یک نمونه آماری است یا جزئی از جامعه آماری، متفاوت خواهد بود. انحراف معیار در آمار اغلب با نماد نشان داده میشود، اما اگر بخواهیم از نماد دقیقتری برای نشان دادن جمعیت یا نمونه بودن دادههای در نظر گرفته شده استفاده کنیم، نماد را برای جمعیت و نماد را برای نمونه بکار میبریم.
فرمول انحراف معیار جمعیت
فرمول محاسبه انحراف معیار جمعیت به صورت زیر است:
- : تعداد کل دادههای نقطهای جمعیت
- : هر داده نقطهای
- : متوسط یا میانگین جمعیت
این فرمول متوسط توان دوم انحراف یا اختلاف تمام دادهها از مقدار میانگین را محاسبه میکند و در انتها ریشه دوم این میانگین را به ما میدهد.
فرمول انحراف معیار نمونه
فرمول محاسبه انحراف معیار نمونه کاملا مشابه فرمول متناظر برای جمعیت است. تنها اختلافی که بین این دو فرمول وجود دارد در مخرج آنها و برخی نمادهای استفاده شده است. همین تفاوت باعث میشود هنگام محاسبه انحراف معیار در اکسل دقت کنیم که از تابع مناسب استفاده شود:
- : تعداد کل دادههای نقطهای نمونه
- : هر داده نقطهای
- : متوسط یا میانگین نمونه
اینکه در فرمول انحراف معیار برای نمونه از مخرج یک واحد کم میشود به علت «تصحیح بسل» (Bessel’s Correction) است. با این تصحیح مطمئن میشویم که بهدرستی از این نمونه برای تخمین جمعیت استفاده کردهایم.
مسیر یادگیری اکسل و کاربردهای آن با فرادرس
نرم افزار صفحه گسترده اکسل جهت مدیریت انواع دادهها و انجام محاسبات آماری مختلف بسیار پرکاربرد است. مزیت مهم این نرمافزار در دسترسی آسان، ارزان بودن و سرعت بالای پردازش دادهها است. مشاهده فیلمهای آموزشی فرادرس با موضوع یادگیری امکانات و کاربردهای مختلف اکسل مانند رسم جدول، ایجاد چکباکس، مغایرتگیری، فیلترگذاری و … به شما کمک میکند تا بهراحتی با این ابزار قدرتمند و دنیای گسترده آن آشنا شوید:

همچنین با توجه به اینکه ممکن است در نسخههای مختلف این نرم افزار تغییراتی در منوها ایجاد شده یا امکانات جدیدی به آن اضافه شود، در ادامه دورههای آموزشی مربوط به نسخههای مختلف اکسل معرفی شدهاند:
- فیلم آموزش اکسل Microsoft Excel 2013 فرادرس
- فیلم آموزش اکسل Microsoft Office Excel 2016 فرادرس
- فیلم آموزش اکسل Microsoft Excel 2019 فرادرس
- فیلم آموزش اکسل Microsoft Excel 2021 فرادرس
جمعبندی
یکی از کمیتهای مهمی که محاسبه آن توسط اکسل انجام میشود، انحراف معیار یا Standard Deviation است. کاربرد انحراف معیار در اقتصاد، انجام انواع پژوهشهای آماری، علوم مهندسی و علوم پایه است. انحراف معیار تخمینی از درستی و قابل اعتماد بودن محاسبات را نشان میدهد و در نتیجه در پیشبینی ریسک میتواند مفید باشد. بنابراین، محاسبه انحراف معیار در اکسل یکی از دقیقترین و سریعترین روشها جهت بررسی قابلاعتماد بودن نتایج بهدست آمده برای هر نوع محاسبات آماری یا آزمودن فرضیهها است.
برای محاسبه انحراف معیار در اکسل، بسته به نوع مجموعه دادهای که در اختیار دارید، میتوانید از توابع داخلی مختلفی استفاده کنید. پس از اینکه دادهها در یک ستون از اکسل و پشت سر هم مرتب شدند، با نوشتن فرمول تابع مناسب در ردیف مربوط به فرمولنویسی و سپس انتخاب بازهای که متناظر با ستون دادههای ما است، کلید اینتر را میزنیم. بلافاصله پس از زدن کلید اینتر میتوانید خروجی را در سلول انتخاب شده مشاهده کنید.
source
