ریاضیات گسسته یا Discrete Mathematics بخشی از علم ریاضی است که به مطالعه ساختارها و عناصر گسسته میپردازد. مباحث مهمی که در ریاضیات گسسته مطرح میشوند عبارتاند از نظریه مجموعهها، نظریه گراف و ترکیبیات. این مفاهیم، پایه و اساس درک الگوریتمها و مدارهای منطقی در علوم کامپیوتر محسوب میشوند. در این مطلب از مجله فرادرس قصد داریم مفاهیم پایه ریاضیات گسسته را به زبانی ساده توضیح دهیم.

به همین منظور، در اولین بخش نظریه مجموعهها را توضیح دادهایم. پس از تعریف مجموعه و ویژگیهای آن مانند کاردینالیتی، به توصیف روابط بین مجموعهها مانند مجموعه مکمل، اجتماع و اشتراک مجموعهها، قوانین دمورگان و اصل شمول و عدم شمول یا قانون PIE پرداختهایم. بخش دوم این نوشته به نظریه گراف اختصاص دارد. به این صورت که ابتدا ویژگیهای یک گراف مانند مرتبه، اندازه و درجه را توضیح دادهایم. سپس فرمول قانون مهمی به نام «قیاس منطقی دست به دست» را بیان کردهایم.
در ادامه، تعریف انواع گراف مانند گرافهای جهتدار، گرافهای همبند، گرافهای منتظم، گرافهای کامل، گراف اویلری و … ارائه شده است. در انتهای این بخش نیز نحوه نمایش گرافها توسط ماتریس مجاورت نشان داده شده است. در سومین بخش به مبحث ساختارهای ترکیبی در ریاضیات گسسته پرداختهایم و موضوعاتی مانند جایگشت و ترکیب را با توجه به تکرار توضیح دادهایم. با مطالعه این مطلب تا انتها و حل مثالهای در نظر گرفته شده برای هر بخش، میتوانید ریاضیات گسسته را بهخوبی بیاموزید.
ریاضیات گسسته چیست؟
ریاضیات گسسته دانشی است که به مطالعه و بررسی ساختارهای ریاضی قابلشمارش، گسسته یا جداشدنی میپردازد. مثالهای رایج برای چنین ساختارهایی در ریاضیات عبارتاند از گرافها، مجموعهها و گزارههای منطقی. ساختارهای گسسته میتوانند متناهی یا نامتناهی (بینهایت) باشند و این قابلیت را دارند که بتوانیم آنها را بشماریم، ترتیبدهی کنیم و یا آنها را در مجموعههای خاص یا در نسبتهای مشخصی نسبت به هم قرار دهیم. به این ترتیب ریاضیات گسسته مجموعهای است از موضوعات مختلف مانند منطق، نظریه مجموعهها، نظریه اعداد، ترکیبیات، نظریه گراف، نظریه احتمال و جبر خطی.
اغلب آن چیزی که مسائل ریاضیات گسسته را جالب و چالشبرانگیز میکند، محدودیتهایی است که در صورت سوال وجود دارند. همچنین نکته جالب دیگر در این شاخه این است که با اینکه در ریاضیات گسسته فرمولهای مشخصی وجود دارد، اما در اکثر موارد برای حل یک نمونه سوال عملا یک فرمول کاملا منطبق بر صورت سوال وجود ندارد. همین مسئله باعث میشود برای حل مسائل این حوزه نیاز داشته باشیم دیدگاههای مختلف حل مسئله را تمرین کنیم تا با بکارگیری روشهای خلاقانه، موفق شویم پاسخ مناسب را پیدا کنیم. در ادامه مفاهیم اساسی مهمترین موضوعات در ریاضیات گسسته یعنی نظریه مجموعهها، نظریه گراف و ترکیبیات را همراه با حل مثال و به زبانی ساده توضیح میدهیم.
نظریه مجموعه ها
در «نظریه مجموعهها» (Set Theory) بهعنوان یکی از مهمترین شاخههای ریاضیات گسسته، به مطالعه اجزای گسسته یک مجموعه میپردازیم. مجموعهها میتوانند گسسته یا پیوسته باشند، و قاعدتا مطالعه ریاضیات گسسته روی مجموعههای گسسته است. در نظریه مجموعهها اینکه مجموعهها چگونه شمارش میشوند، چگونه ترتیببندی شده و یا چگونه ترکیب میشوند، مطالعه میشود.
ابتدا باید ببینیم یک مجموعه در ریاضیات گسسته به چه معنا است. مجموعه تعدادی اجزا است که در یک ویژگی با هم اشتراک دارند و بدون هیچ ترتیب یا نظم خاصی در کنار هم قرار گرفتهاند. سپس لازم است با ویژگیهای یک مجموعه مانند عدد اصلی آن و رابطهای که مجموعههای مختلف با هم دارند (مانند اجتماع و اشتراک) آشنا شویم که در بخشهای بعد به این موضوعات پرداختهایم.
کاردینالیتی یا عدد اصلی مجموعه چیست؟
«کاردینالیتی یا عدد اصلی» (Cardinality) یک مجموعه متناهی برابر است با تعداد اعضای آن مجموعه. برای مثال اگر مجموعهای به نام داشته باشیم، کاردینالیتی آن را با نشان میدهیم. با اینکه این نوع کاردینالیتی قابلشمارش نیست، اما میتوانیم کاردینالیتی مجموعهها را با هم مقایسه کنیم. برای مثال، فرض کنید دو مجموعه و داریم. برای مقایسه کاردینالیتی این دو مجموعه به شکل زیر عمل میکنیم:
- : اگر بین اعضای دو مجموعه A و B رابطه «تناظر دو طرفه» (Bijection) برقرار باشد، در این صورت کاردینالیتی این دو مجموعه با هم برابر است.
- : اگر بین اعضای دو مجموعه A و B رابطه «تناظر یک طرفه» (Injection) برقرار باشد، در این صورت کاردینالیتی این دو مجموعه با هم برابر نیست. چنانچه جهت تناظر از سمت مجموعه A به سمت مجموعه B باشد، در این صورت کاردینالیتی A از کاردینالیتی B کمتر است.
برای نمونه، فرض کنید میخواهیم کاردینالیتی مجموعه اعداد صحیح و مجموعه اعداد زوج صحیح را با هم مقایسه کنیم. در نگاه اول شاید بنظر برسد که امکان ندارد کاردینالیتی این دو مجموعه با هم برابر باشد. اما این دو مجموعه هر دو نامتناهی هستند. اگر بتوانیم تابعی را پیدا کنیم که تناظر دو طرفه بین این دو مجموعه از اعداد را نشان دهد، در این صورت برابر بودن کاردینالیتی این دو مجموعه نیز مشخص میشود. چنین تابعی وجود دارد و بهصورت زیر است:
این تابع یک تناظر دو طرفه را بین هر کدام از اعضای این دو مجموعه یا بین هر عدد صحیح و هر عدد زوج و صحیح توصیف میکند. بنابراین با یافتن چنین تابعی میتوانیم با اطمینان بگوییم که کاردینالیتی این دو مجموعه با هم برابر است.
مجموعه مکمل چیست؟
یکی از مهمترین مباحث در نظریه مجموعهها و در ریاضیات گسسته، مبحث مجموعه «مکمل» (Complement) است. برای یک مجموعه فرضی با نام ، مجموعه مکمل که با یا نشان داده میشود، شامل مجموعه عناصری است که در مجموعه وجود ندارند. مطالعه مجموعههای مکمل به ما کمک میکند تا به روشهای مفیدی جهت محاسبه کاردینالیتی مجموعههای متناهی برسیم. در بخشهای انتهایی، مثالی در این زمینه بررسی میکنیم که نشان میدهد چگونه میتوان از این مفهوم و مبحث ترکیبیات در حل مسائل ریاضیات گسسته استفاده کرد.
اجتماع و اشتراک مجموعه ها
«اجتماع و اشتراک» (Union and Intersection) نیز از جمله مهمترین مفاهیم در بخش نظریه مجموعهها و در ریاضیات گسسته هستند که جهت توصیف نحوه ترکیب مجموعهها بکار میروند. اجتماع دو مجموعه و که با نشان داده میشود، عبارت است از مجموعهای جدید که شامل تمام اعضای دو مجموعه و بدون تکرار است.
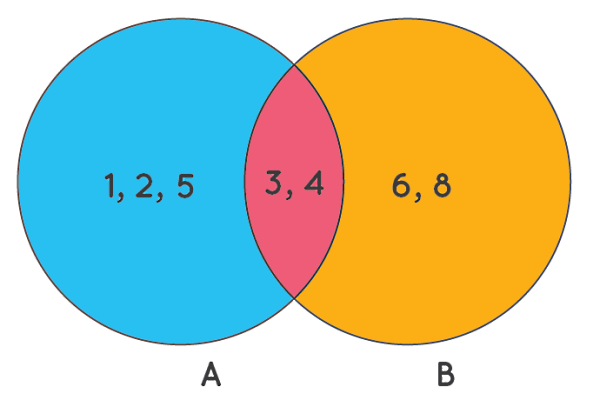
این در حالی است که اشتراک دو مجموعه و که با نمایش داده میشود، بیانگر مجموعه جدیدی است متشکل از اعضایی که بین هر دو مجموعه و مشترک هستند. در تصویر بالا اشتراک دو مجموعه و با ناحیه صورتی رنگ نشان داده شده است. اعداد و متعلق به هر دو مجموعه و هستند.
قوانین دمورگان
مفهوم دیگری که در بخش نظریه مجموعهها به آن میپردازیم، «قوانین دمورگان» (De Morgan’s Laws) است. به کمک این قوانین میتوانیم مشخصات مکملهای اجتماع و اشتراک مجموعهها را بهدست آوریم. نمایش این قوانین در قالب نمودارهایی به نام «نمودار ون» (Venn Diagram) انجام میشود و عبارتاند از:
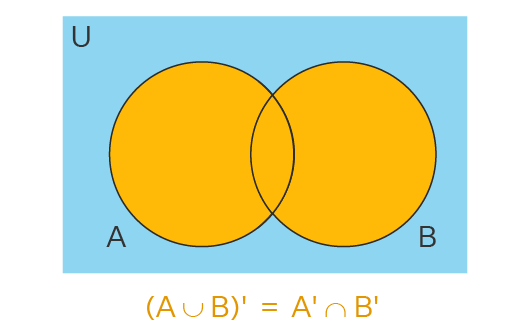
اولین قانون دمورگان بیان میکند که مجموعه مکمل حاصل از اجتماع دو مجموعه و معادل است با اشتراک مکملهای دو مجموعه و . این قانون را قانون اجتماع دمورگان هم مینامند و نمودار ون آن به شکل زیر است:
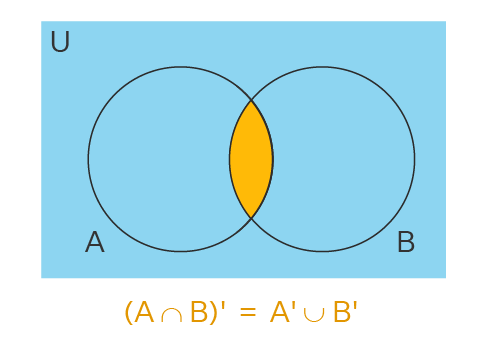
در نمودار ون بالا، ناحیه زرد رنگ نشان دهنده اجتماع دو مجموعه و است، در حالی که ناحیه آبی بیانگر مکمل اجتماع دو مجموعه و است. دومین قانون دمورگان که به قانون اشتراک معروف است، نشان میدهد مجموعه مکمل حاصل از اشتراک دو مجموعه و با اجتماع مکملهای این دو مجموعه برابر است. در نمودار ون زیر که توصیف کننده دومین قانون دمورگان است، ناحیه زرد رنگ نشان دهنده اشتراک دو مجموعه و است، در حالی که ناحیه آبی مکمل این اشتراک را نشان میدهد.
اصل شمول و عدمشمول
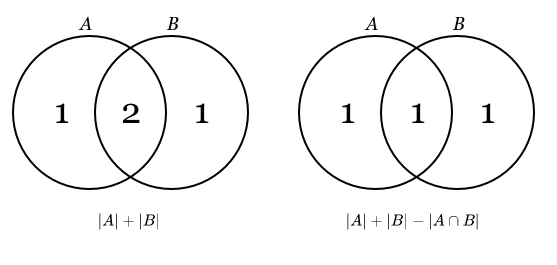
آخرین مبحث مرتبط با نظریه مجموعهها، توضیح «اصل شمول و عدمشمول» (Principle of Inclusion and Exclusion) یا همان قانون PIE است که به ما کمک میکند تا اجتماع یا اشتراک دو یا تعداد بیشتری از دو مجموعه را پیدا کنیم. در مورد دو مجموعه و ، فرمول اصل شمول و عدم شمول به شکل زیر است:
نمودار ون توصیف کننده این فرمول به شکل زیر خواهد بود:
در مواردی که بیشتر از دو مجموعه (برای مثال سه مجموعه) داریم، قانون PIE به شکل زیر خواهد شد:
حل مثال از نظریه مجموعه ها
پس از اینکه مفاهیم و تعاریف اساسی در نظریه مجموعهها از ریاضیات گسسته را تا حدی یاد گرفتیم، در این بخش میخواهیم با حل و بررسی چند مثال به شما کمک کنیم تا به این موضوع کاملا مسلط شوید.
مثال ۱
کاردینالیتی مجموعه اعداد اول کوچکتر از چقدر است؟
پاسخ
برای این منظور، ابتدا باید مجموعه اعداد اول کوچکتر از را بنویسیم که عبارتاند از:
پس از شمارش اعضای این مجموعه، کاردینالیتی یا عدد اصلی این مجموعه برابر خواهد بود با عدد .
مثال ۲
فرض کنید تمام اعداد صحیح کمتر از مدنظر ما است که نه تنها مربع کامل، بلکه مکعب کامل نیز هستند. عدد اصلی مجموعه اعدادی با این مشخصات چیست؟
پاسخ
مربع کامل بودن هر عدد به این معنا است که اگر آن را به شکل یک عدد تواندار بنویسیم، توان آن یک عدد زوج است. همچنین مکعب کامل بودن یک عدد نیز به این معنا است که اگر آن را به شکل یک عدد تواندار بنویسیم، توان این عدد همواره حاصلضربی از عدد است. بنابراین اگر بخواهیم عددی همزمان مربع و مکعب کامل باشد، باید توان آن همزمان مضربی از و یا مضربی از باشد. بنابراین تنها اعداد مثبت و صحیح کوچکتر از ، که اگر آنها را بهصورت یک عدد تواندار بازنویسی کنیم، توان آنها مضربی از عدد است، اعداد زیر هستند:
همچنین نباید فراموش کنیم که علاوهبر این دو عدد، عدد را هم داریم که همواره هم مربع کامل و هم مکعب کامل است:
بنابراین در مجموع عدد با مشخصات خواسته شده خواهیم داشت و کاردینالیتی این مجموعه برابر است با .
مثال ۳
فرض کنید شخص تنها در درصد اوقات حقیقت را میگوید، در حالی که شخص در درصد مواقع حقیقت را میگوید. این دو شخص، در چند درصد موارد ممکن است در بیان یک واقعیت با یکدیگر تناقض داشته باشند؟
پاسخ
اگر هر دو شخص در مورد آن واقعیت حقیقت را بگویند، این احتمال برابر است با:
اما اگر هر دو شخص در مورد واقعیت حقیقت را بیان نکنند، احتمال موردنظر میشود:
بنابراین میتوانیم بگوییم احتمال اینکه این دو شخص در مورد یک واقعیت همنظر باشند، برابر است با:
و به دنبال آن، احتمال اینکه این دو نفر در مورد یک موضوع با هم اختلاف نظر داشته باشند، برابر است با:
مثال ۴
کاردینالیتی مجموعه اعداد صحیح بین و که نه مضرب هستند و نه مضرب ، چقدر است؟
پاسخ
فرض کنید مجموعه مجموعه اعداد صحیح بین و و شامل تمام اعداد مضرب باشد. همچنین مجموعه مجموعه اعداد صحیح بین و و مضرب است. سوال در مورد بهدست آوردن تعداد اعضای مجموعهای به شکل زیر است:
که در آن علامتهای به معنای مجموعههای مکمل برای و است. با بکارگیری اولین قانون دمورگان، میتوانیم بهجای رابطه بالا عبارت سمت راست در رابطه زیر را محاسبه کنیم:
پس باید کاردینالیتی مجموعه بالا یا را پیدا کنیم. میدانیم تعداد عناصر مجموعه یا کاردینالیتی این مجموعه برابر است با . همچنین کاردینالیتی مجموعه نیز برابر است با . پس کاردینالیتی اشتراک این دو مجموعه معادل است با تعداد اعضای مجموعه اعداد صحیح بین و که شامل تمام اعداد مضرب باشند:
از طرفی طبق قانون PIE، عدد اصلی اجتماع این دو مجموعه برابر است با:
در نتیجه برای خواهیم داشت:
بنابراین تعداد اعداد صحیح بین و است که نه مضرب هستند و نه مضرب برابر شد با .
یادگیری ریاضیات گسسته با فرادرس برای دانشآموزان
یکی از مهمترین مباحث ریاضیات در مقطع متوسطه و بهویژه برای دانشآموزان رشته ریاضی، درس ریاضیات گسسته است. البته برخی از مباحث مطرح شده در ریاضیات گسسته از جمله نظریه مجموعهها که در بخش قبل به آن پرداختیم، محدود به کتاب ریاضیات گسسته نیست. این مبحث در سایر کتابهای ریاضی نیز توضیح داده شده است. در این بخش میخواهیم چند فیلم آموزشی از مجموعه فرادرس را به شما معرفی کنیم که در تمام آنها بخشی از مباحث مهم ریاضیات گسسته توضیح داده شده است:
- فیلم آموزش ریاضی پایه نهم فرادرس
- فیلم آموزش ریاضی پایه دهم فرادرس
- فیلم آموزش ریاضیات گسسته پایه دوازدهم فرادرس
- فیلم آموزش ریاضیات گسسته پایه دوازدهم – مرور و حل مساله فرادرس
نظریه گراف
در «نظریه گراف» (Graph Theory) که یکی از زیباترین مباحث در ریاضیات گسسته است، به مطالعه رابطه بین نقاط و خطوط میپردازیم. اهمیت گرافها در این است که به کمک آنها میتوانیم بسیاری از مسائل ریاضی در دنیای واقعی را توسط نمودار نمایش دهیم و این به درک بهتر سوال و به دنبال آن، به حل راحتتر مسئله کمک خواهد کرد. نظریه گراف برای اولین بار توسط «لئونارد اویلر» (Leonhard Euler) مطرح شد. اما پیش از اینکه نظریه گراف را شروع کنیم، پیشنهاد میکنیم اگر تمایل دارید مباحث مختلف در ریاضیات گسسته را در قالب حل تمرین فرا بگیرید، فیلم آمورش ریاضیات گسسته پایه دوازدهم – مرور و حل مساله فرادرس را مشاهده کنید که لینک آن در ادامه نیز برای شما قرار داده شده است:
هر گراف بهعنوان یک ساختار ریاضیاتی و به جهت نمایش یک تابع خاص، از طریق اتصال یک سری نقاط بکار میرود و یک رابطه جفتی بین اجزا را نشان میدهد. کاربرد گرافها نه تنها در ریاضیات گسسته، بلکه در شاخههای دیگری از علوم مانند علوم کامپیوتر، فیزیک، شیمی، زبانشناسی، زیستشناسی و … است. در نظریه گراف، یک گراف مجموعهای از اجزا را نمایش میدهد که به نوعی با هم در ارتباط هستند. اصولا این اجزا همان مفاهیم ریاضیاتی هستند که توسط «رئوس» (Vertices) یا «گرهها» (Nodes) بیان میشوند. همچنین رابطه بین هر جفت گره نیز توسط «یالها» (Edges) نمایش داده میشود.
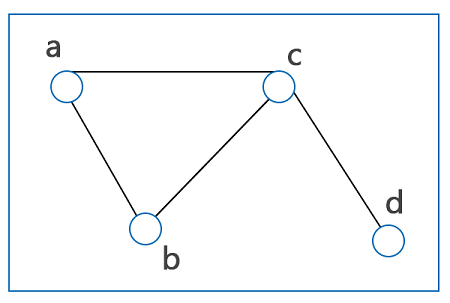
هر گراف با عبارتی به شکل تعریف میشود که در آن نشاندهنده یک مجموعه غیرصفر از راسها یا گرهها و بیانگر مجموعهای متناهی از یالها است. برای مثال، گراف بالا که با عبارت نمایش داده شده است، شامل یک مجموعه از راسها یا و مجموعهای از یالها یا بهصورت زیر است:
در ادامه این بخش قصد داریم گام به گام با تعاریف مهم و انواع گرافها در نظریه گراف آشنا شویم.
مرتبه و اندازه گراف چیست؟
گفتیم گرافها مجموعهای از راسها و یالها هستند. تعداد راسهای یک گراف یا کاردینالیتی مجموعه راسهای گراف یا مجموعه را مرتبه گراف مینامند و با نشان میدهند. همچنین تعداد یالهای هر گراف یا کاردینالیتی مجموعه را اندازه گراف نوعی مینامند و با نشان میدهند.
راسها و یالهای مجاور در گراف
هر دو راسی که توسط یک یال به هم وصل میشوند را راسهای مجاور یا همسایه مینامند. مجموعهای از تمام راسهای گراف نوعی که به راسی به نام توسط یالهای مختلف متصل میشوند، همسایگی باز راس را میسازند. اگر خود این راس را در این مجموعه قرار دهیم، همسایگی بسته راس را داریم. بهعلاوه، تعریف مشابهی برای دو یال مجاور یا همسایه هم داریم، به این صورت که اگر راسی وجود داشته باشد که هر دو یال به آن متصل باشند.
گراف مکمل یا مکمل یک گراف
مکمل گرافی مانند را با یا نشان میدهیم. گراف مکمل یا Complement Graph، گرافی است که مجموعه راسهای آن کاملا با مجموعه راسهای گراف اصلی برابر است، اما شامل تمام یالهایی است که در گراف وجود ندارند.
تفاوت درجه راس و درجه گراف
تعریف بعدی که در نظریه گراف به آن پرداختهایم، درجه یک راس یا Degree of a Vertex است. درجه یک راس یا درجه هر کدام از اعضای مجموعه در یک گراف مانند که با نماد نمایش داده میشود، معادل است با تعداد یالهایی که به آن راس میرسند. در مورد گراف بخش قبل، چهار راس داریم. پس برای هر کدام یک درجه خواهیم داشت. همانطور که گفتیم، درجه هر راس برابر است با تعداد یالهایی که به آن متصل است:
| راس | درجه | زوج یا فرد بودن راس |
| زوج | ||
| زوج | ||
| فرد | ||
| فرد |
ملاحظه کردید که در جدول بالا ستونی را برای مشخص کردن زوج یا فرد بودن درجه هر راس تعیین کردیم. زوج یا فرد بودن درجه هر راس نشان میدهد که آن راس زوج است یا فرد. پس راس زوج راسی است که تعداد یالهای متصل به آن زوج است و راس فرد نیز راسی است که تعداد یالهای رسیده به آن فرد است. حالا میخواهیم ببینم درجه گراف چگونه تعیین میشود. درجه گراف برابر است با بزرگترین درجه راسی که برای آن گراف وجود دارد. برای مثال، در مورد گرافی که مثال زدیم، درجه گراف برابر است با .
قیاس منطقی دست به دست چیست؟
تعریف بعدی در نظریه گراف و ریاضیات گسسته در مورد قانون مهمی است که در هر گراف وجود دارد. همواره مجموع درجات تمام رئوس یک گراف برابر است با دو برابر تعداد یالهای آن گراف. این قانون را «قیاس منطقی دست به دست» (The Handshaking Lemma) مینامند و بهصورت زیر نشان میدهند:
طبق این فرمول میتوانیم به این نتیجه برسیم که مجموع درجات یک گراف همواره یک عدد زوج است.
انواع گراف چیست؟
پس از اینکه با تعاریف مهم نظریه گراف در ریاضیات گسسته آشنا شدیم، در این بخش انواع گراف را معرفی میکنیم. انواع گراف عبارتاند از:
- گراف تهی
- گراف ساده
- گراف چندگانه
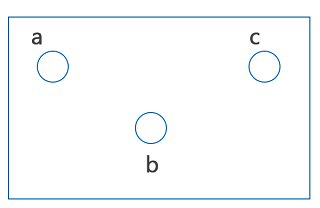
گراف تهی یا Null Graph هیچ یالی ندارد و اگر متشکل از راس باشد، آن را با نشان میدهیم:
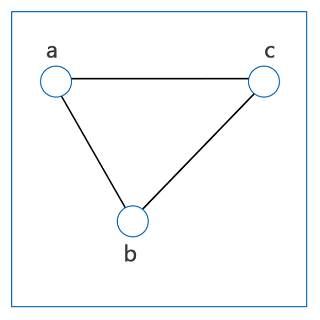
گراف ساده یا Simple Graph همانطور که از نامش مشخص است، به گرافی گفته میشود که تا حد امکان ساده باشد، یعنی دارای حلقه یا دو یا چند یال متصل به رئوس مشابه هم نباشد. برای مثال، گراف زیر یک گراف ساده محسوب میشود:
همچنین یکی دیگر از شرایط ساده بودن یک گراف این است که دارای جهت نباشد. در بخش بعد توضیح میدهیم که منظور از گراف جهتدار و بدون جهت چیست. اما بر خلاف گراف ساده، در گراف چندگانه یا Multi-Graph، حتما حداقل یک حلقه داریم. در این نوع گراف دو یا چند یال بین رئوس مشترک دیده میشوند:
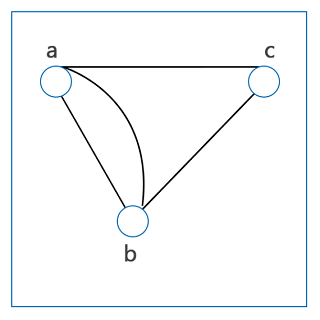
گاهی ممکن است یک یال، یک راس را مجددا به خود آن راس وصل کند. در این صورت چنین یالی طوقه نامیده میشود. تقسیمبندی گرافها بسیار گسترده است و به عوامل مختلفی بستگی دارد. در ادامه تقسیمبندیهای دیگر گرافها را معرفی خواهیم کرد.
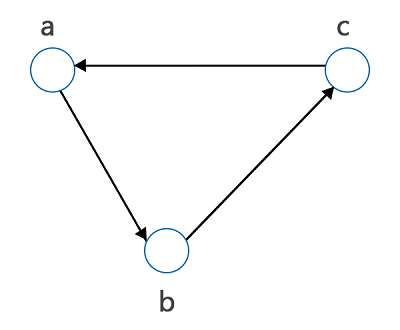
گراف جهتدار چیست؟
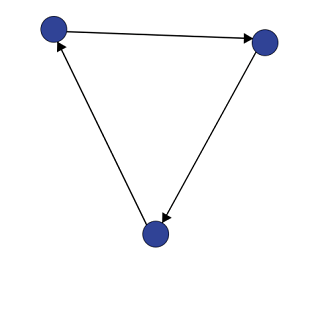
یکی دیگر از تقسیمبندیهای گرافها بر اساس جهت یالهای آن انجام میشود. گراف بدون جهت یا Undirected Graph همان گرافی است که تا اینجا توضیح دادیم. تمام گرافهایی که بالاتر دیدید، گراف بدون جهت محسوب میشوند. چون در هیچکدام از آنها یالها جهت مشخصی ندارند. اما در یک گراف جهتدار مانند تصویر زیر، ترتیب قرار گرفتن اعضای مجموعه گرهها یا رئوس مهم است و یالها جهت مشخصی دارند:
گراف همبند چیست؟
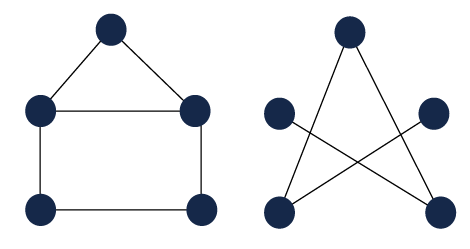
اگر بین هر دو راس از یک گراف حداقل یک مسیر وجود داشته باشد، در این صورت گراف ما همبند (پیوسته یا متصل) است. اما اگر در گراف ما حداقل دو راس وجود داشته باشند که به رئوس دیگر متصل نباشند، در این صورت آن گراف ناهمبند یا Disconnected Graph است. تصاویر زیر تفاوت این دو نوع گراف را بهخوبی نشان میدهند:

در گراف بالا بین هر دو راس انتخابی حداقل یک مسیر وجود دارد. اما در گراف ناهمبند راسهایی داریم که بینشان هیچ مسیری وجود ندارد. مثلا در شکل زیر، بین دو راس و هیچ مسیری وجود ندارد. دقت کنید در مورد یک گراف ناهمبند مانند تصویر زیر، هر کدام از دو زیرگراف جدا از هم، یک مولفه همبند از آن گراف محسوب میشوند.
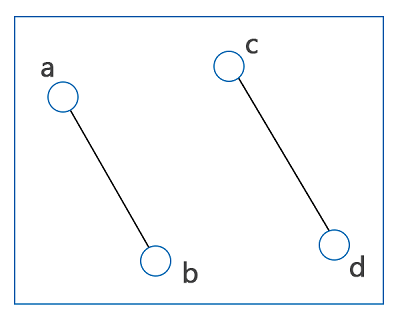
گراف منتظم چیست؟
اگر در یک گراف تمام رئوس آن درجه یکسانی داشته باشند، در این صورت این گراف در ریاضیات گسسته یک گراف منتظم یا Regular Graph نامیده میشود. بنابراین اگر گرافی مانند یک گراف منتظم با درجه است، پس درجه تمام راسهای آن نیز برابر میشود با .
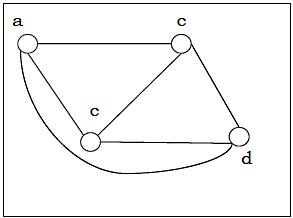
گراف کامل چیست؟
زمانی یک گراف کامل (Complete Graph) است که هر دو راس آن فقط و فقط توسط یک یال به هم متصل شوند. گراف کاملی که شامل راس باشد را با عبارت نمایش میدهیم. به این ترتیب یک گراف ساده با راس نیز میتواند یک گراف کامل باشد، اگر هر دو راس آن فقط و فقط توسط یک یال به هم وصل شده باشند. تعریف دیگری که برای گراف کامل میتوانیم ارائه دهیم به این صورت است: گرافی که هر راس آن با تمام راسهای دیگر مجاور یا همسایه باشد.

همچنین گراف کامل نوعی گراف منتظم با درجه است. در گراف بالا دو راس و توسط یک یال به هم متصل شدهاند. به همین شکل راسهای و و دو راس و نیز فقط و فقط با یک یال به هم وصل هستند. پس این گراف هم یک گراف ساده است و هم یک گراف کامل. برای یک گراف کامل با راس، میتوانیم تعداد کل یالها را با فرمول زیر محاسبه کنیم:
گراف دوری چیست؟
گرافی که شامل یک تک حلقه باشد، را گراف دوری یا Cycle Graph مینامیم. اگر گراف دوری ما از راس تشکیل شده باشد، برای نمایش آن از عبارت استفاده میکنیم. دیاگرام یک گراف دوری را در شکل زیر مشاهده میکنید:
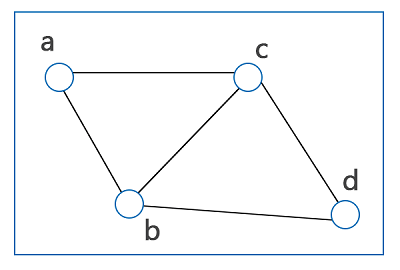
گراف مسطح چیست؟
یکی دیگر از دستهبندی گرافها در ریاضیات گسسته که بر اساس شکل آنها انجام میشود، گراف مسطح یا Planer و غیرمسطح است. تمام اجزای یک گراف مسطح مانند در یک صفحه قرار دارند، بدون اینکه یالی از آن عمود بر صفحه گراف قرار بگیرد. همچنین یالهای یگ گراف مسطح یکدیگر را قطع نمیکنند. اما در مورد گراف غیرمسطح، میتوانیم اجزایی از گراف را پیدا کنیم که در یک صفحه قرار ندارند.
اما گرافی که در شکل زیر ملاحظه میکنید، مسطح نیست. در این گراف یالهایی داریم که یکدیگر را قطع کرده و از هم عبور کردهاند:
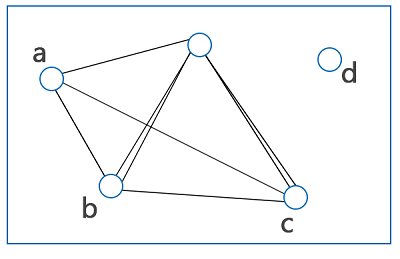
گراف دو بخشی چیست؟
اگر در مورد گرافی بتوانیم مجموعه راسها را به دو مجموعه مانند و تقسیم کنیم، به گونهای که هر یال از گراف راسی از مجموعه را به راسی از مجموعه متصل کند، در این صورت میگوییم یک گراف دو بخشی یا Bipartite Graph داریم. دقت کنید در این نوع گراف بین هر دو راس از مجموعه یا بین هر دو راس از مجموعه هیچ یالی وجود ندارد.
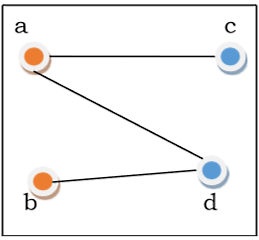
پس از اینکه یاد گرفتیم تعریف گراف دو بخشی در ریاضیات گسسته چیست، با توجه به تعریف گراف کامل از قبل، میتوانیم گراف دو بخشی کامل را نیز تعریف کنیم. گراف دو بخشی کامل به گرافی گفته میشود که در آن هر راس در اولین مجموعه از راسها یا به تمام راسها در مجموعه دوم از راسها یا متصل میشود. این نوع گراف را با نشان میدهیم که در آن گراف شامل راس در اولین مجموعه و راس در دومین مجموعه است. به تفاوت گراف دو بخشی و گراف دو بخشی کامل در تصویر بالا و پایین دقت کنید:
گراف اویلری چیست؟
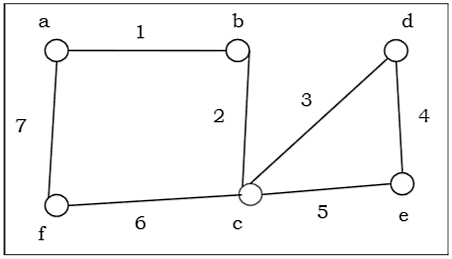
به این ترتیب یک گراف همبند زمانی یک گراف اویلری هم محسوب میشود که فقط و فقط درجه تمام راسهای آن زوج باشد. برای مثال، گراف شکل بالا یک گراف اویلری است، چون مسیر تمام یالهای این گراف را پوشش داده است. همچنین درجه تمام راسهای این گراف نیز عدد زوجی است.
گراف همیلتونی چیست؟
اگر گراف همبند ما دارای یک حلقه باشد، به گونهای که این حلقه تمام راسهای گراف را شامل شود، در این صورت این گراف همبند یا این حلقه را گراف همیلتونی (گراف هامیلتونی) یا Hamiltonian Graph مینامیم. همچنین مسیر همیلتونی در یک گراف همیلتونی به مسیری گفته میشود که از هر راس فقط و فقط یک مرتبه عبور میکند. در ادامه این بخش دو قضیه مهم را معرفی میکنیم که توضیح میدهند چگونه با توجه به ویژگیهای یک گراف میتوانیم در مورد همیلتونی بودن آن نتیجهگیری کنیم.
قضیه دیراک
یکی از مهمترین قضایایی که در مورد گرافهای همیلتونی وجود دارد، «قضیه دیراک» (Dirac’s Theorem) است. قضیه دیراک بیان میکند که اگر گراف یک گراف ساده و شامل راس باشد، به گونهای که همواره ، در این صورت اگر درجه هر راس بزرگتر یا مساوی با باشد، گراف یک گراف همیلتونی خواهد بود.
قضیه اوره
قضیه اوره یا Ore’s Theorem بیان میکند که اگر گراف یک گراف ساده و شامل راس باشد، به گونهای که همواره ، در این صورت اگر برای هر جفت از راسهای غیرمجاور و برقرار باشد، در این صورت گراف یک گراف همیلتونی خواهد بود.
نحوه نمایش گرافها و ماتریس مجاورت
تا اینجا با تعاریف و انواع گراف در ریاضیات گسسته آشنا شدید. مبحث بعدی نحوه نمایش گرافها است. برای نمایش گرافها میتوانیم به دو روش عمل کنیم:
- استفاده از ماتریس مجاورت یا Adjacency Matrix
- استفاده از لیست مجاورت یا Adjacency List
ماتریس مجاورت که با نمایش داده میشود، عبارت است از یک آرایه دو بعدی با ابعاد که در آن برابر است با تعداد راسهای یک گراف بدون جهت. اگر از مجموعه تا یالی وجود داشته باشد، در این صورت درایههای متناظر که بهصورت زیر نمایش داده میشوند، دارای مقدار واحد خواهند بود:
در غیر این صورت، این مقادیر همواره برابر با صفر هستند. همچنین برای یک گراف جهتدار نیز، اگر از مجموعه به سمت مجموعه یالی وجود داشته باشد، در این صورت فقط مقدار درایه زیر برابر با واحد است:
و در صورت نبودن چنین یالی، این مقدار نیز برابر با صفر خواهد بود. پس باید به تفاوت درایهها در گراف جهتدار و بدون جهت توجه کنید. برای مثال فرض کنید گراف بدون جهتی به شکل زیر داریم و میخواهیم ماتریس مجاورت آن را تعیین کنیم:

ابتدا راس را در نظر میگیریم و بررسی میکنیم که از این راس چند یال به هر کدام از راسهای دیگر متصل شده است. طبق تصویر گراف، راس به رئوس و متصل است. اما به راس متصل نیست. به همین ترتیب، اگر راس را در نظر بگیریم، این راس جز به خودش، به تمام راسهای دیگر توسط یک یال وصل شده است. پس در نهایت ماتریس مجاورت ما برای این گراف بدون جهت به شکل زیر خواهد شد:
همانطور که ملاحظه میکنید، هیچ راسی به خودش توسط یک یال متصل نیست. به همین علت تمام درایههای روی قطر اصلی برای این ماتریس مجاورت برابر با صفر هستند. در مثالی دیگر، ماتریس مجاورت را برای گراف جهتداری به شکل زیر تعیین میکنیم تا بهتر متوجه تفاوتهای ماتریسهای مجاورت برای این دو نوع گراف شوید:
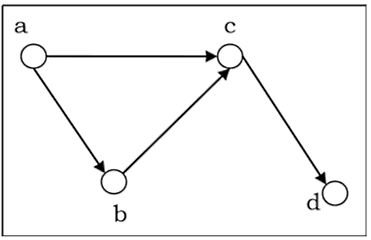
در این ماتریس از راس به سمت راسهای و دو یال جهتدار داریم. شکل ماتریس کاملا مشابه ماتریس بدون جهت است. اما تفاوت واضح این نوع ماتریس با ماتریس بدون جهت در این است که اگر بخواهیم یالی که از به سمت متصل شده است را در نظر بگیریم، چنین یالی در این ماتریس وجود ندارد. در ماتریس جهتدار زمانی یال را در نظر میگیریم که جهت درایه ماتریس مجاورت آن کاملا با جهت یال مشابه باشد. پس با اینکه این یال در ماتریس قبل مخالف صفر بود، در این ماتریس برابر با صفر است. با در نظر گرفتن این نکته، برای ماتریس مجاورت گراف جهتدار داده شده خواهیم داشت:
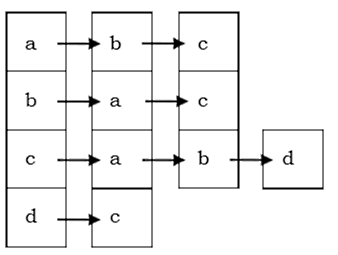
لیست مجاورت چیست؟
گفتیم روش دیگر نمایش گرافها در ریاضیات گسسته استفاده از لیست مجاورت است. در یک لیست مجاورت، آرایهای به شکل از لیستهای متصل شده برای نمایش گراف با تعداد راس بکار میرود. همچنین عبارت نیز به جهت نمایش لیست متصل شده به راسهای مجاور امین راس استفاده میشود. نمونهای از لیست مجاورت گراف بدون جهتی به شکل گراف بدون جهت در بخش قبل به شکل زیر خواهد بود:
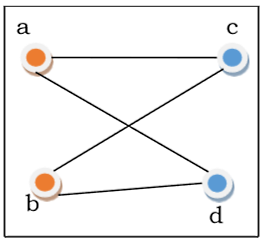
یکریختی گرافها
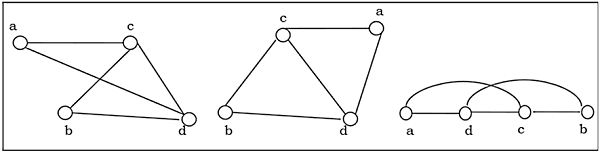
فرض کنید دو گراف مانند و داریم که شامل تعداد راسهای مشابهی هستند و نحوه اتصال راسهای آنها به هم شبیه هم است. این دو گراف را یکریخت یا Isomorphic مینامیم و این رابطه را با عبارت نشان میدهیم. به این ترتیب زمانی میتوانیم بگوییم دو گراف یکریخت محسوب نمیشوند که یکی از شرایط زیر برقرار باشد:
- تعداد مولفههای متصل شده به هم متفاوت است.
- کاردینالیتی مجموعه راسها متفاوت است.
- کاردینالیتی مجموعه یالها متفاوت است.
- توالی درجات متفاوت است.
برای مثال، گرافهای زیر یکریخت هستند:
همریختی گرافها
همریختی یا Homomorphism از گراف به گراف معادل است با نگاشتی به صورت ، به گونهای که برای هر که عضوی از است، همواره عضوی از است. همریختی راسهای مجاور گراف را به رئوس مجاور گراف نگاشت یا متناظر میکند. ویژگیهای همریختی را میتوان به شکل زیر بیان کرد:
- همریختی دو گراف میتواند با یکریختی آنها معادل باشد، اگر تناظر بین دو گراف دو طرفه باشد.
- همریختی همواره یالها و اتصالهای یک گراف را حفظ میکند.
- ترکیبات همریختی نیز همریخت محسوب میشود.
توضیحات ما در مورد نظریه گراف در این بخش به پایان میرسد. اما با توجه به گستردگی این مبحث، پیشنهاد میکنیم اگر تمایل دارید با مبانی مبحث گراف در علوم کامپیوتر آشنا شوید و مروری داشته باشید به آنچه که در این نوشته در مورد گراف آموختید، مطلب «گراف در علوم کامپیوتر – راهنمای مقدماتی» از مجله فرادرس را مطالعه کنید.
حل مثال و تمرین از نظریه گراف
در این قسمت روند حل چند مثال و تمرین را با استفاده از تعاریف و مفاهیمی که توضیح دادیم، بررسی میکنیم. حل این سوالات به شما کمک میکند تا یاد بگیرید چگونه و در چه مواردی از نظریه گراف برای حل مسائل ریاضیات گسسته استفاده کنید.
مثال ۱
فرض کنید شخص در حال دست تکان دادن برای یکدیگر هستند، به گونهای که هر شخص برای تمام افراد دیگر دست تکان میدهد. دست تکان دادن در این موقعیت چند مرتبه اتفاق میافتد؟
پاسخ
میخواهیم با کاربرد نظریه گراف این سوال ریاضیات گسسته را حل کنیم. پرسشی که در اینجا مطرح شده، در حقیقت تعداد یالهای گراف متناظر با این موقعیت را میخواهد. با توجه به اینکه تعداد راسهای این گراف مشخص و معادل با تعداد اشخاص یعنی است، پس هر شخص یا هر راس، برای نفر دیگر دست تکان میدهد و درجه هر راس برابر است با . چون راس داریم، مجموع درجات این گراف برابر میشود با:
در اینجا میتوانیم برای محاسبه تعداد یالها از قانون قیاس منطقی دست به دست استفاده کنیم که فرمول آن به شکل زیر است:
مثال ۲
آیا ممکن است در یک گروه نفری، هر شخص دقیقا با نفر دیگر در همین گروه دوست باشد؟ همچنین بررسی کنید که آیا ممکن است در چنین گروهی هر شخص دقیقا با دیگر در همین گروه دوست باشد:
پاسخ
بله ممکن است. با نظریه گراف این پاسخ را توضیح میدهیم. اگر این پنج نفر را پنج راس یک گراف دوری به شکل در نظر بگیریم، در این صورت هر راس به دو راس دیگر توسط یک یال متصل شده است. در این صورت میتوانیم بگوییم در این گروه هر شخص دقیقا با دو نفر دیگر دوست است.
اما برای برقرار بودن شرایط دوم در صورت سوال، باید گرافی داشته باشیم که دارای تعداد فردی از راسهایی با درجه فرد (درجه ) است و چنین چیزی ممکن نیست. حاصلضرب این دو عدد فرد، یک عدد فرد میشود. در حالی که میدانیم همواره مجموع درجات یک گراف عدد زوجی است.
مثال ۳
آیا ممکن است دو گراف متفاوت (نایکریخت) دارای تعداد برابری از رئوس و یال باشند؟ اگر درجات راسها در این دو گراف یکسان باشد، چه؟ برای مثال هر دو گراف دارای راسهایی با درجات باشند:
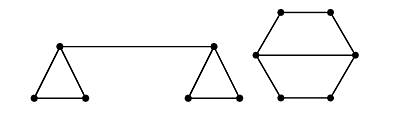
پاسخ
پاسخ هر دو سوال بالا مثبت است. برای مثال، دو گراف زیر را در نظر بگیرید که هر دو دارای تعداد راس، یال و درجات برابری برای این راس بهصورت هستند. طبق ویژگیهایی که برای یکریخت نبودن گرافها بیان شد، این دو گراف یکریخت نیستند، چون توالی درجات آنها با هم فرق دارد. با این وجود شرایط گفته شده در صورت سوال برای هر دو مشابه هم است.
تمرین
گراف شامل دو مجموعه بهصورت زیر است و در ادامه، شکل گراف نیز قرار داده شده است. کدام گزینه در مورد این دو گراف صحیح است؟
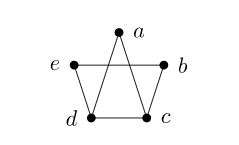
این دو گراف با هم معادل و یکریخت هستند.
این دو گراف با هم معادل نیستند، اما یکریخت محسوب میشوند.
این دو گراف با هم معادل و یکریخت نیستند.
این دو گراف با هم معادل هستند، اما یکریخت محسوب نمیشوند.
گزینه دوم درست است. گرافهای و با هم معادل نیستند، چون برای مثال گراف دارای یالی بهصورت است که در گراف چنین یالی را مشاهده نمیکنید.
اما میتوانیم این دو گراف را یکریخت در نظر بگیریم. کاردینالیتی مجموعه راسها و یالها برای هر دو گراف برابر است. تعداد راسهای هر دو گراف برابر است با و تعداد یالهای هر دو نیز برابر است با . همچنین اگر گراف را رسم کنید، پس از بررسی خواهید دید که توالی درجات این دو گراف نیز مانند هم است.
ترکیبیات (شمارش) در ریاضیات گسسته
«ترکیبیات، ریاضیات انتخاب یا آنالیز ترکیبی» (Combinatorics) ریاضیات شمارش و ترتیبدهی در ریاضیات گسسته است. با اینکه شاید با بیان کلمه شمارش بنظر برسد اغلب انسانها بهراحتی میتوانند بشمارند، اما تفاوت ترکیبیات در این است که در این بخش از ریاضیات گسسته برای انجام شمارش از عملگرهای ریاضیاتی استفاده میشود، بهویژه در مواردی که تعداد اجزا آنقدر زیاد است که کاربرد روش شمارش مرسوم و عادی امکانپذیر نیست.
ترکیبیات بهویژه در علوم کامپیوتر بسیار پرکاربرد است. برای مثال، یکی از اهداف توسعه روشهای ترکیبیاتی این است که بتوانند تخمین بزنند یک الگوریتم کامپیوتری به چه تعداد عملگر نیاز خواهد داشت. همچنین مطالعه ترکیبیات در بررسی احتمال گسسته نیز مفید است. بهعلاوه از روشهای ترکیبیاتی میتوانیم برای شمارش خروجیهای ممکن در یک آزمایش احتمال یکنواخت نیز استفاده کنیم.
در ترکیبیات بیشتر با این موضوع سروکار داریم که اجزای مختلف چگونه و با چه ترتیبی در کنار هم چیده شدهاند. مفهوم مهمی که در اینجا مطرح است این است که هر گونه روش قرارگیری اجزا در کنار هم به معنای گروه شدن آنها است. قوانین پایه ترکیبیات در مورد قرار گرفتن اجزا در کنار هم عبارتاند از قانون ضرب و قانون جمع. این قوانین تعیین میکنند که چگونه با کاربرد عملگرهای ضرب و جمع بتوانیم این گروهها یا روشهای مختلف قرار گرفتن اجزا در کنار هم را بشماریم.
به مثال زیر که نحوه استفاده از قانون ضرب را نشان میدهد، توجه کنید:
در یک اغذیه فروشی محلی، برای دریافت یک ساندویچ انتخابهای زیر وجود دارد:
- انواع نان: سفید، چاودار، گندمی
- انواع پنیر: سوئیسی، چدار، هاوارتی، پروولون
- انواع گوشت: رستبیف، بوقلمون، ژامبون، گوشت گاو، گوشت مرغ
میخواهیم ببینیم اگر مشتری دقیقا یک آیتم از هر کدام از گزینههای بالا را انتخاب کند، چند ساندویچ ممکن میتوان تهیه کرد. در این اغذیه فروشی، سه نوع نان، چهار نوع پنیر و پنج نوع گوشت داریم. پس اگر مشتری حق انتخاب یک آیتم از هر کدام از این گروهها را داشته باشد، با بکارگیری قانون ضرب در ترکیبیات و محاسبه حاصلضرب این سه عدد خواهیم داشت:
بنابراین تعداد ساندویچهای ممکن برابر شد با عدد. در ترکیبیات با دو مفهوم مهم به نامهای «جایگشت و ترکیب» سروکار داریم که در ادامه آنها را معرفی خواهیم کرد. همچنین مباحث پیچیدهتر در ترکیبیات عبارتاند از :
- «پریش» (Derangement): نوعی جایگشت است که در آن هیچ جزئی در مکان اصلی خود قرار ندارد.
- «طی کردن شبکه مستطیلی» (Rectangular Grid Walks): به معنای تعیین تعداد راههایی است که میتوان یک شبکه مستطیلی را طی کرد.
- «توزیع اشیا در سطلها» (Distribution of Objects into Bins): تعیین اینکه چگونه میتوان اشیا را در سطلها گروهبندی کرد.
جایگشت چیست؟
یکی از مهمترین و جالبترین ترتیبهای قرارگیری اجزا در ریاضیات گسسته، «جایگشت» (Permutation) است. در جایگشت ترتیب قرارگیری اجزا بر اساس نظم مشخصی است. برای مثال، فرض کنید در ابتدای یک مسابقه اسبدوانی، تعداد اسب در مزرعه آماده شروع مسابقه هستند. میدانیم که تنها عدد از این اسبها میتوانند در انتهای مسابقه بهعنوان برنده اعلام شوند و اینکه به چه ترتیبی در این جایگاه قرار بگیرند، قطعا مهم است.
اگر بدانیم اسبها در انتهای مسابقه در جایگاههایی به نام و و قرار میگیرند، نکته مهم این است که کدام یک از این جایگاهها جایگاه اول، کدام دوم و کدام سوم است. در حقیقت ترتیب با ترتیب متفاوت است. حالا با کمک گرفتن از مفهوم جایگشت در ریاضیات گسسته میتوانیم بررسی کنیم که چند حالت ممکن برای این اسبها وجود دارد تا جایگاههای اول تا سوم را بگیرند.
برای گرفتن جایگاه اول، اسب یا حالت وجود دارد. به محض پر شدن جایگاه اول، برای جایگاه دوم اسب ممکن یا حالت خواهیم داشت. به همین ترتیب، بلافاصله پس از اشغال دومین جایگاه، برای گرفتن سومین جایگاه اسب خواهیم داشت. پس طبق قانون ضرب برای پر شدن سه جایگاه اول خواهیم داشت:
در این مثال هم مانند مثال قبل از قانون ضرب استفاده کردیم. اما به تفاوت نحوه ضرب کردن اعداد با هم در این مثال و کم شدن تعداد حالتهای ممکن برای دو جایگاه بعدی دقت کنید. همچنین میتوانیم بررسی جایگشت را به دو حالت تقسیم کنیم، زمانی که تکرار مجاز است و زمانی که تکرار مجاز نیست. برای مثال اگر مسئله حالتهای مختلف برای کلمه رمز یک صندوق را در نظر بگیرید، در این مسئله تکرار مجاز است. مثلا عدد میتواند یکی از گزینههای ممکن باشد. اما در مسابقه بالا تکرار مجاز نیست، یعنی امکان ندارد اسبی هم در رتبه دوم قرار بگیرد و هم در رتبه اول. در ادامه تفاوت این دو نوع جایگشت و فرمولهای توصیفکننده هر کدام را توضیح خواهیم داد.
فرمول جایگشت با تکرار چیست؟
در ادامه یادگیری ترکیبیات در ریاضیات گسسته، تا اینجا با مفهوم جایگشت آشنا شدیم. در این بخش توضیح میدهیم اگر تکرار در جایگشت مهم باشد، فرمول محاسبه آن به چه صورت خواهد بود. اگر مسئلهای حالت مختلف داشته باشد، پس هر بار تعداد انتخاب خواهیم داشت. حالا اگر تعداد عدد از این حالت را انتخاب کنیم، جایگشت برابر است با:
یعنی سه مرتبه در خودش ضرب میشود. بنابراین در حالت کلی انتخاب از چیزی که دارای حالت مختلف است، به ما جایگشتی به شکل زیر میدهد:
( مرتبه)
این عبارت به این معنا است که در این نوع جایگشت، حالت برای اولین انتخاب، حالت برای دومین انتخاب، و به همین ترتیب حالت برای امین انتخاب خواهیم داشت. بهتر است عبارت بالا را به شکل یک عدد تواندار نشان دهیم:
= ( مرتبه)
پس در فرمول جایگشت با تکرار بهصورت ، ترتیب مهم و تکرار مجاز است.

برای مثال، فرض کنید میخواهیم جایگشتهای ممکن برای انتخاب رمز سه رقمی یک صندوق را پیدا کنیم. میدانیم در هر جایگاه عددی حالت ( رقم) ممکن میتوانیم داشته باشیم که عبارتاند از:
چون رمز صندوق سه رقمی است، پس در هر انتخاب عدد را باید برگزینیم. به این ترتیب جایگشتهای ما برابر میشوند با:
چون در این انتخاب مجازیم که عدد تکراری هم انتخاب کنیم، پس این مثال یک مسئله جایگشت با تکرار محسوب میشود.
فرمول جایگشت بدون تکرار چیست؟
در جایگشت بدون تکرار، باید در هر بار شمارش تعداد انتخابهای ممکن را کاهش دهیم. مثال مسابقه اسبدوانی نمونهای از یک مسئله جایگشت بدون تکرار است. پس بدون تکرار، انتخابهای ما در هر مرحله از محاسبه جایگشت کاهش خواهد یافت. بهترین روشی که میتوانیم بهصورت ریاضیاتی و خودکار این کاهش را در محاسبات خود وارد کنیم این است که از تابع فاکتوریل با نماد استفاده کنیم.
تابع فاکتوریل هر عدد به معنای این است که آن عدد را با هر بار کاهش به اندازه یک واحد در خودش ضرب کنیم تا زمانی که به عدد برسیم. برای مثال فاکتوریلهای زیر را ببینید:
همچنین توافق شده است که همواره . فرض کنید میخواهیم ببینیم جایگشتهای توپ بیلیارد به چه صورتی محاسبه میشود. در این انتخاب، اگر برای مثال توپ شماره را انتخاب کنیم، دیگر امکان انتخاب این توپ به صورت مجدد وجود ندارد. پس در اینجا یک مسئله جایگشت بدون تکرار داریم. برای اولین انتخاب ما امکان مختلف وجود دارد، برای دومین انتخاب امکان و به همین ترتیب تا انتها، در هر انتخاب یک واحد کم میشود.

پس جایگشت بالا را به شکل زیر میتوانیم بنویسیم:
این عبارت معادل است با . اما ممکن است فقط بخواهیم سه انتخاب داشته باشیم. در این صورت جایگشت برابر است با:
بنابراین برای اینکه از توپ بیلیارد توپ را انتخاب کنیم، حالت مختلف وجود دارد. میتوانیم معادل ریاضیاتی این توصیف را در جایگشت بدون تکرار با عبارت زیر و بر حسب تابع فاکتوریل نشان دهیم:
در حقیقت با حذف و ساده شدن در صورت و مخرج، به پاسخ بالا میرسیم. پس فرمول جایگشت بدون تکرار برای انتخاب از که با نماد نشان داده میشود، عبارت است از:
پس در فرمول جایگشت بدون تکرار بهصورت ، ترتیب مهم و تکرار مجاز نیست. در بخش بعد توضیح میدهیم که اگر در مسئلهای ترتیب مهم نباشد، باید بهجای جایگشت از فرمول ترکیب برای بررسی آن استفاده کنیم.
ترکیب چیست؟
یکی دیگر از انواع ترتیب قرار گرفتن اجزای مختلف در ریاضیات گسسته، «ترکیب» (Combination) است. ترکیب و جایگشت مفاهیمی هستند که به نوعی در مقابل هم قرار میگیرند، به این معنا که در ترکیب ترتیب قرار گرفتن اجزا مهم نیست. اگر دقت کنید، در محاوره عادی هم زمانی که میگوییم چند جزء مختلف مانند چند میوه برای تهیه سالاد با هم ترکیب شدهاند، ترتیب اجزا مهم نیست. مثلا مهم نیست که ترتیب اضافه شده میوهها به سالاد موز، سیب و انگور بوده است یا انگور، سیب و موز.
بنابراین با توجه به توضیحات بخش قبل، میتوانیم جایگشت را نوعی ترکیب در نظر بگیریم که در آن نظم و ترتیب مهم است. برای اینکه با مفهوم ترکیب و تفاوت آن با جایگشت بیشتر آشنا شوید، به مثال زیر توجه کنید. فرض کنید بازیکن متمایز فوتبال داریم که میخواهند یک مسابقه را برگزار کنند. این مسابقه دو کاپیتان با نامهای و دارد که به نوبت در حال انتخاب بازیکن برای تیمهای خود هستند. میخواهیم با کمک گرفتن از مفهوم ترکیب در ریاضیات گسسته، ببینیم چند حالت ممکن برای تقسیمبندی این تیمها وجود دارد.
با توجه به اینکه تعداد کل بازیکنان برابر با است، با شروع یارکشی توسط دو کاپیتان، باید عدد از تعداد کل بازیکنان کم شود، چون نفر از این بازیکن کاپیتانها هستند. پس در شروع انتخاب بازیکن برای هر تیم، بازیکن باقی مانده است. همچنین چون دو تیم داریم، پس هر تیم بازیکن خواهد داشت. اگر از قانون ضرب مانند مثال جایگشت استفاده کنیم، برای تعداد انتخابهای ممکن خواهیم داشت:
اما نتیجه این محاسبه شامل بازیکنان مشابه نیز هست. در حالی که میدانیم این امکان وجود ندارد که یک بازیکن متعلق به هر دو تیم باشد. بنابراین لازم است این عدد را به عدد دیگری تقسیم کنیم که بیانگر تعداد حالتهایی است که بازیکنان مشابه میتوانند مرتب شوند:
با تقسیم این دو عدد بر هم خواهیم داشت:
پس تقسیمبندی اعضای این دو تیم به حالت مختلف ممکن است انجام شود. در ترکیب هم لازم است ببینیم آیا تکرار در مسئله ما مجاز است یا خیر. برای مثال وقتی که از داخل جیب شلوار خود چند سکه بیرون میآورید، ممکن است سکه تکراری هم انتخاب کنید. در این مثال ترتیب مهم نیست و تکرار هم داریم. پس یک ترکیب با تکرار است. اما در انتخاب شمارهها هنگام انجام قرعهکشی، تکرار مجاز نیست. هر شمارهای که انتخاب میشود، برای دور بعدی قرعهکشی حذف میشود.
فرمول ترکیب با تکرار چیست؟
فرض کنید پنج نوع بستنی موجود است، موزی ()، شکلاتی ()، لیمویی ()، توتفرنگی () و وانیلی () و شما حق دارید تنها سه اسکوپ بستنی بردارید. میخواهیم با روشهای ترکیبیات در ریاضیات گسسته این مسئله را بررسی کنیم و ببینیم به چند روش میتوان این سه اسکوپ بستنی را انتخاب کرد. چون ترتیب اهمیت ندارد، پس مسئله محاسبه ترکیب است و چون تکرار هم مجاز است، پس یک ترکیب با تکرار داریم.

برای مثال، ممکن است دوست داشته باشید هر سه اسکوپ را شکلاتی بردارید ()، یا سه طعم متفاوت بهصورت انتخاب کنید. پس حالت ممکن داریم که فقط میتوانیم انتخاب از بین آنها داشته باشیم. روند رسیدن به فرمول در این حالت کمی پیچیده است. بنابراین از توضیح آن در این بخش صرفنظر میکنیم. فرمول مناسب برای این نوع ترکیب به شکل زیر است:
بنابراین در فرمول ترکیب با تکرار بهصورت ، با اینکه ترتیب مهم نیست اما تکرار مجاز است. با این فرمول میتوانیم مسئله انتخاب بستنی را با و به شکل زیر حل کنیم:
فرمول ترکیب بدون تکرار چیست؟
مثالی که در بخش قبل برای انتخاب اعضای تیم توسط کاپیتانها حل شد، نمونه یک مسئله ترکیب بدون تکرار است. گفتیم با توجه به حضور دو کاپیتان، بازیکن برای انتخاب شدن در تیمها باقی میمانند که هر کاپیتان بازیکن را انتخاب خواهد کرد. با اینکه شاید برای خود بازیکنان مهم باشد که با چه ترتیبی توسط کاپیتان انتخاب میشوند (برای مثال بهعنوان اولین انتخاب نام آنها ذکر میشود یا پنجمین!)، اما واقعیت این است که در حل این مسئله و در ترکیببندی تیم این نکته اهمیتی ندارد. به همین دلیل است که میگوییم در ترکیب، ترتیب یا نظم اهمیت ندارد. در ترکیب بدون تکرار مرسوم است محاسبات بالا را به شکل زیر بنویسیم:
این عبارت به معنای ترکیب از است. بهطور کلی ترکیب از بهصورت نمایش داده میشود و روش محاسبه آن بهصورت زیر خواهد بود:
پس در فرمول ترکیب بدون تکرار بهصورت ، علاوهبر اینکه ترتیب مهم نیست، تکرار هم مجاز نیست. در این مثال و است. پس خواهیم داشت:
همانطور که در بخش جایگشت توضیح دادیم، محاسبه فاکتوریل با علامت بهصورت زیر انجام خواهد شد:
ملاحظه میکنید که نتیجه این محاسبه با پاسخ قبل یکسان شد. بنابراین راه برای اینکه کاپیتان تیم بتواند تیم خود را بچیند، وجود دارد. تیم کایپتان تیم نیز بر اساس باقیمانده بازیکنان در هر حالت چیده خواهد شد.
حل مثال و تمرین از جایگشت و ترکیب
پس از اینکه با تعاریف و تفاوتهای جایگشت و ترکیب در مبحث ترکیبیات از ریاضیات گسسته آشنا شدید، در این قسمت چند مثال حل میکنیم تا به فرمولها و روش حل مسائل در این بخش کاملا مسلط شوید.
مثال ۱
به چند روش ممکن است در مسابقهای جایگاه اول و دوم به نفر اختصاص داده شود؟
پاسخ
در کسب جایگاه اول و دوم در مسابقه، ترتیب مهم است. پس مسئله ما محاسبه جایگشت است، نه ترکیب. نکته مهم بعدی این است که بدانیم آیا تکرار مجاز است یا خیر. در انتخاب نفرات، تکرار مجاز نیست، یعنی امکان ندارد یک نفر هم در جایگاه اول قرار بگیرد و هم در جایگاه دوم. بنابراین مسئله ما بررسی جایگشت بدون تکرار است و باید از فرمول زیر برای محاسبه جایگشت استفاده شود:
مثال ۲
جایگشتهای ممکن برای عدد دیجیتالی مختلف که از بین تا انتخاب میشوند، کدام است؟
پاسخ
در صورت سوال اشاره شده که باید جایگشت را بهدست آوریم. همچنین از ما انتخاب سه عدد مختلف خواسته شده است، پس تکرار مجاز نیست. فرمول جایگشت بدون تکرار را مینویسیم و محاسبات را انجام میدهیم:
دقت کنید که است:
مثال ۳
چند کمیته مختلف نفره با انتخاب از بین نفر، میتوان تشکیل داد؟
پاسخ
دقت کنید در انتخاب افراد، ترتیب اهمیتی ندارد. پس باید از فرمولهای ترکیب استفاده کنیم. مسئله بعدی این است که ببینیم آیا تکرار مجاز است یا خیر، که طبق صورت سوال و اینکه ذکر شده کمیتهای از افراد مختلف میخواهیم، پس تکرار هم مجاز نیست. بابراین فرمول ترکیب بدون تکرار را بکار میبریم:
مثال ۴
فرض کنید شخصی مدیریت یک تیم را به عهده دارد و میخواهد نفر را بهعنوان اعضای شورا انتخاب کند. این شخص باید انتخاب خود را از بین نفر متقاضی برای این کار انجام دهد که میدانیم نام سه نفر از این نفر، تامی، جک و مایکل است. میخواهیم ببینیم این فرد به چند روش میتواند اعضای شورا را انتخاب کند، به گونهای که حداقل یکی از سه شخص تامی، جک و مایکل در این شورا باشند:
پاسخ
به این منظور، در اولین قدم بهتر است تعداد حالتهایی که ممکن است هر سه نفری بهصورت تصادفی برای این موقعیت انتخاب شوند را پیدا کنیم. قاعدتا تکرار نداریم و ترتیب هم مهم نیست. پس باید ترکیب از را حساب کنیم:
در مرحله بعدی میتوانیم تعداد حالتهایی که ممکن است هر فردی بهجز سه نفر بالا انتخاب شوند، را محاسبه کنیم. در نتیجه لازم است از کل نفر اعضا، واحد کم شود تا ترکیب از باقیمانده افراد متقاضی که نفر هستند، بهدست آید:
بنابراین با حساب کردن اختلاف دو عددی که بالاتر بهدست آمد، میتوانیم تعداد دفعاتی که افراد مختلف را انتخاب میکنیم، به گونهای که حداقل یکی از سه نفر موردنظر گفته شده در بین آنها باشد را پیدا کردهایم:
دقت کنید برای حل این سوال از مفهوم مجموعه مکمل که در ابتدای مطلب آن را توضیح دادیم، استفاده شده است.
تمرین ۱
فرض کنید میدانیم سارا مسئول یک کمیته است. میخواهیم ببینیم به چند روش میتوان یک کمیته نفره را با حضور سارا از بین نفر انتخاب کرد؟
گزینه سوم درست است. چون حضور سارا در این کمیته الزامی است، پس یک نفر از بین نفر کم میشود. به عبارتی خواهد بود. در این سوال ترتیب اهمیتی ندارد. همچنین امکان ندارد شخصی دو مرتبه انتخاب شود. پس از فرمول ترکیب بدون تکرار استفاده میکنیم:
دقت کنید چون سارا عضو کمیته است، پس انتخاب ما در واقع از است، یعنی است:
تمرین ۲
رمز عبور سیستمی متشکل است از دو حرف از حروف الفبای انگلیسی که به دنبال آن سه رقم بین تا داریم. اگر بدانیم در انتخابها تکرار مجاز است، چند رمز عبور متفاوت خواهیم داشت؟
گزینه سوم صحیح است. با توجه به اینکه در اعلام رمز عبورها همواره ترتیب قرار گرفتن حروف یا اعداد مهم است، پس باید از فرمولهای جایگشت استفاده کنیم. طبق سوال تکرار مجاز است، پس فرمول مناسب است.
از طرفی در این سوال مقدار برای حروف و اعداد متفاوت است. پس باید در دو مرحله جداگانه هر کدام را محاسبه کنیم. با توجه به اینکه تعداد حروف الفبای انگلیسی برابر است با ، برای تعداد حالتهای انتخاب حروف الفبا داریم:
همچنین در مورد تعداد رقمهای انتخابی با در نظر گرفتن و خواهیم داشت:
با ضرب کردن این دو عدد در هم، پاسخ بهدست میآید:
یادگیری ریاضیات گسسته با فرادرس برای دانشجویان
در بخشهای ابتدایی اشاره کردیم که ریاضیات گسسته و مباحث مطرح شده در آن، مبنا و پایهای است برای دانشجویان رشتههای ریاضی، آمار، علوم و مهندسی کامپیوتر. در این بخش چند فیلم آموزشی از مجموعه فرادرس را در این زمینه به شما معرفی میکنیم تا با مشاهده آنها با کاربردهای ریاضیات گسسته کاملا آشنا شوید:

- فیلم آموزش مبانی منطق و نظریه مجموعه ها فرادرس
- فیلم آموزش ترکیبیات و کاربردها فرادرس
- فیلم آموزش گراف ها و گروه ها فرادرس
- فیلم آموزش نظریه گراف و کاربردها فرادرس
- فیلم آموزش ریاضیات گسسته فرادرس
- فیلم آموزش ساختارهای جبری، گراف ها و ماتریس ها فرادرس
- فیلم آموزش جبر خطی فرادرس
- فیلم آموزش ساختمان گسسته با رویکرد حل مساله فرادرس
- فیلم آموزش ساختمان گسسته – مرور و حل تست های کنکور کارشناسی ارشد فرادرس
- فیلم آموزش ریاضیات گسسته – حل تست کنکور کارشناسی ارشد فرادرس
جمعبندی
در این مطلب از مجله فرادرس با مفاهیم و تعاریف در ریاضیات گسسته آشنا شدیم و توضیح دادیم در این شاخه از ریاضیات به چه مباحثی پرداخته میشود. برای مثال یاد گرفتیم در نظریه مجموعهها کاردینالیتی یک مجموعه برابر است با تعداد اعضای آن مجموعه. همچنین با مفاهیمی مانند اجتماع و اشتراک مجموعهها آشنا شدیم.

در بخش دوم به تعاریف مهم در نظریه گراف مانند انواع گراف و نحوه نمایش آنها پرداختیم و در انتها فرمولهای ساختارهای ترکیبی و نحوه استفاده از آنها در حل مسائل ریاضیات گسسته را توضیح دادیم. جدول زیر فرمولهای بخش ترکیبیات را بهطور خلاصه نشان میدهد:
| تکرار مجاز است | تکرار مجاز نیست | |
| جایگشت (ترتیب مهم است) | ||
| ترکیب ( ترتیب مهم نیست) |
source
