در علم فیزیک، انجام کار نوعی انتقال انرژی است که با اعمال یک نیروی مشخصی به جسم و جابجا کردن آن انجام میشود. بنابراین فرمول کار در فیزیک از ضرب کردن نیروی وارد بر جسم در جابجایی آن بهدست میآید و با نشان داده میشود. عبارت در محاسبه کار به این معنا است که فقط مولفهای از نیرو در نظر گرفته میشود که در راستای جابجایی جسم است. به عبارت دیگر، زاویه ، زاویه بین راستای نیرو و جابجایی حاصل از اعمال نیرو است.

در این نوشته از مجله فرادرس، پس از معرفی فرمول کار در فیزیک به بررسی جنبههای مختلف این فرمول خواهیم پرداخت. سپس با حل و بررسی سوالات مختلف راجعبه محاسبه کار در فیزیک مکانیک، یاد میگیرید که چگونه از این فرمول در مورد نیروهای مختلفی مانند نیروی وزن یا کشش طناب و یا نیروهای متغیری مانند نیروی فنر استفاده کنید. همچنین رابطه بین فرمول کار و فرمول انرژی جنبشی نیز در قالب قضیه کار و انرژی توضیح داده میشود.
فرمول کار در فیزیک چیست؟
هرگاه با اعمال یک نیروی مشخص به جسمی، آن جسم در راستای یکی از مولفههای نیرو جابجا شود، کار انجام شده است. بنابراین فرمول کار در فیزیک برای حرکت در یک بعد بهصورت زیر است:
- : کار بر حسب ژول ()
- : جابجایی بر حسب متر ()
- : نیرو بر حسب نیوتن ()
- : زاویه بین نیرو و جابجایی بر حسب درجه
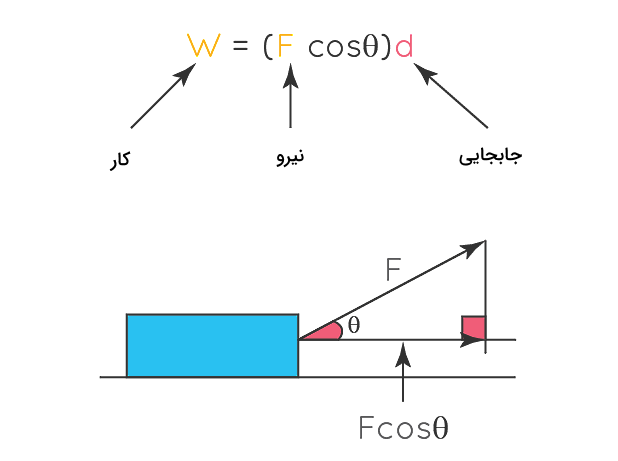
طبق فرمول بالا، واحد کار در سیستم بینالمللی واحدها یا SI برابر میشود با نیوتن در متر () که ژول () نام دارد. پس یک نیوتن در متر برابر است با یک ژول کار انجام شده:
همانطور که دیدیم، در فرمول کار در فیزیک یک عبارت مثلثاتی به شکل داریم. طبق دانش ریاضیات خود، میدانیم بیشترین مقدار مساوی با عدد یک است، پس بیشترین کاری که با مقادیر نیرو و جابجایی مشخص انجام میشود، زمانی است که باشد و این یعنی زاویه بین نیرو جابجایی برابر با صفر باشد:
از طرفی اگر نیرو بر جابجایی عمود باشد، داریم:
بنابراین تشخیص زاویه بین بردار نیرو و جایجایی در محاسبه کار از اهمیت ویژهای برخوردار است.
فرمول کار در فیزیک را میتوانیم با استفاده از مفهوم ضرب داخلی در ریاضیات نیز بنویسیم. ضرب داخلی هر دو برداری مانند و به شکل زیر تعریف میشود:
در محاسبه کار، نیرو و جابجایی هر دو کمیتهای برداری هستند. اگر نیاز دارید در مورد برداری بودن جابجایی و تفاوت آن با مسافت، اطلاعات بیشتری کسب کنید، مطالعه مطلب «مسافت و جابجایی — آنچه باید بدانید به زبان ساده» از مجله فرادرس پیشنهاد میشود. اگر ضرب داخلی این دو کمیت برداری را بهدست آوریم، داریم:
آنچه که از این ضرب داخلی حاصل شد، همان فرمول کار در فیزیک است. پس میتوانیم این فرمول را به شکل زیر هم بنویسیم:
چطور مفهوم و فرمول کار در فیزیک را با فرادرس بهتر بیاموزیم؟
در این بخش چند دوره آموزشی مرتبط با محاسبه کار در سطح کتابهای درسی مقطع متوسطه به شما معرفی خواهد شد. برای اینکه بتوانید محاسبات کار را بهدرستی انجام دهید، ابتدا لازم است مباحث فیزیک مکانیک و تشخیص نیروها را کاملا فرا گرفته باشید. این موضوعات در کتابهای درسی علوم تجربی پایه هفتم و نهم و کتابهای درسی فیزیک پایه دهم و دوازدهم مطرح میشوند. بنابراین مشاهده فیلمهای آموزشی زیر از مجموعه فرادرس در این زمینه بسیار مفید است:
- فیلم آموزش رایگان فرمول کار در فیزیک + مثال های مختلف فرادرس
- فیلم آموزش علوم تجربی پایه هفتم فرادرس
- فیلم آموزش علوم تجربی پایه نهم بخش فیزیک فرادرس
- فیلم آموزش فیزیک پایه دهم فرادرس
- فیلم آموزش فیزیک پایه دهم – مرور و حل تمرین فرادرس
- فیلم آموزش فیزیک پایه دوازدهم فرادرس
- فیلم آموزش فیزیک پایه دوازدهم – سوالات امتحانات نهایی فرادرس
- فیلم آموزش رایگان تبدیل واحد فیزیک دهم + مثالهای عملی فرادرس
تعریف کار در فیزیک چیست؟
برای اینکه بهتر متوجه شویم فرمول کار در فیزیک بر چه اساسی نوشته شده است، لازم است ابتدا با تعریف کار در فیزیک آشنا شویم. در نگاه اول شاید به نظر برسد منظور ما از کار، انجام دادن هر امر سختی مانند امتحان دادن یا بلند کردن یک جسم سنگین از روی زمین است. اما ممکن است از منظر علم فیزیک چنین مواردی کار محسوب نشوند. پس باید تعریف کار بهصورت دقیق برقرار باشد تا بتوانیم انجام دادن یک عمل خاص را کار نامگذاری کنیم.
تعریف علمی کار در ارتباط آن با مفهومی به نام انرژی معنا پیدا میکند، به این شکل که هر زمان کاری انجام شود، حتما مقداری انرژی منتقل شده است. به همین علت است که واحد کار و انرژی مشابه هم است. طبق تعریف کار و فرمول کار در فیزیک، گفتیم واحد کار برابر است با حاصلضرب واحد نیرو در واحد جابجایی. واحد SI برای نیرو، نیوتن و واحد استاندارد جابجایی، متر است. پس یکای استاندارد کار چنین بهدست میآید:

یک نیوتن در متر را با ژول () نشان میدهیم که به شکل زیر تعریف میشود:
یک ژول انرژی زیادی نیست. از این مقدار انرژی میتوان تقریبا برای بلند کردن یک سیب صد گرمی کوچک به اندازه یک متر استفاده کرد. پس واحد کار هم مانند واحد انرژی، ژول است. برای اینکه از نظر علمی کار انجام شود، لازم است دو شرط زیر برقرار باشند:
- نیروی مشخصی به جسم اعمال شود.
- این نیرو باعث شود جسم در راستای آن جابجا شود.
پس با توجه به شرایط بالا، لازم است فرمول کار در فیزیک به این صورت تعریف شود که کار انجام شده روی یک سیستم توسط یک نیروی ثابت برابر است با حاصلضرب مولفهای از نیرو که در راستای حرکت سیستم است در میزان جابجایی که سیستم در اثر دریافت این نیرو داشته است. این بیان در مورد حرکت در یک بعد، به شکل زیر در قالب ریاضیات نمایش داده میشود:
همانطور که در بخش اول توضیح داده شد، زاویه برابر است با زاویهای که بین راستای نیروی و راستای جابجایی وجود دارد. در ادامه با بررسی چند مثال مختلف، بهتر متوجه اثر زاویه روی مقدار کار انجام شده خواهید شد. برای نمونه، بررسی مثالهای مختلف نشان میدهد که کار انجام شده توسط یک نیروی مشخص روی یک سیستم، در حالتهای زیر صفر میشود:
- وقتی که جابجایی سیستم صفر باشد.
- وقتی که نیروی وارد بر سیستم صفر باشد.
- وقتی که نیرو و جابجایی بر هم عمود باشند.
کاربردهای کار در فیزیک
اما شاید این سوال مطرح شود که فایده محاسبه کار چیست. دانستن کار انجام شده در بررسی سیستمهای مکانیکی مانند بالابرها یا ابزارهایی که به منظور کشیدن یا هل دادن اجسام طراحی میشوند، بسیار مهم است و مقدار عددی به دست آمده نشاندهنده میزان انرژی منتقل شده در این فرآیندهای مکانیکی است. فیلم آموزش فیزیک پایه ۱ + حل مثال فرادرس میتواند مسیر یادگیری کاربردهای کار و فرمول کار در فیزیک و تسلط شما بر حل مسائل مرتبط با این فرمول را هموار کند. لینک مشاهده این فیلم آموزشی در ادامه آورده شده است:
همچنین همان طور که ادامه خواهیم دید، کار با تغییرات انرژی جنبشی جسم مرتبط است. همچنین هر کاری که بر خلاف نیروی جاذبه زمین روی اجسام انجام میشود، به شکل انرژی پتانسیل در آنها ذخیره خواهد شد. در سیستمهای ترمودینامیکی، کار در قالب پدیدههایی مانند انقباض و انبساط روی سیستمهای گازی انجام میشود و به علت اصل پایستگی انرژی، انرژی گرمایی سیستم به کار مکانیکی تبدیل خواهد شد. در الکتریسیته و مغناطیس، آشنایی با مفهوم کار برای درک حرکت بارها و چگونگی تولید انرژی الکتریکی لازم است.
حل مثال و تمرین از فرمول کار در فیزیک
پس از اینکه با فرمول کار در فیزیک کاملا آشنا شدیم، در این بخش چند مثال عددی مختلف در این زمینه حل میشود تا نحوه استفاده از این فرمول را در حل مسائل مختلف فیزیک مکانیک تمرین کنید. یکی از مهمترین جنبههای محاسبه کار این است که بتوانیم کار نیروهای مختلف را از هم تفکیک کنیم.
همانطور که میدانید در مسائل مکانیک ممکن است همزمان چند نیرو به یک جسم وارد شود. هر کدام از این نیروها یک مقدار کار روی جسم انجام میدهند که باید از کار نیروی دیگر تمیز داده شود. همچنین چنانچه بخواهیم کار را در یک حرکت دو یا سه بعدی بررسی کنیم، کافی است حرکت دو یا سه بعدی را به دو یا سه حرکت یک بعدی تقسیم کنیم.
مثال ۱
فرض کنید جسمی با جرم به اندازه از سطح افقی مشخصی بلند میشود. کار انجام شده با در نظر گرفتن چقدر است؟ کار نیروی وزن چقدر است؟ کل کار انجام شده در این سوال را محاسبه کنید:
پاسخ
برای محاسبه کار باید از فرمول استفاده کنیم. در اینجا اندازه جابجایی مشخص است، اما نیرویی که برای بلند کردن جسم اعمال شده است، در نگاه اول معلوم نیست. میدانیم به هر جسمی همواره نیرویی از سمت زمین به نام نیروی جاذبه یا نیروی وزن وارد میشود. نیروی وزن هم مانند کار با نشان داده میشود و فرمول محاسبه آن به شکل زیر است:
که در آن جرم جسم بر حسب کیلوگرم ()، شتاب جاذبه زمین بر حسب متر بر مجذور ثانیه () و نیروی وزن بر حسب نیوتن () است. همچنین از قانون اول نیوتن میدانیم زمانی که جسمی از سطح زمین بلند شود، مادامی که جسم ساکن بماند یا با سرعت ثابت حرکت کند، مجموع یا برآیند نیروهای وارد بر آن صفر است:
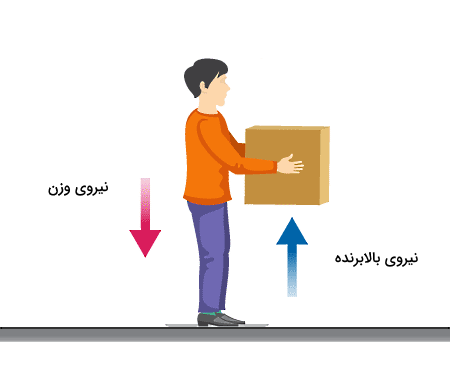
در این سوال چون جسم با سرعت ثابتی به سمت بالا برده میشود، پس مجموع نیروهای وارد بر آن مساوی با صفر است. این نیروها طبق شکل بالا عبارتاند از نیروی وزن و نیرویی که باعت بالا رفتن جسم شده است و ما آن را مینامیم و در حقیقت میخواهیم ابتدا کار همین نیرو را محاسبه کنیم. طبق فرمول قانون اول نیوتن، مجموع این دو نیرو که دو جهت مختلف دارند، برابر با صفر است:
پس نیرو محاسبه شد. حالا با داشتن نیرو و جابجایی، فقط کافی است زاویه نیرو و جابجایی را برای پیدا کردن کار تعیین کنیم. دقت کنید در بخش اول این سوال، کار نیروی بالابرنده یا و در بخش دوم، کار نیروی وزن یا خواسته شده است. در مورد بخش اول، زاویه بین و جابجایی برابر با صفر است. در نتیجه کار این نیرو میشود:
در بخش بعدی سوال، کار نیروی وزن را میخواهیم که باید اندازه نیروی وزن، مقدار جابجایی داده شده در صورت سوال و زاویه بین جهت نیروی وزن و بردار جابجایی مشخص شود. اندازه نیروی وزن را بهدست آوردیم و گفتیم که با اندازه نیروی برابر است. زاویه بین نیروی وزن و جابجایی برابر است با صد و هشتاد درجه. در نتیجه کار نیروی وزن میشود:
دقت کنید در فرمول کار اندازه نیرو قرار داده میشود و جهت آن با در نظر گرفتن زاویه خود به خود اعمال خواهد شد. برای اینکه کل کار را حساب کنیم، باید مجموع کار تمام نیروهای وارد بر این جسم در نظر گرفته شوند. گفتیم دو نیروی و به جسم وارد شده و روی آن کار انجام میدهند. پس کل کار برابر است با:
مثال ۲
شخصی در حال جابجایی یک ماشین چمنزنی با اعمال نیروی به اهرم آن، مطابق شکل زیر است. میخواهیم ببینیم با توجه به فرمول کار در فیزیک، چگونه میتوانیم کار انجام شده توسط این شخص را روی ماشین چمنزنی محاسبه کنیم. دقت کنید با اینکه جهت نیرویی که شخص از طریق اهرم مخصوص به ماشین چمنزنی وارد میکند، کاملا در راستای افقی نیست، اما جابجایی ماشین چمنزنی در راستای مثبت محور افق یا محور xها است.
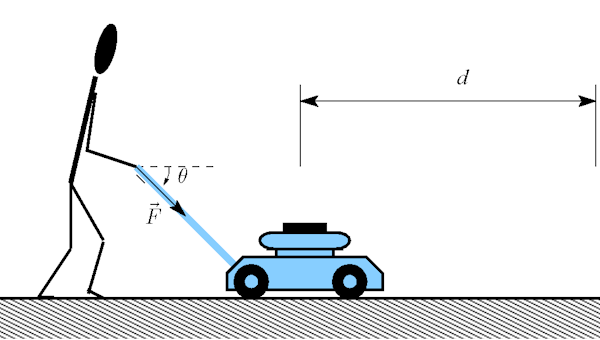
طبق تعریف کار، گفتیم نیرویی باعث انجام کار میشود که یک جابجایی در راستای خودش ایجاد کند. پس در اینجا باید مولفهای از نیرو را در نظر بگیریم که همجهت با جابجایی یا باشد. این مولفه برابر است با . برای اینکه دقیقتر متوجه شوید این مولفه چگونه بهدست میآید، باید به روش تجزیه بردارها مسلط باشید. نیروی در تصویر بالا، دو مولفه در راستای افقی و قائم دارد که عبارتاند از:
اگر بخواهیم کار را محاسبه کنیم، ابتدا باید جهت جابجایی جسم مشخص شود. با وارد کردن نیرویی به شکل به اهرم ماشین چمنزنی، جابجایی آن در جهت مثبت محور xها یا محور افقی است. پس باید مولفهای از نیرو را انتخاب کنیم که در همین راستا باشد، یعنی مولفه . به این ترتیب با ضرب کردن این مولفه از نیرو در جابجایی، کار بهدست میآید:
مثال ۳
فرض کنید شخصی در دو حالت زیر یک کیف را در دست خود نگه میدارد. میخواهیم با استفاده از فرمول کار در فیزیک، کار را برای این دو حالت پیدا کنیم. ابتدا به بررسی تصویر سمت چپ میپردازیم که در آن، کیف هیچگونه جابجایی ندارد. شخص به کیف نیرویی به سمت بالا وارد میکند تا آن را نگه دارد (در مقابل افتادن بر اثر جاذبه زمین)، اما کیف جابجا نمیشود. پس در واقع است و در نتیجه، . پس در این تصویر کاری انجام نمیشود:
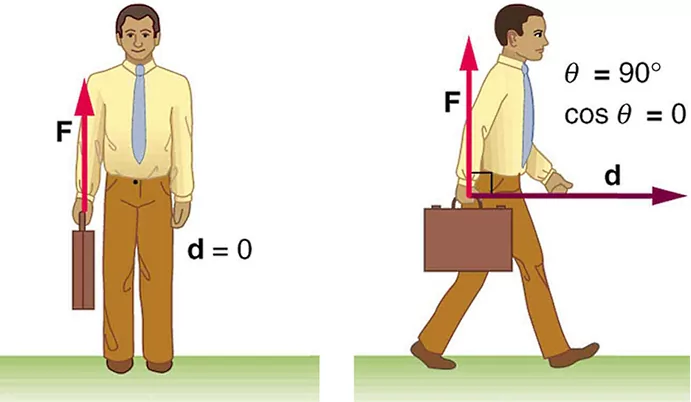
زمانی که میگوییم شخص روی کیف کاری انجام نمیدهد، یعنی هیچ انرژی از شخص به کیف منتقل نمیشود. پس علت خسته شدن شخص در اثر نگه داشتن کیف چیست؟ پاسخ این سوال این است که ماهیچههای بدن با نگه داشتن هر چیزی، نسبت به هم در حال انجام کار هستند. اما این کاری است که یک ماهیچه نسبت به دیگری انجام میدهد و نه نسبت به سیستم کیف و زمین.
در تصویر سمت راست، شخص در حال جابجایی به سمت راست است. طبیعتا کیفی که در دست خود دارد نیز به سمت راست همراه با شخص جابجا میشود. باز هم مانند تصویر سمت چپ، نیرویی که شخص به کیف وارد میکند، برای نگه داشتن آن و در راستای قائم است. اگر بخواهیم مولفهای از نیرو را که در راستای جابجایی است، پیدا کنیم، باید کسینوس زاویه بین نیرو و جابجایی را محاسبه کنیم. زاویه بین نیروی و جابجایی در این شکل برابر است با نود درجه. پس . در نتیجه هیچ مولفهای از نیرو در راستای جابجایی برای این شکل وجود ندارد و کار انجام شده توسط شخص روی کیف، در این تصویر هم مانند تصویر قبلی صفر است:
مثال ۴
در تصویر سمت چپ از شکل زیر، باز هم نیروی لازم برای نگه داشتن کیف به سمت بالا یا در راستای محور y است. اما در این شکل جابجایی کیف یا به موازات راستای پلهها است و در زاویه با نیروی قرار دارد. بنابراین در این مورد، مولفهای از نیرو که در راستای جابجایی کیف باشد، وجود دارد و عبارت است از . پس کار انجام شده روی کیف توسط شخص اگر روی پلهها به اندازه جابجا شود، برابر است با:
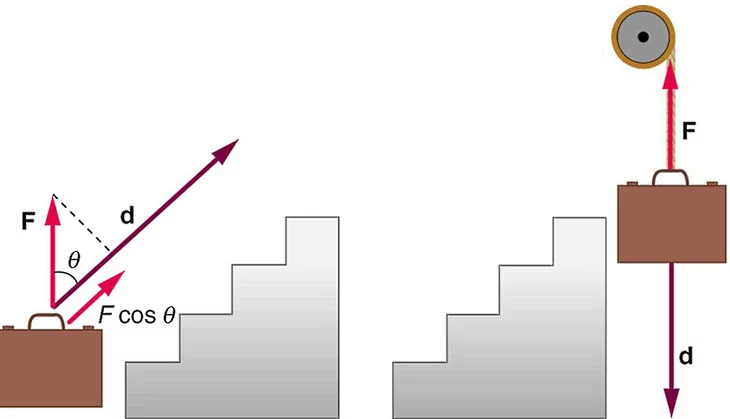
پیش از اینکه به بررسی آخرین تصویر بپردازیم، میتوانیم با توجه به مثالهای بالا به این نتیجه برسیم که برای پیدا کردن مولفهای از نیرو که در راستای جابجایی است، کافی است کسینوس زاویه بین نیرو و جابجایی را محاسبه کنیم. در فرمول کار به شکل نیز، از همین واقعیت استفاده شده است.
در آخرین تصویر، کیفی که توسط یک قرقره نگه داشته شده، به سمت پایین جابجا میشود. نیروی نگه دارنده وارد بر کیف توسط قرقره در جهت مثبت محور y است، در حالی که راستای جابجایی کیف در جهت منفی محور y است. پس اگر بخواهیم مولفهای از نیرو را که در راستای جابجایی است، محاسبه کنیم، کافی است کسینوس زاویه بین نیرو و جابجایی را پیدا کنیم که میشود . پس با قرار دادن این مقدار و اندازه نیرو و جابجایی در فرمول کار در فیزیک، کار منفی خواهد شد:
منفی شدن کار انجام شده توسط قرقره روی کیف، به این معنا است که انرژی از کیف کم میشود و به قرقره اضافه میشود. برخلاف مثالهای قبل که در آنها کار مثبت بود و انرژی از اعمال کننده نیرو به جسم در حال جابجایی منتقل میشد. پس هرگاه کار منفی شود، جهت انتقال انرژی نیز معکوس شده است. یک تفسیر از این وضعیت این است که وزن کیف روی قرقره کاری به اندازه انجام داده و به آن انرژی میدهد. تفسیر دیگر این است که قرقره یک کار منفی برابر با روی کیف انجام میدهد. پس از آن انرژی میگیرد.
مثال ۵
اگر پدری دخترش را که سوار بر واگنی مطابق شکل شده است، حدود جابجا کند، با صرفنظر کردن از اصطکاک، چه مقدار کار انجام داده است؟
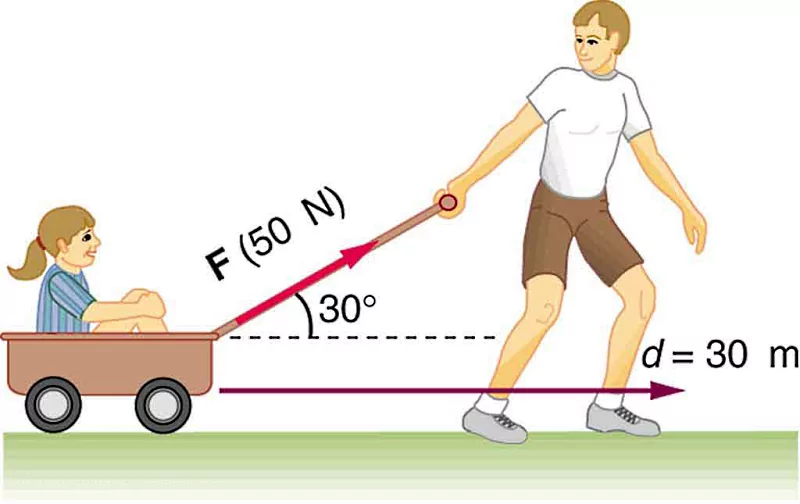
پاسخ
برای محاسبه کار، باید فرمول کار در فیزیک را بنویسیم:
جابجایی، نیرو و زاویه بین بردار نیرو و جابجایی در شکل مشخص است. با قرار دادن این مقادیر در فرمول بالا خواهیم داشت:
مثال ۶
یک ماشین میخکوب تنی از چه فاصلهای باید سقوط کند تا کار انجام دهد؟
پاسخ
برای پاسخ به این سوال کافی است فرمول کار در فیزیک را بنویسیم:
نیرویی که باعث انجام این کار شده است، همان نیروی جاذبه زمین یا نیروی وزن است. میدانیم نیروی وزن یا هر جسم فرضی برابر است با حاصلضرب جرم آن در شتاب جاذبه زمین:
در این سوال جرم ماشین بر حسب تن داده شده است که لازم است به کیلوگرم تبدیل شود. هر تن برابر است با هزار کیلوگرم. از طرفی مقدار شتاب جاذبه زمین معمولا عدد ثابتی و برابر با است. با قرار دادن این دو عدد، نیروی وزن ماشین محاسبه خواهد شد:
مقدار نیرو تعیین شد. زاویه بین نیرو و جابجایی برابر است با صفر درجه. نیروی وزن همواره به سمت پایین به هر جسمی وارد میشود و در این سوال هم سقوط ماشین را داریم که حرکتی رو به پایین است. پس این دو بردار همجهت بوده و دارای زاویه صفر هستند:
در محاسبه بالا میدانیم .
مثال ۷
شخصی با یک سرعت ثابت در حال کشیدن بلوکی به شکل زیر روی یک سطح شیبدار بدون اصطکاک است و جعبه روی این سطح به اندازه جابجا میشود. فرمول کار در فیزیک را برای نیروهای مختلف وارد بر این جعبه بنویسید:
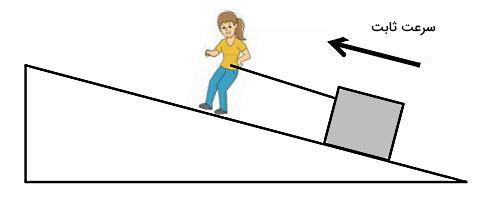
پاسخ
ابتدا باید ببینیم چه نیروهایی بر این جعبه وارد میشوند. اولین نیرو که در شکل هم واضح است، نیروی کشش طنابی است که توسط شخص به جعبه وارد شده و آن را به سمت بالای سطح میکشد. نیروی دیگر، نیروی وزن است که به سمت پایین بر هر چیزی از جمله این جعبه وارد میشود. در شکل زیر، نیروی وزن یا جاذبه زمین با پیکان سیاه نشان داده شده است. اگر این نیرو را در راستای محورهای مختصات فرضی خود تجزیه کنیم، دو مولفه (پیکانهای قرمز) خواهد داشت.
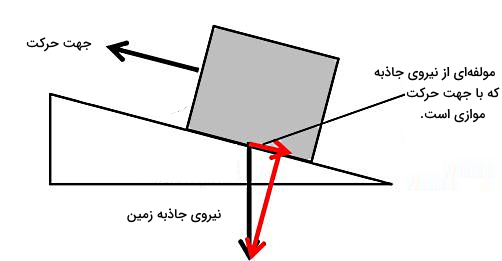
همچنین نیروی دیگری به نام نیروی عمودی سطح داریم، که عمود بر سطح جعبه و به سمت بالا به آن وارد میشود. نیروی عمودی سطح نیرویی است که از طرف سطح شیبدار به جعبه وارد میشود. چون در سوال گفته شده سطح بدون اصطکاک است، پس هیچ نیروی اصطکاکی به جعبه وارد نمیشود. در غیر این صورت، نیروی اصطکاک که در خلاف جهت حرکت جعبه است نیز باید در نظر گرفته میشد.
پس در این سوال سه نیروی مختلف به جعبه وارد میشوند که برای هر کدام یک کار محاسبه میشود. ابتدا فرمول کار نیروی کشش طناب که توسط شخص به جعبه وارد میشود را مینویسیم. این نیرو با نشان داده میشود. جهت این نیرو دقیقا با جهت حرکت جعبه یکی است، پس زاویه بین این دو کمیت برداری برابر با صفر است:
در محاسبات بالا میدانیم که . حالا میرویم سراغ کاری که توسط نیروی جاذبه زمین روی جعبه انجام میشود. این نیرو با پیکان سیاه در شکل نشان داده شده است. در نگاه اول شاید به نظر برسد این نیرو باعث جابجایی جعبه نشده است و در نتیجه کاری روی آن انجام نمیدهد. اما این تصور اشتباه است. اگر این نیرو را تجزیه کنیم، مولفه افقی آن در راستای جابجایی جعبه، اما در خلاف جهت آن است (). اگر نیروی وزن را با مشخص کنیم، مولفه افقی آن برابر است با:
در حالی که برای مولفه قائم نیروی وزن خواهیم داشت:
زاویه زاویه سطح شیبدار است. بنابراین کار نیروی وزن برابر است با مجموع کار هر کدام از مولفههای نیروی وزن:
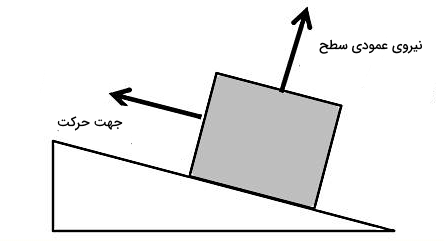
در محاسبات بالا میدانیم و . پس در حقیقت فقط مولفه افقی نیروی وزن روی جعبه کار انجام میدهد. در نهایت سومین نیروی وارد بر جعبه یعنی نیروی عمودی سطح یا نیروی عمودی تکیهگاه () را در نظر میگیریم. این نیرو دقیقا در خلاف جهت مولفه عمودی نیروی وزن است. بنابراین زاویه آن با راستای جابجایی جعبه برابر است با نود درجه و برای کار آن خواهیم داشت:
مثال ۸
چقدر کار باید انجام شود تا شخصی موفق شود یک ماشین چمنزنی را با نیروی ثابتی به اندازه تحت زاویه درجه با محور افقی، به اندازه روی زمین جابجا کند؟ اگر کالری دریافتی روزانه این شخص برابر با باشد، کار بهدست آمده را از ژول به کیلوکالری تبدیل کنید و با این مقدار مقایسه کنید. میتوانید در محاسبات خود از این واقعیت استفاده کنید که هر یک کالری گرما معادل است با مقدار انرژی مورد نیاز برای گرم کردن آب به اندازه درجه سانتیگراد که برابر میشود با ، در حالی که انرژی یک کیلوکالری غذای مصرف شده برابر است با .
پاسخ
ابتدا فرمول کار در فیزیک را مینویسیم. مقدار نیرو و جابجایی مشخص است. راستای جابجایی در راستای افق یا محور xها است. زاویه نیرو با این راستا داده شده است که همان زاویه در فرمول است. پس با داشتن تمام مقادیر، فقط کافی است اعداد را در فرمول کار جایگذاری کنیم:
حالا مقدار کار بهدست آمده را از ژول به کیلوکالری تبدیل میکنیم. با توجه به اینکه در صورت سوال بیان شده است که ، پس میتوانیم این رابطه را به شکل زیر بنویسیم:
بنابراین مقدار کار را از ژول به کیلوکالری تبدیل کردیم. برای مقایسه کار انجام شده با کالری دریافتی روزانه این شخص، کافی است کار محاسبه شده در رابطه بالا را بر تقسیم کنیم:
این نسبت عدد خیلی کوچکی بهدست آمد که نشان میدهد تنها بخش خیلی خیلی کوچکی از انرژی حاصل از مصرف غذا صرف انجام کارهای روزانه خواهد شد و بیشتر این انرژی در قالب چربی در بدن ذخیره میشود.
مثال ۹
ماشینی که با نیروی شروع به حرکت کرده است، اگر طی مدت زمان و با سرعت ثابت به مکان مشخصی برسد، کار انجام شده توسط این نیرو روی ماشین چقدر است؟
پاسخ
برای محاسبه کار به اندازه نیروی وارد شده، جابجایی و زاویه بین جهت نیرو و جابجایی نیاز داریم. در این سوال نیرو و زاویه مشخص است. اما برای محاسبه جابجایی با توجه به دادههای مسئله لازم است از فرمول های سینماتیک استفاده کنیم. فرمول مناسب به شکل زیر است:
در محاسبه بالا تبدیل واحد زمان از دقیقه به ثانیه نباید فراموش شود. حالا میتوانیم از فرمول کار استفاده کنیم:
مثال ۱۰
شخصی با یک نیروی ثابت در حال کشیدن یک بسته روی زمین است و موفق میشود آن را به اندازه جابجا کند. اگر این شخص نیرو را با زاویهای مطابق شکل زیر به بسته وارد کند و فرض کنیم که سطح زمین هموار و صاف و بدون اصطکاک است، کار برآیند را محاسبه کنید:
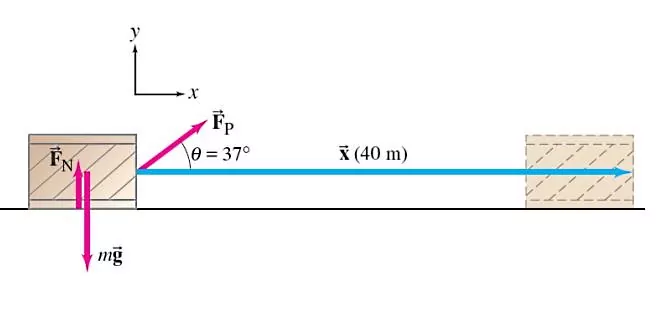
پاسخ
در این سوال کار برآیند یا مجموع نیروهای وارد بر بسته خواسته شده است. بنابراین اولین قدم مشخص کردن نیروهای وارد بر بسته است. طبق صورت سوال، یک نیروی ثابت داریم که به بسته وارد میشود. به علاوه دو نیروی دیگر هم در این شکل به بسته وارد میشوند که عبارتاند از نیروی وزن () و نیروی عمودی سطح (). نیروی وزن از طرف زمین و نیروی عمودی سطح از طرف سطح هر کدام جداگانه به بسته وارد میشوند. حالا کار هر کدام از این سه نیرو را حساب میکنیم:
در دو رابطه آخر نیازی نیست مقادیر نیرو را بهدست آوریم. با توجه به عمود بودن جهت این نیروها بر جابجایی جسم، است و در نتیجه کار این دو نیرو صفر است.پس اگر بخواهیم کار برآیند نیروها را داشته باشیم، کافی است مجموع سه کار بالا را حساب کنیم:
یک راه سادهتر برای حل این سوال این بود که در ابتدا نیروی برآیند وارد بر این بسته را پیدا کنیم و سپس فقط کار آن نیرو را بهدست آوریم. چون نیروی عمودی سطح و نیروی وزن با هم خنثی میشوند، تنها نیروی وارد بر این بسته همان نیروی ثابت است. پس برآیند یا مجموع کار تمام نیروهای وارد بر یک جسم معادل است با کار نیروی برآیند وارد بر آن.
تمرین ۱
فرض کنید شخصی با جرم در حال هل دادن جعبهای به سمت بالا مطابق شکل زیر است. این شخص موفق میشود جعبه را حدود با زاویه درجه نسبت به افق جابجا کند. اگر نیروی وارد شده توسط شخص به جعبه برای این جابجایی بوده باشد، کار انجام شده توسط شخص روی جعبه برابر با کدام گزینه است؟
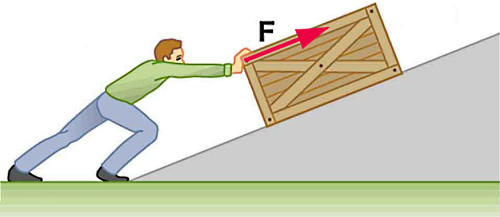
با نوشتن فرمول کار در فیزیک و عددگذاری، گزینه صحیح یعنی گزینه دوم بهدست میآید:
دقت کنید در این سوال نیروی وارد شده به جعبه کاملا در راستای جابجایی آن است. بنابراین زاویه بین بردار نیرو و جابجایی صفر است و نیازی به استفاده از سایر دادههای این سوال در محاسبه کار نیست.
تمرین ۲
اگر نیروی موجب حرکت جعبهای با سرعت در سه حالت زیر شود، کار انجام شده توسط این نیرو از کمترین به بیشترین مقدار معادل با کدام گزینه است؟
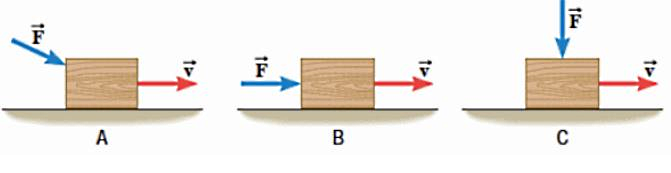
گزینه آخر درست است. طبق فرمول کار در فیزیک یعنی ، عوامل تعیین کننده در مقدار کار انجام شده توسط نیرویی مانند عبارتاند از اندازه نیرو که برای هر سه موقعیت بالا یکسان است، میزان جابجایی که مشخص نیست و زاویه بین بردار نیرو و جابجایی، که در این سوال باید این مسئله بررسی و مقایسه شود. راستای جابجایی با راستای سرعت ثابتی که در هر موقعیت جعبه بهدست آورده است، برابر است.
در موقعیت ، بین بردار و زاویه داریم. در موقعیت ، بین بردار و زاویهای وجود ندارد. به عبارت دیگر، این دو بردار هم جهت هستند و زاویه بین آنها در این حالت صفر است. در ، زاویه بین بردار و نود درجه است. بنابراین کار انجام شده برای هر موقعیت به شکل زیر است:
بنابراین کمترین کار برای موقعیت و بیشترین کار برای است. دقت کنید مقدار همیشه از یک کوچکتر است. پس کار در موقعیت همیشه مقداری کمتر از خواهد داشت.
تمرین ۳
اگر جعبهای در راستای قائم به اندازه جابجا شده و سپس در همان حالت نگه داشته شود، با داشتن وزن و صرفنظر کردن از اصطکاک، کار انجام شده روی جعبه زمانی که در این ارتفاع نگه داشته شده است، چقدر است؟
بیشتر از
کمتر از
کاری انجام نشده است.
گزینه آخر درست است. دقت کنید در این سوال کار برای زمانی که جعبه نگه داشته شده است، خواسته شده است. در این حالت جعبه هیچگونه جابجایی ندارد. پس کاری انجام نمیشود.
قضیه کار و انرژی
در بخشهای قبل با فرمول کار در فیزیک آشنا شدیم و گفتیم که کار و انرژی هر دو دارای واحد یکسانی هستند. در این بخش توضیح میدهیم که رابطه بین کار و انرژی چگونه است. هرگاه نیرویی به جسمی وارد شود، آن جسم تحت تاثیر نیرو میتواند شتاب بگیرد و به دنبال شتابی که بهدست میآورد، یک جابجایی نیز خواهد داشت. شتاب همان تغییر سرعت است، پس حرکت شتابدار جسم همراه با تغییرات سرعت است. بنابراین انرژی جنبشی جسم هم عوض میشود.
طبق قضیه کار و انرژی، تغییرات انرژی جنبشی جسم در اثر اعمال نیرو به آن معادل است با کار انجام شده روی جسم توسط آن نیرو. پس بین کار، نیرو و تغییرات انرژی جنبشی جسم رابطهای به شکل زیر برقرار است:
که در آن انرژی جنبشی جسم است. فرمول انرژی جنبشی جسم به شکل زیر است:
بنابراین با اعمال نیروی و افزایش سرعت جسم از به ، انرژی جنبشی آن از به تبدیل میشود. این تغییرات انرژی جنبشی یا در جسم معادل است با کاری که نیروی روی آن انجام داده است:
به همین علت است که واحد استاندارد کار و انرژی مشابه هم است. همچنین کار هم مانند انرژی یک کمیت عددی یا اسکالر محسوب میشود. توجه به این نکته مهم است که حاصلضرب و برابر است با تغییرات انرژی جسم، نه تغییرات سرعت آن. در ادامه این بخش با حل چند مثال و تمرین، نحوه استفاده از قضیه کار و انرژی و ارتباط آن با فرمول کار در فیزیک را بهتر میآموزید.
نکته: علامت کار میتواند مثبت یا منفی باشد، اما منفی یا مثبت بودن کار به معنای جهت داشتن آن نیست. کار مثبت به این معنا است که نیروی وارد شده به جسم باعث شده است آن جسم در راستای نیرو حرکت کند. این در حالی است که کار منفی به این مفهوم است که نیروی وارد بر جسم با راستای حرکت آن مخالفت میکند.
مثال ۱
چقدر کار لازم است تا کامیونی با انرژی جنبشی در مدت زمان و پس از طی مسیر کاملا متوقف شود؟
پاسخ
اگر کامیون متوقف شود، انرژی جنبشی آن نیز صفر خواهد شد. پس با محاسبه تغییرات انرژی جنبشی میتوانیم کار انجام شده روی کامیون برای توقف را محاسبه کنیم:
علامت منفی برای کار به این معنا است که برای توقف کامیون لازم است انرژی از آن کم شود.
مثال ۲
یک ماشین میخکوب باید با چه سرعتی سقوط کند تا کار انجام دهد؟
پاسخ
وقتی که این ماشین سقوط کند، در اثر برخورد با زمین سرعت آن به صفر میرسد. پس با در نظر گرفتن سرعت نهایی صفر و نوشتن قضیه کار و انرژی خواهیم داشت:
مثال ۳
فرض کنید یک هواپیمای جت با جرم بهصورت افقی و با سرعتی اندازه فرود آمده و طی یک جابجایی قبل از توقف کامل، شتاب آن کاهش مییابد. نیروی برآیندی که توسط موتور به هواپیما وارد میشود، چقدر است؟
پاسخ
با توجه به داشتن مقادیر سرعت و جرم، میتوانیم با نوشتن قضیه کار و انرژی و محاسبه کار، نیروی برآیند را پیدا کنیم. پس داریم:
بازهای که هواپیما جابجایی مشخصی طی میکند تا متوقف شود، مد نظر ما است. در این بازه سرعت اولیه هواپیما مشخص است و در انتها هم متوقف میشود. پس سرعت نهایی هواپیما صفر است:
اما پیش از اینکه سرعت اولیه را در فرمول کار و انرژی قرار دهیم، لازم است واحد آن را به واحد استاندارد سرعت، یعنی متر بر ثانیه تبدیل کنیم. برای تبدیل کیلومتر بر ساعت به متر بر ثانیه به روش زیر عمل میکنیم:
حالا میتوانیم این سرعت را در فرمول بالا جایگذاری کنیم تا کار انجام شده بهدست آید:
با نوشتن فرمول کار در فیزیک و قرار دادن مقدار جابجایی داده شده، نیروی برآیند موتور که باعث توقف هواپیما شده است، پیدا میشود. اما پیش از آن باید زاویه بین نیرو و بردار جابجایی را مشخص کنیم. نیروی موتور باعث میشود هواپیما متوقف شود، بنابراین در خلاف جهت حرکت آن اعمال شده است. پس زاویه مناسب بین این دو بردار زاویه درجه است:
مثال ۴
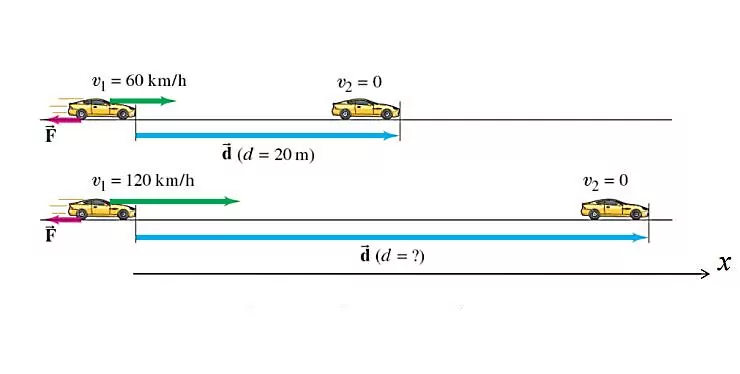
فرض کنید ماشینی که با سرعت در حال حرکت است، ترمز گرفته و پس از طی مسافت بایستد. اگر این ماشین با سرعتی دو برابر سرعت قبل یعنی حرکت کند، مسافت ترمز آن چقدر خواهد شد؟ فرض کنید بیشترین مقدار نیروی ترمز تقریبا از اندازه سرعت ماشین مستقل است.
پاسخ
اگر به کمک قضیه کار و انرژی، کار انجام شده توسط نیروی ترمز را در اولین بخش حرکت پیدا کنیم، با توجه به اینکه ماشین در انتهای مسافت ترمز میایستد، خواهیم داشت:
از طرفی میدانیم تغییرات انرژی جنبشی برابر است با فرمول کار. پس با توجه به اینکه جهت جابجایی در خلاف جهت نیروی ترمز است، برای کار انجام شده توسط نیروی ترمز داریم:
چون در سوال گفته شده مسافت ترمز از نیرو مستقل است و جرم ماشین هم تغییری نکرده است، پس در حالت دوم با دو برابر شدن سرعت خواهیم داشت:
بنابراین بدون اینکه محاسبات را با عددگذاری انجام داده باشیم، میتوانیم با این ضرب ساده مسئله را حل کنیم:
تمرین
اگر انرژی جنبشی کامیونی برابر با باشد، چه نیروی ترمزی میتواند باعث توقف آن پس از طی جابجایی شود؟
گزینه اول درست است. با توجه به اینکه انرژی جنبشی اولیه کامیون مشخص است و پس از توقف نیز انرژی جنبشی نهایی آن برابر با صفر خواهد شد، پس میتوانیم قضیه کار و انرژی را بنویسیم:
طبق گزینهها باید نیرو بر حسب نیوتن محاسبه شود، بنابراین لازم است کار انجام شده نیز بر حسب ژول نوشته شود. میدانیم پسوند مگا در کنار یک واحد برابر است با توان ششم عدد ده:
حالا با نوشتن فرمول کار در فیزیک، قرار دادن جابجایی و اینکه میدانیم نیروی ترمز همیشه در خلاف جهت حرکت است، خواهیم داشت:
روش محاسبه کار یک نیروی متغیر (قانون هوک)
در بخشهای قبل در مورد نیروهایی صحبت کردیم که اندازه ثابتی داشتند، به این مفهوم که اندازه این نیروها تابعی از زمان یا مکان نبود. اما ممکن است با مسائلی روبرو شویم که در آنها اندازه نیرو با مکان تغییر میکند و به آن وابسته است. در این شرایط در فرمول کار در فیزیک تغییر کوچکی خواهیم داشت که در این بخش آن را توضیح میدهیم.
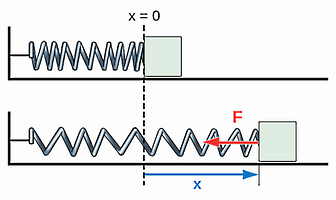
برای مثال، فرض کنید میخواهیم کار انجام شده روی یک جسم مربعی متصل شده به یک فنر را طبق شکل بالا، محاسبه کنیم. نیروی فنر توسط فرمول معروفی به نام قانون هوک بهدست میآید. این فرمول توصیفکننده نیروی بازگرداننده یک فنر با خاصیت کششی ایدهآل است، چه در شرایط فشردگی یا چه در شرایط کشیدگی:
- : نیروی فنر بر حسب نیوتن ()
- : ثابت فنر بر حسب نیوتن بر متر ()
- : میزان فشردگی یا کشیدگی فنر بر حسب متر ()
مشاهده میکنید که نیروی فنر به مکان یا وابسته است. در نتیجه نیروی فنر یک نیروی متغیر محسوب میشود. نکته مهم بعدی در مورد نیروی فنر این است که این نیرو همیشه در خلاف جهت است و این مسئله با درج علامت منفی در قانون هوک توصیف شده است. پس جسم ما به یک فنر متصل است و این فنر نیرویی متناسب با میزان کشیدگی خود به جسم وارد میکند. میخواهیم کار نیروی فنر را پیدا کنیم. چون نیرو متغیر است، باید روی المانهای کوچکی از فاصله به نام انتگرالگیری کنیم:
در رابطه بالا طبق آنچه از فرمولهای انتگرالگیری میدانیم، انتگرال برابر میشود با . پس خواهیم داشت:
مثال
شخصی با کشیدن یک فنر طول آن را به اندازه افزایش میدهد. او برای انجام این کار نیرو به فنر وارد کرده است. کار انجام شده توسط این شخص چقدر است؟ اگر شخص بهجای کشیدن، فنر را به همین اندازه فشرده کند، چقدر کار انجام داده است؟
پاسخ
برای اینکه بتوانیم کار نیروی وارد شده توسط شخص به فنر را پیدا کنیم، لازم است از فرمول زیر استفاده کنیم:
اما در این فرمول باید ثابت فنر مشخص باشد. پس ابتدا قانون هوک را مینویسیم:
دقت کنید ثابت فنر همیشه عدد مثبتی است و فعلا بدون در نظر گرفتن علامت منفی در فرمول، آن را به دست آوردیم. همچنین میزان کشیدگی فنر باید بر حسب متر نوشته شود نه سانتیمتر. بنابراین کار نیروی فنر برابر خواهد شد با:
در حالت بعدی با همان میزان فشردگی، فقط جهت جابجایی عوض میشود. بنابراین در حالت دوم اندازه کار همین مقدار است اما با علامت مثبت:
مسیر یادگیری فیزیک مکانیک دانشگاهی با فرادرس
فیزیک مکانیک از مهمترین مباحث کتابهای فیزیک پایه دانشگاهی محسوب میشود و مبحث کار در فیزیک و فرمول آن نیز در این کتابها با جزئیات بیشتری توضیح داده میشود. فرادرس با تهیه چند فیلم آموزشی در همین زمینه، به شما کمک میکند تا یادگیری عمیقتری داشته باشید. لیست این دورهها در ادامه برای شما قرار داده شده است:
- فیلم آموزش رایگان مقدمه ای بر فیزیک پایه ۱ فرادرس
- فیلم آموزش فیزیک پایه ۱ + حل مثال فرادرس
- فیلم آموزش فیزیک پایه ۱ – مرور و حل مساله فرادرس
- فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله فرادرس
- فیلم آموزش فیزیک پایه ۱ – مرور و حل تست فرادرس
- فیلم آموزش فیزیک پایه ۱ – گرانش و نوسان فرادرس
جمعبندی
در این مطلب از مجله فرادرس یاد گرفتیم فرمول کار در فیزیک عبارت است از یا ضرب داخلی نیرو در جابجایی، که در آن معادل کار انجام شده توسط نیروی روی جسم است و با ژول () اندازهگیری میشود. همان نیروی وارد بر جسم بر حسب نیوتن ()، معادل جابجایی جسم بر حسب متر () و زاویه بین بردار نیرو و جابجایی و بر حسب درجه است. پس طبق این فرمول، یک ژول انرژی یا یک ژول کار برابر است با یک نیوتن در متر.
همچنین بر اساس فرمول کار در فیزیک آموختیم که کار انجام شده توسط یک نیروی مشخص صفر میشود، اگر جسم در اثر دریافت این نیرو هیچگونه جابجایی نداشته باشد یا زاویه بین جابجایی و نیرو قائمه باشد. چنانچه کار انجام شده مقدار مثبتی بهدست آید، به این معنا است که بردارهای نیرو و جابجایی همجهت هستند. در حالی که اگر جهت جابجایی و نیرو مخالف هم باشد، کار انجام شده توسط نیرو روی جسم منفی است.
source
