در مطالب قبلی مجله فرادرس با نحوه رسم نمودار سینوس و کسینوس آشنا شدیم. در این نوشته به بررسی نمودار دو تابع مثلثاتی دیگر به نام تانژانت (tan) و کتانژانت (cot) میپردازیم. توابع تانژانت و کتانژانت در محاسبات موردنیاز جهت پیدا کردن فواصل مختلف، مانند ارتفاع ساختمانها کاربرد گستردهای دارند. بنابراین بهتر است با مراحل رسم نمودار تانژانت و کتانژانت نیز آشنا شویم.

در این مطلب از مجله فرادرس ابتدا یاد میگیریم ویژگیهای توابع تانژانت و کتانژانت از لحاظ دامنه و برد، دوره تناوب و زوج یا فرد بودن به چه صورت است. سپس با در نظر گرفتن همین ویژگیها، نشان میدهیم مراحل رسم نمودار تانژانت و کتانژانت چیست و چگونه میتوانیم محل قرارگیری مجانب قائم یا تغییراتی مانند کشیدگی یا فشردگی نمودار، جابجایی روی محور قائم یا شیفت فاز در راستای افق را برای این توابع محاسبه کنیم.
نمودار تانژانت و کتانژانت
تطابق یا برای متغیری مانند ، تابعی به نام تانژانت یا کتانژانت را تعریف میکند. در مقایسه با توابع سینوس و کسینوس، تانژانت و کتانژانت در نقاط خاصی دارای مقادیر تعریف نشدهاند و هر جا که بینهایت شوند، مجانب قائم داریم.
جدول زیر نشان میدهد چگونه میتوانیم هر نوع نمودار تانژانت و کتانژانت را با پیدا کردن پنج نقطه و اتصال آنها به هم، رسم کنیم:
| مراحل رسم نمودار | tan | cot |
| مقایسه و تعیین و و و | ||
| محاسبه دوره تناوب | ||
| محاسبه مکان اولین مجانب | ||
| محاسبه مکان دومین مجانب | ||
| میزان جابجایی روی محور عمودی | ||
| مختصات نقطه شروع دوره اول | ||
| مختصات نقطه پایانی دوره اول | ||
| مختصات نقطه مرکزی دوره اول | ||
| نقطه بین یک و سه در تناوب اول | ||
| نقطه بین سه و دو در تناوب اول |
پیش از اینکه به توضیح مراحل رسم نمودار تانژانت و کتانژانت بپردازیم، ابتدا لازم است با این دو نوع تابع مثلثاتی و خصوصیات آنها مانند دوره تناوب، زوج یا فرد بودن و … آشنا شویم. دانستن این ویژگیها در رسم نمودار تانژانت و کتانژانت بسیار موثر است.
معرفی توابع مثلثاتی تانژانت و کتانژانت
در ابتدای نوشته به این نکته اشاره کردیم که از توابع تانژانت و کتانژانت جهت محاسبه فواصلی مانند ارتفاع ساختمانها و … استفاده میشود. اما اگر بخواهیم فاصله یا مسافتی که دائما در حال تکرار است را اندازهگیری کنیم، باز هم این توابع میتوانند به ما کمک کنند.

برای مثال، موقعیتی را تصور کنید که یک ماشین پلیس در کنار ساختمانی پارک کرده است، در حالی که چراغ هشدار آن مرتبا در حال چرخیدن و تولید نور قرمز است. نور حاصل از این چراغ روی دیوار ساختمان فواصلی را میپیماید که بهطور دورهای در حال تکرار هستند.
در واقع اگر در این آزمایش ورودی را زمان در نظر بگیریم، خروجی مسافتی خواهد بود که پرتو نور میپیماید. در چنین شرایطی تابع تانژانت میتواند این فواصل را بهطور تقریبی تعیین کند. به علاوه دانستن مجانبهای نمودار تانژانت و کتانژانت در به تصویر کشیدن این دورههای تکرار شده لازم است. بنابراین یکی از مهمترین کاربردهای نمودار تانژانت و کتانژانت، ترسیم و نمایش فواصل تکرار شده است.
توابع تانژانت و کتانژانت هم مانند توابع سینوس و کسینوس، میتوانند بر حسب متغیری مانند یا بیان شوند. در هر دو حالت، جنس این متغیر از زاویه است، یعنی توابع تانژانت و کتانژانت هر دو بر حسب زاویه رسم میشوند که این زاویه میتواند بر حسب درجه یا رادیان باشد.
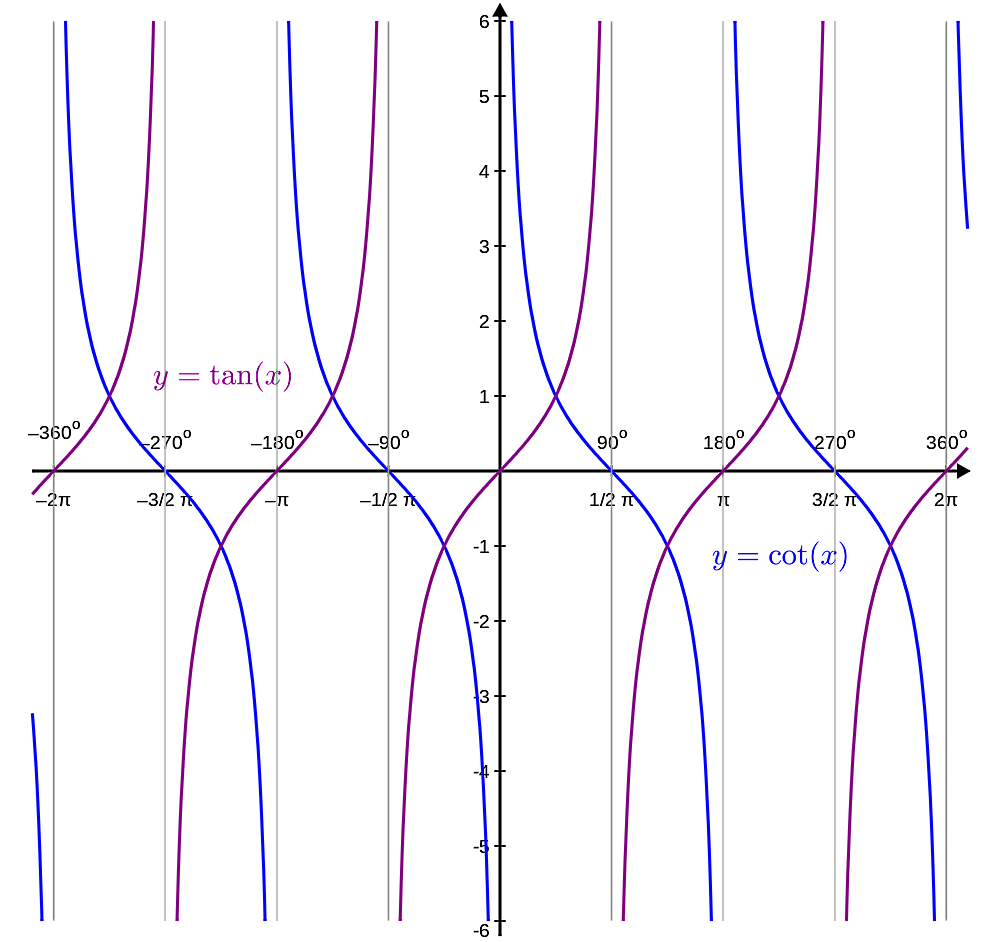
نحوه نمایش کلی این توابع نیز به شکل و است، یعنی معمولا تانژانت یا کتانژانت متغیری مانند را با متغیر دیگری به نام برابر قرار میدهیم. به این ترتیب، رسم نمودار تانژانت و کتانژانت با رسم بر حسب انجام خواهد شد.
تابع تانژانت از تقسیم تابع مثلثاتی سینوس بر کسینوس حاصل میشود:
پس مقادیر تابع تانژانت با استفاده از تعریف بالا بهدست میآیند. در بخش رسم نمودار توضیحات بیشتری در این زمینه خواهیم داد. این در حالی است که تابع کتانژانت از تقسیم تابع مثلثاتی کسینوس بر سینوس بهدست میآید:
پس همینجا میتوانیم بهراحتی رابطه بین توابع تانژانت و کتانژانت را نتیجهگیری کنیم. تابع کتانژانت همواره عکس تابع تانژانت است:
دوره تناوب توابع تانژانت و کتانژانت
یکی از مهمترین خصوصیات توابع مثلثاتی، دورهای یا تناوبی بودن آنها است. به تابعی مانند یک تابع متناوب گفته میشود، در صورتی که تساوی به ازای عدد مثبتی مانند همواره برای آن برقرار باشد. در این صورت به کوچکترین مقدار در صورتی که وجود داشته باشد، دوره تناوب تابع گفته میشود.
گفتیم تمام توابع مثلثاتی متناوباند. برای مثال، توابع سینوس و کسینوس دوره تناوبی برابر با رادیان یا درجه دارند، در حالی که دوره تناوب توابع تانژانت و کتانژانت معادل است با رادیان یا درجه. بنابراین شکل خاص نمودار تانژانت و کتانژانت پس از رادیان مجددا تکرار میشود.
جدول زیر نشان میدهد که چگونه میتوانیم دورهای بودن توابع مثلثاتی را در قالب ریاضیات و با در نظر گرفتن بهعنوان یک عدد صحیح، نشان دهیم:
| تابع مثلثاتی | رابطه دورهای بودن تابع مثلثاتی | دوره تناوب |
| تابع سینوس | ||
| تابع کسینوس | ||
| تابع تانژانت | ||
| تابع کتانژانت |
بنابراین هر بخش از تابع متناوب شامل نقطهای مانند تا نقطهای بهصورت (با توجه به اینکه گفتیم دوره تناوب تابع است)، یک دوره یا یک چرخه از تابع نامیده میشود. برای مثال در مورد تابع تانژانت با دوره تناوب ، دوره میتواند از تا باشد و یا ممکن است از تا بهعنوان دوره در نظر گرفته شود. بنابراین نقاط شروع و انتهای دوره در نمودار تانژانت و کتانژانت میتوانند متفاوت باشند، اما در هر حال میدانیم فاصله بین این دو نقطه همواره با برابر است.
زوج یا فرد بودن توابع تانژانت و کتانژانت
برای اینکه بتوانیم رسم نمودار تانژانت و کتانژانت را بهدرستی انجام دهیم، دانستن زوج یا فرد بودن این توابع مهم است. میدانیم تابعی مانند وقتی زوج است که داشته باشیم:
رابطه بالا بیان میکند که اگر برای تابع ، ورودی منفی شود یا به تبدیل شود، اما در خروجی آن تغییری ایجاد نشود، در این صورت زوج است. این در حالی است که برای تابع فرد تعریف به شکل زیر خواهد بود:
یعنی اگر برای تابع ، ورودی منفی شود یا به تبدیل شود و نتیجه اثر تابع روی متغیر هم منفی شود، در این صورت یک تابع فرد است. برای تشخیص زوج یا فرد بودن توابع تانژانت و کتانژانت میتوانیم از دانش خود در مورد زوج یا فرد بودن تابع سینوس و کسینوس و اینکه چطور توابع تانژانت و کتانژانت از این دو تابع ساخته میشوند، استفاده کنیم. میدانیم سینوس یک تابع فرد و کسینوس یک تابع زوج است، یعنی داریم:
پس با در نظر گرفتن رابطه تانژانت با این دو تابع و تبدیل به برای ، خواهیم داشت:
اگر رابطه بالا را با تعریف تابع فرد مقایسه کنیم، متوجه میشویم که تانژانت یک تابع فرد است. حالا میتوانیم همین روند را برای تابع کتانژانت هم اعمال کنیم تا زوج یا فرد بودن این تابع نیز مشخص شود:
پس کتانژانت نیز یک تابع فرد است. دقت کنید کسینوس تنها تابع مثلثاتی است که زوج محسوب میشود. در جدول زیر خلاصهای از مبحث زوج یا فرد بودن توابع مثلثاتی را مشاهده میکنید:
| تابع مثلثاتی | رابطه زوج یا فرد بودن تابع مثلثاتی | زوج یا فرد |
| تابع سینوس | فرد | |
| تابع کسینوس | زوج | |
| تابع تانژانت | فرد | |
| تابع کتانژانت | فرد |
یکی دیگر از مهمترین جنبههای زوج یا فرد بودن یک تابع، نوع تقارن آن است. این مسئله هنگام رسم نمودار تانژانت و کتانژانت اهمیت خود را بیشتر نشان میدهد. عموما توابع فرد تقارن مرکزی دارند، در حالی که توابع زوج تقارن محوری دارند، یعنی نسبت به یک خط یا یک محور تقارن دارند.
برای مثال، اگر نمودار توابع مثلثاتی در جدول بالا را مطابق شکل زیر رسم کنیم، مشاهده میکنید که برای تابع کسینوس میتوانیم محور عمودی دستگاه مختصات را بهعنوان محور تقارن در نظر بگیریم، به این معنا که هر نقطه از نمودار کسینوس در یک سمت از این خط، متناظر است با نقطه کاملا مشابهی در سمت دیگر.
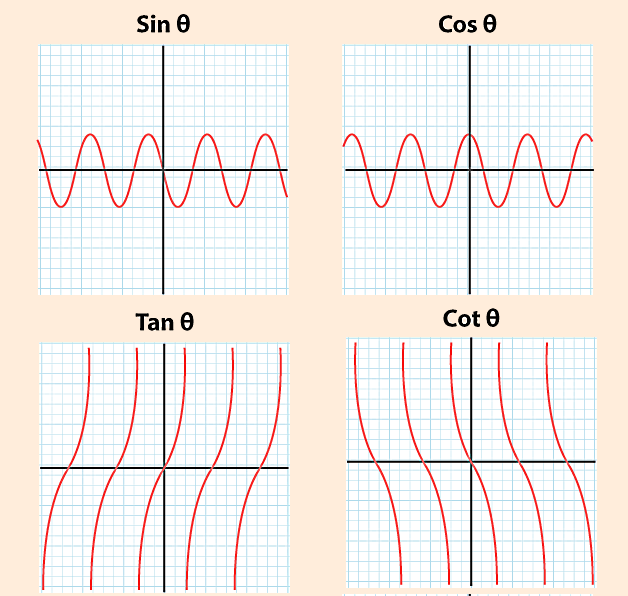
به عبارت دیگر اگر چه برای هر دو نقطه متناظر فرضی در دو طرف خط، مقادیر منفی میشوند، اما مقادیر کاملا مشابه هم هستند. اما در مورد سه نمودار دیگر تقارنی نسبت به محور وجود ندارد، بلکه تقارن نسبت به نقطهای مانند مبدا مختصات است، به این شکل که با منفی شدن مقادیر ، مقادیر توابع مثلثاتی هم منفی میشوند.
دامنه و برد توابع تانژانت و کتانژانت
با نگاه کردن به شکل بخش قبل، میتوان حدس زد که برد توابع تانژانت و کتانژانت مقدار مشخصی ندارند. در فصل دوم از فیلم آموزشی حسابان یازدهم همراه با حل تمرین فرادرس با عنوان «تابع»، به مبحث دامنه و برد پرداخته شده است. همچنین فصل سوم این دوره آموزشی به مبحث مثلثات اختصاص داده شده است. از آنجا که این آموزش همراه با حل تمرین ارائه شده، میتواند در یادگیری شما بسیار موثر باشد. لینک آن را در ادامه برای شما قرار میدهیم:
دامنه یا Domain یک تابع مثلثاتی عبارت است از مجموعه مقادیری از یا که بهعنوان ورودی به یک تابع مثلثاتی داده میشود، در حالی که برد یا Range با خروجی تابع مثلثاتی یا اثر تابع مثلثاتی روی مقادیر یا معادل است. جدول زیر دامنه و برد این دو تابع را همراه با دامنه و برد توابع سینوس و کسینوس جهت مقایسه، نشان میدهد:
| تابع مثلثاتی | دامنه ( یک عدد صحیح است) | برد |
| تابع سینوس | یا اعداد حقیقی | |
| تابع کسینوس | یا اعداد حقیقی | |
| تابع تانژانت | اعداد حقیقی بهجز مضارب فرد | |
| تابع کتانژانت | اعداد حقیقی بهجز مضارب |
چگونه مثلثات در متوسطه را با فرادرس بهتر یاد بگیریم؟
اگر قصد دارید به مبحث مثلثات در مقطع متوسطه مسلط شوید، در این بخش لیستی از چند فیلم آموزشی تهیه شده در مجموعه فرادرس را برای شما جمعآوری کردهایم. مشاهده این دورهها که بر اساس سرفصلهای کتابهای درسی تهیه شدهاند، به شما کمک میکند تا با حل تمرینهای متنوعتر، یادگیری عمیقی در این زمینه داشته باشید:
- فیلم آموزش رایگان سینوس، کسینوس و تانژانت + محاسبه نسبت های مثلثاتی فرادرس
- فیلم آموزش ریاضی دهم فرادرس
- فیلم آموزش ریاضی یازدهم علوم تجربی فرادرس
- فیلم آموزش ریاضی دوازدهم علوم تجربی فرادرس
- فیلم آموزش حسابان یازدهم فرادرس
- فیلم آموزش حسابان یازدهم – حل تمرین فرادرس
- فیلم آموزش رایگان مثلثات– تناوب و تانژانت در حسابان دوازدهم فرادرس
- فیلم آموزش حسابان دوازدهم فرادرس
رسم نمودار Y= tan(x)
در بخشهای قبل گفتیم تابع تانژانت هم مانند سایر توابع مثلثاتی یک تابع تناوبی محسوب میشود. در این بخش با رسم نمودار آن، تناوبی بودن این تابع را بهتر متوجه خواهید شد. پس از اینکه در این بخش و بخش بعد یاد گرفتیم شکل نمودار تانژانت و کتانژانت در سادهترین حالت ممکن به چه صورت است، مراحل رسم این نمودارها را توضیح میدهیم تا بتوانید انواع توابع تانژانت و کتانژانت با مقادیر دوره، دامنه و تغییر فاز متفاوت را رسم کنید.
میخواهیم تابع تانژانت را با در نظر گرفتن نقطه شروع دوره تناوب از زاویهای برابر با رادیان، رسم کنیم. چون دوره تناوب تابع تانژانت برابر با رادیان است، پس واضح است که نقطه انتهای دوره ما در رسم نمودار میشود:
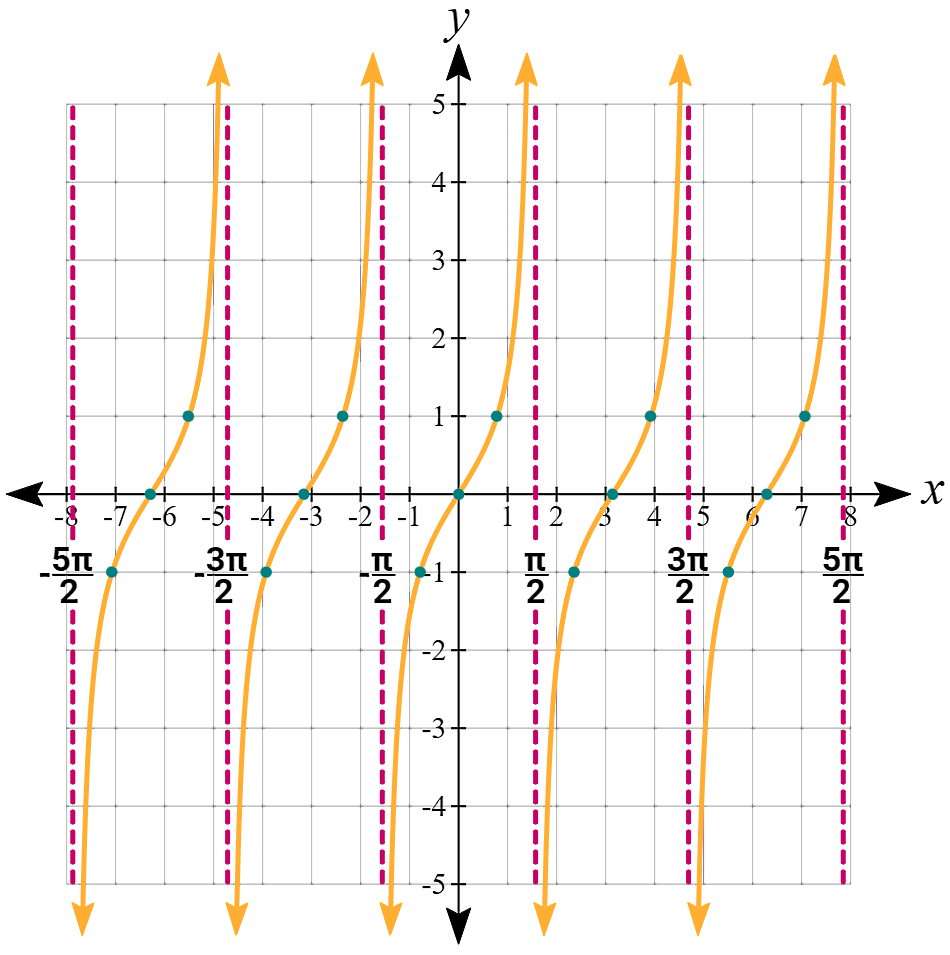
رسم نمودار برای زاویههایی بیشتر از نیاز نیست، چون میدانیم این زاویهها در دوره بعدی قرار میگیرند و شکل نمودار مجددا تکرار میشود. به همین علت است که معمولا رسم یک دوره تناوب از نمودار توابع مثلثاتی کافی است. با در نظر گرفتن نه نقطه، شامل زاویههای ، مقادیر تانژانت برای هر زاویه بهصورت جدول زیر خواهد بود:
| تعریف نشده | |
| تعریف نشده |
برای محاسبه مقادیر تابع تانژانت در هر زاویه داده شده، کافی است از فرمول آن که بر حسب توابع سینوس و کسینوس است، استفاده کنیم. برای نمونه، نقطهای با مختصات را در نظر بگیرید. میخواهیم ببینیم این نقطه چگونه حاصل شده است. فرمول تابع تانژانت را برای زاویهای برابر با رادیان، به شکل زیر مینویسم:
در رابطه بالا از این واقعیت استفاده کردیم که و . همچنین بهتر است برای دو نقطه مهم در دو زاویه و نیز مقدار تانژانت را محاسبه کنیم:
در انتهای رابطه بالا از این نکته کمک گرفتیم که حاصل عدد تقسیم بر صفر همواره با بینهایت برابر است. در ریاضیات بینهایت را تعریف نشده نیز بیان میکنند. بینهایت شدن مقدار تانژانت در زاویه ، از صفر شدن مخرج رابطه بالا ناشی شد. به همین شکل برای زاویه هم همین رابطه تکرار خواهد شد، چون کسینوس این زاویه نیز همیشه برابر با صفر است:
یک تفاوت خیلی کوچک در مقادیر بینهایت برای این دو زاویه وجود دارد و آن، علامت مثبت و منفی است. با رسم نمودار تانژانت و کتانژانت، این تفاوت را بهتر متوجه خواهید شد.
برمیگردیم به ادامه روند رسم نمودار تانژانت. اگر به جدول بالا دقیقتر نگاه کنیم، میتوانیم با تبدیل مقادیر به ، روند مشخصی را برای نمودار تانژانت پیدا کنیم. برای مثال، میتوانیم بهجای بنویسیم ، یا میتوانیم بهطور تقریبی را جایگزین کنیم:
به این ترتیب بهتر متوجه میشویم که با نزدیک شدن به زاویه ، خروجی تابع تانژانت بزرگتر و بزرگتر میشود. چون تانژانت یک تابع فرد است، همین روند را برای مقادیر منفی داریم، اما با علامت منفی:
تفسیر جدول بالا به این صورت میشود که با نزدیک شدن مقادیر به زاویه ، خروجی تابع تانژانت کوچک و کوچکتر میشود. به علامت منفی برای مقادیر تانژانت دقت کنید. بنابراین مهمترین نکته در رسم نمودار تانژانت این است که در نظر داشته باشیم برای برخی از مقادیر زاویهای مقدار تابع کسینوس در مخرج صفر میشود. در نتیجه در این زاویهها، تانژانت بینهایت است.
حالا باید ببینیم در نمودار تانژانت و کتانژانت بینهایت چگونه نشان داده میشود. در این نمودارها در نقاط خاصی ناپیوستگی یا انفصال داریم که نشاندهنده مقادیر بینهایت تابع تانژانتاند. در ریاضیات برای نمایش این ناپیوستگی، از مفهومی به نام مجانب استفاده میشود که به صورت خطوط عمودی (معمولا خطچین) در نمودار نشان داده میشوند.
رای مثال در جدول اول، دو مقدار بینهایت داشتیم که هر کدام متناظر با یک مجانب قائم در نمودار تانژانت خواهند بود. زاویههای زیر محل قرار گرفتن مجانبهای قائم در نمودار را نشان میدهند:
به این ترتیب با در نظر گرفتن نه نقطه در اولین جدول این بخش، اتصال این نقاط به شکل یک منحنی و رسم مجانبها، نمودار به شکل زیر خواهد شد:
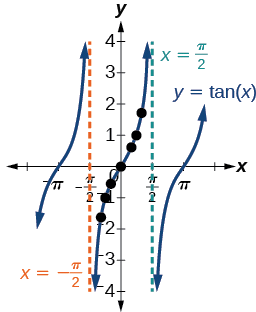
دقت کنید در شکل بالا، نمودار برای دو دوره دیگر هم تکرار شده است. همانطور که از مقادیر جداول مشخص بود، طبق تصویر تانژانت در بازههایی مثل تا و تا مثبت است. این دو بازه با ربع اول و سوم در دایره مثلثاتی متناظر هستند. اگر تمایل دارید در مورد سایر مباحث مرتبط با تانژانت مانند محاسبه آرک تانژانت، اطلاعات بیشتری کسب کنید، میتوانید به مطلب «آرک تانژانت چیست و چگونه محاسبه می شود؟ – به زبان ساده» از مجله فرادرس مراجعه کنید.
رسم نمودار Y= cot(x)
در ادامه رسم نمودار تانژانت و کتانژانت، در این بخش میخواهیم نحوه رسم نمودار کتانژانت را که بسیار شبیه به نمودار تانژانت است، توضیح دهیم. همانطور که گفتیم، فرمول کتانژانت عکس فرمول تانژانت است، یعنی داریم:
طبق رابطه بالا، در زاویههایی که تانژانت برابر است با صفر، کتانژانت بینهایت خواهد شد. بنابراین در این زاویهها مجانب عمودی خواهیم داشت. این زاویهها برای نمودار عبارتاند از:
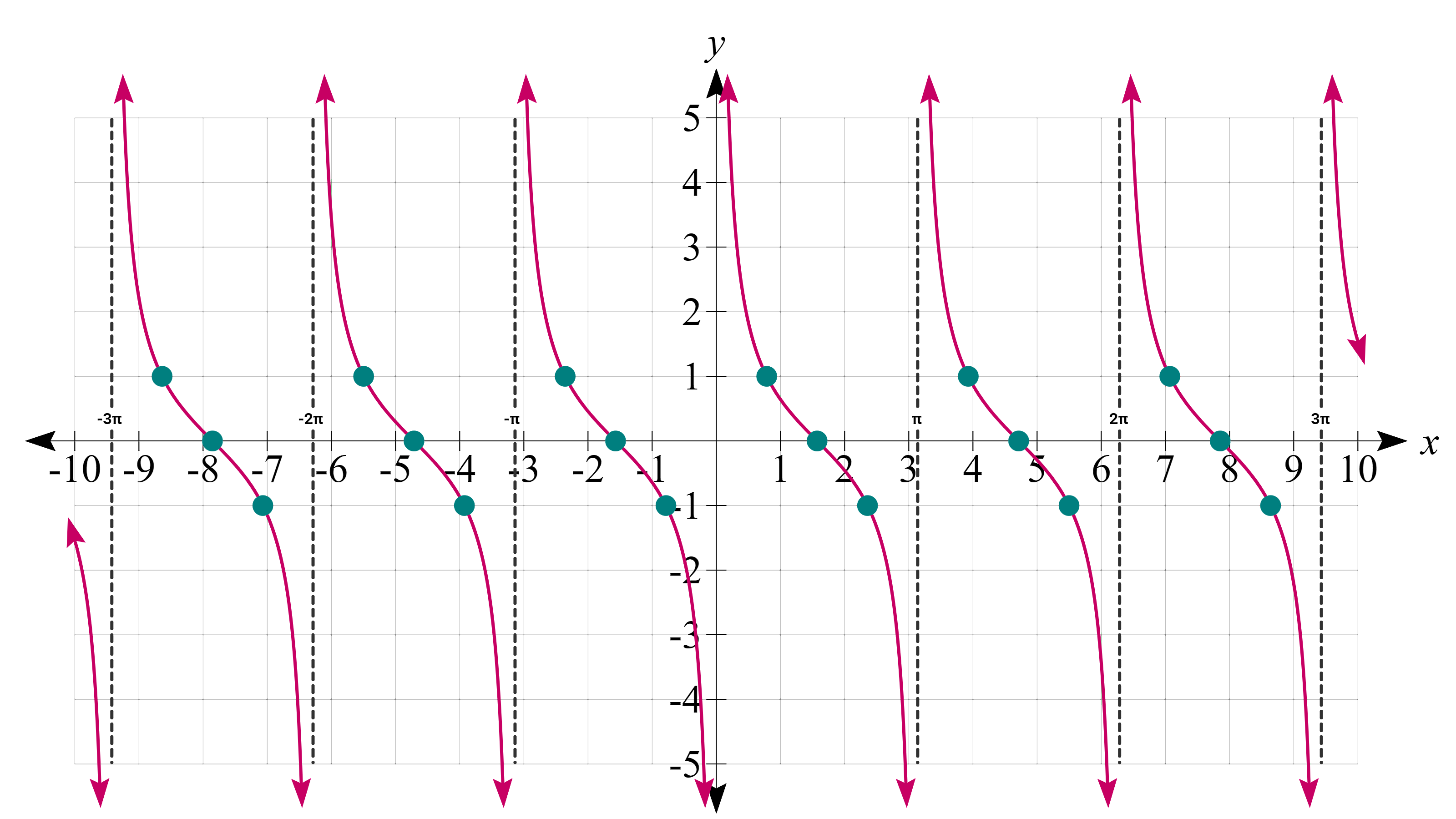
از آنجا که خروجی تابع تانژانت همیشه یک عدد حقیقی است، خروجی تابع کتانژانت نیز همواره در مجموعه اعداد حقیقی قرار میگیرد. از طرفی چون این دو تابع عکس هم هستند، پس هر جایی که تانژانت زیاد میشود، کتانژانت کم میشود و برعکس. برای مثال، مجانبهای قائم نمودار کتانژانت در زاویههایی است که اشاره کردیم. این زاویهها دقیقا معادل هستند با زاویههایی که تانژانت صفر میشود. به همین ترتیب، هر جا که کتانژانت صفر شود، برای تانژانت مجانب قائم داریم.
بنابراین رسم نمودار با تهیه جدولی مانند جدول نمودار تانژانت، اتصال نقاط تعیین شده و تعیین مجانبها انجام میشود:
| تعریف نشده | |
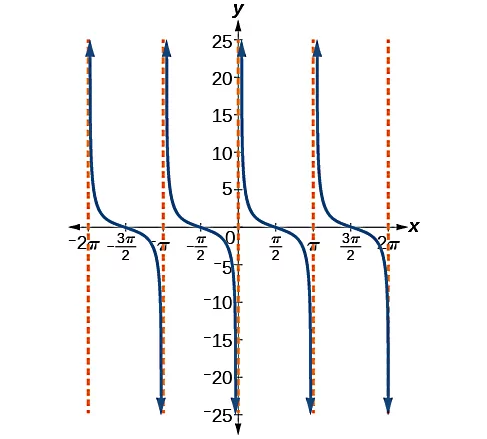
در تصویر زیر نمودار کتانژانت برای چهار دوره رسم شده است، در حالی که بازه در نظر گرفته شده در جدول بالا از تا است.
مراحل رسم نمودار تانژانت و کتانژانت
در بخشهای قبل یاد گرفتیم چگونه نمودار تانژانت و کتانژانت را با عدددهی به سادهترین شکل ممکن رسم کنیم. اما در واقعیت این شیوه برای رسم نمودار توابع مثلثاتی بسیار وقتگیر است. بهویژه اینکه در عمل ممکن است با توابع سادهای مانند یا سروکار نداشته باشیم و تابع مثلثاتی ما دارای کشیدگی یا فشردگی باشد یا نسبت به محور افقی یا قائم دستگاه مختصات، جابجایی داشته باشد.
در این بخش میخواهیم یک روش کلی برای رسم این دو نمودار را به شما معرفی کنیم که با رعایت دقیق مراحل آن، بتوانید هر نوع نمودار تانژانت و کتانژانت را رسم کنید. مراحل رسم نمودار تانژانت و کتانژانت به شکل کلی زیر عبارتاند از:
- مرتب کردن معادله و تشخیص ثوابت
- محاسبه دوره تناوب، فاکتور کشیدگی یا فشردگی و مجانبها
- تعیین جابجایی نمودار روی محور عمودی
- تعیین نقاط اصلی و رسم نمودار
یکی از مهمترین نکات برای رسم نمودار تانژانت و کتانژانت این است که تفاوت این دو نمودار را بدانیم. شکل این دو نمودار ممکن است کاملا شبیه هم باشد، اما چیزی که میتواند به ما در تشخیص این دو از هم کمک کند، مختصات نقاطی است که مجانبها در آن قرار گرفتهاند. در مورد تابع تانژانت، همیشه مجانبهای قائم در زاویههای زیر قرار دارند:
این در حالی است که برای نمودار کتانژانت، مجانبهای قائم در زاویههای زیر دیده میشوند:
برای مثال، اگر نموداری شبیه به نمودار تانژانت و کتانژانت باشد و در مبدا مختصات یا در نقطه ، مجانب قائم داشته باشد، حتما متعلق به یک تابع کتانژانت است. در ادامه توضیحات لازم در مورد مراحل بالا ارائه خواهد شد.
مرحله اول مرتب کردن معادله و تشخیص ثوابت
اولین قدم برای رسم نمودار تانژانت و کتانژانت این است که از مقایسه تابع داده شده با فرم کلی این دو تابع، بتوانیم چند ثابت مهم را پیدا کنیم. دانستن این ثوابت در محاسبه دامنه، دوره تناوب و تغییر فاز برای مرحله بعدی به ما کمک میکند. همانطور که دیدیم، فرم کلی که برای تابع تانژانت و کتانژانت در نظر گرفتهایم، به شکل زیر است:
هدف ما تعیین ثابتهای و و و در معادله تابع تانژانت یا کتانژانت داده شده است. این ثوابت مشخص میکنند که برای مثال، تابع داده شده نسبت به فرم ساده تانژانت و کتانژانت یعنی یا چقدر دچار کشیدگی یا فشردگی شده است. در حالی که کشیدگی و فشردگی توابع تانژانت و کتانژانت به دوره تناوب و در نتیجه به ثابت وابسته است، میزان جابجایی یا تغییر فاز در راستای عمودی و افقی بهترتیب از ثوابت و تعیین میشوند.
نکته ۱: دقت کنید دامنه در این بخش معادل کلمه لاتین Amplitude است و با دامنه بهعنوان ورودی تابع مثلثاتی نباید اشتباه شود.
نکته ۲: چون در مورد توابع تانژانت و کتانژانت بیشترین و کمترین مقادیر مشخص نیستند (بینهایت هستند)، کاربرد کلمه دامنه به آن مفهومی که در مورد توابع سینوس و کسینوس بکار بردیم، چندان رایج نیست. بهجای دامنه بهتر است از عبارت فاکتور کشیدگی یا فشردگی برای بیان استفاده شود.
نکته ۳: در رسم نمودارهای تانژانت و کتانژانت، فرد بودن این توابع و تقارن آنها نسبت به نقطهای مانند مبدا (نه لزوما مبدا) را همواره در نظر داشته باشید.
مرحله دوم محاسبه دوره تناوب، فاکتور کشیدگی یا فشردگی و مجانبها
دومین قدم برای رسم نمودار تانژانت و کتانژانت محاسبه فاکتورهای مهمی مانند فاکتور کشیدگی یا فشردگی (دامنه)، دوره تناوب و تغییر فاز است. این پارامترهای مهم بهصورت زیر تعیین میشوند:
فاکتور کشیدگی یا فشردگی (دامنه) =
در مورد یا فاکتور کشیدگی یا فشردگی، دو حالت خواهیم داشت که باید در رسم نمودار تانژانت به این نکات توجه کنیم:
- اگر ، با شروع از مولفه افقی مجانب با علامت منفی به سمت مجانب با علامت مثبت، مقدار تانژانت زیاد میشود.
- اگر ، با شروع از مولفه افقی مجانب با علامت منفی به سمت مجانب با علامت مثبت، مقدار تانژانت کم میشود.
اما برای نمودار کتانژانت این روند برعکس است:
- اگر ، با شروع از مولفه افقی مجانب با علامت منفی به سمت مجانب با علامت مثبت، مقدار کتانژانت کم میشود.
- اگر ، با شروع از مولفه افقی مجانب با علامت منفی به سمت مجانب با علامت مثبت، مقدار کتانژانت زیاد میشود.
دوره تناوب این دو تابع مثلثاتی از فرمول زیر حاصل میشود:
دوره تناوب =
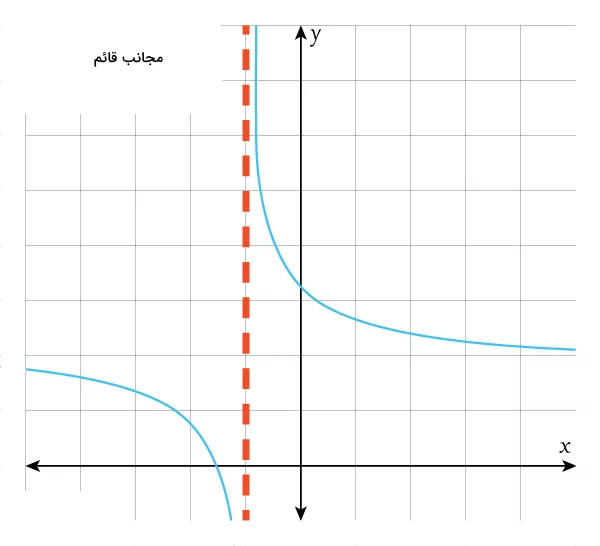
مجانب نقطهای است که مقدار تابع در آن بینهایت میشود. محاسبه دو مجانب تابع تانژانت در یک دوره تناوب، با حل کردن دو معادله زیر انجام میشود:
مقادیر بهدست آمده از این دو فرمول، نشاندهنده مکانهایی روی محور افق هستند که باید خطوط مجانب قائم در آن نقاط رسم شوند. این نقاط را به ترتیب و مینامیم. اما در مودر تابع کتانژانت، مجانبها توسط فرمولهای زیر به دست میآیند:
همانطور که گفتیم محل قرار گرفتن مجانبها برای این دو نمودار، تفاوت بزرگ آنها است. بنابراین معادلهای که این نقاط را تعیین میکند نیز برای این دو متفاوت است.
مرحله سوم تعیین جابجایی نمودار روی محور عمودی
در این مرحله از رسم نمودار تانژانت و کتانژانت، صفر نبودن ثابت مهم است. چنانچه در معادله داده شده مخالف صفر داشتیم، یعنی نمودار ما روی محور قائم مقداری جابجایی دارد. اثر این جابجایی روی مقادیر است و در بخش بعد خواهید دید چگونه باید این ثابت را در بهدست آوردن مختصات نقاط اصلی در نظر بگیریم.
نکته: دقت کنید شیفت فاز در راستای محور افقی برابر است با ، اما جایجایی یا شیفت در راستای قائم به اندازه در معادله داده شده است.
مرحله چهارم تعیین نقاط اصلی و رسم نمودار
همانطور که قبلا هم اشاره کردیم، رسم یک دوره تناوب از نمودارهای توابع مثلثاتی کافی است. معمولا این دوره را طوری در نظر میگیریم که مبدا مختصات را شامل شود. تناوبی بودن این توابع، این امکان را به ما میدهد تا از دو طرف و در محدوده مجاز برای دامنه یا مقادیر مجاز ، تابع را با توجه به تناوباش تکرار کنیم.
اصولا برای رسم یک دوره تناوب از نمودار یک تابع مثلثاتی بهتر است مختصات پنج نقطه را بهعنوان نقاطی اصلی یا بحرانی یا مرجع تعیین کنیم که با اتصال آنها، شکل نمودار بهخوبی مشخص میشود. این پنج نقطه عبارتاند از نقاط ابتدا و انتهای اولین دوره تناوب، نقطه میانی دوره و دو نقطهای که بین نقاط ابتدا/انتهای دوره و نقطه میانی قرار میگیرند. این نقاط را بهترتیب زیر نامگذاری میکنیم:
- : نقطه شروع اولین دوره تناوب
- : نقطه پایانی اولین دوره تناوب
- : نقطه مرکزی اولین دوره تناوب
- : نقطه میانی بین اولین نقطه و نقطه مرکزی اولین دوره تناوب
- : نقطه میانی بین آخرین نقطه و نقطه مرکزی اولین دوره تناوب
هر کدام از این نقاط دارای یک مقدار و یک مقدار یا است که در مجموع مختصات آن نقطه نامیده میشود. برای مثال، اگر بخواهیم تابع تانژانت ساده به شکل را بدون رسم جدول مقادیر و عدددهی رسم کنیم، اولین کار این است که این معادله را با مقایسه کنیم که در نتیجه، و و . بنابراین طبق بخشهای قبل، خواهیم داشت:
فاکتور کشیدگی یا فشردگی (دامنه) =
توجه داریم که چون است، انتظار داریم با رفتن از نقطه به سمت نقطه ، مقدار تانژانت در نمودار زیاد شود که طبق شکل رسم شده برای این نمودار در بخش قبل، همین اتفاق میافتد.
دوره تناوب =
دو مجانب این نمودار نیز به شکل زیر بهدست خواهند آمد:
پس دوره تناوب برابر شد با . چون تابع تانژانت فرد است، پس باید نسبت به یک نقطه متقارن باشد. بهتر است این نقطه را در مبدا مختصات انتخاب کنیم. به این ترتیب، مبدا در نقطه مرکزی دوره تناوب واقع میشود. در ادامه جزئیات بیشتری برای پیدا کردن مکان دقیق این نقاط بیان میکنیم.

تعیین نقاط ابتدا و انتهای دوره تناوب
پس از محاسبه مجانبها و دوره تناوب، دو مولفه نقاط ابتدا و انتهای دوره را باید بهدست آوریم. نقاط ابتدا و انتهای دوره برای تابع تانژانت و کتانژانت همان نقاطی هستند که مجانب داریم. بهعبارت دیگر، با محاسبه دو مجانب قائم، میدانیم که مقدار تابع تانژانت در این دو مقدار از بینهایت میشود.
پس میتوانیم مختصات نقاط ابتدایی و انتهایی دوره تناوب را برای تابع تانژانت بهصورت زیر در نظر بگیریم:
دقت کنید در مختصات بالا میتوانیم بهجای بنویسیم . همچنین به یاد داشته باشید که منظور ما در این نوشته از نقطه دوم، همان نقطه پایانی دوره تناوب اول است. همچنین برای تابع کتانژانت، محل قرار گرفتن دو مجانب روی محور افق برابر است با:
بنابراین مختصات نقاط ابتدا و انتهای دوره در یک نمودار کتانژانت به شکل زیر است:
تعیین نقطه مرکزی دوره تناوب
اگر از مکان نقطه ابتدای دوره روی محور افقی به اندازه نصف دوره در جهت مثبت محور جلو برویم، به سومین نقطه از دوره تناوب که همان نقطه مرکزی است، خواهیم رسید. پس مولفه افقی نقطه سوم در نمودار تانژانت برابر است با:
مولفه قائم سومین نقطه با فرمول زیر تعیین خواهد شد:
پس مختصات سومین نقطه از اولین دوره تناوب برای تانژانت معادل است با:
اما در مورد نمودار کتانژانت برای مولفه افقی سومین نقطه دقیقا مشابه تانژانت عمل میکنیم. با در نظر گرفتن مکان نقطه اول این تابع و پیش رفتن به اندازه نصف دوره، داریم:
مولفه قائم برای این نقطه مشابه با مولفه قائم نقطه سوم نمودار تانژانت است. پس مختصات نقطه سوم در نمودار کتانژانت میشود:
تعیین نقاط چهارم و پنجم دوره تناوب
برای بهدست آوردن مکان چهارمین نقطه از دوره تناوب روی محور افقی، کافی است از نقطه شروع به اندازه یک چهارم دوره در جهت مثبت محور پیش برویم. به این ترتیب این نقطه برای نمودار تانژانت میشود:
مکان افقی نقطه پنجم نیز با طی کردن مسافتی به اندازه سه چهارم دوره روی محور افقی حاصل میشود که در مورد تانژانت به شکل زیر بهدست میآید:
مولفه قائم برای این دو نقطه عبارتاند از:
در مورد اینکه در رابطه بالا کدام علامت باید انتخاب شود، لازم است به علامت ثابت در معادله داده شده و روند نمودار توجه کنیم. در بخش مثالها، متوجه تفاوت کاربرد این دو علامت خواهید شد. به این ترتیب مختصات نقاط چهارم و پنجم از اولین دوره تناوب برابر است با:
در مورد کتانژانت هم مثل تانژانت عمل میکنیم. فقط تفاوت مختصات نقاط ابتدا و انتهای دوره برای این دو نمودار باید در نظر گرفته شود:
فرمول مولفه قائم هم دقیقا مشابه با نمودار تانژانت است:
پس مختصات این دو نقطه در نمودار کتانژانت معادل است با:
حل مثال و تمرین رسم نمودار سینوس و کسینوس
پس از اینکه تمام جزئیات مربوط به رسم نمودار تانژانت و کتانژانت را آموختیم، در این بخش قصد داریم با حل و بررسی مثالهای متنوع به شما کمک کنیم تا به روند رسم این نمودارها کاملا مسلط شوید. همچنین در انتهای این بخش، چند سوال چهار گزینهای بهعنوان تمرین برای شما در نظر گرفته شده است تا با حل آنها بتوانید مهارت خود را در زمینه رسم نمودار تانژانت و کتانژانت بیازمایید.
مثال ۱
نمودار تابع تانژانتی زیر را برای یک دوره تناوب رسم کنید:
پاسخ
اولین قدم برای رسم نمودار تانژانت و کتانژانت این است که فرم کلی این توابع را با معادله داده شده مقایسه کنیم و ثوابت مهم را پیدا کنیم. بنابراین با نوشتن معادله کلی تابع تانژانت خواهیم داشت:
حالا میتوانیم دوره تناوب و مجانبها را محاسبه کنیم:
دوره تناوب =
با توجه به دو مجانبی که بهدست آمد، حالا میدانیم در های متناظر با این ها، ناپیوستگی داریم. بنابراین مختصات نقاط ابتدایی و انتهایی دوره برابر است با:
برای تعیین سومین نقطه در دوره که همان مرکزیترین نقطه محسوب میشود، باید از نقطه ابتدای دوره به اندازه نصف دوره تناوب جلو برویم. طبق محاسبات دیدیم که فرمول نهایی برای مولفه افقی این نقطه به شکل زیر خواهد شد. چون در این سوال ثابت ، پس خواهیم داشت:
با صفر شدن ، میدانیم تانژانت زاویه صفر نیز همیشه برابر است با صفر (). طبق فرمول هم مولفه عمودی برای این نقطه نداریم:
بنابراین سومین نقطه از دوره به شکل زیر است:
همچنین فرمولی که برای تعیین مولفه افقی نقاط چهارم و پنجم داشتیم به شکل زیر میشود:
مولفههای قائم متناظر با این نقاط نیز برابر هستند با:
انتخاب علامت منفی برای نقطه چهارم و علامت مثبت برای نقطه پنجم انجام میشود. با توجه به علامت مثبت در این سوال، لازم است روند افزایشی نمودار تانژانت رعایت شود. پس مولفه قائم نقطه چهارم که به مجانب اول نزدیکتر است، باید نسبت به مولفه قائم نقطه پنجم که به مجانب دوم نزدیکتر است، مقدار کمتر یا منفیتری داشته باشد. به این ترتیب، مختصات نقاط چهارم و پنجم میشود:
پنج نقطه موردنظر ما برای رسم این نمودار بهدست آمدند. با اتصال این نقاط و رسم دو مجانب قائم در نقاط متناظر، نمودار این تابع به شکل زیر خواهد شد:
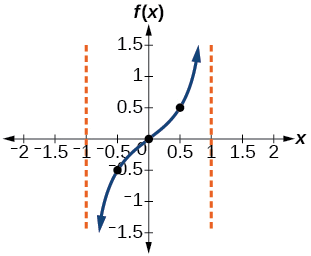
مثال ۲
نمودار تابع تانژانت با معادله را رسم کنید:
پاسخ
ابتدا فرم کلی این توابع را با معادله داده شده مقایسه میکنیم تا ثوابت مهم تعیین شوند:
حالا به محاسبه دوره تناوب و مجانبها میپردازیم:
دوره تناوب =
این دو نقطه بیانگر این هستند که در محل های متناظر با این ها، ناپیوستگی یا مجانب داریم. گفتیم محل قرارگیری مجانبها، مختصات نقاط ابتدا و انتهای دوره را میدهد:
همچنین گفتیم که سومین نقطه در دوره که همان مرکزیترین نقطه است، مولفه افقی بهصورت زیر دارد که چون ثابت در این مثال برابر است با صفر، پس مولفه افقی نقطه مرکزی هم صفر میشود:
از طرفی میدانیم تانژانت صفر برابر با صفر است، پس مختصات این نقطه میشود:
در نهایت با نوشتن فرمولی که برای تعیین مولفه افقی نقاط چهارم و پنجم داشتیم، خواهیم داشت:
مولفه قائم متناظر با این نقاط بهصورت زیر هستند:
پس مختصات این دو نقطه نیز به شکل زیر خواهد شد:
در این مثال هم مانند مثال قبل، چون ثابت مثبت است، پس باید روند افزایشی نمودار تانژانت بین دو مجانب رعایت شود. همین نکته باعث میشود برای مولفه قائم نقطه چهارم علامت منفی و در مورد نقطه پنجم علامت مثبت انتخاب شود. سرانجام با اتصال نقاط بالا و رسم دو مجانب قائم، نموداری به شکل زیر خواهیم داشت:
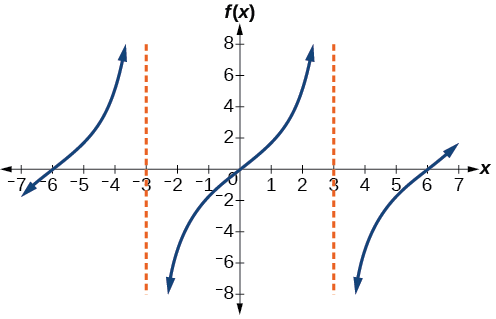
مثال ۳
نمودار تابع مثلثاتی زیر را رسم کنید:
پاسخ
ابتدا این تابع را با فرم قراردادی مقایسه میکنیم تا ببینیم ثوابت مهم ما در این سوال چه هستند:
در این مثال بر خلاف دو مثال قبلی، ثوابت و صفر نیستند. پس احتمالا کمی رسم نمودار پیچیدهتر شود. همچنین دقت کنید در معادله کلی علامت ثابت همیشه منفی در نظر گرفته میشود. بنابراین در این سوال باید برابر با تعیین شود تا طبق معادله عمل کرده باشیم. حالا میتوانیم دوره تناوب و مجانبها را محاسبه کنیم:
دوره تناوب =
گفتیم این دو نقطه که معادل با مکان افقی ابتدا و انتهای اولین دوره تناوب هستند، نقاط مجانب نمودار تانژانت در نظر گرفته میشوند. پس های متناظر با این نقاط بینهایت است. به این ترتیب مختصات نقاط اول و دوم برابر میشود با:
نکته: اگر دقت کنید علامت نماد بینهایت برای این دو نقطه در مقایسه با دو مثال قبل متفاوت است. در دو مثال قبل، چون بود، انتظار داریم با رفتن از مکان افقی مجانب اول به سمت مکان افقی مجانب دوم، مقادیر تانژانت زیاد شوند. پس منطقی است مقدار تانژانت در مجانب اول، منفی بینهایت و در مجانب دوم، مثبت بینهایت شود. اما در این مثال است. یعنی اگر از مکان افقی مجانب اول به سمت مکان افقی مجانب دوم حرکت کنیم، باید مقادیر تانژانت کم شوند. پس لازم است تانژانت در مجانب اول، مثبت بینهایت باشد و در مجانب دوم، منفی بینهایت.
برای تعیین مکان افقی سومین نقطه در دوره، طبق فرمول گفته شده پیش میرویم:
مولفه قائم این نقطه نیز میشود:
بنابراین مختصات نقطه مرکزی دوره تناوب این تابع برابر است با:
به علاوه مولفه افقی نقاط چهارم و پنجم به شکل زیر میشوند:
مولفههای قائم متناظر با این نقاط عبارتاند از:
چون ، پس با حرکت از سمت مجانب اول به سمت مجانب دوم نمودار تانژانت ما کم میشود. این نکته موجب میشود برای مولفه قائم نقطه چهارم که به مجانب اول نزدیکتر است، علامت مثبت را انتخاب کنیم:
در این صورت برای این نقطه مقدار مثبت و بزرگتری خواهد شد. انتخاب علامت منفی برای نقطه پنجم، مقدار بزرگ، اما با علامت منفی به ما میدهد. به این ترتیب روند کم شدن تانژانت رعایت شده است:
پس مختصات نقاط چهارم و پنجم میشود:
در انتها کافی است این پنج نقطه را به هم متصل کنیم تا نمودار تابع داده شده رسم شود:
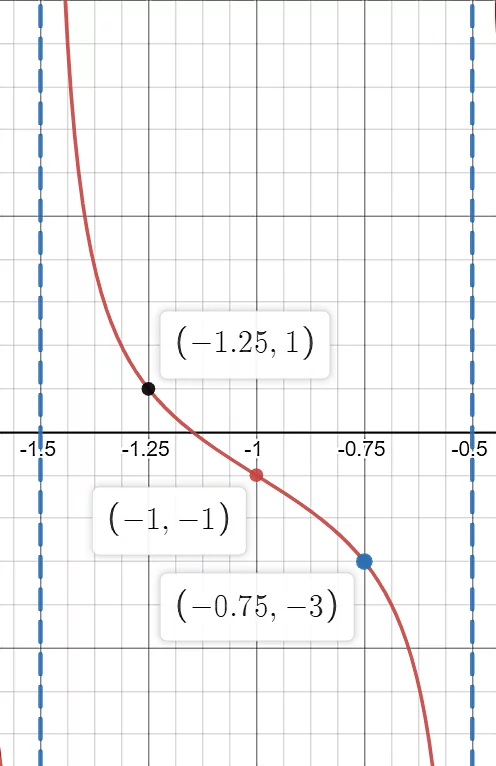
مثال ۴
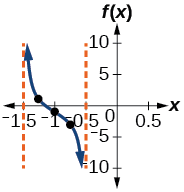
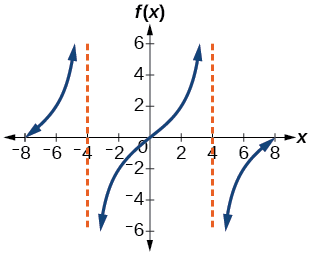
معادله مناسب برای تابعی که نمودار زیر را توصیف کند، بنویسید:
پاسخ
در این سوال با در اختیار داشتن نمودار باید معادله تابع تانژانت را حدس بزنیم. اولین چیزی که در نمودار مشخص است، دوره تناوب این تابع است. یک دوره از این نمودار در فاصله تا رسم شده است. پس میتوانیم با فرمول زیر دوره تناوب را حساب کنیم:
دوره تناوب =
بنابراین ثابت تعیین شد. برای اینکه ببینیم این نمودار تابع تانژانت است یا کتانژانت، کافی است به محل قرار گرفتن مجانبها دقت کنیم. چون در نقطه صفر مجانبی نداریم، میتوانیم نتیجهگیری کنیم که تابع مربوط به این نمودار کتانژانت نیست. در ادامه برای نوشتن معادله به فرم زیر، نیاز داریم تمام ثوابت را از نمودار تشخیص دهیم:
برای تعیین ، کافی است فرمول مختصات افقی نقاطی که مجانبها در آنها قرار دارند را بنویسیم. مجانب اول طبق شکل بالا در نقطهای با قرار گرفته است. پس خواهیم داشت:
با قرار دادن که از مرحله قبل بهدست آمد، داریم:
در مورد بهدست آوردن ، فرمول مولفه قائم نقطه سوم به شکل است، پس به نمودار نگاه میکنیم و مولفه عمودی نقطه مرکزی دوره را پیدا میکنیم:
در نهایت برای پیدا کردن آخرین ثابت یعنی ، کافی است مولفه قائم یکی از نقاط چهارم و پنجم دوره را در نظر بگیریم. طبق نمودار بهطور تقریبی میتوانیم بگوییم:
پس برای مولفه قائم میتوانیم بنویسیم:
اینکه علامت عدد مثبت است یا منفی، با توجه به شکل نمودار مشخص میشود. چون با حرکت از مجانب اول به سمت مجانب دوم، مقدار تانژانت زیاد میشود، پس مثبت است. بنابراین ثوابت ما به شکل زیر هستند و معادله تابع بهصورت زیر خواهد شد:
مثال ۵
نمودار تابع کتانژانتی با معادله زیر را رسم کنید:
پاسخ
تابع کتانژانت داده شده را با معادله کلی به شکل زیر مقایسه میکنیم تا ثوابت بهدست آیند:
حالا با داشتن میتوانیم دوره تناوب و مجانبها را محاسبه کنیم:
دوره تناوب =
در این مرحله باید دقت کنیم مجانبهای نمودار کتانژانت در مکانهایی با زاویهای مانند صفر قرار میگیرند. پس معادله مجانبها برای این تابع با مثالهای قبل که تابع تانژانت داشتیم، فرق میکند:
مولفه قائم در محل مجانبها همیشه بینهایت است. اما اینکه چه علامتی داشته باشد، به علامت بستگی دارد. چون در این سوال مثبت است، انتظار داریم روند نمودار کتانژانت با حرکت از سمت مجانب کمتر به سمت مجانب بیشتر، کاهشی باشد. بنابراین مجانب کوچکتر در مثبت بینهایت و مجانب بزرگتر در منفی بینهایت قرار دارند:
همچنین مولفه افقی سومین نقطه در دوره که همان مرکزیترین نقطه است، از رابطه زیر بهدست میآید:
مولفه قائم برای این نقطه معادل است با مقدار ثابت که طبق تابع داده شده صفر است. پس مختصات سومین نقطه برابر است با:
حالا برای اینکه رسم نمودار ما دقیقتر باشد، نیاز داریم مختصات نقاط چهارم و پنجم را نیز داشته باشیم. کافی است فرمولهای بیان شده در این زمینه را بنویسیم:
مولفه قائم متناظر با این نقاط بهصورت زیر هستند:
که چون مساوی با صفر است، بهصورت زیر خواهد شد:
در اینجا چون روند نمودار کتانژانت کاهشی است، پس لازم است برای نقطه چهارم علامت مثبت و برای نقطه پنجم علامت منفی انتخاب شود. پس مختصات این دو نقطه نیز به شکل زیر خواهد شد:
پس نقاط مهم ما مشخص شدند. حالا کافی است این نقاط را به هم متصل کنیم تا شکل زیر حاصل شود:
مثال ۶
نمودار معادله زیر را رسم کنید:
پاسخ
ابتدا معادله داده شده را با رابطه زیر مقایسه میکنیم:
پس از مشخص شدن و ، دوره تناوب و مجانبهای نمودار بهصورت زیر تعیین میشوند:
دوره تناوب =
گفتیم مقدار در محل مجانبها همیشه بینهایت است. اما علامت این بینهایت، به علامت بستگی دارد. چون در این سوال و مثبت است، پس مقدار کتانژانت ما با حرکت از سمت مجانب کمتر به سمت مجانب بیشتر، باید کم شود، یعنی مجانب کوچکتر در مثبت بینهایت و مجانب بزرگتر در منفی بینهایت قرار میگیرند و مختصات نقاط اول و دوم خواهد شد:
در ادامه با نوشتن فرمول مولفه افقی سومین نقطه در دوره، خواهیم داشت:
مولفه قائم برای این نقطه معادل است با مقدار ثابت . پس مختصات سومین نقطه برابر است با:
در مرحله بعدی لازم است مختصات نقاط چهارم و پنجم را توسط فرمولهای زیر مشخص کنیم:
مولفه قائم متناظر با این نقاط بهصورت زیر هستند:
با قرار دادن مقدار طبق آنچه که تعیین شد، مولفه قائم بهصورت زیر خواهد شد:
در اینجا چون روند نمودار کتانژانت ما باید کاهشی باشد، پس لازم است مولفه عمودی چهارمین نقطه از مولفه عمودی پنجمین نقطه بزرگتر باشد. بنابراین علامتها به شکل زیر باید در نظر گرفته شوند:
به این ترتیب مختصات این دو نقطه برابر است با:
در نهایت کافی است این پنج نقطه را در قالب منحنی به هم متصل کنیم تا نمودار رسم شود. در محل مجانبهای تعیین شده نیز بهتر است خطوط عمودی موازی با محور قائم به شکل خطچین رسم شوند:
مثال ۷
فرض کنید تابعی به شکل توصیف کننده مسافتی است که نور منتشر شده از چراغ یک ماشین پلیس روی دیوار طی میکند. در این تابع، زمان بر حسب ثانیه و مسافت بر حسب فوت است. ابتدا نمودار مسافت نور روی دیوار را در بازه رسم کنید و سپس مسافت نور را در ثانیه اول پیدا کنید.
پاسخ
در سوال اول، رسم نمودار تانژانت خواسته شده است. پس در اولین قدم باید تابع داده شده را با فرم قراردادی مقایسه کنیم تا ببینیم ثوابت مهم ما در این سوال کدامند:
دقت کنید در این سوال تابع تانژانت بر حسب زمان داده شده است که در محاسبات ما تفاوتی ایجاد نمیکند. کافی است معادله کلی بالا را نیز بر حسب زمان بنویسیم تا مقایسه درستتری داشته باشیم. حالا میتوانیم دوره تناوب و مجانبهای این تابع را محاسبه کنیم:
دوره تناوب =
این دو نقطه همان مجانبهای نمودار تانژانت هستند. پس متناظر با این نقاط بینهایت است:
چون است، انتظار داریم با رفتن از مکان افقی مجانب اول به سمت مکان افقی مجانب دوم، مقادیر تانژانت زیاد شوند. پس منطقی است مقدار تانژانت در مجانب اول، منفی بینهایت و در مجانب دوم، مثبت بینهایت انتخاب شود. مکان افقی سومین نقطه در دوره، با رابطه زیر بهدست میآید:
مولفه قائم این نقطه نیز میشود:
در نهایت باید مختصات چهارمین و پنجمین نقاط دوره را پیدا کنیم:
برای این دو مولفه افقی، دو مولفه قائم به شکل زیر وجود دارد:
گفتیم با حرکت از سمت مجانب اول به سمت مجانب دوم، نمودار تانژانت باید روند افزایشی داشته باشد. این نکته موجب میشود برای مولفه قائم نقطه چهارم که به مجانب اول نزدیکتر است، علامت منفی را انتخاب کنیم:
پس مختصات نقاط چهارم و پنجم میشود:
در انتها کافی است این پنج نقطه را به هم متصل کنیم تا نمودار تابع داده شده رسم شود. اما نکته مهم در این سوال این است که از ما خواسته شده تابع داده شده را در یک بازه مشخصی رسم کنیم. این بازه از تا است. آنچه که تا اینجا محاسبه شد، مربوط به اولین دوره تناوب است. اگر مقادیر بهدست آمده با این بازه مقایسه شوند، میبینیم که تقریبا نصف دوره اول در بازه موردنظر قرار دارد. پس از میان پنج نقطه محاسبه شده، نقاط دوم، سوم و پنجم باید در شکل ما قرار بگیرند.
مابقی شکل ما باید به دوره بعدی اختصاص داده شود. شکل نمودار در دوره بعدی دقیقا مانند شکل نمودار در اولین دوره است. فقط کافی است تمام مقادیر را به اندازه واحد در راستای مثبت محور جابجا کنیم. به این ترتیب خواهیم داشت:
برای دوره دوم، پنج نقطه با شمارههای شش، هفت، …، ده در نظر گرفتیم تا با پنج نقطه دوره اول اشتباه نشوند. پس شکل نهایی نمودار این تابع در بازه بهصورت زیر میشود:
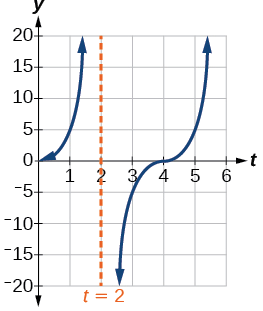
در بخش دوم این مثال، مسافت نور در اولین ثانیه خواسته شده است. طبق شکل بالا، میتوانیم بگوییم ثانیه اول روی محور افقی زمان متناظر است با مسافتی برابر با فوت روی محور قائم. اما میتوانیم برای محاسبه دقیقتر معادله تابع را بنویسیم و به جای زمان، عدد را قرار دهیم:
در محاسبات بالا از این واقعیت استفاده شد که .
تمرین ۱
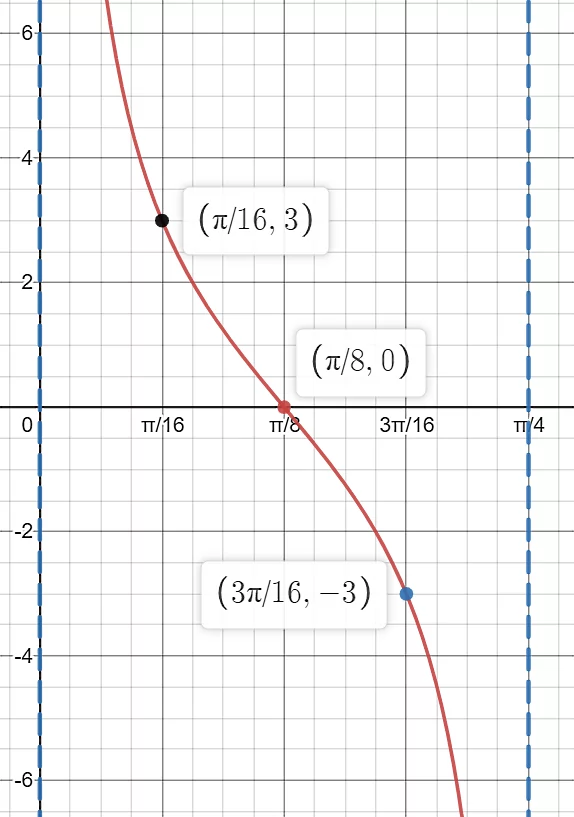
با توجه به نمودار زیر، کدام گزینه بیانگر معادله این تابع است؟
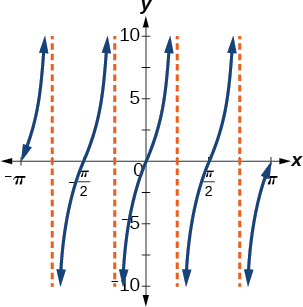
گزینه دوم صحیح است. ابتدا باید ببینیم نمودار داده شده برای این تابع تانژانتی است یا کتانژانتی. با دقت به مبدا و اینکه در این نقطه هیچ مجانب قائمی وجود ندارد، میتوانیم نتیجه بگیریم که تابع ما کتانژانت نیست. برای اینکه بتوانیم از روی نمودار معادله تابع را مشخص کنیم، لازم است با مراجعه به مختصات نقاط اصلی طبق شکل، ثوابت معادله کلی زیر را بهدست آوریم:
اولین چیزی که در نمودار مشخص است، دوره تناوب آن است. در حقیقت باید یک دوره از این نمودار را که چند مرتبه در شکل تکرار شده است، انتخاب کنیم. دوره اول که در بخش مرکزی نمودار بین دو مجانب خطچین حول مبدا قرار گرفته است، از نقطهای با مولفه افقی تا رسم شده است. پس دوره تناوب بهصورت زیر خواهد شد:
دقت کنید لزومی ندارد حتما این دوره انتخاب شود. اگر دوره سمت راست یا سمت چپ را برای محاسبات خود در نظر بگیریم، باز هم جواب یکسانی باید حاصل شود. ما برای راحتی به جهت قرار گرفتن مبدا در این دوره، آن را انتخاب کردیم. با داشتن دوره تناوب، ثابت بهراحتی محاسبه میشود:
دوره تناوب =
برای محاسبه ، به فرمول مختصات افقی یکی از نقاطی که مجانبها در آنها قرار دارند، مراجعه میکنیم. مجانب اول طبق شکل صورت سوال، در نقطهای با قرار دارد. پس داریم:
مقدار را در این رابطه جایگذاری میکنیم:
از طرفی میدانیم فرمول مولفه قائم نقطه سوم به شکل است، پس به نمودار نگاه میکنیم و مولفه عمودی نقطه مرکزی دوره را پیدا میکنیم:
در انتها آخرین ثابت یعنی را باید محاسبه کنیم. برای این منظور، کافی است مولفه قائم یکی از نقاط چهارم و پنجم دوره را در نظر بگیریم. طبق نمودار بهطور تقریبی میتوانیم بگوییم:
پس با توجه به فرمولی که برای مولفه قائم این نقطه معرفی کردیم، میتوانیم بنویسیم:
نکته مهم در این قسمت تعیین علامت ثابت است. با توجه به اینکه روند نمودار تانژانت در صورت سوال افزایشی است، پس علامت مثبت برای انتخاب شود. پس کلیه ثابتهای مهم ما بهصورت زیر خواهند بود:
تمرین ۲
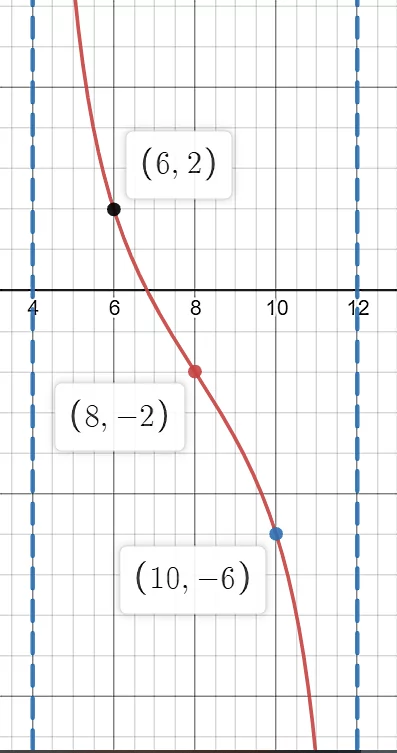
کدام گزینه توصیف دقیقی از نمودار زیر ارائه میدهد؟
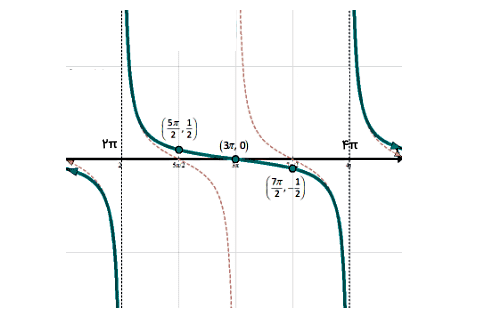
گزینه آخر صحیح است. اول باید ببینیم این نمودار مربوط به تابع تانژانت است یا کتانژانت. چون مجانبها در زاویههایی مانند قرار دارند، میتوانیم نتیجهگیری کنیم که با تابع کتانژانت روبهرو هستیم. در مرحله بعد یک دوره تناوب را روی نمودار در نظر میگیریم.
برای مثال دورهای که بهطور کامل در وسط تصویر بالا قرار دارد (دو دوره دیگر در تصویر کامل نیستند). طبق شکل، دوره تناوب برابر میشود با . پس با نوشتن فرمول زیر میتوانیم یکی از ثوابت را محاسبه کنیم:
دوره تناوب =
حالا با داشتن ، میتوانیم با دقت در مکان مجانبها ثابت را نیز تعیین کنیم. طبق شکل مکان مجانب اول برای دورهای که در نظر گرفتهایم در است. بنابراین با نوشتن معادله مجانب اول خواهیم داشت:
چون توانستیم را پیدا کنیم، دیگر لازم نیست معادله مجانب بعدی بررسی شود. حالا برای پیدا کردن و ، باید به مولفههای قائم نقاط مهم در دوره اول توجه کنیم. برای مثال مولفه عمودی نقطه سوم دوره را در نظر بگیرید:
چون سومین نقطه برابر با صفر دارد، پس هم صفر میشود. در نهایت برای تعیین ابتدا باید به روند نمودار کتانژانت دقت کنیم تا علامت مشخص شود. چون با افزایش مقدار کتانژانت کم میشود، پس میتوانیم بگوییم که مثبت است. مقدار با فرمول زیر برای مولفههای قائم نقاط چهار و پنج بهدست میآید:
کافی است فقط یکی از این دو نقطه، برای مثال نقطه چهارم را انتخاب کنیم که در شکل با نشان داده شده است:
توضیح دادیم که چرا علامت مثبت انتخاب میشود. بنابراین ثوابت زیر، معادلهای بهصورت زیر برای تابع کتانژانت میسازند:
مسیر یادگیری ریاضیات پایه دانشگاهی با فرادرس
یادگیری مثلثات بهعنوان یکی از مهمترین مباحث در ریاضیات، از اهمیت بالایی در حل و بررسی مسائل مختلف حوزه مهندسی برخوردار است. مشاهده دورههای آموزشی زیر از فرادرس به شما کمک میکند تا به این مبحث مسلط شوید:
- فیلم آموزش ریاضی پایه دانشگاهی فرادرس
- فیلم آموزش ریاضی پایه مرور و حل تست کنکور ارشد فرادرس
- فیلم آموزش ریاضی مهندسی فرادرس
- فیلم آموزش ریاضی مهندسی – مرور و حل مساله فرادرس
- فیلم آموزش آزمون های استخدامی – ریاضی و آمار فرادرس
جمعبندی
در این آموزش از مجله فرادرس، یاد گرفتیم که برای رسم نمودار تانژانت و کتانژانت، ابتدا باید معادله تابع تانژانت یا کتانژانت داده شده را با فرم کلی این توابع، یعنی یا مقایسه کنیم و ثوابت مهم را تعیین کنیم تا بتوانیم دوره تناوب، محل قرار گرفتن مجانبها، دامنه و جابجایی عمودی نمودار را مشخص کنیم.
سپس مختصات پنج نقطه مهم مانند نقاط ابتدا و انتهای دوره تناوب اول را پیدا میکنیم و با اتصال این نقاط، نمودار رسم میشود. همانطور که توضیح داده شد، یکی از تفاوتهای مهم توابع تانژانت و کتانژانت در مقایسه با سینوس و کسینوس، فرد بودن و وجود نقاط ناپیوستگی (صفرهای سینوس و کسینوس) در نمودار آنها است. این ناپیوستگیها، مجانب قائم نام دارند. محل قرار گرفتن مجانبهای قائم برای نمودار تانژانت با کتانژانت متفاوت است و همین مسئله میتواند در تشخیص این دو تابع از هم به ما کمک کند.
source
