همزمان با زیاد شدن تعداد ویژگی‌ها یا ابعاد دیتاست، میزان داده لازم برای رسیدن به نتیجه دلخواه نیز افزایش پیدا می‌کند. در چنین شرایطی، احتمال وقوع مشکلاتی همچون بیش‌برازش، زمان محاسبه بالا و کاهش دقت مدل‌های یادگیری ماشین بیش از پیش خواهد بود. برای غلبه‌بر این مشکلات از روش «تحلیل مؤلفه اصلی» (Principal Component Analysis | PCA) استفاده می‌شود. در این مطلب از مجله فرادرس با مفهوم PCA در یادگیری ماشین آشنا شده و توضیح ساده‌ای از نحوه عملکرد آن ارائه می‌دهیم. تکنیک پایه و موثری که بسیار در یادگیری ماشین مورد استفاده قرار می‌گیرد.

در این مطلب ابتدا می‌آموزیم منظور از PCA در یادگیری ماشین چیست و به تعریف مفهوم مؤلفه‌های اصلی و شرح نحوه ایجاد آن‌ها در PCA می‌پردازیم. سپس با مراحل پیاده‌سازی و اجرا PCA در زبان برنامه‌نویسی پایتون آشنا می‌شویم. در انتها این مطلب از مجله فرادرس به مزایا و معایب PCA اشاره می‌کنیم و همچنین به تعدادی از پرسش‌های متداول پیرامون این موضوع پاسخ می‌دهیم.

مفهوم PCA در یادگیری ماشین

تحلیل مؤلفه اصلی یا PCA نوعی روش کاهش ابعاد است که اغلب برای کم کردن از تعداد ویژگی‌های دیتاست به‌کار گرفته می‌شود. روش PCA در یادگیری ماشین این کار را با تبدیل مجموعه بزرگ متغیرها به زیرمجموعه‌ای کوچکتر انجام می‌دهد. اگرچه کاهش تعداد متغیرهای دیتاست اغلب با افت دقت همراه است، در کاهش ابعاد از این موضوع صرف‌نظر کرده و تنها درصد کمی از کارایی و دقت مدل برای سادگی بیشتر هزینه می‌شود. اما بررسی و مصورسازی دیتاست‌های کوچک به مراتب راحت‌تر بوده و تحلیل داده برای الگوریتم‌های یادگیری ماشین با پیچیدگی کمتری همراه است. به بیان ساده، در روش PCA همزمان با کاهش تعداد متغیرها، از اطلاعات ارزشمند دیتاست نیز نگهداری می‌شود.

منظور از مؤلفه اصلی چیست؟

مؤلفه‌های اصلی در واقع ترکیب خطی از متغیرهای اولیه هستند. شکل‌گیری این ترکیب‌ها به گونه‌ایست که مؤلفه‌های اصلی با یک‌دیگر همبستگی نداشته و اکثر اطلاعات پایه در اولین مؤلفه‌ها فشرده و ذخیره می‌شوند. برای مثال در یک دیتاست ۱۰ بعدی، به تعداد ابعاد یعنی ۱۰ عدد مؤلفه اصلی داریم و حداکثر اطلاعات ابتدا در مؤلفه اول و سپس داده‌های باقیمانده به ترتیب در مؤلفه‌های دوم الی آخر جای می‌گیرند. چیزی شبیه به نمودار زیر:

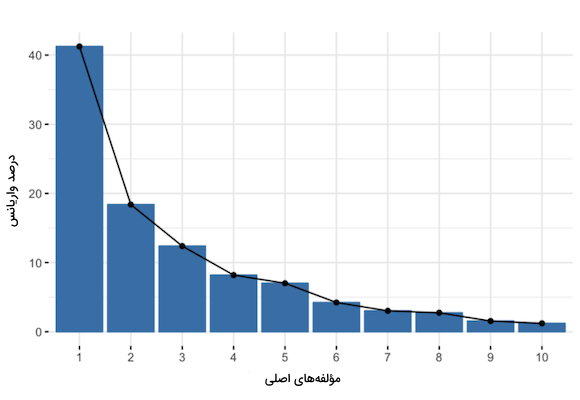
با سازمان‌دهی تاریخچه متغیرها در مؤلفه‌های اصلی، می‌توان بدون از دست دادن اطلاعات زیاد و با حذف مؤلفه‌های کم حجم از نظر تعداد نمونه، تنها مؤلفه‌های باقیمانده را به عنوان متغیرهای جدید در نظر گرفت و فرایند کاهش ابعاد را پیاده‌سازی و اجرا کرد. با این حال به خاطر آنکه مؤلفه‌ها ترکیب خطی از متغیرهای اولیه هستند، مفهوم مشخصی نداشته و تفسیر آن‌ها نیز دشوارتر است. از نظر هندسی، مؤلفه‌های اصلی بیانگر جهتی از داده‌ها با بیشترین واریانس هستند. همان خطی که شامل بیشترین اطلاعات از دیتاست است. هر چه واریانس حاصل از خط بیشتر باشد، پراکندگی نقاط داده نیز بیشتر است و پراکندگی بیشتر در امتداد خط، نشان دهنده حجم بالاتر اطلاعات است.

برای درک بهتر، مؤلفه‌های اصلی را محورهای جدیدی از نمودار در نظر بگیرید که بهترین زاویه دید را برای مشاهده و ارزیابی داده‌ها در اختیار ما قرار می‌دهند. به این صورت تفاضل یا فاصله میان نقاط داده مشهود و قابل تشخیص است.

چگونه کاهش ابعاد را با فرادرس یاد بگیریم؟

الگوریتم تحلیل مؤلفه‌های اصلی (PCA) یکی از ابزارهای موثر و پرکاربرد در حوزه یادگیری ماشین به شمار می‌رود. این الگوریتم نقش مهمی در پردازش و تحلیل داده‌های چند بعدی داشته و به ما کمک می‌کند تا الگوهای پنهان را در داده‌ها کشف کنیم. یکی از مهم‌ترین کاربردهای PCA کاهش ابعاد است. در جهان امروز که با حجم عظیمی از داده‌های پیچیده روبه‌رو هستیم، کاهش ابعاد در حل مسائل مختلفی از جمله مدیریت بهتر داده‌ها، کاهش پیچیدگی محاسباتی و بهبود عملکرد مدل‌های یادگیری ماشین مورد استفاده قرار می‌گیرد.

اما قبل از پیاده‌سازی PCA، باید ابتدا به پیش‌پردازش داده‌ها بپردازیم. پیش‌پردازش داده شامل مراحل مختلفی همچون پاکسازی، تغییر مقیاس و نرمال‌سازی داده‌ها می‌شود. همچنین، انتخاب درست ویژگی‌ها قبل از اعمال PCA بسیار حائز اهمیت است. به این صورت می‌توانیم از ویژگی‌های مرتبط و مفید در تحلیل خود استفاده کنیم و نتایج دقیق‌تری به‌دست آوریم. برای هر کدام از مراحل پیش‌پردازش داده، انتخاب ویژگی و کاهش ابعاد فیلم‌های آموزشی جامع و کاربردی توسط اساتید مجرب در وب‌سایت فرادرس قرار گرفته است که مشاهده آن‌ها را از طریق لینک‌های زیر به شما پیشنهاد می‌کنیم:

نحوه ایجاد مؤلفه های اصلی در PCA

همان‌طور که در بخش‌های قبل در مورد آن بحث شد، تعداد مؤلفه‌های اصلی با تعداد متغیرهای دیتاست برابری می‌کند و اولین مؤلفه، مسئول ایجاد بیشترین واریانس یا پراکندگی میان نقاط داده است. برای مثال در نمودار نقطه‌ای زیر، اولین مؤلفه اصلی برابر با خطی است که در راستای نشانه‌های بنفش رنگ قرار داشته و پراکندگی نقاط داده نگاشت شده بر آن (رنگ قرمز) بیشینه است. یا به زبان ریاضی، خطی است که واریانس را بیشینه می‌کند.

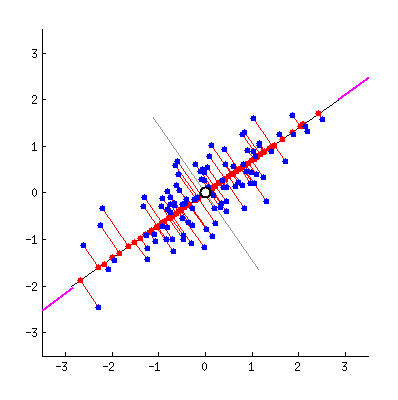
نحوه محاسبه مؤلفه دوم نیز به همین شکل است. با این تفاوت که با مؤلفه اول همبستگی نداشته و عمود بر آن است. اجرا این فرایند تا محاسبه تعداد $$p$$ مؤلفه که برابر با تعداد متغیرهای اصلی دیتاست است ادامه دارد.

شرح قدم به قدم مراحل PCA در یادگیری ماشین

تا اینجا به‌خوبی می‌دانیم PCA در یادگیری ماشین چیست و مؤلفه‌های اصلی چگونه تعریف می‌شوند. الگوریتم PCA در پنج مرحله قابل اجرا است که در این بخش به توضیح جداگانه هر کدام می‌پردازیم. همچنین برای آشنایی بیشتر با مراحل عملیاتی یادگیری ماشین، می‌توانید فیلم آموزش اصول ساخت پروژه در یادگیری ماشین فرادرس را که لینک آن در ادامه آورده شده است مشاهده کنید:

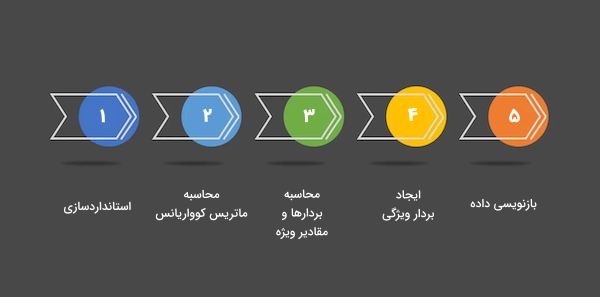
مرحله ۱: استانداردسازی

هدف از این مرحله، استانداردسازی دامنه متغیرهای پیوسته به گونه‌ایست که همه نمونه‌ها مشارکت برابری در تجزیه و تحلیل داشته باشند. روش PCA در یادگیری ماشین، بسیار نسبت به واریانس متغیرها حساس است و از همین جهت، اجرا فرایند استانداردسازی ضرورت دارد. در واقع متغیرهایی با دامنه گسترده‌تر بر متغیرهایی که در بازه کوچکتری قرار می‌گیرند ترجیح داده می‌شوند. برای مثال متغیری با دامنه ۰ تا ۱۰۰ نسبت به متغیر دیگری با دامنه ۰ تا ۱ اولویت داشته و همین موضوع در نتایج نهایی سوگیری ایجاد می‌کند. به همین خاطر با تغییر مقیاس می‌توان از این مشکل جلوگیری کرد.

برای استانداردسازی دیتاست، باید میانگین را از مقادیر هر متغیر به‌طور جداگانه کم و سپس بر انحراف معیار تقسیم کنیم. فرمول استانداردسازی به شرح زیر است:

$$z = frac{Value – Mean}{Standard:Deviation}$$

پس از اجرا کامل استانداردسازی، مقیاس همه متغیرها یکسان خواهد شد.

مرحله ۲: محاسبه ماتریس کوواریانس

با محاسبه ماتریس کوواریانس، فاصله متغیرهای دیتاست از میانگین به‌دست می‌آید و متوجه می‌شویم که آیا رابطه‌ای میان متغیرها وجود دارد یا خیر. گاهی همبستگی میان متغیرها به قدری بالاست که شامل اطلاعات تکراری هستند. به همین خاطر و برای شناسایی همبستگی‌ها، باید ماتریس کوواریانس را محاسبه کنیم. ماتریس کوواریانس، ماتریسی متقارن با اندازه $$p$$ در $$p$$ است (نماد $$p$$ تعداد ابعاد دیتاست را نشان می‌دهد) که از مقادیر کوواریانس مرتبط با جفت متغیرهای اولیه تشکیل می‌شود. به عنوان مثال برای یک دیتاست ۳ بعدی با ۳ متغیر $$y$$، $$x$$ و $$z$$، اندازه ماتریس کواریانس برابر با ۳ در ۳ و مانند زیر خواهد بود:

$$begin{bmatrix}Cov(x, x) & Cov(x, y) & Cov(x, z) \Cov(y, x) & Cov(y, y) & Cov(y, z)\Cov(z, x) & Cov(z, y) & Cov(z, z) end{bmatrix}$$

با توجه به این موضوع که کوواریانس هر متغیر با خودش، برابر با واریانس آن متغیر است ($$(Cov(a, a) = Var(a))$$

هنگام بررسی ماتریس کوواریانس باید به علامت هر عنصر دقت داشته باشید. اگر کوواریانس مثبت باشد یعنی دو متغیر با یک‌دیگر همبستگی داشته و همزمان با هم افزایش یا کاهش می‌یابند. از طرف دیگر، کوواریانس منفی نشان دهنده همبستگی معکوس میان دو متغیر است. یعنی با افزایش یکی، دیگری کاهش می‌یابد و برعکس. در مطلب زیر از مجله فرادرس به‌طور مفصل درباره کوواریانس و نحوه محاسبه آن توضیح داده‌ایم:

مرحله ۳: محاسبه بردارها و مقادیر ویژه از ماتریس کوواریانس

«بردارهای ویژه»‌ (Eigenvectors) و «مقادیر ویژه» (Eigenvalues) مفاهیمی در جبر خطی هستند که از طریق ماتریس کوواریانس و برای تعیین مؤلفه‌های اصلی محاسبه می‌شوند. موضوعی که در ابتدا لازم است درباره بردارها و مقادیر ویژه بدانید این است که همیشه به صورت جفت بوده و هر بردار ویژگی یک مقدار ویژه نیز دارد. همچنین تعداد این دو معیار با ابعاد داده برابر است و برای یک دیتاست ۳ بعدی با ۳ متغیر، ۳ بردار ویژه و ۳ مقدار ویژه متناظر قابل محاسبه است.

در حقیقت بدون این بردارها و مقادیر ویژه، مفهوم مؤلفه‌های اصلی معنی ندارد و بردارهای ویژه ماتریس کوواریانس، بیانگر جهت محورهایی با بیشترین واریانس یا همان مؤلفه‌های اصلی هستند. مقادیر ویژه نیز نقش ضرایب مرتبط با بردارهای ویژه و میزان واریانس متناظر با هر مؤلفه اصلی را ایفا می‌کنند. با مرتب‌سازی بردارهای ویژه بر اساس مقادیر ویژه از بیشترین به کمترین، مهم‌ترین مؤلفه‌های اصلی به‌دست می‌آیند.

فرض کنید دیتاست ما ۲ بعدی بوده و بردارها و مقادیر ویژه ماتریس کوواریانس مانند نمونه در اختیار ما قرار گرفته‌اند:

$$v1 = begin{bmatrix}0.66778736 \0.7351785 end{bmatrix} ; lambda_1 = 1.284028 \v2 = begin{bmatrix}-0.7351785 \0.6778736 end{bmatrix} ; lambda_2 = 0.04908323$$

اگر مقادیر ویژه را به ترتیب نزولی مرتب کنیم، متوجه می‌شویم که مقدار $$lambda_1$$

مرحله ۴: ایجاد بردار ویژگی

همان‌طور که در مرحله قبل یاد گرفتیم، با محاسبه بردارهای ویژه و مرتب‌سازی آن‌ها بر اساس مقادیر ویژه، مهم‌ترین و موثرترین مؤلفه‌های اصلی به‌دست می‌آیند. در این مرحله اما تصمیم می‌گیریم کدام مؤلفه‌ها را نگه داریم و با استفاده از آن‌ها، برداری با عنوان بردار ویژگی تشکیل دهیم. در واقع بردار ویژگی ماتریسی متشکل از بردارهای ویژگی است. این مرحله به نوعی اولین قدم در کاهش ابعاد به حساب می‌آید. چرا که اگر تنها $$p$$ بردار ویژگی را از تعداد کل یا $$n$$ حفظ کنیم، ابعاد دیتاست نهایی برابر با $$p$$ خواهد بود.

در ادامه مثال مرحله قبل، به دو صورت می‌توانیم بردار ویژگی را تشکیل دهیم. در حالت اول هر دو بردار ویژگی $$v1$$ و $$v2$$ مانند زیر حفظ می‌شوند:

$$begin{bmatrix}0.66778736 & -0.7351785 \0.7351785 & 0.6778736 end{bmatrix}$$

در حالت دوم اما بردار کم اهمیت‌تر یعنی $$v2$$ از بردار ویژگی حذف شده و تنها بردار $$v1$$ باقی می‌ماند:

$$begin{bmatrix}0.66778736 \0.7351785 end{bmatrix}$$

حذف بردار ویژگی $$v2$$، ابعاد دیتاست را به اندازه ۱ کاهش داده و موجب هدر رفت اطلاعات در دیتاست نهایی می‌شود. اما با توجه به اینکه بردار $$v2$$ تنها حاوی ۴ درصد از کل اطلاعات است، حذف آن چندان تاثیر مهمی نداشته و همچنان ۹۶ درصد اطلاعات را از طریق بردار $$v1$$ در اختیار خواهیم داشت. بنابراین حذف یا نگه‌داری بردارهای ویژه به شما و مسئله موردنظر بستگی دارد. در صورتی که بخواهید دیتاست خود را بر مبنای متغیرهای جدید یا همان مؤلفه‌های اصلی ناهمبسته توصیف کنید و نیازی به کاهش ابعاد نداشته باشید، حفظ عناصر کم اهمیت مشکلی ایجاد نمی‌کند.

مرحله ۵: بازنویسی داده

در تمام مراحل قبل، به‌جز استانداردسازی تغییر دیگری در دیتاست ایجاد نشد و تنها مؤلفه‌های اصلی را انتخاب و بردار ویژگی را تشکیل دادیم. در این مرحله اما می‌خواهیم با استفاده از بردار ویژگی متشکل از بردارهای ویژه، دیتاست اصلی را با مؤلفه‌های اصلی بازنویسی کنیم. برای این کار باید حالت ترانهاده یا وارون دیتاست اولیه در وارون بردار ویژگی ضرب شود:

$$FinalDataSet = FeatureVector^T * StandaradizedOriginalDataSet^T$$

تا اینجا با مفهوم و همچنین مراحل اجرا PCA در یادگیری ماشین آشنا شدیم. در ادامه این مطلب از مجله فرادرس به شرح نحوه پیاده‌سازی این تکنیک با کمک زبان برنامه‌نویسی پایتون می‌پردازیم.

پیاده ‌سازی PCA در پایتون

برای پیاده‌سازی PCA در زبان برنامه‌نویسی پایتون می‌توانیم به ترتیب مراحل این الگوریتم را خود کدنویسی کنیم و یا از کتابخانه‌های آماده‌ای همچون Scikit-learn کمک بگیریم. در این بخش و برای نمایش نحوه کارکرد PCA در یادگیری ماشین از دیتاست مشخصات بیماران مبتلا به سرطان کتابخانه Sckit-learn استفاده می‌کنیم. همان‌طور که تا اینجا یاد گرفتیم، الگوریتم PCA از تبدیل خطی و حداقل تعداد ابعاد برای حفظ واریانس بیشینه در دیتاست استفاده می‌کند. در مرحله اول پیاده‌سازی باید کتابخانه‌های مورد نیاز را همراه با دیتاست بارگذاری کنیم:

1import pandas as pd
2import numpy as np
3
4# Here we are using inbuilt dataset of scikit learn
5from sklearn.datasets import load_breast_cancer
6
7# instantiating
8cancer = load_breast_cancer(as_frame=True)
9# creating dataframe
10df = cancer.frame
11
12# checking shape
13print('Original Dataframe shape :',df.shape)
14
15# Input features
16X = df[cancer['feature_names']]
17print('Inputs Dataframe shape   :', X.shape)

پس از اجرا این قطعه کد، ابعاد دیتاست اصلی و داده‌های ورودی – بدون متغیر هدف – مانند زیر در خروجی چاپ می‌شود:

Original Dataframe shape : (569, 31)
Inputs Dataframe shape   : (569, 30)

در ادامه قصد داریم داده‌ها را استانداردسازی کنیم و به همین خاطر ابتدا باید مقدار میانگین و انحراف معیار را برای هر ویژگی به‌دست آوریم:

1# Mean
2X_mean = X.mean()
3
4# Standard deviation
5X_std = X.std()
6
7# Standardization
8Z = (X - X_mean) / X_std

با رسم ماتریس کوواریانس به شیوه زیر می‌توانیم میزان وابستگی جفت ویژگی‌ها را به یک‌دیگر نمایش دهیم:

1# covariance
2c = Z.cov()
3
4# Plot the covariance matrix
5import matplotlib.pyplot as plt
6import seaborn as sns
7sns.heatmap(c)
8plt.show()

خروجی مانند زیر خواهد بود:

قدم بعد محاسبه بردارهای ویژه و مقادیر ویژه برای شناسایی مؤلفه‌های اصلی در فضای ویژگی است:

1eigenvalues, eigenvectors = np.linalg.eig(c)
2print('Eigen values:n', eigenvalues)
3print('Eigen values Shape:', eigenvalues.shape)
4print('Eigen Vector Shape:', eigenvectors.shape)

نتیجه اجرای قطعه کد فوق را در بخش زیر ملاحظه می‌کنید:

Eigen values:
 [1.32816077e+01 5.69135461e+00 2.81794898e+00 1.98064047e+00
 1.64873055e+00 1.20735661e+00 6.75220114e-01 4.76617140e-01
 4.16894812e-01 3.50693457e-01 2.93915696e-01 2.61161370e-01
 2.41357496e-01 1.57009724e-01 9.41349650e-02 7.98628010e-02
 5.93990378e-02 5.26187835e-02 4.94775918e-02 1.33044823e-04
 7.48803097e-04 1.58933787e-03 6.90046388e-03 8.17763986e-03
 1.54812714e-02 1.80550070e-02 2.43408378e-02 2.74394025e-02
 3.11594025e-02 2.99728939e-02]
Eigen values Shape: (30,)
Eigen Vector Shape: (30, 30)

سپس مقادیر ویژه را به ترتیب نزولی و در ادامه بردارهای ویژه را مرتب می‌کنیم:

1# Index the eigenvalues in descending order 
2idx = eigenvalues.argsort()[::-1]
3
4# Sort the eigenvalues in descending order 
5eigenvalues = eigenvalues[idx]
6
7# sort the corresponding eigenvectors accordingly
8eigenvectors = eigenvectors[:,idx]

در ادامه، واریانس حفظ شده از طریق انتخاب مؤلفه‌های اصلی محاسبه و در متغیر explained_varذخیره می‌شود:

1explained_var = np.cumsum(eigenvalues) / np.sum(eigenvalues)
2explained_var

خروجی به شرح زیر است:

array([0.44272026, 0.63243208, 0.72636371, 0.79238506, 0.84734274,
       0.88758796, 0.9100953 , 0.92598254, 0.93987903, 0.95156881,
       0.961366  , 0.97007138, 0.97811663, 0.98335029, 0.98648812,
       0.98915022, 0.99113018, 0.99288414, 0.9945334 , 0.99557204,
       0.99657114, 0.99748579, 0.99829715, 0.99889898, 0.99941502,
       0.99968761, 0.99991763, 0.99997061, 0.99999557, 1.        ])

انتخاب تعداد مؤلفه‌های اصلی امری دلخواه بوده و به فرضیات مسئله بستگی دارد. در این مثال مقدار واریانس حاصل از مؤلفه‌های اصلی را بیشتر و برابر با ۵۰ درصد در نظر می‌گیریم:

1n_components = np.argmax(explained_var >= 0.50) + 1
2n_components

خروجی شامل تعداد مؤلفه‌های اصلی است:

2

مطابق با آنچه در خروجی چاپ شده است، تعداد ۲ مؤلفه اصلی حفظ شده‌اند. برای نگاشت داده‌ها بر این مؤلفه‌ها باید «ماتریس تصویر» (Projection Matrix) را به‌دست آوریم. این ماتریس متشکل از بردارهای ویژگی متناظر با بزرگ‌ترین مقادیر ویژه در ماتریس کوواریانس است. ماتریسی که دیتاست با ابعاد بالا را به زیرفضایی با ابعاد پایین‌تر نگاشت می‌کند. همچنین بردارهای ویژه ماتریس کوواریانس به محورهای اصلی داده اشاره داشته و نگاشت نمونه‌های داده بر این محورها، مؤلفه اصلی نام دارد. برای مصورسازی دو مؤلفه اصلی مسئله مانند زیر عمل می‌کنیم:

1# PCA component or unit matrix
2u = eigenvectors[:,:n_components]
3pca_component = pd.DataFrame(u,
4                             index = cancer['feature_names'],
5                             columns = ['PC1','PC2']
6                            )
7
8# plotting heatmap
9plt.figure(figsize =(5, 7))
10sns.heatmap(pca_component)
11plt.title('PCA Component')
12plt.show()

تصویر زیر، نقشه حرارت مرتبط با مؤلفه‌های اصلی را نشان می‌دهد:

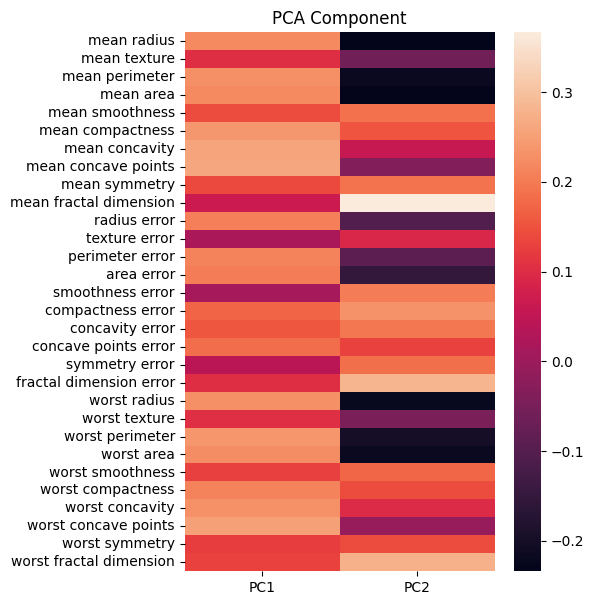
برای نگاشت دیتاست از فرمول زیر کمک می‌گیریم:

$$Projp_i(u) = frac{P_icdot u}{|u|} = P_icdot u$$

سپس برای کاهش ابعاد، تنها مؤلفه‌هایی که بیشترین سهم را در ورایانس کل دارند نگه می‌داریم. برای پیاده‌سازی فرایند نگاشت دیتاست و نمایش مؤلفه‌های اصلی مانند زیر عمل می‌کنیم:

1# Matrix multiplication or dot Product
2Z_pca = Z @ pca_component
3# Rename the columns name
4Z_pca.rename({'PC1': 'PCA1', 'PC2': 'PCA2'}, axis=1, inplace=True)
5# Print the  Pricipal Component values
6print(Z_pca)

در تصویر زیر شاهد مقادیر نهایی دو مؤلفه اصلی مسئله هستید:

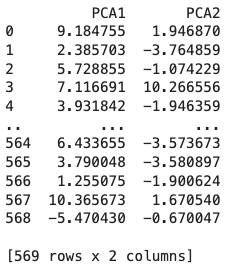
بر همین اساس، فرایند کاهش ابعاد در حفظ ویژگی‌هایی با بیشترین واریانس خلاصه می‌شود.

پیاده سازی PCA با کتابخانه Scikit-learn

با بهره‌گیری از کتابخانه Scikit-learn دیگر نیازی به پیاده‌سازی قدم به قدم مراحل نیست و تنها باید مانند زیر، تعداد مؤلفه‌های اصلی را به عنوان پارامتر ورودی در کلاس PCAمشخص کنیم:

1# Importing PCA
2from sklearn.decomposition import PCA
3
4# Let's say, components = 2
5pca = PCA(n_components=2)
6pca.fit(Z)
7x_pca = pca.transform(Z)
8
9# Create the dataframe
10df_pca1 = pd.DataFrame(x_pca,
11                       columns=['PC{}'.
12                       format(i+1)
13                       for i in range(n_components)])
14print(df_pca1)

ملاحظه می‌کنید که خروجی به‌دست آمده با نتیجه حاصل از روش قبل یکسان است:

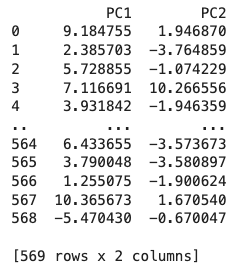
قطعه کد زیر دو مؤلفه اصلی اول و دوم را در نمودار نقطه‌ای به نمایش می‌گذارد:

1# giving a larger plot
2plt.figure(figsize=(8, 6))
3
4plt.scatter(x_pca[:, 0], x_pca[:, 1],
5            c=cancer['target'],
6            cmap='plasma')
7
8# labeling x and y axes
9plt.xlabel('First Principal Component')
10plt.ylabel('Second Principal Component')
11plt.show()

نمودار نقطه‌ای حاصل از اجرا این قطعه کد مانند زیر خواهد بود:

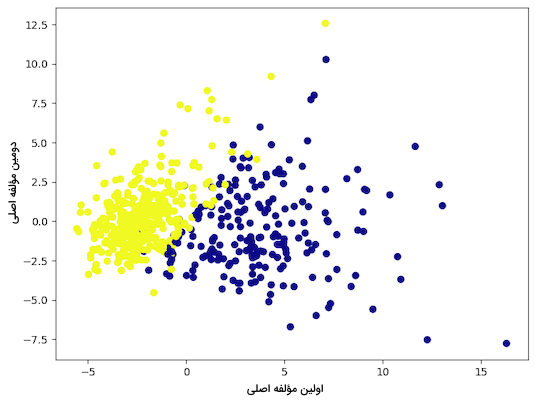
همچنین برای نمایش مقدار مؤلفه‌های اصلی تنها باید ویژگی components_شیء ساخته شده از کلاس PCAرا فراخوانی کنیم:

1# components
2pca.components_

آرایه دو بعدی زیر بیانگر مؤلفه اصلی اول و دوم است:

array([[ 0.21890244,  0.10372458,  0.22753729,  0.22099499,  0.14258969,
         0.23928535,  0.25840048,  0.26085376,  0.13816696,  0.06436335,
         0.20597878,  0.01742803,  0.21132592,  0.20286964,  0.01453145,
         0.17039345,  0.15358979,  0.1834174 ,  0.04249842,  0.10256832,
         0.22799663,  0.10446933,  0.23663968,  0.22487053,  0.12795256,
         0.21009588,  0.22876753,  0.25088597,  0.12290456,  0.13178394],
       [-0.23385713, -0.05970609, -0.21518136, -0.23107671,  0.18611302,
         0.15189161,  0.06016536, -0.0347675 ,  0.19034877,  0.36657547,
        -0.10555215,  0.08997968, -0.08945723, -0.15229263,  0.20443045,
         0.2327159 ,  0.19720728,  0.13032156,  0.183848  ,  0.28009203,
        -0.21986638, -0.0454673 , -0.19987843, -0.21935186,  0.17230435,
         0.14359317,  0.09796411, -0.00825724,  0.14188335,  0.27533947]])

حالا که به‌خوبی می‌دانیم منظور از PCA در یادگیری ماشین چیست و چگونه با استفاده از زبان برنامه‌نویسی پایتون پیاده‌سازی می‌شود، در ادامه به چند مورد از مزایا و معایب این تکنیک اشاره می‌کنیم.

مزایا و معایب PCA در یادگیری ماشین

مانند هر تکنیک دیگر در یادگیری ماشین، الگوریتم PCA نیز دارای مزایا و محدودیت‌هایی است. برخی مزایا PCA عبارت‌اند از:

1. کاهش ابعاد: تحلیل مؤلفه اصلی یا PCA تکنیکی محبوب برای کاهش ابعاد است. فرایندی که طی آن از تعداد متغیرهای دیتاست کم می‌شود. با کاهش ابعاد و بهره‌گیری از PCA، تحلیل داده‌ها راحت‌تر شده، عملکرد مدل ارتقا یافته و مصورسازی داده‌ها نیز آسان‌تر خواهد بود.
2. انتخاب ویژگی: از PCA برای انتخاب موثرترین ویژگی‌های دیتاست نیز استفاده می‌شود. در یادگیری ماشین ممکن است تعداد متغیرها بسیار زیاد باشد و از همین جهت، تنها انتخاب و به‌کارگیری تعداد محدودی از ویژگی‌ها اهمیت بالایی دارد.
3. مصورسازی داده: در PCA تعداد متغیرها کاهش یافته و به همین خاطر می‌توان دیتاست‌هایی با ابعاد بالا را در دو یا سه بعد ترسیم و به راحتی تفسیر کرد.
4. هم‌خطی چندگانه: مشکلی رایج در تحلیل رگرسیون که به وجود همبستگی بالا میان دو یا چند متغیر مستقل اشاره دارد. با کمک PCA ساختار پایه داده‌ها مشخص شده و متغیرهای ناهمبسته و جدیدی برای به‌کارگیری در مدل رگرسیون ایجاد می‌شوند.
5. کاهش نویز: مؤلفه‌هایی که واریانس پایینی دارند، اغلب به عنوان نویز شناسایی می‌شوند و حذف آن‌ها ممکن است در افزایش دقت مدل موثر باشد.
6. فشرده‌سازی داده: نمایش مجموعه داده با تعداد محدودی از مؤلفه‌های اصلی که تنوع میان داده‌ها را به‌خوبی نمایندگی می‌کنند، بسیار در کاهش فضای ذخیره‌سازی و افزایش سرعت پردازش تاثیرگذار است.
7. تشخیص داده‌های پرت: نمونه‌های پرت به نقاط داده‌ای گفته می‌شود که تفاوت چشمگیری با سایر نمونه‌ها در دیتاست دارند. شناسایی نمونه‌های پرت در PCA از طریق جستجو برای نقاط داده دور افتاده در فضای مؤلفه‌های اصلی صورت می‌گیرد.

علاوه‌بر مزایا عنوان شده، الگوریتم PCA معایب و محدودیت‌هایی نیز دارد که در فهرست زیر به چند مورد از آن‌ها اشاره شده است:

1. تفسیر مؤلفه‌های اصلی: مؤلفه‌های اصلی در واقع ترکیبات خطی از متغیرهای اصلی هستند و اغلب نمی‌توان ارتباطی میان آن‌ها و متغیرهای اولیه یافت. در نتیجه شرح نتایج PCA برای دیگران دشوار خواهد بود.
2. مقیاس‌پذیری داده: تکنیک PCA نسبت به مقیاس داده‌ها حساس است. اگر نمونه‌های داده مقیاس هماهنگ و یک‌دستی نداشته باشند، عملکرد PCA تضعیف شده و دقت بالایی به‌دست نمی‌آید. بنابراین بسیار مهم است که پیش از اجرا PCA به یکسان‌سازی مقیاس داده‌ها بپردازیم.
3. اتلاف اطلاعات: استفاده از PCA همزمان با کاهش تعداد متغیرها، ممکن است به هدر رفت اطلاعات ختم شود. میزان این هدر رفت به تعداد مؤلفه‌های اصلی انتخاب شده بستگی دارد و به همین خاطر باید در انتخاب تعداد مؤلفه‌ها دقت داشته باشیم.
4. روابط غیر خطی: در PCA رابطه میان متغیرها از نوع خطی فرض می‌شود و در غیر این‌صورت تضمینی در عملکرد آن نیست.
5. پیچیدگی محاسباتی: محاسبه مؤلفه‌های اصلی از نظر محاسباتی و به‌ویژه برای دیتاست‌های بزرگ با متغیرهای زیاد سنگین و پیچیده است.
6. بیش‌برازش: مدل یادگیری ماشین زمانی بیش‌برازش می‌شود که داده‌های مجموعه آموزشی را با دقت بالا شناسایی کند و نسبت به داده‌های جدید عملکرد ضعیفی ارائه دهد. مشکلی که احتمال رخداد آن در صورت انتخاب مؤلفه‌های اصلی زیاد یا آموزش مدل با دیتاست‌های کوچک افزایش می‌یابد.

یادگیری ماشین را می‌توان به دو رویکرد اصلی یادگیری نظارت شده و یادگیری نظارت نشده تقسیم کرد. در یادگیری نظارت شده، مدل با استفاده از داده‌های برچسب‌دار آموزش می‌بیند. در حالی که در یادگیری نظارت نشده، مدل باید بدون راهنمایی خارجی، الگوها و ساختارهای نهفته را در داده‌ها کشف کند. الگوریتم PCA که در این مطلب به آن پرداختیم، یکی از تکنیک‌های قدرتمند یادگیری نظارت نشده است. این الگوریتم بدون نیاز به برچسب‌های از پیش تعیین شده، به کاهش ابعاد و استخراج ویژگی‌های اصلی از داده‌ها می‌پردازد.

درک عمیق هر دو نوع یادگیری برای متخصصان هوش مصنوعی ضروری است. زیرا هر کدام کاربردها و مزایای خاص خود را دارند. برای کسب دانش جامع در این زمینه، پلتفرم فرادرس دو مجموعه فیلم آموزشی را تهیه و تولید کرده است که از طریق لینک‌های زیر قابل مشاهده هستند:

این دوره‌ها نه تنها مفاهیم پایه و پیشرفته یادگیری نظارت شده و نظارت نشده را پوشش می‌دهند، بلکه با ارائه مثال‌های عملی و پروژه‌های کاربردی، به شما کمک می‌کنند تا مهارت‌های لازم را برای پیاده‌سازی این تکنیک‌ها در دنیای واقعی کسب کنید.

سوالات متداول

اگرچه PCA در گروه الگوریتم‌های پایه و ابتدایی یادگیری ماشین قرار می‌گیرد، آشنایی و تسلط بر آن ممکن است با چالش‌هایی همراه باشد. از همین جهت در این بخش به تعدادی از پرسش‌های متداول پیرامون PCA در یادگیری ماشین پاسخ می‌دهیم.

دلیل بهره گیری از PCA در یادگیری ماشین چیست؟

کاهش تعداد متغیر یا ویژگی‌های دیتاست و حفظ با ارزش‌ترین اطلاعات و الگوها از جمله ویژگی‌های PCA است. این کاهش، از زمان مورد نیاز برای آموزش مدل یادگیری ماشین کاسته و از بیش‌برازش نیز جلوگیری می‌کند.

نمودار PCA شامل چه اطلاعاتی است؟

با بررسی نمودار حاصل از PCA می‌توانیم به شباهت‌های میان دسته‌های مختلف داده در دیتاست پی ببریم. هر نقطه در نمودار PCA نشان دهنده نوعی همبستگی میان متغیر اولیه و مؤلفه اصلی اول و دوم است.

تکنیک PCA چگونه کار می کند؟

مؤلفه‌های اصلی در حقیقت ترکیبات خطی از ویژگی‌های اولیه دیتاست هستند که برای تشخیص حداکثر واریانس به‌کار گرفته می‌شوند.

چه زمان باید از PCA استفاده کنیم؟

عمده کاربرد PCA زمانی است که با مشکل هم‌خطی چندگانه یا دیتاست‌هایی با ابعاد بالا سر و کار داشته باشیم. تکنیکی که نقش ویژه‌ای در استخراج ویژگی، کاهش نویز و پیش‌پردازش داده ایفا می‌کند.

جمع‌بندی

به‌طور خلاصه PCA نه تنها در یادگیری ماشین بلکه در رفع مشکلاتی همچون بیش‌برازش و هم‌خطی چندگانه نیز نقش دارد. در این مطلب از مجله فرادرس به شرح مفهوم PCA در یادگیری ماشین پرداختیم و با جنبه‌های مختلف این الگوریتم از نحوه ایجاد مؤلفه‌های اصلی گرفته تا پیاده‌سازی با زبان پایتون آشنا شدیم. یادگیری PCA قدم مهمی در شروع کار با الگوریتم‌های یادگیری ماشین است و این قابلیت را دارد تا در بسیاری از پروژه‌های جهان حقیقی مورد بهره‌برداری قرار بگیرد.