۲۴ بازدید
آخرین بهروزرسانی: ۲۷ مرداد ۱۴۰۳
زمان مطالعه: ۷ دقیقه
پس از طراحی، پیادهسازی و آموزش، باید نتیجه یا همان پیشبینی مدل یادگیری ماشین مورد ارزیابی قرار بگیرد. از جمله معیارهای کاربردی و رایج برای سنجش کیفیت عملکرد مدل، میتوان به «خطای جذر میانگین مربعات» (Root Mean Square Error | RMSE) اشاره کرد. معیار ارزیابی RMSE میزان تطابق منحنی تابع با دادهها یا فاصله پیشبینیها با مقادیر حقیقی را اندازه میگیرد. در این مطلب از مجله فرادرس، میآموزیم خطای جذر میانگین مربعات چیست و با نحوه محاسبه RMSE آشنا میشویم. معیاری که محاسبه دقیق آن برای تضمین کیفیت مدل یادگیری ماشین ضرورت دارد.

در این مطلب ابتدا یاد میگیریم خطای جذر میانگین مربعات چیست و مثالی از نحوه کارکرد آن در مسائل حقیقی ارائه میدهیم. سپس با فرمول محاسبه RMSE آشنا میشویم و در انتهای این مطلب از مجله فرادرس به معرفی چند مورد از نقاط قوت و ضعف این معیار ارزیابی میپردازیم.
خطای جذر میانگین مربعات چیست؟
خطای جذر میانگین مربعات معیاری است که تفاضل میان مقادیر پیشبینی شده و حقیقی را اندازهگیری میکند. از نظر ریاضیاتی معیار RMSE برابر انحراف معیار «مقادیر باقیمانده» (Residuals) است. مقادیر باقیمانده بیانگر فاصله میان خط رگرسیونی و نقاط داده هستند. در واقع خطای جذر میانگین مربعات یا RMSE، میزان پراکندگی مقادیر باقیمانده یا همان نزدیکی مقادیر حقیقی به پیشبینی شده را اندازه میگیرد. برای آشنایی بیشتر با مباحث ریاضیاتی یادگیری ماشین، میتوانید فیلم آموزش ریاضی برای یادگیری ماشین فرادرس را که در ادامه آورده شده است مشاهده کنید:
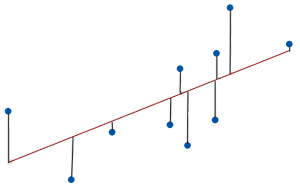
هر چه نقاط داده به خط رگرسیونی نزدیکتر باشند، یعنی خطای مدل و در نتیجه RMSE کمتر است. مدلی که خطای کمتری داشته باشد، نتایج و پیشبینیهای دقیقتری تولید میکند. دامنه مقادیر حاصل از RMSE از صفر تا مثبت بینهایت متغیر است و همچنین واحد اندازهگیری یکسانی با متغیر وابسته یا هدف دارد. از خطای جذر میانگین مربعات برای سنجش میزان خطا در رگرسیون و دیگر مدلهای آماری استفاده میشود. اگر خطا برابر با ۰ باشد، یعنی مقادیر پیشبینی شده با مقادیر حقیقی یکسان هستند که احتمال چنین رخدادی بسیار پایین و بعید است.
پایین بودن مقدار RMSE نشان دهنده این است که مدل یادگیری ماشین بهخوبی بر دادهها برازش شده و پیشبینیهایی با دقت بالا نتیجه میدهد. بهطور متقابل، مقادیر بالا RMSE بیانگر خطا بیشتر و کیفیت پایین پیشبینیها هستند. متخصصان علم داده از خطای جذر میانگین مربعات در زمینههای مختلفی همچون اقلیمشناسی، پیشبینی آب و هوا، اقتصاد و امور مالی بهره میبرند. خطای جذر میانگین مربعات یا RMSE معیار ارزیابی مهمی در «مدلسازی پیشبین» (Predictive Modeling) و آگاهی از عملکرد مدل یادگیری است.
آموزش یادگیری ماشین با فرادرس

یادگیری ماشین یک حوزه گسترده و پیچیده است که به یک رویکرد ساختاریافته برای یادگیری نیاز دارد. یک مسیر جامع برای آموزش یادگیری ماشین از سه بخش زیر تشکیل میشود:
- آموزش مفاهیم آماری: در این مرحله، شما با مفاهیم پایهای آمار و احتمال آشنا میشوید که اساس یادگیری ماشین را تشکیل میدهند. یکی از مهمترین این مفاهیم، معیارهای ارزیابی مدل مانند خطای جذر میانگین مربعات (RMSE) است. درک عمیق این مفاهیم به شما کمک میکند تا بتوانید عملکرد مدلهای خود را به درستی ارزیابی کنید و تصمیمات آگاهانهتری در فرآیند طراحی و آموزش مدل بگیرید.
- آموزش کتابخانههای مهم: پس از آشنایی با مفاهیم پایه، نوبت به یادگیری ابزارهای عملی میرسد. در این مرحله، شما با کتابخانههای کاربردی پایتون مانند Scikit-learn آشنا میشوید. این کتابخانهها امکان پیادهسازی سریع و کارآمد الگوریتمهای یادگیری ماشین را فراهم میکنند. شما یاد میگیرید چگونه از این ابزارها برای پردازش دادهها، ساخت مدلها و ارزیابی نتایج استفاده کنید.
- آموزش کاربردی یادگیری ماشین: در قدم آخر، دانش نظری و مهارتهای عملی خود را در پروژههای واقعی به کار میگیرید. این بخش شامل کار با مجموعه دادههای واقعی، حل مسائل پیچیده و پیادهسازی راهحلهای یادگیری ماشین برای چالشهای جهان حقیقی است. شما یاد میگیرید چگونه از تکنیکهای پیشرفته برای بهبود عملکرد مدلها استفاده و با مشکلاتی مانند بیشبرازش و کمبرازش مقابله کنید.
پلتفرم فرادرس برای هر کدام از بخشهای عنوان شده مجموعه فیلمهای آموزشی را در اختیار شما قرار میدهد که با مشاهده آنها از طریق لینکهای زیر میتوانید به تدریج مهارتهای خود را در حوزه یادگیری ماشین گسترش دهید:
مثالی از خطای جذر میانگین مربعات
حالا که میدانیم منظور از خطای جذر میانگین مربعات چیست، در این بخش با شرح مثالی کاربردی، بیشتر و عمیقتر با نحوه کارکرد این معیار ارزیابی آشنا میشویم. فرض کنید میخواهیم برای پیشبینی نمرات نهایی دانشآموزان یک مدل رگرسیونی طراحی کنیم. متغیر وابسته یا هدف در این مسئله همان نمرات کسب شده از امتحان است. همچنین دو معیار میزان ساعت مطالعه و نمرات میانترم را به عنوان متغیرهای مستقل در نظر میگیریم. اگر مقدار RMSE بهدست آمده از ارزیابی مدل را ۴ فرض کنیم، یعنی اختلافی به اندازه ۴ نمره میان پیشبینی مدل و نمرات اصلی دانشآموزان وجود دارد. در حقیقیت با مقایسه این دو مقدار میتوانیم به کارایی مدل رگرسیون پیببریم.

به عنوان مثال اگر دامنه نمرات نهایی از ۰ تا ۱۰۰ متغیر باشد، خطای RMSE با مقدار ۴ به ما میگوید که پیشبینیهای مدل دقت بالایی داشته و نرخ خطای میانگین تنها ۴ درصد است. در ادامه میتوانیم بررسی کنیم که آیا این حد از خطا برای نیاز و مسئله ما ایدهآل است یا خیر. همچنین از خطای جذر میانگین مربعات برای تخمین فاصله پیشبینی ۹۵ درصدی استفاده میشود. به بیان دیگر، اگر توزیع مقادیر باقیمانده نرمال باشد، بهطور تقریبی ۹۵ درصد از دادههای دیتاست در فاصله از مقادیر پیشبینی شده قرار میگیرند. در مثال ما که RMSE برابر ۴ است، ۹۵ درصد از مقادیر اصلی، ۸ نمره با مقادیر پیشبینی شده فاصله دارند:
توجه داشته باشید که حتی با وجود خطای RMSE پایین، همچنان احتمال کمبرازش شدن مدل وجود دارد. در نتیجه برای اطمینان از این موضوع لازم است تا نمودار مقادیر باقیمانده نیز بررسی شود.
فرمول محاسبه خطای جذر میانگین مربعات چیست؟
پس از پاسخ دادن به پرسش خطای جذر میانگین مربعات چیست و ارائه مثالی از نحوه کارکرد آن، در این بخش به شرح فرمول محاسبه معیار RMSE میپردازیم. شاید فرمول RMSE برای شما آشنا بهنظر برسد، چرا که در واقع همان فرمول محاسبه انحراف معیار است. از طرفی خطای جذر میانگین مربعات همان انحراف معیارِ مقادیر باقیمانده است و پراکندگی مقادیر حقیقی را از پیشبینی شده اندازه میگیرد. فرمول محاسبه RMSE به شرح زیر است:
تعریف هر کدام از نمادهای به کار رفته در این فرمول عبارت است از:
- : مقدار حقیقی برای نمونهای که در جایگاه اُم قرار دارد.
- : مقدار پیشبینی شده برای نمونهای که در جایگاه اُم قرار دارد.
- : تعداد کل نمونهها.
- : تعداد پارامترهای تخمین زده شده از جمله ثابتها.
برای بهدست آوردن خطای جذر میانگین مربعات، باید مربع عبارت برای هر نمونه محاسبه و سپس همه نتایج با یکدیگر جمع شوند. در ادامه، این عبارت بر «درجه آزادی» (Degree of Freedom) مدل یا همان تقسیم شده و خطای میانگین مربعات (MSE) بهدست میآید. در انتها و با جذر گرفتن از MSE، مقدار RMSE حاصل میشود. متخصصان علم آمار، صورت کسر فرمول RMSE را «مجموع مربعات» مینامند. دقت داشته باشید که اگر بخواهیم از کل دادههای دیتاست استفاده کنیم، مخرج کسر برابر با خواهد بود. مطلب کاملتری درباره انواع معیارهای ارزیابی در مجله فرادرس نگارش شده است که با مراجعه به لینک زیر میتوانید آن را مطالعه کنید:
حالا که بهخوبی میدانیم خطای جذر میانگین مربعات چیست و چگونه محاسبه میشود، در بخش بعدی از این مطلب مجله فرادرس با نقاط قوت و ضعف این معیار ارزیابی آشنا میشویم.
نقاط قوت و ضعف خطای جذر میانگین مربعات
مانند هر معیار آماری دیگر، خطای جذر میانگین مربعات نیز نقاط قوت و ضعف منحصر به خود را دارد که در این بخش به برخی از آنها اشاره میکنیم. در طول این بخش، معیار RMSE بهطور مکرر با ضریب تعیین یا R-squared مقایسه میشود. زیرا هر دو کیفیت برازش مدل را در مقیاسهای متفاوت مورد ارزیابی قرار میدهند. خطای جذر میانگین مربعات از مقیاسی استاندارد نشده در بازه ۰ تا مثبت بینهایت و ضریب تعیین از مقیاسی استاندارد شده در بازه ۰ تا ۱۰۰ درصد بهره میبرد. برخی از نقاط قوت RMSE عبارتاند از:
- تفسیر قابل فهم: خطای جذر میانگین مربعات یا RMSE معیار سادهایست که یک تفسیر قابل فهم از خطا مدل ارائه میدهد و حتی توسط افرادی که پیشزمینه محکمی در علم آمار ندارند به کار گرفته میشود. معیاری مطلق از فاصله میانگین نقاط داده تا مقادیر پیشبینی شده که واحد اندازهگیری یکسانی با متغیر وابسته دارد. با بهرهگیری از این معیار، میتوان دقت پیشبینی مدل را به صورت مستقیم اندازه گرفت. از طرف دیگر اما R-squared یک معیار نسبی (درصدی) بوده و برای اندازهگیری کیفیت برازش آن هم بدون واحدی مشخص مناسب است.
- واحد استاندارد: معیار RMSE در بسیاری از زمینهها یک واحد استاندارد بهشمار میرود و برای ارزیابی عملکرد مدل یادگیری ماشین مورد استفاده قرار میگیرد.

از جمله نقاط ضعف معیار ارزیابی RMSE میتوان به موارد زیر اشاره داشت:
- حساس به نمونههای پرت: عملیات به توان رساندن، باعث میشود تا خطای جذر میانگین مربعات وزن نامتناسب بیشتری به خطاهای بالا داده و در نتیجه، نسبت به دیگر معیارهای ارزیابی مانند MAPE و MSD، حساسیت بیشتری به نمونههای پرت داشته باشد.
- حساس به بیشبرازش: با هر بار اضافه شدن یک متغیر مستقل جدید به مدل، از خطای جذر میانگین مربعات کاسته میشود. با تنها اضافه کردن چند متغیر بیشتر -حتی اگر لزومی نداشته باشد- میتوان از خطای RMSE کم کرد و همین موضوع، احتمال بیشبرازش شدن مدل را افزایش میدهد. معیار R-squared نیز مانند RMSE با دو مشکل نمونههای پرت و بیشبرازش مواجه است.
- حساس به مقیاس: خطای جذر میانگین مربعات نسبت به متغیر وابسته حساس است. به بیان سادهتر، تفسیر RMSE به اطلاعات مضاعفی درباره متغیر هدف نیاز دارد. گاهی اوقات ممکن است نتوان خطای RMSE مربوط به چند دیتاست یا واحد اندازهگیری مختلف را با یکدیگر مقایسه کرد. در مقابل و به خاطر استاندارد بودن، مقایسه معیار R-squared حاصل از مسائل یا حتی متغیرهای مختلف راحت بوده و نسبت به مقیاس مقاوم است.
آمار و احتمالات پایه و اساس بسیاری از الگوریتمهای یادگیری ماشین است. تسلط بر این مفاهیم به شما امکان میدهد تا درک عمیقتری از اصول زیربنایی یادگیری ماشین داشته باشید. این دانش نه تنها باعث فهم بهتر الگوریتمها میشود، بلکه توانایی شما را در تحلیل دادهها، تفسیر نتایج و بهینهسازی مدلها افزایش میدهد. از توزیعهای احتمال گرفته تا آزمونهای آماری، هر یک از این مفاهیم، نقش حیاتی در طراحی و ارزیابی مدلهای یادگیری ماشین ایفا میکنند. اگر قصد تقویت دانش آماری خود را دارید، میتوانید با مراجعه به لینک زیر از مجموعه فیلمهای آموزش آمار و احتمالات فرادرس که از سطح مقدماتی تا پیشرفته را پوشش میدهد بهرهمند شوید:
جمعبندی
خطای جذر میانگین مربعات، نقش معیاری ارزشمند را برای اندازهگیری دقت پیشبینی مدل داشته و باعث میشود درک مناسبی از خطا و فاصله میان مقادیر حقیقی و پیشبینی شده بهدست آوریم. در این مطلب از مجله فرادرس آموختیم خطای جذر میانگین مربعات چیست، چگونه محاسبه میشود و نگاهی نیز به نقاط قوت و ضعف این معیار ارزیابی داشتیم. معیاری که به دلیل سادگی و قابل فهم بودن، در حوزههای متنوعی برای سنجش کیفیت مدلهای یادگیری ماشین کاربرد دارد.

امیر حسین فقهی دانشآموخته کارشناسی ارشد مهندسی کامپیوتر است. از علاقهمندیهای او، یادگیری ماشین و برنامهنویسی است و مطالب مرتبط با هوش مصنوعی و توسعه نرمافزار را در مجله فرادرس نگارش میکند.
source
