«انرژی جنبشی» (Kinetic Energy) با حرکت ذرات، امواج یا اجسام مختلف تولید میشود. در واقع، هر جسم یا ذره در حال حرکتی مانند ماشین در جاده، قایق در آب یا الکترون در سیم رسانا دارای انرژی جنبشی است. اگر بخواهیم مقدار این انرژی را محاسبه کنیم، باید از فرمول انرژی جنبشی استفاده کنیم که بهصورت نصف حاصلضرب جرم جسم در مجذور سرعت آن یا تعریف میشود.

در این مطلب از مجله فرادرس قصد داریم توضیح دهیم فرمول انرژی جنبشی چیست و چه نقشی در حل مسائل حرکتشناسی یا سینماتیک دارد. در ادامه پس از آموختن مراحل استفاده از فرمول انرژی جنبشی، با هم مثالهای مختلف را بررسی میکنیم، طوری که در انتها قادر خواهید بود تمرینهای متنوع در این زمینه را به آسانی حل کنید.
فرمول انرژی جنبشی چیست؟
اگر جسمی به جرم m با سرعتی به اندازه v در حال حرکت باشد، آنگاه انرژی جنبشی این جسم که با K یا .K. E نشان داده میشود برابر است با نصف حاصلضرب جرم جسم در مجذور سرعت آن. بنابراین فرمول انرژی جنبشی به شکل زیر است:
در این فرمول برای اینکه انرژی بر حسب واحد استاندارد آن یعنی ژول (J) بهدست آید، لازم است m یا جرم جسم بر حسب کیلوگرم (kg) و v یا سرعت حرکت آن بر حسب متر بر ثانیه (m/s) باشد.
پس تنها با داشتن جرم و سرعت یک جسم یا ذره، میتوانید انرژی جنبشی آن را محاسبه کنید. اهمیت فرمول انرژی جنبشی در این است که این فرمول نحوه ارتباط کمیتهایی مانند جرم و سرعت را با نیروی وارد بر ماده یا جسم را مشخص میکند. بنابراین اگر بدانیم فرمول انرژی جنبشی چیست، میتوانیم وضعیت حرکتی و برهمکنش جسم را با سایر اجسام در دنیای بیرون پیشبینی کنیم. مشخص است که هرچه سرعت یا جرم جسم بیشتر شود، انرژی جنبشی آن نیز بیشتر میشود.
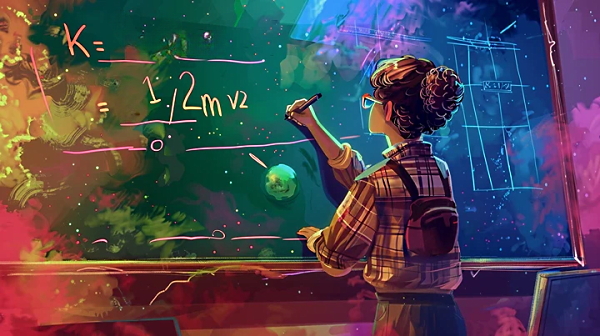
انرژی جنبشی میتواند در فرآیندی به نام ضربه یا برخورد به جسم دیگری منتقل شود. برای مثال، زمانی که طبق شکل زیر یک توپ بسکتبال با سرعت v1 را به سمت توپ ساکن دیگری شوت میکنید، در اثر برخورد دو توپ، انرژی جنبشی توپ بسکتبال به توپ دوم منتقل میشود. در نتیجه توپ دوم با سرعت v2 حرکت میکند. در این فرآیند ممکن است تمام انرژی جنبشی توپ بسکتبال یا فقط بخشی از آن به توپ دوم منتقل شود. استفاده از فرمول انرژی جنبشی به ما کمک میکند تا بتوانیم سرعت توپ دوم را محاسبه کنیم.
تعریف انرژی جنبشی
پیش از اینکه به بررسی جنبههای مختلف فرمول انرژی جنبشی و کاربردهای آن بپردازیم، بهتر است ابتدا کمی با مفهوم این کمیت آشنا شویم. به همین منظور چنانچه دانشآموز پایه دهم مقطع متوسطه هستید، مشاهده فیلم آموزشی فیزیک پایه دهم – مرور و حل تمرین فرادرس به شما کمک میکند تا با حل مثال و تمرینهای مختلف در مورد نحوه استفاده از فرمول انرژی جنبشی به تسلط بهتری دست پیدا کنید. لینک این آموزش از مجموعه فرادرس در ادامه برای شما قرار داده شده است:
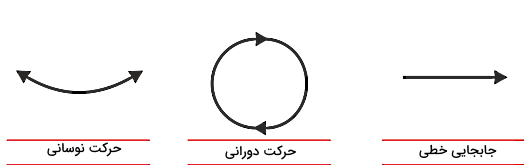
انرژی یک جسم یا ذره در حال حرکت، انرژی جنبشی نام دارد. دقت کنید منظورمان از حرکت در تعریف انرژی جنبشی، انواع مختلفی از حرکت مانند نوسان، چرخش یا جابجایی در یک خط مستقیم است که در شکل زیر تفاوت مسیر حرکت جسم در هر کدام را مشاهده میکنید.
اگر بخواهیم با یک مثال قدرت و اثر انرژی جنبشی را نشان دهیم، برخورد یک ماشین با انرژی جنبشی بالا به یک مانع، مثال مناسبی است. زمانی که یک ماشین در حال حرکت با سرعت بالا ناگهان با مانعی برخورد میکندِ و متوقف میشود، تمام انرژی جنبشی که در اثر حرکت سریع در ماشین ذخیره شده بود، ناگهان آزاد میشود. به همین علت است که کنترل این مقدار انرژی در ماشین هنگام تصادف سخت است.
انرژی جنبشی نوعی انرژی است، پس مانند تمام انواع انرژی در فیزیک، یک کمیت نردهای یا عددی محسوب میشود که جهت ندارد، بلکه فقط اندازه آن مهم است. واحد انرژی جنبشی در سیستم بینالمللی واحدها یا SI، ژول (J) است. یکی از مهمترین جنبههای انرژی این است که میتوان فرمی از انرژی را به فرم دیگر تبدیل کرد. بشر با استفاده از این خاصیت توانسته است به پیشرفتهای گستردهای در کاربرد انرژی برای انجام کارهای مختلف دست پیدا کند. برای مثال در دنیای امروز به جای کاربرد سوختهای فسیلی و تخریب محیط زیست، میتوان با تبدیل فرمی از انرژی به نام نور به فرم دیگر انرژی به نام الکتریسیته، برق تولید کرد. این قابلیت برای انرژی جنبشی نیز وجود دارد که در بخشهای بعد این مبحث را بیشتر توضیح خواهیم داد.
انواع انرژی
در بخش قبل آموختیم فرمول انرژی جنبشی یک جسم با دو مولفه جرم و سرعت آن بهصورت تعریف میشود، که در آن K نشاندهنده انرژی جنبشی است. در این بخش میخواهیم کمی در مورد انواع انرژی صحبت کنیم. شناسایی انواع مختلف انرژی به شما کمک میکند تا در محاسبات و حل مسائل مختلف بهتر بتوانید فرمهای متفاوت انرژی جنبشی را تشخیص دهید.
انرژی به معنای توانایی انجام کار است و فرمهای مختلفی از انرژی در اطراف ما وجود دارد، مثل گرما، نور، انرژی شیمیایی. اما تمام شکلهای مختلف انرژی در دو طبقهبندی بنیادی به نام «انرژی پتانسیل» (Potential Energy) و انرژی جنبشی قرار میگیرند. در ادامه ابتدا انواع انرژی پتانسیل را توضیح میدهیم. سپس با فرمهای مختلف انرژی جنبشی آشنا خواهید شد.
| انواع انرژی | |||||||
| انرژی پتانسیل | انرژی جنبشی | ||||||
| انرژی شیمیایی | انرژی مکانیکی | انرژی هستهای | انرژی گرانشی | انرژی صوتی | انرژی گرمایی | انرژی الکتریکی | انرژی الکترومغناطیسی |
انواع انرژی پتانسیل
انرژی هستهای، انرژی شیمیایی، انرژی گرانشی و انرژی مکانیکی همه انواع مختلفی از انرژی پتانسیل محسوب میشوند. در واقع انرژی پتانسیل، انرژی یک ذره یا جسم در یک موقعیت مکانی ثابت است. تعریف دیگر برای انرژی پتانسیل عبارت است از انرژی ذخیره شده در جسم نسبت به موقعیت مکانی جسم دیگر. برای مثال انرژی شیمیایی، انرژی ذخیره شده در پیوندهای بین اتمها و مولکولها است. این انرژی در منابع طبیعی مانند نفت و گاز یا در باتریها وجود دارد.

یا انرژی مکانیکی که فرم دیگری از انرژی پتانسیل است و با وارد شدن کشش یا تنش، قابل ذخیره شدن در اجسام است. برای مثال یک فنر فشرده شده دارای انرژی مکانیکی است. همچنین انرژی هستهای را داریم که در هسته اتمها ذخیره شده است و با ترکیب یا شکافت هستهای آزاد میشود. اما ملموسترین نوع انرژی پتانسیل، انرژی گرانشی یا جاذبه زمین است که اندازه آن به ارتفاع جسم از سطح زمین بستگی دارد. در بخش بعد فرمول انرژی پتانسیل گرانشی را بیان میکنیم.
فرمول انرژی پتانسیل گرانشی
گفتیم ملموسترین نوع انرژی پتانسیل، انرژی پتانسیل گرانشی است که اندازه آن با دانستن ارتفاع جسم از سطح زمین تعیین میشود. هر جسم یا ذرهای که در ارتفاع مشخصی از سطح زمین قرار گرفته باشد، دارای انرژی گرانشی است. از آنجا که در اکثر مسائل فیزیک مکانیک همواره ارتباط دو طرفهای بین این انرژی با انرژی جنبشی وجود دارد، بنابراین یادگیری فرمول آن در کنار فرمول انرژی جنبشی کمککننده است.
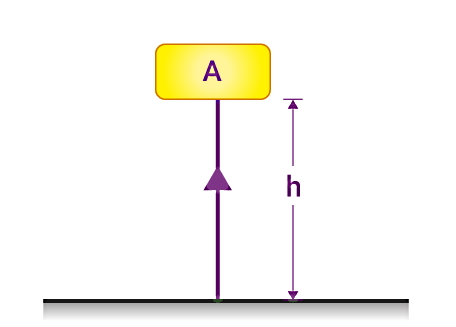
مرسوم است به انرژی پتانسیل گرانشی، انرژی پتانسیل هم گفته شود. اندازه انرژی پتانسیل جسم قرار گرفته در ارتفاع به سه عامل ارتفاع جسم، جرم آن و شتاب جاذبه زمین وابسته است. پس فرمول انرژی پتانسیل گرانشی به شکل زیر خواهد شد:
در این رابطه Ug نشاندهنده انرژی پتانسیل گرانشی و دارای واحد ژول (J) است. همچنین m جرم جسم بر حسب کیلوگرم (kg)، h ارتفاع جسم بر حسب متر (m) و g شتاب جاذبه زمین بر حسب متر بر مجذور ثانیه (m/s2) است. طبق این فرمول، هر چه جسم سنگینتر باشد یا در ارتفاع بالاتری از سطح زمین قرار گرفته باشد، انرژی پتانسیل بیشتری در آن ذخیره خواهد شد.
انواع انرژی جنبشی
در این بخش خواهیم دید که انرژی جنبشی، همانطور که از اسمش پیداست، انرژی ناشی از حرکت جسم است. پس انرژیهایی مانند انرژی الکتریکی، گرما، نور و صدا یا صوت انرژی جنبشی محسوب میشوند. نکته مهمی که در مورد انواع انرژی جنبشی وجود دارد این است که فرمول انرژی جنبشی برای تمام این موارد قابل استفاده است، اما با در نظر گرفتن جزئیات، برای هر کدام فرمول جدیدی محاسبه خواهد شد که موضوع این مطلب نیست. در بخشهای بعد با هر یک از این انرژیها بیشتر آشنا میشوید.
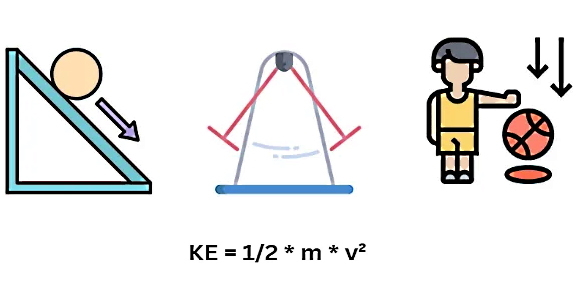
انرژی الکترومغناطیسی یا نور
پس از اینکه تا حدی یاد گرفتیم فرمول انرژی جنبشی چیست، برای اینکه با فرمهای مختلف این انرژی بیشتر آشنا شویم، در این بخش به توضیح یک نوع انرژی جنبشی به نام انرژی الکترومغناطیسی میپردازیم. تمام امواج عرضی مثل امواج الکترومغناطیسی دارای انرژی الکترومغناطیسی یا انرژی تابشی هستند. نور مرئی، اشعه ایکس، اشعه گاما و امواج رادیویی همواره دارای انرژی جنبشی از نوع الکترومغناطیسیاند. البته فرمول محاسبه برای این شکل از انرژی جنبشی کمی متفاوت میشود. بنابراین یاد گرفتیم انرژی خورشید یا نور لامپ ماهیت جنبشی دارد نه پتانسیل.
انرژی گرمایی
نوع دیگری از انرژی جنبشی، انرژی گرمایی یا انرژی حرارتی یا همان گرما است. منشا این انرژی، حرکت ذرات تشکیلدهنده ماده مانند اتمها یا مولکولها است. هر چه این ذرات سریعتر حرکت کنند، گرمای بیشتری بوجود میآید.
انرژی صوتی
این شکل از انرژی جنبشی، در امواج طولی مانند صوت وجود دارد. هر زمان نیرویی باعث شود جسم یا ذرهای نوسان کند، موج طولی تولید میشود که دارای نوعی انرژی جنبشی به نام انرژی صوتی است. معمولا مقدار انرژی صوتی نسبت به سایر انواع انرژی کمتر است.
انرژی الکتریکی
آخرین فرم انرژی که دارای ماهیت جنبشی است، انرژی الکتریکی است. انرژی الکتریکی توسط ذرات باردار کوچکی به نام الکترونها و در قالب جریان الکتریکی در یک سیم رسانا حمل میشود.
یادگیری فرمول انرژی جنبشی با فرادرس
تا اینجا آموختیم که فرمول انرژی جنبشی چیست و مفاهیم مرتبط با این مبحث را با هم مرور کردیم. برای اینکه درک عمیقتری نسبت به نحوه استفاده از این فرمول و کمیت مهم آن یعنی سرعت بهدست آورید، میتوانید از آموزشهای تهیه شده در مجموعه فرادرس به شرح زیر استفاده کنید. مشاهده به ترتیب این فیلمهای آموزشی باعث میشود ابتدا با چیستی حرکت آشنا شوید. سپس انرژی جنبشی و ارتباط آن با مفاهیمی مانند کار و توان را یاد بگیرید و در مباحث کتاب درسی فیزیک پایه دوازدهم، انواع حرکت را بشناسید.
- فیلم آموزش علوم تجربی نهم بخش فیزیک فرادرس
- فیلم آموزش فیزیک دهم فرادرس
- فیلم آموزش فیزیک دهم مرور و حل تمرین فرادرس
- فیلم آموزش فیزیک دوازدهم فرادرس
- فیلم آموزش فیزیک دوازدهم مرور و حل تمرین فرادرس
- فیلم آموزش فیزیک دوازدهم نکته و حل تست کنکور فرادرس
مراحل کاربرد فرمول انرژی جنبشی
تا اینجا یاد گرفتیم که فرمول انرژی جنبشی چیست. در این بخش قصد داریم توضیح دهیم برای حل مسائل مختلف و محاسبه انرژی جنبشی چگونه باید از این فرمول استفاده کنیم. بهطور کلی در فرمول انرژی جنبشی سه کمیت جرم، سرعت و انرژی جنبشی را داریم که در هر سوال دو عدد از این کمیتها مقدار معلومی دارد. در نتیجه کمیت سوم با کمک این فرمول محاسبه میشود. مراحل استفاده از فرمول انرژی جنبشی بهصورت گام به گام در ادامه بیان میشوند.
قدم اول
اولین گام برای کاربرد فرمول انرژی جنبشی این است که به این فرمول کاملا مسلط باشید. در بخش اول دیدیم که فرمول انرژی جنبشی برابر است با که در آن m جرم جسم یا مقدار ماده تشکیلدهنده آن است و v برابر است با سرعت جسم یا نرخ یا آهنگ تغییرات مکانی جسم.
در محاسبه انرژی جنبشی همواره باید پاسخ شما بر حسب واحد ژول باشد، مگر اینکه در خود مسئله ذکر شده باشد برای مثال، انرژی جنبشی چند کیلوژول یا چند کالری است. همچنین طبق تعریف بالا انتظار داریم یک ژول انرژی جنبشی برابر باشد انرژی جنبشی جسمی به جرم یک کیلوگرم که با سرعت یک متر بر ثانیه در حال حرکت است.
قدم دوم
مرحله بعدی برای استفاده از فرمول انرژی جنبشی این است که اول جرم جسم را در سوال تعیین کنید. معمولا اگر سوال محاسبه انرژی جنبشی باشد، جرم داده شده است. اما ممکن است در حال انجام آزمایش باشید و بخواهید انرژی جنبشی جسم را اندازهگیری کنید. در این صورت لازم است جرم جسم را با ترازو اندازهگیری کنید. همچنین حتما باید دقت کنید که جرم اندازهگیری شده با واحد کیلوگرم در فرمول استفاده شود.
قدم سوم
گام بعدی مشخص کردن سرعت جسم است. در مسائل مختلف ممکن است اندازه سرعت به شما داده شود یا لازم باشد اول سرعت جسم را محاسبه کنید و بعد از آن در فرمول انرژی جنبشی استفاده کنید. بنابراین بد نیست نحوه محاسبه سرعت را در این قسمت با هم مرور کنیم. سرعت یک جسم برابر است با میزان جابجایی آن در واحد زمان. بنابراین فرمول سرعت به شکل زیر است:
که در آن Δx برابر با جابجایی جسم بر حسب متر (m) و Δt بر حسب ثانیه (s) معادل مدت زمانی است که طی آن این جابجایی صورت گرفته است. در محاسبه سرعت هم حتما باید دقت کنید که مقدار نهایی سرعت برای قرار گرفتن در فرمول انرژی جنبشی باید بر حسب متر بر ثانیه باشد. برای مثال اگر سرعت در صورت سوال بر حسب کیلومتر بر ساعت یا هر واحد دیگری داده شده بود، لازم است پیش از محاسبه انرژی جنبشی حتما واحد آن را تبدیل کنید.

نکته ۱: میدانیم که سرعت یک کمیت برداری است، یعنی علاوه بر اندازه، دارای جهت نیز هست. بنابراین وقتی که سرعت جسمی را بیان میکنید، همزمان با مقدار سرعت، جهت آن هم باید اعلام شود. همچنین دیدیم که در فرمول انرژی جنبشی، کمیت برداری سرعت را داریم. با این وجود انرژی جنبشی یک کمیت نردهای محسوب میشود. علت این مسئله این است که در فرمول انرژی جنبشی سرعت به توان دوم را داریم نه سرعت با توان یک. بنابراین با وجود بردار بودن، توان دوم سرعت یا هر کمیت برداری دیگری برابر با یک عدد خواهد شد.
نکته ۲: یکی دیگر از روشهای محاسبه سرعت استفاده از فرمولهای شتاب در حرکت با شتاب ثابت است. ما در این مطلب به مسائل حرکت با شتاب ثابت نپرداختهایم، اما اگر در این زمینه نیاز به مطالعه و حل تمرین دارید، میتوانید از مطالب زیر در مجله فرادرس استفاده کنید:
- فرمول شتاب چیست؟ – به زبان ساده + حل مسئله
- حرکت با شتاب ثابت — به زبان ساده
- شتاب لحظه ای چیست؟ – تعریف و فرمول + حل تمرین
- شتاب متوسط چیست؟ – فرمول و محاسبه + حل مسئله
- تقلب نامه (Cheat Sheet) فرمول های فیزیک مکانیک
قدم چهارم
در آخرین مرحله برای درک بهتر این نکته که نحوه کاربرد فرمول انرژی جنبشی چیست، لازم است کمیتهای معلوم و مجهول در سوال را با توجه به فرمول مشخص کنیم. گاهی ممکن است محاسبه خود انرژی جنبشی از شما خواسته شده باشد و گاهی با داشتن مقدار انرژی جنبشی یک جسم، لازم است با کمک گرفتن از فرمول انرژی جنبشی، سرعت یا جرم آن را پیدا کنید. در بخش بعد با حل مثالهای متنوع در این زمینه، به استفاده از فرمول انرژی جنبشی مسلط خواهید شد.
حل مثال فرمول انرژی جنبشی
تا اینجا یاد گرفتیم فرمول انرژی جنبشی چیست و مراحل استفاده از این فرمول را توضیح دادیم. در این بخش با حل چند مثال یاد میگیریم چطور با داشتن دو کمیت معلوم، مقدار کمیت سوم مجهول را به کمک این فرمول پیدا کنیم. برای مثال ممکن است جرم و سرعت جسم در سوال مشخص باشند، در نتیجه خود انرژی جنبشی مجهول مسئله است.
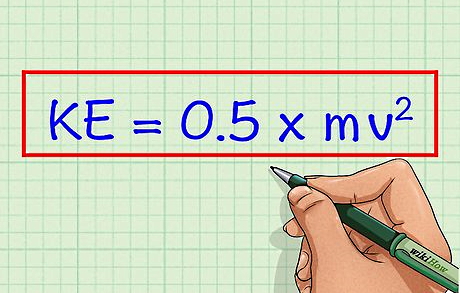
گاهی مقدار انرژی همراه با یکی از دو کمیت سرعت یا جرم جسم داده شده است. در این سوالات هم میتوان با استفاده از فرمول انرژی جنبشی کمیت مجهول را محاسبه کرد. در انتهای این بخش چند تمرین در قالب سوالات چهار گزینهای برای شما قرار داده شده است که میتوانید ابتدا خودتان سوال را حل کنید. سپس در صورت نیاز، پاسخ درست و راهحل را مشاهده کنید.
مثال ۱
انرژی جنبشی شخصی ۵۵ kg که با سرعت ۳٫۸۷ m/s میدود، چقدر است؟
پاسخ
در اولین مثال، جسم در حال حرکت در واقع همان شخصی است که در حال دویدن است. برای محاسبه انرژی جنبشی این شخص کافی است فرمول انرژی جنبشی را بنویسیم و اعداد بالا را در آن جایگذاری کنیم:
در رابطه بالا m=۵۵ و v=۳٫۸۷ است. پس مقدار K خواهد شد:
مثال ۲
جرم جسمی با انرژی ۱۰۰ J و سرعت ۵ m/s چقدر است؟
پاسخ
در این سوال، انرژی جنبشی و سرعت یک جسم داده شده است. با توجه به ذکر کلمه سرعت در صورت سوال، میتوانیم نتیجهگیری کنیم که انرژی جسم از نوع جنبشی است. پس باید از فرمول انرژی جنبشی استفاده کنیم. اگر این فرمول را بنویسید، متوجه خواهید شد که مجهول در این سوال جرم است. پس ابتدا جرم را از فرمول بهدست میآوریم:
حالا میتوانیم بهجای انرژی و سرعت در فرمول بالا عدد قرار دهیم تا جرم محاسبه شود:
مثال ۳
سرعت جسمی با جرم ۳۰ kg و انرژی جنبشی ۵۰۰ J چقدر است؟
پاسخ
در این مثال هم مانند مثال قبل، مقدار انرژی جنبشی مشخص است. همچنین جرم جسم نیز داده شده است. پس مجهول مسئله، سرعت است. بنابراین ابتدا فرمول انرژی جنبشی را طوری بازنویسی میکنیم که سرعت در یک طرف فرمول قرار بگیرد:
در بازنویسی باید دقت کنیم که در فرمول انرژی جنبشی مجذور سرعت جسم را داریم. پس لازم است برای محاسبه توان اول سرعت، حتما عبارت موردنظر را زیر رادیکال ببریم. حالا با قرار دادن مقادیر مربوطه خواهیم داشت:
مثال ۴
انرژی جنبشی ماشینی با جرم ۱۵۰۰ kg که با سرعت ۵۰ km/h در حال حرکت است، چند کیلوژول است؟

پاسخ
در این سوال مقدار جرم و سرعت مشخص است. پس فقط کافی است این اعداد را در فرمول انرژی جنبشی قرار دهیم. اما اگر دقت کنید، واحد سرعت کیلومتر (km) بر ساعت (h) است نه متر بر ثانیه. بنابراین پیش از اینکه مقدار سرعت را در فرمول انرژی جنبشی قرار دهیم، باید واحد آن را تبدیل کنیم. برای تبدیل واحد km/h به m/s بهصورت زیر عمل کنید:
در واقع با شروع از عبارت km/h، لازم است ابتدا در صورت کسر بدانیم یک کیلومتر چند متر است. یک کیلومتر ۱۰۳ یا ۱۰۰۰ متر است. اگر از مبحث واحدهای اندازهگیری بهخاطر داشته باشید، هر زمان پیشوند کیلو در کنار یک واحد اندازهگیری مانند متر قرار بگیرد، به معنای این است که آن واحد را در ۱۰۳ ضرب کردهایم. سپس در مخرج تبدیل ساعت به ثانیه را باید وارد کنیم. یک ساعت برابر ۶۰ دقیقه و هر دقیقه برابر با ۶۰ ثانیه است. پس یک ساعت با ۳۶۰۰ ثانیه برابر است.
بنابراین توانستیم صورت و مخرج را به شکل متر بر ثانیه بنویسیم. حالا از تناسب زیر استفاده میکنیم:
پس از اینکه مقدار سرعت بر حسب واحد استاندارد خود بهدست آمد، حالا میتوانیم ببینیم مقدار مجهول سوال با استفاده از فرمول انرژی جنبشی چیست:
مقدار انرژی بر حسب ژول محاسبه شد. اما در صورت سوال انرژی جنبشی بر حسب کیلوژول خواسته شده است، پس لازم است یک تبدیل واحد دیگر نیز در انتها انجام دهیم. گفتیم پیشوند کیلو به معنای توان سوم ۱۰ است. چون یک کیلوژول برابر است با ۱۰۳ ژول، کافی است عدد بالا را بر ۱۰۰۰ تقسیم کنیم تا به کیلوژول تبدیل شود:
نکته: برای اینکه در حل سایر مسائل نیاز به انجام محاسبات مربوط به تبدیل واحد km/h به m/s نداشته باشید، میتوانید فرمول زیر را به خاطر بسپارید:
بنابراین اگر مقدار سرعت بر حسب کیلومتر بر ساعت داده شده بود، کافی است مقدار سرعت را در ۰٫۲۷ ضرب کنید تا به متر بر ثانیه تبدیل شود.
مثال ۵
فرض کنید جسمی با جرم ۱۰۰۰ kg با سرعت ۱۰ m/s در حال حرکت است. اگر این جسم در اثر برخورد با جسم دیگری، تمام انرژی خود را به جسمی به جرم ۱۰ kg منتقل کند، سرعت جسم دوم چقدر خواهد شد؟
پاسخ
در این سوال جسم اول در اثر برخورد با جسم دوم تمام انرژی خود را به آن منتقل میکند. بنابراین پس از برخورد انرژی جسم دوم با انرژی جنبشی جسم اول برابر است. پس اولین قدم این است که از فرمول انرژی جنبشی استفاده کنیم و ببینیم انرژی جسم اول چقدر بوده است:
حالا که میدانیم تمام این انرژی به جسم دوم منتقل شده است و با داشتن جرم آن، سرعت این جسم برابر خواهد شد با:
نکته: از این مثال میتوانیم نتیجهگیری کنیم که اگر جسم سنگینی با سرعت کم به جسم خیلی سبکتری برخورد کند و تمام انرژی خود را به این جسم منتقل کند، در این صورت جسم سبکتر با سرعت خیلی بیشتری نسبت به جسم اول حرکت خواهد کرد.
مثال ۶
اگر مقدار جرم و سرعت یک جسم در حال حرکت دو برابر شوند، تغییرات انرژی جنبشی آن به چه صورت خواهد بود؟
پاسخ
در این سوال مقایسه وضعیت جسم در دو حالت اولیه و ثانویه خواسته شده است. اگر جرم جسم را در حالت اولیه m1 و سرعت آن را در این حالت v1 در نظر بگیریم، با نوشتن فرمول انرژی جنبشی برای حالت اول خواهیم داشت:
در حالت دوم یا ثانویه، طبق صورت سوال هم جرم و هم سرعت دو برابر شدهاند. پس خواهیم داشت:
بنابراین انرژی جنبشی در حالت دوم یا K2 برابر میشود با:
اگر رابطه بالا را سادهتر کنیم، خواهیم داشت:
حالا با در نظر گرفتن نسبت انرژی جنبشی در حالت دوم به حالت اول، میتوانیم متوجه شویم انرژی جنبشی با این تغییرات در سرعت و جرم در چه وضعیتی خواهد بود:
پس با دو برابر شدن سرعت و جرم جسم، انرژی جنبشی آن هشت برابر خواهد شد.

تمرین ۱
انرژی جنبشی یک کانال آب با عرض 1.85 m، عمق 0.8 m و نرخ جریان 0.4 m/s چقدر است؟ (چگالی آب برابر است با )
انرژی جنبشی قابل محاسبه نیست.
گزینه دوم درست است. در این سوال اگر دقت کنید واحد نرخ جریان آب، همان واحد سرعت است. در واقع نرخ کلمه معادل سرعت است. پس سرعت مشخص است. اما برای محاسبه انرژی جنبشی، طبق فرمول انرژی جنبشی باید جرم هم مشخص باشد.
در اینجا لازم است برای پیدا کردن جرم از رابطه جرم، حجم و چگالی استفاده کنیم. طبق تعریف چگالی (ρ) برابر است با جرم واحد حجم، پس داریم:
در رابطه بالا جرم بر حسب kg و حجم بر حسب متر مکعب است. پس اگر چگالی و حجم را داشته باشیم، جرم برابر خواهد شد با:
پیش از عددگذاری ابتدا حجم را محاسبه میکنیم. اگر آب را بهصورت مجموعهای از اجزایی با ابعاد 1.85 در 0.8 در 0.4 در نظر بگیریم، آنگاه حجم هر جز خواهد شد:
دقت کنید جابجایی در راستای طول لوله طبق عدد نرخ جریان برابر است با 0.4 متر در هر ثانیه. پس یکی از ابعاد جز حجم برابر است با 0.4. عرض و عمق هر جز جریان آب نیز در سوال مشخص است. حالا جرم را از فرمول چگالی حساب میکنیم:
پس از محاسبه جرم و با داشتن سرعت جریان آب، انرژی جنبشی این سیال در کانال طبق فرمول انرژی جنبشی برابر است با:
تمرین ۲
فرض کنید جسم 10 kg که با سرعت 100 m/s در حرکت بوده است، در اثر برخورد با جسم 20 kg تمام انرژی خود را به این جسم منتقل میکند. سرعت جسم دوم پس از برخورد چقدر خواهد شد؟
گزینه اول درست است. برای حل این سوال ابتدا باید انرژی جنبشی جسمی با جرم 10 kg را بهدست آوریم:
حالا با توجه به اینکه در اثر برخورد تمام انرژی جسم اول به جسم دوم متنتقل میشود، پس انتظار داریم انرژی جنبشی جسم دوم برابر شود با 50000 J. بنابراین کافی است با در نظر گرفتن این انرژی و جایگذاری جرم جسم دوم در فرمول انرژی جنبشی، سرعت آن را پیدا کنیم:
قانون پایستگی انرژی
در ادامه برای اینکه بهتر متوجه شوید کاربردهای دیگر فرمول انرژی جنبشی چیست، در این قسمت مثالهایی را تشریح میکنیم که در آنها انرژی پتانسیل گرانشی به انرژی جنبشی تبدیل میشود. فرض کنید طبق شکل زیر اتومبیلی در قله یک کوه در حالت سکون است. بنابراین در این نقطه، اتومبیل دارای مقدار انرژی پتانسیل گرانشی مشخصی است. اگر انرژی آن در این حالت را انرژی در حالت اول یا E1 بنامیم، خواهیم داشت:
حالا اگر این اتومبیل شروع به حرکت در دامنه کوه کند، در حین حرکت به سمت پایین کوه، همواره از انرژی پتانسیل آن کم میشود و به همان اندازه، به انرژی جنبشی آن اضافه میشود. در نهایت، زمانی که اتومبیل به پای کوه برسد، تمام انرژی پتانسیل آن به انرژی جنبشی تبدیل شده است. اگر این شرایط را حالت دوم در نظر بگیریم، انرژی در حالت دوم یا E2 خواهد شد:
از این مثال ساده میتوانیم نتیجه بگیریم که انرژی هیچگاه از بین نمیرود، بلکه از شکلی به شکل دیگر تبدیل میشود. این اصل یکی از بنیادیترین مفاهیم در فیزیک است که قانون پایستگی انرژی نام دارد. طبق این قانون، انرژی جسم در حالت اول با انرژی جسم در حالت دوم همواره برابر است، فقط شکل یا فرم انرژی در این دو حالت عوض شده است. بنابراین طبق قانون پایستگی انرژی داریم:
که در این مثال خواهیم داشت:
حل مثال فرمول انرژی جنبشی – پایستگی انرژی
پس از اینکه یاد گرفتیم در قانون پایستگی انرژی جایگاه فرمول انرژی جنبشی چیست، در این بخش چند مثال از تبدیل انرژی جنبشی و پتانسیل به هم را بررسی میکنیم تا بهتر متوجه شوید کاربرد فرمول انرژی جنبشی چگونه است.
مثال ۱
اگر جعبهای به جرم ۱۰۰ kg از ارتفاع ۲ متری به سمت دریا رها شود، انرژی جنبشی آن چقدر است؟ این جسم با چه سرعتی به سمت دریا حرکت خواهد کرد؟
پاسخ
در این سوال، در حالت اول جعبهای در ارتفاع ۲ متری از سطح دریا در مکان ثابتی قرار گرفته است. پس انرژی اولیه از نوع انرژی پتانسیل گرانشی است. اگر فرمول انرژی پتانسیل گرانشی را بنویسیم و در آن مقادیر عددی را جایگزین کنیم، انرژی جعبه در حالت اول محاسبه میشود:
در نظر داریم که مقدار شتاب جاذبه یا گرانش زمین برابر است با . در ادامه طبق قانون پایستگی انرژی تمام این انرژی پتانسیل به انرژی جنبشی جعبه در حال افتادن تبدیل میشود. پس انرژی در حالت دوم یا انرژی جنبشی برابر است با:
در سوال دوم سرعت جعبه خواسته شده است. با داشتن جرم و انرژی و با استفاده از فرمول انرژی جنبشی، سرعت محاسبه میشود:
مثال ۲
سرعت جسمی با جرم ۵ kg که در ارتفاع ۱۰ m از سطح زمین قرار دارد، در صورت رها شدن چقدر است؟ ()
پاسخ
در این سوال در حالت اول جسمی در یک ارتفاع مشخص، ساکن است. پس در حالت اول دارای انرژی اولیه از نوع پتانسیل گرانشی است:
با استفاده از فرمول انرژی پتانسیل مقدار E1 برابر است با:
دقت کنید که در صورت سوال ذکر شده است شتاب g را 10در نظر بگیرید. پس از رها شدن، تمام انرژی پتانسیل جسم به انرژی جنبشی آن تبدیل خواهد شد. طبق پایستگی انرژی داریم:
اگر فرمول انرژی جنبشی را بدانیم، سرعت جسم پیدا میشود:
تمرین ۱
فرض کنید جعبهای با جرم 10 kg در ارتفاع 20 m نگه داشته شده است. اگر این جعبه رها شود، سرعت آن درست پیش از برخورد با زمین چقدر است؟ (شتاب جاذبه زمین را 10 در نظر بگیرید)
پاسخ صحیح گزینه آخر است. در این سوال هم باید پایستگی انرژی برقرار باشد، به این شکل که انرژی پتانسیل جعبه پس از رها شدن به انرژی جنبشی تبدیل میشود. بنابراین ابتدا انرژی پتانسیل یا انرژی در حالت اولیه یا E1 را محاسبه میکنیم:
با مساوی قرار دادن این مقدار برای انرژی در حالت نهایی یا E2، خواهیم داشت:
حالا با نوشتن فرمول انرژی جنبشی، سرعت جسم پیدا میشود:
تمرین ۲
پیشران یک موشک دارای چگالی انرژی Ed با مقدار 2 MJ/kg است. اگر این موشک دارای جرم 100 kg باشد و با 10000 kg هیدرازین پر شود، چه سرعتی بهدست میآورد؟
گزینه دوم درست است. در این سوال چگالی انرژی پیشران موشک داده شده است. باید دقت کنیم که این پیشران توسط ماده شیمیایی هیدرازین تولید انرژی شیمیایی میکند. پس در این سوال، تبدیل انرژی شیمیایی به انرژی جنبشی موجب حرکت موشک میشود.
برای اینکه انرژی شیمیایی (E1) را پیدا کنیم، کافی است چگالی انرژی (Ed) را در جرم هیدرازین (mh) ضرب کنیم:
دقت کنید چگالی انرژی بر حسب مگاژول (MJ) است. پس انرژی کل در حالت اول (E1) که همان انرژی شیمیایی است، بر حسب MJ محاسبه میشود. حالا طبق پایستگی انرژی داریم:
انرژی در حالت دوم همان انرژی جنبشی است. با نوشتن فرمول انرژی جنبشی، سرعت محاسبه میشود، فقط باید دقت کنید برای محاسبه سرعت، باید حتما انرژی به ژول تبدیل شود. میدانیم پیشوند مگا برابر است با 106. پس با قرار دادن جرم موشک و انرژی، خواهیم داشت:
قضیه کار و انرژی
یکی دیگر از مهمترین مباحثی که در آن از فرمول انرژی جنبشی استفاده میشود، قضیه کار و انرژی است. برای اینکه قضیه کار و انرژی را بهتر درک کنیم، ابتدا لازم است بدانیم تعریف کار و فرمول آن چیست. اگر نیروی F به جسمی وارد شود و باعث شود این جسم به اندازه d جابجا شود، آنگاه کار انجام شده روی جسم توسط این نیرو برابر با W است. فرمول کار به شکل زیر است:
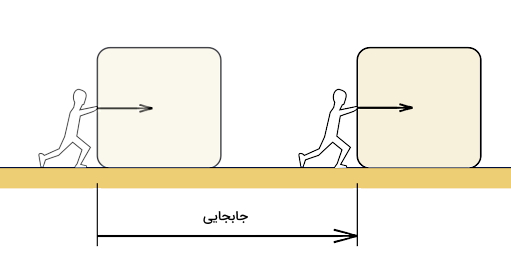
در این رابطه نیرو بر حسب نیوتن (N) و جابجایی بر حسب متر (m) است. بنابراین واحد کار برابر میشود با نیوتن در متر (N.m) که همان ژول است. البته فرمول کاری که در بالا نوشتهایم، حالت خاصی از فرمول کار است و با در نظر گرفتن این فرض نوشته شده است که زاویه بین جهت نیرو و جهت جابجایی همواره صفر است.
حالا اگر از قانون دوم نیوتن بهصورت استفاده کنیم، میتوانیم نیروی F را در رابطه بالا به شکل زیر بنویسیم:
از طرفی طبق فرمول شتاب، بین شتاب a، سرعت اولیه جسم (u) و سرعت نهایی آن (v) ارتباطی به شکل زیر برقرار است:
اگر جابجایی d را به یک سمت این فرمول ببریم، خواهیم داشت:
با قرار دادن d در فرمول کار، رابطه زیر بهدست میآید:
با توجه به اینکه گفتیم سرعت اولیه جسم u است، بنابراین انرژی جنبشی جسم در حالت اول یا K1 برابر خواهد شد با:
به همین ترتیب، انرژی جنبشی جسم در حالت نهایی با سرعت v میشود:
اگر اختلاف این دو مقدار انرژی را حساب کنیم و آن را ΔK بنامیم، خواهیم داشت:
حالا اگر طرف دوم فرمول W و ΔK را مقایسه کنیم، میبینیم که هر دوی این کمیتها با برابر هستند. پس میتوانیم بگوییم کار انجام شده روی جسمی به جرم m برابر است با تغییرات انرژی جنبشی آن:
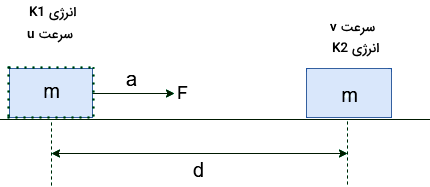
بنابراین با استفاده از فرمول انرژی جنبشی توانسیتم قضیه کار و انرژی را ثابت کنیم. همچنین یاد گرفتیم که یکای کار، همان یکای انرژی است. از این رو میتوانیم بگوییم کار انجام شده روی جسم به نوعی تبدیل به انرژی ذخیره شده در آن جسم خواهد شد. زمانی که توسط اعمال یک نیرو روی جسمی کار انجام شود، آن جسم انرژی به دست میآورد.
این انرژی میتواند از هر نوعی باشد. همانطور که گفتیم، انرژی انواع مختلفی دارد و امکان تبدیل برخی انرژیها به یکدیگر نیز وجود دارد. نکته جالبی که در مورد انرژی جنبشی وجود دارد این است که این انرژی خودش ایجاد نمیشود، بلکه حاصل تبدیل نوع دیگری از انرژی است. انجام کار روی جسم، به معنای تغییرات انرژی در جسم است. ممکن است حتی نوعی از انرژی در جسم به نوع دیگر تبدیل شود. بهطور دقیقتر، تا زمانی که نیرو به جسم وارد میشود، کار انجام شده روی آن باعث تغییرات انرژی در جسم خواهد شد و کار به انرژی تبدیل میشود.
حل مثال فرمول انرژی جنبشی – قضیه کار و انرژی
پس از یادگیری فرمول انرژی جنبشی و حل مثال راجعبه تبدیل انرژی پتانسیل به انرژی جنبشی، در این بخش به بررسی مثالهایی میپردازیم که در آنها از فرمول انرژی جنبشی در قضیه کار و انرژی استفاده میشود.
مثال ۱
فرض کنید به جسم در حال حرکتی نیرویی وارد شده است که کار آن برابر با ۱۰۰ J است. چنانچه سرعت این جسم ۲ m/s باشد، با در نظر گرفتن جرم ۲ kg برای جسم، سرعت جدید آن را پیدا کنید:
پاسخ
طبق توضیحاتی که داده شد، کار انجام شده روی جسم با تغییرات انرژی جنبشی آن برابر است. در این سوال سرعت جسم در حالت اول داده شده است و جرم آن نیز معلوم است. پس میتوانیم به کمک فرمول انرژی جنبشی، انرژی آن را در حالت اول محاسبه کنیم:
حالا طبق فرمول رابطه کار با تغییرات انرژی جنبشی یا قضیه کار و انرژی، انرژی جنبشی جسم در حالت جدید بهصورت زیر بهدست میآید:
با داشتن انرژی جسم در حالت جدید سرعت آن از فرمول انرژی جنبشی به شکل زیر محاسبه میشود:
مثال ۲
کار انجام شده روی جسم در حال حرکتی برابر است با -۵۰ J. با توجه به اینکه این جسم دارای جرم ۲ kg است، اگر سرعت اولیه آن ۱۰ m/s باشد، سرعت نهایی آن را محاسبه کنید:
پاسخ
در این مثال هم مانند مثال اول کار انجام شده داده شده است. با استفاده از فرمول انرژی جنبشی ابتدا انرژی جسم در حالت اولیه محاسبه میشود:
سپس این انرژی را در فرمول رابطه کار و انرژی قرار میدهیم تا انرژی جنبشی نهایی جسم بهدست آید:
حالا میتوانیم با مجهول در نظر گرفتن سرعت نهایی جسم، آن را طبق رابطه زیر پیدا کنیم:
مثال ۳
فرض کنید نیروی افقی F به جسم در حالت سکونی وارد شود و جسم از نقطه x=۰ شروع به حرکت کند. پس از طی مسافت ۸ m در طول سطح افقی بدون اصطکاکی، جسم دارای سرعتی با مقدار ۴ m/s میشود. با در نظر گرفتن شکل زیر برای نیرو بر حسب x، جرم جسم را محاسبه کنید:
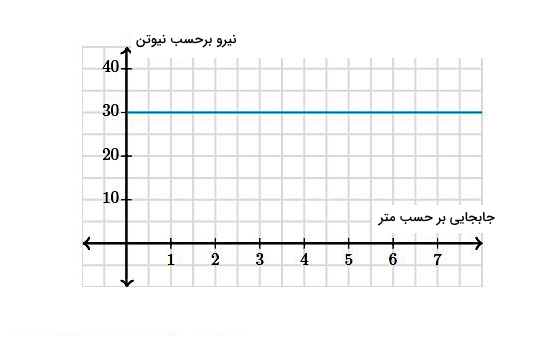
پاسخ
در این سوال مقدار نیرو داده نشده است، اما میتوانیم از شکل استفاده کنیم. اگر دقت کنید جسم از نقطه x=۰ شروع به حرکت کرده است و مقدار نیرو در تمام جابجایی یکسان و برابر با ۳۰ N باقی مانده است. پس با در نظر گرفتن این مقدار برای نیرو و استفاده از فرمول کار داریم:
حالا با کاربرد قضیه کار و انرژی به شکل و با در نظر گرفتن این نکته که در شروع حرکت، جسم در حالت سکون بوده است، پس v1=۰، خواهیم داشت:
با توجه به داشتن سرعت در انتهای جابجایی و برابری مقدار انرژی جنبشی در این حالت با کار انجام شده، کافی است مقدار جرم را به یک سمت فرمول بالا ببریم و عددگذاری کنیم:
تمرین ۱
اگر جسمی از حالت سکون و با نیروی 2 N روی سطح افقی بدون اصطکاکی 5 m جابجا شود، چه مقدار انرژی جنبشی بهدست خواهد آورد؟
چون انرژی جنبشی در ابتدای حرکت مشخص نیست، نمیتوان محاسبه کرد.
پاسخ صحیح گزینه دوم است. طبق قضیه کار و انرژی، گفتیم کار انجام شده روی جسم با تغییرات انرژی جنبشی آن برابر است. پس اگر مقدار کار را محاسبه کنیم، با توجه به اینکه جسم ابتدا در حالت سکون بوده است و K1=0، انرژی جنبشی در انتهای جابجایی محاسبه شده است:
تعریف تکانه
یکی از مفاهیم مهم دیگر در مبحث حرکتشناسی «تکانه یا مومنتوم» (Momentum) است. از آنجا که در مسائل زیادی لازم است ارتباط بین فرمول انرژی جنبشی و تکانه را بدانیم، در این بخش ابتدا تکانه را تعریف میکنیم. سپس با ارائه مثال سعی میکنیم ارتباط فرمول تکانه با فرمول انرژی جنبشی را توضیح دهیم. تکانه یک جسم برابر است با حاصلضرب جرم جسم در سرعت آن.
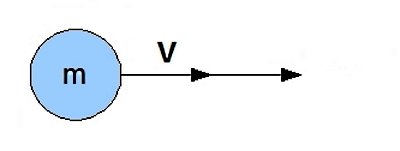
اگر جسمی به جرم m با سرعت v در حال حرکت باشد، تکانه این جسم با p نشان داده میشود که برابر است با:
واحد تکانه برابر است با . در کاربرد فرمول تکانه باید به شباهت آن با فرمول انرژی جنبشی دقت کنید. در فرمول انرژی جنبشی، با توان دوم سرعت کار داریم. بهعلاوه، یک ضریب عددی برابر با 0.5 در فرمول انرژی جنبشی وجود دارد. در بخش بعد خواهیم دید که چطور از این دو فرمول در کنار هم برای حل مسائل سینماتیک میتوان استفاده کرد.
اگر به خاطر داشته باشید، در بخشهای قبل مثالی را بررسی کردیم که در آن جسم در حال حرکتی با برخورد به جسم ساکن دیگر، تمام انرژی جنبشی خود را به این جسم میداد. در نتیجه پس از برخورد، جسم اول ساکن میشد و جسم دوم با سرعتی که بهدست میآورد، حرکت میکرد. در آن مثال، قانون پایستگی انرژی رعایت میشد که شکل دیگر آن قانون پایستگی تکانه است.
حل مثال فرمول انرژی جنبشی – تکانه
در بخشهای قبل یاد گرفتیم فرمول انرژی جنبشی چیست و چگونه در مسائل مربوط به مباحث پایستگی انرژی یا قضیه کار و انرژی از این فرمول استفاده میشود. در ابتدای این بخش با توجه به تعریفی که برای تکانه داشتیم، میتوانیم فرمول انرژی جنبشی را بر حسب تکانه به شکل زیر بازنویسی کنیم:
بنابراین شکل دیگر فرمول انرژی جنبشی برحسب تکانه برابر است با . در ادامه با حل چند مثال، ارتباط بین فرمول انرژی جنبشی و تکانه خطی را بهتر درک خواهید کرد.
مثال ۱
اگر ماشینی با جرم ۲۰۰۰ kg در حال حرکت به سمت شمال با سرعت ثابتی با مقدار ۲۵ m/s باشد، تکانه این ماشین چقدر است؟ انرژی جنبشی آن را نیز محاسبه کنید.
پاسخ
با نوشتن فرمول تکانه و عددگذاری بهجای جرم و سرعت، خواهیم داشت:
در سوال بعدی یا میتوانیم از فرمول انرژی جنبشی اصلی استفاده کنیم و یا با فرمول بیان شده در ابتدای این بخش که بر حسب تکانه یا p بود، مقدار انرژی جنبشی را پیدا کنیم. ما هر دو فرمول را بکار میبریم تا ببینید که نتیجه یکسان خواهد شد. ابتدا با فرمول جدید K را محاسبه میکنیم:
حالا فرمول انرژی جنبشی اصلی را امتحان میکنیم که بر حسب سرعت است:
بنابراین انرژی جنبشی با استفاده از هر دو فرمول مقدار یکسانی بهدست آمد.
مثال ۲
اگر تکانه توپی به جرم ۳ kg برابر با ۳۰ kg.m/s باشد، انرژی جنبشی این توپ چقدر است؟
پاسخ
جرم و تکانه را داریم، با کمک گرفتن از فرمول انرژی جنبشی بر حسب p خواهیم داشت:
یادگیری حرکتشناسی با فرادرس
پس از اینکه نحوه استفاده از فرمول انرژی را خوب یاد گرفتید، در صورت تمایل با مشاهده فیلمهای آموزشی زیر از مجموعه فرادرس میتوانید به مبحث حرکتشناسی یا سینماتیک کاملا مسلط شوید. بهویژه تماشای فیلم آموزشی فیزیک پایه ۱ فرادرس، که در آن مباحثی مانند حرکت در دو و سه بعد، نیروهای پایستار، تکانه، برخورد و انرژی جنبشی در حرکت دورانی آموزش داده شده است و به تکمیل یادگیری شما بسیار کمک میکند. سایر آموزشها بیشتر جنبه حل تمرین، مرور و تمرین در قالب تست هستند که اگر تصمیم به شرکت در آزمونهای مختلف دارید، برای شما مفید خواهند بود.
- فیلم آموزش رایگان بردارها در فیزیک ۱ دانشگاهی فرادرس
- فیلم آموزش رایگان کار و انرژی در فیزیک پایه ۱ فرادرس
- فیلم آموزش فیزیک پایه ۱ فرادرس
- فیلم آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله فرادرس
- فیلم آموزش فیزیک پایه ۱ مرور و حل مساله فرادرس
- فیلم آموزش فیزیک پایه ۱ مرور و حل تست فرادرس
آزمون فرمول انرژی جنبشی
در انتهای این مطلب از مجله فرادرس، پس از اینکه با کاربردهای مختلف فرمول انرژی جنبشی آشنا شدید، اگر تمایل دارید میزان یادگیری خود از مفهوم این فرمول و مهارتتان در حل سوالات مرتبط با آن را محک بزنید، میتوانید به سوالات آزمون زیر پاسخ دهید. پس از پاسخ دهی، با کلیک روی بخش «دریافت نتیجه آزمون» نمره نهایی شما نشان داده میشود.
آیا میتوان انرژی جنبشی یک ذره را فقط با دانستن جرم آن محاسبه کرد؟
خیر، حتما باید سرعت ذره هم مشخص باشد.
بله اگر ارتفاع ذره مشخص باشد.
گزینه اول درست است. برای محاسبه انرژی جنبشی یک جسم، دو مولفه جرم و سرعت جسم هر دو باید مشخص باشند. گزینه دوم در شرایطی صحیح است که بدانیم ذره دارای انرژی پتانسیل است و تمام این انرژی به انرژی جنبشی تبدیل میشود. اما در این سوال اطلاعی راجعبه چنین شرایطی نداریم. پس این گزینه نمیتواند صحیح باشد.
توپی با جرم ۲ kg را در نظر بگیرید که با سرعت ۱۰ m/s حرکت میکند. انرژی جنبشی توپ کدام گزینه است؟
گزینه دوم درست است. با کاربرد فرمول انرژی جنبشی به شکل زیر و قرار دادن مقادیر جرم و سرعت به جای m و v، خواهیم داشت:
اگر جسمی با جرم ۱۰۰ kg در ارتفاع ۸۰ m قرار داشته باشد، در اثر رها شدن از این ارتفاع، سرعت آن درست پیش از رسیدن به زمین چقدر است؟ ()
پاسخ صحیح گزینه سوم است. با توجه به برقراری پایستگی انرژی، تمام انرژی پتانسیل جسم پس از رها شدن و درست پیش از رسیدن به زمین، به انرژی جنبشی آن تبدیل میشود. پس قدم اول محاسبه انرژی پتانسیل یا E1 است:
این مقدار با انرژی در حالت نهایی یا E2 برابر است:
با کمک گرفتن از فرمول انرژی جنبشی، سرعت جسم برابر است با:
اگر توپی از ارتفاع مشخصی رها شود و با سرعت عمودی ۸۵ m/s به زمین برخورد کند، ارتفاع توپ قبل از رها شده چقدر بوده است؟ (فرض کنید از اصطکاک صرفنظر کردهایم و شتاب جاذبه زمین برابر با ۱۰ است)
چون جرم را نداریم، نمیتوان محاسبه کرد.
پاسخ درست گزینه سوم است. در این سوال دو موقعیت داریم که با استفاده از قانون پایستگی انرژی و برابری انرژی کل در این دو موقعیت، میتوانیم ارتفاع توپ را پیدا کنیم. در موقعیت اول توپ در یک ارتفاع مشخص از سطح زمین قرار گرفته است، پس در این حالت دارای انرژی پتانسیل گرانشی است:
اما برای عددگذاری فقط مقدار جاذبه زمین معلوم است، ارتفاع و جرم را نداریم. موقعیت دوم زمانی است که توپ به سطح زمین برخورد میکند و تمام انرژی پتانسیلاش به انرژی جنبشی تبدیل میشود:
Rightarrow 10h= frac{1}{2}times85 times85Rightarrow h= frac{1}{20}times85 times85=361.25 m$$
در صورتی که بدون تغییر دادن جرم، سرعت جسم در حال حرکتی نصف شود، انرژی جنبشی آن چند برابر خواهد شد؟
انرژی نصف میشود.
انرژی دو برابر میشود.
انرژی یک چهارم میشود.
انرژی چهار برابر میشود.
گزینه سوم درست است. اگر سرعت و انرژی جنبشی در حالت اول را به شکل زیر در نظر بگیریم، خواهیم داشت:
در حالت دوم جرم تغییری نمیکند، پس همان m نوشته میشود. اما سرعت نصف میشود، یعنی داریم:
برای اینکه بتوانیم تغییرات انرژی جنبشی را بهراحتی محاسبه کنیم، باید نسبت انرزی جنبشی در حالت دوم به حالت اول را بهدست آوریم:
انرژی جنبشی ماشینی با جرم ۱۵۰۰ kg که با سرعت ۱۴ m/s حرکت میکند، چقدر است؟
‘گزینه اول و سوم هر دو درست هستند.
گزینه آخر صحیح است. با نوشتن فرمول انرژی جنبشی و عددگذاری خواهیم داشت:
میدانیم یک کیلوژول برابر است با 1000 ژول. پس میتوانیم جواب را به شکل زیر هم بنویسیم:
فرض کنید ماشینی با جرم ۲۰۰ kg مسیری حدود ۵ m را طی میکند، در حالی که نیرویی در خلاف جهت با مقدار ۵۰۰ N برای توقف آن اعمال شده است. اگر ماشین در نهایت متوقف شود، سرعت ماشین در ابتدای جابجایی چقدر بوده است؟
گزینه اول درست است. در این مثال با کاربرد قضیه کار و انرژی و محاسبه کار انجام شده روی ماشین با توجه به داشتن جابجایی و نیروی وارد شده، خواهیم داشت:
یک نکته برای محاسبه کار این است که در سوال ذکر شده است نیرو در خلاف جهت حرکت ماشین اعمال میشود. اگر جهت نیرو و جابجایی را در نظر بگیریم، چون دو جهت مختلف دارند، در واقع مقدار کار منفی خواهد شد. پس با در نظر گرفتن جهت نیرو، کار واقعی برابر است با:
از طرفی با توجه به اینکه این نیرو باعث توقف ماشین شده است، پس انرژی جنبشی در حالت نهایی صفر میشود، چون سرعت ماشین در انتهای جابجایی صفر است:
با سادهکردن دو علامت منفی از دو طرف تساوی بالا، خواهیم داشت:
حالا به کمک فرمول انرژی جنبشی سرعت در ابتدای حرکت یا v1 محاسبه خواهد شد:
خرسی با سرعت ۹ m/s و با انرژی جنبشی ۲۳۰۰۰ J در حال دویدن است. جرم خرس تقریبا چند کیلوگرم است؟
گزینه سوم درست است. با داشتن سرعت و انرژی جنبشی، کافی است از فرمول انرژی جنبشی برای پیدا کردن جرم استفاده کنیم:
جسمی با جرم ۲ kg و تکانه خطی ۱۰ kg.m/s، چقدر انرژی جنبشی دارد؟
گزینه آخر صحیح است. برای اینکه سریعتر به جواب برسیم، بهتر است از فرمول زیر استفاده کنیم:
اگر انرژی جنبشی جسمی با سرعت ۲ m/s برابر با ۴۰۰ J باشد، جرم و تکانه آن بهترتیب برابر با کدام گزینه است؟
گزینه اول درست است. ابتدا با نوشتن فرمول انرژی جنبشی جرم را حساب میکنیم:
در مرحله بعد با نوشتن فرمول تکانه میتوانیم p را بهدست آوریم:
source
