الگوریتم مرتب سازی حبابی، الگوریتمی است که برای مرتب کردن رشتهای از اعداد یا سایر عناصر به صورت منظم استفاده میشود. این روش به وسیله بررسی هر مجموعه از عناصر مجاور هم در رشته کار میکند. بررسی عناصر مجاور از سمت چپ به راست انجام میشود. اگر این عنصرها مرتب نباشند، باید جایگاه قرارگیری خود را با هم عوض کنند. سپس الگوریتم این فرایند را برای بار دیگر با حرکت به اندازه یک واحد به سمت راست بر روی جفت عنصر مجاور بعدی انجام میدهد. این عملیات تا زمانی انجام میشود که در طی یک بار بررسی همه جفتعنصرهای مجاور هم در رشته هیچ دو عنصری نیاز به جابهجایی با یکدیگر نداشته باشند.
در این مطلب از مجله فرادرس الگوریتم مرتب سازی حبابی را مورد بررسی قرار دادهایم. همچنین مثالی از کاربرد این الگوریتم به همراه روش پیادهسازی کدهای آن را در چند زبان برنامه نویسی مختلف بیان میکنیم. در نهایت هم با توضیحات کاملی پیچیدگیهای زمانی و فضایی مرتب سازی حبابی را مورد بررسی قرار دادهایم.
الگوریتم مرتب سازی حبابی به چه شکل است؟
اگر برنامه نویس یا تحلیلگر دادهای بخواهد که مجموعه کوچکی از اعداد را به شکل صعودی مرتب کند، به عنوان مثال، الگوریتم «مرتب سازی حبابی» (Bubble Sort) به شکل تصویر زیر خواهد شد.
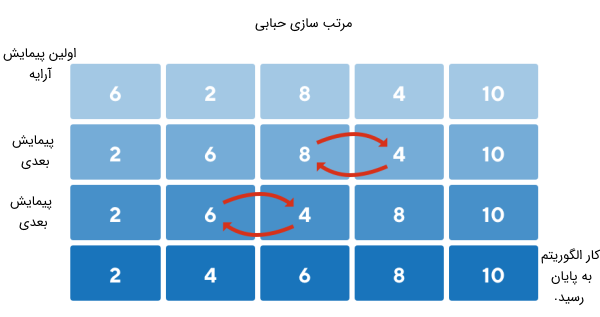
الگوریتم در هر لحظه، دو آیتم را بررسی میکند. جفتهای مجاوری را که از قبل با ترتیب صعودی در کنار یکدیگر قرار نداشتند، از سمت چپ به راست، مرتب میکند. سپس به همین رفتار خود ادامه میدهد تا زمانی که کل صف ساختمان داده را پیمایش کند. بعد از رسیدن به انتهای صف، دوباره از اول عملیات خود را تکرار میکند. این تکرار تا زمانی ادامه مییابد که یک چرخه کامل بر روی عناصر آرایه، بدون جابهجا کردن هیچ عددی طی شود.
روش استفاده از الگوریتم مرتب سازی حبابی در برنامه های کامیپوتری
برنامه نویسان کامپیوتری از الگوریتم مرتب سازی حبابی برای منظم چیدن صفی از اعداد با ترتیب صحیح استفاده میکنند. زیرا این الگوریتم، آسانترین نوع از الگوریتمهای مرتبسازی است. اما در واقع الگوریتم مرتبسازی حبابی در مسائل واقعی دنیای علوم کامیپوتری زیاد استفاده نمیشود. بیشترین استفاده این الگوریتم توسط برنامهنویسان را میتوان در سه مورد فهرست شده زیر خلاصه کرد.
- روشی برای آموزش مرتبسازی اولیه: مرتبسازی حبابی به عنوان روشی برای آموزش مرتبسازی مجموعههای داده به برنامهنویسان مبتدی استفاده میشود. زیرا این الگوریتم هم فرایند آموزش و هم پیادهسازی بسیار ساده و کوتاهی دارد.
- روشی برای مرتبکردن مجموعه دادههای بسیار کوچک: این الگوریتم در هر چرخه باید بر روی کل مجموعه عناصر آرایه پیمایش کند. الگوریتم، فرایند پیمایش را تا زمان رسیدن به جواب، به صورت تکراری ادامه میدهد. در هر مرحله پیمایش هم فقط دو عنصر از صف را با یکدیگر مقایسه میکند. بنابراین الگوریتم مرتب سازی حبابی برای مجموعه دادههای بسیار بزرگ اصلا بهینه نیست. بلکه این الگوریتم فقط میتواند بر روی تعداد بسیار کوچکی از عناصر به خوبی عمل کند.
- روش مرتبسازی برای مجموعه دادههایی که از قبل تقریبا مرتب شده هستند: و در آخر، بعضی از دانشمندان علوم کامیپوتر یا تحلیلگران داده، از این الگوریتم برای بررسی نهایی مجموعه دادههایی استفاده میکنند، که به عقیدهشان از قبل تا حد بسیار زیادی مرتب شدهاند.
مدیران محصول چگونه از مرتب سازی حبابی استفاده می کنند؟
یکی از ضروریترین و مشکلترین مسئولیتهای مدیران محصول این است که ابتکارات رقبا را بسنجد. سپس با توجه به زمان و منابع محدود تیم، تصمیم بگیرد که تمرکز بر روی چه قسمتی باشد.

برای مثال، تیمهای تولید، هزینهها و فواید آیتمهای عقب مانده را میسنجند. بر اثر نتیجه این سنجش، تصمیم میگیرند که کدام یک از آنها در نقشه راه محصول برای تولید گنجانده شود. همچنین آنها برای هر کالای عقب مانده اطلاعات خاصی را ذخیره میکنند تا در نهایت مشخص شود که مقدار تلاش و زمان مورد نیاز هر کالا برای کامل شدن، چقدر است.
برای همه انواع برنامههای امتیازدهی، مدیران محصول باید از رویکرد مرتبسازی استفاده کنند. بر اثر این اقدام میتوانند نحوه اولویتبندی کار تیم خود را مشخص کنند. در چنین مرتبسازیهایی استفاده از الگوریتم مرتب سازی حبابی گزینه خوبی است.
روش های یادگیری طراحی الگوریتم در فرادرس
دنیای کامپیوتر پُر است از الگوریتمهایی که برای حل مسائل مختلف طراحی شدهاند. تقریبا هر مسئلهای امروزه الگوریتم مربوط به خود را دارد. از طرفی میتوان گفت حرفهایترین برنامهنویسها کسانی هستند که توانایی طراحی الگوریتم دارند. طراحی و نوشتن الگوریتم یکی از رشتههای تخصصی در علوم کامپیوتر است. روشهای مختلفی برای آموزش طراحی الگوریتم وجود دارد. یکی از روشهای خوب استفاده از فیلمهای آموزشی است. باید توجه کنیم که فیلمهای آموزشی نسبت به کلاسها از مزیتهای زیادی برخوردار هستند.
فرادرس نیز به عنوان یکی از بهترین تولید کنندگان محتوا آموزشی فارسی، فیلمهای بسیار خوبی در زمینه طراحی الگوریتم تولید و ارائه کرده است. در فهرست پایین، چند مورد از امتیازات فیلمهای آموزشی را نسبت به کلاسهای حضوری، مخصوصا در زمینه طراحی الگوریتم، نوشتهایم.
- اولین مشکل این است که موسسات خیلی کمی برای آموزش طراحی الگوریتم وجود دارند.
- در صورت پیدا کردن چنین موسسهای هزینه مالی زیادتری نسبت به فیلمهای آموزشی باید پرداخت کرد.
- چنین کلاسهایی دارای زمانبندی مشخصی هستند. بنابراین دانشجو مجبور به تنظیم زمان خود با موسسه است.
- کیفیت آموزشی این کلاسها را بهجز از طریق کسب تجربه نمیتوان سنجید.
فرادرس فیلمهای آموزشی زیادی را به صورت اختصاصی درباره آموزش طراحی الگوریتم تولید و منتشر کرده است که در ادامه چند مورد از آنها را معرفی میکنیم.
- فیلم آموزش طراحی الگوریتم فرادرس
- فیلم آموزش طراحی الگوریتم همراه با حل مثال های عملی فرادرس
- فیلم آموزش حل روابط بازگشتی در سایت فرادرس
- فیلم آموزش مروری بر پیچیدگی محاسبات در وب سایت فرادرس
درک عملکرد روش کار الگوریتم مرتب سازی حبابی
برای آشنا شدن به شکل بسیار خوب با روش کار الگوریتم مرتب سازی حبابی، لازم است که شناخت کلی کاملی نسبت به فرایند طراحی الگوریتمها داشته باشیم. یکی از بهترین گزینههای ممکن تماشای فیلم آموزش طراحی الگوریتم همراه با حل مثال های عملی از فرادرس است. برای کمک به مخاطبان عزیز لینک این فیلم آموزشی را در پایین قرار دادهایم.
الگوریتم مرتب سازی حبابی یکی از الگوریتمهای اولیه و ابتدایی مرتبسازی است. این الگوریتم به وسیله تعویض مکرر عناصر مجاور کار میکند. وقتی که دیگر نیازی به جابهجایی عناصر با هم نباشد یعنی آرایه مورد نظر مرتب شده است.
فرض میکنیم که لیست مسئله به نام [fdboutput]{“content”:”list”,”type”:”inline”}[/fdboutput] ، آرایهای از [fdboutput]{“content”:”n”,”type”:”inline”}[/fdboutput] عنصر همسان با مقادیر مختلف است. همچنین تصور میکنیم که تابع [fdboutput]{“content”:”swap”,”type”:”inline”}[/fdboutput] نیز مقادیر عناصر آرایه داده شده را با یکدیگر جابهجا میکند. فرایند انجام این عملیات را در ۵ مرحله میتوان خلاصه کرد.
- بررسی کنیم که آیا عنصر اول آرایه وارد شده از عنصر بعدی در آرایه بزرگتر است یا نه.
- اگر بزرگتر بود که باید دو عنصر را با یکدیگر جابهجا کنیم. در غیر این صورت نشانگر را به اندازه یک واحد در آرایه به جلو حرکت میدهیم.
- مرحله دو را تا زمان رسیدن به انتهای آرایه تکرار میکنیم.
- بررسی میکنیم که آیا عناصر آرایه مرتب شدهاند یا نه؟ اگر مرتب نشده بودند، همان روند مراحل ۱ تا ۳ را دوباره تا به انتها تکرار میکنیم.
- خروجی نهایی که بدست میآید همان لیست مرتب شده است.
Algorithm: Sequential-Bubble-Sort (A)
fori ← 1 to length [A] do
for j ← length [A] down-to i +1 do
if A[A] < A[j-1] then
Exchange A[j] ⟷ A[j-1]شبه کد
تا به اینجای مطلب، دیدیم که الگوریتم مرتب سازی حبابی، هر جفت از عناصر آرایه را با یکدیگر مقایسه میکند، مگر اینکه کل آرایه به طور کامل به شکل صعودی مرتب شده باشد. این مسئله میتواند باعث ایجاد چند مشکل و پیچیدگی شود. مانند اینکه چه میشود اگر آرایه به دلیل از قبل منظم شدن با ترتیب صعودی، نیازی به جابهجایی بیشتر عناصر نداشته باشد؟
برای اینکه این مشکل را رفع کنیم، متغیری را به عنوان پرچم در نظر میگیریم. نام این متغیر را [fdboutput]{“content”:”swapped”,”type”:”inline”}[/fdboutput] میگذاریم. این متغیر کمک میکند که هر جابهجایی اتفاق افتاده یا نیافتاده را تشخیص دهیم. اگر هیچ جابهجایی رخ نداده باشد، آرایه نیازی به پردازش بیشتر برای مرتب شدن ندارد. در نتیجه از حلقه خارج میشویم.
در کادر زیر شبهه کد مربوط به الگوریتم مرتب سازی حبابی را نمایش دادهایم. البته هر برنامهنویس برای هر مسئله، میتواند شبهه کد متفاوتی را ارائه دهد.
voidbubbleSort(int numbers[], intarray_size){
inti, j, temp;
for (i = (array_size - 1); i>= 0; i--)
for (j = 1; j <= i; j++)
if (numbers[j-1] > numbers[j]){
temp = numbers[j-1];
numbers[j-1] = numbers[j];
numbers[j] = temp;
}
}تحلیل الگوریتم
در کادر زیر تعداد مقایسههایی که انجام میشوند را نمایش دادهایم.
1 + 2 + 3 + ... + (n - 1) = n(n - 1)/2 = O(n^2)به وضوح در این کد میتوانیم $$ n^2 $$ مقایسه حبابی را ببینیم.
در این الگوریتم تعداد مقایسهها صرف نظر از مجموعه داده، یکسان هستند. به این معنا که اهمیتی ندارد، دادههای ورودی مرتب شده یا معکوس باشند. حتی اگر با ترتیب تصادفی چیده شده باشند نیز در نتیجه تاثیری نمیگذارد.

نیازمندی های حافظه
با توجه به الگوریتمی که در بالا تعریف کردیم، به وضوح مشخص است که فرایند اجرای الگوریتم مرتب سازی حبابی نیازی به حافظه اضافی ندارد.
مثال
برای نمایش مثال، در این بخش از مطلب، آرایه نامرتبی را به صورت دلخواه انتخاب کردهایم. الگوریتم مرتب سازی حبابی پیچیدگی زمانی برابر با $$ Ο( n^2) $$ دارد. بنابراین آن را کوتاه و دقیق نمایش میدهیم.
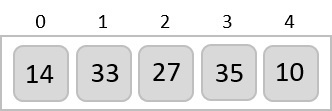
مرتب سازی حبابی با اولین دو عنصر آرایه کار را شروع میکند. این دو عنصر را با یکدیگر مقایسه کرده و بزرگترین آنها را پیدا میکند.
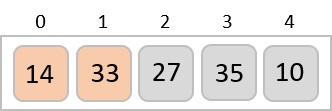
در این مورد خاص مقدار ۳۳ بزرگتر از ۱۴ است. بنابراین، این عناصر از قبل در حالت مرتب شده قرار داشتند. در مرحله بعد باید عدد ۳۳ را با عدد ۲۷ مقایسه کنیم.
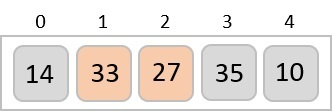
متوجه میشویم که ۲۷ از عدد ۳۳ کوچکتر است. پس این دو مقدار باید با یکدیگر جابهجا شوند.
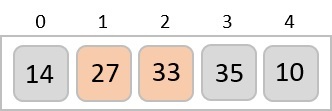
در مرحله بعد باید عدد ۳۳ را با عدد ۳۵ مقایسه کنیم. در این مقایسه مشخص است که هر دو عدد از قبل در حالت مرتب شده قرار دارند.
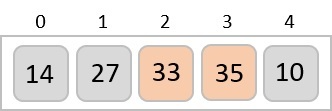
سپس به سمت دو مقدار دیگر حرکت میکنیم. باید این دو مقدار ۳۵ و ۱۰ را با هم مقایسه کنیم.
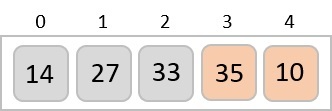
با مقایسه ۳۵ و ۱۰ متوجه میشویم که ۱۰ از ۳۵ کوچکتر است. بنابراین، این دو عنصر هم باید با یکدیگر جابهجا شوند. در نهایت میبینیم که به انتهای آرایه رسیدهایم. بعد از اولین پیمایش آرایه بدست آمده باید به شکل تصویر زیر باشد.
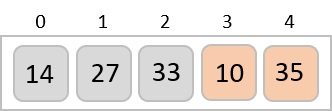
با نگاه دقیقتر میبینیم که اکنون در حال نمایش آرایه بعد از هر پیمایش هستیم. بنابراین بعد از دومین پیمایش آرایه مسئله به شکل زیر خواهد شد.
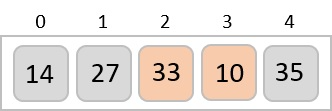
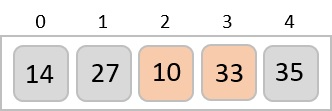
به این نکته توجه کنید که بعد از هر پیمایش حداقل یک مقدار به انتهای آرایه منتقل خواهد شد.
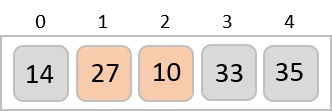
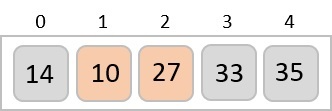
توجه کنید که با هربار پیمایش آرایه یکی از عنصرهای بزرگتر به سمت انتها یا راست آرایه حرکت کرده و عدد ۱۰ نیز در هر پیمایش یک واحد به سمت ابتدا یا چپ آرایه حرکت میکند.
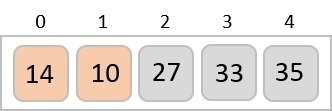
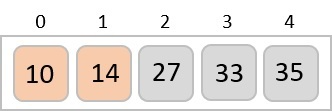
و وقتی که دیگر نیازی به جابهجایی در طول یکبار پیمایش کامل آرایه نباشد، مرتب سازی حبابی متوجه میشود که آرایه به صورت کامل مرتب شده است.
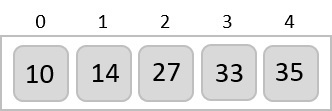
برای اینکه بتوانیم بهتر الگوریتمهای خود را طراحی و پیادهسازی کنید، پیشنهاد میکنیم که مطلب مربوط به آموزش کامل نحوه نوشتن الگوریتم به زبان ساده را از مجله فرادرس مطالعه کنید.
در ادامه مطلب به چند جنبه عملی از پیادهسازی الگوریتم مرتب سازی حبابی نگاه میکنیم.
پیاده سازی
یکی از مهمترین مشکلاتی که در الگوریتم اصلی و شبهه کد فیالبداهه خود مورد اشاره قرار ندادیم، این است که بعد از هر پیمایشی بالاترین مقدار در انتهای آرایه قرار میگیرد. بنابراین، پیمایش بعدی نیازی ندارد شامل عناصر از قبل پیمایش شده شود. برای حل این مسئله، حلقه درونی خود را محدود میکنیم تا از بررسی دوباره مقادیر مرتب شده جلوگیری کنیم. به این حالت الگوریتم، مرتبسازی بهینهسازی شده میگویند.
در این قسمت از مطلب کدهای مربوط به پیادهسازی الگوریتم مرتب سازی حبابی را با زبانهای برنامه نویسی C و ++C و جاوا و پایتون پیادهسازی کردهایم.
کادر زیر مربوط به پیادهسازی کدهای مربوط به الگوریتم مرتب سازی حبابی با زبان برنامه نویسی C است.
#include <stdio.h>
void bubbleSort(int array[], int size){
for(int i = 0; i<size; i++) {
int swaps = 0; //flag to detect any swap is there or not
for(int j = 0; j<size-i-1; j++) {
if(array[j] > array[j+1]) { //when the current item is bigger than next
int temp;
temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
swaps = 1; //set swap flag
}
}
if(!swaps)
break; // No swap in this pass, so array is sorted
}
}
int main(){
int n;
n = 5;
int arr[5] = {67, 44, 82, 17, 20}; //initialize an array
printf("Array before Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ",arr[i]);
printf("n");
bubbleSort(arr, n);
printf("Array after Sorting: ");
for(int i = 0; i<n; i++)
printf("%d ", arr[i]);
printf("n");
}کادر زیر مربوط به پیادهسازی کدهای مربوط به الگوریتم مرتب سازی حبابی با زبان برنامه نویسی ++C است.
#include<iostream>
using namespace std;
void bubbleSort(int *array, int size){
for(int i = 0; i<size; i++) {
int swaps = 0; //flag to detect any swap is there or not
for(int j = 0; j<size-i-1; j++) {
if(array[j] > array[j+1]) { //when the current item is bigger than next
int temp;
temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
swaps = 1; //set swap flag
}
}
if(!swaps)
break; // No swap in this pass, so array is sorted
}
}
int main(){
int n;
n = 5;
int arr[5] = {67, 44, 82, 17, 20}; //initialize an array
cout << "Array before Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
bubbleSort(arr, n);
cout << "Array after Sorting: ";
for(int i = 0; i<n; i++)
cout << arr[i] << " ";
cout << endl;
}کادر زیر مربوط به پیادهسازی کدهای مربوط به الگوریتم مرتب سازی حبابی با زبان برنامه نویسی جاوا است.
import java.io.*;
import java.util.*;
public class BubbleSort {
public static void main(String args[]) {
int n = 5;
int[] arr = {67, 44, 82, 17, 20}; //initialize an array
System.out.print("Array before Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
for(int i = 0; i<n; i++) {
int swaps = 0; //flag to detect any swap is there or not
for(int j = 0; j<n-i-1; j++) {
if(arr[j] > arr[j+1]) { //when the current item is bigger than next
int temp;
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
swaps = 1; //set swap flag
}
}
if(swaps == 0)
break;
}
System.out.print("Array After Sorting: ");
for(int i = 0; i<n; i++)
System.out.print(arr[i] + " ");
System.out.println();
}
}خروجی مربوط به هر سه کد بالا بعد از اجرا به صورت زیر میشود.
[fdboutput]{“content”:”Array%20before%20Sorting%3A%2067%2044%2082%2017%2020%20%0AArray%20After%20Sorting%3A%2017%2020%2044%2067%2082″,”type”:”block”}[/fdboutput]
کادر زیر مربوط به پیادهسازی کدهای مربوط به الگوریتم مرتب سازی حبابی با زبان برنامه نویسی پایتون است.
def bubble_sort(array, size):
for i in range(size):
swaps = 0;
for j in range(0, size-i-1):
if(arr[j] > arr[j+1]):
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
swaps = 1;
if(swaps == 0):
break;
arr = [67, 44, 82, 17, 20]
n = len(arr)
print("Array before Sorting: ")
print(arr)
bubble_sort(arr, n);
print("Array after Sorting: ")
print(arr)خروجی کد بالا بعد از اجرا به صورت زیر در کنسول پایتون نمایش داده میشود.
[fdboutput]{“content”:”Array%20before%20Sorting%3A%20%0A%5B67%2C%2044%2C%2082%2C%2017%2C%2020%5D%0AArray%20after%20Sorting%3A%20%0A%5B17%2C%2020%2C%2044%2C%2067%2C%2082%5D”,”type”:”block”}[/fdboutput]
پیچیدگی های زمانی و فضایی الگوریتم مرتب سازی حبابی
یکی از مهمترین معیارهای تعیین ارزش برای هر الگوریتم، مقادیر مربوط به پیچیدگی زمانی و فضایی الگوریتم است. در این قسمت از مطلب، پیچیدگیهای زمانی و فضایی الگوریتم مرتب سازی حبابی را بررسی کردهایم.
معیار اول پیچیدگی زمانی
«پیچیدگی زمانی» (Time Complexity) به میزان مصرف منبع زمان توسط الگوریتم برای حل مسئله گفته میشود. معمولا برای ارزیابی هر الگوریتم باید پیچیدگی مربوط به آن را در بهترین حالت، حالت متوسط و بدترین حالت اندازه گرفت.
در جدول زیر میزان پیچیدگی زمانی الگوریتم مرتب سازی حبابی را در هر سه حالت بیان کردهایم.
| سطح سختی مسئله | پیچیدگی زمانی |
| بهترین حالت – مسئله ساده | $$ O(n) $$ |
| حالت میانگین – میانگین سختی در مسائل مختلف | $$ O( n^2 ) $$ |
| بدترین حالت – مسئله سخت | $$ O( n^2 ) $$ |
n برابر با تعداد عناصر آرایه است. برای کمک به درک بهتر مطلب، هر سه حالت بالا را در پایین توضیح دادهایم.
- بهترین حالت – مسئله ساده: این اتفاق زمانی رخ میدهد که نیازی به مرتبسازی عناصر لیست نباشد. به این معنا که آرایه از قبل مرتب شده است. بهترین میزان پیچیدگی زمانی مرتب سازی حبابی برابر با $$ O(n) $$ است.
- حالت میانگین – میانگین سختی در مسائل مختلف: این حالت زمانی اتفاق میافتد که عناصر آرایه در یک ترکیب نامرتبی در کنار هم قرار گرفته باشند. ترکیبی که نه به طور مناسبی صعودی و نه به طور مناسبی نزولی شده باشد. در چنین حالتی میانگین پیچیدگی زمانی مرتبسازی حبابی برابر با $$ O( n^2 ) $$ است.

- بدترین حالت – مسئله سخت: این حالت زمانی اتفاق میافتد که عناصر آرایه باید در جهت برعکس مرتب شوند. به این شکل که فرض کنیم باید عناصر آرایه را در حالت صعودی مرتب کنیم، اما عناصر مورد نظر در حالت نزولی قرار دارند. بدترین حالت پیچیدگی زمانی مرتبسازی حبابی برابر با $$ O( n^2 ) $$ است.
معیار دوم پیچیدگی فضایی
«پیچیدگی فضایی» (Space Complexity) به میزان مصرف منبع حافظه توسط الگوریتم برای حل مسئله گفته میشود.
در جدول زیر میزان پیچیدگی فضایی الگوریتم مرتب سازی حبابی را بیان کردهایم.
| پیچیدگی فضایی | $$ O(1) $$ |
| پایداری | بله |
n برابر با تعداد عناصر آرایه است. برای کمک به درک جدول بالا به توضیحات ارائه شده در فهرست زیر توجه کنید.
- پیچیدگی فضایی الگوریتم مرتب سازی حبابی برابر با $$ O(1) $$ است. به این دلیل است که مرتبسازی حبابی نیاز به متغیر اضافی برای جابهجا کردن عناصر با یکدیگر دارد.
- پیچیدگی فضایی مربوط به الگوریتم مرتب سازی حبابی بهینهسازی شده برابر با $$ O(2) $$ است. این مطلب به علت آن است که به دو متغیر اضافی در الگوریتم بهینهسازی شده مرتبسازی حبابی نیاز داریم.
آشنایی با چند مورد از الگوریتم های حرفه ای و مدرن
الگوریتم مرتبسازی حبابی، الگوریتمی نیست که بتوان در برنامههای مدرن و مجموعه دادههای بزرگ استفاده کرد. دنیای علوم کامیپوتر با پیشرفت روز افزون تکنولوژی به مشکلات و مسائل جدیدی نیز برخورد میکند. امروزه صحبت از الگوریتمهایی است که بتوانند با قدرت شگرف کامپیوترهای کوانتومی مسائل بسیار پیچیده را به طرز بهینهای حل کنند.
فرادرس به عنوان وبسایت تولید کننده محتوای آموزشی تلاش کرده تا تعداد متنوعی از الگوریتمهای پیشرفته و قوی را نیز در کنار سایر الگوریتمها معرفی کند. روش پیادهسازی و کار با آنها را توضیح داده و فیلم آموزشی خود را به شکلی ارائه دهد که مخاطب تا حد کاملی به الگوریتمها مسلط شود.
در قسمت پایین چند مورد از این الگوریتمها را معرفی کردهایم. در صورت تمایل با کلیک بر روی تصویر بالا وارد صفحه اصلی این مجموعه آموزشی شده و از الگوریتمهای بیشتر نیز دیدن کنید.
- فیلم آموزش پیاده سازی الگوریتم ژنتیک در پایتون دوره مقدماتی از فرادرس
- فیلم آموزش الگوریتم بهینه سازی گرگ خاکستری GWO و پیاده سازی در متلب با فرادرس
- فیلم آموزش الگوریتم بهینه سازی ملخ GOA و پیاده سازی آن در MATLAB با فرادرس
- فیلم آموزش الگوریتم بهینه سازی شیرمورچه و پیاده سازی در MATLAB با فرادرس
- فیلم آموزش الگوریتم بهینه سازی جهش قورباغه SFLA و پیاده سازی در MATLAB فرادرس
جمع بندی
الگوریتم مرتب سازی حبابی با جابهجایی تکراری عناصر مجاور در لیست کار میکند. این عملیات را تا زمانی انجام میدهد که در پیمایش کامل بر روی لیست دیگر هیچ جابهجایی رخ ندهد. دلیل اصلی نامگذاری این الگوریتم به مرتبسازی حبابی به این علت است که حرکت عناصر آرایه دقیقا شبیه به حرکت حبابهای هوا درون آب است. حبابهای آب به سمت سطح بالای آب حرکت میکنند. به همین هم ترتیب عناصر آرایه در طی هر پیمایش به سمت انتهای لیست حرکت میکنند.
مرتب سازی حبابی یکی از الگوریتمهایی است که هم به سادگی قابل درک است و هم فرایند پیادهسازی آسانی دارد. برای همین یکی از بهترین گزینهها برای شروع کار دانشجویان در درس طراحی و پیادهسازی الگوریتم شده. اما کارآمدی این الگوریتم در دنیای واقعی چندان قابل قبول نیست. زیرا این الگوریتم برای استفاده در مجموعه دادههای بزرگ مناسب نیست.
در این مطلب از مجله فرادرس، الگوریتم مرتبسازی حبابی را معرفی کرده و روش استفاده برنامههای کامپیوتری از این الگوریتم را توضیح دادیم. سپس روش کار این الگوریتم را به صورت کامل بررسی کرده و در نهایت با چند زبان مختلف برنامهنویسی کدهای این الگوریتم را پیادهسازی کردیم. در آخر هم درباره پیچیدگی زمانی و فضایی مرتب سازی حبابی توضیحات شفاف و کاملی را ارئه کردیم.
نوشته توضیح الگوریتم مرتب سازی حبابی و پیاده سازی در زبان های مختلف اولین بار در فرادرس – مجله. پدیدار شد.
source