مساحت جانبی منشور برابر با حاصلضرب محیط قاعده منشور در ارتفاع منشور است. منشورها، یکی از انواع حجمهای هندسی به شمار میروند که از دو قاعده یکسان موازی و یک وجه جانبی تشکیل میشوند. وجه جانبی منشور، بین دو قاعده آن قرار میگیرد. اندازه سطح این وجه، به محیط قاعده و فاصله عمودی بین دو قاعده (ارتفاع) بستگی دارد. البته در حالتهای خاص مانند منشور با قاعده دایره یا منشور با وجههای مربعی، امکان محاسبه مساحت جانبی با شعاع قاعده یا اندازه ضلع (یال) نیز وجود دارد. در این مطلب از مجله فرادرس، نحوه محاسبه مساحت جانبی منشور را به همراه حل چندین مثال و تمرین متنوع آموزش میدهیم.

در ادامه، ضمن معرفی رابطه محاسبه مساحت جانبی منشور، تعریف این اندازه را به کمک مفهوم گسترده بیان میکنیم. سپس، به ارائه فرمول جبری محاسبه اندازه سطح جانبی برای انواع منشور میپردازیم. در نهایت، پس از بررسی تفاوت بین مساحت جانبی و مساحت کل منشور، میزان یادگیری شما را با حل چندین تمرین در قالب یک آزمون چهارگزینهای میسنجیم.
مساحت جانبی منشور چگونه بدست می آید؟
مساحت جانبی استوانه با استفاده از رابطه زیر به دست میآید:
ارتفاع منشور × محیط قاعده منشور = مساحت جانبی منشور
در ادامه و با حل دو مثال، نحوه استفاده از فرمول مساحت جانبی منشورها را آموزش میدهیم.
مثال ۱: محاسبه مساحت جانبی منشور
تصویر زیر، یک منشور را نمایش میدهد. محیط قاعده این منشور برابر با ۱۵ سانتیمتر و ارتفاع آن برابر با ۱۰ سانتیمتر است.
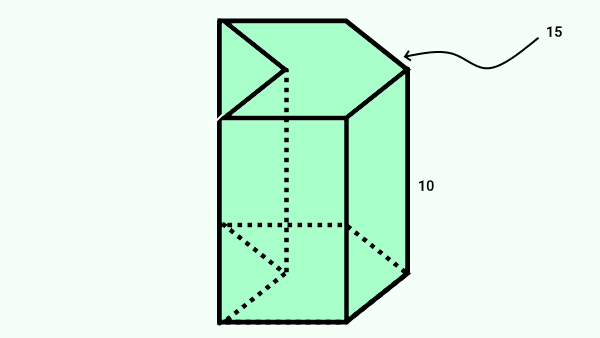
با توجه به اطلاعات مسئله، مساحت جانبی حجم بالا را به دست بیاورید.
برای به دست آوردن اندازه سطح جانبی منشور، از رابطه زیر استفاده میکنیم:
ارتفاع منشور × محیط قاعده منشور = مساحت جانبی منشور
بر اساس اطلاعات داده شده، محیط قاعده برابر با ۱۵ سانتیمتر و ارتفاع آن برابر با ۱۰ سانتیمتر است. اندازههای معلوم را درون رابطه بالا قرار میدهیم:
۱۰ × ۱۵ = مساحت جانبی منشور
۱۵۰ = مساحت جانبی
بنابراین، مساحت جانبی برابر با ۱۵۰ سانتیمتر مربع میشود. در حل سوالات مربوط به محاسبه مساحت و مساحت جانبی، به واحد (یکا) دقت کنید. یکای مساحت، طول به توان دو یا طول مربع است.
مثال ۲: محاسبه مساحت جانبی منشور پنج پهلو
یک منشور با قاعده پنجضلعی را در نظر بگیرید. اگر یالهای این منشور مانند تصویر زیر باشد، مساحت جانبی آن چقدر خواهد بود؟
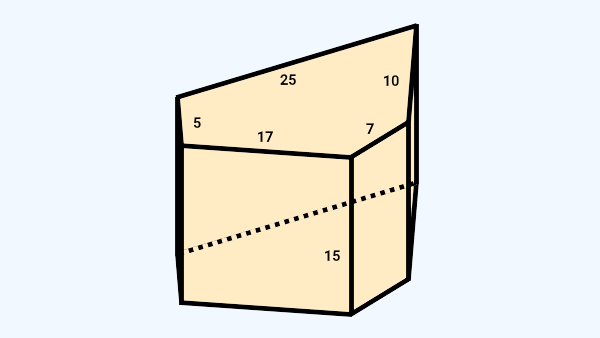
برای شروع حل این مثال، ابتدا رابطه محاسبه اندازه سطح جانبی منشور را مینویسیم:
ارتفاع منشور × محیط قاعده منشور = مساحت جانبی منشور
بر اساس این رابطه، باید محیط قاعده و ارتفاع منشور را داشته باشیم. ارتفاع منشور برابر با ۱۵ واحد طول است. محیط قاعده نیز از جمع اندازه ضلعهای آن به دست میآید:
۷ + ۱۰ + ۲۵ + ۵ + ۱۷ = محیط پنجضلعی
۶۴ = محیط پنجضلعی
اکنون میتوانیم ارتفاع و محیط را درون رابطه مساحت جانبی جایگذاری کنیم:
ارتفاع منشور × محیط قاعده منشور = مساحت جانبی منشور
۱۵ × ۶۴ = مساحت جانبی
۹۶۰ = مساحت جانبی
در نتیجه، مساحت جانبی برابر با ۹۶۰ واحد سطح (واحد طول مربع) است. در ادامه، برای یادگیری بهتر نحوه محاسبه مساحت جانبی منشورها، به تعریف این مفهوم میپردازیم.
تعریف مساحت جانبی منشور چیست؟
منشور (+)، یکی از انواع حجمهای هندسی است که از گسترش یک شکل دوبعدی در بعد سوم به دست میآید.
منشورها، از دو قاعده یکسان و چند سطح جانبی تشکیل میشوند. به قاعدهها و سطوح جانبی منشور، وجه میگویند. تصویر زیر، چند حجم منشوری را نمایش میدهد.
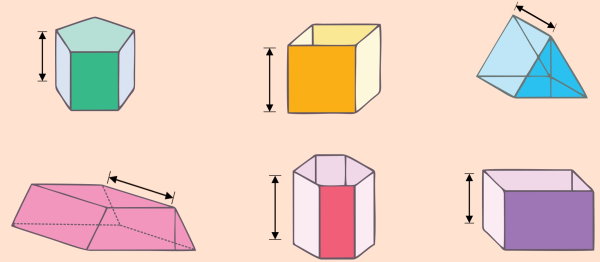
در منشورهای بالا، ارتفاع مشخص شده است. قاعدهها در هر یک از منشورها، موازی و مساوی هستند. سطحهای بین دو قاعده، وجههای جانبی منشور را تشکیل میدهند. همانطور که مشاهده میکنید، تمام وجههای جانبی در منشورها، به شکل مستطیل است. بنابراین، مساحت جانبی منشور، از جمع مساحت تمام این مستطیلها به دست میآید. یک منشور با قاعده ذوزنقه و اندازههای زیر را در نظر بگیرید.
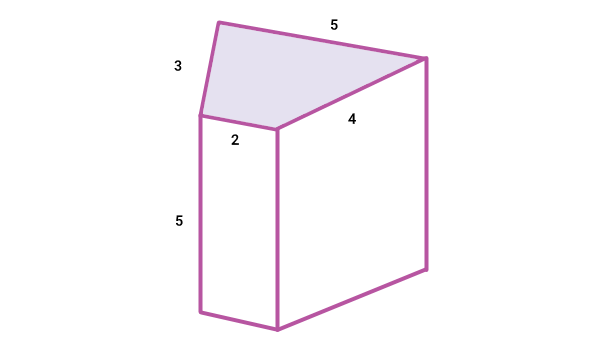
اگر این منشور را در راستای ارتفاعش بر روی کاغذ قرار دهیم و دور آن را خط بکشیم، یک مستطیل به وجود میآید.
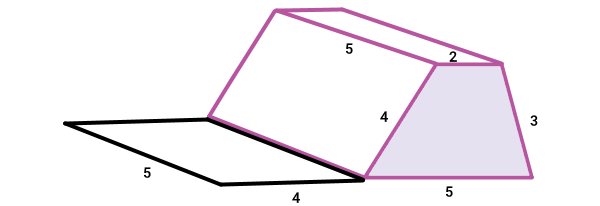
با چرخاندن منشور، قرار دادن سطح دیگر روی کاغذ و خط کشیدن دور آن، یک مستطیل دیگر تشکیل میشود. در صورت تکرار این فرآیند برای تمام وجههای جانبی، به شکلی مشابه تصویر زیر میرسیم.
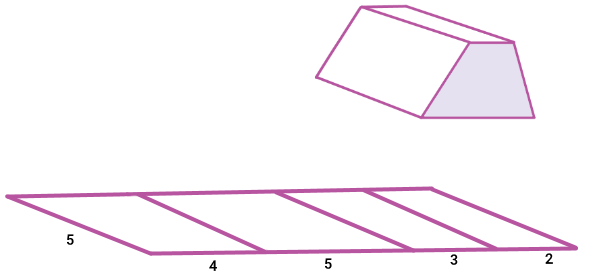
مستطیلهای بالا، وجههای جانبی منشور با قاعده ذوزنقه هستند. از اینرو، مساحت جانبی این منشور، از محاسبه مجموع مساحتهای این چهار مستطیل به دست میآید. توجه داشته باشید که در تمام این مستطیلها، یکی از ضلعها برابر با ارتفاع منشور است. در نتیجه:
۲۰ = ۵ × ۴ = مساحت مستطیل اول
۲۵ = ۵ × ۵ = مساحت مستطیل دوم
۱۵ = ۵ × ۳ = مساحت مستطیل سوم
۱۰ = ۵ × ۲ = مساحت مستطیل چهارم
به این ترتیب، با جمع تمام مساحتها به مساحت جانبی منشور ذوزنقهای میرسیم:
۷۰ = ۱۵ + ۲۵ + ۲۰ + ۱۰ = مساحت جانبی
البته یک نکته مهم در اینجا وجود دارد که به درک شما از فرمول مساحت جانبی منشور کمک میکند. در مساحت مستطیلها، یک عدد (طول ارتفاع) همواره ثابت بود. اگر هنگام جمع کردن مساحتها، از این عدد فاکتور بگیریم، به رابطه زیر میرسیم:
(۳ + ۵ + ۴ + ۲) × ۵ = مساحت تمام مستطیلها
به عبارت درون پرانتز دقت کنید (۳ + ۵ + ۴ + ۲). این عبارت، جمع ضلعهای قاعده منشور را نمایش میدهند. به عبارت دیگر:
(۱۴) × ۵ = مساحت تمام مستطیلها
عدد ۱۴، جمع ضلعهای قاعده منشور ذوزنقهای یا همان محیط ذوزنقه است. بنابراین میتوانیم بگوییم:
محیط ذوزنقه × ارتفاع منشور = مساحت جانبی منشور ذوزنقهای
مثال ۳: محاسبه مساحت جانبی منشور شش پهلو
یک منشور با قاعده ششضلعی منتظم را در نظر بگیرید. اگر اندازه ضلعهای قاعده منشور برابر با ۲ سانتیمتر و ارتفاع آن برابر با ۵ سانتیمتر باشد، مساحت جانبی منشور ششپهلو چقدر خواهد بود؟
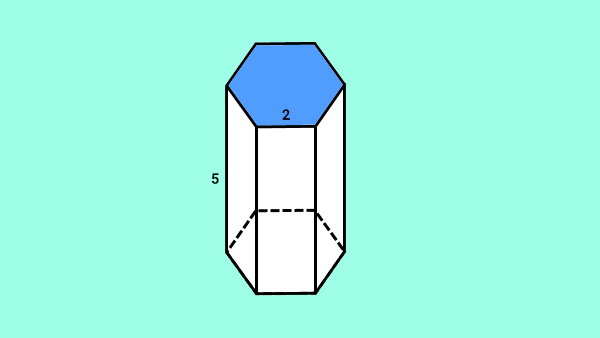
برای به دست آوردن اندازه سطح جانبی منشور، به ارتفاع و محیط قاعده آن نیاز داریم. ارتفاع منشور برابر با ۵ است. محیط قاعده، از رابطه زیر محاسبه میشود:
اندازه ضلع × تعداد ضلعها = محیط چندضلعی منتظم
۲ × ۶ = محیط ششضلعی منتظم
۱۲ = محیط ششضلعی منتظم
به این ترتیب، داریم:
ارتفاع منشور × محیط قاعده منشور = مساحت جانبی منشور
۵ × ۱۲ = مساحت جانبی
۶۰ = مساحت جانبی
در نتیجه، اندازه سطح جانبی منشور ششپهلو با قاعده ششضلعی منتظم برابر با ۶۰ سانتیمتر مربع است.
مثال ۴: محاسبه ارتفاع منشور از روی مساحت جانبی
مجموع مساحت وجههای جانبی یک منشور برابر با ۸۶۷ متر مربع است. اگر قاعده این منشور، یک مثلث متساویالاضلاع به ضلع ۱۷ متر باشد، اندازه ارتفاع چقدر خواهد بود؟
صورت سوال، مساحت جانبی را به ما داده است و مقدار ارتفاع را از ما میخواهد. رابطه بین مساحت جانبی و ارتفاع منشور، به صورت زیر نوشته میشود:
ارتفاع منشور × محیط قاعده منشور = مساحت جانبی منشور
همانطور که مشاهده میکنید، برای به دست آوردن ارتفاع با داشتن مساحت جانبی یا برعکس، باید محیط قاعده را داشته باشیم. قاعده منشور مورد سوال، یک مثلث متساویالاضلاع (دارای ضلعهای برابر) است. بنابراین، داریم:
۱۷ + ۱۷ + ۱۷ = محیط قاعده مثلثی
۵۱ = محیط قاعده
این مقدار را به همراه مساحت جانبی، در رابطه قرار میدهیم:
ارتفاع منشور × ۵۱ = ۸۶۷
۵۱ ÷ ۸۶۷ = ارتفاع منشور
۱۷ = ارتفاع منشور
در نتیجه، ارتفاع منشور مورد سوال برابر با ۱۷ متر است. در مطلب آموزش محاسبه مساحت جانبی استوانه از مجله فرادرس، راجع به نحوه محاسبه اندازه سطح جانبی یکی از انواع خاص منشور و فرمولهای مربوط به آن به طور کامل صحبت کردیم. در ادامه این مطلب از مجله فرادرس، به معرفی فرمول جبری مساحت جانبی تمام منشورها میپردازیم.
یادگیری حل مسائل مساحت جانبی منشور با فرادرس

مباحث مربوط به حجمهای هندسی و منشورها، در فصل ششم کتاب ریاضی هفتم به دانشآموزان تدریس میشوند. درس سوم فصل ششم ریاضی هفتم، به مبحث «مساحت جانبی و کل» اختصاص دارد. با مطالعه این درس میتوانید مفاهیم اولیه مرتبط با مساحت جانبی منشور را یاد بگیرید. با این وجود، برای تقویت مهارت حل مسئله خود، بهتر است پس از مرور مثالها و تمرینهای کتاب، به سراغ منبعی بروید که ضمن ارائه کامل نکات تئوری، روشهای مختلف حل مسئله را به شما آموزش دهد. فرادرس، یک فیلم آموزشی مفید و جامع را در رابطه با نکات و فرمولهای ریاضی هفتم تهیه کرده است که میتواند شما در یادگیری سریع و راحت درسهای ریاضی هفتم کمک کند. لینک مشاهده این فیلم در ادامه آورده شده است:
در ادامه، به معرفی فرمول جبری محاسبه اندازه سطح جانبی منشور میپردازیم.
فرمول جبری مساحت جانبی منشور چیست؟
فرمول جبری مساحت جانبی منشور به صورت زیر نوشته میشود:
- : مساحت جانبی
- : محیط قاعده
- : ارتفاع
برای آشنایی با نحوه استفاده از فرمول بالا، به حل چند مثال میپردازیم.
مثال ۵: محاسبه مساحت جانبی منشور سه پهلو
اندازه سطح جانبی منشور زیر را به دست بیاورید.
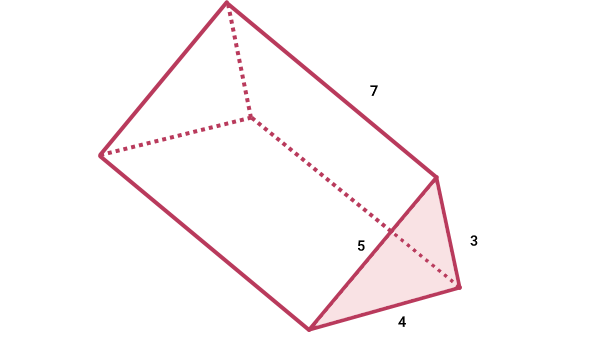
تصویر، یک منشور با قاعده مثلثی را نمایش میدهد. فرمول محاسبه مساحت جانبی این منشور، به صورت زیر نوشته میشود:
- : مساحت جانبی
- : محیط قاعده
- : ارتفاع برابر با ۷ واحد طول
محیط قاعده مثلثی را نداریم اما میتوانیم آن را با استفاده از فرمول زیر به دست بیاوریم:
- : محیط مثلث
- : اندازه ضلع اول مثلث برابر با ۵ واحد طول
- : اندازه ضلع دوم مثلث برابر با ۴ واحد طول
- : اندازه ضلع سوم مثلث برابر با ۳ واحد طول
به این ترتیب، داریم:
اکنون، اندازه محیط را به همراه ارتفاع در فرمول مساحت جانبی قرار میدهیم:
در نتیجه، مساحت جانبی منشور مثلثی برابر با ۸۴ واحد سطح (طول به توان دو) است.
مثال ۶: محاسبه مساحت جانبی منشور چهار پهلو
منشور زیر، دارای ارتفاع ۶ متر و قاعدهای مستطیلی شکل به طول ۳ متر و عرض ۲ متر است.
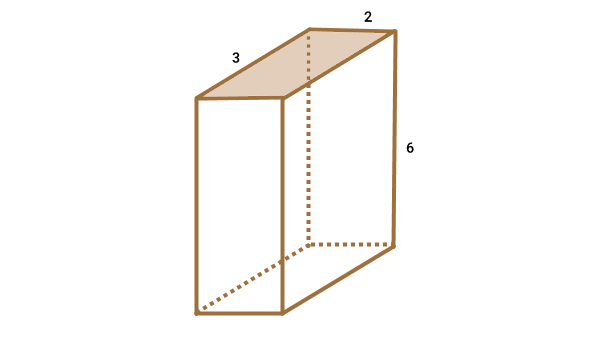
مساحت جانبی این منشور چهارپهلو را به دست بیاورید.
برای به دست آوردن اندازه سطح جانبی منشور مورد سوال، از فرمول زیر استفاده میکنیم:
- : مساحت جانبی
- : محیط قاعده
- : ارتفاع برابر با ۶ متر
- : محیط مستطیل
- : طول مستطیل برابر با ۳ متر
- : عرض مستطیل برابر با ۲ متر
در نتیجه، مساحت جانبی منشور با قاعده مستطیلی برابر با ۶۰ متر مربع شد.
مساحت جانبی انواع منشور
در این بخش، به معرفی انواع منشورها و نحوه محاسبه مساحت جانبی آنها میپردازیم.
مساحت جانبی مکعب مربع
مکعب مربع، یکی از انواع حجمهای منشوری است که از شش وجه مربعیشکل و برابر تشکیل میشود. بنابراین، چهار وجه جانبی مکعب، چهار مربع با اندازههای یکسان هستند.
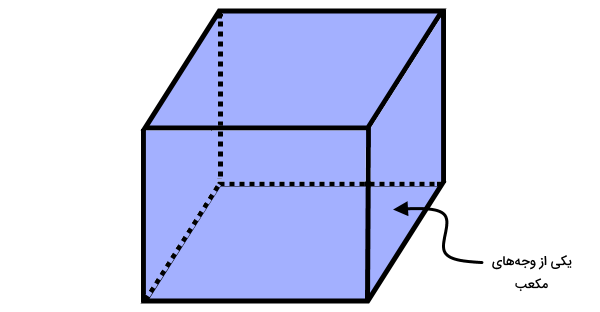
به این ترتیب، اندازه سطح جانبی مکعب از رابطه زیر به دست میآید:
مساحت هر وجه مکعب × ۴ = مساحت جانبی مکعب
به دلیل مربعی بودن وجههای مکعب، به جای مساحت هر وجه، از فرمول مساحت مربع استفاده میکنیم:
۲(اندازه ضلع مکعب) × ۴ = مساحت جانبی مکعب
فرمول جبری مساحت جانبی مکعب مربع عبارت است از:
- : مساحت جانبی مکعب
- : اندازه ضلع مکعب
مثال ۵: محاسبه مساحت جانبی مکعب
مکعب مربعی به ضلع ۲a را در نظر بگیرید. مساحت جانبی این مکعب چند برابر a است؟
مساحت جانبی مکعب از رابطه زیر به دست میآید:
- : مساحت جانبی مکعب
- : اندازه ضلع مکعب
به جای اندازه ضلع مکعب ، را قرار میدهیم:
در نتیجه، مساحت جانبی مکعب برابر با میشود.
مساحت جانبی استوانه
استوانه، یک حجم منشوری با قاعدههای دایرهای است. برخلاف حجمهای منشوری با قاعدههای چندضلعی، سطح جانبی استوانه، نه از چند سطح مستطیلیشکل، بلکه تنها از یک سطح مستطیلی تشکیل نمیشود. البته، این مستطیل به صورت یک سطح منحنی درآمده است.
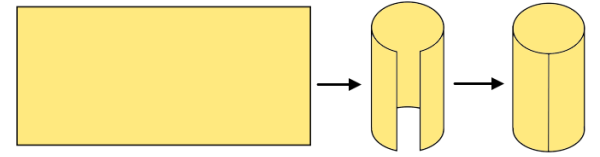
فرمول کلی مساحت جانبی حجمهای منشوری را برای استوانه نیز میتوان استفاده کرد. این فرمول، عبارت بود از:
ارتفاع منشور × محیط قاعده منشور = مساحت جانبی منشور
- : مساحت جانبی
- : محیط قاعده
- : ارتفاع
به دلیل دایرهای شکل بودن قاعده استوانه، به جای محیط قاعده در رابطه بالا مینویسیم:
ارتفاع منشور × محیط دایره = مساحت جانبی استوانه
فرمول محیط دایره عبارت است از:
شعاع × عدد پی × ۲ = محیط دایره
به این ترتیب، برای محاسبه مساحت جانبی استوانه داریم:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
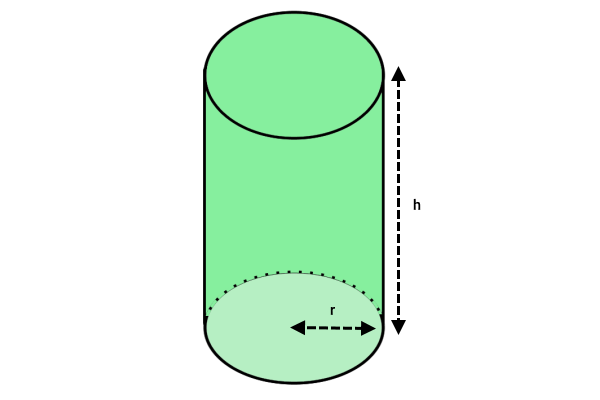
- : مساحت جانبی استوانه
- : عدد پی
- : شعاع قاعده استوانه
- : ارتفاع استوانه
مثال ۷: محاسبه مساحت جانبی استوانه
استوانهای به ارتفاع ۲۰ سانتیمتر و شعاع قاعده ۱۰ سانتیمتر را در نظر بگیرید. مساحت جانبی استوانه را به دست بیاورید.
مساحت جانبی استوانه با استفاده از رابطه زیر به دست میآید:
- : مساحت جانبی استوانه
- : عدد پی برابر با ۳/۱۴
- : شعاع قاعده استوانه برابر با ۱۰ سانتیمتر
- : ارتفاع استوانه برابر با ۲۰ سانتیمتر
مقادیر معلوم را درون فرمول قرار میدهیم:
در نتیجه، مساحت جانبی استوانه برابر با ۱۲۵۶ سانتیمتر مربع است.
مساحت جانبی منشور منتظم
منشور منتظم، منشوری با قاعده چندضلعی منتظم است. محیط چندضلعیهای منتظم با استفاده از رابطه زیر محاسبه میشود:
- : اندازه ضلع چندضلعی منتظم
- : تعداد ضلعهای چندضلعی منتظم
بنابراین، اگر قاعده منشور، یک n ضلعی با ضلعهای برابر باشد، فرمول محاسبه مساحت جانبی منشور به شکل زیر درمیآید:
- : مساحت جانبی
- : اندازه ضلع چندضلعی منتظم
- : تعداد ضلعهای چندضلعی منتظم
- : ارتفاع
مثال ۸: محاسبه مساحت جانبی منشور منتظم
مساحت جانبی یک منشور با قاعده چهارضلعی منتظم به ضلع ۳ میلیمتر و ارتفاع ۳ میلیمتر را محاسبه کنید.
برای به دست آوردن مساحت جانبی منشورهای منتظم، از رابطه زیر استفاده میکنیم:
- : مساحت جانبی
- : اندازه ضلع چندضلعی منتظم برابر با ۳ میلیمتر
- : تعداد ضلعهای چندضلعی منتظم برابر با ۴
- : ارتفاع برابر با ۳ میلیمتر
مقادیر معلوم را درون فرمول جایگذاری میکنیم:
در نتیجه، مساحت جانبی منشور برابر با ۳۶ میلیمتر مربع است. توجه داشته باشید که میتوانستیم این مثال را به صورت دیگری حل کنیم. چهارضلعی منتظم، همان مربع است. به دلیل برابر بودن اندازه ضلع این مربع (قاعده) با ارتفاع، با یک مکعب سر و کار داریم. بنابراین، مساحت جانبی با استفاده از فرمول مساحت جانبی مکعب نیز قابل محاسبه است:
- : مساحت جانبی مکعب
- : اندازه ضلع مکعب برابر با ۳ میلیمتر
مساحت جانبی منشور غیر منتظم
قاعده حجمهای منشوری، همیشه یک شکل منتظم نیست. در بخشهای قبلی، چندین مثال در رابطه با نحوه محاسبه مساحت جانبی منشورهای غیرمنتظم حل کردیم. اگر قاعده منشور، یک n ضلعی بوده و تمام ضلعها با هم برابر نباشند، فرمول کلی مساحت جانبی منشور به صورت زیر نوشته میشود:
- : مساحت جانبی
- تا : اندازه ضلعهای اول تا n ام چندضلعی منتظم
- : تعداد ضلعهای چندضلعی منتظم
- : ارتفاع
مثال ۹: محاسبه مساحت جانبی منشور غیر منتظم
مساحت جانبی منشور زیر را به دست بیاورید.
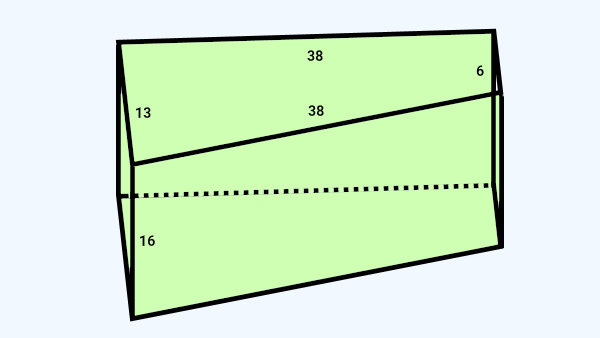
تصویر بالا، یک منشور غیرمنتظم با قاعده چهارضلعی را نمایش میدهد. مساحت سطح جانبی این منشور با استفاده از فرمول زیر به دست میآید:
- : مساحت جانبی
- تا : اندازه ضلعهای اول تا n ام چندضلعی منتظم
- : تعداد ضلعهای چندضلعی منتظم برابر با ۴
- : ارتفاع
- : اندازه ضلع اول برابر با ۳۸
- : اندازه ضلع دوم برابر با ۶
- : اندازه ضلع سوم برابر با ۳۸
- : اندازه ضلع چهارم برابر با ۱۳
- : ارتفاع برابر با ۱۶
به این ترتیب داریم:
در نتیجه، مساحت جانبی منشور برابر با ۱۵۲۰ واحد سطح است.
تفاوت مساحت جانبی و مساحت کل منشور چیست؟
هنگامی بحث در مورد مساحت منشور، مساحت قاعدهها به همراه مساحت جانبی مورد نظر است.
به عنوان مثال، یک استوانه را در نظر بگیرید. گسترده این استوانه، مانند تصویر زیر نمایش داده میشود.
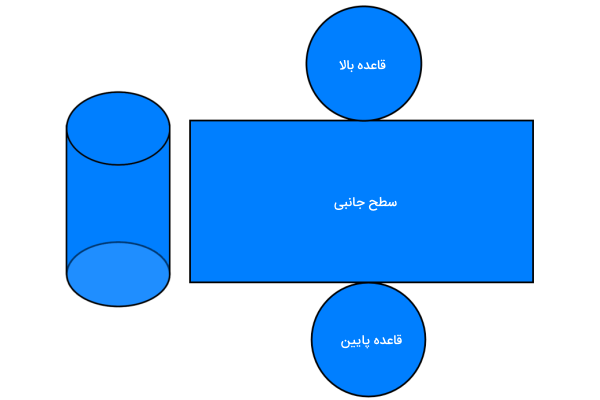
مساحت کل استوانه، مجموع مساحتهای قاعده بالا، قاعده پایین و سطح جانبی است.
مثال ۱۰: محاسبه مساحت کل منشور از روی مساحت جانبی
مساحت جانبی استوانهای برابر با ۲۰۱۶ سانتیمتر مربع است. اگر ارتفاع استوانه برابر با ۲۴ سانتیمتر باشد، مساحت کل این استوانه چقدر خواهد بود؟ (عدد پی را برابر با ۳ در نظر بگیرید.) برای به دست آوردن مساحت کل استوانه، به مساحت جانبی و مساحت قاعدههای دایرهای آن نیاز داریم.
مساحت دو قاعده دایرهای + مساحت جانبی = مساحت کل استوانه
مساحت جانبی در صورت سوال داده شده است. مساحت هر قاعده استوانه از رابطه زیر به دست میآید:
۲(شعاع قاعده) × عدد پی = مساحت قاعده
برای تعیین این مساحت، به شعاع قاعده نیاز داریم. این پارامتر، با استفاده از مساحت جانبی و ارتفاع قابل محاسبه است:
ارتفاع × شعاع قاعده × عدد پی × ۲ = مساحت جانبی استوانه
۲۴ × شعاع قاعده × ۳ × ۲ = ۲۰۱۶
شعاع قاعده × ۸۴ = ۲۰۱۶
۱۴۴ ÷ ۲۰۱۶ = شعاع قاعده
۱۴ = شعاع قاعده
اکنون، با استفاده از شعاع قاعده میتوانیم مساحت آن را به دست بیاوریم. به دلیل دایرهای شکل بودن قاعده استوانه، داریم:
۲(۱۴) × ۳ = مساحت قاعده
۱۹۶ × ۳ = مساحت قاعده
۵۸۸ = مساحت قاعده
مساحت هر یک از قاعدههای استوانه برابر با ۵۸۸ سانتیمتر مربع است. هر استوانه، دو قاعده دارد. بنابراین، مجموع مساحت قاعدهها برابر میشود با:
۵۸۸ × ۲ = مساحت قاعدههای استوانه
۱۱۷۶ = مساحت قاعدههای استوانه
اکنون، با داشتن مساحت قاعدهها و مساحت جانبی، میتوانیم مساحت کل را به دست بیاوریم:
مساحت قاعدهها + مساحت جانبی = مساحت کل استوانه
۱۱۷۶ + ۲۰۱۶ = مساحت کل استوانه
۳۱۹۲ = مساحت کل استوانه
در نتیجه، مساحت کل استوانه برابر با ۳۱۹۲ سانتیمتر مربع است. در آخرین بخش این مطلب از مجله فرادرس، به حل چندین تمرین متنوع در قالب یک آزمون چندگزینهای میپردازیم.
آزمون سنجش یادگیری مساحت جانبی منشور
در این بخش، سطح اطلاعات شما در مبحث اندازه سطح جانبی منشور را با طرح سوالهای چندگزینهای میسنجیم.
پس از جواب دادن به تمام سوالها، نتیجه آزمون برای شما به نمایش درمیآید.
مساحت جانبی منشور مثلث شکل زیر را به دست بیاورید.
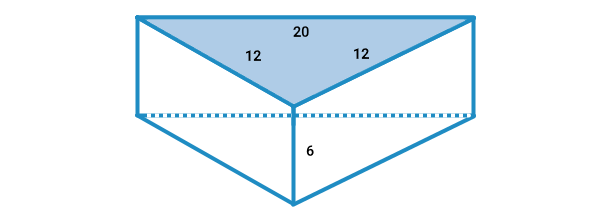
برای محاسبه مساحت جانبی منشور مثلثی، ابتدا محیط قاعده آن را تعیین میکنیم. این محیط برابر است با:
۲۰ + ۱۲ + ۱۲ = محیط قاعده
۴۴ = محیط قاعده
در مرحله بعد، اندازه محیط را درون فرمول زیر قرار میدهیم:
ارتفاع منشور × محیط قاعده منشور = مساحت جانبی منشور
۶ × ۴۴ = مساحت جانبی
۲۶۴ = مساحت جانبی
در نتیجه، مساحت جانبی منشور با قاعده مثلث برابر با ۲۶۴ واحد سطح است.
مساحت جانبی یک منشور پنج پهلو منتظم برابر با ۳۴۰ سانتیمتر مربع است. اگر ارتفاع منشور برابر با ۱۷ سانتیمتر باشد، اندازه هر یک از ضلعهای قاعده آن چقدر خواهد بود؟
صورت سوال، مساحت جانبی و ارتفاع یک منشور را به ما داده است. از این اطلاعات میتوانیم محیط قاعده منشور را به دست بیاوریم:
ارتفاع منشور × محیط قاعده منشور = مساحت جانبی منشور
۱۷ × محیط قاعده = ۳۴۰
۱۷ ÷ ۳۴۰ = محیط قاعده
۲۰ = محیط قاعده
منشور مورد سوال، یک منشور پنجپهلو (دارای قاعده پنجضلعی) و منتظم (دارای قاعدهای با ضلعهای برابر) است. بنابراین، رابطه بین محیط قاعده و اندازه ضلعها به صورت زیر نوشته میشود:
اندازه ضلع × تعداد ضلعها = محیط پنجضلعی منتظم
اندازه ضلع × ۵ = ۲۰
۵ ÷ ۲۰ = اندازه ضلع
۴ = اندازه ضلع
در نتیجه، اندازه هر یک از ضلعهای قاعده منشور برابر با ۴ سانتیمتر است.
تصویر زیر، گسترده یک منشور با قاعده مثلث قائمالزاویه را نمایش میدهد. مساحت جانبی این منشور، کدامیک از گزینههای زیر است؟
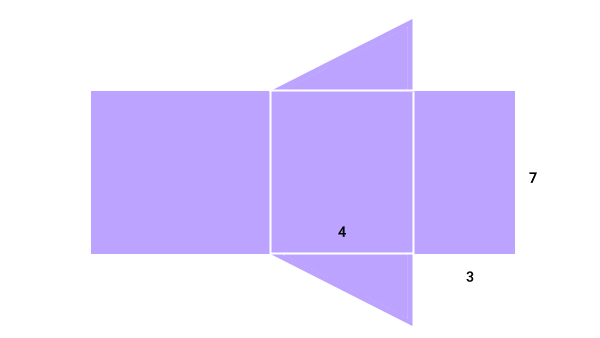
به منظور محاسبه مساحت جانبی منشور، به محیط قاعده و ارتفاع آن نیاز داریم. با توجه به اندازههای نمایش داده شده در تصویر، ارتفاع (۷) را داریم. محیط، از جمع ضلعهای مثلث قائمالزاویه (قاعده منشور) به دست میآید. در تصویر، اندازه دو ضلع مثلث (ساقهای مثلث قائمالزاویه) داده شده است. با استفاده از این اندازهها و رابطه فیثاغورس میتوانیم اندازه زاویه سوم را نیز تعیین کنیم. رابطه فیثاغورس به صورت زیر نوشته میشود:
- c: وتر مثلث قائمالزاویه
- a: یکی از ساقهای مثلث قائمالزاویه برابر با ۳
- b: ساق دیگر مثلث قائمالزاویه برابر با ۴
اکنون، تمام ضلعهای قاعده منشور را داریم. این اندازهها را با هم جمع میکنیم تا محیط قاعده به دست آید:
۵ + ۴ + ۳ = محیط قاعده
۱۲ = محیط قاعده
با قرار دادن محیط قاعده و ارتفاع در فرمول مساحت جانبی، خواهیم داشت:
ارتفاع × محیط قاعده = مساحت جانبی
۷ × ۱۲ = مساحت جانبی
۸۴ = مساحت جانبی
در نتیجه، مساحت جانبی منشور برابر با ۸۴ واحد سطح است.
دانشآموزی قصد دارد مساحت جانبی یک مکعب مربع را به دست بیاورد. کدامیک از فرمولهای زیر برای این کار مناسب هستند؟
ارتفاع × محیط قاعده
۲(ضلع منشور) × ۴
مساحت یک وجه × ۴
مکعب مربع، یک منشور است. به همین دلیل میتوان مساحت جانبی آن را با استفاده از فرمول کلی مساحت جانبی منشور به دست آورد. این فرمول به صورت زیر نوشته میشود:
ارتفاع × محیط قاعده = مساحت جانبی منشورها
در مکعب مربع، اندازه ضلع و ارتفاع با هم برابرند. به همین دلیل، میتوانیم فرمول بالا را به صورت زیر بازنویسی کنیم:
ضلع منشور × محیط مربع = مساحت جانبی
ضلع منشور × (ضلع منشور) ۴ = مساحت جانبی
۲(ضلع منشور) × ۴ = مساحت جانبی
2(ضلع منشور)، مساحت یک وجه مکعب مربع را نمایش میدهد. بنابراین، به جای فرمول بالا میتوانیم بنویسیم:
مساحت یک وجه × ۴
در نتیجه، تمام گزینهها درست هستند.
اگر مساحت یکی از وجههای یک منشور هشتپهلو و منتظم، برابر با ۱۴ سانتیمتر مربع باشد، مساحت جانبی، کدامیک از گزینههای زیر است؟
اطلاعات مسئله کافی نیست.
در یک منشور منتظم، تمام وجهها با یکدیگر برابرند. بنابراین، منشور هشتپهلو، هشت وجه با اندازه برابر دارد. با توجه به اطلاعات مسئله، داریم:
مساحت هر وجه × تعداد وجهها = مساحت جانبی
۱۴ × ۸ = مساحت جانبی
۱۱۲ = مساحت جانبی
به این ترتیب، اندازه سطح جانبی منشور مورد سوال برابر با ۱۱۲ سانتیمتر مربع است.
مساحت جانبی استوانهای به قطر قاعده ۶ و ارتفاع ۸ متر، کدامیک از گزینههای زیر است؟
استوانه، یک نوع منشور است. بنابراین، مساحت جانبی این منشور از رابطه زیر به دست میآید:
ارتفاع × محیط قاعده = مساحت جانبی استوانه
قاعده استوانه، دایره است. رابطه محیط دایره به صورت زیر نوشته میشود:
شعاع × عدد پی × ۲ = محیط دایره
بنابراین:
ارتفاع × شعاع × عدد پی × ۲ = مساحت جانبی استوانه
شعاع دایره، برابر با نصف قطر (۳ = ۲ ÷ ۶) است. به این ترتیب، داریم:
۸ × ۳ × ۳/۱۴ × ۲ = مساحت جانبی
۱۵۰/۷۲ = مساحت جانبی
در نتیجه، مساحت جانبی استوانه برابر با ۱۵۰/۷۲ متر مربع است.
میخواهیم دیوارهای یک کانتینر حمل بار را رنگ کنیم. اگر این کانتینر به شکل مکعب مستطیل و به صورت زیر باشد، مساحت سطح قابل رنگ، کدامیک از گزینههای زیر خواهد بود؟
- ارتفاع کانتینر: ۲/۲۶ متر
- طول کانتینر: ۱۲/۱۹ متر
- عرض کانتینر: ۲/۴۴ متر
اندازه سطح قابل رنگ، مساحت دیوارههای جانبی کانتینر است. این مساحت، از رابطه زیر به دست میآید:
ارتفاع × محیط کف = مساحت دیوارهها
ارتفاع × محیط مستطیل = مساحت جانبی
۲/۲۶ × (۲/۴۴ + ۱۲/۱۹) × ۲ = مساحت جانبی
۶۶/۱۳ = مساحت جانبی
در نتیجه، مساحت دیوارههای کانتینر یا همان مساحت قابل رنگ برابر با ۶۶/۱۳ متر مربع است.
آکواریومهای خانگی، از شیشه ساخته میشوند. اغلب این آکواریومها، به شکل مکعب مستطیل هستند. اگر طول، عرض و ارتفاع یک آکواریوم، به ترتیب برابر با ۲۰۰، ۳۰ و ۷۰ سانتیمتر باشد، اندازه شیشه به کاررفته در اطراف آن چند متر مربع است؟

۳۲۲۰۰۰ سانتیمتر مربع
۱۶۲۰۰ سانتیمتر مربع
اندازه شیشه به کار رفته در آکواریوم، همان مساحت جانبی است. از آنجایی که در اینجا با یک آکواریوم مکعب مستطیل سر و کار داریم، برای محاسبه مساحت جانبی میتوانیم از رابطه زیر استفاده کنیم:
- : مساحت جانبی آکواریوم
- : ارتفاع آکواریوم برابر با ۷۰ سانتیمتر
- : طول آکواریوم برابر با ۲۰۰ سانتیمتر
- : عرض آکواریوم برابر با ۳۰ سانتیمتر
صورت سوال، مساحت شیشه را برحسب متر مربع از ما خواسته است. بنابراین، مقادیر را از سانتیمتر به متر تبدیل میکنیم:
- : ارتفاع آکواریوم برابر با ۰/۷ متر
- : طول آکواریوم برابر با ۲ متر
- : عرض آکواریوم برابر با ۰/۳ متر
در نتیجه، مساحت شیشه دور آکواریوم برابر با ۳/۲۲ متر مربع است.
شخصی قصد دارد کاشیکاری یک استخر کوچک با شکل نامنظم را انجام دهد. او قصد دارد برای این کار، از کاشیهایی با مساحت ۲۲۵ سانتیمتر مربع استفاده کند. به منظور سفارش تعداد کاشیها، کاشیکار، محیط استخر را اندازه میگیرد و عدد ۱۶ متر را به دست میآورد. اگر عمق استخر برابر با ۱/۵ متر باشد، حداقل تعداد کاشیهای مورد نیاز برای کار بر روی دیواره داخلی استخر چقدر خواهد بود؟

برای محاسبه تعداد کاشیهای مورد نیاز برای کار بر روی دیواره داخلی استخر، باید مساحت جانبی استخر را به دست بیاوریم. به این منظور، میتوانیم از فرمول مساحت جانبی منشور کمک بگیریم. بر اساس این فرمول، داریم:
- : مساحت جانبی استخر
- : محیط قاعده استخر برابر با ۱۶ متر
- : ارتفاع استخر برابر با ۱۵ متر
مساحت جانبی استخر برابر با ۲۴ متر مربع است. باید این مساحت را با کاشیهای ۲۳۰ سانتیمتر مربعی پر کنیم. به این منظور، میتوانیم مساحت جانبی را بر مساحت کاشیها تقسیم کنیم. البته پیش از این کار، باید یکسانسازی واحد مساحتها را انجام دهیم. ۲۴ متر مربع برابر با ۲۴۰۰۰۰ سانتیمتر مربع است. از اینرو:
در نتیجه، برای کاشیکاری دیواره داخلی استخر، به حداقل ۱۰۶۷ کاشی ۲۲۵ سانتیمتر مربعی نیاز داریم.
مساحت کل یک مکعب مربع برابر با ۳۴۲ سانتیمتر مربع است. کدامیک از گزینههای زیر، مساحت جانبی مکعب را نمایش میدهند؟
۴۵۶ سانتیمتر مربع
۳۴۲ سانتیمتر مربع
۲۲۸ سانتیمتر مربع
۵۷ سانتیمتر مربع
برای به دست آوردن مساحت جانبی مکعب، به اندازه ضلع آن یا اندازه سطح هر یک از وجههای آن نیاز داریم. اندازه هر وجه مکعب از رابطه آن با مساحت کل به دست میآید:
مساحت یک وجه × ۶ = مساحت کل مکعب
مساحت یک وجه × ۶ = ۳۴۲
۶ ÷ ۳۴۲ = مساحت یک وجه
۵۷ = مساحت یک وجه
هر وجه مکعب، ۵۷ سانتیمتر مربع مساحت دارد. اکنون میتوانیم از فرمول زیر برای به دست آوردن مساحت جانبی مکعب استفاده کنیم:
مساحت یک وجه × ۴ = مساحت جانبی مکعب
۵۷ × ۴ = مساحت جانبی مکعب
۲۲۸ = مساحت جانبی مکعب
در نتیجه، مساحت جانبی مکعب برابر با ۲۲۸ سانتیمتر مربع است.
source
