۵۰ بازدید

آخرین به‌روزرسانی: ۱۱ تیر ۱۴۰۳

زمان مطالعه: ۸ دقیقه

مساحت جانبی مکعب، چهار برابر مساحت هر یک از وجه‌های آن است. مکعب، از شش وجه مربعی تشکیل می‌شود. بنابراین، مساحت این حجم منشوری، از ضرب عدد ۴ در مساحت وجه‌های مربعی آن به دست می‌آید. مکعب یا به طور دقیق‌تر، مکعب مربع، یکی از حالت‌های خاص مکعب مستطیل است که طول، عرض و ارتفاع آن برابرند. برای محاسبه مساحت جانبی مکعب مستطیل، باید محیط قاعده آن را در ارتفاعش ضرب کنیم. مساحت جانبی تمام حجم‌های منشوری، به این شکل به دست می‌آید. در این مطلب از مجله فرادرس، به آموزش نحوه محاسبه مساحت جانبی مکعب و مکعب مستطیل می‌پردازیم و چندین مثال و تمرین متنوع را حل می‌کنیم.

در ادامه، ضمن تعریف مفهوم مساحت جانبی در مکعب، به معرفی فرمول‌های محاسبه این اندازه می‌پردازیم. علاوه بر این، تفاوت بین اندازه سطح جانبی مکعب مربع و مکعب مستطیل را توضیح می‌دهیم. در نهایت، میزان یادگیری شما را با حل چند تمرین در قالب یک آزمون چندگزینه‌ای می‌سنجیم.

مساحت جانبی مکعب چگونه بدست می آید؟

مساحت جانبی مکعب، از رابطه زیر به دست می‌آید:

اندازه ضلع مکعب × اندازه ضلع مکعب × ۴ = مساحت جانبی مکعب

یا

^۲(اندازه ضلع مکعب) × ۴ = مساحت جانبی مکعب

منظور از اندازه ضلع در رابطه‌های بالا، طول ضلع یکی از وجه‌های مکعب است. از آنجایی که تمام وجه‌های مکعب با هم برابر و به شکل مربع هستند، اندازه اضلاع وجه‌های مختلف، تفاوت ندارد. بر این اساس می‌توانیم رابطه بالا را به صورت زیر ساده کنیم:

مساحت یک وجه × ۴ = مساحت جانبی مکعب

در ادامه برای درک بهتر روابط معرفی شده، به حل یک مثال می‌پردازیم.

مثال ۱: محاسبه اندازه سطح دور جعبه مکعبی

جعبه زیر را در نظر بگیرید. این جعبه از وجه‌‌های مربعی شکل تشکیل می‌شود.

اگر اندازه هر ضلع مکعب برابر با ۳۰ سانتی‌متر باشد، مساحت جانبی جعبه چقدر خواهد بود؟

به منظور محاسبه مساحت جانبی جعبه، از رابطه زیر استفاده می‌کنیم:

مساحت یک وجه × ۴ = مساحت جانبی مکعب

مساحت یک وجه جعبه × ۴ = مساحت جانبی جعبه

برای به دست آوردن مساحت جانبی جعبه مکعبی، به مساحت یکی از وجه‌های آن نیاز داریم. به دلیل مربعی بودن وجه‌های جعبه، مساحت هر وجه آن از رابطه زیر به دست می‌آید:

ضلع × ضلع = مساحت مربع

ضلع جعبه × ضلع جعبه = مساحت یک وجه جعبه

بنابراین، داریم:

۳۰ × ۳۰ = مساحت یک وجه جعبه

۹۰۰ = مساحت یک وجه جعبه

مساحت یکی از وجه‌‌‌های جعبه برابر با ۹۰۰ سانتی‌متر مربع است. به این ترتیب، محاسبه مساحت جانبی جعبه، از ضرب این مقدار در عدد ۴ انجام می‌گیرد:

۹۰۰ × ۴ = مساحت جانبی جعبه

۳۶۰۰ = مساحت جانبی جعبه

در نتیجه، اندازه سطح جانبی جعبه مکعبی برابر با ۳۶۰۰ سانتی‌متر مربع است.

تعریف مساحت جانبی مکعب چیست؟

مساحت جانبی مکعب، اندازه سطحی است که دور این شکل را تشکیل می‌دهد.

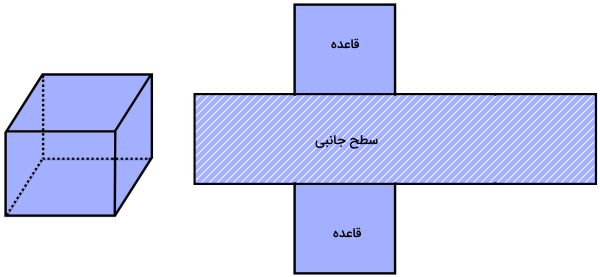
مکعب، به عنوان یک شکل سه‌بعدی یا به طور دقیق‌تر، یک حجم منشوری در نظر گرفته می‌شود. این حجم، از کنار هم قرار گرفتن شش سطح مربعی شکل به وجود می‌آید.

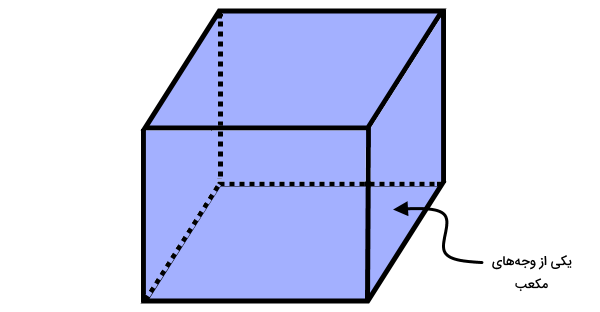
تصویر بالا، نمونه‌ای از یک مکعب را نمایش می‌دهد. اگر این مکعب را باز کنیم، به سطحی مشابه تصویر زیر می‌رسیم. به این سطح، گسترده مکعب گفته می‌شود.

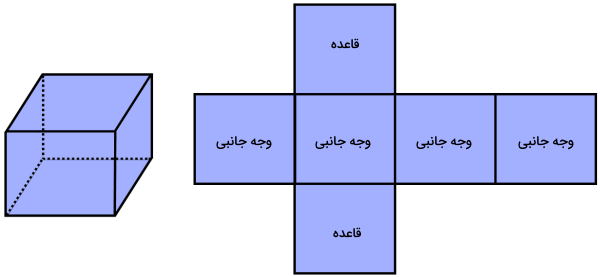
همان‌طور که مشاهده می‌کنید، گسترده مکعب، شامل شش مربع است. چهار مربعی که در کنار یکدیگر قرار دارند، سطح جانبی مکعب را تشکیل می‌دهند. مساحت این چهار مربع، به عنوان مساحت جانبی مکعب در نظر گرفته می‌شود. در حجم‌های منشوری دیگر، مساحت جانبی را بهتر و ساده‌تر می‌توان درک کرد؛ زیرا در این اشکال هندسی، تمام وجه‌‌ها با یکدیگر برابر نیستند. برای درک این موضوع، یک استوانه را در نظر بگیرید. اگر می‌خواهید اطلاعات بیشتری در مورد «استوانه» کسب کنید، می‌توانید مطلب مجله فرادرس در رابطه با «استوانه و مفاهیم آن در هندسه» را مطالعه کنید.

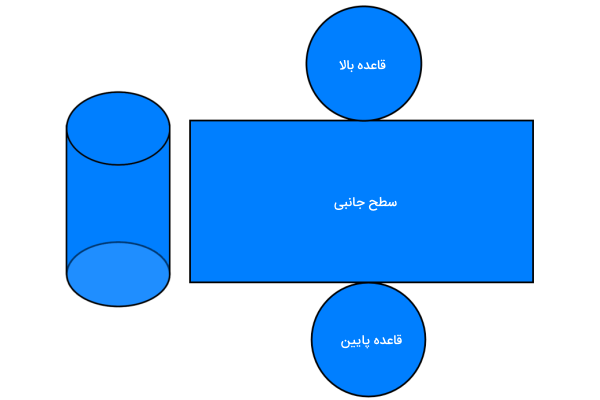
استوانه‌ها، از یک سطح جانبی منحنی شکل و دو قاعده دایره‌ای شکل تشکیل می‌شوند. اگر استوانه را دوران دهیم، موقعیت سطح جانبی و قاعده‌‌های آن، تغییر می‌کنند. در این حالت، نمی‌توانیم بگوییم وجه‌های دایره‌ای، سطح جانبی استوانه هستند.

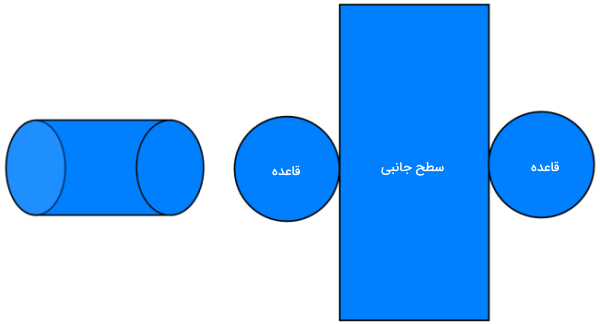
اکنون، یک مکعب را در نظر بگیرید. تمام وجه‌های مکعب به یک شکل هستند. بنابراین، اگر مکعب را دوران دهیم، شکل آن هیچ تغییری نمی‌کند. به عبارت دیگر، دوباره می‌توانیم وجه‌‌های بالایی و پایینی را به عنوان قاعده‌های مکعب و وجه‌های دیگر را به عنوان سطح جانبی مکعب در نظر بگیریم.

مبحث مساحت جانبی، از مباحث ارائه شده در ریاضی هفتم است. فرادرس، یک فیلم آموزشی مفید با عنوان «فیلم آموزش ریاضی پایه هفتم – جامع و با نکات مهم» را تهیه کرده است که می‌تواند شما را در یادگیری سریع و راحت دروس ریاضی هفتم و حل مسائل مربوط به مساحت جانبی کمک کند. لینک مشاهده این فیلم در ادامه آورده شده است.

تفاوت مساحت مکعب با مساحت جانبی مکعب چیست؟

یکی از سوالاتی که هنگام مطالعه و یادگیری مبحث مساحت جانبی مکعب برای دانش‌آموزان پیش می‌آید، تفاوت این مساحت با مساحت کل است. مساحت کل شکل‌های سه‌بعدی، اندازه تمام وجه‌های تشکیل‌دهنده آن‌ها است. مساحت جانبی، اندازه سطح دور شکل‌های سه‌بعدی را نمایش می‌دهد. مکعب، از شش وجه مربعی تشکیل می‌شود. بنابراین، مساحت کل مکعب از رابطه زیر به دست می‌آید:

مساحت یک وجه × ۶ = مساحت کل مکعب

یا

(اندازه ضلع × اندازه ضلع) × ۶ = مساحت کل مکعب

به عبارت دیگر، مساحت کل مکعب، همواره شش برابر مساحت یک وجه آن است. در طرف دیگر، مساحت جانبی مکعب، با چهار برابر مساحت یک وجه آن برابری می‌کند.

مثال ۲: محاسبه مساحت جانبی و مساحت کل مکعب

چگونه مساحت جانبی مکعب و دیگر حجم ها را یاد بگیریم؟

دنیای اطراف ما پر از اشکال هندسی و احجام سه‌بعدی است. یادگیری نحوه انجام محاسبات مربوط به این اشکال و احجام، در زندگی روزمره به کار می‌آید. به عنوان مثال، شخصی که می‌خواهد دور یک زمین حصار بکشد، باید با نحوه محاسبه سطح جانبی، مخصوصا سطح جانبی مکعب مربع و مکعب مستطیل آشنا باشد. نقاشی که قصد رنگ کردن دیوارهای یک اتاق را دارد، باید بتواند مساحت جانبی اتاق را به دست بیاورد. به دلیل اهمیت و کاربرد زیاد مساحت و حجم اشکال، نحوه محاسبه آن‌ها در دوره‌ها و پایه‌های مختلف تحصیلی به دانش‌آموزان آموزش داده می‌شود. دانش‌آموزان، مساحت جانبی مکعب و دیگر حجم‌های منشوری را در کتاب ریاضی هفتم یاد می‌گیرند. فرادرس، یک فیلم آموزشی مفید را تهیه کرده است که می‌تواند به شما در یادگیری راحت و سریع درس‌های این کتاب به همراه حل چندین مثال و تمرین متنوع کمک کند. لینک مشاهده این فیلم در ادامه آورد شده است:

در مطلب «مساحت مکعب مستطیل و محاسبه آن | به زبان ساده (+ دانلود فیلم آموزش رایگان)»، راجع به فرمول محاسبه مساحت حجم‌های مکعبی صحبت کردیم. در ادامه، به معرفی فرمول جبری مساحت جانبی مکعب می‌پردازیم.

فرمول جبری مساحت جانبی مکعب چیست؟

فرمول جبری مساحت جانبی مکعب به صورت زیر نوشته می‌شود:

$$S _ l = ۴ a ^ ۲$$

• $$S _ l$$
• $$a$$: اندازه ضلع مکعب

مثال ۳: محاسبه جبری اندازه سطح جانبی مکعب

مثال ۴: محاسبه مساحت جانبی مکعب روبیک ۳ در ۳

یک مکعب روبیک ۳ در ۳ را در نظر بگیرید. هر وجه این مکعب، از ۹ مربع تشکیل می‌شود. اگر اندازه هر ضلع این مربع‌ها، برابر با ۱/۹ سانتی‌متر باشد، اندازه سطح جانبی مکعب روبیک چقدر است؟

برای به دست آوردن اندازه سطح جانبی مکعب روبیک، باید مساحت یک وجه آن را به دست بیاوریم. اندازه هر ضلع روبیک، برابر است با:

ضلع یک مربع × ۳ = ضلع مکعب روبیک

۱/۹ × ۳ = ضلع مکعب روبیک

۵/۷ = ضلع مکعب روبیک

اندازه هر ضلع روبیک برابر با ۵/۷ سانتی‌متر است. بنابراین، داریم:

۵/۷ × ۵/۷ = مساحت وجه مکعب روبیک

۳۲/۴۹ = مساحت وجه مکعب روبیک

مساحت هر وجه مکعب روبیک برابر با ۳۲/۴۹ سانتی‌متر مربع است. با داشتن مساحت وجه می‌توانیم مساحت سطح جانبی روبیک را به دست بیاوریم:

مساحت وجه × ۴ = مساحت جانبی روبیک

۳۲/۴۹ × ۴ = مساحت جانبی روبیک

۱۲۹/۹۶ = مساحت جانبی روبیک

در نتیجه، اندازه سطح جانبی مکعب روبیک برابر با ۱۲۹/۹۶ سانتی‌متر مربع است.

تفاوت مساحت جانبی مکعب و مکعب مستطیل در چیست؟

مکعب یا به عبارت دقیق‌تر، مکعب مربع، یکی از حالت‌های خاص مکعب مستطیل است. در بخش‌های قبلی، راجع به نحوه محاسبه مساحت جانبی مکعب مربع صحبت کردیم. در این بخش، به معرفی فرمول مساحت جانبی مکعب مستطیل می‌پردازیم.

مکعب مستطیل، یک حجم منشوری است که قاعده آن از مستطیل تشکیل می‌شوند. تصویر زیر، اجزای مکعب مستطیل را نمایش می‌دهد.

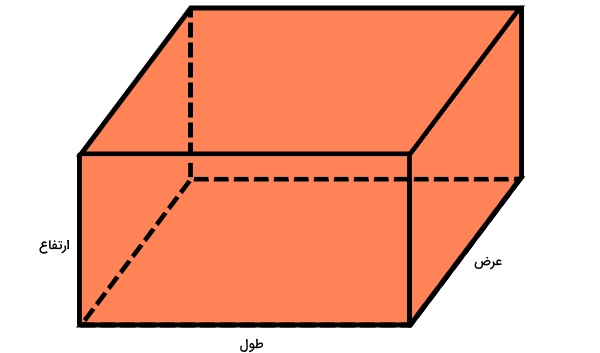
مساحت جانبی حجم‌های منشوری، از ضرب محیط قاعده آن‌ها در ارتفاع‌شان به دست می‌آید. بنابراین، مساحت جانبی مکعب مستطیل برابر است با:

محیط قاعده مستطیلی × ارتفاع = مساحت جانبی مکعب مستطیل

محیط مستطیل، با استفاده از رابطه زیر محاسبه می‌شود:

( عرض + طول ) ۲ = محیط مستطیل

به این ترتیب، داریم:

( عرض + طول ) ۲ × ارتفاع = مساحت جانبی مکعب مستطیل

فرمول جبری روابط بالا به صورت زیر نوشته می‌شود:

$$S _ l = h P$$

$$S _ l = h times ۲ ( l + b )$$

• $$S _ l$$
• $$h$$: ارتفاع مکعب مستطیل
• $$P$$: محیط قاعده مکعب مستطیل
• $$l$$: طول قاعده مستطیلی
• $$b$$: عرض قاعده مستطیلی

دقت داشته باشید که این فرمول، برای محاسبه اندازه سطح جانبی مکعب مربع نیز قابل استفاده است. برای یادگیری نحوه استفاده از این فرمول‌ها، به حل چند مثال می‌پردازیم.

مثال ۵: محاسبه میزان رنگ کاری دیوار اتاق

یک اتاق ۳ در ۴ متر مربعی را در نظر بگیرید. می‌خواهیم دیوارهای این اتاق را رنگ کنیم. اگر ارتفاع اتاق برابر با ۲/۵ متر باشد، مساحت ناحیه قابل رنگ چقدر خواهد بود؟ (اتاق را بدون پنجره فرض کرده و از مساحت در نیز چشم‌پوشی کنید.)

اغلب اتاق‌ها و فضاهای داخلی ساختمان‌ها، به شکل مکعب مستطیل هستند. دیوارها، سطح جانبی اتاق‌ها را تشکیل می‌دهند. بنابراین، مجموع مساحت آن‌ها را می‌توان با استفاده از فرمول مساحت جانبی مکعب مستطیل به دست آورد. به این ترتیب، داریم:

$$S _ l = h times ۲ ( l + b )$$

• $$S _ l$$
• $$h$$: ارتفاع اتاق برابر با ۲/۵ متر
• $$l$$: طول کف اتاق برابر با ۴ متر
• $$b$$: عرض کف اتاق برابر با ۳ متر

برای محاسبه سطح قابل رنگ، مقادیر معلوم را درون فرمول قرار می‌دهیم:

$$S _ l = ۲/۵ times ۲ ( ۳ + ۴ )$$

$$S _ l = ۲/۵ times ۲ ( ۷ )$$

$$S _ l = ۲/۵ times ۱۴$$

$$S _ l = ۳۵$$

در نتیجه، ۳۵ متر مربع از مساحت دیوارهای اتاق قابل رنگ است.

در آخرین بخش این مطلب از مجله فرادرس، به حل چند تمرین می‌پردازیم.

آزمون سنجش یادگیری مساحت جانبی مکعب

در این بخش، سطح اطلاعات شما در مبحث اندازه سطح جانبی مکعب را با طرح سوال‌های چندگزینه‌ای می‌سنجیم.

پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.

با کدامیک از گزینه‌های زیر می‌توان مساحت جانبی یک مکعب مربع را به دست آورد؟

( عرض + طول ) ۲ × ارتفاع

^۲(اندازه ضلع مکعب) × ۴

مساحت وجه مکعب × ۶

گزینه اول و دوم

مشاهده جواب

گزینه اول، اندازه سطح جانبی یک مکعب مستطیل را نمایش می‌دهد. مکعب مربع، یکی از انواع مکعب مستطیل است. بنابراین، می‌توانیم از رابطه معرفی شده در این گزینه برای به دست آوردن مساحت جانبی مکعب استفاده کنیم. گزینه دوم، متداول‌ترین رابطه برای محاسبه انداطه سطح جانبی مکعب مربع است. از این‌رو، این گزینه نیز درست است. گزینه سوم،‌ مساحت کل مکعب مربع را نشان می‌دهد که مقدار آن برابر با مساحت جانبی نیست. در نتیجه، گزینه چهارم صحیح است.

یکی از ضلع‌های یک مکعب برابر با ۵ میلی‌متر است. کدامیک از گزینه‌های زیر، مساحت جانبی این مکعب را نمایش می‌دهد؟

۱۵۰ سانتی‌متر مربع

۱۰۰ سانتی‌متر مربع

۱۵۰ میلی‌متر مربع

۱۰۰ میلی‌متر مربع

مشاهده جواب

اندازه سطح جانبی مکعب از رابطه زیر به دست می‌آید:

^۲(اندازه ضلع مکعب) × ۴ = مساحت جانبی مکعب

اندازه ضلع مکعب × اندازه ضلع مکعب × ۴ = مساحت جانبی

۵ × ۵ × ۴ = مساحت جانبی

۱۰۰ = مساحت جانبی

در نتیجه، مساحت جانبی برابر با ۱۰۰ میلی‌متر مربع است.

مساحت جانبی یک مکعب برابر با ۲۱۶ سانتی‌متر مربع است. مساحت هر یک از وجه‌های مکعب، کدامیک از گزینه‌های زیر است؟

$$۵۴$$ سانتی‌متر مربع

$$۳۶$$ سانتی‌متر مربع

مشاهده جواب

برای حل این سوال، فرمول محاسبه مساحت جانبی مکعب را می‌نویسیم:

^۲(اندازه ضلع مکعب) × ۴ = مساحت جانبی مکعب

این فرمول، به صورت زیر نیز نوشته می‌شود:

مساحت یک وجه مکعب × ۴ = مساحت جانبی مکعب

با توجه به اطلاعات مسئله، داریم:

مساحت یک وجه مکعب × ۴ = ۲۱۶

۴ ÷ ۲۱۶ = مساحت یک وجه مکعب

۵۴ = مساحت یک وجه مکعب

در نتیجه، هر یک از وجه‌های مکعب، ۵۴ سانتی‌متر مربع مساحت دارد.

جعبه‌ای مکعبی شکل را در نظر بگیرید که محیط کف آن برابر با ۲۴ سانتی‌متر است. می‌خواهیم دور این جعبه را با کاغذ کادو بپوشانیم. مساحت کاغذ مورد نیاز چقدر خواهد بود؟

۲۴ سانتی‌متر مربع

۳۶ سانتی‌متر مربع

۹۶ سانتی‌متر مربع

۱۴۴ سانتی‌متر مربع

مشاهده جواب

قاعده مکعب، یک مربع است. بنابراین و بر اساس صورت سوال، محیط کف جعبه برابر می‌شود با:

محیط مربع = محیط کف جعبه

ضلع × ۴ = محیط کف جعبه

ضلع × ۴ = ۲۴

۴ ÷ ۲۴ = ضلع

۶ = ضلع

به این ترتیب، اندازه هر ضلع جعبه برابر با ۶ سانتی‌متر است. اکنون، اندازه ضلع و محیط قاعده جعبه را داریم. اگر این اندازه‌ها را در هم ضرب کنیم، مساحت جانبی جعبه مکعبی به دست می‌آید:

۲۴ × ۶ = مساحت جانبی جعبه

۱۴۴ = مساحت جانبی جعبه

در نتیجه، اندازه سطح جانبی جعبه مکعبی برابر با ۱۴۴ سانتی‌متر مربع است. توجه داشته باشید که در صورت استفاده از فرمول دیگر مساحت جانبی مکعب نیز به مقدار بالا می‌رسیدیم:

^۲(اندازه ضلع جعبه) × ۴ = مساحت جانبی جعبه

^۲(۶) × ۴ = مساحت جانبی جعبه

۳۶ × ۴ = مساحت جانبی جعبه

۱۴۴ = مساحت جانبی جعبه

یک آکواریوم مکعبی شکل را در نظر بگیرید. اگر اندازه ضلع‌های این آکواریوم برابر با ۳۰ سانتی‌متر باشد، شیشه مورد استفاده برای ساخت این آکواریوم، چند متر مربع است؟

مشاهده جواب

مساحت شیشه‌ای که برای ساخت آکواریوم استفاده می‌شود، همان مساحت جانبی آکواریوم است که از رابطه زیر به دست می‌آید:

^۲(اندازه ضلع آکواریوم) × ۴ = مساحت جانبی آکواریوم

^۲(۳۰) × ۴ = مساحت جانبی آکواریوم

۹۰۰ × ۴ = مساحت جانبی آکواریوم

۳۶۰۰ = مساحت جانبی آکواریوم

مساحت جانبی آکواریوم یا همان شیشه مورد استفاده برای ساخت آن برابر با ۳۶۰۰ سانتی‌متر مربع است. صورت سوال، این مساحت را با واحد متر مربع از ما خواسته است. برای تبدیل سانتی‌متر مربع به متر مربع، عدد به دست آمده را بر ۱۰۰۰۰ تقسیم می‌کنیم:

$$frac { ۳۶۰۰ } { ۱۰۰۰۰ } = ۰/۳۶$$

در نتیجه، مساحت شیشه مورد استفاده در ساخت آکواریوم برابر با ۰/۳۶ متر مربع است.

مساحت جانبی یک مکعب برابر با ۳۲۴ متر مربع است. اندازه ضلع این مکعب، کدامیک از گزینه‌های زیر است؟

مشاهده جواب

برای به دست آوردن اندازه ضلع یک مکعب بر اساس مساحت جانبی آن، از فرمول مساحت جانبی استفاده می‌کنیم. این فرمول به صورت زیر نوشته می‌شود:

$$S _ l = ۴ a ^ ۲$$

• $$S _ l$$
• $$a$$: اندازه ضلع مکعب

با جایگذاری مقادیر معلوم در فرمول، خواهیم داشت:

$$۳۲۴ = ۴ a ^ ۲$$

$$a ^ ۲ = frac { ۳۲۴ } { ۴ }$$

$$a ^ ۲ = ۸۱$$

$$a = sqrt { ۸۱ }$$

$$a = ۹$$

در نتیجه، اندازه هر یک از اضلاع مکعب برابر با ۹ متر است.

تصویر زیر، مکعبی را نمایش می‌دهد که داخل آن یک فضای خالی مکعبی شکل وجود دارد. اندازه سطح داخلی و خارجی شکل چند است؟

مشاهده جواب

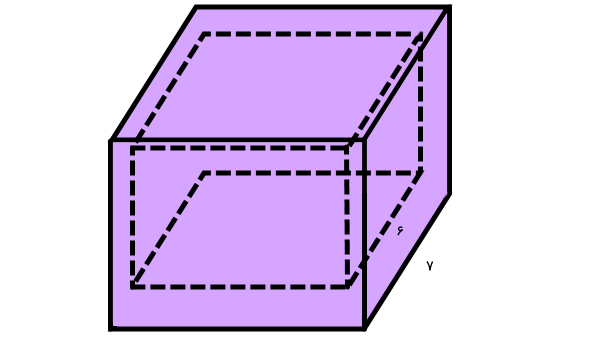
برای به دست آوردن اندازه سطح داخلی و خارجی، فضای خالی درون مکعب را به عنوان یک مکعب کوچک‌تر در نظر می‌گیریم. سپس، مساحت هر دو مکعب را به دست می‌آوریم و با هم جمع می‌کنیم. دقت داشته باشید که صورت سوال، مساحت کل (مجموع مساحت وجه‌ها) را می‌خواهد. مساحت مکعب بزرگ برابر است با:

$$S _ b = ۶ a _ b ^ ۲$$

• $$S _ b$$
• $$a _ b$$

$$S _ b = ۶ times ۷ ^ ۲$$

$$S _ b = ۶ times ۴۹$$

$$S _ b = ۲۹۴$$

مساحت مکعب بزرگ برابر با ۲۹۴ واحد سطح است. به همین ترتیب، برای مکعب کوچک داریم:

$$S _ s = ۶ a _ s ^ ۲$$

• $$S _ s$$
• $$a _ s$$

$$S _ b = ۶ times ۶ ^ ۲$$

$$S _ b = ۶ times ۳۶$$

$$S _ b = ۲۱۶$$

مساحت مکعب کوچک، برابر با ۲۱۶ واحد سطح شد. در نتیجه، مجموع مساحت‌های داخلی و خارجی شکل مورد سوال برابر می‌شود با:

$$S _ t = S _ b + S _ s$$

$$S _ t = ۲۹۴ + ۲۱۶$$

$$S _ t = ۵۱۰$$

یک جعبه میوه را در نظر بگیرید. اگر طول، عرض و ارتفاع این جعبه به ترتیب برابر با ۵۰، ۴۱ و ۳۱ سانتی‌متر باشد، مساحت چوب به کار رفته در آن چقدر است؟

$$۲۰۵۰$$ سانتی‌متر مربع

$$۵۶۴۲$$ سانتی‌متر مربع

$$۷۶۹۲$$ سانتی‌متر مربع

$$۹۷۴۲$$ سانتی‌متر مربع

مشاهده جواب

جعبه‌های میوه، معمولا به شکل مکعب مستطیل ساخته می‌شوند. البته به دلیل باز بودن بالای جعبه‌ها، شکل آن‌ها، یک مکعب مستطیل بدون قاعده بالایی است. بنابراین، برای اینکه مساحت چوب به کار رفته در جعبه مورد سوال را به دست بیاوریم، به اندازه سطح جانبی جعبه و کف آن نیاز داریم. کف جعبه، مستطیلی به طول ۵۰ سانتی‌متر و عرض ۴۱ سانتی‌متر است. مساحت این مستطیل با استفاده از رابطه زیر محاسبه می‌شود:

$$S _ b = l times b$$

• $$S _ b$$
• $$l$$: طول قاعده جعبه برابر با ۵۰ سانتی‌متر
• $$b$$: عرض قاعده جعبه برابر با ۴۱ سانتی‌متر

$$S _ b = ۵۰ times ۴۱ = ۲۰۵۰$$

مساحت کف جعبه برابر با ۲۰۵۰ سانتی‌متر مربع است. مساحت جانبی جعبه، از رابطه زیر به دست می‌آید:

$$S _ l = h times ۲ ( l + b )$$

• $$S _ l$$
• $$h$$: ارتفاع جعبه برابر با ۳۱ سانتی‌متر
• $$l$$: طول قاعده جعبه برابر با ۵۰ سانتی‌متر
• $$b$$: عرض قاعده جعبه برابر با ۴۱ سانتی‌متر

$$S _ l = ۳۱ times ۲ ( ۵۰ + ۴۱ )$$

$$S _ l = ۳۱ times ۲ ( ۹۱ )$$

$$S _ l = ۳۱ times ۱۸۲$$

$$S _ l = ۵۶۴۲$$

اندازه سطح جانبی جعبه برابر با ۵۶۴۲ سانتی‌متر مربع است. گر از فاصله بین قطعات چوب صرف‌نظر کنیم، مساحت چوب مصرفی برای ساخت جعبه برابر می‌شود با:

$$S _ t = S _ b + S _ l$$

$$S _ t = ۲۰۵۰ + ۵۶۴۲$$

$$S _ t = ۷۶۹۲$$

در نتیجه، مساحت چوب جعبه برابر با ۷۶۹۲ سانتی‌متر مربع است.

یک مکعب به ضلع x را در نظر بگیرید. اگر یک مکعب مشابه را در کنار مکعب اول قرار دهیم، یک مکعب مستطیل به وجود می‌آید. مساحت جانبی مکعب مستطیل با مساحت جانبی مکعب اول چه رابطه‌ای دارد؟

اندازه سطح جانبی مکعب مستطیل، دو برابر اندازه سطح جانبی مکعب می‌شود.

اندازه سطح جانبی مکعب مستطیل، یک و نیم برابر اندازه سطح جانبی مکعب می‌شود.

اندازه سطح جانبی مکعب مستطیل برابر با اندازه سطح جانبی مکعب می‌شود.

اندازه سطح جانبی مکعب مستطیل، نصف اندازه سطح جانبی مکعب می‌شود.

مشاهده جواب

مساحت جانبی مکعب به ضلع x برابر است با:

$$S _ ۱ = ۴ a ^ ۲$$

• $$S _ ۱$$
• $$a$$: ضلع مکعب برابر با x

$$S _ ۱ = ۴ x ^ ۲$$

اگر یک مکعب دیگر به ضلع $$x$$ را کنار مکعب اول قرار دهیم، مکعب مستطیلی به طول $$۲ x$$، عرض $$x$$ و ارتفاع $$x$$ به وجود می‌آید. مساحت جانبی این مکعب مستطیل برابر است با:

$$S _ ۲ = h times ۲ ( l + b )$$

• $$S _ ۲$$
• $$h$$: ارتفاع مکعب مستطیل برابر با $$x$$
• $$l$$: طول مکعب مستطیل برابر با $$۲ x$$
• $$b$$: عرض مکعب مستطیل برابر با $$x$$

$$S _ ۲ = x times ۲ ( ۲ x + x )$$

$$S _ ۲ = x times ۲ ( ۳ x)$$

$$S _ ۲ = x times ۶ x$$

$$S _ ۲ = ۶ x ^ ۲$$

نسبت مساحت جانبی مکعب مستطیل به مکعب، برابر می‌شود با:

$$frac { S _ ۲ } { S _ ۱ } = frac { ۶ x ^ ۲ } { ۴ x ^ ۲ } = ۱/۵$$

در نتیجه، مساحت جانبی مکعب مستطیل، یک و نیم برابر مساحت جانبی شکل اول شد.

می‌خوایم دور یک زمین مستطیلی شکل را تا ارتفاع ۲/۵ متر فنس بکشیم. اگر طول و عرض زمین برابر با ۱۶ و ۱۱ متر باشد، مساحت فنس مورد نیاز چقدر خواهد بود؟

$$۶۷/۵$$ متر مربع

$$۱۳۵$$ سانتی‌متر مربع

$$۲۷۰$$ متر مربع

$$۱۳۵$$ متر مربع

مشاهده جواب

با کشیدن فنس به طور یک زمین مستطیلی، شکل مکعب مستطیل به وجود می‌آید. فنس، سطح جانبی این مکعب مستطیل را تشکیل می‌دهد. بنابراین، اگر بخواهیم مساحت فنس دور زمین را حساب کنیم، باید مساحت جانبی مکعب مستطیل با ابعاد ارائه شده در صورت سوال را به دست بیاوریم. این مساحت برابر است با:

$$S _ l = h times ۲ ( l + b )$$

• $$S _ l$$
• $$h$$: ارتفاع فنس برابر با ۲/۵ متر
• $$l$$: طول زمین برابر با ۱۶ متر
• $$b$$: عرض زمین برابر با ۱۱ متر

$$S _ l = ۲/۵ times ۲ ( ۱۶ + ۱۱ )$$

$$S _ l = ۲/۵ times ۲ ( ۲۷ )$$

$$S _ l = ۲/۵ times ۵۴$$

$$S _ l = ۱۳۵$$

در نتیجه، برای فنس کشی دور زمین، به ۱۳۵ متر مربع فنس نیاز داریم.