اگر تجربه کار کردن با دیتاستهای بزرگ، یعنی دیتاستهایی با چندین هزار ویژگی را داشته باشید، بهطور حتم میدانید که چه فرایند دشواری برای پردازش دادهها در انتظار شما قرار دارد. دسترسی به این تعداد متغیر باعث افزایش دقت تجزیه و تحلیل نهایی شده اما از طرف دیگر، مدیریت این حجم از اطلاعات نیز چالشهای خود را دارد. از آنجا که بررسی تک به تک متغیرها بسیار هزینهبر است، به روش بهتری برای استخراج الگو از دادههایی با ابعاد بالا نیاز داریم. در چنین شرایطی میتوان از انواع روشهای کاهش ابعاد یا Dimensionality Reduction کمک گرفت. رویکردی که ما را قادر میسازد تا بدون کاهش تعداد ویژگیهای دیتاست و از دست دادن اطلاعات حیاتی، عملکرد خوب مدلهای یادگیری ماشین را حفظ و یا حتی ارتقاء دهیم. در این مطلب از مجله فرادرس یاد میگیریم منظور از Dimensionality Reduction چیست و به بررسی کاربردهای کاهش ابعاد در یادگیری ماشین میپردازیم.

در این مطلب، ابتدا با مفهوم کاهش ابعاد آشنا میشویم و به اهمیت آن در یادگیری ماشین اشاره میکنیم. سپس به این پرسش پاسخ میدهیم که چرا به کاهش ابعاد نیاز داریم و چه تکنیکهایی بیشترین استفاده را دارند. در انتهای این مطلب از مجله فرادرس و پس از آشنایی با انواع روشهای کاهش ابعاد، علاوهبر معرفی کاربردها و همچنین شرح مزایا و معایب این فرایند، به چند مورد از پرسشهای متداول پیرامون کاهش ابعاد پاسخ میدهیم.
منظور از کاهش ابعاد چیست؟
هر زمان که در علوم و حوزههای مختلفی مانند یادگیری ماشین و یا آمار و احتمال از «ابعاد» صحبت میکنیم، در واقع به تعداد ویژگیها یا همان متغیرهای ورودی یک دیتاست اشاره داریم. به عنوان مثال، دیتاستی را با ۲ ویژگی بسیار ساده «قد» و «وزن» در نظر بگیرید. این دیتاست و هر نمونه دادهای از آن را میتوان در قالب یک نمودار دو بعدی مانند زیر به نمایش گذاشت:
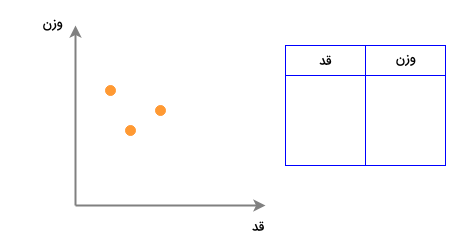
اگر بُعد دیگری را نیز با عنوان «سن» به این دیتاست اضافه کنیم، تعداد ابعاد آن به ۳ ارتقاء یافته و هر نمونه را میتوان بر روی فضایی سه بعدی مانند زیر ترسیم کرد:
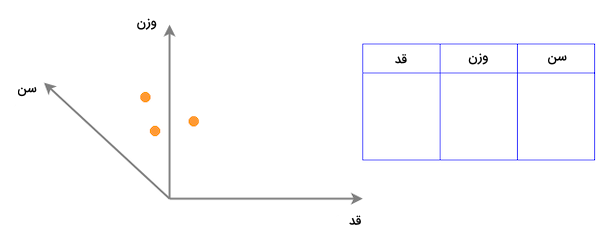
به همین شکل، اغلب دیتاستهای کاربردی در جهان حقیقی نیز ویژگیهای زیادی دارند. نمونه دادههایی که در فضایی با ابعاد بالا قرار داشته و مصورسازی آنها کار دشواری است. دانشمندان علم داده و همچنین مهندسین یادگیری ماشین، دیتاست را موجودیتی شامل چندین سطر و ستون تعریف میکنند که هر ستون بیانگر بُعدی از فضای بُعدی ویژگی، و سطرها همان نقاط داده ترسیم شده در فضای چند بُعدی هستند. به بیان سادهتر، کاهش ابعاد فرایندی است که همزمان با حفظ حداکثری تنوع دادهها، تعداد ویژگیهای دیتاست اصلی را کاهش میدهد. کاهش ابعاد بخشی از مرحله پیشپردازش داده بهحساب میآید. به این معنی که فرایند Dimensionality Reduction باید پیش از آموزش مدل یادگیری ماشین اجرا شود. حالا و پس از آشنایی با مفاهیم اولیه، در ادامه به بررسی اهمیت کاهش ابعاد در یادگیری ماشین میپردازیم.
اهمیت کاهش ابعاد در یادگیری ماشین
برای بیان اهمیت فرایند کاهش ابعاد در یادگیری ماشین، میتوان از مثال شهودی و ساده طبقهبندی ایمیلهای اسپم و عادی کمک گرفت. مسئله طبقهبندی ایمیلهای اسپم شامل ویژگیهای زیادی از قبیل «عنوان»، «محتوا» و «قالب» است. اگر چه امکان دارد برخی از این ویژگیها با یکدیگر همپوشانی داشته باشند. از طرف دیگر، بهخاطر همبستگی که میان ویژگیها در مسئلهای مانند شرایط آبوهوایی وجود دارد، دو ویژگی «رطوبت» و «میزان بارندگی» را میتوان به تنها یک ویژگی واحد تبدیل کرد. در حالی که مصورسازی و درک مسائل طبقهبندی سه بعدی کمی پیچیده است، اما دو ویژگی را میتوان در یک فضای دو بعدی و مسائل تک بعدی را با یک خط ساده به تصویر کشید. همانطور که در تصویر زیر مشاهده میکنید، فضای ویژگی سه بعدی به ۲ فضای دو بعدی مجزا تقسیم شده است:
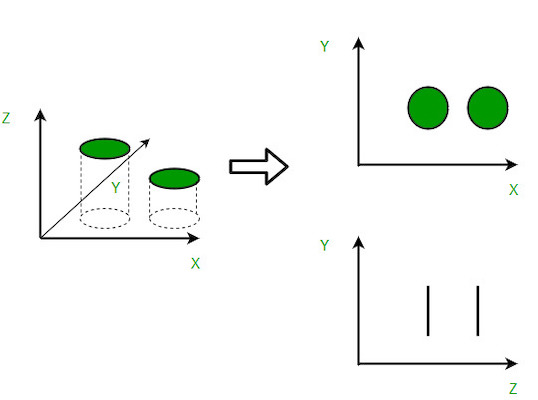
آموزش کاهش ابعاد در یادگیری ماشین با فرادرس

وقتی از دادههایی با ابعاد بالا حرف میزنیم، در واقع منظورمان دیتاستهایی است که ویژگیها یا متغیرهای زیادی دارند. تکههای اطلاعاتی بسیاری که باید کنار یکدیگر قرار گیرند. پیچیدگی این دیتاستها از حجم زیاد دادهها سرچشمه میگیرد. به عنوان مثال، دیتاستی را در نظر بگیرید که شامل اطلاعات مربوط به هزاران محصول فروشگاهی است. هر محصول ویژگیهای منحصربهفردی مانند قیمت، اندازه و رنگ دارد. واضح است که مرتبسازی چنین اطلاعاتی نیازمند صرف هزینه و زمان زیادی است. در اینجا تکنیکهای کاهش یا تقلیل ابعاد بهکار میآیند. روشهایی که از طریق کشف الگوها و روابط میان متغیرها، باعث سادهسازی دادهها شده و به درک راحتتر اطلاعات کمک میکند.
از طرف دیگر، فضایی با ابعاد پایین، نسخهای ساده شده از فضایی با ابعاد بالا است. در کاهش ابعاد بهجای استفاده از همه ویژگیها یا نقاط داده، تنها شمار اندکی از ویژگیها را جدا میکنیم. این سادهسازی به درک، تحلیل و تفسیر موثرتر دادهها منجر میشود. با توجه به اهمیت این موضوع، پلتفرم فرادرس دورهای را در قالب ویدئوهای آموزشی تولید کرده است که با مراجعه به لینک زیر میتوانید بهطور رایگان آن را مشاهده کنید:
چرا به تکنیک های کاهش ابعاد نیاز داریم؟
پس از آشنایی با اهمیت کاهش ابعاد در یادگیری ماشین، این بخش را به شرح برخی از دلایل استفاده از تکنیکهای کاهش ابعاد اختصاص میدهیم. در فهرست زیر چند مورد از مزایای کاهش ابعاد را برای دیتاستها ملاحظه میکنید:

- با کاهش تعداد ویژگیها، فضای لازم برای ذخیرهسازی نیز کاهش پیدا میکند.
- ابعاد کمتر به محاسبات و زمان آموزش کمتری نیاز دارد.
- در برخی الگوریتمها، ابعاد بالا به عملکردی ضعیف ختم میشود و از همین جهت لازم است تا ابتدا فرایند کاهش ابعاد اجرا شود.
- کاهش ابعاد با حذف ویژگیهای اضافی از وضعیت «همخطی چندگانه» (Multicollinearity) جلوگیری میکند. به عنوان مثال دو متغیر «زمان سپری شده روی تردمیل به دقیقه» و «میزان کالری سوزانده شده» را در نظر بگیرید. این دو ویژگی همبستگی بالایی با یکدیگر دارند. چرا که صرف زمان بیشتر برای دویدن روی تردمیل برابر با سوزاندن کالری بیشتر است. در نتیجه نیازی به ذخیره هر دو این ویژگیها نیست و تنها یک مورد از آنها اطلاعات مورد نیاز را در اختیار ما قرار میدهد.
- به مصورسازی دادهها کمک میکند. همانگونه که پیشتر نیز توضیح دادیم، مصورسازی دادهها در ابعاد بالا کار دشواری است و با کاهش فضا به دو یا سه بُعد، میتوان درک بهتری از توزیع دادهها بهدست آورد.
موارد ذکر شده تنها بخشی از دلایلی است که نیاز ما را به کاهش ابعاد توجیه میکند. در ادامه با معرفی انواع روشهای کاهش ابعاد در یادگیری ماشین، بهتر به ضرورت استفاده از این فرایند پی میبریم.
روش های کاهش ابعاد در یادگیری ماشین
برای معرفی روشهای کاهش ابعاد در یادگیری ماشین، ابتدا باید بگوییم که کاهش ابعاد یا Dimensionality Reduction به دو شیوه زیر قابل انجام است:
- تکنیک انتخاب ویژگی با حفظ مرتبطترین ویژگیهای دیتاست.
- یافتن زیرمجموعه کوچکتری از متغیرهای جدید که هر کدام ترکیبی از متغیرهای ورودی اصلی با اطلاعات مشابه هستند.
در این بخش از مطلب مجله فرادرس علاوهبر معرفی، به پیادهسازی برخی از رایجترین روشهای کاهش ابعاد در یادگیری ماشین با استفاده از زبان برنامه نویسی پایتون و دیتاستی متشکل از اطلاعات ۱۵۵۹ محصول فروشگاهی جمعآوری شده از ۱۰ فروشگاه مختلف میپردازیم.
۱. نسبت مقادیر گمشده
هنگامی که دیتاستی در اختیار شما قرار میگیرد، اولین قدم بررسی و ارزیابی دادهها پیش از ساخت هر گونه مدل یادگیری است. در بیشتر اوقات متوجه برخی مقادیر گمشده در دیتاست میشوید که باید یا جایگذاری و یا حذف شوند. اما چه میشود اگر حجم زیادی از دادهها، برای مثال ۵۰ درصد از یک ویژگی را مقادیر گمشده تشکیل داده باشند. در چنین شرایطی بهتر است ویژگی بهطور کامل حذف شود اما، میتوان این کار را با تعیین حد آستانهای مشخص انجام داد. یعنی تنها در صورتی ویژگی حذف شود که درصد مقادیر گمشده از حد آستانه فراتر رود. برای پیادهسازی روش «نسبت مقادیر گمشده» (Missing Value Ratio)، ابتدا کتابخانههای مورد نیاز را فراخوانی کرده و دیتاست را در متغیری با نام df
ذخیره میکنیم:
1# importing required libraries
2import pandas as pd
3import numpy as np
4import matplotlib.pyplot as plt
5
6
7# read the data
8df = pd.read_csv("df_train.csv")سپس برای بررسی درصد مقادیر گمشده در هر متغیر یا ویژگی، از دو متد isnull()
و sum()
کمک میگیریم:
1# checking the percentage of missing values in each variable
2df.isnull().sum() / len(df)*100همانطور که در تصویر زیر مشاهده میکنید، تنها دو متغیر Item_Weight و Outlet_Size با مشکل مقادیر گمشده روبهرو هستند:

برای حل این مشکل میتوان از تکنیکهای جایگذاری استفاده کرد و یا مانند زیر و با تعیین حد آستانهای ۲۰ درصدی، متغیرهایی که بیش از ۲۰ درصد از مقادیر آنها گمشده است را حذف و در نهایت لیست متغیرهای باقیمانده را در خروجی چاپ کنیم:
1# saving missing values in a variable
2m_values = df.isnull().sum() / len(df)*100
3# saving column names in a variable
4variables = train.columns
5variable = [ ]
6for i in range(0, 12):
7 if m_values[i] <= 20: # setting the threshold as 20%
8 variable.append(variables[i])
9
10print(variable)خروجی مانند زیر است:
['Item_Identifier', 'Item_Weight', 'Item_Fat_Content', 'Item_Visibility', 'Item_Type', 'Item_MRP', 'Outlet_Identifier', 'Outlet_Establishment_Year', 'Outlet_Location_Type', 'Outlet_Type', 'Item_Outlet_Sales']
با توجه به خروجی فوق، تنها ویژگی که بیش از ۲۰ درصد از مقادیر آن گمشده بودند یعنی Outlet_Size از دیتاست حذف شده است.
۲. فیلتر واریانس پایین
متغیری در دیتاست را در نظر بگیرید که مقدار تمام نمونههای آن برابر با ۱ است. چنین متغیری در ساخت مدل یادگیری ماشین مفید نخواهد بود. زیرا واریانسی برابر با صفر دارد. در روش «فیلتر واریانس پایین» (Low Variance Filter)، ابتدا واریانس هر ویژگی حساب شده و پس از مقایسه، ویژگیها با واریانس پایین حذف میشوند. زیرا متغیرهایی که واریانس پایین داشته باشند، تاثیری بر متغیر هدف نمیگذارند. برای پیادهسازی این روش، ابتدا مقادیر گمشده دو ستون Item_Weight و Outlet_Size را به ترتیب با مقادیر میانه و نما همان ستون جایگزین میکنیم:
1df['Item_Weight'].fillna(df['Item_Weight'].median(), inplace=True)
2df['Outlet_Size'].fillna(df['Outlet_Size'].mode()[0], inplace=True)در مرحله بعد و پس از جایگذاری، مجدد نگاهی به تعداد مقادیر گمشده هر ویژگی میاندازیم:
1df.isnull().sum() / len(train)*100خروجی مانند زیر است:
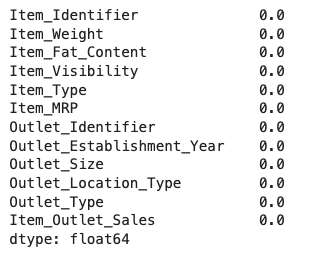
همانطور که ملاحظه میکنید دیگر هیچ متغیری داده گمشده ندارد. در مرحله بعد با فراخوانی متد var()
بر روی ویژگیهای عددی دیتاست، مقدار واریانس آنها را محاسبه میکنیم:
1df[['Item_Weight', 'Item_Visibility', 'Item_MRP',
2 'Outlet_Establishment_Year', 'Item_Outlet_Sales']].var()مطابق با نتایج بهدست آمده، واریانس ویژگی Item_Visibility (مشخص شده با رنگ قرمز) بسیار کمتر از سایر متغیرها است:

با اعمال یک فیلتر واریانس پایین، بهراحتی میتوانیم ستون Item_Visibility را حذف کنیم:
1numeric = df[['Item_Weight', 'Item_Visibility', 'Item_MRP',
2 'Outlet_Establishment_Year', 'Item_Outlet_Sales']]
3var = numeric.var()
4numeric = numeric.columns
5variable = []
6for i in range(0, len(var)):
7 if var[i] >= 10: # setting the threshold as 10%
8 variable.append(numeric[i])
9
10print(variable)پس از اجرای قطعه کد بالا، خروجی مانند نمونه حاصل میشود:
['Item_Weight', 'Item_MRP', 'Outlet_Establishment_Year', 'Item_Outlet_Sales']
تنها ستونهایی در خروجی مشاهده میشوند که واریانس بیشتر از ۱۰ داشتهاند.
۳. فیلتر همبستگی بالا
وجود همبستگی بالا میان دو متغیر یعنی الگوهای مشابهی داشته و اطلاعات یکسانی از هر دو قابل برداشت است. موقعیتی که در عملکرد برخی از مدلهای یادگیری ماشین مانند رگرسیون خطی و لجستیک تاثیر منفی میگذارد. اگر فرض بگیریم ضریب همبستگی از حد آستانهای مشخص میگذرد، به راحتی میتوان همبستگی میان دو متغیر عددی را محاسبه و یکی از آنها را حذف کرد. توجه داشته باشید که حذف متغیر عملی حساس است و باید بسته به پیشنیازهای مسئله و دامنه دیتاست انجام شود. بهطور معمول، متغیرهایی حفظ میشوند که همبستگی بالایی با متغیر هدف دارند. برای آشنایی بیشتر با مفهوم همبستگی، میتوانید فیلم آموزش همبستگی و رگرسیون خطی فرادرس را از طریق لینک زیر دنبال کنید:
برای محاسبه همبستگی با استفاده از زبان برنامه نویسی پایتون، ابتدا متغیر وابسته یا همان Item_Outlet_Sales را در دیتافریم جدیدی با عنوان df_co
ذخیره و متد corr()
را فراخوانی میکنیم:
1df_co = df.drop('Item_Outlet_Sales', axis=1)
2df_co[['Item_Weight', 'Item_Visibility', 'Item_MRP',
3 'Outlet_Establishment_Year']].corr()جدول زیر همبستگی میان متغیرهای عددی را نشان میدهد:

بهطور معمول اگر همبستگی میان دو متغیر بیش از ۰/۵ باشد، بهتر است یکی از آنها را حذف کنیم. با این حال، در دیتاست ما هیچ دو متغیری همبستگی بالا ندارند و نیازی به حذف متغیر نیست.
۴. جنگل تصادفی
از «جنگل تصادفی» (Random Forest) به عنوان یکی از رایجترین الگوریتمهای مورد استفاده در انتخاب ویژگی یاد میشود. معیار اهمیت ویژگیها در این الگوریتم از پیش مشخص شده و دیگر نیازی به تشخیص ما نیست. در نتیجه راحتتر میتوانیم زیرمجموعهای کوچک از ویژگیها را انتخاب کنیم. برای پیادهسازی الگوریتم جنگل تصادفی از کلاس RandomForestRegressor
کتابخانه Scikit-learn استفاده میکنیم که تنها متغیرهای عددی را به عنوان پارامتر ورودی قبول میکند. به همین خاطر، از تکنیک «کدبندی وان هات» (One Hot Encoding) برای تبدیل دادهها به نوع عددی بهره میبریم. همچنین دو ستون Item_Identifier و Outlet_Identifier را که فاقد اطلاعات ارزشمند هستند و از مقادیر عددی منحصربهفردی تشکیل شدهاند، از دیتاست حذف میکنیم:
1from sklearn.ensemble import RandomForestRegressor
2
3
4df_rf = df.drop(['Item_Identifier', 'Outlet_Identifier'], axis=1)
5model = RandomForestRegressor(random_state=1, max_depth=10)
6df_rf = pd.get_dummies(df_rf)
7model.fit(df_rf, train.Item_Outlet_Sales)پس از برازش مدل، نمودار اهمیت ویژگیها را مانند زیر رسم میکنیم:
1features = df_rf.columns
2importances = model.feature_importances_
3indices = np.argsort(importances)[-9:] # top 10 features
4plt.title('Feature Importances')
5plt.barh(range(len(indices)), importances[indices], color='b', align='center')
6plt.yticks(range(len(indices)), [features[i] for i in indices])
7plt.xlabel('Relative Importance')
8plt.show()خروجی، تصویری مانند زیر است:

مطابق با نمودار بهدست آمده، میتوانیم مهمترین ویژگیها را برای کاهش ابعاد انتخاب کنیم. کتابخانه Scikit-learn نیز کلاسی تحت عنوان SelectFromModel
دارد که همین کار را بر اساس اهمیت ویژگیها بهطور خودکار برای ما انجام میدهد:
1from sklearn.feature_selection import SelectFromModel
2
3
4feature = SelectFromModel(model)
5fit_rf = feature.fit_transform(df_rf, df.Item_Outlet_Sales)۵. حذف ویژگی رو به عقب
روش «حذف ویژگی رو به عقب» (Backward Feature Elimination) یکی دیگر از رویکردهایی است که برای کاهش ابعاد در یادگیری ماشین از آن استفاده میشود. مراحل اجرای این تکنیک به شرح زیر است:
- ابتدا مدل را با همه ویژگیهای دیتاست آموزش میدهیم.
- عملکرد مدل را ارزیابی میکنیم.
- هر بار یکی از ویژگیها را حذف کرده و مدل را با ویژگی باقیمانده آموزش میدهیم.
- ویژگی که کمترین تاثیر را در عملکرد مدل داشته شناسایی و از دیتاست حذف میکنیم.
- قدمهای فوق را تا جایی تکرار میکنیم که دیگر هیچ ویژگی قابل حذف نباشد.
برای پیادهسازی این الگوریتم باید تعداد ویژگیهای انتخابی را از طریق پارامتر n_features_to_select
کلاس RFE
مشخص کنیم. همچنین برای تحلیل اهمیت هر کدام از ویژگیها، خروجی دستور rfe.ranking_
را چاپ میکنیم:
1# importing required libraries
2import pandas as pd
3from sklearn.linear_model import LinearRegression
4from sklearn.feature_selection import RFE
5
6
7# seperate the target and independent variable
8X = df.drop(columns = ['Item_Outlet_Sales', 'Item_Identifier',
9 'Item_Fat_Content', 'Item_Type', 'Outlet_Identifier',
10 'Outlet_Size', 'Outlet_Location_Type', 'Outlet_Type'], axis=1)
11y = df['Item_Outlet_Sales']
12
13# create the object of the model
14lreg = LinearRegression()
15
16# specify the number of features to select
17rfe = RFE(lreg, n_features_to_select=2)
18
19# fit the model
20rfe = rfe.fit(X, y)
21
22print('nnFEATUERS SELECTEDnn')
23print(rfe.support_)
24
25print('nnRANKING OF FEATURESnn')
26print(rfe.ranking_)خروجی به شرح زیر است:
FEATUERS SELECTED [False True True False] RANKING OF FEATURES [3 1 1 2]
از آنجا که خواستهایم تنها ۲ ویژگی را از میان ۴ ویژگی ورودی انتخاب کنیم، الگوریتم، ویژگیهای دوم و سوم یعنی Item_Visibility و Item_MRP را برگزیده و در بخش ردهبندی یا Ranking نیز میزان اهمیت آنها با عدد ۱، بالاتر از ویژگیهای اول و چهارم قرار گرفته است.
۶. انتخاب ویژگی رو به جلو
در «انتخاب ویژگی رو به جلو» (Forward Feature Selection)، همانطور که از نام آن مشخص است، بر عکس روش حذف ویژگی رو به عقب عمل میکنیم. در واقع بهجای حذف، تمرکزمان را بر پیدا کردن ویژگیهایی میگذاریم که بیشترین تاثیر را بر عملکرد مدل یادگیری ماشین میگذارند. روند اجرای این تکنیک که با عنوان استخراج ویژگی نیز شناخته میشود به شرح زیر است:
- ابتدا با یک ویژگی شروع کرده و سپس مدل را مرتبه و هر بار با یکی از ویژگی آموزش میدهیم.
- متغیری که بهترین عملکرد را نتیجه دهد، به عنوان متغیر شروع انتخاب میشود.
- سپس این فرایند را تکرار کرده و در هر مرحله، یک متغیر دیگر به متغیرهای قبلی اضافه میکنیم. متغیری حفظ میشود که بیشترین تاثیر مثبت را در عملکرد مدل داشته باشد.
- همین فرایند را تا جایی تکرار میکنیم که دیگر بهبود چشمگیری در دقت مدل مشاهده نشود.
برای پیادهسازی این روش مانند نمونه عمل میکنیم:
1from sklearn.feature_selection import f_regression
2
3
4X = df.drop(columns = ['Item_Outlet_Sales', 'Item_Identifier',
5 'Item_Fat_Content', 'Item_Type', 'Outlet_Identifier',
6 'Outlet_Size', 'Outlet_Location_Type', 'Outlet_Type'], axis=1)
7ffs = f_regression(X, df.Item_Outlet_Sales )
8
9print(ffs)در بخش زیر، خروجی اجرای این قطعه کد را مشاهده میکنید:
(array([8.00638865e-01, 1.43345451e+02, 4.04945623e+03, 2.06215699e+01]), array([3.70927701e-01, 9.04128718e-33, 0.00000000e+00, 5.67308211e-06]))
خروجی، دو آرایه را با مقادیری تحت عنوان F-values و p-values برای هر ویژگی نشان میدهد. هر چه رابطه خطی میان ویژگی با متغیر هدف بیشتر باشد، مقدار F-value بیشتر و p-value کمتر است. در اینجا هدف را انتخاب ویژگیهایی میگذاریم که مقدار F-value بیشتر از ۱۰ داشته باشند و سپس نتایج ذخیره شده در متغیر variable
را در خروجی چاپ میکنیم:
1variable = [ ]
2for i in range(0, len(X.columns)-1):
3 if ffs[0][i] >= 10:
4 variable.append(X.columns[i])
5
6print(variable)خروجی مانند زیر است:
['Item_Visibility', 'Item_MRP']
همانطور که ملاحظه میکنید، دو متغیر Item_Visibility و Item_MRP توسط الگوریتم انتخاب شدهاند.
روشهایی که تا اینجا برای کاهش ابعاد در یادگیری ماشین معرفی کردهایم از جمله حذف ویژگی رو به عقب و انتخاب ویژگی رو به جلو، بسیار زمانبر بوده و از نظر محاسباتی نیز تنها برای دیتاستهای کوچک با تعداد متغیرهای کم بهصرفه هستند. از همین جهت، در ادامه با بهکارگیری دیتاست Fashion MNIST که متشکل از تصاویر انواع پوشاک مانند پیراهن، شلوار و کیف است، به بررسی الگوریتمهای متناسب با دیتاستهای بزرگ میپردازیم. این دیتاست شامل ۷۰ هزار تصویر است که ۶۰ هزار مورد آن در مجموعه آموزشی و ۱۰ هزار تصویر دیگر در مجموعه آزمایشی ذخیره شدهاند. برای الگوریتمهای بعدی، استفاده از تصاویر مجموعه آموزشی کفایت میکند.
۷. تحلیل عاملی
دیتاستی را با دو متغیر «درآمد» و «تحصیلات» تصور کنید. با توجه به همبستگی بالایی که میان این دو متغیر وجود دارد، در اکثر مواقع، سطح تحصیلات بالاتر به درآمد بیشتری منجر میشود. در روش «تحلیل عاملی» (Factor Analysis) متغیرها بر اساس معیار همبستگی گروهبندی میشوند. به بیان دیگر، متغیرهای هر گروه با یکدیگر همبستگی بالا و با متغیرهای سایر گروهها همبستگی پایینی دارند. مجموعه متغیرهای مرتبط با هم در یک گروه را «عامل» (Factor) مینامند. هنگام سادهسازی انواع معیارها و همچنین مدلسازی خطی، تکنیکهایی مانند «نگاشت ویژگی» (Feature Projection) و «تحلیل تشخیصی خطی» (Linear Discriminant Analysis | LDA) به کار میآیند.
در قدم اول، همه تصاویر موجود در مجموعه آموزشی را خوانده و در متغیر images
ذخیره میکنیم:
1import pandas as pd
2import numpy as np
3from glob import glob
4import cv2
5
6
7images = [cv2.imread(file) for file in glob('MNIST_train/*.png')]سپس برای اجرای عملیاتهای ریاضی و مصورسازی، فرمت تصاویر را به آرایه کتابخانه Numpy تغییر میدهیم:
1images = np.array(images)
2images.shapeهمانطور که در خروجی ملاحظه میکنید، تعداد ۶۰ هزار تصویر با ابعاد ۲۸ پیکسل در ۲۸ پیکسل و پروفایل رنگی RGB در متغیر images
ذخیره شدهاند:
(60000, 28, 28, 3)
از آنجا که ورودی اغلب تکنیکهای رایج تک بعدی است، باید ابعاد تصاویر را به یک بعد کاهش دهیم:
1image = []
2for i in range(0, images.shape[0]):
3 img = images[i].flatten()
4 image.append(img)
5
6image = np.array(image)بهتر است آرایه Numpy را به دیتافریمی از کتابخانه Pandas تبدیل کنیم که در آن، مقادیر پیکسلی و برچسب مربوط به هر تصویر ذخیره شده است:
1df_train = pd.read_csv('MNIST_train.csv')
2feat_cols = ['pixel'+str(i) for i in range(image.shape[1])]
3df = pd.DataFrame(image, columns=feat_cols)
4df['label'] = df_train['label']سپس با استفاده از روش تحلیل عاملی، دیتاست را به سه بخش مجزا تقسیم میکنیم:
1from sklearn.decomposition import FactorAnalysis
2
3
4fa = FactorAnalysis(n_components = 3).fit_transform(df[feat_cols].values)با مقداردهی پارامتر n_components
در کلاس FactorAnalysis
، تعداد کل دستههای دیتاست مشخص میشود. پس از تبدیل دادهها، نوبت به رسم نتایج میرسد:
1%matplotlib inline
2import matplotlib.pyplot as plt
3
4
5plt.figure(figsize=(12, 8))
6plt.title('Factor Analysis')
7plt.scatter(fa[:, 0], fa[:, 1])
8plt.scatter(fa[:, 1], fa[:, 2])
9plt.scatter(fa[:, 2], fa[:, 0])توزیع دادههای تبدیل شده به شکل زیر است:

با توجه به تصویر فوق، دادهها به سه گروه تقسیم و با رنگهای سبز، نارنجی و آبی مشخص شدهاند. مقادیر هر نمونه داده در محور افقی و عمودی نمودار قرار دارند. تشخیص جداگانه نمونهها کار دشواری است اما، فرایند کاهش ابعاد با موفقیت انجام شده است.
۸. تحلیل مؤلفه اصلی
با بهرهگیری از روش «تحلیل مؤلفه اصلی» (Principal Component Analysis | PCA) میتوانیم زیرمجموعه جدیدی را از مجموعه متغیرهای اصلی استخراج کنیم. هر کدام از متغیرهای جدید بهدست آمده مؤلفه اصلی نام دارند. توجه به نکات زیر درباره PCA بسیار حائز اهمیت است:
- هر مؤلفه اصلی، ترکیبی خطی از متغیرهای دیتاست است.
- استخراج مؤلفههای اصلی بهگونهای انجام میشود که مؤلفه اول بیانگر حداکثر واریانس باشد و سایر مؤلفهها بدون همبستگی به یکدیگر، باقیمانده واریانس را در دیتاست به نمایش بگذارند.
ابتدا و بهصورت تصادفی، تعدادی از تصاویر دیتاست را در خروجی رسم میکنیم:
1rndperm = np.random.permutation(df.shape[0])
2plt.gray()
3fig = plt.figure(figsize=(20, 10))
4for i in range(0, 15):
5 ax = fig.add_subplot(3, 5, i+1)
6 ax.matshow(df.loc[rndperm[i],feat_cols].values.reshape((28, 28*3)).astype(float))همانگونه که مشاهده میکنید، تصویر ۱۵ محصول در خروجی نمایان شده است:

سپس از کلاس PCA
کتابخانه Scikit-learn برای تبدیل دادهها استفاده میکنیم:
1from sklearn.decomposition import PCA
2
3
4pca = PCA(n_components=4)
5pca_result = pca.fit_transform(df[feat_cols].values)پارامتر n_components
در کلاس PCA
، تعداد مؤلفههای اصلی دیتاست را مشخص میکند. در ادامه، میزان واریانس توصیف شده با ۴ مؤلفه را به تصویر میکشیم:
1plt.plot(range(4), pca.explained_variance_ratio_)
2plt.plot(range(4), np.cumsum(pca.explained_variance_ratio_))
3plt.title("Component-wise and Cumulative Explained Variance")نمودار حاصل مانند زیر است:

در این نمودار، خط آبی، واریانس مؤلفهای را نشان میدهد و خط نارنجی بیانگر واریانس انباشته شده یا تجمعی است. در واقع تنها با چهار مؤلفه توانستیم ۶۰ درصد از کل واریانس دیتاست را توصیف کنیم. با اجرای قطعه کد زیر، هر کدام از چهار مؤلفه اصلی را ترسیم میکنیم:
1import seaborn as sns
2
3
4plt.style.use('fivethirtyeight')
5fig, axarr = plt.subplots(2, 2, figsize=(12, 8))
6sns.heatmap(pca.components_[0, :].reshape(28, 84), ax=axarr[0][0], cmap='gray_r')
7sns.heatmap(pca.components_[1, :].reshape(28, 84), ax=axarr[0][1], cmap='gray_r')
8sns.heatmap(pca.components_[2, :].reshape(28, 84), ax=axarr[1][0], cmap='gray_r')
9sns.heatmap(pca.components_[3, :].reshape(28, 84), ax=axarr[1][1], cmap='gray_r')
10axarr[0][0].set_title(
11"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[0]*100),
12fontsize=12
13)
14axarr[0][1].set_title(
15"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[1]*100),
16fontsize=12
17)
18axarr[1][0].set_title(
19"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[2]*100),
20fontsize=12
21)
22axarr[1][1].set_title(
23"{0:.2f}% Explained Variance".format(pca.explained_variance_ratio_[3]*100),
24fontsize=12
25)
26axarr[0][0].set_aspect('equal')
27axarr[0][1].set_aspect('equal')
28axarr[1][0].set_aspect('equal')
29axarr[1][1].set_aspect('equal')
30
31plt.suptitle('4-Component PCA')خروجی به شرح زیر است:

هر بُعد جدیدی که به تکنیک PCA اضافه شود، واریانس کمتری را نسبت به سایر ابعاد در مدل جذب میکند. مؤلفههای اول، دوم و سوم به ترتیب بیشترین اهمیت را دارند.
همچنین میتوانیم از روش «تجزیه مقادیر منفرد» (Singular Value Decomposition | SVD) برای کاهش ابعاد در یادگیری ماشین بهره ببریم. در SVD متغیرهای اصلی به سه ماتریس تجزیه شده و متغیرهای اضافی از دیتاست حذف میشوند. تعیین این سه ماتریس از طریق «مقادیر ویژه» (Eigenvalues) و «بردارهای ویژه» (Eigenvectors) صورت میگیرد. مجله فرادرس مطلب جامعی را درباره مقادیر و بردارهای ویژه تهیه کرده است که با مراجعه به لینک زیر میتوانید آن را مطالعه کنید:
برای کاهش ابعاد با روش SVD از کلاس TruncatedSVD
کمک میگیریم:
1from sklearn.decomposition import TruncatedSVD
2
3
4svd = TruncatedSVD(n_components=3, random_state=42).fit_transform(df[feat_cols].values)مصورسازی متغیرهای تبدیل شده با رسم سه مؤلفه اصلی اول مانند زیر انجام میشود:
1plt.figure(figsize=(12, 8))
2plt.title('SVD Components')
3plt.scatter(svd[:, 0], svd[:, 1])
4plt.scatter(svd[:, 1], svd[:, 2])
5plt.scatter(svd[:, 2],svd[:, 0])خروجی مانند تصویر زیر خواهد بود:

نمودار نقطهای فوق بهخوبی مؤلفههای تجزیه شده را نشان میدهد. همانطور که مشاهده میکنید، همبستگی چندانی میان مؤلفهها وجود ندارد.
۹. تحلیل مؤلفه مستقل
«تحلیل مؤلفه مستقل» (Independent Component Analysis | ICA) یکی از مورد استفادهترین روشهای کاهش ابعاد در یادگیری ماشین است. در PCA، هدف پیدا کردن معیارهای ناهمبسته است اما در ICA، این معیارهای مستقل هستند که دنبال میشوند. دو متغیر را ناهمبسته مینامیم اگر هیچ رابطه خطی میان آنها وجود نداشته باشد. اما مستقل بودن به معنی عدم وابستگی به سایر متغیرها است. به عنوان مثال، سن یک نفر مستقل از غذای او یا میزان زمانی است که صرف تماشای تلویزیون میکند. این الگوریتم، متغیرهای دیتاست را خطی و مستقل از هم در نظر میگیرد. به همین خاطر و از آنجا که هیچ متغیری به دیگر متغیرها وابستگی ندارد، به آنها مؤلفه مستقل گفته میشود. برای مقایسه بهتر PCA و ICA به دو تصویر زیر توجه کنید:
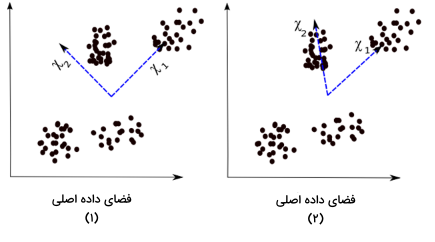
تصاویر ۱ و ۲ به ترتیب نتایج الگوریتم PCA و ICA را نسبت به دیتاستی مشابه نشان میدهند. فرمول محاسبه PCA عبارت است از:
در این عبارت، به نمونه داده، به ماتریس «آمیخته» (Mixing) و به مؤلفههای مستقل اشاره دارد. حالا باید ماتریس «نا آمیختهای» (Un-mixing) پیدا کنیم که مؤلفهها را تا حد امکان از یکدیگر جدا کند. رایجترین روش برای اندازهگیری میزان استقلال مؤلفهها، «نا گاوسی» (Non-Gaussianity) نام داشته و مانند زیر عمل میکند:
- بر اساس «قضیه حد مرکزی» (Central Limit Theorem)، توزیع مؤلفههای مستقل به سمت نرمال (گاوسی) میل میکند.
- تبدیلات بیشینهکننده معیار «کشیدگی» (Kurtosis) هر مؤلفه پیدا میشوند. گشتاور مربته سوم توزیع دادهها را کشیدگی میگویند.
- با بیشینهسازی معیار کشیدگی، توزیع دیتاست از حالت گاوسی خارج شده و مؤلفهها مستقل میشوند.
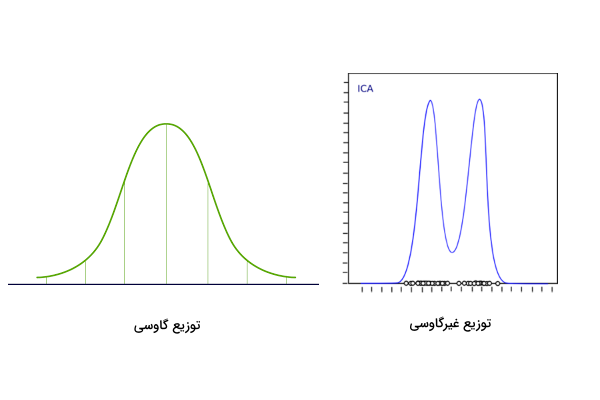
برای پیادهسازی الگوریتم ICA در پایتون از کتابخانه FastICA
استفاده میکنیم:
1from sklearn.decomposition import FastICA
2
3
4ica = FastICA(n_components=3, random_state=12)
5X = ica.fit_transform(df[feat_cols].values)با مشخص کردن پارامتر n_components
، تعداد مؤلفهها را برابر با ۳ قرار میدهیم. قطعه کد لازم برای مصورسازی دادههای تبدیل شده مانند نمونه است:
1plt.figure(figsize=(12, 8))
2plt.title('ICA Components')
3plt.scatter(X[:, 0], X[:, 1])
4plt.scatter(X[:, 1], X[:, 2])
5plt.scatter(X[:, 2], X[:, 0])با توجه به تصویر زیر، دیتاست به سه مؤلفه مستقل تقسیم شده است:

محورهای افقی و عمودی، بیانگر مقادیر مؤلفههای مستقل هستند. در بخش بعد به معرفی تعدادی از روشهای کاهش ابعاد در یادگیری ماشین میپردازیم که از تکنیکهای «نگاشتی» (Projection) استفاده میکنند.
۱۰. روش های مبتنی بر نگاشت
برای شروع، بهتر است یاد بگیریم منظور از «تصویر کردن» یا «نگاشت» چیست. دو بردار با نامهای و را در نظر بگیرید:
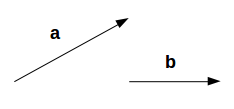
میخواهیم نگاشت یا تصویر بردار را بر پیدا کنیم. زاویه بین این دو بردار را با نمایش میدهیم. نگاشت بردار برابر است با :
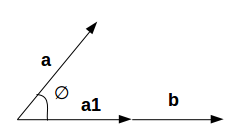
بردار با موازی است و در نتیجه میتوانیم از طریق معادله زیر، نگاشت بردار را محاسبه کنیم:
در این معادله همان نگاشت بردار بر و بردار واحدی است که در جهت بردار قرار دارد. تصویر کردن یک بردار بر بردار دیگر راهی برای کاهش ابعاد است. در تکنیکهای نگاشتی، تحلیل داده چند بُعدی با تصویر کردن نقاط داده بر فضایی با ابعاد پایین انجام میشود. انواع روشهای نگاشت را میتوان به دو دسته «نگاشت بر جهت» (Projection onto Directions) و «نگاشت بر خمیده» (Projection onto Manifolds) تقسیم کرد. در ادامه به بررسی دقیقتر این دو روش میپردازیم.
نگاشت بر جهت
در هر مسئله، جهتی که قرار است بر آن نگاشت صورت گیرد متفاوت است. اما بهطور معمول جهتی انتخاب میشود که توزیع مقادیر تصویر شده بر آن گاوسی نباشد. مشابه الگوریتم ICA که در بخش قبل در مورد آن توضیح دادیم، در اینجا نیز جهتی برای نگاشت مناسب است که کشیدگی مقادیر تصویر شده را بیشینه کند.

نگاشت بر خمیده
زمانی باور این بود که زمین صاف است. هر جا که قدم بگذارید (بهجز کوهها) زمین صاف بهنظر میرسد. اما اگر در یک جهت حرکت کرده و ادامه دهید، سرانجام به همان موقعیت اول میرسید. اگر زمین صاف بود چنین نمیشد. ما فکر میکنیم زمین صاف است چرا که در مقایسه با آن بسیار کوچکتر هستیم. این قسمتهای کوچکی که باعث میشوند زمین را صاف تصور کنیم، «خمیده» (Manifolds) نام دارند. ترکیب این خمیدهها دید وسیعتری از زمین به ما میدهد. بهطرز مشابهی، در یک منحنی بعدی نیز قسمتهای صاف نشانگر خمیدهها هستند. با ترکیب این خمیدهها میتوانیم منحنی بعدی اصلی را بازسازی کنیم. مراحل اجرای روش نگاشت بر خمیده به شرح زیر است:
- ابتدا بهدنبال خمیدهای نزدیک به نمونه داده میگردیم.
- سپس داده را بر خمیده تصویر میکنیم.
- در انتها و برای نمایش بهتر، خمیده را بسط میدهیم.
روشهای متنوعی برای خمیدهیابی وجود دارد که همه آنها از رویکردی سه مرحلهای تشکیل میشوند. این مراحل عبارتاند از:
- ایجاد نموداری که در آن نقاط داده نقش رئوس را دارند.
- تبدیل نمودار ساخته شده در مرحله قبل به ورودی مناسب مسئله.
- محاسبه مقادیر ویژه.
خمیدهای را که نسبت به هر مرتبهای مشتقپذیر باشد، به اصطلاح خمیده «نرم» (Smooth) گویند. با استفاده از الگوریتم ISOMAP، تصویر یک خمیده غیرخطی با ابعاد پایین قابل بازیابی است. البته با این فرض که خمیده مشتقپذیر بوده و بهازای هر دو نقطه، فاصله «ژئودزیک» (Geodesic) برابر با فاصله «اقلیدسی» (Euclidean) باشد. کوتاهترین مسیر بین دو نقطه روی سطح منحنی و خط صاف را به ترتیب ژئودزیک و اقلیدسی گویند که در تصویر زیر مشخص شده است:
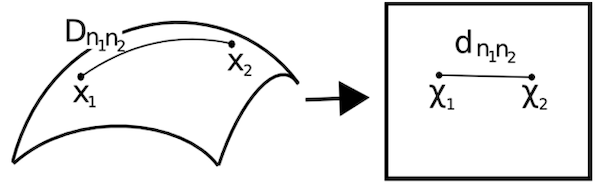
در این مثال، فاصله ژئودزیک و فاصله اقلیدسی را بین دو نقطه و نشان میدهد. در الگوریتم ISOMAP هر دو این فواصل یکسان فرض میشوند. مراحل اجرای این الگوریتم به سه بخش محاسبه گراف مجاورت، محاسبه «فاصله گرافها» (Graph Distance) و «جانمایی» (Embedding) تقسیم میشود که در ادامه توضیح بیشتری از هر بخش ارائه میدهیم.
محاسبه گراف مجاورت
ابتدا و طبق معادله زیر، فاصله میان هر جفت نقطه داده بهدست میآید:
در این معادله، فاصله ژئودزیک و فاصله اقلیدسی بین دو نقطه و را نشان میدهد. پس از محاسبه فاصله، همسایههای خمیده را مشخص کرده و در نهایت گراف همسایگی را مانند نمونه ایجاد میکنیم:
نماد بیانگر مجموعهای از رئوس به عنوان نقاط داده ورودی و شامل یالهایی است که همسایگی میان نقاط را نشان میدهند.
محاسبه فاصله گراف
در این مرحله فاصله ژئودزیک جفت نقاط داده روی خمیده بهدست میآید. فاصل گراف برابر با کوتاهترین مسیر بین تمام جفت نقاط داده در گراف است.

جانمایی
حالا که فواصل را بهدست آوردیم، ماتریسی در از مربع فاصله گراف ایجاد و بردارهایی برای کمینه کردن تفاضل میان فاصله ژئودزیک و گراف انتخاب میکنیم. در مجله فرادرس مطلب کاملتری در زمینه گراف تالیف شده که از طریق لینک زیر قابل دسترسی است:
جهت پیادهسازی الگوریتم ISOMAP ابتدا نوعی تکنیک غیرخطی را بر روی زیرمجموعهای از دیتاست اجرا میکنیم:
1from sklearn import manifold
2
3
4trans_data = manifold.Isomap(n_neighbors=5, n_components=3, n_jobs=-1).fit_transform(df[feat_cols][:6000].values)در کلاس Isomap
که در قطعه کد بالا فراخوانی شده است، دو پارامتر n_neighbors
و n_components
به ترتیب تعداد همسایههای هر نقطه داده و مختصات خمیده را مشخص میکنند. همچنین مقدار پارامتر n_jobs
را برابر با ۱- قرار میدهیم تا از همه قدرت پردازنده استفاده شود. نحوه رسم توزیع دادهها پس از کاهش ابعاد به شکل زیر است:
1plt.figure(figsize=(12, 8))
2plt.title('Decomposition using ISOMAP')
3plt.scatter(trans_data[:, 0], trans_data[:, 1])
4plt.scatter(trans_data[:, 1], trans_data[:, 2])
5plt.scatter(trans_data[:, 2], trans_data[:, 0])همانطور که ملاحظه میکنید، همبستگی کمی میان مؤلفهها وجود دارد:

در الگوریتم ISOMAP همبستگی مؤلفهها به یکدیگر حتی از روش SVD نیز کمتر است.
۱۱. t-توکاری همسایگی تصادفی توزیع شده
تا اینجا یاد گرفتیم که PCA انتخاب مناسبی برای کاهش ابعاد در یادگیری ماشین و مصورسازی دیتاستهای بزرگ است. با این حال، تکنیکهای پیشرفتهتری مانند «t-توکاری همسایگی تصادفی توزیع شده» (t-Distributed Stochastic Neighbor Embedding | t-SNE) الگوها را به شیوهای غیرخطی پیدا میکنند. برای نگاشت نقاط داده از دو رویکرد اصلی استفاده میشود:
- رویکرد «محلی» (Local): نگاشت نقاط داده همسایه روی خمیده بر نقاط داده همسایه در ابعاد پایین.
- رویکرد «سراسری» (Global): در این رویکرد تلاش میشود تا موقعیت نمونهها در هر مقیاس حفظ شود. به عنوان مثال نقاط داده همسایه روی خمیده به نقاط داده همسایه در ابعاد پایین و نقاط دورتر به نقاط مشابهی نگاشت میشوند.
قطعه کد زیر نحوه پیادهسازی تکنیک t-SNE را در پایتون نشان میدهد:
1from sklearn.manifold import TSNE
2
3
4tsne = TSNE(n_components=3, n_iter=300).fit_transform(df[feat_cols][:6000].values)پارامتر n_components
بیانگر تعداد مؤلفهها بوده و برای رسم دادههای تبدیل شده مانند نمونه عمل میکنیم:
1plt.figure(figsize=(12, 8))
2plt.title('t-SNE components')
3plt.scatter(tsne[:, 0], tsne[:, 1])
4plt.scatter(tsne[:, 1], tsne[:, 2])
5plt.scatter(tsne[:, 2], tsne[:, 0])خروجی به شرح زیر است:

در نمودار حاصل از تکنیک t-SNE، سه نوع مؤلفه متفاوت دیده میشود.
۱۲. نگاشت و برآورد خمیده یکسان
با وجود عملکرد بسیار خوب روش t-SNE نسبت به دیتاستهای بزرگ، سرعت محاسبه پایینی داشته و نمایش قابل قبولی از اطلاعات ارائه نمیدهد. روش «نگاشت و برآورد خمیده یکسان» (Uniform Manifold Approximation and Projection | UMAP) در کاهش ابعاد کاربرد زیادی داشته و علاوهبر مزایای t-SNE، در مدت زمان کوتاهتری نیز اجرا میشود. به عنوان برخی از مزایای روش UMAP میتوان به موارد زیر اشاره کرد:
- مدیریت آسان دیتاستهای بزرگ و دادههایی با ابعاد بالا.
- مصورسازی دادههای تبدیل شده.
- قابلیت نگاشت دادههای همسایه روی خمیده بر نقاط دادهای در ابعاد پایینتر و همچنین نگاشت نقاط داده دور افتاده بر نقاطی متناظر.
این روش از مفهوم الگوریتم K-نزدیکترین همسایه یا KNN برای بهینهسازی نتایج حاصل از «گرادیان کاهشی تصادفی» (Stochastic Gradient Descent) استفاده میکند. نحوه کار UMAP به این شکل است که ابتدا فاصله میان نقاط داده نگاشت شده به ابعاد پایین بهدست آمده و سپس از الگوریتم گرادیان کاهشی در کمینهسازی تفاضل میان فواصل استفاده میشود. برای پیادهسازی روش UMAP در پایتون ابتدا لازم است کتابخانه umap-learn را مانند زیر نصب کنیم:
pip install umap-learn
سپس کتابخانه را فراخوانی کرده و شیای از کلاس UMAP
با عنوان umap_data
میسازیم:
1import umap
2
3
4umap_data = umap.UMAP(n_neighbors=5, min_dist=0.3, n_components=3).fit_transform(df[feat_cols][:6000].values)در کلاس UMAP
پارامتر n_neighbors
، تعداد نقاطه همسایه و پارامتر min_dist
میزان پراکندگی دادهها را مشخص میکند. بهمنظور ترسیم توزیع دادهها مانند زیر عمل میکنیم:
1plt.figure(figsize=(12, 8))
2plt.title('Decomposition using UMAP')
3plt.scatter(umap_data[:, 0], umap_data[:, 1])
4plt.scatter(umap_data[:, 1], umap_data[:, 2])
5plt.scatter(umap_data[:, 2], umap_data[:, 0])مطابق با انتظار، ابعاد داده کاهش یافته و میتوانیم مؤلفههای مختلف را مشاهده کنیم:

همبستگی کمی میان متغیرهای تبدیل شده وجود دارد. با مقایسه نتایج حاصل از دو روش UMAP و t-SNE متوجه میشویم که در UMAP، همبستگی بهمراتب کمتری میان مؤلفهها وجود دارد. به بیان سادهتر، روش UMAP عملکرد بهتری در جداسازی و درک مؤلفههای مستقل از خود نشان میدهد.
تا اینجا با ۱۲ مورد از انواع روشهای کاهش ابعاد در یادگیری ماشین آشنا شدیم و نحوه پیادهسازی هر کدام را نیز یاد گرفتیم. در بخش بعدی، بهطور خلاصه از کاربرد روشهای کاهش ابعاد و موارد استفاده آنها میگوییم.
کاربرد تکنیک های کاهش ابعاد
در این بخش میخواهیم کاربرد هر کدام از روش های کاهش ابعاد در یادگیری ماشین را شرح دهیم و یاد بگیریم استفاده از آنها در چه مسائلی باعث صرفهجویی در زمان و هزینه محاسباتی میشود. در بخش زیر موارد استفاده تکنیکهای کاهش ابعاد فهرست شده است:

- نسبت مقادیر گمشده: اگر بخش زیادی از مقادیر دیتاست به اصطلاح گمشده باشد، از این روش برای کاهش تعداد متغیرها بهره میبریم. در حقیقت متغیرهایی با درصد بالا از دادههای گمشده حذف میشوند.
- فیلتر واریانس پایین: زمانی از این روش استفاده میشود که بخواهیم متغیرهای ثابت را از دیتاست شناسایی و حذف کنیم. متغیر هدف، تحت تاثیر متغیرهایی با واریانس پایین قرار نمیگیرد و به سادگی میتوان این قبیل از متغیرها را حذف کرد.
- فیلتر همبستگی بالا: با توجه به احتمال رخداد شرایط همخطی چندگانه در دیتاست، از این تکنیک برای یافتن و حذف ویژگیهای همبسته استفاده میکنند.
- جنگل تصادفی: یکی از رایجترین تکنیکهایی که نمایانگر اهمیت هر ویژگی در دیتاست است. در نتیجه تنها ویژگیهایی حفظ میشوند که بیشترین اهمیت را داشته و از ابعاد دیتاست کاسته میشود.
- حذف ویژگی رو به عقب و انتخاب ویژگی رو به جلو: این دو روش از نظر محساباتی بسیار زمانبر بوده و تنها مناسب دیتاستهای کوچک هستند.
- تحلیل معیار: مناسب برای مسائلی که در آنها درصد همبستگی متغیرها زیاد است. در این روش، متغیرها بر اساس معیار همبستگی به گروههای مختلف تقسیم میشوند.
- تحلیل مؤلفه اصلی یا PCA: از جمله پر کاربردترین تکنیکهای کاهش ابعاد در یادگیری ماشین برای دادههای خطی. تقسیم دادهها در PCA بر اساس معیار واریانس صورت میگیرد.
- تحلیل مؤلفه مستقل یا ICA: مورد استفاده در تبدیل دادهها به مؤلفههای مستقلی که نمونهها را در ابعاد پایینتری به نمایش میگذارند.
- ISOMAP: این الگوریتم زمانی بهکار گرفته میشود که دادهها غیرخطی باشند.
- t-SNE: بیشترین کاربرد را برای دادههای غیرخطی داشته و مصورسازی با آن راحت است.
- UMAP: برای دادههایی با ابعاد بالا مناسب بوده و زمان اجرای کوتاهتری نسبت به الگوریتم t-SNE دارد.
کاهش ابعاد چه مزایا و معایبی دارد؟
پس از آنکه با مفهوم و کاربرد کاهش ابعاد در یادگیری ماشین آشنا شدیم، حالا زمان خوبی است تا در این بخش تعدادی از مزایا و معایب کاهش ابعاد را مورد بررسی قرار دهیم. از جمله مزایای کاهش ابعاد میتوان به موارد زیر اشاره کرد:
- در فشردهسازی دادهها موثر بوده و باعث کاهش فضای لازم برای ذخیرهسازی میشود.
- زمان محاسبات را کاهش میدهد.
- ویژگیهای اضافه را شناسایی و حذف میکند.
- تسهیل مصورسازی و ارزیابی راحتتر نتایج.
- جلوگیری از مشکل بیشبرازش و کاستن از پیچیدگی دادهها.
- استخراج ویژگیهای مهم از دادههایی با ابعاد بالا و آموزش موثر مدلهای یادگیری ماشین.
- بهکارگیری به عنوان بخشی از فرایند پیشپردازش داده و ارتقاء عملکرد مدل.

همچنین باید معایب زیر را نیز در نظر داشته باشیم:
- فراموش شدن بخشی از اطلاعات.
- گاهی هدف روش PCA که یافتن همبستگی خطی میان متغیرها است، مطلوب و مورد نیاز نیست.
- اگر دو معیار میانگین و کوواریانس برای تعریف دیتاست کافی نباشند، روش PCA موفق نخواهد بود.
- ممکن است تشخیص تعداد مؤلفههای اصلی کار راحتی نباشد.
- گاهی تفسیر و درک ارتباط میان ویژگیهای تبدیل شده و دادههای اصلی دشوار است.
- انتخاب مؤلفهها بر اساس دادههای آموزشی، احتمال وقوع مشکل بیشبرازش را افزایش میدهد.
- برخی تکنیکهای کاهش ویژگی به «نمونههای پرت» (Outliers) حساس هستند. به این معنی که در انتها نمایش سوگیرانهای از دادهها حاصل میشود.
- کاهش ویژگی فرایندی هزینهبر از نظر محاسبات است. بهویژه اگر با دیتاست بزرگی سروکار داشته باشیم.
کاهش ابعاد یکی از تکنیکهای بسیار مهم در پیشپردازش دادهها برای یادگیری ماشین است. در بسیاری از پروژههای دادهکاوی، باید با دیتاستهایی کار کنیم که دارای تعداد زیادی ویژگی یا بُعد هستند. همانطور که تا اینجا خواندیم، تکنیکهای کاهش ابعاد همراه با حفظ اطلاعات مهم، دادهها را به فضایی با ابعاد کمتر انتقال میدهند. علاوهبر کاهش ابعاد، مرحله پیشپردازش شامل مجموعهای از فرایندها میشود که هدف آنها آمادهسازی و تبدیل دادههای خام به ورودیهای معتبر برای مدلهای یادگیری ماشین است. اگر قصد دارید در مسیر دادهکاوی و یادگیری ماشین گام بردارید و به یک متخصص حرفهای در این زمینه تبدیل شوید، مجموعه فرادرس فیلمهای آموزشی متنوعی را با زبان برنامه نویسی پایتون از مقدماتی تا پیشرفته تدارک دیده است که مشاهده آنها را به ترتیبی که در ادامه آورده شده به شما پیشنهاد میکنیم:
سوالات متداول
حالا که با کاهش ابعاد در یادگیری ماشین و انواع روشهای آن آشنا شدیم، در این بخش به برخی از پرتکرارترین سوالات افراد مبتدی درباره کاهش ابعاد پاسخ میدهیم.

کاربرد تکنیک های کاهش ابعاد چیست؟
تکنیکهای کاهش ابعاد با انتخاب ویژگیهای مهم، تبدیل داده و مدیریت دادههای گمشده، نقش مهمی در سادهسازی دیتاستها ایفا میکنند.
چرا کاهش ابعاد مهم است؟
استفاده از تکنیکهای کاهش ابعاد به دلایل زیر اهمیت دارد:
- کاهش احتمال بیشبرازش.
- بهبود عملکرد مدل یادگیری.
- صرفهجویی در منابع و کاهش پیچیدگی محاسباتی.
- مصورسازی راحتتر نمونه دادهها.
آیا PCA نوعی روش کاهش ابعاد به حساب می آید؟
بله. روش PCA همزمان با حفظ اطلاعات ارزشمند، فضای دادهها را به ابعاد پایینتری تغییر میدهد. پیادهسازی PCA در پروژههای یادگیری ماشین به مدیریت و پردازش سریعتر دادهها کمک میکند.
بیشتر از چه تکنیک هایی برای کاهش ابعاد استفاده می شود؟
پاسخ این سوال به نوع مسئله و اندازه دیتاست بستگی دارد. به عنوان مثال اگر تعداد ویژگیها کم باشد، تکنیکهایی مانند جنگل تصادفی و انتخاب ویژگی بیشترین کاربرد را دارند. در غیر اینصورت بهرهگیری از الگوریتمهایی مانند t-SNE و UMAP توصیه میشود.
جمعبندی
مدیریت و تعامل مناسب با هزاران یا حتی میلیونها ویژگی برای هر دانشمند علم داده یا علاقهمند به حوزه یادگیری ماشین مهارتی لازم و ضروری بهشمار میرود. در جهان اطلاعات، حجم دادههای تولیدی آنقدر زیاد است که باید به فکر یافتن راهکارهای مختلفی برای استفاده مناسب از آنها باشیم. همانطور که در این مطلب از مجله فرادرس خواندیم، تکنیکهای کاهش ابعاد در یادگیری ماشین بهخوبی پاسخگوی این نیاز هستند. فرایندی که هم کارکرد حرفهای داشته و هم در پروژههای آموزشی بهکار گرفته میشود.
source

