به فرایند انجام عملیات جستوجو بر روی ساختمان داده درختی پیمایش درخت گفته میشود. در هر لحظه گرهای جستوجو میشود و عملیاتی مانند بررسی یا بهروزرسانی داده درون گره انجام میشود. اگر برنامه نویس حرفهای یا کسی هستیم که برای چندسال در صنعت نرمافزار کار کرده، ممکن است که با این مفهوم آشنا شده باشیم. در عین حال، موارد کاربرد چنین الگوریتمهایی شاید برای افراد تازهکار کمی گمراهکننده باشد. در این مطلب از مجله فرادرس تلاش کردیم هر آنچه که نیاز است درباره پیمایش درخت در ساختمان داده را همراه با تصاویر کمکی برای درک مطلب ارائه دهیم.

بنابراین در ادامه مطلب، ابتدا درباره ساختمان داده درخت توضیحاتی ارائه کرده و سپس به بررسی پیمایش درختی پرداختهایم. انواع الگوریتمهای پیمایش بر روی درختها را معرفی کردهایم. درنهایت، چهار نوع الگوریتم پیمایش درختی را همراه با مثالهای کدنویسی شده به طور کامل بررسی کردیم.
پیمایش درخت در ساختمان داده چیست؟
پیمایش درخت به معنای جستوجو و بررسی کردن گرهها در ساختمان داده درخت است. این کار را به صورت بررسی یک گره در هر لحظه، همراه با اجرای توابعی برای بررسی دادههای درون گره یا بهروزرسانی این دادهها انجام میدهیم. برای الگوریتمهای پیمایش درختی دو رویکرد کلی وجود دارد.
- الگوریتمهای «جستوجوی عمقاول» (Depth-First Search | DFS)
- الگوریتمهای «جست وجوی سطح اول» (Breadth-First Search | BFS)
الگوریتمهای جستوجوی عمقاول، پیمایش را از گره ریشه شروع می کنند و در ابتدا قبل از اینکه عقبنشینی کنند همه گرههای ممکن بر روی یک شاخه را بررسی میکنند. الگوریتمهای جستوجوی سطحاول، پیمایش خود را از گره ریشه شروع میکنند و قبل از اینکه به گرههای لایه پایینی بروند همه گرههای موجود در عمق فعلی را بررسی میکنند.

در این مطلب تئوریهای مربوط به این الگوریتمها را آموزش داده و روش پیادهسازی این الگوریتمها را به وسیله کدنویسی بررسی کردهایم.
ساختمان داده درخت چیست؟
قبل از پرداختن به مبحث الگوریتمهای پیمایش درختی در ساختمان داده، در ابتدا باید درخت را به عنوان عضوی از ساختمان داده تعریف کنیم. این مسئله کمک میکند که بسیار ساده، مفاهیم را به صورتی عمیق و مفهومی درک کنیم.
درخت نوعی از ساختمانهای داده سلسلهمراتبی است. در این نوع از ساختمانهای داده اطلاعات را به شکل سلسلهمراتبی ذخیره میکنند، برعکس ساختارهای ذخیره داده خطی مانند لیستهای پیوندی، پشتهها و غیره. درخت شامل گرهها -داده- و اتصالات بین گرهها -یال- میشود. هرگز اتصالات بین گرهها و یالها در درخت تشکیل حلقه نمیدهند.
لغات تخصصی مربوط به درخت در ساختمان داده
در این بخش، پُراستفادهترین لغات تخصصی مربوط به ساختمان داده درخت را بررسی خواهیم کرد. تلاش کردیم که مهمترین و پرتکرارترین لغات را در فهرست زیر جمعآوری کنیم.
- «گره» (Node): گره، ساختاری است که میتواند حاوی مقدار یا شرایط خاصی باشد. گره حتی میتواند نماینده ساختمان داده جداگانهای هم باشد.
- «ریشه» (Root): به بالاترین گره درخت، ریشه میگویند. به عنوان جد اول نیز شناخته میشود.
- «فرزند» (Child): گرهای که در جهت دور شدن از گره ریشه، به صورت مستقیم به گره دیگری متصل باشد. به عنوان نواده فوری یا نسلی از گره بالای سر خود -به طرف ریشه- نیز شناخته میشود.
- «والد» (Parent): به مفهوم معکوس فرزند میگویند. به عنوان جد بدون فاصله و فوری نیز شناخته میشود.
- «برگ» (Leaf): گرهای که هیچ فرزندی ندارد.
- «گره داخلی» (Internal Node): گرهای که حداقل یک فرزند داشته باشد.
- «یال» (Edge): به اتصالات بین گرهها یال میگویند.
- «عمق» (Depth): به فاصله بین هر گره تا ریشه، عمق آن گره گفته میشود.
- «سطح» (Level): به تعداد یالهای بین گره و ریشه به علاوه یک، سطح گره گفته میشود.
- «ارتفاع» (Height): به تعداد یالهای طولانیترین مسیر در درخت، بین گره ریشه و یکی از نوادگان برگ شده، ارتفاع درخت میگویند.
- «دامنه» (Breadth): به تعداد برگهای هر درخت گفته میشود.
- «زیردرخت» (Subtree): زیردرخت T درختی است که ریشه آن فرزند گره دیگری در درخت اصلی باشد. زیردرخت T شامل گره T و همه فرزندان آن گره است.
- «درخت دودویی» (Binary Tree): درخت دودویی یا باینری، به نوعی از ساختار داده درختی میگویند که در آن هر درخت، به صورت بیشینه دو فرزند دارد. به این فرزندها با عنوان فرزند چپ و فرزند راست اشاره میشود.
- «درخت جستوجوی دودویی» (Binary Search Tree): درخت جست وجوی دودویی نوع خاصی از درخت دودویی است. این درخت، ویژگیهای خاصی دارد که در فهرست زیر نوشتهایم.
- زیردرخت سمت چپ هر گره فقط شامل گرههایی میشود که کلیدشان کوچکتر از کلید گره والد است.
- زیردرخت سمت راست هر گره فقط شامل گرههایی میشود که کلیدشان بزرگتر از کلید گره والد است.
- ضروری است که هر دو زیردرختهای راست و چپ، خودشان نیز از نوع درختهای جستوجوی باینری باشند.

بهخاطر سادگی و درک بهتر الگوریتمهای پیمایش درختی، از درختهای باینری برای نمایش مثالها استفاده کردهایم. اما به خوبی میتوان این الگوریتمها را برای کار بر روی سایر انواع درختها نیز تعمیم داد.
تسلط به ساختمان داده با فرادرس
درختها نوع خاصی از ساختارهای داده هستند. در مبحث ساختمان داده انواع مختلفی از این ساختارها مانند صف، پشته، درخت و غیره وجود دارد. خود حوزه ساختمان داده یکی از مهمترین بخشهایی است که هر توسعهدهندهای باید با آن آشنا باشد. زیرا این حوزه یکی از بخشهای بنیادین و تخصصی علوم کامپیوتری را شامل میشود. وبسایت آموزشی فرادرس نیز به عنوان قدرتمندترین وبسایت آموزشی فارسی زبان درباره این مبحث علمی فیلمهای آموزشی حرفهای تولید کرده است. فیلمهای آموزشی فرادرس متناسب با همه دانشجویان و علاقهمندان برنامهنویسی و علوم کامپیوتر طراحی و تولید شدهاند. در نتیجه مخاطبان فرادرس در هر سطح دانش و با هر مهارتی که هستند میتوانند فیلم مربوط به خود را پیدا کنند.
در ادامه چند مورد از این فیلمهای آموزشی مربوط به مبحث ساختمان داده را معرفی کردهایم.
در صورتی که تمایل به دیدن فیلمهای بیشتر دارید با کلیک بر روی تصویر پایین، یا مراجعه به سایت فرادرس میتوانید گزینههای بسیار بیشتری حتی در رشتهها و زمینههای دیگر نیز پیدا کنید.

در ادامه مطلب، قبل از صحبت درباره آموزش پیمایش درخت در ساختمان داده باید به بررسی خود پیمایش درخت و انواع آن بپردازیم.
پیمایش درختی چیست؟
پیمایش درختی به عنوان جستوجوی درختی نیز شناخته میشود. این نوع از پیمایش، به فرایندی درباره بازدید هر گره از ساختمان داده درخت اشاره میکند. در طول پیمایش درخت، هر گره از درخت را دقیقا یکبار مشاهده میکنیم و در همان دفعه عملیات خاصی مانند جستوجو در دادههای درون گره یا بهروزرسانی این دادهها را انجام میدهیم.
الگوریتمهای پیمایش درختی را بر اساس نظم گرههایی که بازدید میشوند، به طور گسترده میتوان در دو دسته زیر طبقهبندی کرد.
- «الگوریتمهای جستوجوی عمقاول» (Depth-First Search |DFS): در این نوع از الگوریتمها عمل پیمایش را از گره اول شروع میکنیم. در ابتدا قبل از عقب نشینی از هر شاخه، همه گرههای آن شاخه را به ترتیب تا عمیقترین سطح ممکن بازدید میکنیم. سپس گرههای همه شاخههای دیگر نیز طبق همین روش باید بازدید شوند. سه نوع الگوریتم، از این روش جستوجو استفاده میکنند که در ادامه این مطلب آنها را پوشش دادهایم.
- «الگوریتم جستوجوی سطحاول» (Breadth-First Search |BFS): این الگوریتم نیز از ریشه شروع به کار میکند. روش کار به این صورت است که قبل از رفتن به هر سطحی در درخت، در ابتدا همه گرههای سطح بالاتر بررسی میشود. در بخش بعدی الگوریتمی از نوع BFS را بررسی کردهایم.
انواع الگوریتم های پیمایش درخت در ساختمان داده
در این بخش به درک مفهوم پیمایش درخت، از طریق روشهای عملی پرداختهایم. با اینکه در ادامه این مطلب، برای پیادهسازی الگوریتمها از زبان برنامه نویسی Java استفاده کردهایم، اما همه الگوریتمها را میتوانید با زبان برنامهنویسی مورد نظر خودتان به همین روشی که در Java پیادهسازی شده برای خود بنویسید.
چهار نوع از الگوریتم های پیمایش درخت
با توجه به دستهبندی بالا، الگوریتمهای پیمایش درخت را به صورت جزئیتر میتوان در چهار دسته مختلف دستهبندی کرد. این دستهها را در ادامه فهرست کردهایم.
- «پیمایش میانترتیب» (Inorder Traversal): در ابتدا همه گرههای درون زیردرخت سمت چپ را بازدید میکنیم و سپس گره فعلی را نیز قبل از بازدید هر گرهای در زیردرختهای سمت راست بازدید میکنیم.
- «پیمایش پیشترتیب» (Preorder Traversal): قبل از اینکه هر گره درون زیردرختهای سمت راست یا چپ را بازدید کنیم باید گره فعلی را بررسی کنیم.
- «پیمایش پسترتیب» (Postorder Traversal): بعد از اینکه همه گرههای درون زیردرختهای چپ و راست را بازدید کردیم، گره فعلی را بازدید میکنیم.
- «پیمایش سطحترتیب» (Level order Traversal): همه گرهها را به صورت سطح به سطح بازدید میکنیم. در هر سطح بازدید گرهها را از سمت چپ به راست انجام میدهیم.
در کدهای پایین طرح اولیهای از کلاس گره خود را میبینیم. کلاس گرهای که تعریف کردیم به عنوان عضو اصلی ساختمان داده درختی عمل میکند. این کلاس را به نام TreeNode
نامگذاری میکنیم. در این کلاس دادهها را به شکل مقادیر عدد صحیح نگهداری میکنیم. فرزندان چپ و راست نیز از همان نوع کلاس هستند. هر نوع ساختار دادهای را میتوان برای نگهداری به عنوان داده در کلاس TreeNode
بهکار برد.
1public class TreeNode {
2 int data;
3 TreeNode left;
4 TreeNode right;
5
6 public TreeNode(int data) {
7 this.data = data;
8 this.left = this.right = null;
9 }
10}پیمایش میان ترتیب
الگوریتم Inorder Traversal یکی از پر استفادهترین نوع الگوریتمهای پیمایش درخت از نوع DFS است.

همانطور که DFS پیشنهاد میدهد در ابتدا بر روی بررسی عمیق گره انتخاب شده تمرکز میکنیم، سپس به بررسی بقیه گرهها در همان سطح میپردازیم. به همین ترتیب به هر گره که میرسیم اول تمام عمق آن گره را ملاقات میکنیم. بنابراین، از گره ریشه درخت شروع خواهیم کرد. سپس با رویکرد بازگشتی از زیر درخت سمت چپ، پیمایش خود را به صورت عمقی ادامه میدهیم.
وقتی که با پیروی از مراحل بالا به چپترین گره یا برگ درخت یا رسیدیم، بررسی گرهها را شروع میکنیم. اول از همه این برگ ملاقات میشود، سپس به سراغ چپترین گره در زیردرخت سمت راست همین برگ-البته در صورت وجود داشتن- میرویم.
برای کامل کردن پیمایش میانترتیب باید همین مراحل با روش بازگشتی دنبال شوند. ترتیب انجام این مراحل شبیه به کار با توابع بازگشتی است. در فهرست پایین همین مراحل را به صورت الگوریتم سطح بالا نوشتهایم.
- به زیردرخت سمت چپ حرکت میکنیم.
- گره را ملاقات میکنیم.
- به زیردرخت سمت راست حرکت میکنیم.
در پایین، کدهای مربوط به پیادهسازی این الگوریتم را با زبان جاوا پیادهسازی کردهایم.
1public void inorderTraversal(TreeNode root) {
2 if (root != null) {
3 inorderTraversal(root.left);
4 System.out.print(root.data + " ");
5 inorderTraversal(root.right);
6 }
7}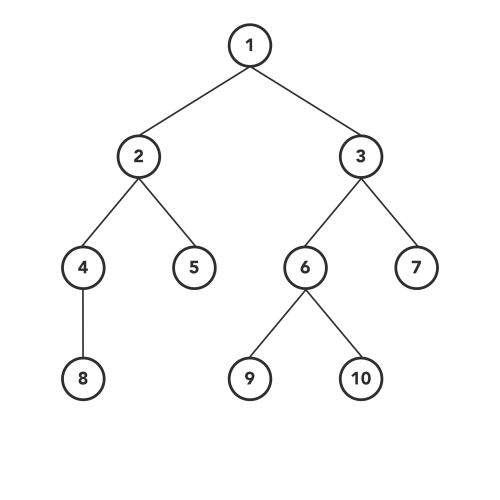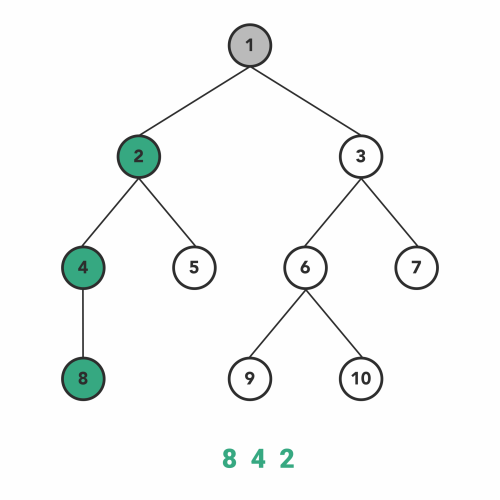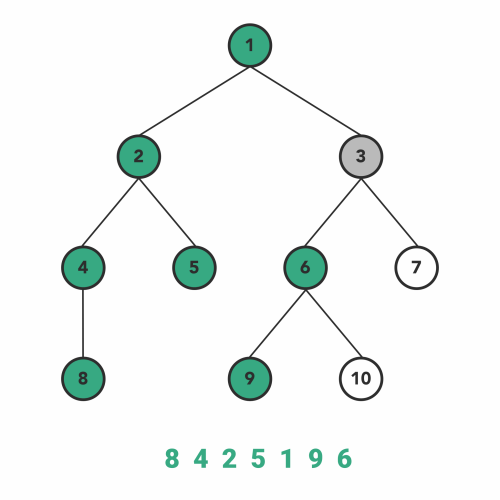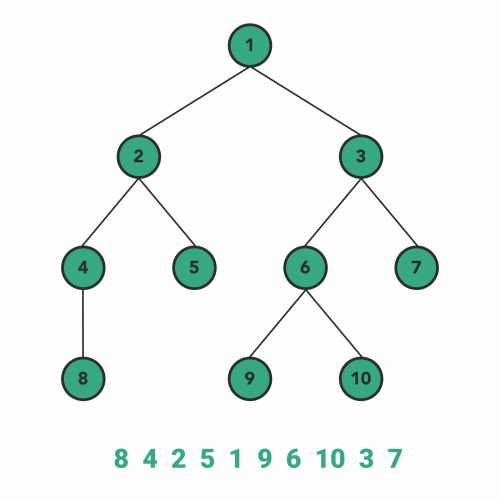
الگوریتم پیمایش میانترتیب بر روی درخت جستوجوی باینری، همیشه گرهها را به صورت منظم برمیگرداند.
پیمایش پیش ترتیب
پیمایش پیشترتیب، نوع دیگری از الگوریتمهای DFS است. عملیات درون توابع بازگشتی شبیه به پیمایش میانترتیب است با این تفاوت که با نظم متفاوتی اجرا میشود.
درصورتی که نسبت به درخت جستوجوی دودویی و ساختار این درخت هنوز به طور کامل آشنایی پیدا نکردهاید، پیشنهای میکنیم که مطلب درخت جستجوی دودویی (BST) — ساختار داده و الگوریتم ها را از مجله فرادرس مطالعه کنید.
در این نوع از پیمایش پیشترتیب، ابتدا گره فعلی را ملاقات میکنیم و سپس به زیردرخت سمت چپ منتقل میشویم. بعد از اینکه همه گرههای زیر درخت سمت چپ را پوشش دادیم، به طرف زیردرخت سمت راست حرکت میکنیم. زیر درخت سمت راست را نیز با همان ترتیب مانند یک درخت دیگر پیمایش میکنیم.
ترتیب مراحل پیمایش به صورت زیر است.
- گره را ملاقات میکنیم
- سپس به طرف زیردرخت سمت چپ حرکت میکنیم.
- بعد به طرف زیردرخت سمت راست حرکت میکنیم.
در پایین، کدهای مربوط به پیادهسازی این الگوریتم را با زبان جاوا پیادهسازی کردهایم.
1public void preorderTraversal(TreeNode root) {
2 if (root != null) {
3 System.out.print(root.data + " ");
4 preorderTraversal(root.left);
5 preorderTraversal(root.right);
6 }
7}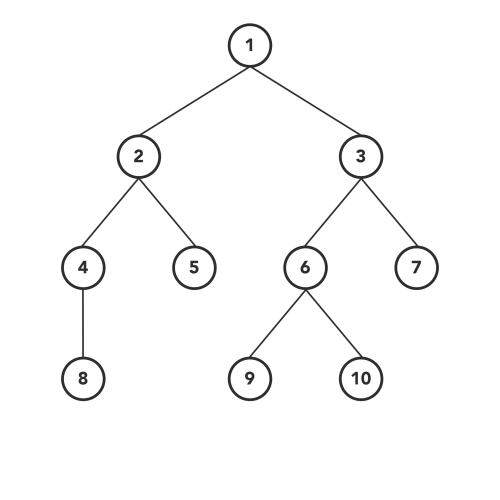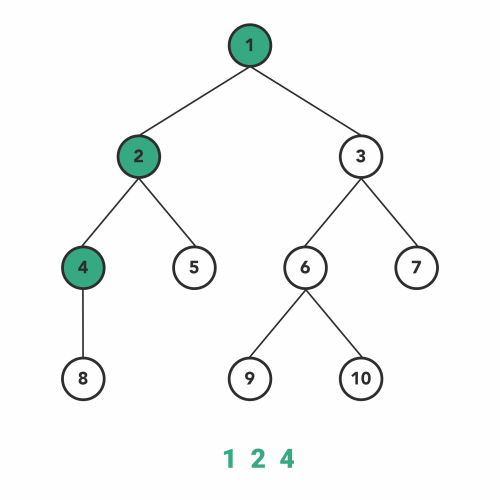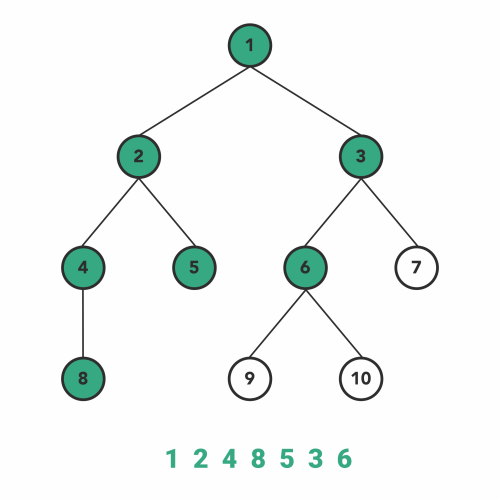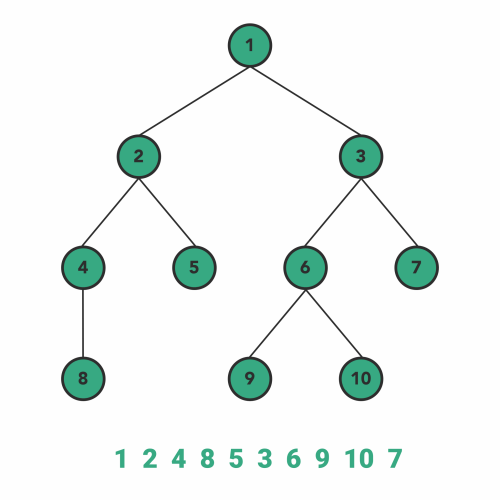
پیمایش پس ترتیب
در الگوریتم پیمایش پسترتیب نیز تقریبا فرایندی مشابه با فرایند اجرای الگوریتمهای بالا رخ میدهد. به این ترتیب که در ابتدا قبل از مشاهده هر گره، زیر درخت سمت چپ و سپس زیر درخت سمت راست آن گره را به صورت بازگشتی مشاهده میکنیم. سپس نوبت به ملاقات خود گره میرسد.
بنابراین ترتیب مراحل پیمایش در این الگوریتم به صورت زیر خواهد شد.
- برای بازدید گرهها اول به طرف زیردرخت سمت چپ حرکت میکنیم.
- سپس به طرف زیر درخت سمت راست حرکت میکنیم.
- در نهایت هم خود گره را ملاقات میکنیم.
کدهای مربوط به پیادهسازی این الگوریتم به زبان جاوا را در ادامه پیادهسازی کردهایم.
1public void postorderTraversal(TreeNode root) {
2 if (root != null) {
3 postorderTraversal(root.left);
4 postorderTraversal(root.right);
5 System.out.print(root.data + " ");
6 }
7}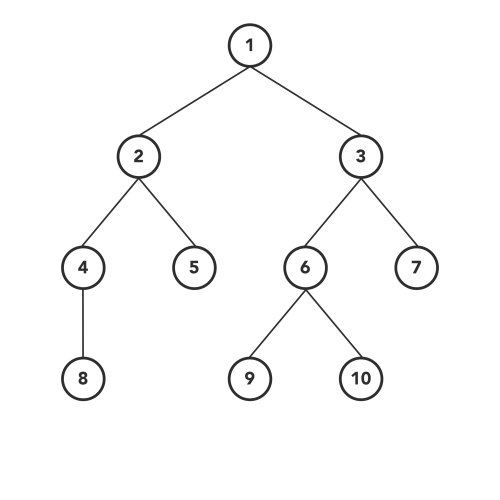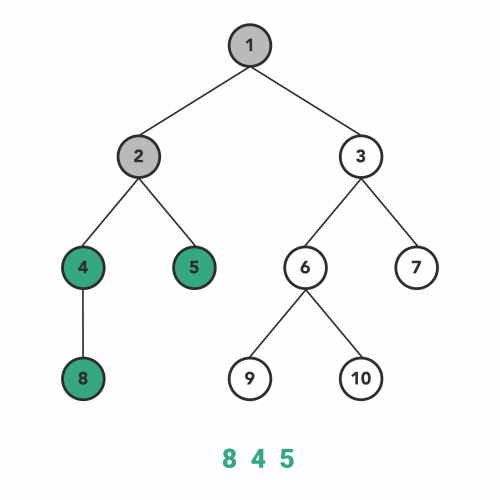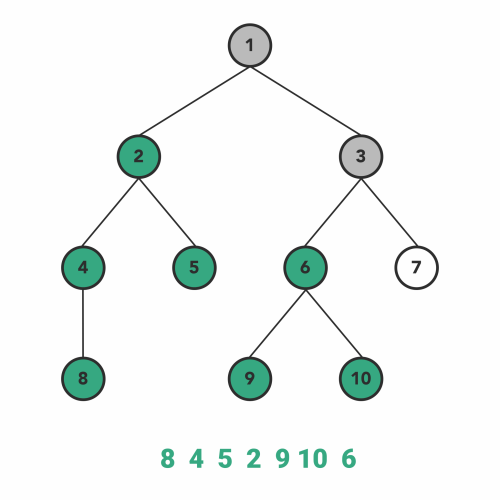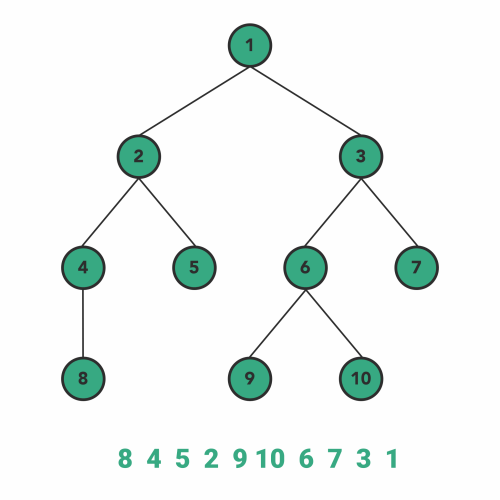
پیمایش سطح ترتیب
این روش پیمایش با موارد پوشش داده شده در بالا فرق میکند. الگوریتم پیمایش سطحترتیب از تکنیک الگورتیم جستوجوی سطحاول برای بررسی یا تغییر دادن هر گره در درخت پیروی میکند.
همینطور که تکنیک پیمایش BFS پیشنهاد میدهد، اولویت اول پیمایش با پهنای درخت است. در ابتدا پهنای هر سطح در درخت به طور کامل پیمایش میشود سپس به یک لایه عمیقتر منتقل میشویم. به عبارت سادهتر، در ابتدا همه گرههای موجود در یک سطح را به صورت یک به یک از چپ به راست، بازدید میکنیم سپس در عمق به سطح بعدی منتقل میشویم. در سطح جدید هم در ابتدا همه گرهها را از چپ به راست بازدید میکنیم و سپس همین فرایند را تا بازدید آخرین گره در درخت ادامه میدهیم.

نسبت به پیادهسازی الگوریتمهای پیمایش درختی که در بالا دیدیم، پیادهسازی الگوریتم سطحترتیب کمی پیچیدهتر است. برای پیادهسازی الگوریتم پیمایش سطحترتیب باید از ساختمان داده صف با الگوی FIFO استفاده کنیم. به این ترتیب که بعد از ملاقات هر گرهای، فرزندان چپ و راست آن گره را به ترتیب پشت سر هم در صف قرار میدهیم.
در اینجا نظم اضافه کردن گرههای فرزند به صف مهم است. برای اینکه باید در هر سطح پیمایش را از چپ به راست انجام دهیم. برای درک بهتر مطلب، به کدهای پیادهسازی شده زیر توجه کنید.
1public void levelorderTraversal(TreeNode root) {
2 if (root == null) {
3 return;
4 }
5
6 Queue<TreeNode> queue = new LinkedList<>();
7 queue.add(root);
8
9 while (!queue.isEmpty()) {
10 TreeNode node = queue.remove();
11 System.out.print(node.data + " ");
12
13 if (node.left != null) {
14 queue.add(node.left);
15 }
16
17 if (node.right != null) {
18 queue.add(node.right);
19 }
20 }
21}آشنایی با انواع زبانهای برنامهنویسی در فرادرس
الگوریتمهای پیمایش خطی و به طور کل همه الگوریتمهای مربوط به ساختمان داده باید حالت جامعیت داشته باشند. به این معنی که بتوان با هر زبان برنامهنویسی این الگوریتمها را پیادهسازی کرد. این مسئله درباره تمام مباحث مطرح در حوزه ساختمان داده صدق میکند. با توجه به اینکه هر کسی متناسب با علایق و هدفی که در پیش دارد، آموزش زبان برنامهنویسی خاصی را دنبال میکند، در فرادرس تلاش کردیم که تقریبا برای همه زبانهای برنامهنویسی پرکاربرد آموزش مربوطه را طراحی، تولید و ارائه کنیم.

در این بخش چند آموزش درباره زبانهای برنامهنویسی مختلف را معرفی کردهایم. در صورت علاقه با کلیک بر روی تصویر بالا میتوانید به صفحه اصلی این مجموعه آموزش رفته و فیلمهای بیشتری درباره همین زبانها یا سایر زبانهای برنامهنویسی مشاهده کنید.
دسته بندی الگوریتم های پیمایش درخت در ساختمان داده
الگوریتمهای پیمایش درخت را به طور کلی در دو دسته اصلی میتوان طبقهبندی کرد.
- الگوریتمهای جستوجوی عمقاول یا DFS
- الگوریتم جستوجوی سطحاول یا BFS

خود الگوریتمهای جستوجوی عمقاول نیز شامل سه نوع متفاوت از هم میشوند.
- الگوریتم «پیمایش پیشترتیب» (Preorder Traversal): در این رویکرد، در ابتدا گره فعلی را بررسی میکنیم سپس به سراغ بررسی گرههای درون زیردرختهای چپ و راست میرویم. به این رویکرد «Current-Left-Right» نیز میگویند.
- الگوریتم «پیمایش میانترتیب» (Inorder Traversal): در این رویکرد، گره فعلی را بعد از ملاقات همه گرههای درون زیردرخت سمت چپ و قبل از ملاقات گرههای درون زیر درخت سمت راست ملاقات میکنیم. به این رویکرد «Left-Current-Right» نیز میگویند.
- الگوریتم «پیمایش پسترتیب» (Postorder Traversal): در این رویکرد، گره فعلی را بعد از ملاقات همه گرههای درون زیردرختهای سمت چپ و راست ملاقات میکنیم. پیمایش گرهها مثل همیشه به ترتیب از چپ به راست است. به این رویکرد «Left-Right-Current» نیز میگویند.
الگوریتم جستوجوی سطحاول یا BFS تنها شامل یک نوع است.
- «الگوریتم پیمایش سطحترتیب» (Level Order Traversal): در این روش حل مسئله، گرهها را سطح به سطح و در هر سطح از چپ به راست ملاقات میکنیم.
جمع بندی
پیمایش درخت در ساختمان داده یا جستوجوی درختی، به بررسی همه گرههای موجود در ساختمان داده درخت اشاره دارد. به این صورت که در هر واحد زمانی یک گره بازدید میشود و هر گره هم فقط یکبار بازدید میشود. پیمایش درختها اغلب زمانی استفاده میشوند که نیاز به اجرای عملیات خاصی بر روی دادههای هر گره در درخت داریم. در این مطلب از مجله فرادرس، در ابتدا نوع ساختمان داده درخت را بررسی کردیم. سپس به بحث درباره پیمایش درختی پرداختیم. برای کمک به درک و یادگیری بهتر هم انواع الگوریتمهای پیمایش درخت را توضیح داده و با زبان برنامهنویسی جاوا پیادهسازی کردیم. در نهایت هم همه این الگوریتمها را به صورت مختصر و مفید در کنارهم دستهبندی کردیم.
پیمایش درختی یکی از تکنیکهای مهم کار با ساختار داده درخت است. از موارد کاربرد این ساختمان داده میتوان به استفاده در پایگاههای داده و مباحث مربوط به هوش مصنوعی اشاره کرد. در آخر باید بدانیم که همه الگوریتمهای بررسی شده در این مطلب را میتوانیم با سایر زبانهای برنامهنویسی نیز پیادهسازی کنیم.
source
