تکنیکهای مرتبسازی و الگوریتمهای مرتبطی که در علوم کامپیوتر وجود دارند، به ما کمک میکنند تا با راه و روشی مشخص، عناصر یک ساختمان داده مانند لیست را با ترتیب مشخصی مرتب کنیم. بهطور مثال، لیستی از اعداد را به صورت صعودی یا غیره مرتب میکنند. این دسته از الگوریتمها، انواع گوناگونی دارند و نحوه کار آنها در مرتبسازی عناصر، با هم فرق دارد. از آنجاییکه برخی الگوریتمها به دادههای ورودی مرتبشده نیاز دارند الگوریتمهای مرتبسازی میتوانند نقش مهمی را در عملکرد آنها ایفا کنند. در این مطلب از مجله فرادرس، ضمن ارائه تعریفی از «الگوریتم مرتب سازی سریع» یا Quicksort، که یکی از الگوریتمهای شناخته شده از دسته الگوریتمهای مرتبسازی بهشمار میرود، خصوصیات، کاربردها و پیچیدگی زمانی آن را نیز بیان میکنیم. همچنین نحوه پیادهسازی این الگوریتم را در زبان برنامهنویسی پایتون شرح میدهیم.
الگوریتم مرتب سازی سریع، یکی از الگوریتمهای بسیار مفید و پرکاربرد کنونی است که کارایی بالایی را در این زمینه ارائه میدهد. این الگوریتم، که یکی از چندین الگوریتم مرتبسازی موجود محسوب میشود، در طول سالهای ۱۹۵۹ تا ۱۹۶۱ میلادی توسط آقای «تونی هور» طراحی و معرفی شد. این الگوریتم را اگر بخواهیم برای دادههای تصادفی بهکار ببریم، کارایی و سرعت اجرای بهتری نسبت به الگوریتمهایی نظیر مرتبسازی هرمی و مرتبسازی ادغامی از خود نشان میدهد و این مورد هنگامیکه پراکندگی دادهها بیشتر باشد، ملموستر است.

الگوریتم مرتب سازی سریع چیست؟
الگوریتم «مرتب سازی سریع» (Quicksort)، نوعی الگوریتم مرتبسازی محسوب میشود که دادههای موجود در یک ساختمان داده را برایمان مرتب میکند. این الگوریتم، کارایی بالایی دارد و از روش تقسیم و غبله یا «تقسیم و حل» (Divide and Conquer) برای مرتبسازی استفاده میکند.
بهطور کلی در این الگوریتم، یکی از عناصر آرایه بهعنوان عنصر «لولا | محور» (Pivot)، انتخاب شده و آرایه از همان نقطه به ۲ زیرآرایه تقسیم میشود. سپس، عناصری که از عنصر Pivot کوچکتر هستند به زیرآرایه سمت چپ منتقل میشوند و همچنین عناصر بزرگتر از عنصر Pivot در زیرآرایه سمت راست قرار میگیرند. بههمین ترتیب، هر یک از این زیرآرایهها دوباره با یک عنصر Pivot به ۲ زیرآرایه تقسیم شده و این روند بهصورت بازگشتی ادامه پیدا میکند. در نهایت به نقطهای خواهیم رسید که تمامی زیرآرایهها تنها یک عنصر دارند. اکنون میتوانیم با ترکیب زیرآرایهها در قالب یک لیست، به دادههای مرتب شده خود دست پیدا کنیم. تصویر زیر، جایگاه عنصر Pivot و پارتیشنهای ساخته شده را نشان میدهد.

برای درک بهتر، اگر لیست دادههای ما بهصورت 7 2 1 6 8 5 3 4
باشد، آنگاه اجرای الگوریتم مرتب سازی سریع روی این لیست به ما کمک میکند تا این لیست را مرتب کرده و به لیستی شبیه به 1 2 3 4 5 6 7 8
دست پیدا کنیم.
الگوریتم مرتبسازی سریع بهطور کلی و در شرایط استاندارد، برای اینکه عناصر آرایه عنصری n
عنصری ما را مرتب کند، nlogn
مرتبه مقایسه انجام میدهد. به همین دلیل، گزینه مناسبی برای مرتبسازی دادههایی با حجم بسیار زیاد محسوب میشود.
عنصر محوری یا Pivot را چگونه انتخاب کنیم؟
همانطور که گفته شد، مجموعهای که قصد مرتبسازی آن را داریم از یک نقطه، یا بهتر بگوییم از یک عنصر محوری شکسته شده و به ۲ مجموعه دیگر تبدیل میشود و این روند در زیرمجموعهها نیز ادامه پیدا میکند. اینکه کدام عنصر میتواند برای این نقطه شکست انتخاب شود را در ادامه گفتهایم.
- میتوانیم همیشه اولین عنصر از دادههای خود را بهعنوان Pivot انتخاب کنیم.
- یا اینکه عنصر انتهایی از مجموعه دادههای خود را بهعنوان Pivot انتخاب کنیم.
- میتوانیم عنصر Pivot را بهصورت رندوم یا تصادفی انتخاب کنیم که در اینصورت هریک از عناصر مجموعه، شانس Pivot شدن را خواهند داشت.
- همچنین، امکان انتخاب عنصر میانی مجموعه، بهعنوان Pivot نیز وجود دارد.
پس بهطور خلاصه، میتوانیم اولین یا آخرین داده و یا عناصر میانی از لیست عناصر خود را بهعنوان Pivot انتخاب کنیم.

مراحل سه گانه الگوریتم مرتب سازی سریع چیست؟
در ادامه، ۳ مرحله اصلی لازم برای مرتبسازی دادهها به روش الگوریتم مرتب سازی سریع را آوردهایم.
- انتخاب عنصر محوری: عنصری را از مجموعه دادههای خود انتخاب میکنیم. این عنصر که به عنصر محوری یا Pivot معروف است، نقطه شکست آرایه یا لیست دادههای اولیه را مشخص میکند.
- تقسیم: دادههای مسئله را از عنصر انتخابی، به ۲ نیمه تقسیم میکنیم. عناصر کوچکتر از Pivot را در یک سمت و عناصر بزرگتر از آن را در سمت دیگر آن قرار میدهیم.
- تکرار و ترکیب: همین مراحل را تا دستیابی به آرایههای تکعضوی، بارها و بارها تکرار میکنیم. در نهایت زیرآرایههای مرتبشده را با هم ترکیب میکنیم.
گام های الگوریتم مرتب سازی سریع
در الگوریتم مرتب سازی سریع برای انجام عمل «تقسیمبندی» (Partitioning) دادههای اصلی، طبق مراحل زیر پیش میرویم.
- گام ۱: نخستین عنصر «لیست» ( list
) را بهعنوان عنصر Pivot در نظر میگیریم. البته، این یکی از روشهای انتخاب عنصر محوری است.
- گام ۲: دو متغیر بهنامهای i
و j
تعریف کرده و آنها را بهترتیب به عناصر اول و آخر لیست منتسب میکنیم.
- گام ۳: تا زمانیکه شرط list[i] > pivot
برقرار شود، مقدار i
افزایش مییابد. سپس متوقف میشود.
- گام ۴: تا هنگام برقراری شرط list[j] < pivot
، مقدار j
کاهش پیدا میکند.
- گام ۵: اگر i < j
باشد آنگاه، عناصر list[i]
و list[j]
را جا به جا میکنیم.
- گام ۶: تا پیش از اینکه i > j
شود، گامهای ۳، ۴ و ۵ را تکرار میکنیم.
- گام ۷: عنصر Pivot را با عنصر list[j]
جابهجا میکنیم.

چگونه الگوریتم ها را با فرادرس یاد بگیریم؟
در حال حاضر، آموزشهای ویدیویی یکی از بهترین روشهای یادگیری مهارتهای گوناگون بهخصوص مهارتهای مرتبط با علوم کامپیوتر محسوب میشوند. فرادرس بهعنوان یکی از بزرگترین پلتفرمهای آموزشی، در رابطه با ساختمان دادهها و الگوریتمها، فیلمهای آموزشی متعددی منتشر کرده است که میتوانید از آنها بهرهمند شوید. یکی از این موارد، فیلم آموزش ساختمان دادهها از فرادرس است که با مشاهده آن مباحث مربوط به ساختمان دادهها را بهطور کامل یاد میگیرید.
در این فیلم آموزشی از فرادرس، علاوه بر بخش آموزش کامل مرتبسازی که الگوریتمهای مرتبسازی سریع، حبابی، انتخابی، درجی، ادغامی، سریع و هرمی را توضیح میدهد، به آموزش بخشهای دیگر ساختمان داده نظیر مرتبه اجرایی، زیربرنامههای بازگشتی، آرایه، صف و پشته، لیست پیوندی، درخت، گراف، درهمسازی و غیره نیز میپردازد.
پیچیدگی الگوریتم مرتب سازی سریع
برای فهمیدن میزان کارایی الگوریتمها بهطور معمول از ۲ معیار پیچیدگی زمانی و پیچیدگی فضایی استفاده میشود. اگر به زبان ساده بخواهیم بگوییم، پیچیدگی زمانی یک الگوریتم بیان میکند که اگر دادههای ورودی به الگوریتم را افزایش دهیم، زمان اجرای آن به چه صورتی رشد میکند. بهطور مثال اگر دادههای ورودی به الگوریتم را ۲ برابر کنیم و زمان اجرای آن نیز ۲ برابر شود میگوییم که پیچیدگی زمانی خطی دارد. پیچیدگی فضایی نیز، به ارزیابی میزان حافظه مورد نیاز برای اجرای الگوریتم میپردازد. در ادامه، پیچیدگی الگوریتم مرتب سازی سریع را بیان کردهایم.
در یکی از مطالب پیشین مجله فرادرس به توضیح مرتبه اجرایی در ساختمان داده به زبان ساده، رایگان و کامل پرداختهایم که مطالعه آن میتواند اطلاعات بیشتری را در این مورد در اختیار شما قرار دهد.
به فضایی که برای اجرای الگوریتم مرتب سازی سریع، علاوه بر دادههای ورودی نیاز است، پیچیدگی فضایی Quicksort میگویند. با توجه به اینکه مرتبسازی سریع، یک الگوریتم درجا محسوب میشود، به همین دلیل به فضای اضافی خیلی زیادی نسبت به دادههای ورودی نیاز ندارد. اما از سوی دیگر به فضایی نیاز دارد تا فراخوانیهای بازگشتی تابع و پشته فراخوانی را در حین اجرا ذخیره کند.
پیچیدگی زمانی
برای اینکه بتوانیم لیستی نامرتب شامل n
عنصر را مرتب کنیم، در بدترین حالت، میبایست (n (n-1))/2
مقایسه انجام دهیم که از رابطه زیر بهدست آمده است.
((n-1)+(n-2)+(n-3)+......+1)
جدول زیر، پیچیدگی الگوریتم مرتب سازی سریع را در بدترین و بهترین حالت و همچنین حالت متوسط نشان میدهد.
| بدترین حالت | Ο(n²) |
| بهترین حالت | Ο(n log n) |
| حالت متوسط | Ο(n log n) |
پیچیدگی فضایی
میزان پیچیدگی فضایی الگوریتم مرتبسازی سریع، بهطور متوسط برابر با Ο(log n) است. همچنین در بدترین حال آن، بهدلیل انجام n
فراخوانی بازگشتی، پیچیدگی فضایی برابر با Ο(n) خواهد بود.

کاربردهای الگوریتم مرتب سازی سریع
همانطور که گفتیم، الگوریتم مرتب سازی سریع دارای کاربردهای گوناگونی است و برای مسائلی با دادههای زیاد بسیار خوب عمل میکند. در ادامه، برخی از کاربردهای آن را آوردهایم.
- آنالیز عددی: برای اینکه محاسبات با دقت مناسبی انجام شود، بسیاری از الگوریتمهای بهینه یک صف اولویت را مورد استفاده قرار داده و برای مرتبسازی دادههای این صف، Quicksort را بهکار میبرند.
- مدیریت پایگاه داده: با توجه به اینکه مرتبسازی سریع، الگوریتم بسیار سریعی است، بههمین دلیل، بهعنوان روش خوبی برای جست و جو در این زمینه استفاده میشود.
- یافتن اطلاعات مورد نظر در یک مجموعه داده که مرتب شده است، راحتتر و بهینهتر انجام میشود.
- در پژوهشهای عملیاتی و شبیهسازی مبتنی بر رویداد بهکار میرود.
- این الگوریتم در بسیاری از مراکز خصوصی و دولتی برای مرتبسازی انواع مختلفی از دادهها همچون مرتبسازی فایلها بر مبنای نام، قیمت و تاریخ آنها، مرتبسازی پروندههای دانشجویان بر اساس شماره دانشجویی آنها، مرتبسازی پروفایل کاربری با شناسه آنها و غیره بهکار میرود.
- بهطور معمول، هنگامی که بخواهیم مواردی را بهصورت کارآمد مرتب کنیم، الگوریتم مرتبسازی سریع را با توجه به بهینه بودن پیچیدگی زمانی آن بهکار میبریم.
- از کاربردهای تخصصیتر الگوریتم مرتبسازی سریع میتوان به استفاده آن در دیتاستها، سیستم عاملها و سیستمهای توصیهگر تجارت الکترونیک اشاره کرد.
مزایای الگوریتم مرتب سازی سریع
از مزیتهای بهکارگیری الگوریتم مرتب سازی سریع میتوان به بازدهی بالا، مرتبسازی درجا و پیادهسازی سریع اشاره کرد که در ادامه آنها را توضیح دادهایم.
- بازدهی: الگوریتم مرتب سازی سریع روی دادههای حجیم، بهرهوری بالایی دارد.
- مرتبسازی درجا: الگوریتم مرتب سازی سریع، فرایند مرتبسازی را بهصورت «in-Place» (درجا) انجام میدهد. به زبان ساده، یعنی نیازی به حافظه کمکی برای ذخیرهسازی نتایج و دادههای موقتی ندارد.
- پیادهسازی راحت: الگوریتم مرتبسازی سریع، نسب به سایر الگوریتمهای مرتبسازی پیچیده، منطق سادهای دارد بههمین دلیل هم به راحتی میتوان نحوه کار آن را متوجه شد و هم اینکه به سادگی قابل پیادهسازی است.

معایب الگوریتم مرتب سازی سریع
اکنون که با مزایای Quicksort آشنا شدید خوب است تا معایب آن را نیز بدانید. در ادامه، برخی از نقاط ضعف الگوریتم مرتبسازی سریع را آوردهایم.
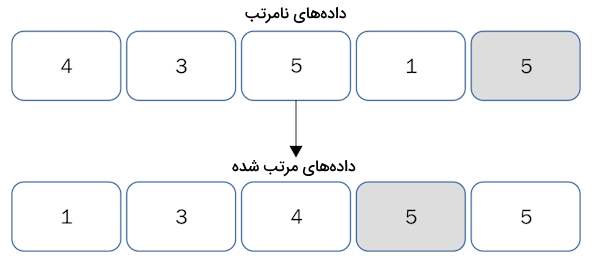
- مرتبسازی ناپایدار: مرتب سازی سریع جزو الگوریتمهای مرتبسازی «ناپایدار» (Unstable) محسوب میشود. یعنی، اگر عناصر یکسانی در دادههای مرتب نشده وجود داشته باشد، ممکن است ترتیب آنها پس از مرتبسازی تغییر کند. تصویر زیر این مورد را بهخوبی نشان میدهد. در این مثال جایگاه نسبی ۲ عنصر 5
و 5 با همان ترتیب اولیه حفظ نشده است.
- کارایی الگوریم در بدترین حالت: فرض کنید Pivot انتخابی، بزرگترین یا کوچکترین عنصر موجود در دادههایمان باشد. در اینصورت تقسیمبندیهایی که صورت میگیرد ممکن است منجر به تولید قسمتهای نامتعادل شود. در نتیجه، این الگوریتم در بدترین حالت خود میتواند پیچیدگی زمانی برابر با Ο(n²) داشته باشد.
- تأثیر عنصر Pivot انتخابی: اینکه کدام عنصر را بهعنوان Pivot انتخاب کنیم میتواند تأثیر بسیار زیادی روی عملکرد الگوریتم مرتبسازی سریع داشته باشد. این مشکل، بهخصوص هنگامی به چشم میآید که که دادههای ما از قبل، بهطور کامل یا تقریبی مرتب شده باشند.
- سربار بازگشتی: فراخوانیهای بازگشتی متعددی که در الگوریتم مرتبسازی سریع انجام میشود باعث مصرف بیشتر حافظه شده و در نتیجه احتمال وقوع خطاهای سرریز پشته یا به اصلاح Stack Overflow هنگام کار با دادههای حجیم وجود دارد.
- تطبیق ناپذیری: الگوریتم مرتبسازی سریع، به اینکه دادههای ورودی از قبل دارای ترتیب خاصی هستند یا اینکه تا حدی مرتب شدهاند توجهی ندارد. بههمین دلیل، حتی اگر قسمتی از دادهها مرتب باشند هم این الگوریتم عملیات تقسیمبندی را روی کل مجموعه داده ما انجام میدهد.
- بازدهی ناکارآمد برای دادههای کم: فراخوانی بازگشتی در الگوریتم مرتب سازی سریع و شکل تقسیمبندی مجموعه دادهها در این الگوریتم ممکن است برای مجموعه دادههای کوچک بازده خوبی نداشته باشد. بهطور کلی، هنگامیکه با مجموعه داده کوچک سر و کار داریم، این الگوریتم سربار بیشتری نسبت به الگوریتمهای مرتبسازی سادهتر تولید میکند.
پیشگیری از بدترین حالت در الگوریتم مرتب سازی سریع
در ادامه، روشهایی را برای پیشگیری از وقوع «بدترین حالت» (Worst Case) الگوریتم مرتب سازی سریع آوردهایم.
- تصادفی بودن
- انتخاب هوشمندانه عنصر محوری یا Pivot
- Introspection
- پیشپردازش مجموعه دادههای اولیه
۱. الگوریتم مرتب سازی سریع تصادفی
نوعی دیگر از الگوریتم مرتبسازی سریع بهنام «مرتب سازی سریع تصادفی» (Randomized Quicksort) وجود دارد. در این نوع Quicksort، بهجای اینکه همیشه اولین عنصر، آخرین عنصر یا غیره را بهعنوان عنصر Pivot انتخاب کنیم، به انتخاب تصادفی آن از بین دادههایمان میپردازیم. این رویکرد به دنبال این است که با انتخاب تصادفی Pivot از بروز بدترین حالت الگوریتم جلوگیری کند.
در این فرایند که عنصر Pivot بهصورت اتفاقی انتخاب میشود، معمولاً احتمال مواجهه با موارد بدترین حالت الگوریتم با پیچیدگی Ο(n²) کمتر میشود.

برخی خصوصیات این نوع الگوریتم مرتب سازی سریع را در ادامه آوردهایم.
- عنصر Pivot در Randomized Quicksort به صورت رندوم از زیرآرایه تولید شده انتخاب میشود.
- رندوم بودن انتخاب Pivot باعث میشود تا از تأثیر انتخاب همیشگی این عنصر از جایگاه خاصی در دادهها – مانند اولین یا آخرین عنصر آرایه – کاسته شده و احتمال تولید زیرآرایههای نامتوازن کمتر شود.
تأثیر این روش روی پیچیدگی زمانی را در ادامه آوردهایم.
- پیچیدگی زمانی Quicksort تصادفی در حالت متوسط، مشابه معادل آن در Quicksort معمولی یعنی Ο(n log n) است.
- با توجه به این که عنصر Pivot را بهصورت رندوم یا تصادفی انتخاب میکنیم، احتمال رو به رو شدن با موقعیتهای بدترین حالت – و پیچیدگی زمانی Ο(n²) – کمتر میشود.
- همانطور که پیشتر گفتیم، اگر دادههای ورودی به الگوریتم از قبل مرتب شده باشند، ممکن است که الگوریتم بدترین حالت خود و پیچیدگی زمانی Ο(n²) را ارائه دهد. با انتخاب تصادفی Pivot، اینگونه مشکلات کمتر رخ میدهد و در نتیجه قسمتهای متوازنتری تولید شده و عمل مرتبسازی، سریعتر انجام شود.
- با وجود اینکه پیچیدگی زمانی در حالت متوسط، تغیری نمیکند اما به دلیل سربار ایجاد عدد تصادفی برای انتخاب Pivot، ممکن است فاکتور ثابت مرتبط با پیچیدگی زمانی کمی افزایش پیدا کند. هر چند که مقدار این سربار در مقابل پیچیدگی زمانی کلی بهخصوص برای دادههای ورودی حجیم بسیار کم است.
۲. انتخاب هوشمندانه عنصر Pivot
رویکرد انتخاب هوشمندانه Pivot باعث میشود تا احتمال رویارویی با بدترین حالت الگوریتم مرتبسازی سریع، کاهش پیدا کند. در این روش، هنگام پارتیشنبندی یا شکستن مجموعه داده به زیرآرایهها سعی میشود تا زیرآرایههایی متوازنتر تشکیل شوند. بهطور مثال، یکی از کارهایی که در این رابطه میتوانیم انجام دهیم، این است که میانه عناصر موجود در مجموعهدادهمان را بهعنوان Pivot بهکار ببریم.
ایده اصلی این روش بیان میکند که بهجای انتخاب اولین و آخرین عنصر یا عنصر میانی به عنوان Pivot که برای ورودیهای خاص میتواند منجر به بروز بدترین حالت الگوریتم مرتبسازی سریع شود، بر مبنای میانه ۳ عنصر، pivot را انتخاب کنیم. در این حالت، میانه عناصر اول، آخر و میانی از دادهها محاسبه میشود. اگر عنصر Pivot را نزدیک به میانه حقیقی دادههایمان انتخاب کنیم، احتمال اینکه زیرآرایهها متوازنتر شوند بیشتر میشود.

۳ مرحلهای که در این روش وجود دارد را در ادامه آوردهایم.
- عنصرهای ابتدایی، میانی و انتهایی مجموعه داده را پیدا میکنیم.
- مقدار Median یا میانه آن را محاسبه میکنیم.
- این میانه را بهعنوان Pivot بهکار میبریم و تابع پارتیشنبندی را روی دادهها اجرا میکنیم.
تأثیر این روش روی پیچیدگی زمانی را در ادامه آوردهایم.
- حالت متوسط: اینکه میانه ۳ عنصر را بهعنوان عنصر Pivot در نظر بگیریم، «حالت متوسط» عملکرد الگوریتم مرتبسازی سریع را بهبود میدهد. همچنین اگر یک عنصر Pivot انتخاب کنیم که به میانه واقعی دادههایمان نزدیکتر باشد، احتمال متوازنتر شدن زیرآرایهها یا همان پارتیشنها افزایش خواهد یافت. در نتیجه، درخت بازگشتی با پارتیشنبندی متوازنتری خواهیم داشت که باعث بهبود عملکرد کلی میشود. همچنین خوب است بدانید که پیچیدگی زمانی در حالت متوسط Ο(n log n) باقی خواهند ماند.
- بدترین حالت: روش محاسبه میانه ۳ عنصر بهعنوان Pivot گرچه احتمال موقعیتهای بدترین حالت را بهطور کامل از بین نمیبرد اما تا حد زیادی از بروز آن پیشگیری میکند. اگر عنصر Pivot را به درستی انتخاب کنیم، یعنی از انتخاب همیشگی اولین یا آخرین عنصر به عنوان Pivot پرهیز کنیم، احتمال بهوجود آمدن زیرآرایهها و پارتیشنهای بسیار نامتوازن تا حد زیادی کاهش مییابد. در نتیجه، پیچیدگی زمانی الگوریتم در بدترین حالت، نسبت به زمانیکه از روشهای پایهای انتخاب Pivot استفاده میکنیم بهتر میشود. با این وجود، پیچیدگی زمانی در بدترین حالت و در معدود مواردی که Pivot انتخابی زیرآرایههای بسیار نامتوزان تولید میکند، Ο(n²) باقی میماند.
۳. روش Introspection
در این روش، برای فراخوانیهای بازگشتی هنگام انجام مرتبسازی، یک حد آستانه تعیین میشود و در صورتی که عمق بازگشتیها از آن مقدار بیشتر شد، از الگوریتمی دیگر بهعنوان جایگزین استفاده میشود.

در ادامه، مؤلفههای این رویکرد را آوردهایم.
- زیر نظر داشتن عمق بازگشتیها در فرایند مرتبسازی: همانطور که میدانیم، الگوریتم Quicksort تابعی را بهصورت بازگشتی فراخوانی میکند. در رویکرد «خودنگری» (Introspection) که سعی در جلوگیری از بروز بدترین حالت در الگوریتم مرتبسازی سریع دارد، عمق بازگشتی که به زبان ساده به تعداد فراخوانیهای بازگشتی در حین مرتبسازی اشاره دارد، زیرنظر گرفته میشود.
- تعیین مقدار حد آستانه یا Threshold: برای اینکه مقدار مناسب حد آستانه را بیابیم میبایست برخی عوامل را مورد توجه قرار دهیم. مواردی مانند اندازه مجموعه دادههای ورودی و برخی خصوصیات مربوط به کارایی الگوریتم از این دست عوامل هستند. در صورتیکه هنگام مرتبسازی، میزان فراخوانی بازگشتی از این مقدار آستانه بیشتر شد، ممکن است با بدترین حالت الگوریتم مواجه شویم. بههمین دلیل، روش کار فرایند مرتبسازی میبایست تغییر کند.
- بهکارگیری الگوریتمهای جایگزین: پس از اینکه احتمال وقوع بدترین حالت الگوریتم Quicksort بیشتر شد، از یک الگوریتم جایگزین برای مرتبسازی استفاده میکنیم که احتمال کمتری برای بروز بدترین حالت – به لحاظ پیچیدگی زمانی – را داشته باشد. از الگوریتمهای مناسب برای استفاده در اینگونه مواقع میتوان به «مرتبسازی هرمی» (Heapsort) یا Introsort اشاره کرد که مورد دوم خود در واقع، ترکیبی از Quicksort و Heapsort است و بهطور کلی این الگوریتمها به لحاظ بدترین حالت، بهتر از Quicksort عمل میکنند.
تأثیر این روش روی پیچیدگی زمانی را در ادامه آوردهایم.
- ارائه عملکردی بهتر در بدترین حالت الگوریتم: این تکنیک که در هنگام افزایش فراخوانیهای بازگشتی بیش از یک حد تعیین شده، الگوریتم مرتبسازی را تغییر میدهیم، میتواند احتمال وقوع بدترین حالتها و ارائه علمکرد ضعیف را کاهش دهد. الگوریتمهایی نظیر Heapsort یا Introsort بهطور معمول در بدترین حالت خود – به لحاظ پیچیدگی زمانی – عملکرد بهتری مانند Ο(n log n) را ارائه میدهند که از بدترین حالت Quicksort یعنی پیچیدگی زمانی Ο(n²) بهتر است.
- توازن بین پیچیدگی زمانی و پیچیدگی فضایی: این روش میتواند باعث بهتر شدن عملکرد الگوریتم مرتبسازی سریع در «بدترین حالت» شود اما از سویی دیگر، ممکن است یک «Trade off» به لحاظ پیچیدگی فضایی بیشتر یا کمی افزایش در پیچیدگی زمانی در حالت متوسط را نیز بههمراه داشته باشد. بهعنوان مثال، هنگامیکه از الگوریتم Introsort استفاده میکنیم، به فضایی بیشتر برای نگهداری ساختمان داده Heap نیاز دارد و از این طریق میتواند روی پیچیدگی فضایی تأثیر بگذارد.
- سربار الگوریتمی: گفتیم که Introspection میزان فراخوانیهای بازگشتی را زیر نظر دارد و تعویض الگوریتمها را در مواقع نیاز انجام میدهد. به همین دلیل، سربار بیشتری را ایجاد میکند. البته لازم به ذکر است که این سربار اضافی در مقابل مزیتی که ارائه میدهد – یعنی پرهیز از بروز بدترین حالت – ناچیز است.

۴. پیش پردازش
اگر لیست یا آرایه شامل دادههای مرتب نشده و اولیه را بتوانیم با پیشپردازش آن، بهبود دهیم و سپس عنصر Pivot را انتخاب کنیم، احتمال مواجهه با بدترین حالت کاهش مییابد. در این روش معمولاً پیش از انجام مرتبسازی، خصوصیات دادههایمان را تحلیل کرده و عنصری را بهعنوان Pivot انتخاب میکنیم که در فرایند پارتیشنبندی، زیرآرایههای متوازنتری را تولید کند.
بررسی مجموعه دادههای اولیه و بهبود آن برای انتخاب عنصر Pivot میتواند تأثیر بسیار زیادی روی عملکرد و پیچیدگی زمانی الگوریتم مرتبسازی سریع داشته باشد و احتمال وقوع بدترین حالت آن را کاهش دهد. تأثیر این روش روی پیچیدگی زمانی را در ادامه آوردهایم.
- حالت متوسط: انتخاب راهبردی عنصر Pivot هنگامیکه دادههای ما توزیعی یکنواخت دارند یا اینکه بهصورت رندوم درهمریخته باشند، شاید حالت متوسط پیچیدگی زمانی این الگوریتم را خیلی تحت تأثیر قرار ندهد و Ο(n log n) باقی بماند. با این وجود ممکن است احتمال بروز بدترین حالت این الگوریتم مرتبسازی را کاهش دهد و عملکرد بهتری را در عمل از خود نشان دهد.
- بدترین حالت: هنگامیکه عنصر Pivot را بهصورت راهبردی انتخاب میکنیم احتمال رویارویی با موقعیتهای بدترین حالت الگوریتم Quicksort یعنی پیچیدگی زمانی Ο(n²) تا حد زیادی کاهش مییابد، درست مانند هنگامیکه از روشهایی مانند انتخاب تصادفی یا انتخاب میانه ۳ عنصر برای انتخاب Pivot استفاده میکنیم، این مورد هنگامیکه دادههای ما بدترین حالت را دارند – مانند زمانیکه از قبل مرتب شده هستند – میتواند عملکرد بهتری را ارائه دهد.
پیاده سازی الگوریتم مرتب سازی سریع در پایتون
مرتبسازی سریع بر اساس تکنیک تقسیم و غلبه حل عمل میکند. عنصری را بهعنوان Pivot انتخاب کرده و مجموعه دادهها را از آن نقطه به ۲ قسمت تقسیم میکند. پیش از این گفتیم که عنصر Pivot را به چهصورت میتوان انتخاب کرد و اکنون ما از عنصر آخر دادههایمان به عنوان Pivot استفاده خواهیم کرد.
مهمترین فرایندی که در پیادهسازی Quicksort وجود دارد، عمل تقسیمبندی یا تابع partition()
است. ما آرایهای از دادهها را برای مرتبسازی و همچنین عنصری از آن بهنام x
را بهعنوان عنصر Pivot در نظر میگیریم. عناصر کوچکتر از x
را به پیش از آن و عناصر بزرگتر از Pivot را به بعد از آن منتقل میکنیم. نکته بسیار مهمی که میبایست مدنظر داشته باشیم این است که تمامی فرایندها باید در زمان خطی انجام شوند.

شبه کدهای الگوریتم مرتب سازی سریع
در ادامه، شبهکدهای مربوط به تابع بازگشتی quickSort()
را آوردهایم.
1quickSort(arr[], low, high) {
2 if (low < high) {
3 pi = partition(arr, low, high);
4 quickSort(arr, low, pi - 1);
5 quickSort(arr, pi + 1, high);
6 }
7}در ادامه توضیحات مربوط به این شبهکدها را بیان کردهایم.
- خط شماره ۱: با در نظر گرفتن این کدها، توجه داشته باشید که پارامترهای low
و high
بهترتیب ایندکس شروع و ایندکس پایان را نشان میدهند.
- خط شماره ۲: تا هنگامیکه ایندکس شروع، کوچکتر از ایندکس پایان باشد یعنی low < high
، دستورات مشخص شده در بلوک شرطی را اجرا میکند.
- خط شماره ۳: pi
ایندکس نقطه تقسیمبندی را نشان میدهد.
- خط شماره ۴: تابع مرتبسازی سریع برای پارتیشن یا قسمت چپی دادهها اجرا میشود.
- خط شماره ۵: تابع مرتبسازی سریع برای قسمت راستی دادهها اجرا میشود.
کدهای الگوریتم مرتب سازی سریع در پایتون
در ادامه، کدهای برنامه پایتون برای پیادهسازی الگوریتم مرتبسازی سریع را آوردهایم. در این برنامه، آخرین عنصر لیست بهعنوان عنصر Pivot در نظر گرفته شده است. در این برنامه اشارهگری داریم که عناصر کوچکتر از Pivot را زیر نظر گرفته و در انتهای اجرای تابع partition()
این اشارهگر با عنصر Pivot جا به جا میشود تا دادههای مرتب شدهای را نسبت به Pivot داشته باشیم.
کدهای مربوط به تابع partition()
را در ادامه آوردهایم.
1def partition(array, low, high):
2
3 pivot = array[high]
4
5 i = low - 1
6
7 for j in range(low, high):
8 if array[j] <= pivot:
9
10 i = i + 1
11
12 (array[i], array[j]) = (array[j], array[i])
13
14 (array[i + 1], array[high]) = (array[high], array[i + 1])
15
16 return i + 1این کدها را در ادامه، توضیح دادهایم.
- خط شماره ۱: در این خط تابع partition()
را تعریف کردهایم که مکان پارتیشن را پیدا میکند.
- خط شماره ۳: در این خط، راستترین عنصر بهعنوان Pivot انتخاب میشود.
- خط شماره ۵: اشارهگری برای عنصر بزرگتر تعریف شده است.
- خطوط شماره ۷ و ۸: تمامی عناصر، پیمایش شده و هر یک از آنها با عنصر Pivot مقایسه میشوند.
- خط شماره ۱۰: اگر عنصری پیدا شد که از Pivot کوچکتر بود، آن را با عنصر بزرگتر که توسط i
نشان داده شده جا به جا میکند.
- خط شماره ۱۲: عناصر موجود در i
و j
را با هم جا به جا میکند.
- خط شماره ۱۴: در این خط، عنصر Pivot با عنصری بزرگتری که توسط i
مشخص شده جا به جا میشود.
- خط شماره ۱۶: این خط، جاییکه تقسیمبندی انجام شده را بر میگرداند.

کدهای مربوط به تابع quickSort()
را در ادامه آوردهایم.
1def quickSort(array, low, high):
2 if low < high:
3
4 pi = partition(array, low, high)
5
6 quickSort(array, low, pi - 1)
7
8 quickSort(array, pi + 1, high)این کدها را در ادامه، توضیح دادهایم.
- خط شماره ۱: در این خط تابع quickSort()
را تعریف کردهایم که آرایهای از دادههای نامرتب را بههمراه ایندکس ابتدایی و ایندکس انتهایی آرایه دریافت میکند.
- خط شماره ۴: عنصر محوری را پیدا کرده و در pi
قرار میدهد. به این صورت که عنصر کوچکتر از Pivot در سمت چپ آن و عنصر بزرگتر از Pivot در سمت راست آن قرار میگیرد.
- خط شماره ۶: تابع quickSort()
بهصورت بازگشتی برای زیرآرایه سمت چپ Pivot فراخوانی میشود.
- خط شماره ۸: تابع quickSort()
بهصورت بازگشتی برای زیرآرایه سمت راست Pivot فراخوانی میشود.
در ادامه، این تابع را در برنامه استفاده کردهایم. کدهای مربوطه در ادامه آورده شده است.
1data = [1, 7, 4, 1, 10, 9, -2]
2print("Unsorted Array")
3print(data)
4
5size = len(data)
6
7quickSort(data, 0, size - 1)
8
9print('Sorted Array in Ascending Order:')
10print(data)این کدها را در ادامه، توضیح دادهایم.
- خط شماره ۱ تا ۳: دادههای اولیه خود یعنی [1, 7, 4, 1, 10, 9, -2]
را در لیستی بهنام data
قرار داده و در خروجی چاپ کردهایم.
- خط شماره ۵: اندازه لیست data
را محاسبه و در size
قرار میدهیم.
- خط شماره ۷: تابع quickSort()
را صدا زدهایم. پارامترهای آن بهترتیب شامل دادهها اولیه و نامرتب، ایندکس اولین عنصر لیست و ایندکس آخرین عنصر لیست است. به زبان ساده، اگر از اندازه یک لیست بهمیزان یک واحد کم کنیم، ایندکس آخرین عنصر آن بهدست خواهد آمد.
- خط شماره ۹ و ۱۰: لیست مرتب شده با الگوریتم مرتبسازی سریع را در خروجی چاپ کردهایم.

خروجی این برنامه پس از اجرا بهصورت زیر خواهد بود.
Unsorted Array [1, 7, 4, 1, 10, 9, -2] Sorted Array in Ascending Order: [-2, 1, 1, 4, 7, 9, 10]
همانطور که در خروجی مشاهده میشود، پس از اجرای الگوریتم مرتبسازی روی دادههای نامرتب [1, 7, 4, 1, 10, 9, -2]
، لیست مرتب شده [-2, 1, 1, 4, 7, 9, 10]
را دریافت کردیم.
تقویت مهارت های خود در ساختمان داده ها با فرادرس
با مشاهده فیلم آموزش ساختمان دادهها و پیادهسازی در C++ از فرادرس، هر ۲ جنبه تئوری و عملی ساختمان دادهها را یاد میگیرید. یکی از فصول این فیلم آموزشی به توضیح و پیادهسازی الگوریتمهای مرتبسازی از جمله الگوریتم مرتب سازی سریع پرداخته است.

با توجه محبوبیت و همهمنظوره بودن زبان برنامهنویسی پایتون، با مشاهده فیلم آموزش الگوریتمهای مرتبسازی در زبان برنامهنویسی پایتون با مثال از فرادرس، الگوریتمهای مرتبسازی شامل مرتبسازی حبابی، مرتبسازی درجی، مرتبسازی انتخابی، مرتبسازی ادغامی و مرتبسازی سریع را بهطور عملی در این زبان یاد میگیرید.
جمعبندی
در این مطلب از مجله فرادرس به بررسی یکی از الگوریتمهای پرکاربرد مرتبسازی یعنی Quicksort پرداختیم و با مفاهیم اصلی آن آشنا شدیم.
الگوریتم مرتبسازی سریع از روش تقسیم و غلبه برای انجام مرتبسازی دادههای مورد نظر استفاده میکند. به این صورت که مجموعه اصلی ما را از عنصری مشخص به ۲ بخش تقسیم کرده و سپس، عناصر کوچکتر از آن نقطه را در یک زیرآرایه و عناصر بزرگتر از آن را در زیرآرایه دیگر قرار میدهد. این روال برای هر یک از زیرآرایهها تکرار شده تا در نهایت به زیرآرایههایی با یک عضو دست پیدا کنیم. سپس با ترکیب این زیرآرایهها به مجموعهای مرتب شده دست خواهیم یافت. مرتب سازی سریع، یکی از مهمترین مفاهیمی است که توصیه میشود تا برنامهنویسان آن را درک کرده و پیادهسازی کنند. این الگوریتم، بهخصوص برای دادههای حجیم عملکرد بسیار خوبی ارائه میدهد و میتواند در موارد گوناگونی استفاده شود.
source