ریاضی نهم، در سال سوم دوره اول متوسطه یا همان مقطع نهم به دانشآموزان تدریس میشود. این درس، حاوی هشت فصل است که مباحثی نظیر مجموعهها، عددهای حقیقی، استدلا و اثبات در هندسه، توان و ریشه، عبارتهای جبری، خط و معادلههای خطی، عبارتهای گویا و حجم و مساحت را پوشش میدهند. مباحث ریاضی نهم، اهمیت بسیار بالایی برای دانشآموزان دارد؛ زیرا این مباحث، نه تنها تکمیلکننده مباحث ارائه شده در ریاضی هفتم و ریاضی هشتم هستند، بلکه زمینه یادگیری بهتر ریاضیات مقاطع بالاتر را نیز فراهم میکنند. به همین دلیل، دانشآموزان، همواره به دنبال منبعی هستند که فرمول های ریاضی نهم و نکات مهم فصلهای مختلف آن را برایشان خلاصه کرده باشد. در مطالب قبلی مجله فرادرس، نکات و فرمولهای مهم ریاضی هشتم را به همراه مثال جمعبندی کردیم. در این مطلب نیز قصد داریم با همان رویکرد، ضمن معرفی تمام فرمول های ریاضی نهم، به حل مثال در رابطه با موضوع هر درس بپردازیم. شما میتوانید این مطلب را برای مرور سریع فرمول های ریاضی نهم ذخیره کنید.
۱. مجموعه ها: فرمول های فصل اول ریاضی نهم
فصل اول کتاب ریاضی نهم، شامل چهار درس با عنوانهای «معرفی مجموعه»، «مجموعههای برابر و نمایش مجموعهها»، «اجتماع، اشتراک و تفاضل مجموعهها» و «مجموعهها و احتمال» است.
این فصل از ریاضی نهم فرمول های خاصی ندارد اما پر از علامتها و مفاهیم جدید است. این علامتها را در جدول زیر آوردهایم.
| عنوان | توضیحات |
| علامت عضو بودن | $$ in $$ |
| علامت عضو نبودن | $$ notin $$ |
| علامت مجموعه تهی | $$ emptyset $$ یا $$ { } $$ |
| علامت برابری مجموعهها | $$ = $$ |
| علامت نابرابری مجموعهها | $$ ne $$ |
| علامت زیرمجموعه بودن | $$ subseteq $$ |
| علامت زیرمجموعه نبودن | $$ nsubseteq $$ |
| علامت بهطوری که | $$ | $$ |
| علامت اجتماع مجموعهها | $$ cup $$ |
| علامت اشتراک مجموعهها | $$ cap $$ |
| علامت تعداد عضوهای یک مجموعه مانند $$ A $$ | $$ n ( A ) $$ |
| علامت احتمال رخ دادن پیشامد $$ A $$ | $$ P ( A ) $$ |
| فرمول احتمال رخ دادن پیشامد | $$ P ( A ) = frac { n ( A ) } { n ( S ) } $$ |
درس اول: معرفی مجموعه
مجموعه، یکی از مفاهیم پایه ریاضی است که به منظور بیان و نمایش دستهای از اشیای مشخص و متمایز (غیرتکراری) مورد استفاده قرار میگیرد. به عنوان مثال، اعداد زوج بین $$ ۱ $$ تا $$ ۹ $$ را میتوان به عنوان یک مجموعه در نظر گرفت. این مجموعه به صورت زیر نمایش داده میشود:
$$ { ۲ , ۴ , ۶ , ۸ } $$
در این مجموعه، هیچ عدد تکراری وجود ندارد و تمام عضوهای مجموعه مشخص هستند. در طرف مقابل، چهار شاعر ایرانی را در نظر بگیرید. از آنجایی که نام این چهار شاعر را مشخص نیست و هر کسی ممکن است شاعرهای متفاوتی را در نظر بگیرید، نمیتوانیم بگوییم آنها در یک مجموعه قرار میگیرند.

عضویت در مجموعه با $$ in $$ نمایش داده میشود. به عنوان مثال، اگر مجموعه اعداد زوج بین $$ ۱ $$ تا $$ ۹ $$ را برابر با $$ A $$ در نظر بگیریم، میتوانیم بگویم:
$$ ۲ in A $$
عبارت بالا، یعنی $$ ۲ $$، عضوی از مجموعه $$ A $$ است. علامت عضو نبودن در یک مجموعه به صورت $$ notin $$ نوشته میشود. به عنوان مثال، در مجموعه $$ A $$، داریم:
$$ ۱ notin A $$
عبارت بالا، یعنی عدد $$ ۱ $$، عضوی از مجموعه $$ A $$ نیست. از مهمترین ویژگیهای مجموعهها میتوان به موارد زیر اشاره کرد:
- در نمایش یک مجموعه، ترتیب نوشتن عضوهای آن، مهم نیست.
- با جابجایی عضوهای یک مجموعه و یا تکرار عضوهای آن، مجموعه جدیدی ساخته نمیشود.
- به مجموعه بدون عضو، مجموعه تهی میگوییم و آن را با $$ emptyset $$ یا $$ { } $$ نمایش میدهیم.
- مجموعه $$ { emptyset } $$ یا $$ { ۰ } $$، تهی نیستند و هرکدام یک عضو دارند.
مجموعه اعداد حاوی هشت ضریب اول عدد $$ ۷ $$ چیست؟
برای نوشتن مجموعه مورد سوال، ضرایب عدد $$ ۷ $$ را مینویسیم:
$$ ۷ times ۱ = ۷ $$
$$ ۷ times ۲ = ۱۴ $$
$$ ۷ times ۳ = ۲۱ $$
$$ ۷ times ۴ = ۲۸ $$
$$ ۷ times ۵ = ۳۵ $$
$$ ۷ times ۶ = ۴۲ $$
$$ ۷ times ۷ = ۴۹ $$
$$ ۷ times ۸ = ۵۶ $$
$$ ۷ times ۹ = ۶۳ $$
$$ ۷ times ۱۰ = ۷۰ $$
هشت ضریب اول عدد $$ ۷ $$ عبارت هستند از:
$$ ۱ $$
$$ ۷ $$
$$ ۱۴ $$
$$ ۲۱ $$
$$ ۲۸ $$
$$ ۳۵ $$
$$ ۴۲ $$
$$ ۴۹ $$
$$ ۵۶ $$
بنابراین، مجموعه اعداد حاوی هشت ضریب اول عدد $$ ۷ $$ به صورت زیر نوشته میشود:
$$
A = { ۱, ۷, ۱۴, ۲۱, ۲۸, ۳۵, ۴۲, ۴۹, ۵۶ }
$$
درس دوم: مجموعه های برابر و نمایش مجموعه ها
به مجموعههای دارای عضوهای یکسان، مجموعههای برابر میگویند. دو مجموعه $$ A $$ و $$ B $$ را در نظر بگیرید. اگر هر عضو $$ A $$، عضوی از $$ B $$ و هر عضو $$ B $$، عضوی از $$ A $$ باشد، $$ A $$ و $$ B $$ برابر هستند. برای نمایش برابری این مجموعه، عبارت $$ A = B $$ را مینویسیم. اگر $$ A $$ و $$ B $$ برابر نباشند، برابر نبودن آنها را به صورت $$ A ne B $$ نشان میدهیم.
اگر هر عضو از مجموعهای به نام $$ C $$، عضوی از مجموعهای به نام $$ B $$ باشد، میگوییم $$ C $$ زیرمجموعه $$ B $$ است. زیرمجموعهها با علامت $$ subseteq $$ نمایش داده میشود. به عنوان مثال:
$$ C subseteq B $$
اگر حتی یکی از عضوهای $$ C $$ در $$ B $$ وجود نداشته باشد، مینویسیم:
$$ C nsubseteq B $$
$$ nsubseteq $$، یعنی $$ C $$ زیرمجموعه $$ B $$ نیست. به خاطر داشته باشید که مجموعه تهی ($$ emptyset $$)، زیرمجموعه تمام مجموعهها است. در فصل اول ریاضی نهم، نحوه نمایش مجموعههای اعداد با استفاده از نمادهای ریاضی آموزش داده میشود. به عنوان مثال، نمایش مجموعه عددهای طبیعی با نماد $$ mathbb { N } $$، به صورت زیر است:
$$ mathbb { N } = {۱, ۲, ۳, ۴, ۵, … } $$
برای نمایش مجموعه اعداد زوج طبیعی، مینویسیم:
$$
mathbb { E } = { ۲ k | k in mathbb { N } }
$$
عبارتهای بالا را اینگونه میخوانیم؛ $$ E $$ برابر است با مجموعه عددهایی به شکل $$ ۲ k $$ بهطوری که $$ k $$ متعلق به مجموعه عددهای طبیعی است. معادل کلامی علامت $$ | $$، «بهطوری که» است.
رابطه بین مجموعههای زیر چیست و چگونه نمایش داده میشود؟
$$ A = { ۱, ۷, ۱۴, ۲۱, ۲۸, ۳۵, ۴۲, ۴۹, ۵۶ } $$
$$ B = { ۱, ۷, ۱۴, ۲۱, ۲۸, ۳۵, ۴۲, ۴۹, ۵۶, ۶۳, ۷۰ } $$
با بررسی عضوهای دو مجموعه $$ A $$ و $$ B $$، میتوان مشاهده کرد که تمام عضوهای مجموعه $$ A $$ در مجموعه $$ B $$ وجود دارند اما تمام عضوهای $$ B $$ در $$ A $$ وجود ندارند. بنابراین، $$ A $$، زیرمجموعه $$ B $$ است. این رابطه به صورت زیر نوشته میشود:
$$
A subset B
$$
درس سوم: اجتماع، اشتراک و تفاضل مجموعه ها
مهمترین تعاریف مربوط به انجام عملیات روی مجموعهها عبارت هستند از:
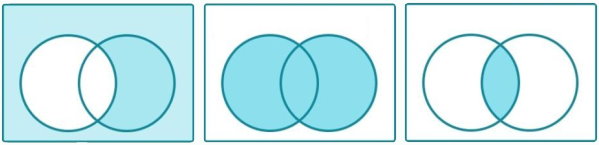
- اشتراک: اشتراک دو مجموعه $$ A $$ و $$ B $$، مجموعهای شامل همه عضوهایی است که هم در $$ A $$ و هم در $$ B $$ حضور دارند. اشتراک با علامت $$ cap $$ نمایش داده میشود ($$ A cap B $$).
- اجتماع: اجتماع دو مجموعه $$ A $$ و $$ B $$، مجموعهای شامل همه عضوهایی است که حداقل در یکی از مجموعههای $$ A $$ یا $$ B $$ حضور دارند. اجتماع با علامت $$ cup $$ نمایش داده میشود ($$ A cup B $$).
- تفاضل: مجموعه $$ A $$ منهای $$ B $$ یا $$ A – B $$، مجموعهای شامل همه عضوهایی است که در $$ A $$ حضور دارند اما در $$ B $$ حضور ندارند.
تصویر زیر، مفهوم اشتراک، اجتماع و تفاضل را نمایش میدهد.
تعداد عضوهای هر مجموعه مانند $$ A $$، با $$ n ( A ) $$ نمایش داده میشود. به عنوان مثال، اگر $$ A $$، مجموعهای $$ k $$-عضوی باشد، مینویسیم:
$$ n ( A ) = k $$
دو مجموعه $$ A = { – ۱ , ۰ , ۲ , ۳ , ۵ , ۷ } $$ و $$ B = { ۰ , ۱ , ۲ , ۳ , ۵ , ۶ } $$ را در نظر بگیرید. $$ A cup B $$ چیست؟
در مبحث مجموعهها، اجتماع دو مجموعه را با علامت $$ cup $$ نمایش میدهند. اجتماع د و مجموعه، مجموعهای است که همه عضوهای آن مجموعهها را دربرمیگیرد. در اینجا، داریم:
$$ A = { – ۱ , ۰ , ۲ , ۳ , ۵ , ۷ } $$
$$ B = { ۰ , ۱ , ۲ , ۳ , ۵ , ۶ } $$
در نتیجه:
$$ A cup B = { – ۱ , ۰ , ۱ , ۲ , ۳ , ۵ , ۶ , ۷ } $$
توجه داشته باشید که در اجتماع، نیازی به نوشتن دوباره عضوهای مشترک نیست.
درس چهارم: مجموعه ها و احتمال
بر اساس کتاب ریاضی هشتم، احتمال هر پیشامد به صورت زیر تعریف میشود:
احتمال رخ دادن پیشامد
=
تعداد همه حالتهای ممکن ÷ تعداد حالتهای مطلوب
بر اساس نمادهای معرفی شده در ریاضی نهم میتوانیم این رابطه را به زبان ریاضی بنویسم. به این منظور، ابتدا پارامترهای زیر را تعریف میکنیم:
- $$ S $$: مجموعهای شامل همه حالتهای ممکن
- $$ A $$: مجموعهای شامل همه حالتهای مطلوب
- $$ P ( A ) $$: احتمال رخ دادن پیشامد $$ A $$
به این ترتیب، فرمول احتمال رخ دادن پیشامد به صورت زیر نوشته میشود:
$$ P ( A ) = frac { n ( A ) } { n ( S ) } $$
در یک آزمایش احتمالاتی، سه سکه را $$ ۱۰۰۰ $$ بار به طور همزمان پرتاب میکنیم. در این آزمایش، با نتایج زیر روبهرو میشویم:
- ظاهر شدن سه خط: $$ ۱۶۰ $$ بار
- ظاهر شدن دو خط و یک شیر: $$ ۲۶۰ $$ بار
- ظاهر شدن یک خط و دو شیر: $$ ۳۲۰ $$ بار
- ظاهر شدن سه شیر: $$ ۲۶۰ $$ بار
اگر یک بار دیگر سکه را همزمان پرتاب کنیم، احتمال اینکه دو خط و یک شیر بیاید چقدر است؟
برای پاسخگویی به این سوال، از مفهوم احتمال رخ دادن پیشامد استفاده میکنیم. بر اساس این مفهوم، داریم:
$$ P ( A ) = frac { n ( A ) } { n ( S ) } $$
- $$ P ( A ) $$: احتمال رخ دادن پیشامد $$ A $$
- $$ n ( A ) $$: تعداد رخداد حالت مطلوب $$ A $$ برابر با $$ ۲۶۰ $$
- $$ n ( S ) $$: تعداد تمام رخدادها برابر با $$ ۱۰۰۰ $$
در $$ ۱۰۰۰ $$ پرتاب قبلی، $$ ۲۶۰ $$ بار با حالت دو خط و یک شیر مواجه شدیم. بنابرین، در پرتاب بعدی،احتمال رخ دادن این پیشامد روبهرو میشویم:
$$ P ( A ) = frac { ۲۶۰ } { ۱۰۰۰ } $$
$$ P ( A ) = ۰/۲۶ $$
به این ترتیب، به احتمال $$ ۰/۲۶ $$ یا $$ ۲۶ $$ درصد، در پرتاب $$ ۱۰۰۱ $$ با دو خط و یک شیر رو به رو میشویم.
فرادرس، یک فیلم آموزشی جامع و مفید را برای دانشآموزان پایه نهم تهیه کرده است که مفاهیم و فرمول های موجود در درسهای کتاب ریاضی نهم را به خوبی توضیح میدهد. برای مشاهده این فیلم آموزشی، بر روی لینک زیر کلیک کنید:

۲. عددهای حقیقی: فرمول های فصل دوم ریاضی نهم
فصل دوم کتاب ریاضی نهم، شامل درسهای «عددهای گویا»، «عددهای حقیقی» و «قدر مطلق و محاسبه تقریبی» است. فرمول های خاصی در این فصل ریاضی نهم وجود ندارد. البته، در رابطه با ویژگیهای مجموعههای اعداد و قدر مطلق صبحت میشود.
جدول زیر، مهمترین این ویژگیها را نمایش میدهد.
| تعریف | عبارت جبری |
| اشتراک مجموعههای عددهای گویا و گنگ برابر با مجموعه تهی | $$ Q cap Q ‘ = emptyset $$ |
| مجموعه عددهای طبیعی، زیرمجموعه عددهای صحیح است. | $$ mathbb{ N } subseteq mathbb{ Z } $$ |
| مجموعه عددهای صحیح، زیرمجموعه عددهای گویا است. | $$ mathbb{ Z } subseteq mathbb{ Q } $$ |
| مجموعه عددهای گویا، زیرمجموعه عددهای حقیقی است. | $$ mathbb{ Q } subseteq mathbb{ R } $$ |
| مجموعه عددهای گنگ، زیرمجموعه عددهای حقیقی است. | $$ mathbb{ Q ‘ } subseteq mathbb{ R } $$ |
| قدر مطلق صفر | $$ a = ۰ Rightarrow | a | = ۰ $$ |
| قدر مطلق عدد مثبت | $$ a gt ۰ Rightarrow | a | = a $$ |
| قدر مطلق عدد منفی | $$ a lt ۰ Rightarrow | a | = – a $$ |
| جذر مربع یک عدد | $$ sqrt { a ^ ۲ } = | a | $$ |
در این فصل با علامتهای جدیدی روبهرو میشوید که در ادامه آنها را به طور خلاصه معرفی میکنیم:
درس اول: عددهای گویا
عددهای گویا، عددهایی هستند که میتوان آنها به صورت نسبت دو عدد صحیح نمایش داد. درس اول فصل دوم ریاضی نهم، به موضوع مرتبسازی و مقایسه اعداد گویا میپردازد. از مهمترین اصطلاحات جدید در این درس میتوان به موارد زیر اشاره کرد.
- عدد اعشاری متناهی یا مختوم: در نمایش اعشاری کسر، تمام رقمهای اعشار مشخص است. مانند:
$$ frac { ۱ } { ۴ } = ۰/۲۵ $$
- عدد اعشاری متناوب: در نمایش اعشاری کسر، رقم آخر آن به طور متناوب و بدون انتها تکرار میشود. مانند:
$$frac { ۱ } { ۳ } = ۰/۳۳۳۳۳ …… = ۰ / overline { ۳ } $$
در ادامه، یکی از تمرینهای این درس را حل میکنیم.
حاصل عبارت زیر را به دست بیاورید و تا حد امکان ساده کنید:
$$ – frac { ۱ } ۲ + frac { – ۵ } { ۶ } div frac { ۷ } { ۳ } times frac { ۷ } { ۵ } + frac { ۲ } {۳ } $$
در انجام عملیاتهای ریاضی بر روی چند عدد، همواره به خاطر داشته باشید که اولویت انجام عملیات به صورت زیر است:
- عبارت داخل پرانتز
- ضرب و تقسیم
- جمع و تفریق
در عبارت $$ – frac { ۱ } ۲ + frac { – ۵ } { ۶ } div frac { ۷ } { ۳ } times frac { ۷ } { ۵ } + frac { ۲ } {۳ } $$، هیچ پرانتزی وجود ندارد. بنابراین، پیش از هر چیزی، حاصل عبارت زیر را به دستت میآوریم:
$$ frac { – ۵ } { ۶ } div frac { ۷ } { ۳ } times frac { ۷ } { ۵ } $$
بر اساس قوانین تقسیم کسرها، میتوانیم عبارت بالا را به صورت زیر بازنویسی کنیم:
$$
frac { – ۵ } { ۶ } times frac { ۳ } { ۷ } times frac { ۷ } { ۵ }
$$
به این ترتیب و بر اساس قوانین ضرب کسرها، داریم:
$$
frac { – ۵ } { ۶ } times frac { ۳ } { ۷ } times frac { ۷ } { ۵ } = frac { – ۵ times ۳ times ۷ }{ ۶ times ۷ times ۵} = – frac { ۱ } { ۲ }
$$
این نتیجه را درون عبارت اول قرار میدهیم:
$$
– frac { ۱ } ۲- frac { ۱ } { ۲ } + frac { ۲ } {۳ }
$$
اکنون، با استفاده از اصول جمع و تفریق کسرها و گرفتن مخرج مشترک، حاصل عبارت بالا را به دست میآوریم:
$$
– frac { ۱ } ۲ – frac { ۱ } { ۲ } + frac { ۲ } {۳ } = – ۱ + frac { ۲ } {۳ }
$$
$$
– ۱ + frac { ۲ } {۳ } = frac { – ۳ + ۲ } { ۳ } = – frac { ۱ } { ۳ }
$$
درس دوم: عددهای حقیقی
به مجموعه همه عددهای گویا و گنگ، عددهای حقیقی میگویند. در برخی از مسائل ریاضی، با عددهایی رو به رو میشوید که در نمایش اعشاری آنها، تعداد ارقام اعشاری بیشمار بوده و هیچ تناوبی ندارد. این عددها با عنوان عددهای گنگ یا اصم شناخته میشوند. مجموعه عددهای گنگ را با $$ Q ‘ $$ یا $$ Q ^ c $$ نمایش میدهند. عدد پی ($$ pi $$)، یک عدد گنگ است. شاید در اغلب موارد، مقدار این عدد برابر با $$ ۳/۱۴ $$ در نظر گرفته شود اما رقمهای اعشار آن هیچ انتهایی ندارد:
$$ pi = ۳/۱۴۱۵۹۲۶۵۳۵۸۹۷۹۳۲۳۸۴۶۲۶۴۳۳۸۳۲۷۹ ….. $$
تصویر زیر، نمودار ون مجموعههای عددهای طبیعی، صحیح، گویا و گنگ را نمایش میدهد.
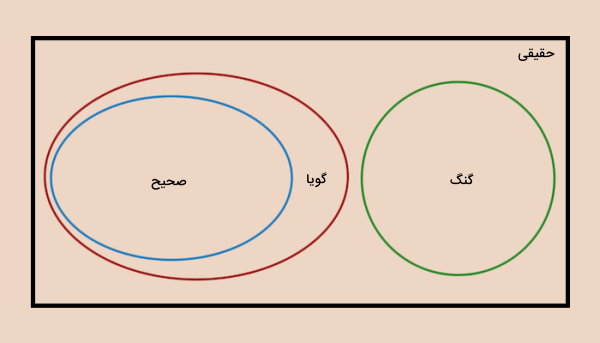
بر اساس این نمودار میتوانیم بگوییم:
$$ Q cap Q ‘ = emptyset $$
$$ mathbb{ N } subseteq mathbb{ Z } $$
$$ mathbb{ Z } subseteq mathbb{ Q } $$
$$ mathbb{ Z } nsubseteq mathbb{ Q ‘ } $$
$$ mathbb{ N } nsubseteq mathbb{ Q ‘ } $$
به این ترتیب میتوانیم بگوییم عددها، به دو دسته عددهای گویا و عددهای گنگ تقسیم میشوند. به اجتماع مجموعه عددهای گویا و گنگ، مجموعه عددهای حقیقی میگویند و آن را با $$ mathbb { R } $$ نمایش میدهند:
$$ mathbb { R } = Q cup Q ‘ $$
کدامیک از اعداد زیر، حقیقی هستند؟
$$ sqrt { ۶ } $$
$$ – ۳ $$
$$ ۳/۱۵ $$
$$ sqrt { – ۵ } $$
عدد $$ sqrt { ۶ } $$، یک عدد گنگ است. عدد $$ – ۳ $$، یک عدد صحیح منفی است. عدد $$ ۳/۱۵ $$، یک عدد اعشاری گویا است. تمام این اعداد، در مجموعه اعداد حقیقی قرار دارند. با این وجود، عدد $$ sqrt { -۵ } $$، در هیچ یک از زیرمجموعههای مجموعه اعداد حقیقی جای ندارد. از آنجایی که عدد زیر رادیکال نمیتواند منفی باشد، این عدد با عنوان یک عدد موهومی یا عدد مختلط شناخته میشود.
درس سوم: قدر مطلق و محاسبه تقریبی
فاصله یک نقطه تا مبدا محور اعداد، با عنوان قدر مطلق آن عدد شناخته میشود. این فاصله، یک عدد با مبدا صفر را نمایش میدهد. علامت قدر مطلق، $$ | | $$ است. قدر مطلق، علامت اعداد را مثبت میکند. به عنوان مثال، قدر مطلق $$ – ۲ $$ برابر است با:
$$ | – ۲ | = ۲ $$
به طور کلی، سه قانون اصلی در رابطه با قدر مطلق وجود دارد. این سه قانون عبارت هستند از:
- قدر مطلق صفر، برابر با صفر است.
- قدر مطلق عددهای مثبت، برابر با خود آن عددها است.
- قدر مطلق عددهای منفی، برابر با قرینه آن عددها است.
عبارت جبری قوانین بالا به صورت زیر نوشته میشود:
$$ a = ۰ Rightarrow | a | = ۰ $$
$$ a gt ۰ Rightarrow | a | = a $$
$$ a lt ۰ Rightarrow | a | = – a $$
قدر مطلق، با مفهوم جذر و ریشهیابی نیز ارتباط دارد. اگر از مربع کامل یک عدد جذر یا رادیکال بگیریم، خروجی آن برابر با قدر مطلق عدد میشود. به عبارت دیگر:
$$ sqrt { a ^ ۲ } = | a | $$
حاصل عبارت $$ left | frac { – ۳ } { ۵ } right | times left | frac { ۵ } { ۶ } right | $$ را به دست بیاورید.
برای به دست آوردن حاصل عبارت مورد سوال، ابتدا مقدار قدر مطلق آنها را تعیین میکنیم. میدانیم که قدر مطلق، علامت منفی اعداد را به علامت مثبت تبدیل میکند. بنابراین:
$$
left | frac { – ۳ } { ۵ } right | = frac { ۳ } { ۵ }
$$
$$
left | frac { ۵ } { ۶ } right | = frac { ۵ } { ۶ }
$$
به این ترتیب داریم:
$$
left | frac { – ۳ } { ۵ } right | times left | frac { ۵ } { ۶ } right | = frac { ۳ } { ۵ } times frac { ۵ } { ۶ }
$$
$$
left | frac { – ۳ } { ۵ } right | times left | frac { ۵ } { ۶ } right | = frac { ۳ times ۵ } { ۵ times ۶ }
$$
$$
left | frac { – ۳ } { ۵ } right | times left | frac { ۵ } { ۶ } right | = frac { ۳ } { ۶ }
$$
$$
left | frac { – ۳ } { ۵ } right | times left | frac { ۵ } { ۶ } right | = frac { ۱ } { ۲ }
$$
در مطالب قبلی مجله فرادرس، با فرمولهای ریاضی پایه هشتم آشنا شدیم. در ادامه، بهترین راه برای یادگیری و تسلط بر روی فرمول های ریاضی نهم را معرفی میکنیم.
چگونه فرمول های ریاضی نهم را یاد بگیریم؟
پایه نهم، آخرین پایه در دوره متوسطه اول است. دانشآموزان نهم، برای موفقیت در درسهای خود و ورود قوی به دوره متوسطه دوم، باید بر روی مفاهیم و فرمول های ریاضی هفتم و هشتم نیز تسلط داشته باشند. زیرا این مفاهیم و فرمولها، پیشزمینه فرمول های ریاضی نهم هستند. اغلب فرمول های ریاضی نهم، در مقاطع بالاتر و حتی دانشگاه نیز مورد استفاده قرار میگیرند. از اینرو، دانشآموزان باید به طور اصولی، ریاضیات هفتم، هشتم و نهم را یاد بگیرند. به این منظور، فرادرس، فیلمهای آموزشی جامع و مفیدی را تهیه کرده است که تمام نیازهای دانشآموزان برای یادگیری ریاضیات پایه را برطرف میکنند. لینک مشاهده این فیلمها در ادامه آورده شده است:
در صورت علاقه به یادگیری دیگر درسهای دوره متوسطه اول و دوم، مشاهده مجموعه فیلمهای آموزشی زیر را به شما پیشنهاد میکنیم:
۳. استدلال و اثبات در هندسه: فرمول های فصل سوم ریاضی نهم
فصل سوم کتاب ریاضی نهم مفاهیم مرتبط با استدلال و اثبات در هندسه را طی پنح درس با عنوانهای «استدلال»، «آشنایی با اثبات در هندسه»، «همنهشتی مثلثها»، «حل مسئله در هندسه» و «شکلهای متشابه» آموزش میدهد.
فرمول های خاصی در این فصل از کتاب ریاضی نهم ارائه نمیشوند و اغلب مطالب به صورت تئوری یا اثباتی هستند. در ادامه، مهمترین نکات فصل سوم ریاضی نهم را مرور میکنیم.
درس اول: استدلال
استدلال، یعنی دلیل آوردن و استفاده از دانستههای قبلی برای معلوم کردن موضوعی که در ابتدا مجهول بوده است. به استدلالی که موضوع مورد نظر را به درستی نتیجه بدهد، اثبات میگوییم. یکی از روشهای اثبات نادرستی یک موضوع، بیان مثال نقض است. به عنوان مثال، فرض کنید شخصی به شما میگوید «در هر مثلث، محل برخورد هر دو ارتفاع، درون مثلث قرار میگیرد». شما با بیان «در مثلثهای دارای زاویه باز یا منفرجه، امکان قرارگیری محل برخورد دو ارتفاع در بیرون مثلث وجود دارد»، یک مثال نقض میآورید. با این کار، نادرستی جمله اول را اثبات میکنید.
درس دوم: آشنایی با اثبات در هندسه
به اطلاعات یا دادههای مسئله به همراه حقایق و اصولی که درستی آنها از قبل برایمان معلوم شده است، فرض میگوییم. خواسته مسئله که قرار است برای رسیدن به آن و اثباتش از فرض استفاده کنیم را نیز با عنوان حکم بیان میکنیم. به عنوان مثال، لوزی نمایش داده شده در تصویر زیر را در نظر بگیرید.

میخواهیم ثابت کنیم زاویههای روبهرویی لوزی با هم برابرند. فرض، حکم و استدلال ما برای ثابت این مدعا به صورت زیر خواهند بود:
- فرض: شکل نمایش داده شده، لوزی است.
- حکم: زاویههای روبهرویی لوزی با هم برابرند.
- استدلال
- لوزی نوعی متوازیالاضلاع است.
- در متوازیالاضلاع، زاویههای روبهرویی با هم برابرند.
- نتیجه: در لوزی، زاویههای روبهرویی با هم برابرند.
اولین قدم برای اثبات، تشخیص فرض، حکم و واقعیتهای مرتبط با مسئله است. برخی از حکمهایی که در این درس با آنها آشنا میشوید عبارت هستند از:
- اگر در دو مثلث، دو زاویه داخلی با هم برابر باشند، زاویه سوم از دو مثلث نیز برابر است.
- اگر در یک مثلث، دو زاویه نابرابر باشد، ضلع روبهرو به زاویه بزرگتر، از ضلع روبهرو به زاویه کوچکتر بزرگتر است.
- در هر مثلث، اندازه هر زاویه خارجی با مجموع دو زاویه داخلی غیرمجاور آن برابر است.
- قطر مربع، نیمساز زاویههای داخلی است.
درس سوم: هم نهشتی مثلث ها
به شکلهایی که با یک یا چند تبدیل هندسی (دوران، انتقال، تقارن)، کاملا بر روی هم منطبق میشوند، شکلهای همنهشت میگویند. در کتاب ریاضی هشتم، حالتهای مختلف همنهشتی مثلثها بیان شدهاند. یکی از این حالتها، برابر بودن دو ضلع و زاویه بین آنها (ض ز ض) است. اگر بخواهیم این همنهشتی را به زبان ریاضی و برای دو مثلث فرضی $$ A B C $$ و $$ A ‘ B ‘ C ‘ $$ بنویسیم، خواهیم داشت:
$$
left.begin{array}
mathrm { A B } = mathrm { A } ^ {prime} mathrm { B } ^ { prime } \
mathrm { A C } = mathrm { A } ^ { prime } mathrm { C } ^ { prime } \
hat { mathrm { A } } = hat { mathrm { A } } ^ { prime }
end {array} right } Rightarrow mathrm{ A B C } cong mathrm { A } ^ { prime } mathrm { B } ^ { prime } mathrm { C } ^ { prime }
$$
درس چهارم: حل مسئله در هندسه
بر اساس کتاب ریاضی نهم، مراحل حل مسئلههای هندسی به صورت زیر خلاصه میشود:
- خواندن دقیق مسئله و مفاهیم تشکیلدهنده آن
- رسم شکل مناسب برای مسئله (در صورت عدم وجود)
- تشخیص دادههای مسئله (فرض) و خواستههای مسئله (حکم) در یک جدول
- پیدا کردن راهحل برای رسیدن از فرض به حکم
یکی از نکاتی که هنگام مطالعه این درس خواهید آموخت، این است که در یک دایره، اگر دو کمان برابر باشند، وترهای نظیر آنها با هم برابرند و اگر دو وتر برابر باشند، کمانهای نظیر آنها نیز با هم برابرند.
درس پنجم: شکل های متشابه
هرگاه در دو چندضلعی، همه ضلعها به یک نسبت تغییر کرده باشد و اندازه زاویهها تغییر نکرده باشد، آن دو چندضلعی با هم متشابهاند.

در بخش بعدی این مطلب از مجله فرادرس، فرمول های ریاضی نهم در مبحث توان و ریشه را معرفی میکنیم.
۴. توان و ریشه: فرمول های فصل چهارم ریاضی نهم
فصل چهارم کتاب ریاضی نهم، به مبحث توان و ریشه اختصاص دارد. در این فصل، مفاهیمی نظیر «توان صحیح»، «نماد علمی»، «ریشهگیری» و «جمع و تفریق رادیکالها» پوشش داده میشود.
جدول زیر، مهمترین فرمول های فصل چهارم ریاضی نهم را نمایش میدهد.
| عنوان | فرمول |
| عدد به توان صفر | $$ a ^ ۰ = ۱ $$ |
| عدد به توان منفی | $$ a ^ { – n } = frac { ۱ } { a ^ n } a ne ۰ , n in mathbb { N } $$ |
| ضرب دو عدد تواندار با پایه یکسان | $$ a ^ m times a ^ n = a ^ { m + n } $$ |
| تقسیم دو عدد تواندار با پایه یکسان | $$ frac { a ^ m }{ a ^ n } = a ^ { m – n } $$ |
| تقسیم دو تواندار با توان یکسان | $$ frac { a ^ m }{ b ^ m } = left ( frac { a } { b }right ) ^ m $$ |
| عدد تواندار به توان عدد دیگر | $$ ( a ^ m ) ^ n = a ^ { m n } $$ |
| به توان رساندن ضرب دو عدد | $$ ( a b ) ^ m = a ^ m cdot b ^ m $$ |
| نماد علمی | $$ a times ۱۰ ^ n $$ |
| رادیکال ضرب دو عدد |
$$ sqrt { a b } = sqrt { a } times sqrt { b } $$ |
| رادیکال تقسیم دو عدد | $$ sqrt { frac { a } { b } } = frac { sqrt { a } }{ sqrt { b } } $$ |
| رادیکال با فرجه $$ ۳ $$ ضرب دو عدد | $$ sqrt [ ۳ ] { a b } = sqrt [ ۳ ] { a } times sqrt [ ۳ ] { b } $$ |
| رادیکال با فرجه $$ ۳ $$ تقسیم دو عدد | $$ sqrt [ ۳ ] { frac { a } { b } } = frac { sqrt [ ۳ ] { a } }{ sqrt [ ۳ ] { b } } $$ |
در ادامه، به مرور نکات مهم درسهای این فصل و حل چند مثال میپردازیم.
درس اول: توان صحیح
عددهای تواندار، عددهایی هستند که به فرم زیر نوشته میشوند:
$$ a ^ n $$
$$ a $$، پایه و $$ n $$، توان عدد بالا است. توان میتواند یک عدد طبیعی یا صحیح باشد. به عبارت دیگر، توان میتواند علامت منفی داشته باشد. به طور کلی، اگر $$ a ne ۰ $$ و $$ n in mathbb { N } $$، خواهیم داشت:
$$ a ^ { – n } = frac { ۱ } { a ^ n } a ne ۰ , n in mathbb { N } $$
$$
a ^ { – n } = frac { ۱ } { a ^ n } = left ( frac { ۱ } { a }right ) ^ n
$$
اکنون، ضرب دو عدد تواندار با پایه یکسان را در نظر بگیرید. حاصل این ضرب به صورت زیر نوشته میشود:
$$ a ^ m times a ^ n = a ^ { m + n } $$
در این فرمول، $$ a $$، یک عدد دلخواه غیرصفر است. $$ m $$ و $$ n $$ نیز دو عدد صحیح هستند. برای تقسیم دو عدد تواندار، میتوانیم از فرمولهای زیر استفاده کنیم:
$$ frac { a ^ m }{ a ^ n } = a ^ { m – n } $$
$$ frac { a ^ m }{ b ^ m } = left ( frac { a } { b }right ) ^ m $$
اثبات فرمولهای بالا به سادگی و با استفاده از فرمولهای قبلی انجام میگیرد. از دیگر فرمول های فصل چهارم ریاضی نهم میتوان به موارد زیر اشاره کرد:
$$ ( a ^ m ) ^ n = a ^ { m n } $$
$$ ( a b ) ^ m = a ^ m cdot b ^ m $$
حاصل عبارت $$ ۴ ^ { – ۲ } $$ چند است؟
$$ ۴ ^ { – ۲ } $$، یک عدد تواندار با توان صحیح منفی را نمایش میدهد. بر اساس قوانین اعداد تواندار، میتوان این عدد را به صورت زیر بازنویسی کرد:
$$ ۴ ^ { – ۲ } = frac { ۱ } { ۴ ^ ۲ } $$
حاصل کسر بالا عبارت است از:
$$ frac { ۱ } { ۴ ^ ۲ } = frac { ۱ } { ۱۶ } $$
بنابراین:
$$ ۴ ^ { – ۲ } = frac { ۱ } { ۱۶ } $$
البته میتوانیم این عدد را به صورت اعشاری نیز نشان دهیم:
$$ ۴ ^ { – ۲ } = frac { ۱ } { ۱۶ } = ۰/۰۶۲۵ $$
درس دوم: نماد علمی
نماد علمی، نمایش اعداد به صورت ضرب یک عدد صحیح در توانی از عدد $$ ۱۰ $$ است. نماد علمی، برای بیان ساده و قابل فهم اعداد نسبتا بزرگ و کوچک مورد استفاده قرار میگیرد. به عنوان مثال عدد زیر را در نظر بگیرید:
$$ ۳۰۰۰۰۰۰۰۰ $$
خواندن صفرهای این عدد، کمی دشوار است و امکان رخ دادن خطا را افزایش میدهد. اکنون، آن را به صورت نماد علمی مینویسیم:
$$ ۳۰۰۰۰۰۰۰۰ = ۳ times ۱۰ ^ ۸ $$
همانطور که میبینید، خوانایی و درک نماد علمی بهتر از نمایش معمولی عدد است. به طور کلی، نماد علمی یک عدد اعشاری مثبت به صورت زیر نوشته میشود:
$$ a times ۱۰ ^ n $$
در اینجا، $$ ۱ le a lt ۱۰ $$ بوده و $$ n $$، عدی صحیح است. با ترکیب قوانین ضرب و تقسیم عددهای تواندار با نماد علمی، انجام محاسبات بر روی اعداد بزرگ سادهتر میشود.
شعاع خورشید، تقریبا $$ ۶۹۵۰۰۰ $$ کیلومتر است. این عدد را با نماد علمی و بر حسب متر نمایش دهید.
برای نمایش شعاع خورشید ($$ ۶۹۵۰۰۰ $$ کیلومتر) با نماد علمی، تعداد صفرهای آن را میشماریم. $$ ۶۹۵۰۰۰ $$، سه صفر دارد. این صفرها را حذف کرده و به جای آنها، بخش باقیمانده عدد را ضرب در عدد $$ ۱۰ $$ به توان تعداد صفرها ($$ ۳ $$) میکنیم. با این کار، خواهیم داشت:
$$ ۶۹۵۰۰۰ = ۶۹۵ times ۱۰ ^ ۳ $$
این عدد با نماد علمی و بر حسب کیلومتر است. صورت سوال، عدد را با نماد علمی و بر حسب متر میخواهد. برای تبدیل کیلومتر به متر، عدد بالا را در $$ ۱۰ ^ ۳ $$ ضرب میکنیم:
$$ ۶۹۵ times ۱۰ ^ ۳ times ۱۰ ^ ۳ = ۶۹۵ times ۱۰ ^ { ۳ + ۳ } = ۶۹۵ times ۱۰ ^ ۶ $$
بنابراین، شعاع خورشید، تقریبا $$ ۶۹۵ times ۱۰ ^ ۶ $$ متر است.
درس سوم: ریشه گیری
عبارتهای $$ sqrt { b } $$ و $$ – sqrt { b } $$، ریشههای دوم عدد حقیقی و مثبت $$ b $$ هستند. عددهای منفی، ریشه دوم ندارند. اگر $$ b $$، یک عدد حقیقی باشد، ریشه سوم آن به صورت $$ sqrt [ ۳ ] { b } $$ نمایش داده میشود. هر عدد فقط یک ریشه سوم دارد.
مبحث ریشهگیری، ارتباط بسیار نزدیکی به مفهوم رادیکال دارد. از فرمول های نهم ریاضی در رابطه با محاسبه ضرب و تقسیم رادیکالها میتوان به موارد زیر اشاره کرد:
$$ sqrt { a b } = sqrt { a } times sqrt { b } $$
$$ sqrt { frac { a } { b } } = frac { sqrt { a } }{ sqrt { b } } $$
$$ sqrt [ ۳ ] { a b } = sqrt [ ۳ ] { a } times sqrt [ ۳ ] { b } $$
$$ sqrt [ ۳ ] { frac { a } { b } } = frac { sqrt [ ۳ ] { a } }{ sqrt [ ۳ ] { b } } $$
توجه داشته باشید که به دلیل حضور $$ b $$ در مخرج کسر، شرط $$ b ne ۰ $$ برقرار است.
حاصل عبارت $$ sqrt { left ( – frac { ۳ }{ ۵ } right ) ^ ۲} $$ چیست؟
برای به دست آوردن عبارت مورد سوال، از رابطه زیر استفاده میکنیم:
$$ sqrt { x ^ ۲ } = | x | $$
اگر $$ left ( – frac { ۳ }{ ۵ } right ) $$ را برابر با $$ x $$ در نظر بگیریم، خواهیم داشت:
$$
sqrt { left ( – frac { ۳ }{ ۵ } right ) ^ ۲} = left | – frac { ۳ }{ ۵ } right |
$$
میدانیم که قدر مطلق، علامت عدد درون خود را مثبت میکند. بنابراین:
$$
sqrt { left ( – frac { ۳ }{ ۵ } right ) ^ ۲} = frac { ۳ }{ ۵ }
$$
در نتیجه، حاصل عبارت $$ sqrt { left ( – frac { ۳ }{ ۵ } right ) ^ ۲} $$ برابر با $$ frac { ۳ } { ۵ } $$ یا $$ ۰/۶ $$ است.

درس چهارم: جمع و تفریق رادیکال ها
درس آخر فصل چهارم ریاضی نهم، به توضیح روشهای جمع و تفریق رادیکالها، ساده کردن عبارتهای رادیکالی و گویا کردن مخرج کسرها میپردازید. اگر قسمتهای رادیکالی دو عدد با یکدیگر برابر باشند، میتوانیم جمع و تفریق آنها را به صورت زیر بنویسیم:
$$ a sqrt { b } pm c sqrt { b } = ( a pm c ) sqrt { b } $$
در صورتی که عدد زیر رادیکال، بر یک عدد مربع کامل بخشپذیر باشد، میتوانیم عدد مربع کامل را از درون رادیکال بیرون بکشیم. به عنوان مثال، $$ sqrt { ۵۰ } $$ را در نظر بگیرید. عدد زیر رادیکال برابر با $$ ۵۰ $$ است. میتوانیم این عدد را به صورت ضرب عدد مربع کامل $$ ۲۵ $$ در عدد $$ ۲ $$ بنویسیم:
$$ ۵۰ = ۲۵ times ۲ $$
به این ترتیب، داریم:
$$ sqrt { ۵۰ } = sqrt { ۲۵ times ۲ } $$
بر اساس قوانین ضرب رادیکالها، داریم:
$$ sqrt { ۲۵ times ۲ } = sqrt { ۲۵ } times sqrt { ۲ } = ۵ sqrt { ۲ } $$
در برخی از مواقع، با اعداد کسری روبهرو میشوید که مخرج آنها، یک عبارت رادیکالی است. برای ساده کردن این اعداد، باید مخرج کسر را از حالت رادیکالی خارج کنیم. این کار، با ضرب عدد کسری در کسری با صورت و مخرج عبارت رادیکالی صورت میگیرد. به عنوان مثال، کسر $$ frac { ۱ } { sqrt { ۳ }} $$ را در نظر بگیرید. اگر بخواهیم مخرج این کسر را گویا کنیم، مینویسیم:
$$
frac { ۱ } { sqrt { ۳ }} times frac { sqrt { ۳ } } { sqrt { ۳ } } = frac { ۱ times sqrt { ۳ } } { sqrt { ۳ } times sqrt { ۳ } } = frac { sqrt { ۳ } } { ۳ }
$$
عبارت $$ ۲ sqrt { ۵۰ } + sqrt { ۳۲ } + ۲ sqrt { ۷۲ } $$ را ساده کنید.
برای سادهسازی عبارت $$ ۲ sqrt { ۵۰ } + sqrt { ۳۲ } + ۲ sqrt { ۷۲ } $$، ابتدا هر یک از جملههای آن را به طور جداگانه ساده میکنیم:
$$ ۲ sqrt { ۵۰ } = ۲ sqrt { ۲۵ times ۲ } = ۲ sqrt { ۲۵ } sqrt { ۲ } = ۲ times ۵ sqrt { ۲ } = ۱۰ sqrt { ۲ } $$
$$ sqrt { ۳۲ } = sqrt { ۱۶ times ۲ } = ۴ sqrt { ۲ } $$
$$ ۲ sqrt { ۷۲ } = ۲ sqrt { ۳۶ times ۲ } = ۲ times ۶ sqrt { ۲ } = ۱۲ sqrt { ۲ } $$
اکنون، فرم ساده شده جملات را درون عبارت مورد سوال قرار میدهیم:
$$ ۱۰ sqrt { ۲ } + ۴ sqrt { ۲ } + ۱۲ sqrt { ۲ } $$
در مرحله بعد، از بخش مشترک در جملات بالا ($$ sqrt { ۲ } $$) فاکتور میگیریم:
$$ sqrt { ۲ } ( ۱۰ + ۴ + ۱۲ ) = ۲۶ sqrt { ۲ } $$
$$ ۲ sqrt { ۵۰ } + sqrt { ۳۲ } + ۲ sqrt { ۷۲ } = ۲۶ sqrt { ۲ } $$
در بخش بعدی این مطلب، فرمول های ریاضی نهم در مبحث عبارتهای جبری را معرفی میکنیم.
۵. عبارت های جبری: فرمول های فصل پنجم ریاضی نهم
فصل پنجم کتاب ریاضی نهم، «عبارتهای جبری» نام دارد. این فصل، از درسهای «عبارتهای جبری و مفهوم اتحاد»، «چند اتحاد دیگر، تجزیه و کاربردها» و «نابرابریها و نامعادلهها» تشکیل میشود. جدول زیر، مهمترین فرمول های فصل پنجم ریاضی نهم را نشان میدهد.
| عنوان | فرمول |
| اتحاد مربع مجموع دوجملهای | $$ ( a + b ) ^ ۲ = a ^ ۲ + ۲ a b + b ^ ۲ $$ |
| اتحاد مربع تفاضل دوجملهای | $$ ( a – b ) ^ ۲ = a ^ ۲ – ۲ a b + b ^ ۲ $$ |
| اتحاد مزدوج | $$ ( a + b ) ( a – b ) = a ^ ۲ – b ^ ۲ $$ |
| اتحاد جمله مشترک | $$ ( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b $$ |
درس اول: عبارت های جبری و مفهوم اتحاد
به عبارتهای جبری متشکل از یک جمله، یکجملهای یا تکجملهای میگویند. البته شرط تکجملهای بودن یک عبارت جبری، وجود ضریب حقیقی به همراه توان صحیح و غیرمنفی است. به عنوان مثال، عبارت زیر، یک تکجملهای در نظر گرفته میشود:
$$ ۵ x ^ { ۱۰ } $$
در طرف مقابل، عبارت زیر را نمیتوان به عنوان یک تکجملهای در نظر گرفت:
$$ ۲ x ^ { frac { ۱ } { ۲ } } $$
درجه تکجملهایها نسبت به یک متغیر، بر اساس توان آن متغیر تعیین میشود. به عنوان مثال، درجه تکجملهای $$ a x ^ ۲ $$ نسبت به متغیر $$ a $$ برابر با $$ ۱ $$ است. دو تکجملهای میتوانند متشابه یا غیرمتشابه باشند:
- تکجملهایهای متشابه: تکجملهایهایی که قسمت حرفی آنها یکسان است.
- تکجملهایهای غیرمتشابه: تکجملهایهایی که قسمت حرفی آنها یکسان نیست
حاصل جمع یا تفریق دو یا چند تکجملهای، یک چندجملهای است. درجه چندجملهای نسبت به یک متغیر، بالاترین توان آن متغیر در چندجملهای است.
یکی از مهمترین مفاهیمی که در کتاب ریاضی نهم تدریس میشود، مفهوم اتحاد است. اگر دو عبارت جبری، به ازای هر مقدار برای متغیرهایشان، حاصل یکسانی داشته باشند، به برابری حاصل از آنها، اتحاد جبری میگوییم. به عنوان مثال، برابری عبارتهای جبری زیر را در نظر بگیرید:
$$ ( x + ۳ ) ^ ۲ = x ^ ۲ + ۶ x + ۹ $$
به ازای تمامی مقادیر $$ x $$، تساوی بالا برقرار است. بنابراین، این تساوی با عنوان یک اتحاد شناخته میشود. اتحاد زیادی در دنیای ریاضی وجود دارند. مهمترین اتحاد معرفی شده در این درس، اتحاد مربع دوجملهای است. فرمول های اتحاد مربع دوجملهای در ریاضی نهم به صورت زیر نوشته میشوند:
$$ ( a + b ) ^ ۲ = a ^ ۲ + ۲ a b + b ^ ۲ $$
$$ ( a – b ) ^ ۲ = a ^ ۲ – ۲ a b + b ^ ۲ $$
عبارت $$ ( ۷ x + ۴ y ) ^ ۲ + ( ۷ x – ۴ y ) ^ ۲ $$ را ساده کنید.
به منظور سادهسازی $$ ( ۷ x + ۴ y ) ^ ۲ + ( ۷ x – ۴ y ) ^ ۲ $$ میتوانیم از اتحاد مربع مجموع دوجملهای و اتحاد مربع تفاضل دوجملهای استفاده کنیم. اتحاد مربع مجموع دوجملهای به صورت زیر نوشته میشود:
$$ ( a + b ) ^ ۲ = a ^ ۲ + ۲ a b + b ^ ۲ $$
بر اساس این اتحاد، برای $$ ( ۷ x + ۴ y ) ^ ۲ $$ داریم:
$$ a = ۷ x $$
$$ b = ۴ y $$
$$ ( ۷ x + ۴ y ) ^ ۲ = ( ۷ x ) ^ ۲ + ۲ ( ۷ x ) ( ۴ y ) + ( ۴ y ) ^ ۲ $$
$$
( ۷ x + ۴ y ) ^ ۲ = ۴۹ x ^ ۲ + ۵۶ x y + ۱۶ y ^ ۲
$$
اتحاد مربع تفاضل دوجملهای عبارت است از:
$$ ( a – b ) ^ ۲ = a ^ ۲ – ۲ a b + b ^ ۲ $$
بر اساس این اتحاد، برای $$ ( ۷ x – ۴ y ) ^ ۲ $$ داریم:
$$ a = ۷ x $$
$$ b = ۴ x $$
$$ ( ۷ x – ۴ y ) ^ ۲ = ( ۷ x ) ^ ۲ – ۲ ( ۷ x ) ( ۴ y ) + ( ۴ y ) ^ ۲ $$
$$
( ۷ x – ۴ y ) ^ ۲ = ۴۹ x ^ ۲ – ۵۶ x y + ۱۶ y ^ ۲
$$
در نتیجه:
$$
( ۷ x + ۴ y ) ^ ۲ + ( ۷ x – ۴ y ) ^ ۲ =۴۹ x ^ ۲ + ۵۶ x y + ۱۶ y ^ ۲ + ۴۹ x ^ ۲ – ۵۶ x y + ۱۶ y ^ ۲
$$
$$
( ۷ x + ۴ y ) ^ ۲ + ( ۷ x – ۴ y ) ^ ۲ =۴۹ x ^ ۲ + ۱۶ y ^ ۲ + ۴۹ x ^ ۲ + ۱۶ y ^ ۲
$$
$$
( ۷ x + ۴ y ) ^ ۲ + ( ۷ x – ۴ y ) ^ ۲ =۴۹ x ^ ۲ + ۴۹ x ^ ۲ + ۱۶ y ^ ۲ + ۱۶ y ^ ۲
$$
$$
( ۷ x + ۴ y ) ^ ۲ + ( ۷ x – ۴ y ) ^ ۲ = ۹۸ x ^ ۲ + ۳۲ y ^ ۲
$$

درس دوم: چند اتحاد دیگر، تجزیه و کاربردها
از دیگر اتحادهایی که در کتاب ریاضی نهم معرفی میشوند، میتوان به اتحاد مزدوج و اتحاد جمله مشترک اشاره کرد. فرمول های اتحاد مزدوج و اتحاد جمله مشترک در ریاضی نهم عبارت هستند از:
$$ ( a + b ) ( a – b ) = a ^ ۲ – b ^ ۲ $$
$$ ( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b $$
حاصل عبارت $$ left ( z – sqrt { ۳ } right ) left ( z + sqrt { ۳ } right ) $$ را با استفاده از اتحاد مناسب به دست بیاورید.
عبارت $$ left ( z – sqrt { ۳ } right ) left ( z + sqrt { ۳ } right ) $$، شباهت زیادی به اتحاد مزدوج دارد. این اتحاد به صورت زیر نوشته میشود:
$$ ( a + b ) ( a – b ) = a ^ ۲ – b ^ ۲ $$
بنابراین، اگر فرض کنیم:
$$ a = z $$
$$ b = sqrt { ۳ } $$
خواهیم داشت:
$$
left ( z – sqrt { ۳ } right ) left ( z + sqrt { ۳ } right ) = z ^ ۲ – left ( sqrt { ۳ } right ) ^ ۲
$$
$$
left ( z – sqrt { ۳ } right ) left ( z + sqrt { ۳ } right ) = z ^ ۲ – ۳
$$
درس سوم: نابرابری ها و نامعادله ها
هرگاه $$ a $$ و $$ b $$، دو عدد حقیقی باشد، به طوری که $$ a gt b $$، در این صورت، عدد حقیقی مثبتی مانند $$ p $$ وجود دارد که در رابطه زیر صدق میکند:
$$ a = b + p $$
علامت بزرگتر ($$ gt $$) یا کوچکتر ($$ lt $$)، نابرابری را نمایش میدهند. در مبحث نابرابریها و نامعادلهها، چندین نکته مهم وجود دارد که در فهرست زیر به بیان آنها میپردازیم:
- اگر دو طرف یک نابرابری را با عددی مانند $$ c $$ جمع کنیم، نابرابری همچنان برقرار است. یعنی اگر $$ a gt b $$، آنگاه $$ a + c gt b + c $$.
- اگر دو طرف یک نابرابری را با در عدد مثبتی مانند $$ c $$ ضرب کنیم، نابرابری همچنان برقرار است. یعنی اگر $$ a gt b $$ و $$ c gt ۰ $$، آنگاه $$ a c gt b c $$.
- اگر دو طرف نابرابری $$ a gt b $$ را در عدد منفی $$ c $$ (یعنی $$ c lt ۰ $$) ضرب کنیم. مانند $$ c $$ جمع کنیم، نابرابری همچنان برقرار است. یعنی اگر $$ a gt b $$، آنگاه $$ a + c gt b + c $$.
- به نامعادلهای که دارای یک متغیر با حداکثر توان $$ ۱ $$ باشد، نامعادله یک مجهولی درجه اول میگوییم.
- مجموعه مقادیری که به ازای آنها، نامعادله به نابرابری درست تبدیل شود، مجموعه جواب نامعادله میگوییم.
جواب نامعادله $$ frac { x – ۳ } { ۵ } ge – ۲ $$ را به دست بیاورید.
برای به دست آوردن جواب نامعادله $$ frac { x – ۳ } { ۵ } ge – ۲ $$، ابتدا هر دو طرف آن را در مخرج کسر (عدد $$ ۵ $$) ضرب میکنیم:
$$
۵ times frac { x – ۳ } { ۵ } ge ۵ times ( – ۲ )
$$
$$
not ۵ times frac { x – ۳ } { not ۵ } ge ۵ times ( – ۲ )
$$
$$
x – ۳ ge -۱۰
$$
سپس، مجهول (متغیر $$ x $$) را به یک طرف نامعادله و اعداد معلوم را به طرف دیگر میبریم:
$$
x ge -۱۰ + ۳
$$
$$
x ge -۷
$$
در نتیجه، $$ x $$ بزرگتر مساوی $$ – ۷ $$ است.
در بخش بعدی این مطلب از مجله فرادرس، فرمول های ریاضی نهم در مبحث خط و معادلههای خطی را معرفی میکنیم.
۶. خط و معادله های خطی: فرمول های فصل ششم ریاضی نهم
فصل ششم کتاب ریاضی نهم، مبحث خط و معادلههای خطی را در سه درس با عنوانهای «معادله خط»، «شیب خط و عرض از مبدا» و «دستگاه معادلههای خطی» ارائه میکند.
مهمترین فرمول های این بخش از ریاضی هشتم در جدول زیر آورده شدهاند.
| عنوان | فرمول |
| معادله خط | $$ y = a x + b $$ |
| معادله خط گذرنده از مبدا مختصات | $$ y = a x $$ |
| شیب خط گذرنده از دو نقطه | $$ a = frac { y _ ۲ – y _ ۱ } { x _ ۲ – x _ ۱ } $$ |
درس اول: معادله خط
از اتصال دو نقطه به یکدیگر، یک خط به وجود میآید. در ریاضیات، خط را میتوان به صورت یک معادله بیان کرد. معادله خط، معمولا به صورت زیر نوشته میشود:
$$ y = a x + b $$
هر معادلهای که فرم کلی آن، مانند معادله بالا باشد، یک خط را نمایش میدهد. در ادامه، کاربرد معادله خط را با حل یک مثال آموزش میدهیم.
$$ y = – ۲ x + ۳ $$، معادله یک خط راست است. آیا نقطه $$ ( ۱ , ۱ ) $$ بر روی این خط قرار دارد؟
برای بررسی قرار داشتن یک نقطه بر روی یک خط، مختصات آن نقطه را درون معادله خط قرار میدهیم. در اینجا، داریم:
$$ y = – ۲ x + ۳ $$
$$ x = ۱ $$
$$ y = ۱ $$
$$ ۱ = – ۲ ( ۱ ) + ۳ $$
$$ ۱ = – ۲ + ۳ $$
$$ ۱ = ۱ checkmark $$
در نتیجه، نقطه $$ ( ۱ , ۱ ) $$، بر روی خط $$ y = – ۲ x + ۳ $$ قرار دارد.
درس دوم: شیب خط و عرض از مبدا
در معادله خط $$ y = a x + b $$، داریم:
- $$ a $$: شیب یا گرادیان خط
- $$ b $$: عرض از مبدا (محل برخورد خط با محور عرضها یا همان محور عمودی)
با تغییر $$ a $$، زاویه خط با جهت مثبت محور طولها (محور افقی یا محور $$ x $$) تغییر میکند. اگر خطی از مبدا مختصات عبور کند، $$ b = ۰ $$ میشود. برای این شرایط، معادله خط عبارت است از:
$$ y = a x $$
معادله خط راست گذرنده از نقاط $$ ( ۱ , ۳ ) $$ و $$ ( – ۲ , ۴ ) $$ را بنویسید. عرض از مبدا را برابر با $$ frac { ۱۰ } { ۳ } $$ در نظر بگیرید.
برای جواب دادن به این سوال، ابتدا فرم کلی معادله خط راست را مینویسیم:
$$ y = a x + b $$
با توجه به اطلاعات مسئله (مختصات دو نقطه)، میتوانیم شیب خط ($$ a $$) را به دست بیاوریم. به این منظور، از رابطه زیر استفاده میکنیم:
$$ a = frac { y _ ۲ – y _ ۱ } { x _ ۲ – x _ ۱ } $$
در این رابطه داریم:
$$ y _ ۲ = ۴ $$
$$ y _ ۱ = ۳ $$
$$ x _ ۲ = – ۲ $$
$$ x _ ۱ = ۱ $$
این مقادیر را درون رابطه شیب خط راست قرار میدهیم:
$$ a = frac { ۴ – ۳ } { – ۲ – ۱ } $$
$$ a = – frac { ۱ } { ۳ } $$
به این ترتیب، معادله خط به شکل زیر تغییر میکند:
$$ y = – frac { ۱ } { ۳ } + b $$
بر اساس اطلاعات مسئله، میدانیم که عرض از مبدا یا همان $$ b $$ برابر با $$ frac { ۱۰ } { ۳ } $$ است. در نتیجه، معادله خط مورد نظر، عبارت است از:
$$ y = – frac { ۱ } { ۳ } + frac { ۱۰ } { ۳ } $$
درس سوم: دستگاه معادله های خطی
دستگاه معادله خطی، مجموعهای از معادلات حاوی یک یا چند متغیر مجهول است. به عنوان مثال، مجموعه معادلات زیر، به عنوان یک دستگاه معادلات خطی در نظر گرفته میشود:
$$
begin{cases}
x- y = ۳\
۲ x + ۲ y = ۶
end{cases}
$$
دستگاههای معادله خطی، با به دست آوردن مقادیر متغیرهای مجهول (در اینجا $$ x $$ و $$ y $$) انجام میگیرد. روشهای متعددی برای این کار وجود دارد. یکی از روشهای رایج و ساده حل دستگاه معادلههای خطی، روش حذفی است. این روش به صورت زیر اجرا میشود:
- انتخاب یکی از متغیرها برای حذف
- یکسان کردن ضریب متغیر انتخابی در هر دو معادله
- قرینه کردن ضریب متغیر انتخابی در یکی از معادلهها
- جمع دو معادله
- حل معادله به دست آمده از مجموع دو معادله
سعی کنید جواب سوال زیر را با استفاده از مراحل بالا به دست بیاورید.
مقادیر متغیرهای دستگاه معادله خطی $$ begin{cases} ۲x – ۵ y = ۲۱\ x + y = ۳
end{cases} $$ چه هستند؟
روشهای مختلفی برای حل دستگاه معادله خطی وجود دارند. در اینجا از روش حذفی برای حل دستگاه استفاده میکنیم. اولین مرحله در این روش، انتخاب یکی از متغیرها برای حذف است. با توجه به ضرایب متغیرها در معادلات، شاید بهتر باشد متغیر $$ x $$ را حذف کنیم. به این منظور، معادله دوم را در عدد $$ ۲ $$ ضرب میکنیم تا ضریب $$ x $$ در هر دو معادله، یکسان شود:
$$
begin{cases} ۲x + ۵ y = ۲۱\ ۲times (x + y = ۳)
end{cases} to begin{cases} ۲x + ۵ y = ۲۱\ ۲ x + ۲ y = ۶
end{cases}
$$
در مرحله بعدی، یکی از معادلهها را در عدد $$ – ۱ $$ ضرب میکنیم تا ضرایب $$ x $$ در معادلهها، قرینه یکدیگر شوند:
$$
begin{cases} ۲x + ۵ y = ۲۱\ – ۱ times ( ۲ x + ۲ y = ۶ )
end{cases} to begin{cases} ۲x + ۵ y = ۲۱\ – ۲ x – ۲ y = – ۶
end{cases}
$$
اکنون، دو معادله را با هم جمع میکنیم. توجه داشته باشید که جملات سمت راست با هم و جملات سمت چپ نیز با هم جمع شوند:
$$
begin{cases} ۲x + ۵ y = ۲۱\ – ۲ x – ۲ y = – ۶
end{cases} to ( ۲ x + ۵ y ) + ( – ۲ x – ۲ y ) = ۲۱ – ۶
$$
به این ترتیب، خواهیم داشت:
$$
۲ x + ۵ y- ۲ x – ۲ y = ۲۱ – ۶
$$
$$
۵ y- ۲ y = ۱۵
$$
$$
۳ y = ۱۵
$$
$$ y = frac { ۱۵ } { ۳ } $$
$$ y = ۵ $$
اکنون، مقدار یکی از متغیرها را به دست آوریم. برای به دست آوردن مقدار متغیر دیگر، مقدار معلوم را درون یکی از معادلههای دستگاه قرار میدهیم:
$$ x + y = ۳ $$
$$ y = ۵ $$
$$ x + ۵ = ۳ $$
$$ x = ۳ – ۵ $$
$$ x = – ۲ $$
شما میتوانید این مسئله را با حذف متغیر $$ y $$ نیز انجام دهید.
روش حذفی را میتوان به صورت زیر نیز اجرا کرد:
- نوشتن یکی از معادلهها بر حسب $$ x $$ یا $$ y $$
- قرار دادن جملههای معادل با $$ x $$ یا $$ y $$ در معادله دیگر (حذف یکی از متغیرها)
- حل معادله دوم بر حسب متغیر موجود و به دست آوردن مقدار آن
- جایگذاری مقدار به دست آمده برای یکی از متغیرهای مجهول در یکی از معادلهها برای تعیین مقدار متغیر دوم
این روش با عنوان روش جایگزینی نیز شناخته میشود. در بخش بعدی این مطلب از مجله فرادرس، به معرفی بهترین منابع برای یادگیری اصولی فرمول های ریاضی نهم میپردازیم.
مسیر یادگیری فرمول های ریاضی نهم از پایه
یادگیری فرمول های ریاضی نهم و دیگر پایهها، بسیار آسان و لذتبخش است؛ اگر به صورت اصولی انجام شود. بهترین روش یادگیری اصولی، تقویت دانش پایه با مطالعه کتابهای دورههای گذشته و حل مثالهای متنوع است. فرمول های ریاضی نهم، تکمیلکننده فرمول های ریاضی هفتم و هشتم هستند. بنابراین، اگر میخواهید در مسیر درست قدم بردارید، بهتر است یادگیری ریاضی دوره متوسطه اول را از ریاضی هفتم شروع کنید. پس از آن، به سراغ ریاضی هشتم و نهم بروید. فرادرس، فیلمهای آموزشی جامع و مفیدی را در زمینه ریاضی نهم و دیگر دورههای متوسطه اول تهیه کرده است. شما میتوانید این فیلمها را در لینکهای زیر مشاهده کنید:
پس از تسلط بر روی ریاضیات هفتم، هشتم و نهم، میتوانید به سراغ ریاضیات دوره متوسطه دوم بروید و با پایه قوی، به راحتی آنها را فرا بگیرید. در صورت علاقه به یادگیری این درسها، فیلمهای موجود در لینک زیر را مشاهده کنید:
در بخش بعدی این مطلب از مجله فرادرس، فرمول های ریاضی نهم در مبحث عبارتهای گویا را معرفی میکنیم.
۷. عبارت های گویا: فرمول های فصل هفتم ریاضی نهم
فصل هفتم کتاب ریاضی نهم، به مبحث عبارتهای گویا اختصاص دارد. این فصل، به «معرفی و ساده کردن عبارتهای گویا»، «محاسبات عبارتهای گویا» و «تقسیم چندجملهایها» میپردازد.
فرمول های فصل هفتم ریاضی هشتم، در جدول زیر آورده شدهاند.
| عنوان | فرمول |
| ضرب عبارتهای گویا | $$ frac { a } { b } times frac { c } {d } = frac { a c } { b d } $$ |
| تقسیم عبارتهای گویا | $$ frac { a } { b } div frac { c } {d } = frac { a } { b } times frac { d } { c } = frac { a d } { b c } $$ |
| تقسیم چندجملهای بر تکجملهای | $$ frac { a + b + c } { d } = frac { a } { d } + frac { b } { d } + frac { c } { d } $$ |
همانطور که مشاهده میکنید، تعداد فرمول های ریاضی نهم در فصل هفتم این کتاب، زیاد نیست. البته، مفاهیم و نکات مهمی در این فصل وجود دارند که در ادامه به مرور آنها میپردازیم.
درس اول: معرفی و ساده کردن عبارت های گویا
به کسری که صورت و مخرج آن از چندجملهایها تشکیل شده باشد، یک عبارت گویا میگویند. به عنوان مثال، عبارت کسری زیر، فرمول تندی متوسط را نمایش میدهد:
$$ v _ { a v } = frac { Delta x } { Delta t } = frac { x _ ۲ – x _ ۱ } { t _ ۲ – t _ ۱ } $$
این فرمول فیزیک، نمونهای از یک عبارت گویا است. عبارتهای گویا در دنیای ریاضی نیز حضور دارند. به عنوان مثال، رابطه میانگین حسابی دو عدد، به صورت زیر نوشته میشود:
$$ frac { a + b } { ۲ } $$
توجه داشته باشید که عبارتهای رادیکالی و قدر مطلق، عبارتهای گویا نیستند. یک نکته مهم در مبحث عبارتهای گویا، مقدار مخرج آنها است. مخرج عبارتهای گویا نمیتواند صفر باشد. بنابراین، مقادیری که مخرج کسر را صفر میکنند، نباید به عنوان ورودی عبارتهای گویا در نظر گرفته شوند.
عبارت $$ frac { ۳ – x }{ x ^ ۲ – ۵ x + ۶} $$ را به سادهترین شکل ممکن بنویسید. به ازای کدام مقادیر $$ x $$، این عبارت، تعریف نشده است؟
برای سادهسازی عبارت $$ frac { ۳ – x }{ x ^ ۲ – ۵ x + ۶} $$، ابتدا صورت و مخرج را به دقت بررسی میکنیم تا ببینیم آیا امکان تجزیه آنها توسط اتحادها وجود دارد. مخرج این عبارت برابر است با:
$$ x ^ ۲ – ۵ x + ۶ $$
برای تجزیه چندجملهای بالا، میتوانیم از اتحاد جمله مشترک کمک بگیریم. این اتحاد به صورت زیر نوشته میشود:
$$ ( x + a ) ( x + b ) = x ^ ۲ + ( a + b ) x + a b $$
بر اساس این اتحاد، باید $$ a $$ و $$ b $$ را پیدا کنیم؛ به طوری که مجموع $$ a $$ و $$ b $$ برابر با $$ – ۵ $$ و حاصلضرب آنها برابر با $$ ۶ $$ شود. با انجام آزمون و خطا، به دو مقدار زیر میرسیم:
$$ a = – ۲ $$
$$ b = – ۳ $$
به این ترتیب، داریم:
$$ x ^ ۲ – ۵ x + ۶ = ( x – ۲ ) ( x – ۳ )$$
این عبارت را درون عبارت کسری اولیه قرار میدهیم:
$$
frac { ۳ – x }{ x ^ ۲ – ۵ x + ۶} = frac { ۳ – x }{( x – ۲ ) ( x – ۳ )}
$$
صورت کسر ($$ ۳ – x $$)، قرینه یکی از جملههای مخرج کسر ($$ x – ۳ $$) است. بنابراین، میتوانیم آنها را با یکدیگر ساده کنیم و به جایشان عدد $$ – ۱ $$ را بنویسیم. به این ترتیب، خواهیم داشت:
$$
frac { ۳ – x }{ x ^ ۲ – ۵ x + ۶} = frac { – ۱ }{( x – ۲ )}
$$
$$
frac { ۳ – x }{ x ^ ۲ – ۵ x + ۶} = – frac { ۱ }{( x – ۲ )}
$$
برای تعیین مقادیر تعریف نشده عبارت $$ frac { ۳ – x }{ x ^ ۲ – ۵ x + ۶} $$، باید مقادیری را به دست بیاوریم که مخرج کسر را صفر میکنند (ریشههای مخرج). با توجه به عبارت بازنویسی شده $$ frac { ۳ – x }{ x ^ ۲ – ۵ x + ۶} = frac { ۳ – x }{( x – ۲ ) ( x – ۳ )} $$، این مقادیر عبارت هستند از:
$$ x = ۳ $$
$$ x = ۲ $$
البته پس از سادهسازی $$ frac { ۳ – x }{ x ^ ۲ – ۵ x + ۶} $$، به عبارت $$ – frac { ۱ }{( x – ۲ )} $$ میرسیم. در این عبارت، فقط $$ x = ۲ $$ باعث غیرقابل تعریف شدن کسر میشود. دلیل این موضوع، وجود ابهام $$ frac { ۰ } { ۰ } $$ در عبارت ساده نشده با $$x = ۳ $$ است.

درس دوم: محاسبات عبارت های گویا
انجام عملیاتهای ریاضی بر روی عبارتهای گویا، مشابه انجام عملیاتهای ریاضی بر روی عبارتهای کسری است. ضرب و تقسیم عبارتهای گویا به صورت زیر انجام میشود:
$$ frac { a } { b } times frac { c } {d } = frac { a c } { b d } $$
$$ frac { a } { b } div frac { c } {d } = frac { a } { b } times frac { d } { c } = frac { a d } { b c } $$
نحوه استفاده از این فرمولها را با حل مثال توضیح میدهیم.
حاصل عبارت $$ frac { a ^ ۲ – ۱۶ } { a + ۴ } times frac { a + ۲ } { a ^ ۲ – ۸ a + ۱۶ } $$ چیست؟
پیش از انجام ضرب کسرها، سعی میکنیم صورت و مخرج آنها را تا حد امکان ساده کنیم. صورت کسر اول، ما را به یاد اتحاد مزدوج میاندازد که به صورت زیر نوشته میشود:
$$ ( a + b ) ( a – b ) = a ^ ۲ – b ^ ۲ $$
بر اساس این اتحاد داریم:
$$ a ^ ۲ – ۱۶ = ( a – ۴ ) ( a + ۴ ) $$
به این ترتیب، میتوانیم کسر اول را به صورت زیر ساده کنیم:
$$
frac { a ^ ۲ – ۱۶ } { a + ۴ } = frac { ( a – ۴ ) ( a + ۴ ) }{ a + ۴ } = a – ۴
$$
مخرج کسر دوم، به اتحاد جمله مربع تفاضل دوجملهای یا اتحاد جمله مشترک شباهت دارد. بر اساس این اتحادها، مخرج مذکور به صورت زیر بازنویسی میشود:
$$
a ^ ۲ – ۸ a + ۱۶ = ( a – ۴ ) ^ ۲
$$
بنابراین، خواهیم داشت:
$$
frac { a + ۲ } { a ^ ۲ – ۸ a + ۱۶ } = frac { a + ۲ } { ( a – ۴ ) ^ ۲ }
$$
اکنون، فرم ساده شده کسرها را در هم ضرب میکنیم:
$$
frac { a ^ ۲ – ۱۶ } { a + ۴ } times frac { a + ۲ } { a ^ ۲ – ۸ a + ۱۶ } = ( a – ۴ ) times frac { a + ۲ } { ( a – ۴ ) ^ ۲ }
$$
$$
( a – ۴ ) times frac { a + ۲ } { ( a – ۴ ) ^ ۲ } = frac { a – ۴ } { ۱ } times frac { a + ۲ } { ( a – ۴ ) ^ ۲ }
$$
$$
( a – ۴ ) times frac { a + ۲ } { ( a – ۴ ) ^ ۲ } = frac { ( a – ۴ ) times ( a + ۲ ) } { ۱ times ( a – ۴ ) ^ ۲ }
$$
$$
( a – ۴ ) times frac { a + ۲ } { ( a – ۴ ) ^ ۲ } = frac { a + ۲ } { a – ۴ }
$$
$$
frac { a ^ ۲ – ۱۶ } { a + ۴ } times frac { a + ۲ } { a ^ ۲ – ۸ a + ۱۶ } = frac { a + ۲ } { a – ۴ }
$$
درس سوم: تقسیم چندجمله ای ها
در تقسیم چندجملهایها، یکی از سهحالتهای زیر به وجود میآید:
- تقسیم تکجملهای بر تکجملهای
- تقسیم چندجملهای بر تکجملهای
- تقسیم چندجملهای بر چندجملهای
برای انجام تقسیم تکجملهای بر تکجملهای، از قوانین ساده کردن کسرها و ساده کردن توانها استفاده میکنیم.
حاصل تقسیم $$ frac { – ۲ x ^ ۲ y ^ ۳ z ^ ۷ } { ۱۸ x z ^ ۵ } $$ را تعیین کنید.
عبارت کسری $$ frac { – ۲ x ^ ۲ y ^ ۳ z ^ ۷ } { ۱۸ x z ^ ۵ } $$، تقسیم تکجملهای بر تکجملهای را نمایش میدهد. برای به دست آوردن حاصل این عبارت، جملههای مشابه صورت و مخرج را با هم ساده میکنیم. عدد $$ ۲ $$ با عدد $$ ۱۸ $$ ساده میشود و عدد $$ ۹ $$ در مخرج باقی میماند:
$$
frac { – ۲ x ^ ۲ y ^ ۳ z ^ ۷ } { ۱۸ x z ^ ۵ } = frac { – x ^ ۲ y ^ ۳ z ^ ۷ } { ۹ x z ^ ۵ }
$$
$$ x ^ ۲ $$ در صورت با $$ x $$ در مخرج ساده میشود و $$ x $$ در صورت باقی میماند:
$$
frac { – ۲ x ^ ۲ y ^ ۳ z ^ ۷ } { ۱۸ x z ^ ۵ } = frac { – x y ^ ۳ z ^ ۷ } { ۹ z ^ ۵ }
$$
متغیر $$ y $$، فقط در صورت حضور دارد. بنابراین نمیتوان آن را ساده کرد. $$ z ^ ۷ $$ در صورت با $$ z ^ ۵ $$ در مخرج ساده میشود و $$ z ^ ۲ $$ در صورت باقی میماند:
$$
frac { – ۲ x ^ ۲ y ^ ۳ z ^ ۷ } { ۱۸ x z ^ ۵ } = frac { – x y ^ ۳ z ^ ۲ } { ۹ }
$$
به این ترتیب توانستیم حاصل تقسیم یک تکجملهای بر تکجملهای را به دست بیاوریم.
تقسیم چندجملهای بر تکجملهای، فرمول مخصوص خود را دارد که به صورت زیر نوشته میشود:
$$ frac { a + b + c } { d } = frac { a } { d } + frac { b } { d } + frac { c } { d } $$
حاصل عبارت کسری $$ frac { ۲ a ^ ۳ y – a ^ ۴ y ^ ۲ + ۱۵ x y } { – ۵ y ^ ۲} $$ چه میشود؟
برای تقسیم چندجملهای بر تکجملهای، میتوانیم جملههای صورت کسر را به صورت جداگانه بر مخرج تقسیم کنیم و حاصل تقسیمها را با یکدیگر جمع کنیم. به این ترتیب، داریم:
$$
frac { ۲ a ^ ۳ y – a ^ ۴ y ^ ۲ + ۱۵ x y } { – ۵ y ^ ۲} = frac {۲ a ^ ۳ y}{ – ۵ y ^ ۲} + frac { a ^ ۴ y ^ ۲}{ – ۵ y ^ ۲} + frac { ۱۵ x y }{ – ۵ y ^ ۲}
$$
با این کار، چند تقسیم تکجملهای بر تکجملهای به وجود میآید. حاصل این تقسیمها عبارت است از:
$$
frac {۲ a ^ ۳ y}{ – ۵ y ^ ۲} = frac { ۲ a ^ ۳}{ – ۵ y } = – frac { ۲ a ^ ۳}{ ۵ y }
$$
$$
frac { a ^ ۴ y ^ ۲}{ – ۵ y ^ ۲} = frac {- a ^ ۴}{ – ۵ } = frac { a ^ ۴}{ ۵ }
$$
$$
frac { ۱۵ x y }{ – ۵ y ^ ۲} = frac { ۳ x } { – ۵ y } = – frac { ۳ x } { ۵ y }
$$
اکنون، این تقسیمها را با هم جمع میکنیم:
$$
frac { ۲ a ^ ۳ y – a ^ ۴ y ^ ۲ + ۱۵ x y } { – ۵ y ^ ۲} = – frac { ۲ a ^ ۳}{ ۵ y } + frac { a ^ ۴}{ ۵ } – frac { ۳ x } { ۵ y }
$$
اگر از این کسرها مخرج مشترک بگیریم، به عبارت زیر میرسیم:
$$
frac { ۲ a ^ ۳ y – a ^ ۴ y ^ ۲ + ۱۵ x y } { – ۵ y ^ ۲} = frac { – ۲ a ^ ۳ + a ^ ۴ y + ۱۵ x} {۵ y}
$$
توجه داشته باشید که اگر در همان ابتدای حل، از $$ y $$ (مشترک در همه جملهها)، فاکتور میگرفتیم و آن را با مخرج کسر ساده میکردیم، دوباره به عبارت بالا میرسیدیم.
روند تقسیم چندجملهای بر چندجملهای، کمی پیچیدهتر از دو حالت دیگر از تقسیم عبارتهای گویا است. انجام این تقسیم، بر اساس اصول و مراحل زیر صورت میگیرد:
- مرتبسازی جملههای مقسوم و مقسومعلیه بر اساس توان متغیر از بزرگ به کوچک
- تقسیم اولین جمله مقسوم بر اولین جمله مقسومعلیه (تقسیم تکجملهای بر تکجملهای)
- ضرب جمله به دست آمده از مرحله قبل بر مقسومعلیه
- کم کردن عبارت به دست آمده از مرحله قبل از مقسوم
- تکرار مراحل بالا برای باقیمانده و مقسومٰعلیه
- تکرار مراحل بالا تا رسیدن به باقیمانده صفر
وقتی باقیمانده صفر شود، مقسوم بر مقسومعلیه بخشپذیر است.
حاصل تقسیم $$ ۶ x ^ ۲ + ۷ x – ۲۰ $$ بر $$ ۲ x + ۵ $$ چه میشود؟
برای تقسیم یک چندجملهای بر چندجملهای دیگر، ابتدا جملههای مقسوم و مقسومعلیه را بر اساس توان، از بزرگ به کوچک مرتب میکنیم. در عبارتهای $$ ۱۶ x ^ ۲ + ۷ x – ۲۰ $$ و $$ ۲ x + ۵ $$، نیازی به این کار نیست. زیرا جملههای این عبارتها، به همان شکلی هستند که میخواهیم. در مرحله بعد، اولین جمله مقسوم ($$ ۶ x ۲ $$) را بر اولین جمله مقسومعلیه ($$ ۲ x $$) تقسیم میکنیم:
$$ frac { ۶ x ^ ۲ } { ۲ x } = ۳ x $$
$$ ۳ x $$، اولین جمله خارج قسمت تقسیم است:
$$
( ۶ x ^ ۲ + ۷ x – ۲۰ ) div ( ۲ x + ۵ ) = ۳ x + …
$$
سپس، حاصل این تقسیم ($$ ۳ x $$) را در مقسومعلیه ($$ ۲ x + ۵ $$) ضرب میکنیم:
$$ ۳ x ( ۲ x + ۵ ) = ۶ x ^ ۲ + ۱۵ x $$
در ادامه، عبارت بالا را از مقسوم کم میکنیم:
$$
( ۶ x ^ ۲ + ۷ x – ۲۰ ) – ( ۶ x ^ ۲ + ۱۵ x ) = – ۸ x – ۲۰
$$
اکنون، بار دیگر، اولین عبارت بالا ($$ – ۸ x $$) را بر اولین جمله مقسومعلیه ($$ ۲ x $$) تقسیم میکنیم:
$$
frac { – ۸ x } { ۲ x } = – ۴
$$
به این ترتیب، جمله بعدی خارج قسمت تقسیم نیز به دست میآید:
$$
( ۶ x ^ ۲ + ۷ x – ۲۰ ) div ( ۲ x + ۵ ) = ۳ x – ۴
$$
برای اطمینان از صحت نتیجه تقسیم و عدم وجود باقیمانده، $$ ۲ x + ۵ $$ را در $$ ۳ x – ۴ $$ ضرب کنید.
در بخش بعدی این مطلب از مجله فرادرس، فرمول های ریاضی نهم در مبحث حجم و مساحت را معرفی میکنیم.

۸. حجم و مساحت: فرمول های فصل هشتم ریاضی نهم
فصل آخر کتاب ریاضی نهم، به مبحث حجم و مساحت میپردازد. در این فصل، سه درس با عنوانهای «حجم و مساحت کره»، «حجم هرم و مخروط» و «سطح و حجم» آموزش داده میشود.
مهمترین فرمول های فصل هشتم ریاضی نهم، در جدول زیر آورده شدهاند.
| عنوان | فرمول |
| حجم کره | $$ V = frac { ۴ } { ۳ } pi R ^ ۲ $$ |
| مساحت کره | $$ S = ۴ pi R ^ ۲ $$ |
| حجم استوانه | $$ V = pi r ^ ۲ h $$ |
| مساحت استوانه | $$ S = ۲ pi r h + ۲ pi r ^ ۲ $$ |
| حجم هرم | $$ V = frac { ۱ } { ۳ } S h $$ |
| حجم مخروط | $$ V = frac { ۱ } { ۳ } pi r ^ ۲ h $$ |
در ادامه، مهمترین نکات و فرمول های موجود در درسهای فصل هشتم ریاضی نهم را به همراه حل مثال، مرور میکنیم.
درس اول: حجم و مساحت
کره مجموعه نقاطی از فضا است که فاصله آنها از یک نقطه ثابت (مرکز کره) به یک اندازه است. به این اندازه، شعاع کره میگویند و آن را معمولا با حرف $$ R $$ یا $$ r $$ نمایش میدهند.

حجم کره از رابطه زیر به دست میآید:
$$ V = frac { ۴ } { ۳ } pi R ^ ۲ $$
- $$ V $$: حجم کره
- $$ pi $$: عدد پی، تقریبا برابر با $$ ۳/۱۴ $$
- $$ R $$: شعاع کره
فرمول جبری مساحت کره نیز به صورت زیر نوشته میشود:
$$ S = ۴ pi R ^ ۲ $$
- $$ S $$: مساحت رویه کره
- $$ pi $$: عدد پی، تقریبا برابر با $$ ۳/۱۴ $$
- $$ R $$: شعاع کره
در سوالات مربوط به حجم و مساحت کره، امکان ادغام سوال با مسائل مربوط به حجم و مساحت استوانه نیز وجود دارد. فرمولهای حجم و مساحت استوانه عبارت هستند از:
$$ V = pi r ^ ۲ h $$
- $$ V $$: حجم استوانه
- $$ pi $$: عدد پی، تقریبا برابر با $$ ۳/۱۴ $$
- $$ r $$: شعاع مقطع دایرهای استوانه
- $$ h $$: ارتفاع استوانه (فاصله عمودی بین مقاطع بالایی و پایینی)
$$ S = ۲ pi r h + ۲ pi r ^ ۲ $$
- $$ S $$: مساحت رویه استوانه (مجموع مساحتهای مقاطع بالایی و پایینی و سطح جانبی دور استوانه)
- $$ pi $$: عدد پی، تقریبا برابر با $$ ۳/۱۴ $$
- $$ r $$: شعاع مقطع دایرهای استوانه
- $$ h $$: ارتفاع استوانه
شعاع قاعده استوانهای به حجم $$ ۴۴۰ $$ سانتیمتر مکعب و ارتفاع $$ ۳۵ $$ سانتیمتر را به دست بیاورید. عدد پی را برابر با $$ frac { ۲۲ } { ۷ } $$ در نظر بگیرید.
برای پاسخگویی به این سوال، فرمول حجم استوانه را مینویسیم:
$$ V = pi r ^ ۲ h $$
- $$ V $$: حجم استوانه $$ ۴۴۰ $$ سانتیمتر مکعب
- $$ pi $$: عدد پی برابر با $$ frac { ۲۲ } { ۷ } $$
- $$ r $$: شعاع قاعده دایرهای استوانه
- $$ h $$: ارتفاع استوانه برابر با $$ ۳۵ $$ سانتیمتر
در این رابطه، فقط شعاع مقطع استوانه را نداریم. به منظور محاسبه این کمیت، مقادیر معلوم را درون رابطه قرار میدهیم:
$$ ۴۴۰ cm ^ ۳ = frac { ۲۲ } { ۷ } times r ^ ۲ times ۳۵ cm $$
$$
frac { ۴۴۰ cm ^ ۳ times ۷ } { ۲۲ times ۳۵ cm } = r ^ ۲
$$
$$
r ^ ۲ = frac { ۳۰۸۰ cm ^ ۳ } { ۷۷۰ cm }
$$
$$
r ^ ۲ = ۴ cm ^ ۲
$$
$$ r = ۲ cm $$
شعاع قاعده استوانه برابر با $$ ۲ $$ سانتیمتر است.
درس دوم: حجم هرم و مخروط
هرم، یک شکل فضایی با یک وجه زیرین به شکل چندضلعی است که بر روی ضلعهای آن، چندین سطح قرار دارند. این سطحها یا وجههای جانبی، یکدیگر را در نقطهای مشترک قطع میکنند. به وجه زیرین هرم، قاعده و نقطه اتصال وجههای جانبی آن، راس میگویند. فاصله راس تا قاعده هرم نیز با عنوان ارتفاع هرم شناخته میشود. این اجزا، در محاسبه حجم و مساحت هرم مورد استفاده قرار میگیرند.
[تصویر-نمونه]
حجم هرم از رابطه زیر به دست میآید:
$$ V = frac { ۱ } { ۳ } S h $$
- $$ V $$: حجم هرم
- $$ S $$: مساحت قاعده هرم
- $$ h $$: ارتفاع هرم
از مهمترین نکات و ویژگیهای مرتبط با هرمها میتوان به موارد زیر اشاره کرد:
- به هرم دارای قاعده چندضلعی منتظم و وجههای جانبی همنهشت، هرم منتظم میگویند.
- اگر دو هرم دارای قاعدههای هممساحت و ارتفاعهای مساوی باشند، حجم آنها با هم برابر خواهد بود.
مخروط، یک شکل فضایی مشابه هرم منتظم اما با قاعده دایرهای شکل است. در این شکل، ارتفاع به مرکز دایره وارد میشود. فرمول حجم مخروط، به صورت زیر نوشته میشود:
$$ V = frac { ۱ } { ۳ } pi r ^ ۲ h $$
- $$ V $$: حجم مخروط
- $$ pi $$: عدد پی، تقریبا برابر با $$ ۳/۱۴ $$
- $$ r $$: شعاع قاعده دایرهای مخروط
- $$ h $$: ارتفاع مخروط
حجم هرمی با قاعده مستطیلی به ابعاد $$ ۷ $$ و $$ ۶ $$ و ارتفاع $$ ۹ $$ را به دست بیاورید.
حجم هرم با یکسوم مساحت قاعده در ارتفاع آن برابری میکند. فرمول این حجم به صورت زیر نوشته میشود:
$$ V = frac { ۱ } { ۳ } S h $$
- $$ V $$: حجم هرم
- $$ S $$: مساحت قاعده هرم برابر با مساحت مستطیل
- $$ h $$: ارتفاع هرم برابر با $$ ۹ $$ سانتیمتر
قاعده هرم، یک مستطیل به ابعاد $$ ۷ $$ و $$ ۶ $$ سانتیمتر است. بنابراین، مساحت قاعده هرم از رابطه مساحت مستطیل به دست میآید. این رابطه عبارت است از:
طول در عرض = مساحت مستطیل
$$ ۷ times ۶ = ۴۲ $$ = مساحت مستطیل
این مقدار را به همراه ارتفاع، در فرمول محاسبه حجم هرم قرار میدهیم:
$$ V = frac { ۱ } { ۳ } times ۴۲ times ۹ $$
$$ V = ۱۲۶ cm ^ ۳ $$
در نتیجه، حجم هرم برابر با $$ ۱۲۶ $$ سانتیمتر مکعب است.

درس سوم: سطح و حجم
درس آخر ریاضی نهم، به توضیح نحوه محاسبه سطح رویههای شکلهای سهبعدی میپردازد. در این درس، نحوه ایجاد شکلهای فضایی با دوران شکلهای مسطح نیز آموزش داده میشود. برخی از نکات مهم درس سوم از فصل هشتم ریاضی نهم عبارت هستند از:
- مساحت سطح رویه شکلهای فضایی، از مجموع مساحتهای وجههای آنها به دست میآید. به عنوان مثال، مساحت هرم، مجموع مساحتهای وجههای جانبی و مساحت قاعده است.
- از دوران یک مستطیل حول یکی از ضلعهایش، استوانه به وجود میآید.
- از دوران یک مثلث قائمالزاویه حول یکی از ساقهایش، مخروط به وجود میآید.
- از دوران یک نیمدایره حول قطرش، یک کره به وجود میآید.
- از دوران یک ربعدایره حول شعاع، یک نیمکره به وجود میآید.
- مقطع کره، دایرهای است.
- مقطع گذرنده از قطر مکعب مربع، یک مستطیل است.
استوانهای به شعاع قاعده و ارتفاع $$ a $$، کرهای به شعاع $$ a $$ و مکعب مربعی به ضلع $$ a $$ را در نظر بگیرید. حجم و سطح کل این شکلها را با هم مقایسه کنید. عدد پی را برابر با $$ ۳/۱۴ $$ در نظر بگیرید.
حل این سوال را با نوشتن فرمول حجم استوانه شروع میکنیم. این فرمول، عبارت است از:
$$ V _ { cylinder } = pi r ^ ۲ h $$
- $$ V _ { cylinder } $$: حجم استوانه
- $$ pi $$: عدد پی برابر با $$ ۳/۱۴ $$
- $$ r $$: شعاع قاعده استوانه برابر با $$ a $$
- $$ h $$: ارتفاع استوانه برابر با $$ a $$
$$ V _ { cylinder } = ۳/۱۴ times a ^ ۲ times a $$
$$ V _ { cylinder } = ۳/۱۴ a ^ ۳ $$
سطح کل استوانه، از جمع مساحت سطح جانبی (ضرب محیط قاعده در ارتفاع استوانه) و مساحتهای دو قاعده (مساحت دو دایره) به دست میآید. فرمول این سطح به صورت زیر نوشته میشود:
$$ A _ { cylinder } = ۲ pi r h + ۲ pi r ^ ۲ $$
- $$ A _ { cylinder } $$: سطح کل استوانه
- $$ pi $$: عدد پی برابر با $$ ۳/۱۴ $$
- $$ r $$: شعاع قاعده استوانه برابر با $$ a $$
- $$ h $$: ارتفاع استوانه برابر با $$ a $$
$$ A _ { cylinder } = ( ۲ times ۳/۱۴ times a times a ) + ( ۲ times ۳/۱۴ a ^ ۲ ) $$
$$ A _ { cylinder } = ۶/۲۸ a ^ ۲ + ۶/۲۸ a ^ ۲ = ۱۲/۵۶ a ^ ۲ $$
در مرحله بعد، فرمول حجم کره را مینویسیم:
$$ V _ { sphere } = frac { ۴ } { ۳ } pi r ^ ۳ $$
- $$ V _ { sphere} $$: حجم کره
- $$ pi $$: عدد پی برابر با $$ ۳/۱۴ $$
- $$ r $$: شعاع کره برابر با $$ a $$
$$ V _ { sphere } = frac { ۴ } { ۳ } times ۳/۱۴ times a ^ ۳ $$
$$ V _ { sphere } = ۴/۱۹ a ^ ۳ $$
سطح کل کره از فرمول زیر به دست میآید:
$$ A _ { sphere } = ۴ pi r ^ ۲ $$
- $$ A _ { sphere} $$: سطح کل ;vi
- $$ pi $$: عدد پی برابر با $$ ۳/۱۴ $$
- $$ r $$: شعاع کره برابر با $$ a $$
$$ A _ { sphere } = ۴ times ۳/۱۴ a ^ ۲ $$
$$ A _ { sphere } = ۱۲/۵۶ a ^ ۲ $$
در نهایت، به سراغ محاسبه حجم مکعب میرویم:
$$ V _ { cube } = a ^ ۳ $$
- $$ V _ { cube } $$: حجم مکعب
- $$ a $$: یک ضلع مکعب برابر با $$ a $$
$$ V _ { cube } = a ^ ۳ $$
سپس، سطح مکعب را محاسبه میکنیم:
$$ A _ { cube } = ۶ a ^ ۲ $$
- $$ A _ { cube } $$: سطح کل مکعب
- $$ a $$: یک ضلع مکعب برابر با $$ a $$
$$ A _ { cube } = ۶ a ^ ۲ $$
برای مقایسه حجم و سطح شکلها، نتایج به دست آمده را در کنار یکدیگر مینویسیم:
$$ V _ { cylinder } = ۳/۱۴ a ^ ۳ $$
$$ V _ { sphere } = ۴/۱۹ a ^ ۳ $$
$$ V _ { cube } = a ^ ۳ $$
همانطور که مشاهده میکنید، حجم کره از بقیه شکلهای مورد سوال بیشتر است. برای سطح کل داریم:
$$ A _ { cylinder } = ۱۲/۵۶ a ^ ۲ $$
$$ A _ { sphere } = ۱۲/۵۶ a ^ ۲ $$
$$ A _ { cube } = ۶ a ^ ۲ $$
بر اساس نتایج به دست آمده، سطح کل استوانه و کره برابر شدند. سطح کل استوانه و کره، بزرگتر از سطح کل مکعب شد.
source