در ریاضیات همواره نیازمند ابزارهایی هستیم که تا حد امکان، پیچیدگی‌ها را کم‌تر و مسائل را آسان‌تر کنند. یکی از این ابزارها، «اتحاد» (Identity) است. در آموزش‌های قبلی فرادرس مباحثی مانند اتحاد و تجزیه بیان شده‌اند و فرمول‌ انواع اتحاد نیز کاملا تشریح شده‌ است. در این مطلب از مجله فرادرس قصد داریم تمرکز خود را روی اولین و پرکاربردترین اتحاد، یعنی «اتحاد مربع کامل» (Perfect Square Identity) قرار دهیم. این اتحاد، همان اتحاد مربع دو‌جمله‌ای است. در این اتحاد مجموع یا تفاضل دو جمله به توان دوم می‌رسد و حاصل بر حسب سه جمله بیان می‌شود که جمله اول و سوم، مربع کامل هستند.

در ادامه این مطلب، ابتدا یاد می‌گیریم که فرمول اتحاد مربع کامل چیست. سپس خواهیم دید چگونه از این اتحاد در حل مسائل مختلف می‌توانیم استفاده کنیم. همچنین در انتها آزمونی جهت سنجش یادگیری این مبحث برای شما تهیه شده است که پس از حل درست سوالات آن، می‌توانید مطمئن باشید مفهوم اتحاد مربع کامل را به‌خوبی فرا گرفته‌‌اید.

اتحاد مربع کامل چیست؟

اتحاد مربع کامل اتحادی است که در آن توان دوم یا مربع مجموع یا تفاضل دو جمله با مجموع سه جمله برابر است، به گونه‌ای که جملات اول و سوم مربع کامل هستند. فرمول اتحاد مربع کامل برای هر a و b که جز «اعداد حقیقی» (Real Numbers) باشند، به‌صورت زیر است:

$$begin{cases}(a+b)^2=a^2+2ab+b^2 \ \ (a-b)^2=a^2-2ab+b^2 end{cases}$$

این اتحاد، به اتحاد اول و دوم یا اتحاد مربع مجموع دو‌جمله‌ای و اتحاد مربع تفاضل دوجمله‌ای نیز معروف است. برای مثال $$(x+3)^2=x^2+6x+9$$ نمونه‌ای از اتحاد مربع کامل یا اتحاد اول است.

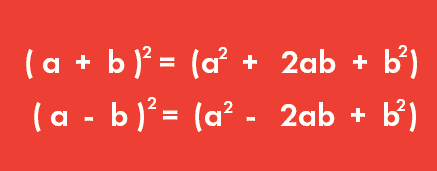
در واقع این اتحاد شامل دو فرمول است. در فرمول اتحاد اول، علامت بین دو جمله a و b، علامت جمع (+) است و در فرمول اتحاد دوم، علامت بین دو جمله a و b، علامت تفریق (-) است. پس اتحاد اول، مربع مجموع دو جمله را بیان ‌می‌کند و اتحاد دوم، مربع تفاضل دو جمله را به‌دست می‌دهد. همچنین می‌دانیم که منظور از مربع، همان توان دوم است.

مهم‌ترین کاربرد این اتحاد علاوه‌بر حل مسائل تجزیه، در فرآیندهای فاکتورگیری جهت حل معادلات ریاضی یا حل معادلات درجه دوم و پیدا کردن ریشه این نوع معادلات است. نام‌گذاری این اتحاد به‌صورت مربع کامل، به این علت است که جملات اول و سوم در سمت راست فرمول این اتحاد، جملاتی هستند که مربع کامل‌اند. این خاصیت باعث می‌شود تا از اتحاد مربع کامل در حل معادلات درجه دوم به روش مربع کامل کردن استفاده شود. در ادامه و در قالب مثال‌های مختلف، کاربرد این نوع اتحاد توضیح داده شده است.

تعمیم فرمول اتحاد مربع کامل

اگر جای طرفین تساوی در فرمو‌ل‌های اتحاد مربع کامل را عوض کنیم و جمله 2ab را به سمتی که مربع مجموع یا تفاضل قرار دارد ببریم، شکل دیگری از فرمول‌های اتحاد مربع کامل به‌صورت زیر به‌دست خواهد آمد:

$$begin{cases}a^2+b^2=(a+b)^2-2ab \ \ a^2+b^2=(a-b)^2+2ab end{cases}$$

اتحاد جبری چیست؟

اتحاد جبری یک گزاره ریاضی است که اگر به جای هر کدام از اجزای آن یک عدد حقیقی قرار دهید، به ازای تمام اعداد جای‌گذاری شده، تساوی جبری دو طرف همیشه برقرار و صادق است. در این تعریف می‌دانیم اعداد حقیقی به مجموعه همه اعداد گویا (اعداد کسری) و اعداد گنگ در مجموعه اعداد گفته می‌شود که با R نمایش داده می‌شوند. چنانچه دانش‌آموز مقطع تحصیلی نهم هستید و تمایل دارید با مباحث مربوط به «عبارت‌های جبری، اتحاد و تجزیه» به‌‌طور کامل آشنا شوید، می‌توانید فیلم آموزشی ریاضی پایه نهم را مشاهده کنید که لینک آن در ادامه قرار داده شده است.

برای مثال، برابری جبری بین دو طرف رابطه $$(x+5)^2=x^2+10x+25$$، یک اتحاد است. اتحادها علاوه‌بر اتحادهای جبری، شامل مجموعه گسترده‌تری مانند اتحادهای مثلثاتی، اتحادهای نمایی و اتحادهای لگاریتمی نیز می‌شوند. هدف از استفاده اتحادها، ساد‌ه‌سازی فرآیندهای جبری و محاسبات عددی در ریاضیات است.

تجزیه چیست؟

یکی دیگر از ابزارهایی که مانند اتحاد به منظور ساده کردن مسائل در ریاضیات استفاده می‌شود، تجزیه است. تجزیه معادل است با شکستن یک عبارت ریاضیاتی پیچیده به چند عبارت کوچکتر و ساده‌تر، به گونه‌ای که حاصل‌ضرب این عبارت‌ها با عبارت اصلی برابر شود. یکی از بهترین روش‌ها در تجزیه یک عبارت ریاضی، استفاده از اتحادها است.

توضیح فرمول اتحاد مربع کامل

شکل زیر یک اتحاد مربع کامل را نشان می‌دهد. در فرمول اتحاد مربع کامل، تمام اعداد ۲ چه به‌عنوان توان ۲ یا چه به‌عنوان عدد ۲ که در a و b یا x ضرب می‌شود، همیشه ثابت‌اند. اما به‌جای مقادیر a و b یا x می‌توانیم از هر عدد حقیقی استفاده کنیم. اگر به جای مقادیر a و b و x اعداد حقیقی را جایگزین کنیم، همیشه تساوی بین دو طرف علامت مساوی در فرمول، برقرار است.

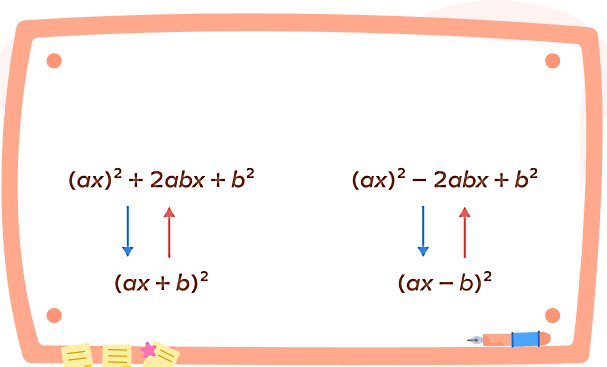
همچنین در این فرمول‌ها، فاصله بین هر علامت + یا – به‌عنوان یک جمله در نظر گرفته می‌شود. تعریف دقیق‌تر تک‌جمله‌ای یا یک‌جمله‌ای در ریاضیات برابر است با حاصل‌ضرب هر عدد حقیقی در توان‌های صحیح و نامنفی یک یا چند متغیر. بنابراین یک سمت فرمول اتحاد مربع کامل، شامل سه جمله و یک سمت آن شامل دو جمله است.

اگر بخواهیم دو طرف اتحاد اول را در شکل بالا تشریح کنیم، ابتدا دو جمله ax و b با هم جمع می‌شوند و سپس به توان دو می‌رسند یا مربع می‌شوند. در سمت دیگر این اتحاد، حاصل این فرآیند به‌صورت مجموع سه جمله بیان شده است. جمله اول، مربع جمله اول است. جمله دوم دو برابر حاصل‌ضرب جمله اول و دوم یعنی ax و b است. جمله سوم نیز، مربع جمله دوم است. در ادامه با عددگذاری، این اتحاد را بهتر می‌شناسید، اما پیش از آن بهتر است ابتدا مفهوم مربع کامل را توضیح دهیم.

برای مثال اتحاد مربع کامل $$(x+4)^2=x^2+8x+16$$ را در نظر بگیرید. اگر بخواهیم تساوی در این اتحاد را با شکل نشان دهیم، از شکل زیر می‌توانیم استفاده کنیم. در شکل مساحت مربع بزرگ برابر است با حاصل‌ضرب دو ضلع مربع با اندازه $$x+4$$ که می‌شود $$(x+4)^2$$.

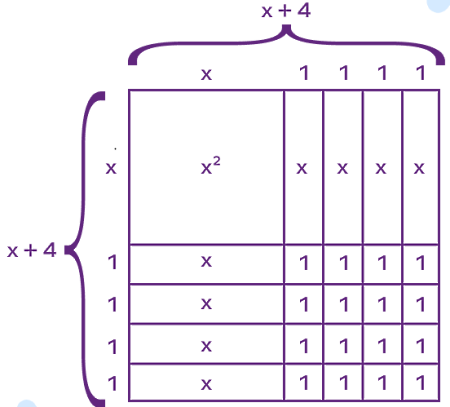
از طرفی اگر به داخل این مربع دقت کنیم، مشاهده می‌کنیم که این مساحت با مربعی به مساحت $$x^2$$، هشت مستطیل با مساحت x و ۱۶ مربع با مساحت ۱ پر شده است. پس در واقع مساحت مربع بزرگ با مجموع سه جمله $$x^2+8x+16$$ معادل است. به این ترتیب با شکل توانسیتم درستی اتحاد و مفهوم مربع کامل را بهتر توضیح دهیم.

عددگذاری در اتحاد مربع کامل

فرض کنید a=-۱ و b=۳ است. در این صورت برای سمت چپ اتحاد اول که در آن مجموع دو جمله a و b به توان ۲ می‌رسد، خواهیم داشت:

$$((-1)+3)^2=2^2=4$$

مقدار عددی سمت راست فرمول اتحاد اول نیز با عددگذاری می‌شود:

$$a^2+2ab+b^2=(-1)^2+2(-1)3+3^2=1+(-6)+9=9-5=4$$

پس دو طرف فرمول اتحاد اول بعد از عددگذاری با هم برابر شدند.

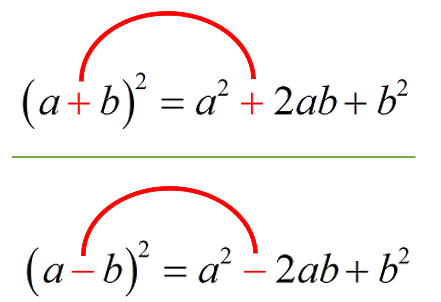
حالا فرض کنید a=-۱/۲ و b=۲ است. می‌خواهیم درستی اتحاد دوم را با این اعداد که شامل یک عدد گویا یا کسری هم هستند، امتحان کنیم. مقدار عددی سمت چپ اتحاد دوم، با قرار دادن این مقادیر خواهد شد:

$$(a-b)^2=((-1/2)-2)^2=(-3/2)^2=9/4$$

و با عددگذاری در سمت راست اتحاد دوم، خواهیم داشت:

$$a^2-2ab+b^2=(-1/2)^2-2(-1/2)2+2^2=1/4-2+4=2+1/4=9/4$$

بنابراین دو طرف این اتحاد نیز با قرار دادن هر دو عدد حقیقی به جای a و b مساوی به‌دست آمد. در مسائل ریاضیات، معمولا از اتحادها به شکل‌های مختلفی استفاده می‌شود. در ادامه با بررسی مثال‌های مختلف از این فرمول، به شما در به‌کارگیری سریع این فرمول کمک می‌کنیم.

مسیر یادگیری اتحاد با فرادرس

پیش از اینکه به ادامه مباحث بپردازیم، اگر دانش‌آموز پایه نهم یا دهم رشته انسانی هستید و تمایل دارید مباحث مرتبط با عبارت‌های جبری یا حل معادلات درجه دوم با استفاده از اتحادها را بهتر بیاموزید، پیشنهاد می‌کنیم از فیلم‌های آموزشی تهیه شده در فرادرس حتما استفاده کنید:

1. فیلم آموزش ریاضی پایه نهم فرادرس
2. فیلم آموزش ریاضی و آمار پایه دهم انسانی فرادرس
3. مجموعه فیلم آموزش دروس پایه نهم فرادرس
4. مجموعه فیلم آموزش دروس پایه دهم فرادرس

اثبات اتحاد مربع کامل

برای اثبات اتحاد مربع کامل، ابتدا اتحاد نوع اول را در نظر می‌گیریم. با شروع از سمت چپ و باز کردن این عبارت، داریم:

$$(a+b)^2=(a+b)(a+b)=a(a+b)+b(a+b)$$

$$Rightarrow (a+b)^2=a^2+ab+ba+b^2$$

در این قسمت توجه داریم که در مورد عبارت جبری ab، همواره رابطه ab=ba برقرار است. پس خواهیم داشت:

$$Rightarrow (a+b)^2=a^2+2ab+b^2$$

به این ترتیب با شروع از سمت چپ فرمول اتحاد اول، سه جمله طرف دوم این فرمول به‌دست آمدند. برای اتحاد دوم نیز، همین روند برقرار است، فقط علامت‌ها فرق دارند.

مربع کامل چیست؟

همان‌طور که گفتیم علت نام‌گذاری اتحاد مربع دو‌جمله‌ای به شکل اتحاد مربع کامل این است که در این اتحاد با جملاتی روبرو می‌شویم که «مربع کامل» (Perfect Square) هستند. فرض کنید دو عدد «صحیح» (Integer) و مشابه در هم ضرب شوند، در این صورت توان دوم آن عدد حاصل شده است. حالا اگر ریشه دوم یا جذر حاصل را بگیریم، عدد صحیحی به‌دست می‌آید. در این صورت مقادیر توان دوم را مربع کامل می‌نامیم.

برای مثال اعدای مانند ۱۶، ۴۹ یا ۱۲۱ که به ترتیب حاصل‌ضرب اعداد ۴، ۷ و ۱۱ در خودشان هستند، مربع کامل‌اند. اما ۱۸۱ مربع کامل نیست. چون اگر جذر این عدد را محاسبه کنیم، $$sqrt{181}=pm 13.45$$ را خواهیم داشت که حاصل یعنی ۱۳٫۴۵ یک عدد صحیح نیست.

به عبارتی فرمول آن را می‌توانیم به این صورت تعریف کنیم که اگر x یک عدد صحیح باشد، مربع کامل آن برابر است با $$x^2$$. در این تعریف باید دقت داشته باشیم که عدد صحیح می‌تواند یک عدد منفی باشد. برای مثال عدد ۱۶ یک مربع کامل است که از به توان دوم رساندن عدد ۴ یا ۴- به‌دست می‌آید.

$$4^2=(-4)^2=16$$

نکته دیگری که از فرمول در مورد مربع کامل می‌توانیم برداشت کنیم این است که مربع کامل نمی‌تواند یک عدد منفی باشد. اما جذر آن می‌تواند عدد صحیح منفی باشد. مفهوم مربع کامل فقط محدود به اعداد نیست، بلکه در اتحادهای جبری نیز دیده می‌شود. به‌ویژه با تکنیک‌هایی مانند فاکتورگیری در حل برخی مسائل می‌توان این مفهوم را به‌کار گرفت.

همان‌طور که گفتیم، دو اتحادی که به‌خوبی این مفهوم را نمایش می‌دهند، اتحادهای مربع دوجمله‌ای هستند. به همین دلیل است که آن‌ها را با واژه مربع کامل نام‌گذاری کرده‌اند. به صورت دقیق‌تر، عبارت جبری که از مربع دوجمله‌ای به‌دست می‌آید، «سه‌جمله‌ای مربع کامل» (Perfect Square Trinomial) نامیده می‌شود. برای نمونه در عبارت جبری $$(x+3)^2=x^2+6x+9$$، مربع دوجمله‌ای برابر است با $$(x+3)^2$$، در حالی که $$x^2+6x+9$$ به‌عنوان سه‌جمله‌ای مربع کامل شناخته می‌شود.

بنابراین هر زمان که عبارت سه‌جمله‌ای به شکل $$a^2+2ab+b^2$$ یا $$a^2-2ab+b^2$$ دیدیم، می‌توانیم از مربع کامل استفاده کنیم. در برخی مسائل لازم است چنین عبارتی را با فاکتورگیری بسازیم. در بخش بعدی با حل مثال این فرآیند را بهتر درک خواهید کرد. البته پیش‌تر نیز در مجله فرادرس راجع به «اتحاد مربع» صحبت کرده‌ایم که لینک این مطلب در ادامه آورده شده و برای اطلاعات بیشتر می‌توانید آن را مطالعه کنید.

مثال اتحاد مربع کامل

تا این‌جا آموختیم که فرمول اتحاد مربع کامل چیست. در این بخش با حل مثال، یادگیری خود را در مورد این فرمول و نحوه استفاده از آن گسترش می‌دهیم. به‌ویژه خواهیم دید چگونه کاربرد این اتحاد باعث می‌شود تا در حل مسائل به نوعی از یک مسیر میان‌بر استفاده کرده باشیم.

مثال ۱

حاصل هر کدام از عبارت‌های $$(frac{c}{2}+frac{d}{3})^2$$ و $$(w-frac{t}{3})^2$$ را بر حسب مجموع سه جمله بنویسید:

پاسخ

برای عبارت اول که مربع مجموع دو جمله است، از فرمول اتحاد اول استفاده می‌کنیم، با این تفاوت که در اینجا $$a=frac{c}{2}$$ و $$b=frac{d}{3}$$ است:

$$(a+b)^2=a^2+2ab+b^2$$

$$(frac{c}{2}+frac{d}{3})^2=(frac{c}{2})^2+2(frac{c}{2})(frac{d}{3})+(frac{d}{3})^2$$

$$Rightarrow(frac{c}{2}+frac{d}{3})^2=frac{c^2}{4}+frac{cd}{3}+frac{d^2}{9}$$

عبارت دوم مربع تفاضل دو جمله است و باید از فرمول اتحاد دوم برای گسترش این رابطه استفاده کنیم:

$$(a-b)^2=a^2-2ab+b^2$$

$$(w-frac{t}{3})^2=w^2-2w(frac{t}{3})+(frac{t}{3})^2$$

$$Rightarrow(w-frac{t}{3})^2=w^2-frac{2wt}{3}+frac{t^2}{9}$$

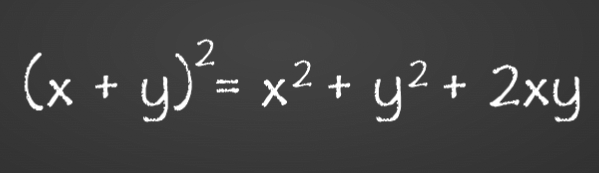
مثال ۲

اگر $$x+y=10$$ و $$xy=5$$ باشد، حاصل $$x^2+y^2$$ را به‌دست آورید:

پاسخ

با استفاده از فرمول تعمیم یافته، می‌توانیم عبارت خواسته شده را به‌راحتی محاسبه کنیم:

$$begin{cases}a^2+b^2=(a+b)^2-2ab \ \ a^2+b^2=(a-b)^2+2ab end{cases}$$

در این سوال چون مجموع دو جمله داده شده است، پس فرمول اول را به‌کار می‌بریم و به جای a و b از x و y استفاده می‌کنیم. پس با جای‌گذاری عبارت‌های داده شده در صورت سوال خواهیم داشت:

$$ x^2+y^2=(x+y)^2-2xy$$

$$x^2+y^2=10^2-2times5=100-10=90$$

مثال ۳

اگر $$c-d=8$$ و $$cd=-3$$ باشد، حاصل $$d^2+c^2$$ را به‌دست آورید:

پاسخ

در این سوال هم مشابه مثال قبل با استفاده از فرمول تعمیم یافته، می‌توانیم عبارت خواسته شده را به‌راحتی محاسبه کنیم:

$$begin{cases}a^2+b^2=(a+b)^2-2ab \ \ a^2+b^2=(a-b)^2+2ab end{cases}$$

در این مثال تفاضل دو جمله داده شده است، پس فرمول دوم را به‌کار می‌بریم و به جای a و b از c و d استفاده می‌کنیم. پس با جای‌گذاری عبارت‌های داده شده در صورت سوال خواهیم داشت:

$$ c^2+d^2=(c-d)^2+2cd$$

$$c^2+d^2=8^2+2times(-3)=64-6=58$$

دقت داریم که حاصل $$ c^2+d^2$$ با $$ d^2+c^2$$ برابر است.

مثال ۴

اگر $$x-frac{1}{x}=4$$ باشد، حاصل $$x^2+frac{1}{x^2}$$ چقدر است؟

پاسخ

با نوشتن فرمول تعمیم یافته اتحاد مربع، داریم:

$$begin{cases}a^2+b^2=(a+b)^2-2ab \ \ a^2+b^2=(a-b)^2+2ab end{cases}$$

در این مثال هم تفاضل دو جمله داده شده است، پس فرمول دوم را به‌کار می‌بریم و به جای a و b از جملات داده شده استفاده می‌کنیم. با جای‌گذاری خواهیم داشت:

$$x^2+frac{1}{x^2}=(x-frac{1}{x})^2+2(x)(frac{1}{x})$$

$$x^2+frac{1}{x^2}=4^2+2(x)(frac{1}{x})=16+2=18$$

دقت داریم که $$(x)(frac{1}{x})=1$$ است.

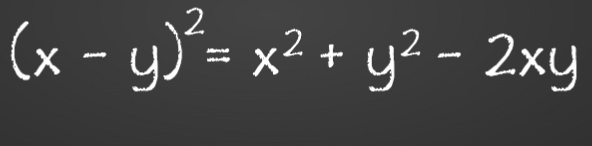
مثال ۵

حاصل عبارت عددی $${53}^2-{50}^2-3^2$$ چقدر است؟

پاسخ

می‌خواهیم برای اینکه بتوانیم حاصل این عبارت تقریبا پیچیده را به آسانی و سریع محاسبه کنیم، از اتحاد مربع دوجمله‌ای استفاده کنیم. جمله اول این عبارت را به شکل زیر می‌نویسیم:

$${53}^2-{50}^2-3^2=(50+3)^2-{50}^2-3^2$$

حالا اگر دقت کنید طرف دوم این رابطه معادل رابطه زیر بر اساس فرمول اتحاد مربع کامل است:

$$(a+b)^2=a^2+b^2+2abRightarrow(a+b)^2-a^2-b^2=2ab $$

پس می‌توانیم بنویسیم:

$$(a+b)^2-a^2-b^2=2ab Rightarrow (50+3)^2-{50}^2-3^2=2times50times3=300$$

مثال ۶

اگر $$6a-b=2$$ باشد، حاصل عبارت $$-36a^2+12ab-b^2$$ چقدر خواهد شد؟

پاسخ

برای اینکه بتوانیم به این سوال جواب دهیم، لازم است بتوانیم آن را به شکل یکی از فرمول‌های اتحاد مربع تبدیل کنیم. در این سوال عبارت خواسته شده در جمله اول و سوم علامت منفی دارد. پس برای اینکه آن را شبیه فرمول اتحاد دوم کنیم، می‌توانیم از یک منفی فاکتورگیری کنیم:

$$-36a^2+12ab-b^2=-(36a^2-12ab+b^2)$$

طبق فرمول اتحاد دوم داریم:

$$a^2-2ab+b^2=(a-b)^2$$

$$a^2-2ab+b^2=-(36a^2-12ab+b^2)$$

$$Rightarrow-[(6a)^2-2(6a)b+b^2]=-(6a-b)^2=-(2^2)=-4$$

مثال ۷

حاصل عبارت $$9y^2+42y+49$$ را به‌صورت مربع کامل بنویسید و سپس به ازای $$y=-2$$ مقدار آن را محاسبه کنید:

پاسخ

در بخش اول این سوال، از مقایسه این عبارت با اتحاد اول خواهیم داشت:

$$a^2+2ab+b^2=(a+b)^2$$

$$9y^2+42y+49$$

$$Rightarrow begin{cases}a=3y \ \b=7 end{cases}$$

حالا با استفاده از طرف دیگر اتحاد اول، می‌توانیم بنویسیم:

$$9y^2+42y+49=(3y+7)^2$$

پس حاصل عبارت جبری داده شده به شکل مربع کامل می‌شود $$(3y+7)^2$$ که اگر به ازای y عددگذاری انجام دهیم، حاصل خواهد شد:

$$(3(-2)+7)^2=(-6+7)^2=1^2=1$$

در واقع با استفاده از اتحاد اول توانستیم مقدار عبارت جبری داده شده را سریع‌تر و آسان‌تر محاسبه کنیم.

مثال ۸

اگر r یک عدد باشد، به گونه‌ای که داشته باشیم $$r^2-10r+25=64$$، آن‌گاه مقدار $$(r-5)^4$$ چقدر است؟

پاسخ

با توجه به اینکه سمت چپ رابطه داده شده کاملا با سمت راست اتحاد نوع دوم مطابقت دارد، پس با در نظر گرفتن اتحاد نوع دوم و مقایسه این دو عبارت، خواهیم داشت:

$$(a-b)^2=a^2-2ab+b^2$$

$$r^2-10r+25=64$$

$$Rightarrow begin{cases}a=r \ \ b=5 end{cases}$$

از طرفی با توجه به سمت چپ فرمول اتحاد نوع دوم، داریم:

$$ (r-5)^2=64$$

$$Rightarrow r-5=sqrt{64}=pm 8$$

بنابراین برای به‌دست آوردن حاصل عبارتی که در صورت سوال خواسته شده است، کافی است که عدد ۸± را به توان ۴ برسانیم. در این محاسبه عدد ۸ چه علامت مثبت داشته باشد چه منفی، تفاوتی در پاسخ ایجاد نمی‌کند. چون توان چهارم خواسته شده است که یک توان زوج است و به هر حال حاصل مثبت می‌شود. پس با دانستن اینکه حاصل‌ضرب علامت منفی در منفی مثبت است، داریم:

$$ (r-5)^4=(pm 8)^4=begin{cases}(+8)^4=4096 \(-8)^4=4096 end{cases}$$

بنابراین در این مثال دیدیم که چگونه با استفاده از اتحاد دوم توانستیم حاصل عبارت خواسته شده در صورت سوال را بدون نیاز به حل معادله درجه دوم و پیدا کردن مقدار r، محاسبه کنیم.

مثال ۹

مقدار عبارت زیر چقدر می‌شود؟

$${73}^2+2times73times27+{27}^2$$

پاسخ

در این سوال می‌خواهیم حاصل عبارت عددی بالا را بدون انجا‌م محاسبات سخت و پیچیده، تنها با به‌کارگیری اتحاد ممربع دوجمله‌ای محاسبه کنیم. از مقایسه این عبارت عددی با اتحاد اول داریم:

$${73}^2+2times73times27+{27}^2$$

$$a^2+2ab+b^2=(a+b)^2$$

$$Rightarrow{73}^2+2times73times27+{27}^2=a^2+2ab+b^2$$

بنابراین مقدار a و b به‌صورت زیر خواهند شد:

$$Rightarrowbegin{cases}a=73 \ \b=27 end{cases}$$

از طرفی طبق فرمول اتحاد اول می‌توانیم بنویسیم:

$${73}^2+2times73times27+{27}^2=(73+27)^2=(100)^2=10000$$

پس با استفاده از اتحاد مربع، توانستیم حاصل این عبارت را سریع‌تر و راحت‌تر به‌دست آوریم.

مثال ۱۰

آیا عبارت $$9y^2+36y+4$$ یک اتحاد مربع کامل محسوب می‌شود؟

پاسخ

ابتدا این عبارت را با فرمول اتحاد اول مقایسه می‌کنیم:

$$a^2+2ab+b^2=(a+b)^2$$

$$9y^2+36y+4$$

$$Rightarrow begin{cases}a=3y \ \b=2 end{cases}$$

اگر فرض کنیم برای a و b مقادیر بالا را داشته باشیم، باید جمله وسط در عبارت صورت سوال به‌صورت 2ab باشد، یعنی مقدار آن باید $$12y$$ باشد. اما جمله وسط در این عبارت $$36y$$ است. پس این عبارت، یک اتحاد مربع کامل محسوب نمی‌شود.

مثال ۱۱

در عبارت جبری $$4x^2-20x+25$$، مقدار جمله 3ab چقدر است؟

پاسخ

طبق فرمول اتحاد دوم داریم:

$$a^2-2ab+b^2=(a-b)^2$$

اگر این عبارت را با این فرمول مقایسه کنیم، می‌توانیم a و b را به‌دست آوریم و سپس جمله 3ab را محاسبه کنیم:

$$Rightarrow begin{cases}a=2x \ \b=5 end{cases}$$

$$Rightarrow 3ab=3(2x)5=30x$$

مثال ۱۲

کدام یک از تساوی‌های زیر یک عبارت معتبر و صحیح است؟

$$(2x+y)(4x-2y)=2(4x^2+8xy-y^2)$$

$$(n+2)^2-n^2=4(n+1)$$

$$(a+b)(2a+1)-b=a(2a+2b+1)$$

پاسخ

ابتدا عبارت اول را بررسی می‌کنیم. برای شروع، دو جمله اول پرانتز اول را در دو جمله پرانتز بعدی ضرب می‌کنیم:

$$(2x+y)(4x-2y)=2x(4x-2y)+y(4x-2y)$$

$$(2x+y)(4x-2y)=8x^2-4xy+4xy-2y^2$$

با حذف شدن دو جمله 4xy که علامت‌های مخالف هم دارند، خواهیم داشت:

$$(2x+y)(4x-2y)=8x^2-2y^2=2(4x^2-y^2)$$

 مشاهده می‌کنید که حاصل این عبارت با $$2(4x^2+8xy-y^2)$$ برابر نشد. برای عبارت دوم هم با باز کردن پرانتز اول که در واقع اتحاد اول است، خواهیم داشت:

$$(n+2)^2-n^2=(n^2+4n+4)-n^2=4n+4=4(n+1)$$

طرف دوم رابطه به‌دست آمد. پس این تساوی درست است. عبارت سوم نیز این چنین خواهد شد:

$$(a+b)(2a+1)-b=a(2a+1)+b(2a+1)-b$$

$$(a+b)(2a+1)-b=2a^2+a+2ab+b-b=2a^2+a+2ab$$

با ساده‌سازی بیشتر رابطه به‌دست آمده از طریق فاکتورگیری از a، خواهیم داشت:

$$(a+b)(2a+1)-b=a(2a+1+2b)$$

پس برای این رابطه هم طرف دوم محاسبه شد و تساوی سوم نیز معتبر است.

مثال ۱۳

حاصل عبارت $$(7x+4y)^2+(7x-47)^2$$ را به ساده‌ترین شکل ممکن محاسبه کنید:

پاسخ

در این عبارت، پرانتز اول همان اتحاد اول و پرانتز دوم، اتحاد دوم است. با استفاده از دو فرمول اتحاد مربع کامل و بیان هر کدام بر حسب سه جمله، خواهیم داشت:

$$(a+b)^2+(a-b)^2=a^2+2ab+b^2+a^2-2ab+b^2=2a^2+2b^2$$

بنابراین بهتر است پیش از عددگذاری در فرمول، ابتدا دو فرمول را با هم جمع کنیم تا مسئله راحت‌تر حل شود. حالا با قرار دادن مقادیر داده شده به‌جای a و b خواهیم داشت:

$$(7x+4y)^2+(7x-47)^2=2(7x)^2+2(4y)^2=98x^2+32y^2$$

حل معادله درجه ۲ با اتحاد مربع کامل

یک روش مهم حل معادلات درجه دوم، روش مربع کامل است. در این روش، گاهی لازم است معادله درجه دوم را با کم کردن یا افزودن جملات عددی، طوری بازنویسی کنیم که یک طرف معادله به شکل اتحاد مربع کامل دربیاید. در برخی مسائل هم نیازی به این کار نیست و خود معادله، یک اتحاد مربع کامل است. بنابراین با استفاده از اتحاد مربع کامل می‌توانیم ریشه‌های معادله درجه دوم را به‌دست آوریم. مزیت استفاده از اتحاد مربع کامل در حل معادلات درجه دوم، سرعت بالاتر حل معادلات است.

مثال ۱

معادله $$x^2+6x+9=0$$ را حل کنید:

پاسخ

این معادله در واقع یک طرف اتحاد اول است. طبق فرمول اتحاد مربع، خواهیم داشت:

$$(a+b)^2=a^2+2ab+b^2$$

بنابراین $$Rightarrow a^2+2ab+b^2=x^2+(2)(3)x+3^2$$. پس می‌توانیم بنویسیم:

$$Rightarrow x^2+(2)(3)x+3^2= (x+3)^2=0$$

$$Rightarrow (x+3)=0 $$

$$Rightarrow x=-3$$

بنابراین معادله حل شد.

مثال ۲

ریشه معادله $$16x^2-40x+25=0$$ را به‌دست آورید:

پاسخ

در این معادله با توجه به اینکه جملات اول و سوم مربع کامل هستند ($$(4x)^2=16x^2$$ و $$5^2=25$$)، می‌توانیم خیلی راحت از اتحاد مربع دوجمله‌ای استفاده کنیم. با توجه به اینکه جمله دوم منفی است، اتحاد دوم در اینجا به‌کار می‌رود:

$$(a-b)^2=a^2-2ab+b^2$$

$$a^2-2ab+b^2=(4x)^2-2(4x)(5)+5^2$$

$$16x^2-40x+25=(4x-5)^2=0$$

$$Rightarrow 4x-5=0 $$

$$Rightarrow 4x=5 Rightarrow x=5/4$$

خلاصه‌ای از مهم‌ترین اتحادها

همان‌طور که گفتیم، اتحادها بسیار گسترده هستند. در این مطلب ما فقط به اتحاد مربع کامل پرداختیم. اگر تمایل دارید چند مورد از پرکاربردترین اتحادها را با هم مقایسه کنید، می‌توانید از جدول زیر استفاده کنید.

ترکیب اتحاد مربع کامل با سایر اتحادها

پس از فراگیری فرمول سایر اتحادهای مهم، در این بخش می‌خواهیم مثال‌هایی را با هم حل کنیم که در آن‌ها از دو یا چند اتحاد در حل مسئله استفاده می‌شود. بنابراین باید این اتحاد و تفاوت آن با اتحادهایی مانند اتحاد جمله مشترک یا اتحاد مزدوج را به‌خوبی یاد گرفته باشیم تا بتوانیم به این سوالات به‌درستی پاسخ دهیم.

مثال ۱

عبارت جبری $$n^4+4$$ را به‌صورت حاصل‌ضرب دو عبارت جبری دیگر بر حسب n و 2 بنویسید:

پاسخ

برای اینکه بتوانیم این عبارت را گسترش دهیم و بر حسب حاصل‌ضرب دو عبارت بنویسیم، لازم است به آن یک جمله یا جملاتی را اضافه کنیم. بنابراین باید از روش مربع کامل کردن استفاده کنیم. اگر به این عبارت دو جمله به‌صورت $$4n^2-4n^2$$ اضافه کنیم، در واقع گویی هیچ جمله‌ای را به آن اضافه نکرده‌ایم. چون عبارت $$4n^2-4n^2$$ شامل دو جمله برابر و با علامت‌های مختلف است، طوری که این دو جمله هم را خنثی می‌کنند:

$$n^4+4+4n^2-4n^2=n^4+4n^2+4-4n^2$$

حالا برای بخشی از این عبارت (سه جمله اول در سمت راست عبارت بالا) می‌توانیم از اتحاد اول استفاده کنیم:

$$n^4+4n^2+4=(n^2+2)^2$$

بنابراین خواهیم داشت:

$$n^4+4=(n^2+2)^2-4n^2$$

اگر عبارت $$4n^2$$ را به شکل $$(2n)^2$$ بنویسیم، خواهیم داشت:

$$n^4+4=(n^2+2)^2-(2n)^2$$

از طرفی با مقایسه فرمول اتحاد مزدوج و عبارت بالا داریم:

$$a^2-b^2=(a-b)(a+b)$$

$$a^2-b^2=(n^2+2)^2-(2n)^2$$

$$Rightarrowbegin{cases}a=(n^2+2) \ \b=2n end{cases}$$

در نهایت عبارت صورت سوال به‌صورت زیر به ساده‌ترین شکل ممکن خواهد شد:

$$Rightarrow n^4+4=(n^2+2-2n)(n^2+2+2n)$$

مثال ۲

اگر داشته باشیم $$a+b=2$$ و $$ab=-1$$، آن‌گاه مقدار $$a^3+b^3$$ چقدر است؟

پاسخ

در صورت سوال مجموع مکعب دو جمله خواسته شده است. طبق فرمولی که برای این مجموع در جدول داشتیم، می‌توانیم بنویسیم:

$$a^3+b^3=(a+b)(a^2-ab+b^2)$$

از طرفی برای مجموع مربع دو جمله a و b هم از فرمول تعمیم‌یافته اتحاد مربع کامل می‌توانیم استفاده کنیم:

$$a^2+b^2=(a+b)^2-2ab $$

با ترکیب کردن این دو رابطه خواهیم داشت:

$$ Rightarrow a^3+b^3=(a+b)((a+b)^2-2ab-ab)$$

با عددگذاری در نهایت خواهیم داشت:

$$ Rightarrow a^3+b^3=(a+b)((a+b)^2-3ab)=2(2^2-3(-1))=2(4+3)=2(7)=14$$

مثال ۳

ثابت کنید چگونه فرمول اتحاد مکعب مجموع دو جمله $$(a+b)^3=a^3+3a^2b+3ab^2+b^3$$ با استفاده از روابط اتحاد اول و دوم به‌دست خواهد آمد:

پاسخ

از سمت چپ این رابطه، یعنی توان سوم یا مکعب مجموع دو جمله a و b شروع می‌کنیم و این عبارت را باز می‌کنیم:

$$(a+b)^3=(a+b)(a+b)^2$$

حالا به‌جای $$(a+b)^2$$ از اتحاد مربع استفاده می‌کنیم:

$$(a+b)^2=a^2+2ab+b^2$$

$$(a+b)^3=(a+b)(a^2+2ab+b^2)$$

با ضرب کردن دو جمله اول، در سه‌جمله‌ای مربع کامل خواهیم داشت:

$$(a+b)^3=a(a^2+2ab+b^2)+b(a^2+2ab+b^2)$$

$$(a+b)^3=a^3+2a^2b+ab^2+ba^2+2ab^2+b^3$$

پس از مرتب کردن جملات و جمع جملات مشابه $$2a^2b+ba^2$$ و $$ab^2+2ab^2$$، می‌بینیم که طرف دوم این رابطه حاصل شده است:

$$(a+b)^3=a^3+3a^2b+3ab^2+b^3$$

مثال ۴

حاصل عبارت جبری عددی زیر چقدر می‌شود؟

$$(5sqrt{3}+2)(5sqrt{3}-2)+(5sqrt{3}+2)^2-(5sqrt{3}-2)^2$$

پاسخ

اگر به جمله اول این عبارت خوب دقت کنیم، متوجه خواهیم شد که کاملا با یک طرف اتحاد مزدوج معادل است. جملات دوم و سوم هم اتحادهای مربع دوجمله‌ای هستند. بدون عدد‌گذاری اگر از فرمول اتحادهای گفته شده استفاده کنیم، خواهیم داشت:

$$(a-b)(a+b)=a^2-b^2$$

$$(a+b)^2=a^2+2ab+b^2$$

$$(a-b)^2=a^2-2ab+b^2$$

پس با فرض اینکه $$a=5sqrt{3}$$ و $$b=2$$ هستند، داریم:

$$(5sqrt{3}+2)(5sqrt{3}-2)+(5sqrt{3}+2)^2-(5sqrt{3}-2)^2=(a+b)(a-b)+(a+b)^2-(a-b)^2$$

$$(5sqrt{3}+2)(5sqrt{3}-2)+(5sqrt{3}+2)^2-(5sqrt{3}-2)^2=a^2-b^2+a^2+2ab+b^2-[a^2-2ab+b^2]$$

$$(5sqrt{3}+2)(5sqrt{3}-2)+(5sqrt{3}+2)^2-(5sqrt{3}-2)^2=a^2-b^2+a^2+2ab+b^2-a^2+2ab-b^2$$

$$(5sqrt{3}+2)(5sqrt{3}-2)+(5sqrt{3}+2)^2-(5sqrt{3}-2)^2=a^2-b^2+4ab$$

$$a^2-b^2+4ab=(5sqrt{3})^2-2^2+4(5sqrt{3})(2)=25(3)-4+40sqrt{3}=71+40sqrt{3}$$

تکمیل یادگیری اتحاد با فرادرس

در انتهای این مطلب آموزشی از مجله فرادرس، پیشنهاد می‌کنیم اگر در مقاطع دانشگاهی هستید و نیاز دارید یادگیری خود در زمینه ریاضیات پایه، به‌ویژه مباحث مربوط به اتحادهای جبری را بهبود ببخشید یا چنانچه قصد دارید در آزمون‌های مختلف با سوالاتی در این زمینه شرکت کنید، فیلم‌های آموزشی زیر از فرادرس را مشاهده کنید:

1. مجموعه فیلم آموزش ریاضیات مقدماتی تا پیشرفته فرادرس
2. فیلم آموزش ریاضی پایه دانشگاهی فرادرس
3. فیلم آموزش ریاضی پایه مرور و حل تست کنکور ارشد فرادرس
4. فیلم آموزش رایگان اتحاد و تجزیه در ریاضی پایه دانشگاهی فرادرس
5. فیلم آموزش آزمون های استخدامی ریاضی و آمار فرادرس
6. فیلم آموزش المپیاد ریاضی مبحث ترکیبیات فرادرس

آزمون اتحاد مربع کامل

آموختیم اتحاد مربع کامل چیست و چگونه باید از فرمول‌های آن استفاده کنیم. حالا می‌توانیم یادگیری خود را با پاسخ‌دهی به سوالات آزمون محک بزنیم. پس از اینکه به سوالات آزمون جواب دادید، با کلیک روی گزینه «دریافت پاسخ آزمون»‌ می‌توانید نتیجه آزمون خود را مشاهده کنید. ضمن اینکه پاسخ‌های تشریحی هر سوال در باکس زیر آن درج شده است و در صورت نیاز می‌توانید به این توضیحات نیز مراجعه کنید.