یکی از مهمترین ابزارهایی که ریاضیات در اختیار ما قرار داده است، «انتگرال» (Integral) است. اگر با مفهوم انتگرال و کاربرد آن آشنا باشید، احتمالا در استفاده از آن با قواعد و فرمولهای پیچیدهای مواجه شدهاید. در این مطلب از مجله فرادرس سعی داریم به بخشی از قواعد انتگرالگیری که مربوط به «انتگرالگیری از یک عدد ثابت» (Integration of a Constant Number) است، بپردازیم. انتگرال عدد ثابت، در واقع سادهترین نوع انتگرال در مقایسه با انتگرالهایی شامل توابع پیچیده ریاضی است.
پس از مطالعه چگونگی محاسبه انتگرال عدد ثابت، با تمرین مثالهای مختلفی که در این مطلب قرار داده شده است و انجام آزمون انتهایی، قادر خواهید بود این نوع انتگرالها را با سرعت و دقت بیشتری و بهدرستی حل کنید.
انتگرال عدد ثابت چیست؟
انتگرال عدد ثابتی مانند c نسبت به متغیری مانند x بهصورت $$ int c dx$$ نوشته میشود و حاصل آن برابر است با $$ cx+A$$، که در آن A یک عدد ثابت اختیاری است. پس حاصل انتگرال یک عدد ثابت نسبت به متغیری مثل x، حاصلضرب آن عدد ثابت در متغیر x خواهد شد:
$$int cdx=cx+A $$
از آنجا که این مطلب محدود به انتگرال عدد ثابت است، برای یادگیری انواع انتگرال میتوانید فیلم آموزش ریاضی عمومی ۱ فرادرس که لینک آن در ادامه آورده شده است را مشاهده کنید.
در فرمول بالا اگر حدود انتگرالگیری مشخص باشد، میتوانیم حاصل انتگرال عدد ثابت را به صورت یک عدد به دست آوریم. در ادامه برای اینکه با مفاهیم فرمول ارائه شده برای انتگرال عدد ثابت بیشتر آشنا شویم، لازم است ابتدا یاد بگیریم انتگرال چیست، چگونه نشان داده میشود و قواعد محاسبه آن چگونه است. همچنین باید بدانیم انتگرال معین و نامعین یک عدد ثابت چه تفاوتهایی با هم دارند.
تعریف انتگرال
منحنی تابع f(x) را در دستگاه مختصات بهصورت شکل زیر در نظر بگیرید. فرض کنید مساحت زیر این منحنی یعنی S، شامل تعداد خیلی زیادی از سطوح خیلی خیلی کوچک با طولی به اندازه dx روی محور x است. انتگرال ابزاری است که با استفاده از تابع f(x) و با جمع تمام این مقادیر خیلی خیلی کوچک، مساحت زیر منحنی f(x) یعنی S را محاسبه میکند. ∫ نمادی است که برای نشان دادن انتگرال بهکار میرود.
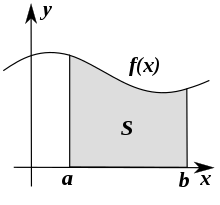
برای بیان محاسبه انتگرال تابع f(x) نسبت به متغیر x از a تا b به زبان ریاضیات، از رابطه زیر استفاده میکنیم:
$$int_{a}^{b} f(x) dx =S$$
- همانطور که گفتیم، در این رابطه f(x) تابعی بر حسب x است که می خواهیم انتگرال آن را نسبت به متغیر x محاسبه کنیم. تابع f «انتگرالده» (Integrand) یا «تابع زیر انتگرال» نامیده میشود. همچنین، در این مطلب تابع f(x) برابر با یک عدد ثابت در نظر گرفته میشود، اما این تابع در حالت کلی میتواند شکلهای مختلف و پیچیدهتری داشته باشد.
- a و b حدود انتگرالگیری هستند، طوری که داریم a ≤ x ≤ b. در واقع a حد پایین و b حد بالای انتگرال نامیده میشوند و همیشه a<b است.
- dx دیفرانسیل انتگرال است و نشاندهنده این است که انتگرالگیری نسبت به چه متغیری انجام میشود. در فرمول بالا، انتگرالگیری نسبت به x است.
قواعد محاسبه انتگرال
محاسبه انتگرال در حالت کلی دارای قواعدی است که برای تمام توابع صدق میکند. مهمترین این قواعد عبارتاند از:
- مشتق یا دیفرانسیل یک انتگرال که با d نشان داده میشود، با خود انتگرالده برابر است:
$$text{d} [int f(x)] =f(x)$$
- انتگرال مجموع دو تابع نسبت به یک متغیر برابر است با مجموع انتگرالهای هر تابع نسبت به آن متغیر:
$$int [f(x)+g(x)] dx =int f(x)dx +int g(x) dx + A$$
- انتگرال حاصلضرب یک عدد ثابت مثل k در تابعی مثل f(x) برابر است با حاصلضرب عدد ثابت در حاصل انتگرال f(x):
$$int kf(x) dx =kint f(x)dx + A$$
انتگرال معین و نامعین عدد ثابت
بهطور کلی محاسبه انتگرال برای دو گروه از مسائل استفاده میشود:
- مسئله یافتن مساحت محدود شده زیر نمودار یک تابع.
- مسئله یافتن تابعی که مشتق آن داده شده است.
میدانیم انتگرالگیری فرآیند معکوس مشتقگیری یا دیفرانسیلگیری محسوب میشود. اگر مشتق تابعی مثل g(x) برابر با تابع f(x) شود $$acute{g(x)} = f(x) $$، در این صورت انتگرال f(x) روی متغیر x با g(x) برابر است. بر این اساس، انتگرالها به دو گروه تقسیمبندی میشوند:
- «انتگرال معین (Definite Integral): انتگرالی که در آن حدود انتگرالگیری مشخص است. برای مثال $$int_{a}^{b} f(x) dx $$، یک انتگرال معین است که حاصل آن یک عدد مشخص خواهد شد:
$$int_{a}^{b} f(x) dx=g(b)-g(a) $$
- «انتگرال نامعین» (Indefinite Integral): در انتگرال نامعین حدود انتگرالگیری مشخص نیست. $$int f(x) dx $$، یک انتگرال نامعین بهشمار میرود و جواب این انتگرال نامعین است:
$$int {f(x)} dx = g(x) + A$$
یادگیری انتگرال با فرادرس
انتگرال عدد ثابت یا تابع ثابت، سادهترین نوع انتگرالگیری است که در این مطلب توضیح داده شده است. اما معمولا در محاسبات انتگرال، با توابع پیچیدهتری مانند توابع مثلثاتی، توابع نمایی، توابع گنگ، توابع کسری، توابع رادیکالی، توابع چندجملهای و … روبرو میشویم که محاسبه چنین انتگرالهایی نیازمند یادگیری قواعد پیشرفتهتر و استفاده از روشهایی مانند روش جز به جز یا تغییر متغیر است. بنابراین اگر علاقهمند هستید که در مبحث انتگرالگیری کاملا مسلط شوید، پیشنهاد میکنیم یادگیری خود را با این فیلمهای آموزشی فرادرس به ترتیب زیر ادامه دهید:
مفهوم انتگرال عدد ثابت
در بخش انتگرال عدد ثابت گفتیم حاصل انتگرالی به فرم cdx∫ برابر خواهد شد با cx+A، که در آن A یک عدد ثابت دلخواه است. در این بخش میخواهیم با استفاده از نمودار، این نوع انتگرالگیری را بیشتر توضیح دهیم تا مفهوم آن را بهتر درک کنید. همانطور که در تعریف انتگرال بیان شد، انتگرالگیری به معنای محاسبه مساحت زیر نموداری است که بهعنوان تابع زیر انتگرال یا انتگرالده در نظر گرفته میشود. معمولا این تابع یعنی f(x) را برابر با y (y=f(x)) در نظر میگیریم، در حالی که در دستگاه مختصات انتگرالگیری روی متغیر x انجام میشود.
در این مطلب تمرکز ما روی انتگرالگیری از عدد ثابت یا به بیان دقیقتر انتگرال تابعی با مقدار ثابت است. بنابراین داریم y=f(x)=c که در آن c یک عدد ثابت است و میتواند تمام اعداد مثبت، منفی و صفر را شامل شود. طبق شکل زیر، تابع y=c برابر است با یک خط صاف موازی محور افقی یا محور xها. این خط به اندازه عدد c از روی محور x به سمت بالا یا پایین جابجا شده است. اگر c منفی باشد، این خط در ربع چهارم دستگاه مختصات خواهد بود.
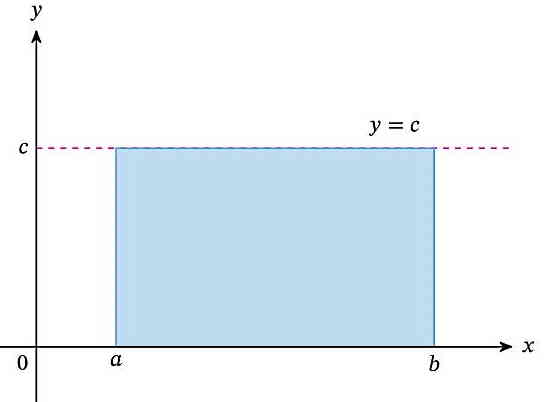
حالا اگر انتگرالگیری روی این تابع ثابت یک انتگرالگیری معین باشد، یعنی محدوده انتگرالگیری مطابق شکل بالا مشخص است و از a تا b است. بنابراین حاصل این انتگرال برابر خواهد بود با مقداری از مساحت زیر این تابع ثابت، که بین a و b قرار دارد. طبق شکل بالا، چنین مساحتی برای این مورد برابر خواهد بود با مساحت مستطیلی به طول b-a و عرض c. پس میتوانیم بنویسیم:
$$int_{a}^{b} f(x) dx=int_{a}^{b} c dx=c(b-a) $$
حالا اگر بخواهیم مساحت بهدست آمده را در قالب فرمول بنویسیم، مشاهده میکنیم که c(b-a) در واقع همان حاصلضرب مقدار تابع ثابت در حاصل تفریق حد بالا و حد پایین است. در ابتدای این مطلب فرمول انتگرال عدد ثابت را در انتگرالگیری نامعین بیان کردیم. اگر این فرمول را برای انتگرال معین استفاده کنیم، داریم:
$$int_{a}^{b} c dx=(cx+A)Big|_a^b =(cb+A)-(ca+A)=c(b-a)$$
پس میبینیم که مقدار ثابت اختیاری A که در پاسخ انتگرال نامعین در نظر گرفته میشد، برای انتگرال معین تاثیری ندارد، چون درمحاسبات با جایگذاری دو حد بالا و پایین به هر حال حذف خواهد شد.
فرمول انتگرال عدد ثابت
اگر بخواهیم تا اینجا یک جمعبندی داشته باشیم، دو فرمول انتگرال عدد ثابت برای انتگرالگیری معین و نامعین بهصورت زیر است. همچنین در این جدول برای درک بهتر ارتباط بین مشتق و انتگرال عدد ثابت، مشتقگیری از جواب انتگرال عدد ثابت نیز آورده شده است:
| $$int_{a}^{b} c dx=c(b-a)$$ | فرمول انتگرال معین عدد ثابت c |
| $$int c dx=cx+A$$ | فرمول انتگرال نامعین عدد ثابت c |
| $$ frac{text{d}(cx+A)}{text{d}x}=c$$ | فرمول مشتق جواب انتگرال عدد ثابت c |
احتمالا با توجه به ردیف آخر این جدول بهتر متوجه خواهید شد که علت قرار دادن ثابت A در فرمول پاسخ انتگرال نامعین چیست. همانطور که گفتیم انتگرال و مشتق معکوس یکدیگر عمل میکنند. پس باید مشتق حاصل انتگرال نامعین یعنی مشتق cx+A با انتگرالده یعنی c برابر باشد. مشتق cx+A طبق قواعد مشتقگیری برابر است با c که همان انتگرالده است. پس از یک عدد ثابت اختیاری مثل A استفاده میکنیم تا با صفر شدن مشتق آن، در انتگرالگیری بهدرستی عمل کرده باشیم.
حل مثال انتگرال عدد ثابت
پس از اینکه یاد گرفتیم انتگرال عدد ثابت چیست و چگونه محاسبه میشود، در ادامه میخواهیم انتگرال اعداد مختلف را محاسبه کنیم، با انتگرالگیری عدد ثابت روی متغیرهای مختلف آشنا شویم، انتگرال مجموع دو عدد ثابت را بررسی کنیم، مساحت زیر منحنی ثابت را حساب کنیم و کاربرد این مبحث در فیزیک را در قالب حل مثال توضیح دهیم. همچنین اگر میخواهید خلاصهای از تمام فرمولهای انتگرال در اختیار داشته باشید، میتوانید از مطلب «فرمول های انتگرال و انتگرال گیری در یک نگاه با مثال» در مجله فرادرس استفاده کنید.
مثال انتگرال عدد صفر
حاصل $$int 0 dx$$ و $$int_{0}^{2} 0 dx$$ چقدر میشود؟
پاسخ
انتگرال اول یک انتگرال نامعین و دومی یک انتگرال معین است. در مورد انتگرال نامعین حاصل برابر میشود با عدد ثابت A، چون مقدار انتگرالده یعنی c=۰ است.
$$int 0dx=0x+A=A $$
برای حل انتگرال معین، میدانیم حاصلضرب عدد صفر در هر چیزی برابر با صفر خواهد شد. پس حاصل این انتگرال فارغ از این که a و b چه مقداری داشته باشند، همیشه برابر با صفر است.
$$int_{0}^{2} 0 dx=0(2-0)=0$$
مثال انتگرال عدد یک
انتگرالهای $$int_{-1}^{3} dx$$ و $$int dx$$ را محاسبه کنید:
پاسخ
انتگرال اول، یک انتگرال معین است که حدود آن مشخص هستند. نکته مهم این است که در انتگرالده قبل از dx عددی وجود ندارد، اما در واقع عدد یک در اینجا قرار دارد. چون میدانیم حاصلضرب عدد یک در هر چیزی با خود آن برابر است. پس در واقع داریم:
$$int_{-1}^{3} dx=int_{-1}^{3} 1times dx=1times(3-(-1))=4$$
و برای انتگرال نامعین که در آن انتگرالده بهصورت عدد ثابت ۱ است، خواهیم داشت:
$$int dx=1x+A=x+A$$
مثال انتگرال عدد منفی یک
جواب $$int -dx$$ چیست؟ اگر حدود انتگرال را از ۳- تا ۵ در نظر بگیریم، حاصل چقدر خواهد شد؟
پاسخ
در این مثال عدد ثابت، عدد منفی یک است. بخش اول این سوال یک انتگرالگیری نامعین است، چون در فرمول داده شده حد بالا و پایین انتگرال مشخص نیست. طبق فرمول انتگرال نامعین عدد ثابت داریم:
$$int -dx=int -1times dx=-1x+A=-x+A $$
ولی در سوال دوم، حدود انتگرالگیری مشخص شده است. پس برای حل این انتگرال معین میتوانیم بنویسیم:
$$int_{-3}^{5} -dx=-1(5-(-3))=-1(8)=-8$$
مثال انتگرال عدد پی
حاصل انتگرال عدد پی (π) به شکل $$int pi dx $$ و $$int_{-1}^{0} pi dx$$ چیست؟
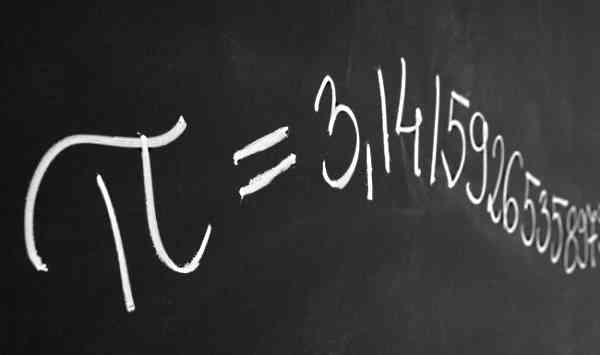
پاسخ
انتگرال اول، یک انتگرال نامعین و دومی یک انتگرال معین است. جواب این دو انتگرال خواهد شد:
$$int pi dx =pi x+A=3.14x+A$$
$$int_{-1}^{0} pi dx=pi(0-(-1))=pi=3.14$$
مثال انتگرال مجموع دو عدد ثابت
با این فرض که دو پارامتر a و v اعداد ثابتی هستند، انتگرال $$int_{0}^{4} (a+v) dx$$ را محاسبه کنید:
پاسخ
سوال یک انتگرال معین است که در آن جمع دو عدد ثابت a و v قرار دارد. با دانستن اینکه جمع دو عدد ثابت برابر با یک عدد ثابت دیگر است، باز هم میتوانیم از فرمول انتگرال معین عدد ثابت استفاده کنیم:
$$int_{0}^{4} (a+v) dx=(a+v)(4-0)=4(a+v)$$
مثال انتگرال عدد ثابت روی متغیر y
حاصل $$int 5 dy$$ و $$int_{-2}^{2} 5 dy$$ چقدر است؟
پاسخ
دقت شود در این سوال متغیری که روی آن انتگرالگیری انجام میشود، y است. فرمول استفاده شده هیچ تفاوتی با قبل ندارد، فقط به جای x در فرمول انتگرال نامعین از y استفاده میکنیم:
$$int 5 dy=5y+A$$
$$int_{-2}^{2} 5 dy=5(2-(-2))=20$$
در این مثال ممکن بود در بخش دیفرانسیل انتگرال بهجای y از z یا r یا t یا هر حرف دیگری استفاده شود. در این صورت پاسخ انتگرال نامعین به ترتیب برابر میشد با ۵z+A و ۵r+A و ۵t+A. پس انتگرالگیری لزوما روی x انجام نمیشود. برای مثال در مسائل فیزیک معمولا انتگرالگیری روی زمان که با t نشان داده میشود، انجام میشود.
مثال پیدا کردن ثابت اختیاری
اگر برای تمام مقادیر x داشته باشیم $$int kdx=2x-3 $$، مقدار k و ثابت اختیاری چقدر است؟
پاسخ
طبق فرمول انتگرال نامعین میدانیم:
$$int kdx=kx+A $$
چون طبق صورت سوال در اینجا $$kx+A =2x-3 $$ شده است، پس k=۲ و ثابت اختیاری A=-۳ است.
مثال محاسبه مساحت با انتگرال عدد ثابت
مساحت زیر نمودار y=۷ از x=-۳ تا x=-۱ چقدر است؟
پاسخ
دقت شود متغیری که در اینجا روی آن انتگرال را حل میکنیم، y است. y=۷ خطی است موازی محور xها که به اندازه ۷ واحد روی محور y جابجا شده است. مساحت زیر این نمودار برای محدوده گفته شده معادل مساحت یک مستطیل است با یک ضلع به اندازه ۷ و یک ضلع برابر با (۳-)-۱- که می شود ۲. مساحت این مستطیل در واقع همان جواب انتگرال $$int_{-3}^{-1} 7 dy$$ است:
$$int_{-3}^{-1} 7 dy=7(-1-(-3))=14$$
کاربرد انتگرال عدد ثابت در فیزیک
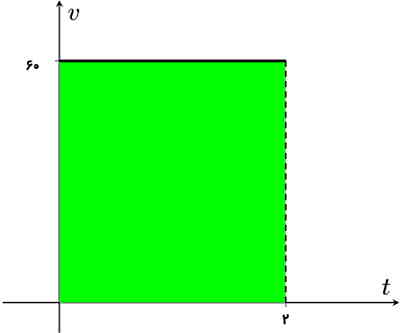
فرض کنید میخواهیم ببینیم اگر اتومبیلی از مکان و زمان صفر با سرعت ثابت ۶۰ km/h شروع به حرکت کند، در مدت زمان دو ساعت چه مسافتی طی کرده است. طبق فرمولهای حرکتشناسی در فیزیک میدانیم $$v=frac{triangle x}{triangle t}$$ است. در این فرمول، v سرعت بر حسب m/s است. همچنین مسافت طی شده Δx بر حسب متر (m) و مدت زمان جابجایی Δt بر حسب ثانیه (s) است.

پس میتوانیم بگوییم سرعت به نوعی مشتق مکان نسبت به زمان است ($$v=frac{d x}{d t}$$). اگر این رابطه را بهصورت زیر بنویسیم و از دو طرف آن انتگرال بگیریم، داریم:
$$dx=v dt$$
$$int dx=int v dt$$
برای پیدا کردن جواب لازم است انتگرال دو طرف این رابطه را محاسبه کنیم. ابتدا انتگرال سمت چپ را بررسی میکنیم. همانطور که گفتیم، انتگرال dx در واقع همان انتگرال عدد ثابت یک، روی متغیر x است:
$$int dx=int 1 dx=1x+A =x+A$$
با توجه به صورت سوال میدانیم اتومبیل از مکان یا x اولیه برابر با صفر شروع به حرکت کرده است. مکان نهایی آن همان مسافتی است که پاسخ سوال است. اگر مکان اولیه را با x۱ و مکان نهایی را با x۲ نشان دهیم، این دو مقدار معادل حد پایین و حد بالای انتگرال نامعین بالا هستند. پس انتگرال معینی به شکل زیر را حل میکنیم:
$$int_{x_1}^{x_2} dx=int_{0}^{x_2} dx=(x+A)Big|_0^{x_2}$$
$$Rightarrow int_{0}^{x_2} dx=({x_2}+A)-(0+A)={x_2}$$
بنابراین تا اینجا متوجه شدیم که حاصل انتگرال سمت چپ در رابطه $$int dx=int v dt$$ برابر با x۲ است. حالا انتگرال سمت راست را محاسبه میکنیم:
$$int_{t_1}^{t_2} v dt=int_{0}^{t_2} v dt=vBig|_0^{t_2}$$
نکته مهم این است که در این حرکت مقدار سرعت ثابت میماند. بنابراین v=۶۰ در زیر انتگرالده، یک عدد ثابت است. متغیر انتگرالگیری در این انتگرال زمان یا t است که از صفر شروع میشود و در انتها زمان به دو ساعت میرسد. پس میتوانیم بگوییم t۲=۲ و در نتیجه با عددگذاری در فرمول بالا داریم:
$$Rightarrow int_{0}^{t_2} v dt=int_{0}^{2} 60 dt=60(2-0)=120 km$$
از آنجایی که دو طرف $$int dx=int v dt$$ با هم برابر بودند، پس مسافت طی شده محاسبه شد:
$$Rightarrow x_2=120 km$$
بنابراین با استفاده از مفهوم انتگرال عدد ثابت میتوانیم این نتیجهگیری را داشته باشیم که مساحت زیر منحنی سرعت بر حسب زمان برابر با مسافت طی شده است.
حل انتگرال عدد ثابت به روش دیگر
در این بخش میخواهیم به حل انتگرال عدد ثابت با استفاده یک فرمول مهم در مبحث انتگرال بپردازیم. این فرمول مهم بیان میکند که اگر تابع زیر انتگرال یا انتگرالده ما به صورت xn باشد، در این صورت حاصل چنین انتگرالی برابر است با:
$$int x^n dx=frac{x^{n+1}}{n+1}+A$$
در این رابطه n یک عدد صحیح است که میتواند صفر، مثبت یا منفی باشد اما نباید برابر با ۱- باشد تا مخرج جواب صفر نشود. حالا فرض کنید میخواهیم انتگرال عدد ثابت ۳- را به کمک این فرمول بهدست آوریم. برای این کار $$int -3dx$$ را به شکل $$int -3x^0dx$$ مینویسیم، چون میدانیم همیشه رابطه x۰=۱ برقرار است و حاصلضرب یک در ۳- نیز برابر است با ۳-. حالا با در نظر گرفتن n=۰ و اینکه عدد ثابت ۳- را میتوانیم از داخل انتگرال خارج کنیم، خواهیم داشت:
$$int -3x^0dx=-3int x^0dx=-3(frac{x^{0+1}}{0+1}+A)=-3 (x+A)=-3x+B$$
مشاهده میکنید که جواب با این روش با جواب بهدست آمده از فرمولهای بیان شده در بخشهای قبل، یکسان است.
تکمیل یادگیری انتگرال با فرادرس
اگر با مراجعه به فیلمهای آموزشی فرادرس در بخش «یادگیری انتگرال با فرادرس» توانستید به مبحث انتگرالگیری از توابع مختلف مسلط شوید، مشاهده فیلمهای آموزشی زیر میتواند به پیشرفت شما در کاربرد برنامهنویسی برای انجام محاسبات انتگرالی یا کاربرد مبحث انتگرال در فیزیک نیز بسیار کمککننده باشد:
آزمون انتگرال عدد ثابت
در این مطلب از مجله فرادرس آموختیم که انتگرال عدد ثابت چگونه محاسبه میشود. در بخش آخر، با حل سوالات آزمون میتوانید سرعت و دقت خود را در حل انتگرال عدد ثابت بیازمایید. پس از اتمام آزمون، با کلید روی قسمت «دریافت نتیجه آزمون» نمره خود را مشاهده خواهید کرد.
اگر به ازای تمام مقادیر z، حاصل انتگرال $$int pdz$$ برابر با $$-4z-3$$ باشد، مقدار انتگرالده چقدر است؟
طبق فرمول انتگرال نامعین داریم:
$$int c dx=cx+A$$
اگر این فرمول را با رابطه زیر مقایسه کنیم:
$$int pdz=-4z-3 $$
در این رابطه انتگرالده با p بهجای c نشان داده شده است. پس p همان انتگرالده است که برابر با ۴- است.
مساحت بالای منحنی y=-1 در فاصله ۰ تا ۴ چقدر است؟
با استفاده از فرمول انتگرال معین داریم:
$$int_{0}^{4} (-1) dx=-1(4-0)=-4$$
اما مساحت همیشه یک کمیت مثبت است. پس باید اندازه حاصل انتگرال بهدست آمده را صرفنظر از علامت در نظر بگیریم. گزینه صحیح ۲ است.
اگر s یک عدد ثابت باشد، حاصل $$int sdx +int sdy$$ چقدر میشود؟
گزینه ۴ صحیح است. در این سوال باید دو انتگرال جداگانه حل شوند و پس از جمع میتوان مجموع دو ثابت اختیاری را یک ثابت به نام A در نظر گرفت. پس داریم:
$$int sdx +int sdy=(sx+B)+(sy+C)=sx+sy+(B+C)=sx+sy+A$$
$$int_{0}^{2} 4dx+int_{-2}^{0} 4dy$$ برابر است با؟
صورت سوال مجموع دو انتگرال معین است:
$$int_{0}^{2} 4dx+int_{-2}^{0} 4dy=4(2-0)+4(0-(-2))=8+8=16$$
پس گزینه ۳ گزینه صحیح است.
اگر اتوبوسی با سرعت ثابت ۵۰ km/h در جادهای حرکت کند، پس از گذشت یک ساعت چه مسافتی طی کرده است؟
طبق آنچه در بخش کاربرد انتگرال عدد ثابت در فیزیک گفته شد، مسافت طی شده برابر است با سطح زیر نمودار سرعت بر حسب زمان. بنابراین اگر انتگرال سرعت روی متغیر زمان را حل کنیم، مسافت طی شده بهدست میآید.
دقت کنید چون اشارهای به زمان و مکان اولیه نشده است، مقدار هر دو را صفر در نظر میگیریم:
$$ int_{0}^{1} 50 dt=50(1-0)=50 km$$
همچنین باید دقت شود در سوال سرعت بر حسب کیلومتر بر ساعت ذکر شده است. چون برای زمان و سرعت واحدهای گفته شده در صورت سوال استفاده شده است، پس مسافت در نهایت بر حسب کیلومتر به دست میآید.
اما در گزینهها گزینه درستی بر حسب کیلومتر وجود ندارد بلکه گزینه درست برحسب متر و برابر با ۵۰۰۰۰ است.
$$ Rightarrow x=50 km=50times 1000=50000 m$$
در مورد مجموع انتگرال صفر و عدد پی کدام گزینه درست است؟
گزینه اول و سوم هر دو درست هستند.
گفتیم حاصل انتگرال صفر یک عدد ثابت اختیاری مثل B است و برای انتگرال عدد پی حاصل برابر است با:
$$int pi dx =pi x+A=3.14x+A$$
بنابراین با در نظر گرفتن A+B=C، داریم:
$$int 0 dx + int pi dx =B+3.14x+A=3.14x+C$$
اما چون در صورت سوال مشخص نشده است که انتگرالگیری روی چه متغیری انجام میشود، گزینه سوم هم به نوعی درست است. پس گزینه ۴ بهترین گزینه برای انتخاب است.
کدام گزینه در مورد تعریف انتگرال معین یک عدد ثابت اشتباه است؟
جواب این انتگرال همیشه یک عدد است.
جواب این انتگرال همیشه یک عدد به اضافه یک ثابت اختیاری است.
جواب این انتگرال نامشخص و تابعی از متغیر x است.
هیچ گزینهای درست نیست.
انتگرال معین دارای حدود مشخصی بهصورت عدد است. انتگرالده نیز عدد ثابت و دارای مقداری مشخص است. پس طبق فرمول انتگرال معین یک عدد ثابت، با قرار دادن مقادیر عددی در نهایت یک عدد به دست میآید. گزینه اول درست است.
در مورد گزینه دوم، دقت شود که اگر انتگرال نامعین عدد ثابت را در نظر بگیریم، پس از جایگذاری مقادیر عددی، دو ثابت یکدیگر را حذف میکنند. بنابراین ثابتی در جواب نهایی باقی نخواهد ماند.
انتگرال dz- برای بازه ۱- تا ۵ چقدر میشود؟
$$int_{-1}^{5} -dz=-1(5-(-1))=-6$$
کدام گزینه در مورد انتگرال عدد ثابت درست نیست؟
انتگرالگیری معین عدد ثابت دارای حد بالا و پایین مشخصی است.
انتگرالگیری نامعین یک عدد ثابت همیشه با تابعی بر حسب متغیری مانند x برابر است.
انتگرال معین عدد ثابت برابر است با مساحت مستطیلی که از تقاطع نمودار عدد ثابت با محورهای مختصات شکل میگیرد.
انتگرال نامعین عدد ثابت برابر است با مساحت مستطیلی که از تقاطع نمودار عدد ثابت با محورهای مختصات شکل میگیرد.
گزینه آخر اشتباه است. در انتگرالگیری معین برای یک عدد ثابت، چون حدود انتگرال مشخص هستند، میتوانیم سطح زیر نمودار را یک مستطیل در نظر بگیریم. اما در انتگرالگیری نامعین یک عدد ثابت، حد بالا و پایین مشخص نیست و در واقع مستطیلی با یک ضلع در بینهایت داریم.
اگر a یک عدد ثابت باشد، حاصل عبارت زیر چقدر میشود؟
$$int_{0}^{2} (7+a)dt$$
$$int_{0}^{2} (7+a)dt= (7+a) (2-0)=14+2a$$
source